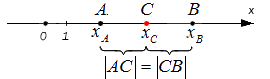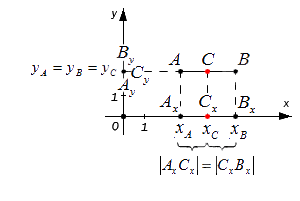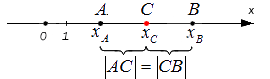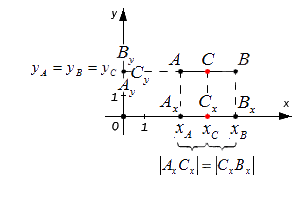В статье ниже будут освещены вопросы нахождения координат середины отрезка при наличии в качестве исходных данных координат его крайних точек. Но, прежде чем приступить к изучению вопроса, введем ряд определений.
Отрезок – прямая линия, соединяющая две произвольные точки, называемые концами отрезка. В качестве примера пусть это будут точки A и B и соответственно отрезок AB.
Если отрезок AB продолжить в обе стороны от точек A и B, мы получим прямую AB. Тогда отрезок AB – часть полученной прямой, ограниченный точками A и B. Отрезок AB объединяет точки A и B, являющиеся его концами, а также множество точек, лежащих между. Если, к примеру, взять любую произвольную точку K, лежащую между точками A и B, можно сказать, что точка K лежит на отрезке AB.
Длина отрезка – расстояние между концами отрезка при заданном масштабе (отрезке единичной длины). Длину отрезка AB обозначим следующим образом: AB.
Середина отрезка – точка, лежащая на отрезке и равноудаленная от его концов. Если середину отрезка AB обозначить точкой C, то верным будет равенство: AC=CB
И далее мы рассмотрим, как же определять координаты середины отрезка (точки C) при заданных координатах концов отрезка (A и B), расположенных на координатной прямой или в прямоугольной системе координат.
Середина отрезка на координатной прямой
Исходные данные: координатная прямая Ox и несовпадающие точки на ней: A и B. Этим точкам соответствуют действительные числа xA и xB. Точка C – середина отрезка AB: необходимо определить координату xC.
Поскольку точка C является серединой отрезка АВ, верным будет являться равенство: |АС| = |СВ|. Расстояние между точками определяется модулем разницы их координат, т.е.
|АС| = |СВ|⇔xC-xA=xB-xC
Тогда возможно два равенства: xC-xA=xB-xC и xC-xA=-(xB-xC)
Из первого равенства выведем формулу для координаты точки C : xC=xA+xB2 (полусумма координат концов отрезка).
Из второго равенста получим: xA=xB , что невозможно, т.к. в исходных данных — несовпадающие точки. Таким образом, формула для определения координат середины отрезка AB с концами A(xA) и B(xB):
xA+xB2
Полученная формула будет основой для определения координат середины отрезка на плоскости или в пространстве.
Середина отрезка на плоскости
Исходные данные: прямоугольная система координат на плоскости Оxy, две произвольные несовпадающие точки с заданными координатами AxA, yA и BxB, yB . Точка C – середина отрезка AB. Необходимо определить координаты xC и yC для точки C.
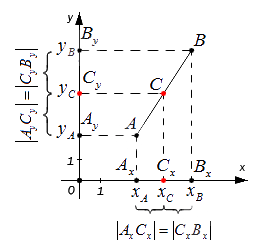
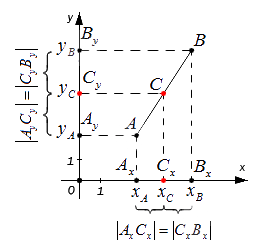
Возьмем для анализа случай, когда точки A и B не совпадают и не лежат на одной координатной прямой или прямой, перпендикулярной одной из осей.Ax, Ay ; Bx, By и Cx ,Cy — проекции точек A, B и C на оси координат (прямые Ох и Оy).
Согласно построению прямые AAx, BBx, CCx параллельны; прямые также параллельны между собой. Совокупно с этим по теореме Фалеса из равенства АС = СВ следуют равенства: АxСx = СxВx и АyСy = СyВy, и они в свою очередь свидетельствуют о том, что точка Сx – середина отрезка АxВx, а Сy – середина отрезка АyВy. И тогда, опираясь на полученную ранее формулу, получим:
xC=xA+xB2 и yC=yA+yB2
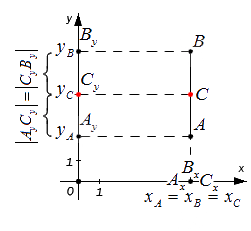
Этими же формулами можно воспользоваться в случае, когда точки A и B лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. Проводить детальный анализ этого случая не будем, рассмотрим его лишь графически:
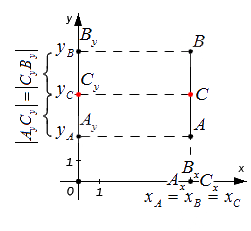
Резюмируя все выше сказанное, координаты середины отрезка AB на плоскости с координатами концов A (xA,yA) и B (xB, yB) определяются как:
(xA+xB2, yA+yB2)
Середина отрезка в пространстве
Исходные данные: система координат Оxyz и две произвольные точки с заданными координатами A(xA, yA, zA) и B (xB, yB, zB). Необходимо определить координаты точки C, являющейся серединой отрезка AB.
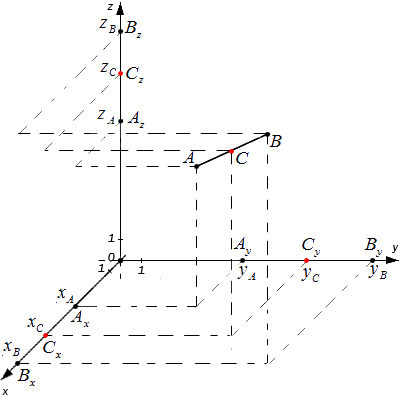
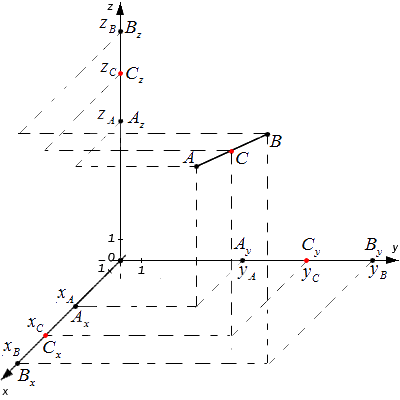
Ax, Ay, Az ; Bx, By,Bz и Cx, Cy, Cz — проекции всех заданных точек на оси системы координат.
Согласно теореме Фалеса верны равенства: AxCx=CxBx, AyCy=CyBy,AzCz=CzBz
Следовательно, точки Cx, Cy,Cz являются серединами отрезков AxBx, AyBy, AzBz соответственно. Тогда, для определения координат середины отрезка в пространстве верны формулы:
xC=xA+xB2, yc=yA+yB2, zc=zA+ZB2
Полученные формулы применимы также в случаях, когда точки A и B лежат на одной из координатных прямых; на прямой, перпендикулярной одной из осей; в одной координатной плоскости или плоскости, перпендикулярной одной из координатных плоскостей.
Определение координат середины отрезка через координаты радиус-векторов его концов
Формулу для нахождения координат середины отрезка также можно вывести согласно алгебраическому толкованию векторов.
Исходные данные: прямоугольная декартова система координат Oxy, точки с заданными координатами A(xA,yA) и B(xB, xB) . Точка C – середина отрезка AB.
Согласно геометрическому определению действий над векторами верным будет равенство: OC→=12·OA→+OB→ . Точка C в данном случае – точка пересечения диагоналей параллелограмма, построенного на основе векторов OA→ и OB→ , т.е. точка середины диагоналей.Координаты радиус-вектора точки равны координатам точки, тогда верны равенства: OA→=(xA, yA), OB→=(xB,yB) . Выполним некоторые операции над векторами в координатах и получим:
OC→=12·OA→+OB→=xA+xB2, yA+yB2
Следовательно, точка C имеет координаты:
xA+xB2, yA+yB2
По аналогии определяется формула для нахождения координат середины отрезка в пространстве:
C(xA+xB2, yA+yB2, zA+zB2)
Примеры решения задач на нахождение координат середины отрезка
Среди задач, предполагающих использование полученных выше формул, встречаются, как и те, в которых напрямую стоит вопрос рассчитать координаты середины отрезка, так и такие, что предполагают приведение заданных условий к этому вопросу: зачастую используется термин «медиана», ставится целью нахождение координат одного из концов отрезка, а также распространены задачи на симметрию, решение которых в общем также не должно вызывать затруднений после изучения настоящей темы. Рассмотрим характерные примеры.
Исходные данные: на плоскости – точки с заданными координатами А (-7,3) и В (2,4). Необходимо найти координаты середины отрезка АВ.
Решение
Обозначим середину отрезка AB точкой C. Координаты ее буду определяться как полусумма координат концов отрезка, т.е. точек A и B.
xC=xA+xB2=-7+22=-52yC=yA+yB2=3+42=72
Ответ: координаты середины отрезка АВ -52, 72.
Исходные данные: известны координаты треугольника АВС: А (-1,0), В (3,2), С (9,-8). Необходимо найти длину медианы АМ.
Решение
- По условию задачи AM – медиана, а значит M является точкой середины отрезка BC. В первую очередь найдем координаты середины отрезка BC, т.е. точки M:
xM=xB+xC2=3+92=6yM=yB+yC2=2+(-8)2=-3
- Поскольку теперь нам известны координаты обоих концов медианы (точки A и М), можем воспользоваться формулой для определения расстояния между точками и посчитать длину медианы АМ:
AM=(6-(-1))2+(-3-0)2=58
Ответ: 58
Исходные данные: в прямоугольной системе координат трехмерного пространства задан параллелепипед ABCDA1B1C1D1 . Заданы координаты точки C1(1, 1, 0), а также определена точка M, являющаяся серединой диагонали BD1 и имеющая координаты M (4, 2, -4) . Необходимо рассчитать координаты точки А.
Решение
Диагонали параллелепипеда имеют пересечение в одной точке, которая при этом является серединой всех диагоналей. Исходя из этого утверждения, можно иметь в виду, что известная по условиям задачи точка М является серединой отрезка АС1. Опираясь на формулу для нахождения координат середины отрезка в пространстве, найдем координаты точки А: xM=xA+xC12 ⇒xA=2·xM-xC1=2·4-1+7yM=yA+yC12⇒yA=2·yM-yC1=2·2-1=3zM=zA+zC12⇒zA=2·zM-zC1=2·(-4)-0=-8
Ответ: координаты точки А (7,3,-8).
Определение.
Середина отрезка — это точка, которая лежит на отрезке и находится на равном расстоянии от конечных точек.
В геометрических задачах часто можно столкнуться с необходимостью найти середину отрезка заданного координатами точек его концов, например в задачах поиска медианы, средней линии, …
Каждая координата середины отрезка равна полусумме соответствующих координат концов отрезка.
Формулы вычисления расстояния между двумя точками:
- Формула вычисления координат середины отрезка с концами A(xa, ya) и B(xb, yb) на плоскости:
xc = xa + xb yc = ya + yb 2 2 - Формула вычисления координат середины отрезка с концами A(xa, ya, za) и B(xb, yb, zb) в пространстве:
xc = xa + xb yc = ya + yb zc = za + zb 2 2 2
Примеры задач на вычисление середины отрезка
Примеры вычисления координат середины отрезка на плоскости
Пример 1.
Найти координаты точки С, середины отрезка AB заданного точками A(-1, 3) и B(6, 5).
Решение.
| xc = | xa + xb | = | -1 + 6 | = | 5 | = 2.5 |
| 2 | 2 | 2 |
| yc = | ya + yb | = | 3 + 5 | = | 8 | = 4 |
| 2 | 2 | 2 |
Ответ: С(2.5, 4).
Пример 2.
Найти координаты точки В, если известны координаты точки C(1; 5), середины отрезка AB и точки A(-1, 3).
Решение.
xc =
xa + xb2
=> xb = 2xc — xa = 2·1-(-1)=2+1=3
yc =
ya + yb2
=> yb = 2yc — ya = 2·5-3=10-3=7
Ответ: B(3, 7).
Примеры вычисления координат середины отрезка в пространстве
Пример 3.
Найти координаты точки С середины отрезка AB заданного точками A(-1, 3, 1) и B(6, 5, -3).
Решение.
| xc = | xa + xb | = | -1 + 6 | = | 5 | = 2.5 |
| 2 | 2 | 2 |
| yc = | ya + yb | = | 3 + 5 | = | 8 | = 4 |
| 2 | 2 | 2 |
| zc = | za + zb | = | 1 + (-3) | = | -2 | = -1 |
| 2 | 2 | 2 |
Ответ: С(2.5, 4, -1).
Пример 4.
Найти координаты точки В если известны координаты точки C(1, 5, 2), середины отрезка AB и точки A(-1, 3, 10).
Решение.
xc =
xa + xb2
=> xb = 2xc — xa = 2·1-(-1)=2+1=3
yc =
ya + yb2
=> yb = 2yc — ya = 2·5-3=10-3=7
zc =
za + zb2
=> zb = 2zc — za = 2·2-10=4-10=-6
Ответ: B(3, 7, -6).
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Загрузить PDF
Загрузить PDF
Поиск середины отрезка – легкая задача когда вам известны координаты двух конечных точек. Самый распространенный способ сделать это состоит в использовании формулы для нахождения середины отрезка; но есть еще один способ найти середину отрезка, если линия вертикальная или горизонтальная. Если вы хотите знать, как найти середину отрезка в течение нескольких минут, выполните следующие действия.
-
1
Определение. Середина отрезка — точка, которая находится на равном расстоянии от конечных точек отрезка и лежит на нем. Таким образом, ее координаты – среднее из двух координат х и двух координат у.
-
2
Формула. Формула записывается в виде суммы двух координат х (конечных точек), деленной на два, и суммы двух координат у (конечных точек), деленной на два. Это даст среднее значение х и у координат. Формула:[(x1 + x2)/2,( y1 + y2)/2]
-
3
Найдите координаты конечных точек. Вы не можете использовать формулу, не зная х и у координаты конечных точек. Например, необходимо найти середину (точку О) отрезка, ограниченного точками М (5,4 ) и N (3, -4). Таким образом, (x1, y1) = (5, 4) и (x2, y2) = (3, -4).
- Обратите внимание, что любая пара координат может обозначаться как (x1, y1) или (x2, y2). Так как вы будете просто складывать координаты и делить результат на два, не имеет значения, какую пару координат выбрать в первую очередь.
-
4
Подставьте координаты в формулу. Теперь, когда вам известны координаты конечных точек, подставьте их в формулу. Вот как это делается:
- [(5 + 3)/2, (4 + -4)/2]
-
5
Решите. После того как вы подставили координаты в формулу, проделайте арифметические действия для вычисления середины. Вот как это делается:
- [(5 + 3)/2, (4 + -4)/2] =
- [(8/2), (0/2)] =
- (4, 0)
- Середина отрезка между точками (5,4) и (3, -4) есть точка (4,0).
Реклама
-
1
Рассмотрим вертикальную или горизонтальную линию.
- Линия горизонтальная, если две у- координаты конечных точек равны. Например, отрезок с концами ( -3 , 4) и (5, 4) расположен горизонтально.
- Линия расположена вертикально, если две х -координаты конечных точек равны. Например, отрезок с концами (2, 0 ) и (2 , 3) находится в вертикальном положении.
- Линия горизонтальная, если две у- координаты конечных точек равны. Например, отрезок с концами ( -3 , 4) и (5, 4) расположен горизонтально.
-
2
Найдите длину отрезка. Вот как это сделать:
- Длина горизонтального отрезка с конечными точками (-3 , 4) и ( 5, 4) равна 8. Вы можете найти это сложением абсолютных величин координат х: | -3| + |5| = 8.
- Длина вертикального отрезка с конечными точками (2 ,0) и (2,3) равна 3. Вы можете найти это сложением абсолютных величин координат у: |0| + |3| = 3.
- Длина горизонтального отрезка с конечными точками (-3 , 4) и ( 5, 4) равна 8. Вы можете найти это сложением абсолютных величин координат х: | -3| + |5| = 8.
-
3
Разделите длину отрезка на два. Теперь, когда вы нашли длину отрезка, нужно разделить его на два.
- 8/2 = 4
- 3/2 = 1,5
- 8/2 = 4
-
4
Вычислите координаты середины. Вот как это делается:
- Чтобы найти середину отрезка, ограниченного точками (-3,4) и (5,4), прибавьте или вычтите 4 из х-координаты первой или второй конечной точки соответственно. Для точки (-3 , 4) это будет -3+4=1 и координаты середины: (1, 4) (Вам не нужно менять у- координаты, так как линия горизонтальная и у-координаты постоянны). Итак, середина отрезка (-3,4) и (5,4) есть точка (1,4).
- Чтобы найти середину отрезка, ограниченного точками (2, 0) и (2,3), прибавьте или вычтите 1,5 из у-координаты первой или второй конечной точки соответственно. Для точки (2 ,0) это будет -0+1,5=1,5 и координаты середины: (2,1,5) (Вам не нужно менять х-координаты, так как линия вертикальная и х-координаты постоянны). Итак, середина отрезка (2, 0 ) и (2,3) есть точка (2,1,5).
Реклама
- Чтобы найти середину отрезка, ограниченного точками (-3,4) и (5,4), прибавьте или вычтите 4 из х-координаты первой или второй конечной точки соответственно. Для точки (-3 , 4) это будет -3+4=1 и координаты середины: (1, 4) (Вам не нужно менять у- координаты, так как линия горизонтальная и у-координаты постоянны). Итак, середина отрезка (-3,4) и (5,4) есть точка (1,4).
Что вам понадобится
- Карандаш
- Лист бумаги
- Линейка
Об этой статье
Эту страницу просматривали 31 374 раза.
Была ли эта статья полезной?
Нахождение координат середины отрезка: примеры, решения
В статье ниже будут освещены вопросы нахождения координат середины отрезка при наличии в качестве исходных данных координат его крайних точек. Но, прежде чем приступить к изучению вопроса, введем ряд определений.
Отрезок – прямая линия, соединяющая две произвольные точки, называемые концами отрезка. В качестве примера пусть это будут точки A и B и соответственно отрезок A B .
Если отрезок A B продолжить в обе стороны от точек A и B , мы получим прямую A B . Тогда отрезок A B – часть полученной прямой, ограниченный точками A и B . Отрезок A B объединяет точки A и B , являющиеся его концами, а также множество точек, лежащих между. Если, к примеру, взять любую произвольную точку K , лежащую между точками A и B , можно сказать, что точка K лежит на отрезке A B .
Длина отрезка – расстояние между концами отрезка при заданном масштабе (отрезке единичной длины). Длину отрезка A B обозначим следующим образом: A B .
Середина отрезка – точка, лежащая на отрезке и равноудаленная от его концов. Если середину отрезка A B обозначить точкой C , то верным будет равенство: A C = C B
И далее мы рассмотрим, как же определять координаты середины отрезка (точки C ) при заданных координатах концов отрезка ( A и B ), расположенных на координатной прямой или в прямоугольной системе координат.
Середина отрезка на координатной прямой
Исходные данные: координатная прямая O x и несовпадающие точки на ней: A и B . Этим точкам соответствуют действительные числа x A и x B . Точка C – середина отрезка A B : необходимо определить координату x C .
Поскольку точка C является серединой отрезка А В , верным будет являться равенство: | А С | = | С В | . Расстояние между точками определяется модулем разницы их координат, т.е.
| А С | = | С В | ⇔ x C — x A = x B — x C
Тогда возможно два равенства: x C — x A = x B — x C и x C — x A = — ( x B — x C )
Из первого равенства выведем формулу для координаты точки C : x C = x A + x B 2 (полусумма координат концов отрезка).
Из второго равенста получим: x A = x B , что невозможно, т.к. в исходных данных — несовпадающие точки. Таким образом, формула для определения координат середины отрезка A B с концами A ( x A ) и B ( x B ):
Полученная формула будет основой для определения координат середины отрезка на плоскости или в пространстве.
Середина отрезка на плоскости
Исходные данные: прямоугольная система координат на плоскости О x y , две произвольные несовпадающие точки с заданными координатами A x A , y A и B x B , y B . Точка C – середина отрезка A B . Необходимо определить координаты x C и y C для точки C .
Возьмем для анализа случай, когда точки A и B не совпадают и не лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. A x , A y ; B x , B y и C x , C y — проекции точек A , B и C на оси координат (прямые О х и О y ).
Согласно построению прямые A A x , B B x , C C x параллельны; прямые также параллельны между собой. Совокупно с этим по теореме Фалеса из равенства А С = С В следуют равенства: А x С x = С x В x и А y С y = С y В y , и они в свою очередь свидетельствуют о том, что точка С x – середина отрезка А x В x , а С y – середина отрезка А y В y . И тогда, опираясь на полученную ранее формулу, получим:
x C = x A + x B 2 и y C = y A + y B 2
Этими же формулами можно воспользоваться в случае, когда точки A и B лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. Проводить детальный анализ этого случая не будем, рассмотрим его лишь графически:
Резюмируя все выше сказанное, координаты середины отрезка A B на плоскости с координатами концов A ( x A , y A ) и B ( x B , y B ) определяются как:
( x A + x B 2 , y A + y B 2 )
Середина отрезка в пространстве
Исходные данные: система координат О x y z и две произвольные точки с заданными координатами A ( x A , y A , z A ) и B ( x B , y B , z B ) . Необходимо определить координаты точки C , являющейся серединой отрезка A B .
A x , A y , A z ; B x , B y , B z и C x , C y , C z — проекции всех заданных точек на оси системы координат.
Согласно теореме Фалеса верны равенства: A x C x = C x B x , A y C y = C y B y , A z C z = C z B z
Следовательно, точки C x , C y , C z являются серединами отрезков A x B x , A y B y , A z B z соответственно. Тогда, для определения координат середины отрезка в пространстве верны формулы:
x C = x A + x B 2 , y c = y A + y B 2 , z c = z A + Z B 2
Полученные формулы применимы также в случаях, когда точки A и B лежат на одной из координатных прямых; на прямой, перпендикулярной одной из осей; в одной координатной плоскости или плоскости, перпендикулярной одной из координатных плоскостей.
Определение координат середины отрезка через координаты радиус-векторов его концов
Формулу для нахождения координат середины отрезка также можно вывести согласно алгебраическому толкованию векторов.
Исходные данные: прямоугольная декартова система координат O x y , точки с заданными координатами A ( x A , y A ) и B ( x B , x B ) . Точка C – середина отрезка A B .
Согласно геометрическому определению действий над векторами верным будет равенство: O C → = 1 2 · O A → + O B → . Точка C в данном случае – точка пересечения диагоналей параллелограмма, построенного на основе векторов O A → и O B → , т.е. точка середины диагоналей.Координаты радиус-вектора точки равны координатам точки, тогда верны равенства: O A → = ( x A , y A ) , O B → = ( x B , y B ) . Выполним некоторые операции над векторами в координатах и получим:
O C → = 1 2 · O A → + O B → = x A + x B 2 , y A + y B 2
Следовательно, точка C имеет координаты:
x A + x B 2 , y A + y B 2
По аналогии определяется формула для нахождения координат середины отрезка в пространстве:
C ( x A + x B 2 , y A + y B 2 , z A + z B 2 )
Примеры решения задач на нахождение координат середины отрезка
Среди задач, предполагающих использование полученных выше формул, встречаются, как и те, в которых напрямую стоит вопрос рассчитать координаты середины отрезка, так и такие, что предполагают приведение заданных условий к этому вопросу: зачастую используется термин «медиана», ставится целью нахождение координат одного из концов отрезка, а также распространены задачи на симметрию, решение которых в общем также не должно вызывать затруднений после изучения настоящей темы. Рассмотрим характерные примеры.
Исходные данные: на плоскости – точки с заданными координатами А ( — 7 , 3 ) и В ( 2 , 4 ) . Необходимо найти координаты середины отрезка А В .
Решение
Обозначим середину отрезка A B точкой C . Координаты ее буду определяться как полусумма координат концов отрезка, т.е. точек A и B .
x C = x A + x B 2 = — 7 + 2 2 = — 5 2 y C = y A + y B 2 = 3 + 4 2 = 7 2
Ответ: координаты середины отрезка А В — 5 2 , 7 2 .
Исходные данные: известны координаты треугольника А В С : А ( — 1 , 0 ) , В ( 3 , 2 ) , С ( 9 , — 8 ) . Необходимо найти длину медианы А М .
Решение
- По условию задачи A M – медиана, а значит M является точкой середины отрезка B C . В первую очередь найдем координаты середины отрезка B C , т.е. точки M :
x M = x B + x C 2 = 3 + 9 2 = 6 y M = y B + y C 2 = 2 + ( — 8 ) 2 = — 3
- Поскольку теперь нам известны координаты обоих концов медианы (точки A и М ), можем воспользоваться формулой для определения расстояния между точками и посчитать длину медианы А М :
A M = ( 6 — ( — 1 ) ) 2 + ( — 3 — 0 ) 2 = 58
Ответ: 58
Исходные данные: в прямоугольной системе координат трехмерного пространства задан параллелепипед A B C D A 1 B 1 C 1 D 1 . Заданы координаты точки C 1 ( 1 , 1 , 0 ) , а также определена точка M , являющаяся серединой диагонали B D 1 и имеющая координаты M ( 4 , 2 , — 4 ) . Необходимо рассчитать координаты точки А .
Решение
Диагонали параллелепипеда имеют пересечение в одной точке, которая при этом является серединой всех диагоналей. Исходя из этого утверждения, можно иметь в виду, что известная по условиям задачи точка М является серединой отрезка А С 1 . Опираясь на формулу для нахождения координат середины отрезка в пространстве, найдем координаты точки А : x M = x A + x C 1 2 ⇒ x A = 2 · x M — x C 1 = 2 · 4 — 1 + 7 y M = y A + y C 1 2 ⇒ y A = 2 · y M — y C 1 = 2 · 2 — 1 = 3 z M = z A + z C 1 2 ⇒ z A = 2 · z M — z C 1 = 2 · ( — 4 ) — 0 = — 8
Ответ: координаты точки А ( 7 , 3 , — 8 ) .
Онлайн калькулятор. Середина отрезка
Предлагаю вам воспользоваться онлайн калькулятором для вычисления середины отрезка AB.
Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление координат середины отрезка и закрепить пройденный материал.
Калькулятор для вычисления координат середины отрезка AB
Выберите необходимую вам размерность:
Введите координаты точек.
Ввод данных в калькулятор для вычисления координат середины отрезка
В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.
Дополнительные возможности калькулятора для вычисления координат середины отрезка
- Используйте кнопки и на клавиатуре, для перемещения между полями калькулятора.
Теория. Середина отрезка.
В геометрических задачах часто можно столкнуться с необходимостью найти координаты середины отрезка заданного координатами точек его концов, например в задачах поиска медианы, средней линии, .
Каждая координата середины отрезка равна полусумме соответствующих координат концов отрезка.
В случае плоской задачи. Координаты середины отрезка с концами A( xa , ya ) и B( xb , yb ) вычисляются по формулам:
| xc = | xa + xb | ; | yc = | ya + yb |
| 2 | 2 |
В случае пространственной задачи. Координаты середины отрезка с концами A( xa , ya , za ) и B( xb , yb , zb ) вычисляются по формулам:
| xc = | xa + xb | ; | yc = | ya + yb | ; | zc = | za + zb |
| 2 | 2 | 2 |
Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.
Геометрия
Лучшие условия по продуктам Тинькофф по этой ссылке
Дарим 500 ₽ на баланс сим-карты и 1000 ₽ при сохранении номера
. 500 руб. на счет при заказе сим-карты по этой ссылке
Лучшие условия по продуктам
ТИНЬКОФФ по данной ссылке
План урока:
Прямоугольная система координат
В планиметрии мы уже рассматривали прямоугольную систему координат. Ее образовывали 2 перпендикулярные друг другу оси – Ох и Оу. С ее помощью можно было определить положение любой точки на координатной плоскости, просто указав две ее координаты – абсциссу х и ординату у.
В стереометрии необходимо определять положение точки уже не на плоскости, а в пространстве. Для этого добавляется третья ось Оz, которую ещё называют осью апликат. Каждые пара осей образует свою отдельную координатную плоскость, всего получается три таких плос-ти: Оху, Охz и Oуz.
Точка О именуется началом координат. Она делит каждую ось на два луча, один из которых – это положительная полуось, а второй – отрицательная полуось.
Для каждой точки в пространстве можно указать три координаты, однозначно определяющие ее положение в пространстве. Пусть в пространстве есть некоторая точка М. Опустим из нее перпендикуляры на координатные плоскости. В свою очередь из этих проекций точки М опустим перпендикуляры уже на координатные оси. В результате будет построен прямоугольный параллелепипед. Измерения этого параллелепипеда и будут координатами точки М:
Если точка M находится в одной из координатных плоскостей, то одна из ее координат будет нулевой. Например, если М принадлежит плоскости Охz, то нулю будет равна координата у. Если же точка располагается на одной из координатных осей, то у нее уже две координаты будут нулевыми. Так, если точка находится на оси Ох, то только координата х может быть ненулевой, а у и z окажутся нулевыми координатами.
На показанном рисунке ребра параллелепипеда лежат на положительных полуосях, поэтому все координаты положительны. Если же какие-то ребра будут лежать на отрицательных полуосях, то и соответствующие координаты будут отрицательными.
Координаты вектора
Введем в пространстве прямоугольную систему коорд-т, а далее от ее начала отложим вектора i, j и k, которые соответственно будут лежать на координатных осях Ох, Оу и Оz, и длина которых составит единицу. Эти вектора именуют координатными векторами, единичными векторами или просто ортами.
Ясно, что орты находятся в разных плоскостях, то есть они образуют тройку некомпланарных векторов. Это означает, что любой вектор а в пространстве можно разложить на орты:
где х, у и z – какие-то действительные числа. Они как раз и считаются координатами вектора а. Записываются коорд-ты вектора в фигурных скобках. На следующем рисунке показан вектор а<3; – 2; – 4>.
Задание. Разложите на орты вектор
Если начало вектора ОМ располагается в начале системы координат О, то вектор ОМ именуют радиус-вектором. В таком случае коорд-ты точки конца вектора, то есть точки М, совпадают с коорд-тами самого вектора ОМ.
Это свойство радиус-вектора мы уже изучали в 9 классе в планиметрии, и в стереометрии оно сохраняется.
Задание. О – начало координат, а точка М имеет коорд-ты (2; 5; – 3). Найдите коорд-ты вектора ОМ.
Решение. Всё очень просто – коорд-ты вектора будут совпадать с коорд-тами его конца, так его начало совпадает с началом коорд-т:
Также в стереометрии остаются справедливыми ещё несколько правил, которые были доказаны в курсе планиметрии:
Задание. Найдите сначала сумму, а потом разность векторов а <3; 7; 5>и b<2; 4; 6>.
Решение. Будем обозначать коорд-ты векторов через индексы. Например, коорд-ты вектора а – это ха, уа и zа. Пусть сумма векторов будет вектором с, а их разность – вектором d. Для вычисления суммы надо складывать соответствующие координаты:
Для вычисления разности надо из коорд-т вектора а вычитать коорд-ты вектора b:
Задание. Вычислите коорд-ты вектора р, зная, что:
Решение. Для вычисления координат надо в выражении для вектора р сами векторы заменить на их координаты:
Получается, что вектор p имеет координаты <0; – 2; 3>.
Теперь мы можем доказать ещё одно утверждение, уже известное из курса планиметрии:
Действительно, пусть есть некоторый вектор АВ, причем коорд-ты точек А и В известны. Построим радиус-вектора OА и OВ:
Координаты радиус-векторов будут совпадать с координатами их концов:
Задание. Определите коорд-ты вектора CD, если даны коорд-ты точек С и D: С(3; 8; – 5) и D(5; 4; 1).
Решение. Здесь надо просто из коорд-т точки D, являющейся концом вектора, вычесть коорд-ты точки С:
Задание. От точки K(10; 6; 13) отложен вектор m<3; 2; 5>, конец совпал в точку H. Найдите коорд-ты точки H.
Решение. Коорд-ты вектора m и его концов связаны формулами:
Координаты середины отрезка
Пусть в пространстве есть отрезок АВ, и координаты его концов известны. Точка М – середина этого отрезка. Как вычислить ее координаты? Рассмотрим взаимосвязь векторов АМ, МВ и АВ:
Раз М – середина АВ, то вектора АМ и МВ имеют равные длины, и при этом они находятся на одной прямой. Значит, эти вектора равны и потому у них одинаковые коорд-ты:
Аналогично можно получить аналогичные формулы для коорд-т у и z:
Рассмотрим несколько задач на координаты точек.
Задание. Найдите коорд-ты середины отрезка, соединяющего точки А(3; 7; 12) и В(1; 5; – 4).
Решение. Просто используем только что выведенные формулы. Середину также обозначаем буквой М:
Задание. Известно, что K середина отрезка CD. Даны координаты точек С и K: С(12; 9; – 3) и K(15; 7; 3). Найдите коорд-ты D.
Решение. Сначала запишем формулу для коорд-ты х:
Вычисление длины векторов и расстояния между точками
Рассмотрим радиус-вектор ОМ с коорд-тами . Попытаемся найти его длину. Мы можем построить прямоугольный параллелепипед, в котором этот вектор окажется диагональю:
Напомним, что квадрат длины диагонали в прямоугольном параллелепипеде равен сумме квадратов его измерений. Но в полученном параллелепипеде измерения – это коорд-ты х, у и z, поэтому можно записать:
Так как равные вектора имеют как одинаковы и коорд-ты, и длина, то ясно, что каждый вектор с коорд-тами будет равен рассмотренному радиус-вектору, а значит и его длина будет рассчитываться по такой же формуле.
Задание. Найдите длину вектора m<– 2; 9; 6>.
Решение. Просто используем формулу:
Рассмотрим отрезок АВ с известными коорд-тами его концов. Можно построить вектор АВ, его коорд-ты будут определяться так:
Задание. Найдите расстояние между точкой K(10; 15; 5) и M(16; 21; – 2).
Решение. Просто подставляем коорд-ты точек в формулу:
Задание. Найдите длину медианы KM в ∆ KPN, если известны коорд-ты его вершин: P(2; 5; 8), N (6; 9; 12) и K(16; 11; 13).
Решение. Для нахождения длины медианы достаточно знать коорд-ты ее концов. Коорд-ты K уже известны, а M – середина PN, что позволяет вычислить и ее коорд-ты:
Коллинеарность векторов
Напомним, что если два вектора а и b коллинеарны друг другу, то должно существовать такое число k, что
Полученное отношение (1) является одновременно и признаком коллинеарных векторов, и их свойством. Слово «признак» означает, что любые вектора, чьи координаты соответствуют условию (1), будут коллинеарны. Слово «свойство» означает обратное – если известно, что вектора коллинеарны, то для них обязательно выполняется условие (1). В таких случаях в математике может использоваться словосочетание «тогда и только тогда»:
Очень важно то, что это правило действует только в случае, если все коорд-ты векторов ненулевые. Теперь рассмотрим случай, когда какие-то коорд-ты вектора b (одна или две из них) равны нулю. Например, пусть
В результате мы выяснили, что если коорд-та одного вектора нулевая, то и у любого вектора, коллинеарному ему, эта же коорд-та также должна быть нулевой. Особняком стоит случай с нулевым вектором с коорд-тами <0; 0; 0>. Он условно признается коллинеарным любому вектору.
Задание. Выясните, какие из этих пар векторов коллинеарны:
Решение. В первом задании просто делим друг на друга соответствующие коорд-ты и находим значение коэффициента k:
Значение коэффициента k оказалось одинаковым для каждой пары коорд-т, значит, вектора коллинеарны.
Повторяем эти действия в задании б):
На этот раз коэффициенты k оказались различными, значит, вектора неколлинеарны.
В задании в) у вектора е коорд-та z нулевая. Значит, если и у вектора f, если он коллинеарен z, эта координата должна быть нулевой, но это не так. Значит, вектора e и f неколлинеарны.
В задании г) снова указаны вектора с нулевыми коорд-тами. Но у обоих векторов коорд-та z нулевая, поэтому они могут быть коллинеарными. Однако необходимо проверить, что отношение ненулевых координат одинаково:
Коэффициент k получился одинаковым, поэтому вектора коллинеарны.
В последнем задании д) вектор n – нулевой, ведь все его коорд-ты нулевые. Нулевой вектор всегда коллинеарен другим векторам, в том числе и в этом задании.
Ответ: а) да; б) нет; в) нет; г) да; д) да.
Задание. Выясните, располагаются ли на одной прямой точки А(3; 5; 12), В(5; 7; 16) и С(0; 2; 6).
Решение. Ясно, что если эти точки находятся на одной прямой, то вектора АВ и ВС будут коллинеарными. Если же эти вектора неколлинеарны, то и точки должны находиться на разных прямых.
Сначала вычислим коорд-ты векторов АВ и ВС:
Теперь проверяем, коллинеарны ли эти вектора:
Коэффициенты k одинаковы, а потому АВ и ВС – коллинеарные векторы. Значит, точки А, В и С находятся на одной прямой.
Определение компланарности векторов
Пусть у нас есть три вектора с известными коорд-тами:
Как определить, компланарны ли эти вектора, то есть располагаются ли они в одной плоскости? Если эти вектора компланарны, то, по признаку компаланарности, вектор а можно разложить на вектора b и с:
где х и y – некоторые числа. Но если такое разложение существует, то коорд-ты векторов а, b и с будут связаны равенствами:
Получили систему из 3 уравнений с двумя неизвестными (х и y). Если такая система имеет решение, то вектора компланарны. Если же решения нет, то вектора не компланарны.
Задание. Определите, компланарны ли вектора
Имеем систему с тремя уравнениями. Из последних двух уравнений очевидно, что его решением может быть только пара чисел:
Значит, рассмотренная тройка векторов компланарна.
Задание. Располагаются ли в одной плос-ти вектора:
Решение. Нам надо проверить компаланарность векторов, поэтому действуем также, как и в предыдущей задаче. Если вектора компланарны, то существует разложение:
Получилось неверное равенство. Это означает, что у системы уравнений решения нет, и потому тройка векторов некомпланарна.
Скалярное произведение векторов
В 9 классе мы уже изучали скалярное произведение векторов.
Для нахождения угла между векторами необходимо отложить их от одной точки, тогда они образуют такой угол.
Задание. Угол между векторами с и d составляет 60°, а их длины соответственно равны 5 и 6. Найдите их скалярное произведение.
Решение. Здесь для расчета просто перемножаем длины векторов и косинус 60°:
Напомним несколько уже известных нам фактов о скалярном произведении, остающихся верными и в стереометрии:
Формула для расчета скалярного произведения по коорд-там векторов, используемая в стереометрии, несколько отличается от формулы из курса планиметрии. Напомним, что в планиметрии произведение векторов аа; уа> и b<хb; yb> можно было рассчитать так:
Задание. Вычислите скалярное произведение векторов:
На практике скалярное произведение обычно используется для расчета углов между векторами, а также отрезками и прямыми. Рассмотрим несколько задач.
Задание. Вычислите угол между векторами:
Теперь через скалярное произведение возможно рассчитать косинус искомого нами угла, а затем и сам угол, который мы обозначим как α:
Задание. Рассчитайте углы в ∆АВС, зная коорд-ты его вершин: А(1; – 1; 3), В(3; – 1; 1) и С(– 1; 1; 3).
Решение. Чтобы найти ∠В, необходимо просто рассчитать угол между векторами ВС и ВА также, как это сделано в предыдущей задаче. Но сначала найдем коорд-ты векторов ВС и ВА и их длины:
Далее рассчитываем скалярное произведение векторов:
Теперь найдем угол А, который представляет собой угол между векторам AВ и AС. Вектор AВ – это вектор, противоположный ВA, то у него та же длина, но противоположный знак у коорд-т:
Задание. В прямоугольном параллелепипеде АВСDA1B1C1D1 ребра имеют длину:
Рассчитайте угол между векторами DB1 и BC1.
Решение. Введем систему коорд-т Охуz и расположим в нем параллелепипед следующим образом:
При этом построении граничные точки векторов будут иметь следующие коорд-ты:
Находим коорд-ты векторов, а также их длины:
Рассчитываем скалярное произведение DB1 и BC1:
Получили ноль. Из этого вытекает, что вектора перпендикулярны, то есть искомый нами угол составляет 90°.
Сегодня мы научились использовать координаты для решения стереометрических задач. Почти все формулы, используемые в методе координаты, аналогичны тем формулам, которые были выведены ещё в курсе планиметрии. Надо лишь учитывать существование ещё одной, третьей координаты z.
http://ru.onlinemschool.com/math/assistance/cartesian_coordinate/p_center/
http://100urokov.ru/predmety/koordinaty-v-stereometrii
Содержание материала
- Нахождение координат середины отрезка: примеры, решения
- Видео
- Правила нахождения координат середины отрезка, формулы
- Середина отрезка на координатной прямой
- Середина отрезка на плоскости
- Середина отрезка в пространстве
- Координаты середины отрезка
- Определение координат середины отрезка через координаты радиус-векторов его концов
- Середина отрезка на плоскости
- Как построить середину отрезка с помощью циркуля и линейки?
Нахождение координат середины отрезка: примеры, решения
В статье ниже будут освещены вопросы нахождения координат середины отрезка при наличии в качестве исходных данных координат его крайних точек. Но, прежде чем приступить к изучению вопроса, введем ряд определений.
Отрезок – прямая линия, соединяющая две произвольные точки, называемые концами отрезка. В качестве примера пусть это будут точки A и B и соответственно отрезок A B .
Если отрезок A B продолжить в обе стороны от точек A и B , мы получим прямую A B . Тогда отрезок A B – часть полученной прямой, ограниченный точками A и B . Отрезок A B объединяет точки A и B , являющиеся его концами, а также множество точек, лежащих между. Если, к примеру, взять любую произвольную точку K , лежащую между точками A и B , можно сказать, что точка K лежит на отрезке A B .
Длина отрезка – расстояние между концами отрезка при заданном масштабе (отрезке единичной длины). Длину отрезка A B обозначим следующим образом: A B .
Середина отрезка – точка, лежащая на отрезке и равноудаленная от его концов. Если середину отрезка A B обозначить точкой C , то верным будет равенство: A C = C B
И далее мы рассмотрим, как же определять координаты середины отрезка (точки C ) при заданных координатах концов отрезка ( A и B ), расположенных на координатной прямой или в прямоугольной системе координат.
Правила нахождения координат середины отрезка, формулы
Середина отрезка на координатной прямой
Предположим, что несовпадающие точки A и B лежат на координатной прямая Ох. Известно, что A и B соответствуют действительные числа xA и xB, а точка С делит AB пополам. Определите координату xC, соответствующую С.
Так как C — это середина AB, то справедливо следующее равенство:
(left|ACright|=left|CBright|)
Вычислим расстояние между A и C, а также между C и B. Для этого определим модуль разницы их координат. На математическом языке это будет иметь вид:
(left|ACright|=left|CBright|Leftrightarrowleft|x_C-x_Aright|=left|x_B-x_Cright|)
Опустим знак модуля и получим справедливость двух выражений:
(x_C-x_A=x_B-x_C)
(x_C-x_A=-left(x_B-x_Cright))
Исходя из первого равенства, получим формулу нахождения xC, согласно которой координата точки С равна половине суммы координат A и B:
(x_C=frac{x_A+x_B}2)
Следствием второго равенства будет следующее утверждение:
(x_A=x_B)
Это противоречит заданным условиям, следовательно, формула определения координат середины отрезка выглядит так:
(x_C=frac{x_A+x_B}2)
Середина отрезка на плоскости
В декартовой системе координат Oxy расположены две точки A(xA,yA) и B(xB,yB), которые не совпадают между собой. Точка C является центром AB. Необходимо произвести вычисление координат xC и yC, соответствующих С.
Пусть произвольные точки А и В лежат на одной координатной прямой, а также не принадлежат прямым, располагающимся перпендикулярно к оси абсцисс или ординат. Опустим от заданных точек A, B, C перпендикуляры на ось x на ось y. Полученные точки пересечения с осями координат Ax, Ay; Bx, By; Cx, Cy — это проекции исходных точек.
По построению прямые AAx, BBx, CCx относительно друг друга находятся параллельно. Прямые AAy, BBy, CCy не пересекаются, то есть являются параллельными. Согласно равенству AB=BC, далее применим теорему Фалеса и получим:
(A_xC_x=C_xB_x)
(A_yC_y=C_yB_y)
Это значит, что Cx и Cy являются серединами отрезков AxBx и AyBy соответственно. Теперь воспользуемся формулой определения координат середины отрезка на координатной прямой и получим:
(x_C=frac{x_A+x_B}2)
(y_C=frac{y_A+y_B}2)
Данные формулы подходят для вычисления координат середины отрезка в случае его расположения на осях абсцисс и ординат, а также при перпендикулярности одной из них. Следовательно, координаты центра отрезка AB, находящегося в плоскости и ограниченного точками A(xA,yA) и B(xB,yB), вычисляются следующим образом:
(left(frac{x_A+x_B}2,frac{y_A+y_B}2right))
Середина отрезка в пространстве
Допустим, что в трехмерной системе координат Oxyz любые две точки с соответствующими им координатами A(xA, yA, zA) и B(xB, yB, zB). C(xC, yC, zC) — это центр АВ. Задание заключается в том, чтобы определить xC, yC, zC.
Проведем от исходных точек перпендикуляры к прямым Ox, Oy и Oz. Образовавшиеся точки пересечения с координатными осями — Ax, Ay, Az; Bx, By, Bz;Cx, Cy, Cz — проекции точек A, B, C на них.
Воспользуемся теоремой Фалеса:
(left|A_xC_xright|=left|C_xB_xright|)
(left|A_yC_yright|=left|C_yB_yright|)
(left|A_zC_zright|=left|C_zB_zright|)
Исходя из полученных равенств следует, что Cx, Cy, Cz — делят AxBx, AyBy, AzBz пополам, то есть являются серединами перечисленных отрезков. Значит, для определения координат центра AB с концами A(xA,yA,zA) и B(xB,yB,zB) используем формулу:
(left(frac{x_A+x_B}2,frac{y_A+y_B}2,;frac{z_A+z_B}2right))
Видео
Координаты середины отрезка
Пусть в пространстве есть отрезок АВ, и координаты его концов известны. Точка М – середина этого отрезка. Как вычислить ее координаты? Рассмотрим взаимосвязь векторов АМ, МВ и АВ:
Раз М – середина АВ, то вектора АМ и МВ имеют равные длины, и при этом они находятся на одной прямой. Значит, эти вектора равны и потому у них одинаковые коорд-ты:
Аналогично можно получить аналогичные формулы для коорд-т у и z:
Рассмотрим несколько задач на координаты точек.
Задание. Найдите коорд-ты середины отрезка, соединяющего точки А(3; 7; 12) и В(1; 5; – 4).
Решение. Просто используем только что выведенные формулы. Середину также обозначаем буквой М:
Задание. Известно, что K середина отрезка CD. Даны координаты точек С и K: С(12; 9; – 3) и K(15; 7; 3). Найдите коорд-ты D.
Решение. Сначала запишем формулу для коорд-ты х:
Определение координат середины отрезка через координаты радиус-векторов его концов
Формулу для нахождения координат середины отрезка также можно вывести согласно алгебраическому толкованию векторов.
Исходные данные: прямоугольная декартова система координат Oxy, точки с заданными координатами A(xA,yA) и B(xB, xB) . Точка C – середина отрезка AB.
Согласно геометрическому определению действий над векторами верным будет равенство: OC→=12·OA→+OB→ . Точка C в данном случае – точка пересечения диагоналей параллелограмма, построенного на основе векторов OA→ и OB→ , т.е. точка середины диагоналей.Координаты радиус-вектора точки равны координатам точки, тогда верны равенства: OA→=(xA, yA), OB→=(xB,yB) . Выполним некоторые операции над векторами в координатах и получим:
OC→=12·OA→+OB→=xA+xB2, yA+yB2
Следовательно, точка C имеет координаты:
xA+xB2, yA+yB2
По аналогии определяется формула для нахождения координат середины отрезка в пространстве:
C(xA+xB2, yA+yB2, zA+zB2)
Середина отрезка на плоскости
Исходные данные: прямоугольная система координат на плоскости Оxy, две произвольные несовпадающие точки с заданными координатами AxA, yA и BxB, yB . Точка C – середина отрезка AB. Необходимо определить координаты xC и yC для точки C.
Возьмем для анализа случай, когда точки A и B не совпадают и не лежат на одной координатной прямой или прямой, перпендикулярной одной из осей.Ax, Ay ; Bx, By и Cx ,Cy — проекции точек A, B и C на оси координат (прямые Ох и Оy).
Согласно построению прямые AAx, BBx, CCx параллельны; прямые также параллельны между собой. Совокупно с этим по теореме Фалеса из равенства АС = СВ следуют равенства: АxСx = СxВx и АyСy = СyВy, и они в свою очередь свидетельствуют о том, что точка Сx – середина отрезка АxВx, а Сy – середина отрезка АyВy. И тогда, опираясь на полученную ранее формулу, получим:
xC=xA+xB2 и yC=yA+yB2
Этими же формулами можно воспользоваться в случае, когда точки A и B лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. Проводить детальный анализ этого случая не будем, рассмотрим его лишь графически:

Резюмируя все выше сказанное, координаты середины отрезка AB на плоскости с координатами концов A (xA,yA) и B (xB, yB) определяются как:
(xA+xB2, yA+yB2)
Как построить середину отрезка с помощью циркуля и линейки?
Еще можно построить середину отрезка с помощью циркуля, линейки. Сделать это намного проще, чем в предыдущем варианте. Вам не понадобится рисовать множество окружностей разного диаметра, а достаточно построить лишь две одинаковые, а после провести перпендикуляр через точки пересечения с линиями окружности. Еще этот перпендикуляр называют серединным, что означает прямую, которую проводят под углом 90 градусов к отрезку.
Далее будет представлен мастер-класс на эту тему в подробностях и наглядно:
- Нарисуйте нужный отрезок на листке в клеточку, так вам удобнее будет разобраться в данной теме.
- Возьмите циркуль и нарисуйте две окружности с радиусом большим, чем середина отрезка или радиусом с длину отрезка – нет особой надобности рисовать слишком большие окружности, особенно, если отрезок большой длины.
- На рисунке выше видно, что окружности образуют две точки пересечения (вверху и внизу). Теперь понадобится линейка. Соедините эти две точки серединным перпендикуляром. Точка пересечения линии и отрезка и будет серединой.
Итак, среднюю точку отрезка нашли, теперь еще и не помешает доказать, что именно CD – срединный перпендикуляр, и он делит отрезок пополам. Это сделать просто. Ведь две окружности, что образуют линию, имеют одинаковый радиус, диаметр. А у окружностей все точки на линии одинаково удалены от ее центра. Значит точки C и D также находятся на одинаковых расстояниях от точек A и B. Прямая которая соединяет точки D и C может быть лишь одна в плоскости. И точка пересечения на отрезке находится на одном и том же расстоянии. Все это и требовалось прояснить.