Как найти середину полосы

Как найти середину

Иногда в повседневной деятельности может возникнуть необходимость найти середину отрезка прямой линии. Скажем, если предстоит сделать выкройку, эскиз изделия или просто распилить на две равные части деревянный брусок. На помощь приходит геометрия и немного житейской смекалки.

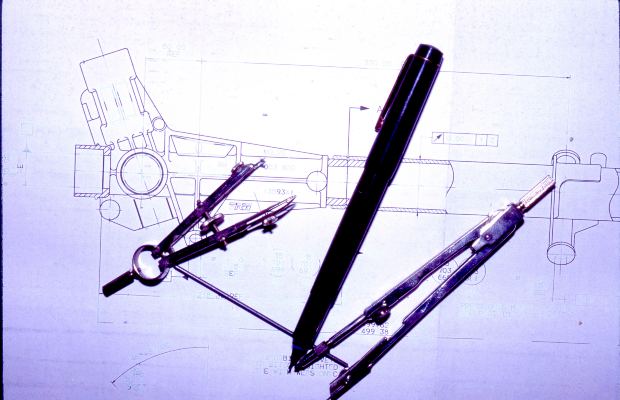
Вам понадобится

• Циркуль, линейка; булавка, карандаш, нить

Инструкция

Воспользуйтесь обычными инструментами, предназначенными для измерения длины. Это самый простой способ отыскать середину отрезка. Измерьте линейкой или рулеткой длину отрезка, разделите полученное значение пополам и отмерьте от одного из концов отрезка полученный результат. Вы получите точку, соответствующую середине отрезка.

Существует более точный способ нахождения середины отрезка, известный из курса школьной геометрии. Для этого возьмите циркуль и линейку, причем линейку может заменить любой предмет подходящей длины с ровной стороной.

Установите расстояние между ножками циркуля так, чтобы оно было равным длине отрезка или же большим, чем половина отрезка. Затем поставьте иглу циркуля в один из концов отрезка и проведите полуокружность так, чтобы она пересекала отрезок. Переставьте иглу в другой конец отрезка и, не меняя размах ножек циркуля, проведите вторую полуокружность точно таким же образом.

Вы получили две точки пересечения полуокружностей по обе стороны от отрезка, середину которого мы хотим найти. Соедините эти две точки при помощи линейки или ровного бруска. Соединительная линия пройдет в точности посередине отрезка.

Если под рукой не оказалось циркуля или длина отрезка существенно превышает допустимый размах его ножек, можно воспользоваться простым приспособлением из подручных средств. Изготовить его можно из обычной булавки, нитки и карандаша. Привяжите концы нитки к булавке и карандашу, при этом длина нитки должна немного превышать длину отрезка. Таким импровизированным заменителем циркуля остается проделать шаги, описанные выше.

Видео по теме

Полезный совет

Достаточно точно найти середину доски или бруска вы можете, использовав обычную нитку или шнур. Для этого отрежьте нить так, чтобы она соответствовала длине доски или бруска. Остается сложить нить точно пополам и разрезать на две равные части. Приложите один конец полученной мерки к концу измеряемого предмета, а второй конец будет соответствовать его середине.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Как найти среднюю линию треугольника?

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Понятие треугольника

Треугольник — это геометрическая фигура, которая получилась из трех отрезков. Их соединили тремя точками, которые не лежат на одной прямой. Отрезки принято называть сторонами, а точки — вершинами.

• Прямоугольный. Один угол прямой, то есть равен 90 градусам, два других меньше 90 градусов.
• Остроугольный. Градусная мера всех углов больше 0, но меньше 90 градусов.
• Тупоугольный. Один угол тупой, два других — острые.

Треугольник считают равнобедренным, если две его стороны равны. Эти стороны называют боковыми сторонами, а третью — основанием.

Треугольник, у которого все стороны равны, называется равносторонним или правильным.

Треугольник называется прямоугольным, если у него есть прямой угол, то есть угол в 90°. Сторона прямоугольного треугольника, которая лежит напротив прямого угла — гипотенуза, а две другие стороны — катеты.

Правильный (равносторонний или равноугольный) треугольник — это правильный многоугольник, в котором все стороны равны между собой, все углы также равны и составляют 60°. В равностороннем треугольнике высота является и биссектрисой, и медианой.

Свойства треугольников:

• В треугольнике против большего угла лежит большая сторона — и наоборот.
• Сумма углов треугольника равна 180 градусов.
• Все углы равностороннего треугольника равны 60 градусам.
• В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

Понятие средней линии треугольника

Определение средней линии треугольника подходит для любого вида этой фигуры.

​Средняя линия треугольника — отрезок, который соединяет середины двух сторон. В любом треугольнике можно провести три средних линии.

​Основанием считается сторона, которой параллельна средняя линия.

Как найти среднюю линию треугольника — расскажем дальше, а для начала еще немного разберемся со всеми определениями.

Понятие средней линии прямоугольного треугольника

Математики говорят: в любом треугольнике можно провести три средних линии. В прямоугольном треугольнике этот отрезок будет равен половине основания — это и есть формула средней линии прямоугольного треугольника.

Прямой угол помогает нам применить другие признаки равенства и подобия. Для углов в прямоугольном треугольнике можно использовать геометрические тождества без дополнительных построений, а любую из сторон можно найти по теореме Пифагора.

В прямоугольном треугольнике две средние линии перпендикулярны катетам, а третья равна медиане, проведенной к гипотенузе. Средние линии острого и разностороннего треугольника не обладают подобными свойствами.

Свойства средней линии треугольника

Признак средней линии треугольника: если отрезок в треугольнике проходит через середину одной из его сторон, пересекает вторую и параллелен третьей — этот отрезок можно назвать средней линией этого треугольника.

Свойства:

1. Средняя линия равна половине длины основания и параллельна ему.
2. Средняя линия отсекает треугольник, подобный данному с коэффициентом 1/2; его площадь равна четверти площади данного.
3. Три средние линии разделяют исходную фигуру на четыре равных треугольника. Центральный из них называют дополнительным.
4. Три средние линии разделяют исходный прямоугольный треугольник на четыре равных прямоугольных треугольника.

Теорема о средней линии треугольника

Теорема о средней линии треугольника звучит так:

Средняя линия треугольника параллельна основанию и равна его половине. А так выглядит формула нахождения средней линии треугольника:

Докажем теорему:

По условию нам дано, что MA = MB, NA = NC

Рассмотрим два образовавшихся треугольника ΔAMN и ΔABC.

(по второму признаку подобия треугольников).

△ABC, то Следовательно, ВС = 2МN. Значит, доказано, что средняя линия равна половине основания.

△ABC, то ∠1 = ∠2 . Так как ∠1 и ∠2 — соответственные углы, то по признаку параллельности прямых MN || BC.

Параллельность средней линии и соответствующего ей основания доказана.

Пример 1. В треугольнике ΔABC AB = 8, BC = 7, CA = 5, точки M, K, N — середины сторон AB, BC, CA соответственно. Найти периметр ΔMNK.

Соединим середины сторон треугольника ΔABC и получим его средние линии, которые образуют треугольник ΔMNK. Найдем их длины по теореме о средней линии:

Ответ: периметр треугольника ΔMNK равен 10.

Пример 2. В прямоугольном треугольнике АВС есть две средние линии: MN и NP, равные 3 и 4 соответственно. Найти площадь большого прямоугольного треугольника.

Площадь треугольника равна половине произведения основания на высоту. Так как треугольник прямоугольный, то его площадь найдем как половину произведения катетов:

Так как MN — средняя линия, то по теореме о средней линии она равна половине катета AC:

Значит, AC = 2MN = 2 × 3 = 6.

Так как NP — средняя линия, то по теореме о средней линии она равна половине катета BC:

Значит, BC = 2NP = 2 × 4 = 8.

Тогда найдем площадь большого треугольника, используя формулу, указанную выше:

S = ½ × 6 × 8 = ½ × 48 = 24.

Ответ: площадь большого прямоугольного треугольника равна 24.

Что такое средняя линия треугольника

В данной публикации мы рассмотрим определение, свойства и признак средней линии треугольника, а также разберем пример решения задачи для лучшего понимания теоретического материала.

Определение средней линии треугольника

Отрезок, который соединяет середины двух сторон треугольника, называется его средней линией.

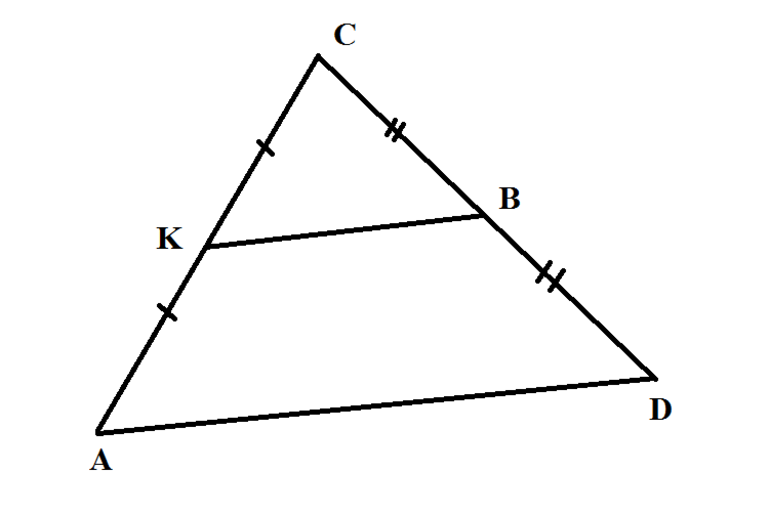
• KL – средняя линия треугольника ABC
• K – середина стороны AB: AK = KB
• L – середина стороны BC: BL = LC

Свойства средней линии треугольника

Свойство 1

Средняя линия треугольника параллельна одной из его сторон (которую не пересекает) и в два раза меньше этой стороны.

На рисунке выше:

Свойство 2

Средняя линия треугольника отсекает от него подобный треугольник (в соотношении 1:2), площадь которого в 4 раза меньше исходного.

На рисунке выше:

• △KBL ∼ △ABC (подобие по пропорциональности всех сторон)
• Стороны △KBL в два раза меньше соответствующих сторон △ABC:
  AB = 2KB, BC = 2BL, AC = 2KL.
• S_△ABC = 4 ⋅ S_△KBL

Свойство 3

В любом треугольнике можно провести три средние линии.

KL, KM и ML – средние линии треугольника ABC.

Свойство 4

Три средние линии треугольника делят его на 4 равных по площади треугольника.

Признак средней линии треугольника

Отрезок, проходящий через середину одной из сторон треугольника, пресекающий вторую и параллельный третьей стороне, является средней линией этого треугольника.

Пример задачи

Дан треугольник, две стороны которого равны 6 и 8 см. Найдите длину средней линии, соединяющей эти стороны.

Треугольник с заданными сторонами является прямоугольным, причем известные значения – это длины катетов. Средняя линия, которая соединяет катеты, параллельна гипотенузе и равна половине ее длины.

Мы можем найти гипотенузу, воспользовавшись теоремой Пифагора.

BC 2 = AB 2 + AC 2 = 6 2 + 8 2 = 100.
BC = 10.

Таким образом, средняя линия LM = 1 /₂ ⋅ BC = 1 /₂ ⋅ 10 = 5.

Длина средней линии треугольника — формула, признаки подобия и свойства

Фигура с тремя вершинами

Прежде чем понять, как найти ср. линию треугольника, необходимо рассмотреть фигуру, о которой пойдет речь. Каждый человек, даже плохо знакомый с геометрией, все же отчетливо представляет объект на плоскости, состоящий из трех вершин и трех сторон. Каждая вершина соединяется с двумя другими прямыми отрезками. Они называются сторонами.

Существующие типы

Рассматриваемый геометрический объект бывает нескольких типов. Наиболее известные из них следующие:

• равносторонний, у которого все стороны и углы равны между собой;
• равнобедренный, который имеет лишь две равные по длине стороны и отличающуюся от них третью;
• прямоугольный, у которого один из трех углов составляет 90 градусов, то есть является прямым.

Одним из важных свойств рассматриваемой фигуры произвольного типа является равенство 180 градусам суммы его трех углов. Именно по этой причине фигура может иметь либо три острых угла, либо один тупой и два меньше 90 градусов. Два прямых угла он также не может иметь, поскольку третья вершина должна будет лежать в бесконечности, чтобы иметь нулевой угол (90 + 90 + 0 = 180).

Основные геометрические элементы

К ним относятся типичные для треугольника отрезки, которые обладают определенными характеристиками. Наиболее известны из них следующие:

1. Медиана. Она опускается из любой из трех вершин на середину противоположной стороны. Медиана делит треугольник на две равные по площади части, а точка пересечения трех подобных отрезков является геометрическим и гравитационным центром фигуры.
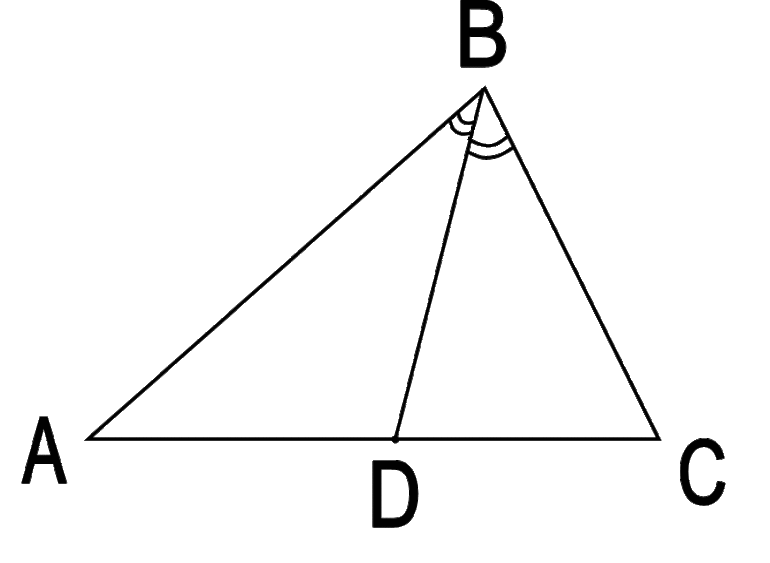
2. Биссектриса. Этот отрезок делит пополам угол вершины, из которой он проведен.
3. Высота. Она представляет собой перпендикулярный к противоположной стороне отрезок, опущенный из любой вершины треугольника. Высота делит фигуру на два прямоугольных геометрических объекта, сама является общей для них стороной и катетом.
4. Средняя линия. Это отрезок, который соединяет любые две точки треугольника, лежащие на серединах его сторон. В рассматриваемой фигуре можно провести три различных таких линии.

В общем случае первые три линейных элемента из списка не совпадают друг с другом, однако для определенных типов треугольников они могут быть одинаковыми. Например, для равносторонней фигуры не существует разницы между биссектрисами, медианами и высотами.

В случае треугольника равнобедренного лишь биссектриса, выходящая из вершины, образованной одинаковыми сторонами, также является медианой и высотой одновременно.

Признаки подобия

Важно рассмотреть признаки подобия треугольников, чтобы понимать все свойства, связанные со средним отрезком фигуры. Подобными являются геометрические объекты, которые имеют полностью идентичную форму, но разный размер. Например, два любых квадрата всегда подобны друг другу, поскольку один из них является увеличенной/уменьшенной копией другого.

Применительно к треугольникам существуют следующие признаки их подобия:

1. Равенство любых двух углов. Поскольку сумма трех углов является величиной постоянной, то этот признак свидетельствует о факте равенства всех трех рассматриваемых элементов.
2. Одинаковое соотношение всех трех сторон. Например, даны треугольники ABC и A1B1C1, для которых справедливо равенство: AB/A1B1 = BC/B1C1 = AC/A1C1 = k. Это означает, что обе фигуры подобны друг другу, при этом коэффициент их подобия равен k.
3. Существует коэффициент подобия для двух любых сторон рассматриваемых треугольников, а угол между ними является одинаковым. Математически это записывается так: A = A1 и AB/A1B1=AC/A1C1 = k.

Любой из этих признаков является достаточным, чтобы подтвердить подобие двух изучаемых треугольников. При доказательстве свойств среднего отрезка используют отмеченные признаки.

Средняя линия

Чтобы понять, как найти середину треугольника, можно воспользоваться обычной линейкой. Для этого необходимо выбрать произвольные две стороны фигуры. Затем отметить на каждой из них точки, отстоящие на одинаковом расстоянии от соответствующих вершин, которые ограничивают данную сторону. Полученные две точки следует соединить, чтобы начертить средний отрезок. Его название является интуитивно понятным каждому, поскольку он соединяет середины двух сторон.

Важные свойства

Существует три основных свойства, которыми обладает рассматриваемый отрезок. Пусть имеется треугольник произвольного типа ABC, в котором точки P и Q лежат на серединах сторон AB и AC соответственно. При таком обозначении отрезок PQ будет средней линией треугольника ABC. Справедливы следующие геометрические свойства:

1. Полученный треугольник APQ является подобным исходной фигуре ABC. Доказать это утверждение несложно, если обратить внимание на два факта: во-первых, угол A у обеих фигур является общим, во-вторых, отношение AB/AP равно величине AC/AQ и составляет 2 согласно выполненным геометрическим построениям. Таким образом, выполняется один из признаков подобия.
2. Длина средней линии PQ оказывается в два раза меньше, чем сторона BC. Кроме того, оба отрезка параллельны друг другу. Утверждение о равенстве PQ = ½*BC следует из факта подобия треугольников APQ и ABC, коэффициент которых составляет 2. Это равенство также можно доказать, если воспользоваться координатным методом.
3. Треугольник APQ имеет в 4 раза меньшую площадь, чем исходная фигура ABC.

Утверждение № 3 из списка справедливо для произвольного треугольника. Для его доказательства следует воспользоваться формулой Герона. Согласно ей, площадь рассматриваемой фигуры может быть вычислена следующим образом:

Здесь p = (a+b+c)/2 — полупериметр фигуры. Буквами a, b и c обозначены длины ее сторон. Пусть таким же образом обозначаются стороны для треугольника ABC. Тогда для фигуры APQ они будут иметь длины a/2, b/2 и c/2. Полупериметр для APQ составит величину p1 = (a+b+c)/4 = ½*p. Теперь необходимо подставить все известные величины в формулу Герона, получается площадь S1:

Иными словами, площадь треугольника APQ составляет четвертую часть от этой величины для ABC.

Решение задачи

В треугольнике ABC проведен средний отрезок PQ, граничные точки которой P и Q находятся на сторонах AB и AC соответственно. Необходимо с использованием метода координат доказать, что эта линия имеет в два раза меньшую длину, чем сторона BC.

Прежде чем находить решение этой задачи, следует обозначить координаты вершин исходной фигуры. Они будут следующие:

Поскольку точка P делит ровно пополам сторону AB, то для нахождения ее координат необходимо провести следующие вычисления:

Аналогичным образом рассчитываются координаты точки Q:

Вспоминая формулу для длины вектора, координаты конца и начала которого известны, для средней линии PQ можно произвести следующие вычисления:

PQ = (((x1+x3)/2 — (x1+x2)/2)^2 + ((y1+y3)/2 — (y1+y2)/2)^2)^0,5 = ½*((x3-x2)^2 + (y3-y2)^2)^0,5.

В свою очередь, длина стороны BC равна:

BC = ((x3-x2)^2 + (y3-y2)^2)^0,5.

Из сопоставления этих двух равенств следует искомая формула, которую требовалось доказать:

Поскольку в процессе доказательства были использованы произвольные координаты для вершин треугольника, полученный вывод является общим и универсальным для любого типа рассматриваемых фигур.

Срединный треугольник

Это особый вид фигуры с тремя вершинами, который строится на средних линиях. Поскольку любой треугольник имеет всего три линии указанного вида, то вместе они образуют новую фигуру, вершины которой расположены на серединах сторон исходной.

Построенный геометрический объект делит исходную фигуру на четыре одинаковые части. Доказать это можно следующим образом: если начертить срединный треугольник и обозначить черточками все его стороны, а также длины сторон исходного геометрического объекта, то можно увидеть, что сам он, а также три других фигуры при вершинах исходной имеют по три одинаковых стороны. Иными словами, выполняется признак их подобия. Равенство сторон всех четырех фигур говорит об одинаковом значении их площадей.

Еще одним интересным свойством срединной фигуры является возможность построения внутри нее точно такого же геометрического объекта. Он также будет подобен исходному треугольнику, но уже будет иметь в 8 раз меньшую площадь. Если продолжать такие геометрические построения, то площади срединных треугольников будут становиться все меньше, а пространство на плоскости, которое они будут покрывать, стремится к гравитационному центру исходной фигуры.

Таким образом, формула длины средней линии получается исходя из признака подобия треугольников по углу и двум прилежащим сторонам. Она всегда составляет половину от противоположной стороны. При выполнении геометрического построения срединного треугольника образуются четыре новых фигуры, которые подобны исходной. Гравитационные центры первоначального геометрического объекта и срединной фигуры совпадают.

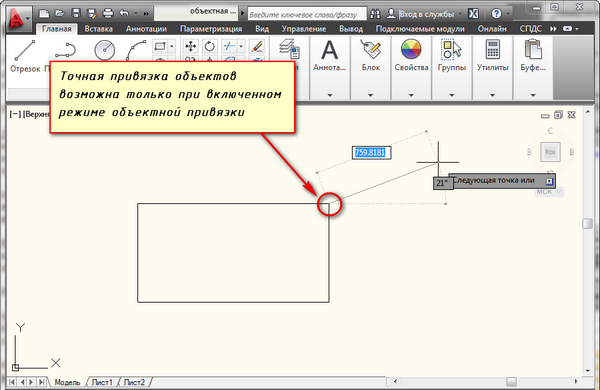
Как включить привязки в Автокаде и как настроить привязки в Автокаде? Почти всегда в AutoCAD требуется чертить объекты, точно привязывая их друг к другу. Например, точно построить отрезок, начинающийся из угла уже построенного прямоугольника. Далее мы вам расскажем как работать с Автокадом, включить привязки и правильно их настроить.

Для того чтобы подобные построения можно было выполнять с помощью мыши, в системе AutoCAD предусмотрен режим «объектной привязки». При этом когда мы начнем строить отрезок и подведем курсор к углу прямоугольника, то курсор автоматически как бы «притянется» к нужной точке.

Чтобы осуществить объектную привязку в (autocad) автокад, необходимо выполнить следующие шаги:

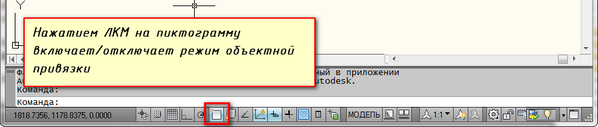
Включение/выключение привязки в автокаде осуществляется нажатием ЛКМ (левой кнопки мыши) на пикторгамму «Привязка» на строке состояния. Но я больше использую горячую клавишу вызова — F3.

У этого режима «объектной привязки» в autocad имеется множество методов. Например, один метод привязки в автокаде (autocad) указывает, как курсор должен привязываться к прямолинейным отрезкам, другой — дает возможнсть привязаться к середине отрезка, и так далее.

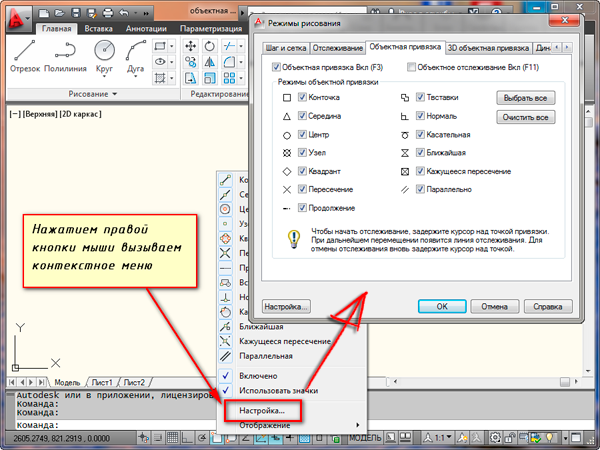
Настроить режим объектной привязки в автокаде можно в диалоговом окне «Режимы рисования» ➾ вкладка «Объектная привязка».

Я это окно вызываю следующим образом.

Наводим курсор мыши на пиктограмму «Объектная привязка» и нажимаем ПКМ (Правой кнопки мыши). В появившемся контекстном меню выбираем пункт «Настройка».

Вот как выглядит вкладка «Объектная приязка» в окне «Режимы рисования» в autocad.

На вкладке содержится перечень всевозможных методов объектной привязки в автокаде. Каждый метод имеет свои характерные точки, связанные с определенными объектами.

Возле каждого метода объектной привязки в autocad (автокад) показан внешний вид маркера, появляющегося в районе соответствующей характерной точки при «привязывании» к ней курсора.

Для наглядности описание методов объектной привязки я свел в таблицу.

Метод объектной привязки

Объекты, к которым применяется привязка	Характерные точки метода объектной привязки

Конечные точки объектовПривязка будет осуществляться к серединам объектовЦентры кругов, эллипсов и дугПривязка в автокаде (autocad) осуществляется к центру точкиТочки, делящие указанные объекты на квадранты (четверти). Это точки, соответствующие углам 0, 90,180 и 270 градусовТочки пересечения объектовТочки на линиях, образующих продолжение отрезков, дуг и полилиний. Для срабатывания данного метода необходимо установить курсор на конец отрезка или дуги и немного подождать. Затем следует двигать курсор, как бы продолжая линию или дугу. Появится пунктирная линия, которая является условным продолжением объекта. А на пунктире появится привязка в виде косого знака «+».Для блоков привязка привязка в автокаде (autocad) будет производиться к базовым точкам вставки. О тексте в autocad и его характерных точках вставки читайте в другом уроке. Точки на объектах в предполагаемом месте окончания перпендикуляра. Этот метод позволяет строить перпендикуляры к различным объектам в автокаде.Характерная точка появляется в предполагаемой точке касания. Этот метод позволяет строить касательные к дугам, кругам и эллипсамПривязка происходит к точке, в данный момент наиболее близко расположенной к курсоруПозволяет осуществить привязку к воображаемому пересечению объектов. При этом характерная точка высвечивается в воображаемой точке пересеченияПозволяет строить отрезки параллельно выбранным. В начале надо построить первую точку параллельного отрезка. Затем подвести курсор к исходному объекту, т.е параллельно которому мы будем строить отрезок. Необходимо немного подождать, пока маркер связи не изменит вид на знак «+». Затем перемещайте курсор из начальной точки параллельно выбранному объекту. При этом появится вспомогательная пунктирная линия, проходящая точно параллельно выбранному объекту.

Далее (для еще большей наглядности) приведу пример каждого из методов объектной привязки в autocad на рисунках.

Как сделать привязку в Автокаде и настройку привязок в Автокаде, теперь для нас не проблема!

В этом уроки мы поговорим о том, как правильно работать с отрезками в Автокаде.

В уроке разбираются следующие насущные темы:

– Как объединять отрезки в Полилинию в Автокаде;

– Как работать с опорным отрезком, как масштабировать с ним чертежи AutoCAD;

– Как сделать отрезок в Автокаде;

– Как разделить отрезок на одинаковые части;

– Как строить отрезки в Автокаде под определенным углом.

Видео версия урока:

Освой AutoCAD за 40 минут пройдя базовый курс от Максима Фартусова.

Текстовая версия урока:

Здравствуйте дорогой коллега! В этом уроке, мы с Вами подробней рассмотрим возможности команды “отрезок”. Предлагаю не тянуть чертеж за ватман и приступить к изучению вопросов!

Вопрос 1. Как построить отрезок в Автокаде под углом?

Шаг 1. Вызываем команду “отрезок”.

Шаг 2. Ставим первую точку нашего отрезка.

Шаг 3. Если Вы хотите чертить отрезок под углами определенной кратности (5,10,15,18,23,30 градусов) используйте режим под названием “полярное отслеживание”. Находится она на панели режимов.

Для выбора кратности угла, нажмите на “треугольник”. Когда появится список, выберите нужную кратность и Ваш отрезок будет чертиться под этими углами.

Теперь, когда мы поставим первую точку нашего отрезка и начнем крутить курсор, то в определенный момент появиться вспомогательная зеленная линия к которой наш отрезок как бы “прилипнет” и которая даст понять, что это угол 45 градусов или кратен 45-ти градусам.

Шаг 4. Для задания произвольного угла отрезка в Автокаде, сначала мы ставим первую точку нашего отрезка и вводим длину нашего отрезка.

Для указания угла наклона к горизонтали, требуется нажать кнопку TAB. Обращаю Ваше внимание на то, что углы в Автокаде отсчитываются так: против часовой стрелки со знаком плюс, по часовой стрелке со знаком минус.

После ввода длины отрезка (не обязательно вводить длину отрезка, можно указать произвольное значение), необходимо переключиться на ввод значения угла, для этого нажимаем кнопку TAB

После нажатия TAB вводим нужное значение угла, например 32 градуса и нажимаем enter для подтверждения.

Вопрос 2. Как найти середину отрезка в Автокаде?

Шаг 1. Делается это достаточно просто. Первым делом, убедитесь, что у Вас включены и настроены привязки. Привязки находятся вот тут (см. картинку ниже).

В случае, если Вы никогда не заходили в настройки привязок, следует кликнуть по стрелочке и вызвать окно, в котором нужно поставить галочку напротив “середина”.

Шаг 2. Итак, включили привязки (пиктограмма горит синим цветом). Теперь, когда мы возьмем любой инструмент для рисования, допустим новый отрезок и наведем на существующий отрезок, у нас появиться подсказка в виде зеленого треугольника. Это и есть привязка к середине нашего предыдущего отрезка.

Вопрос 3. Как разделить отрезок в Автокаде на равные части?

Допустим, у нас есть отрезок. И наша задача состоит в том, чтобы разделить его на четыре равные части. (обратите внимание, даже на глаз я сделал это очень не точно. Поэтому и есть такая возможность, которая помогает в некоторых моментах сделать точное деление на части)

Шаг 1. Для решения этой задачи, требуется зайти в панель “рисование” и раскрыть ее нажав на треугольник. Панель находится на вкладке “главная”.

Шаг 2. В новом окне нас интересует команда “поделить на равные части”, нажимаем на нее и смотрим, что делать дальше.

Шаг 3. Теперь требуется выбрать объект для деления, это наш отрезок.

Шаг 4. Теперь требуется ввести число сегментов, которые мы хотим получить в итоге. Обратите внимание, если у Вас включен динамический ввод, то подсказка будет около курсора. Если нет, то вводить значение нужно в командной строке.

Шаг 5. После ввода значения нажимаем enter и смотрим на результат. Обращаю Ваше внимание на тот факт, что деление отрезка происходит за счет использования инструмента “точка” в Автокаде. И по умолчанию, точка практически не видима, ее следует настроить.

Вопрос 4. Как объединять отрезки в полилинию в Автокаде?

Имея несколько отрезков на чертеже мы можем их преобразовать в одну полилинию в Автокаде.

Шаг 1. Раскрываем панель “редактирования”, нас интересует команда “редактировать полилинию”.

Шаг 2. Далее, выбираем любой из отрезков.

Шаг 3. Программа Автокад просит преобразовать отрезок в “полилинию”, мы соглашаемся и нажимаем enter. Данной процедурой мы преобразовали один из отрезков в полилинию.

Шаг 4. Сейчас нам требуется опять с помощью команды “добавить” выбрать оставшиеся отрезки и затем два раза нажать на enter. Тем самым мы объединили все наши отрезки в одну полилинию.

Выбираем отрезки, которые мы присоединим к нашей созданной полилинии.

Итог наших работ, наши отрезки стали одной полилинией и теперь мы можем задать ей новые параметры, например присвоить единую ширину.

Вопрос 5. Как сделать масштаб с помощью опорного отрезка в Автокаде?

После вставки изображения в Автокад иногда возникает вопрос, а как подогнать картинку по масштабу?

Т.е. чтобы она была скажем М 1:1? Это делается достаточно просто, требуется найти лишь размер любой линии и с помощью масштаба сделать подгонку.

Шаг 1. Найдем на нашем изображении линию с размером.

Шаг 2. На вкладке “главная” найдем команду “отрезок” и активируем ее.

Шаг 3. Начертим нашу линию. Причем первая точка нашего отрезка, будет совпадать с началом линии на картинке. Как видите, на нашем примере мы поставили первую точку отрезка в начале линии на рисунке, направили ее ровно вверх и задачи значение 200. Проще говоря, мы провели линию поверх картинки, началом отрезка послужило начало линии на картинке.

Шаг 4. Выбрали наш отрезок в Автокаде и придадим ему в свойствах другой цвет, например красный. Для чего? Так он будет более заметным на фоне нашей картинки. Напомню, что цвет можно поменять в “свойствах”, которые находятся на вкладке “главная”. Требуется кликнуть по треугольнику и выбрать нужный цвет, как на примере ниже.

Шаг 5. Отлично! Теперь наш отрезок стал красным и нам нужно выделить нашу картинку. Просто нажмите на рамку, что очерчивает рисунок или просто выделите всю картинку. И в том и другом случае Вы увидите синие маркеры, это сигнал о том, что объект выделен.

Шаг 6. Когда мы выделили нашу картинку, которую мы вставили в Автокад, нам нужно кликнуть где нибудь рядом или на самой картинке “правой кнопкой мышки”, чтобы появилось контекстное меню, где нам нужно выбрать команду “Масштаб”.

Шаг 7. После того, как мы выбрали команду “масштаб”, программа Автокад попросит нас выбрать базовую точку. В нашем и Вашем случае, это точка начала нашего отрезка и линии на картинке. Выбираем эту точку. Обратите внимание, чтобы линия была видна еще лучше, следует настроить веса в автокаде и включить их отображение.

Шаг 8. После того, как мы выбрали базовую точку, следует нажать в командной строке на слова “опорный отрезок” или нажать правую кнопку мышки и выбрать ее в контекстном меню.

Шаг 9. Теперь важная тонкость. Сейчас нам нужно указать длину опорного отрезка. Т.е. отрезка на который мы будем опираться при изменении масштаба, в нашем случае это линия на нашем рисунке, которая имеет длину 200 мм. В итоге, мы два раза кликнем левой кнопкой мышки, сначала на начале линии, потом на ее конце.

Шаг 10. Теперь нам нужно указать новую длину. Соответственно, указываем конечную точку нашего отрезка. Когда Вы начнете это делать увидите, что все изображение будет пропорционально изменяться в размерах относительно базовой точки. Завершаем команду кликом левой кнопки мыши.

Шаг 11. Как видите, теперь наш отрезок и линия стали почти одного размера. Почему почти? Я считаю, что на практике довольно сложно выровнять изображение к масштабу 1:1, погрешность в 1.2-1.5% всегда будет.

Это был последний вопрос, который мы разберем в этом уроке. Предлагаю подвести итоги.

Как и вся музыка состоящая из всего 12 нот (7 нот + тона), так и все чертежи состоят только из отрезков. Но зато какое многообразие проектов можно создать используя только одну команду “отрезок”. Не нужно недооценивать данную команду, она несет большой потенциал и возможности, да Вы и сами убедились в этом уже. Конечно, в некоторых ситуациях лучше использовать только полилинии в Автокаде, но и даже полилиния состоит из простых отрезков.

Как включить привязки в Автокад или как их настроить, т.е. как работать с помощью мыши точно, не прибегая к вводу координат в командную строку – цель нашего урока.

Правильная настройка привязок, и какие привязки включить для вычерчивания чертежа – это общая тема раздела, а непосредственно мы разберем объектную привязку и шаговую. Конечно, для настройки шаговой привязки разберем, что такое координатная сетка AutoCAD, ее настройку, а также не упустим момент и рассмотрим объектное отслеживание.

Объектная привязка AutoCAD

Например, при включенном режиме «Объектная привязка» курсор может прилипать к конечным точкам отрезка (привязка «Конточка») или к серединной точке отрезка (привязка «Середина») в зависимости какие объектные привязки на данный момент включены.

Общая настройка в Автокад объектных привязок

Общая настройка привязок в Автокад осуществляется в диалоговом окне «Режимы рисования». Режимы объектных привязок находятся на его вкладке «Объектная привязка».

Вызвать данное окно можно несколькими способами (приступить к настройке привязок):

настроить режимы объектных привязок можно из строки меню пункт «Сервис» – строка «Режимы рисования» – вкладка «Объектная привязка»;

Виды объектных привязок в Автокад, описание привязок

Объектная привязка Автокад «Конточка»

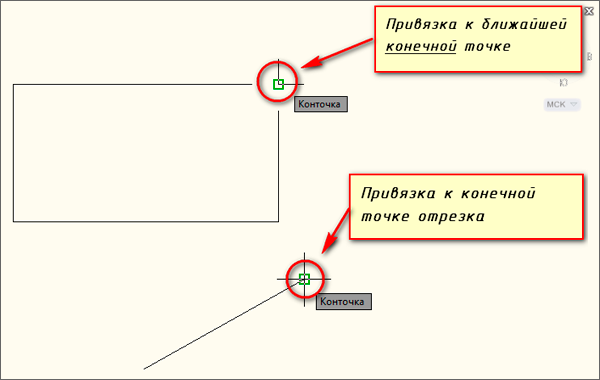
В Автокад 2D можно привязываться к оконечным точкам следующих объектов (другими словами — объекты с которыми работает привязка «Конточка» в AutoCAD): дуги, эллиптические дуги, сегменты мультилинии, отрезки, сегменты полилинии, к начальной точке луча.

Для привязки в Автокад к конечной точке объекта необходимо подвести курсор в область этой точки. В момент появления в AutoCAD маркера привязки (квадрат), щелкнуть мышкой. Как только режим автопривязки Автокад «Конточка» сработает, курсор захватывает координаты конечной точки объекта, а не той точки, на которой находился указатель-перекрестие в момент щелчка.

Объектная привязка в Автокад «Середина»

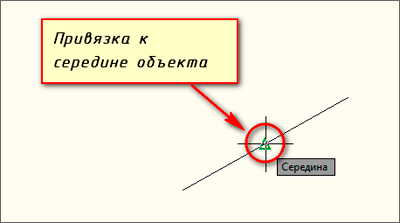
В Автокад 2D можно привязываться к средним точкам следующих объектов (другими словами — объекты с которыми работает привязка «Середина» в AutoCAD): дуги, эллиптические дуги, сегменты мультилинии, отрезки, сегменты полилинии, сплайны, прямые (базовая точка прямой в роле средней точки прямой). Средняя точка сплайнов и эллиптических дуг находится посередине между начальной и конечной точками.

Для привязки в Автокад к средней точке объекта необходимо подвести курсор в область этой точки. В момент появления маркера привязки (треугольник) в Автокад, щелкнуть мышкой. Как только режим автопривязки сработает, курсор захватывает координаты средней точки объекта, а не той точки, на которой находился указатель-перекрестие в момент щелчка.

Объектная привязка в Автокад «Пересечение»

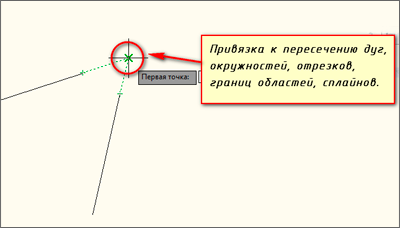
В программе можно привязываться к точкам пересечения объектов следующих типов в любой комбинации (другими словами — объекты с которыми работает привязка «Пересечение» в AutoCAD): дуги, окружности, эллипсы, эллиптические дуги, мультилинии, отрезки, прямые, полилинии, лучи, сплайны. Привязка в Автокад «Пересечение« срабатывает также к точке пересечения границ областей и кривых.

Для привязки в AutoCAD к точке пересечения объектов необходимо подвести курсор в область этой точки. В момент появления маркера привязки (пересекающиеся линии, крестик), щелкнуть мышкой. Как только режим автопривязки в Автокад сработает, курсор захватывает координаты точки пересечения объектов, а не той точки, на которой находился указатель-перекрестие в момент щелчка.

Объектная привязка Автокад «Кажущееся пересечение»

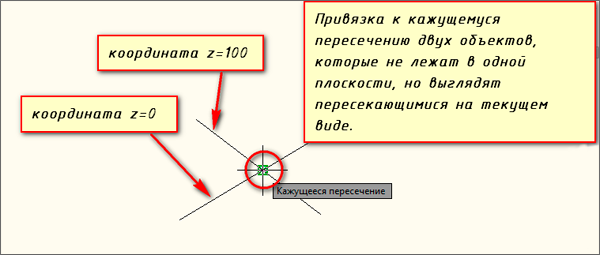
Так как в Автокад объектная привязка «Кажущееся пересечение» относится к моделированию, поэтому перейдем сразу к следующему виду привязки.

Объектная привязка в Автокад «Продолжение»

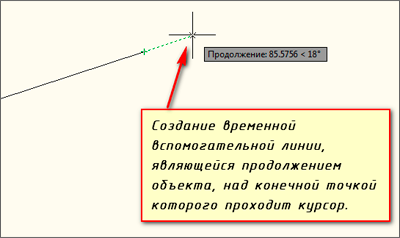
Для привязки в Автокад к произвольной точке, расположенной на условной штриховой линии продолжения объекта (дуги, линии), необходимо подвести курсор к оконечной точке линии или дуги. В месте расположения курсора появится знак «плюс, +». Затем следует вести курсор вдоль штриховой линии, появляющейся из выбранной точки. Режим привязки «Продолжение» в AutoCAD называется отслеживанием объектной привязки и является формой автоматического отслеживания!.

Обычно в Автокад привязку «Продолжение» используют совместно с другими видами привязок: конточка, пересечение, кажущееся пересечение и т.д.

Привязка «Продолжение» также позволяет привязываться сразу к нескольким объектам и вести их объектное отслеживание (тип мнимого продолжения объектов в AutoCAD), тем самым появляется возможность находит точку воображаемого пересечения объектов, не производя, каких либо дополнительных построений.

Объектная привязка «Продолжение» в Автокад напоминает метод «Направление и расстояние» при вводе координат. Использование этого вида привязки AutoCAD позволяет осуществлять отступ на определенное расстояние от объекта по его направлению и ввода расстояния с клавиатуры, совместное использование динамического ввода.

Объектная привязка Автокад «Центр»

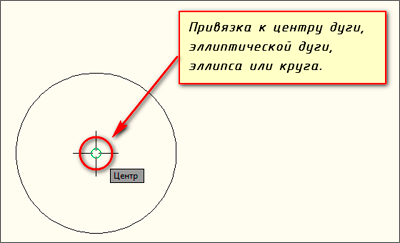
В системе можно привязываться к центральным точкам следующих объектов (другими словами — объекты с которыми работает привязка «Центр» в AutoCAD): дуги, окружности, эллипсы, эллиптические дуги, дуговому (криволинейному) сегементу полилинии.

Для привязки в Автокад к центральной точке криволинейного объекта, необходимо выбрать любую точку видимой части криволинейного объекта.

Объектная привязка в Автокад «Квадрант»

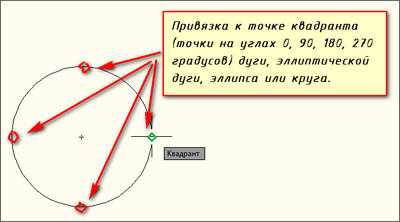
В программе можно осуществить привязку к ближайшему квадранту дуги, окружности, эллипса, эллиптической дуги, кливолинейнного сегмента полилинии.

Объектная привязка «Автокад» Касательная

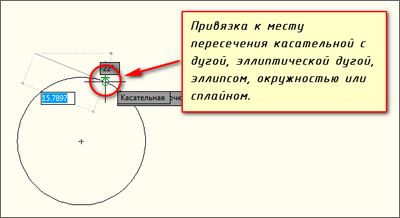
В программе можно привязываться к точке касания следующих объектов (другими словами — объекты с которыми работает привязка «Касательная» в AutoCAD): дуги, окружности, эллипса, эллиптической дуги, дугового сегмента полилинии.

Два режима работы привязки «Касательная» в Автокад:

• режим привязки к точке касания;
• режим привязки Автокад задающей касательную.

Например, привязка к точке касания в Автокад срабатывает, когда строится привязка конечной (второй) точки отрезка к точке касания окружности, которая при соединении ее с предыдущей выбранной точкой — первой точкой отрезка, образует касательную к этому объекту (первая точка отрезка уже была задана).

Объектная привязка Автокад «Нормаль»

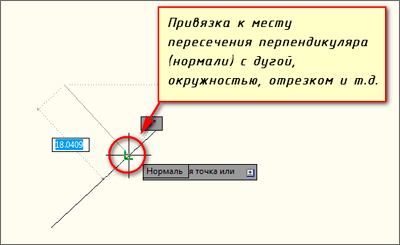
В программе привязка «Нормаль» может привязаться к дуге, окружности, эллипсу, эллиптической дуге, мультилинии, отрезку, прямой, полилинии, лучу, сплайну.

Режим объектной привязки «Нормаль» в Автокад работает в двух режимах:

• режим привязки к точке объекта, в которой обеспечивается условие перпендикулярности;
• режим привязки, задающей перпендикуляр в Автокад.

Например, привязка к точке объекта, в которой обеспечивается условие перпендикулярности срабатывает, когда строится в Автокад привязка конечной (второй) точки отрезка к точке «нормали» прямой, которая при соединении ее с предыдущей выбранной точкой — первой точкой отрезка, образует перпендикуляр к этому объекту (первая точка отрезка уже была задана).

Объектная привязка в Автокад «Параллельная»

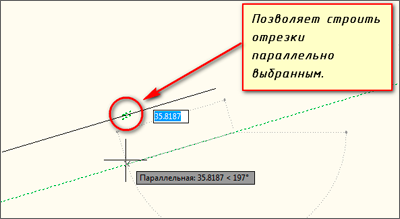
Построение прямолинейного объекта в Автокад параллельного другому прямолинейному объекту с использованием привязки «Параллельная» осуществляется следующим способом: начните построение прямолинейного объекта, например, укажем первую точку отрезка, а затем поместим курсор над прямолинейным сегментов имеющегося объекта — прямой, т.е. мы выбрали тем самым прямую, параллельно которой следует строить отрезок. Система пометит базовый объект (прямую) маркером привязки «Параллельная» в Автокад. Отведем курсор от базового объекта в сторону возможного возникновения параллельности объектов в Автокад. Как только система выполнит условие параллельности прямолинейных объектов при помощи объектной привязки AutoCAD «Параллельная», маркер привязки «Параллельная» на базовом объекте (прямой) будет отображаться штриховыми линиями, а через строющийся объект (отрезок) будет проведена временная штриховая линия, параллельную базовому объекту (прямой). Теперь вы можете указать вторую точку отрезка в любом месте временной штриховой линии.

Объектная привязка в Автокад «Узел»

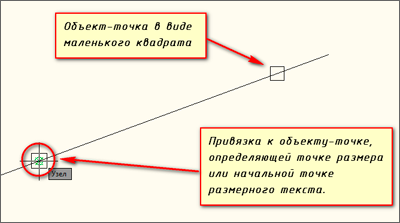
Для привязки в AutoCAD к узловой точке объекта необходимо подвести курсор над объектом.

Объектная привязка Автокад «Твставка»

Для привязки в Автокад к точке вставки объекта необходимо подвести курсор над объектом.

Объектная привязка в Автокад «Ближайшая»

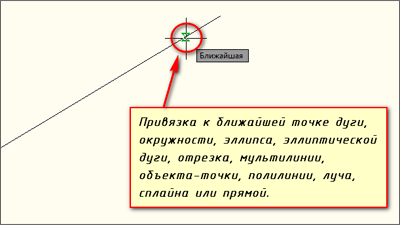
В AutoCAD можно привязываться к ближайшим точкам следующих объектов: дуги, эллиптические дуги, окружности, эллипсы, мультилинии, отрезки, прямые, точки, полилинии, лучи, сплайны.

Индивидуальный (разовый) вызов режимов объектных привязок в Автокад

Пользоваться автопривязками в Автокад очень удобно, но есть и свои минусы:

• сложный чертеж содержит высокую плотность линий, поэтому происходит путаница привязок Автокад и по ошибке можно выбрать другую привязку;
• в общих настройках автопривязки Автокад которые мы рассмотрели выше, постоянно отключать все типы привязок и оставлять нужный режим привязки, а затем снова заходить в настроки привязки и снова включать отключенные ранее привязки AutoCAD — не целесоорбразно;
• в общих настроках автопривязки Автокад нет всех режимов объектных привязок!

Разработчики нашли выход как включить/выключить нужные привязки в Автокад отдельно (разово) и таких способов три (Автокад 2017):

1. Использование «Меню объектной привязки Автокад».
2. Использование панели инструментов «Объектная привязка».
3. Ввод наименования объектной привязки в командную строку.

Далее мы рассмотрим все спобы вызова отдельных привязок в Автокад, как отключить на одну операцию (действие) все автопривязки Автокад, а также привязки в Автокад которые вызываются только разово (отдельно) и отсутствуют в настройках автопривязки.

Разовый (индивидуальный) вызов объектных привязок в Автокад с помощью меню Объектных привязок

Специальное контекстное меню объектных привязок можно вызвать щелчком правой кнопкой мыши с одновременным удерживанием клавиши «Shift».

При выборе в контекстном меню «Объектных привязок» нужной разовой привязки — все включенные автопривязки отключаются на одну операцию.