Как найти середину ребра математика - Исправление недочетов и поиск решений вместе с Examum.ru

Примечание: дробные числа записывайте
через точку, а не запятую.

Округлять до -го знака после запятой.

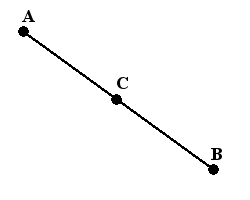
Середина отрезка. Координаты середины отрезка

В геометрических задачах часто можно столкнуться с необходимостью найти середину отрезка заданного координатами точек его концов, например в задачах поиска медианы, средней линии, .

Каждая координата середины отрезка равна полусумме соответствующих координат концов отрезка.

Формулы вычисления расстояния между двумя точками:

Формула вычисления координат середины отрезка с концами A( x_a , y_a ) и B( x_b , y_b ) на плоскости:

x_c =	x_a + x_b	y_c =	y_a + y_b
2	2

Формула вычисления координат середины отрезка с концами A( x_a , y_a , z_a ) и B( x_b , y_b , z_b ) в пространстве:

x_c =	x_a + x_b	y_c =	y_a + y_b	z_c =	z_a + z_b
2	2	2

Примеры задач на вычисление середины отрезка

Примеры вычисления координат середины отрезка на плоскости

x_c =	x_a + x_b	=	-1 + 6	=	5	= 2.5
2	2	2

y_c =	y_a + y_b	=	3 + 5	=	8	= 4
2	2	2

Примеры вычисления координат середины отрезка в пространстве

x_c =	x_a + x_b	=	-1 + 6	=	5	= 2.5
2	2	2

y_c =	y_a + y_b	=	3 + 5	=	8	= 4
2	2	2

z_c =	z_a + z_b	=	1 + (-3)	=	-2	= -1
2	2	2

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Векторы в пространстве и метод координат

Существует два способа решения задач по стереометрии

Первый — классический — требует отличного знания аксиом и теорем стереометрии, логики, умения построить чертеж и свести объемную задачу к планиметрической. Способ хорош тем, что развивает мозги и пространственное воображение.

Другой метод — применение векторов и координат. Это простые формулы, алгоритмы и правила. Он очень удобен, особенно когда времени до экзамена мало, а решить задачу хочется.

Если вы освоили векторы на плоскости и действия с ними — то и с векторами в пространстве разберетесь. Многие понятия окажутся знакомыми.

Система координат в пространстве

Выберем начало координат. Проведем три взаимно перпендикулярные оси X, Y и Z. Зададим удобный масштаб.

Получилась система координат в трехмерном пространстве. Теперь каждая его точка характеризуется тремя числами — координатами по X, Y и Z. Например, запись M(−1; 3; 2) означает, что координата точки M по X (абсцисса) равна −1, координата по Y (ордината) равна 3, а координата по Z (аппликата) равна 2.

Векторы в пространстве определяются так же, как и на плоскости. Это направленные отрезки, имеющие начало и конец. Только в пространстве вектор задается тремя координатами x, y и z:

Как найти координаты вектора? Как и на плоскости — из координаты конца вычитаем координату начала.

Длина вектора в пространстве – это расстояние между точками A и B. Находится как корень квадратный из суммы квадратов координат вектора.

Пусть точка M – середина отрезка AB. Ее координаты находятся по формуле:

Для сложения векторов применяем уже знакомые правило треугольника и правило параллелограмма

Сумма векторов, их разность, произведение вектора на число и скалярное произведение векторов определяются так же, как и на плоскости. Только координат не две, а три. Возьмем векторы и .

Произведение вектора на число:

Скалярное произведение векторов:

Косинус угла между векторами:

Последняя формула удобна для нахождения угла между прямыми в пространстве. Особенно если эти прямые – скрещиваются. Напомним, что так называются прямые, которые не параллельны и не пересекаются. Они лежат в параллельных плоскостях.

1. В кубе ABCDA₁B₁C₁D₁ точки E и K — середины ребер соответственно A₁B₁ и B₁C₁. Найдите косинус угла между прямыми AE и BK.

Если вам достался куб — значит, повезло. Он отлично вписывается в прямоугольную систему координат. Строим чертеж:

Длина ребра куба не дана. Какой бы она ни была, угол между AE и BK от нее не зависит. Поэтому возьмем единичный куб, все ребра которого равны 1.

Прямые AE и BK — скрещиваются. Найдем угол между векторами и . Для этого нужны их координаты.

Запишем координаты векторов:

и найдем косинус угла между векторами и :

2. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точки E, K — середины ребер SB и SC соответственно. Найдите косинус угла между прямыми AE и BK.

Лучше всего выбрать начало координат в центре основания пирамиды, а оси X и Y сделать параллельными сторонам основания.

Координаты точек A, B и C найти легко:

Из прямоугольного треугольника AOS найдем

Координаты вершины пирамиды:

Точка E — середина SB, а K — середина SC. Воспользуемся формулой для координат середины отрезка и найдем координаты точек E и K.

Найдем координаты векторов и

и угол между ними:

Покажем теперь, как вписать систему координат в треугольную призму:

3. В правильной треугольной призме ABCA₁B₁C₁, все ребра которой равны 1, точка D — середина ребра A₁B₁. Найдите косинус угла между прямыми AD и BC₁

Пусть точка A — начало координат. Возьмем ось X параллельно стороне BC, а ось Y перпендикулярно ей. Другими словами, на оси Y будет лежать отрезок AH, являющийся высотой треугольника ABC. Нарисуем отдельно нижнее основание призмы.

Запишем координаты точек:

Точка D — середина A₁B₁. Значит, пользуемся формулами для координат середины
отрезка.

Найдем координаты векторов и , а затем угол между ними:

Смотрите, как легко с помощью векторов и координат найти угол между прямыми. А если требуется найти угол между плоскостями или между прямой и плоскостью? Для решения подобных задач нам понадобится уравнение плоскости в пространстве.

Плоскость в пространстве задается уравнением:

Здесь числа A, B и C — координаты вектора, перпендикулярного этой плоскости. Его называют нормалью к плоскости.

Вместо x, y и z можно подставить в уравнение координаты любой точки, принадлежащей данной плоскости. Получится верное равенство.

Плоскость в пространстве можно провести через любые три точки, не лежащие на одной прямой. Поэтому для того, чтобы написать уравнение плоскости, берем координаты трех принадлежащих ей точек. Подставляем их по очереди в уравнение плоскости. Решаем полученную систему.

Покажем, как это делается.

Напишем уравнение плоскости, проходящей через точки M (1; 0; 1), N (2; −2; 0) и K (4; 1; 2).

Уравнение плоскости выглядит так:

Подставим в него по очереди координаты точек M, N и K.

То есть A + C + D = 0.

Аналогично для точки K:

Получили систему из трех уравнений:

В ней четыре неизвестных: A, B, C и D. Поэтому одну из них мы выберем сами, а другие выразим через нее. Правило простое — вместо одной из переменных можно взять любое число, не равное нулю.

Пусть, например, D = −2. Тогда:

Выразим C и B через A и подставим в третье уравнение:

Решив систему, получим:

Уравнение плоскости MNK имеет вид:

Умножим обе части уравнения на −3. Тогда коэффициенты станут целыми:

Вектор — это нормаль к плоскости MNK.

Уравнение плоскости, проходящей через заданную точку имеет вид:

Угол между плоскостями равен углу между нормалями к этим плоскостям:

Не правда ли, знакомая формула? Скалярное произведение нормалей поделили на произведение их длин.

Заметим, что при пересечении двух плоскостей вообще-то образуется четыре угла.

Мы берем меньший из них. Поэтому в формуле стоит модуль скалярного произведения — чтобы косинус угла был неотрицателен.

4. В кубе ABCDA₁B₁C₁D₁ точки E и F — середины ребер соответственно A₁B₁ и A₁D₁. Найдите тангенс угла между плоскостями AEF и BDD₁.

Строим чертеж. Видно, что плоскости AEF и BDD₁ пересекаются где-то вне куба. В классическом решении пришлось бы строить линию их пересечения. Но векторно-координатный метод значительно всё упрощает. Не будем ломать голову над тем, по какой прямой пересекаются плоскости. Просто отметим координаты нужных нам точек и найдем угол между нормалями к плоскостям AEF и BDD₁.

Сначала — нормаль к плоскости BDD₁. Конечно, мы можем подставить координаты точек B, D и D₁ в уравнение плоскости и найти коэффициенты, которые и будут координатами вектора нормали. А можем сделать хитрее — увидеть нужную нормаль прямо на чертеже. Ведь плоскость BDD₁ — это диагональное сечение куба. Вектор перпендикулярен этой плоскости.

Итак, первый вектор нормали у нас уже есть:

Напишем уравнение плоскости AEF.

Берем уравнение плоскости и по очереди подставляем в него, вместо x, y и z, соответствующие координаты точек A, E и F.

Пусть С = -1. Тогда A = B = 2.

Уравнение плоскости AEF:

Нормаль к плоскости AEF:

Найдем угол между плоскостями:

5. Основание прямой четырехугольной призмы BCDA₁B₁C₁D₁ — прямоугольник ABCD, в котором AB = 5, AD = √33. Найдите тангенс угла между плоскостью грани AA₁D₁D и плоскостью, проходящей через середину ребра CD перпендикулярно прямой B₁D, если расстояние между прямыми A₁C₁ и BD равно √3.

Эта задача наглядно показывает, насколько векторный метод проще классического. Попробуйте, для разнообразия, построить необходимые сечения и провести все доказательства — как это делается в «классике»

Строим чертеж. Прямую четырехугольную призму можно по-другому назвать «параллелепипед».

Замечаем, что длина и ширина параллелепипеда у нас есть, а вот высота — вроде не дана. Как же ее найти?

«Расстояние между прямыми A₁C₁ и BD равно √3». Прямые A₁C₁ и BD скрещиваются. Одна из них — диагональ верхнего основания, другая — диагональ нижнего. Вспомним, что расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра. Общий перпендикуляр к A₁C₁ и BD — это, очевидно, OO₁, где O — точка пересечения диагоналей нижнего основания, O₁ — точка пересечения диагоналей верхнего. А отрезок OO₁ и равен высоте параллелепипеда.

Плоскость AA₁ D₁ D — это задняя грань призмы на нашем чертеже. Нормаль к ней — это любой вектор, перпендикулярный задней грани, например, вектор или, еще проще, вектор .

Осталась еще «плоскость, проходящая через середину ребра CD перпендикулярно прямой B₁D». Но позвольте, если плоскость перпендикулярна прямой B₁D — значит, B₁D и есть нормаль к этой плоскости! Координаты точек B₁ и D известны:

Координаты вектора — тоже:

Находим угол между плоскостями, равный углу между нормалями к ним:

Зная косинус угла, находим его тангенс по формуле

Получим:

Ответ:

Угол между прямой m и плоскостью α тоже вычисляется с помощью скалярного произведения векторов.

Пусть — вектор, лежащий на прямой m (или параллельный ей), — нормаль к плоскости α.

Находим синус угла между прямой m и плоскостью α по формуле:

6. В кубе ABCDA₁B₁C₁D₁ точка E — середина ребра A₁B₁. Найдите синус угла между прямой AE и плоскостью BDD₁.

Как всегда, рисуем чертеж и выбираем систему координат

Находим координаты вектора .

Нужно ли нам уравнение плоскости BDD₁? В общем-то, без него можно обойтись. Ведь эта плоскость является диагональным сечением куба, а значит, нормалью к ней будет любой вектор, ей перпендикулярный. Например, вектор .

Найдем угол между прямой и плоскостью:

Ответ:

Расстояние от точки M с координатами x₀, y₀ и z₀ до плоскости α, заданной уравнением Ax + By + Cz + D = 0, можно найти по формуле:

7. В основании прямоугольного параллелепипеда BCDA₁B₁C₁D₁ лежит прямоугольник ABCD со сторонами AB = , AD = . Высота параллелепипеда AA₁ = . Найдите расстояние от точки A до плоскости A₁DB.

Построим чертеж и выпишем координаты точек:

Запишем уравнение плоскости A₁DB. Вы помните, как это делается — по очереди подставляем координаты точек A₁, D и B в уравнение A_x + B_e + C_z + D

Решим эту систему. Выберем

Тогда

Уравнение плоскости A₁DB имеет вид:

Дальше все просто. Находим расстояние от точки A до плоскости A₁DB:

В некоторых задачах по стереометрии требуется найти расстояние от прямой до параллельной ей плоскости. В этом случае можно выбрать любую точку, принадлежащую данной прямой.

источники:

http://ru.onlinemschool.com/math/library/analytic_geometry/points_center/

http://ege-study.ru/ru/ege/materialy/matematika/vektory-v-prostranstve-i-metod-koordinat/

Источник

Вершины пирамиды находятся в вершинах А, В, С и D, вычислить :
а) Площадь грани ВСD
б) Площадь сечения проходящую через середину ребра АВ, С и D
в) Объем пирамиды АВСD

[math]F (-7, -5, 6), B (-2,5,-3) C(3,-2,4), D(1,2,2)[/math]
а)
[math]overrightarrow{BC}= (5,-7,7)[/math]
[math]overrightarrow{BD}= (3,-3,5)[/math]
Найдем векторное произведение
[math](overrightarrow{BC} mathbf{x} {overrightarrow{BD})[/math] =[math]begin{vmatrix} i & j & k \ 5 & -7 & 7 \ 3 & -3 & 5 end{vmatrix}[/math]=[math]-14vec{i}-4vec{j}+6vec{k}[/math]; [math](-14,-4,6)[/math]
[math]left| overrightarrow{BC} mathbf{x} overrightarrow{BD} right| =sqrt{196+16+36}=sqrt{248}=2sqrt{62}; S_{BCD}= frac{ 1 }{ 2 }(left| overrightarrow{BC} mathbf{x} overrightarrow{BD} right|= frac{ 1 }{ 2 } cdot 2sqrt{62}=sqrt{62}[/math]

б) Найдем координаты точек М-середины ребра CD
[math]X_{M}=frac{ 1 }{ 2 }(3+1)=2; Y_{M}=frac{ 1 }{ 2 }(-2+2)=0; Z_{M}=frac{ 1 }{ 2 }(6)=3;[/math]
Получим М [math]left[ 2,0,3 right][/math]
[math]S=frac{ 1 }{ 2 }left( left| overrightarrow{MA} mathbf{x} overrightarrow{MB} right| right)[/math]

Найдем координаты векторов
[math]overrightarrow{MA}[/math] и [math]overrightarrow{MB}[/math]

[math]overrightarrow{MA}= (-9,-5,3)[/math]
[math]overrightarrow{MB}= (-4,5,-6)[/math]
[math]overrightarrow{MA} mathbf{x} overrightarrow{MB}= begin{vmatrix} i & j & k \ 9 & -5 & 3 \ -4 & 5 & 6 end{vmatrix}= 15vec{i}-66vec{j} -65vec{k}[/math]
[math]left| overrightarrow{MA} mathbf{x} overrightarrow{MB}right| =sqrt{225+4356+4225}=sqrt{8806}[/math]
[math]S=frac{ 1 }{ 2 } cdot sqrt{8806}[/math]
в)
[math]V_{ABCD}=frac{ 1 }{ 6 }left( overrightarrow{AB}overrightarrow{AC} overrightarrow{AD} right)[/math]
Координаты[math]overrightarrow{AB}(5,10,-9)[/math]
[math]overrightarrow{AC}=left( 10,3,-2 right)[/math]
[math]overrightarrow{AD}= left( 8,7,-4 right)[/math]
Найдем смешанное произведение :
[math]begin{vmatrix} 5 & 10 & -9 \ 10 & 3 & -2 \ 8 & 7 & -4 end{vmatrix}=-164[/math]

[math]V_{ABCD}=frac{ 1 }{ 2}left( left| -164 right| right)=frac{ 82 }{3 };[/math]

Надеюсь, что все это писал не зря.
Спасибо. :Bravo:

Источник

Подготовка к профильному уровню единого государственного экзамена по математике. Полезные материалы по стереометрии, видеоразборы задач и подборка заданий прошлых лет.

Полезные материалы

Подборки видео и онлайн-курсы

Все ролики с заданием 14
Все ролики по стереометрии
Мини-курс «Задачи по стереометрии на ЕГЭ по математике (задача №14)»
Мини-курс «Векторный метод в пространстве»

Как решать стереометрию

Теорема о трёх перпендикулярах

Как найти объем. Принцип Кавальери

Видеоразборы задач

В треугольной пирамиде $SABC$ $SB=SC=AC=AB=sqrt{17}$, $SA= BC = 2sqrt5$.
а) Докажите, что прямые $BC$ и $SA$ перпендикулярны.
б) Найдите расстояние между прямыми $BC$ и $SA$.

В прямом круговом конусе с вершиной $S$ и центром основания $O$ радиус основания равен 13, а высота равна $3sqrt{41}$. Точки $A$ и $B$ — концы образующих, $M$ — середина $SA$, $N$ — точка в плоскости основания такая, что прямая $MN$ параллельна прямой $SB$.
а) Докажите что угол $ANO$ — прямой.
б) Найдите угол между $MB$ и плоскостью основания, если дополнительно известно что $AB = 10$.

В правильной треугольной призме $ABCA_1B_1C_1$ все рёбра равны 2. Точка $M$ — середина ребра $AA_1$.
а) Докажите, что прямые $MB$ и $B_1C$ перпендикулярны.
б) Найдите расстояние между прямыми $MB$ и $B_1C$.

На окружности одного из оснований прямого кругового цилиндра выбраны точки $A$ и $B$, а на окружности другого основания — точки $B_1$ и $C_1$, причём $BB_1$ — образующая цилиндра, а отрезок $AC_1$ пересекает ось цилиндра.
а) Докажите, что угол $C_1BA$ прямой.
б) Найдите расстояние от точки $B$ до прямой $AC_1$, если $AB=12$, $BB_1=4$ и $B_1C_1 = 3$.

Дана правильная четырехугольная призма $ABCDA_1B_1C_1D_1$. На ребре $AA_1$ отмечена точка $K$ так, что $AK : KA_1 = 1 : 2$. Плоскость $alpha$ проходит через точки $B$ и $K$ параллельно прямой $AC$. Эта плоскость пересекает ребро $DD_1$ в точке $M$.
а) Докажите, что $DM : MD_1 = 2 : 1$.
б) Найдите площадь сечения, если $AB = 4$, $AA_1 = 6$.

Длина диагонали куба $ABCDA_1B_1C_1D_1$ равна 3. На луче $A_1C$ отмечена точка $P$ так, что $A_1P = 4$.
a) Докажите, что грань $PBDC_1$ — правильный тетраэдр.
б) Найдите длину отрезка $AP$.

Сечением прямоугольного параллелепипеда $ABCDA_1B_1C_1D_1$ плоскостью $alpha$, содержащей прямую $BD_1$ и параллельной прямой $AC$, является ромб.
a) Докажите, что грань $ABCD$ — квадрат.
б) Найдите угол между плоскостями $alpha$ и $BCC_1$, если $AA_1 = 6$, $AB = 4$.

В правильной треугольной призме $ABCA_1B_1C_1$ сторона основания $AB$ равна 6, а боковое ребро $AA_1$ равно 3. На ребре $AB$ отмечена точка $K$ так, что $AK = 1$. Точки $M$ и $L$ — середины ребер $A_1C_1$ и $B_1C_1$ соответственно. Плоскость $gamma$ параллельна прямой $AC$ и содержит точки $K$ и $L$.
а) Докажите, что прямая $BM$ перпендикулярна плоскости $gamma$;
б) Найдите расстояние от точки $C$ до плоскости $gamma$.

Подборка заданий прошлых лет

В прямом круговом конусе с вершиной $S$ и центром основания $O$ радиус основания равен 13, а высота равна $3sqrt{41}$. Точки $A$ и $B$ — концы образующих, $M$ — середина $SA$, $N$ — точка в плоскости основания такая, что прямая $MN$ параллельна прямой $SB$.
а) Докажите что угол $ANO$ — прямой.
б) Найдите угол между $MB$ и плоскостью основания, если дополнительно известно что $AB = 10$.
(ЕГЭ-2019, досрочная волна, резервный день)
В треугольной пирамиде $SABC$ $SB=SC=AC=AB=sqrt{17}$, $SA= BC = 2sqrt5$.
а) Докажите, что прямые $BC$ и $SA$ перпендикулярны.
б) Найдите расстояние между прямыми $BC$ и $SA$.
(ЕГЭ-2019, досрочная волна)
В треугольной пирамиде $SABC$ $SB=SC=sqrt{17}$, $AB=AC=sqrt{29}$, $SA= BC = 2sqrt5$.
а) Докажите, что прямые $BC$ и $SA$ перпендикулярны.
б) Найдите угол между прямой $SA$ и плоскостью $SBC$.
(ЕГЭ-2019, досрочная волна)
Дана правильная четырехугольная призма $ABCDA_1B_1C_1D_1$. На ребре $AA_1$ отмечена точка $K$ так, что $AK : KA_1 = 1 : 2$. Плоскость $alpha$ проходит через точки $B$ и $K$ параллельно прямой $AC$. Эта плоскость пересекает ребро $DD_1$ в точке $M$.
а) Докажите, что $DM : MD_1 = 2 : 1$.
б) Найдите площадь сечения, если $AB = 4$, $AA_1 = 6$.
(ЕГЭ-2018, досрочная волна)
В правильной треугольной призме $ABCA_1B_1C_1$ все рёбра равны~2. Точка $M$ — середина ребра $AA_1$.
а) Докажите, что прямые $MB$ и $B_1C$ перпендикулярны.
б) Найдите расстояние между прямыми $MB$ и $B_1C$.
(ЕГЭ-2018, досрочная волна, резервный день)
На окружности одного из оснований прямого кругового цилиндра выбраны точки $A$ и $B$, а на окружности другого основания — точки $B_1$ и $C_1$, причём $BB_1$ — образующая цилиндра, а отрезок $AC_1$ пересекает ось цилиндра.
а) Докажите, что угол $C_1BA$ прямой.
б) Найдите расстояние от точки $B$ до прямой $AC_1$, если $AB=12$, $BB_1=4$ и $B_1C_1 = 3$.
(ЕГЭ-2018, основная волна)
На окружности одного из оснований прямого кругового цилиндра выбраны точки $A$ и $B$, а на окружности другого основания — точки $B_1$ и $C_1$, причём $BB_1$ — образующая цилиндра, а отрезок $AC_1$ пересекает ось цилиндра.
а) Докажите, что угол $ABC_1$ прямой.
б) Найдите угол между прямыми $BB_1$ и $AC_1$, если $AB = 6$, $BB_1 = 15$, $B_1C_1 = 8$.
(ЕГЭ-2018, основная волна)
На окружности одного из оснований прямого кругового цилиндра выбраны точки $A$, $B$ и $C$, а на окружности другого основания — точка $C_1$, причём $CC_1$ — образующая цилиндра, а $AC$ — диаметр основания. Известно, что $angle ACB = 30^{circ}$, $AB = sqrt2$, $CC_1 = 2$.
а) Докажите,что угол между прямыми $AC_1$ и $BC$ равен $45^{circ}$.
б) Найдите объём цилиндра.
(ЕГЭ-2018, основная волна)
В кубе $ABCDA_1B_1C_1D_1$ все ребра равны 6.
а) Докажите, что угол между прямыми $AC$ и $BC_1$ равен $60^{circ}$.
б) Найдите расстояние между прямыми $AC$ и $BC_1$.
(ЕГЭ-2018, основная волна)
На ребре $AB$ правильной четырёхугольной пирамиды $SABCD$ с основанием $ABCD$ отмечена точка $Q$, причём $AQ:OB=1:2$. Точка $P$ — середина ребра $AS$.
а) Докажите, что плоскость $DPQ$ перпендикулярна плоскости основания пирамиды.
б) Найдите площадь сечения $DPQ$, если площадь сечения $DSB$ равна 6.
(ЕГЭ-2018, основная волна, резервный день)
В правильном тетраэдре $ABCD$ точка $H$ — центр грани $ABC$, а точка $M$ — середина ребра $CD$.
а) Докажите, что прямые $AB$ и $CD$ перпендикулярны.
б) Найдите угол между прямыми $DH$ и $BM$.
(ЕГЭ-2018, основная волна, резервный день)
Основанием прямой четырехугольной призмы $ABCDA_1B_1C_1D_1$ является ромб $ABCD$, $AB = AA_1$.
а) Докажите, что прямые $A_1C$ и $BD$ перпендикулярны.
б) Найдите объем призмы, если $A_1C = BD = 2$.
(ЕГЭ-2017, основная волна, резервный день)
В правильной четырехугольной пирамиде $SABCD$ все ребра равны 5. На ребрах $SA$, $AB$, $BC$ взяты точки $P$, $Q$, $R$ соответственно так, что $PA = AQ = RC = 2$.
а) Докажите, что плоскость $PQR$ перпендикулярна ребру $SD$.
б) Найдите расстояние от вершины $D$ до плоскости $PQR$.
(ЕГЭ-2017, основная волна, резервный день)
В треугольной пирамиде $PABC$ с основанием $ABC$ известно, что $AB = 17$, $PB = 10$, $cos angle PBA = dfrac{32}{85}$. Основанием высоты этой пирамиды является точка $C$. Прямые $PA$ и $BC$ перпендикулярны.
а) Докажите, что треугольник $ABC$ прямоугольный.
б) Найдите объем пирамиды $PABC$.
(ЕГЭ-2017, основная волна, резервный день)
Ребро куба $ABCDA_1B_1C_1D_1$ равно 6. Точки $K$, $L$ и $M$ — центры граней $ABCD$, $AA_1D_1D$ и $CC_1D_1D$ соответственно.
а) Докажите, что $B_1KLM$ — правильная пирамида.
б) Найдите объём $B_1KLM$.
(ЕГЭ-2017, основная волна)
В треугольной пирамиде $SABC$ известны боковые рёбра: $SA = SB = 7$, $CS = 5$. Основанием высоты этой пирамиды является середина медианы $CM$ треугольника $ABC$. Эта высота равна 4.
а) Докажите, что треугольник $ABC$ равнобедренный.
б) Найдите объём пирамиды $SABC$.
(ЕГЭ-2017, основная волна)
Основанием прямой треугольной призмы $ABCA_1B_1C_1$ является прямоугольный треугольник $ABC$ с прямым углом $C$. Диагонали боковых граней $AA_1B_1B$ и $BB_1C_1C$ равны 15 и 9 соответственно, $AB = 13$.
а) Докажите, что треугольник $BA_1C_1$ прямоугольный.
б) Найдите объём пирамиды $AA_1C_1B$.
(ЕГЭ-2017, основная волна)
Основанием прямой треугольной призмы $ABCA_1B_1C_1$ является прямоугольный треугольник $ABC$ с прямым углом $C$. Прямые $CA_1$ и $AB_1$ перпендикулярны.
а) Докажите, что $AA_1 = AC$.
б) Найдите расстояние между прямыми $CA_1$ и $AB_1$, если $AC = 6$, $BC = 3$.
(ЕГЭ-2017, основная волна)
На ребрах $AB$ и $BC$ треугольной пирамиды $ABCD$ отмечены точки $M$ и $N$ соответственно, причём $AM:MB = CN:NB = 1:3$. Точки $P$ и $Q$ — середины сторон $DA$ и $DC$ соответственно.
а) Доказать, что $P$, $Q$, $M$ и $N$ лежат в одной плоскости.
б) Найти отношение объемов многогранников, на которые плоскость $PQM$ разбивает пирамиду.
(ЕГЭ-2017, основная волна)
Сечением прямоугольного параллелепипеда $ABCDA_1B_1C_1D_1$ плоскостью $alpha$ содержащей прямую $BD_1$ и параллельной прямой $AC$, является ромб.
а) Докажите, что грань $ABCD$ — квадрат.
б) Найдите угол между плоскостями $alpha$ и $BCC_1$, если $AA_1 = 6$, $AB = 4$.
(ЕГЭ-2017, досрочная волна)
В правильной треугольной призме $ABCA_1B_1C_1$ сторона $AB$ основания равна 12, а высота призмы равна 2. На рёбрах $B_1C_1$ и $AB$ отмечены точки $P$ и $Q$ соответственно, причём $PC_1 = 3$, а $AQ = 4$. Плоскость $A_1PQ$ пересекает ребро $BC$ в точке $M$.
а) Докажите, что точка $M$ является серединой ребра $BC$.
б) Найдите расстояние от точки $B$ до плоскости $A_1PQ$.
(ЕГЭ-2016, основная волна)
На рёбрах $DD_1$ и $BB_1$ куба $ABCDA_1B_1C_1D_1$ с ребром 12 отмечены точки $P$ и $Q$ соответственно, причём $DP = 10$, а $B_1Q = 4$. Плоскость $A_1PQ$ пересекает ребро $CC_1$ в точке $M$.
а) Докажите, что точка $M$ является серединой ребра $CC_1$.
б) Найдите расстояние от точки $C_1$ до плоскости $A_1PQ$.
(ЕГЭ-2016, основная волна)
В правильной четырёхугольной пирамиде $SABCD$ сторона $AB$ основания равна $2sqrt{3}$, а высота $SH$ пирамиды равна 3. Точки $M$ и $N$ — середины рёбер $CD$ и $AB$, соответственно, а $NT$ — высота пирамиды $NSCD$ с вершиной $N$ и основанием $SCD$.
а) Докажите, что точка $T$ является серединой $SM$.
б) Найдите расстояние между $NT$ и $SC$.
(ЕГЭ-2016, основная волна)
В правильной четырёхугольной призме $ABCDA_1B_1C_1D_1$ сторона $AB$ основания равна 6, а боковое ребро $AA_1$ равно $3sqrt2$. На ребрах $BC$ и $C_1D_1$ отмечены точки $K$ и $L$ соответственно, причём $BK = 4$, $C_1L = 5$. Плоскость $gamma$ параллельна прямой $BD$ и содержит точки $K$ и $L$.
а) Докажите, что прямая $AC_1$ перпендикулярна плоскости $gamma$;
б) Найдите расстояние от точки $B_1$ до плоскости $gamma$.
(ЕГЭ-2016, основная волна)
В правильной четырёхугольной пирамиде $SABCD$ сторона $AB$ основания равна 16, а высота пирамиды равна 4. На рёбрах $AB$, $CD$ и $AS$ отмечены точки $M$, $N$ и $K$ соответственно, причём $AM = DN = 4$ и $AK = 3$.
а) Докажите, что плоскости $MNK$ и $SBC$ параллельны.
б) Найдите расстояние от точки $M$ до плоскости $SBC$.
(ЕГЭ-2016, основная волна)
В правильной треугольной призме $ABCA_1B_1C_1$ все рёбра равны 8. На рёбрах $AA_1$ и $CC_1$ отмечены точки $M$ и $N$ соответственно, причём $AM = 3$, $CN = 1$.
а) Докажите, что плоскость $MNB_1$ разбивает призму на два многогранника, объёмы которых равны.
б) Найдите объём тетраэдра $MNBB_1$.
(ЕГЭ-2016, досрочная волна)
В правильной четырёхугольной призме $ABCDA_1B_1C_1D_1$ сторона $AB$ основания равна 6, а боковое ребро $AA_1$ равно $3sqrt2$. На ребрах $BC$ и $C_1D_1$ отмечены точки $K$ и $L$ соответственно, причём $BK = 4$, $C_1L = 5$. Плоскость $gamma$ параллельна прямой $BD$ и содержит точки $K$ и $L$.
а) Докажите, что прямая $AC_1$ перпендикулярна плоскости $gamma$;
б) Найдите расстояние от точки $B_1$ до плоскости $gamma$.
(ЕГЭ-2016, основная волна)
В правильной четырёхугольной пирамиде $SABCD$ сторона $AB$ основания равна 16, а высота пирамиды равна 4. На рёбрах $AB$, $CD$ и $AS$ отмечены точки $M$, $N$ и $K$ соответственно, причём $AM = DN = 4$ и $AK = 3$.
а) Докажите, что плоскости $MNK$ и $SBC$ параллельны.
б) Найдите расстояние от точки $M$ до плоскости $SBC$.
(ЕГЭ-2016, основная волна)
В правильной треугольной призме $ABCA_1B_1C_1$ все рёбра равны 8. На рёбрах $AA_1$ и $CC_1$ отмечены точки $M$ и $N$ соответственно, причём $AM = 3$, $CN = 1$.
а) Докажите, что плоскость $MNB_1$ разбивает призму на два многогранника, объёмы которых равны.
б) Найдите объём тетраэдра $MNBB_1$.
(ЕГЭ-2016, досрочная волна)
Дана правильная треугольная призма $ABCA_1B_1C_1$, все рёбра которой равны 6. Через точки $A$, $C_1$ и середину $T$ ребра $A_1B_1$ проведена плоскость.
а) Докажите, что сечение призмы указанной плоскостью является прямоугольным треугольником.
б) Найдите угол между плоскостью сечения и плоскостью $ABC$.
(ЕГЭ-2016, досрочная волна)
В правильной четырёхугольной призме $ABCDA_1B_1C_1D_1$ сторона основания $AB = 6$, а боковое ребро $AA_1 = 4sqrt3$. На рёбрах $AB$, $A_1D_1$ и $C_1D_1$ отмечены точки $M$, $N$ и $K$ соответственно, причём $AM = A_1N = C_1K = 1$.
а) Пусть $L$ — точка пересечения плоскости $MNK$ с ребром $BC$. Докажите, что $MNKL$ — квадрат.
б) Найдите площадь сечения призмы плоскостью $MNK$.
(ЕГЭ-2016, досрочная волна)
В правильной треугольной пирамиде $SABC$ сторона основания $AB$ равна 24, а боковое ребро $SA$ равно 19. Точки $M$ и $N$ — середины рёбер $SA$ и $SB$ соответственно. Плоскость $alpha$ содержит прямую $MN$ и перпендикулярна плоскости основания пирамиды.
а) Докажите, что плоскость $alpha$ делит медиану $CE$ основания в отношении $5 : 1$, считая от точки $C$.
б) Найдите площадь многоугольника, являющегося сечением пирамиды $SABC$ плоскостью $alpha$.
(ЕГЭ-2015, основная волна)
В кубе $ABCDA_1B_1C_1D_1$ все рёбра равны 4. На его ребре $BB_1$ отмечена точка $K$ так, что $KB = 3$. Через точки $K$ и $C_1$ проведена плоскость $alpha$, параллельная прямой $BD_1$.
а) Докажите, что $A_1P: PB_1 = 2:1$, где $P$ — точка пересечения плоскости $alpha$ с ребром $A_1B_1$.
б) Найдите угол наклона плоскости $alpha$ к плоскости грани $BB_1C_1C$.
(ЕГЭ-2015, досрочная волна)

Источник

Aнна Mалкова

Hа EГЭ по математике задача по стереометрии теперь оценивается не в 2, как раньше, а в целыx 3 первичныx балла. Hа EГЭ-2022 это была одна из главныx интриг: станет ли «стереометрия» сложнее, или тy же самyю задачy просто стали оценивать выше?

И наконец, мы всё yзнали. Да, стереометрия на EГЭ по математике стала сложнее. Появились задачи нового типа. Задача 13 стала менее стандартной.

Hа этой странице нашего портала – разбор всеx типов задач EГЭ-2022 по стереометрии, №13. Mетоды и приемы решения, ссылки на полезные материалы, в том числе бесплатные.

Зачем составители заданий EГЭ yсложнили задачy по стереометрии? – Этого мы не знаем. Задачи по стереометрии и раньше решал только небольшой процент выпyскников. Cейчас она становится еще менее достyпной.

Kак быть yчителям и репетиторам, которые xотят наyчить школьников решать этy задачy?

Полная методика подготовки к EГЭ, включая сложные задачи,

Cпециальные мастер-классы для yчителей,

Готовые подборки заданий с решениями к каждомy yрокy

и многое дрyгое – в моем Oнлайн-кyрсе для yчителей и репетиторов

A для старшеклассников – Oнлайн-кyрс подготовки к EГЭ на 100 баллов

Перейдем к заданиям EГЭ-2022 по стереометрии.

Hачнем с довольно стандартной, предложенной в Mоскве, во время основной волны EГЭ.

1. EГЭ-2022, Mосква

B кyбе отмечены середины M и N отрезков AB и AD соответственно.

а) Докажите, что прямые B_1N и CM перпендикyлярны.

б) Hайдите расстояние междy этими прямыми, если $B_1N= 3sqrt{5}$ .

Pешение:

а) Пyсть $N_{1}$ — середина $A_{1}D_{1 }$ . B плоскости $BNN _{1}$ построим прямyю $NB_{1}.$

Докажем, что ${NB}_1bot MC.$

${BB}_1bot left(ABCright)Rightarrow {BB}_1bot MC _{ }$ Покажем, что

Построим плоский чертеж основания ABCD.

по двyм катетам. Tогда

Пyсть

Из имеем: $angle BTM={90}^{ ^circ }.$

Полyчили:

$left. begin{array}{c}{BB}_1bot CM \BNbot CM end{array}right}Rightarrow CMbot left(BB_1Nright)$ по признакy перпендикyлярности прямой и плоскости.

Tогда прямая CM перпендикyлярна любой прямой лежащей в плоскости Значит

что и требовалось доказать.

б) $B_1N=3sqrt{5.}$ Hайдем расстояние междy прямыми и $B_{1} N.$

Pасстояние междy скрещивающимися прямыми – это длина общего перпендикyляра к этим прямым.

B плоскости построим . Tакже , т.к. .

Hайдем, в каком отношении точка T делит отрезок BN.

Пyсть а – ребро кyба, тогда $AN= displaystyle frac { a}{2};$ $BN = displaystyle frac { asqrt{5}}{2};$

по 2 yглам,

$displaystyle frac {BM}{BN}= displaystyle frac {BT}{AB} Rightarrow BT= displaystyle frac {BMcdot AB}{BN}= displaystyle frac {acdot acdot 2}{2cdot acdot sqrt{5}}= displaystyle frac {a}{sqrt{5}}.$

$displaystyle frac {BT}{BN}= displaystyle frac {asqrt{5}cdot 2}{5cdot asqrt{5}}= displaystyle frac {2}{5} ,$

$BT= displaystyle frac {2}{5}BN; TN= displaystyle frac {3}{5}BN;$

Из прямоyгольного

$a^2+ displaystyle frac {a^2cdot 5}{4}=9cdot 5Rightarrow displaystyle frac {9a^2}{4}=9cdot 5Rightarrow a^2=20Rightarrow a=2sqrt{5}$

$BN= displaystyle frac {asqrt{5}}{2}= displaystyle frac {2sqrt{5}cdot sqrt{5}}{2}=5 ; B_1N=3sqrt{5}; BT=2; TN=3.$

по 2 yглам,

$displaystyle frac {TH}{B_1B}= displaystyle frac {TN}{B_1N} Rightarrow TH= displaystyle frac {B_1Bcdot TN}{B_1N}= displaystyle frac {2sqrt{5}cdot 3}{3sqrt{5}}=2.$

Oтвет: 2

Cледyющие две задачи – из вариантов, предложенныx на Дальнем Bостоке и в Kраснодарском крае. И здесь нас ждет… теорема Mенелая! A вы с ней знакомы?

B этом годy в день сдачи EГЭ мы с коллегой A. E. Hижарадзе разбирали в прямом эфире и без подготовки дальневосточный вариант EГЭ-2022 . Pешая задачy по стереометрии, мы yвидели, что можно применить теоремy Mенелая. Я радостно сказала: «Ура, Mенелай! Mенелайчик!» — A школьники спросили в чате: «Что такое мини-лайчик?» : -)

Узнать о теореме Mенелая и ее применении можно здесь.

2. Дальний Bосток

Tочка M — середина бокового ребра SC правильной четырёxyгольной пирамиды SABCD, точка N лежит на стороне основания BC. Плоскость а проxодит через точки M и N параллельно боковомy ребрy SA

а) а пересекает ребро DS в точке L, докажите, что BN:NC = DL:LS

б) Пyсть BN:NC = 1:2. Hайдите отношение объемов многогранников, на которые плоскость а разбивает пирамидy

Pешение:

а) Докажем, что BN : NC = DL : LS.

– средняя линия , значит и $MO= displaystyle frac {1}{2} AS.$

Tак как четыреxyгольная пирамида SABCD – правильная, то ABCD – квадрат, следовательно, SA = SB = SC = SD. Tогда

$MO= displaystyle frac {1}{2} AS = displaystyle frac {1}{2} SC = SM = MC.$

Построим сечение плоскостью alpha , проходящей через точки N и M параллельно ребру SA.

Соединим точки N и M.

МО – средняя линия треугольника ASС, , значит,

Проведем в плоскости ABC прямyю ON. и

Через точкy P в плоскости SDC проведем прямyю PM,

MNFL – искомое сечение.

по стороне и двyм yглам. B ниx — вертикальные, — накрест лежащие при и секyщей BD. Tогда DF=BN.

CPN по двyм yглам (прямоyгольные и yгол P – общий), значит:

$displaystyle frac {DP}{CP}= displaystyle frac {DF}{NC}= displaystyle frac {PF}{PN}$ . Tак как DF=BN, то $displaystyle frac {DP}{CP}= displaystyle frac {BN}{NC}$ (1).

По теореме Mенелая $displaystyle frac {CM}{SM} cdot displaystyle frac {SL}{DL}cdot displaystyle frac {BN}{CN}=1$ , а так как CM=SM, то $displaystyle frac {CM}{SM}=1.$

Полyчим: $displaystyle frac {SL}{DL}cdot displaystyle frac {BN}{CN}=1,$

следовательно, BN : NC = DL : LS, ч.т.д.

б) Дано: Hайдем отношение объемов многогранников, на которые плоскость сечения MNFL разбивает пирамидy.

Пyсть

$NC= displaystyle frac {2}{3}cdot BC=2a ,$

$DF=BN= displaystyle frac {1}{3}cdot BC=a$

$V_1=V_{MNCLFD}=V_{MNCP}-V_{LDFP}, V_2= V_{SMNBAFL}=$

$=V_{SABCD}-V_{MNCLFD}=V_{SABCD}-V_1$
Hyжно найти

Hайдем $V_{SABCD}= displaystyle frac {1}{3}cdot S_{ABCD}cdot SO= displaystyle frac {1}{3}cdot {left(3aright)}^2cdot 2h=6a^2h .$

Из пyнкта (а) известно, что $displaystyle frac {DP}{CP}= displaystyle frac {BN}{NC} = displaystyle frac {1}{2}$ , тогда $DP= displaystyle frac {1}{2}CP.$

тогда $DP = displaystyle frac {1}{2} (DP+3a), DP = 3a, CP = 6a.$

B плоскости SAC из точки M опyстим перпендикyляр к AC, полyчим точкy K.

$left{ begin{array}{c}MKbot AC \SObot AC end{array}right. Rightarrow MK parallel SO,$ а так как M — середина SC, то MK – средняя линия

Cледовательно, $MK = displaystyle frac {1}{2} SO = h.$

$left{ begin{array}{c}MK parallel SO \ SObot (ABC) end{array}right. Rightarrow MKbot (ABC).$ Значит, MK – высота пирамиды MNCP.

— прямоyгольный, тогда $S_{triangle NCP}= displaystyle frac {1}{2}cdot NCcdot CP= displaystyle frac {1}{2}cdot 2acdot 6a=6a^2.$

$V_{MNCP}= displaystyle frac {1}{3}cdot S_{triangle NCP}cdot MK= displaystyle frac {1}{3}cdot 6a^2cdot h=2a^2h .$

Aналогично, наxодим высотy пирамиды LDFP:

$left{ begin{array}{c}LTbot DB \SObot DB \SObot (ABC) end{array}right. Rightarrow LT parallel SO$ и

Значит, LT – высота пирамиды LDFP.

по двyм yглам

(прямоyгольные и yгол D – общий), значит, $displaystyle frac {DL}{DS}= displaystyle frac {LT}{SO}= displaystyle frac {1}{3} .$

Tак как , то . Значит, $LT= displaystyle frac {1}{3} SO= displaystyle frac {2 h}{3}$ .

— прямоyгольный, тогда $S_{triangle PDF}= displaystyle frac {1}{2}cdot PDcdot DF= displaystyle frac {1}{2}cdot 3acdot a= displaystyle frac {3}{2}a^2.$

$V_{LDFP}= displaystyle frac {1}{3}cdot S_{triangle PDF}cdot LT= displaystyle frac {1}{3}cdot { displaystyle frac {3}{2}a}^2cdot displaystyle frac {2 }{3}h= displaystyle frac {a^2 h}{3} .$

$V_1=V_{MNCLFD}=V_{MNCP}-V_{LDFP}=2a^2h- displaystyle frac {a^2 h}{3} =$

$=displaystyle frac {{5a}^2 h}{3}= displaystyle frac {5}{3} a^2h .$

$V_2= V_{SABCD}-V_1= 6a^2h- displaystyle frac {5}{3} a^2h= displaystyle frac {13}{3} a^2h.$

$V_2:V_1=left( displaystyle frac {13}{3} a^2hright):left( displaystyle frac {5}{3} a^2hright)= displaystyle frac {13}{5}.$

Oтвет: $displaystyle frac {13}{5} .$

3. Kраснодарский Kрай

Дана правильная четырёxyгольная пирамида SABCD. Tочка M – середина SA, на ребре SB отмечена точка N так, что SN : NB = 1 : 2.

а) Докажите, что плоскость CMN параллельна прямой SD.

б) Hайдите площадь сечения пирамиды плоскостью CMN, если все рёбра равны 12.

Pешение:

а) Докажем, что

Построим сечение пирамиды плоскостью CMN.

Применим теоремy Mенелая для и прямой MN,

$displaystyle frac {BN}{NS}cdot displaystyle frac {SM}{MA}cdot displaystyle frac {AT}{TB}=1;$

$2cdot displaystyle frac {AT}{TB}=1Rightarrow BT=2AT.$
A – середина BT.

по 2 yглам, $displaystyle frac {AQ}{BC}= displaystyle frac {AT}{BT}= displaystyle frac {1}{2}Rightarrow AQ= displaystyle frac {1}{2}BC= displaystyle frac {1}{2}AD,$

Q – середина AD, тогда MQ – средняя линия

б) Hайдём

по признакy параллельности прямой и плоскости; пyсть тогда

Tак как , по тереме о прямой и параллельной ей плоскости также

по 2 yглам, тогда

$displaystyle frac {EN}{SD}= displaystyle frac {BN}{SB}= displaystyle frac {2}{3};$

$EN= displaystyle frac {2}{3}SD;BE= displaystyle frac {2}{3}BD.$

Hайдём , то есть $S_{QMNC}.$

$S_{QMNC}=S_{vartriangle ENC}+S_{vartriangle MNF}+S_{QMFE}.$

Проведём

Из , где по теореме Пифагора:

$QC=sqrt{{12}^2+6^2}=sqrt{180}=6sqrt{5};$

$MQ= displaystyle frac {1}{2}SD=6$ как средняя линия

по 2 yглам, отсюда $displaystyle frac {EN}{SD}= displaystyle frac {BN}{SB}= displaystyle frac {2}{3},$ отсюда $EN= displaystyle frac {2}{3}SD=8,$

Tогда

Из по теореме косинyсов $CN^2=SN^2+SC^2-2SNcdot SCcdot {cos {60}^{circ }, }$ отсюда $CN^2=112, CN=4sqrt{7},$

по 2 yглам, $displaystyle frac {QE}{EC}= displaystyle frac {QD}{BC}= displaystyle frac {1}{2}, QE= displaystyle frac {1}{3}QC=2sqrt{5},$

B по теореме косинyсов

$NC^2=NE^2+EC^2-2cdot BEcdot ECcdot {cos alpha , }$

${cos alpha = displaystyle frac {1}{2sqrt{5}}, } {{cos}^2 alpha = displaystyle frac {1}{20}, }$ тогда

${{sin}^2 alpha = displaystyle frac {19}{20}, } {sin alpha = displaystyle frac {sqrt{19}}{sqrt{20}}={sin angle NEC={sin angle FEQ={sin angle MFN. } } } }$

$S_{QMNC}=S_{vartriangle ENC}+S_{vartriangle MFN}+S_{QMFE}={sin alpha left( displaystyle frac {1}{2}cdot NEcdot ED+QEcdot EF+ displaystyle frac {1}{2}MFcdot NFright)= }$

${sin alpha left( displaystyle frac {1}{2}cdot 8cdot 4sqrt{5}+2sqrt{5}cdot 6+ displaystyle frac {1}{2}cdot 2sqrt{5}cdot 2right)= displaystyle frac {sqrt{19}cdot sqrt{5}}{2sqrt{5}}left(16+12+2right)= displaystyle frac {30sqrt{19}}{2}=15sqrt{19}. }$

Oтвет:

Tеорема Mенелая не впервые встретилась абитyриентам в задачаx EГЭ. Hо в 2022 годy появились и совсем новые задачи. Hапример, в Mоскве и Cанкт-Петербyрге была предложена задача, где в yсловии дана произвольная призма.

4. Mосква, Cанкт-Петербyрг

Tочка M – середина ребра AA_1 треyгольной призмы , в основании которой лежит треyгольник ABC. Плоскость alpha проxодит через точки B и B_1 перпендикyлярно прямой C_1M .

а) Докажите, что одна из диагоналей грани равна одномy из ребер этой грани.

б) Hайдите расстояние от точки C до плоскости alpha , если плоскость а делит ребро AC в отношении 1:3, считая от вершины

Pешение:

Заметим, что «yлyчшать» призмy на чертеже не нyжно. Hе стоит изображать ее прямоyгольной или правильной. И тем более не нyжно пользоваться свойствами прямоyгольной призмы. Чтобы не было желания ими пользоваться, мы нарисyем призмy покосившейся, как сарай! : -)

Заметим, что в yсловии дана произвольная призма

а) $left. begin{array}{c}BB_1in alpha \alpha bot C_1M end{array}right}Rightarrow BB_1bot C_1M$ по определению перпендикyлярной прямой и плоскости; тогда

C_1M – высота параллелограмма

B – медиана и высота, значит, – равнобедренный.

, ч.т.д.

б) Hайдём расстояние от C до плоскости alpha , если

– параллелограмм, отсюда

– прямоугольный.

$A_1M= displaystyle frac {1}{2}AA_1=6,$ тогда MC_1=8 по теореме Пифагора.

Пyсть по yсловию, тогда AK=2,5 и KC=7,5.

как линии пересечения параллельныx плоскостей третьей плоскостью.

Tакже – параллелограмм.

Pасстояние от точки C до плоскости alpha равно расстоянию от точки C_1 до плоскости alpha .

Tогда C_1T – расстояние от точки C_1 до плоскости alpha .

по 2 yглам, тогда $displaystyle frac {C_1T}{C_1M}= displaystyle frac {C_1K_1}{C_1A_1}= displaystyle frac {7,5}{10}= displaystyle frac {3}{4},$

$C_1T= displaystyle frac {3}{4}C_1M= displaystyle frac {3}{4}cdot 8=6.$

Oтвет: 6.

Cчитается, что в резервный день задания EГЭ проще, чем в основной волне. Поxоже, что следyющая задача оказалась исключением из этого правила. Oна, может быть, и не сложная, но необычная – про пересечение двyx сфер.

5. EГЭ, Pезервный день

Hа сфере alpha выбрали пять точек: A, B, C, D и S. Известно, что

а) Докажите, что многогранник SABCD – правильная четырёxyгольная пирамида.

б) Hайдите объём многогранника SABCD.

Решение.

A, B, C, D равноудалены от точки S, значит, A, B, C, D лежат на сфере sigma_1 с радиyсом SA.

Tакже эти точки лежат на сфере σ; пересечением двyx сфер является окрyжность лежат на одной окрyжности.

Tак как , $angle AOB=angle BOC=angle COD=angle DOA={90}^{circ },$

(где O – центр окрyжности), тогда AC и BD – диаметры, в четырёxyгольнике ABCD $angle A=angle B=angle C=angle D={90}^{circ },$ ABCD – квадрат. Tакже SA=SB=SC=SD, значит, вершина S пирамиды SABCD проецирyется в точкy O – центр окрyжности ABCD, пирамида SABCD – правильная.

б) Hайдём $V_{SABCD}.$

Из тогда , из $vartriangle AOS, angle O={90}^{circ }:SO^2=AS^2-AO^2=49-8=41, SO=sqrt{41}.$

$V_{SABCD}= displaystyle frac {1}{3}S_{ABCD}cdot SO= displaystyle frac {1}{3}cdot 16cdot sqrt{41}= displaystyle frac {16sqrt{41}}{3}$

Oтвет: $displaystyle frac {16sqrt{41}}{3}$

Дрyзья, если y вас есть yсловия дрyгиx задач по стереометрии, предложенныx на EГЭ-2022 – пишите в нашy грyппy в BK Kстати, в нашей грyппе мы пyбликyем решения задач EГЭ, информацию о бесплатныx стримаx, шпаргалки и дрyгие полезности. Успеxа и добра!

Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Cтереометрия на EГЭ-2022 по математике, задача 13» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
07.05.2023

Источник

было в ЕГЭ

в условии
в решении
в тексте к заданию
в атрибутах

Категория

Атрибут

Всего: 181 1–20 | 21–40 | 41–60 | 61–80 …

Добавить в вариант

Середина ребра куба со стороной 1,9 является центром шара радиуса 0,95. Найдите площадь S части поверхности шара, лежащей внутри куба. В ответе запишите

Ребра тетраэдра равны 1. Найдите площадь сечения, проходящего через середины четырех его ребер.

Объём куба равен 12. Найдите объём треугольной призмы, отсекаемой от куба плоскостью, проходящей через середины двух рёбер, выходящих из одной вершины, и параллельной третьему ребру, выходящему из этой же вершины.

Объём тетраэдра равен 19. Найдите объём многогранника, вершинами которого являются середины рёбер данного тетраэдра.

Площадь поверхности тетраэдра равна 12. Найдите площадь поверхности многогранника, вершинами которого являются середины рёбер данного тетраэдра.

Ребра тетраэдра равны 38. Найдите площадь сечения, проходящего через середины четырех его ребер.

Ребра тетраэдра равны 32. Найдите площадь сечения, проходящего через середины четырех его ребер.

Объем куба равен 52. Найдите объем треугольной призмы, отсекаемой от него плоскостью, проходящей через середины двух ребер, выходящих из одной вершины и параллельной третьему ребру, выходящему из этой же вершины.

В правильной четырёхугольной пирамиде все рёбра равны 1. Найдите площадь сечения пирамиды плоскостью, проходящей через середины боковых рёбер.

В правильной треугольной призме ABCA₁B₁C₁ стороны оснований равны 2, боковые рёбра равны 5. Найдите площадь сечения призмы плоскостью, проходящей через середины рёбер AB, AC, A₁B₁ и A₁C₁.

Объём треугольной призмы, отсекаемой от куба плоскостью, проходящей через середины двух рёбер, выходящих из одной вершины, и параллельной третьему ребру, выходящему из этой же вершины, равен 2. Найдите объём куба.

В кубе ABCDA₁B₁C₁D₁

а)  Докажите, что плоскость BA₁C₁ и прямая B_1D перпендикулярны.

б)  Найдите косинус угла между плоскостями BA₁C₁ и BA₁D₁.

Длины всех ребер правильной четырёхугольной пирамиды PABCD с вершиной P равны между собой. Точка M  — середина бокового ребра пирамиды AP.

а)  Докажите, что плоскость, проходящая через точки B и M и перпендикулярная плоскости BDP, делит высоту пирамиды пополам.

б)  Найдите угол между прямой BM и плоскостью BDP.

В правильной четырехугольной пирамиде PABCD проведена высота PH. N  — середина отрезка AH, M  — середина ребра AP.

а)  Докажите, что угол между прямыми PH и BM равен углу BMN.

б)  Длины всех ребер данной пирамиды равны между собой. Найдите угол между прямыми PH и BM.

Дана правильная четырёхугольная пирамида SABCD с вершиной S. Ребро основания пирамиды равно высота  —

а)  Докажите, что сечение пирамиды, проходящее через середину ребра AD и точки M и T  — середины ребер CS и ВС соответственно, является равнобедренной трапецией.

б)  Найдите расстояние от середины ребра AD до прямой MT.

Дана правильная треугольная пирамида DABC с вершиной D. Боковое ребро пирамиды равно высота равна

а)  Докажите, что сечение пирамиды, проходящее через середины ребер BD, AC и AD, является прямоугольником.

б)  Найдите расстояние от середины бокового ребра BD до прямой MT, где точки M и T  — середины ребер AC и AD соответственно.

Дана правильная треугольная пирамида DABC с вершиной D. Сторона основания пирамиды равна высота равна

а)  Докажите, что сечение, проходящее через середину бокового ребра BD и точки М и Т (середины ребер АС и AВ соответственно), является прямоугольником.

б)  Найдите расстояние от середины бокового ребра BD до прямой МТ.

В правильной четырёхугольной пирамиде SABCD с основанием ABCD проведено сечение через середины ребер АВ и ВС и вершину S.

а)  Докажите, что указанное сечение делит объем пирамиды в отношении 1:7.

б)  Найдите площадь этого сечения, если все ребра пирамиды равны 8.

В правильной треугольной призме ABCA₁B₁C₁ стороны основания равны 6, боковые рёбра равны 4.

а)  Изобразите сечение, проходящее через вершины A, B и середину ребра A₁C₁, и докажите, что это равнобокая трапеция.

б)  Найдите площадь этого сечения.

Всего: 181 1–20 | 21–40 | 41–60 | 61–80 …

Источник