Как найти середину ребра правильного треугольника

Примечание: дробные числа записывайте
через точку, а не запятую.

Округлять до -го знака после запятой.

Середина отрезка. Координаты середины отрезка

В геометрических задачах часто можно столкнуться с необходимостью найти середину отрезка заданного координатами точек его концов, например в задачах поиска медианы, средней линии, .

Каждая координата середины отрезка равна полусумме соответствующих координат концов отрезка.

Формулы вычисления расстояния между двумя точками:

• Формула вычисления координат середины отрезка с концами A( x_a , y_a ) и B( x_b , y_b ) на плоскости:

xc =	xa + xb	yc =	ya + yb
2	2

Формула вычисления координат середины отрезка с концами A( x_a , y_a , z_a ) и B( x_b , y_b , z_b ) в пространстве:

xc =	xa + xb	yc =	ya + yb	zc =	za + zb
2	2	2

Примеры задач на вычисление середины отрезка

Примеры вычисления координат середины отрезка на плоскости

xc =	xa + xb	=	-1 + 6	=	5	= 2.5
2	2	2

yc =	ya + yb	=	3 + 5	=	8	= 4
2	2	2

Примеры вычисления координат середины отрезка в пространстве

xc =	xa + xb	=	-1 + 6	=	5	= 2.5
2	2	2

yc =	ya + yb	=	3 + 5	=	8	= 4
2	2	2

zc =	za + zb	=	1 + (-3)	=	-2	= -1
2	2	2

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Векторы в пространстве и метод координат

Существует два способа решения задач по стереометрии

Первый — классический — требует отличного знания аксиом и теорем стереометрии, логики, умения построить чертеж и свести объемную задачу к планиметрической. Способ хорош тем, что развивает мозги и пространственное воображение.

Другой метод — применение векторов и координат. Это простые формулы, алгоритмы и правила. Он очень удобен, особенно когда времени до экзамена мало, а решить задачу хочется.

Если вы освоили векторы на плоскости и действия с ними — то и с векторами в пространстве разберетесь. Многие понятия окажутся знакомыми.

Система координат в пространстве

Выберем начало координат. Проведем три взаимно перпендикулярные оси X, Y и Z. Зададим удобный масштаб.

Получилась система координат в трехмерном пространстве. Теперь каждая его точка характеризуется тремя числами — координатами по X, Y и Z. Например, запись M(−1; 3; 2) означает, что координата точки M по X (абсцисса) равна −1, координата по Y (ордината) равна 3, а координата по Z (аппликата) равна 2.

Векторы в пространстве определяются так же, как и на плоскости. Это направленные отрезки, имеющие начало и конец. Только в пространстве вектор задается тремя координатами x, y и z:

Как найти координаты вектора? Как и на плоскости — из координаты конца вычитаем координату начала.

Длина вектора в пространстве – это расстояние между точками A и B. Находится как корень квадратный из суммы квадратов координат вектора.

Пусть точка M – середина отрезка AB. Ее координаты находятся по формуле:

Для сложения векторов применяем уже знакомые правило треугольника и правило параллелограмма

Сумма векторов, их разность, произведение вектора на число и скалярное произведение векторов определяются так же, как и на плоскости. Только координат не две, а три. Возьмем векторы и .

Произведение вектора на число:

Скалярное произведение векторов:

Косинус угла между векторами:

Последняя формула удобна для нахождения угла между прямыми в пространстве. Особенно если эти прямые – скрещиваются. Напомним, что так называются прямые, которые не параллельны и не пересекаются. Они лежат в параллельных плоскостях.

1. В кубе ABCDA₁B₁C₁D₁ точки E и K — середины ребер соответственно A₁B₁ и B₁C₁. Найдите косинус угла между прямыми AE и BK.

Если вам достался куб — значит, повезло. Он отлично вписывается в прямоугольную систему координат. Строим чертеж:

Длина ребра куба не дана. Какой бы она ни была, угол между AE и BK от нее не зависит. Поэтому возьмем единичный куб, все ребра которого равны 1.

Прямые AE и BK — скрещиваются. Найдем угол между векторами и . Для этого нужны их координаты.

Запишем координаты векторов:

и найдем косинус угла между векторами и :

2. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точки E, K — середины ребер SB и SC соответственно. Найдите косинус угла между прямыми AE и BK.

Лучше всего выбрать начало координат в центре основания пирамиды, а оси X и Y сделать параллельными сторонам основания.

Координаты точек A, B и C найти легко:

Из прямоугольного треугольника AOS найдем

Координаты вершины пирамиды:

Точка E — середина SB, а K — середина SC. Воспользуемся формулой для координат середины отрезка и найдем координаты точек E и K.

Найдем координаты векторов и

и угол между ними:

Покажем теперь, как вписать систему координат в треугольную призму:

3. В правильной треугольной призме ABCA₁B₁C₁, все ребра которой равны 1, точка D — середина ребра A₁B₁. Найдите косинус угла между прямыми AD и BC₁

Пусть точка A — начало координат. Возьмем ось X параллельно стороне BC, а ось Y перпендикулярно ей. Другими словами, на оси Y будет лежать отрезок AH, являющийся высотой треугольника ABC. Нарисуем отдельно нижнее основание призмы.

Запишем координаты точек:

Точка D — середина A₁B₁. Значит, пользуемся формулами для координат середины
отрезка.

Найдем координаты векторов и , а затем угол между ними:

Смотрите, как легко с помощью векторов и координат найти угол между прямыми. А если требуется найти угол между плоскостями или между прямой и плоскостью? Для решения подобных задач нам понадобится уравнение плоскости в пространстве.

Плоскость в пространстве задается уравнением:

Здесь числа A, B и C — координаты вектора, перпендикулярного этой плоскости. Его называют нормалью к плоскости.

Вместо x, y и z можно подставить в уравнение координаты любой точки, принадлежащей данной плоскости. Получится верное равенство.

Плоскость в пространстве можно провести через любые три точки, не лежащие на одной прямой. Поэтому для того, чтобы написать уравнение плоскости, берем координаты трех принадлежащих ей точек. Подставляем их по очереди в уравнение плоскости. Решаем полученную систему.

Покажем, как это делается.

Напишем уравнение плоскости, проходящей через точки M (1; 0; 1), N (2; −2; 0) и K (4; 1; 2).

Уравнение плоскости выглядит так:

Подставим в него по очереди координаты точек M, N и K.

То есть A + C + D = 0.

Аналогично для точки K:

Получили систему из трех уравнений:

В ней четыре неизвестных: A, B, C и D. Поэтому одну из них мы выберем сами, а другие выразим через нее. Правило простое — вместо одной из переменных можно взять любое число, не равное нулю.

Пусть, например, D = −2. Тогда:

Выразим C и B через A и подставим в третье уравнение:

Решив систему, получим:

Уравнение плоскости MNK имеет вид:

Умножим обе части уравнения на −3. Тогда коэффициенты станут целыми:

Вектор — это нормаль к плоскости MNK.

Уравнение плоскости, проходящей через заданную точку имеет вид:

Угол между плоскостями равен углу между нормалями к этим плоскостям:

Не правда ли, знакомая формула? Скалярное произведение нормалей поделили на произведение их длин.

Заметим, что при пересечении двух плоскостей вообще-то образуется четыре угла.

Мы берем меньший из них. Поэтому в формуле стоит модуль скалярного произведения — чтобы косинус угла был неотрицателен.

4. В кубе ABCDA₁B₁C₁D₁ точки E и F — середины ребер соответственно A₁B₁ и A₁D₁. Найдите тангенс угла между плоскостями AEF и BDD₁.

Строим чертеж. Видно, что плоскости AEF и BDD₁ пересекаются где-то вне куба. В классическом решении пришлось бы строить линию их пересечения. Но векторно-координатный метод значительно всё упрощает. Не будем ломать голову над тем, по какой прямой пересекаются плоскости. Просто отметим координаты нужных нам точек и найдем угол между нормалями к плоскостям AEF и BDD₁.

Сначала — нормаль к плоскости BDD₁. Конечно, мы можем подставить координаты точек B, D и D₁ в уравнение плоскости и найти коэффициенты, которые и будут координатами вектора нормали. А можем сделать хитрее — увидеть нужную нормаль прямо на чертеже. Ведь плоскость BDD₁ — это диагональное сечение куба. Вектор перпендикулярен этой плоскости.

Итак, первый вектор нормали у нас уже есть:

Напишем уравнение плоскости AEF.

Берем уравнение плоскости и по очереди подставляем в него, вместо x, y и z, соответствующие координаты точек A, E и F.

Пусть С = -1. Тогда A = B = 2.

Уравнение плоскости AEF:

Нормаль к плоскости AEF:

Найдем угол между плоскостями:

5. Основание прямой четырехугольной призмы BCDA₁B₁C₁D₁ — прямоугольник ABCD, в котором AB = 5, AD = √33. Найдите тангенс угла между плоскостью грани AA₁D₁D и плоскостью, проходящей через середину ребра CD перпендикулярно прямой B₁D, если расстояние между прямыми A₁C₁ и BD равно √3.

Эта задача наглядно показывает, насколько векторный метод проще классического. Попробуйте, для разнообразия, построить необходимые сечения и провести все доказательства — как это делается в «классике»

Строим чертеж. Прямую четырехугольную призму можно по-другому назвать «параллелепипед».

Замечаем, что длина и ширина параллелепипеда у нас есть, а вот высота — вроде не дана. Как же ее найти?

«Расстояние между прямыми A₁C₁ и BD равно √3». Прямые A₁C₁ и BD скрещиваются. Одна из них — диагональ верхнего основания, другая — диагональ нижнего. Вспомним, что расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра. Общий перпендикуляр к A₁C₁ и BD — это, очевидно, OO₁, где O — точка пересечения диагоналей нижнего основания, O₁ — точка пересечения диагоналей верхнего. А отрезок OO₁ и равен высоте параллелепипеда.

Плоскость AA₁ D₁ D — это задняя грань призмы на нашем чертеже. Нормаль к ней — это любой вектор, перпендикулярный задней грани, например, вектор или, еще проще, вектор .

Осталась еще «плоскость, проходящая через середину ребра CD перпендикулярно прямой B₁D». Но позвольте, если плоскость перпендикулярна прямой B₁D — значит, B₁D и есть нормаль к этой плоскости! Координаты точек B₁ и D известны:

Координаты вектора — тоже:

Находим угол между плоскостями, равный углу между нормалями к ним:

Зная косинус угла, находим его тангенс по формуле

Получим:

Ответ:

Угол между прямой m и плоскостью α тоже вычисляется с помощью скалярного произведения векторов.

Пусть — вектор, лежащий на прямой m (или параллельный ей), — нормаль к плоскости α.

Находим синус угла между прямой m и плоскостью α по формуле:

6. В кубе ABCDA₁B₁C₁D₁ точка E — середина ребра A₁B₁. Найдите синус угла между прямой AE и плоскостью BDD₁.

Как всегда, рисуем чертеж и выбираем систему координат

Находим координаты вектора .

Нужно ли нам уравнение плоскости BDD₁? В общем-то, без него можно обойтись. Ведь эта плоскость является диагональным сечением куба, а значит, нормалью к ней будет любой вектор, ей перпендикулярный. Например, вектор .

Найдем угол между прямой и плоскостью:

Ответ:

Расстояние от точки M с координатами x₀, y₀ и z₀ до плоскости α, заданной уравнением Ax + By + Cz + D = 0, можно найти по формуле:

7. В основании прямоугольного параллелепипеда BCDA₁B₁C₁D₁ лежит прямоугольник ABCD со сторонами AB = , AD = . Высота параллелепипеда AA₁ = . Найдите расстояние от точки A до плоскости A₁DB.

Построим чертеж и выпишем координаты точек:

Запишем уравнение плоскости A₁DB. Вы помните, как это делается — по очереди подставляем координаты точек A₁, D и B в уравнение A_x + B_e + C_z + D

Решим эту систему. Выберем

Тогда

Уравнение плоскости A₁DB имеет вид:

Дальше все просто. Находим расстояние от точки A до плоскости A₁DB:

В некоторых задачах по стереометрии требуется найти расстояние от прямой до параллельной ей плоскости. В этом случае можно выбрать любую точку, принадлежащую данной прямой.

Как найти середину треугольника

Геометрические задачи на построение, в которых использовались только циркуль и линейка, зародились еще в древней Греции. Уже во времена Евклида и Платона математики умели решать множество геометрических задач. Например, строить правильные треугольники, квадраты, разбивать отрезки на равные части и находить центр треугольника.

Вам понадобится

• — лист бумаги или тетрадь (лучше в клеточку)
• — линейка
• — карандаш
• — циркуль

Инструкция

Отметьте на плоскости три точки А, В и С, причём так, чтобы они не лежали на одной прямой. Соедините полученные точки между собой отрезками АВ, ВС и СВ. У вас получился треугольник АВС – геометрическая фигура, имеющая три стороны, три вершины и три угла.

Найдите середину отрезка АВ. Для этого возьмите циркуль и проведите две окружности одинакового радиуса, равного отрезку АВ с центрами в вершинах А и В. Найдите точки пересечения P и Q двух построенных окружностей. С помощью линейки постройте отрезок, концами которого будут точки P и Q. Найдите искомую середину отрезка АВ – ею будет являться точка пересечения стороны АВ с отрезком PQ.

Найдите середины стороны ВС. Для этого возьмите циркуль и проведите две окружности одинакового радиуса равного отрезку ВС с центрами в вершинах В и С. Найдите точки пересечения H и G двух построенных окружностей. С помощью линейки постройте отрезок, концами которого будут точки H и G. Найдите искомую середину отрезка BC – ею будет являться точка пересечения стороны BC с отрезком HG.

Найдите середины стороны СА. Для этого возьмите циркуль и проведите две окружности одинакового радиуса, равного отрезку СА с центрами в вершинах С и А. Найдите точки пересечения M и N двух построенных окружностей. С помощью линейки постройте отрезок, концами которого будут точки M и N. Найдите искомую середину отрезка СА – ею будет являться точка пересечения стороны СА с отрезком MN.

Постройте медианы треугольника. Для этого с помощью линейки и карандаша проведите отрезки, соединяющие вершины треугольника с серединами противолежащих сторон этого треугольника. В результате правильно построения медианы должны пересечься в одной точке.

Найдите центр треугольника. Им будет являться точка пересечения медиан. Центр треугольника ещё по-другому называют центром тяжести.

Полезный совет

Помните о точности построений, иначе вы не получите желаемого результата.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

• Задание 1

  В пра­виль­ной тре­уголь­ной приз­ме  бо­ко­вое ребро равно  а ребро ос­но­ва­ния равно 1. Точка D — се­ре­ди­на ребра BB₁. Най­ди­те объём пя­ти­гран­ни­ка .

  Разбор задания
  Свернуть

• Задание 2

  В пра­виль­ной тре­уголь­ной пи­ра­ми­де SABC с ос­но­ва­ни­ем ABC угол ASB равен . На ребре SC взята точка M так, что AM — бис­сек­три­са угла SAC. Пло­щадь се­че­ния пи­ра­ми­ды, про­хо­дя­ще­го через точки A, M и B, равна Най­ди­те сто­ро­ну ос­но­ва­ния.

  Разбор задания
  Свернуть

  Нуж­ное се­че­ние — тре­уголь­ник AMB.

  Рас­смот­рим тре­уголь­ник ASC. Он рав­но­бед­рен­ный, и Зна­чит,

  Рас­смот­рим те­перь тре­уголь­ник CAM. Сумма его углов , зна­чит, Сле­до­ва­тель­но, тре­уголь­ник CAM рав­но­бед­рен­ный, и по­это­му AC=AM. Ана­ло­гич­но на­хо­дим, что BM=BC.

  Таким об­ра­зом, тре­уголь­ник AMB рав­но­сто­рон­ний, и его сто­ро­на AB од­но­вре­мен­но яв­ля­ет­ся сто­ро­ной ос­но­ва­ния. По усло­вию со­ста­вим урав­не­ние от­ку­да AB = 10.

  Ответ: 

• Задание 3

  Пло­щадь бо­ко­вой по­верх­но­сти пра­виль­ной четырёхуголь­ной пи­ра­ми­ды SABCD равна 108, а пло­щадь пол­ной по­верх­но­сти этой пи­ра­ми­ды равна 144. Най­ди­те пло­щадь се­че­ния, про­хо­дя­ще­го через вер­ши­ну S этой пи­ра­ми­ды и через диа­го­наль её ос­но­ва­ния.

  Разбор задания
  Свернуть

  Пло­щадь ос­но­ва­ния пи­ра­ми­ды равна 144 − 108 = 36, по­это­му AB = 6 (в основании квадрат). Пло­щадь бо­ко­вой грани равна  Пусть SM — вы­со­та грани SAB. Тогда  по­это­му SM = 9. Пусть SH — вы­со­та пи­ра­ми­ды. Имеем

  

  Тогда

  Ответ: 

• Задание 4

  В пра­виль­ной тре­уголь­ной приз­ме , все рёбра ко­то­рой равны 1, най­ди­те рас­сто­я­ние между пря­мы­ми  и .

  Разбор задания
  Свернуть

• Задание 5

  Дана пра­виль­ная тре­уголь­ная пи­ра­ми­да DABC с вер­ши­ной D. Сто­ро­на ос­но­ва­ния пи­ра­ми­ды равна , вы­со­та равна . Най­ди­те рас­сто­я­ние от се­ре­ди­ны бо­ко­во­го ребра BD до пря­мой МТ, где точки М и Т — се­ре­ди­ны ребер АС и AВ со­от­вет­ствен­но.

  Разбор задания
  Свернуть

  Пусть Q — се­ре­ди­на ребра CD; P — се­ре­ди­на ребра BD. По тео­ре­ме о сред­ней линии тре­уголь­ни­ка сле­до­ва­тель­но, точки M, T, P, Q лежат в одной плос­ко­сти.

   Далее,  сле­до­ва­тель­но, точки M, T, P, Q яв­ля­ют­ся вер­ши­на­ми па­рал­ле­ло­грам­ма. Кроме того,  а по тео­ре­ме о трёх пер­пен­ди­ку­ля­рах, так как по­лу­чим  по­это­му этот па­рал­ле­ло­грамм — пря­мо­уголь­ник. Зна­чит, ис­ко­мое рас­сто­я­ние есть длина от­рез­ка PT. Проведём высоту DO, тогда точка O есть точка пересечения диагоналей квадрата, следовательно, от­ре­зок AO равен

  По тео­ре­ме Пи­фа­го­ра 

  

  Ответ: 

• Задание 6

  В пра­виль­ной ше­сти­уголь­ной пи­ра­ми­де SABCDEF, сто­ро­ны ос­но­ва­ния ко­то­рой равны 1, а бо­ко­вые рёбра равны 2, най­ди­те рас­сто­я­ние от точки C до пря­мой SA.

  Разбор задания
  Свернуть

• Задание 7

  Сто­ро­на ос­но­ва­ния пра­виль­ной тре­уголь­ной приз­мы  равна 2, а диа­го­наль бо­ко­вой грани равна Най­ди­те угол между плос­ко­стью  и плос­ко­стью ос­но­ва­ния приз­мы.

  Разбор задания
  Свернуть

• Задание 8

  В пра­виль­ной четырёхуголь­ной пи­ра­ми­де SABCD с ос­но­ва­ни­ем ABCD точка M — се­ре­ди­на ребра SA, точка K — се­ре­ди­на ребра SC. Най­ди­те угол между плос­ко­стя­ми BMK и ABC, если AB = 8, SC = 6.

  Разбор задания
  Свернуть

  Про­ведём из точки B пер­пен­ди­ку­ляр BQ к MK, Q — се­ре­ди­на MK. Точка Q яв­ля­ет­ся се­ре­ди­ной вы­со­ты SO. Пря­мая MK па­рал­лель­на пря­мой пе­ре­се­че­ния плос­ко­стей, ,  (так как OB перпендикулярна параллельной MK прямой AC). Сле­до­ва­тель­но,  — ли­ней­ный угол ис­ко­мо­го угла. Найдём стороны прямоугольного треугольника QBO.

  

  

  

  Зна­чит,

  

  Ответ: 

• Задание 9

  Дана пря­мая приз­ма . Ос­но­ва­ние приз­мы — ромб со сто­ро­ной 8 и ост­рым углом . Вы­со­та приз­мы равна 6. Най­ди­те угол между плос­ко­стью  и плос­ко­стью ABD.

  Разбор задания
  Свернуть

  По­стро­им се­че­ние приз­мы плос­ко­стью . По­лу­чим па­рал­ле­ло­грамм . Из точки D про­ведём пер­пен­ди­ку­ляр DH к пря­мой AB. Тогда по тео­ре­ме о трех пер­пен­ди­ку­ля­рах . Плос­кий угол  — ис­ко­мый. Сле­до­ва­тель­но,

  

  Ответ: 

• Задание 10

  Длины всех ребер пра­виль­ной четырёхуголь­ной пи­ра­ми­ды PABCD с вер­ши­ной P равны между собой. Най­ди­те угол между пря­мой BM и плос­ко­стью BDP, если точка M — се­ре­ди­на бо­ко­во­го ребра пи­ра­ми­ды AP.

  Разбор задания
  Свернуть

• Задание 11

  Длина ребра пра­виль­но­го тет­ра­эд­ра ABCD равна 1. Най­ди­те угол между пря­мы­ми DM и CL, где M — се­ре­ди­на ребра BC, L — се­ре­ди­на ребра AB.

  Разбор задания
  Свернуть

• Задание 12

  В пра­виль­ной ше­сти­уголь­ной пи­ра­ми­де SABCDEF сто­ро­ны ос­но­ва­ния ко­то­рой равны 1, а бо­ко­вые ребра равны 2, най­ди­те ко­си­нус угла между пря­мы­ми SB и AD.

  Разбор задания
  Свернуть

  Сведём угол между скрещивающимися прямыми к плоскому углу. Пря­мая AD па­рал­лель­на пря­мой BC. Сле­до­ва­тель­но, ис­ко­мый угол равен углу SBC. В рав­но­бед­рен­ном тре­уголь­ни­ке SBC про­ведём ме­ди­а­ну и вы­со­ту SM. Имеем:

  

  Из пря­мо­уголь­но­го тре­уголь­ни­ка SBM по­лу­ча­ем: 

  Ответ: 

• Задание 13

  В конус, ра­ди­ус ос­но­ва­ния ко­то­ро­го равен 3, впи­сан шар ра­ди­у­са 1,5.

  а) Изоб­ра­зи­те осе­вое се­че­ние ком­би­на­ции этих тел.

  б) Най­ди­те от­но­ше­ние пло­ща­ди пол­ной по­верх­но­сти ко­ну­са к пло­ща­ди по­верх­но­сти шара.

  Разбор задания
  Свернуть

  Осе­вым се­че­ни­ем яв­ля­ет­ся рав­но­бед­рен­ный тре­уголь­ник ABC бо­ко­вые сто­ро­ны ко­то­ро­го яв­ля­ют­ся об­ра­зу­ю­щи­ми ко­ну­са, а ос­но­ва­ни­ем — его диа­метр, и впи­сан­ная в тре­уголь­ник окруж­ность, ра­ди­ус ко­то­рой равен ра­ди­у­су шара (см. рис.).

   Введём обо­зна­че­ния, как по­ка­за­но на ри­сун­ке. Пусть O — центр впи­сан­ной окруж­но­сти, от­ре­зок CO — бис­сек­три­са угла ACB и пусть  имеем:

   

  Тогда  Для пло­ща­дей по­верх­но­стей ко­ну­са и шара имеем: Тем самым, ис­ко­мое от­но­ше­ние равно или 8:3.

  Ответ: 8:3

• Задание 14

  В пра­виль­ную четырёхуголь­ную пи­ра­ми­ду, бо­ко­вое ребро ко­то­рой равно 17, а вы­со­та равна 7, впи­са­на сфера. (Сфера ка­са­ет­ся всех гра­ней пи­ра­ми­ды.) Най­ди­те пло­щадь этой сферы.

  Разбор задания
  Свернуть

  Пусть MH — вы­со­та пра­виль­ной четырёхуголь­ной пи­ра­ми­ды MABCD с вер­ши­ной M, тогда тре­уголь­ник AMH — пря­мо­уголь­ный,  от­ку­да

  

  Тре­уголь­ник ABH — пря­мо­уголь­ный рав­но­бед­рен­ный, сле­до­ва­тель­но, В тре­уголь­ни­ке AMB вы­со­та

  В рав­но­бед­рен­ном пря­мо­уголь­ном тре­уголь­ни­ке ABH вы­со­та  (формула работает для медианы в прямоугольном треугольнике, но в равнобедренном треугольнике высота, проведённая к основанию, совпадает с медианой).

  Центр O сферы, впи­сан­ной в пра­виль­ную четырёхуголь­ную пи­ра­ми­ду, лежит на её вы­со­те MH, точка K ка­са­ния сферы и бо­ко­вой грани AMB лежит на от­рез­ке MN. Тре­уголь­ни­ки MOK и MNH по­доб­ны, по­это­му

  

  

  где r — ра­ди­ус сферы.

  Пло­щадь сферы

  Ответ:  

• Задание 15

  В пра­виль­ную ше­сти­уголь­ную пи­ра­ми­ду, бо­ко­вое ребро ко­то­рой равно 10, а вы­со­та равна 6, впи­са­на сфера. (Сфера ка­са­ет­ся всех гра­ней пи­ра­ми­ды.) Най­ди­те пло­щадь этой сферы.

  Разбор задания
  Свернуть

  Пусть MH — вы­со­та пра­виль­ной ше­сти­уголь­ной пи­ра­ми­ды MABCDEF с вер­ши­ной M, тогда тре­уголь­ник AMH пря­мо­уголь­ный, MA=10, MH=6 от­ку­да

   

  Тре­уголь­ник ABH рав­но­сто­рон­ний, сле­до­ва­тель­но, AB=AH=8. В тре­уголь­ни­ке AMB вы­со­та

  

  В пра­виль­ном тре­уголь­ни­ке AHB вы­со­та

  Центр O сферы, впи­сан­ной в пра­виль­ную ше­сти­уголь­ную пи­ра­ми­ду, лежит на её вы­со­те MH, точка K ка­са­ния сферы и бо­ко­вой грани AMB лежит на от­рез­ке MN. Тре­уголь­ни­ки MOK и MNH по­доб­ны, по­это­му

  

  где r — ра­ди­ус сферы. Пло­щадь сферы 

  Ответ:  

• а) В плос­ко­сти  через точку К про­ве­дем пря­мую, па­рал­лель­но . Пусть эта пря­мая пе­ре­се­ка­ет диа­го­наль  в точке L. В плос­ко­сти ос­но­ва­ния  про­ве­дем пря­мую , пусть она пе­ре­се­ка­ет сто­ро­ну  в точке P. Тре­уголь­ник — се­че­ние, про­хо­дя­щее через точки К и па­рал­лель­но пря­мой . Дей­стви­тель­но, пря­мая  па­рал­лель­на плос­ко­сти се­че­ния, так как па­рал­лель­на ле­жа­щей в нем пря­мой KL.

  В плос­ко­сти ос­но­ва­ния через точку  про­ве­дем пря­мую па­рал­лель­но . Пусть она пе­ре­се­ка­ет в точке М. За­ме­тим, что  и , по­это­му . По тео­ре­ме Фа­ле­са па­рал­лель­ные пря­мые вы­се­ка­ют на сто­ро­нах угла  про­пор­ци­о­наль­ные от­рез­ки, по­это­му . Что и тре­бо­ва­лось до­ка­зать.

  б) Пусть те­перь точка N — ос­но­ва­ние вы­со­ты  тре­уголь­ни­ка , яв­ля­ю­ще­го­ся про­ек­ци­ей на­клон­ной PN на плос­кость . Тогда угол — ли­ней­ный угол ис­ко­мо­го дву­гран­но­го угла. Имеем: 

  

  

  

  Тем самым,

  Ответ:  

Как найти среднюю линию треугольника

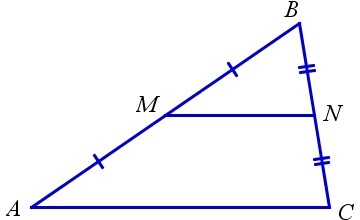
​Средняя линия треугольника — отрезок, соединяющий середины двух его сторон.

Свойства и признаки

Признак средней линии: если отрезок в треугольнике проходит через середину одной из его сторон, пересекает вторую и параллелен третьей, то этот отрезок называется средней линией данного треугольника.

Свойства:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

1. Равна половине длины основания и параллельна ему.
2. Отсекает треугольник, подобный данному с коэффициентом 1/2; его площадь равна четверти площади данного.
3. Три средние линии разделяют исходную фигуру на четыре равных треугольника. Центральный из них называют дополнительным треугольником.
4. Три средние линии разделяют исходный прямоугольный треугольник на четыре равных прямоугольных треугольника.

Формула для расчета

Теорема

Средняя линия треугольника параллельна основанию и равна её половине.

Доказательство

(A_1C_1) — средняя линия

Рассмотрим (triangle BA_1C_1) и (triangle BAC) :

Из этого следует, что треугольники подобны по двум пропорциональным сторонам и углу между ними.

Следовательно, (angle BA_1C_1=angle BAC) , как соответственные элементы подобных треугольников. Следовательно (A_1C_1parallel AC) по признаку параллельности.

Кроме того, из подобия следует, что (frac=frac12)

Примечание

Данная формула одинаково работает для любого треугольника: равнобедренного, равностороннего (правильного).

Задачи на использование теоремы

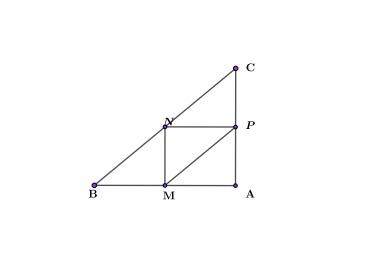
Задача 1

В прямоугольном треугольнике ABC проведены средние линии: MN; NP; MP. При этом MN=NP=2. Найти площадь треугольника ABC.

Рассмотрим прямоугольный треугольник NMP:

(S_=frac12times MNtimes NP=frac12times2times2=2)

Все маленькие треугольники равны, следовательно (S_=2times4=8)

Задача 2

Площадь треугольника ABC равна 8. MN — средняя линия. Необходимо вычислить площадь треугольника BMN.

Задача 3

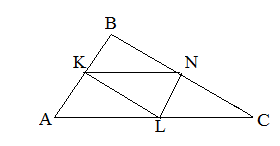
В треугольнике ABC точки M, N, K – середины сторон AB, BC, AC соответственно, MN=12, MK=10, KN=8. Необходимо узнать периметр треугольника ABC.

Средняя линия треугольника

Найдем площадь треугольника :

Так как средняя линия отсекает треугольник , площадь которого равна одной четвёртой площади исходного треугольника , то площадь треугольника равна:

см см см

Теперь можно найти периметр треугольника как сумму длин всех его сторон:

см

Что такое средняя линия треугольника

В данной публикации мы рассмотрим определение, свойства и признак средней линии треугольника, а также разберем пример решения задачи для лучшего понимания теоретического материала.

• Определение средней линии треугольника
• Свойства средней линии треугольника
  • Свойство 1
  • Свойство 2
  • Свойство 3
  • Свойство 4

  Определение средней линии треугольника

  Отрезок, который соединяет середины двух сторон треугольника, называется его средней линией.

  

  • KL – средняя линия треугольника ABC
  • K – середина стороны AB: AK = KB
  • L – середина стороны BC: BL = LC

  Свойства средней линии треугольника

  Свойство 1

  Средняя линия треугольника параллельна одной из его сторон (которую не пересекает) и в два раза меньше этой стороны.

  На рисунке выше:

  • KL параллельна AC
  • KL = 1 /₂ ⋅ AC

  Свойство 2

  Средняя линия треугольника отсекает от него подобный треугольник (в соотношении 1:2), площадь которого в 4 раза меньше исходного.

  На рисунке выше:

  • △KBL ∼ △ABC (подобие по пропорциональности всех сторон)
  • Стороны △KBL в два раза меньше соответствующих сторон △ABC:
    AB = 2KB, BC = 2BL, AC = 2KL.
  • S_△ABC = 4 ⋅ S_△KBL

  Свойство 3

  В любом треугольнике можно провести три средние линии.

  

  KL, KM и ML – средние линии треугольника ABC.

  • KL || AC, KL = 1 /₂ ⋅ AC
  • KM || BC, KM = 1 /₂ ⋅ BC
  • ML || AB, ML = 1 /₂ ⋅ AB

  Свойство 4

  Три средние линии треугольника делят его на 4 равных по площади треугольника.

  

  Признак средней линии треугольника

  Отрезок, проходящий через середину одной из сторон треугольника, пресекающий вторую и параллельный третьей стороне, является средней линией этого треугольника.

  Пример задачи

  Дан треугольник, две стороны которого равны 6 и 8 см. Найдите длину средней линии, соединяющей эти стороны.

  Треугольник с заданными сторонами является прямоугольным, причем известные значения – это длины катетов. Средняя линия, которая соединяет катеты, параллельна гипотенузе и равна половине ее длины.

  

  Мы можем найти гипотенузу, воспользовавшись теоремой Пифагора.

  BC 2 = AB 2 + AC 2 = 6 2 + 8 2 = 100.
  BC = 10.

  Таким образом, средняя линия LM = 1 /₂ ⋅ BC = 1 /₂ ⋅ 10 = 5.

Правильный треугольник. Площадь правильного треугольника

Правильный треугольник — треугольник, у которого все стороны равны. Каждый угол правильного треугольника равен  градусов.
Правильный треугольник называют еще равносторонним.

Каждая из высот правильного треугольника является также его медианой и биссектрисой.
Центры вписанной и описанной окружностей правильного треугольника совпадают.

Пусть сторона правильного треугольника равна .

Высота правильного треугольника:
Радиус окружности, вписанной в правильный треугольник:
Радиус описанной окружности в два раза больше:
Площадь правильного треугольника:

Все эти формулы легко доказать. Если вы нацелены на решение задач части  — докажите их самостоятельно.

. Сторона правильного треугольника равна . Найдите радиус окружности, вписанной в этот треугольник.

Задача решается в одну строчку. Радиус вписанной окружности .

. Найдите радиус окружности, вписанной в правильный треугольник, высота которого равна .

Сравним формулы для высоты правильного треугольника и радиуса вписанной окружности. Очевидно, радиус вписанной окружности равен высоты.

Ответ: .

. Сторона правильного треугольника равна . Найдите радиус окружности, описанной около этого треугольника.

Радиус окружности, описанной вокруг правильного треугольника, равен .

Ответ: .