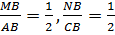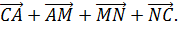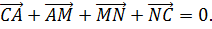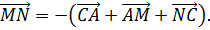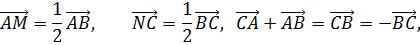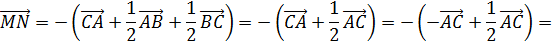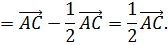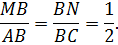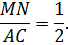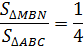Как найти середину стороны равнобедренного треугольника - Исправление недочетов и поиск решений вместе с Examum.ru

Как найти среднюю линию треугольника?

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Понятие треугольника

Треугольник — это геометрическая фигура, которая получилась из трех отрезков. Их соединили тремя точками, которые не лежат на одной прямой. Отрезки принято называть сторонами, а точки — вершинами.

Прямоугольный. Один угол прямой, то есть равен 90 градусам, два других меньше 90 градусов.
Остроугольный. Градусная мера всех углов больше 0, но меньше 90 градусов.
Тупоугольный. Один угол тупой, два других — острые.

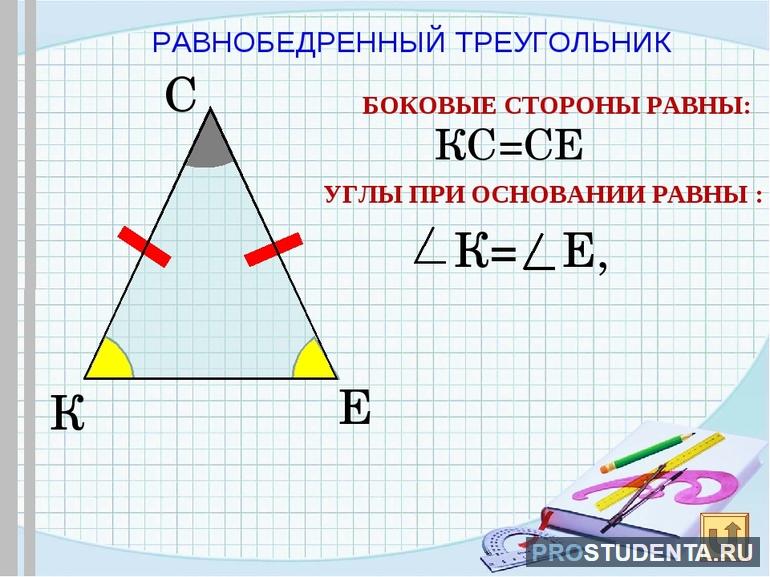
Треугольник считают равнобедренным, если две его стороны равны. Эти стороны называют боковыми сторонами, а третью — основанием.

Треугольник, у которого все стороны равны, называется равносторонним или правильным.

Треугольник называется прямоугольным, если у него есть прямой угол, то есть угол в 90°. Сторона прямоугольного треугольника, которая лежит напротив прямого угла — гипотенуза, а две другие стороны — катеты.

Правильный (равносторонний или равноугольный) треугольник — это правильный многоугольник, в котором все стороны равны между собой, все углы также равны и составляют 60°. В равностороннем треугольнике высота является и биссектрисой, и медианой.

Свойства треугольников:

В треугольнике против большего угла лежит большая сторона — и наоборот.
Сумма углов треугольника равна 180 градусов.
Все углы равностороннего треугольника равны 60 градусам.
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

Понятие средней линии треугольника

Определение средней линии треугольника подходит для любого вида этой фигуры.

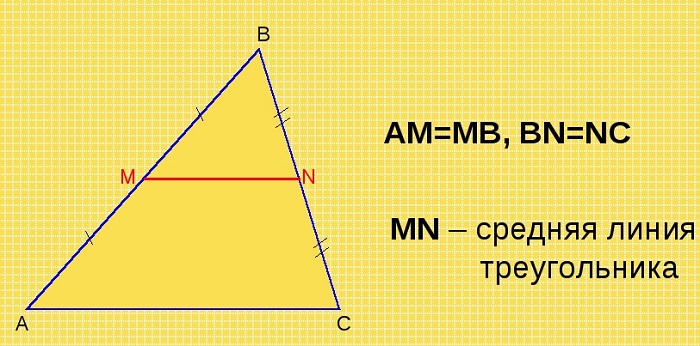
Средняя линия треугольника — отрезок, который соединяет середины двух сторон. В любом треугольнике можно провести три средних линии.

Основанием считается сторона, которой параллельна средняя линия.

Как найти среднюю линию треугольника — расскажем дальше, а для начала еще немного разберемся со всеми определениями.

Понятие средней линии прямоугольного треугольника

Математики говорят: в любом треугольнике можно провести три средних линии. В прямоугольном треугольнике этот отрезок будет равен половине основания — это и есть формула средней линии прямоугольного треугольника.

Прямой угол помогает нам применить другие признаки равенства и подобия. Для углов в прямоугольном треугольнике можно использовать геометрические тождества без дополнительных построений, а любую из сторон можно найти по теореме Пифагора.

В прямоугольном треугольнике две средние линии перпендикулярны катетам, а третья равна медиане, проведенной к гипотенузе. Средние линии острого и разностороннего треугольника не обладают подобными свойствами.

Свойства средней линии треугольника

Признак средней линии треугольника: если отрезок в треугольнике проходит через середину одной из его сторон, пересекает вторую и параллелен третьей — этот отрезок можно назвать средней линией этого треугольника.

Свойства:

Средняя линия равна половине длины основания и параллельна ему.
Средняя линия отсекает треугольник, подобный данному с коэффициентом 1/2; его площадь равна четверти площади данного.
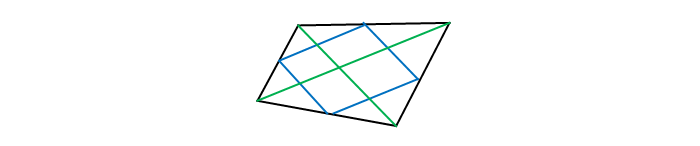
Три средние линии разделяют исходную фигуру на четыре равных треугольника. Центральный из них называют дополнительным.
Три средние линии разделяют исходный прямоугольный треугольник на четыре равных прямоугольных треугольника.

Теорема о средней линии треугольника

Теорема о средней линии треугольника звучит так:

Средняя линия треугольника параллельна основанию и равна его половине. А так выглядит формула нахождения средней линии треугольника:

Докажем теорему:

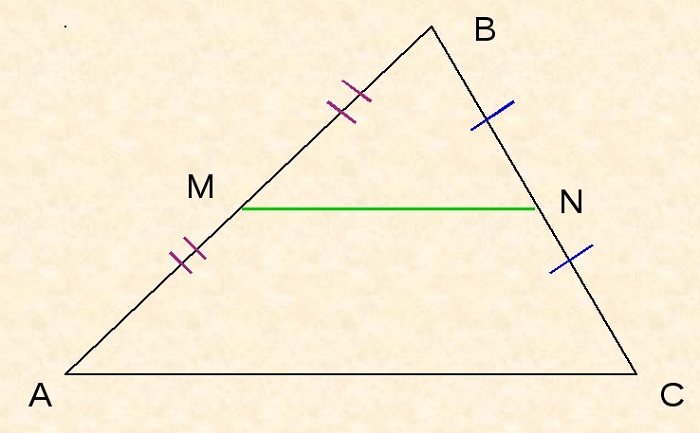
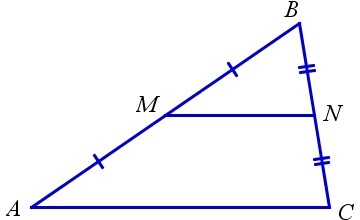
По условию нам дано, что MA = MB, NA = NC

Рассмотрим два образовавшихся треугольника ΔAMN и ΔABC.

(по второму признаку подобия треугольников).

△ABC, то Следовательно, ВС = 2МN. Значит, доказано, что средняя линия равна половине основания.

△ABC, то ∠1 = ∠2 . Так как ∠1 и ∠2 — соответственные углы, то по признаку параллельности прямых MN || BC.

Параллельность средней линии и соответствующего ей основания доказана.

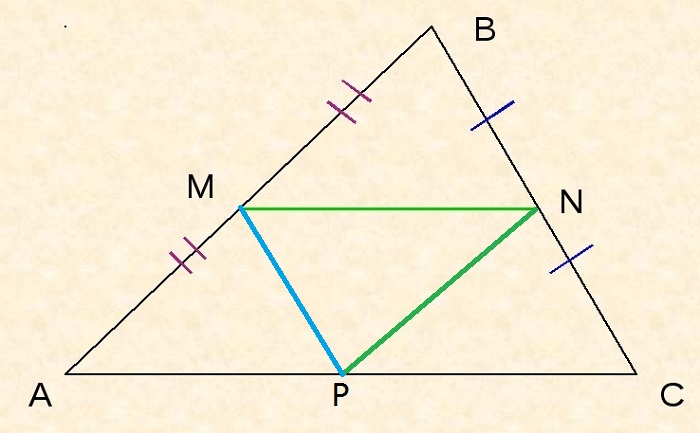
Пример 1. В треугольнике ΔABC AB = 8, BC = 7, CA = 5, точки M, K, N — середины сторон AB, BC, CA соответственно. Найти периметр ΔMNK.

Соединим середины сторон треугольника ΔABC и получим его средние линии, которые образуют треугольник ΔMNK. Найдем их длины по теореме о средней линии:

Ответ: периметр треугольника ΔMNK равен 10.

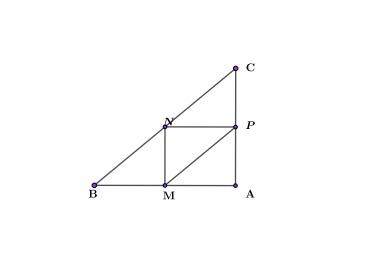
Пример 2. В прямоугольном треугольнике АВС есть две средние линии: MN и NP, равные 3 и 4 соответственно. Найти площадь большого прямоугольного треугольника.

Площадь треугольника равна половине произведения основания на высоту. Так как треугольник прямоугольный, то его площадь найдем как половину произведения катетов:

Так как MN — средняя линия, то по теореме о средней линии она равна половине катета AC:

Значит, AC = 2MN = 2 × 3 = 6.

Так как NP — средняя линия, то по теореме о средней линии она равна половине катета BC:

Значит, BC = 2NP = 2 × 4 = 8.

Тогда найдем площадь большого треугольника, используя формулу, указанную выше:

S = ½ × 6 × 8 = ½ × 48 = 24.

Ответ: площадь большого прямоугольного треугольника равна 24.

Что такое средняя линия треугольника

В данной публикации мы рассмотрим определение, свойства и признак средней линии треугольника, а также разберем пример решения задачи для лучшего понимания теоретического материала.

Определение средней линии треугольника

Отрезок, который соединяет середины двух сторон треугольника, называется его средней линией.

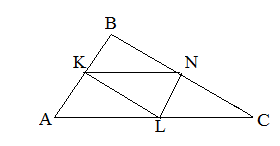
KL – средняя линия треугольника ABC
K – середина стороны AB: AK = KB
L – середина стороны BC: BL = LC

Свойства средней линии треугольника

Свойство 1

Средняя линия треугольника параллельна одной из его сторон (которую не пересекает) и в два раза меньше этой стороны.

На рисунке выше:

Свойство 2

Средняя линия треугольника отсекает от него подобный треугольник (в соотношении 1:2), площадь которого в 4 раза меньше исходного.

На рисунке выше:

△KBL ∼ △ABC (подобие по пропорциональности всех сторон)
Стороны △KBL в два раза меньше соответствующих сторон △ABC:
AB = 2KB, BC = 2BL, AC = 2KL.
S_△ABC = 4 ⋅ S_△KBL

Свойство 3

В любом треугольнике можно провести три средние линии.

KL, KM и ML – средние линии треугольника ABC.

Свойство 4

Три средние линии треугольника делят его на 4 равных по площади треугольника.

Признак средней линии треугольника

Отрезок, проходящий через середину одной из сторон треугольника, пресекающий вторую и параллельный третьей стороне, является средней линией этого треугольника.

Пример задачи

Дан треугольник, две стороны которого равны 6 и 8 см. Найдите длину средней линии, соединяющей эти стороны.

Треугольник с заданными сторонами является прямоугольным, причем известные значения – это длины катетов. Средняя линия, которая соединяет катеты, параллельна гипотенузе и равна половине ее длины.

Мы можем найти гипотенузу, воспользовавшись теоремой Пифагора.

BC 2 = AB 2 + AC 2 = 6 2 + 8 2 = 100.
BC = 10.

Таким образом, средняя линия LM = 1 /₂ ⋅ BC = 1 /₂ ⋅ 10 = 5.

Средняя линия треугольника — свойства, признаки и формулы

Одним из важных понятий, с помощью которого легко решается целый класс задач по геометрии, является средняя линия треугольника.

Разберём данное понятие, рассмотрим свойства, и научимся правильно решать задачи на эту тему.

Определение и признаки средней линии треугольника

Отрезок, соединяющий середины двух сторон треугольника, называется его средней линией.

Отрезок, у которого один из концов совпадает с серединой одной из сторон, другой находится на второй стороне, проведённый параллельно третьей стороне, является средней линией треугольника.

Доказательство следует из теоремы Фалеса.

Теорема о средней линии треугольника

Средняя линия треугольника параллельна основанию (третьей стороне) и равна её половине.

Существует три вида доказательств этого положения. Каждое из них базируется на одной из ключевых позиций планиметрии.

Пусть дан треугольник ABC, M – середина стороны AB, N – середина BC.

По определению, MN – средняя линия ΔABC.

Необходимо доказать, что MN II AC, MN = ½AC.

Доказательства

Пусть прямая MK II AC. Тогда по теореме Фалеса MK пересекает сторону BC в её середине. В этом случае отрезок MN лежит на прямой MK.

Следовательно, MN II AC.

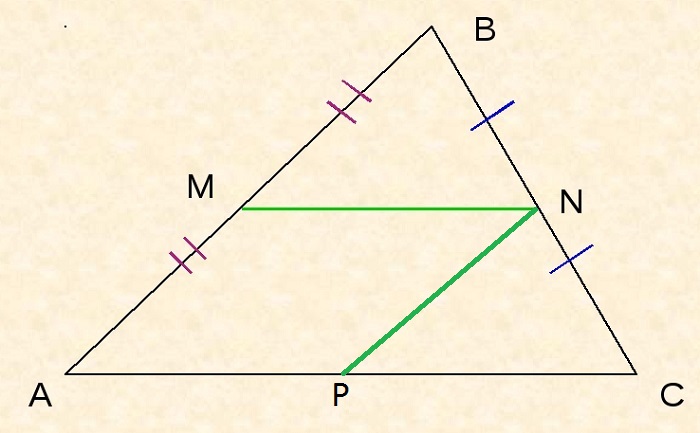
Тогда NP – средняя линия по теореме Фалеса, то есть AP = PC.

Так как AMNP – параллелограмм по определению, то AP = MN. Из этого и предыдущего утверждения следует, что длина MN равна ½AC.

Рассматриваются треугольники MBN и ABC. В них угол B является общим,

По второму признаку подобия треугольников ΔMBN ∼ ΔABC. Следовательно, углы BMN и BAC равны.

Поскольку эти углы являются соответственными, то прямые MN и AC параллельны.

Формула MN = ½AC следует из условий

поскольку пропорциональность двух пар сторон влечёт соответствующее отношение для третьей пары сторон.

Рассматривается сумма векторов

Поскольку в результате образуется замкнутая ломаная, то

Отсюда следует, что

Из последнего равенства следуют условия теоремы.

Следствия из теоремы с доказательствами

Следствие №1

Средняя линия отсекает треугольник, подобный данному, с коэффициентом подобия ½ и площадью, составляющий ¼ площади заданного треугольника.

По определению стороны AB и BC делятся пополам, поэтому

Из третьего признака подобия вытекает рассматриваемое свойство.

Поскольку площади подобных фигур относятся как квадрат коэффициента подобия, то получается вторая часть свойства, то есть площадь маленького треугольника относится к площади большого как

Следствие №2

Поскольку MN – средняя линия, то MN II AC, поэтому ∠BMN = ∠BAP, ∠BNM = ∠BCA как соответственные при MN II AC и секущей AB или BC соответственно.

Поскольку MP – средняя линия, то MP II BC, поэтому ∠MPA = ∠BCA как соответственные при MP II BC и секущей AC.

Таким образом: ∠BNM = ∠BCA = ∠MPA.

Так как MN – средняя линия, то сторона MN = ½AC, поэтому MN = AP.

Следовательно, ΔAMP = ΔMBN по второму признаку равенства треугольников.

Равенство остальных пар треугольников доказывается аналогично.

По основному свойству ΔMBN ∼ ΔABC с коэффициентом подобия ½. Так как все полученные маленькие треугольники равны между собой, то каждый из них, следовательно, подобен большому с тем же коэффициентом.

Свойства средней линии треугольника

Теорема и следствия из неё составляют основные свойства средней линии треугольника.

Согласно второму утверждению, вид большого треугольника такой же, как и у маленьких. То есть для равностороннего и равнобедренного треугольников средние линии отсекают равносторонние и равнобедренные треугольники.

Высоты тупоугольного треугольника, проведённые к тупому углу из вершин острых, располагаются вне треугольника. Поэтому часто рассматривают не саму среднюю линию, а её продолжение. Учитывая подобие получаемых фигур, можно утверждать, что точкой пересечения с продолжением средней линии высота делится на две равные части.

Биссектриса угла треугольника точкой пересечения со средней линией также делится пополам.

Средняя линия прямоугольного треугольника

Для прямоугольного треугольника две средние линии перпендикулярны катетам, а третья равна медиане, проведённой к гипотенузе.

Остроугольный разносторонний треугольник не имеет средних линий, обладающих подобными характеристиками.

Пример решения задачи

Доказать, что середины сторон произвольного выпуклого четырёхугольника являются вершинами параллелограмма.

Проводя диагональ четырёхугольника, получают разбиение на два треугольника, в каждом из которых построена средняя линия, параллельная по основной теореме диагонали, как основанию.

Так как две прямые, параллельные третьей, параллельны между собой, то противолежащие стороны образованного средними линиями четырёхугольника параллельны.

Аналогично доказывается параллельность двух других сторон нового четырёхугольника. По определению четырёхугольник, полученный соединением середин сторон заданного четырёхугольника, является параллелограммом.

источники:

Что такое средняя линия треугольника

http://nauka.club/matematika/geometriya/srednyaya-liniya-treugolnika.html

Источник

Как найти среднюю линию треугольника

Средняя линия треугольника — отрезок, соединяющий середины двух его сторон.

Свойства и признаки

Признак средней линии: если отрезок в треугольнике проходит через середину одной из его сторон, пересекает вторую и параллелен третьей, то этот отрезок называется средней линией данного треугольника.

Свойства:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Равна половине длины основания и параллельна ему.
Отсекает треугольник, подобный данному с коэффициентом 1/2; его площадь равна четверти площади данного.
Три средние линии разделяют исходную фигуру на четыре равных треугольника. Центральный из них называют дополнительным треугольником.
Три средние линии разделяют исходный прямоугольный треугольник на четыре равных прямоугольных треугольника.

Формула для расчета

Теорема

Средняя линия треугольника параллельна основанию и равна её половине.

Доказательство

(A_1C_1) — средняя линия

Рассмотрим (triangle BA_1C_1) и (triangle BAC) :

Из этого следует, что треугольники подобны по двум пропорциональным сторонам и углу между ними.

Следовательно, (angle BA_1C_1=angle BAC) , как соответственные элементы подобных треугольников. Следовательно (A_1C_1parallel AC) по признаку параллельности.

Кроме того, из подобия следует, что (frac=frac12)

Примечание

Данная формула одинаково работает для любого треугольника: равнобедренного, равностороннего (правильного).

Задачи на использование теоремы

Задача 1

В прямоугольном треугольнике ABC проведены средние линии: MN; NP; MP. При этом MN=NP=2. Найти площадь треугольника ABC.

Рассмотрим прямоугольный треугольник NMP:

(S_=frac12times MNtimes NP=frac12times2times2=2)

Все маленькие треугольники равны, следовательно (S_=2times4=8)

Задача 2

Площадь треугольника ABC равна 8. MN — средняя линия. Необходимо вычислить площадь треугольника BMN.

Задача 3

В треугольнике ABC точки M, N, K – середины сторон AB, BC, AC соответственно, MN=12, MK=10, KN=8. Необходимо узнать периметр треугольника ABC.

Средняя линия треугольника

Найдем площадь треугольника :

$[S_{ABC} =frac{1}{2} ACcdot BK=frac{1}{2} cdot 12cdot 5=30 cm^{2} ]$

Так как средняя линия отсекает треугольник , площадь которого равна одной четвёртой площади исходного треугольника , то площадь треугольника равна:

$[S_{MBN} =frac{1}{4} S_{ABC} =frac{1}{4} cdot 30=7,5 cm^{2} ]$

см см см

Теперь можно найти периметр треугольника как сумму длин всех его сторон:

$P_{ABC} =AC+AB+BC=8+10+16=34$

см

Что такое средняя линия треугольника

Определение средней линии треугольника
Свойства средней линии треугольника
- Свойство 1
- Свойство 2
- Свойство 3
- Свойство 4
Определение средней линии треугольника

Отрезок, который соединяет середины двух сторон треугольника, называется его средней линией.
- KL – средняя линия треугольника ABC
- K – середина стороны AB: AK = KB
- L – середина стороны BC: BL = LC
Свойства средней линии треугольника

Свойство 1

Средняя линия треугольника параллельна одной из его сторон (которую не пересекает) и в два раза меньше этой стороны.

На рисунке выше:
- KL параллельна AC
- KL = 1 /₂ ⋅ AC
Свойство 2

Средняя линия треугольника отсекает от него подобный треугольник (в соотношении 1:2), площадь которого в 4 раза меньше исходного.

На рисунке выше:
- △KBL ∼ △ABC (подобие по пропорциональности всех сторон)
- Стороны △KBL в два раза меньше соответствующих сторон △ABC:
  AB = 2KB, BC = 2BL, AC = 2KL.
- S_△ABC = 4 ⋅ S_△KBL
Свойство 3

В любом треугольнике можно провести три средние линии.

KL, KM и ML – средние линии треугольника ABC.
- KL || AC, KL = 1 /₂ ⋅ AC
- KM || BC, KM = 1 /₂ ⋅ BC
- ML || AB, ML = 1 /₂ ⋅ AB
Свойство 4

Три средние линии треугольника делят его на 4 равных по площади треугольника.

Признак средней линии треугольника

Отрезок, проходящий через середину одной из сторон треугольника, пресекающий вторую и параллельный третьей стороне, является средней линией этого треугольника.

Пример задачи

Дан треугольник, две стороны которого равны 6 и 8 см. Найдите длину средней линии, соединяющей эти стороны.

Треугольник с заданными сторонами является прямоугольным, причем известные значения – это длины катетов. Средняя линия, которая соединяет катеты, параллельна гипотенузе и равна половине ее длины.

Мы можем найти гипотенузу, воспользовавшись теоремой Пифагора.

BC 2 = AB 2 + AC 2 = 6 2 + 8 2 = 100.
BC = 10.

Таким образом, средняя линия LM = 1 /₂ ⋅ BC = 1 /₂ ⋅ 10 = 5.

Источник

У равнобедренного треугольника 2 равных по длине стороны. Каждая из них — боковая сторона равнобедренного треугольника, а третья будет основанием. Их часто просят найти при решении различных задач в геометрии. Зная основные способы решения, формулы, теоремы и свойства геометрической фигуры, учащийся может легко справиться с предложенным заданием.

Оглавление:

Основные свойства

Важная теорема

Полезные формулы

Примеры решения задач

Основные свойства

Свойства основания равнобокого треугольника применяются на практике. Фигуру будет проще воспринимать визуально, если расположить чертеж таким образом, чтобы основание располагалось снизу.

Принято считать, что равносторонний треугольник — это частный случай равнобедренного. Каждая его сторона может считаться и основанием, и боковой.

Помимо равенства боковых сторон, при решении задач используют совпадение биссектрисы с высотой. Решить задание, как найти основание равнобедренного треугольника, зная боковые стороны, невозможно в следующих случаях:

Известно лишь основание или углы.
По условию дана только величина характеризующих отрезков — биссектрисы, высоты.

А также решение задачи невозможно, если заданы только две боковые стороны. В остальных случаях найти решение можно, даже если известен только один угол или площадь.

Важная теорема

Для решения задач на построение, когда задана боковая сторона треугольника, используется теорема, связанная с высотой. Применяется она и для медианы с биссектрисой.

Ее суть в следующем:

Биссектриса, которая проведена к основанию, будет не только высотой. Она считается и медианой.
Высота, проведенная к основанию, не только медиана. А также она может быть названа биссектрисой.
Медиана, которая проведена к основанию, будет не только высотой, но и биссектрисой.

Теорема доказывается следующим образом: если в заданном треугольнике ABC из точки B провести высоту BD, он будет разделен на треугольники ABD и CBD. Помимо общего катета, у них равны гипотенузы. Что касается прямых AC и BD, они будут перпендикуляром.

Получается, что в ABD и CBD углы BAD и BCD, а также AB и BC равны. А также — AD и CD. Следовательно, фигуры равны, а BD считается как высотой, так и медианой и биссектрисой.

Полезные формулы

Когда по условию не даны углы, но известны все стороны, поможет формула для косинусов: cos A = (b² + с² — а²)/ 2bc = (b² + a² — а²)/2ba = b²/2ba = b/2a. При этом cos В = (а² + а² — b²)/ 2bc = (b² + a² — а²)/2а² = (2 a² — b²)/2а².

Медиана вычисляется по следующей формуле: √(2 a² + 2b² — а²)/2 = √(a² + 2b²)/2. Биссектрису можно вычислить с помощью формулы √ ab (2a+b)(a+b-a)/(a+b) = b√ a (2a+b)/(a+b).

Средняя линия, параллельная основанию равнобедренного треугольника, считается равной его половине. Равны между собой и средние линии, которые параллельны его боковым сторонам.

Если необходимо вычислить радиус описанной вокруг равнобедренного треугольника окружности, используется формула R = a²/√(4а² — b²). Когда окружность вписана в фигуру действует формула r= b/2√(2a-b)/(2a+b).

Примеры решения задач

Вот примеры заданий, как узнать боковую сторону равнобедренного треугольника АВС. Так, если основание АС = 8 см, а опущенная на его середину высота (являющаяся медианой) BH =3 см, то AH = AC = 4 см. По теореме Пифагора боковая сторона AB = √ AH ² + BH ² = √ 16+9 = √25 = 5 см.

Можно привести и следующий пример задачи. Если площадь равнобедренного треугольника АВС = 40√ 3 см², а углы при основании (A и C) = 30°, угол B будет равен 180° — 2 * ∠АС = 180° — 2 * 30° = 120°.

В этом случае действует формула S = ½ АВ*АС * sin ∠B = ½ * AB ² * sin 120° = 40√ 3 см². Значит, AB ² = 2*40√ 3/ sin 120 = 80 √ 3:√ 3/2 = 160. Тогда АВ = 4√ 10 см.

Еще пример задачи — если боковая сторона равна 1, а угол при вершине 120°, диаметр окружности, описанной вокруг него, можно найти так: угол при основании будет равен (180−120)/2, то есть 30°. В таком случае диаметр будет 1/sin 30° = 2 см.

Задачи, связанные с нахождением боковой стороны треугольника, часто встречаются в геометрии. Для их решения необходимо знать перечисленные формулы и свойства.

Источник

Как посчитать стороны равнобедренного треугольника

Главная
/
Математика
/
Геометрия
/
Как посчитать стороны равнобедренного треугольника

Чтобы посчитать чему равны стороны равнобедренного треугольника воспользуйтесь нашим удобным онлайн калькулятором:

Онлайн калькулятор

Чтобы вычислить длины сторон равнобедренного треугольника вам нужно знать следующие параметры (либо-либо):

для стороны a:

длину основания (b) и угол α
длину основания (b) и угол β
длину основания (b) и высоту (h)

для стороны b:

длину двух равных сторон (a) и угол α
длину двух равных сторон (a) и угол β
длину двух равных сторон (a) и высоту (h)

Введите их в соответствующие поля и получите результат.

Как посчитать сторону a равнобедренного треугольника

Если известна сторона b и угол α

Чему равна сторона a равнобедренного треугольника если длина основания

b =

, а угол

α =?

Ответ:

a =

Чему равна сторона a у равнобедренного треугольника если известны длина основания (сторона b) и угол α?

Формула

a = ^b/_{2⋅cos α}

Пример

Если сторона b = 10 см, а ∠α = 30°, то:

a = ¹⁰/_{2⋅cos 30°} = 10/(2⋅0.8660) = 5.77см

Если известна сторона b и угол β

Чему равна сторона a равнобедренного треугольника если длина основания

b =

, а угол

β =?

Ответ:

a =

Чему равна сторона a у равнобедренного треугольника если известны длина основания (сторона b) и угол β?

Формула

a = ^b/_{2⋅sin ^β/₂}

Пример

Если сторона b = 10 см, а ∠β = 30°, то:

a = ¹⁰/_{2⋅sin 15} = 10/(2⋅0.2588) = 19.31см

Если известна сторона b и высота h

Чему равна сторона a равнобедренного треугольника если длина основания

b =

, а высота

h =?

Ответ:

a =

Чему равна сторона a у равнобедренного треугольника если известны длина основания (сторона b) и высота h?

Формула

a = √¹/_b² + h²

Пример

Если сторона b = 10 см, а высота h = 20 см, то:

a = √¹/_10² + 20² = √0.01+400 = 20.61см

Как посчитать сторону b (основание) равнобедренного треугольника

Если известна сторона a и угол α

Чему равна сторона b равнобедренного треугольника если длина стороны

a =

, а угол

α =?

Ответ:

b =

Чему равна сторона b у равнобедренного треугольника если известны длина стороны a и угол α?

Формула

b = 2⋅a⋅cos α

Пример

Если сторона a = 10 см, а ∠α = 30°, то:

b = 2⋅10⋅cos 30° = 2⋅10⋅0.8660 = 17.32см

Если известна сторона a и угол β

Чему равна сторона b равнобедренного треугольника если длина стороны

a =

, а угол

β =?

Ответ:

b =

Чему равна сторона b у равнобедренного треугольника если известны длина стороны a и угол β?

Формула

b = 2⋅a⋅sin ^β/₂

Пример

Если сторона a = 10 см, а ∠β = 40°, то:

b = 2⋅10⋅sin ⁴⁰/₂ = 2⋅10⋅0.342 = 6.84см

Если известна сторона a и высота h

Чему равна сторона b равнобедренного треугольника если длина стороны

a =

, а высота

h =?

Ответ:

b =

Чему равна сторона b у равнобедренного треугольника если известны длина стороны a и высота h?

Формула

b = 2⋅√a² — h² , h < a

Пример

Если сторона a = 10 см, а высота h = 5 см, то:

b = 2⋅√10² — 5² = 2⋅√75 = 17.32см

См. также

Источник

Калькулятор длин сторон треугольника онлайн умеет вычислять длину сторон 14 способами.
Калькулятор может:

Найти все стороны треугольника.
Найти все углы треугольника.
Найти площадь (S) и периметр (P) треугольника.
Найти радиус (r) вписанной окружности.
Найти радиус (R) описанной окружности.
Найти высоту (h) треугольника.

Просто введите любые имеюшиеся данные и, если их достаточно, то калькулятор сам подберет нужные формулы для вычислений и покажет подробный расчет с выводом формул.

Сторона треугольника (или длина сторон) может быть найдена различными методами.
В большинстве случаев достаточно воспользоваться одной из ниже приведенных формул. Однако не редки случаи когда для нахождения искомой стороны понадобиться обратиться к дополнительным материалам или решения в два действия.

Как найти длину стороны треугольника?

Найти длину сторон треугольника очень просто на нашем онлайн калькуляторе. Так же длина может быть найдена самостоятельно по формулам. Выбор нужной формулы зависит от того какие данные известны.