Онлайн калькулятор. Середина отрезка
Предлагаю вам воспользоваться онлайн калькулятором для вычисления середины отрезка AB.
Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление координат середины отрезка и закрепить пройденный материал.
Калькулятор для вычисления координат середины отрезка AB
Выберите необходимую вам размерность:
Размерность:
Введите координаты точек.
Вводить можно числа или дроби (-2.4, 5/7, …). Более подробно читайте в правилах ввода чисел.
Вычислить координаты середины отрезка AB
На данной странице калькулятор поможет найти координаты между двумя точками онлайн в плоскости и пространстве. Для расчета задайте координаты.
Середина между двумя точками
Формула вычисления середины отрезка A(xa; ya) и B(xb; yb) на плоскости:
Вывод формулы для вычисления расстояния между двумя точками на плоскости
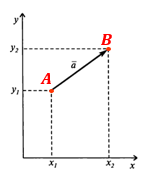
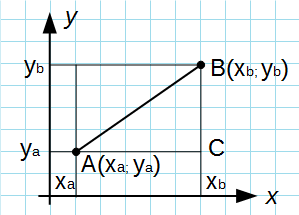
Из точек A и B опустим перпендикуляры на оси координат x и y.
Рассмотрим прямоугольный треугольник ∆ABC. Катеты этого треугольника равны:
Спомощью теоремы Пифагора, вычислим длину отрезка AB:
Подставив в это выражение длины отрезков AC и BC, выраженные через координаты точек A и B, получим формулу для вычисления расстояния между точками на плоскости.
Формула для вычисления расстояния между двумя точками в пространстве выводится аналогично.
Онлайн калькулятор. Середина отрезка
Предлагаю вам воспользоваться онлайн калькулятором для вычисления середины отрезка AB.
Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление координат середины отрезка и закрепить пройденный материал.
Калькулятор для вычисления координат середины отрезка AB
Выберите необходимую вам размерность:
Введите координаты точек.
Ввод данных в калькулятор для вычисления координат середины отрезка
В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.
Дополнительные возможности калькулятора для вычисления координат середины отрезка
- Используйте кнопки и на клавиатуре, для перемещения между полями калькулятора.
Теория. Середина отрезка.
В геометрических задачах часто можно столкнуться с необходимостью найти координаты середины отрезка заданного координатами точек его концов, например в задачах поиска медианы, средней линии, .
Каждая координата середины отрезка равна полусумме соответствующих координат концов отрезка.
В случае плоской задачи. Координаты середины отрезка с концами A( xa , ya ) и B( xb , yb ) вычисляются по формулам:
| xc = | xa + xb | ; | yc = | ya + yb |
| 2 | 2 |
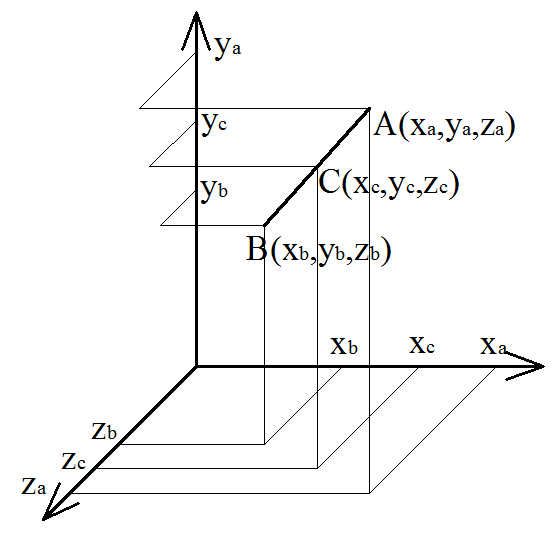
В случае пространственной задачи. Координаты середины отрезка с концами A( xa , ya , za ) и B( xb , yb , zb ) вычисляются по формулам:
| xc = | xa + xb | ; | yc = | ya + yb | ; | zc = | za + zb |
| 2 | 2 | 2 |
Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.
51. Планиметрия Читать 0 мин.
51.143. Векторы
ОСИ КООРДИНАТ:
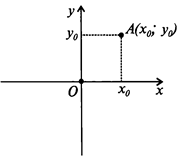
Для понимания темы «вектор», надо сначала разобраться с понятием «декартовы координаты».
- ось x — ось абсцисс;
- ось y — ось ординат,
- точка О — начало координат.
Любой точке плоскости сопоставляются два числа:
Эти числа называются декартовыми координатами данной точки.
ВЕКТОР:
Вектор — направленный отрезок прямой. То есть это отрезок, для которого указано, какая из его точек является началом, а какая — концом.
Пусть имеются две точки:
Тогда мы имеем вектор $,overline <!AB,>$, который обозначим за $overline a.$
На примере вектора рассмотрим основные понятия, связанные с векторами.
Во-первых, для каждого вектора можно найти его координаты и модуль.
КООРДИНАТЫ ВЕКТОРА И МОДУЛЬ ВЕКТОРА:
Координаты вектора — разности координат конца и начала вектора. На примере вектора $overline a$ его координатами будут: $(a_x;,a_y).$ Свойства координат вектора:
- Координаты вектора не изменяются при параллельном переносе.
- У равных векторов соответствующие координаты равны.
Нахождение координат вектора:
Координаты вектора $overline a;(a_x;,a_y)colon$
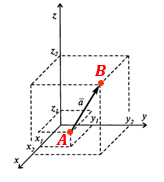
То есть, координаты вектора $overline acolon (x_2-x_1;,y_2-y_1;,z_2-z_1).$
Модуль вектора — длина вектора (обозначается ). Находится как квадратный корень из суммы квадратов координат вектора.
Если рассмотреть пространственный вектор, то в эти формулы добавляется третья координата — z.
Координаты вектора $overline a;(a_x;,a_y;,a_z)$:
$begin&a_x = x_2-x_1 \ &a_y = y_2-y_1 \ &a_z = z_2 — z_1end$
То есть, координаты вектора $overline acolon (x_2-x_1;,y_2-y_1;,z_2-z_1).$
Модуль вектора $overline acolon$
СЕРЕДИНА ВЕКТОРА:
Чтобы найти середину вектора по координатам нужно:
1. Вычислить сумму координат начала и конца вектора.
2. Разделить на два.
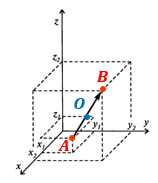
НА ПЛОСКОСТИ
В ПРОСТРАНСТВЕ
O — середина вектора $,overline <!AB,>$
ВИДЫ ВЕКТОРОВ:
Единичный вектор — вектор, длина которого равна 1.
Нулевой вектор — отдельные точки плоскости. У такого вектора конец и начало совпадают, а его длина (его модуль) равен нулю.
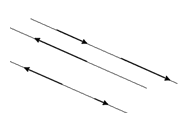
Коллинеарные и компланарные векторы
Коллинеарные векторы — векторы, которые параллельны одной прямой или которые лежат на одной прямой.
Два коллинеарных вектора $|overline a| и |b|$ называются сонаправленными только тогда, когда их направления соответствуют друг другу:
Компланарные векторы — векторы, которые параллельны одной плоскости или которые лежат на общей плоскости.
В любое мгновение существует плоскость одновременно параллельная двум любым векторам, поэтому два произвольных вектора являются компланарными.
АЛГЕБРАИЧЕСКИЕ ДЕЙСТВИЯ НАД ВЕКТОРАМИ:
| НА ПЛОСКОСТИ | В ПРОСТРАНСТВЕ | |
| Координаты вектора $overline $ |
Сложение векторов: $overline =overline a + overline b$ |
|
| $x$ | $c_x = a_x + b_x$ | $c_x = a_x + b_x$ |
| $y$ | $c_y = a_y + b_y$ | $c_y = a_y + b_y$ |
| $z$ | — | $c_z = a_z + b_z$ |
| Координаты вектора $overline $ |
Вычитание векторов: $overline =overline a — overline b$ |
|
| $x$ | $c_x = a_x — b_x$ | $c_x = a_x — b_x$ |
| $y$ | $c_y = a_y — b_y$ | $c_y = a_y — b_y$ |
| $z$ | — | $c_z = a_z — b_z$ |
| Координаты вектора $overline $ |
Умножение вектора на число: $overline b = lambdaoverline a$ |
|
| $x$ | $overline b_x = lambda a_x$ | $overline b_x = lambda a_x$ |
| $y$ | $overline b_y = lambda a_y$ | $overline b_y = lambda a_y$ |
| $z$ | — | $overline b_z = lambda a_z$ |
| Значение числа $s$ | Скалярное умножение векторов: $s = overline acdotoverline b$ |
|
| $s=a_x!cdot b_x + a_y!cdot b_y$ | $s=a_x!cdot b_x + a_y!cdot b_y + a_z!cdot b_z$ |
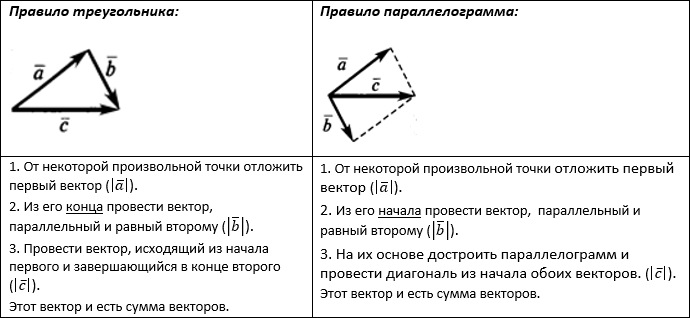
ГЕОМЕТРИЧЕСКОЕ СЛОЖЕНИЕ И ГЕОМЕТРИЧЕСКАЯ РАЗНОСТЬ ВЕКТОРОВ:
СЛОЖЕНИЕ
Сумма двух векторов находится с помощью правила треугольника или правила параллелограмма: $overline = overline a + overline b$.
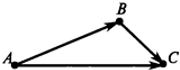
$<mathbf <Теоремаcolon>>\ Для любых трёх точек A,,B,,C справедливо соотношениеcolon overline<!AB,>+,overline<!BC,>=,overline<!AC,>!.$
$<mathbf <РАЗНОСТЬ>>\Разность двух векторов overline a и overline b;— это вектор overline , который в сумме с вектором overline b даёт вектор overline a \ overline b + overline = overline aquadRightarrowquadoverline = overline a — overline b$
$Вектор overline можно найти также, складывая с вектором overline a вектор bigl(-overline bbigr), противоположный вектору overline bcolon \ overline = overline a + bigl(-overline bbigr)$
http://ru.onlinemschool.com/math/assistance/cartesian_coordinate/p_center/
http://reshutest.ru/theory/7?theory_id=275
Формула вычисления середины отрезка A(xa; ya) и B(xb; yb) на плоскости:
Формула вычисления середины отрезка A(xa; ya; za) и B(xb; yb; zb) в пространстве:
Вывод формулы для вычисления расстояния между двумя точками на плоскости
Из точек A и B опустим перпендикуляры на оси координат x и y.
Рассмотрим прямоугольный треугольник ∆ABC. Катеты этого треугольника равны:
AC = xb — xa;
BC = yb — ya.
Спомощью теоремы Пифагора, вычислим длину отрезка AB:
Подставив в это выражение длины отрезков AC и BC, выраженные через координаты точек A и B, получим формулу для вычисления расстояния между точками на плоскости.
Формула для вычисления расстояния между двумя точками в пространстве выводится аналогично.
Середина отрезка
Операции над векторами
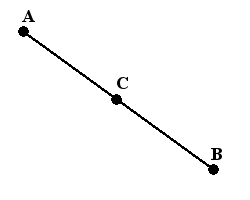
Если от точки А провести прямую к точке В, то мы получим отрезок АВ, т.е отрезок — часть прямой, ограниченная с двух сторон двумя точками с определенными параметрами. Точки А и В будут концами этого отрезка. Точка, расположенная на данном отрезке и равноудаленная от обоих его концов, называется серединой отрезка. Если отрезок АВ в двухмерной системе координат имеет координаты: А (х1;у1); В (х2;у2), то координаты середины данного отрезка (точки С) можно рассчитать как сумму абсцисс (Х1+Х2) и ординат (Y1+Y2), каждую из которых нужно разделить пополам. Середина отрезка АВ (точка С) будет иметь координаты {(Х1+Х2)/2,(Y1+Y2)/2}.
Чтобы найти координаты середины отрезка АВ, расположенного в трехмерном пространстве, введем дополнительно координаты оси Z.
Пусть в прямоугольной системе координат Oxyz отрезок АВ имеет координаты A (xa, ya, za) и B (xb, yb, zb), тогда координаты середины отрезка — точки С в пространстве рассчитываем по координатам его концов:
хC = (хA+хB) / 2, yC = (уA+уB)/2, zC = (zA + zB)/2
или
С ( (хA+хB) / 2; (уA+уB)/2; (zA + zB)/2)
Рассчитать середину отрезка можно с помощью онлайн-калькулятора. Для этого вводим данные точек Х,Y,Z для трехмерного пространства; Х, Y — для отрезка на плоскости.
Координаты точки середины отрезка в пространстве онлайн
Калькулятор рассчитывает координаты середины отрезка в пространстве по координатам конца отрезка с подробным порядком вычислений. В поля можно вводить целые или десятичные числа.
Введите координаты точки A
Введите координаты точки B
Определение середины отрезка
Середина отрезка — это точка которая лежит на отрезке, делит этот отрезок пополам и находится на равном расстоянии от начала и конца отрезка.
Формула расчёта координаты середины отрезка в пространстве
Каждая координата середины отрезка равна полусумме соответствующих координат его концов.
xc=(xa+xb)/2
yc=(ya+yb)/2
zc=(za+zb)/2
A(xa, ya, za), B(xb, yb, zb) — координаты концов отрезка
C(xc, yc, zc) — координаты середины отрезка
Разберём пример
Найдите координаты середины отрезка AC заданного точками A(4,5,7), C(10,11,5)
По формуле найдём координаты середины отрезка
x=(4+10)/2=7
y=(5+11)/2=8
z=(7+5)/2=6
Найдите координаты точки C середины отрезка AB заданного точками A(3,4,5), B(9,10,11)
xc=(3+9)/2=6
yc=(4+10)/2=7
yc=(5+11)/2=8
Найти координаты середины отрезка AB если A(5, 5, 3), B(3, 1, 2).
Найти координаты середины отрезка AB если A(1, 4, 0), B(6, 6, 5).
Найти координаты середины отрезка AB если A(2, 0, 4), B(3, 4, 3).
Похожие калькуляторы