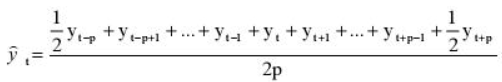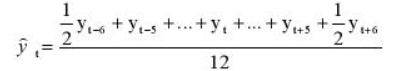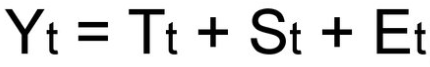Сезонная составляющая (сезонная компонента) и её оценка.
Известны данные по ВВП в России за 2008-2012 г.
|
год |
квартал |
объём ВВП, млрд.руб |
|
2008 |
1 |
8878 |
|
2 |
10238 |
|
|
3 |
11542 |
|
|
4 |
10619 |
|
|
2009 |
1 |
8335 |
|
2 |
9245 |
|
|
3 |
10411 |
|
|
4 |
10816 |
|
|
2010 |
1 |
9617 |
|
2 |
10693 |
|
|
3 |
11843 |
|
|
4 |
13019 |
|
|
2011 |
1 |
11680 |
|
2 |
13038 |
|
|
3 |
14406 |
|
|
4 |
15462 |
Построить аддитивную модель временного ряда, выделив сезонную и трендовую составляющие
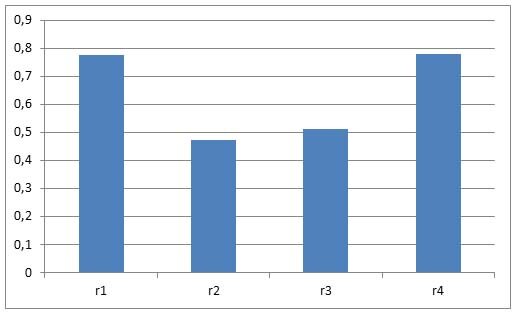
Найдём коэффициенты автокорреляции
| r1 |
0,777705 |
| r2 |
0,475503 |
| r3 |
0,513819 |
| r4 |
0,781028 |
Построим коррелограмму
По высоким значениям коэффициентов автокорреляции 1 и 4 порядка выдвигаем гипотезу о наличии тренда и сезонной составляющей .
Для оценки сезонной компоненты аддитивной модели составим таблицу
Для этого:
- Просуммируем уровни ряда последовательно за 4 квартала со сдвигом на один сезон (итого за 4 квартала)
- Найдем скользящие средние, делением каждой суммы на 4.
- Приведем скользящие средние с помощью центрирования, найдя средние значения из двух последовательных скользящих средних.
- Найдем оценки сезонной компоненты как разность между фактическим y и центрированной скользящей средней
|
t |
y |
Итого за 4 кв. |
Скользящая средняя за 4 кв. |
Центрированная скользящая средняя |
Оценка сезонной компоненты |
|
1 |
8878 |
— |
— |
— |
— |
|
2 |
10238 |
41277 |
10319,3 |
— |
— |
|
3 |
11542 |
40734 |
10183,5 |
10251,38 |
1290,63 |
|
4 |
10619 |
39741 |
9935,3 |
10059,38 |
559,63 |
|
5 |
8335 |
38610 |
9652,5 |
9793,88 |
-1458,88 |
|
6 |
9245 |
38807 |
9701,8 |
9677,13 |
-432,13 |
|
7 |
10411 |
40089 |
10022,3 |
9862,00 |
549,00 |
|
8 |
10816 |
41537 |
10384,3 |
10203,25 |
612,75 |
|
9 |
9617 |
42969 |
10742,3 |
10563,25 |
-946,25 |
|
10 |
10693 |
45172 |
11293,0 |
11017,63 |
-324,63 |
|
11 |
11843 |
47235 |
11808,8 |
11550,88 |
292,13 |
|
12 |
13019 |
49580 |
12395,0 |
12101,88 |
917,13 |
|
13 |
11680 |
52143 |
13035,8 |
12715,38 |
-1035,38 |
|
14 |
13038 |
54586 |
13646,5 |
13341,13 |
-303,13 |
|
15 |
14406 |
— |
— |
— |
— |
|
16 |
15462 |
— |
— |
— |
— |
Рассчитаем значения сезонной компоненты
|
Показатели |
Год |
Квартал |
|||
|
1 кв. |
2 кв. |
3 кв. |
4 кв. |
||
|
1 |
1290,63 |
559,63 |
|||
|
2 |
-1458,88 |
-432,13 |
549,00 |
612,75 |
|
|
3 |
-946,25 |
-324,63 |
292,13 |
917,13 |
|
|
4 |
-1035,38 |
-303,13 |
|||
| Итого за сезон |
-3440,50 |
-1059,88 |
2131,75 |
2089,50 |
|
| Средняя оценка сезонной компоненты, |
-1146,83 |
-353,29 |
710,58 |
696,50 |
|
| Скорректированная сезонная компонента, |
-1123,57 |
-330,03 |
733,84 |
719,76 |
Все значения для расчетов возьмем из колонки «Оценка сезонной компоненты», последовательно внося их в таблицу
Сумма «Скорректированной сезонной компоненты» равна нулю.
Для расчета скорректированной сезонной компоненты определим корректирующий коэффициент.
Составим таблицу, где T + ε колонка с возможным трендом (за вычетом сезонности)
|
t |
y |
Si (скорректированная S) |
y – S = T + ε |
|
1 |
2301 |
-373,48 |
2674,48 |
|
2 |
2567 |
-139,52 |
2706,52 |
|
3 |
3050 |
266,48 |
2783,52 |
|
4 |
3064 |
246,52 |
2817,48 |
|
5 |
2891 |
-373,48 |
3264,48 |
|
6 |
3149 |
-139,52 |
3288,52 |
|
7 |
3671 |
266,48 |
3404,52 |
|
8 |
3696 |
246,52 |
3449,48 |
|
9 |
3522 |
-373,48 |
3895,48 |
|
10 |
3984 |
-139,52 |
4123,52 |
|
11 |
4645 |
266,48 |
4378,52 |
|
12 |
4979 |
246,52 |
4732,48 |
|
13 |
4441 |
-373,48 |
4814,48 |
|
14 |
5070 |
-139,52 |
5209,52 |
|
15 |
5897 |
266,48 |
5630,52 |
|
16 |
6354 |
246,52 |
6107,48 |
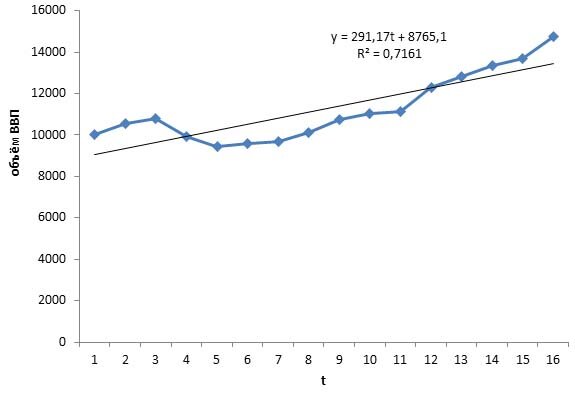
Строим график модели за вычетом сезонной компоненты
Коэффициенту детерминации очень высок (близок к 1), таким образом, полученная линейная модель может использоваться для прогнозирования
Оценим качество такой модели с помощью инструмента регрессия
| ВЫВОД ИТОГОВ | ||||
|
Регрессионная статистика |
||||
| Множественный R |
0,846 |
|||
| R-квадрат |
0,716 |
|||
| Нормированный R-квадрат |
0,696 |
|||
| Стандартная ошибка |
903,55 |
|||
| Наблюдения |
16 |
|||
| Дисперсионный анализ | ||||
|
df |
SS |
MS |
F |
|
| Регрессия |
1 |
28826034 |
28826034 |
35,30883 |
| Остаток |
14 |
11429564 |
816397,4 |
|
| Итого |
15 |
40255598 |
||
|
Коэффи-циенты |
Стандартная ошибка |
t-статистика |
P-Значение |
|
| Y-пересечение |
8765,144 |
473,824 |
18,499 |
3,09E-11 |
| t |
291,174 |
49,002 |
5,942 |
3,6E-05 |
Модель y = 291,174t + 8765,144 высокого качества, поскольку коэффициент корреляции очень высок и модель значима в целом и по параметрам при уровне значимости 95%, т.к. уровни значимости критерия Фишера и Стьюдента намного меньше 5% (0,05) – см. колонки Значимость F и P-Значение.
Материалы сайта
Обращаем Ваше внимание на то, что все материалы опубликованы для образовательных целей.
Определение сезонной составляющей временного ряда
В зависимости от
характера сезонных колебаний различают
два вида моделей – аддитивная и
мультипликативная.
По аддитивной
модели временной ряд с сезонными
колебаниями представляется в виде:
где:
— значение прогнозируемой переменной
для
-го
момента времени;
— трендовая составляющая
;
— сезонная составляющая
;
— случайная ошибка.
По мультипликативной
модели временной ряд с сезонными
колебаниями имеет в вид:
Для решения вопроса
о том какая из рассматриваемых моделей
должна быть выбрана для конкретного
временного ряда, необходимо построить
график изменения прогнозируемой величины
во времени и проанализировать изменение
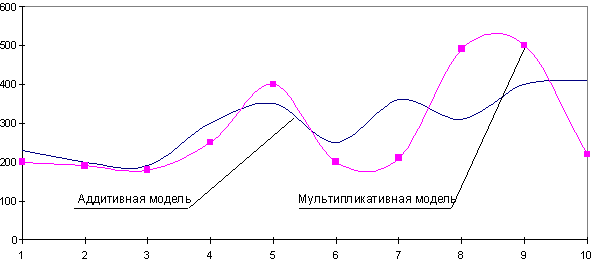
амплитуды сезонных колебаний (Рис.16.).
В случае если амплитуда сезонных
колебаний не имеет ярко выраженной
тенденции к изменению во времени, то
тогда может быть выбрана аддитивная
модель (a), в противном
случае предпочтительна мультипликативная
(б).
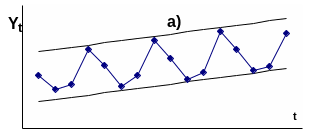

Рис 16. Временные
ряды, характерные для аддитивной (а) и
мультипликативной(б)моделей.
Наиболее просто
сезонная составляющая может быть
определена с помощью скользящих средних
с периодом осреднения равным периоду
сезонных колебаний L.
Скользящая средняя
– это переменная значения которой равны
среднему арифметическому значения
исследуемой величины в точке для которой
она вычисляется и значений всех точек,
отстоящих от нее на 0.5*(L
— 1) слева и справа в случае если L
нечетное и 0.5L – если L
четное. При вычислении значения скользящей
средней для следующей точки временного
ряда номера точек, участвующих в
вычислении смещаются на единицу. Длинна
периода сезонных колебаний – это
число временных интервалов, через
которые характер изменения временного
ряда повторяется.
Таким образом для
их вычисления скользящей средней вначале
необходимо определить длину периода
сезонных колебаний L. В
простейшем случае найти ее можно на
основании визуального анализа данных.
Затем для каждой точки исходного
временного ряда необходимо вычислить
средние значения переменной
.
В случае если L четное,
полученный ряд скользящих средних ССt
оказывается смещенным относительно
на величину равную половине временного
интервала. Значения скользящей средней
при этом соответствуют уже не конкретным
интервалам, например первому или второму
интервалу, а второй половине интервала
1 и первой половине интервала 2 (рис. 17).
Следующее значение скользящей средней
соответствует половинам интервалов 2
и 3 и т.д. Смещенная на пол интервала
скользящая средняя называется
межинтервальной скользящей средняй.
Для устранения возникшего смещения
полученные скользящие средние с любым
четным периодом осреднения необходимо
еще раз усреднить с периодом усреднения,
равным двум. Полученная в результате
повторного осреднения скользящая
средняя называется центрированной
скользящей средней.

Рис. 17. Получение
центрированных скользящих средних с
периодом осреднения равным двум. Где:
— значения yt;
— межинтервальные
скользящие средние для точек 1-2 и 2-3
соответственно;
—
интервальная скользящая средняя для
точки 2.
Как видно из схемы
расчетов в результате усреднения число
значений скользящей средней оказывается
меньше числа точек исходного временного
ряда на величину равную периоду осреднения
L так как на краях временного
ряда отсутствуют точки необходимые для
нахождения скользящей средней. Потеря
L точек приводит к тому,
что минимальная длительность временного
ряда должна быть равной хотя бы трем
периодам колебаний.
Схема расчета
скользящих средних для периода осреднения
равного четырем (ежеквартальные данные
за несколько лет) представлена в таблице
1.
Таблица 1.
|
номер перио-да |
фактические |
межинтервальные |
интервальные |
|
|
|
||
|
|
|
||
|
|
|||
|
3 |
|
|
|
|
|
|||
|
4 |
|
|
|
|
|
|||
|
5 |
|
|
|
|
|
|||
|
6 |
|
||
|
7 |
|
||
Дальнейшая схема
определения сезонных колебаний различна
для аддитивной и мультипликативной
моделей, по этому рассмотрим их по
отдельности.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
В прошлой статье мы уже разобрали, что такое временной ряд и функцию тренда. Теперь подробнее разберемся с терминологией и остановимся на одной из моделей временного ряда.
Из чего состоит временной ряд
Уровни временного ряда (Yt) представляют из себя сумму двух компонент:
- Регулярную составляющую
- Случайную составляющую
В свою очередь регулярная составляющая состоит из:
- Тренда
- Сезонности
- Циклической составляющей
Однако, в модели необязательно наличие всех этих компонент сразу.
Случайная компонента отражает влияние случайных возмущений на модель, которые по отдельности имеют незначительное воздействие, но суммарно их влияние ощущается.
То есть, в общем случае временной ряд представляет из себя наличие четырех составляющих:
- Тренд (Tt)
- Сезонность (St)
- Цикличность (Ct)
- Случайные возмущения (Et)
Циклическая компонента, по сравнению с сезонностью, имеет более длительный эффект и меняется от цикла к циклу. Поэтому, ее обычно объединяют с трендом.
Виды моделей временного ряда
Обычно, выделяют две модели временного ряда и третью — смешанную.
- Аддитивная модель
-
Мультипликативная модель
-
Смешанная модель
При выборе необходимой модели временного ряда смотрят на амплитуду колебаний сезонной составляющей. Если ее колебания относительно постоянны, то выбирают аддитивную модель. То есть, амплитуда колебаний примерно одинакова:
Если амплитуда сезонных колебаний возрастает или уменьшается, строят мультипликативную модель временного ряда, которая ставит уровни ряда в зависимость от значений сезонной компоненты.
Построение этих моделей сводится к расчету тренда (Tt), сезонности (St) и случайных возмущений (Et) для каждого уровня ряда (Yt).
Алгоритм построения модели
- Выравниваем ряд с помощью скользящей средней, то есть сглаживаем ряд и отфильтровываем высокочастотные колебания.
- Рассчитываем значение сезонной компоненты St.
- Рассчитываем значения Tt с использованием полученного уравнения тренда.
- Используя полученные значения St и Tt, находим прогнозные значения уровней временного ряда.
- Оцениваем качество модели.
Реализация на практике
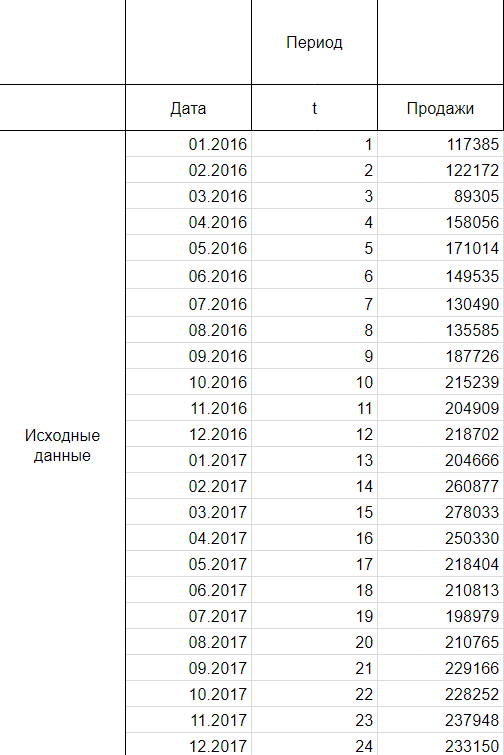
Итак, мы имеем на руках данные о продажах за 2016 и 2017 год и хотим спрогнозировать продажи на 2018 год.
Шаг 1
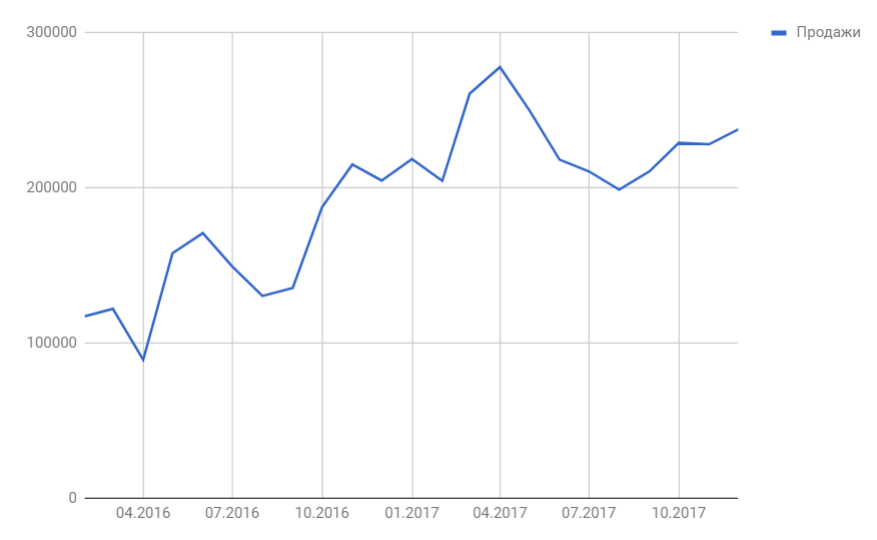
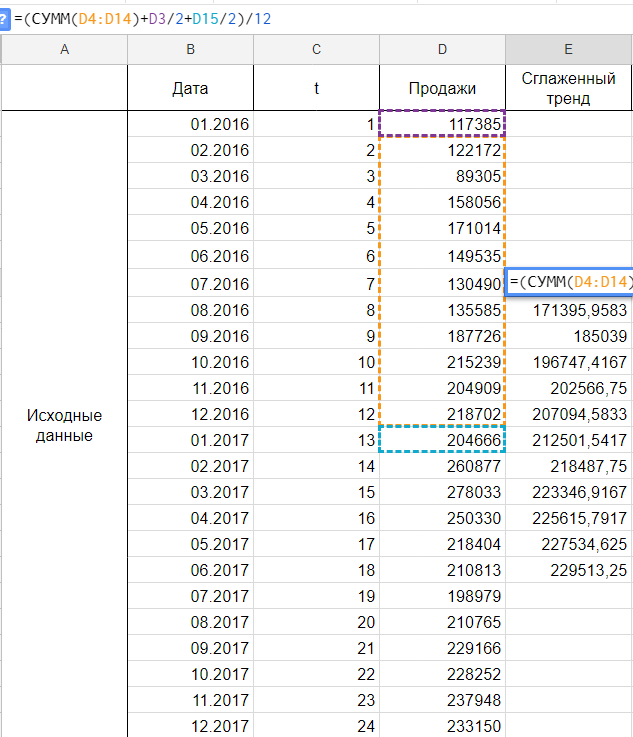
Следуя нашему алгоритму, мы должны сгладить временной ряд. Воспользуемся методом скользящей средней. Видим, что в каждом году есть большие пики (май-июнь 2016 и апрель 2017), поэтому возьмем период сглаживания пошире, например, месячную динамику, т.е. 12 месяцев.
Удобнее брать период сглаживания в виде нечетного числа, тогда формула для расчета уровней сглаженного ряда:
yi — фактическое значение i-го уровня ряда,
yt — значение скользящей средней в момент времени t,
2p+1 — длина интервала сглаживания.
Но так как мы решили использовать месячную динамику в виде четного числа 12, то данная формула нам не подойдет и мы воспользуемся этой:
Иными словами, мы учитываем половины от крайних уровней ряда в диапазоне, в остальном формула не претерпела больше никаких изменений. Вот ее точный вид для нашей задачи:
Сглаживаем наши уровни ряда и растягиваем формулу вниз:
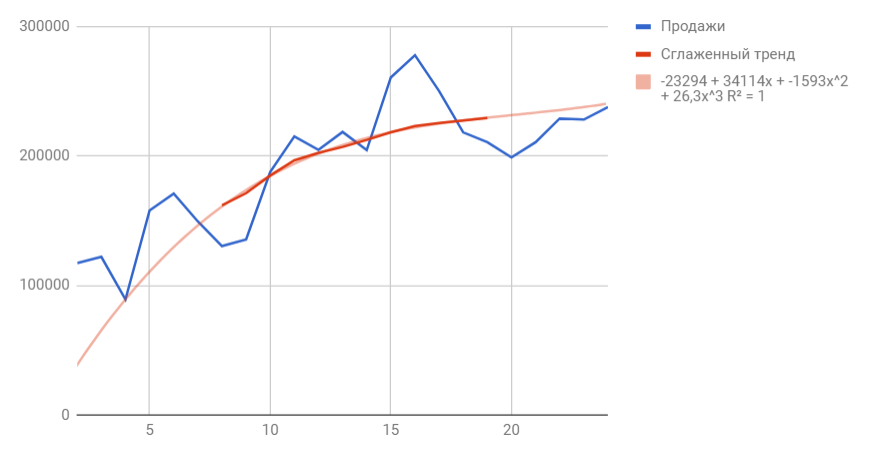
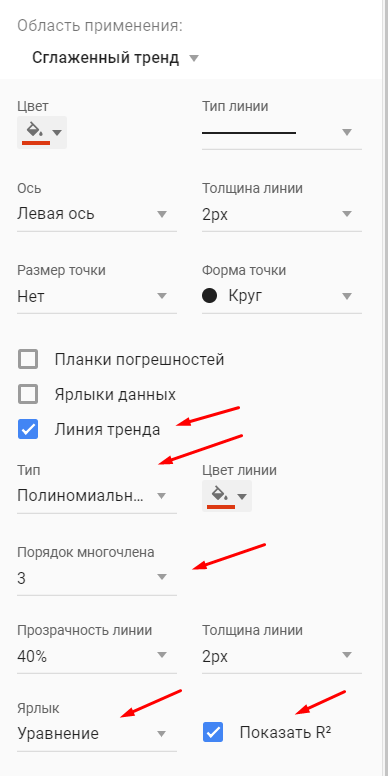
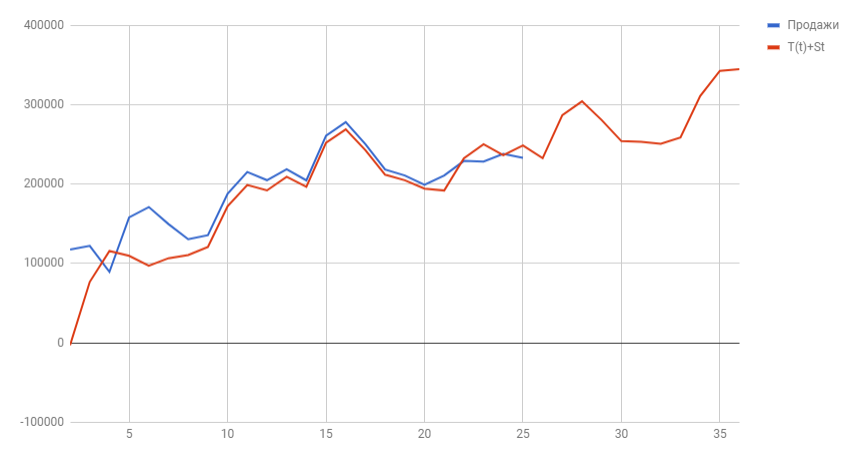
Сразу можем построить график из известных значений уровня продаж и их сглаженной. Выведем ее уравнение и значение коэффициента детерминации R^2:
В качестве сглаженной я выбрала полином третьей степени, так как он лучше всего описывал уровни временного ряда и имел наибольший R^2.
Шаг 2
Так как мы рассматриваем аддитивную модель вида:
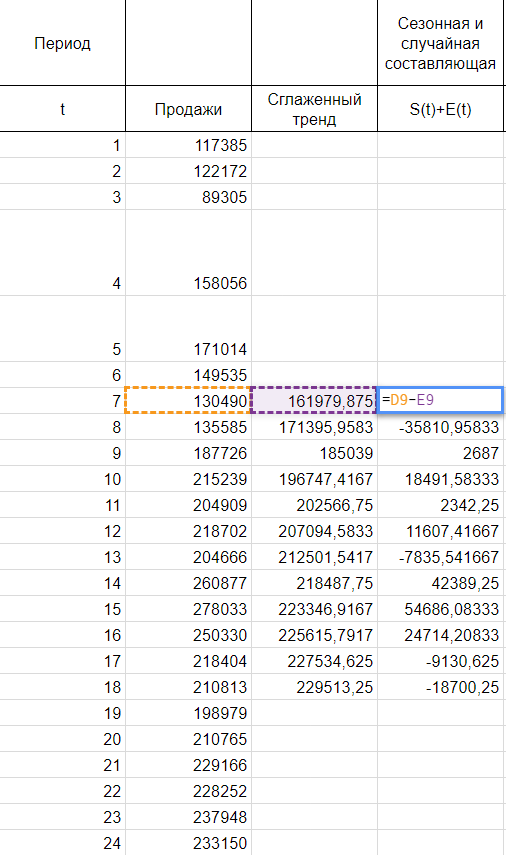
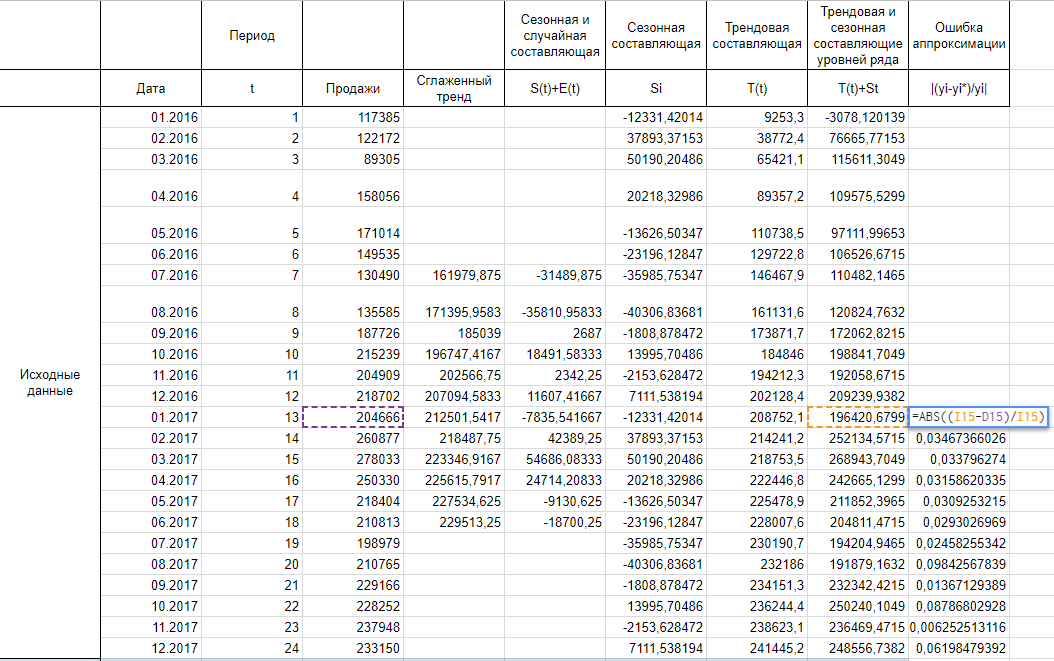
Найдем оценки сезонной компоненты как разность между фактическими уровнями ряда и значениями скользящей средней St+Et = Yt-Tt, так как Yt и Tt мы уже знаем.
Используем оценки сезонной компоненты (St+Et) для расчета значений сезонной компоненты St. Для этого найдем средние за каждый интервал (по всем годам) оценки сезонной компоненты St.
Средняя оценка сезонной компоненты находится как сумма по столбцу, деленная на количество заполненных строк в этом столбце. В нашем случае оценки сезонной составляющей расположились в строках без пересечений, поэтому сумма по столбцам состоит из одиночных значений, следовательно и среднее будет таким же. Если бы мы располагали периодом побольше, например с 2015, у нас бы добавилась еще одна строка и мы смогли бы полноценно найти среднее, поделив сумму на 2.
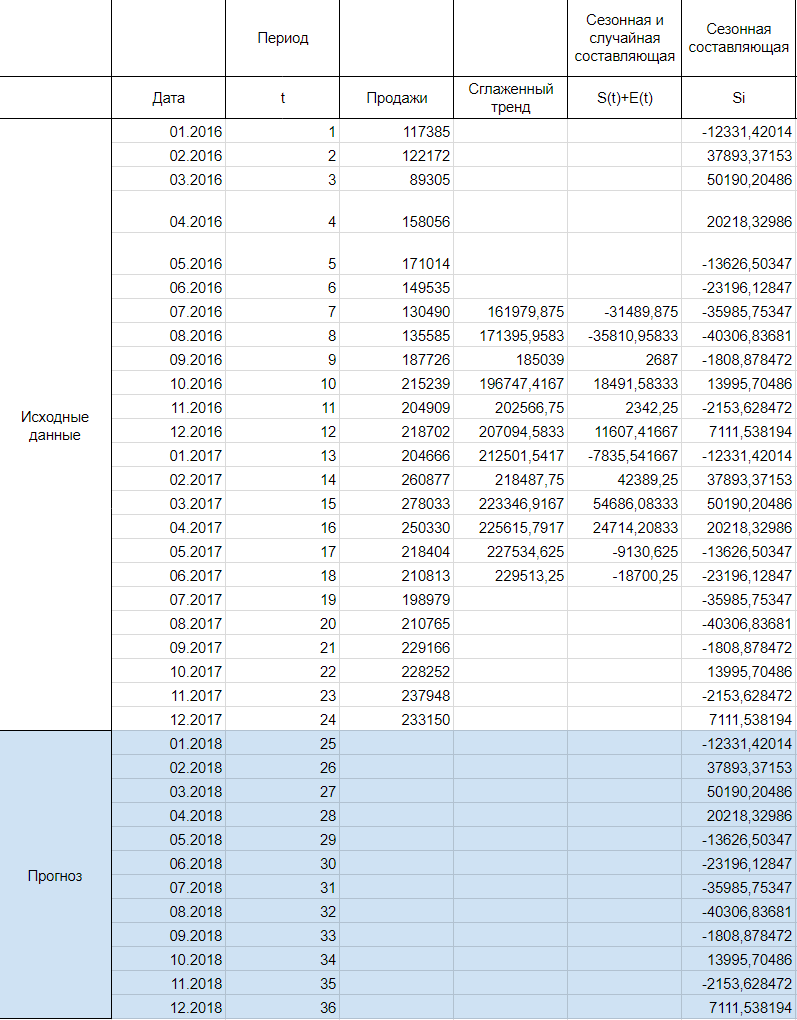
В моделях с сезонной компонентой обычно предполагается, что сезонные воздействия за период взаимопогашаются. В аддитивной модели это выражается в том, что сумма значений сезонной компоненты по всем интервалам должна быть равна нулю. Поэтому найдя значение случайной составляющей, поделив сумму средних оценок сезонной составляющей на 12, мы вычитаем ее значение из каждой средней оценки и получаем скорректированную сезонную компоненту, St.
Далее, заполняем нашу таблицу значениями сезонной составляющей дублируя ряд каждые 12 месяцев, то есть три раза:
Шаг 3
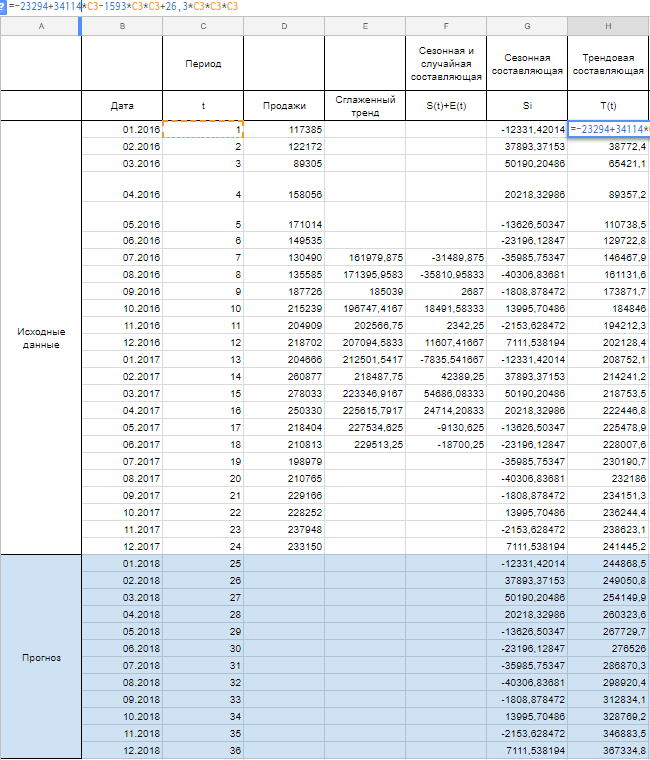
Теперь рассчитываем значения уровня тренда T(t) по тому уравнению, которое мы получили при построении сглаженного тренда на первом шаге.
T(t) = -23294+34114*t-1593*t^2+26,3*t^3
Вместо t используем значения из столбца Период из соответствующей строки.
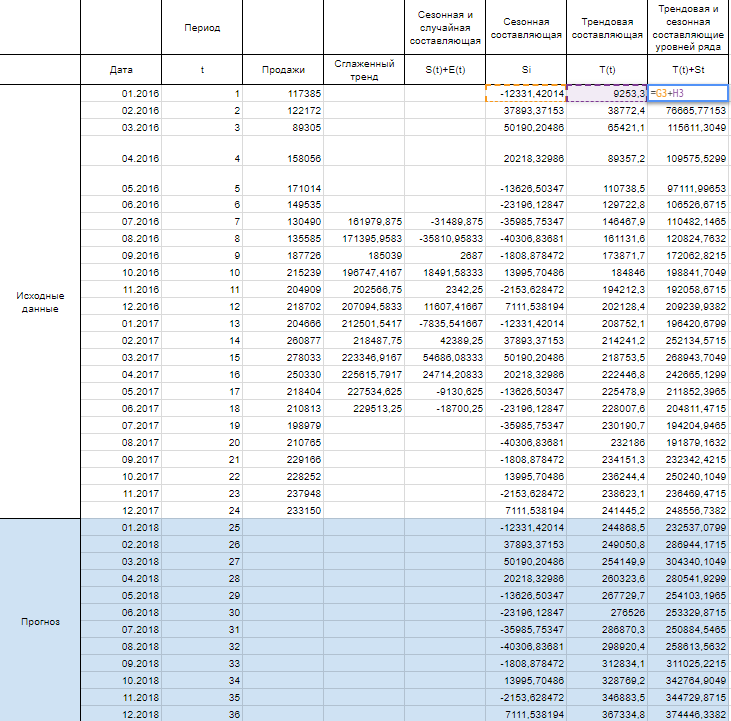
Шаг 4
Имея рассчитанные значения S(t) и T(t) мы можем рассчитать прогнозные значения уровней ряда Y(t). Для этого накладываем уровни сезонности на тренд.
Теперь построим график известных значений Y(t) и спрогнозированных за 2018 год.
Вот мы и нашли спрогнозированные значения уровней продаж на 2018 год. Значения отражают возрастающую тенденцию и сезонные пики. Конечно, эти данные не дают 100% точности, ведь существует множество внешних воздействий, которые могут изменить направление тренда, поэтому к прогнозным значениям обычно строят доверительный интервал, это такой коридор, внутри которого могут колебаться прогнозные значения с заданной вероятностью (чаще всего выбирают 95%). Но об этом я расскажу в следующей статье.
Шаг 5
Осталось оценить точность модели. Для этого будем использовать среднюю ошибку аппроксимации, которая поможет рассчитать ошибку в относительном выражении. Иными словами, это среднее отклонение расчетных значений от фактических, которое вычисляется по формуле:
yi — спрогнозированные уровни ряда,
yi* — фактические уровни ряда,
n — количество складываемых элементов.
Модель может считаться адекватной, если:
Итак, рассчитываем ошибку аппроксимации для нашего случая. Так как в основе нашего тренда лежит полином третьей степени, прогнозные значения начинают хорошо повторять фактические значения к концу 2016 года, думаю, я думаю, поэтому корректнее было бы рассчитать ошибку аппроксимации для значений 2017 года.
Сложив весь столбец с ошибками аппроксимации и поделив на 12, получаем среднюю ошибку аппроксимации 4,13%. Это значение меньше 15% и можем сделать вывод об адекватности модели.
Не забывайте, что прогнозы не бывают точными на 100%. Любые неожиданные внешние воздействия могут развернуть значения уровней ряда в неизвестном направлении 🙂
Полезные ссылки:
- Ссылка на пример Google Sheets
- Построение функции тренда в Excel. Быстрый прогноз без учета сезонности
- Бывшев В.А. Эконометрика
- Об авторе
- Свежие записи
Как рассчитать коэффициент сезонности
Для того, чтобы сформировать заказ поставщикам, распределить запасы РЦ по филиалам и сбалансировать первые между вторыми, необходимо спрогнозировать спрос. Но важно понимать, что спрос не равно продажи.
Одним из факторов, влияющих на формирование спроса, является сезонность. В этой статье мы расскажем, что такое коэффициент сезонности и как его посчитать, почему для его расчёта лучше брать медиану, как и для чего нужно считать недельную сезонность и на какие ещё особенности этого показателя обратить внимание при прогнозировании спроса.
Формула коэффициента сезонности
Коэффициент сезонности показывает, как возрастают или падают продажи в определённый период. Одни товары лучше продаются летом, другие зимой, на третьи – высокий спрос один месяц в году. Расчёт коэффициента сезонности можно проводить разными методами. Рассмотрим два основных.
Классический метод по средним продажам
Для того чтобы рассчитать коэффициент сезонности, нужно найти средние продажи товаров для каждого года. Агрегируем данные по месяцам и считаем средние продажи за год. Затем делим продажи каждого месяца на год и получаем набор коэффициентов.
Для того чтобы рассчитать коэффициент сезонности, нужно найти средние продажи товаров для каждого года. Агрегируем данные по месяцам и считаем средние продажи за год. Затем делим продажи каждого месяца на год и получаем набор коэффициентов.
Коэффициент сезонности каждого месяца = продажи в штуках этого месяца/ продажи за год.
Коэффициент сезонности = среднее значение из коэффициентов по конкретным месяцам.
Рассмотрим на примере.
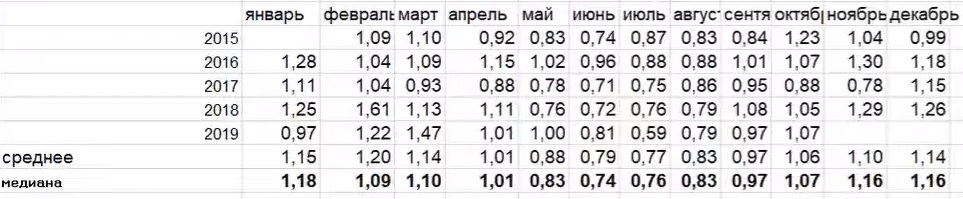
В строке 21 посчитаны средние продажи за год. Показатель февраля – 8307. Затем мы посчитали средние продажи за второй год. Цифра за февраль – 14243, и так далее для каждого года. После реальные продажи за каждый месяц (строка 20) поделили на средние – за год (строка 21).
7322/8307 = 0,8814 – это коэффициент сезонности для февраля.
Получаем набор коэффициентов для каждого месяца. Чтобы найти общий суммарный коэффициент по месяцу, берём среднее значение и получаем коэффициент сезонности.
Расчёт сезонности с очисткой от тренда
Первый шаг будет таким же, как и в предыдущем методе – суммируем продажи по месяцам. Затем вместо средних продаж рассчитываем тренд. В Exel это можно сделать с помощью функции «Тенденция». Затем проводим расчёт коэффициента сезонности для каждого месяца.
Итак, как считается коэффициент сезонности?
Коэффициент сезонности = Продажи в месяц/ тренд
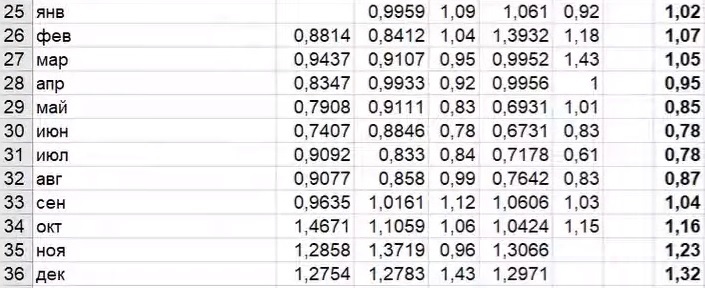
После того как мы получили набор коэффициентов для каждого месяца, ищем не средние значения, а медиану. Это число, которое находится в середине. Половина получившихся значений выше его, а половина ниже. Рассмотрим на примере.
Итак, у нас есть данные по спросу по месяцам. Строим функцию тренда (с помощью функции «Тенденция» в Excel). Не забываем исключать дефициты и прочие факторы, которые могут привести к ошибкам в расчётах. Делим спрос на получившееся значение тренда и получаем коэффициент сезонности.
И так для каждого месяца:
В чём ключевые отличия этого метода от классического? Во-первых, в расчёт коэффициента сезонности идёт не показатель средних продаж, а тренд. Во-вторых, вместо средних значений – медиана. Так, например, за апрель у нас всего шесть значений сезонности: два по 1,01, два ниже этого показателя и два выше. Значит, медианой для апреля будет показатель 1,01.
Почему лучше брать медиану?
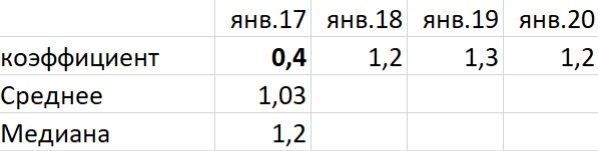
Этот показатель наиболее стабилен к выбросу. Посмотрим на таблице ниже.
Мы видим: в январе 2017 года по товару был низкий коэффициент сезонности – 0,4. При этом в аналогичные периоды других лет продажи были стабильными – 1,2 – 1,3. Если посчитать среднее значение, мы получим, коэффициент 1,03. Это означает, что товар в этом месяце не обладает сезонностью, но это то не так. Медиана более устойчивый показатель. Если брать в расчёт её, то коэффициент будет 1,2. Это уже говорит об умеренной сезонности и ближе к правде.
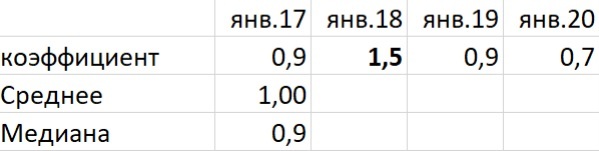
Может быть и обратная ситуация. Например, товар в январе традиционно продаётся хуже, но в каком-то году был всплеск продаж. Возможно, на товар была акция или сработал какой-то другой фактор.
Если взять в расчёт средний показатель, мы увидим, что товар не обладает сезонностью. По медиане же мы получили коэффициент 0,9, который говорит, что продажи в январе ниже средних. Поэтому для расчёта сезонности по каждому месяцу лучше брать медиану.
Как считать: по отдельному товару или по группе?
Как правило, у продаж каждого отдельного товара внутри склада велик случайный фактор. И он в разы больше, чем влияние сезонности. Если считать коэффициенты сезонности по отдельным товарам, могут возникнуть сложности. Случайный фактор даст погрешность в расчётах, и коэффициенты сезонности будут посчитаны неправильно. Мы рекомендуем считать сезонность для группы товаров.
Как считается коэффициент сезонности в этом случае? Для начала агрегируем данные по группе товаров с похожей сезонностью. Считаем не по эскимо конкретной марки, а по всем эскимо, которые есть в продаже, или по всему мороженому.
Исключением могут быть только товары группы АХ в продуктовой рознице. Это позиции, которые стабильно и часто продаются. По ним допускается считать сезонность отдельно по каждому товару. В остальных случаях рекомендуем считать коэффициент сезонности по группам.
Нужно ли агрегировать данные для расчёта?
Чтобы минимизировать влияние случайного фактора, можно агрегировать данные для расчёта. Но делать это нужно только по складам и магазинам одинакового формата и похожего географического положения. Например, по всем магазинам у дома ЦФО или по супермаркетам Дальнего Востока. Возможно объединять похожие по географии магазины внутри города. Например, отдельно считать сезонность по проходным точкам, отдельно по магазинам в спальных районах и т.д. Делать прогноз с учётом сезонности одновременно для точки во Владивостоке и в Москве не имеет никакого смысла.
Как посчитать недельную сезонность?
Иногда этот показатель важен. Например, перед 8 марта традиционно растёт спрос на конфеты. Как считается коэффициент сезонности в таких случаях? Мы можем посчитать недельную сезонность так же, как и месячную. Агрегируем данные по неделям, даём им номера и считаем коэффициенты. Но у вас получится уже на 12, а 52 коэффициента. А чем больше декомпозиция данных, тем сложнее расчёты и их интерпретация. Если вам важен показатель недельной сезонности, рассчитывайте его отдельно.
Помимо недельной сезонности существует и внутринедельная. Например, продажи по алкогольным напиткам по пятницам и субботам всегда значительно выше, чем в другие дни недели. Нужно ли это учитывать? Если мы строим прогноз с учётом сезонности на месяц или больший период, то смысла в этом нет. В месяце будет примерно одинаковое количество пятниц, суббот и других дней недели. Но если мы делаем заказ на какие-то скоропортящиеся продукты, конечно, показатель внутринедельной сезонности важен. Например, если мы заказываем молоко с маленьким сроком хранения на четверг и пятницу, логичнее опираться на данные по продажам в эти дни. Если же мы делаем заказ пастеризованного молока на месяц вперёд, то этот показатель не имеет значения.
From Wikipedia, the free encyclopedia
In time series data, seasonality is the presence of variations that occur at specific regular intervals less than a year, such as weekly, monthly, or quarterly. Seasonality may be caused by various factors, such as weather, vacation, and holidays[1] and consists of periodic, repetitive, and generally regular and predictable patterns in the levels[2] of a time series.
Seasonal fluctuations in a time series can be contrasted with cyclical patterns. The latter occur when the data exhibits rises and falls that are not of a fixed period. Such non-seasonal fluctuations are usually due to economic conditions and are often related to the «business cycle»; their period usually extends beyond a single year, and the fluctuations are usually of at least two years.[3]
Organisations facing seasonal variations, such as ice-cream vendors, are often interested in knowing their performance relative to the normal seasonal variation. Seasonal variations in the labour market can be attributed to the entrance of school leavers into the job market as they aim to contribute to the workforce upon the completion of their schooling. These regular changes are of less interest to those who study employment data than the variations that occur due to the underlying state of the economy; their focus is on how unemployment in the workforce has changed, despite the impact of the regular seasonal variations.[3]
It is necessary for organisations to identify and measure seasonal variations within their market to help them plan for the future. This can prepare them for the temporary increases or decreases in labour requirements and inventory as demand for their product or service fluctuates over certain periods. This may require training, periodic maintenance, and so forth that can be organized in advance. Apart from these considerations, the organisations need to know if variation they have experienced has been more or less than the expected amount, beyond what the usual seasonal variations account for.
Motivation[edit]
There are several main reasons for studying seasonal variation:
-
- The description of the seasonal effect provides a better understanding of the impact this component has upon a particular series.
- After establishing the seasonal pattern, methods can be implemented to eliminate it from the time-series to study the effect of other components such as cyclical and irregular variations. This elimination of the seasonal effect is referred to as de-seasonalizing or seasonal adjustment of data.
- To use the past patterns of the seasonal variations to contribute to forecasting and the prediction of the future trends, such as in climate normals.
Detection[edit]
The following graphical techniques can be used to detect seasonality:
- A run sequence plot will often show seasonality
A seasonality plot of US electricity usage
- A seasonal plot will show the data from each season overlapped[4]
- A seasonal subseries plot is a specialized technique for showing seasonality
- Multiple box plots can be used as an alternative to the seasonal subseries plot to detect seasonality
- An autocorrelation plot (ACF) and a spectral plot can help identify seasonality.
A really good way to find periodicity, including seasonality, in any regular series of data is to remove any overall trend first and then to inspect time periodicity.[5]
The run sequence plot is a recommended first step for analyzing any time series. Although seasonality can sometimes be indicated by this plot, seasonality is shown more clearly by the seasonal subseries plot or the box plot. The seasonal subseries plot does an excellent job of showing both the seasonal differences (between group patterns) and also the within-group patterns. The box plot shows the seasonal difference (between group patterns) quite well, but it does not show within group patterns. However, for large data sets, the box plot is usually easier to read than the seasonal subseries plot.
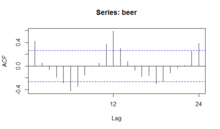
The seasonal plot, seasonal subseries plot, and the box plot all assume that the seasonal periods are known. In most cases, the analyst will in fact, know this. For example, for monthly data, the period is 12 since there are 12 months in a year. However, if the period is not known, the autocorrelation plot can help. If there is significant seasonality, the autocorrelation plot should show spikes at lags equal to the period. For example, for monthly data, if there is a seasonality effect, we would expect to see significant peaks at lag 12, 24, 36, and so on (although the intensity may decrease the further out we go).
An autocorrelation plot (ACF) can be used to identify seasonality, as it calculates the difference (residual amount) between a Y value and a lagged value of Y. The result gives some points where the two values are close together ( no seasonality ), but other points where there is a large discrepancy. These points indicate a level of seasonality in the data.
An ACF (autocorrelation) plot, of Australia beer consumption data.
Semiregular cyclic variations might be dealt with by spectral density estimation.
Calculation[edit]
Seasonal variation is measured in terms of an index, called a seasonal index. It is an average that can be used to compare an actual observation relative to what it would be if there were no seasonal variation. An index value is attached to each period of the time series within a year. This implies that if monthly data are considered there are 12 separate seasonal indices, one for each month. The following methods use seasonal indices to measure seasonal variations of a time-series data.
-
- Method of simple averages
- Ratio to trend method
- Ratio-to-moving-average method
- Link relatives method
Method of simple averages[edit]
The measurement of seasonal variation by using the ratio-to-moving-average method provides an index to measure the degree of the seasonal variation in a time series. The index is based on a mean of 100, with the degree of seasonality measured by variations away from the base. For example, if we observe the hotel rentals in a winter resort, we find that the winter quarter index is 124. The value 124 indicates that 124 percent of the average quarterly rental occur in winter. If the hotel management records 1436 rentals for the whole of last year, then the average quarterly rental would be 359= (1436/4). As the winter-quarter index is 124, we estimate the number of winter rentals as follows:
359*(124/100)=445;
Here, 359 is the average quarterly rental. 124 is the winter-quarter index. 445 the seasonalized winter-quarter rental.
This method is also called the percentage moving average method. In this method, the original data values in the time-series are expressed as percentages of moving averages. The steps and the tabulations are given below.
Ratio to trend method[edit]
- Find the centered 12 monthly (or 4 quarterly) moving averages of the original data values in the time-series.
- Express each original data value of the time-series as a percentage of the corresponding centered moving average values obtained in step(1). In other words, in a multiplicative time-series model, we get (Original data values) / (Trend values) × 100 = (T × C × S × I) / (T × C) × 100 = (S × I ) × 100.
This implies that the ratio–to-moving average represents the seasonal and irregular components. - Arrange these percentages according to months or quarter of given years. Find the averages over all months or quarters of the given years.
- If the sum of these indices is not 1200 (or 400 for quarterly figures), multiply then by a correction factor = 1200 / (sum of monthly indices). Otherwise, the 12 monthly averages will be considered as seasonal indices.
Ratio-to-moving-average method[edit]
Let us calculate the seasonal index by the ratio-to-moving-average method from the following data:
| Year/Quarters | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 1996 | 75 | 60 | 54 | 59 |
| 1997 | 86 | 65 | 63 | 80 |
| 1998 | 90 | 72 | 66 | 85 |
| 1999 | 100 | 78 | 72 | 93 |
Now calculations for 4 quarterly moving averages and ratio-to-moving-averages are shown in the below table.
| Year | Quarter | Original Values(Y) | 4 Figures Moving Total | 4 Figures Moving Average | 2 Figures Moving Total | 2 Figures Moving Average(T) | Ratio-to-Moving-Average(%)(Y)/ (T)*100 |
|---|---|---|---|---|---|---|---|
| 1996 | 1 | 75 | — | — | — | ||
| — | — | ||||||
| 2 | 60 | — | — | — | |||
| 248 | 62.00 | ||||||
| 3 | 54 | 126.75 | 63.375 | 85.21 | |||
| 259 | 64.75 | ||||||
| 4 | 59 | 130.75 | 65.375 | 90.25 | |||
| 264 | 66.00 | ||||||
| 1997 | 1 | 86 | 134.25 | 67.125 | 128.12 | ||
| 273 | 68.25 | ||||||
| 2 | 65 | 141.75 | 70.875 | 91.71 | |||
| 294 | 73.50 | ||||||
| 3 | 63 | 148.00 | 74.00 | 85.13 | |||
| 298 | 74.50 | ||||||
| 4 | 80 | 150.75 | 75.375 | 106.14 | |||
| 305 | 76.25 | ||||||
| 1998 | 1 | 90 | 153.25 | 76.625 | 117.45 | ||
| 308 | 77.00 | ||||||
| 2 | 72 | 155.25 | 77.625 | 92.75 | |||
| 313 | 78.25 | ||||||
| 3 | 66 | 159.00 | 79.50 | 83.02 | |||
| 323 | 80.75 | ||||||
| 4 | 85 | 163.00 | 81.50 | 104.29 | |||
| 329 | 82.25 | ||||||
| 1999 | 1 | 100 | 166.00 | 83.00 | 120.48 | ||
| 335 | 83.75 | ||||||
| 2 | 78 | 169.50 | 84.75 | 92.03 | |||
| 343 | 85.75 | ||||||
| 3 | 72 | — | — | — | |||
| — | — | ||||||
| 4 | 93 | — | — | — | |||
| Years/Quarters | 1 | 2 | 3 | 4 | Total |
|---|---|---|---|---|---|
| 1996 | — | — | 85.21 | 90.25 | |
| 1997 | 128.12 | 91.71 | 85.13 | 106.14 | |
| 1998 | 117.45 | 92.75 | 83.02 | 104.29 | |
| 1999 | 120.48 | 92.04 | — | — | |
| Total | 366.05 | 276.49 | 253.36 | 300.68 | |
| Seasonal Average | 122.01 | 92.16 | 84.45 | 100.23 | 398.85 |
| Adjusted Seasonal Average | 122.36 | 92.43 | 84.69 | 100.52 | 400 |
Now the total of seasonal averages is 398.85. Therefore, the corresponding correction factor would be 400/398.85 = 1.00288. Each seasonal average is multiplied by the correction factor 1.00288 to get the adjusted seasonal indices as shown in the above table.
Link relatives method[edit]
1. In an additive time-series model, the seasonal component is estimated as:
- S = Y – (T + C + I )
where
- S : Seasonal values
- Y : Actual data values of the time-series
- T : Trend values
- C : Cyclical values
- I : Irregular values.
2. In a multiplicative time-series model, the seasonal component is expressed in terms of ratio and percentage as
- Seasonal effect
;
However, in practice the detrending of time-series is done to arrive at 
This is done by dividing both sides of 

3. The deseasonalized time-series data will have only trend (T ), cyclical (C ) and irregular (I ) components and is expressed as:
-
- Multiplicative model :
- Multiplicative model :
-
- Additive model: Y – S = (T + S + C + I ) – S = T + C + I
Modeling[edit]
A completely regular cyclic variation in a time series might be dealt with in time series analysis by using a sinusoidal model with one or more sinusoids whose period-lengths may be known or unknown depending on the context. A less completely regular cyclic variation might be dealt with by using a special form of an ARIMA model which can be structured so as to treat cyclic variations semi-explicitly. Such models represent cyclostationary processes.
Another method of modelling periodic seasonality is the use of pairs of Fourier terms. Similar to using the sinusoidal model, Fourier terms added into regression models utilize sine and cosine terms in order to simulate seasonality. However, the seasonality of such a regression would be represented as the sum of sine or cosine terms, instead of a single sine or cosine term in a sinusoidal model. Every periodic function can be approximated with the inclusion of Fourier terms.
The difference between a sinusoidal model and a regression with Fourier terms can be simplified as below:
Sinusoidal Model:
Regression With Fourier Terms:
Seasonal adjustment[edit]
Seasonal adjustment or deseasonalization is any method for removing the seasonal component of a time series. The resulting seasonally adjusted data are used, for example, when analyzing or reporting non-seasonal trends over durations rather longer than the seasonal period. An appropriate method for seasonal adjustment is chosen on the basis of a particular view taken of the decomposition of time series into components designated with names such as «trend», «cyclic», «seasonal» and «irregular», including how these interact with each other. For example, such components might act additively or multiplicatively. Thus, if a seasonal component acts additively, the adjustment method has two stages:
- estimate the seasonal component of variation in the time series, usually in a form that has a zero mean across series;
- subtract the estimated seasonal component from the original time series, leaving the seasonally adjusted series:
.[3]
If it is a multiplicative model, the magnitude of the seasonal fluctuations will vary with the level, which is more likely to occur with economic series.[3] When taking seasonality into account, the seasonally adjusted multiplicative decomposition can be written as 
The multiplicative model can be transformed into an additive model by taking the log of the time series;
SA Multiplicative decomposition: 
Taking log of the time series of the multiplicative model: 
One particular implementation of seasonal adjustment is provided by X-12-ARIMA.
In regression analysis[edit]
In regression analysis such as ordinary least squares, with a seasonally varying dependent variable being influenced by one or more independent variables, the seasonality can be accounted for and measured by including n-1 dummy variables, one for each of the seasons except for an arbitrarily chosen reference season, where n is the number of seasons (e.g., 4 in the case of meteorological seasons, 12 in the case of months, etc.). Each dummy variable is set to 1 if the data point is drawn from the dummy’s specified season and 0 otherwise. Then the predicted value of the dependent variable for the reference season is computed from the rest of the regression, while for any other season it is computed using the rest of the regression and by inserting the value 1 for the dummy variable for that season.
[edit]
It is important to distinguish seasonal patterns from related patterns.
While a seasonal pattern occurs when a time series is affected by the season or the time of the year, such as annual, semiannual, quarterly, etc.
A cyclic pattern, or simply a cycle, occurs when the data exhibit rises and falls in other periods, i.e., much longer (e.g., decadal) or much shorter (e.g., weekly) than seasonal.
A quasiperiodicity is a more general, irregular periodicity.
See also[edit]
- Oscillation
- Periodic function
- Periodicity (disambiguation)
- Photoperiodism
References[edit]
- ^ «Seasonality». |title=Influencing Factors|
- ^ «Archived copy». Archived from the original on 2015-05-18. Retrieved 2015-05-13.
{{cite web}}: CS1 maint: archived copy as title (link) - ^ a b c d e 6.1 Time series components — OTexts.
- ^ 2.1 Graphics — OTexts.
- ^ «time series — What method can be used to detect seasonality in data?». Cross Validated.
- Barnett, A.G.; Dobson, A.J. (2010). Analysing Seasonal Health Data. Springer. ISBN 978-3-642-10747-4.
- Complete Business Statistics (Chapter 12) by Amir D. Aczel.
- Business Statistics: Why and When (Chapter 15) by Larry E. Richards and Jerry J. Lacava.
- Business Statistics (Chapter 16) by J.K. Sharma.
- Business Statistics, a decision making approach (Chapter 18) by David F. Groebner and Patric W. Shannon.
- Statistics for Management (Chapter 15) by Richard I. Levin and David S. Rubin.
- Forecasting: practice and principles by Rob J. Hyndman and George Athansopoulos
External links[edit]
Media related to Seasonality at Wikimedia Commons
- Seasonality at NIST/SEMATECH e-Handbook of Statistical Methods
This article incorporates public domain material from NIST/SEMATECH e-Handbook of Statistical Methods. National Institute of Standards and Technology.