Как найти шаг от периода - Исправление недочетов и поиск решений вместе с Examum.ru

Все курсы > Вводный курс > Занятие 20

Понятие временного ряда

Временной ряд (time series) — это данные, последовательно собранные в регулярные промежутки времени.

К таким данным относятся, например, цены на акции, объемы продаж чего-либо, изменения температуры с течением времени и т.д. Посмотрим на изменение обычных данных и временных рядов.

Основное отличие: перекрестные данные предполагают независимость наблюдений, во временных рядах будущее зависит от прошлого.

Работа с временными рядами предполагает два аспекта:

Анализ временного ряда (time series analysis), т.е. понимание его структуры и закономерностей; и
Моделирование и построение прогноза на будущее (time series forecasting)

Договоримся о терминах:

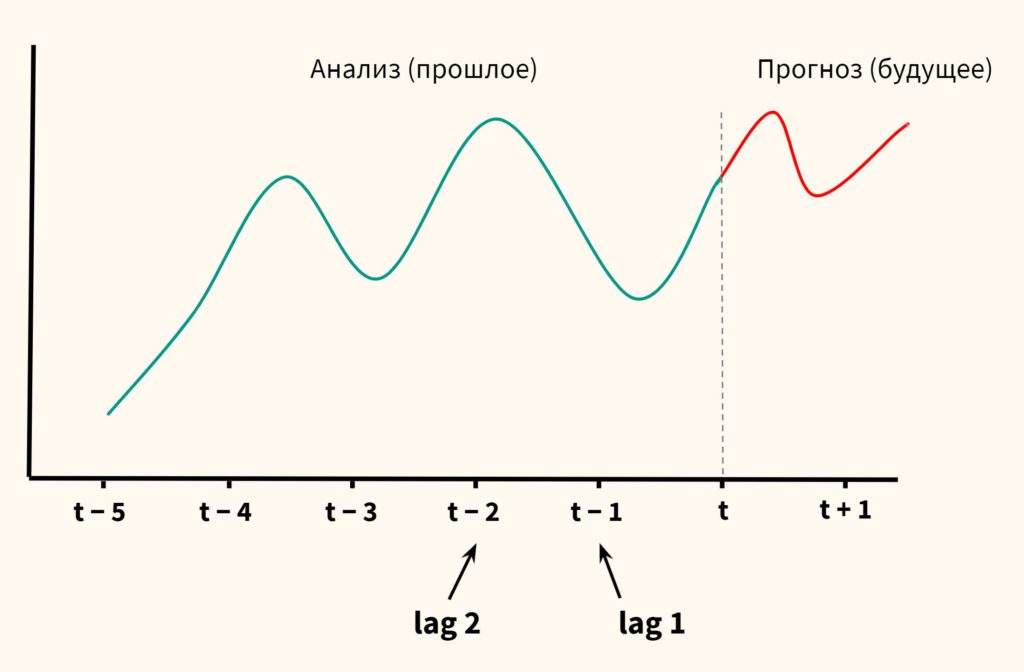
Во-первых, определим нотацию периодов. Временем t обозначим настоящее, t−1, t−2,… прошлое, t+1, t+2,… будущее.
Во-вторых, введем важное понятие временного лага (lag), т.е. запаздывания по сравнению с заданным периодом.

Датасеты

Мы будем использовать два популярных набора данных, а именно (1) ежемесячные данные о количестве пассажиров, перевезенных одной американской авиакомпанией с 1949 по 1960 годы и (2) ежедневные данные о родившихся в Калифорнии в 1959 году девочках.

Подгружать внешние данные в ноутбук Google Colab мы уже умеем. Можем переходить непосредственно к работе с кодом.

Откроем ноутбук к этому занятию⧉

Анализ временных рядов

# импортируем необходимые библиотеки

import pandas as pd

import numpy as np

import matplotlib.pyplot as plt

Импорт данных и работа в библиотеке Pandas

Для начала давайте импортируем данные. Пока что мы будем использовать только первый набор данных с информацией об авиаперевозках.

# импортируем файл с данными о пассажирах

passengers = pd.read_csv(«/content/passengers.csv»)

passengers.head()

Сделаем дату индексом.

# превратим дату в индекс и сделаем изменение постоянным

passengers.set_index(‘Month’, inplace = True)

passengers.head()

Питон воспринимает дату как число. Это не очень удобно, если мы хотим делать срезы и в целом изменять данные во времени. Дату можно преобразовать в специальный объект datetime.

# превратим дату (наш индекс) в объект datetime

passengers.index = pd.to_datetime(passengers.index)

# посмотрим на первые пять дат и на тип данных

passengers.index[:5]

DatetimeIndex([‘1949-01-01’, ‘1949-02-01’, ‘1949-03-01’, ‘1949-04-01’,

‘1949-05-01’],

dtype=’datetime64[ns]’, name=’Month’, freq=None)

Все эти операции также можно проделать в одну строчку.

passengers = pd.read_csv(‘/content/passengers.csv’, index_col = ‘Month’, parse_dates = True)

Теперь мы можем делать срезы за определенный период, например, с августа 1949 по март 1950 года.

passengers[‘1949-08’:‘1950-03’]

Обратите внимание, что в отличие от других перечней в Питоне (например, списков), во временном ряде мы получаем данные и по начальной, и по конечной дате среза (в частности, март 1950 года вошел в наш интервал).

Изменение шага временного ряда, сдвиг и скользящее среднее

Отдельно хотелось бы поговорить про возможность обобщения и изменения данных. Помимо прочего, мы можем изменить шаг (resample) нашего временного ряда, и посмотреть средние показатели перевозок, например, за год.

passengers.resample(rule = ‘AS’).mean().head()

Кроме того, мы можем сдвинуть (shift) наши данные на n периодов вперед или назад.

# произведем сдвиг на два периода (в данном случае месяца) вперед

passengers.shift(2, axis = 0).head()

Что логично, после сдвига первые два значения определяются как пропущенные (NaN или Not a number).

Мы также можем рассчитать скользящее среднее (moving average, rolling average) за n предыдущих периодов. Вначале посмотрим, что это такое.

Теперь давайте рассчитаем его для наших данных. Период, за который рассчитывается скользящее среднее, также называется окном (window).

# рассчитаем скользящее среднее для трех месяцев

passengers.rolling(window = 3).mean().head()

Опять же, так как в данном случае мы использовали три месяца для расчета скользящего среднего, этот показатель недоступен для первых двух значений. В целом, скользящее среднее сглаживает временные показатели (мы это увидим на графике в следующем разделе).

Построение графиков

Для того чтобы построить график временного ряда мы можем воспользоваться инструментами, которые уже содержатся в библиотеке Pandas. Например, простым методом .plot().

График можно усложнить.

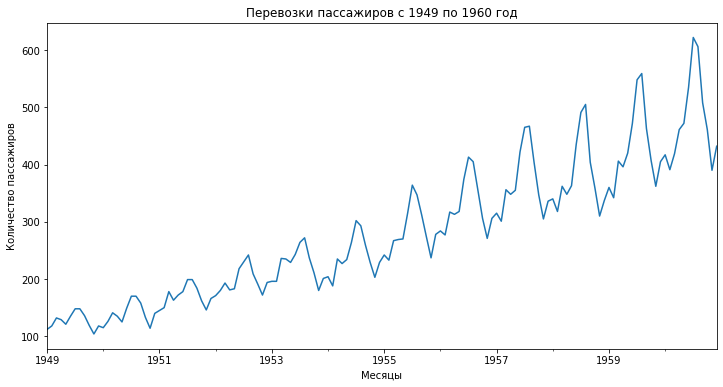
# изменим размер графика, уберем легенду и добавим подписи

ax = passengers.plot(figsize = (12,6), legend = None)

ax.set(title = ‘Перевозки пассажиров с 1949 по 1960 год’, xlabel = ‘Месяцы’, ylabel = ‘Количество пассажиров’)

Визуализацию можно также построить с помощью библиотеки Matplotlib. Давайте выведем на одном графике перевозки пассажиров и скользящее среднее.

# зададим размер графика

plt.figure(figsize = (15,8))

# поочередно зададим кривые (перевозки и скользящее среднее) с подписями и цветом

plt.plot(passengers, label = ‘Перевозки пассажиров по месяцам’, color = ‘steelblue’)

plt.plot(passengers.rolling(window = 12).mean(), label = ‘Скользящее среднее за 12 месяцев’, color = ‘orange’)

# добавим легенду, ее положение на графике и размер шрифта

plt.legend(title = », loc = ‘upper left’, fontsize = 14)

# добавим подписи к осям и заголовки

plt.xlabel(‘Месяцы’, fontsize = 14)

plt.ylabel(‘Количество пассажиров’, fontsize = 14)

plt.title(‘Перевозки пассажиров с 1949 по 1960 год’, fontsize = 16)

# выведем обе кривые на одном графике

plt.show()

Как вы видите, скользящее среднее сильно сглаживает показатели. Также обратите внимание, что так как в данном случае мы взяли окно равное двенадцати месяцам, то первое значение скользящего среднего мы получили только за декабрь 1949 года (самое начало желтой кривой на графике).

В целом не стоит недооценивать важность визуальной оценки ряда на графике. Многие особенности можно выявить именно так.

Разложение временного ряда на компоненты

Выявление компонентов временного ряда (time series decomposition) предполагает его разложение на тренд, сезонность и случайные колебания. Дадим несколько неформальных определений.

Тренд — долгосрочное изменение уровня ряда
Сезонность предполагает циклические изменения уровня ряда с постоянным периодом
Случайные колебания — непрогнозируемое случайное изменение ряда

В Питоне в модуле statsmodels есть функция seasonal_decompose(). Воспользуемся ей для визуализации компонентов ряда.

Перед этим импортируем второй датасет для последующего сравнения.

# для наглядности импортируем второй датасет

# сразу превратим дату в индекс и преобразуем ее в объект datetime

births = pd.read_csv(‘/content/births.csv’, index_col = ‘Date’, parse_dates = True)

births.head(3)

Теперь давайте разложим наш временной ряд по авиаперевозкам на компоненты.

# импортируем функцию seasonal_decompose из statsmodels

from statsmodels.tsa.seasonal import seasonal_decompose

# задаем размер графика

from pylab import rcParams

rcParams[‘figure.figsize’] = 11, 9

# применяем функцию к данным о перевозках

decompose = seasonal_decompose(passengers)

decompose.plot()

plt.show()

Сделаем то же самое с данными о рождаемости.

decompose = seasonal_decompose(births)

decompose.plot()

plt.show()

Как мы видим, графики совершенно разные. В следующем разделе мы изучим это различие более подробно.

Стационарность

Стационарность (stationarity) временного ряда как раз означает, что такие компоненты как тренд и сезонность отсутствуют. Говоря более точно, среднее значение и дисперсия не меняются со смещением во времени.

Понимание того, стационарные ли у нас данные или нестационарные важно для последующего моделирования.

Стационарность процесса можно оценить визуально. Датасет о перевозках демонстрирует очевидный тренд и сезонность, в то время как в наборе данных о рождаемости этого не видно (см. графики выше).

Для более точной оценки стационарности можно применить тест Дики-Фуллера (Dickey-Fuller test). О том, что такое статистический вывод мы с вами уже говорили.

В данном случае гипотезы звучат следующим образом.

Нулевая гипотеза предполагает, что процесс нестационарный
Альтернативная гипотеза соответственно говорит об обратном

Применим этот тест к обоим датасетам. Используем пороговое значение, равное 0,05 (5%).

# импортируем необходимую функцию

from statsmodels.tsa.stattools import adfuller

# передадим ей столбец с данными о перевозках и поместим результат в adf_test

adf_test = adfuller(passengers[‘#Passengers’])

# выведем p-value

print(‘p-value = ‘ + str(adf_test[1]))

p-value = 0.9918802434376409

Как мы видим, вероятность (p-value) для данных о перевозках существенно выше 0,05. Мы не можем отвергнуть нулевую гипотезу. Процесс нестанионарный. Проведем тест для второго набора данных.

# теперь посмотрим на данные о рождаемости

adf_test = adfuller(births[‘Births’])

# выведем p-value

print(‘p-value = ‘ +str(adf_test[1]))

p-value = 5.243412990149865e-05

Результат существенно меньше 5%. Временной ряд стационарен.

Надо сказать, что наша визуальная оценка полностью совпала с математическими вычислениями.

Автокорреляция

Изучая статистику, мы с вами уже познакомились с корреляцией. Корреляция показывает силу взаимосвязи двух переменных и позволяет строить модель.

Автокорреляция также показывает степень взаимосвязи в диапазоне от –1 до 1, но только не двух переменных, а одной и той же переменной в разные моменты времени.

Допустим, у нас есть временной ряд и этот же ряд, взятый с лагом 1, 2 и 3.

Мы можем посчитать автокорреляцию ряда с лагом 1.

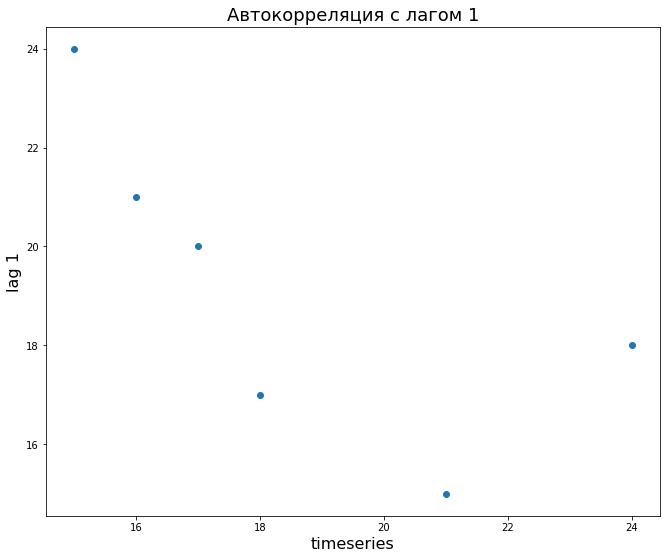
# для начала возьмем искусственные данные

data = np.array([16, 21, 15, 24, 18, 17, 20])

# для сдвига на одно значение достаточно взять этот ряд, начиная со второго элемента

lag_1 = data[1:]

# посчитаем корреляцию для лага 1 (у исходных данных мы убрали последний элемент)

# так как мы получим корреляционную матрицу, возьмем первую строку и второй столбец [0, 1]

np.round(np.corrcoef(data[:—1], lag_1)[0,1], 2)

Визуально это будет выглядеть следующим образом (вспомните график обычной корреляции).

# построим точечную диаграмму

plt.scatter(data[:—1], lag_1)

# добавим подписи

plt.xlabel(‘timeseries’, fontsize = 16)

plt.ylabel(‘lag 1’, fontsize = 16)

plt.title(‘Автокорреляция с лагом 1’, fontsize = 18)

Аналогично мы можем посчитать корреляцию для лагов 2 и 3 и на самом деле любого другого лага. Такие измерения автокорреляции удобно вычислить и изобразить с помощью графика автокорреляционной функции (autocorrelation function, ACF).

# импортируем автокорреляционную функцию (ACF)

from statsmodels.graphics.tsaplots import plot_acf

# применим функцию к нашему набору данных

plot_acf(data, alpha = None)

plt.show()

В частности, мы видим, что автокорреляция ряда с самим собой (первый столбец) равна 1, что логично. Второй столбец (то есть лаг 1) как раз примерно равен – 0,71.

Разные значения, полученные через np.corrcoef() и plot_acf(), объясняются небольшим различием в заложенных в этих функциях формулах.

Теперь построим график ACF для наших данных о перевозках.

# импортируем функцию для построения автокорреляционной функции (ACF)

from statsmodels.graphics.tsaplots import plot_acf

# применим ее к данным о пассажирах

plot_acf(passengers)

plt.show()

Автокорреляция позволяет выявлять тренд и сезонность, а также используется при подборе параметров моделей. В частности, мы видим, что лаг 12 сильнее коррелирует с исходным рядом, чем соседние лаги 10 и 11. То же самое можно сказать и про лаг 24. Такая автокорреляция позволяет предположить наличие (ежегодных) сезонных колебаний.

То, что корреляция постоянно положительная говорит о наличии тренда. Все это согласуется с тем, что мы узнали о данных, когда раскладывали их на компоненты.

Также замечу, что синяя граница позволяет оценить статистическую значимость корреляции. Если столбец выходит за ее пределы, то автокорреляция достаточно сильна и ее можно использовать при построении модели.

Сравним полученный выше график с графиком автокорреляционной функции данных о рождаемости.

# построим аналогичный график для данных о рождаемости

plot_acf(births)

plt.show()

Во-первых, важно отметить, что автокорреляция в данном случае намного слабее. Во-вторых, мы не можем выявить четкой сезонности и тренда.

Моделирование и построение прогноза

На сегодняшнем занятии мы познакомимся с двумя типами моделей: экспоненциальное сглаживание и модель ARMA (и ее более продвинутые версии, ARIMA, SARIMA и SARIMAX).

Экспоненциальное сглаживание

Вновь обратимся к скользящему среднему (см. выше). В этой модели (1) всем предыдущим наблюдениям задавался одинаковый вес и (2) количество таких наблюдений было ограничено (мы называли это размером окна).

Однако логично предположить, что недавние наблюдения более важны для прогноза, чем более отдаленные. Кроме того, мы можем взять все, а не некоторые из имеющихся у нас наблюдений.

В модели экспоненциального сглаживания (exponential smoothing) или экспоненциального скользящего среднего мы как раз (1) берем все предыдущие значения и (2) задаем каждому из наблюдений определенный вес и (экспоненциально) уменьшаем этот вес по мере углубления в прошлое.

Приведем формулу.

$$ hat{y}_{t+1} = alpha cdot y_t + (1-alpha) cdot hat{y}_{t} $$

где ŷ_t+1 — это прогнозное значение, y_t — истинное значение в текущий период, ŷ_t — прогнозное значение в текущий период.

Как мы видим, прогнозное значение зависит как от истинного, так и от прогнозного значений. Важность этих значений определяется параметром альфа, который варьируется от 0 до 1. Чем альфа больше, тем больший вес у истинного наблюдения.

Формула рекурсивна, т.е. каждый раз мы умножаем (1 – α) на очередное прогнозное значение и так до конца временного ряда.

Практика

На Питоне эту модель не сложно прописать руками.

alpha = 0.2

# первое значение совпадает со значением временного ряда

exp_smoothing = [births[‘Births’][0]]

# в цикле for последовательно применяем формулу ко всем элементам ряда

for i in range(1, len(births[‘Births’])):

exp_smoothing.append(alpha * births[‘Births’][i] + (1 — alpha) * exp_smoothing[i — 1])

# выведем прогнозное значение для 366-го дня (1 января 1960 года)

exp_smoothing[—1]

Для временного ряда, состоящего из 365 наблюдений (весь 1959 год), мы получим 365 прогнозных значений (вплоть до 1 января 1960 года включительно).

len(births), len(exp_smoothing)

Теперь добавим эти данные в исходный датафрейм births.

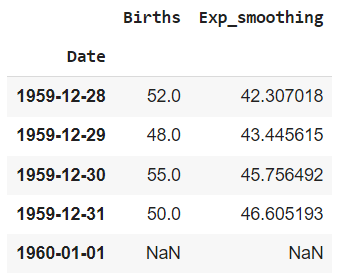
# добавим кривую сглаживаия в качестве столбца в датафрейм

births[‘Exp_smoothing’] = exp_smoothing

births.tail(3)

Единственный нюанс, так как фактические значения описывают период с 1 января по 31 декабря 1959 года, а прогнозные со 2 января 1959 года по 1 января 1960, мы не можем просто их соединить. Второй столбец нужно сдвинуть на один день вперед.

# для этого импортируем класс timedelta

from datetime import timedelta

# возьмём последний индекс (31 декабря 1959 года)

last_date = births.iloc[[—1]].index

# # «прибавим» один день

last_date = last_date + timedelta(days = 1)

last_date

# добавим его в датафрейм

births = births.append(pd.DataFrame(index = last_date))

# значения за этот день останутся пустыми

births.tail()

Сдвинем второй столбец.

births[‘Exp_smoothing’] = births[‘Exp_smoothing’].shift(1)

И посмотрим на начало и конец датафрейма.

# как и должно быть первое прогнозное значение совпадает с предыдущим фактическим

births.head()

# и у нас есть прогноз на один день вперед

births.tail()

Проверим правильность расчетов, найдя последнее прогнозное значение по формуле выше.

$$ hat{y}_{366} = 0,2 times y_{355} + 0,8 times hat{y}_{355} = 0,2 times 50 + 0,8 times 45.756492 = 46.6051936 $$

Результаты совпадают. Теперь выведем фактические и прогнозные значения на графике.

# зададим размер

plt.figure(figsize = (15,8))

# выведем данные о рождаемости и кривую экспоненциального сглаживания

plt.plot(births[‘Births’], label = ‘Данные о рождаемости’, color = ‘steelblue’)

plt.plot(births[‘Exp_smoothing’], label = ‘Экспоненциальное сглаживание’, color = ‘orange’)

# добавим легенду, ее положение на графике и размер шрифта

plt.legend(title = », loc = ‘upper left’, fontsize = 14)

# добавим подписи к осям и заголовки

plt.ylabel(‘Количество родившихся’, fontsize = 14)

plt.xlabel(‘Месяцы’, fontsize = 14)

plt.title(‘Рождаемость в 1959 году. Прогноз на 1 января 1960 года’, fontsize = 16)

plt.show()

Очень советую в качестве упражнения попробовать построить график с несколькими значениями альфа от 0 до 1.

Модель экспоненциального сглаживания можно усложнить и тогда она будет улавливать тренд и сезонность. Кроме того, усложненные модели способны предсказывать более одного значения (обратите внимание, здесь мы смогли сделать прогноз лишь на один день вперёд).

Работа над ошибками. На видео в формуле экспоненциального сглаживания есть ошибка.

alpha = 0.2

# первое значение совпадает со значением временного ряда

exp_smoothing = [births[‘Births’][0]]

# в цикле for последовательно применяем формулу ко всем элементам ряда

for i in range(0, len(births[‘Births’])):

exp_smoothing.append(alpha * births[‘Births’][i] + (1 — alpha) * exp_smoothing[i — 1])

Должно быть.

alpha = 0.2

# первое значение совпадает со значением временного ряда

exp_smoothing = [births[‘Births’][0]]

# в цикле for последовательно применяем формулу ко всем элементам ряда

for i in range(1, len(births[‘Births’])):

exp_smoothing.append(alpha * births[‘Births’][i] + (1 — alpha) * exp_smoothing[i — 1])

Как вы видите расчет прогнозного значения в цикле следовало начинать с наблюдения
[births[‘Births’][1], а не
[births[‘Births’][0]. Из-за этого последующие результаты оказались некорректными. В лекции и ноутбуке код исправлен.

Теперь поговорим про модели семейства ARMA.

Модель ARMA

Модель ARMA состоит из двух компонентов.

компоненты модели ARMA: авторегрессия и скользящее среднее

Авторегрессия (autoregressive model, AR) — это регрессия ряда на собственные значения в прошлом. Другими словами, наши признаки в модели обычной регрессии мы заменяем значениями той же переменной, но за предыдущие периоды.

Когда мы прогнозируем значение в период t с помощью данных за предыдущий период (AR(1)), уравнение будет выглядеть следующим образом.

$$ y_t = c + varphi cdot y_{t-1} $$

где c — это константа, $varphi$ — вес модели, y_t–1 — значение в период t – 1.

То, сколько предыдущих периодов использовать определяется параметром p. Обычно записывается как AR(p).

Модель скользящего среднего (moving average, MA) помогает учесть случайные колебания или отклонения (ошибки) истинного значения от прогнозного. Можно также сказать, что модель скользящего среднего — это авторегрессия на ошибку.

Обратите внимание, что скользящее среднее временного ряда, которое мы рассмотрели выше, и модель скользящего среднего — это разные понятия.

Если использовать ошибку только предыдущего наблюдения, то уравнение будет выглядеть следующим образом.

$$ y_t = mu + varphi cdot varepsilon_{t-1} $$

где μ — это среднее значение временного ряда, φ — вес модели, ε_t–1 — ошибка в период t – 1.

Такую модель принято называть моделью скользящего среднего с параметром q = 1 или MA(1). Разумеется, параметр q может принимать и другие значения (MA(q)).

Модель ARMA с параметрами (или как еще говорят порядками, orders) p и q или ARMA(p, q) позволяет описать любой стационарный временной ряд.

ARMA предполагает, что в данных отсутствует тренд и сезонность (данные стационарны). Если данные нестационарны, нужно использовать более сложные версии этих моделей:

ARIMA, здесь добавляется компонент Integrated (I), который отвечает за удаление тренда (сам процесс называется дифференцированием); и
SARIMA, эта модель учитывает сезонность (Seasonality, S)
SARIMAX включает еще и внешние или экзогенные факторы (eXogenous factors, отсюда и буква X в названии), которые напрямую не учитываются моделью, но влияют на нее.

Параметров у модели SARIMAX больше. Их полная версия выглядит как SARIMAX(p, d, q) x (P, D, Q, s). В данном случае, помимо известных параметров p и q, у нас появляется параметр d, отвечающий за тренд, а также набор параметров (P, D, Q, s), отвечающих за сезонность.

Теперь давайте воспользуемся моделью SARIMAX для прогнозирования авиаперевозок.

Практика

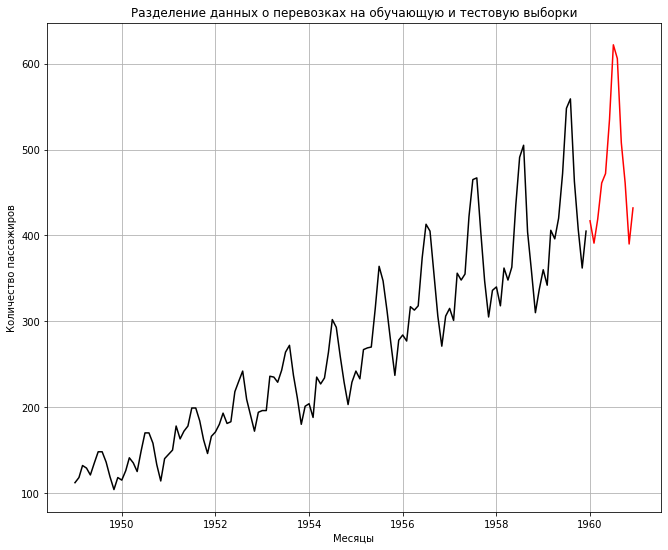
В первую очередь нужно разбить данные на обучающую и тестовую выборки. Как мы помним, у нас есть данные с января 1949 года по декабрь 1960 года.

# обучающая выборка будет включать данные до декабря 1959 года включительно

train = passengers[:‘1959-12’]

# тестовая выборка начнется с января 1960 года (по сути, один год)

test = passengers[‘1960-01’:]

Посмотрим на разделение на графике.

plt.plot(train, color = «black»)

plt.plot(test, color = «red»)

# заголовок и подписи к осям

plt.title(‘Разделение данных о перевозках на обучающую и тестовую выборки’)

plt.ylabel(‘Количество пассажиров’)

plt.xlabel(‘Месяцы’)

# добавим сетку

plt.grid()

plt.show()

Далее нам нужно обучить модель. При обучении модели SARIMAX, самое важное — правильно подобрать гиперпараметры, о которых говорилось выше. Процесс подбора гиперпараметров достаточно сложен, и сегодня мы воспользуемся уже готовыми значениями.

# принудительно отключим предупреждения системы

import warnings

warnings.simplefilter(action = ‘ignore’, category = Warning)

# обучим модель с соответствующими параметрами, SARIMAX(3, 0, 0)x(0, 1, 0, 12)

# импортируем класс модели

from statsmodels.tsa.statespace.sarimax import SARIMAX

# создадим объект этой модели

model = SARIMAX(train,

order = (3, 0, 0),

seasonal_order = (0, 1, 0, 12))

# применим метод fit

result = model.fit()

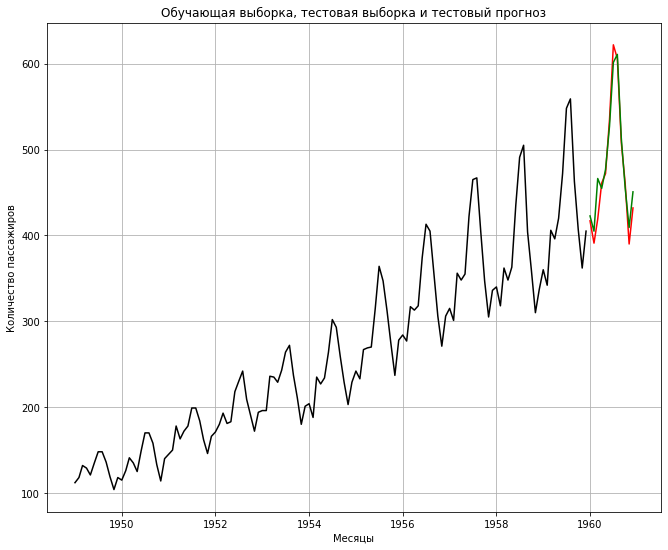
Теперь мы готовы делать прогноз. Вначале сделаем тестовый прогноз, соответствующий периоду тестовой выборки (1960 год), для того, чтобы оценить качество работы модели.

# тестовый прогнозный период начнется с конца обучающего периода

start = len(train)

# и закончится в конце тестового

end = len(train) + len(test) — 1

# применим метод predict

predictions = result.predict(start, end)

predictions

1960-01-01 422.703385

1960-02-01 404.947178

1960-03-01 466.293258

1960-04-01 454.781295

1960-05-01 476.848627

1960-06-01 527.162825

1960-07-01 601.449809

1960-08-01 610.821690

1960-09-01 513.229987

1960-10-01 455.692618

1960-11-01 409.200046

1960-12-01 450.754160

Freq: MS, Name: predicted_mean, dtype: float64

Построим соответствующий график.

# выведем три кривые (обучающая, тестовая выборка и тестовый прогноз)

plt.plot(train, color = «black»)

plt.plot(test, color = «red»)

plt.plot(predictions, color = «green»)

# заголовок и подписи к осям

plt.title(«Обучающая выборка, тестовая выборка и тестовый прогноз»)

plt.ylabel(‘Количество пассажиров’)

plt.xlabel(‘Месяцы’)

# добавим сетку

plt.grid()

plt.show()

В целом модель хорошо описывает временной ряд. Мы также можем использовать знакомые нам метрики среднеквадратической ошибки (MSE) и корня среднеквадратической ошибки (RMSE) для оценки качества.

# импортируем метрику

from sklearn.metrics import mean_squared_error

# рассчитаем MSE

print(mean_squared_error(test, predictions))

# и RMSE

print(np.sqrt(mean_squared_error(test, predictions)))

317.39564617023217

17.815601201481588

Теперь можно делать прогноз на будущее. Возьмём горизонт равный трем годам (1961, 1962 и 1963 год). Всего должно получиться 36 прогнозных значений.

# прогнозный период с конца имеющихся данных

start = len(passengers)

# и закончится 36 месяцев спустя

end = (len(passengers) — 1) + 3 * 12

# теперь построим прогноз на три года вперед

forecast = result.predict(start, end)

# посмотрим на весь 1963 год

forecast[—12:]

1963-01-01 518.603433

1963-02-01 497.908985

1963-03-01 556.406781

1963-04-01 542.133831

1963-05-01 561.524759

1963-06-01 609.244560

1963-07-01 681.016634

1963-08-01 687.950661

1963-09-01 587.995797

1963-10-01 528.167673

1963-11-01 479.454532

1963-12-01 518.856113

Freq: MS, Name: predicted_mean, dtype: float64

Посмотрим на прогнозные значения на графике.

# выведем две кривые (фактические данные и прогноз на будущее)

plt.plot(passengers, color = ‘black’)

plt.plot(forecast, color = ‘blue’)

# заголовок и подписи к осям

plt.title(‘Фактические данные и прогноз на будущее’)

plt.ylabel(‘Количество пассажиров’)

plt.xlabel(‘Месяцы’)

# добавим сетку

plt.grid()

plt.show()

Подведем итог

Занятие было насыщенным. Мы узнали, (1) чем временные ряды отличаются от структурных данных, (2) научились анализировать временные ряды с помощью Питона, а также (3) строить графики.

При прогнозировании временных рядов мы (4) использовали модель экспоненциального сглаживания и (5) познакомились с семейством моделей ARMA.

Вопросы для закрепления

Чем структурные/перекрестные данные отличаются от временных рядов?

Посмотреть правильный ответ

Ответ: во временных рядах значение наблюдаемой величины зависит от времени, в структурных данных — от других величин или переменных.

Что определяет параметр альфа в модели экспоненциального сглаживания?

Посмотреть правильный ответ

Ответ: значение параметра альфа близкое к единице повышает значимость текущего истинного наблюдения, если альфа близка к нулю — превалирует предыдущее прогнозное значение.

Из каких компонентов состоит модель ARMA?

Посмотреть правильный ответ

Ответ: модель ARMA состоит из компонента авторегрессии (AR), т.е. регрессии на собственные значения в прошлом, и модели скользящего среднего (MA), учитывающей отклонение от среднего значения или ошибку.

В рамках вводного курса осталась одна тема, основы нейронных сетей.

Ответы на вопросы

Вопрос. Вы не могли бы более детально рассказать, как подбираются параметры в модели SARIMAX. В частности, как были подобраны параметры (3, 0, 0)x(0, 1, 0, 12)?

Ответ. Параметры SARIMAX можно подобрать с помощью функции auto_arima. Выбор наиболее удачных параметров осуществляется на основе определенного критерия.

По умолчанию используется, так называемый, Akaike Information Criterion или AIC, который рассчитывается для каждой комбинации параметров. Чем ниже AIC модели, тем лучше.

Я привел код auto_arima в конце ноутбука⧉.

Вопрос. У меня уточнение: скажите, там, где мы считаем экспоненциальное сглаживание,

# в цикле for последовательно применяем формулу ко всем элементам ряда

for i in range(0, len(births[‘Births’])):

exp_smoothing.append(alpha * births[‘Births’][i] + (1 — alpha) * exp_smoothing[i — 1])

там, может быть, нужно в цикле
for i in range(0, len(births[‘Births’])): поставить начальное значение счетчика = 1:
for i in range(1, len(births[‘Births’]))?

Я проверял выкладки в Экселе — и, когда цикл стартует с нуля, получается ошибка. Возможно, это потому, что в начале списка получается задублированное значение первого элемента (мы сначала вручную вносим в список
[births[‘Births’][0]], а потом это же делаем на первой итерации, когда значение счетчика = 0)

Ответ. Да, действительно, первое прогнозное значение мы вносим вручную (оно совпадает с первым фактическим значением), поэтому должно быть

for i in range(1, len(births[‘Births’])):

Внес изменения в ноутбук и текст лекции.

Источник

Всем привет. Строю график. Нужна формула, которая на основании минимального и максимального значений задаёт интервал (шаг) между отсчётами. То бишь допустим, что макс=95; мин=8; интервал при этом, примерно, должен составлять около ~5. Или же макс=672; мин=35; интервал при этом, примерно, должен составлять ~50. Заранее спасибо за помощь.

Вопрос задан

более трёх лет назад
912 просмотров

Источник

Чтобы описать колебательные процессы и отличить одни колебания от других, используют 6 характеристик. Они называются так (рис. 1):

амплитуда,
период,
частота,
циклическая частота,
фаза,
начальная фаза.

Рис. 1. Основные характеристики колебаний – это амплитуда, период и начальная фаза

Такие величины, как амплитуду и период, можно определить по графику колебаний.

Начальную фазу, так же, определяют по графику, с помощью интервала времени (large Delta t), на который относительно нуля сдвигается начало ближайшего периода.

Частоту и циклическую частоту вычисляют из найденного по графику периода, по формулам. Они находятся ниже в тексте этой статьи.

А фазу определяют с помощью формулы, в которую входит интересующий нас момент времени t колебаний. Читайте далее.

Что такое амплитуда

Амплитуда – это наибольшее отклонение величины от равновесия, то есть, максимальное значение колеблющейся величины.

Измеряют в тех же единицах, в которых измерена колеблющаяся величина. К примеру, когда рассматривают механические колебания, в которых изменяется координата, амплитуду измеряют в метрах.

В случае электрических колебаний, в которых изменяется заряд, ее измеряют в Кулонах. Если колеблется ток – то в Амперах, а если – напряжение, то в Вольтах.

Часто обозначают ее, приписывая к букве, обозначающей амплитуду индекс «0» снизу.

К примеру, пусть колеблется величина ( large x ). Тогда символом ( large x_{0} ) обозначают амплитуду колебаний этой величины.

Иногда для обозначения амплитуды используют большую латинскую букву A, так как это первая буква английского слова «amplitude».

С помощью графика амплитуду можно определить так (рис. 2):

Рис. 2. Амплитуда – это максимальное отклонение от горизонтальной оси либо вверх, либо вниз. Горизонтальная ось проходит через уровень нуля на оси, на которой отмечены амплитуды

Что такое период

Когда колебания повторяются точно, изменяющаяся величина принимает одни и те же значения через одинаковые кусочки времени. Такой кусочек времени называют периодом.

Обозначают его обычно большой латинской буквой «T» и измеряют в секундах.

( large T left( c right) ) – период колебаний.

Одна секунда – достаточно большой интервал времени. Поэтому, хотя период и измеряют в секундах, но для большинства колебаний он будет измеряться долями секунды.

Чтобы по графику колебаний определить период (рис. 3), нужно найти два одинаковых значения колеблющейся величины. После, провести от этих значений к оси времени пунктиры. Расстояние между пунктирами – это период колебаний.

Рис. 3. Период колебаний – это горизонтальное расстояние между двумя похожими точками на графике

Период – это время одного полного колебания.

На графике период найти удобнее одним из таких способов (рис. 4):

Рис. 4. Удобно определять период, как расстояние между двумя соседними вершинами, либо между двумя впадинами

Что такое частота

Обозначают ее с помощью греческой буквы «ню» ( large nu ).

Частота отвечает на вопрос: «Сколько полных колебаний выполняется за одну секунду?» Или же: «Сколько периодов умещается в интервал времени, равный одной секунде?».

Поэтому, размерность частоты — это единицы колебаний в секунду:

( large nu left( frac{1}{c} right) ).

Иногда в учебниках встречается такая запись ( large displaystyle nu left( c^{-1} right) ), потому, что по свойствам степени ( large displaystyle frac{1}{c} = c^{-1} ).

Начиная с 1933 года частоту указывают в Герцах в честь Генриха Рудольфа Герца. Он совершил значимые открытия в физике, изучал колебания и доказал, что существуют электромагнитные волны.

Одно колебание в секунду соответствует частоте в 1 Герц.

[ large displaystyle boxed{ frac{ 1 text{колебание}}{1 text{секунда}} = 1 text{Гц} }]

Чтобы с помощью графика определить частоту, нужно на оси времени определить период. А затем посчитать частоту по такой формуле:

[ large boxed{ nu = frac{1}{T} }]

Существует еще один способ определить частоту с помощью графика колеблющейся величины. Нужно отмерить на графике интервал времени, равный одной секунде, и сосчитать количество периодов колебаний, уместившихся в этот интервал (рис. 5).

Рис. 5. На графике частота – это количество периодов, уместившихся в одну секунду

Что такое циклическая частота

Колебательное движение и движение по окружности имеют много общего – это повторяющиеся движения. Одному полному обороту соответствует угол (large 2pi) радиан. Поэтому, кроме интервала времени 1 секунда, физики используют интервал времени, равный (large 2pi) секунд.

Число полных колебаний для такого интервала времени, называется циклической частотой и обозначается греческой буквой «омега»:

( large displaystyle omega left( frac{text{рад}}{c} right) )

Примечание: Величину ( large omega ) так же называют круговой частотой, а еще — угловой скоростью (ссылка).

Циклическая частота отвечает на вопрос: «Сколько полных колебаний выполняется за (large 2pi) секунд?» Или же: «Сколько периодов умещается в интервал времени, равный (large 2pi) секунд?».

Обычная ( large nu ) и циклическая ( large omega ) частота колебаний связаны формулой:

[ large boxed{ omega = 2pi cdot nu }]

Слева в формуле количество колебаний измеряется в радианах на секунду, а справа – в Герцах.

Чтобы с помощью графика колебаний определить величину ( large omega ), нужно сначала найти период T.

Затем, воспользоваться формулой ( large displaystyle nu = frac{1}{T} ) и вычислить частоту ( large nu ).

И только после этого, с помощью формулы ( large omega = 2pi cdot nu ) посчитать циклическую ( large omega ) частоту.

Для грубой устной оценки можно считать, что циклическая частота превышает обычную частоту примерно в 6 раз численно.

Определить величину ( large omega ) по графику колебаний можно еще одним способом. На оси времени отметить интервал, равный (large 2pi), а затем, сосчитать количество периодов колебаний в этом интервале (рис. 6).

Рис. 6. На графике циклическая (круговая) частота – это количество периодов, уместившихся в 2 пи секунд

Что такое начальная фаза и как определить ее по графику колебаний

Отклоним качели на некоторый угол от равновесия и будем удерживать их в таком положении. Когда мы отпустим их, качели начнут раскачиваться. А старт колебаний произойдет из угла, на который мы их отклонили.

Такой, начальный угол отклонения, называют начальной фазой колебаний. Обозначим этот угол (рис. 7) какой-нибудь греческой буквой, например, (large varphi_{0} ).

(large varphi_{0} left(text{рад} right) ) — начальная фаза, измеряется в радианах (или градусах).

Начальная фаза колебаний – это угол, на который мы отклонили качели, перед тем, как их отпустить. Из этого угла начнется колебательный процесс.

Рис. 7. Угол отклонения качелей перед началом колебаний

Рассмотрим теперь, как величина (large varphi_{0} ) влияет на график колебаний (рис. 8). Для удобства будем считать, что мы рассматриваем колебания, которые происходят по закону синуса.

Кривая, обозначенная черным на рисунке, начинает период колебаний из точки t = 0. Эта кривая является «чистым», не сдвинутым синусом. Для нее величину начальной фазы (large varphi_{0} ) принимаем равной нулю.

Рис. 8. Вертикальное положение стартовой точки в момент времени t = 0 и сдвиг графика по горизонтали определяется начальной фазой

Вторая кривая на рисунке обозначена красным цветом. Начало ее периода сдвинуто вправо относительно точки t = 0. Поэтому, для красной кривой, начавшей новый период колебаний спустя время (large Delta t), начальный угол (large varphi_{0} ) будет отличаться от нулевого значения.

Определим угол (large varphi_{0} ) с помощью графика колебаний.

Обратим внимание (рис. на то, что время, лежащее на горизонтальной оси, измеряется в секундах, а величина (large varphi_{0} ) — в радианах. Значит, нужно связать формулой кусочек времени (large Delta t) и соответствующий ему начальный угол (large varphi_{0} ).

Как вычислить начальный угол по интервалу смещения

Алгоритм нахождения начального угла состоит из нескольких несложных шагов.

Сначала определим интервал времени, обозначенный синими стрелками на рисунке. На осях большинства графиков располагают цифры, по которым это можно сделать. Как видно из рис. 8, этот интервал (large Delta t) равен 1 сек.
Затем определим период. Для этого отметим одно полное колебание на красной кривой. Колебание началось в точке t = 1, а закончилось в точке t =5. Взяв разность между этими двумя точками времени, получим значение периода.

[large T = 5 – 1 = 4 left( text{сек} right)]

Из графика следует, что период T = 4 сек.

Рассчитаем теперь, какую долю периода составляет интервал времени (large Delta t). Для этого составим такую дробь (large displaystyle frac{Delta t }{T} ):

[large frac{Delta t }{T} = frac{1}{4} ]

Полученное значение дроби означает, что красная кривая сдвинута относительно точки t = 0 и черной кривой на четверть периода.

Нам известно, что одно полное колебание — один полный оборот (цикл), синус (или косинус) совершает, проходя каждый раз угол (large 2pi ). Найдем теперь, как связана найденная доля периода с углом (large 2pi ) полного цикла.

Для этого используем формулу:

[large boxed{ frac{Delta t }{T} cdot 2pi = varphi_{0} }]

(large displaystyle frac{1}{4} cdot 2pi = frac{pi }{2} =varphi_{0} )

Значит, интервалу (large Delta t) соответствует угол (large displaystyle frac{pi }{2} ) – это начальная фаза для красной кривой на рисунке.

В заключение обратим внимание на следующее. Начало ближайшего к точке t = 0 периода красной кривой сдвинуто вправо. То есть, кривая запаздывает относительно «чистого» синуса.

Чтобы обозначить запаздывание, будем использовать знак «минус» для начального угла:

[large varphi_{0} = — frac{pi }{2} ]

Примечание: Если на кривой колебаний начало ближайшего периода лежит левее точки t = 0, то в таком случае, угол (large displaystyle frac{pi }{2} ) имеет знак «плюс».

Для не сдвинутого влево, либо вправо, синуса или косинуса, начальная фаза нулевая (large varphi_{0} = 0 ).

Для синуса или косинуса, сдвинутого влево по графику и опережающего обычную функцию, начальная фаза берется со знаком «+».

А если функция сдвинута вправо и запаздывает относительно обычной функции, величину (large varphi_{0} ) записываем со знаком «-».

Примечания:

Физики начинают отсчет времени из точки 0. Поэтому, время в задачах будет величиной не отрицательной.
На графике колебаний начальная фаза ( varphi_{0}) влияет на вертикальный сдвиг точки, из которой стартует колебательный процесс. Значит, можно для простоты сказать, что колебания имеют начальную точку.

Благодаря таким допущениям график колебаний при решении большинства задач можно изображать, начиная из окрестности нуля и преимущественно в правой полуплоскости.

Что такое фаза колебаний

Рассмотрим еще раз обыкновенные детские качели (рис. 9) и угол их отклонения от положения равновесия. С течением времени этот угол изменяется, то есть, он зависит от времени.

Рис. 9. Угол отклонения от равновесия – фаза, изменяется в процессе колебаний

В процессе колебаний изменяется угол отклонения от равновесия. Этот изменяющийся угол называют фазой колебаний и обозначают (varphi).

Различия между фазой и начальной фазой

Существуют два угла отклонения от равновесия – начальный, он задается перед началом колебаний и, угол, изменяющийся во время колебаний.

Первый угол называют начальной ( varphi_{0}) фазой (рис. 10а), она считается неизменной величиной. А второй угол – просто ( varphi) фазой (рис. 10б) – это величина переменная.

Рис. 10. Перед началом колебаний задаем начальную фазу — начальный угол отклонения от равновесия. А угол, который изменяется во время колебаний, называют фазой

Как на графике колебаний отметить фазу

На графике колебаний фаза (large varphi) выглядит, как точка на кривой. С течением времени эта точка сдвигается (бежит) по графику слева направо (рис. 11). То есть, в разные моменты времени она будет находиться на различных участках кривой.

На рисунке отмечены две крупные красные точки, они соответствуют фазам колебаний в моменты времени t1 и t2.

Рис. 11. На графике колебаний фаза – это точка, скользящая по кривой. В различные моменты времени она находится в разных положениях на графике

А начальная фаза на графике колебаний выглядит, как место, в котором находится точка, лежащая на кривой колебаний, в момент времени t=0. На рисунке дополнительно присутствует одна мелкая красная точка, она соответствует начальной фазе колебаний.

Как определить фазу с помощью формулы

Пусть нам известны величины (large omega) — циклическая частота и (large varphi_{0}) — начальная фаза. Во время колебаний эти величины не изменяются, то есть, являются константами.

Время колебаний t будет величиной переменной.

Фазу (large varphi), соответствующую любому интересующему нас моменту t времени, можно определить из такого уравнения:

[large boxed{ varphi = omega cdot t + varphi_{0} }]

Левая и правая части этого уравнения имеют размерность угла (т. е. измеряются в радианах, или градусах). А подставляя вместо символа t в это уравнение интересующие нас значения времени, можно получать соответствующие им значения фазы.

Что такое разность фаз

Обычно понятие разности фаз применяют, когда сравнивают два колебательных процесса между собой.

Рассмотрим два колебательных процесса (рис. 12). Каждый имеет свою начальную фазу.

Обозначим их:

( large varphi_{01}) – для первого процесса и,

( large varphi_{02}) – для второго процесса.

Рис. 12. Для двух колебаний можно ввести понятие разности фаз

Определим разность фаз между первым и вторым колебательными процессами:

[large boxed{ Delta varphi = varphi_{01} — varphi_{02} }]

Величина (large Delta varphi ) показывает, на сколько отличаются фазы двух колебаний, она называется разностью фаз.

Как связаны характеристики колебаний — формулы

Движение по окружности и колебательное движение имеют определенную схожесть, так как эти виды движения могут быть периодическими.

Поэтому, основные формулы, применимые для движения по окружности, подойдут так же, для описания колебательного движения.

Связь между периодом, количеством колебаний и общим временем колебательного процесса:

[large boxed{ T cdot N = t }]

( large T left( c right) ) – время одного полного колебания (период колебаний);

( large N left( text{шт} right) ) – количество полных колебаний;

( large t left( c right) ) – общее время для нескольких колебаний;

Период и частота колебаний связаны так:

[large boxed{ T = frac{1}{nu} }]

(large nu left( text{Гц} right) ) – частота колебаний.

Количество и частота колебаний связаны формулой:

[large boxed{ N = nu cdot t}]

Связь между частотой и циклической частотой колебаний:

[large boxed{ nu cdot 2pi = omega }]

(large displaystyle omega left( frac{text{рад}}{c} right) ) – циклическая (круговая) частота колебаний.

Фаза и циклическая частота колебаний связаны так:

[large boxed{ varphi = omega cdot t + varphi_{0} }]

(large varphi_{0} left( text{рад} right) ) — начальная фаза;

(large varphi left( text{рад} right) ) – фаза (угол) в выбранный момент времени t;

Между фазой и количеством колебаний связь описана так:

[large boxed{ varphi = N cdot 2pi }]

Интервал времени (large Delta t ) (сдвигом) и начальная фаза колебаний связаны:

[large boxed{ frac{Delta t }{T} cdot 2pi = varphi_{0} }]

(large Delta t left( c right) ) — интервал времени, на который относительно точки t=0 сдвинуто начало ближайшего периода.

Источник

Что такое шаг арифметической прогрессии?

Если для некой последовательности величина разности между соседними членами будет величиной постоянной, то такую последовательность называют арифметической.

Рассмотрим последовательность: a1, a2, a3, a4, a5.

Где d у нас некая постоянная величина, которую обычно называют шагом арифметической прогрессии.

Примеры арифметических прогрессий:

5, 10, 15, 20, 25. Здесь мы имеем арифметическую прогрессию с шагом 5 (10-5=5).

Каковы 6 шага к решению уравнения?

Точно так же, каковы 4 шага к решению уравнения? У нас есть 4 способа решения одношаговых уравнений: Сложение, вычитание, умножение и деление. Если мы прибавим одно и то же число к обеим частям уравнения, обе стороны останутся равными. Если мы вычтем одно и то же число из обеих частей уравнения, обе части останутся равными.

Какие 3 шагов для решения уравнения?

Похожие страницы:Блог

Какие есть 3 вида налогов?

Как найти среднюю точку между двумя точками?

Как вы делаете кадровые прогнозы?

Как найти начальную скорость, зная только время?

Каковы шаги решения стандартного уравнения или неравенства? Шаг 1: Распределите 2 на (x + 2), умножив на 2. Шаг 2: Объедините одинаковые термины, вычтя 9 из 15 (15 – 9 = 6). Шаг 3: Переместите все переменные в одну часть уравнения, вычитая 2x из обеих сторон. Шаг 4: Вычтите 6 с обеих сторон.

Во-вторых, каково золотое правило решения уравнений? Делайте с одной частью уравнения то, что вы делаете с другой!

Если мы что-то надеваем или снимаем с одной стороны, шкала (или уравнение) становится несбалансированной. При решении математических уравнений мы должны всегда сохраняйте баланс «шкалы» (или уравнения), чтобы обе стороны ВСЕГДА были равны.

Каков первый шаг алгебры?

Самое первое, что вам нужно освоить в алгебре, это понятие переменной. Переменные — это буквы, которые служат заполнителями для чисел, значение которых вам неизвестно. Так, например, в уравнении 1 + 2 = x, x является заполнителем для 3, который должен занимать другую сторону уравнения.

тогда Как вы решаете простые уравнения?

Что такое одношаговое уравнение? Одношаговое уравнение уравнение, для решения которого требуется один шаг. Решать, используйте обратную операцию, чтобы изолировать переменную саму по себе. Помните, что вы делаете с одной стороной, вы должны делать и с другой. Чтобы проверить решение, просто подставьте значение в переменную, чтобы увидеть, верно ли уравнение.

Что такое пятишаговый метод математики?

Как сделать многошаговый?

Что такое решения в математике?

Научные определения решения

Математика Значение или значения, которые при замене переменной в уравнении делают уравнение верным. Например, решения уравнения x2 = 4 равны 2 и -2.

Что такое пример уравнения? Уравнение — это математическое предложение, в котором две равные стороны разделены знаком равенства. 4 + 6 = 10 это пример уравнения. Мы можем видеть слева от знака равенства 4 + 6 и справа от знака равенства 10.… Например, 12 — это коэффициент в уравнении 12n = 24.

Что является правильным первым шагом в решении неравенства?

Ответ: Первым шагом в решении данного неравенства является использовать распределительное свойство и открыть скобки, то есть -8x + 4 > 5 — 3x.

Можешь объяснить мне алгебру?

Алгебра помогает в представлении проблем или ситуаций в виде математических выражений. Он включает в себя переменные, такие как x, y, z, и математические операции, такие как сложение, вычитание, умножение и деление, для формирования осмысленного математического выражения. … Простой пример выражения в алгебре: 2x + 4 = 8.

Что на первом месте в математических уравнениях? Порядок операций можно запомнить по аббревиатуре PEMDAS, которая означает: круглые скобки, показатели степени, умножение и деление слева направо, сложение и вычитание слева направо. Первый, упрости скобки. Затем сделайте показатели. Далее умножайте.

Что обозначают буквы в алгебре? В алгебраических выражениях буквы представляют переменные. Эти буквы на самом деле являются замаскированными числами. В этом выражении переменные x и y. Мы называем эти буквы «переменными», потому что числа, которые они представляют, могут быть разными, то есть мы можем заменить буквы в выражении одним или несколькими числами.

Как начать преподавать алгебру?

8 нестандартных идей для преподавания алгебры и геометрии

Используйте интересные видео. …
Добавьте художественный компонент в подход STEAM. …
Свяжите своих учеников с личным тренером по математике. …
Сделайте это игрой! …
Войдите в мир реалити-шоу. …
Используйте примеры из реальной жизни. …
Рассмешите их. …
Используйте стены слов.

Что такое базовая алгебра? Основная алгебра область математики, которая на шаг абстрактнее арифметики. … Алгебра вводит переменную, которая обозначает неизвестное число или может быть заменена целой группой чисел.

Могу ли я сам выучить алгебру?

Вы можете сами выучить алгебру, так как их много. образовательные ресурсы доступны для тех, кто может бороться с этой темой. Вы можете получить доступ к множеству книг и курсов, которые позволят вам изучать алгебру в свободное время, если вы уделяете время практике.

Как легко выучить алгебру? Вот 7 советов, которые ваш ребенок может использовать при изучении алгебры.

Что такое шаг в алгебре

Шаг [step] — в многошаговом расчете (например, при решении задач нелинейного программирования) этап, дающий промежуточный результат, позволяющий обычно судить о приближении или, наоборот, удалении расчета от цели. Одной из разновидностей шага является итерация в машинном расчете, которая отличается от других его этапов лишь значениями переменных величин, а не составом процедур обработки информации. Пример см. в статье Алгоритм.

Экономико-математический словарь: Словарь современной экономической науки. — М.: Дело . Л. И. Лопатников . 2003 .

Смотреть что такое «Шаг» в других словарях:

шаг — шаг/ … Морфемно-орфографический словарь

ШАГ — шага (шагу) и (с колич. числит.) шага, предл. п. о шаге и на (в) шагу, мн. шаги, м. 1. Движение ногой при ходьбе. Сделать шаг вперед. Два шага. Крупные шаги. Мелкие шаги. Размеренные шаги. «Услышав его шаги, она вздрогнула.» Тургенев. «Она… … Толковый словарь Ушакова

шаг — сущ., м., употр. часто Морфология: (нет) чего? шага и шагу, чему? шагу, (вижу) что? шаг, чем? шагом, о чём? о шаге и в шагу; мн. что? шаги, (нет) чего? шагов, чему? шагам, (вижу) что? шаги, чем? шагами, о чём? о шагах о движении человека 1.… … Толковый словарь Дмитриева

Шаг — Шаг: В Викисловаре есть статья «шаг» Шаг движение ногой при ходьбе. Шаг способ передвижения военнослужащего (строевой и походный шаг) Шаг расстояние между основными поперечными несущими конструкциями (колоннами, стенами). Шаг … … Википедия

шаг — Выступка, поступь, ход, походка, па. Шаг бодрый, вольный, сдержанный, тихий, форсированный, черепаший. Выделывать па.. Ср. . См. аллюр, действие, походка бодрым шагом, ленивым шагом, ловкий шаг, ложный шаг, первый шаг, прибавить шагу, сделать шаг … Словарь синонимов

шаг — а ( у); (с числительными: два, три, четыре шага); предл. в шаге и в шагу; мн. шаги; м. 1. Движение ноги, перемещающее человека, животное с одного места на другое (при ходьбе, беге). Идти медленным, быстрым шагом. Сделать ш. в сторону. Шагу нельзя … Энциклопедический словарь

ШАГ — (1) расстояние между одноимёнными профилями, точками или осями изделия; напр. шаг резьбы, шаг заклёпок, шаг зубьев, шаг зацепления и др.; (2) Ш. алгоритма ступень (этап) исполнения (см.), состоящая в выполнении одной или нескольких простых команд … Большая политехническая энциклопедия

ШАГ — ШАГ, а ( у) и а, о шаге, на (в) шагу, мн. и, ов, муж. 1. Движение ногой при ходьбе, беге, а также расстояние от ноги до ноги при таком движении. Сделать ш. Отмерить шагами. Услышать чьи н. шаги (звуки, возникающие при ходьбе). В нескольких или… … Толковый словарь Ожегова

шаг — шаг, а и у и (с колич. числит. 2, 3, 4) а, предл. п. в ш аге и в шаг у, мн. ч. и, ов … Русский орфографический словарь

шаг — бодрый (П.Я.); журавлиный (Давыдов); легкий (Цензор); медлительный (Жуковский); увесистый (Златовратский); унылый (П.Я.); хлюпающий (Гусев Оренбургский); черепаший (Гончаров, Мельников Печерский, Писемский, Салтыков Щедрин) Эпитеты литературной… … Словарь эпитетов

шаг — [шаг] шага/, м. (на) шагу/, мн. шаги/, шаг і/y (моне/та) … Орфоепічний словник української мови

Источник

Вычисление перемещения по графику проекции скорости

Из кодификатора по физике, 2020.
«1.1.3. Вычисление перемещения по графику зависимости υ(t).»

Теория

Пусть задан график зависимости проекции скорости ${ v }_{ x }$ от времени t (рис. 1).

Проекция перемещении тела ${ s }_{ x }$ за промежуток времени от ${ t }_{ 1 }$ до ${ t }_{ 2 }$ численно равна по величине площади фигуры, ограниченной графиком ${ v }_{ x }(t)$ , осью времени 0t и перпендикулярами к ${ t }_{ 1 }$ и ${ t }_{ 2 }$ (см. рис. 1, площадь выделена штриховкой).

Проекцию перемещения на ось 0Х будем считать:

— положительной, если проекция скорости на данную ось будет положительной (тело движется по направлению оси) (см. рис. 1);

— отрицательной, если проекция скорости на данную ось будет отрицательной (тело движется против оси) (рис. 2).

Путь s может быть только положительным:

Напоминаем формулы для расчета площадей фигур:

— прямоугольника –

— треугольника – $S=frac { acdot h }{ 2 }$

— трапеции – $S=frac { a+b }{ 2 } cdot h$

Задачи

Задача 1. По графику проекции скорости тела (рис. 3) определите проекцию его перемещения между 1 и 5 с.

Ответ: ____ м.

Решение. Проекция перемещения за промежуток времени Δt= ${ t }_{ 2 }$ – ${ t }_{ 1 }$ =5с–1с=4c численно равна площади фигуры, ограниченной графиком ${ v }_{ x }(t)$ , осью времени 0t и перпендикулярами к ${ t }_{ 1 }=1$ с и ${ t }_{ 2 }=5$ с (рис. 4, площадь выделена штриховкой). Фигура ABCD — это трапеция, ее площадь равна

$S=frac { a+b }{ 2 } cdot h=frac { AD+BC }{ 2 } cdot DC$

где DC = Δt = 4 c, AD = 3 м/c, BC = 5 м/c. Тогда S = 16 м.
Проекция перемещения ${ s }_{ x }>0$ , т.к. проекция скорости ${ v }_{ x }>0$ .
${ s }_{ x }=S=16$ м.

Ответ: 16.

Задача 2. Автомобиль движется по прямой улице вдоль оси X. На рисунке 5 представлен график зависимости проекции скорости автомобиля от времени. Определите путь, пройденный автомобилем в течение указанных интервалов времени.

Интервал времени	Путь
от 0 до 10 с	Ответ: м.
от 30 до 40 с	Ответ: м.

В бланк ответов перенесите только числа, не разделяя их пробелом или другим знаком.

Решение. Путь за промежуток времени Δt = ${ t }_{ 2 }$ – ${ t }_{ 1 }$ численно равна площади фигуры, ограниченной графиком ${ v }_{ x }(t),$ осью времени 0t и перпендикулярами к ${ t }_{ 1 }$ и ${ t }_{ 2 }$ .

На интервале [0 с, 10 с] ищем площадь треугольника (рис. 6).

${ S }_{ 1 }=frac { acdot h }{ 2 }$ ,

где a = 20 м/c, $h=triangle { t }_{ 1 }=10c-0c=10c$ . Тогда ${ S }_{ 1 }=100$ м.

Путь равен значению площади (путь всегда положительный, т.е. s > 0).

${ s }_{ 1 }={ S }_{ 1 }=100$ м.

На интервале [30 с, 40 с] ищем площадь трапеции (см. рис. 6).

${ S }_{ 2 }=frac { a+b }{ 2 } cdot h$ ,

где a = 10 м/c, b = 15 м/c, h = Δt = 40 c – 30 с = 10 с. Тогда ${ s }_{ 2 }={ S }_{ 2 }=125$ м.

Ответ: 100125.

Задача 3. Определите за первые 4 с (рис. 7):

а) проекцию перемещения тела;

б) пройденный путь.

Ответ: а) ____ м; б) ____ м.

Решение. Проекция перемещения за время $triangle t={ t }_{ 2 }-{ t }_{ 1 }=4c-0=4c$ (пер-вые 4 с) численно равна площади фигуры, ограниченной графиком ${ v }_{ x }(t)$ , осью времени 0t и перпендикулярами к ${ t }_{ 1 }=0$ с и ${ t }_{ 2 }=4$ с (рис. 8, площадь выделена штриховкой).

Так как при ${ t }_{ 0 }=3$ с проекция скорости поменяла знак, то получили две фигуры, два треугольника, площади которых равны:

${ S }_{ 1 }=frac { { a }_{ 1 }cdot { h }_{ 1 } }{ 2 } ,quad { S }_{ 2 }=frac { { a }_{ 2 }cdot { h }_{ 2 } }{ 2 }$ ,

где

${ a }_{ 1 }=30quad$ м/с, $quad { h }_{ 1 }=triangle { t }_{ 1 }=3c-0c=3c$

${ a }_{ 2 }$ =|-10 м/c|=10 м/c, $quad { h }_{ 2 }=triangle { t }_{ 2 }=4c-3c=1c$ .

Тогда ${ S }_{ 1 }=45$ м, $quad { S }_{ 2 }=5$ м.

а) Проекция перемещения ${ s }_{ 1x }>0$ , т.к. проекция скорости ${ v }_{ 1x }>0$ ; проекция перемещения ${ s }_{ 2x }<0$ , т.к. проекция скорости ${ v }_{ 2x }<0$ . В итоге получаем: ${ s }_{ x }={ s }_{ 1x }+{ s }_{ 2x }={ S }_{ 1 }-{ S }_{ 2 },quad { s }_{ 1x }=$ 45м — 5м = 40 м. б) Путь равен значению площади (путь всегда положительный, т.е. s>0).

$s={ S }_{ 1 }+{ S }_{ 2 }$ , s = 45 м + 5 м = 50 м.

Ответ: а) 40; б) 50.

Задача 4. График зависимости проекции скорости материальной точки, движущейся вдоль оси 0Х, от времени изображен на рисунке 9. Определите перемещение точки, которое она совершила за первые 6 с.

Ответ: ____ м.

Решение. Проекция перемещения за время $triangle t={ t }_{ 2 }-{ t }_{ 1 }=6c-0=6c$ (пер-вые 6 с) численно равна площади фигуры, ограниченной графиком ${ v }_{ x }(t)$ , осью времени 0t и перпендикулярами к ${ t }_{ 1 }=0 c$ и ${ t }_{ 2 }=6 c$ (рис. 10, площадь выделена штриховкой).

Так как при ${ t }_{ 01 }=2c$ и ${ t }_{ 02 }=4c$ проекция скорости меняет знак, то получили три фигуры, три треугольника, площади которых равны:

${ S }_{ 1 }=frac { { a }_{ 1 }cdot { h }_{ 1 } }{ 2 } ,quad { S }_{ 2 }=frac { { a }_{ 2 }cdot { h }_{ 2 } }{ 2 } ,quad { S }_{ 3 }=frac { { a }_{ 3 }cdot { h }_{ 3 } }{ 2 } ,$

где

${ a }_{ 1 }=3$ м/с, $h_{ 1 }=triangle { t }_{ 1 }=2c-0c=2c$

${ a }_{ 2 }=$ |-2 м/c| = 2 м/с, $h_{ 2 }=triangle { t }_{ 2 }=4c-2c=2c$

${ a }_{ 2 }=$ 3м/c, $h_{ 3 }=triangle { t }_{ 3 }=6c-4c=2c$ .

Тогда ${ S }_{ 1 }=3$ м, ${ S }_{ 2 }=2$ м, ${ S }_{ 3 }=3$ м.

Проекция перемещения ${ s }_{ 1x }>0$ , т.к. проекция скорости ${ v }_{ 1x }>0$ .

Проекция перемещения ${ s }_{ 2x }<0$ , т.к. проекция скорости ${ v }_{ 2x }<0$ . Проекция перемещения ${ s }_{ 3x }>0$ , т.к. проекция скорости ${ v }_{ 3x }>0$ . В итоге получаем:

${ s }_{ x }={ s }_{ 1x }+{ s }_{ 2x }+{ s }_{ 3x }={ S }_{ 1 }-{ S }_{ 2 }+{ S }_{ 3 },quad { s }_{ x }=$ 3 м – 2 м + 3 м = 4 м.

Ответ: 4.

Задача 5. На рисунке приведен график зависимости v_x скорости тела от времени .

Определите путь, пройденный телом в интервале времени от 0 до 5 с.

Ответ: ____ м.

Решение. Решение любых графических задач основывается на умении «читать» графики. В данной задаче рассматривается зависимость проекции скорости тела от времени. На интервале от 0 до 3с проекция скорости уменьшается от значения 15 м/с до 0. На интервале от 3 до 5с модуль проекции начинает возрастать от нулевого значения до 10 м/с. Причем важно «увидеть», что тело в этом временном интервале начинает движение в направлении, противоположном оси ОХ.

Пройденный путь будет определяться площадью геометрической фигуры, образованной под графиком проекции скорости.

Рис.1

Дальнейшее решение задачи сводится к нахождению площадей двух треугольников, заштрихованных на рис.1

$S_1=frac{15cdot 3}{2}=22,5$ (м).

$S_2=frac{10cdot 2}{2}=10$ (м).

Тогда, общий путь в интервале времени от 0 до 5с будет определяться суммой отдельных путей S_1 и S_2 .

(м).
Ответ: 32,5 м

По условию этой задачи можно поставить второй вопрос: найти проекцию перемещения в интервале времени от 0 до 5с.

В этом случае надо учесть, что проекция перемещения в интервале времени от 0 до 3 с положительная и её значение равно пройденному пути на этом интервале.

$S_{1x}=S_1=22,5$ (м).

В интервале времени от 3 с до 5 с проекция перемещения отрицательная, так как тело движется в направлении противоположном оси ОХ.

$S_{2x}=-10$ (м).

Проекция перемещения за весь интервал времени будет равна $S_{o.x}=S_{1x}+S_{2x}$
$S_{o.x}=22,5+(-10)=12,5$ (м).

Ответ: 12,5 м

Задача 6. На рисунке представлен график зависимости модуля скорости v прямолинейно движущегося тела от времени t. Определите по графику путь, пройденный телом в интервале времени от 1 до 5 с.

Ответ: ____ м.

Решение. Для нахождения пройденного пути в интервале времени от 1с до 5с необходимо рассчитать площадь геометрической фигуры под графиком модуля скорости.

Рис.1

Дальнейшее решение сводится к расчету площади трапеции, заштрихованной на графике (см. рис.1).

$S=frac{4+2}{2}cdot 10=30$ (м).

Особенностью подобной задачи является то, что при решении, необходимо внимательно отследить временной интервал, на котором требуется рассчитать пройденный путь.
Ответ: 30 м.

Задача 7. Из двух городов навстречу друг другу с постоянной скоростью двиижутся два автомобиля. На графике показана зависимость расстояния между автомобилями от времени. Скорость первого автомобиля равна 15 м/с. Какова скорость второго автомобиля?

Ответ: ____ м.

Решение. При движении навстречу друг к другу расстояние между двумя автомобилями уменьшается от значения 144 км до 0. На графике видно, что встреча автомобилей произошла в момент времени 60 минут, так как расстояние между автомобилями стало равным 0. Расчеты в этой задаче требуют обязательного применения системы «СИ».

144 км = 144000 м; 60 мин = 3600 с.
Используя эти данные, можно рассчитать скорость сближения автомобилей.

$v=frac{144000}{3600}=40$ м/с

Так как автомобили движутся навстречу друг другу, то отсюда скорость второго автомобиля можно выразить как

(м/с)

Ответ: 25 м/с.

Задача 8. На рисунке представлен график зависимости модуля скорости тела от времени. Найдите путь, пройденный телом за время от момента времени 0 с до момента времени 5 с. (Ответ дайте в метрах.)

Ответ: ____ м.

Решение. Для нахождения пройденного пути необходимо рассчитать площадь геометрической фигуры (трапеции) под графиком модуля скорости (см.рис.1). Это относится к интервалу времени от 0 до 3 с. От 3 с до 5 с скорость тела равна 0, следовательно, тело находилось в состоянии покоя и пройденный путь в этом интервале равен 0.

Рис.1

$S_1=frac{3+1}{2}cdot 10=20$ (м).
S_2=0
(м).

Сакович А.Л., 2020

Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Вычисление перемещения по графику проекции скорости» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
08.05.2023

Источник