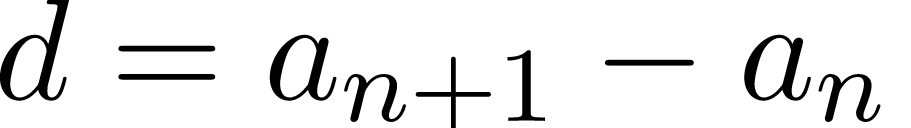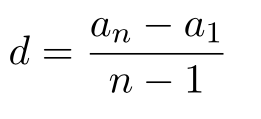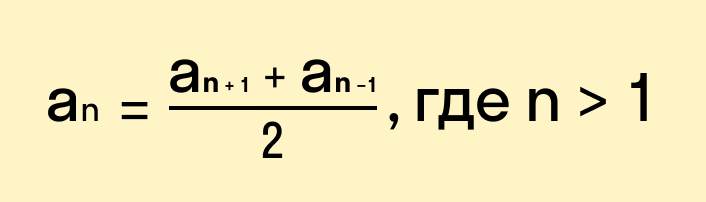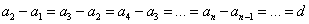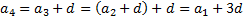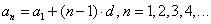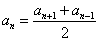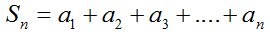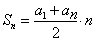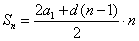Как найти шаг ряда чисел - Исправление недочетов и поиск решений вместе с Examum.ru

Сразу отметим, что единой универсальной методики для решения задач на числовые ряды нет. Закономерности, по которым числа следуют друг за другом, могут быть самыми разными, и научиться быстро решать такого рода задачи можно только путём практики — прорешав большое количество других задач на ряды.

Рассмотрим самые простые случаи.

Надо продолжить ряд

1) 2 4 6 8 …

В этом случае всё просто — каждое следующее число на 2 больше предыдущего (т.е. это ряд чётных чисел, или арифметическая прогрессия с шагом 2), поэтому следующее число будет 10

2) 4 8 16 32 …

Тут каждое следующее число в 2 раза больше предыдущего (геометрическая прогрессия), поэтому следующим будет число 64

3) 6 11 17 24 …

Этот случай уже чуть сложнее. В этом числовом ряду разница между соседними числами на 1 больше, чем разница между предыдущими

11 — 6 = 5

17 — 11 = 6

24 -17 = 7

Как видим, шаг (разница) между соседними числами каждый раз увеличивается на 1.

Соответственно, после 24 будет число, которое на 8 больше, то есть 32

Хотите, чтобы ваш ребёнок обучался самостоятельно?
Вам поможет наш ВИДЕОКУРС

Пример 1

Ряд: 18 10 6 4 …

Взглянув на этот ряд, можно достаточно быстро понять, что разница между соседними числами с каждым шагом сокращается в 2 раза

18 – 10 = 8

10 — 6 = 4 (8:4 = 2)

6 – 4 = 2 (4:2 = 2)

Следовательно, следующий шаг — это 2:2 = 1, то есть число будет 4-1 = 3

Пример 2

Ряд: 7 15 31 63

Этот ряд противоположен предыдущему. Тут разница между соседними числами с каждым шагом увеличивается в 2 раза

15 – 7 = 8

31 – 15 = 16 (16:8 = 2)

63 – 31 = 32 (32:16 = 2)

Следующий шаг будет 32∙2 = 64, соответственно, следующее число будет 63 + 64 = 127

Ответ: 127

Пример 3

Ряд: 2 4 8 10 20 22 44 46 92 94

Взглянем на этот ряд подробнее.

4 – 2 = 2

8:4 = 2

10 – 8 =2

20:10 = 2

То есть одно число на 2 больше предыдущего, а следующее — в 2 раза больше предыдущего.

Далее опять — на 2 больше, и потом в два раза больше.

Следующие числа в этом ряду:

22 – 20 = 2

44:22 = 2

46 – 44 = 2

92:46 = 2

94 – 92 = 2

Соответственно, следующее число будет в 2 раза больше, чем 94. Т.е. это будет 94∙2 = 188

Ответ: 188

ВИДЕОКУРС 2plus2.online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов в 5-й класс физматшколы.

Пример 4

Ряд: 1 2 3 5 7 11 13 17 19

В этом ряду бесполезно искать закономерности, насколько соседние числа отличаются друг от друга. Все числа в этом ряду — простые, то есть без остатка делятся только на 1 и на само себя. Соответственно, следующим в ряду будет следующее после 19 простое число, то есть 23.

После того, как вы поняли, что это ряд простых чисел, то вы поняли, почему иные закономерности в этом ряду искать бесполезно — ведь математики до сих пор не нашли закона, по которому распределяются простые числа, и как можно по формуле (а не путём перебора) найти следующее простое число, зная предыдущие.

Ответ: 23

Дата публикации
02.05.2020

Источник

Интервальный вариационный ряд и его характеристики

Построение интервального вариационного ряда по данным эксперимента
Гистограмма и полигон относительных частот, кумулята и эмпирическая функция распределения
Выборочная средняя, мода и медиана. Симметрия ряда
Выборочная дисперсия и СКО
Исправленная выборочная дисперсия, стандартное отклонение выборки и коэффициент вариации
Алгоритм исследования интервального вариационного ряда
Примеры

п.1. Построение интервального вариационного ряда по данным эксперимента

Интервальный вариационный ряд – это ряд распределения, в котором однородные группы составлены по признаку, меняющемуся непрерывно или принимающему слишком много значений.

Общий вид интервального вариационного ряда

Интервалы, (left.left[a_{i-1},a_iright.right))	(left.left[a_{0},a_1right.right))	(left.left[a_{1},a_2right.right))	…	(left.left[a_{k-1},a_kright.right))
Частоты, (f_i)	(f_1)	(f_2)	…	(f_k)

Здесь k — число интервалов, на которые разбивается ряд.

Размах вариации – это длина интервала, в пределах которой изменяется исследуемый признак: $$ F=x_{max}-x_{min} $$

Правило Стерджеса
Эмпирическое правило определения оптимального количества интервалов k, на которые следует разбить ряд из N чисел: $$ k=1+lfloorlog_2 Nrfloor $$ или, через десятичный логарифм: $$ k=1+lfloor 3,322cdotlg Nrfloor $$

Скобка (lfloor rfloor) означает целую часть (округление вниз до целого числа).

Шаг интервального ряда – это отношение размаха вариации к количеству интервалов, округленное вверх до определенной точности: $$ h=leftlceilfrac Rkrightrceil $$

Скобка (lceil rceil) означает округление вверх, в данном случае не обязательно до целого числа.

Алгоритм построения интервального ряда
На входе: все значения признака (left{x_jright}, j=overline{1,N})
Шаг 1. Найти размах вариации (R=x_{max}-x_{min})
Шаг 2. Найти оптимальное количество интервалов (k=1+lfloorlog_2 Nrfloor)
Шаг 3. Найти шаг интервального ряда (h=leftlceilfrac{R}{k}rightrceil)
Шаг 4. Найти узлы ряда: $$ a_0=x_{min}, a_i=1_0+ih, i=overline{1,k} $$ Шаг 5. Найти частоты (f_i) – число попаданий значений признака в каждый из интервалов (left.left[a_{i-1},a_iright.right)).
На выходе: интервальный ряд с интервалами (left.left[a_{i-1},a_iright.right)) и частотами (f_i, i=overline{1,k})

Заметим, что поскольку шаг h находится с округлением вверх, последний узел (a_kgeq x_{max}).

Например:
Проведено 100 измерений роста учеников старших классов.
Минимальный рост составляет 142 см, максимальный – 197 см.
Найдем узлы для построения соответствующего интервального ряда.
По условию: (N=100, x_{min}=142 см, x_{max}=197 см).
Размах вариации: (R=197-142=55) (см)
Оптимальное число интервалов: (k=1+lfloor 3,322cdotlg ⁡100rfloor=1+lfloor 6,644rfloor=1+6=7)
Шаг интервального ряда: (h=lceilfrac{55}{5}rceil=lceil 7,85rceil=8) (см)
Получаем узлы ряда: $$ a_0=x_{min}=142, a_i=142+icdot 8, i=overline{1,7} $$

(left.left[a_{i-1},a_iright.right)) cм

(left.left[142;150right.right))

(left.left[150;158right.right))

(left.left[158;166right.right))

(left.left[166;174right.right))

(left.left[174;182right.right))

(left.left[182;190right.right))

(left[190;198right])

п.2. Гистограмма и полигон относительных частот, кумулята и эмпирическая функция распределения

Относительная частота интервала (left.left[a_{i-1},a_iright.right)) — это отношение частоты (f_i) к общему количеству исходов: $$ w_i=frac{f_i}{N}, i=overline{1,k} $$

Гистограмма относительных частот интервального ряда – это фигура, состоящая из прямоугольников, ширина которых равна шагу ряда, а высота – относительным частотам каждого из интервалов.
Площадь гистограммы равна 1 (с точностью до округлений), и она является эмпирическим законом распределения исследуемого признака.

Полигон относительных частот интервального ряда – это ломаная, соединяющая точки ((x_i,w_i)), где (x_i) — середины интервалов: (x_i=frac{a_{i-1}+a_i}{2}, i=overline{1,k}).

Накопленные относительные частоты – это суммы: $$ S_1=w_1, S_i=S_{i-1}+w_i, i=overline{2,k} $$ Ступенчатая кривая (F(x)), состоящая из прямоугольников, ширина которых равна шагу ряда, а высота – накопленным относительным частотам, является эмпирической функцией распределения исследуемого признака.
Кумулята – это ломаная, которая соединяет точки ((x_i,S_i)), где (x_i) — середины интервалов.

Например:
Продолжим анализ распределения учеников по росту.
Выше мы уже нашли узлы интервалов. Пусть, после распределения всех 100 измерений по этим интервалам, мы получили следующий интервальный ряд:

i	1	2	3	4	5	6	7
(left.left[a_{i-1},a_iright.right)) cм	(left.left[142;150right.right))	(left.left[150;158right.right))	(left.left[158;166right.right))	(left.left[166;174right.right))	(left.left[174;182right.right))	(left.left[182;190right.right))	(left[190;198right])
(f_i)	4	7	11	34	33	8	3

Найдем середины интервалов, относительные частоты и накопленные относительные частоты:

(x_i)	146	154	162	170	178	186	194
(w_i)	0,04	0,07	0,11	0,34	0,33	0,08	0,03
(S_i)	0,04	0,11	0,22	0,56	0,89	0,97	1

Построим гистограмму и полигон:

Построим кумуляту и эмпирическую функцию распределения:

Эмпирическая функция распределения (относительно середин интервалов): $$ F(x)= begin{cases} 0, xleq 146\ 0,04, 146lt xleq 154\ 0,11, 154lt xleq 162\ 0,22, 162lt xleq 170\ 0,56, 170lt xleq 178\ 0,89, 178lt xleq 186\ 0,97, 186lt xleq 194\ 1, xgt 194 end{cases} $$

п.3. Выборочная средняя, мода и медиана. Симметрия ряда

Выборочная средняя интервального вариационного ряда определяется как средняя взвешенная по частотам: $$ X_{cp}=frac{x_1f_1+x_2f_2+…+x_kf_k}{N}=frac1Nsum_{i=1}^k x_if_i $$ где (x_i) — середины интервалов: (x_i=frac{a_{i-1}+a_i}{2}, i=overline{1,k}).
Или, через относительные частоты: $$ X_{cp}=sum_{i=1}^k x_iw_i $$

Модальным интервалом называют интервал с максимальной частотой: $$ f_m=max f_i $$ Мода интервального вариационного ряда определяется по формуле: $$ M_o=x_o+frac{f_m-f_{m-1}}{(f_m-f_{m-1})+(f_m+f_{m+1})}h $$ где
(h) – шаг интервального ряда;
(x_o) — нижняя граница модального интервала;
(f_m,f_{m-1},f_{m+1}) — соответственно, частоты модального интервала, интервала слева от модального и интервала справа.

Медианным интервалом называют первый интервал слева, на котором кумулята превысила значение 0,5. Медиана интервального вариационного ряда определяется по формуле: $$ M_e=x_o+frac{0,5-S_{me-1}}{w_{me}}h $$ где
(h) – шаг интервального ряда;
(x_o) — нижняя граница медианного интервала;
(S_{me-1}) накопленная относительная частота для интервала слева от медианного;
(w_{me}) относительная частота медианного интервала.

Расположение выборочной средней, моды и медианы в зависимости от симметрии ряда аналогично их расположению в дискретном ряду (см. §65 данного справочника).

Например:
Для распределения учеников по росту получаем:

(x_i)	146	154	162	170	178	186	194	∑
(w_i)	0,04	0,07	0,11	0,34	0,33	0,08	0,03	1
(x_iw_i)	5,84	10,78	17,82	57,80	58,74	14,88	5,82	171,68

$$ X_{cp}=sum_{i=1}^k x_iw_i=171,68approx 171,7 text{(см)} $$ На гистограмме (или полигоне) относительных частот максимальная частота приходится на 4й интервал [166;174). Это модальный интервал.
Данные для расчета моды: begin{gather*} x_o=166, f_m=34, f_{m-1}=11, f_{m+1}=33, h=8\ M_o=x_o+frac{f_m-f_{m-1}}{(f_m-f_{m-1})+(f_m+f_{m+1})}h=\ =166+frac{34-11}{(34-11)+(34-33)}cdot 8approx 173,7 text{(см)} end{gather*} На кумуляте значение 0,5 пересекается на 4м интервале. Это – медианный интервал.
Данные для расчета медианы: begin{gather*} x_o=166, w_m=0,34, S_{me-1}=0,22, h=8\ \ M_e=x_o+frac{0,5-S_{me-1}}{w_me}h=166+frac{0,5-0,22}{0,34}cdot 8approx 172,6 text{(см)} end{gather*} begin{gather*} \ X_{cp}=171,7; M_o=173,7; M_e=172,6\ X_{cp}lt M_elt M_o end{gather*} Ряд асимметричный с левосторонней асимметрией.
При этом (frac{|M_o-X_{cp}|}{|M_e-X_{cp}|}=frac{2,0}{0,9}approx 2,2lt 3), т.е. распределение умеренно асимметрично.

п.4. Выборочная дисперсия и СКО

Выборочная дисперсия интервального вариационного ряда определяется как средняя взвешенная для квадрата отклонения от средней: begin{gather*} D=frac1Nsum_{i=1}^k(x_i-X_{cp})^2 f_i=frac1Nsum_{i=1}^k x_i^2 f_i-X_{cp}^2 end{gather*} где (x_i) — середины интервалов: (x_i=frac{a_{i-1}+a_i}{2}, i=overline{1,k}).
Или, через относительные частоты: $$ D=sum_{i=1}^k(x_i-X_{cp})^2 w_i=sum_{i=1}^k x_i^2 w_i-X_{cp}^2 $$

Выборочное среднее квадратичное отклонение (СКО) определяется как корень квадратный из выборочной дисперсии: $$ sigma=sqrt{D} $$

Например:
Для распределения учеников по росту получаем:

$x_i$	146	154	162	170	178	186	194	∑
(w_i)	0,04	0,07	0,11	0,34	0,33	0,08	0,03	1
(x_iw_i)	5,84	10,78	17,82	57,80	58,74	14,88	5,82	171,68
(x_i^2w_i) — результат	852,64	1660,12	2886,84	9826	10455,72	2767,68	1129,08	29578,08

$$ D=sum_{i=1}^k x_i^2 w_i-X_{cp}^2=29578,08-171,7^2approx 104,1 $$ $$ sigma=sqrt{D}approx 10,2 $$

п.5. Исправленная выборочная дисперсия, стандартное отклонение выборки и коэффициент вариации

Исправленная выборочная дисперсия интервального вариационного ряда определяется как: begin{gather*} S^2=frac{N}{N-1}D end{gather*}

Стандартное отклонение выборки определяется как корень квадратный из исправленной выборочной дисперсии: $$ s=sqrt{S^2} $$

Коэффициент вариации это отношение стандартного отклонения выборки к выборочной средней, выраженное в процентах: $$ V=frac{s}{X_{cp}}cdot 100text{%} $$

Подробней о том, почему и когда нужно «исправлять» дисперсию, и для чего использовать коэффициент вариации – см. §65 данного справочника.

Например:
Для распределения учеников по росту получаем: begin{gather*} S^2=frac{100}{99}cdot 104,1approx 105,1\ sapprox 10,3 end{gather*} Коэффициент вариации: $$ V=frac{10,3}{171,7}cdot 100text{%}approx 6,0text{%}lt 33text{%} $$ Выборка однородна. Найденное значение среднего роста (X_{cp})=171,7 см можно распространить на всю генеральную совокупность (старшеклассников из других школ).

п.6. Алгоритм исследования интервального вариационного ряда

На входе: все значения признака (left{x_jright}, j=overline{1,N})
Шаг 1. Построить интервальный ряд с интервалами (left.right[a_{i-1}, a_ileft.right)) и частотами (f_i, i=overline{1,k}) (см. алгоритм выше).
Шаг 2. Составить расчетную таблицу. Найти (x_i,w_i,S_i,x_iw_i,x_i^2w_i)
Шаг 3. Построить гистограмму (и/или полигон) относительных частот, эмпирическую функцию распределения (и/или кумуляту). Записать эмпирическую функцию распределения.
Шаг 4. Найти выборочную среднюю, моду и медиану. Проанализировать симметрию распределения.
Шаг 5. Найти выборочную дисперсию и СКО.
Шаг 6. Найти исправленную выборочную дисперсию, стандартное отклонение и коэффициент вариации. Сделать вывод об однородности выборки.

п.7. Примеры

Пример 1. При изучении возраста пользователей коворкинга выбрали 30 человек.
Получили следующий набор данных:
18,38,28,29,26,38,34,22,28,30,22,23,35,33,27,24,30,32,28,25,29,26,31,24,29,27,32,24,29,29
Постройте интервальный ряд и исследуйте его.

1) Построим интервальный ряд. В наборе данных: $$ x_{min}=18, x_{max}=38, N=30 $$ Размах вариации: (R=38-18=20)
Оптимальное число интервалов: (k=1+lfloorlog_2⁡ 30rfloor=1+4=5)
Шаг интервального ряда: (h=lceilfrac{20}{5}rceil=4)
Получаем узлы ряда: $$ a_0=x_{min}=18, a_i=18+icdot 4, i=overline{1,5} $$

(left.left[a_{i-1},a_iright.right)) лет

(left.left[18;22right.right))

(left.left[22;26right.right))

(left.left[26;30right.right))

(left.left[30;34right.right))

(left.left[34;38right.right))

Считаем частоты для каждого интервала. Получаем интервальный ряд:

(left.left[a_{i-1},a_iright.right)) лет	(left.left[18;22right.right))	(left.left[22;26right.right))	(left.left[26;30right.right))	(left.left[30;34right.right))	(left.left[34;38right.right))
(f_i)	1	7	12	6	4

2) Составляем расчетную таблицу:

(x_i)	20	24	28	32	36	∑
(f_i)	1	7	12	6	4	30
(w_i)	0,033	0,233	0,4	0,2	0,133	1
(S_i)	0,033	0,267	0,667	0,867	1	—
(x_iw_i)	0,667	5,6	11,2	6,4	4,8	28,67
(x_i^2w_i)	13,333	134,4	313,6	204,8	172,8	838,93

3) Строим полигон и кумуляту

Эмпирическая функция распределения: $$ F(x)= begin{cases} 0, xleq 20\ 0,033, 20lt xleq 24\ 0,267, 24lt xleq 28\ 0,667, 28lt xleq 32\ 0,867, 32lt xleq 36\ 1, xgt 36 end{cases} $$ 4) Находим выборочную среднюю, моду и медиану $$ X_{cp}=sum_{i=1}^k x_iw_iapprox 28,7 text{(лет)} $$ На полигоне модальным является 3й интервал (самая высокая точка).
Данные для расчета моды: begin{gather*} x_0=26, f_m=12, f_{m-1}=7, f_{m+1}=6, h=4\ M_o=x_o+frac{f_m-f_{m-1}}{(f_m-f_{m-1})+(f_m+f_{m+1})}h=\ =26+frac{12-7}{(12-7)+(12-6)}cdot 4approx 27,8 text{(лет)} end{gather*}
На кумуляте медианным является 3й интервал (преодолевает уровень 0,5).
Данные для расчета медианы: begin{gather*} x_0=26, w_m=0,4, S_{me-1}=0,267, h=4\ M_e=x_o+frac{0,5-S_{me-1}}{w_{me}}h=26+frac{0,5-0,4}{0,267}cdot 4approx 28,3 text{(лет)} end{gather*} Получаем: begin{gather*} X_{cp}=28,7; M_o=27,8; M_e=28,6\ X_{cp}gt M_egt M_0 end{gather*} Ряд асимметричный с правосторонней асимметрией.
При этом (frac{|M_o-X_{cp}|}{|M_e-X_{cp}|} =frac{0,9}{0,1}=9gt 3), т.е. распределение сильно асимметрично.

5) Находим выборочную дисперсию и СКО: begin{gather*} D=sum_{i=1}^k x_i^2w_i-X_{cp}^2=838,93-28,7^2approx 17,2\ sigma=sqrt{D}approx 4,1 end{gather*}
6) Исправленная выборочная дисперсия: $$ S^2=frac{N}{N-1}D=frac{30}{29}cdot 17,2approx 17,7 $$ Стандартное отклонение (s=sqrt{S^2}approx 4,2)
Коэффициент вариации: (V=frac{4,2}{28,7}cdot 100text{%}approx 14,7text{%}lt 33text{%})
Выборка однородна. Найденное значение среднего возраста (X_{cp}=28,7) лет можно распространить на всю генеральную совокупность (пользователей коворкинга).

Источник

Определение числовой последовательности

Числовая последовательность — это множество чисел, каждому из которых можно присвоить уникальный номер.

Последовательности можно задавать разными способами:

Словесно — когда правило последовательности объясняется словами:
«Последовательность простых чисел: 2, 3, 5, 7, 11, 13, 17, 19, 23…»

Аналитически — когда указана формула ее n-го члена: y_n = f(n).
Последовательность y_n = C называют постоянной или стационарной.

Рекуррентно — когда указывается правило, которое помогает вычислить n-й член последовательности, если известны её предыдущие члены.
Последовательность Фибоначчи — когда каждое следующее число равно сумме двух предыдущих чисел: a_n+1 = a_n + a_n-1.

Пример: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55…

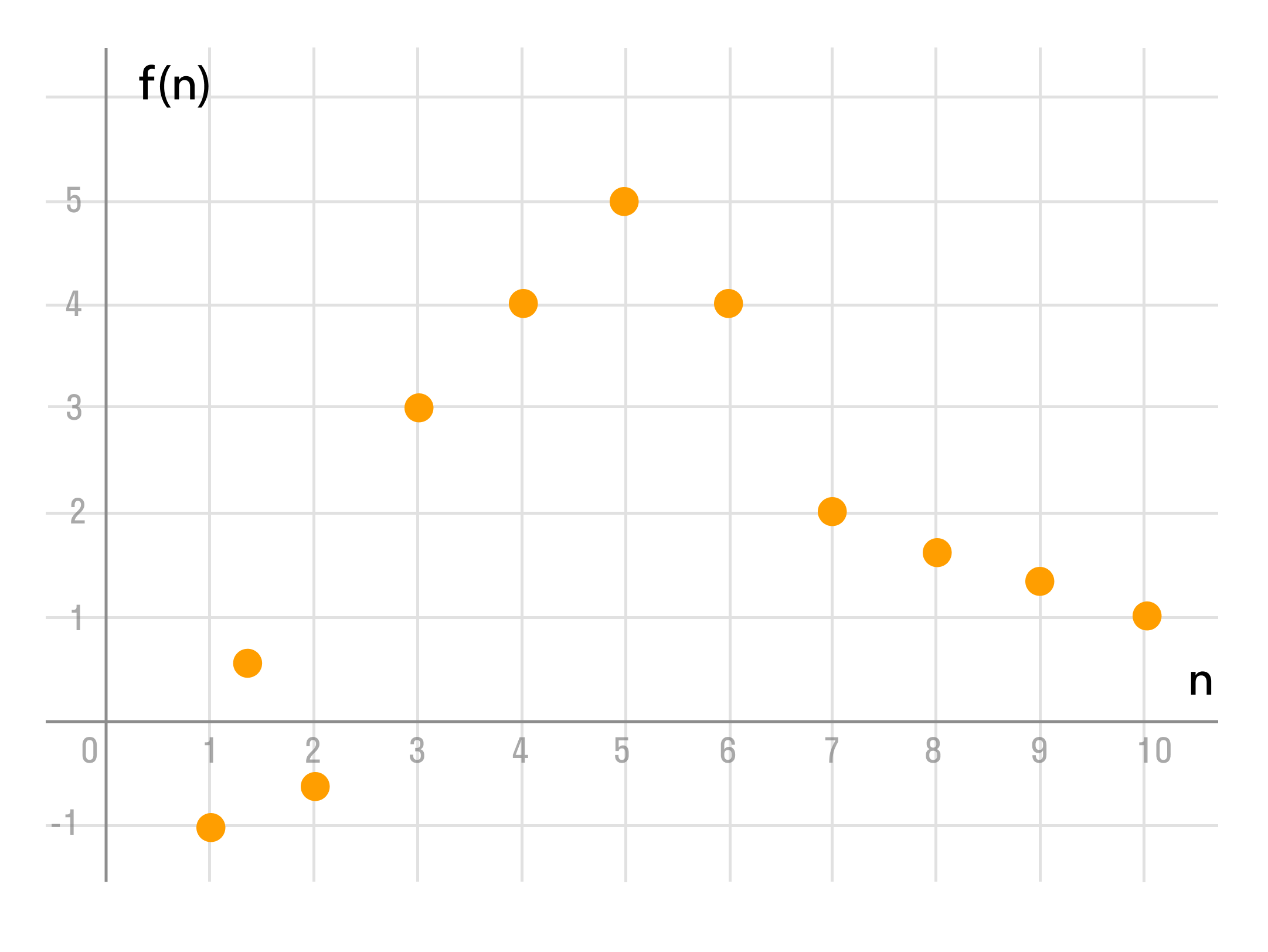
Графически — когда график последовательности состоит из точек с абсциссами
1, 2, 3, 4…

Так как алгебраическая числовая последовательность — это частный случай числовой функции, то ряд свойств функций рассматриваются и для последовательностей.

Свойства числовых последовательностей:

Последовательность {y_n} называют возрастающей, если каждый ее член кроме первого больше предыдущего:
y₁ < y₂ < y₃ < … < y_n < y_n+1 < …

Последовательность {y_n} называют убывающей, если каждый ее член кроме первого меньше предыдущего:
y₁ > y₂ > y₃ > … > y_n > y_n+1 > …

Возрастающие и убывающие последовательности называют монотонными последовательностями.

Последовательность можно назвать периодической, если существует такое натуральное число T, что начиная с некоторого N, выполняется равенство: y_n = y_n+T. Число T — длина периода.

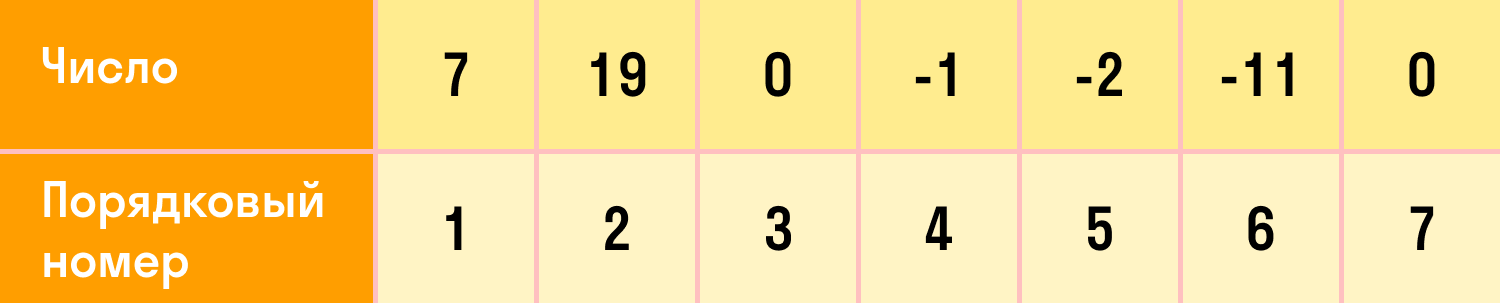
Запишем числа, которые первые пришли в голову: 7, 19, 0, −1, −2, −11, 0… Сколько бы чисел не написали, всегда можно сказать, какое из них первое, какое — второе и так до последнего. То есть мы можем их пронумеровать.

Пример числовой последовательности выглядит так:

В такой математической последовательности каждый номер соответствует одному числу. Это значит, что в последовательности не может быть двух первых чисел и т.д. Первое число (как и любое другое) — всегда одно.

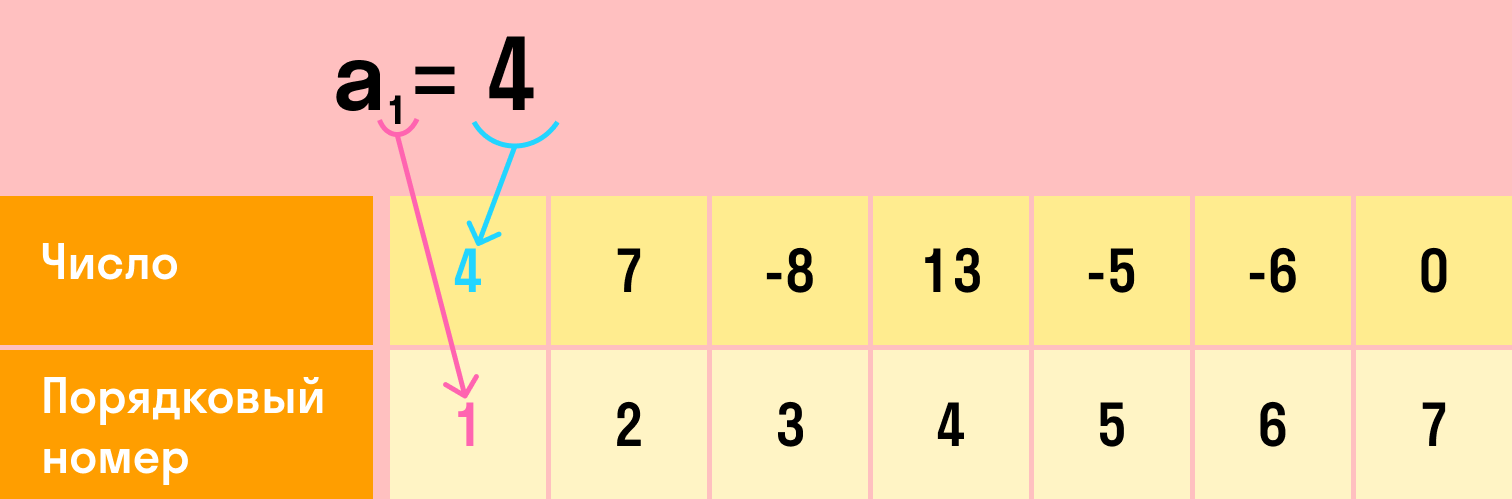
N-ный член алгебраической последовательности — это число с порядковым номером n.

Всю последовательность можно обозначить любой буквой латинского алфавита, например, a. Каждый член этой последовательности — той же буквой с индексом, который равен номеру этого члена: a₁, a₂,…, a₁₀…, a_n.

N-ый член последовательности можно задать формулой. Например:

Формула a_n = 3n − 5 задает последовательность: −2, 1, 4, 7, 10…
Формула a_n = 1 : (n + 2) задает последовательность: 1/3, 1/4, 1/5, 1/6…

Получай лайфхаки, статьи, видео и чек-листы по обучению на почту

Реши домашку по математике на 5.

Подробные решения помогут разобраться в самой сложной теме.

Определение арифметической прогрессии

Так как числовая последовательность — это частный случай функции, которая определена на множестве натуральных чисел, арифметическую прогрессию можно назвать частным случаем числовой последовательности.

Рассмотрим основные определения и как найти арифметическую прогрессию.

Арифметическая прогрессия — это числовая последовательность a₁, a₂,…, a_n,… для которой для каждого натурального n выполняется равенство:

a_n+1= a_n + d, где d — это разность арифметической прогрессии.

Описать словами эту формулу можно так: каждый член арифметической прогрессии равен предыдущему, сложенному с одним и тем же числом d.

Разность между последующим и предыдущим членами, то есть разность арифметической прогрессии можно найти по формуле:

Если известны первый член a₁ и n-ый член прогрессии, разность можно найти так:

Арифметическая прогрессия бывает трех видов:

Возрастающая — арифметическая прогрессия, у которой положительная разность, то есть d > 0.
Пример: последовательность чисел 11, 14, 17, 20, 23… — это возрастающая арифметическая прогрессия, так как ее разность d = 3 > 0.

Убывающая — арифметическая прогрессия, у которой отрицательная разность, то есть d < 0.
Пример: последовательность чисел 50, 48, 46, 44, 42… — это убывающая арифметическая прогрессия, так как ее разность d = –2 < 0.

Стационарная — арифметическая прогрессия, у которой разность равна нулю, то есть d = 0.
Пример: последовательность чисел 23, 23, 23, 23, 23… — это стационарная арифметическая прогрессия, так как ее разность d = 0.

Экзамены — это почти всегда стресс. Подготовка к ЕГЭ по математике онлайн в школе Skysmart поможет снять волнение перед экзаменом и придаст уверенности в своих знаниях.

Свойство арифметической прогрессии

Переведем с языка формул на русский: каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому двух соседних с ним членов. Что как раз объясняет название «арифметическая» прогрессия.

Формула n-го члена арифметической прогрессии

Из определения арифметической прогрессии следует, что равенство истинно:

Поэтому:

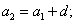
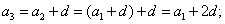
и т.д.

Значит,

Переведем с языка формул на русский: если мы знаем первый член и разность арифметической прогрессии, то можем найти любой ее член.

Арифметическую прогрессию можно назвать заданной, если известен ее первый член и разность.

Формулу a_n = a₁ + d * (n — 1) называют формулой n-го члена арифметической прогрессии.

Формулы арифметической прогрессии

В 9 классе проходят все формулы арифметической прогрессии. Давайте узнаем, какими способами ее можно задать:

Рекуррентной формулой:

Формулой n-го члена: a_n = a₁+ d · (n — 1).

Формулой вида a_n = kn + b, где k и b — числа, n — число членов последовательности.

Сумма первых n членов арифметической прогрессии (а_n) обозначается S_n:

Формулы нахождения суммы n членов арифметической прогрессии:

Чтобы быстрее запомнить формулы можно использовать такую табличку с основными определениями:

Рассмотрим пример арифметической прогрессии.

Дано: арифметическая прогрессия (a_n), где a₁ = 0 и d = 2.

Найти: первые пять членов прогрессии и десятый член прогрессии.

Решение арифметической прогрессии:

Чтобы найти последующий член прогрессии, нужно к предыдущему прибавить разность:
a₂ = a₁ + d = 0 + 2 = 2;

a₃ = a₂ + d = 2 + 2 = 4;

a₄ = a₃ + d = 4 + 2 = 6;

a₅ = a₄ + d = 6 + 2 = 8.

Используем общую формулу a_n = a₁ + d * (n — 1).
По условиям задачи n = 10, подставляем в формулу:

a₁₀ = a₁ + 2 * (10 — 1) = 0 + 2⋅9 = 18.

Геометрическая прогрессия

Геометрическая прогрессия — это последовательность (b_n), в которой каждый последующий член можно найти, если предыдущий член умножить на одно и то же число q.

Если последовательность (b_n) является геометрической прогрессией, то для любого натурального значения n справедлива зависимость:

b_n+1 = b_n * q, где q — знаменатель геометрической прогрессии

Если в геометрической прогрессии (b_n) известен первый член b₁ и знаменатель q, то можно найти любой член прогрессии:

b₂ = b₁ * q;
b₃ = b₂ * q = b₁ * q * q = b₁ * q²;
b₄ = b₁ * q³;
и т. д.

Общий член геометрической прогрессии bn можно вычислить при помощи формулы:

b_n = b₁ * qⁿ⁻¹, где n — порядковый номер члена прогрессии, b₁ — первый член прогрессии, q — знаменатель.

Пример 1. 2, 6, 18, 54,… — геометрическая прогрессия b = 2, q = 3.

Пример 2. 3, -3, 3, -3,… — геометрическая прогрессия b = 3, q = -1.

Пример 3. 7, 7, 7, 7,… — геометрическая прогрессия b = 7, q = 1.

Источник

Что такое шаг арифметической прогрессии?

Если для некой последовательности величина разности между соседними членами будет величиной постоянной, то такую последовательность называют арифметической.

Рассмотрим последовательность: a1, a2, a3, a4, a5.

Где d у нас некая постоянная величина, которую обычно называют шагом арифметической прогрессии.

Примеры арифметических прогрессий:

5, 10, 15, 20, 25. Здесь мы имеем арифметическую прогрессию с шагом 5 (10-5=5).

Каковы 6 шага к решению уравнения?

Точно так же, каковы 4 шага к решению уравнения? У нас есть 4 способа решения одношаговых уравнений: Сложение, вычитание, умножение и деление. Если мы прибавим одно и то же число к обеим частям уравнения, обе стороны останутся равными. Если мы вычтем одно и то же число из обеих частей уравнения, обе части останутся равными.

Какие 3 шагов для решения уравнения?

Похожие страницы:Блог

Какие есть 3 вида налогов?

Как найти среднюю точку между двумя точками?

Как вы делаете кадровые прогнозы?

Как найти начальную скорость, зная только время?

Каковы шаги решения стандартного уравнения или неравенства? Шаг 1: Распределите 2 на (x + 2), умножив на 2. Шаг 2: Объедините одинаковые термины, вычтя 9 из 15 (15 – 9 = 6). Шаг 3: Переместите все переменные в одну часть уравнения, вычитая 2x из обеих сторон. Шаг 4: Вычтите 6 с обеих сторон.

Во-вторых, каково золотое правило решения уравнений? Делайте с одной частью уравнения то, что вы делаете с другой!

Если мы что-то надеваем или снимаем с одной стороны, шкала (или уравнение) становится несбалансированной. При решении математических уравнений мы должны всегда сохраняйте баланс «шкалы» (или уравнения), чтобы обе стороны ВСЕГДА были равны.

Каков первый шаг алгебры?

Самое первое, что вам нужно освоить в алгебре, это понятие переменной. Переменные — это буквы, которые служат заполнителями для чисел, значение которых вам неизвестно. Так, например, в уравнении 1 + 2 = x, x является заполнителем для 3, который должен занимать другую сторону уравнения.

тогда Как вы решаете простые уравнения?

Что такое одношаговое уравнение? Одношаговое уравнение уравнение, для решения которого требуется один шаг. Решать, используйте обратную операцию, чтобы изолировать переменную саму по себе. Помните, что вы делаете с одной стороной, вы должны делать и с другой. Чтобы проверить решение, просто подставьте значение в переменную, чтобы увидеть, верно ли уравнение.

Что такое пятишаговый метод математики?

Как сделать многошаговый?

Что такое решения в математике?

Научные определения решения

Математика Значение или значения, которые при замене переменной в уравнении делают уравнение верным. Например, решения уравнения x2 = 4 равны 2 и -2.

Что такое пример уравнения? Уравнение — это математическое предложение, в котором две равные стороны разделены знаком равенства. 4 + 6 = 10 это пример уравнения. Мы можем видеть слева от знака равенства 4 + 6 и справа от знака равенства 10.… Например, 12 — это коэффициент в уравнении 12n = 24.

Что является правильным первым шагом в решении неравенства?

Ответ: Первым шагом в решении данного неравенства является использовать распределительное свойство и открыть скобки, то есть -8x + 4 > 5 — 3x.

Можешь объяснить мне алгебру?

Алгебра помогает в представлении проблем или ситуаций в виде математических выражений. Он включает в себя переменные, такие как x, y, z, и математические операции, такие как сложение, вычитание, умножение и деление, для формирования осмысленного математического выражения. … Простой пример выражения в алгебре: 2x + 4 = 8.

Что на первом месте в математических уравнениях? Порядок операций можно запомнить по аббревиатуре PEMDAS, которая означает: круглые скобки, показатели степени, умножение и деление слева направо, сложение и вычитание слева направо. Первый, упрости скобки. Затем сделайте показатели. Далее умножайте.

Что обозначают буквы в алгебре? В алгебраических выражениях буквы представляют переменные. Эти буквы на самом деле являются замаскированными числами. В этом выражении переменные x и y. Мы называем эти буквы «переменными», потому что числа, которые они представляют, могут быть разными, то есть мы можем заменить буквы в выражении одним или несколькими числами.

Как начать преподавать алгебру?

8 нестандартных идей для преподавания алгебры и геометрии

Используйте интересные видео. …
Добавьте художественный компонент в подход STEAM. …
Свяжите своих учеников с личным тренером по математике. …
Сделайте это игрой! …
Войдите в мир реалити-шоу. …
Используйте примеры из реальной жизни. …
Рассмешите их. …
Используйте стены слов.

Что такое базовая алгебра? Основная алгебра область математики, которая на шаг абстрактнее арифметики. … Алгебра вводит переменную, которая обозначает неизвестное число или может быть заменена целой группой чисел.

Могу ли я сам выучить алгебру?

Вы можете сами выучить алгебру, так как их много. образовательные ресурсы доступны для тех, кто может бороться с этой темой. Вы можете получить доступ к множеству книг и курсов, которые позволят вам изучать алгебру в свободное время, если вы уделяете время практике.

Как легко выучить алгебру? Вот 7 советов, которые ваш ребенок может использовать при изучении алгебры.

Что такое шаг в алгебре

Шаг [step] — в многошаговом расчете (например, при решении задач нелинейного программирования) этап, дающий промежуточный результат, позволяющий обычно судить о приближении или, наоборот, удалении расчета от цели. Одной из разновидностей шага является итерация в машинном расчете, которая отличается от других его этапов лишь значениями переменных величин, а не составом процедур обработки информации. Пример см. в статье Алгоритм.

Экономико-математический словарь: Словарь современной экономической науки. — М.: Дело . Л. И. Лопатников . 2003 .

Смотреть что такое «Шаг» в других словарях:

шаг — шаг/ … Морфемно-орфографический словарь

ШАГ — шага (шагу) и (с колич. числит.) шага, предл. п. о шаге и на (в) шагу, мн. шаги, м. 1. Движение ногой при ходьбе. Сделать шаг вперед. Два шага. Крупные шаги. Мелкие шаги. Размеренные шаги. «Услышав его шаги, она вздрогнула.» Тургенев. «Она… … Толковый словарь Ушакова

шаг — сущ., м., употр. часто Морфология: (нет) чего? шага и шагу, чему? шагу, (вижу) что? шаг, чем? шагом, о чём? о шаге и в шагу; мн. что? шаги, (нет) чего? шагов, чему? шагам, (вижу) что? шаги, чем? шагами, о чём? о шагах о движении человека 1.… … Толковый словарь Дмитриева

Шаг — Шаг: В Викисловаре есть статья «шаг» Шаг движение ногой при ходьбе. Шаг способ передвижения военнослужащего (строевой и походный шаг) Шаг расстояние между основными поперечными несущими конструкциями (колоннами, стенами). Шаг … … Википедия

шаг — Выступка, поступь, ход, походка, па. Шаг бодрый, вольный, сдержанный, тихий, форсированный, черепаший. Выделывать па.. Ср. . См. аллюр, действие, походка бодрым шагом, ленивым шагом, ловкий шаг, ложный шаг, первый шаг, прибавить шагу, сделать шаг … Словарь синонимов

шаг — а ( у); (с числительными: два, три, четыре шага); предл. в шаге и в шагу; мн. шаги; м. 1. Движение ноги, перемещающее человека, животное с одного места на другое (при ходьбе, беге). Идти медленным, быстрым шагом. Сделать ш. в сторону. Шагу нельзя … Энциклопедический словарь

ШАГ — (1) расстояние между одноимёнными профилями, точками или осями изделия; напр. шаг резьбы, шаг заклёпок, шаг зубьев, шаг зацепления и др.; (2) Ш. алгоритма ступень (этап) исполнения (см.), состоящая в выполнении одной или нескольких простых команд … Большая политехническая энциклопедия

ШАГ — ШАГ, а ( у) и а, о шаге, на (в) шагу, мн. и, ов, муж. 1. Движение ногой при ходьбе, беге, а также расстояние от ноги до ноги при таком движении. Сделать ш. Отмерить шагами. Услышать чьи н. шаги (звуки, возникающие при ходьбе). В нескольких или… … Толковый словарь Ожегова

шаг — шаг, а и у и (с колич. числит. 2, 3, 4) а, предл. п. в ш аге и в шаг у, мн. ч. и, ов … Русский орфографический словарь

шаг — бодрый (П.Я.); журавлиный (Давыдов); легкий (Цензор); медлительный (Жуковский); увесистый (Златовратский); унылый (П.Я.); хлюпающий (Гусев Оренбургский); черепаший (Гончаров, Мельников Печерский, Писемский, Салтыков Щедрин) Эпитеты литературной… … Словарь эпитетов

шаг — [шаг] шага/, м. (на) шагу/, мн. шаги/, шаг і/y (моне/та) … Орфоепічний словник української мови

Источник

Арифметическая прогрессия — это некая последовательность чисел, каждый следующий член которой отличается от предыдущего на одно и то же число d, называемое шаг прогрессии или разность прогрессии. Калькулятор арифметической прогрессии, используя следующие формулы, может найти первый член арифметической прогрессии , n-ный член прогрессии, найти сумму первых членов или разность.

Арифметическая прогрессия как последовательность, составленная из действительных чисел, связывает их между собой заданной закономерностью ряда. Как правило, числовой ряд начинается с того, что дан первый член арифметической прогрессии, как отправная точка. Далее каждый следующий член прогрессии получается путем прибавления к предыдущему одного и того же параметра, называемого разность арифметической прогрессии или шаг арифметической прогрессии. Если разность является положительным числом, то вся последовательность будет стремиться к плюс бесконечности, так как значения членов будут увеличиваться по мере возрастания их порядковых номеров.

Если разность арифметической прогрессии представлена отрицательным числом, каждый следующий член будет меньше предыдущего и вся последовательность будет стремиться к минус бесконечности. В некоторых случаях предел арифметической прогрессии будет конкретным числом. Это происходит, если шаг прогрессии (разность) равен нулю, тогда первый член арифметической прогрессии совпадает со всеми остальными.

Формулы арифметической прогрессии включают в себя следующие равенства:

• формула первого члена арифметической прогрессии;

• формула n-ного члена прогрессии;

• формула разности арифметической прогрессии;

• формула суммы первых членов арифметической прогрессии или суммы определенной выборки членов.

По всем формулам онлайн калькулятор рассчитывает необходимые значения, используя условия, по которым дана арифметическая прогрессия. Числа, выстроенные в симметричной последовательности, дают возможность вычислить любой член или сумму прогрессии, опираясь всего на два или три параметра в зависимости от уровня сложности задания.

Источник