Как найти шаг статистика - Исправление недочетов и поиск решений вместе с Examum.ru

Группировка. Формула Стерджесса

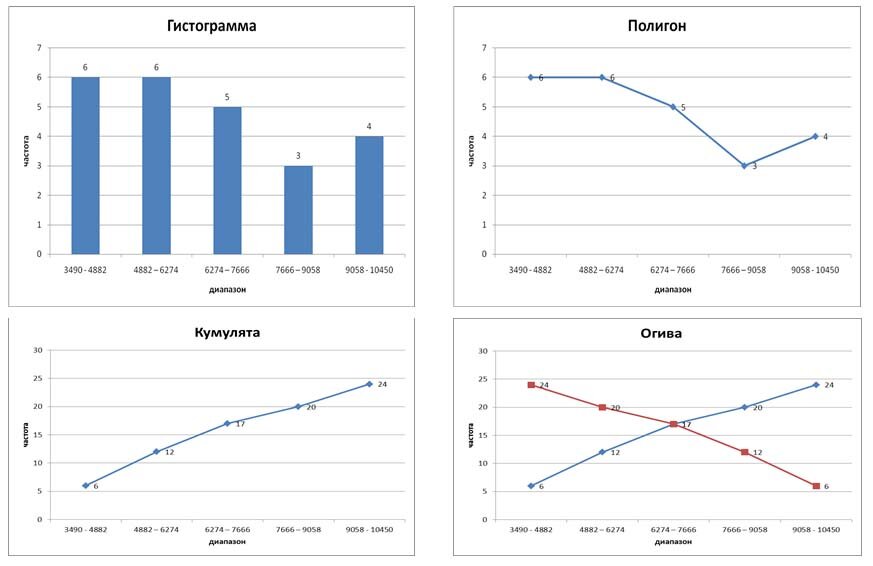
Провести группировку жителей поселка по доходу с равными интервалами и оптимальным числом групп и представить полученные данные в виде статистического ряда распределения и гистограммы. На основе гистограммы построить полигон, кумуляту и огиву распределения жителей поселка по доходу.

№	Дох.	№	Дох.
1	3820	13	6660
2	9470	14	5490
3	3490	15	5980
4	7790	16	6250
5	4210	17	8390
6	3870	18	3630
7	4490	19	6090
8	9620	20	10450
9	6200	21	6800
10	6350	22	6470
11	7430	23	9160
12	7670	24	5110

Определяем число групп по формуле Стерджесса:

n = 1 + 3,322lgN = 1 + 3,322lg24 = 5,6

принимаем n = 5

Определяем шаг интервала:

Xmax, Xmin- максимальное и минимальное значение
n – число групп

Произведем группировку с равными интервалами

Интервалы	Диапазон	частота, f	Накопленная частота, f
1	3490 — 4882	6	6
2	4882 – 6274	6	12
3	6274 – 7666	5	17
4	7666 – 9058	3	20
5	9058 — 10450	4	24

Гистограмма. Полигон. Кумулята. Огива

Если Вас интересуют задачи по статистике заходите сюда.

Материалы сайта

Обращаем Ваше внимание на то, что все материалы опубликованы для образовательных целей.

Источник

Интервальный вариационный ряд и его характеристики

Построение интервального вариационного ряда по данным эксперимента
Гистограмма и полигон относительных частот, кумулята и эмпирическая функция распределения
Выборочная средняя, мода и медиана. Симметрия ряда
Выборочная дисперсия и СКО
Исправленная выборочная дисперсия, стандартное отклонение выборки и коэффициент вариации
Алгоритм исследования интервального вариационного ряда
Примеры

п.1. Построение интервального вариационного ряда по данным эксперимента

Интервальный вариационный ряд – это ряд распределения, в котором однородные группы составлены по признаку, меняющемуся непрерывно или принимающему слишком много значений.

Общий вид интервального вариационного ряда

Интервалы, (left.left[a_{i-1},a_iright.right))	(left.left[a_{0},a_1right.right))	(left.left[a_{1},a_2right.right))	…	(left.left[a_{k-1},a_kright.right))
Частоты, (f_i)	(f_1)	(f_2)	…	(f_k)

Здесь k — число интервалов, на которые разбивается ряд.

Размах вариации – это длина интервала, в пределах которой изменяется исследуемый признак: $$ F=x_{max}-x_{min} $$

Правило Стерджеса
Эмпирическое правило определения оптимального количества интервалов k, на которые следует разбить ряд из N чисел: $$ k=1+lfloorlog_2 Nrfloor $$ или, через десятичный логарифм: $$ k=1+lfloor 3,322cdotlg Nrfloor $$

Скобка (lfloor rfloor) означает целую часть (округление вниз до целого числа).

Шаг интервального ряда – это отношение размаха вариации к количеству интервалов, округленное вверх до определенной точности: $$ h=leftlceilfrac Rkrightrceil $$

Скобка (lceil rceil) означает округление вверх, в данном случае не обязательно до целого числа.

Алгоритм построения интервального ряда
На входе: все значения признака (left{x_jright}, j=overline{1,N})
Шаг 1. Найти размах вариации (R=x_{max}-x_{min})
Шаг 2. Найти оптимальное количество интервалов (k=1+lfloorlog_2 Nrfloor)
Шаг 3. Найти шаг интервального ряда (h=leftlceilfrac{R}{k}rightrceil)
Шаг 4. Найти узлы ряда: $$ a_0=x_{min}, a_i=1_0+ih, i=overline{1,k} $$ Шаг 5. Найти частоты (f_i) – число попаданий значений признака в каждый из интервалов (left.left[a_{i-1},a_iright.right)).
На выходе: интервальный ряд с интервалами (left.left[a_{i-1},a_iright.right)) и частотами (f_i, i=overline{1,k})

Заметим, что поскольку шаг h находится с округлением вверх, последний узел (a_kgeq x_{max}).

Например:
Проведено 100 измерений роста учеников старших классов.
Минимальный рост составляет 142 см, максимальный – 197 см.
Найдем узлы для построения соответствующего интервального ряда.
По условию: (N=100, x_{min}=142 см, x_{max}=197 см).
Размах вариации: (R=197-142=55) (см)
Оптимальное число интервалов: (k=1+lfloor 3,322cdotlg ⁡100rfloor=1+lfloor 6,644rfloor=1+6=7)
Шаг интервального ряда: (h=lceilfrac{55}{5}rceil=lceil 7,85rceil=8) (см)
Получаем узлы ряда: $$ a_0=x_{min}=142, a_i=142+icdot 8, i=overline{1,7} $$

(left.left[a_{i-1},a_iright.right)) cм

(left.left[142;150right.right))

(left.left[150;158right.right))

(left.left[158;166right.right))

(left.left[166;174right.right))

(left.left[174;182right.right))

(left.left[182;190right.right))

(left[190;198right])

п.2. Гистограмма и полигон относительных частот, кумулята и эмпирическая функция распределения

Относительная частота интервала (left.left[a_{i-1},a_iright.right)) — это отношение частоты (f_i) к общему количеству исходов: $$ w_i=frac{f_i}{N}, i=overline{1,k} $$

Гистограмма относительных частот интервального ряда – это фигура, состоящая из прямоугольников, ширина которых равна шагу ряда, а высота – относительным частотам каждого из интервалов.
Площадь гистограммы равна 1 (с точностью до округлений), и она является эмпирическим законом распределения исследуемого признака.

Полигон относительных частот интервального ряда – это ломаная, соединяющая точки ((x_i,w_i)), где (x_i) — середины интервалов: (x_i=frac{a_{i-1}+a_i}{2}, i=overline{1,k}).

Накопленные относительные частоты – это суммы: $$ S_1=w_1, S_i=S_{i-1}+w_i, i=overline{2,k} $$ Ступенчатая кривая (F(x)), состоящая из прямоугольников, ширина которых равна шагу ряда, а высота – накопленным относительным частотам, является эмпирической функцией распределения исследуемого признака.
Кумулята – это ломаная, которая соединяет точки ((x_i,S_i)), где (x_i) — середины интервалов.

Например:
Продолжим анализ распределения учеников по росту.
Выше мы уже нашли узлы интервалов. Пусть, после распределения всех 100 измерений по этим интервалам, мы получили следующий интервальный ряд:

i	1	2	3	4	5	6	7
(left.left[a_{i-1},a_iright.right)) cм	(left.left[142;150right.right))	(left.left[150;158right.right))	(left.left[158;166right.right))	(left.left[166;174right.right))	(left.left[174;182right.right))	(left.left[182;190right.right))	(left[190;198right])
(f_i)	4	7	11	34	33	8	3

Найдем середины интервалов, относительные частоты и накопленные относительные частоты:

(x_i)	146	154	162	170	178	186	194
(w_i)	0,04	0,07	0,11	0,34	0,33	0,08	0,03
(S_i)	0,04	0,11	0,22	0,56	0,89	0,97	1

Построим гистограмму и полигон:

Построим кумуляту и эмпирическую функцию распределения:

Эмпирическая функция распределения (относительно середин интервалов): $$ F(x)= begin{cases} 0, xleq 146\ 0,04, 146lt xleq 154\ 0,11, 154lt xleq 162\ 0,22, 162lt xleq 170\ 0,56, 170lt xleq 178\ 0,89, 178lt xleq 186\ 0,97, 186lt xleq 194\ 1, xgt 194 end{cases} $$

п.3. Выборочная средняя, мода и медиана. Симметрия ряда

Выборочная средняя интервального вариационного ряда определяется как средняя взвешенная по частотам: $$ X_{cp}=frac{x_1f_1+x_2f_2+…+x_kf_k}{N}=frac1Nsum_{i=1}^k x_if_i $$ где (x_i) — середины интервалов: (x_i=frac{a_{i-1}+a_i}{2}, i=overline{1,k}).
Или, через относительные частоты: $$ X_{cp}=sum_{i=1}^k x_iw_i $$

Модальным интервалом называют интервал с максимальной частотой: $$ f_m=max f_i $$ Мода интервального вариационного ряда определяется по формуле: $$ M_o=x_o+frac{f_m-f_{m-1}}{(f_m-f_{m-1})+(f_m+f_{m+1})}h $$ где
(h) – шаг интервального ряда;
(x_o) — нижняя граница модального интервала;
(f_m,f_{m-1},f_{m+1}) — соответственно, частоты модального интервала, интервала слева от модального и интервала справа.

Медианным интервалом называют первый интервал слева, на котором кумулята превысила значение 0,5. Медиана интервального вариационного ряда определяется по формуле: $$ M_e=x_o+frac{0,5-S_{me-1}}{w_{me}}h $$ где
(h) – шаг интервального ряда;
(x_o) — нижняя граница медианного интервала;
(S_{me-1}) накопленная относительная частота для интервала слева от медианного;
(w_{me}) относительная частота медианного интервала.

Расположение выборочной средней, моды и медианы в зависимости от симметрии ряда аналогично их расположению в дискретном ряду (см. §65 данного справочника).

Например:
Для распределения учеников по росту получаем:

(x_i)	146	154	162	170	178	186	194	∑
(w_i)	0,04	0,07	0,11	0,34	0,33	0,08	0,03	1
(x_iw_i)	5,84	10,78	17,82	57,80	58,74	14,88	5,82	171,68

$$ X_{cp}=sum_{i=1}^k x_iw_i=171,68approx 171,7 text{(см)} $$ На гистограмме (или полигоне) относительных частот максимальная частота приходится на 4й интервал [166;174). Это модальный интервал.
Данные для расчета моды: begin{gather*} x_o=166, f_m=34, f_{m-1}=11, f_{m+1}=33, h=8\ M_o=x_o+frac{f_m-f_{m-1}}{(f_m-f_{m-1})+(f_m+f_{m+1})}h=\ =166+frac{34-11}{(34-11)+(34-33)}cdot 8approx 173,7 text{(см)} end{gather*} На кумуляте значение 0,5 пересекается на 4м интервале. Это – медианный интервал.
Данные для расчета медианы: begin{gather*} x_o=166, w_m=0,34, S_{me-1}=0,22, h=8\ \ M_e=x_o+frac{0,5-S_{me-1}}{w_me}h=166+frac{0,5-0,22}{0,34}cdot 8approx 172,6 text{(см)} end{gather*} begin{gather*} \ X_{cp}=171,7; M_o=173,7; M_e=172,6\ X_{cp}lt M_elt M_o end{gather*} Ряд асимметричный с левосторонней асимметрией.
При этом (frac{|M_o-X_{cp}|}{|M_e-X_{cp}|}=frac{2,0}{0,9}approx 2,2lt 3), т.е. распределение умеренно асимметрично.

п.4. Выборочная дисперсия и СКО

Выборочная дисперсия интервального вариационного ряда определяется как средняя взвешенная для квадрата отклонения от средней: begin{gather*} D=frac1Nsum_{i=1}^k(x_i-X_{cp})^2 f_i=frac1Nsum_{i=1}^k x_i^2 f_i-X_{cp}^2 end{gather*} где (x_i) — середины интервалов: (x_i=frac{a_{i-1}+a_i}{2}, i=overline{1,k}).
Или, через относительные частоты: $$ D=sum_{i=1}^k(x_i-X_{cp})^2 w_i=sum_{i=1}^k x_i^2 w_i-X_{cp}^2 $$

Выборочное среднее квадратичное отклонение (СКО) определяется как корень квадратный из выборочной дисперсии: $$ sigma=sqrt{D} $$

Например:
Для распределения учеников по росту получаем:

$x_i$	146	154	162	170	178	186	194	∑
(w_i)	0,04	0,07	0,11	0,34	0,33	0,08	0,03	1
(x_iw_i)	5,84	10,78	17,82	57,80	58,74	14,88	5,82	171,68
(x_i^2w_i) — результат	852,64	1660,12	2886,84	9826	10455,72	2767,68	1129,08	29578,08

$$ D=sum_{i=1}^k x_i^2 w_i-X_{cp}^2=29578,08-171,7^2approx 104,1 $$ $$ sigma=sqrt{D}approx 10,2 $$

п.5. Исправленная выборочная дисперсия, стандартное отклонение выборки и коэффициент вариации

Исправленная выборочная дисперсия интервального вариационного ряда определяется как: begin{gather*} S^2=frac{N}{N-1}D end{gather*}

Стандартное отклонение выборки определяется как корень квадратный из исправленной выборочной дисперсии: $$ s=sqrt{S^2} $$

Коэффициент вариации это отношение стандартного отклонения выборки к выборочной средней, выраженное в процентах: $$ V=frac{s}{X_{cp}}cdot 100text{%} $$

Подробней о том, почему и когда нужно «исправлять» дисперсию, и для чего использовать коэффициент вариации – см. §65 данного справочника.

Например:
Для распределения учеников по росту получаем: begin{gather*} S^2=frac{100}{99}cdot 104,1approx 105,1\ sapprox 10,3 end{gather*} Коэффициент вариации: $$ V=frac{10,3}{171,7}cdot 100text{%}approx 6,0text{%}lt 33text{%} $$ Выборка однородна. Найденное значение среднего роста (X_{cp})=171,7 см можно распространить на всю генеральную совокупность (старшеклассников из других школ).

п.6. Алгоритм исследования интервального вариационного ряда

На входе: все значения признака (left{x_jright}, j=overline{1,N})
Шаг 1. Построить интервальный ряд с интервалами (left.right[a_{i-1}, a_ileft.right)) и частотами (f_i, i=overline{1,k}) (см. алгоритм выше).
Шаг 2. Составить расчетную таблицу. Найти (x_i,w_i,S_i,x_iw_i,x_i^2w_i)
Шаг 3. Построить гистограмму (и/или полигон) относительных частот, эмпирическую функцию распределения (и/или кумуляту). Записать эмпирическую функцию распределения.
Шаг 4. Найти выборочную среднюю, моду и медиану. Проанализировать симметрию распределения.
Шаг 5. Найти выборочную дисперсию и СКО.
Шаг 6. Найти исправленную выборочную дисперсию, стандартное отклонение и коэффициент вариации. Сделать вывод об однородности выборки.

п.7. Примеры

Пример 1. При изучении возраста пользователей коворкинга выбрали 30 человек.
Получили следующий набор данных:
18,38,28,29,26,38,34,22,28,30,22,23,35,33,27,24,30,32,28,25,29,26,31,24,29,27,32,24,29,29
Постройте интервальный ряд и исследуйте его.

1) Построим интервальный ряд. В наборе данных: $$ x_{min}=18, x_{max}=38, N=30 $$ Размах вариации: (R=38-18=20)
Оптимальное число интервалов: (k=1+lfloorlog_2⁡ 30rfloor=1+4=5)
Шаг интервального ряда: (h=lceilfrac{20}{5}rceil=4)
Получаем узлы ряда: $$ a_0=x_{min}=18, a_i=18+icdot 4, i=overline{1,5} $$

(left.left[a_{i-1},a_iright.right)) лет

(left.left[18;22right.right))

(left.left[22;26right.right))

(left.left[26;30right.right))

(left.left[30;34right.right))

(left.left[34;38right.right))

Считаем частоты для каждого интервала. Получаем интервальный ряд:

(left.left[a_{i-1},a_iright.right)) лет	(left.left[18;22right.right))	(left.left[22;26right.right))	(left.left[26;30right.right))	(left.left[30;34right.right))	(left.left[34;38right.right))
(f_i)	1	7	12	6	4

2) Составляем расчетную таблицу:

(x_i)	20	24	28	32	36	∑
(f_i)	1	7	12	6	4	30
(w_i)	0,033	0,233	0,4	0,2	0,133	1
(S_i)	0,033	0,267	0,667	0,867	1	—
(x_iw_i)	0,667	5,6	11,2	6,4	4,8	28,67
(x_i^2w_i)	13,333	134,4	313,6	204,8	172,8	838,93

3) Строим полигон и кумуляту

Эмпирическая функция распределения: $$ F(x)= begin{cases} 0, xleq 20\ 0,033, 20lt xleq 24\ 0,267, 24lt xleq 28\ 0,667, 28lt xleq 32\ 0,867, 32lt xleq 36\ 1, xgt 36 end{cases} $$ 4) Находим выборочную среднюю, моду и медиану $$ X_{cp}=sum_{i=1}^k x_iw_iapprox 28,7 text{(лет)} $$ На полигоне модальным является 3й интервал (самая высокая точка).
Данные для расчета моды: begin{gather*} x_0=26, f_m=12, f_{m-1}=7, f_{m+1}=6, h=4\ M_o=x_o+frac{f_m-f_{m-1}}{(f_m-f_{m-1})+(f_m+f_{m+1})}h=\ =26+frac{12-7}{(12-7)+(12-6)}cdot 4approx 27,8 text{(лет)} end{gather*}
На кумуляте медианным является 3й интервал (преодолевает уровень 0,5).
Данные для расчета медианы: begin{gather*} x_0=26, w_m=0,4, S_{me-1}=0,267, h=4\ M_e=x_o+frac{0,5-S_{me-1}}{w_{me}}h=26+frac{0,5-0,4}{0,267}cdot 4approx 28,3 text{(лет)} end{gather*} Получаем: begin{gather*} X_{cp}=28,7; M_o=27,8; M_e=28,6\ X_{cp}gt M_egt M_0 end{gather*} Ряд асимметричный с правосторонней асимметрией.
При этом (frac{|M_o-X_{cp}|}{|M_e-X_{cp}|} =frac{0,9}{0,1}=9gt 3), т.е. распределение сильно асимметрично.

5) Находим выборочную дисперсию и СКО: begin{gather*} D=sum_{i=1}^k x_i^2w_i-X_{cp}^2=838,93-28,7^2approx 17,2\ sigma=sqrt{D}approx 4,1 end{gather*}
6) Исправленная выборочная дисперсия: $$ S^2=frac{N}{N-1}D=frac{30}{29}cdot 17,2approx 17,7 $$ Стандартное отклонение (s=sqrt{S^2}approx 4,2)
Коэффициент вариации: (V=frac{4,2}{28,7}cdot 100text{%}approx 14,7text{%}lt 33text{%})
Выборка однородна. Найденное значение среднего возраста (X_{cp}=28,7) лет можно распространить на всю генеральную совокупность (пользователей коворкинга).

Источник

Каждое
значение непрерывного признака как
правило имеет частоту встречаемости
равную 1, поэтому построение вариационного
ряда по типу дискретного ряда здесь
невозможно. Для непрерывного признака
строится интервальный вариационный
ряд. Интервальный вариационный ряд
может быть построен также и по
дискретному признаку в том случае
если он принимает значения в очень
широком диапазоне ( например число
жителей в населенном пункте может
изменяться от 1-го до нескольких
миллионов ). В интервальном вариационном
ряду в левой колонке таблицы вместо
отдельных значений записываются их
интервалы, а в правой – вместо частот
для отдельных значений признака
записываются частоты интервалов, то
есть сколько единиц имеют значения
признака в пределах того или иного
интервала. Следовательно, макет
интервального вариационного ряда
выглядит так :

Таблица
2.2.2

Интервальный
вариационный ряд распределения …………

Интервалы значений признака	Частота Частота интервала (
от до
от до
……………
Итого	Сумма частот ( )

Построение
интервального ряда распределения
включает в себя несколько этапов.

На
первом этапе определяется число
интервалов ( групп ) на которое
подразделяется совокупность. Наиболее
часто используемыми формулами для
определения числа интервалов являются
две :
и, гдечисло интервалов . а— общая численность совокупности.
Эти формулы дают схожую оценку числа
интервалов при общей численности
совокупности примерно до 50 единиц.
При большей совокупности обнаруживаются
большие различия. Например, приN
= 100, по первой формуле число интервалов
равно 10, а по второй -7, при N
=1000 соответственно 32 и 10. и предпочтение
следует отдавать второй формуле.

Любой
интервал содержит нижнюю и верхнюю
границы На втором этапе следует
рассчитать шаг интервала., то есть
разницу между этими границами . Эта
разница для всех интервалов должна
быть одинаковой. Для расчета шага
интервала обычно используется формула
:
,
где—
искомый шаг интервала ;—
максимальное в совокупности значение
признака ;— минимальное в совокупности значение
признака ;число интервалов. Если при изучении
ранжированного ряда обнаружится, что
максимальное или минимальное ( или
даже несколько значений ) сильно
отличаются от остальных, то при расчете
шага интервала следует использовать
соответственно не максимальное, а
предшествующее ему значение, не
минимальное , а следующее в ранжированном
ряду значение признака. В противном
случае может получиться , что в одном-
двух интервалах будут сосредоточены
все наблюдения.

Шаг
интервала обычно рассчитывают с той
же точностью с какой представлены
значения признака в изучаемой
совокупности. Иногда шаг интервала
берут с точностью на один знак меньше
той , какая имеет место в исходной
совокупности. Если при расчете шага
интервала требуется округление до
заданной точности , то округление
производят всегда в большую
сторону.

После
определения шага интервала следует
найти границы интервалов : первый
интервал в качестве нижней границы
имеет
, в качестве верхней+;
второй интервал в качестве нижней
имеет верхнюю границу первого интервала
,то есть+,
для получения верхней границы этого
интервала надо вновь прибавить шаг
интервала , то есть+,+=+
2и так далее. Если при определении
шага интервала пришлось отказаться
от,
то в первом интервале сразу находится
верхняя граница, для чего к значению,
которое использовалось при расчете
шага интервала следует прибавить шаг
интервала, нижняя граница первого
интервала не обозначается . Сам интервал
будет открыт снизу. Если при расчете
шага интервала пришлось отказаться
от максимального значения, для того
, чтобы и это значение присутствовало
в интервальном ряду, открытым сверху
делают последний интервал. Определив
границы интервалов, далее следует
подсчитать сколько единиц попало в
каждый интервал. Для этого удобнее
всего воспользоваться ранжированным
рядом, обозначив на нем границы
интервалов. Если единица имеет значение
признака на границе интервала, то она
может вой- ти только в один интервал
; в какой именно решает сам исследователь
– в нижний ( принцип включительно) или
верхний ( принцип исключительно ).
Результаты подсчетов оформляются в
таблице, представленной ранее на
макете. Графически интервальный
вариационный ряд отображается в
виде гистограммы распределения, при
этом на оси абсцисс откладываются
интервалы, а на оси ординат — частоты
интервалов Вид такого графика следующий

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Варианты для выполнения работы

I. Установление закономерностей, которым подчинены массовые случайные явления, основано на изучении методами теории вероятностей статистических данных — результатов наблюдений.

Почти все встречающиеся в жизни величины (урожайность сельскохозяйственных растений, продуктивности скота, производительность труда и заработная плата рабочих, объем производства продукции и т.д.) принимают неодинаковые значения у различных членов совокупности. Поэтому возникает необходимость в изучении их изменяемости. Это изучение начинается с проведения соответствующих наблюдений, обследований.

В результате наблюдений получают сведения о численной величине изучаемого признака у каждого члена данной совокупности.

Пример. Имеются данные о размере прибыли 100 коммерческих банков. Прибыль, млн. рублей.

30,2	51,9	43,1	58,9	34,1	55,2	47,9	43,7	53,2	34,9
47,8	65,7	37,8	68,6	48,4	67,5	27,3	66,1	52,0	55,6
54,1	26,9	53,6	42,5	59,3	44,8	52,8	42,3	55,9	48,1
44,5	69,8	47,3	35,6	70,1	39,5	70,3	33,7	51,8	56,1
28,4	48,7	41,9	58,1	20,4	56,3	46,5	41,8	59,5	38,1
41,4	70,4	31,4	52,5	45,2	52,3	40,2	60,4	27,6	57,4
29,3	53,8	46,3	40,1	50,3	48,9	35,8	61,7	49,2	45,8
45,3	71,5	35,1	57,8	28,1	57,6	49,6	45,5	36,2	63,2
61,9	25,1	65,1	49,7	62,1	46,1	39,9	62,4	50,1	33,1
33,3	49,8	39,8	45,9	37,3	78,0	64,9	28,8	62,5	58,7

Из данной таблицы видно, что интересующий нас признак (прибыль банков) меняется от одного члена совокупности к другому, варьирует. Варьирование есть изменяемость признака у отдельных членов совокупности.

Вариационным рядом называется последовательность вариант, записанных в возрастающем порядке и соответствующих им частот.

Число, показывающее, сколько раз повторяется в данной совокупности каждое значение признака, называется частотой.

Составим ранжированный вариационный ряд (выпишем варианты в порядке возрастания):

20,4	25,1	26,9	27,3	27,6	28,1	28,4	28,8	29,3	30,2
31,4	33,1	33,3	33,7	34,1	34,9	35,1	35,6	35,8	36,2
37,3	37,8	38,1	39,5	39,8	39,9	40,1	40,2	41,4	41,8
41,9	42,3	42,5	43,1	43,7	44,5	44,8	45,2	45,3	45,5
45,8	45,9	46,1	46,3	46,5	47,3	47,8	47,9	48,1	48,4
48,7	48,9	49,2	49,6	49,7	49,8	50,1	50,3	51,8	51,9
52,0	52,3	52,5	52,8	53,2	53,6	53,8	54,1	55,2	55,6
55,9	56,1	56,3	57,4	57,6	57,8	58,1	58,7	58,9	59,3
59,5	60,4	61,7	61,9	62,1	62,4	62,5	63,2	64,9	65,1
65,7	66,1	67,5	68,6	69,8	70,1	70,3	70,4	71,5	78,0

В нашем случае каждое значение признака (варианта вариационного ряда) повторилось только один раз, т.е. значение частоты для всех вариант равно единице. Перейдем к интервальному вариационному ряду, так как интересующий нас признак принимает дробные, практически не повторяющиеся значения.

Для этого необходимо определить число интервалов (классов) и длину интервала (классного промежутка), после чего произвести разноску, т.е. подсчитать для каждого интервала число вариант, попавших в него.

Количество классов устанавливают в зависимости от степени точности, с которой ведется обработка, и количества объектов в выборке. Считается удобным при объеме выборки (n) в пределах от 30 до 60 вариант распределять их на 6-7 классов, при n от 60 до 100 вариант — на 7-8 классов, при n от 100 и более вариант — на 9-17 классов.

Нужное количество групп также может быть ориентировочно вычислено по формуле Стерджесса:

где — число групп (классов, интервалов) ряда распределения; n — объем выборки.

Можно также использовать выражение:

При они дают примерно одинаковые результаты.

В рассматриваемом примере о размере прибыли коммерческих банков, n=100. Применяя формулу Стерджесса, получим:

Однако Таким образом, число интервалов может быть равно 8, 9, 10 и т.д.

Нахождение нужного количества групп и их размеров часто бывает взаимообусловлено. Для того, чтобы как-то определиться с числом интервалов, найдем размах вариации — разность между наибольшей и наименьшей вариантой:

$[R=x_{max}-x_{min}]$

где — размах вариации,

$x_{max}$ — наибольшее значение варьирующего признака,

$x_{min}$ — наименьшее значение варьирующего признака.

Найдем размах вариации для рассматриваемой задачи:

Для того, чтобы найти длину интервала (величину классового промежутка) необходимо разделить размах вариации на число классов и полученную величину округлить таким образом, чтобы было удобно производить сначала разноску, а затем и различные вычисления. Рекомендую округлять до единиц, до которых округлены варианты в исходной таблице, в нашем случае до десятых.

$[happrox frac{R}{k}]$

Согласно формуле получаем

$[happrox frac{57,6}{8}=7,2]$

Теперь необходимо определиться с началом первого интервала. Для этого можно использовать формулу:

$[x_1approx x_{min}-frac{h}{2}]$

$[x_1approx 20,4-frac{7,2}{2}=16,8.]$

Замечание. За начало первого интервала можно принять некоторое значение, несколько меньшее $x_{min}$ или само значение $x_{min}$ . Далее в табличном виде я покажу оба варианта.

Прибавив к началу первого интервала (нижней границе) шаг, получим верхнюю границу первого интервала и одновременно нижнюю границу второго интервала. Выполняя последовательно указанные действия, будем находить границы последующих интервалов до тех пор, пока не будет получено или перекрыто $x_{max}$ .

Таким образом, верхняя граница одного интервала одновременно является нижней границей другого интервала. Чтобы не возникало сомнений, в какой интервал отнести варианту, попавшую на границу, условимся относить ее к верхнему интервалу.

Составим теперь рабочую таблицу для построения интервального вариационного ряда и произведем подсчет частот вариант, попавших в тот или иной интервал.

Как и обещал покажу две таблицы построения ряда:

1. Отсчет ведем от $x_{min}$ , т.е. нижняя граница первого интервала совпадает с $x_{min}$ .

Группы банков по размеру прибыли (границы интервалов)	Количество банков, принадлежащих данной группе (частоты, )	Накопленные частоты,
20,4 — 27,6	4	4
27,6 — 34,8	11	15
34,8 — 42	16	31
42 — 49,2	21	52
49,2 — 56,4	21	73
56,4 — 63,6	15	88
63,6 — 70,8	10	98
70,8 — 78	2	100

2. Начало первого интервала определяем с помощью формулы: $x_1approx x_{min}-frac{h}{2}$ .

Группы банков по размеру прибыли (границы интервалов)	Количество банков, принадлежащих данной группе (частоты, )	Накопленные частоты,
16,8 — 24	1	1
24 — 31,2	9	10
31,2 — 38,4	13	23
38,4 — 45,6	17	40
45,6 — 52,8	23	63
52,8 — 60	18	81
60 — 67,2	11	92
67,2 — 74,4	7	99
74,4 — 81,6	1	100

Как мы видим в 1-м случае у нас получилось восемь интервалов, что полностью совпадает с результатом, который нам дала формула Стерджесса. Во втором случае у нас получилось девять интервалов, так как при поиске начала первого интервала пользовались специальной формулой.

Для дальнейшего исследования я буду пользоваться результатами второй таблицы, так как там ярко выражен модальный интервал (одна мода) и медиана практически точно попадает на середину вариационного ряда.

Мы получили интервальный вариационный ряд — упорядоченную совокупность интервалов варьирования значений случайной величины с соответствующими частотами попаданий в каждый из них значений величины.

II. Графическая интерпретация вариационных рядов.

№ п/п	Границы интервалов, $[x_{i}; x_{i+1})$	Середины интервалов, $x_{i}^{*}=frac{x_i+x_{i+1}}{2}$	Частоты интервалов,	Относительные частоты $W_i=frac{n_i}{n}$	Плотность относит. частоты $frac{W_i}{h}$	Плотность частоты $frac{n_i}{h}$
1	16,8 — 24	20,4	1	0,01	0,001	0,139
2	24 — 31,2	27,6	9	0,09	0,013	1,250
3	31,2 — 38,4	34,8	13	0,13	0,018	1,806
4	38,4 — 45,6	42	17	0,17	0,024	2,361
5	45,6 — 52,8	49,2	23	0,23	0,032	3,194
6	52,8 — 60	56,4	18	0,18	0,025	2,500
7	60 — 67,2	63,6	11	0,11	0,015	1,528
8	67,2 — 74,4	70,8	7	0,07	0,010	0,972
9	74,4 — 81,6	78	1	0,01	0,001	0,139

Строим графики:

Далее найдем моду вариационного ряда:

$[M_o(X)=x_{M_o}+hfrac{(n_2-n_1)}{(n_2-n_1)+(n_2-n_3)}]$

где

$x_{M_o}$ — начало модального интервала;

— длина частичного интервала (шаг);

n_1 — частота предмодального интервала;

n_2 — частота модального интервала;

— частота послемодального интервала.

Определим модальный интервал — интервал, имеющий наибольшую частоту. Из таблицы видно, что модальным является интервал (45,6 — 52,8).

$[M_o(X)=45,6+7,2frac{(23-17)}{(23-17)+(23-18)}=]$

$[=45,6+7,2cdot frac{6}{6+5}=45,6+3,93=49,5]$

Медиана

Для интервального ряда медиана находится по формуле:

$[M_e(X)=x_{M_e}+hfrac{0,5n-S_{M_{e}-1}}{n_{M_e}}]$

где

$x_{M_e}$ — начало медианного интервала;

— длина частичного интервала (шаг);

— объем совокупности;

$S_{M_{e}-1}$ — накопленная частота интервала, предшествующая медианному;

$n_{M_e}$ — частота медианного интервала.

Определим медианный интервал — интервал, в котором впервые накопленная частота превышает половину объема выборки.Так как объем выборки n=100, то n/2=50. По таблице найдем интервал, где впервые накопленные частоты превысят это значение. Таким является интервал (45,6 — 52,8).

Получаем,

$[M_e(X)=45,6+7,2frac{0,5cdot 100-40}{23}approx 48,7.]$

III. Расчет сводных характеристик выборки.

Для определения $x_B, D_{B}, sigma_{B}$ составим расчетную таблицу. Для начала определимся с ложным нулем С. В качестве ложного нуля можно принять любую варианту. Максимальная простота вычислений достигается, если выбрать в качестве ложного нуля варианту, которая расположена примерно в середине вариационного ряда (часто такая варианта имеет наибольшую частоту).

Варианте, которая принята в качестве ложного нуля, соответствует условная варианта, равная нулю. В нашем случае С=49,2.

Равноотстоящими называют варианты, которые образуют арифметическую прогрессию с разностью h.

Условными называют варианты, определяемые равенством:

$[U_i=frac{(x_i-C)}{h}]$

Произведем расчет условных вариант согласно формуле:

$[U_1=frac{20,4-49,2}{7,2}=-4]$

$[U_2=frac{27,6-49,2}{7,2}=-3]$

$[U_3=frac{34,8-49,2}{7,2}=-2]$

$[U_4=frac{42-49,2}{7,2}=-1]$

$[U_5=frac{49,2-49,2}{7,2}=0]$

$[U_6=frac{56,4-49,2}{7,2}=1]$

$[U_7=frac{63,6-49,2}{7,2}=2]$

$[U_8=frac{70,8-49,2}{7,2}=3]$

$[U_9=frac{78-49,2}{7,2}=4]$

N п/п	Середины интервалов, $x_{i}^{*}$	Частоты интервалов,	Условные варианты,	Произведения частот и условных вариант,	Произведения частот и условных вариант,	Произведения частот и условных вариант,	Произведения частот и условных вариант,	Произведения частот и условных вариант,	Произведения частот и условных вариант,
1	20,4	1	-4	-4	16	-64	256	9	81
2	27,6	9	-3	-27	81	-243	729	36	144
3	34,8	13	-2	-26	52	-104	208	13	13
4	42	17	-1	-17	17	-17	17	0	0
5	49,2	23	0	0	0	0	0	23	23
6	56,4	18	1	18	18	18	18	72	288
7	63,6	11	2	22	44	88	176	99	891
8	70,8	7	3	21	63	189	567	112	1792
9	78	1	4	4	16	64	256	25	625

Контроль:

$[sum n_i U_i^2 + 2sum n_iU_i+n=sum n_i{(U_i+1)}^2]$

$[sum n_i{(U_i+1)}^2=389]$

Контроль:

$[sum n_i U_i^4 + 4sum n_iU_i^3+6sum n_iU_i^2+4sum n_iU_i+n=sum n_i{(U_i+1)}^4]$

$[sum n_i{(U_i+1)}^4=3857]$

Равенство выполнено, следовательно вычисления произведены верно.

Вычислим условные моменты 1-го, 2-го, 3-го и 4-го порядков:

$[M_1^{*}=frac{sum n_iU_i}{n}=frac{-9}{100}=-0,09;]$

$[M_2^{*}=frac{sum n_iU_i^2}{n}=frac{307}{100}=3,07;]$

$[M_3^{*}=frac{sum n_iU_i^3}{n}=frac{-69}{100}=-0,69;]$

$[M_4^{*}=frac{sum n_iU_i^4}{n}=frac{2227}{100}=22,27.]$

Найдем выборочные среднюю, дисперсию и среднее квадратическое отклонение :

$[x_{B}=M_1^{*}cdot h+C=-0,09cdot 7,2+49,2=48,552;]$

$[D_{B}=(M_2^{*}-{(M_1^{*})}^2)h^2=(3,07-{(-0,09)}^2){7,2}^2approx 158,73.]$

$[sigma_{B}=sqrt{D_B}=sqrt{158,73}=12,6.]$

Также для оценки отклонения эмпирического распределения от нормального используют такие характеристики, как асимметрия и эксцесс.

Асимметрией теоретического распределения называют отношение центрального момента третьего порядка к кубу среднего квадратического отклонения:

$[a_s=frac{m_3}{sigma_B^3}]$

Асимметрия положительна, если «длинная часть» кривой распределения расположена справа от математического ожидания; асимметрия отрицательна, если «длинная часть» кривой расположена слева от математического ожидания. Практически определяют знак асимметрии по расположению кривой распределения относительно моды (точки максимума дифференциальной функции): если «длинная часть» кривой расположена правее моды, то асимметрия положительна, если слева — отрицательна.

Эксцесс эмпирического распределения определяется равенством:

$[e_k=frac{m_4}{sigma_B^4}-3]$

где — центральный эмпирический момент четвертого порядка.

Для нормального распределения эксцесс равен нулю. Поэтому если эксцесс некоторого распределения отличен от нуля, то кривая этого распределения отличается от нормальной кривой: если эксцесс положительный, то кривая имеет более высокую и «острую» вершину, чем нормальная кривая; если эксцесс отрицательный, то сравниваемая кривая имеет более низкую и «плоскую» вершину, чем нормальная кривая. При этом предполагается, что нормальное и теоретическое распределения имеют одинаковые математические ожидания и дисперсии.

Вычисляем центральные эмпирические моменты третьего и четвертого порядков:

$[m_3=(M_3^*-3M_1^*M_2^*+2{(M_1^*)}^3)cdot h^3=51,3;]$

$[m_4=(M_4^*-4M_3^*M_1^*+6M_2^*{(M_1^*)}^2-3{(M_1^*)}^4)cdot h^4=59580,97;]$

Найдем асимметрию и эксцесс:

$[a_s=frac{51,3}{{12,6}^3}=0,026]$

$[e_k=frac{59580,97}{{12,6}^4}-3=-0,635]$

IV. Проверка гипотезы о нормальном распределении генеральной совокупности. Критерий согласия Пирсона.

Проверим генеральную совокупность значений размера прибыли банков по критерию Пирсона

Правило. Для того, чтобы при заданном уровне значимости проверить нулевую гипотезу : генеральная совокупность распределена нормально, надо сначала вычислить теоретические частоты, а затем наблюдаемое значение критерия:

$[chi^2_{nabl}=sum frac{ {(n_i-n_i^{'})}^2}{n_i^{'}}]$

и по таблице критических точек распределения , по заданному уровню значимости и числу степеней свободы найти критическую точку $chi^2_{kp}(alpha;k)$ , где s — количество интервалов.

Если $chi^2_{nabl}<chi^2_{kp}$ — нет оснований отвергнуть нулевую гипотезу.

Если $chi^2_{nabl}>chi^2_{kp}$ — нулевую гипотезу отвергают.

Найдем теоретические частоты , для этого составим следующую таблицу.

Середины интервалов, $x_{i}^{*}$	Частоты интервалов,	Произведем расчет, $x_{i}^{*}-x_B$	Произведем расчет, $V_i=frac{(x_{i}^{*}-x_B)}{sigma_B}$	Значения функции Гаусса,	Произведем расчет, $frac{nh}{sigma_B}$	Теоретические частоты, $n_i^{'}=57 cdotvarphi(V_i)$
20,4	1	-28,152	-2,23	0,0332	57	2
27,6	9	-20,952	-1,66	0,1006	57	6
34,8	13	-13,752	-1,09	0,2203	57	13
42	17	-6,552	-0,52	0,3485	57	20
49,2	23	0,648	0,05	0,3984	57	23
56,4	18	7,848	0,62	0,3292	57	19
63,6	11	15,048	1,19	0,1965	57	11
70,8	7	22,248	1,77	0,0833	57	5
78	1	29,448	2,34	0,0258	57	1
						$sum n_i^{'}=100$

Вычислим $chi^2_{nabl}$ , для чего составим расчетную таблицу.

		$n_i^{'}$	$n_i-n_i^{'}$	${(n_i-n_i^{'})}^2$	$frac{{(n_i-n_i^{'})}^2}{n_i^'}$		$frac{n_i^2}{n_i^{'}}$
1	1	2	-1	1	0,5	1	0,5
2	9	6	3	9	1,5	81	13,5
3	13	13	0	0	0	169	13
4	17	20	-3	9	0,45	289	14,45
5	23	23	0	0	0	529	23
6	18	19	-1	1	0,05	324	17,05
7	11	11	0	0	0	121	11
8	7	5	2	4	0,8	49	9,8
9	1	1	0	0	0	1	1
	100	100			Наблюдаемое значение критерия, $chi^2_{nabl}=3,30$		103,30

Контроль:

$[sumfrac{n_i^2}{n_i^{'}}-n=sum frac{{(n_i-n_i^{'})}^2}{n_i^'}]$

$[sumfrac{n_i^2}{n_i'}-n=103,3-100=3,3]$

$[sum frac{{(n_i-n_i')}^2}{n_i'}=3,3]$

Вычисления произведены правильно.

Найдем число степеней свободы, учитывая, что число групп выборки (число различных вариант) s=9;

По таблице критических точек распределения по уровню значимости и числу степеней свободы k=6 находим $chi^2_{kp}(0,025;6)=14,4.$

Так как $chi^2_{nabl}<chi^2_{kp}$ — нет оснований отвергнуть нулевую гипотезу. Другими словами, расхождение эмпирических и теоретических частот незначительное. Следовательно, данные наблюдений согласуются с гипотезой о нормальном распределении генеральной совокупности.

На рисунке построены нормальная (теоретическая) кривая по теоретическим частотам (зеленый график) и полигон наблюдаемых частот (коричневый график). Сравнение графиков наглядно показывает, что построенная теоретическая кривая удовлетворительно отражает данные наблюдений.

V. Интервальные оценки.

Интервальной называют оценку, которая определяется двумя числами — концами интервала, покрывающего оцениваемый параметр.

Доверительным называют интервал, который с заданной надежностью покрывает заданный параметр.

Интервальной оценкой (с надежностью ) математического ожидания (а) нормально распределенного количественного признака Х по выборочной средней при известном среднем квадратическом отклонении sigma генеральной совокупности служит доверительный интервал

$[x_B-frac{tsigma}{sqrt{n}}<a<x_B+frac{tsigma}{sqrt{n}},]$

где $frac{tsigma}{sqrt{n}}=delta$ — точность оценки, n — объем выборки, t — значение аргумента функции Лапласа (см. приложение 2), при котором $phi(t)=frac{gamma}{2}$ ;

при неизвестном среднем квадратическом отклонении sigma (и объеме выборки n<30)

$[x_B-frac{t_{gamma}cdot S}{sqrt{n}}<a<x_B+frac{t_{gamma}cdot S}{sqrt{n}},]$

$[S=sqrt{frac{n}{n-1}D_B}]$

где S — исправленное выборочное среднее квадратическое отклонение, $t_{gamma}$ находят по таблице приложения по заданным n и .

В нашем примере среднее квадратическое отклонение известно, . А также , , . Поэтому для поиска доверительного интервала используем первую формулу:

$[x_B-frac{tsigma}{sqrt{n}}<a<x_B+frac{tsigma}{sqrt{n}}]$

Все величины, кроме t, известны. Найдем t из соотношения $phi(t)=frac{0,95}{2}=0,475.$ По таблице приложения находим t=1,96. Подставив t=1,96, , , в формулу, окончательно получим искомый доверительный интервал:

$[48,55-frac{1,96cdot 12,6}{10}<a<48,55+frac{1,96cdot 12,6}{10}]$

Интервальной оценкой (с надежностью ) среднего квадратического отклонения нормально распределенного количественного признака Х по «исправленному» выборочному среднему квадратическому отклонению S служит доверительный интервал

(при q<1), (*)

(при q>1),

где q — находят по таблице приложения по заданным n и .

По данным и n=100 по таблице приложения 4 найдем q=0,143. Так как q<1, то, подставив $S=sqrt{frac{n}{n-1}D_B}=sqrt{frac{100}{99}cdot 158,73}approx 12,66, quad quad q=0,143$ в соотношение (*), получим доверительный интервал:

Источник