Download Article
Download Article
Hexadecimal notation (base sixteen) is used throughout the Web and computer systems to indicate values. One good example is the notation for color in HTML pages. Reading and using hexadecimal takes some practice, but the basic concept is no more difficult to understand than the ordinary decimal (base ten) system you’ve been using all your life.
-
1
Learn what hexadecimal is. Just like the
decimal
number system uses
ten
different symbols to denote values from Zero to Nine, the
hexadecimal
number system uses
sixteen
different symbols to denote values from Zero to Fifteen. Any number can be written in either system.[1]
Here’s how to start counting in hexadecimal:- zero through fifteen: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
- sixteen through thirty-two: 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 1A, 1B, 1C, 1D, 1E, 1F, 20
-
2
Learn how to write bases. The ten symbols used in the decimal number system form the base of the decimal number system.[2]
Similarly, the sixteen symbols used in the hexadecimal number system form the base of the hexadecimal number system. Whenever it’s unclear which base is being used, subscript numbers are added to show the base. For example, 10010 is «100 in base 10» and 10016 is «100 in base 16» (which equals 25610).- Another term for «base» is «radix» (pluralized «radixes» or «radices»).
Advertisement
-
3
Understand place values in decimal. We can understand long numbers written in base 10 without even pausing to think, but that’s only because we’ve had a lot of practice.[3]
We know automatically that «583410» means 5×103 + 8×102 + 3×101 + 4×100. Each digit in a multi-digit number has its own place value. Here are the place values in decimal, from right to left:- 10010 = 1
- 10110 = 1010
- 102 = 10×10 = 100
- 103 = 10x10x10 = 1000
- 104 = 10x10x10x10 = 10000
- 105 = 10x10x10x10x10 = 100000 & so on.
-
4
Learn the hexadecimal place values. Since hexadecimal is base sixteen, the place values are based on powers of sixteen, not powers of ten. Here are the powers of sixteen, written in decimal.[4]
- 16010 = 1
- 16110 = 1610
- 162=16×16=256
- 163=16x16x16=4096
- 164=16x16x16x16=65536
- 165=16x16x16x16x16=1048576 & so on.
- If we write these in hexadecimal, these would instead be written as 1016, 100, 1000, etc.
-
5
Convert from hexadecimal to decimal. Converting between two bases is a good way to become familiar with how each system works. Here’s how to convert from any number in hexadecimal to the same number written in decimal:[5]
- Write out your hexadecimal number: 15B3016
- Write each digit out as a decimal multiplication problem, using the place value in the chart above: 15B30 = (1 x 6553610) + (5 x 409610) + (B x 25610) + (3 x 1610) + (0 x 1)
- Convert non-decimal symbols into decimal numbers. In our example, B = 1110, so that digit can be converted to 1110 x 25610
- Solve the problem. Use a calculator or work it out by hand, and you’ll get the answer in decimal. 15B30 = 65536 + 20480 + 2816 + 48 + 0 = 8888010
Advertisement
-
1
Understand how colors on a computer screen are determined. All colors on a computer screen are determined by three values: red, green, and blue. All colors of light can be created by combining these three types of light in different proportions. On a computer screen, red, green, and blue can each be assigned any value from 0 to 255 (for a total of 256 possible values).[6]
- This doesn’t match the «primary» colors you learned in school, because that color system is based on physical pigment (like paint), not light. The paint system is sometimes called «subtractive color system» and the light system (the RGB system described here) «additive.»
-
2
Learn why hexadecimal is used for colors. HTML uses hexadecimal to describe colors. This is convenient, since a two-digit hexadecimal number can communicate exactly 25610 possible values. This isn’t a coincidence; the number 25610 is due to limitations of old hardware, which could only handle 1000000002 colors, or 25610. Because 24 = 1610, any binary system can be easily converted to a hexadecimal system with ¼ as many digits.
- The subscript numbers tell you which base the numbers is written in. Base2 is binary, base10 is ordinary decimal, and base16 is hexadecimal.
-
3
Understand how the system works. The hexadecimal color system is easy to understand, once you know how it works. The first two digits are the red value, the next two are the green value, and the last two are the blue value.[7]
Here are some examples:- #FFFFFF is white, while #000000 is black.
- Any color with equal r, g, and b values (besides black and white) is a shade of grey, such as #121212, #5A5A5A, or #C0C0C0
- #003000 is a very dark green. #003F00 is barely any lighter (you’ve only added F, or 1610 green), but #00FF00 is the brightest possible green (adding an additional C0, or 19210).
- More complex colors are created by using all three types of light. Try to guess #7FFFD4, #8A2BE2, or #A0522D.
Advertisement
-
1
Teach yourself to read hexadecimal intuitively. Use the examples below as «milestones» to help you estimate the size of a hexadecimal number. This will give you a more intuitive understanding of hexadecimal, and let you read hexadecimal numbers without laboriously converting to decimal every time. As you’ll see, one advantage to hexadecimal is that the number of digits doesn’t increase nearly as fast as it does in decimal:
- Humans have A fingers, or 1416 if you count the toes too. (Remember, the subscript 16 means a number is written in base sixteen.)
- In a residential area, drive below 1916 miles per hour (or 2816 kilometers per hour).
- A typical highway driving speed is 3C mph (or 6416 kph).
- Water boils at D4 ºFahrenheit (6416 º Celsius).
- The median U.S. income is roughly C350 dollars a year.
- The population of the world is over 1A0,000,000.
-
2
Learn hexadecimal addition. You can do hexadecimal addition problems without ever converting to another system. It does take some mental effort and practice to remember the new rules. Here are a few methods and tips:[8]
- Count up one by one, using hexadecimal digits. For instance to solve 7+5 in hex, count 7, 8, 9, A, B, C.
- Learn the addition tables. A much faster method is to memorize the hexadecimal addition tables, which you can practice with an online quiz.[9]
Once you know that A + 7 = 1116, you don’t have to laboriously count it out any more. - Carry the one when needed. If your addition gets you past F, you «carry the one» as you would in a normal addition problem. For example, A+5 = F, A+6 = 1016, A+7 = 1116, and so on. Similarly, 3A+6 = 4016, 3A+7 = 4116, etc.
-
3
Learn hexadecimal multiplication. Just like regular multiplication, the best way to become competent at hexadecimal multiplication is to memorize the multiplication tables. Here’s the hex «6 times table» as an example (all numbers are hexadecimal):[10]
- 6 x 1 = 6
- 6 x 2 = C
- 6 x 3 = 12
- 6 x 4 = 18
- 6 x 5 = 1E
- 6 x 6 = 24
- 6 x 7 = 2A
- 6 x 8 = 30
- 6 x 9 = 36
- 6 x A = 3C
- 6 x B = 42
- 6 x C = 48
- 6 x D = 4E
- 6 x E = 54
- 6 x F = 5A
Advertisement
Add New Question
-
Question
How did this work in the movie The Martian as satellite communication?
ASCII was used; it is the American Standard Code for Information Interchange. For example, 6E was the lowercase letter «n» and 6F was the lowercase letter «o.» Combining these gives us 6E6F for «no.»
-
Question
Convert the decimal number 64 to hexadecimal.
It’s 40, which indicates 4 sixteens and zero ones.
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
-
Any binary number can be easily represented in hexadecimal. Divide the binary number into four-digit sections (adding initial 0s if necessary), then replace each section with the equivalent hexadecimal digit. For example, 00002 = 016, 00012 = 116… all the way up to 11112 = F16.[11]
-
Computers actually use the «complement» method to add and subtract numbers (in hexadecimal or any other base), not the «carrying» method we’re used to. The complement method is not a very useful method for humans, but if you program calculating software, you should learn it to make your program more efficient.
Thanks for submitting a tip for review!
Advertisement
Video
References
About This Article
Article SummaryX
To understand hexadecimal, first learn that in this number system there are 16 different symbols used to denote values from 0 to 15. The 16 symbols used in the hexadecimal number system form the base. Since hexadecimal is based on 16, the place values are based on powers of 16. To convert from hexadecimal to decimal, write out the hexadecimal number, convert non-decimal symbols into decimal numbers, and solve the problem. To learn how to understand the hexadecimal color system, keep reading!
Did this summary help you?
Thanks to all authors for creating a page that has been read 278,152 times.
Did this article help you?
На чтение 4 мин Просмотров 12.7к. Опубликовано 18.05.2022 Обновлено 19.05.2022
Шестнадцатеричная система (англ. — Hexadecimal system ) — это базовая система счисления с снованием 16. Она, наряду с десятичной и двоичной, является одной из наиболее часто встречающихся систем счисления в мире электроники и программирования. Важно понимать, как она работает, потому что во многих случаях имеет смысл представлять число в ней, а не в двоичной или десятичной.
Шестнадцатеричная система счисления — позиционная система счисления по основанию 16.
Википедия
Существует 16 возможных цифр, которые используют для представления чисел. 10 числовых значений, которые вы привыкли видеть в десятичных числах: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9; эти значения по-прежнему представляют то же значение, что и в десятичной системе. Остальные шесть цифр представлены как A, B, C, D, E и F, которые соответствуют числам 10, 11, 12, 13, 14 и 15.
Возможно, Вы столкнетесь с представлением чисел от 10 до 15 в верхнем и нижнем регистрах. Оба варианта считаются верными. Например, A3F — это то же число, что и a3f.
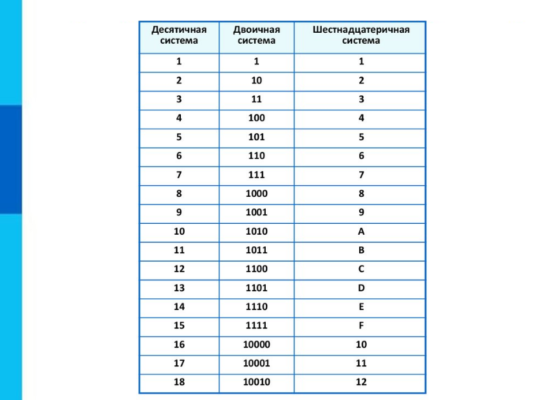
Эта таблица показывает какой шестнадцатеричной цифре эквивалентно значение в десятичном и двоичном формате.
| Десятичный (основание 10) | Двоичный (основание 2) | Шестнадцатеричный (основание 16) |
| 0 | 0000 | 0 |
| 1 | 0001 | 1 |
| 2 | 0010 | 2 |
| 3 | 0011 | 3 |
| 4 | 0100 | 4 |
| 5 | 0101 | 5 |
| 6 | 0110 | 6 |
| 7 | 0111 | 7 |
| 8 | 1000 | 8 |
| 9 | 1001 | 9 |
| 10 | 1010 | А |
| 11 | 1011 | B |
| 12 | 1100 | С |
| 13 | 1101 | D |
| 14 | 1110 | Е |
| 15 | 1111 | F |
Содержание
- Перевод из шестнадцатеричной системы и в нее
- Преобразование из десятичной в шестнадцатеричную систему и обратно
- Преобразование из двоичной в шестнадцатеричную систему и обратно
- Использование шестнадцатеричной системы
- Цвета
Перевод из шестнадцатеричной системы и в нее
Преобразование из десятичной в шестнадцатеричную систему и обратно
Чтобы перевести десятичное число в шестнадцатеричное, нужно следовать простому алгоритму преобразования:
- Делим десятичное число на 16.
- Записываем остаток и переводим его в шестнадцатеричный формат.
- Делим результат прошлого действия снова на 16.
- Повторяем, пока в результате мы не получим 0.
- Переписываем записанные остатки в обратном порядке.
- Пример:
Переведем десятеричное число 1515 в шестнадцатеричную систему
| Деление | Частное | Остаток | Порядок записи (от последнего к первому) |
| 1515/16 | 94 | 11 = B | 3 |
| 94/16 | 5 | 14 = E | 2 |
| 5/16 | 0 | 5 = 5 | 1 |
Ответ: 5EB
Читайте также: Проверяю стратегию Мартингейла на Python и показываю, почему она не работает
Чтобы перевести шестнадцатеричное число в десятичное, нужно каждую цифру с конца этого числа умножить на 16 в степени, соответствующей разряду этой цифры.
- Пример:
Переведем шестнадцатеричное число 5EB в десятеричную систему
5EB = (5 × 16²) + (14 × 16¹) + (11 × 16⁰) = 1515
Ответ: 1515
Преобразование из двоичной в шестнадцатеричную систему и обратно
Чтобы перевести двоичное число в шестнадцатеричное, нужно разделить его на группы по 4 цифры и заменить каждую группу на эквивалент из таблицы
- Пример:
Переведем двоичное число 1010000011111 в шестнадцатеричную систему
Для этого разбиваем число на группу по 4 цифры: 0001 0100 0001 1111
0001 = 1; 0100 = 4; 0001 = 1; 1111 = F
Ответ: 141F
Чтобы сделать обратное преобразование, нужно просто каждую цифру шестнадцатеричного числа заменить на эквивалент по таблице
- Пример:
Переведем шестнадцатеричное число 141F в двоичную систему
1= 0001; 4 = 0100; 1 = 0001; F = 1111
Ответ: 1010000011111
Использование шестнадцатеричной системы
По большей части, шестнадцатеричные коды используются во многих областях вычислительной техники для сокращения двоичного кода до более понятной формы. Шестнадцатеричный код переводится в двоичный для использования на компьютере. Вот некоторые примеры использования шестнадцатеричного кода:
- Ссылки на цвета в HTML и CSS
- Язык ассемблера
- Сообщения об ошибках
Цвета
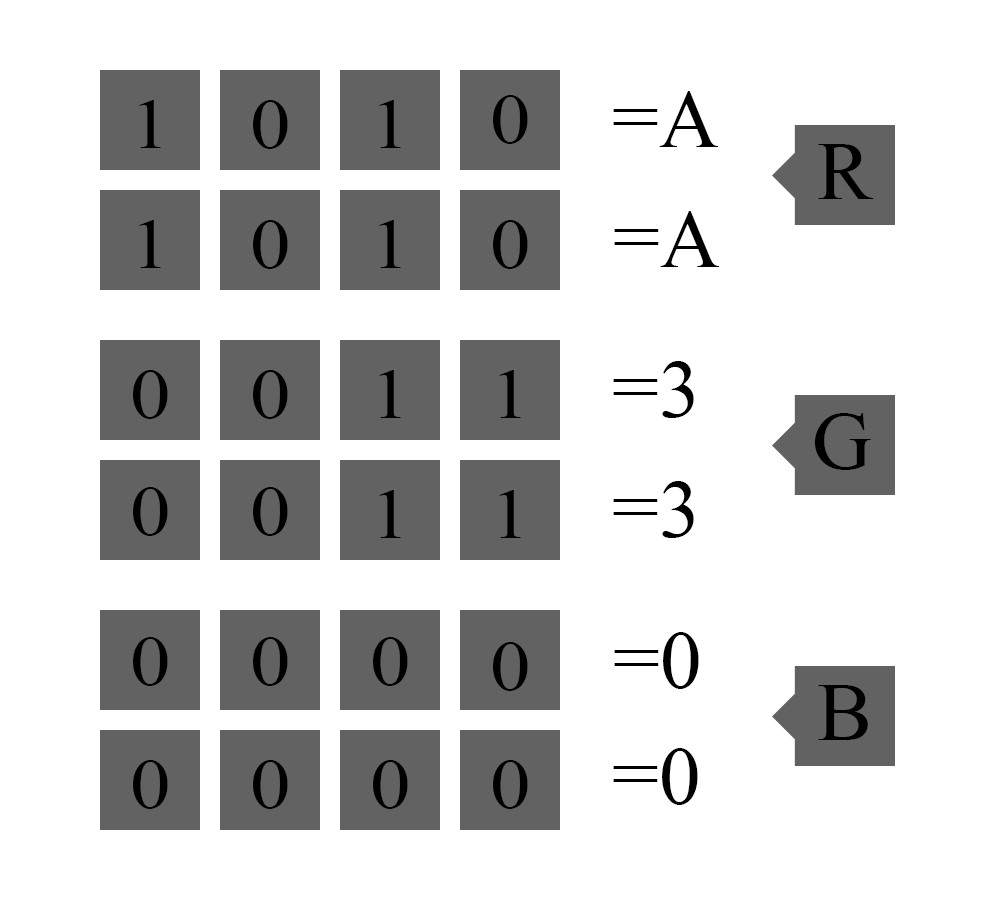
Hex система счисления может использоваться для представления цветов на сайтах и в программах редактирования изображений в формате #RRGGBB (# = показатель того, что число было записано в шестнадцатеричном формате, RR = красный, GG = зеленый, BB = синий). Этот система использует две шестнадцатеричных цифры для каждого цвета, например, #AA3300.
Как одна шестнадцатеричная цифра представляет 4 бита, так две шестнадцатеричные цифры вместе составляют 8 бит (1 байт). Значения для каждого цвета находятся в диапазоне от 00 до FF. В двоичной системе, 00 — это 00000000, а FF — это 11111111. Это дает 256 возможных значений для каждого из трех цветов (256 красных х 256 зеленых х 256 синих), а в сумме это больше 16 миллион цветов.
- #FF0000 будет самым чистым красным цветом — Максимум красного, 0 зеленого и 0 синего.
- Черный это #000000 — ни красного, ни зеленого, ни синего.
- Белый — это #FFFFFF — при смешении всех цветов.
Системы счисления – одна из самых главных основ информатики. Практически ни в одной школе и ни в одном университете не пропускают данную тему, но зачастую именно с переводом шестнадцатеричной системы у многих возникают проблемы, хотя это не такая уж сложная задача, и её перевод практически не отличается от других систем счисления.
Давайте рассмотрим эту систему поподробнее.
Для чего нужна шестнадцатеричная система
Итак, шестнадцатеричная система счисления, как следует из названия, имеет в своём основании число 16. Почему так? Дело в том, что единица информации в информатике – это бит. Восемь бит образуют байт. Также информационной среде существует такое понятие, как машинное слово – это минимальная единица данных, представляющая собой шестнадцать бит, то есть два байта. Считается, что машинное слово – это минимальная величина разрядности регистров процессора, при которой можно работать с ЭВМ.
Так вот, как мы знаем, компьютер работает на двоичном коде. Однако, если Вы когда-нибудь переводили числа из двоичной системы в десятичную, то замечали, что в ней бывает довольно много разрядов, особенно при переводе больших чисел, например, перевод числа 5132 в двоичной системе будет записано так:
Как можно увидеть, при переводе в двоичную систему этого числа у нас получилось аж 13 разрядов (с 0 до 12). Довольно муторно, а главное, занимает много места на письме и отнимает много времени для перевода.
Именно для этого придумали восьмеричную и шестнадцатеричную системы счисления, для этого придумали и байты. Эти системы помогают сократить затраты на перевод чисел и привести их к более приятному визуальному виду.
Если перевести то же число 5132 в восьмеричную систему счисления, то получится «более сокращённая версия» двоичного кода:
Как мы видим, количество символов сократилось, так как разрядность уменьшилась до 5 (с 0 до 4).
Как можно уже понять, шестнадцатеричная система ещё сильнее сокращает разрядность (с 0 до 3) и ещё сильнее сжимает на письме переведённое число:
Человеку такой вид записи в любом случае удобнее, чем бесконечные нули и единицы.
Таким образом, шестнадцатеричная система используется довольно широко в современных информационных системах. Например, при помощи неё указываются коды цветовых схем, данная система используется для записи кодов ошибок, а также для программирования на языках низкого уровня типа Ассемблера, шестнадцатеричную систему зачастую используют для предоставления данных и адресов в малоразрядных ЭВМ.
Как перевести из десятичной системы в шестнадцатеричную
Выше мы уже немного затронули процесс перевода чисел. Теперь мы рассмотрим его подробнее и на примерах.
Но прежде чем начать, надо узнать одну очень важную особенность шестнадцатеричной системы.
Так как система имеет своим основанием число 16, то, следовательно, всего в этой системе имеется 16 цифр, но если первые десять цифр (0-9) вполне привычные для нас, то остальные имеют вид не совсем цифровой, но, тем не менее, являются цифрами, а именно значения A, B, C, D, E, F, которые соответствуют нашим привычным числам с 10 до 15. Все цифры шестнадцатеричной системы и их «аналоги» в десятичной записаны в таблице ниже.
Итак, допустим, у нас есть число 40 563 в десятичной системе счисления. Переведём его в шестнадцатеричную.
- Сначала мы просто делим наше исходное число 40 563 на 16 в столбик. В частном у нас получилось 2 535, если умножить это число на 16, то получится 40 560, а в остатке 3. Эту тройку мы выделяем.
- Теперь мы делим 2 535, и тоже на 16, и тоже абсолютно таким же образом. Частное – 158, 16*158 = 2 528, а в остатке 7. Остаток так же, как и в тот раз, выделяем.
- Делим полученные частные до тех пор, пока они не станут меньше 16, тогда деление заканчивается. Делим 158 на 16, и находим остаток от этого деления.
Остаток от деления – 14, а частное, полученное при делении 158 на 16 равно 9. Так как 9 меньше 16, то процесс вычислений закончен, а 9 также выделяется.
- Процесс преобразования десятичного числа в шестнадцатеричное почти окончен. Для того, чтобы получить его, надо всего лишь выписать выделенные числа справа налево (т.е. в данном случае от девятки к тройке), НО, как мы писали выше, у шестнадцатеричной системы свой особый «алфавит» с 10 по 15. И как раз один из наших «остатков» (число 14) вписывается в этот диапазон, поэтому надо посмотреть в таблице, либо просто самостоятельно посчитать, что в шестнадцатеричной системе 14 будет буквой Е.
Итого весь процесс преобразования приведён на следующем изображении:
Таким образом мы научились переводить числа из десятичной системы в шестнадцатеричную. Теперь давайте попробуем сделать обратное преобразование, но уже с другим числом.
Как перевести из шестнадцатеричной системы в десятичную
Перевести шестнадцатеричное число в привычное нам десятичное также совсем не сложно, более того, мы уже делали это в самом начале статьи, когда сравнивали двоичную, восьмеричную и шестнадцатеричную системы счислений, теперь же разберём этот процесс более подробно.
Давайте сразу приступим к примеру и переведём шестнадцатеричное число 1C3B3 в десятичную систему.
По сути, процесс перевода можно разделить на 2 этапа:
- Мы справа налево отделяем от числа все цифры и умножаем каждую из них на 16, и всё это складываем:
Также обязательно необходимо перевести буквенные обозначения шестнадцатеричной системы в числовые, чтобы можно было посчитать их в десятичном виде, то есть, для данного случая, перевести B в 11 и C в 12.
- После того, как мы сделали этот шаг, нам необходимо пронумеровать разряды чисел. Делается это просто – мы приписываем ко всем числам 16, на которые мы умножали наши исходные цифры, степени, начиная с нулевой:
Теперь нам остаётся только перемножить и сложить всё это:
Таким образом, мы превратили шестнадцатеричное число 1C3B3 в десятичное число 115 635.
Как видите, ничего сложного. Также у нас на сайте имеется статья, описывающая процесс перевода чисел из шестнадцатеричной системы в двоичную.
Спасибо за прочтение!
Шестнадцатиричная система счисления

4.1
Средняя оценка: 4.1
Всего получено оценок: 202.
4.1
Средняя оценка: 4.1
Всего получено оценок: 202.
Для записи адресов и содержимого ячеек памяти компьютера используется шестнадцатеричная система счисления. Запись числовых значений в шестнадцатеричной системе счисления, а также выполнение арифметических операций над ними имеет ряд особенностей, о чем можно прочитать в данной статье.
Что такое шестнадцатеричная система счисления
Шестнадцатеричная система счисления использует для записи числовых значений шестнадцать символов: арабские цифры от 0 до 9 и буквы латинского алфавита A, B, C, D, E, F. Соответственно, основанием такой системы счисления будет число 16.
При использовании шестнадцатеричных чисел следует помнить, что в числовом ряду шестнадцатеричных чисел после числа 9 идет А, а после F следует двузначное число 10.
Перевод 16 –10
Для прямого перевода шестнадцатеричного числа в десятичную систему удобно пользоваться развернутой формой записи, когда число представляют в виде суммы, в которой слагаемые получаются путем умножения символа разряда (числа или числового эквивалента буквы) на 16 в степени соответствующего разряда.
Например, 1F4 = 1 * (16^2) + 15 * (16^1) + 4 * (16^0) = 256 + 240 + 4 = 500
Обратный перевод выполняется последовательным делением десятичного числа на 16 и взятия остатков от деления. Причем полученные остатки в диапазоне от 10 до 15 надо заменить соответствующей буквой.
Выполняя обратный перевод, следует помнить, что результирующее значение получают путем записи полученных от деления остатков в обратном порядке, начиная с последнего частного. Каждый остаток от деления должен получаться всегда меньше шестнадцати.
Например: 500 / 16 = 31 (остаток 4)
31 / 16 = 1 (остаток 15 заменяем на букву F)
Таким образом, получено шестнадцатеричное число 1F4.
Перевод 16 – 2
Для перевода шестнадцатеричного числа в десятичную систему каждую его цифру заменяют группой из четырех нулей и единиц, которую принято называть «тетрадой». Для перевода обычно пользуются таблицей соответствия шестнадцатеричных символов и двоичных тетрад.
Например, 1F4 = (0001)(1111)(0100).
Арифметические действия в шестнадцатеричной системе счисления
Сложение и вычитание
Операции сложения и вычитания удобно выполнять с использованием таблицы сложения шестнадцатеричных чисел. И сложение или вычитание выполняются поразрядно, начиная с младшего разряда.
Если при сложении двух чисел одинакового разряда получается двузначное число, то значение его старшего разряда (единицу) добавляют в старший разряд.
Например, 1F + 2D = 4C.
Сначала складываются значения младших разрядов F + D. По таблице получается двузначное число1С, единицу старшего разряда которого переносим и добавляем к сумме следующих по величине разрядов суммируемых шестнадцатеричных чисел.
Сумма цифр старших разрядов 1 + 2 равна 3 и еще прибавляется переносимая единица, то есть получается в сумме 4.
Таким образом, получается число 4C.
При выполнении вычитания часто возникает ситуация, когда необходимо выполнять заем из старшего разряда, если уменьшаемое конкретного разряда меньше вычитаемого. Тогда занимается единица из старшего разряда. Значение разности смотрится по таблице.
Например, 2D – 1F = E.
Сначала находят разность цифр младших разрядов, то есть D – F (в десятичном представлении 13-15). Уменьшаемое меньше вычитаемого, поэтому происходит заем единицы из старшего разряда исходного числа. То есть вычисляют разность 1D – F = E.
После выполненных манипуляций с младшими разрядами переходят к следующим по величине. В текущем примере следует вычислить 2 – 1. Но ранее произошел заем единицы и в старшем разряде уменьшаемого остается не 2, а 1. Поэтому вычисляется разность 1 – 1 = 0.
Умножение и деление
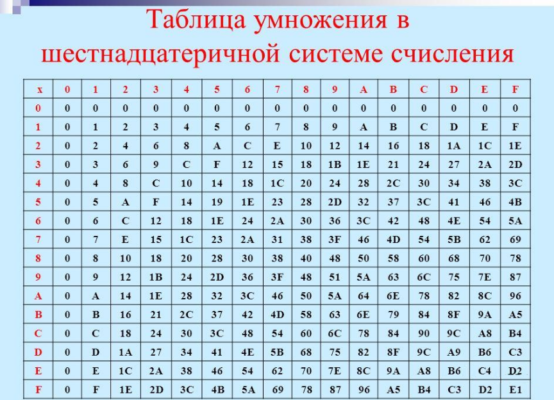
Умножать и делить числа в шестнадцатеричной системе следует также поразрядно. При вычислениях удобно пользоваться таблицей умножения шестнадцатеричной системы счисления.
Например, 1С * 2 = 38. Используя распределительный закон умножения: (10 + С) * 2 = 10 * 2 + С * 2 = 20 + 18 = 38
Операция деления также выполняется столбиком с использованием таблицы умножения: 1С / 2 = Е. В строке таблицы для числа 2, то есть делителя, находится значение 1С (делимое) и пересечение этой строки и столбца, где расположено 1С даст значение частного от деления числа, то есть Е.
Что мы узнали?
В шестнадцатеричной системе счисления для записи числовых значений используются цифры от 0 до 9 и латинские буквы от A до F. Прямой перевод шестнадцатеричного числа в десятичную систему выполняется с использованием развернутой формы записи числа. Обратный перевод выполняется путем деления и записи остатков. Каждую шестнадцатеричную цифру в числе можно заменить тетрадой двоичных чисел. Арифметические операции в шестнадцатеричной системе удобнее всего выполнять поразрядно с использованием таблиц сложения и умножения шестнадцатеричных чисел
Тест по теме
Доска почёта

Чтобы попасть сюда — пройдите тест.
-
Роман Журавлев
10/10
-
Татьяна Лазарева
10/10
-
Коля Приходько
8/10
-
Андрей Букин
10/10
-
Игорь Карабута
1/10
-
Александра Цалко
8/10
Оценка статьи
4.1
Средняя оценка: 4.1
Всего получено оценок: 202.
А какая ваша оценка?
Содержание:
Что такое шестнадцатеричная система счисления
Как перевести целое десятичное число в шестнадцатеричную систему счисления
Как перевести десятичную дробь в шестнадцатеричную систему счисления
Как перевести число из шестнадцатеричной системы счисления в десятичную
Как перевести дробное шестнадцатеричное число в десятичное
Таблица значений десятичных чисел от 0 до 100 в шестнадцатеричной системе счисления
Что такое шестнадцатеричная система счисления
шестнадцатеричная система счисления, является позиционной системой счисления, то есть имеется зависимость от позиции цифры в записи числа.
Для записи числа в шестнадцатеричной системе счисления используется десять цифр и шесть
букв 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E и F.
Для определения в какой системе счисления записано число, внизу, справа от числа ставят цифру, которая называется основанием системы счисления.
Например, F24516 или 123A16
Если вам необходимо перевести число любой системы счисления в другую систему счисления, воспользуйтесь
калькулятором систем счисления с подробным решением онлайн.
Как перевести целое десятичное число в шестнадцатеричную систему счисления
Для того, чтобы перевести целое десятичное число в шестнадцатеричную систему счисления нужно десятичное число делить на 16
до тех пор, пока неполное частное не будет равно нулю.
В результате будет получено число из остатков деления записанное справа налево.
Например, переведем число 32394710 в шестнадцатеричную систему счисления:
323947 : 16 = 20246 остаток: 11, 11 = B
20246 : 16 = 1265 остаток: 6
1265 : 16 = 79 остаток: 1
79 : 16 = 4 остаток: 15, 15 = F
4 : 16 = 0 остаток: 4
32394710 = 4F16B16
Как перевести десятичную дробь в шестнадцатеричную систему счисления
Для того чтобы перевести десятичную дробь в шестнадцатеричную систему счисления необходимо сначала перевести целую часть десятичной дроби в
шестнадцатеричную систему счисления,
а затем дробную часть, последовательно умножать на 16, до тех пор, пока в дробной части произведения не получиться ноль
(результатом произведения будет целое число)
или не будет достигнуто необходимое количество знаков после запятой. Если в результате умножения целая часть не равна нулю,
тогда необходимо заменить значение целой части на ноль.
В результате будет получено число из целых частей произведений, записанное слева направо.
Например, переведем десятичное число 842.99082088510 в шестнадцатеричную систему счисления:
Переведем целую часть
842 : 16 = 52 остаток: 10, 10 = A
52 : 16 = 3 остаток: 4
3 : 16 = 0 остаток: 3
84210 = 34A16
Переведем дробную часть
0.990820885 · 16 = 15.85313416, 15 = F
0.85313416 · 16 = 13.65014656, 13 = D
0.65014656 · 16 = 10.40234496, 10 = A
0.40234496 · 16 = 6.43751936
0.43751936 · 16 = 7.00030976
0.00030976 · 16 = 0.00495616
0.00495616 · 16 = 0.07929856
0.07929856 · 16 = 1.26877696
0.26877696 · 16 = 4.30043136
0.30043136 · 16 = 4.80690176
0.99082088510 = 0.FDA670014416
842.99082088510 = 34A.FDA670014416
Шестнадцатеричные дроби, как и десятичные могут быть как конечными, так и бесконечными. Не всегда конечная десятичная дробь может быть
представлена конечной шестнадцатеричной.
В данном примере получается бесконечная шестнадцатеричная дробь, поэтому умножение на 16 можно производить бесконечное число раз
и все равно дробная часть частного не будет равна нулю.
В данном случае десятичная дробь 842.99082088510 не может быть точно представлена в шестнадцатеричной системе счисления.
Как перевести число из шестнадцатеричной системы счисления в десятичную
Для того, чтобы перевести число из шестнадцатеричной системы счисления в десятичную систему счисления, необходимо записать позиции
каждой цифры в числе с права на лево начиная с нуля.
Каждая позиция цифры будет степенью числа 16, так как система счисления 16-ичная.
Необходимо последовательно умножить каждое число на 16 в
степени соответствующей позиции числа и затем сложить с последующим произведением следующего числа в степени соответствующей его позиции.
Например, переведем число AE1916 в десятичную систему счисления:
| Позиция в числе | 4 | 3 | 2 | 1 | 0 |
| Число | A | F | 2 | D | 6 |
A16 = 1010
D16 = 1310
F16 = 1510
AF2D616 = 10 ⋅ 164 + 15 ⋅ 163 + 2 ⋅ 162 + 13 ⋅ 161 + 6 ⋅ 160 = 71752610
Как перевести дробное шестнадцатеричное число в десятичное
Для того, чтобы перевести дробное шестнадцатеричное число в десятичное, необходимо записать дробное шестнадцатеричное число, убрав точку и
затем сверху расставить индексы.
Индексы в дробной части числа начинаются от -1 и продолжаются на уменьшение вправо, индексы в целой части начинаются с 0 и ставятся с
права на лево по возрастанию.
Каждая позиция цифры (индекс) будет степенью числа 16, так как система счисления 16-ичная. Необходимо последовательно умножить каждое число на
16 в степени соответствующей позиции числа и затем сложить с последующим произведением следующего числа в степени соответствующей его позиции.
Например, переведем дробное шестнадцатеричное число 69.F316 в десятичное:
| Позиция в числе | 1 | 0 | -1 | -2 |
| Число | 6 | 9 | F | 3 |
F16 = 1510
69.F316 = 6 ⋅ 161 + 9 ⋅ 160 + 15 ⋅ 16-1 + 3 ⋅ 16-2 = 105.9492187510
Таблица значений десятичных чисел от 0 до 100 в шестнадцатеричной системе счисления
| Значение числа в десятичной системе счисления | Значение числа в шестнадцатеричной системе счисления |
| 010 | 016 |
| 110 | 116 |
| 210 | 216 |
| 310 | 316 |
| 410 | 416 |
| 510 | 516 |
| 610 | 616 |
| 710 | 716 |
| 810 | 816 |
| 910 | 916 |
| 1010 | A16 |
| 1110 | B16 |
| 1210 | C16 |
| 1310 | D16 |
| 1410 | E16 |
| 1510 | F16 |
| 1610 | 1016 |
| 1710 | 1116 |
| 1810 | 1216 |
| 1910 | 1316 |
| 2010 | 1416 |
| 2110 | 1516 |
| 2210 | 1616 |
| 2310 | 1716 |
| 2410 | 1816 |
| 2510 | 1916 |
| 2610 | 1A16 |
| 2710 | 1B16 |
| 2810 | 1C16 |
| 2910 | 1D16 |
| 3010 | 1E16 |
| 3110 | 1F16 |
| 3210 | 2016 |
| 3310 | 2116 |
| 3410 | 2216 |
| 3510 | 2316 |
| 3610 | 2416 |
| 3710 | 2516 |
| 3810 | 2616 |
| 3910 | 2716 |
| 4010 | 2816 |
| 4110 | 2916 |
| 4210 | 2A16 |
| 4310 | 2B16 |
| 4410 | 2C16 |
| 4510 | 2D16 |
| 4610 | 2E16 |
| 4710 | 2F16 |
| 4810 | 3016 |
| 4910 | 3116 |
| 5010 | 3216 |
| Значение числа в десятичной системе счисления | Значение числа в шестнадцатеричной системе счисления |
| 5110 | 3316 |
| 5210 | 3416 |
| 5310 | 3516 |
| 5410 | 3616 |
| 5510 | 3716 |
| 5610 | 3816 |
| 5710 | 3916 |
| 5810 | 3A16 |
| 5910 | 3B16 |
| 6010 | 3C16 |
| 6110 | 3D16 |
| 6210 | 3E16 |
| 6310 | 3F16 |
| 6410 | 4016 |
| 6510 | 4116 |
| 6610 | 4216 |
| 6710 | 4316 |
| 6810 | 4416 |
| 6910 | 4516 |
| 7010 | 4616 |
| 7110 | 4716 |
| 7210 | 4816 |
| 7310 | 4916 |
| 7410 | 4A16 |
| 7510 | 4B16 |
| 7610 | 4C16 |
| 7710 | 4D16 |
| 7810 | 4E16 |
| 7910 | 4F16 |
| 8010 | 5016 |
| 8110 | 5116 |
| 8210 | 5216 |
| 8310 | 5316 |
| 8410 | 5416 |
| 8510 | 5516 |
| 8610 | 5616 |
| 8710 | 5716 |
| 8810 | 5816 |
| 8910 | 5916 |
| 9010 | 5A16 |
| 9110 | 5B16 |
| 9210 | 5C16 |
| 9310 | 5D16 |
| 9410 | 5E16 |
| 9510 | 5F16 |
| 9610 | 6016 |
| 9710 | 6116 |
| 9810 | 6216 |
| 9910 | 6316 |
| 10010 | 6416 |