Гистограмма распределения — это инструмент, позволяющий визуально оценить величину и характер разброса данных. Создадим гистограмму для непрерывной случайной величины с помощью встроенных средств MS EXCEL из надстройки Пакет анализа и в ручную с помощью функции
ЧАСТОТА()
и диаграммы.
Гистограмма (frequency histogram) – это
столбиковая диаграмма MS EXCEL
, в каждый столбик представляет собой интервал значений (корзину, карман, class interval, bin, cell), а его высота пропорциональна количеству значений в ней (частоте наблюдений).
Гистограмма поможет визуально оценить распределение набора данных, если:
- в наборе данных как минимум 50 значений;
- ширина интервалов одинакова.
Построим гистограмму для набора данных, в котором содержатся значения
непрерывной случайной величины
. Набор данных (50 значений), а также рассмотренные примеры, можно взять на листе
Гистограмма AT
в
файле примера.
Данные содержатся в диапазоне
А8:А57
.
Примечание
: Для удобства написания формул для диапазона
А8:А57
создан
Именованный диапазон
Исходные_данные.
Построение гистограммы с помощью надстройки
Пакет анализа
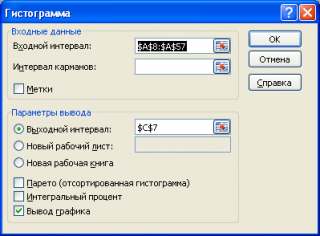
Вызвав диалоговое окно
надстройки Пакет анализа
, выберите пункт
Гистограмма
и нажмите ОК.
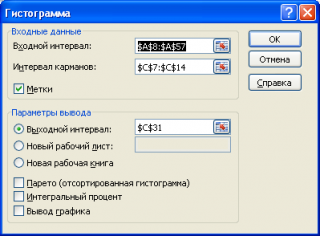
В появившемся окне необходимо как минимум указать:
входной интервал
и левую верхнюю ячейку
выходного интервала
. После нажатия кнопки
ОК
будут:
- автоматически рассчитаны интервалы значений (карманы);
- подсчитано количество значений из указанного массива данных, попадающих в каждый интервал (построена таблица частот);
-
если поставлена галочка напротив пункта
Вывод графика
, то вместе с таблицей частот будет выведена гистограмма.
Перед тем как анализировать полученный результат —
отсортируйте исходный массив данных
.
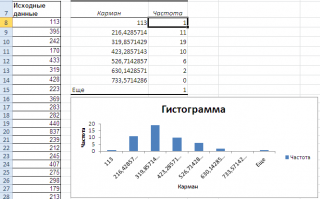
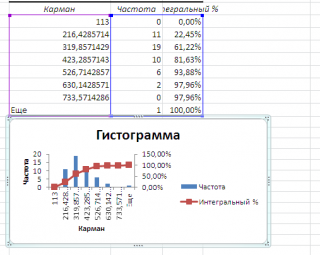
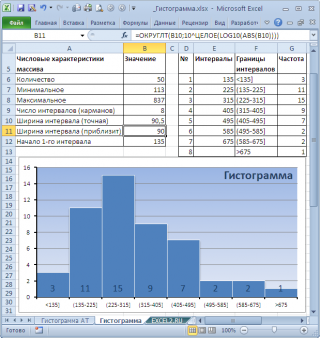
Как видно из рисунка, первый интервал включает только одно минимальное значение 113 (точнее, включены все значения меньшие или равные минимальному). Если бы в массиве было 2 или более значения 113, то в первый интервал попало бы соответствующее количество чисел (2 или более).
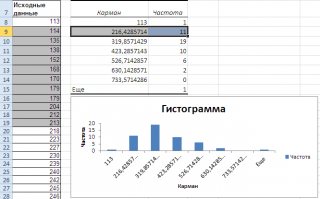
Второй интервал (отмечен на картинке серым) включает значения больше 113 и меньше или равные 216,428571428571. Можно проверить, что таких значений 11. Предпоследний интервал, от 630,142857142857 (не включая) до 733,571428571429 (включая) содержит 0 значений, т.к. в этом диапазоне значений нет. Последний интервал (со странным названием
Еще
) содержит значения больше 733,571428571429 (не включая). Таких значений всего одно — максимальное значение в массиве (837).
Размеры карманов одинаковы и равны 103,428571428571. Это значение можно получить так:
=(МАКС(
Исходные_данные
)-МИН(
Исходные_данные
))/7
где
Исходные_данные –
именованный диапазон
, содержащий наши данные.
Почему 7? Дело в том, что количество интервалов гистограммы (карманов) зависит от количества данных и для его определения часто используется формула √n, где n – это количество данных в выборке. В нашем случае √n=√50=7,07 (всего 7 полноценных карманов, т.к. первый карман включает только значения равные минимальному).
Примечание
:
Похоже, что инструмент
Гистограмма
для подсчета общего количества интервалов (с учетом первого) использует формулу
=ЦЕЛОЕ(КОРЕНЬ(СЧЕТ(
Исходные_данные
)))+1
Попробуйте, например, сравнить количество интервалов для диапазонов длиной 35 и 36 значений – оно будет отличаться на 1, а у 36 и 48 – будет одинаковым, т.к. функция
ЦЕЛОЕ()
округляет до ближайшего меньшего целого
(ЦЕЛОЕ(КОРЕНЬ(35))=5
, а
ЦЕЛОЕ(КОРЕНЬ(36))=6)
.
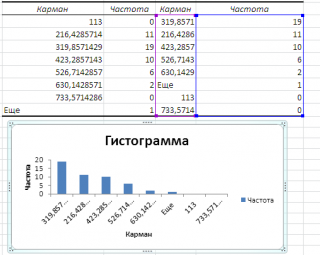
Если установить галочку напротив поля
Парето (отсортированная гистограмма)
, то к таблице с частотами будет добавлена таблица с отсортированными по убыванию частотами.
Если установить галочку напротив поля
Интегральный процент
, то к таблице с частотами будет добавлен столбец с
нарастающим итогом
в % от общего количества значений в массиве.
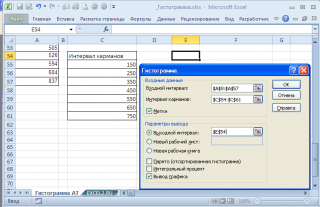
Если выбор количества интервалов или их диапазонов не устраивает, то можно в диалоговом окне указать нужный массив интервалов (если интервал карманов включает текстовый заголовок, то нужно установить галочку напротив поля
Метка
).
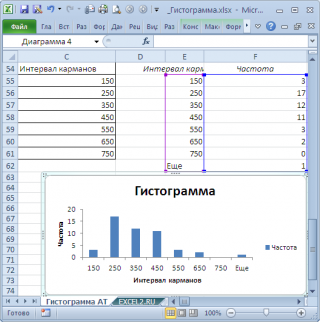
Для нашего набора данных установим размер кармана равным 100 и первый карман возьмем равным 150.
В результате получим практически такую же по форме
гистограмму
, что и раньше, но с более красивыми границами интервалов.
Как видно из рисунков выше, надстройка
Пакет анализа
не осуществляет никакого
дополнительного форматирования диаграммы
. Соответственно, вид такой гистограммы оставляет желать лучшего (столбцы диаграммы обычно располагают вплотную для непрерывных величин, кроме того подписи интервалов не информативны). О том, как придать диаграмме более презентабельный вид, покажем в следующем разделе при построении
гистограммы
с помощью функции
ЧАСТОТА()
без использовании надстройки
Пакет анализа
.
Построение гистограммы распределения без использования надстройки Пакет анализа
Порядок действий при построении гистограммы в этом случае следующий:
- определить количество интервалов у гистограммы;
- определить ширину интервала (с учетом округления);
- определить границу первого интервала;
- сформировать таблицу интервалов и рассчитать количество значений, попадающих в каждый интервал (частоту);
- построить гистограмму.
СОВЕТ
: Часто рекомендуют, чтобы границы интервала были на один порядок точнее самих данных и оканчивались на 5. Например, если данные в массиве определены с точностью до десятых: 1,2; 2,3; 5,0; 6,1; 2,1, …, то границы интервалов должны быть округлены до сотых: 1,25-1,35; 1,35-1,45; … Для небольших наборов данных вид гистограммы сильно зависит количества интервалов и их ширины. Это приводит к тому, что сам метод гистограмм, как инструмент
описательной статистики
, может быть применен только для наборов данных состоящих, как минимум, из 50, а лучше из 100 значений.
В наших расчетах для определения количества интервалов мы будем пользоваться формулой
=ЦЕЛОЕ(КОРЕНЬ(n))+1
.
Примечание
: Кроме использованного выше правила (число карманов = √n), используется ряд других эмпирических правил, например, правило Стёрджеса (Sturges): число карманов =1+log2(n). Это обусловлено тем, что например, для n=5000, количество интервалов по формуле √n будет равно 70, а правило Стёрджеса рекомендует более приемлемое количество — 13.
Расчет ширины интервала и таблица интервалов приведены в
файле примера на листе Гистограмма
. Для вычисления количества значений, попадающих в каждый интервал, использована
формула массива
на основе функции
ЧАСТОТА()
. О вводе этой функции см. статью
Функция ЧАСТОТА() — Подсчет ЧИСЛОвых значений в MS EXCEL
.
В MS EXCEL имеется диаграмма типа
Гистограмма с группировкой
, которая обычно используется для построения
Гистограмм распределения
.
В итоге можно добиться вот такого результата.
Примечание
: О построении и настройке макета диаграмм см. статью
Основы построения диаграмм в MS EXCEL
.
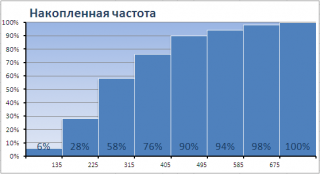
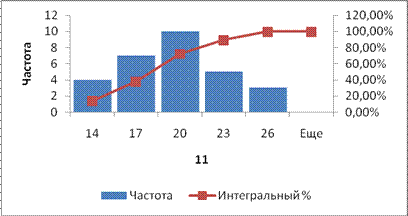
Одной из разновидностей гистограмм является
график накопленной частоты
(cumulative frequency plot).
На этом графике каждый столбец представляет собой число значений исходного массива, меньших или равных правой границе соответствующего интервала. Это очень удобно, т.к., например, из графика сразу видно, что 90% значений (45 из 50) меньше чем 495.
СОВЕТ
: О построении
двумерной гистограммы
см. статью
Двумерная гистограмма в MS EXCEL
.
Примечание
: Альтернативой
графику накопленной частоты
может служить
Кривая процентилей
, которая рассмотрена в
статье про Процентили
.
Примечание
: Когда количество значений в выборке недостаточно для построения полноценной
гистограммы
может быть полезна
Блочная диаграмма
(иногда она называется
Диаграмма размаха
или
Ящик с усами
).
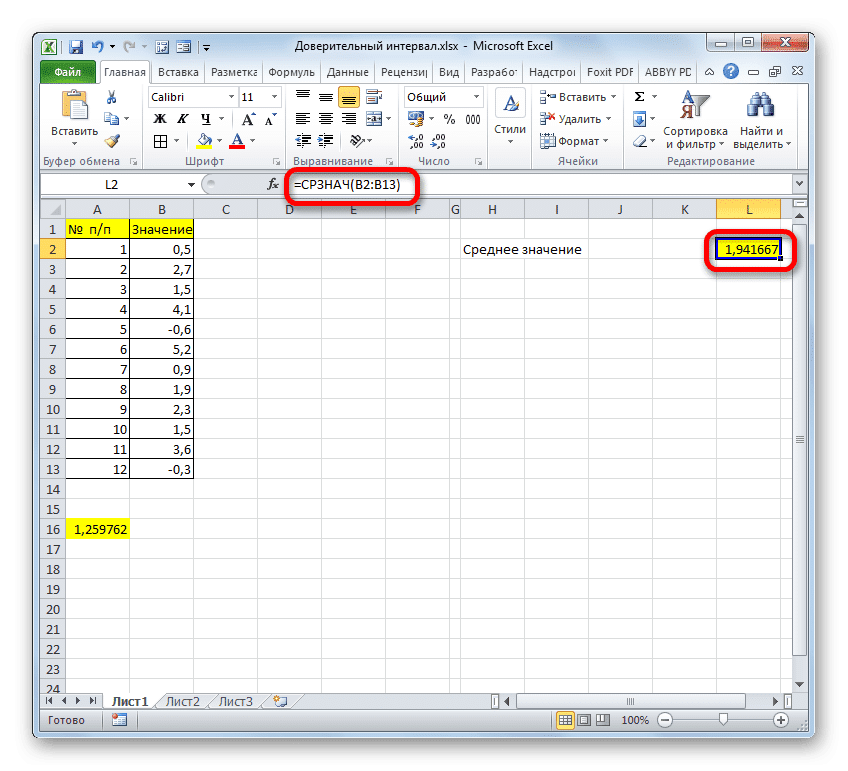
Вычисление доверительного интервала для среднего значения
Для вычисления
доверительного интервала в MS
Excel
можно использовать специальную функцию
ДОВЕРИТ или инструмент Описательная
статистика.
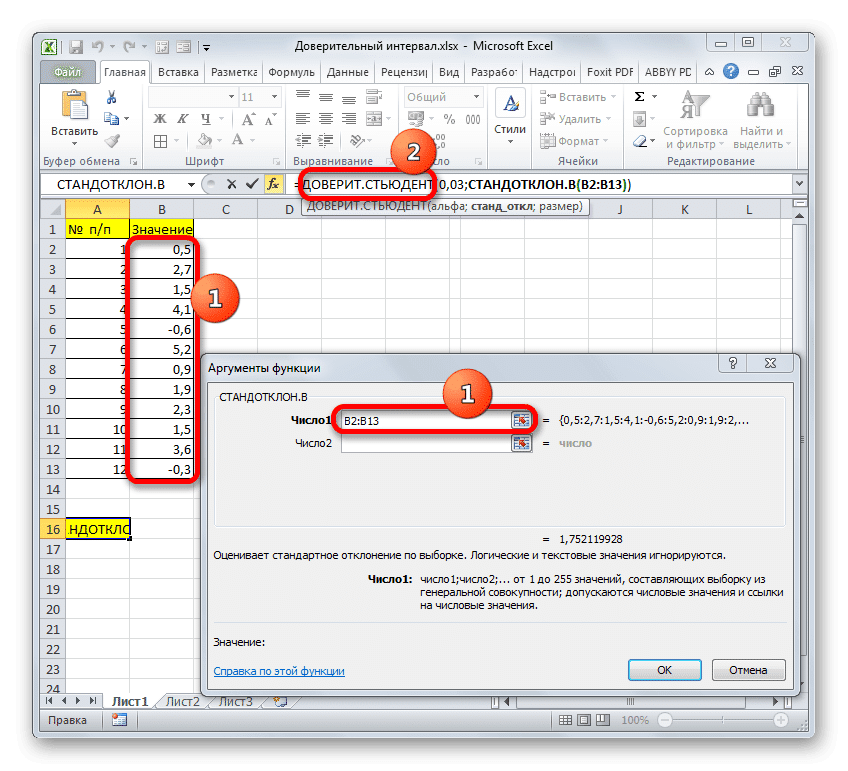
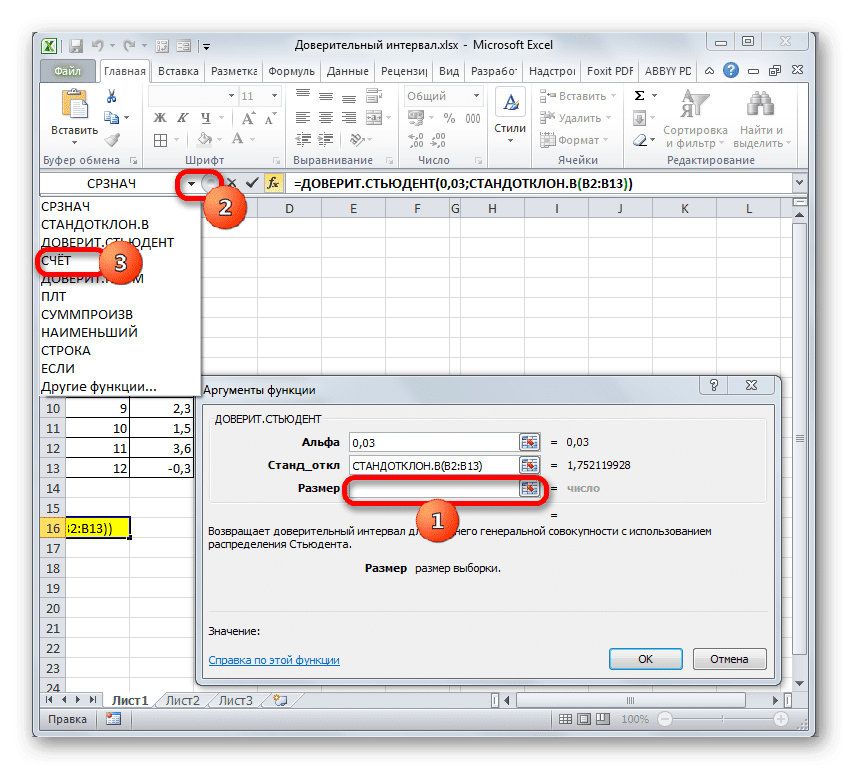
Функция ДОВЕРИТ
(альфа;
станд_откл; размер) вычисляет
ширину доверительного интервала. Ее
параметрами являются:
-
альфа —
уровень значимости, используемый для
вычисления доверительной вероятности; -
станд_откл —
стандартное отклонение генеральной
совокупности для интервала данных
(предполагается известным или
предварительно вычисляется); -
размер — размер
выборки.
Пример 2.12 Требуется
найти границы 90% интервала для среднего
значения, если по результатам 24 торгов
среднее значение стоимости доллара
составило 28 руб., а стандартное отклонение
— 35 коп.
Решение
-
Установим курсор
в любую свободную ячейку рабочего листа
и установим для нее денежный формат. -
Выполним команду
меню Вставка/Функция.
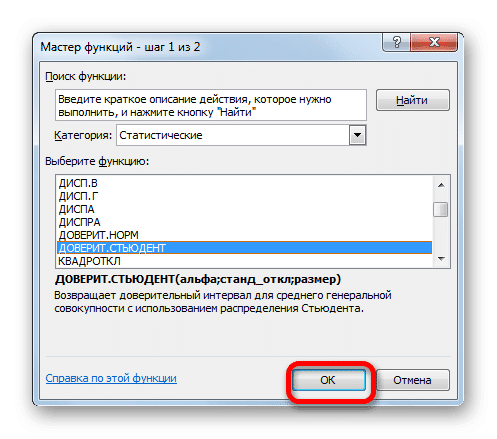
В окне Мастер
функций в
категории Статистические
выберем из
списка функцию ДОВЕРИТ. -
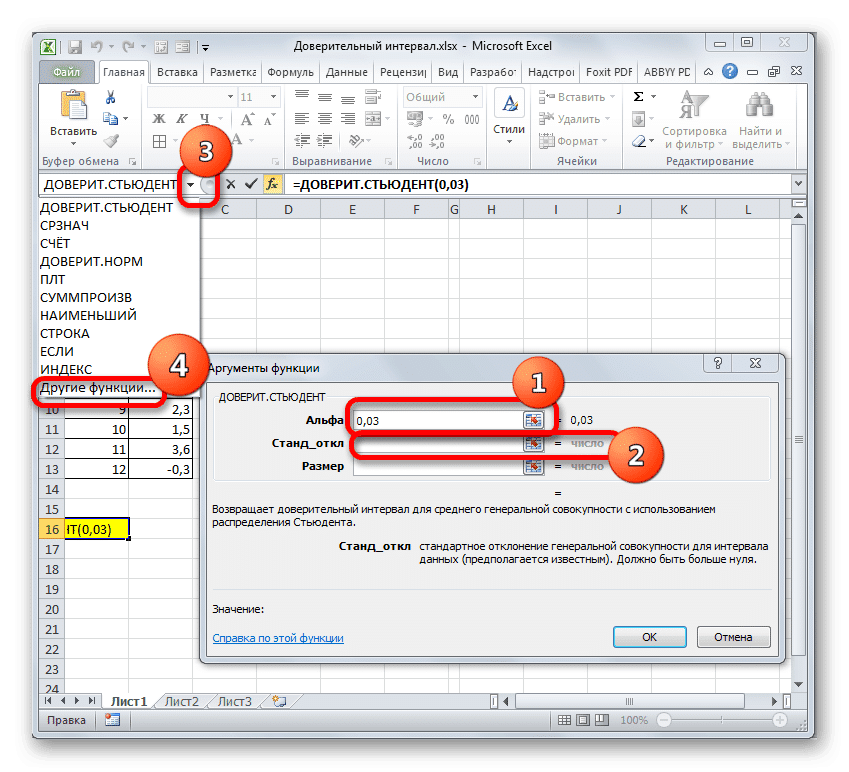
В поля аргументов
окна ДОВЕРИТ
введем
исходные данные: альфа
— 0,1; станд_откл
— 0,35; размер
— 24.
После щелчка на
ОК в ячейке будет вычислена полуширина
90% доверительного интервала для среднего
значения выборки — 0,12 руб.
Таким образом, с
90%-ным уровнем надежности можно утверждать,
что средняя стоимость доллара в диапазоне
27 руб. 88 коп. – 28 руб. 12 коп
(рис. 2.16).

Рис. 2.16
Пример 2.13 Дана
выборка стоимости валюты: 27,70; 27,85; 28,12;
28,20; 28,10; 27,75; 28,25 (рублей). Необходимо
определить границы 95% доверительного
интервала для среднего.
Решение
-
Введем в диапазон
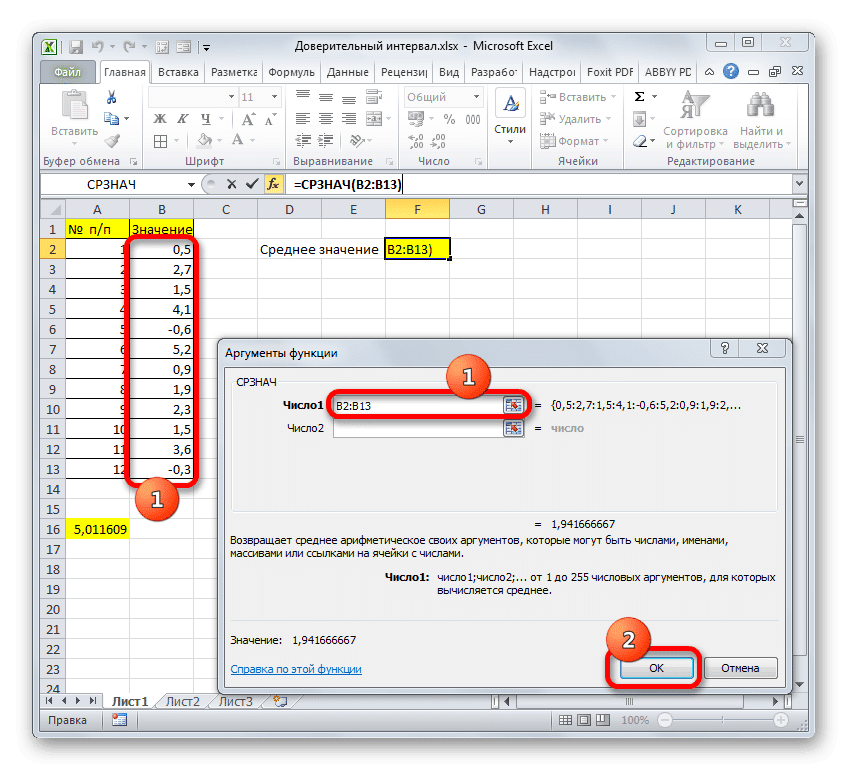
ячеек А2:А8 заданный массив чисел. -
Включим инструмент
Описательная
статистика. -
В поле
Входной интервал диалогового
окна Описательная
статистика укажем
ссылку на диапазон, содержащий выборку
(А1:А8). Включим переключатель Выходной
диапазон и в
соответствующем поле укажем ссылку на
ячейку, где будет размещен верхний
левый угол результирующей таблицы
(В2). Установим флажок Уровень
надежности и
в соответствующем поле введем число
95%. Установим флажок Метки
в первой строке. -
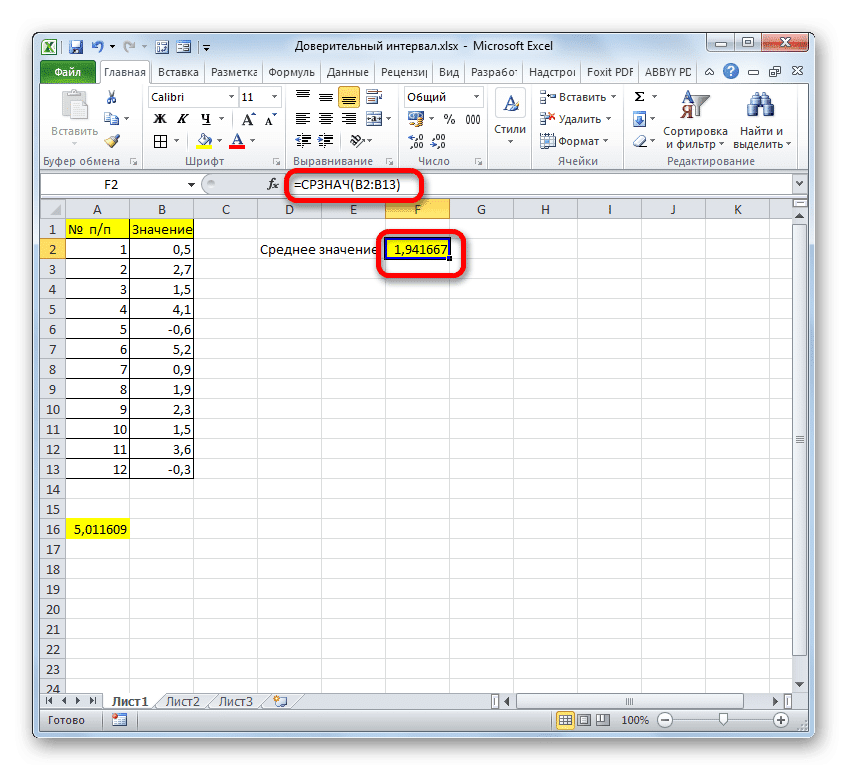
Щелкнем на ОК — на
рабочий лист в указанный диапазон будет
выведен результат (рис. 2.17).
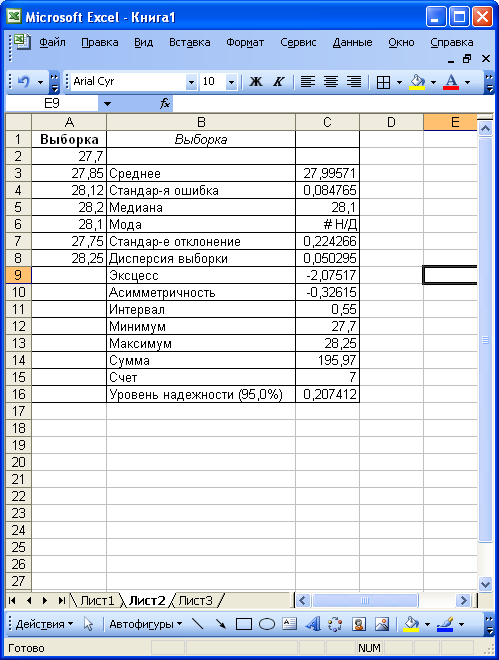
Рис. 2.17
В результате
вычислений для доверительной вероятности
0,95 и графе Уровень надежности получим
величину доверительного интервала
0,207412. Это означает, что с вероятностью
0,95 для заданной Генеральной совокупности
среднее значение будет находиться в
интервале 27,99571 +/- 0,207412 (нижняя граница
доверительного интервала 27,7883, верхняя
граница — 28,20312).
Технология проверки соответствия данных, полученных экспериментально, теоретическому распределению
При решении
практических задач закон распределения
случайных величин и его параметры
неизвестны. Однако для решения задачи
необходимо иметь информацию о том, каков
закон распределения и каковы его
параметры. В этом случае решают задачу
проверки гипотезы. Исходя из предположения
(гипотезы), что распределение случайных
чисел подчиняется тому или иному закону,
выполняют проверку этой гипотезы. Суть
задачи проверки соответствия сводится
к оценке меры соответствия экспериментальных
данных и какого-либо теоретического
распределения. Методом проверки
соответствия теоретическому распределению
является использование критерия
согласия. Одним из них является критерий
согласия хи-квадрат.
В табличном
процессоре проверка согласия по критерию
хи-квадрат реализуется функцией ХИ2ТЕСТ.
Эта функция вычисляет вероятность
совпадения наблюдаемых (фактических)
значений и теоретических (гипотетических)
значений. Если вычисленная вероятность
ниже уровня значимости (
< 0,05), то утверждается, что экспериментальные
значения не соответствуют теоретическому
распределению.
Функция имеет
параметры:
ХИ2ТЕСТ(фактический
интервал; ожидаемый интервал);
где фактический
интервал — диапазон
данных, который содержит результаты
наблюдения, подлежащие сравнению с
ожидаемыми значениями;
ожидаемый интервал
— диапазон
данных, который содержит теоретические
(ожидаемые) значения для соответствующих
наблюдаемых.
Для получения
правильных результатов необходимо,
чтобы объем выборки был не менее 40,
выборочные данные сгруппированы в
интервальный ряд с количеством интервалов
не менее 7, а количество наблюдений в
каждом интервале (частот) не менее 5.
Пример 2.14 Требуется
проверить соответствие нормальному
закону распределения выборочных данных
результатов сдачи экзамена, оцененных
в следующих баллах: 48, 51, 67, 70, 64, 71, 85, 79,
80, 83, 86, 01,99, 56, 66, 65, 84,84,84, 75, 76, 77, 78, 80, 86, 88,
58, 69, 65, 81, 75, 78, Ь 80, 80, 83, 86, 80, 89, 60, 68, 55, 82,
64, 71, 72, 72, 73, 74, 74, 79.
Решение
-
В диапазон ячеек
рабочего листа введем исходные данные
в виде таблицы, содержащей баллы из
приведенной выборки. -
Выберем ширину
интервала, равную 5 баллам, начиная от
50 до 100, и введем в диапазон F2.F12
граничные значения интервалов. -
Подготовим
заголовки создаваемой таблицы (ячейки
G1,
H1,
I1). -
Применяя функцию
ЧАСТОТА, рассчитаем абсолютные частоты
попаданий случайных величин в
установленные интервалы — столбец
Абсолютные частоты. -
В ячейке Н15 вычислим
общее количество наблюдений, используя
формулу =CУMM(G2:GH)
(рис.2.18).

Рис. 2.18
-
В ячейке Н16
вычислим среднее значение выборки, а
в ячейке Н17 — стандартное отклонение. -
Вычислим
теоретические частости распределения.
Поскольку мы проверяем соответствие
заданной совокупности случайных величин
нормальному закону распределения, то
для расчета применим функцию НОРМРАСП.
Установим курсор в ячейку Н2 и вызовем
из Мастера функций функцию НОРМРАСП.
Заполним поля аргументов: х
— F2,
среднее — $Н$16, стандартное_откл. — $Н$17,
интегральный — 0, щелкнем на ОК. -
В ячейку НЗ введем
формулу =НОРМРАСП(F3;$Н$16;
$Н$17;1)-СУММ($Н$2:Н2). -
Скопируем введенную
формулу в ячейки диапазона Н4:Н12.
Для вычисления
теоретических частот установим курсор
в ячейку 12 и введем формулу = $Н$16* Н2.
Скопируем содержимое этой ячейки в
ячейки диапазона I3:I12
(рис. 2.19).
Применяя функцию
ХИ2ТЕСТ, определим соответствие данных
выборки нормальному закону распределения.
Для этого:
-
установим курсор
в свободную ячейку 114, включим Мастер
функций,
выберем категорию Статистические,
а в списке
функций — функцию ХИ2ТЕСТ; -
заполним поля
аргументов функции: фактический
— введем адрес
диапазона абсолютных частот G2:G12,
ожидаемый —
адрес диапазона
теоретических частот I2:I12.
После щелчка на кнопке ОК в ячейке I14
будет вычислено значений вероятности
того, что выборочные данные соответствуют
нормальному закону распределения —
0,917143314.
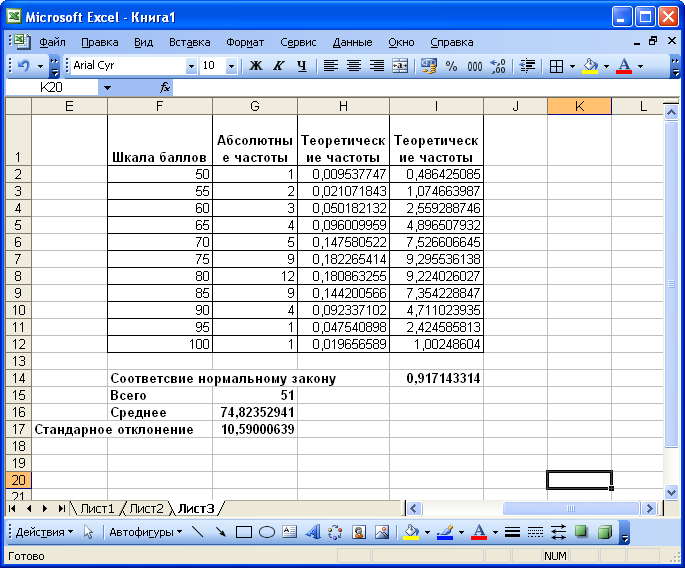
Рис. 2.19
Поскольку полученная
вероятность соответствия экспериментальных
данных р =
0,917143314 намного
больше уровня значимости
=0,05,
то можно утверждать, нулевая гипотеза
не может быть отвергнута и экспериментальные
данные не противоречат нормальному
закону распределения. Но так как
полученное значение вероятности очень
мало отличается от 1, то можно говорить
о высокой степени вероятности того, что
экспериментальные данные соответствуют
нормальному закону.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Программа Эксель используется для выполнения различных статистических задач, одной из которых является вычисление доверительного интервала, который применяется как наиболее подходящая замена точечной оценки при малом объеме выборки.
Хотим сразу заметить, что сама процедура вычисления доверительного интервала довольно непростая, однако, в Excel существует ряд инструментов, призванных облегчить выполнение данной задачи. Давайте рассмотрим их.
Содержание
- Вычисление доверительного интервала
- Метод 1: оператор ДОВЕРИТ.НОРМ
- Метод 2: оператор ДОВЕРИТ.СТЬЮДЕНТ
- Заключение
Вычисление доверительного интервала
Доверительный интервал нужен для того, чтобы дать интервальную оценку каким-либо статическим данным. Основная цель этой операции – убрать неопределенности точечной оценки.
В Microsoft Excel существует два метода выполнения данной задачи:
- Оператор ДОВЕРИТ.НОРМ – применяется в случаях, когда дисперсия известна;
- Оператор ДОВЕРИТ.СТЬЮДЕНТ– когда дисперсия неизвестна.
Ниже мы пошагово разберем оба метода на практике.
Метод 1: оператора ДОВЕРИТ.НОРМ
Данная функция впервые была внедрена в арсенал программы в редакции Эксель 2010 года (до этой версии ее заменял оператор “ДОВЕРИТ”). Оператор входит в категорию “статистические”.
Формула функции ДОВЕРИТ.НОРМ выглядит так:
=ДОВЕРИТ.НОРМ(Альфа;Станд_откл;Размер)
Как мы видим, у функции есть три аргумента:
- “Альфа” – это показатель уровня значимости, который берется за основу при расчете. Доверительный уровень считается так:
1-"Альфа". Это выражение применимо в случае, если значение “Альфа” представлено в виде коэффициента. Например, 1-0,7=0,3, где 0,7=70%/100%.(100-"Альфа")/100. Применятся это выражение, если мы считаем доверительным уровень со значением “Альфа” в процентах. Например, (100-70)/100=0,3.
- “Стандартное отклонение” — соответственно, стандартное отклонение анализируемой выборки данных.
- “Размер” – объем выборки данных.
Примечание: У данной функции наличие всех трех аргументов является обязательным условием.
Оператор “ДОВЕРИТ”, который применялся в более ранних редакциях программы, содержит такие же аргументы и выполняет те же самые функции.
Формула функции ДОВЕРИТ выглядит следующим образом:
=ДОВЕРИТ(Альфа;Станд_откл;Размер)
Отличий в самой формуле нет никаких, лишь название оператора иное. В редакциях приложения Эксель 2010 года и последующих этот оператор находится в категории “Совместимость”. В более же старых версиях программы он находится в разделе статических функций.
Граница доверительного интервала определяется следующей формулой:
X+(-)ДОВЕРИТ.НОРМ
где Х – это среднее значение по заданному диапазону.
Теперь давайте разберемся, как применять эти формулы на практике. Итак, у нас есть таблица с различными данными 10-ти проведенных замеров. При этом, стандартное отклонение совокупности данных равняется 8.
Перед нами стоит задача – получить значение доверительного интервала с 95%-ым уровнем доверия.
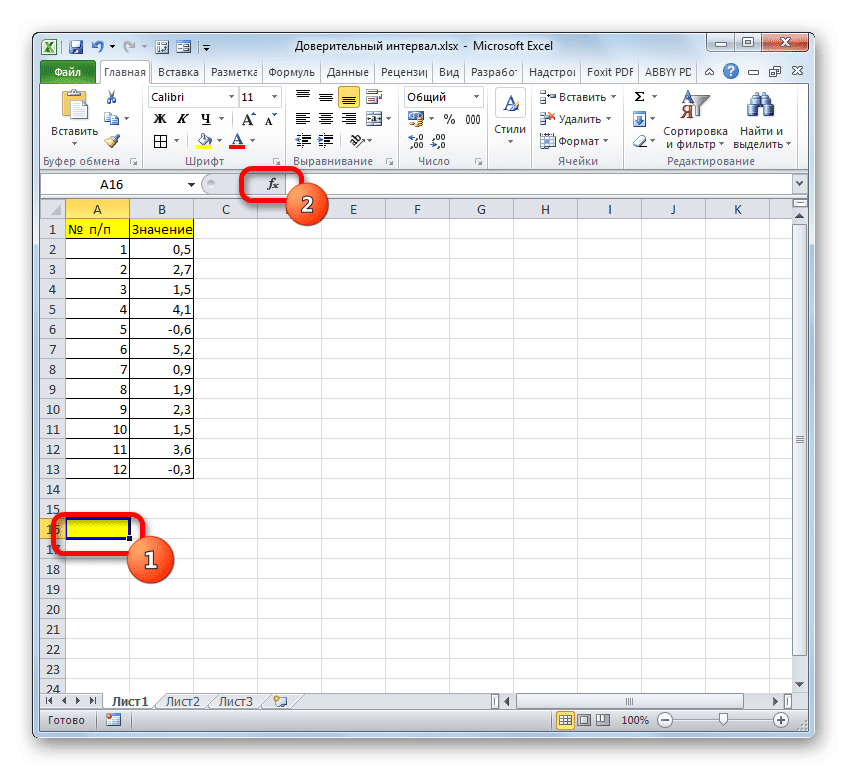
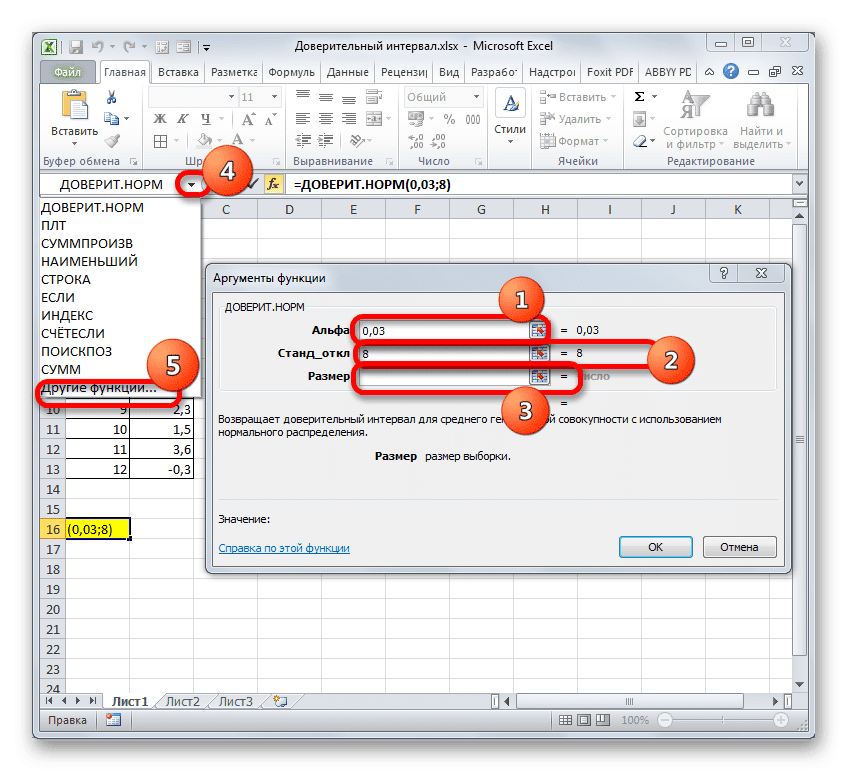
- Первым делом выбираем ячейку для вывода результата. Затем кликаем по кнопке “Вставить функцию” (слева от строки формул).
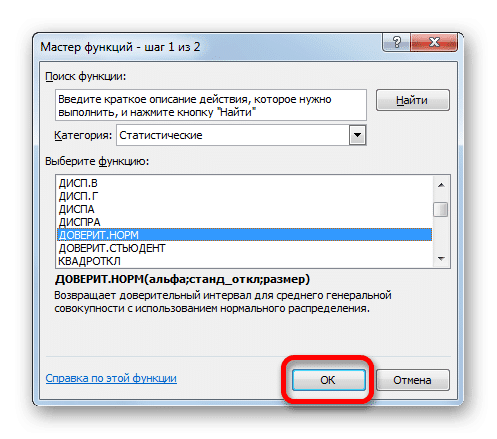
- Откроется окно Мастера функций. Кликнув по текущей категории функций, раскрываем список и щелкаем в нем по строке “Статистические”.
- В предложенном перечне кликаем по оператору “ДОВЕРИТ.НОРМ”, затем жмем OK.
- Перед нами появится окно с настройками аргументов функции, заполнив которые нажимаем кнопку OK.
- в поле “Альфа” указываем уровень значимости. В нашей задаче предполагается 95%-ый уровень доверия. Подставив данное значение в формулу расчета, которую мы рассматривали выше, получаем выражение:
(100-95)/100. Пишем его в поле аргумента (или можно сразу написать результат вычисления, равный 0,05). - в поле “Станд_откл” согласно нашим условия, пишем цифру 8.
- в поле “Размер” указываем количество исследуемых элементов. В нашем случае было проведено 10 замеров, значит пишем цифру 10.
- в поле “Альфа” указываем уровень значимости. В нашей задаче предполагается 95%-ый уровень доверия. Подставив данное значение в формулу расчета, которую мы рассматривали выше, получаем выражение:
- Чтобы при изменении данных не пришлось заново настраивать функцию, можно автоматизировать ее. Для это применим функцию “СЧЁТ”. Ставим указатель в область ввода информации аргумента “Размер”, затем щелкаем по значку треугольника с левой стороны от строки формул и кликаем по пункту “Другие функции…”.
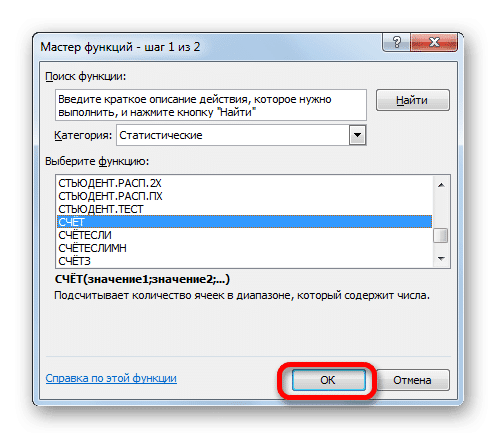
- В результате откроется еще одно окно Мастера функций. Выбрав категорию “Статистические”, кликаем по функции “СЧЕТ”, затем – OK.
- На экране отобразится еще одно окно с настройками аргументов функции, которая применяется для определения числа ячеек в заданном диапазоне, в которых находятся числовые данные.
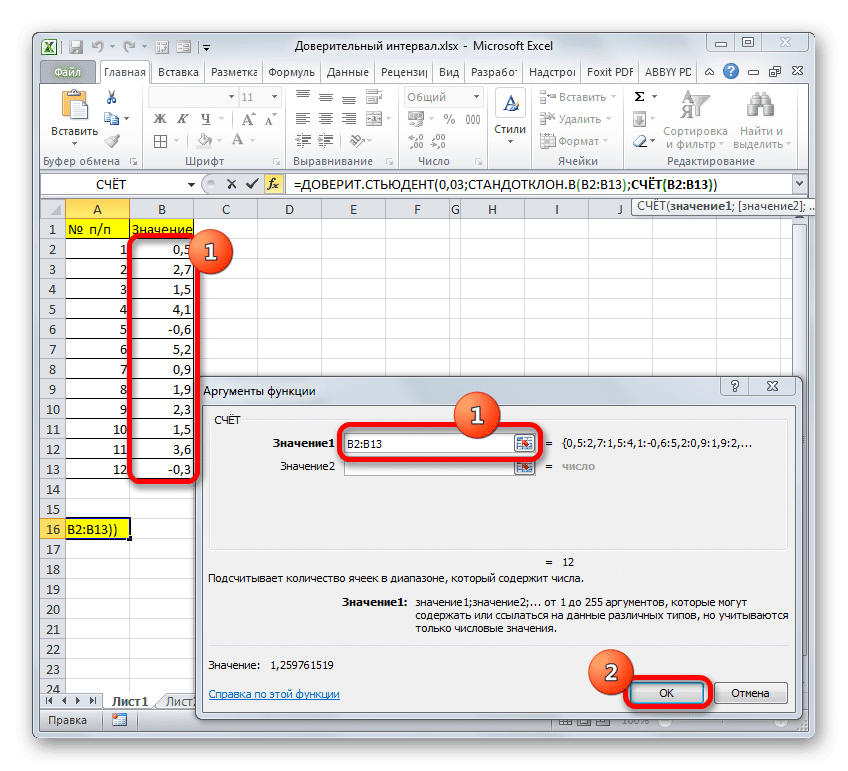
Формула функции СЧЕТ пишется так:=СЧЁТ(Значение1;Значение2;...).
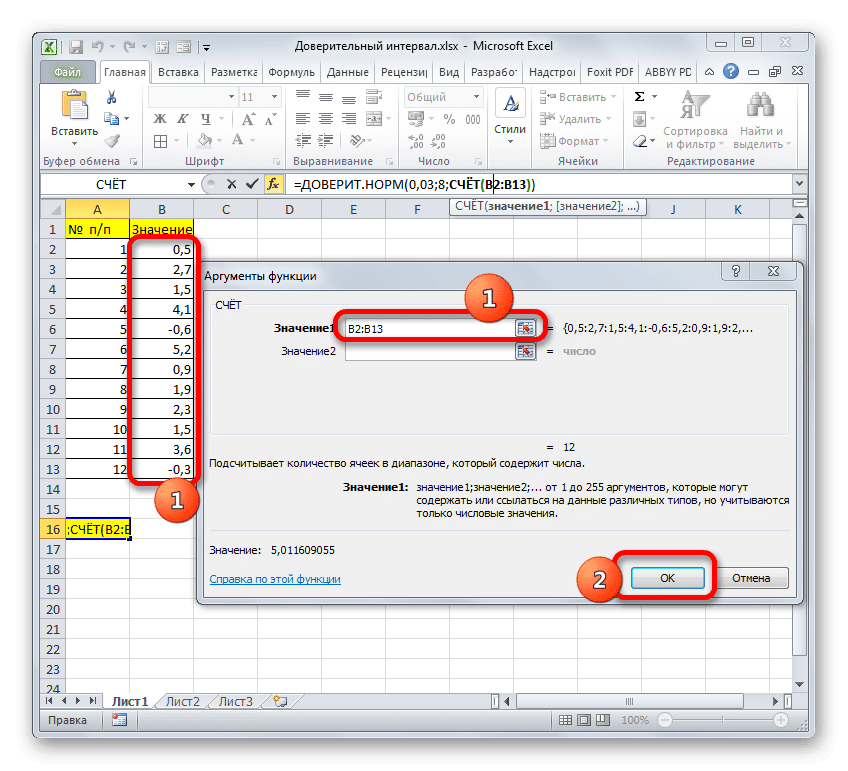
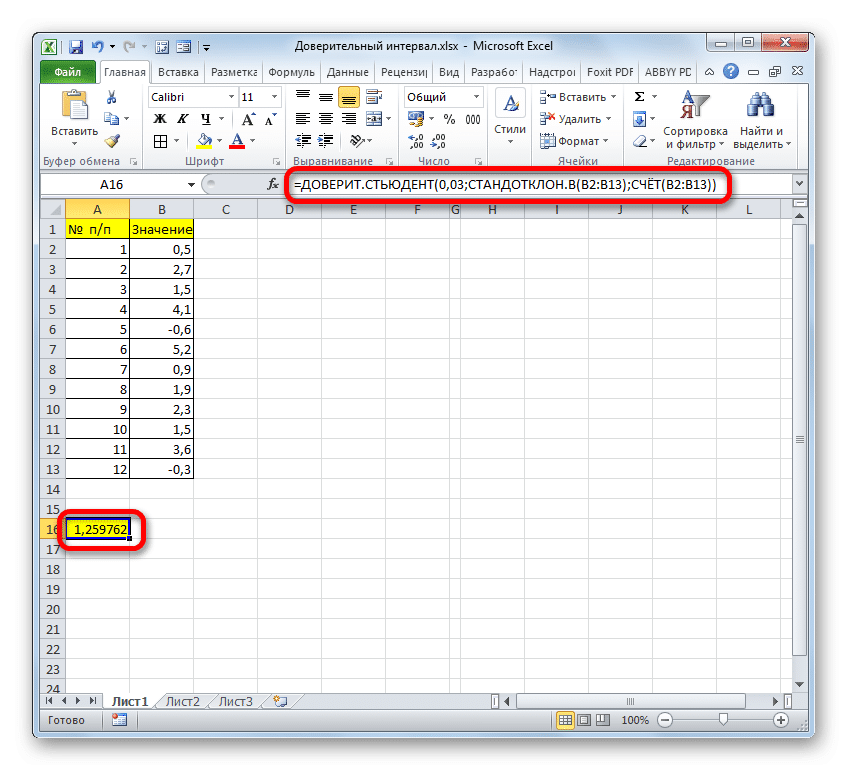
Количество доступных аргументов этой функции может достигать 255 штук. Здесь можно прописать, либо конкретные числа, либо адреса ячеек, либо диапазоны ячеек. Мы воспользуемся последним вариантом. Для этого кликаем по области ввода информации для первого аргумента, затем зажав левую кнопку мыши выделяем все ячейки одного из столбцов нашей таблицы (не считая шапки), после чего жмем кнопку OK. - В результате проделанных действий в выбранной ячейке будет выведено результат расчетов по оператору ДОВЕРИТ.НОРМ. В нашей задаче его значение оказалось равным 4,9583603.
- Но это еще не конечный результат в нашей задаче. Далее требуется рассчитать среднее значение по заданному интервалу. Для этого потребуется применить функцию “СРЗНАЧ”, которая выполняет задачу по вычислению среднего значения в пределах указанного диапазона данных.
Формула оператора пишется так:=СРЗНАЧ(число1;число2;...).
Выделяем ячейку, куда планируем вставить функцию и жмем кнопку “Вставить функцию”. - В категории “Статистические” выбираем нудный оператор “СРЗНАЧ” и кликаем OK.
- В аргументах функции в значении аргумента “Число” указываем диапазон, в который входят все ячейки со значениями всех замеров. Затем кликаем OK.
- В результате проделанных действий среднее значение будет автоматически подсчитано и выведено в ячейку с только что вставленной функцией.
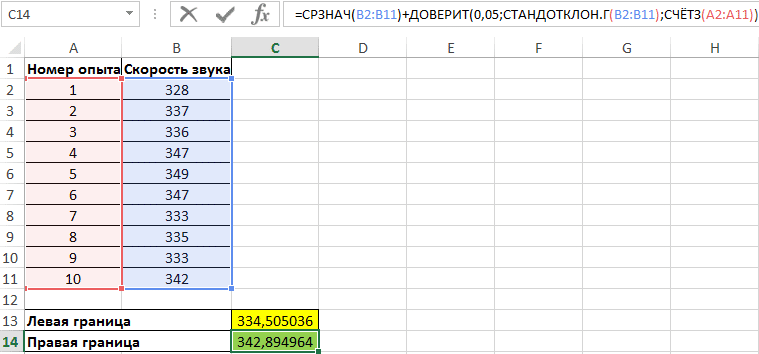
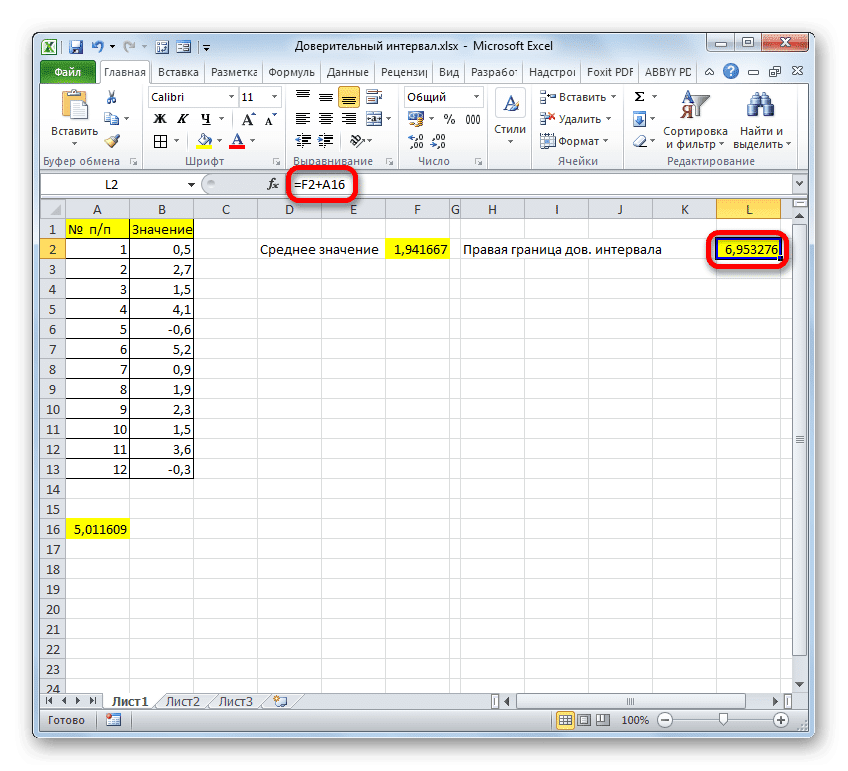
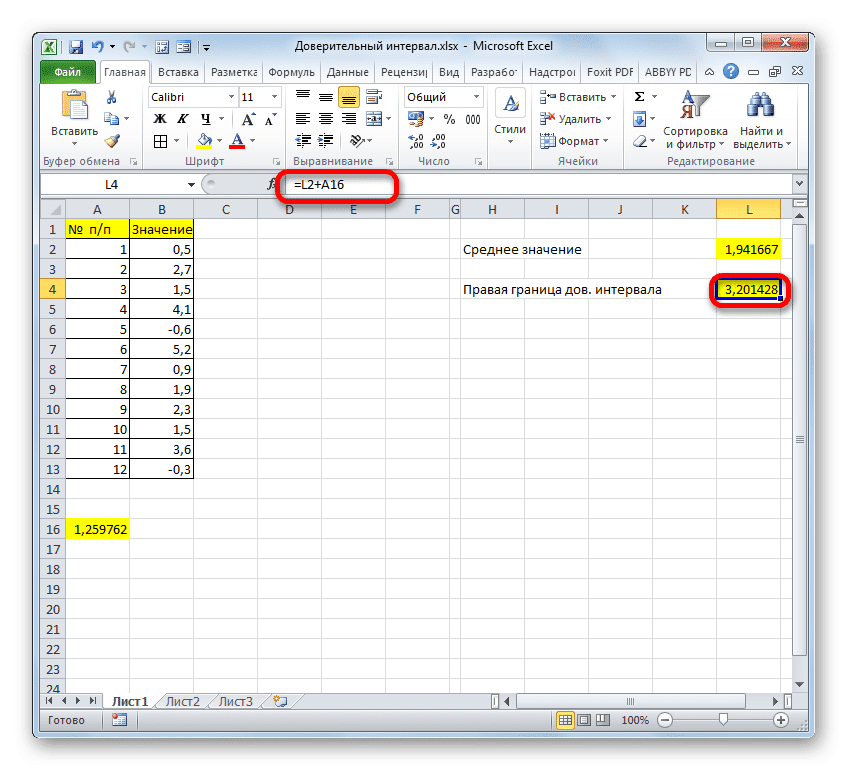
- Теперь нам нужно рассчитать границы ДИ (доверительного интервала). Начнем с расчета значения правой границы. Выбираем ячейку, куда хотим вывести результат, и выполняем в ней сложение результатов, полученных с помощью операторов “СРЗНАЧ” и “ДОВЕРИТ.НОРМ”. В нашем случае формула выглядит так:
A14+A16. После ее набора жмем Enter. - В результате будет произведен расчет и результат немедленно отобразится в ячейке с формулой.
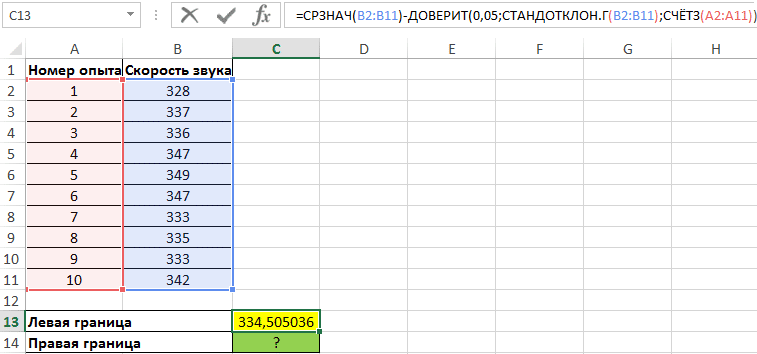
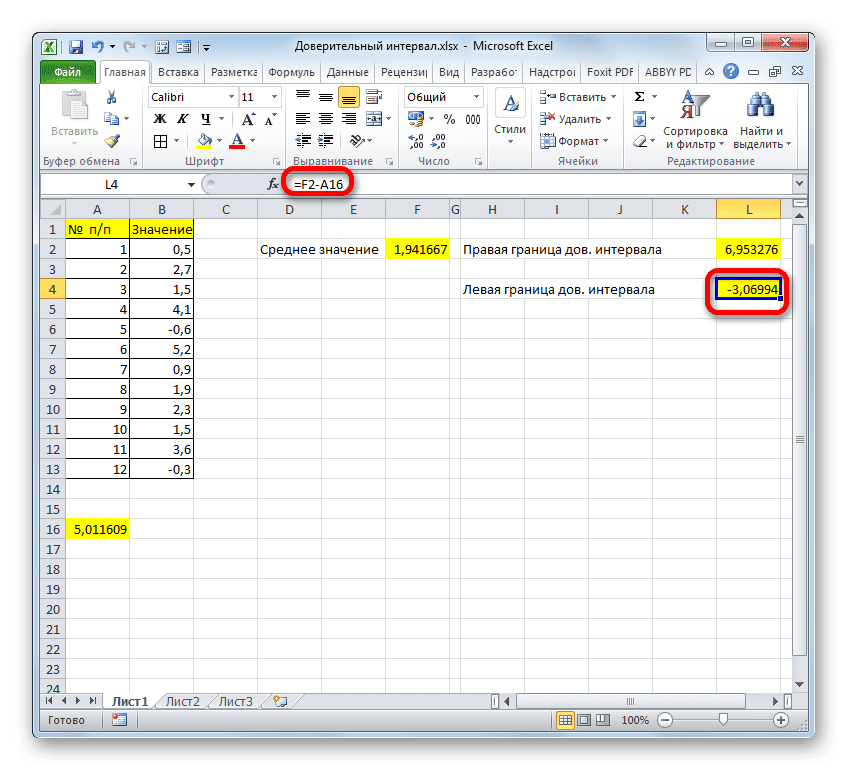
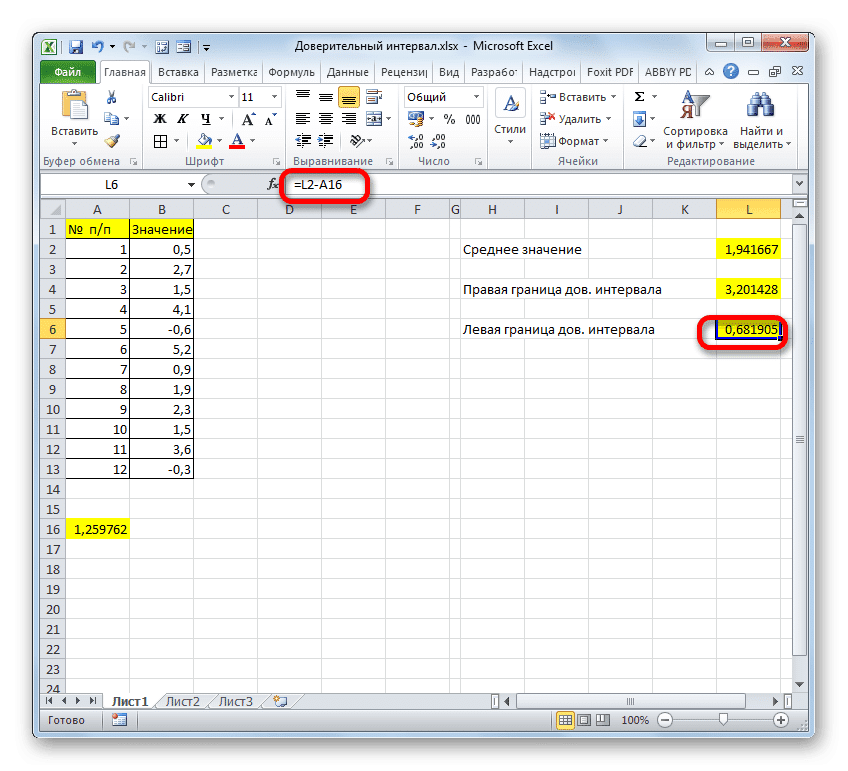
- Затем аналогичным способом выполняем расчет для получения значения левой границы ДИ. Только в этом случае значение результата “ДОВЕРИТ.НОРМ” нужно не прибавлять, а вычитать из результата, полученного при помощи оператора “СРЗНАЧ”. В нашем случае формула выглядит так:
=A16-A14. - После нажатия Enter мы получим результат в заданной ячейке с формулой.
Примечание: В пунктах выше мы постарались максимально подробно расписать все шаги и каждую применяемую функцию. Однако все прописанные формулы можно записать вместе, в составе одной большой:
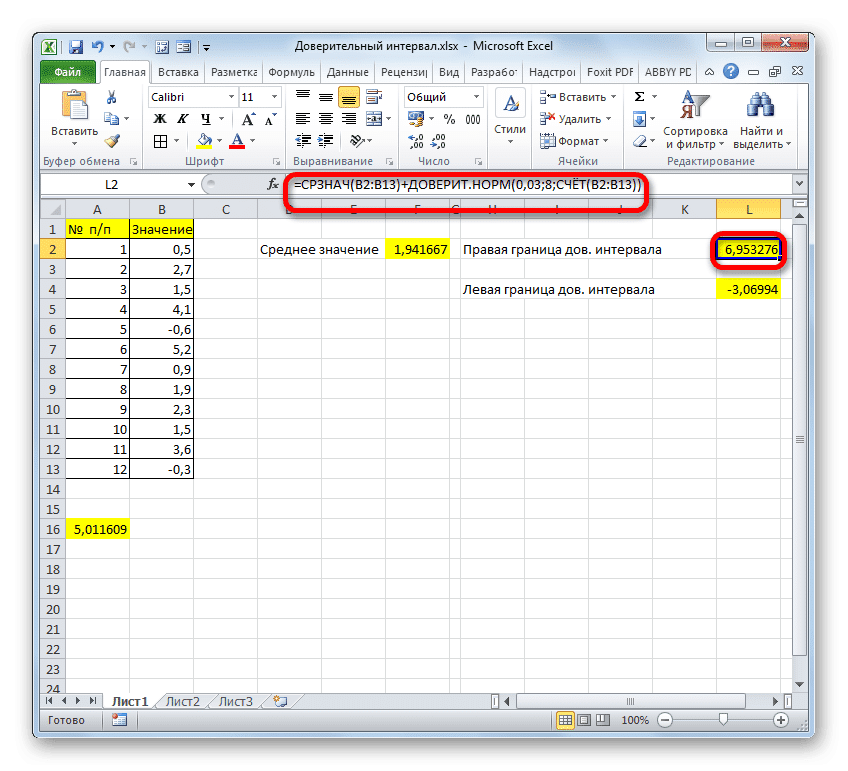
- Для определения правой границы ДИ общая формула будет выглядеть так:
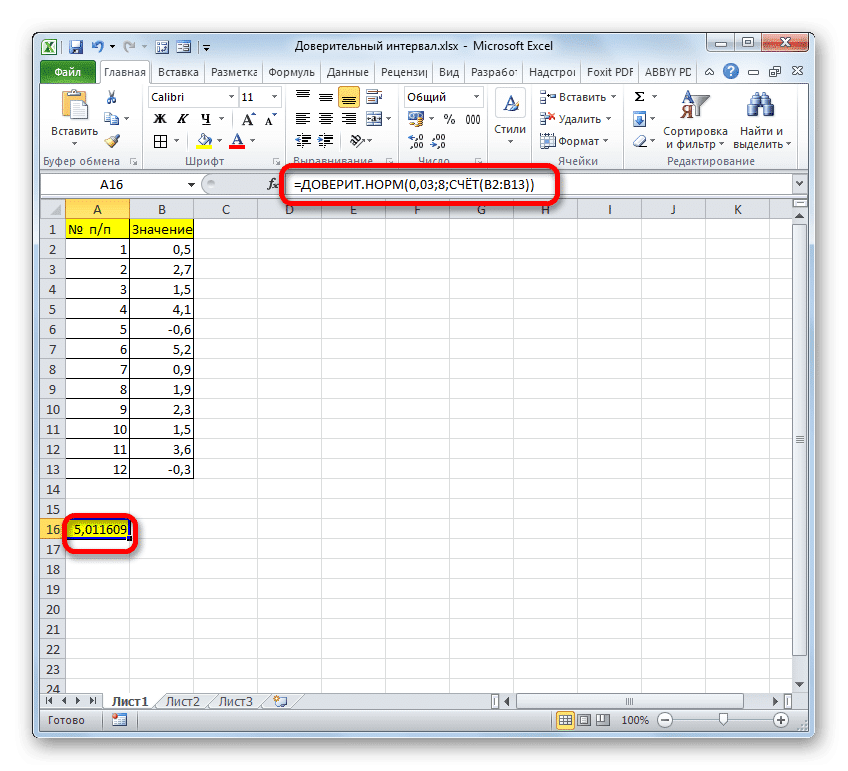
=СРЗНАЧ(B2:B11)+ДОВЕРИТ.НОРМ(0,05;8;СЧЁТ(B2:B11)). - Точно также и для левой границы, только вместо плюса нужно поставить минус:
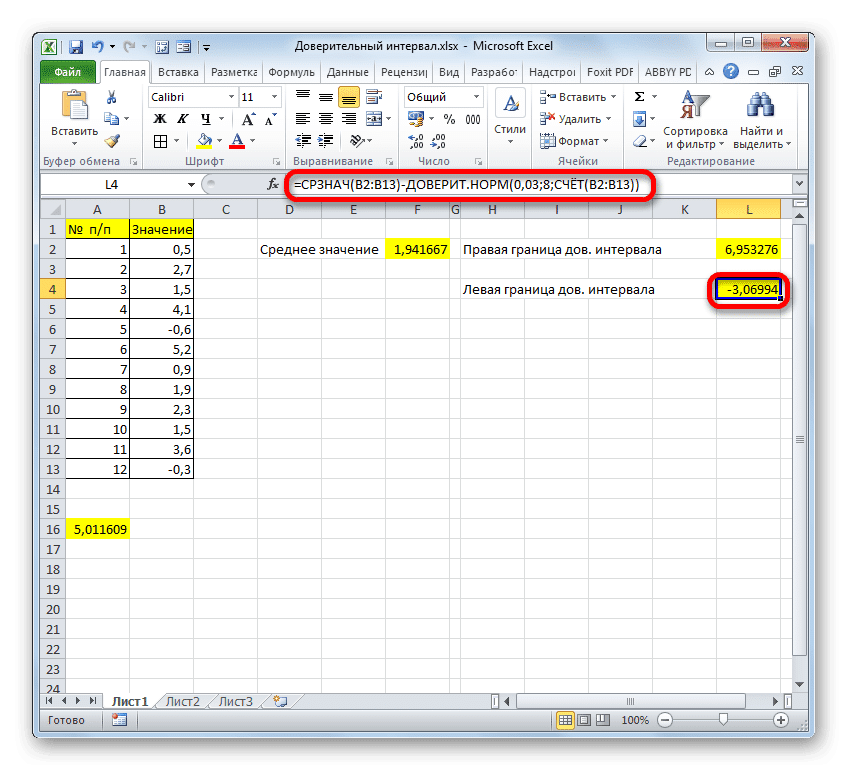
=СРЗНАЧ(B2:B11)-ДОВЕРИТ.НОРМ(0,05;8;СЧЁТ(B2:B11)).
Метод 2: оператор ДОВЕРИТ.СТЬЮДЕНТ
Теперь давайте познакомимся со вторым оператором для определения доверительного интервала – ДОВЕРИТ.СТЬЮДЕНТ. Данная функция была внедрена в программу относительно недавно, начиная с версии Эксель 2010, и направлена на определение ДИ выбранной совокупности данных с применением распределения Стьюдента, при неизвестной дисперсии.
Формула функции ДОВЕРИТ.СТЬЮДЕНТ выглядит следующим образом:
=ДОВЕРИТ.СТЬЮДЕНТ(Альфа;Cтанд_откл;Размер)
Давайте разберем применение данного оператора на примере все той же таблицы. Только теперь стандартное отклонение по условиям задачи нам неизвестно.
- Сначала выбираем ячейку, куда планируем вывести результат. Затем кликаем по значку “Вставить функцию” (слева от строки формул).
- Откроется уже хорошо знакомое окно Мастера функций. Выбираем категорию “Статистические”, затем из предложенного списка функций щелкаем по оператору “ДОВЕРИТ.СТЬЮДЕНТ”, после чего – OK.
- В следующем окне нам нужно настроить аргументы функции:.
- В выбранной ячейке отобразится значение доверительного интервала согласно заданным нами параметрам.
- Далее нам нужно рассчитать значения границ ДИ. А для этого потребуется получить среднее значение по выбранному диапазону. Для этого снова применим функцию “СРЗНАЧ”. Алгоритм действий аналогичен тому, что был описан в первом методе.
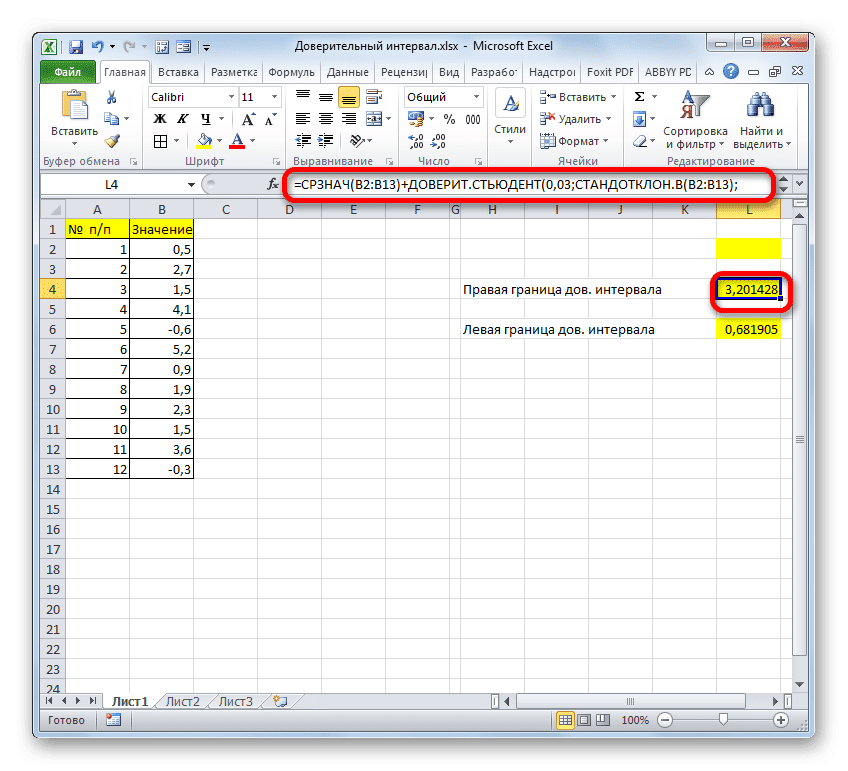
- Получив значение “СРЗНАЧ”, можно приступать к расчетам границ ДИ. Сами формулы ничем не отличаются от тех, что использовались с оператором “ДОВЕРИТ.НОРМ”:
- Правая граница ДИ=СРЗНАЧ+ДОВЕРИТ.СТЬЮДЕНТ
- Левая граница ДИ=СРЗНАЧ-ДОВЕРИТ.СТЬЮДЕНТ
Заключение
Арсенал инструментов Excel невероятно большой, и наряду с распространенными функциями, программа предлагает большое разнообразие специальных функций, которые помогут существенно облегчить работу с данными. Возможно, описанные выше шаги некоторым пользователям, на первый взгляд, могут показаться сложными. Но после детального изучения вопроса и последовательности действий, все станет намного проще.
При изучении величины, принимающей случайные значения (результатов физических измерений в серии экспериментов, экономических показателей, параметров технологических процессов и т.п.), мы имеем дело с выборками. Выборочное наблюдение — это способ наблюдения, при котором обследуется не вся совокупность значений изучаемой величины, а лишь часть ее, отобранная по определенным правилам выборки и обеспечивающая получение данных, характеризующих всю совокупность в целом.
При выборочном наблюдении обследованию подвергается определенная, заранее обусловленная часть совокупности, а результаты обследования распространяются на всю совокупность.
Ту часть единиц, которая отобрана для наблюдения, принято называть выборочной совокупностью или выборкой, а всю совокупность единиц, из которых производится отбор, — генеральной совокупностью.
Число единиц (элементов) статистической совокупности называется ее объемом. Объем генеральной совокупности обозначается N, а объем выборочной совокупности п.
Качество результатов выборочного наблюдения зависит от того, насколько состав выборки представляет генеральную совокупность, иначе говоря, от того, насколько выборка репрезентативна (представительна).
Элементами выборки (x1 х2, . хп) являются числовые значения, называемые вариантами, которые могут быть дискретными, т.е. изолированными (например, целыми числами), или могут принимать значения из некоторого интервала (а, b).
Вариационный ряд получается из выборки упорядочением по возрастанию (или убыванию) и подсчетом частоты каждого значения. Если вариационный ряд содержит значения признака и соответствующие ему частоты,то такой ряд носит название дискретный вариационный ряд. Если нам известно, что исследуемый показатель может принимать любые значения из некоторого интервала, то строим интервальный вариационный.
Удобнее всего ряды распределения анализировать с помощью их графического изображения, позволяющего судить о форме распределения. Наглядное представление о характере изменения частот вариационного ряда дают полигон и гистограмма.
Пример 2.1.
Известны следующие данные о результатах сдачи студентами экзамена (в баллах):
| 18 | 16 | 20 | 17 | 19 | 20 | 17 |
| 17 | 12 | 15 | 20 | 18 | 19 | 18 |
| 18 | 16 | 18 | 14 | 14 | 17 | 19 |
| 16 | 14 | 19 | 12 | 15 | 16 | 20 |
Необходимо построить ряд распределения числа студентов по баллу, представить графически результаты.
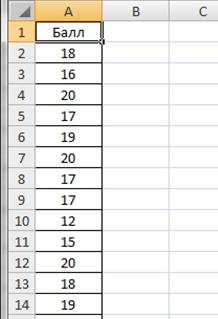
Введем данные в диапазоне A1: A29, в ячейку A1 введем текст «Балл» (рис.2.6).
Рисунок 2.6. Баллы успеваемости студентов
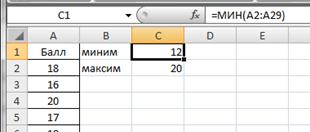
Определим наименьший и наибольший балл по выборке. Для этого введем в ячейках С1 и С2 соответственно введем формулы =МИН(A2:A29) и =МАКС(A2:A29). Получим значения 12 и 20 соответственно (рис.2.7).
Рисунок 2.7. Минимальный и максимальный балл
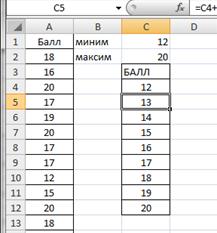
Построим вариационный ряд. Для каждого значения необходимо подсчитать частоту. Так как значения признака (балл) отличаются на единицу, то можно воспользоваться следующим способом. В ячейку С4 введем формулу =С1, в С5 соответственно С4+1. Ячейку С5 протянем маркером заполнения (правый нижний угол ячейки) вниз до С12. Результаты представлены на рисунке 2.8.
Рисунок 2.8. Значения признака
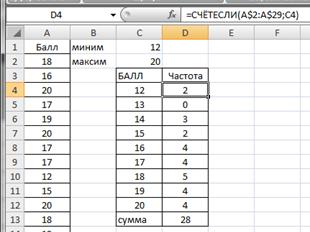
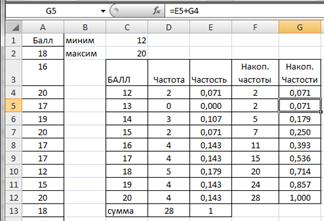
Вычислим частоту для каждого значения признака. В ячейку D4 введем формулу =СЧЕТЕСЛИ(A$2:A$29;C4) и протянем D4 маркером вниз до заполнения D12. В ячейке D13 просуммируем частоты с помощью формулы =СУММ(D4:D12).
Получим вариационный ряд (значения признака и соответствующие им частоты) на рисунке 2.9.
Рис.2.9. Частоты вариационного ряда
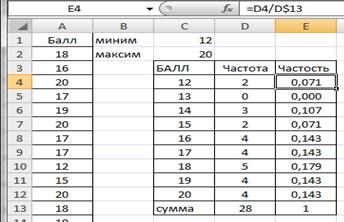
Вычислим частость (относительную частоту) для каждого значения признака. В ячейку Е4 введем формулу = D4/D$13. Протянем Е4 маркером заполнения вниз до Е12 (рис.2.10).
Рисунок 2.10. Частости ряда распределения
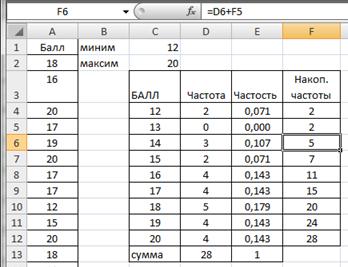
Вычислим накопленные частоты. В ячейку F4 введем формулу =D4, а в ячейку F5 – формулу = D5+F4. Протянем F5 маркером заполнения вниз до F12 (рис.2.11).
Рисунок 2.11. Накопленные частоты ряда
Построим эмпирическую функцию распределения, т.е. найдем наколенные частости. Выделим F4:F12 и маркером заполнения протянем вправо на соседний столбец (рис.2.12). В G4 получим формулу = Е4, в ячейке G5 формулу =Е5+ G4 и т.д.
Рисунок 2.12. Накопленные частости ряда
Построим полигон распределения частот и частостей. Выделим диапазон ячеек С4:D12. Выполним команду меню «Диаграмма» и выберем тип «Точечная», вариант «Точечная с прямыми отрезками и маркерами». Полигон распределения частот представлен на рисунке 2.13.
Рисунок 2.13. Полигон распределения частот
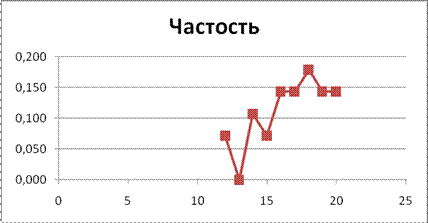
Выделим диапазон ячеек С4:С12 и, удерживая клавишу CTRL, диапазон Е4:Е12. Выполним команду меню «Диаграмма» и выберем тип «Точечная», вариант «Точечная с прямыми отрезками и маркерами». Полигон распределения частостей представлен на рисунке 2.14.
Рисунок 2.14. Полигон распределения частостей
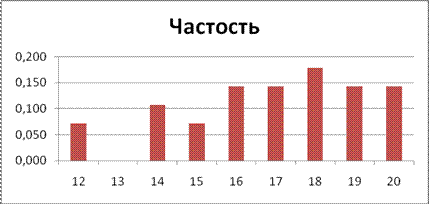
Построим гистограмму распределения частостей, для чего выделим диапазон Е4:Е12, выберем тип диаграммы «Гистограмма». Щелкнем правой кнопкой в области диаграммы, выберем «Выбрать данные», выберете «Ряд» — «Изменить», левой кнопкой щелкнем в строке «Подписи оси Х» и выделим диапазон С4:С12 (рис.2.15).
Рисунок 2.15. Гистограмма распределения частостей
Построим кумуляту частостей, для чего выделим диапазон ячеек С4:С12 и, удерживая клавишу CTRL, диапазон G4:G12. Выполним команду меню «Диаграмма» и выберем тип «Точечная», вариант «Точечная с прямыми отрезками». Кумулята представлена на рис.2.16.
Рисунок 2.16. Кумулята
Пример 2.2.
В таблице 2.7 представлены значения процентных ставок по кредитам по 30 коммерческим банкам.
Банковские процентные ставки
| № Банка | Процентная ставка, % |
| 1 | 20,3 |
| 2 | 17,1 |
| 3 | 14,2 |
| 4 | 11,0 |
| 5 | 17,3 |
| 6 | 19,6 |
| 7 | 20,5 |
| 8 | 23,6 |
| 9 | 14,6 |
| 10 | 17,5 |
| 11 | 20,8 |
| 12 | 13,6 |
| 13 | 24,0 |
| 14 | 17,5 |
| 15 | 15,0 |
| 16 | 21,1 |
| 17 | 17,6 |
| 18 | 15,8 |
| 19 | 18,8 |
| 20 | 22,4 |
| 21 | 16,1 |
| 22 | 17,9 |
| 23 | 21,7 |
| 24 | 18,0 |
| 25 | 16,4 |
| 26 | 26,0 |
| 27 | 18,4 |
| 28 | 16,7 |
| 29 | 12,2 |
| 30 | 13,9 |
Построим интервальный вариационный ряд. Для этого вычислим границы интервалов (карманов) с использованием формулы Стэрджесса.
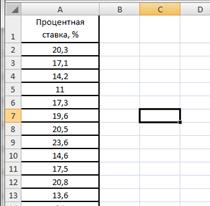
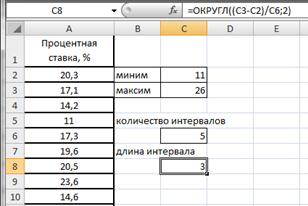
Введем данные в диапазоне A1:A31 (рис.2.17). Определим максимальное и минимальное значения (ячейки С2 и С3 соответственно) так же как и в примере 2.1. Определим число интервалов по формуле Стэрджесса, для чего в ячейку С6 введем формулу =ЦЕЛОЕ(1+3,322*LOG10(30)) (рис.2.18).
Рисунок 2.17. Процентные ставки банков
Рисунок 2.18. Число интервалов
Вычислим длину интервалов, для чего в ячейке С8 введем формулу =ОКРУГЛ((C3-C2)/C6;2) (рис.2.19).
Рисунок 2.19. Длина интервала
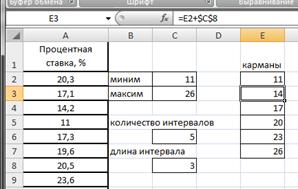
Определим нижние и верхние границы интервалов (карманы), для чего в ячейке Е2 запишем формулу =С2, в ячейке Е3 запишем ==E2+$C$8. Протянем Е3 маркером заполнения вниз до Е7 (рис.2.20).
Рисунок 2.20. Границы интервалов
Подсчитаем частоты – в интервал считаем те значения, которые больше нижней границы интервала или равны ей и меньше верхней границы.
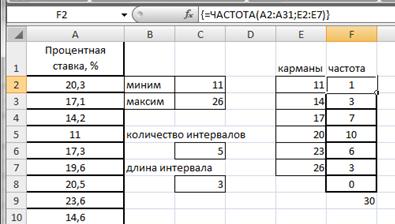
Воспользуемся функцией ЧАСТОТА. Для этого в ячейке F2 введем формулу =ЧАСТОТА(A2:A31;E2:E7). Протянем F2 маркером заполнения вниз до F8.
Формулу в этом примере необходимо ввести как формулу массива. Выделим диапазон F2:F8, нажмем клавишу F2, а затем нажмем клавиши CTRL+SHIFT+ВВОД (рис.2.21).
Если формула не будет введена как формула массива, отобразится только одно ее значение в ячейке F2.
Рисунок 2.21. Частоты значений признака
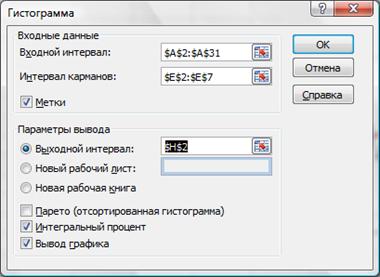
Также можно воспользоваться средством Пакета анализа (Анализ данных в Office 2007) ГИСТОГРАММА (рис.2.22). Выберем входной интервал, интервал карманов, метки, интегральный процент, поместим результаты на этом же листе (укажем ячейку $H$2).
Рисунок 2.22. Построение гистограммы
Полученная гистограмма представлена на рис.2.23.
Рис.2.23. Гистограмма частот
Замечание. Если диапазон карманов не был введен, то набор отрезков, равномерно распределенных между минимальным и максимальным значениями данных, будет создан автоматически.
Дата добавления: 2018-11-12 ; просмотров: 1066 | Нарушение авторских прав
Вариационный ряд может быть:
— дискретным, когда изучаемый признак характеризуется определенным числом (как правило целым).
— интервальным, когда определены границы «от» и «до» для непрерывно варьируемого признака. Интервальный ряд также строят если множество значений дискретно варьируемого признака велико.
Рассмотрим пример построения дискретного вариационного ряда.
Пример 1. Имеются данные о количественном составе 60 семей.

Построить вариационный ряд и полигон распределения
Решение .
Алгоритм построения вариационного ряда:
1) Откроем таблицы Excel.
2) Введем массив данных в диапазон А1:L5. Если вы изучаете документ в электронной форме (в формате Word, например), для этого достаточно выделить таблицу с данными и скопировать ее в буфер, затем выделить ячейку А1 и вставить данные – они автоматически займут подходящий диапазон.
3) Подсчитаем объем выборки n – число выборочных данных, для этого в ячейку В7 введем формулу =СЧЁТ(А1:L5). Заметим, что для того, чтобы в формулу ввести нужный диапазон, необязательно вводить его обозначение с клавиатуры, достаточно его выделить.
4) Определим минимальное и максимальное значение в выборке, введя в ячейку В8 формулу =МИН(А1:L5), и в ячейку В9: =МАКС(А1:L5).
Рис.1.1 Пример 1. Первичная обработка статистических данных в таблицах Excel

5) Далее, подготовим таблицу для построения вариационного ряда, введя названия для столбца интервалов (значений варианты) и столбца частот. В столбец интервалов введем значения признака от минимального (1) до максимального (6), заняв диапазон В12:В17.
6) Выделим столбец частот, введем формулу =ЧАСТОТА(А1:L5;В12:В17) и нажмем сочетание клавиш CTRL+SHIFT+ENTER
Рис.1.2 Пример 1. Построение вариационного ряда

7) Для контроля вычислим сумму частот при помощи функции СУММ (значок функции S в группе «Редактирование» на вкладке «Главная»), вычисленная сумма должна совпасть с ранее вычисленным объемом выборки в ячейке В7.
Построим полигон:
1) выделив полученный диапазон частот, выберем команду «График» на вкладке «Вставка». По умолчанию значениями на горизонтальной оси будут порядковые числа — в нашем случае от 1 до 6, что совпадает со значениями варианты (номерами тарифных разрядов).
2) Название ряда диаграммы «ряд 1» можно либо изменить, воспользовавшись той же опцией «выбрать данные» вкладки «Конструктор», либо просто удалить.
Рис.1.3. Пример 1. Построение полигона частот
В реальных социально-экономических системах нельзя проводить активные эксперименты, поэтому данные обычно представляют собой наблюдения за происходящим процессом, например: курс валюты на бирже в течение месяца, урожайность пшеницы в хозяйстве за 30 лет, производительность труда рабочих за смену и т.д. Результаты наблюдений — это в общем случае ряд чисел, расположенных в беспорядке, который для изучения необходимо упорядочить (проранжи- ровать).
Операция, заключающаяся в расположении значений признака по возрастанию, называется ранжированием опытных данных.
После операции ранжирования опытные данные можно сгруппировать так, чтобы в каждой группе признак принимал одно и то же значение, которое называется вариантом (х,). Число элементов в каждой группе называется частотой варианта («,).
Размахом вариации называется число
где хтах — наибольший вариант;
x min — наименьший вариант.
Сумма всех частот равна определенному числу л, которое называется объемом совокупности:
Отношение частоты данного варианта к объему совокупности называется относительной частотой, или частостью, этого варианта:
Последовательность вариант, расположенных в возрастающем порядке, называется вариационным рядом (вариация — изменение).
Вариационные ряды бывают дискретными и непрерывными. Дискретным вариационным рядом называется ранжированная последовательность вариант с соответствующими частотами и (или) частостями.
Пример 1. В результате тестирования группа из 24 человек набрала баллы: 4, 0, 3, 4, 1, 0, 3, 1, 0, 4, 0, 0, 3, 1, 0, 1, 1, 3, 2, 3, 1, 2, 1, 2. Построить дискретный вариационный ряд.
Решение. Проранжируем исходный ряд, подсчитаем частоту и частость вариант: 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 3, 3, 3, 3, 3, 4, 4, 4.
В результате получим дискретный вариационный ряд (табл. 3.10).
Ранжированный ряд успеваемости
Число студентов, л,
Относительная частота, А
В Excel проранжируем исходный ряд. Для этого введем все данные в диапазон А1 :А24 и воспользуемся кнопкой Щ (Сортировка по возрастанию).
Подсчитаем частоту и частость вариант. Построим таблицу в диапазоне D2:G7 (рис. 3.13).
Рис. 3.13. Контекстное меню строки состояния
Рассмотрим два варианта подсчета частот:
- 1) выделим диапазон, в котором находятся нули. Щелкнем в нижней правой части окна Excel правой кнопкой мыши и выберем в контекстном меню вид итога, который по умолчанию будет появляться в итоговой строке при выделении произвольного диапазона (см. рис. 3.13) — количество. Таким образом, последовательно выделяя диапазоны с одинаковыми значениями вариант, мы получим все частоты;
- 2) выполним команду Сервис — Анализ данных — Гистограмма. Заполним диалоговое окно в соответствии с рис. 3.14.
Рис. 3.14. Диалоговое окно инструмента пакета анализа «Гистограмма»
В результате получим таблицу с частотами вариантов и соответствующий график (рис. 3.15).
Рис. 3.15. Результаты применения инструмента «Гистограмма)
Найдем объем выборки, заполнив все частоты вариант в диапазоне ЕЗ:Е7, выделим его левой кнопкой мыши и щелкнем по кнопке ? (автосумма).
В ячейку F3 введем формулу «=ЕЗ/$Е$8», за маркер заполнения (крест в правом нижнем углу ячейки) с помощью мыши скопируем до F7 и выберем кнопку автосумма, в результате получим частоты вариантов и их сумму (1). В ячейку G3 введем частоту варианта 0 — цифру 6 (или ссылку на ячейку, ее содержащую — ЕЗ), в ячейку G4 введем формулу «=G3+E4» и скопируем ее до ячейки G7, в результате получим накопленные частоты. Таким образом, мы получили дискретный вариационный ряд. Естественно, частоты необходимо округлить, но таким образом, чтобы их сумма равнялась 1. Для этого выделим левой кнопкой мыши диапазон частот (F3:F7), щелкнув по правой кнопке, откроем контекстное меню и выполним команду Формат ячеек — Числовой — Число знаков 3 — ОК. Преобразовав обозначения, получим дискретный вариационный ряд, представленный в табл. 3.11.
Подсчет чисел, попадающих в диапазон, — обычная задача — с помощью функции СЧЁТЕСЛИ (). Усложняем задачу, делаем интервал легко настраиваемым.
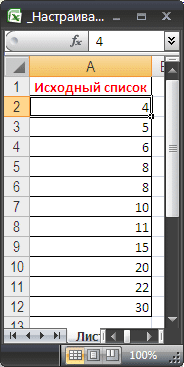
В качестве примера подсчета чисел возьмем список с числовыми значениями от 4 до 30 (см. Файл примера).
Мы будем считать значения, попадающие в диапазон, например (4; 15. Кроме того, пределы диапазона «include » и «не включают ()» будут выбраны из раскрывающегося меню. (выпадающее меню.
Примечание. Решение без выбора диапазона = СЧЁТЕСЛИМН (A2: A12; «>» & D2; A2: A12; «Предполагается, что границы диапазона вводятся в ячейки D2 и F2. Эти ячейки не должны быть пустыми, даже если одна из the limits = 0. Если диапазон A2: A12 содержит числовые значения в текстовом формате, они будут проигнорированы.
Чтобы установить пределы диапазона, используйте проверку данных с типом данных List. В качестве источника мы указываем для левой границы>;> = и для правой СЧЁТЕСЛИМН (A2: A12; C2 & D2; A2: A12; E2 & F2)
- = COUNTIF ($ A $ 2: $ A $ 12; C2 & D2) — (COUNT ($ A $ 2: $ A $ 12) -COUNTIF ($ A $ 2: $ A $ 12; E2 & F2))
- Формула = РАСЧЕТ (A1: A12; A1; H2: I3) требует, чтобы вы сначала создали таблицу с условиями. Заголовки этой таблицы должны точно соответствовать заголовкам исходной таблицы.
Функция УВЕРЕННОСТЬ в Excel предназначена для определения доверительного интервала для среднего, найденного для генеральной совокупности с нормальным распределением.
Другими словами, рассматриваемая функция позволяет определять допустимые отклонения для найденного среднего значения с учетом известных уровней значимости (заданная вероятность того, что определенное значение находится в доверительном интервале) и стандартного отклонения (мера степень разброса значений относительно среднего значения для генеральной совокупности).
Поскольку диапазон значений, в котором находится какое-то неизвестное, совпадает с областью, в которой значения этой величины могут изменяться, вероятность правильности оценки этой величины стремится к нулю. Поэтому принято устанавливать определенное значение вероятности нахождения границ изменения определенного значения. Значения между этими пределами называются доверительным интервалом.
Эта функция была заменена функцией CONFIDENCE.NORM в Excel 2010. Функция CONFIDENCE была сохранена для совместимости с документами, созданными в более ранних версиях редактора электронных таблиц.
Пример расчета доверительного интервала в Excel
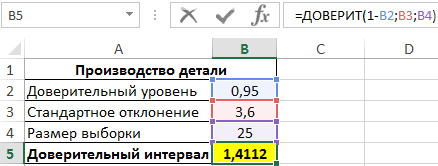
Пример 1. В заводском цехе изготавливается деталь, длина которой должна составлять 200 мм. Стандартное отклонение от длины составляет 3,6 мм. Для проверки качества деталей партии (генеральной совокупности) делается выборка из 25 деталей. Определите интервал с доверительной вероятностью 95%.
Просмотр таблицы данных:
Для определения доверительного интервала воспользуемся функцией:
- 1-В2 — уровень значимости (рассчитывается с учетом зависимости от уровня достоверности);
- B3 — значение стандартного отклонения;
- B4 — количество деталей в образце.
То есть пределы доверительного интервала соответствуют: (Xav-1.4112; Xav + 1.4112). Допустим, определилось среднее значение образца — 199,5 мм. Следовательно, доверительный интервал примерно определяется как (198,1; 200,9), а номинальная длина детали (200 мм) находится в доверительном интервале, то есть процесс изготовления не нарушается.
Как найти границы доверительного интервала в Excel
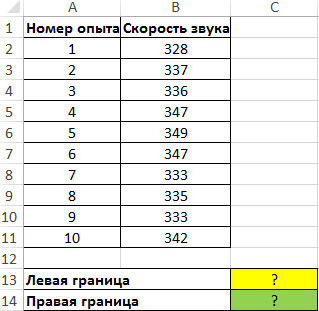
Пример 2. Были проведены эксперименты по определению скорости распространения звуковой волны в воздухе. Результаты 10 экспериментов занесены в таблицу. Определите левую и правую границы доверительного интервала для среднего.
Просмотр таблицы данных:
Чтобы найти левый край, используйте формулу:
В этом случае выборка и генеральная совокупность берутся в качестве доступных данных для 10 выполненных экспериментов. Среднее значение выборки рассчитывается с использованием функции СРЕДНЕЕ. Чтобы получить левый край доверительного интервала из этого значения, вычтите число, полученное в результате функции УВЕРЕННОСТЬ, где значение второго аргумента определяется с помощью функции СТАНДОТКЛОН, а количество экспериментов определяется путем подсчета количества ячейки с функцией СЧЁТ.
Поскольку уровень значимости не указан, мы используем значение по умолчанию 0,05.
Правая граница определяется аналогично, с той разницей, что результат вычисления функции УВЕРЕННОСТЬ прибавляется к среднему значению выборки:
Как посчитать доверительный интервал по функции ДОВЕРИТ в Excel
Функция имеет следующий синтаксис:
- альфа — требуется, принимает числовое значение, которое характеризует уровень значимости — вероятность отклонения нулевой (неправильной) гипотезы, если она действительно верна. Он определяется как 1-, где — уровень достоверности (вероятность найти истинное значение оценочного значения в определенном интервале, называемом уровнем достоверности).
- standard_dev — обязательный, принимает значение стандартного отклонения значения для генеральной совокупности значений (Excel предоставляет функцию для определения этого значения — STDEV.Y).
- size — обязательный, принимает числовое значение, характеризующее количество точек данных в анализируемой выборке (ее размер).
- Все аргументы функции должны быть указаны как числовые значения или данные, которые можно преобразовать в числа (например, текстовые строки с числами, логическое ИСТИНА, ЛОЖЬ). В противном случае выполнение функции УВЕРЕННОСТЬ приведет к появлению кода ошибки # ЧИСЛО!
- Буква должна быть числовым значением от 0 до 1 (оба включительно). В противном случае функция УВЕРЕННОСТЬ вернет код ошибки # ЧИСЛО! Аналогичная ошибка возникает, когда standard_dev — отрицательное или нулевое число.
- Допустимый диапазон измерения — от 1 до бесконечности со знаком плюс.
Одним из методов решения статистических задач является расчет доверительного интервала. Он используется как предпочтительная альтернатива точечной оценке в небольших выборках. Следует отметить, что сам процесс расчета доверительного интервала довольно сложен. Но инструменты программы Excel позволяют несколько ее упростить. Давайте узнаем, как это делается на практике.
Процедура вычисления
Этот метод используется для оценки диапазона различных статистических величин. Основная задача этого расчета — исключить неопределенности точечной оценки.
В Excel есть два основных варианта выполнения вычислений с использованием этого метода: когда известна дисперсия и когда она неизвестна. В первом случае для расчетов используется функция КОНФИДЕНТ.НОРМ, а во втором — функция КОНФИДЕНТ.СТУДЕНТ.
Способ 1: функция ДОВЕРИТ.НОРМ
Оператор CONFIDENT.NORM, который принадлежит к совокупной группе функций, был впервые представлен в Excel 2010. В более ранних версиях программы используется эквивалент CONFIDENCE. Цель этого оператора — вычислить нормально распределенный доверительный интервал для средней совокупности.
Его синтаксис следующий:
Альфа — это аргумент, который указывает уровень значимости, используемый для расчета уровня достоверности. Уровень достоверности равен следующему выражению:
«Стандартное отклонение» — это аргумент, подсказанный названием. Это стандартное отклонение предложенной выборки.
«Размер» — это аргумент, определяющий размер выборки.
Все аргументы для этого оператора обязательны.
Функция УВЕРЕННОСТЬ имеет те же аргументы и возможности, что и предыдущая. Его синтаксис следующий:
Как видите, отличия только в названии оператора. По соображениям совместимости эта функция сохраняется в Excel 2010 и более поздних версиях в специальной категории «Совместимость». В версиях Excel 2007 и ранее он присутствует в основной группе статистических операторов.
Предел доверительного интервала определяется по формуле следующего вида:
Где X — это среднее значение выборки, которое находится в центре выбранного диапазона.
Теперь давайте посмотрим, как рассчитать доверительный интервал на конкретном примере. Было проведено 12 тестов, в результате которых были получены различные результаты, приведенные в таблице. Это наша совокупность. Стандартное отклонение равно 8. Нам нужно рассчитать доверительный интервал с уровнем достоверности 97%.
- Выберите ячейку, в которой будет отображаться результат обработки данных. Нажмите кнопку «Вставить функцию».
Появится мастер. Перейдите в категорию «Статистика» и выберите название «КОНФИДЕНТ.НОРМ». Затем нажмите кнопку «ОК».
Откроется окно темы. Его поля естественно соответствуют именам аргументов.
Установите курсор в первое поле — «Альфа». Здесь следует указать уровень значимости. Как мы помним, уровень нашей уверенности составляет 97%. При этом мы сказали, что он рассчитывается так:
Это означает, что для расчета уровня значимости, т. Е. Для определения значения «Альфа», должна применяться формула следующего типа:
То есть, подставляя значение, получаем:
Путем несложных вычислений мы обнаруживаем, что аргумент «Альфа» равен 0,03. Введите это значение в поле.
Как известно, по условию стандартное отклонение равно 8. Поэтому в поле «Стандартное отклонение» просто напишите это число.
В поле «Размер» необходимо ввести количество элементов выполненных тестов. Как мы помним, их 12. Но чтобы автоматизировать формулу и не менять ее каждый раз при выполнении нового теста, мы задаем это значение не обычным числом, а с помощью оператора COUNT. Затем установите ползунок в поле «Размер», затем щелкните треугольник, который находится слева от строки формул.
Отображается список недавно использованных функций. Если вы недавно использовали оператор COUNT, он должен быть в этом списке. В этом случае просто нажмите на его название. В противном случае, если вы не можете его найти, перейдите в «Другие функции…».
Появляется уже знакомый нам мастер функции. Вернитесь в группу «Статистика». Выделяем там название «АККАУНТ». Нажимаем на кнопку «ОК».
Отображается окно аргументов для предыдущего оператора. Эта функция предназначена для вычисления количества ячеек в указанном диапазоне, содержащих числовые значения. Его синтаксис следующий:
Группа аргументов «Значения» — это ссылка на диапазон, в котором вы хотите вычислить количество ячеек, заполненных числовыми данными. Всего может быть до 255 аргументов этого типа, но в нашем случае нам нужен только один.
Поместите курсор в поле «Value1» и, удерживая левую кнопку мыши, выберите диапазон, содержащий нашу коллекцию на листе. Тогда ваш адрес отобразится в поле. Нажимаем на кнопку «ОК».
Далее приложение выполнит расчет и отобразит результат в ячейке, в которой оно находится. В нашем конкретном случае формула получилась так:
Общий результат расчета составил 5,011609.
Но это еще не все. Как мы помним, предел доверительного интервала вычисляется путем сложения и вычитания выборочного среднего результата вычисления CONFIDENCE.NORM. Это вычисляет правую и левую границы доверительного интервала соответственно. Само выборочное среднее можно рассчитать с помощью оператора AVERAGE.
Этот оператор предназначен для вычисления среднего арифметического выбранного диапазона чисел. Он имеет следующий довольно простой синтаксис:
Аргумент Number может быть одним числовым значением или ссылкой на ячейки или даже целые диапазоны, которые их содержат.
Затем выберите ячейку, в которой будет отображаться расчет среднего значения, и нажмите кнопку «Вставить функцию».
Мастер откроется. Снова перейдите в категорию «Статистика» и выберите из списка название «СРЕДНИЙ». Как всегда, нажмите кнопку «ОК».
Откроется окно темы. Установите курсор в поле «Число 1» и, удерживая левую кнопку мыши, выделите весь диапазон значений. После того, как координаты отобразятся в поле, нажмите кнопку «ОК».
Затем СРЕДНИЙ отображает результат расчета в элементе листа.
Вычисляем правый край доверительного интервала. Для этого выделите отдельную ячейку, введите знак «=» и добавьте содержимое элементов листа, где находятся результаты расчетов функций СРЕДНИЙ и КОНФИДЕНТ.НОРМ. Чтобы выполнить расчет, нажмите клавишу Enter. В нашем случае мы получили следующую формулу:
Результат расчета: 6.953276
Точно так же мы вычисляем левый край доверительного интервала, только на этот раз мы вычитаем результат вычисления оператора CONFIDENCE.NORM из результата вычисления AVERAGE. Результатом является формула для нашего примера следующего типа:
Результат расчета: -3.06994
Мы постарались подробно описать все этапы расчета доверительного интервала, поэтому подробно описали каждую формулу. Но вы можете объединить все действия в одну формулу. Расчет правой границы доверительного интервала можно записать следующим образом:
Аналогичный расчет левого края будет выглядеть так:
Способ 2: функция ДОВЕРИТ.СТЮДЕНТ
Кроме того, в Excel есть еще одна функция, связанная с вычислением доверительного интервала: ДОВЕРИЙ УЧАЩИХСЯ. Он появился только в Excel 2010. Этот оператор вычисляет доверительный интервал генеральной совокупности с использованием t-распределения Стьюдента. Это очень удобно, когда дисперсия и, следовательно, стандартное отклонение неизвестны. Синтаксис оператора следующий:
Как видите, в этом случае названия операторов остались без изменений.
Давайте посмотрим, как рассчитать границы доверительного интервала с неизвестным стандартным отклонением, используя тот же пример популяции, который мы рассматривали в предыдущем методе. Уровень доверия, как и в прошлый раз, 97%.
- Выберите ячейку, в которой будет производиться расчет. Нажмите кнопку «Вставить функцию».
В открывшемся мастере перейдите в категорию «Статистика». Выбираем название «КОНФИДЕНТ.СТУДЕНТ». Нажимаем на кнопку «ОК».
Откроется окно аргументов для указанного оператора.
В поле «Альфа», поскольку уровень достоверности 97%, обратите внимание на число 0,03. Второй раз останавливаться на принципах расчета этого параметра не будем.
Затем поместите курсор в поле «Стандартное отклонение». На этот раз этот показатель нам неизвестен, и нам нужно его рассчитать. Это делается с помощью специальной функции — СТАНДОТКЛОН. B. Чтобы открыть это окно оператора, щелкните треугольник слева от строки формул. Если мы не находим нужное имя в открывшемся списке, переходим в «Другие функции…».
Мастер запускается. Перейдите в категорию «Статистика» и отметьте в ней имя «STDEV.V». Затем нажимаем кнопку «ОК».
Откроется окно темы. Задача оператора STDEV.B — определить стандартное отклонение выборки. Его синтаксис выглядит так:
Как вы понимаете, аргумент Number — это адрес элемента выбора. Если выделение помещено в один массив, то, используя только один аргумент, вы можете предоставить ссылку на этот диапазон.
Поместите курсор в поле «Число 1» и, как всегда, зажмите левую кнопку мыши и выберите популяцию. После того, как координаты были введены в поле, не спешите нажимать кнопку «ОК», так как результат будет некорректным. Во-первых, нам нужно вернуться в окно аргументов оператора CONFIDENCE.STUDENT, чтобы вставить последний аргумент. Для этого щелкните соответствующее имя в строке формул.
Снова открывается окно аргументов для знакомой функции. Установите курсор в поле «Размер». Еще раз нажмите на уже знакомый нам треугольник, чтобы перейти к выбору операторов. Как вы понимаете, нам нужно название «COUNT». Поскольку мы использовали эту функцию в расчетах в предыдущем методе, она присутствует в этом списке, поэтому просто щелкните по ней. Если вы его не нашли, действуйте по алгоритму, описанному в первом способе.
Оказавшись в окне СЧЁТ аргументов, поместите курсор в поле «Число 1» и, удерживая кнопку мыши, выберите агрегат. Затем нажимаем кнопку «ОК».
Далее программа рассчитывает и отображает значение доверительного интервала.
Чтобы определить границы, нам все равно нужно будет вычислить выборочное среднее. Но, поскольку алгоритм расчета по формуле СРЕДНИЙ такой же, как и в предыдущем методе, и результат также не изменился, мы не будем подробно останавливаться на этом второй раз.
Суммируя результаты вычислений СРЕДНЕГО и УВЕРЕННОГО СТУДЕНТА, мы получаем правый край доверительного интервала.
Вычитая результат вычисления CONFIDENCE STUDENT из результатов вычисления оператора AVERAGE, мы получаем левый край доверительного интервала.
Если расчет записать по формуле, расчет правого края в нашем случае будет выглядеть так:
Следовательно, формула расчета левого края будет выглядеть так:
Как видите, инструменты Excel значительно упрощают расчет доверительного интервала и его пределов. Для этого используются отдельные операторы для выборок, для которых дисперсия известна и неизвестна.