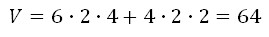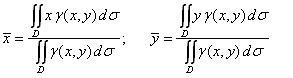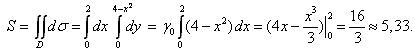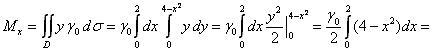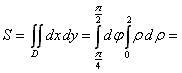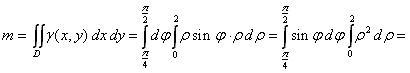Как найти ширину пластины - Исправление недочетов и поиск решений вместе с Examum.ru

Ширина — пластина

Cтраница 4

С уменьшением ширины пластины время нагрева также уменьшается.
[47]

Длину и ширину пластин магнитопровода определяют из размеров сечения стержня и ярма, расстояния между осями стержней и их высоты. При этом принимают, что края пластин прилегают друг к другу вплотную, без зазоров.
[49]

При дальнейшем увеличении ширины пластины и щели диафрагмы амплитуда колебаний светового потока уменьшается и они становятся негармоническими.
[50]

Однако с уменьшением ширины пластины даже при длинном индукторе нижний предел частоты, как это следует из формулы ( 12 — 22) и графиков на рис. 12 — 2, повышается и при 62 / D2 1 достигает того же значения, что и для цилиндра. При этом в формулы ( 11 — 22) и ( 11 — 23) следует вместо D2 подставлять сторону квадрата.
[51]

Выбор оптимального отношения ширины пластины к ее высоте способствует выравниванию скорости потока по ширине канала и, следовательно, улучшению использования теплооб-менной поверхности. Это достигается также при равномерном распределении турбулизирующих элементов по поверхности пластин, устранении прямых проходов, применении плавных очертаний зон расширения при входе жидкости и зон сужения при ее выходе.
[52]

Напряжения изменяются по ширине пластины так, как это показано на фиг.
[54]

Кроме различия в ширине пластин, сердечники усилителей серии УМ1П имеют три размера по толщине пакета для каждой ширины пластины.
[55]

Для штучных грузов принимается ширина пластин на 100 — 150 мм больше максимального размера груза.
[56]

Положим далее, что ширина пластины А существенно больше ее длины / ив пределе стремится к бесконечности. Это позволяет пренебречь боковым течением жидкости в зазоре и свести более сложную пространственную задачу к плоской с осями х и у, сохраняя интересующую нас физику явления.
[57]

Очевидно, что увеличение ширины пластин не может производиться в неограниченных пределах, поскольку в этом случае пластина заполнит волновод, который приобретет обратимые свойства, и дифференциальный сдвиг фазы уменьшится до нуля.
[59]

Здесь же требуется найти неизвестную ширину пластины, которая будет находиться в равновесии в изогнутом состоянии при известном сжимающем напряжении о. В обоих случаях получается одно и то же соотношение между шириной полоски и напряжением, единственное различие состоит в том, что принимать за известное и что за неизвестное.
[60]

Страницы:

Источник

✖нагрузка на плоскую пластину определяется как сила, действующая на поверхность или корпус плоской пластины.ⓘ Нагрузка на плоскую пластину [P]			+10% -10%
✖Толщина листа — это толщина или минимальный размер рассматриваемого листа или металлического листа.ⓘ Толщина пластины [t]			+10% -10%
✖Номинальное напряжение – это значение напряжения в минимальном поперечном сечении.ⓘ Номинальное напряжение [σ_o]			+10% -10%
✖Диаметр поперечного отверстия в пластине — это длина прямой линии, проходящей из стороны в сторону через центр отверстия (отверстия в чем-либо), особенно окружности.ⓘ Диаметр поперечного отверстия в пластине [d_h]			+10% -10%

Источник

Как найти площадь поверхности детали

Площадь поверхности многогранника. В данной рубрике в опубликованных статьях » Общий обзор. Формулы стереометрии » и » Что ещё необходимо знать для решения по стереометрии » мы уже рассмотрели теоретические моменты, которые необходимы для решения.

В составе ЕГЭ по математике имеется целый ряд задач на определение площади поверхности и объема составных многогранников. Это, наверное, одни из самых простых задач по стереометрии. НО! Имеется нюанс. Не смотря на то, что сами вычисления просты, ошибку при решении такой задачи допустить очень легко.

В чём же дело? Далеко не все обладают хорошим пространственным мышлением, чтобы сразу увидеть все грани и параллелепипеды из которых «состоят» многогранники. Даже если вы умеете делать это очень хорошо, можете мысленно сделать такую разбивку, всё-таки следует не торопиться и воспользоваться рекомендациями из этой статьи.

Кстати, пока работал над данным материалом, нашёл ошибку в одной из задач на сайте. Нужна внимательность и ещё раз внимательность, вот так.

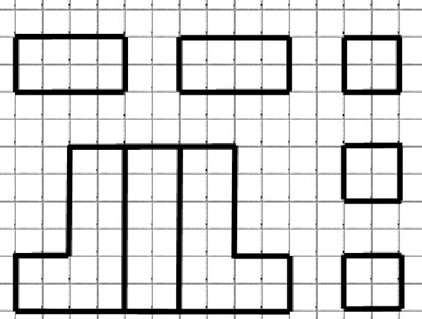
Итак, если стоит вопрос о площади поверхности, то на листе в клетку постройте все грани многогранника, обозначьте размеры. Далее внимательно вычисляйте сумму площадей всех полученных граней. Если будете предельно внимательны при построении и вычислении, то ошибка будет исключена.

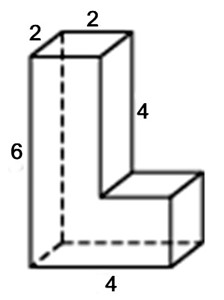
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Используем оговоренный способ. Он нагляден. На листе в клетку строим все элементы (грани) в масштабе. Если длины рёбер будут большими, то просто подпишите их.

Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Ещё задачи 25881 , 77155 , 77156 . В них приведены решения другим способом (без построения), постарайтесь разобраться — что откуда взялось. Также решите уже представленным способом.

Если требуется найти объём составного многогранника. Разбиваем многогранник на составляющие его параллелепипеды, записываем внимательно длины их рёбер и вычисляем.

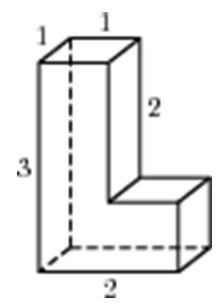
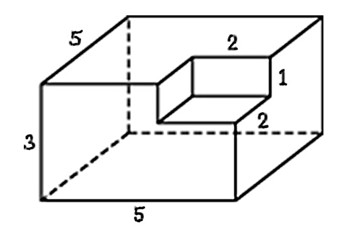
Найдите объем многогранника, изображенного на рисунке (все двугранные углы многогранника прямые).

Объем многогранника, изображенного на рисунке равен сумме объёмов двух многогранников с рёбрами 6,2,4 и 4,2,2

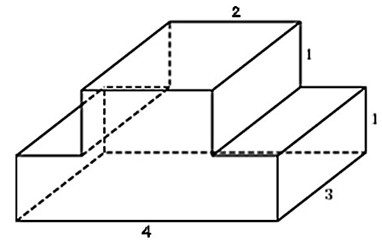
Найдите объем многогранника, изображенного на рисунке (все двугранные углы многогранника прямые).

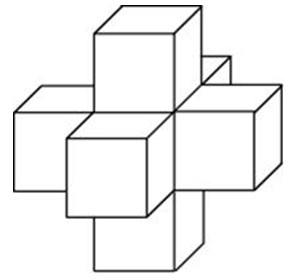
Найдите объем пространственного креста, изображенного на рисунке и составленного из единичных кубов.

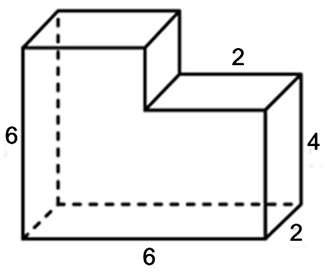
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

Казалось бы, данные задачи можно вообще не рассматривать, они же просты и понятны. Но в их решении важна практика. Повторюсь, что ошибиться очень легко, попрактикуйтесь с подобными задачами и вы убедитесь.

В отк рытом банке задач много примеров аналогичных задач (смотрите здесь и здесь ). Договоритесь с одноклассниками решить одни и те же задачи, затем сверьтесь.

Мы продолжим рассматривать задачи данной части, не пропустите! Успехов вам.

Задание 8 (№ 25641) из Открытого банка заданий для подготовки к ЕГЭ по математике.

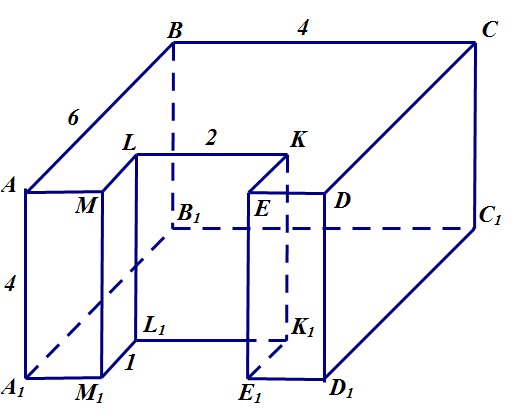
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые)

Решение. Площадь поверхности многогранника равна сумме площадей всех его граней. Так как все грани этого многогранника — прямоугольники, то для нахождения площади каждой грани мы используем формулу площади прямоугольника:

S=ab, где a и b — длины двух смежных сторон прямоугольника.

Обозначим вершины многогранника:

1.Найдем сначала площадь боковой поверхности. Для этого, чтобы не пропустить ни одной грани, обойдем наш многогранник по часовой стрелке, и запишем площадь каждой грани:

2. Найдем площадь верхней грани. Для этого из площади прямоугольника ABCD вычтем площадь прямоугольника MLKE:

3. Площадь нижней грани равна площади верхней грани и равна 22.

4. Сложим получившиеся площади: 88+22+22=132.

Задание 8_1. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Площадь поверхности многогранника можно вычислить как сумму площадей всех его граней. Причем площади передней и задней граней, равны

и вся площадь поверхности равна

Задание 8_2. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

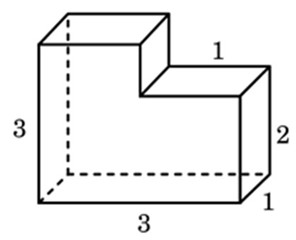
Найдем площадь поверхности как площадь поверхности прямоугольного параллелепипеда со сторонами 3, 3, 5 и вычтем площади двух граней 1х1 прямоугольного параллелепипеда со сторонами 1, 1 и 3 (см. рисунок).

Площадь поверхности большого параллелепипеда, равна

Площади двух граней 1х1 малого параллелепипеда, равны:

и площадь поверхности фигуры

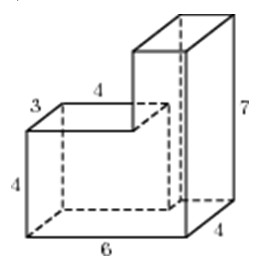
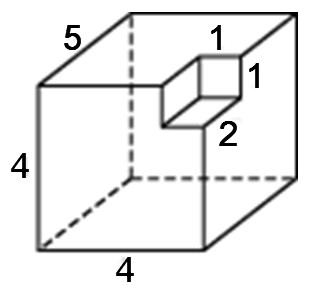
Задание 8_3. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Из рисунка видно, что площадь поверхности фигуры будет меньше площади прямоугольного параллелепипеда со сторонами 3, 4 и 5 на площади двух квадратов, размером 1х1, имеем:

Задание 8_4. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Можно заметить, что площадь поверхности данной фигуры будет в точности совпадать с площадью поверхности прямоугольного параллелепипеда со сторонами 5, 3 и 5 и равна

Замечание. Не путайте вычисление объема фигуры и площади его поверхности!

Задание 8_5. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Площадь поверхности данной фигуры равна площади поверхности прямоугольного параллелепипеда со сторонами 3, 5 и 4, и равна

Замечание. Не путайте вычисление объема фигуры и площади его поверхности!

Задание 8_6. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Площадь поверхности данной фигуры можно вычислить как площадь поверхности прямоугольного параллелепипеда со сторонами 4, 4 и 6 плюс две грани 1х4 площадью 4 (см. рисунок) и минус две грани площадью 2х1 (они вычитаются из оснований). Таким образом, площадь фигуры равна

Задание 8_7. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Площади нижней и верхней граней равны , площади боковых граней можно вычислить как , площади передней и задней граней соответственно и еще нужно учесть две площади внутренней нижней и верхней граней . Таким образом, вся площадь поверхности фигуры равна

Задание 8_8. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Площадь поверхности фигуры можно вычислить как площадь поверхности прямоугольного параллелепипеда со сторонами 4, 3 и 2, минус четыре площади боковых квадратов, размером 1х1. Имеем:

Задание 8_9. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

На рисунке изображен прямоугольный параллелепипед с вырезом. Площадь поверхности такой фигуры будет равна площади поверхности всего параллелепипеда со сторонами 5, 7 и 1 минус две площади фронтального выреза площадью 2х1=2 и плюс четыре площади внутренних сторон выреза размерами 1х1 и 2х1. Таким образом, вся площадь поверхности многогранника равна

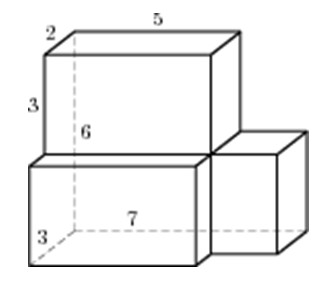
Задание 8_10. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Площадь поверхности многогранника можно найти как сумму площадей двух прямоугольных параллелепипедов со сторонами 5, 4, 3 и 3, 2, 3 минус две площади основания нижнего параллелепипеда площадью 2х3 (две площади, т.к. она будет дважды учтена в большом и малом параллелепипедах). Таким образом, получаем:

Задание 8_11. Найдите площадь поверхности многогранника, изображенного на рисунке, все двугранные углы которого прямые.

Найдем площадь поверхности фигуры как площадь прямоугольного параллелепипеда со сторонами 2, 2, 1 и вычтем две площади граней 1х1 во фронтальных плоскостях (передней и задней), получим:

Задание 8_12. Найдите площадь поверхности пространственного креста, изображенного на рисунке и составленного из единичных кубов.

Площадь поверхности данной фигуры можно найти как сумму площадей поверхности 6 кубов минус площадь поверхности одного куба (тот что внутри и эти грани не входят в площадь поверхности), получаем:

Задание 8_13. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Найдем площадь поверхности этого многогранника как сумму площадей поверхности большого (6х6х2) и малого (3х3х4) прямоугольных параллелепипедов и вычтем дважды площадь поверхности соприкосновения граней этих параллелепипедов, которая имеет размер 3х4, получим:

Задание 8_14. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Площадь поверхности этого многогранника можно найти как сумму площадей поверхности каждого из трех параллелепипедов размерами 2х5х6, 2х5х3 и 2х3х2 минус удвоенные площади соприкосновения этих параллелепипедов, то есть минус удвоенные площади двух граней размерами 3х5 и 2х3 соответственно. В результате получаем площадь поверхности фигуры:

Задание 8_15. Через среднюю линию основания треугольной призмы, проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности призмы, если площадь боковой поверхности отсеченной треугольной призмы равна 37.

Так как плоскость сечения проведена через среднюю линию, то она делит боковую плоскость пополам. Следовательно, площадь боковой поверхности большей призмы в 2 раза больше площадь боковой поверхности малой призмы и равна 74.

Определить площадь пластин плоского воздушного конденсатора электроемкостью 1 мкФ

Определить площадь пластин плоского воздушного конденсатора электроемкостью 1 мкФ, если расстояние между пластинами 1 мм.

Задача №6.4.10 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Решение задачи:

Электроемкость плоского конденсатора определяется по следующей известной формуле:

Выразим из этой формулы искомую площадь пластин конденсатора (S):

Задача решена в общем виде, остается только произвести расчет. Напомним, что электрическая постоянная (varepsilon _0) равна 8,85·10 -12 Ф/м, диэлектрическая проницаемость воздуха (varepsilon) равна 1. Не забывайте переводить численные значения величин в систему СИ.

Мы получили какое-то огромное число, тем не менее в ответах в конце сборника указан такой же ответ.

Ответ: 113 м 2 .

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Масса пластины

Масса тела — это его объем , умноженный на плотность его материала rho (см. таблицы плотностей):
, умноженная на ее толщину :
Площадь прямоугольника: — длина пластины, — ширина пластины. Тогда масса:

2. Масса треугольной пластины

Площадь треугольника: — основание треугольника, — высота треугольника. Тогда масса:

3. Масса круглой пластины

Площадь круга: — диаметр круга.
Тогда масса:

4. Масса эллиптической пластины

Площадь эллипса: — длина эллипса, — ширина эллипса. Тогда масса:

Масса пластины более сложной формы может быть вычислена как сумма (или разность) масс пластин простой формы. Примеры:

5. Масса овальной пластины

Овал — это круг, разрезанный пополам и раздвинутый вставленным в него прямоугольником. Площадь круга: Это прямоугольник, из которого вырезан треугольник. Площадь прямоугольника:

Источник

3 Приложения
двойных интегралов

3.1 Теоретическое
введение

Рассмотрим приложения двойного интеграла
к решению ряда геометрических задач и
задач механики.

3.1.1 Вычисление площади и массы плоской
пластины

Рассмотрим тонкую материальную
пластину D,
расположенную в плоскости Оху.

Площадь
S
этой пластины может быть найдена с
помощью двойного интеграла по формуле:

(1)

Пусть в каждой точке пластины
задана ее поверхностная плотность γ
= γ (x,
y) ≥ 0. Будем считать,
что функция γ = γ (x,
y) непрерывна в области
D.
Тогда масса
m
этой пластины равна двойному интегралу
от функции плотности γ (x,
y) по области D:

(2)

3.1.2
Статические моменты. Центр масс плоской
пластины

Статическим моментом
M_x
относительно оси Ox
материальной точки P(x;y),
лежащей в плоскости Oxy
и имеющей массу m,
называется произведение массы точки
на ее ординату, т.е. M_x=
my. Аналогично
определяется статический момент M_y
относительно оси Oy:
M_y
= mx.
Статические
моменты плоской
пластины с поверхностной плотностью γ
= γ (x,
y) вычисляются по
формулам:

(3)

(4)

Как известно из механики,
координаты x_c
, y_c
центра масс плоской материальной системы
определяются равенствами:

(5)

где m
– масса системы, а M_x
и M_y
– статические моменты системы. Масса
плоской пластины m
определяется формулой (1), статические
моменты плоской пластины можно вычислить
по формулам (3) и (4). Тогда, согласно
формулам (5), получаем выражение для
координат центра масс плоской пластины:

(6)

3.2 Содержание
типового расчета

Типовой расчет содержит
две задачи. В каждой задаче задана
плоская пластина D,
ограниченная линиями, указанными в
условии задачи. Г(x,y)
– поверхностная плотность пластины D.
Для этой пластины найти:
1. S
– площадь;
2. m
– массу;
3. M_y
, M_x
– статические моменты относительно
осей Оy
и Ох
соответственно;
4.
,
–
координаты центра масс.

3.3 Порядок
выполнения типового расчета

При решении каждой задачи
необходимо:
1. Выполнить чертеж заданной
области. Выбрать систему координат, в
которой будут вычисляться двойные
интегралы.
2. Записать область в виде
системы неравенств в выбранной системе
координат.
3. Вычислить площадь S
и массу m
пластины по формулам (1) и (2).
4. Вычислить
статические моменты M_y
, M_x
по формулам (3) и (4).
5. Вычислить
координаты центра масс
,
по
формулам (6). Нанести центр масс на чертеж.
При этом возникает визуальный
(качественный) контроль полученных
результатов.
Численные ответы должны
быть получены с тремя значащими цифрами.

3.4 Примеры
выполнения типового расчета

Задача 1.
Пластина D
ограничена линиями: y
= 4 – x²;
х =
0; y
= 0 (x
≥ 0; y
≥ 0) Поверхностная плотность γ₀
= 3.
Решение.
Область, заданная в задаче, ограничена
параболой y
= 4 – x²,
осями координат и лежит в первой четверти
(рис. 1). Задачу будем решать в декартовой
системе координат. Эта область может
быть описана системой неравенств:

Рис.
1

Площадь S
пластины равна (1):

Так
как пластина однородная, ее масса m
= γ₀S
= 3·
= 16.
По формулам (3), (4) найдем статические
моменты пластины:

Координаты
центра масс находятся по формуле (6):

Ответ:
S ≈
5,33; m
= 16; M_x
= 25,6; M_y
= 12;
=
0,75;
=
1,6.

Задача 2.
Пластина D
ограничена линиями: х²
+ у²
= 4; х
= 0, у
= х
( х
≥ 0, у
≥ 0). Поверхностная плотность γ(x,y)
= у.

Решение.
Пластина ограничена окружностью и
прямыми, проходящими через начало
координат (рис. 2). Поэтому для решения
задачи удобно использовать полярную
систему координат. Полярный угол φ
меняется от π/4 до π/2. Луч, проведенный
из полюса через пластину, «входит» в
неё при ρ = 0 и «выходит» на окружность,
уравнение которой: х²
+ у²
= 4 <=> ρ = 2.

Рис.
2

Следовательно, заданную
область можно записать системой
неравенств:

Площадь
пластины найдем по формуле (1):

Массу
пластины найдем по формуле (2), подставив
γ(x,y)
= у = ρ
sinφ:

Для
вычисления статических моментов пластины
используем формулы (3) и (4):

Координаты
центра масс получим по формулам (6):

Ответ:
S ≈
1,57; m
≈ 1,886; M_x
= 2,57; M_y
= 1;
=
0,53;
=
1,36.

3.5 Оформление
отчета

В отчете должны быть представлены все
выполненные расчеты, аккуратно выполненные
чертежи. Численные ответы должны быть
получены с тремя значащими цифрами.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Автор:
Judy Howell

Дата создания:
25 Июль 2021

Дата обновления:
18 Май 2023

Видео: Как рассчитать вес металлического листа исходя из его габаритных размеров и толщины

Вы можете легко измерить длину и ширину прямоугольной пластины с помощью метрической линейки. Однако прямое измерение третьего размера (толщины) пластины не будет точным, если пластина достаточно тонкая. Вы можете рассчитать толщину пластины как отношение объема пластины к площади ее поверхности.

Измерьте или узнайте в другом месте длину и ширину пластины.

Умножьте длину и ширину, если они указаны в дюймах, на коэффициент 2,54, чтобы преобразовать размеры в сантиметры. Например, размеры пластины составляют 5 на 3 дюйма, которые будут преобразованы в 12,7 и 7,62 см.

Умножьте длину на ее ширину, чтобы вычислить площадь поверхности пластины в квадратных сантиметрах. В этом примере площадь поверхности составляет 12,7 х 7,62 или 96,774 кв.

Рассчитать или измерить объем тарелки; если плотность пластины известна, разделите вес пластины на плотность. Например, тарелка изготовлена из алюминия (плотность 2,7 г / куб. См) и весит 41,85 г. Тогда объем пластины составляет 41,85 / 2,7 = 15,5 куб. См.

Разделите объем пластины на площадь поверхности, чтобы рассчитать толщину. В этом примере толщина составляет 15,5 куб. См / 96,774 кв. См = 0,16 см или 1,6 мм.

Источник