Как найти ширину зуба зубчатого колеса

За многие тысячелетия технического прогресса передача многократно усовершенствовалась, и сегодня они применяются практически в любом транспортном средстве от велосипеда до космического корабля и подводной лодки. Используются они также в любом станке и механизме, больше всего шестеренок используется в механических часах.

Что такое модуль зубчатого колеса

Современные шестерни далеко ушли от своих деревянных шестизубых предков, изготавливаемых механиками с помощью воображения и мерной веревочки. Конструкция передач намного усложнилась, тысячекратно возросли скорость вращения и усилия, передаваемые через такие передачи. В связи с этим усложнились и методы их конструирования. Каждую шестеренку характеризует несколько основных параметров

• диаметр;
• число зубьев;
• шаг;
• высота зубца;
• и некоторые другие.

Одним из самых универсальных характеристик является модуль зубчатого колеса. Существует для подвида — основной и торцевой.

Скачать ГОСТ 9563-60

В большинстве расчетов используется основной. Он рассчитывается применительно к делительной окружности и служит одним из важнейших параметров. Для расчета этого параметра применяют следующие формулы:

m=t/π,

где t — шаг. Модуль зубчатого колеса можно рассчитать и следующим образом:

m=h/2,25,

где h — высота зубца. И, наконец,

m=De/(z+2),

где De — диаметр окружности выступов,а z — число зубьев.

Что же такое модуль шестерни?

это универсальная характеристика зубчатого колеса, связывающая воедино такие его важнейшие параметры, как шаг, высота зуба, число зубов и диаметр окружности выступов. Эта характеристика участвует во всех расчетах, связанных с конструированием систем передач.

Формула расчета параметров прямозубой передачи

Чтобы определить параметры прямозубой шестеренки, потребуется выполнить некоторые предварительные вычисления. Длина начальной окружности равна π×D, где D — ее диаметр.Шаг зацепления t – это расстояние между смежными зубами, измеренное по начальной окружности. Если это расстояние умножить на число зубов z, то мы должны получить ее длину:

π×D=t×z,

проведя преобразование, получим:

D=(t /π)×z

Если разделить шаг на число пи, мы получим коэффициент, постоянный для данной детали зубчатой передачи. Он и называется модулем зацепления m.

t/π=m,

размерность модуля шестерни — миллиметры. Если подставить его в предыдущее выражение, то получится:

В=m×z;

выполнив преобразование, находим:

m=D / z.

Отсюда вытекает физический смысл модуля зацепления: он представляет собой длину дуги начальной окружности, соответствующей одному зубцу колеса. Диаметр окружности выступов D_e получается равным

De=d+2× h’,

где h’- высота головки. Высоту головки приравнивают к m:

 h’=m.

Проведя математические преобразования с подстановкой, получим:

De=m×z+2m = m(z+2),

откуда вытекает:

m=De/(z+2).

Диаметр окружности впадин D_i соответствует D_e за вычетом двух высот основания зубца:

D_i=D-2h“,

где h“- высота ножки зубца. Для колес цилиндрического типа h“ приравнивают к значению в 1,25m:

h’ = 1,25m.Выполнив подстановку в правой части равенства, имеем:

D_i = m×z-2×1,25m = m×z-2,5m;

что соответствует формуле:

D_i = m(z-2,5m).

Полная высота:

h = h’+h“,

и если выполнить подстановку, то получим:

h = 1m+1,25m=2,25m.

Иначе говоря, головка и ножка зубца относятся друг к другу по высоте как 1:1,25. Следующий важный размер, толщину зубца s принимают приблизительно равной:

• для отлитых зубцов: 1,53m:
• для выполненных путем фрезерования-1,57m, или 0,5×t

Поскольку шаг t приравнивается к суммарной толщине зубца s и впадины s_в, получаем формулы для ширины впадины

• для отлитых зубцов: s_в=πm-1,53m=1,61m:
• для выполненных путем фрезерования- s_в= πm-1,57m = 1,57m

Характеристики конструкции оставшейся части зубчатой детали определяются следующими факторами:

• усилия, прикладываемые к детали при эксплуатации;
• конфигурация деталей, взаимодействующих с ней.

Детальные методики исчисления этих параметров приводятся в таких ВУЗовских курсах, как «Детали машин» и других. Модуль шестерни широко используется и в них как один из основных параметров.

Для отображения шестеренок методами инженерной графики используются упрощенные формулы. В инженерных справочниках и государственных стандартов можно найти значения характеристик, рассчитанные для типовых размеров зубчатых колес.

Исходные данные и замеры

На практике перед инженерами часто встает задача определения модуля реально существующей шестерни для ее ремонта или замены. При этом случается и так, что конструкторской документации на эту деталь, как и на весь механизм, в который она входит, обнаружить не удается. Самый простой метод — метод обкатки. Берут шестерню, для которой характеристики известны. Вставляют ее в зубья тестируемой детали и пробуют обкатать вокруг. Если пара вошла в зацепление — значит их шаг совпадает. Если нет — продолжают подбор. Для косозубой выбирают подходящую по шагу фрезу.

Такой эмпирический метод неплохо срабатывает для зубчатых колес малых размеров. Для крупных, весящих десятки, а то и сотни килограмм, такой способ физически нереализуем.

Результаты расчетов

Для более крупных потребуются измерения и вычисления. Как известно, модуль равен диаметру окружности выступов, отнесенному к числу зубов плюс два:

m=De/(z+2)

Последовательность действий следующая:

• измерить диаметр штангенциркулем;
• сосчитать зубцы;
• разделить диаметр на z+2;
• округлить результат до ближайшего целого числа.

Данный метод подходит как для прямозубых колес, так и для косозубых.

Расчет параметров колеса и шестерни косозубой передачи

Расчетные формулы для важнейших характеристик шестерни косозубой передачи совпадают с формулами для прямозубой. Существенные различия возникают лишь при прочностных расчетах.

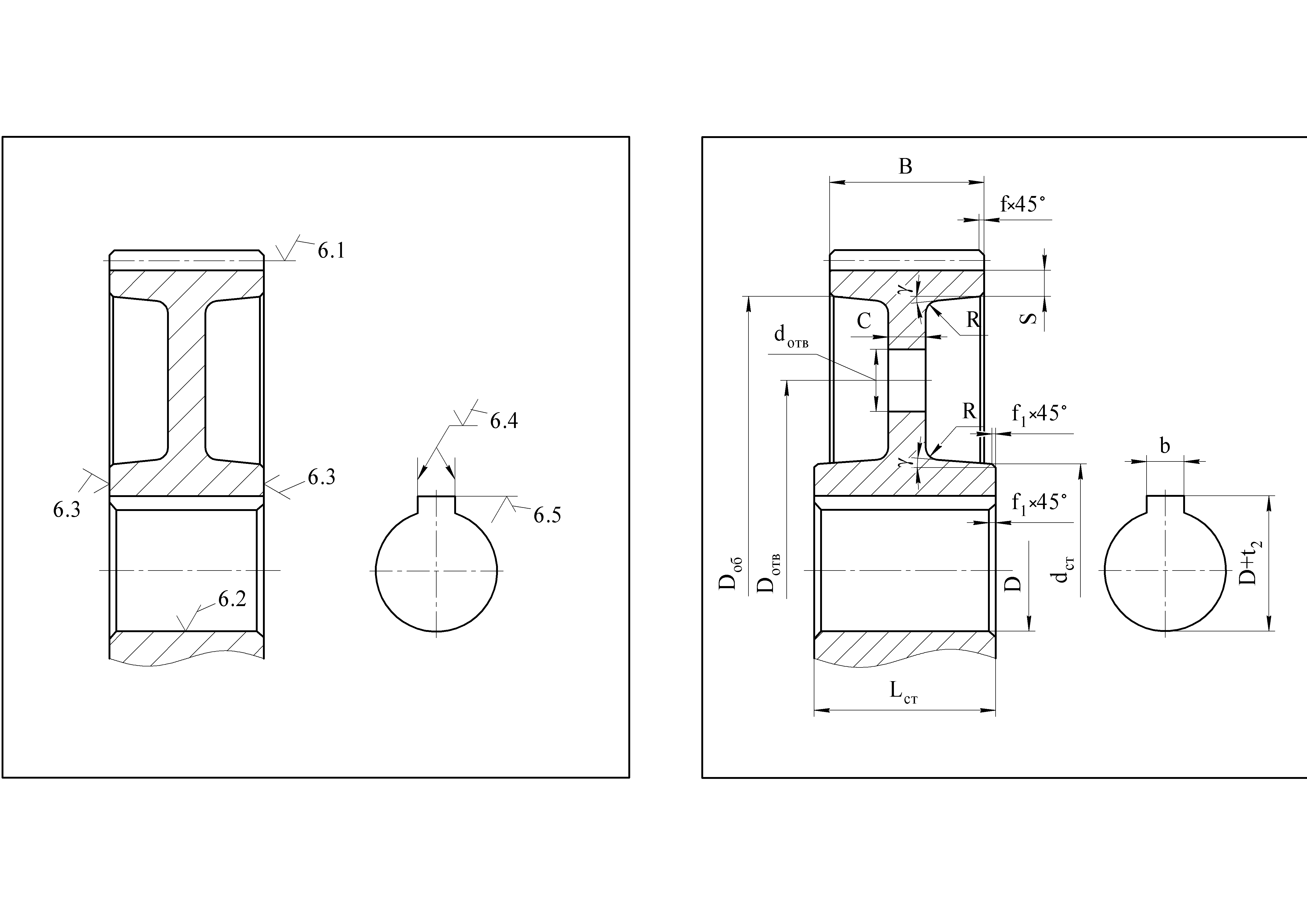
Размеры зубчатого
колеса (рис. 3.1) могут быть известны
заранее по предыдущим расчетам или
приняты по натурным образцам. Исходные
данные для расчета основных геометрических
размеров цилиндрического зубчатого
колеса приведены во второй части
методических указаний (прил. 1). Этот
расчет необходимо выполнять в следующем
порядке:

делительный диаметр
вычисляется по формуле:

,

(3.1)

где m
– модуль передачи, мм; z
– число зубьев; 
– угол наклона линии зу­ба, град;

диаметр окружности
вершин зубьев –

;

(3.2)

диаметр окружности
впадин –

;

(3.3)

диаметр посадочного
отверстия –

;

(3.4)

диаметр ступицы
–

;

(3.5)

длина ступицы –

.

(3.6)

Ширину зубчатого
венца можно принять равной величине
посадочного отверстия:

.

(3.7)

	Если окажется меньше ширины зубчатого венца B, то следует принять . Значение длины и диаметра ступицы следует согласовать со стандартными значениями, приведенными в табл. 3.1 (ГОСТ 6636-69). Толщина обода колеса рассчитывается по формуле: (3.8) Диаметр обода колеса – (3.9)
Рис. 3.1

Таблица
3.1

Нормальные линейные
размеры, мм (ГОСТ 6636-69)

3,2	5,6	10	18	32	56	100	180	320	560
3,4	6,0	10,5	19	34/35	60/62	105	190	340	600
3,6	6,3	11	20	36	63/65	110	200	360	630
3,8	6,7	11,5	21	38	67/70	120	210	380	670
4,0	7,1	12	22	40	71/72	125	220	400	710
4,2	7,5	13	24	42	75	130	240	420	750
4,5	8,0	14	25	45/47	80	140	250	450	800
4,8	8,5	15	26	48	85	150	260	480	850
5,0	9,0	16	28	50/52	90	160	280	500	900
5,3	9,5	17	30	53/55	95	170	300	530	950

Примечание.
Под косой чертой приведены размеры
посадочных мест для подшипников качения.

Диаметр окружности,
по которому располагаются центры
технологи­ческих отверстий, вычисляется
по формуле:

(3.10)

Диаметр технологических
отверстий, предназначенных для уменьшения
массы колеса и транспортировки,
принимается из интервала

Толщина диска
колеса рассчитывается по уравнению:

(3.11)

Если в результате
расчета толщина диска получилась менее
10 мм, то ее следует принять равной 10 мм.

Значения диаметра
посадочного отверстия D,
ширины зубчатого венца B,
диаметра d_ст и
длины L_ст
ступицы, диаметра обода колеса
D_об, координатного
диаметра технологических отверстий
D_отв, диаметра
технологических отверстий d_отв
и толщины диска C следует
округлять до стандартных значений из
ряда нормальных линейных размеров,
приведенных в табл. 3.1 (ГОСТ 6636-69).

На торцах зубчатого
венца выполняются фаски в зависимости
от величины делительного диаметра d
(табл. 3.2).

Таблица
3.2

Размеры фасок
торца зубчатого колеса (ГОСТ 10948-64)

d, мм	30 – 40	40 – 50	50 – 80	80 – 120	120 – 150	150 – 250
f, мм	1,2	1,6	2,0	2,5	3,0	4,0

Размер фасок
посадочного отверстия и торца ступицы
f₁ может быть принят
в соответствии с ГОСТ 12080-66 как для
цилиндрических валов в зависи­мости
от диаметра D (табл. 3.3).

Таблица
3.3

Размеры фасок
торца ступицы

D, мм	20 – 28	28 – 45	45 – 80	80 – 120	120 – 150
f1, мм	1,0	1,6	2,0	2,5	3,0

Размеры шпонки,
шпоночного паза (ширина b
и глубина t₂)
выбираются по стандарту в зависимости
от типа шпонки и диаметра отверстия:
для призматических шпонок – по ГОСТ
23360-78 [3, табл. 9.1, с. 204], сегментных – по

ГОСТ 24071-80 [3, табл. 9.3, с. 207]. Для
призматических шпонок размеры приведены
во второй части методических указаний
(прил. 2).

Для обеспечения
свободной выемки заготовки зубчатого
колеса из штампа штамповочные уклоны
 и радиусы R
закругления принимаются более 7° и

6
мм соответственно.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

 

Рисунок 3. Параметры эвольвентного зубчатого колеса.

К основным геометрическим параметрам эвольвентного зубчатого колеса относятся: модуль m, шаг p, угол профиля α, число зубьев z и коэффициент относительного смещения x.

Виды модулей: делительный, основной, начальный. 

Для косозубых колес дополнительно различают: нормальный, торцевой и осевой. 

Для ограничения числа модулей ГОСТом установлен стандартный ряд его значений, которые определяются по делительной окружности.

Модуль − это число миллиметров диаметра делительной окружности зубчатого колеса, приходящееся на один зуб.  

m =p /π

Делительная окружность − это теоретическая окружность зубчатого колеса, на которой модуль и шаг принимают стандартные значения 

d = Z · m

Делительная окружность делит зуб на головку и ножку.

Начальная окружность – это теоретическая окружность зубчатого колеса, принадлежащая его начальной поверхности.

 

Головка зуба – это часть зуба, расположенная между делительной ок-ружностью зубчатого колеса и его окружностью вершин.

Ножка зуба – это часть зуба, расположенная между делительной окружностью зубчатого колеса и его окружностью впадин.

Сумма высот головки ha и ножки hf  соответствует высоте зубьев h:

h = ha  + hf

Окружность вершин – это теоретическая окружность зубчатого колеса, соединяющая вершины его зубьев.

 d_a=d+2(h^*_a + x — Δy)m

Окружность впадин – это теоретическая окружность зубчатого колеса, соединяющая все его впадины.

 d_f = d — 2(h^*_a — C^* — x) · m

Согласно ГОСТ 13755-81 α = 20°,   С* = 0,25.

Коэффициент уравнительного смещения Δу:

Окружной шаг, или шаг p − это расстояние по дуге делительной окружности между одноименными точками профилей соседних зубьев.

p = m·π

Угловой шаг − это центральный угол, охватывающий дугу делительной окружности, соответствующий окружному шагу

 

Шаг по основной окружности − это расстояние по дуге основной ок-ружности между одноименными точками профилей соседних зубьев

p_b = p · cos α

Толщина зуба s по делительной окружности − это расстояние по дуге делительной окружности между разноименными точками профилей одного зуба

S = 0,5 · ρ + 2 · х · m · tg α

Ширина впадины e по делительной окружности − это расстояние по дуге делительной окружности между разноименными точками профилей со-седних зубьев

е = p — S

Толщина зуба Sb по основной окружности − это расстояние по дуге основной окружности между разноименными точками профилей одного зуба.

Толщина зуба Sa  по окружности вершин − это расстояние по дуге ок-ружности вершин между разноименными точками профилей одного зуба.

Угол профиля α − это острый угол между касательной t – t к профилю зуба в точке, лежащей на делительной окружности зубчатого колеса и радиус-вектором, проведенным в данную точку из его геометрического центра

 

1.1. Пример расчета прямозубого внешнего эвольвентного зубчатого зацепления.

1.2. Вычерчивание элементов зубчатого зацепления