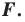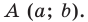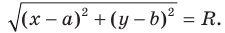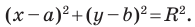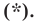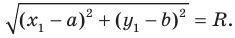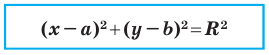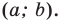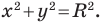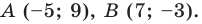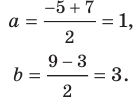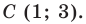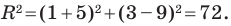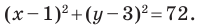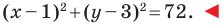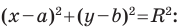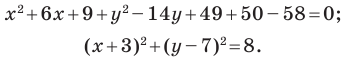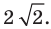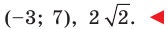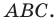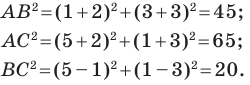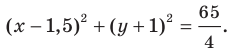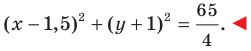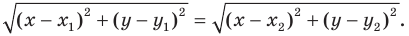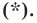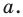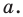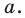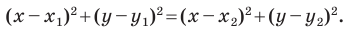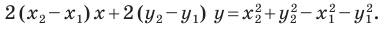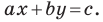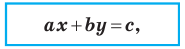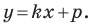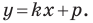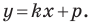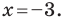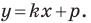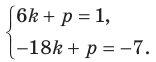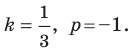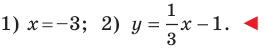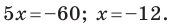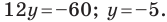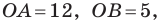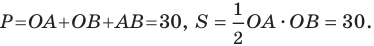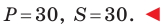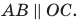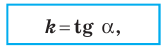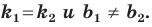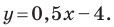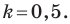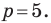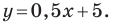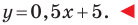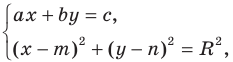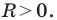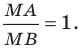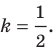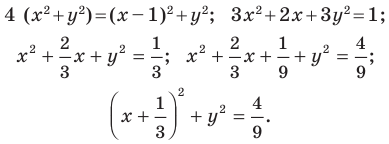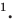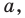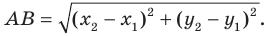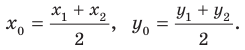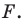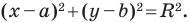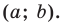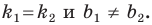Определение геодезических координат по топографической карте.
Северная
и южная линии внутренней рамки листа
топографической карты являются
параллелями, западная и восточная –
меридианами. Во всех четырех углах листа
карты подписаны значения широты и
долготы.
Между
внутренней и внешней рамками выделена
градусная рамка в виде двойной линии с
переменной заливкой белым и черным
цветами. Каждый интервал (белый или
черный) равен 1’. Этот минутный интервал
разделен с помощью точек на 10-секундные
отрезки. Если соединить аналогичные
точки на северной и южной стороне листа
получим меридиан с известной долготой.
Соответственно при соединении аналогичных
точек на западной и восточной стороне
получим параллель с известной широтой.
Чтобы
определить геодезические координаты
(широту и долготу) точки нужно через нее
провести перпендикуляры к градусной
рамке листа топографической карты (рис.
1).
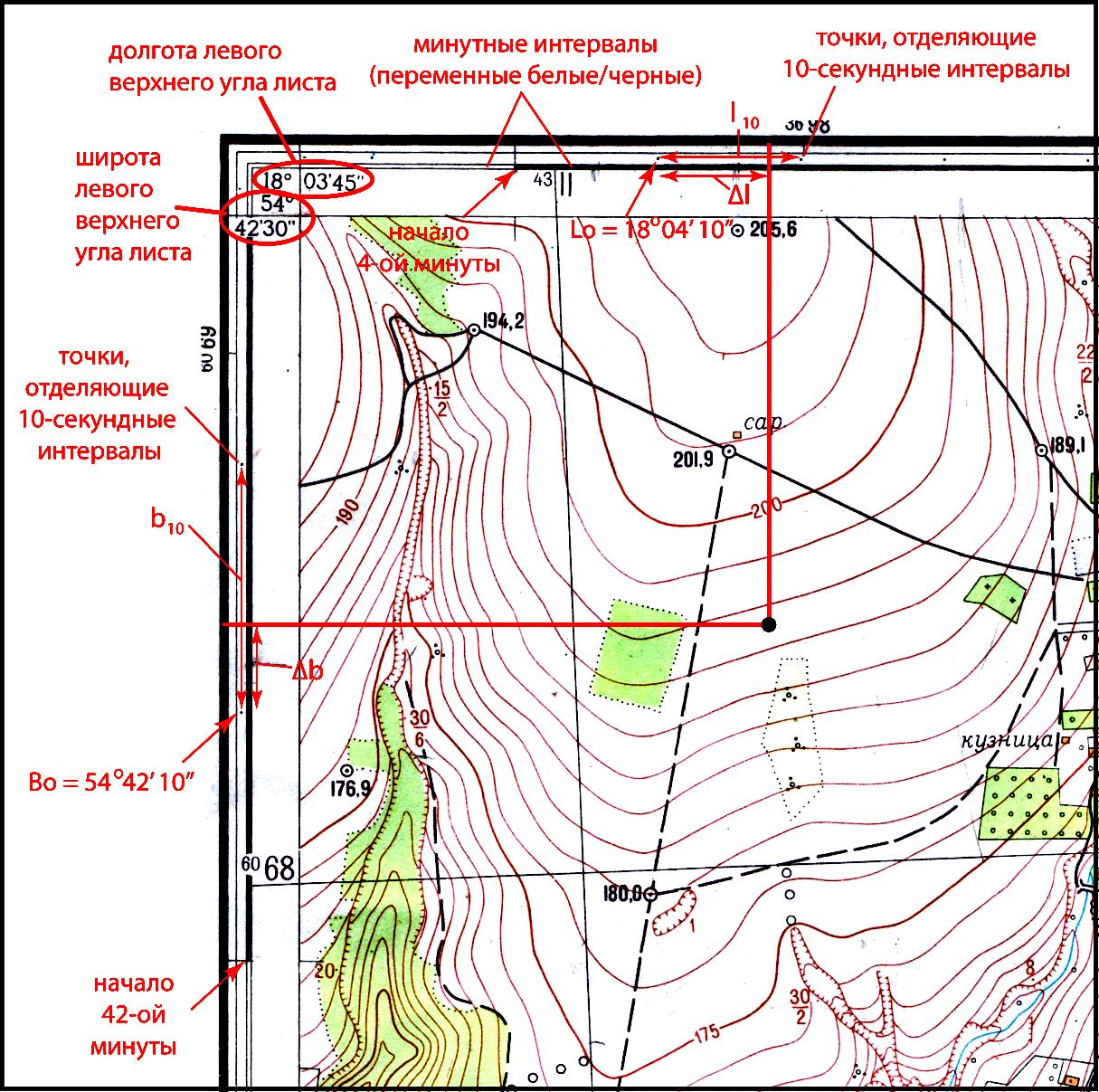
Рис.
1. Определение геодезических координат.
Проводим
перпендикуляр к западной стороне листа.
Находим пересечение с градусной рамкой.
Далее определяем широту ближайшей южной
точки, отделяющей 10-секундные интервалы
(В0).
Измеряем длину 10-секундного интервала
(b10)
и расстояние от ближайшей точки до
отметки пересечения перпендикуляра с
градусной рамкой (∆b).
Широту
заданной точки можно вычислить по
формуле B
= В0
+ (∆b
* 10’’ / b10).
Чтобы
определить долготу заданной точки,
необходимо опустить перпендикуляр на
южную сторону листа карты, определить
долготу ближайшей западной точки,
отделяющей 10-секундные интервалы (L0).
Далее процесс аналогичен предыдущему,
формула выглядит как L
= L0
+ (∆l
* 10’’ / l10).
Масштаб
– величина, характеризующая степень
уменьшения длины отрезка на местности
при его отображении на карте. На картах
масштаб указывается обязательно. Подпись
масштаба возможна в нескольких вариантах.
Численный
масштаб
представляется в виде дроби с единицей
в числителе, например, 1 : 10 000, 1 : 100 000
и т.д. Именованный масштаб
– это запись вида «в 1 сантиметре 100
метров», «в 1 сантиметре 1 километр».
Линейный
масштаб
дается в виде масштабной линейки, которая
облегчает измерение длин по топографической
карте. На топографических картах, как
правило, даются все три варианта (рис.
2).
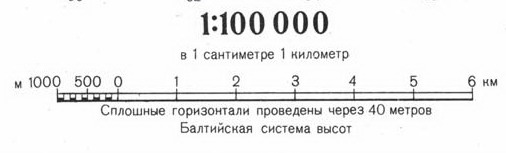
Рис.
2. – Подписи масштаба топографических
карт (сверху вниз: численный, именованный,
линейный).
К
артографическая
проекция
– математически определенный способ
изображения эллипсоида на плоскости.
В России для составления топографических
карт используют проекцию
Гаусса-Крюгера.
Это поперечно-цилиндрическая равноугольная
зональная проекция.
В
проекции Гаусса-Крюгера размер зон для
топографических карт ограничен 6-ю
градусами по долготе. Зоны располагаются
последовательно от нулевого (Гринвичского
меридиана) в направлении с запада на
восток. Т.е. 1-я зона ограничена меридианами
00
и 60
в.д., 2-я – 60
и 120
в.д., 60-я – 60
и 00
з.д.
Через
центр зоны проходит осевой
меридиан,
являющийся касательным к боковой
поверхности гипотетического цилиндра.
Таким образом, для 1-й зоны осевой меридиан
будет иметь долготу 30
в.д.,
2-й — 90
в.д. и т.д. Чтобы определить долготу
осевого меридиана по номеру зоны, можно
воспользоваться формулами:
для
восточного полушария L
= 6*n
– 3
для
западного полушария L
= 180 – 6*(n
– 30) + 3,
где
n
– номер зоны.
Прямоугольные
координаты.
На
топографических картах применяется
зональная прямоугольная система
координат. Координаты – абсцисса и
ордината – определяются в метрах. За
ось
ординат Y
принята линия экватора (рис. 3), а за ось
абсцисс X
– северное направление осевых меридианов
зон. Начало отсчета по оси ординат
смещено на 500 км к западу, чтобы исключить
отрицательные значения ординат.
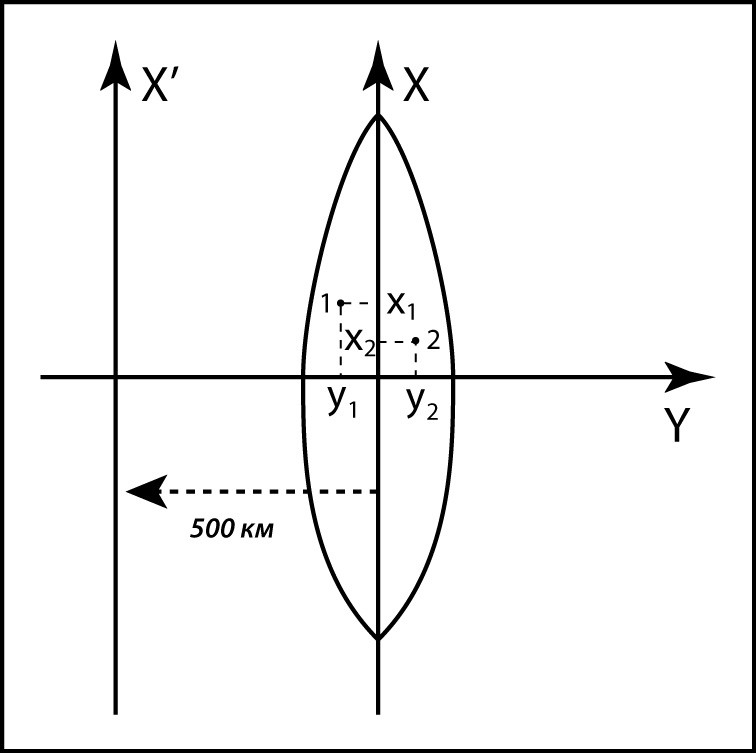
Рис.
3. Система плоских прямоугольных координат
Для
устранения неоднозначности определения
ординат, в ее состав вводится номер зоны
(первые одна или две цифры). Таким образом,
запись ординаты вида «4 312 000»
означает, что заданная точка находится
в 4-й зоне на расстоянии 312 км от смещенного
осевого меридиана (число меньше 500 км,
т.е. точка западнее осевого меридиана).
Абсцисса вида «6 066 000» означает,
что точка находится на расстоянии 6 066
км от экватора.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #

ЕГЭ-2018. География. Сдаем без проблем!
В книге содержатся материалы для успешной сдачи ЕГЭ по географии: краткие теоретические сведения по всем темам, задания разных типов и уровней сложности, методические комментарии, ответы и критерии оценивания. Учащимся не придется искать дополнительную информацию в интернете и покупать другие пособия. В данной книге они найдут все необходимое для самостоятельной и эффективной подготовки к экзамену. Издание содержит теоретические сведения по географии по всем темам, проверяемым на ЕГЭ, а также задания для самоконтроля. В конце пособия приведены ответы и комментарии. Издание окажет неоценимую помощь учащимся при подготовке к ЕГЭ по географии, а также может быть использовано учителями при организации учебного процесса.
Купить
Задание 32
(«Земля как планета, современный облик планеты Земля. Форма, размеры, движение Земли»). max 2 балла!
Тип 1. Определите, в каком из обозначенных буквами на карте Северного полушария пунктов, 20 декабря солнце раньше (по времени Гринвичского меридиана) поднимется над горизонтом. Ход ваших рассуждений запишите.
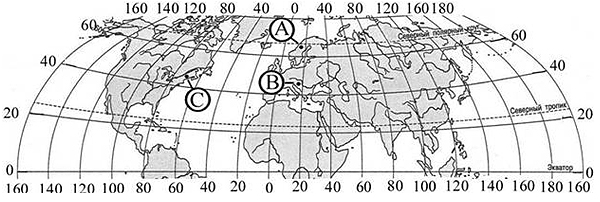
Задание 32 – одно из самых сложных в ЕГЭ по географии. По статистике, его решают менее 30% сдававших экзамен. В то же время, оно не так трудно, как кажется на первый взгляд, если точно придерживаться алгоритма его решения.
В первом из типов задания 32 необходимо найти точку, в которой солнце раньше (или позже) всего поднимется над горизонтом. Это зависит от двух факторов:
1. Долготы точки. Солнце встаёт на востоке, следовательно, чем восточнее расположена точка, тем раньше солнце будет подниматься в ней над горизонтом.
2. Широты точки. Здесь важно время года.
Летом северного полушария (с 21 марта по 23 сентября) продолжительность дня будет возрастать от Южного полюса к Северному, следовательно, чем дальше на север будет расположена точка, тем раньше там будет всходить солнце.
Зимой же всё меняется с точностью до наоборот. Продолжительность дня будет возрастать при движении на юг, следовательно, чем южнее расположена точка, тем раньше там будет всходить солнце.
В приведённом задании точки А и В расположены восточнее точки С, следовательно, в точке С солнце взойдёт позже. Так как точки А и В лежат на одном меридиане, то время восхода солнца будет зависеть от продолжительности светового дня в них. 20 декабря день будет длиннее в точке В, т.к. она лежит южнее точки А.
Следовательно, солнце раньше поднимется над горизонтом в точке B.
Алгоритм 1
(при поиске точки, где солнце взойдёт раньше всего):
- Выбираем точку(и), лежащую(ие) восточнее всего.
- Если на одном меридиане располагаются две точки, то выбираем ту, в которой продолжительность дня в данное время года больше.
Эмпирическая подсказка: примерно в 85% случаев искомая точка располагается «в вершине» угла, образуемого тремя точками. Т.е. на одной параллели с одной из точек и на одном из меридианов с другой.
Тип 2. Определите, в какой из точек, географические координаты которых указаны в таблице, 18 марта Солнце будет находиться выше всего над горизонтом в 15 часов по солнечному времени гринвичского меридиана. Запишите обоснование Вашего ответа.
|
точка |
географические координаты |
|
|
широта |
долгота |
|
|
А |
30° ю.ш. |
40° з.д. |
|
Б |
40° ю.ш. |
40° з.д. |
|
В |
30° ю.ш. |
70° з.д. |
Во втором типе задания 32 требуется найти точку, в которой солнце расположено выше всего над горизонтом. Что характерно, это также зависит от двух факторов:
1. Широты точки. Чем ближе к экватору расположена точка, тем выше в ней стоит солнце над горизонтом*.
2. Долготы точки. Чем ближе к полуденному меридиану находится точка, тем выше в ней стоит солнце над горизонтом.
Таким образом, основная сложность при выполнении этого типа задания связана с нахождением полуденного меридиана – меридиана, на котором в данный момент времени полдень. Т.к. окружность Земли составляет 360°, а в сутках 24 часа, то за один час Земля поворачивается на 360 : 24 = 15°. Следовательно, чтобы найти полуденный меридиан, нужно разницу во времени нулевого и полуденного меридиана умножить на 15°.
В приведённом задании на Гринвиче 15 часов, следовательно, разница со временем полуденного меридиана составляет 3 часа (15 – 12), а градусная мера последнего составит (15 – 12) · 15° = 45° з.д. Долгота западная потому, что полуденный меридиан лежит к западу от Гринвича (там уже три часа дня, а солнце движется с востока на запад)**.
Точки А и Б лежат ближе к полуденному меридиану, чем точка В. При этом точка А расположена ближе к экватору, следовательно, именно там солнце и будет располагаться выше всего над горизонтом.
Алгоритм 2
(при поиске точки, в которой солнце стоит выше всего над горизонтом):
- Находим точку(и), расположенную(ые) ближе всего к полуденному меридиану. Долготу полуденного меридиана рассчитываем по формуле λ = (t – 12) · 15°, где λ – долгота, t – время гринвичского меридиана. Если число отрицательное, то долгота восточная.
- Если на одном меридиане располагаются две точки, то выбираем ту, которая расположена ближе к экватору.
Эмпирическая подсказка: если вы лучше воспринимаете информацию в графическом виде, нежели чем в табличном, то нарисуйте схематически на черновике две параллели и два меридиана и расположите на их пересечениях указанные точки.
* Из этого правила есть исключения, когда точка расположена между тропиками, но такие точки практически не попадаются в заданиях ЕГЭ.
** А ёщё можно посмотреть на долготу данных точек – в 90% случаев полушария совпадают.
Тип 3. Определите географические координаты пункта, расположенного в США, если известно, что 23 сентября в 17 часов по солнечному времени Гринвичского меридиана в этом пункте полдень и солнце находится на высоте 53° над горизонтом. Ход ваших рассуждений запишите.
Этот тип задания 32 требует исключительно математических расчётов.
Для нахождения широты точки воспользуемся известной нам высотой солнца над горизонтом (он же – угол падения солнечных лучей) в полдень. В дни равноденствий* солнечные лучи падают отвесно (под 90°) на экваторе, т.е. на 0° широты. А на полюсах (90° широты) солнце находится точно на горизонте, т.е. угол падения лучей равен 0°.
Следовательно, между географической широтой и углом падения солнечных лучей наблюдается обратная зависимость, которую можно выразить формулой φ = 90°– α, где φ – широта точки, α – угол падения солнечных лучей в полдень в дни равноденствия.
Чтобы найти долготу точки, нам потребуется выполнить вычисления, аналогичные таковым для типа 2, т.е. найти полуденный меридиан, градусная мера которого и будет долготой искомой точки, по формуле λ = (t – 12) · 15°, где λ – долгота точки, t – время гринвичского меридиана.
В данном задании широта составит φ = 90° – 53° = 37° с.ш. Широта северная только потому, что точка, как мы помним, расположена на территории США.
Долгота точки будет равна λ = (17 – 12) · 15° = 75° з.д., долгота западная потому, что время в данной точке отстаёт от Гринвича.
Алгоритм 3
(при поиске координат точки, для которой известна высота полуденного солнца и разница во времени с Гринвичем):
- Находим широту точки, используя формулу φ = 90° – α, где φ – широта точки, α – угол падения солнечных лучей в полдень в дни равноденствия.
- Находим долготу точки по формуле λ = (t – 12) · 15°, где λ – долгота точки, t – время гринвичского меридиана. Если число отрицательное, то долгота восточная.
- Записываем полученные координаты с указанием значения широты и долготы.
* В этом типе заданий дело происходит либо 23 сентября, либо 21 марта, т.е. в дни равноденствий.

ЕГЭ-2018. География. Тематические тренировочные задания
Пособие содержит задания, максимально приближенные к реальным, используемым на ЕГЭ, но распределенные по темам в порядке их изучения в 10-11-х классах старшей школы. Работая с книгой, можно последовательно отработать каждую тему, устранить пробелы в знаниях, а также систематизировать изучаемый материал. В конце пособия приводятся тренировочные варианты, благодаря которым можно ознакомиться со структурой экзаменационного теста, выполнить его на время и сразу же проверить ответы. Такая структура книги поможет эффективнее подготовиться к ЕГЭ. Это издание адресовано учащимся старших классов для подготовки к ЕГЭ по географии. Тренировочные задания позволят систематически, при прохождении каждой темы, готовиться к экзамену.
Купить
Система координат — комплекс определений, реализующий метод координат, то есть способ определять положение и перемещение точки или тела с помощью чисел или других символов. Совокупность чисел, определяющих положение конкретной точки, называется координатами этой точки. В математике координаты — совокупность чисел, сопоставленных точкам многообразия в некоторой карте определённого атласа.
Координаты на прямой
Если на прямой задано направление, то такую прямую называют направленной, а выбранное направление — положительным. Например, на горизонтальной прямой можно отметить направление вправо, тогда будем говорить, что направленная прямая имеет положительное направление вправо. Можно с таким же правом считать положительным и направление влево. Направление прямой будем указывать стрелкой (рис. 1).
Выберем на направленной прямой точку, которую назовем началом отсчета или началом координат, и будем обозначать ее буквой О.
Кроме того, выберем отрезок, длину которого будем считать единицей длины. Этот отрезок назовем единицей масштаба.
Определение:
Прямая линия, на которой указаны: начало отсчета, единица масштаба и направление отсчета, называется осью координат.
Рассмотрим отрезок, расположенный на оси координат. Если одну из точек, ограничивающих отрезок, назовем началом отрезка, а другую—его концом, то отрезок будем называть направленным отрезком. Направленный отрезок обозначают двумя буквами, например: АВ, СМ, КР, причем на первом месте ставят букву, обозначающую начало, на втором—букву, обозначающую конец. Таким образом, запись АВ показывает, что начало отрезка есть точка А, а конец — точка В. Направление отрезка считается от начала к концу.
Если направление отрезка совпадает с направлением оси, то отрезок называют положительно направленным; если же его направление противоположно направлению оси, то — отрицательно направленным. Таким образом, отрезки АВ и ВА имеют противоположные направления. Это записывают так:
Отметим, что положительный отрезок может находиться в любом месте координатной оси, только его направление должно совпадать с направлением оси.
Сложение направленных отрезков производится по следующему правилу:
Для того чтобы сложить два направленных отрезка, нужно к концу первого приложить начало второго; тогда отрезок, имеющий началом начало первого отрезка и концом конец второго, называют суммой двух направленных отрезков.
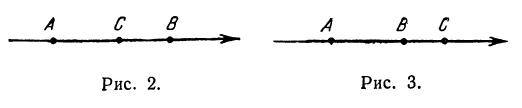
Из этого определения вытекает, что сумма отрезков АВ и ВС равна отрезку АС при любом расположении точек А, В, С, т. е. всегда:
(рис. 2 и 3).
Координатным отрезком точки А называется направленный отрезок, имеющий начало в точке О (т. е. в начале координат), а концом — рассматриваемую точку А.
Всякий направленный отрезок, лежащий на оси, можно выразить через координатные отрезки его начала и конца. В самом деле, рассмотрим направленный отрезок АВ. На основании равенства (2) можно написать
(здесь вместо точки В поставлена точка О, а вместо точки С точка В) или
Отрезок ОВ есть координатный отрезок (его начало есть точка О), но отрезок АО не является координатным, поскольку его начало не является началом координат. Но в силу равенства (1)
поэтому можно написать
Получен следующий результат:
Направленный отрезок равен разности координатного отрезка его конца и координатного отрезка его начала.
Это верно для любого отрезка, лежащего на координатной оси.
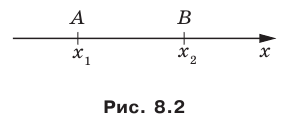
Теперь дадим одно из самых важных определений: Координатой точки на координатной оси называется число, равное по абсолютной величине длине координатного отрезка этой точки и по знаку совпадающее со знаком координатного отрезка.
Точку А, имеющую координатной число х, будем обозначать А (х).
Указанные на рис. 4 точки имеют следующие координаты:
Будем также писать
Если даны точки А(х1) и В(х2), то на основании формул (3) и (4) получим
т. е. направленный отрезок равен разности координат его конца и начала.
Отсюда сразу получаем, что длина отрезка равна абсолютной величине разности координат его конца и начала.
Длину отрезка будем обозначать, пользуясь знаком | |, т. е. знаком абсолютной величины. Таким образом, длина отрезка АВ будет записываться так:
Пример:
Если даны точки А (+4), В (+8), то отрезок АВ = (+8) — (+4), а его длина |АВ|= |+ 4 | = 4.
Если даны точки М (+5) и Р (+3), то отрезок МР = (+3)—(+5) = —2, а его длина |МР| = | —2| = 2. Даны две точки: Q (+ 3) и S (—4). Длина отрезка
Даны две точки R (— 6) и Т (—2); отрезок RТ = ( — 2) — (—6) = +4, а его длина | RТ | = 4.
Пример:
Начало отрезка АВ находится в точке А (—950), а конец—в точке В ( —1200); найти его направление и длину.
Отрезок АВ = ( — 1200)—( — 950) = —250. Так как он
получился отрицательным, то его направление противоположно направлению оси. Его длина равна | АВ | = | —250 | = 250.
Задача:
На координатной оси даны две точки: A (x1) и В (x2) Найти точку С, лежащую между ними и делящую отрезок АВ в отношении т : п.
Чтобы найти точку, надо найти ее координату. По условию задачи должно быть
Обозначая координату искомой точки С через х и выражая отрезки через координаты, т. е. применяя формулу (5), получим, что АС = х—х1, СВ = х2 — х. Подставляя эти выражения в равенство (6), будем иметь
Решая последнее уравнение относительно х, найдем:
Это и есть координата искомой точки.
Пример:
Найти точку С, делящую отрезок АВ в отношении 1:2, если даны начало отрезка А (+ 3) и конец В ( + 5) (рис. 5).
Здесь т = 1, п = 2, х1=-3, х2 = 5. Применяя формулу (7), получим
Пример:
Найти точку М, делящую расстояние между точками Р ( — 2) и Q (—9) в отношении 3:4 (рис. 5). Здесь т = 3, п = 4, х1 = —2, х2 = —9. По формуле (7) находим
Если т = n т. е. точка С делит отрезок АВ пополам, тогда формула (7) перепишется так:
Таким образом, координата точки, делящей отрезок пополам, равна средней арифметической координат его начала и конца.
Пример:
Найдем середину отрезка, заключенного между точками А (—6) и B (4) (рис. 6).
Применяя формулу (8), получим, что
Координаты на плоскости
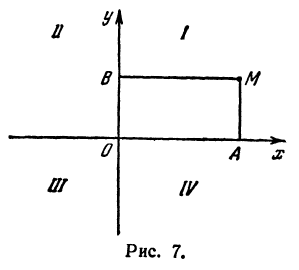
Возьмем на плоскости две взаимно перпендикулярные прямые, пересекающиеся в точке О. На каждой из этих прямых зададим направление, указав его стрелкой (рис. 7).
Установим масштаб, общий для обеих прямых, а за начало отсчета выберем точку О.
Определение:
Координатными осями на плоскости называются две взаимно перпендикулярные прямые, на которых установлены: 1) на-правления, 2) масштаб и 3) общая точка отсчета.
Назовем одну из осей осью Ох или осью абсцисс, другую — осью Оу или осью ординат. Точку их пересечения назовем началом координат.
Возьмем произвольную точку M, лежащую на плоскости, и опустим из нее перпендикуляры на оси координат, т. е. найдем ее проекции на оси. Обозначим проекцию на ось Ох через А, а проекцию на ось Оу через В. Обозначим координату точки А (по оси Ох) через х, а координату точки В (по оси Оу) через у. Введем определение:
Определение:
Абсциссой точки называется координата ее проекции на ось Ох. Ординатой точки называется координата ее проекции на ось Оу.
Абсциссу точки обычно обозначают буквой х, ординату— буквой у. Точку М, имеющую абсциссу х и ординату у, обозначают следующим образом: пишут скобку и в ней на первом месте ставят абсциссу, на втором ординату и разделяют эти два числа запятой или точкой с запятой. Таким образом, запись точки выглядит так: М(х, у).
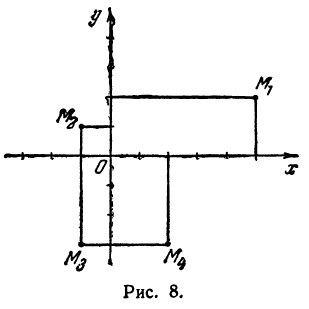
Координатные оси разделяют плоскость на четыре части, которые называют четвертями.
Первой четвертью называется та часть плоскости, в которой абсцисса и ордината положительны.
Второй четвертью — та часть, в которой абсцисса отрицательна, а ордината положительна.
Третьей четвертью — та часть, в которой абсцисса и ордината отрицательны, и, наконец, четвертой, — та часть, в которой абсцисса положительна, а ордината отрицательна (рис. 7), На рис. 8 указаны точки M1 (5, 2), М2 ( — 1, 1), М3 (-1, -3), М4 (2, -3). Заметим, что абсцисса х = ОА по абсолютной величине равна расстоянию точки от оси ординат, так как ОА = ВМ (см. рис. 7), а ордината — расстоянию точки М от оси абсцисс, так как ОВ = АМ.
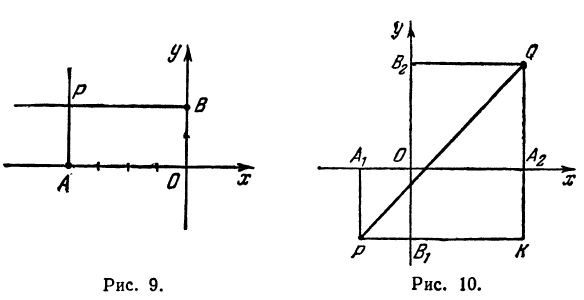
Пример:
Найти точку Р( — 4, 2) (рис. 9), Возьмем на оси Ох точку А с координатой —4, ее координатный отрезок ОА = —4. На оси Оу возьмем точку В с координатным отрезком ОВ= 2. Восставим перпендикуляры к осям из точек А и В, точка их пересечения и даст искомую точку Р.
Задача:
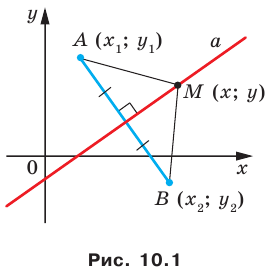
Найти расстояние между точками Р (х1, у1) и Q( х1, у1 ). Иначе говоря, нужно найти длину отрезка РQ(рис. 10).
Обозначим проекцию точки Р на ось Ох через А1, а ее проекцию на ось Оу — через В1. Проекцию точки Q на ось Ох обозначим через А2 и через В2— ее проекцию на ось Oy. Тогда ОА1 = х1, ОВ1 = y1, ОА2 = х2, ОВ2 = у2. Из точки Р проведем прямую, параллельную оси Ох, до пересечения с прямой A2Q в точке К. Рассмотрим треугольник PKQ. По теореме Пифагора имеем
Но РК = А1А2, KQ = B1B2, как противоположные стороны прямоугольников; кроме того, на основании формулы (3 из § 1) направленные отрезки А1А2 и В1В2 будут равны
Подставляя полученные выражения в (*), получим
откуда
т. е. расстояние между двумя точками равно корню квадратному из суммы квадратов разностей координат.
Примечание:
Расстояние между двумя точками, так же как длина отрезка, всегда положительно, поэтому в формуле (1) перед квадратным корнем берут только знак плюс.
Пример:
Найти расстояние между точками Р (— 2, — 1) и Q (2, 2). Применяя формулу (1), получим
Пример:
Найти длину отрезка MN, если даны М (8, 2) и N(2, 10). Применяя формулу (1), получим
Задача:
Найти точку С, делящую отрезок PQ в отношении т : п, если известны координаты точек Р (х1, у1) и Q (х2, у2). По условию задачи надо найти такую точку С, чтобы было выполнено равенство
Решение:
Обозначим, как и выше, проекции точки Р на оси через А1 и В1, а проекции точки Q—через А2 и В2; тогда ОА1 = х1 , OB1 = y1, ОА2 =х2, ОВ2=у2 (рис. 11). Кроме того, обозначим координаты искомой точки С через х и у, а ее проекции на оси — через А и В, т. е. ОА = х, ОВ = у.
Так как прямые А1Р, АС и А2Q параллельны между собой, то на основании теоремы о пропорциональных отрезках можно записать, что
Но А1А = ОА — ОА1 = х—х1, АА2 = ОА2 — ОА = х2—х; поэтому, подставляя в равенство (*), будем иметь уравнение
решая которое найдем абсциссу точки С:
Рассуждая аналогично о проекциях на ось Оу, т. е. о точках В1, В и В2, получим ординату точки С, делящей отрезок в отношении т : п,
Итак, искомая точка С имеет координаты, определяемые равенствами (2) и (3).
Пример:
Найти точку, делящую в отношении 1:2 отрезок PQ, где Р (4, —3) и Q (8, 0). Здесь х1 = 4, у1 = — 3, х2 = 8, у2 = 0, т = 1, п = 2. Применяя формулы (2) и (3), получим:
Пример:
Найти точку, делящую расстояние между точками А (4, 2) и B (8, 10) в отношении 3 : 1. Здесь х1=-4, у1 = 2, х2 = 8, у2= 10, т = 3, п = 1. По формулам (2) и (3) находим:
Следствие (из формул (2) и (3)). Если точка С делит отрезок РQ пополам, то т = n, поэтому
т. е. абсцисса середины отрезка равна средней арифметической абсцисс его начала и конца; ордината середины отрезка равна средней арифметической ординат его начала и конца.
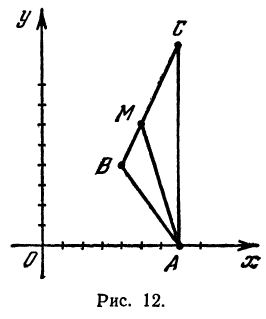
Задача:
Даны три вершины треугольника: А (7, 0), В (4, 4) и С (7, 10). Найти длину биссектрисы угла A (рис. 12).
Найдем длины сторон АВ и АС. Для этого применим формулу (1):
Обозначим точку пересечения биссектрисы угла А с противоположной стороной ВС через М, а ее координаты—через х и у. Помня, что биссектриса внутреннего угла треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам, можно утверждать, что точка М делит отрезок ВС в отношении 5 : 10 = 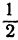
т. е. М (5, 6).
Теперь вычисляем длину биссектрисы между точками А(7, 0) и М(5, 6):
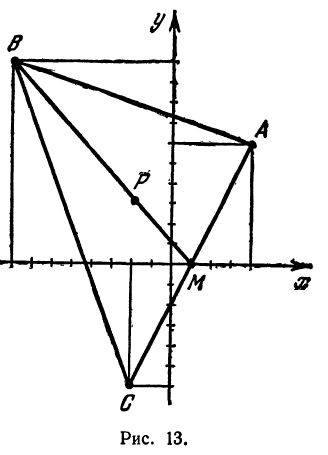
Задача:
Найти точку пересечения медиан треугольника, вершинами которого являются точки А(4, 6), В(—8, 10), С( —2, —6) (рис. 13).
Точка пересечения медиан делит каждую из медиан в отношении 2:1, считая от вершины треугольника. Обозначим через М середину стороны АС; по формулам (4) и (5) можно найти ее координаты:
т. е. М(19 0). Точка Р пересечения медиан делит отрезок ВМ в отношении 2:1, поэтому ее координаты найдутся по формулам (2)
и (3):
Итак, искомая точка
Задача:
Записать условие того, что точка М (х, у) находится на расстоянии По формуле (1) имеем
или, возводя обе части равенства в квадрат, получим
Это равенство есть уравнение с двумя неизвестными х и у. Этому уравнению удовлетворяют координаты любой точки, лежащей на расстоянии 5 от точки С. Иначе говоря, ему удовлетворяют координаты любой точки, принадлежащей геометрическому месту точек, расстояние которых от точки С равно 5. Это геометрическое место есть окружность.
Следовательно, можно сказать, что уравнение (*) есть уравнение окружности с центром в точке С и радиуса 5.
В следующих главах будут рассмотрены уравнения с двумя неизвестными х и у и те линии (геометрические места), точки которых имеют координаты, удовлетворяющие этим уравнениям.
Числовая ось
Числовой осью называют направленную прямую, на которой указывается начальная точка О и задается некоторый «эталон» длины Е. Каждой точке 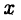
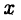
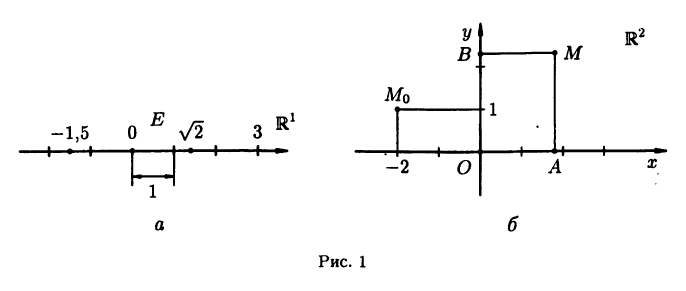
длине со знаком минус — в противном случае (см. рис. 1 а). Числовую ось будем обозначать 
Указанное соответствие между точками числовой оси 
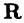
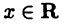
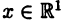
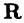

Декартова система координат
Декартовой (прямоугольной) системой координат на плоскости называют две взаимно перпендикулярные числовые оси 
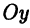

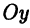
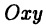
Пусть М — произвольная точка координатной плоскости. Опустим из нее перпендикуляры МА и МВ на оси 
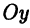
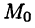
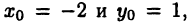
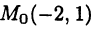
Полярная система координат
В плоскости зададим луч 
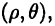
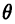

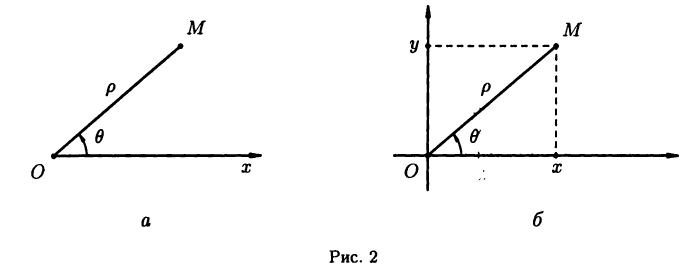
Полярные и декартовы координаты, заданные на одной плоскости (см. рис. 2 6), связаны очевидными равенствами:
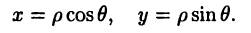
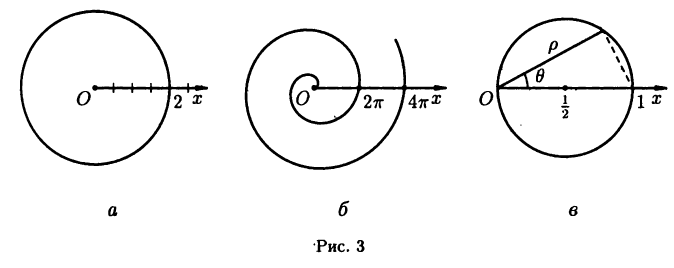
Полярные координаты удобны для задания многих кривых. Например, уравнение р=2 описывает окружность, изображенную на рис. За. Уравнение 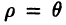
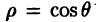
Системы координат в пространстве
Декартова система координат в пространстве определяется тремя взаимно перпендикулярными осями 
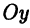
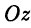
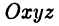
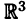
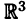
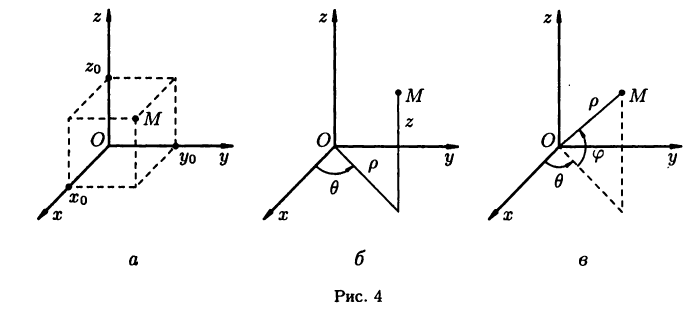
Аналогами полярной системы координат в пространстве служат цилиндрическая и сферическая системы координат.
Цилиндрическая система координат (рис. 4 б) представляет собой объединение полярной системы координат в плоскости 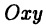
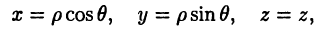
где
Сферическая система координат (рис. 4 в) связана с декартовой системой равенствами
где
Пространство
Пространство
На плоскости и в пространстве положение точки в декартовых координатах полностью определяется соответственно, парой и тройкой чисел вида [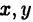
Упорядоченную систему из 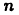

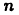
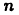
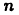
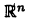
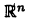
Понятие пространства 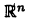
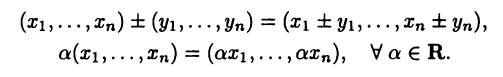
Наконец, обобщая известную из аналитической геометрии формулу, определяют расстояние между двумя точками 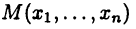
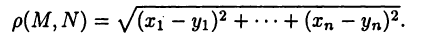
Прямую, плоскость и пространство можно рассматривать как пространства 

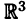
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
Каждое место на земле может быть идентифицировано глобальной системой координат широты и долготы. Зная эти параметры, легко найти любое местоположение на планете. В этом вот уже несколько столетий подряд помогает людям система координат.
Исторические предпосылки возникновения географических координат
Когда люди стали путешествовать на большие расстояния по пустыням и морями, им нужен был способ зафиксировать свое положение и знать, в каком направлении двигаться, чтобы не заблудиться. Прежде чем появились широта и долгота на карте, финикийцы (600 г. до н. э.) и полинезийцы (400 г. н. э.) использовали звездное небо для вычисления широты.
На протяжении веков были разработаны довольно сложные устройства, такие как квадрант, астролябия, гномон и арабский камаль. Все они использовались для измерения высоты солнца и звезд над горизонтом и тем самым измерения широты. И если гномон — это всего лишь вертикальная палка, которая бросает тень от солнца, то камаль — очень своеобразное приспособление.
Лондон – столица Королевства Великобритания, одного из самых влиятельных государств мира в…
Он состоял из прямоугольной деревянной дощечки размером 5,1 на 2,5 см, к которой через отверстие в середине была прикреплена веревка с несколькими одинаково расположенными узлами.
Этими инструментами определяли широту даже после изобретения магнитного компаса, до того времени, пока не изобрели надежный метод определения широты и долготы на карте.
Навигаторы на протяжении сотен лет не имели точного представления о местоположении из-за отсутствия понятия значения долготы. В мире не существовало точного устройства времени, такого как хронометр, поэтому расчет долготы был просто невозможным. Не удивительно, что ранняя навигация была проблематичной и часто приводила к кораблекрушениям.
Без сомнения, пионером революционной навигации был капитан Джеймс Кук, который путешествовал по просторам Тихого океана благодаря техническому гению Генри Томасу Харрисону. В 1759 году Харрисон разработал первые навигационные часы. Сохраняя точное среднее время по Гринвичу, часы Харрисона позволяли морякам определить, сколько часов было в точке нулевого меридиана и в точке нахождения, после чего стало возможным определить долготу от востока до запада.
Архипелаг Кергелен – это группа, состоящая из 301 острова, самым большим из которых считается…
Географическая система координат
Географическая система координат определяет двумерные координаты, основанные на поверхности Земли. Он имеет угловую единицу измерения, первичный меридиан и экватор с нулевой широтой. Земной шар условно разделен на 180 градусов широты и 360 градусов долготы. Линии широты размещаются параллельно экватору, на карте они горизонтальные. Линии долготы соединяют Северный и Южный полюса, на карте они вертикальные. В результате наложения образовываются географические координаты на карте — широта и долгота, с помощью которых можно определить положение на поверхности Земли.
Эта географическая сетка дает уникальную широту и долготу для каждой позиции на Земле. Чтобы повысить точность измерений, они дополнительно подразделяются на 60 минут, а каждая минута — на 60 секунд.
Определение широты
Экватор расположен под прямым углом к оси Земли, примерно посередине между Северным и Южным полюсами. При угле 0 градусов он используется в географической системе координат как отправная точка для вычисления широты и долготы на карте.
Точкой отсчета долготы является нулевой, или Гринвичский, меридиан. Но так было не всегда….
Широта определяется как угол между экваториальной линией центра Земли и местоположением ее центра. Северный и Южный полюс имеют угол ширины 90. Чтобы отличить места в Северном полушарии от Южного полушария, ширина дополнительно предоставляется в традиционном написании с N для севера или S для юга.
Земля наклонена примерно на 23,4 градуса, поэтому, чтобы найти широту в летнее солнцестояние, нужно добавить 23,4 градуса к углу, который измеряют.
Как определить широту и долготу на карте во время зимнего солнцестояния? Для этого нужно вычесть 23,4 градуса от угла, который измеряется. А в любой другой промежуток времени нужно определить угол, зная, что он изменяется на 23,4 градуса каждые шесть месяцев и, следовательно, около 0,13 градуса в день.
В северном полушарии можно рассчитать угол наклона Земли и, следовательно, широту, взглянув на угол Полярной звезды. На Северном полюсе он будет на 90 от горизонта, а на экваторе он будет прямо впереди наблюдателя, 0 градусов от линии горизонта.
Важные широты:
- Северный и Южный полярные круги, каждый находится на 66 градусе 34 минуты северной и, соответственно, южной широты. Эти широты ограничивают области вокруг полюсов, где солнце не устанавливается в летнее солнцестояние, поэтому там преобладает полуночное солнце. В зимнее солнцестояние солнце здесь не поднимается, наступает полярная ночь.
- Тропики находятся на 23 градусе 26 минуте в северной и южной широтах. Эти широтные круги отмечают солнечный зенит летним солнцестоянием северного и южного полушария.
- Экватор лежит на широте 0 градусов. Экваториальная плоскость проходит примерно в середине оси Земли между северным и южным полюсами. Экватор – это единственный круг широты, соответствующий окружности Земли.
Определение долготы
Широта и долгота на карте – важные географические координаты. Долготу намного сложнее рассчитать, чем широту. Земля вращается на 360 градусов в день, или 15 градусов в час, поэтому существует прямая связь между долготой и временем, когда солнце поднимается и опускается. Гринвичский меридиан обозначается 0 градусом долготы. Солнце устанавливает час раньше каждые 15 градусов к востоку от этого и на час позже через каждые 15 градусов на запад. Если знать разницу между временем заката местоположения и другим известным местом, то можно понять, как далеко от него находится восток или запад.
Линии долготы проходят с севера на юг. Они сходятся на полюсах. И координаты долготы находятся между -180 и +180 градусами. Гринвичский меридиан является нулевой линией долготы, которой измеряют направление «восток-запад» в системе географических координат (таких как широта и долгота на карте). Фактически нулевая линия проходит через Королевскую обсерваторию в Гринвиче (Англия). Гринвичский меридиан как нулевой является отправной точкой для расчета долготы. Долгота задается как угол между центром нулевого меридиана центра Земли и центром центра Земли. Гринвичский меридиан имеет угол 0, а противоположная долгота, вдоль которой проходит линия даты, имеет угол 180 градусов.
Как найти широту и долготу на карте?
Определение точного географического положения на карте зависит от ее масштаба. Для этого достаточно иметь карту с масштабом 1/100000, или лучше — 1/25000.
Вначале определяют долготу D по формуле:
D =G1 + (G2 — G1) * L2 / L1,
где G1, G2 – величина правого и левого ближайших меридианов в градусах;
L1 – расстояние между этими двумя меридианами;
L2 – расстояние от точки определения к левому ближайшему.
Расчет долготы, например, для г. Москвы:
G1 = 36°,
G2 = 42°,
L1 = 252,5 мм,
L2 = 57,0 мм.
Искомая долгота = 36 + (6) * 57,0 / 252,0 = 37° 36′.
Определяем широту L, она определяется по формуле:
L =G1 + (G2 — G1) * L2 / L1,
где G1, G2 – величина нижней и верхней ближайшей широты в градусах;
L1 – расстояние между этими двумя широтами, мм;
L2 – расстояние от точки определения к левому ближайшему.
Например, для г. Москвы:
G1 = 56°,
G2 = 52°,
L1 = 371,0 мм,
L2 = 320,5 мм.
Искомая ширина L = 52 ‘+ (4) * 273,5 / 371,0 = 55 ° 45.
Проверяем правильность вычисления, для этого надо по онлайн-сервисам в интернете найти координаты широты, долготы по карте.
Устанавливаем, что географические координаты для г. Москвы соответствуют проведенным вычислениям:
- 55° 45′ 07″ (55° 45′ 13) северной широты;
- 37° 36′ 59″ (37° 36′ 93) восточной долготы.
Определение координат местонахождения с помощью iPhone
Ускорение темпа научно-технического прогресса на современном этапе привело к революционным открытиям мобильной техники, с помощью которой стало доступным быстрое и более точное определение географических координат.
Для этого существуют различные мобильные приложения. В телефонах iPhone это очень легко сделать с использованием приложения Compass.
Порядок определения:
- Для этого нажмите «Настройки», а затем — «Конфиденциальность».
- Теперь нажмите «Службы местоположения» на самом верху.
- Прокрутите вниз до тех пор, пока вы не увидите компас и не коснетесь его.
- Если вы видите, что он сообщает «При использовании на правой стороне», можно начинать определение.
- Если нет, коснитесь его и выберите «При использовании приложения».
- Откройте приложение Compass, и вы увидите свое текущее местоположение и текущие координаты GPS в нижней части экрана.
Определение координат в телефоне Android
К сожалению, Android не имеет официального встроенного способа получить GPS-координаты. Тем не менее есть возможность получить координаты Google Maps, что требует некоторых дополнительных шагов:
- Откройте Google Maps на устройстве Android и найдите необходимую точку определения.
- Нажмите и удерживайте ее в любом месте экрана и перенесите на Карты Google.
- В нижней части появится информационная или подробная карта.
- Найти опцию Share на информационной карте в верхнем правом углу. Это вызовет меню с опцией Share.
Такую настройку можно выполнить в Google Maps на iOS.
Это отличный способ получить координаты, который не требует устанавливать какие-либо дополнительные приложения.
Содержание:
Декартовы координаты на плоскости:
Изучая материал этой лекции, вы расширите свои знания о координатной плоскости.
Вы научитесь находить длину отрезка и координаты его середины, зная координаты его концов.
Сформируете представление об уравнении фигуры, выведете уравнения прямой и окружности.
Ознакомитесь с методом координат, позволяющим решать геометрические задачи средствами алгебры.
Расстояние между двумя точками с заданными координатами. Координаты середины отрезка
В 6 классе вы ознакомились с координатной плоскостью, то есть с плоскостью, на которой изображены две перпендикулярные координатные прямые (ось абсцисс и ось ординат) с общим началом отсчета (рис. 8.1). Вы умеете отмечать на ней точки по их координатам и наоборот, находить координаты точки, отмеченной на координатной плоскости.
Договорились координатную плоскость с осью
Координаты точки на плоскости 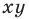
Вы знаете, как находить расстояние в между двумя точками, заданными своими координатами на координатной прямой. Для точек 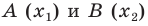
Научимся находить расстояние между точками 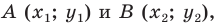
Рассмотрим случай, когда отрезок 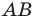
Через точки 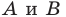
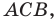
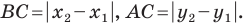
Тогда формулу расстояния между точками 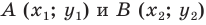
Докажите самостоятельно, что эта формула остается верной и для случая, когда отрезок 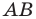
Пусть 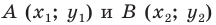
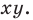
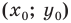
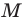
Рассмотрим случай, когда отрезок 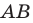
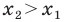
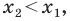
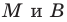
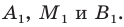
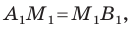
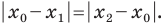
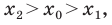
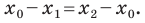

Формулы для нахождения координат середины отрезка остаются верными и для случая, когда отрезок 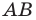
Пример №1
Докажите, что треугольник с вершинами в точках 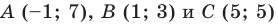
Решение:
Используя формулу расстояния между двумя точками, найдем стороны данного треугольника:
Следовательно, 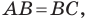
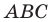
Поскольку 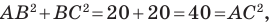
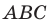
Пример №2
Точка 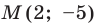
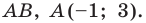
Решение:
Обозначим 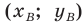
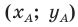
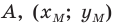
Поскольку 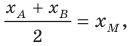
Аналогично
Ответ:
Пример №3
Докажите, что четырехугольник 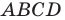
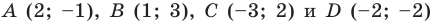
Решение:
Пусть точка 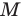
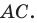
Следовательно,
Пусть точка 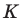
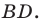
Следовательно,
Таким образом, точки 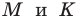
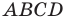
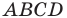
Найдем диагонали параллелограмма:
Следовательно, диагонали параллелограмма 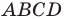
Уравнение фигуры. Уравнение окружности
Из курса алгебры 7 класса вы знаете, какую фигуру называют графиком уравнения. В этом пункте вы ознакомитесь с понятием уравнения фигуры.
Координаты 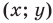
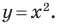
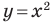
Определение. Уравнением фигуры 
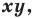
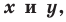
- если точка принадлежит фигуре
то ее координаты являются решением данного уравнения;
- любое решение
данного уравнения является координатами точки, принадлежащей фигуре
Например, уравнение прямой, изображенной на рисунке 9.2, имеет вид 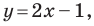
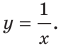
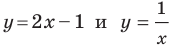
Если данное уравнение является уравнением фигуры 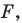
Пользуясь этими соображениями, выведем уравнение окружности радиуса 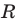
Пусть 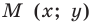
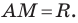
Отсюда
Мы показали, что координаты 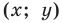
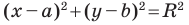
Пусть пара чисел 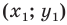
Тогда 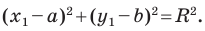
Это равенство показывает, что точка 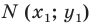
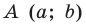
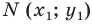
Итак, мы доказали следующую теорему.
Теорема 9.1. Уравнение окружности радиуса 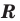
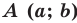
Верно и такое утверждение: любое уравнение вида 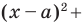
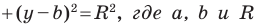
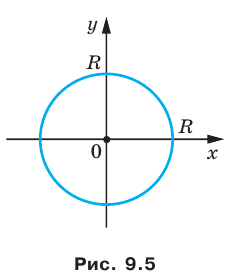
Если центром окружности является начало координат (рис. 9.5), то 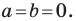
Пример №4
Составьте уравнение окружности, диаметром которой является отрезок 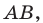
Решение:
Поскольку центр окружности является серединой диаметра, то можем найти координаты 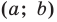
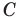
Следовательно,
Радиус окружности 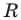
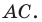
Следовательно, искомое уравнение имеет вид
Ответ:
Пример №5
Докажите, что уравнение 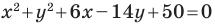
Решение:
Представим данное уравнение в виде
Следовательно, данное уравнение является уравнением окружности с центром в точке 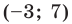
Ответ:
Пример №6
Докажите, что треугольник с вершинами в точках 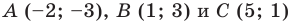
Решение:
Найдем квадраты сторон данного треугольника:
Поскольку 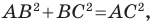
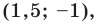
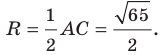
Ответ:
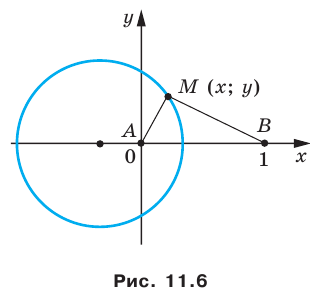
Уравнение прямой
В предыдущем пункте, рассматривая окружность как ГМТ, равноудаленных от данной точки, мы вывели ее уравнение. Для того чтобы вывести уравнение прямой, рассмотрим ее как ГМТ, равноудаленных от двух данных точек.
Пусть 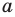
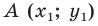
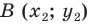
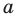
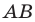
Пусть 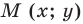
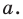
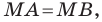
Мы показали, что координаты 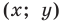
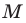
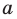
Теперь покажем, что любое решение уравнения 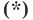
Пусть 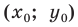
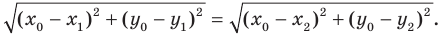
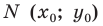
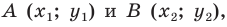
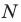
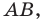
Итак, мы доказали, что уравнение 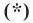
Однако из курса алгебры 7 класса вы знаете, что уравнение прямой выглядит гораздо проще, а именно: 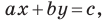
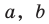
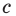
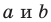
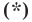
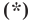
Раскроем скобки и приведем подобные слагаемые. Получим:
Обозначив 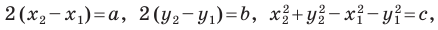
Поскольку точки 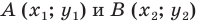
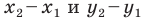
Итак, мы доказали следующую теорему.
Теорема 10.1. Уравнение прямой имеет вид?
где 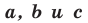
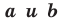
Верно и такое утверждение: любое уравнение вида 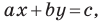
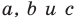
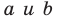
Если 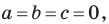
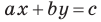
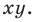
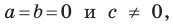
Из курса алгебры 7 класса вы знаете, что уравнение вида 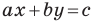
на уроках алгебры в 7 классе мы приняли без доказательства тот факт, что графиком линейной функции 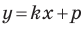
Перепишем уравнение 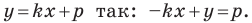
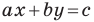
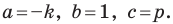
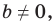
А любую ли прямую на плоскости можно задать уравнением вида 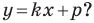
Дело в том, что прямая, перпендикулярная оси абсцисс, не может являться графиком функции, а следовательно, не может быть задана уравнением вида
Вместе с тем, если в уравнении прямой 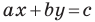
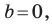
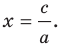
Если 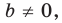
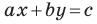
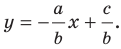
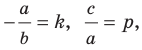
Следовательно, если 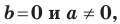
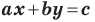
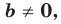
Уравнение невертикальной прямой удобно записывать в виде
Данная таблица подытоживает материал, рассмотренный в этом пункте.
Пример №7
Составьте уравнение прямой, проходящей через точки:
Решение:
1) Поскольку данные точки имеют равные абсциссы, то прямая 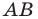
2) Поскольку данные точки имеют разные абсциссы, то прямая 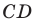
Подставив координаты точек 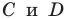
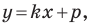
Решив эту систему уравнений, находим, что
Ответ:
Пример №8
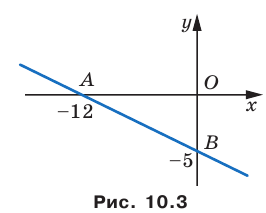
Найдите периметр и площадь треугольника, ограниченного прямой 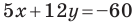
Решение:
Найдем точки пересечения данной прямой с осями координат.
С осью абсцисс: при 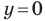
С осью ординат: при 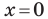
Следовательно, данная прямая и оси координат ограничивают прямоугольный треугольник 
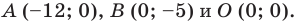
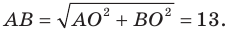
Ответ:
Угловой коэффициент прямой
Рассмотрим уравнение 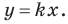
Покажем, что прямые 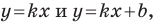
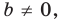
Точки 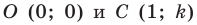
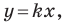
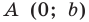
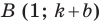
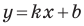
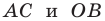
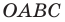
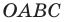
Теперь мы можем сделать такой вывод: если 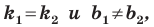
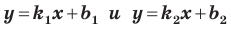
Пусть прямая 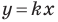
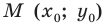
Если прямая 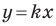
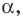
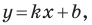
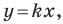
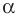
Рассмотрим прямую 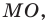
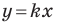
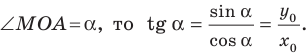
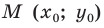
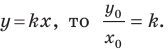
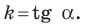
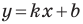
где 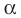
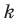
Если невертикальные прямые параллельны, то они образуют равные углы с положительным направлением оси абсцисс. Тогда тангенсы этих углов равны, следовательно, равны и их угловые коэффициенты. Таким образом,
если прямые 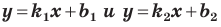
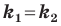
Выводы (1) и (2) объединим в одну теорему.
Теорема 11.1. Прямые 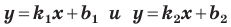
Пример №9
Составьте уравнение прямой, которая проходит через точку 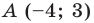
Решение:
Пусть уравнение искомой прямой 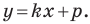
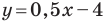
Следовательно, искомое уравнение имеет вид 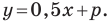
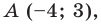
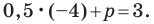
Искомое уравнение имеет вид
Ответ:
Метод координат
Мы часто говорим: прямая 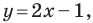
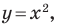
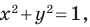
Проиллюстрируем сказанное на таком примере.
Из наглядных соображений очевидно, что прямая и окружность имеют не более двух общих точек. Однако это утверждение не является аксиомой, поэтому его надо доказывать.
Эта задача сводится к исследованию количества решений системы уравнений
где числа 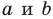
Решая эту систему методом подстановки, мы получим квадратное уравнение, которое может иметь два решения, одно решение или вообще не иметь решений. Следовательно, для данной системы существует три возможных случая:
- система имеет два решения — прямая и окружность пересекаются в двух точках;
- система имеет одно решение — прямая касается окружности;
- система не имеет решений — прямая и окружность не имеют общих точек.
С каждым из этих случаев вы встречались, решая задачи 10.17-10.19.
Метод координат особенно эффективен в тех случаях, когда требуется найти фигуру, все точки которой обладают некоторым свойством, то есть найти геометрическое место точек.
Отметим на плоскости две точки 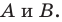
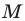
Это серединный перпендикуляр отрезка 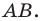
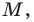
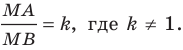
Плоскость, на которой отмечены точки 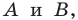
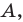
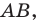
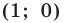
Пусть 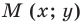
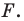
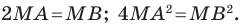
Следовательно, если точка 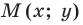
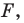
Пусть 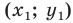
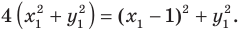
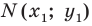
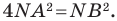
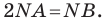
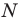
Таким образом, уравнением фигуры 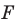
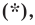
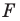
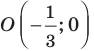
Мы решили задачу для частного случая, когда 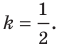
Как строили мост между геометрией и алгеброй
Идея координат зародилась очень давно. Ведь еще в старину люди изучали Землю, наблюдали звезды, а по результатам своих исследований составляли карты, схемы.
Во II в. до н. э. древнегреческий ученый Гиппарх впервые использовал идею координат для определения места расположения объектов на поверхности Земли.
Только в XIV в. французский ученый Николя Орем (ок. 1323-1382) впервые применил в математике идею Гиппарха: он разбил плоскость на клетки (как разбита страница вашей тетради) и стал задавать положение точек широтой и долготой.
Однако огромные возможности применения этой идеи были раскрыты лишь в XVII в. в работах выдающихся французских математиков Пьера Ферма и Рене Декарта. В своих трудах эти ученые показали, как благодаря системе координат можно переходить от точек к числам, от линий к уравнениям, от геометрии к алгебре.
Несмотря на то что П. Ферма опубликовал свою роботу на год раньше Р. Декарта, систему координат, которой мы сегодня пользуемся, называют декартовой. Р. Декарт в своей работе «Рассуждение о методе» предложил новую удобную буквенную символику, которой с незначительными изменениями мы пользуемся и сегодня. Вслед за Декартом мы обозначаем переменные последними буквами латинского алфавита 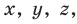
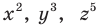
Справочный материал
Расстояние между двумя точками
Расстояние между точками 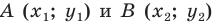
Координаты середины отрезка
Координаты 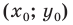
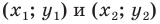
Уравнение фигуры
Уравнением фигуры 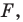
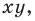
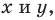
1) если точка принадлежит фигуре 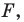
2) любое решение 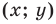
Уравнение окружности
Уравнение окружности радиуса 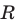
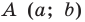
Любое уравнение вида 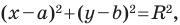
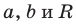
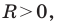
Уравнение прямой
Уравнение прямой имеет вид 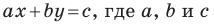
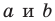
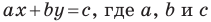
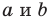
Если 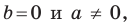
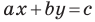
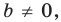
Угловой коэффициент прямой
Коэффициент 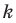
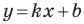
Необходимое и достаточное условие параллельности невертикальных прямых
Прямые 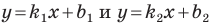
- Декартовы координаты в пространстве
- Геометрические преобразования в геометрии
- Планиметрия — формулы, определение и вычисление
- Стереометрия — формулы, определение и вычисление
- Перпендикулярность прямой и плоскости
- Взаимное расположение прямых в пространстве, прямой и плоскости
- Перпендикулярность прямых и плоскостей в пространстве
- Ортогональное проецирование





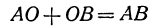
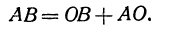
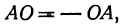


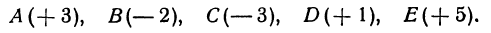


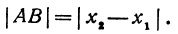
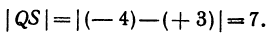

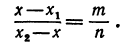
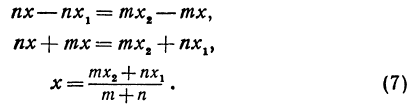
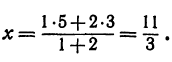
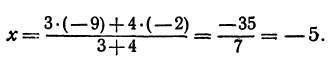

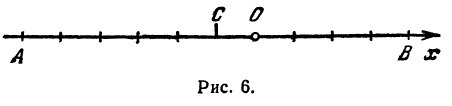
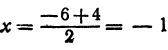
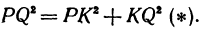
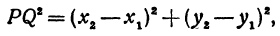
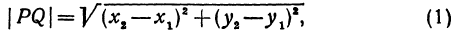
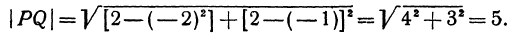
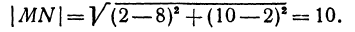
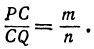

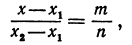
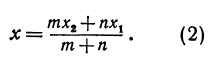

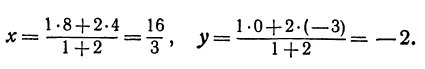
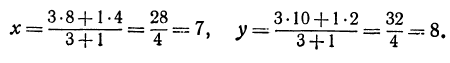

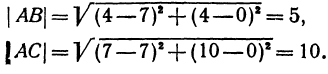
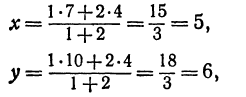
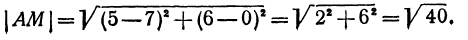
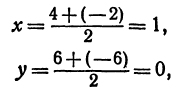
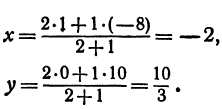
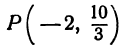
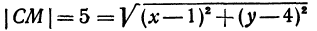
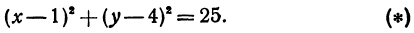
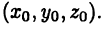
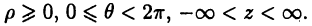
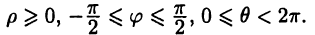










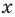
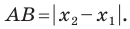
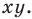
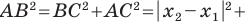
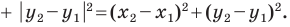

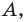
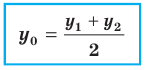
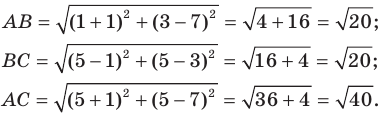

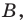
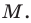
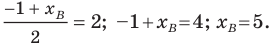
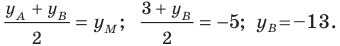
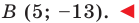
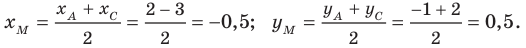
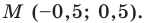
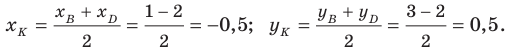
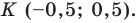
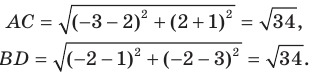

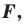 то ее координаты являются решением данного уравнения;
то ее координаты являются решением данного уравнения;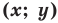 данного уравнения является координатами точки, принадлежащей фигуре
данного уравнения является координатами точки, принадлежащей фигуре