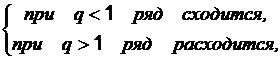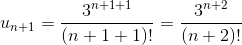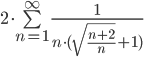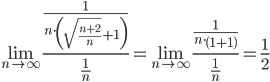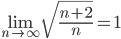Исследовать на сходимость числовой ряд
Числовой ряд в общем виде задаётся следующей формулой: $$sum_{n=1}^infty a_n.$$ Разберем из чего состоит ряд. $a_n$ — это общий член ряда. $n$ — это переменная суммирования, которая может начинаться с нуля или любого натурального числа. Таким образом ряд расписывается следующим образом: $$sum_{n=1}^infty a_n = a_1+a_2+a_3+…$$ Слагаемые $a_1,a_2,a_3,…$ называются членами ряда. Если они неотрицательные, то ряд называется положительными числовым рядом.
Ряд расходится, если сумма его членов равна бесконечности: $$sum_{n=1}^infty n^2+1 = 2+5+10+…$$Ряд сходится, если сумма его членов равна конечному числу. Например, бесконечно убывающая геометрическая прогрессия: $$sum_{n=0}^infty frac{1}{2^n} = 1+frac{1}{2} + frac{1}{4}+frac{1}{8}+…$$ Её сумма вычисляется по следующей формуле $S = frac{A}{1-q}$, где $A$ — первый член прогрессии, а $q$ — основание. В данном случае сумма равна $S = frac{1}{1 — frac{1}{2}} = 2$.
Стоит заметить, что вычислить сумму ряда в большинстве случаев просто так не получится. Поэтому используют признаки сходимости, выполнение которых достаточно для установления сходимости ряда. Например, признаки Коши и Даламбера. Зависит это от общего члена ряда.
Необходимый признак сходимости ряда
Необходимый признак сходимости ряда нужно применять мысленно перед тем, как использовать достаточные признаки. Именно благодаря ему, можно заранее установить, что ряд расходится и не тратить время на проверку достаточными признаками. Для этого, нужно найти предел общего члена ряда и в зависимости от его значения сделать вывод.
- Если ряд сходится, то $limlimits_{nto infty} a_n = 0$
- Если $limlimits_{nto infty} a_n neq 0$ или не существует, то ряд расходится
ЗАМЕЧАНИЕ ! Первый пункт не работает в обратную сторону и нужно использовать достаточный признак сходимости. То есть, если предел общего члена ряда равен нулю, то это ещё не значит, что ряд сходится! Требуется использовать один из достаточных признаков сходимости.
| Пример 1 |
| Проверить сходимость числового ряда $sum_{nto 1}^infty n^2 + 1$ |
| Решение |
| Применяем необходимый признак сходимости ряда $$lim_{ntoinfty} n^2+1 = infty$$Так как получили бесконечность, то значит ряд расходится и на этом исследование заканчивается. Если бы предел равнялся нулю, то действовали бы дальше применяя достаточные признаки. |
| Ответ |
| Ряд расходится |
| Пример 2 |
| Проверить сходимость $sum_{nto 1}^infty frac{1}{n^2+1}$ |
| Решение |
| Ищем предел общего члена ряда $$lim_{xtoinfty} frac{1}{n^2+1} = 0$$Так как предел получился равным нулю, то нельзя сказать сходится или расходится ряд. Нужно применить один из достаточных признаков сходимости. |
| Ответ |
| Требуется дополнительное исследование |
Признаки сравнения
Обобщенный гармонический ряд записывается следующим образом $ sum_{n=1} ^infty frac{1}{n^p} $.
- Если $ p = 1 $, то ряд $ sum_{n=1} ^infty frac{1}{n} $ расходится
- Если $ p leqslant 1 $, то ряд расходится. Пример,$ sum_{n=1} ^infty frac{1}{sqrt{n}} $, в котором $ p = frac{1}{2} $
- Если $ p > 1 $, то ряд сходится. Пример, $ sum_{n=1} ^infty frac{1}{sqrt{n^3}} $, в котором $ p = frac{3}{2} > 1 $
Этот ряд пригодится нам при использовании признаков сравнения, о которых пойдет речь дальше.
Признак сравнения
Пусть даны два знакоположительных числовых ряда $sum_{n=1}^infty a_n$ и $sum_{n=1}^infty b_n$, причем второй ряд сходящийся. Тогда, если начиная с некоторого номера $n$ выполнено неравенство $a_n le b_n$, то ряд $sum_{n=1}^infty a_n$ сходится вместе с $sum_{n=1}^infty b_n$.
Предельный признак сравнения
Если предел отношения общих членов двух рядов $sum_{n=1}^infty a_n$ и $sum_{n=1}^infty b_n$ равен конечному числу и отличается от нуля $$lim_{ntoinfty} frac{a_n}{b_n} = A,$$то оба ряда сходятся или расходятся одновременно.
ЗАМЕЧАНИЕ. Предельный признак удобно применять когда хотя бы один из общих членов ряда представляет собой многочлен.
| Пример 3 |
| Исследовать сходимость ряда с помощью признака сравнения $$sum_{n=1}^infty frac{1}{n^3+n^2+1}$$ |
| Решение |
|
Проверяем ряд на необходимый признак сходимости и убеждаемся в его выполнении $$lim_{ntoinfty} frac{1}{n^3+n^2+1} = 0.$$ Теперь данный ряд нужно сравнить с одним из гармонических рядов. В данном случае видим, что в знаменателе старшая степень $n^3$, значит подойдет гармонический ряд $frac{1}{n^3}$, а он как известно сходится. Но нужно дополнительно мысленно проверить, что выполняется неравенство $n^3 le n^3+n^2+1$. Убедившись в этом получаем, что $$frac{1}{n^3+n^2+1} le frac{1}{n^3}.$$Это означает, что $sum_{n=1}^infty frac{1}{n^3+n^2+1}$ сходится. |
| Ответ |
| Ряд сходится |
| Пример 4 |
| Исследовать сходимость ряда с помощью признака сравнения $$sum_{n=1}^infty frac{1}{n^2-2n}$$ |
| Решение |
| Воспользуемся предельным признаком сравнения. Сравним данный ряд со сходящимся рядом $sum_{n=1}^infty frac{1}{n^2}$. Найти предел отношения общих членов двух рядов $$lim_{ntoinfty} frac{frac{1}{n^2}}{frac{1}{n^2-2n}} = lim_{ntoinfty} frac{n^2-2n}{n^2} =$$Выносим за скобку $n^2$ и сокращаем на него числитель и знаменатель $$lim_{ntoinfty} frac{n^2(1-frac{2}{n})}{n^2} = lim_{ntoinfty} (1-frac{2}{n}) = 1.$$ Итак, получили конечное число отличное от нуля, значит оба ряда сходятся одновременно. |
| Ответ |
| Ряд сходится |
Признак Даламбера
Признак рекомендуется использовать, если в общем члене ряда есть:
- Число в степени. Например, $2^n, 3^{n+1}$
- Присутствует факториал. Например, $(n+1)!,(2n-3)!$
Для исследования сходимости ряда по признаку Даламбера нужно найти предел отношения двух членов ряда: $$lim_{ntoinfty} frac{a_{n+1}}{a_n} = L$$
В зависимости от значения предела делается вывод о сходимости или расходимости ряда:
- При $0 le L le 1$ ряд сходится
- При $L > 1$ или $L = infty$ ряд расходится
- При $L = 1$ признак не даёт ответа и нужно пробовать другой
| Пример 5 |
| Исследовать ряд на сходимость по признаку Даламбера $$sum_{n=1}^infty frac{2^{n+1}}{n!}$$ |
| Решение |
|
Общий член ряда $a_n = frac{2^{n+1}}{n!}$, тогда следующий член ряда будет $$a_{n+1} = frac{2^{(n+1)+1}}{(n+1)!} = frac{2^{n+2}}{(n+1)!}$$ Теперь находим предел предыдущего и последующего членов ряда $$L=lim_{ntoinfty} frac{a_{n+1}}{a_n} = lim_{ntoinfty} frac{frac{2^{n+2}}{(n+1)!}}{frac{2^{n+1}}{n!}} = lim_{ntoinfty} frac{2^{n+2} n!}{(n+1)! 2^{n+1}}$$ Выполняем сокращение на $2^{n+1}$ и $n!$ и находим значение предела $$L=lim_{ntoinfty} frac{2}{n+1} = 0$$ Так как предел равен нулю ($L=0$), то ряд сходится по признаку Даламбера. |
| Ответ |
| Числовой ряд сходится |
| Пример 6 |
| Исследовать сходимость ряда по признаку Даламбера $$sum_{n=1}^infty frac{3^{n+1}}{sqrt{2n+5}}$$ |
| Решение |
|
Начинаем с того, что выписываем общий член ряда $$a_n = frac{3^{n+1}}{sqrt{2n+5}}.$$ Подставляем в него $n = n + 1$ и раскрываем скобки $$a_{n+1} = frac{3^{(n+1)+1}}{sqrt{2(n+1)+5}} = frac{3^{n+2}}{sqrt{2n+7}}.$$ Находим отношение следующего общего члена к предыдущему и упрощаем $$frac{a_{n+1}}{a_n} = frac{frac{3^{n+2}}{sqrt{2n+7}}}{frac{3^{n+1}}{sqrt{2n+5}}} = frac{(3^{n+2})sqrt{2n+5}}{sqrt{2n+7}(3^{n+1})} = frac{3sqrt{2n+5}}{sqrt{2n+7}}$$ Теперь вычисляем предел последней дроби, чтобы проверить признаком Даламбера сходимость. Для этого сократим числитель и знаменатель на $n$ $$L = limlimits_{ntoinfty} frac{3sqrt{2n+5}}{sqrt{2n+7}} = 3limlimits_{ntoinfty} frac{sqrt{2+frac{5}{n}}}{sqrt{2+frac{7}{n}}} = 3frac{sqrt{2}}{sqrt{2}} = 3.$$ Так как получился $L > 0$, то по признаку Даламбера представленный ряд расходится. Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| Ряд расходится |
Радикальный признак Коши
Для установления сходимости ряда по радикальному признаку Коши нужно вычислить предел корня $n$ степени из общего члена ряда $$L = limlimits_{ntoinfty} sqrt[n]{a_n}.$$
- Если $L<1$, то ряд сходится,
- если $L>1$, то ряд расходится,
- если $L=1$, то признак не даёт ответа о сходимости.
Применяется данный признак в случаях, когда общий член ряда находится в степени содержащей $n$.
| Пример 7 |
| Исследовать ряд на сходимость $$sum_{n=1}^infty bigg(frac{3n+1}{2n+7}bigg)^{3n}.$$ |
| Решение |
|
Так как у общего члена есть тепень, в составе которой, присутствует $n$, то есть смысл попробовать применить радикальный признак сходимости Коши. Для этого, извлекаем корень $n$ степени из общего члена. $$sqrt[n]{bigg(frac{3n+1}{2n+7}bigg)^{3n}} = bigg(frac{3n+1}{2n+7}bigg)^3.$$ Теперь вычисляем предел полученного выражения. $$L = limlimits_{ntoinfty} bigg(frac{3n+1}{2n+7}bigg)^3 = limlimits_{ntoinfty}frac{(3n+1)^3}{(2n+7)^3}$$ Осталось вынести за скобки $n^3$ одновременно в числетеле и знаменателе. $$L=limlimits_{ntoinfty} frac{n^3(3+frac{1}{n})^3}{n^3(2+frac{7}{n})^3} = limlimits_{ntoinfty} frac{(3+frac{1}{n})^3}{2+frac{7}{n}} = frac{3}{2}.$$ Делаем вывод: так как $L > 1$, то представленный ряд расходится. |
| Ответ |
| Ряд расходится |
| Пример 8 |
| Исследовать сходимость ряда $$sum_{n=1}^infty frac{1}{3^n} bigg(frac{n}{n+1}bigg)^n.$$ |
| Решение |
|
Выписываем общий член ряда и извлекаем из него корень $n$ степени. $$sqrt[n]{frac{1}{3^n} bigg(frac{n}{n+1}bigg)^n} = frac{1}{3}frac{n}{n+1}$$ Вычисляем предел $$L = limlimits_{ntoinfty} frac{1}{3}frac{n}{n+1} = frac{1}{3} cdot 1 = frac{1}{3}.$$ Так как предел меньше единицы $L = frac{1}{3} < 1$, то данный ряд сходится. |
| Ответ |
| Ряд сходится |
Сходимость ряда и признаки сходимости числовых рядов
- Определение сходимости ряда. Сумма ряда
- Признаки сходимости и расходимости числовых рядов
- Необходимый признак сходимости и критерий Коши
- Признак сравнения
- Предельный признак сравнения
- Признак Даламбера
- Признак Коши
- Интегральный признак Коши
Определение сходимости ряда. Сумма ряда
Числовой ряд
называется сходящимся, если его частичная сумма
имеет предел при
. Величина
называется при этом суммой ряда, а число
остатком ряда.
Если предел
не существует, то ряд называется расходящимся.
Пример 1
Исследовать на сходимость
ряд, рассматривая последовательность его частичных сумм. В случае сходимости
найти сумму ряда.
Решение
Преобразуем выражение под
знаком суммы:
Данный ряд — сумма
геометрических прогрессий со знаменателями
и
ряд сходится
Признаки сходимости и расходимости числовых рядов
Необходимый признак сходимости и критерий Коши
Если ряд сходится, то
Обратное утверждение неверно
Критерий Коши
Для сходимости ряда необходимо и достаточно, чтобы для всякого
положительного числа
можно подобрать такое
,
чтобы при
и любом положительном
выполнялось неравенство
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Сходимость или расходимость ряда не нарушится, если прибавить или
отбросить конечное число его членов.
Пример 2
Исследовать на сходимость
ряд:
Решение
Воспользуемся
необходимым признаком сходимости:
Необходимый
признак сходимости не выполняется — ряд расходится.
Признак сравнения
Если
,
начиная с некоторого
,
и ряд
сходится, то ряд
также сходится. Если ряд (**) расходится,
то расходится и ряд (*).
В качестве рядов для сравнения удобно, в частности, выбирать
геометрическую прогрессию:
которая сходится при
и расходится при
,
и гармонический ряд
являющийся рядом расходящимся.
Пример 3
Решение
Этот ряд сходится, так как
Причем геометрическая прогрессия
знаменатель которой
,
сходится
Предельный признак сравнения
Если существует конечный и отличный от нуля предел
(в частности, если
,
то ряды
сходятся или расходятся одновременно.
Пример 4
Ряд
Решение
Сравним заданный ряд с расходящимся гармоническим рядом
Таким образом ряды одновременно
расходятся, так как найденный предел конечный и отличный от нуля.
Признак Даламбера
Пусть
(начиная с некоторого
)
и существует предел
Тогда ряд
сходится, если
,
и расходится, если
.
Если
,
то вопрос о сходимости ряда остается открытым.
Пример 5
Решение
Воспользуемся признаком
Даламбера
Ряд
сходится
Признак Коши
Пусть
(начиная с некоторого
)
и существует предел
Тогда ряд
сходится, если
,
и расходится, если
.
Если
,
то вопрос о сходимости ряда остается открытым.
Пример 6
Решение
Воспользуемся признаком
Коши:
Ряд расходится
Интегральный признак Коши
Если
,
где функция
положительна, монотонно убывает и непрерывна
при
,
то ряд
и интеграл
сходится или расходится одновременно.
С помощью интегрального признака доказывается, что ряд Дирихле
сходится, если
,
и расходится, если
.
Сходимость многих рядов можно исследовать при помощи сравнения с
соответствующим рядом Дирихле.
Пример 7
Исследовать на сходимость
числовой ряд:
Решение
Используем интегральный признак Коши.
Соответствующий интеграл:
расходится, следовательно, расходится исходный ряд
Признаки сходимости ряда
Определение. Числовым рядом называется бесконечная сумма членов последовательности:
.
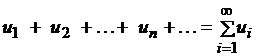
Признаки сходимости знакопостоянного числового ряда можно разделить на необходимый и достаточные.
Необходимый признак сходимости состоит в том, что: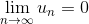 
.
Если этот признак не выполняется, то ряд расходится.
- Решение онлайн
- Видеоинструкция
Правила ввода данных
- В качестве переменной используйте только n.
- Все математические операции выражаются через общепринятые символы (+ , - , * , / , ^ ). Например,
4n, записываем как 4^n.
Примеры
≡ n^2/(n+2)
≡ n+sqrt(n-1)
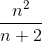
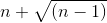
Это поле предназначено для ввода знаменателя дроби.
Правила ввода данных
- Все математические операции выражаются через общепринятые символы ( + , - , * , / , ^ ). Например, 4n, записываем как 4^n.
Примеры
≡ n^2/(n+2)
≡ n+sqrt(n-1)
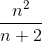
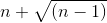
Рассмотрим четыре достаточных признака сходимости числового ряда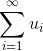 
.
1. Признак Даламбера.
Если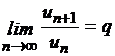 
, то 
при q = 1 получаем неопределенность.
2. Радикальный признак Коши.
Если 
,
при q = 1 получаем неопределенность.
3. Интегральный признак Коши.
Если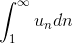 
существует, то ряд сходится; если интеграл не существует (т. е. равен ±∞) – ряд расходится.
4. Признак сравнения.
Если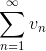 
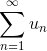
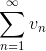
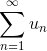
сходится и un ≤ vn, то 
также сходится, если расходится и un ≥ vn, то также расходится.
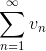
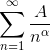
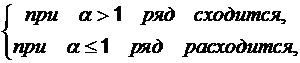
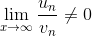
Для признака сравнения в качестве ряда часто используется 
, который 
, A — произвольная постоянная величина; причем 
.
5. Предельный признак сравнения.
Если предел отношений исходного ряда un с расходимым рядом vn равен конечному числу, отличному от нуля, то ряд un расходится.
Если предел отношений исходного ряда un со сходимым рядом vn равен конечному числу, отличному от нуля, то ряд vn сходится.
Схема определения сходимости или расходимости ряда
ДаНетДаНетДаНетДаДаНетДаНетДаНетПреобразование и упрощениеЗамена на замечательные эквивалентностиФункция ограниченаЗамена на VnПризнаки сходимостиПризнаки сходимостиVn сходитсяUn≤VnVn расходитсяРяд Un сходитсяСходимость не определенаUn≥VnРяд Un расходитсяСходимость не определенаРяд сходитсяРяд Un сходитсяРяд расходитсяРяд Un расходитсяСходимость не определена
Пример 1. Исследовать ряд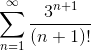 
на сходимость.
Решение:
Применим признак Даламбера:
; 
= 
= 
ряд сходится.
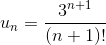
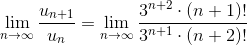
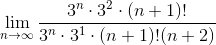
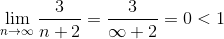
Пример 2. Исследовать ряд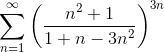 
на сходимость.
Решение:
Применим радикальный признак Коши:
ряд сходится.
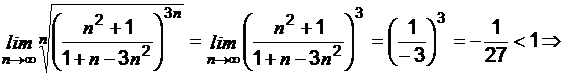
Замечание: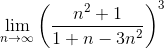 
вычисляем следующим образом: так как в числителе и знаменателе дроби старшие степени переменной n равны, то выписываем коэффициенты при n2 соответственно из числителя и знаменателя.
Пример 3. Исследовать ряд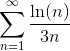 
на сходимость.
Решение:
Применим интегральный признак Коши:
, так как интеграл не существует, то ряд расходится.
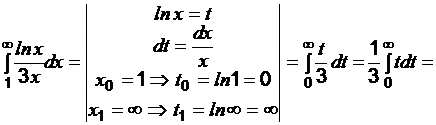
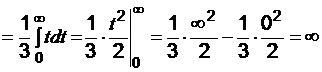
Пример 4. Исследовать ряд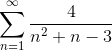 
на сходимость.
Решение:
Сравним ряд с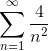 
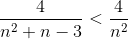
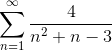
, который сходится, так как степень α переменной n: α=2 > 1. При этом 
, следовательно ряд 
также сходится.
Пример 5. Исследовать ряд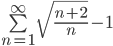 
на сходимость.
Решениие.
Исходное выражение преобразуем к виду:
Тогда исходный ряд можно представить в виде:
Коэффициент общего члена не влияет на сходимость или расходимость ряда, поэтому выносим его за пределы суммы:
Применим сравнительный признак. Рассмотрим ряд: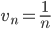 
, 
.
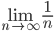
Поскольку un≤vn, то если ряд vn будет сходиться, то будет сходиться и исходный un.
По определению этот ряд расходится, здесь α≤1.
Проведя анализ ряда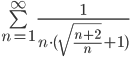 
можно сделать вывод, что признак сравнения здесь не применим (по условию ряд должен был сходиться, а он расходится). Поэтому продолжаем исследования далее. Используем предельный признак сравнения.
Сравним исследуемый ряд с расходящимся рядом:
здесь 
Получено конечное число, отличное от нуля, значит, исследуемый ряд расходится.
Следовательно, ряд 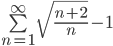расходится.
(схема 48)
Числовым рядом (или просто рядом) называется бесконечная сумма вида
, (9.1)
где 
– действительные или комплексные числа, называемые членами
ряда, un –
общим
членом ряда.
Если известен общий член ряда как функция его номера n: un=f(n), то ряд
считают заданным.
Сумма первых n членов ряда (9.1) называется n-ой частичной суммой ряда Sn, то есть Sn = u1 + u2 +…+ un.
Рассмотрим последовательность частичных сумм ряда
(9.1):
. (9.2)
Если существует конечный предел 
последовательности
частичных сумм (9.2), то этот предел называют суммой
ряда, а сам ряд – сходящимся числовым рядом. При этом
записывают:
.
Если 
не существует или 
, то ряд (9.1) называют расходящимся. Говорят, что такой ряд
суммы не имеет.
Ряд 
называется остатком
ряда после n-го члена или n-ым остатком ряда.
Сформулируем некоторые свойства числовых рядов.
1. Если ряд (9.1) сходится и его сумма равна S, то ряд
(9.3)
где
c – произвольное
число, также сходится и его сумма равна cS. Если же ряд (9.1) расходится и c ≠ 0, то и ряд (9.3) расходится.
2. Если сходится ряд (9.1) и сходится ряд 
, при этом S1 и S2 – их соответствующие суммы, то сходятся также ряды
, причём сумма каждого равна
соответственно S1± S2.
Следствие.
Сумма (разность)
сходящегося и расходящегося рядов есть расходящийся ряд 
Примечание. Сумма (разность) двух расходящихся рядов
может быть как сходящимся, так и расходящимся рядом.
3. Если к ряду (9.1) прибавить или отбросить конечное
число членов, то полученный ряд и ряд (9.1) сходятся или расходятся
одновременно.
Следствие. Если ряд (9.1) сходится, то
его n-ый остаток rn
стремится к нулю при n→∞, то есть 
.
Теорема 9.1
(необходимый признак сходимости числового ряда). Если ряд (9.1)
сходится, то его общий член un стремится к нулю при неограниченном возрастании n, то есть 
.
Следствие (достаточное
условие расходимости ряда). Если 
или этот предел не
существует, то ряд расходится
Таким образом, из того, что общий член
ряда стремится к нулю при n→∞, еще не следует, что ряд сходится.
Пример 9.1. Исследовать на сходимость ряд 
.
Решение. Вычислим предел общего члена ряда:
, то есть выполняется достаточное условие расходимости ряда.
Следовательно, заданный ряд расходится
Во многих случаях на вопрос о
сходимости или расходимости числового ряда можно ответить с помощью достаточных
признаков.
Сходимость или расходимость знакоположительного ряда
часто устанавливается путем сравнения его с другим рядом, о котором известно,
сходится он или нет. Подобное сравнение базируется на теоремах 9.2 и 9.3.
Теорема 9.2
(признак сравнения числовых знакоположительных рядов). Пусть даны два знакоположительных ряда
(9.4) и 
(9.5)
Если для всех n, начиная с некоторого номера N, выполняется неравенство 
, то из сходимости ряда (9.5) следует сходимость ряда (9.4),
а из расходимости ряда (9.4) следует расходимость ряда (9.5)
В этом случае ряд (9.4) называется минорантным,
а ряд (9.5) – мажорантным рядом.
Пример 9.2. Исследовать на сходимость ряд 
.
Решение. Общий член заданного ряда
. Рассмотрим минорантный ряд с общим членом
, который расходится (гармонический ряд (9.6)). Следовательно, заданный по условию ряд
(мажорантный) расходится и подавно
Теорема 9.3.
(признак сравнения в предельной форме)
Пусть даны два знакоположительных ряда (9.4) и (9.5).
Если существует конечный, отличный от нуля, предел 
, то ряды (9.4) и (9.5) сходятся или расходятся одновременно
Теорема 9.4
(признак Даламбера). Если в ряде (9.1) с положительными членами отношение последующего члена ряда к
предыдущему при n→∞ имеет конечный или бесконечный предел 
, то при
l<1 ряд сходится и расходится
при l>1
Примечание. Если l=1, то ряд (9.1) может быть как сходящимся, так и
расходящимся
Признак Даламбера целесообразно применять, когда общий
член ряда содержит факториалы и показательные выражения.
Пример 9.3. Исследовать на сходимость ряд
.
Решение. Согласно теореме 9.4 вычислим величину 
. Следовательно, по признаку Даламбера
заданный ряд сходится
Теорема 9.5
(радикальный признак Коши). Если для ряда (9.1) с положительными членами существует
конечный или бесконечный предел 
, то при при
l<1 ряд сходится и расходится
при l>1
Пример 9.4. Исследовать на сходимость ряд 
.
Решение. Учитывая теорему 9.5 и второй замечательный предел (3.13), вычисляем:
. Следовательно, по
радикальному признаку Коши заданный ряд сходится
Теорема 9.6
(интегральный признак Коши). Если
члены знакоположительного числового ряда 
могут быть
представлены как числовые значения некоторой непрерывной монотонно убывающей на
промежутке [1;∞) функции f(x) так, что u1= f(1), u2= f(2), …,
un= f(n), …, то если 
сходится, то сходится
и ряд (9.1); если расходится, то
расходится также и ряд (9.1)
Пример 9.5. Исследовать на сходимость ряд 
.
Решение. Для исследования ряда на сходимость применим интегральный признак Коши – рассмотрим несобственный интеграл
.
Так как несобственный интеграл от общего члена ряда сходится, то и исходный ряд также сходится (согласно теореме 9.6)
Особое значение в теории числовых рядов (в частности,
при их сравнении) имеет обобщенный гармонический ряд
, (9.6)
где
p>0 –
действительное число. Для
исследования ряда (9.6) применим теорему 9.6 (интегральный признак Коши).
Рассмотрим функцию 
. Она непрерывна и монотонно убывает на промежутке [1;∞), при этом 
. При p ≠ 1 имеем:
.
При p = 1
имеем гармонический ряд 
, который расходится 
. Итак, ряд (9.6) сходится при p>1, расходится при p≤1.
Примечание. Знакоотрицательный ряд переходит в
знакоположительный путем умножения его
на (–1), что не влияет на сходимость
ряда
Помимо знакоположительных числовых рядов существует
важный класс знакопеременных рядов, в которых члены ряда имеют произвольные
знаки.
Числовой ряд 
, содержащий бесконечное множество положительных и
бесконечное множество отрицательных членов, называется знакопеременным.
Теорема 9.7
(общий достаточный признак сходимости). Пусть
дан знакопеременный ряд
u1 + u2 +…+ un (9.7)
Если сходится ряд
(9.8)
составленный
из модулей членов данного ряда, то сходится и сам знакопеременный ряд (9.7)
Знакопеременный ряд называется абсолютно сходящимся,
если ряд, составленный из модулей его членов, сходится.
Знакопеременный ряд называется условно сходящимся, если
сам он сходится, а ряд, составленный из модулей его членов, расходится.
Сформулируем основные свойства абсолютно сходящихся
рядов.
1. Если ряд абсолютно сходится и имеет сумму S, то ряд,
полученный из него перестановкой членов, также сходится и имеет ту же сумму S, что и
исходный ряд.
2. Абсолютно сходящиеся ряды с суммами S1 и S2 можно
почленно складывать (вычитать). В результате получается абсолютно сходящийся
ряд, сумма которого равна S1 + S2 (S1 – S2).
3. Произведение двух абсолютно сходящихся рядов с
суммами S1 и S2 есть абсолютно сходящийся ряд, сумма которого равна S1 ∙ S2.
Примечание. В случае условно сходящихся рядов подобные свойства,
вообще говоря, места не имеют.
Используя указанные свойства, математические действия и операции производят только над абсолютно сходящимися
рядами. Для установления абсолютной сходимости используют все признаки
сходимости знакоположительных рядов, заменяя всюду общий член ряда его модулем.
Частным случаем знакопеременных рядов являются знакочередующиеся
ряды, члены которых имеют строго
чередующиеся знаки:
, (9.9)
где
un>0 для всех 
.
Для знакочередующихся рядов имеет место следующий
достаточный признак сходимости.
Теорема 9.8
(признак Лейбница). Знакочередующийся
ряд (9.9) сходится, если последовательность абсолютных величин его членов монотонно убывает (u1 > u2 > u3>…> un>) и общий член ряда по абсолютной величине стремится к
нулю при n→∞, то есть 
. При этом сумма S ряда (9.9) удовлетворяет неравенствам 0 < S < u1
Пример 9.6. Исследовать на сходимость ряд 
.
Решение. Это знакочередующийся ряд, для которого выполняются
условия теоремы 9.8. Действительно, предел общего члена ряда 
и члены ряда монотонно
убывают по абсолютной величине:
. Следовательно, заданный ряд сходится. Однако, ряд,
составленный из модулей его членов, то есть ряд 
– расходится, так как
является гармоническим. Значит, заданный по условию знакочередующийся ряд
сходится условно
Ряд, членами которого являются функции от переменной x, называется функциональным:
(9.10)
Придавая x определённое значение x0, мы
получим числовой ряд 
, который может быть как сходящимся, так и расходящимся.
Если полученные числовой ряд сходится, то точка x0 называется точкой сходимости ряда (9.10); если
же ряд расходится – точкой расходимости функционального ряда. Совокупность числовых
значений аргумента x, при которых функциональный ряд сходится, называется
его областью
сходимости.
В области сходимости функционального ряда его сумма
является некоторой функцией от x: S= S(x), которая определяется равенством:
– частичная сумма
ряда.
Частным случаем
функционального ряда является степенной ряд, члены которого представляют
собой степенные функции аргумента x:
(9.11)
Действительные (или комплексные) числа
называются коэффициентами
ряда (9.11), 
– действительная
переменная.
Ряд (9.11) называется разложением по степеням x. На практике часто работают со
степенным рядом, разложенным по степеням (x
– x0):
(9.12)
где x0 –
некоторое постоянное число.
Рассмотрим вопрос о нахождении области сходимости
степенного ряда.
Теорема 9.9
(Абеля о сходимости степенного ряда). Если
степенной ряд сходится при некотором значении x0 ≠ 0, то
он абсолютно сходится при всех значениях x, удовлетворяющих неравенству |x|<| x0|; если ряд
(9.11) расходится при x = x1, то он
расходится при всех x,
удовлетворяющих неравенству |x|>| x1|
Из теоремы Абеля следует, что если x0 ≠ 0 есть точка сходимости степенного ряда, то интервал (–|x0|;|x0|) весь
состоит из точек сходимости данного ряда; при всех значениях x вне этого
интервала ряд (9.11) расходится (рис. 9.1). Интервал (–|x0|;|x0|)
называют интервалом сходимости степенного ряда. Положив |x0|=R, интервал сходимости можно записать в виде (–R;R). Число R называют радиусом
сходимости степенного ряда, то есть R > 0 – это
такое число, что при всех x, для которых |x| < R,
ряд (9.11) абсолютно сходится, а при |x| > R
ряд расходится.
Если ряд (9.11) сходится в одной точке x0 = 0, то полагают, что R=0. Если же он сходится при всех действительных
значениях x, то его радиус сходимости R=∞.
На практике радиус сходимости степенного ряда (9.11)
отыскивают с помощью признака Даламбера. Для этого составляют ряд из модулей
членов ряда:
и применим к нему
признак Даламбера. Допустим, что существует предел
.
По теореме 9.4 ряд сходится, если
, то есть ряд сходится при тех значениях x, для
которых
. Ряд, составленный из
модулей членов ряда (9.11), расходится при тех значениях x, для
которых 
. Таким образом, для ряда (9.11) радиус абсолютной сходимости
вычисляется по формуле:
. (9.13)
С помощью радикального признака Коши (теоремы 9.5) можно
показать, что радиус сходимости также вычисляется по формуле:
. (9.14)
Примечание. Интервал сходимости степенного ряда (9.12) находят из
неравенства |x– x0| < R; он имеет вид (x0–R; x0+R)
Пример 9.7. Найти область сходимости ряда 
.
Решение. Воспользуемся формулой (9.13) 
: 
.
Следовательно,
данный ряд абсолютно сходится в единственной точке х = 0.
Область
сходимости степенного ряда (9.11) уточняют на концах полученного интервала
сходимости, симметричного относительно начала координат. На его левом конце,
при 
получают
знакочередующийся числовой ряд, сходимость которого исследуют с помощью
признака Лейбница (теорема 9.8). На правом конце интервала сходимости, при x=R получают
числовой ряд с положительными членами, который исследуют на сходимость с
помощью рассмотренных выше достаточных признаков – теорем
9.2-9.6. Если при и (или) x=R получают
сходящийся числовой ряд, то
соответствующую точку включают в область сходимости степенного ряда. Если при и (или) x=R получают
расходящийся числовой ряд, то
соответствующую точку включают в область расходимости степенного ряда.
Уточненный на концах интервал сходимости представляет собой область сходимости
степенного ряда (9.11).
Пример 9.8. Написать первые три члена ряда 
и найти его область сходимости.
Решение. Беря последовательно n = 1, 2, 3, …, запишем данный ряд в виде:
Для нахождения области сходимости ряда применим
признак Даламбера:
.
Данный ряд сходится абсолютно при тех значениях x, которые удовлетворяют неравенству
.
Исследуем сходимость ряда на концах полученного
интервала.
При 
заданный ряд принимает
вид 
. Последний ряд является знакочередующимся; абсолютная
величина его общего члена стремится к нулю при n→∞; члены ряда убывают по абсолютной
величине. Следовательно, по признаку
Лейбница этот ряд сходится. Значит, принадлежит области
сходимости данного ряда.
При 
ряд принимает вид 
. Исследуем его сходимость при помощи интегрального признака
сходимости Коши. Рассмотрим несобственный интеграл
.
Так как несобственный интеграл сходится, то сходится и
исследуемый ряд. Значит, при исходный ряд сходится.
Таким образом,
– область сходимости заданного
по условию ряда
Вопросы для самопроверки