Исследовать на сходимость числовой ряд
Числовой ряд в общем виде задаётся следующей формулой: $$sum_{n=1}^infty a_n.$$ Разберем из чего состоит ряд. $a_n$ — это общий член ряда. $n$ — это переменная суммирования, которая может начинаться с нуля или любого натурального числа. Таким образом ряд расписывается следующим образом: $$sum_{n=1}^infty a_n = a_1+a_2+a_3+…$$ Слагаемые $a_1,a_2,a_3,…$ называются членами ряда. Если они неотрицательные, то ряд называется положительными числовым рядом.
Ряд расходится, если сумма его членов равна бесконечности: $$sum_{n=1}^infty n^2+1 = 2+5+10+…$$Ряд сходится, если сумма его членов равна конечному числу. Например, бесконечно убывающая геометрическая прогрессия: $$sum_{n=0}^infty frac{1}{2^n} = 1+frac{1}{2} + frac{1}{4}+frac{1}{8}+…$$ Её сумма вычисляется по следующей формуле $S = frac{A}{1-q}$, где $A$ — первый член прогрессии, а $q$ — основание. В данном случае сумма равна $S = frac{1}{1 — frac{1}{2}} = 2$.
Стоит заметить, что вычислить сумму ряда в большинстве случаев просто так не получится. Поэтому используют признаки сходимости, выполнение которых достаточно для установления сходимости ряда. Например, признаки Коши и Даламбера. Зависит это от общего члена ряда.
Необходимый признак сходимости ряда
Необходимый признак сходимости ряда нужно применять мысленно перед тем, как использовать достаточные признаки. Именно благодаря ему, можно заранее установить, что ряд расходится и не тратить время на проверку достаточными признаками. Для этого, нужно найти предел общего члена ряда и в зависимости от его значения сделать вывод.
- Если ряд сходится, то $limlimits_{nto infty} a_n = 0$
- Если $limlimits_{nto infty} a_n neq 0$ или не существует, то ряд расходится
ЗАМЕЧАНИЕ ! Первый пункт не работает в обратную сторону и нужно использовать достаточный признак сходимости. То есть, если предел общего члена ряда равен нулю, то это ещё не значит, что ряд сходится! Требуется использовать один из достаточных признаков сходимости.
| Пример 1 |
| Проверить сходимость числового ряда $sum_{nto 1}^infty n^2 + 1$ |
| Решение |
| Применяем необходимый признак сходимости ряда $$lim_{ntoinfty} n^2+1 = infty$$Так как получили бесконечность, то значит ряд расходится и на этом исследование заканчивается. Если бы предел равнялся нулю, то действовали бы дальше применяя достаточные признаки. |
| Ответ |
| Ряд расходится |
| Пример 2 |
| Проверить сходимость $sum_{nto 1}^infty frac{1}{n^2+1}$ |
| Решение |
| Ищем предел общего члена ряда $$lim_{xtoinfty} frac{1}{n^2+1} = 0$$Так как предел получился равным нулю, то нельзя сказать сходится или расходится ряд. Нужно применить один из достаточных признаков сходимости. |
| Ответ |
| Требуется дополнительное исследование |
Признаки сравнения
Обобщенный гармонический ряд записывается следующим образом $ sum_{n=1} ^infty frac{1}{n^p} $.
- Если $ p = 1 $, то ряд $ sum_{n=1} ^infty frac{1}{n} $ расходится
- Если $ p leqslant 1 $, то ряд расходится. Пример,$ sum_{n=1} ^infty frac{1}{sqrt{n}} $, в котором $ p = frac{1}{2} $
- Если $ p > 1 $, то ряд сходится. Пример, $ sum_{n=1} ^infty frac{1}{sqrt{n^3}} $, в котором $ p = frac{3}{2} > 1 $
Этот ряд пригодится нам при использовании признаков сравнения, о которых пойдет речь дальше.
Признак сравнения
Пусть даны два знакоположительных числовых ряда $sum_{n=1}^infty a_n$ и $sum_{n=1}^infty b_n$, причем второй ряд сходящийся. Тогда, если начиная с некоторого номера $n$ выполнено неравенство $a_n le b_n$, то ряд $sum_{n=1}^infty a_n$ сходится вместе с $sum_{n=1}^infty b_n$.
Предельный признак сравнения
Если предел отношения общих членов двух рядов $sum_{n=1}^infty a_n$ и $sum_{n=1}^infty b_n$ равен конечному числу и отличается от нуля $$lim_{ntoinfty} frac{a_n}{b_n} = A,$$то оба ряда сходятся или расходятся одновременно.
ЗАМЕЧАНИЕ. Предельный признак удобно применять когда хотя бы один из общих членов ряда представляет собой многочлен.
| Пример 3 |
| Исследовать сходимость ряда с помощью признака сравнения $$sum_{n=1}^infty frac{1}{n^3+n^2+1}$$ |
| Решение |
|
Проверяем ряд на необходимый признак сходимости и убеждаемся в его выполнении $$lim_{ntoinfty} frac{1}{n^3+n^2+1} = 0.$$ Теперь данный ряд нужно сравнить с одним из гармонических рядов. В данном случае видим, что в знаменателе старшая степень $n^3$, значит подойдет гармонический ряд $frac{1}{n^3}$, а он как известно сходится. Но нужно дополнительно мысленно проверить, что выполняется неравенство $n^3 le n^3+n^2+1$. Убедившись в этом получаем, что $$frac{1}{n^3+n^2+1} le frac{1}{n^3}.$$Это означает, что $sum_{n=1}^infty frac{1}{n^3+n^2+1}$ сходится. |
| Ответ |
| Ряд сходится |
| Пример 4 |
| Исследовать сходимость ряда с помощью признака сравнения $$sum_{n=1}^infty frac{1}{n^2-2n}$$ |
| Решение |
| Воспользуемся предельным признаком сравнения. Сравним данный ряд со сходящимся рядом $sum_{n=1}^infty frac{1}{n^2}$. Найти предел отношения общих членов двух рядов $$lim_{ntoinfty} frac{frac{1}{n^2}}{frac{1}{n^2-2n}} = lim_{ntoinfty} frac{n^2-2n}{n^2} =$$Выносим за скобку $n^2$ и сокращаем на него числитель и знаменатель $$lim_{ntoinfty} frac{n^2(1-frac{2}{n})}{n^2} = lim_{ntoinfty} (1-frac{2}{n}) = 1.$$ Итак, получили конечное число отличное от нуля, значит оба ряда сходятся одновременно. |
| Ответ |
| Ряд сходится |
Признак Даламбера
Признак рекомендуется использовать, если в общем члене ряда есть:
- Число в степени. Например, $2^n, 3^{n+1}$
- Присутствует факториал. Например, $(n+1)!,(2n-3)!$
Для исследования сходимости ряда по признаку Даламбера нужно найти предел отношения двух членов ряда: $$lim_{ntoinfty} frac{a_{n+1}}{a_n} = L$$
В зависимости от значения предела делается вывод о сходимости или расходимости ряда:
- При $0 le L le 1$ ряд сходится
- При $L > 1$ или $L = infty$ ряд расходится
- При $L = 1$ признак не даёт ответа и нужно пробовать другой
| Пример 5 |
| Исследовать ряд на сходимость по признаку Даламбера $$sum_{n=1}^infty frac{2^{n+1}}{n!}$$ |
| Решение |
|
Общий член ряда $a_n = frac{2^{n+1}}{n!}$, тогда следующий член ряда будет $$a_{n+1} = frac{2^{(n+1)+1}}{(n+1)!} = frac{2^{n+2}}{(n+1)!}$$ Теперь находим предел предыдущего и последующего членов ряда $$L=lim_{ntoinfty} frac{a_{n+1}}{a_n} = lim_{ntoinfty} frac{frac{2^{n+2}}{(n+1)!}}{frac{2^{n+1}}{n!}} = lim_{ntoinfty} frac{2^{n+2} n!}{(n+1)! 2^{n+1}}$$ Выполняем сокращение на $2^{n+1}$ и $n!$ и находим значение предела $$L=lim_{ntoinfty} frac{2}{n+1} = 0$$ Так как предел равен нулю ($L=0$), то ряд сходится по признаку Даламбера. |
| Ответ |
| Числовой ряд сходится |
| Пример 6 |
| Исследовать сходимость ряда по признаку Даламбера $$sum_{n=1}^infty frac{3^{n+1}}{sqrt{2n+5}}$$ |
| Решение |
|
Начинаем с того, что выписываем общий член ряда $$a_n = frac{3^{n+1}}{sqrt{2n+5}}.$$ Подставляем в него $n = n + 1$ и раскрываем скобки $$a_{n+1} = frac{3^{(n+1)+1}}{sqrt{2(n+1)+5}} = frac{3^{n+2}}{sqrt{2n+7}}.$$ Находим отношение следующего общего члена к предыдущему и упрощаем $$frac{a_{n+1}}{a_n} = frac{frac{3^{n+2}}{sqrt{2n+7}}}{frac{3^{n+1}}{sqrt{2n+5}}} = frac{(3^{n+2})sqrt{2n+5}}{sqrt{2n+7}(3^{n+1})} = frac{3sqrt{2n+5}}{sqrt{2n+7}}$$ Теперь вычисляем предел последней дроби, чтобы проверить признаком Даламбера сходимость. Для этого сократим числитель и знаменатель на $n$ $$L = limlimits_{ntoinfty} frac{3sqrt{2n+5}}{sqrt{2n+7}} = 3limlimits_{ntoinfty} frac{sqrt{2+frac{5}{n}}}{sqrt{2+frac{7}{n}}} = 3frac{sqrt{2}}{sqrt{2}} = 3.$$ Так как получился $L > 0$, то по признаку Даламбера представленный ряд расходится. Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| Ряд расходится |
Радикальный признак Коши
Для установления сходимости ряда по радикальному признаку Коши нужно вычислить предел корня $n$ степени из общего члена ряда $$L = limlimits_{ntoinfty} sqrt[n]{a_n}.$$
- Если $L<1$, то ряд сходится,
- если $L>1$, то ряд расходится,
- если $L=1$, то признак не даёт ответа о сходимости.
Применяется данный признак в случаях, когда общий член ряда находится в степени содержащей $n$.
| Пример 7 |
| Исследовать ряд на сходимость $$sum_{n=1}^infty bigg(frac{3n+1}{2n+7}bigg)^{3n}.$$ |
| Решение |
|
Так как у общего члена есть тепень, в составе которой, присутствует $n$, то есть смысл попробовать применить радикальный признак сходимости Коши. Для этого, извлекаем корень $n$ степени из общего члена. $$sqrt[n]{bigg(frac{3n+1}{2n+7}bigg)^{3n}} = bigg(frac{3n+1}{2n+7}bigg)^3.$$ Теперь вычисляем предел полученного выражения. $$L = limlimits_{ntoinfty} bigg(frac{3n+1}{2n+7}bigg)^3 = limlimits_{ntoinfty}frac{(3n+1)^3}{(2n+7)^3}$$ Осталось вынести за скобки $n^3$ одновременно в числетеле и знаменателе. $$L=limlimits_{ntoinfty} frac{n^3(3+frac{1}{n})^3}{n^3(2+frac{7}{n})^3} = limlimits_{ntoinfty} frac{(3+frac{1}{n})^3}{2+frac{7}{n}} = frac{3}{2}.$$ Делаем вывод: так как $L > 1$, то представленный ряд расходится. |
| Ответ |
| Ряд расходится |
| Пример 8 |
| Исследовать сходимость ряда $$sum_{n=1}^infty frac{1}{3^n} bigg(frac{n}{n+1}bigg)^n.$$ |
| Решение |
|
Выписываем общий член ряда и извлекаем из него корень $n$ степени. $$sqrt[n]{frac{1}{3^n} bigg(frac{n}{n+1}bigg)^n} = frac{1}{3}frac{n}{n+1}$$ Вычисляем предел $$L = limlimits_{ntoinfty} frac{1}{3}frac{n}{n+1} = frac{1}{3} cdot 1 = frac{1}{3}.$$ Так как предел меньше единицы $L = frac{1}{3} < 1$, то данный ряд сходится. |
| Ответ |
| Ряд сходится |
Признаки сходимости ряда
Определение. Числовым рядом называется бесконечная сумма членов последовательности:
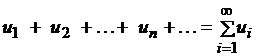
Признаки сходимости знакопостоянного числового ряда можно разделить на необходимый и достаточные.
Необходимый признак сходимости состоит в том, что: 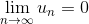
Если этот признак не выполняется, то ряд расходится.
- Решение онлайн
- Видеоинструкция
Правила ввода данных
- В качестве переменной используйте только n.
- Все математические операции выражаются через общепринятые символы (+ , - , * , / , ^ ). Например,
4n, записываем как 4^n.
Примеры
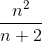
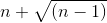
Это поле предназначено для ввода знаменателя дроби.
Правила ввода данных
- Все математические операции выражаются через общепринятые символы ( + , - , * , / , ^ ). Например, 4n, записываем как 4^n.
Примеры
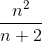
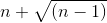
Рассмотрим четыре достаточных признака сходимости числового ряда 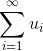
1. Признак Даламбера.
Если 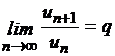
при q = 1 получаем неопределенность.
2. Радикальный признак Коши.
Если ,
при q = 1 получаем неопределенность.
3. Интегральный признак Коши.
Если 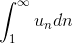
4. Признак сравнения.
Если 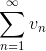
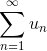
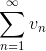
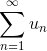
Для признака сравнения в качестве ряда 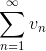
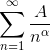
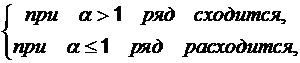
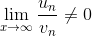
5. Предельный признак сравнения.
Если предел отношений исходного ряда un с расходимым рядом vn равен конечному числу, отличному от нуля, то ряд un расходится.
Если предел отношений исходного ряда un со сходимым рядом vn равен конечному числу, отличному от нуля, то ряд vn сходится.
Схема определения сходимости или расходимости ряда
ДаНетДаНетДаНетДаДаНетДаНетДаНетПреобразование и упрощениеЗамена на замечательные эквивалентностиФункция ограниченаЗамена на VnПризнаки сходимостиПризнаки сходимостиVn сходитсяUn≤VnVn расходитсяРяд Un сходитсяСходимость не определенаUn≥VnРяд Un расходитсяСходимость не определенаРяд сходитсяРяд Un сходитсяРяд расходитсяРяд Un расходитсяСходимость не определена
Пример 1. Исследовать ряд 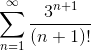
Решение:
Применим признак Даламбера:
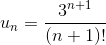
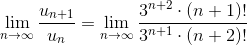
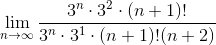
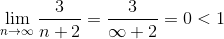
Пример 2. Исследовать ряд 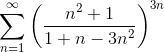
Решение:
Применим радикальный признак Коши:
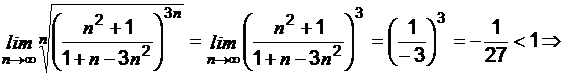
Замечание: 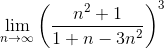
Пример 3. Исследовать ряд 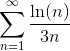
Решение:
Применим интегральный признак Коши:
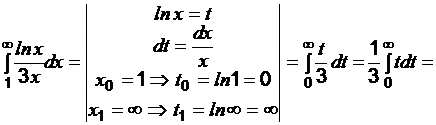
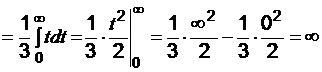
Пример 4. Исследовать ряд 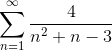
Решение:
Сравним ряд с 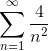
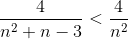
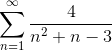
Пример 5. Исследовать ряд 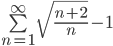
Решениие.
Исходное выражение преобразуем к виду:
Тогда исходный ряд можно представить в виде:
Коэффициент общего члена не влияет на сходимость или расходимость ряда, поэтому выносим его за пределы суммы:
Применим сравнительный признак. Рассмотрим ряд: 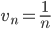
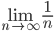
Поскольку un≤vn, то если ряд vn будет сходиться, то будет сходиться и исходный un.
По определению этот ряд расходится, здесь α≤1.
Проведя анализ ряда 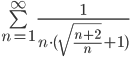
Сравним исследуемый ряд с расходящимся рядом:
здесь
Получено конечное число, отличное от нуля, значит, исследуемый ряд расходится.
Следовательно, ряд 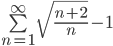
Признак Д’Аламбера. Первая часть.
Перед началом работы с этой темой советую посмотреть раздел с терминологией для числовых рядов. Особенно стоит обратить внимание на понятие общего члена ряда. Если у вас есть сомнения в правильности выбора признака сходимости, советую глянуть тему «Выбор признака сходимости числовых рядов».
Признак Д’Аламбера (или признак Даламбера) используется для исследования сходимости рядов, общий член которых строго больше нуля, т.е. $u_n > 0$. Такие ряды называют строго положительными. В стандартных примерах признак Д’Аламбера используют в предельной форме.
Признак Д’Аламбера (в предельной форме)
Если ряд $sumlimits_{n=1}^{infty}u_n$ строго положителен и
$$
lim_{ntoinfty}frac{u_{n+1}}{u_n}=L,
$$
то при $L<1$ ряд сходится, а при $L>1$ (и при $L=infty$) ряд расходится.
Формулировка довольно проста, но остаётся открытым следующий вопрос: что будет, если $L=1$? Ответа на данный вопрос признак Д’Аламбера дать не в состоянии. Если $L=1$, то ряд может как сходиться, так и расходиться.
Чаще всего в стандартных примерах признак Д’Аламбера применяется, если в выражении общего члена ряда присутствуют многочлен от $n$ (многочлен может быть и под корнем) и степень вида $a^n$ или $n!$. Например, $u_n=frac{5^ncdot(3n+7)}{2n^3-1}$ (см. пример №1) или $u_n=frac{sqrt{4n+5}}{(3n-2)!}$ (см. пример №2). Вообще, для стандартного примера наличие $n!$ – это своеобразная «визитная карточка» признака Д’Аламбера.
Что обозначает выражение «n!»? показатьскрыть
Кроме того, нередко признак Д’Аламбера используют для выяснения сходимости ряда, общий член которого содержит произведение такой структуры: $u_n=frac{3cdot 5cdot 7cdotldotscdot(2n+1)}{2cdot 5cdot 8cdotldotscdot(3n-1)}$.
Для вычисления пределов будем использовать методы, изложенные в темах «Пределы с иррациональностями», «Предел отношения двух многочленов», а также в теме «Второй замечательный предел».
Пример №1
Исследовать ряд $sumlimits_{n=1}^{infty}frac{5^ncdot(3n+7)}{2n^3-1}$ на сходимость.
Решение
Так как нижний предел суммирования равен 1, то общий член ряда записан под знаком суммы: $u_n=frac{5^ncdot(3n+7)}{2n^3-1}$. Так как при $n≥ 1$ имеем $3n+7 > 0$, $5^n>0$ и $2n^3-1 > 0$, то $u_n > 0$. Следовательно, наш ряд является строго положительным.
Проверять выполнение необходимого условия сходимости здесь несколько затруднительно, поэтому эту проверку мы пропустим.
Что мы можем сказать про общий член ряда? Он содержит многочлены $3n+7$, $2n^3-1$ и степень $5^n$. Это сразу наводит на мысль о применении признака Д’Аламбера.
Чтобы применить данный признак, нам придётся найти предел отношения $frac{u_{n+1}}{u_n}$. Общий член ряда у нас есть, вот он: $u_n=frac{5^ncdot(3n+7)}{2n^3-1}$. А формулу для $u_{n+1}$ запишем отдельно. Чтобы записать $u_n$, нужно в формулу $u_n=frac{5^ncdot(3n+7)}{2n^3-1}$ вместо $n$ подставить $n+1$:
$$
u_{n+1}=frac{5^{n+1}cdot(3(n+1)+7)}{2(n+1)^3-1}=frac{5^{n+1}cdot(3n+10)}{2(n+1)^3-1}.
$$
При желании знаменатель можно записать без скобок, так как $2(n+1)^3-1=2n^3+6n^2+6n+1$, однако в этом нет необходимости. Итак, найдём чему же равно значение $lim_{ntoinfty}frac{u_{n+1}}{u_n}$. При упрощении получившегося выражения учтём, что $frac{5^{n+1}}{5^n}=5^{n+1-n}=5^1=5$.
$$
lim_{ntoinfty}frac{u_{n+1}}{u_n}=lim_{ntoinfty}frac{frac{5^{n+1}cdot(3n+10)}{2(n+1)^3-1}}{frac{5^ncdot(3n+7)}{2n^3-1}}=
lim_{ntoinfty}frac{5cdot(3n+10)left(2n^3-1right)}{left(2(n+1)^3-1right)(3n+7)}=5cdotlim_{ntoinfty}frac{(3n+10)left(2n^3-1right)}{left(2(n+1)^3-1right)(3n+7)}.
$$
Чтобы вычислить получившийся предел, нужно разделить и числитель и знаменатель на $n^4$ (см. пример №1 на этой странице):
$$
5cdotlim_{ntoinfty}frac{(3n+10)left(2n^3-1right)}{left(2(n+1)^3-1right)(3n+7)}=left|frac{infty}{infty}right|=
5cdotlim_{ntoinfty}frac{frac{(3n+10)left(2n^3-1right)}{n^4}}{frac{left(2(n+1)^3-1right)(3n+7)}{n^4}}=
5cdotlim_{ntoinfty}frac{frac{3n+10}{n}cdotfrac{2n^3-1}{n^3}}{frac{left(2(n+1)^3-1right)}{n^3}cdotfrac{3n+7}{n}}=\
=5cdotlim_{ntoinfty}frac{left(frac{3n}{n}+frac{10}{n}right)cdotleft(frac{2n^3}{n^3}-frac{1}{n^3}right)}{left(2left(frac{n}{n}+frac{1}{n}right)^3-frac{1}{n^3}right)cdotleft(frac{3n}{n}+frac{7}{n}right)}=5cdotlim_{ntoinfty}frac{left(3+frac{10}{n}right)cdotleft(2-frac{1}{n^3}right)}{left(2left(1+frac{1}{n}right)^3-frac{1}{n^3}right)cdotleft(3+frac{7}{n}right)}=5cdotfrac{3cdot 2}{2cdot 3}=5.
$$
Так как $lim_{ntoinfty}frac{u_{n+1}}{u_n}=5>1$, то согласно признаку Д’Аламбера заданный ряд расходится.
Честно говоря, признак Д’Аламбера – не единственный вариант в данной ситуации. Можно использовать, например, радикальный признак Коши. Однако применение радикального признака Коши потребует знания (или доказательства) дополнительных формул. Поэтому использование признака Д’Аламбера в данной ситуации более удобно.
Ответ: ряд расходится.
Пример №2
Исследовать ряд $sumlimits_{n=1}^{infty}frac{sqrt{4n+5}}{(3n-2)!}$ на сходимость.
Решение
Так как нижний предел суммирования равен 1, то общий член ряда записан под знаком суммы: $u_n=frac{sqrt{4n+5}}{(3n-2)!}$. Заданный ряд является строго положительным, т.е. $u_n>0$.
Общий член ряда содержит многочлен под корнем, т.е. $sqrt{4n+5}$, и факториал $(3n-2)!$. Наличие факториала в стандартном примере – почти стопроцентная гарантия применения признака Д’Аламбера.
Чтобы применить данный признак, нам придётся найти предел отношения $frac{u_{n+1}}{u_n}$. Чтобы записать $u_{n+1}$, нужно в формулу $u_n=frac{sqrt{4n+5}}{(3n-2)!}$ вместо $n$ подставить $n+1$:
$$
u_{n+1}=frac{sqrt{4(n+1)+5}}{(3(n+1)-2)!}=frac{sqrt{4n+9}}{(3n+1)!}.
$$
Так как
$$(3n+1)!=(3n-2)!cdot (3n-1)cdot 3ncdot(3n+1),$$
то формулу для $u_{n+1}$ можно записать по-иному:
$$
u_{n+1}=frac{sqrt{4n+9}}{(3n+1)!}=frac{sqrt{4n+9}}{(3n-2)!cdot (3n-1)cdot 3ncdot(3n+1)}.
$$
Эта запись удобна для дальнейшего решения, когда нам придётся сокращать дробь под пределом. Если равенство с факториалами требует пояснений, то прошу раскрыть примечание ниже.
Как мы получили равенство $(3n+1)!=(3n-2)!cdot (3n-1)cdot 3ncdot(3n+1)$? показатьскрыть
Вычислим значение $lim_{ntoinfty}frac{u_{n+1}}{u_n}$:
$$
lim_{ntoinfty}frac{u_{n+1}}{u_n}=lim_{ntoinfty}frac{frac{sqrt{4n+9}}{(3n-2)!cdot (3n-1)cdot 3ncdot(3n+1)}}{frac{sqrt{4n+5}}{(3n-2)!}}=
lim_{ntoinfty}left(frac{sqrt{4n+9}}{sqrt{4n+5}}cdotfrac{(3n-2)!}{(3n-2)!cdot (3n-1)cdot 3ncdot(3n+1)}right)=\
=lim_{ntoinfty}frac{sqrt{4n+9}}{sqrt{4n+5}}cdotlim_{ntoinfty}frac{1}{(3n-1)cdot 3ncdot(3n+1)}=
lim_{ntoinfty}frac{sqrt{4+frac{9}{n}}}{sqrt{4+frac{5}{n}}}cdotlim_{ntoinfty}frac{1}{(3n-1)cdot 3ncdot(3n+1)}=1cdot 0=0.
$$
Так как $lim_{ntoinfty}frac{u_{n+1}}{u_n}=0<1$, то согласно признаку Д’Аламбера заданный ряд сходится.
Ответ: ряд сходится.
Пример №3
Исследовать ряд $sumlimits_{n=1}^{infty}frac{(2n+5)!}{4^{3n+2}}$ на сходимость.
Решение
Так как нижний предел суммирования равен 1, то общий член ряда записан под знаком суммы: $u_n=frac{(2n+5)!}{4^{3n+2}}$. Заданный ряд ряд является строго положительным, т.е. $u_n>0$.
Общий член ряда содержит как факториал $(2n+5)!$, так и степень $4^{3n+2}$. Применяем признак Д’Аламбера.
Нам потребуется $u_{n+1}$. Подставляя в формулу $u_n=frac{(2n+5)!}{4^{3n+2}}$ вместо $n$ выражение $n+1$, будем иметь:
$$
u_{n+1}=frac{(2(n+1)+5)!}{4^{3(n+1)+2}}=frac{(2n+7)!}{4^{3n+5}}
$$
Вычислим значение $lim_{ntoinfty}frac{u_{n+1}}{u_n}$. При сокращении станем учитывать, что $(2n+7)!=(2n+5)!(2n+6)(2n+7)$ (см. примечание в предыдущем примере №2) и $frac{4^{3n+2}}{4^{3n+5}}=4^{3n+2-(3n+5)}=4^{-3}=frac{1}{4^3}=frac{1}{64}$.
$$
lim_{ntoinfty}frac{u_{n+1}}{u_n}=lim_{ntoinfty}frac{frac{(2n+7)!}{4^{3n+5}}}{frac{(2n+5)!}{4^{3n+2}}}=lim_{ntoinfty}left(frac{4^{3n+2}}{4^{3n+5}}cdotfrac{(2n+7)!}{(2n+5)!}right)
=lim_{ntoinfty}left(frac{1}{64}cdot(2n+6)(2n+7)right)=infty.
$$
Так как $lim_{ntoinfty}frac{u_{n+1}}{u_n}=infty$, то согласно признаку Д’Аламбера заданный ряд расходится.
Ответ: ряд расходится.
Продолжение темы исследования сходимости рядов с помощью признака Д’Аламбера рассмотрим во второй и третьей частях.
Исследование сходимости рядов является важным с точки зрения их оценки и необходимым в случае вычисления суммы ряда. Признаков сходимости рядов несколько, популярный и достаточно прост в применении для рядов с положительными членами — признак сходимости Даламбера. Ниже будет разобран ряд примеров на установление сходимости ряда по признаку Даламбера, советую для себя взять максимум полезного.
Напомним что предпосылками для применения признака Даламбера служит наличие степенной зависимости (2, 3, a в степени n) или факториалов в формуле общего члена ряда. Будет это знаменатель или числитель дроби совсем не имеет значения, важно что имеем подобную зависимость, ну или факториал и степенную зависимость в одном наборе. С факториалами у многих на первых порах возникают проблемы но с практикой Вы заметете что ничего сложного в факториалах нет. Надо только расписать факториал подробно до тех пор когда в числителе или знаменателе дроби поучим одинаковые множителе. На словах это звучит не всем понятно, но следующие примеры помогут Вам в этом разобраться. Ну и самые сложные примеры предполагают наличие комбинаций факториалов и степенных зависимостей, два или более факториала, тоже и для степенной фунции, всевозможные цепочки множителей и другие каверзные комбинации. Ниже приведены базовые примеры с которых и начинается практика проверки сходимости ряда по Даламберу.
Пример: 2.5 Исследовать сходимость рядов
а) 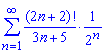
Вычисления: Поскольку данный ряд имеет положительные члены то исследовать его на сходимость можем с помощью признака Даламбера:
Если А<1 ряд сходящийся, А>1 — ряд расходящийся и при A=0 следует использовать другие признаки сходимости рядов.
Записываем общий член ряда и следующий, идущий после него
И находим границу их доли
Поскольку граница бесконечна 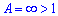
б) 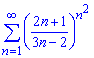
Вычисления: Члены ряда положительные поетому исследуем на сходимость по признаку Даламбера — записываем формулы последовательных членов ряда
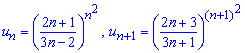
И находим предел отношения следующего члена к предыдущему при n стремящемуся к бесконечности
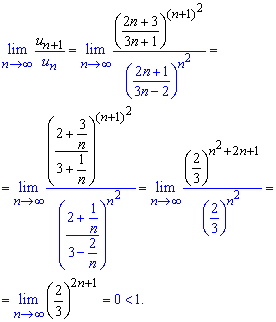
Граница равна нулю так как показатель стремится к бесконечности, а в скобках имеем значение меньше единицы.
По теореме Даламбера A = 0 <1 ряд сходится!
Пример: 2.14 Исследовать ряд на сходимость
а)
В отличие от
признаков сравнения, где все зависит
от догадки и записи известных сходящихся
и расходящихся рядов признак Даламбера
позволяет решить вопрос о сходимости
ряда, проделав лишь некоторые операции
над самим рядом.
Теорема. Пусть
дан ряд с положительными членами и
существует конечный или бесконечный
предел
,
тогда ряд сходится прии
расходится при.
Доказательство:
Так как
,
то по определению предела для любогонайдется натуральное число
такое, что при
выполняется неравенство
или
(2).
Пусть.
Можно подобратьтак,
что число.
Обозначим.
Тогда из правой части неравенства (2)
получаемили
.
В силу свойств всех 3 числовых рядов
можно считать, чтодля всех
.
Давая номеруэти значения получим целый набор
неравенств:
………..
Т.е. члены ряда
меньше соответствующих членов ряда
,
который сходится как геометрическая
прогрессия со знаменателем.
Но тогда на основании признака сходимости
сходится и ряд.
Следовательно, сходится и исходный ряд.
Пусть
.
В этом случае.
Отсюда следует, что, начиная с некоторого
номера,
выполняется неравенствоили
,
т.е. члены ряда с увеличением номеравозрастают, поэтому
.
На основании следствия из необходимого
признака этот ряд расходится.
-
Если
,
то рядможет быть как сходящимся, так и
расходящимся. -
Признак Даламбера
целесообразно применять, когда общий
член ряда содержит выражения вида
.
Пример.
Исследовать на
сходимость ряд.
Находим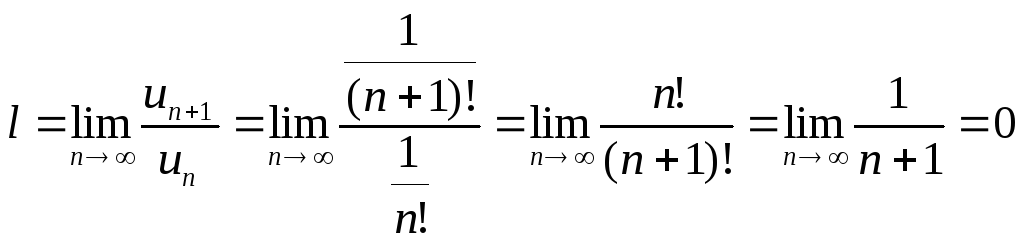
Так как,
то данный ряд по признаку Даламбера
сходится.
5.5. Радикальный признак Коши
Иногда удобно
пользоваться радикальным признаком
Коши для исследования сходимости
знакоположительного ряда. Этот признак
во многом схож с признаком Даламбера.
Теорема. Пусть
дан ряд
с положительными членами и существует
конечный или бесконечный предел.
Тогда ряд сходится прии расходится при
.
При
вопрос о сходимости остается открытым.
(Без доказательства).
Пример. Исследовать
на сходимость ряд
.
Так как,
то применим признак Коши к ряду.
Вычисляем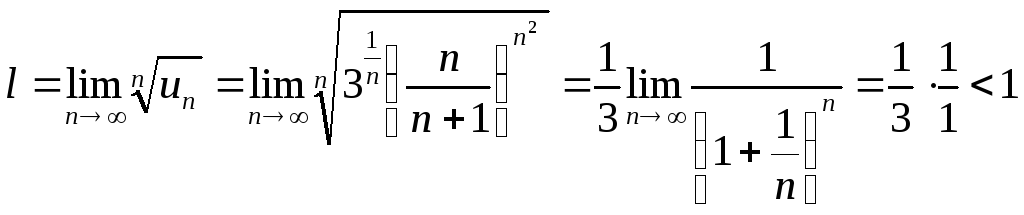
т.е. этот ряд сходится, значит, сходится
и исходный ряд согласно свойству 1
числовых рядов.
5.6. Интегральный признак Коши. Обобщенный гармонический ряд
Теорема. Если
члены знакоположительного ряда
могут быть представлены как числовые
значения некоторой непрерывно монотонно
убывающей на промежуткефункции
так, что
то
-
е
сли
сходится,
то сходится и ряд.
-
если
расходится, то расходится также и ряд
.
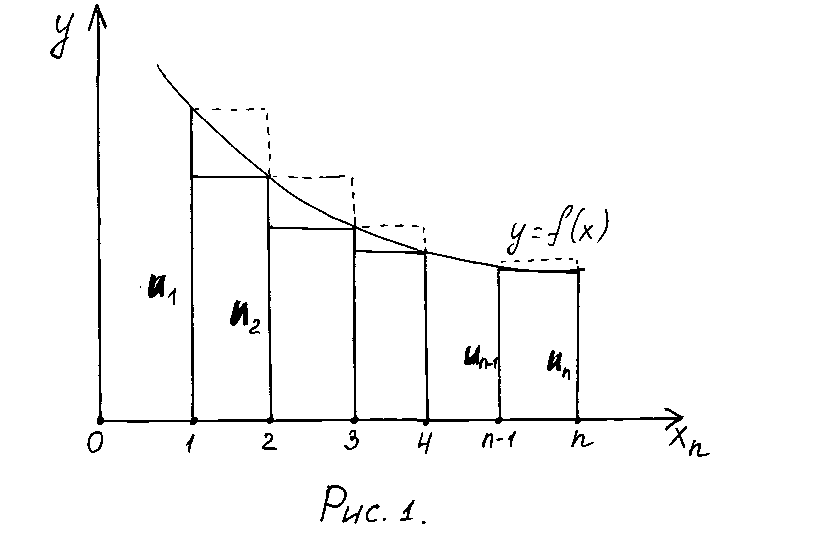
Рассмотрим
криволинейную трапецию, ограниченную
сверху графиком функции
,
основанием которой служит отрезок осиот
до
(рис.1). Построим входящие и выходящие
прямоугольники, основаниями которых
служат отрезки.
Учитывая геометрический смысл
определенного интеграла можно записатьили
или
(1).
Случай 1.
несобственный интеграл
сходится, т.е.
.
Поскольку<
,
то с учетом неравенства (1) имеем
,
т.е..Так
как последовательность частичных сумм
монотонно возрастает и ограничена
сверху (числом
),
то по признаку существования предела,
имеет предел. Следовательно, рядсходится.
Случай 2.
Несобственный
интеграл
расходится, тогда
и интеграл
неограниченно возрастает при
.
Учитывая, что(см. 1) получаем, что
при
.
Следовательно, рядрасходится.
Пример. Исследовать
на сходимость ряд
.
Воспользуемся интегральным признаком
Коши. Функцияудовлетворяет условиям теоремы. Поэтому
находим.
Значит, ряд с общим членомрасходится.
Ряд,
где– действительное число называетсяобобщенным
гармоническим рядом.
Для исследования этого ряда на сходимость
применим интегральный признак Коши.
Рассмотрим функцию
.
Эта функция непрерывна, монотонно
убывает на промежуткеи
.
Приимеем:
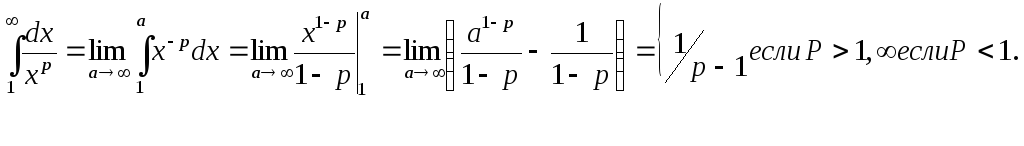
Приимеем
гармонический ряд,
который расходится (второй способ).
Итак, гармонический ряд сходится при,
расходится при.
Рассмотренные
признаки сходимости знакоположительных
рядов позволяют судить о сходимости
практически любого положительного
ряда.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #

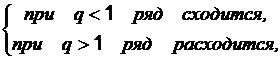
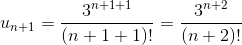
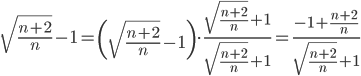
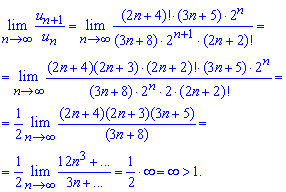
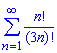
 сли
сли