Как найти сходимость ряда в точке - Исправление недочетов и поиск решений вместе с Examum.ru

Лекция
4 1

4.1.
Функциональные ряды: основные понятия,
область сходимости 1

4.2.
Степенные ряды: основные понятия,
теорема Абеля 2

4.3.
Свойства степенных рядов 5

4.4.
Формула Тейлора 5

4.1. Функциональные ряды: основные понятия, область сходимости

Определение
1.
Ряд, члены которого являются функциями
одной
или нескольких независимых переменных,
определёнными
на некотором множестве,
будем называть функциональным
рядом.

Рассмотрим
функциональный ряд,
члены которого являются функциями одной
независимой переменной х.
Сумма первых n
членов ряда

является частичной суммой данного
функционального ряда. Общий член

есть функция от х,
определенная в некоторой области. Если
положить
,
получим числовой ряд
,
и если он сходится, т.е. существует предел
частичных сумм этого ряда,
где

− сумма числового ряда, тогда говорят,
что

− точка сходимости функционального
ряда
,
а если числовой ряд

расходится, то

называется точкой расходимости
функционального ряда.

Определение
2.
Областью
сходимости
функционального ряда

называется множество всех таких значений
х,
при которых функциональный ряд сходится.
Область сходимости, состоящая из всех
точек сходимости, обозначается
.
Отметим, что
.

Будем
говорить, что функциональный ряд сходится
в области
,
если для любого

он сходится как числовой, при этом его
сумма будет некоторой функцией

(это так называемая предельная
функция
последовательности
:
).

Как
находить область сходимости функционального
ряда
?
Можно использовать признак, аналогичный
признаку Даламбера. Для ряда

составляем

и рассматриваем предел при фиксированном
х:
.
Тогда

является решением неравенства

и решением уравнения

(берем только те решения уравнения, в
которых соответствующие числовые ряды
сходятся).

Пример
1.
Найти область сходимости ряда
.

Решение.
Обозначим
,
.
Составим и вычислим предел
,
тогда область сходимости определяется
неравенством

и уравнением
.
Исследуем дополнительно сходимость
исходного ряда в точках, являющимися
корнями уравнения: а) если
,
,
то получается расходящийся ряд
;
б) если
,
,
то ряд

сходится условно (по признаку Лейбница,
пример 1, лекция 3).
Таким образом,
область сходимости

ряда

имеет вид:
.

4.2. Степенные ряды: основные понятия, теорема Абеля

Рассмотрим
частный случай функционального ряда,
так называемый степенной
ряд:
,
где
.

Определение
3.
Степенным
рядом
называется функциональный ряд вида
,
где

−
постоянные числа, называемые
коэффициентами
ряда.

Степенной
ряд есть «бесконечный многочлен»,
расположенный по возрастающим степеням
.
(Любой числовой ряд

является частным случаем степенного
ряда при
.)

Рассмотрим
частный случай степенного ряда при
:
.
Выясним, какой вид имеет область
сходимости данного ряда
.

Теорема
1 (теорема Абеля).
1) Если степенной ряд
(*)
сходится в точке
,
то он абсолютно сходится при всяком х,
для которого справедливо неравенство
.
2)
Если же степенной ряд расходится при
,
то он расходится при всяком х,
для
которого
.

Доказательство.
1) По условию степенной ряд сходится в
точке
,
т е. сходится числовой ряд
(**),
а значит, по необходимому признаку
сходимости его общий член стремится к
0, т.е.
.
Следовательно, существует такое число
,
что все члены ряда ограничены этим
числом:
.

Рассмотрим
теперь любое х,
для которого
,
и составим ряд из абсолютных величин:
.
Запишем этот ряд в другом виде: т.к.
,
то
(***).

Из
неравенства

получаем
,
т.е. ряд
(****)
состоит из членов, которые больше
соответствующих членов ряда (***). Ряд

представляет собой сходящийся ряд
геометрической прогрессии с знаменателем
,
причем
,
т.к.
.
Следовательно, ряд (***) сходится при
.
Таким образом, степенной ряд

абсолютно сходится.

2)
Пусть теперь ряд

расходится при
,
иными словами, расходится числовой ряд
.
Докажем, что для любого х
()
ряд расходится. Доказательство ведется
от противного. Пусть при некотором
фиксированном

()
ряд сходится, тогда он сходится при всех

(см. первую часть данной теоремы), в
частности, при
,
что противоречит условию 2 теоремы.
Теорема доказана.

Следствие.
Теорема Абеля позволяет судить о
расположении точки сходимости степенного
ряда.
Если точка

является точкой сходимости степенного
ряда, то интервал

заполнен точками сходимости; если точкой
расходимости является точка
,
то бесконечные интервалы

заполнены точками расходимости (см.
рис. 1).

Рис.
1.

Можно
показать, что существует такое число
,
что при всех

степенной ряд

абсолютно сходится, а при

− расходится. Будем считать, что если
ряд сходится только в одной точке 0, то
,
а если ряд сходится при всех
,
то
.

Определение
4.
Интервалом
сходимости
степенного ряда

называется такой интервал
,
что при всех

этот ряд сходится и притом абсолютно,
а для всех х,
лежащих вне этого интервала, ряд
расходится. Число R
называется радиусом
сходимости
степенного ряда.

Замечание.
На концах интервала

вопрос о сходимости или расходимости
степенного ряда решается отдельно для
каждого конкретного ряда.

Покажем
один из способов определения интервала
и радиуса сходимости степенного ряда.

Рассмотрим
степенной ряд

и обозначим
.
Составим ряд из абсолютных величин его
членов:

и применим к нему признак
Даламбера.

Пусть
существует
,
где
.
По признаку Даламбера ряд сходится,
если
,
и расходится, если
.
Отсюда ряд сходится при
,
тогда интервал сходимости:
.
При

ряд расходится, т.к.
.
Используя обозначение
,
получим формулу для определения радиуса
сходимости степенного ряда:
,
где

− коэффициенты степенного ряда. Если
окажется, что предел
,
то полагаем
.

Для
определения интервала и радиуса
сходимости степенного ряда также можно
использовать радикальный признак Коши,
радиус сходимости ряда определяется
из соотношения
.

Определение
5.
Обобщенным
степенным рядом называется ряд вида
.
Его также называют рядом по степеням
.
Для такого ряда интервал сходимости
имеет вид:
,
где

− радиус сходимости.

Покажем,
как находится радиус сходимости для
обобщенного степенного ряда.

,
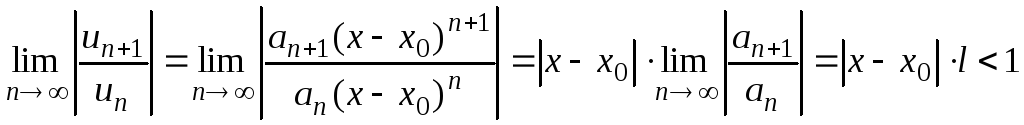
т.е.
,
где
.

Если
,
то
,
;
если
,
то

и область сходимости
.

Пример
2.
Найти область сходимости ряда
.

Решение.
Обозначим
.
Составим предел
.
Решаем неравенство:
,

,
следовательно, интервал сходимости
имеет вид:
,
причем R
= 5. Дополнительно исследуем концы
интервала сходимости: а)
,
,
получаем ряд
,
который
расходится;
б)
,

,
получаем ряд
,
который сходится условно. Таким образом,
область сходимости:
,
.

Пример
3.
Ряд

расходится для всех
,
т.к.

при
,
радиус сходимости
.

Пример
4.
Ряд

сходится при всех
,
радиус сходимости
.

Источник

Функциональные последовательности и ряды
в комплексной области

Основные понятия, связанные с функциональными последовательностями и рядами в комплексной области, вводятся так же, как и в действительной.

Определение функциональной последовательности

1. Рассмотрим функции f_1(z),f_2(z),ldots,f_n(z) , определенные на некотором множестве . Для любой точки z_0 этого множества (z_0in M) получаем последовательность комплексных чисел ${c_n},~n=1,2ldots$ , где c_n=f_n(z_0) . Если последовательность ${c_n}$ сходится, т.е. существует предел последовательности $lim_{ntoinfty}c_n=A$ , или, что то же самое, $lim_{ntoinfty}f_n(z_0)=A$ , то говорят, что функциональная последовательность ${f_n(z_0)}$ сходится в точке z_0 .

Множество точек , для которых существует предел последовательности $bigl{f_n(z)bigr}_{ninmathbb{N}}$ , называется областью сходимости функциональной последовательности (область ).

Пределом функциональной последовательности является функция, которая называется предельной функцией последовательности: $lim_{ntoinfty}f_n(z)=f(z),~zin D$ , что можно записать, учитывая определение сходимости числовой последовательности, следующим образом:

$lim_{ntoinfty}f_n(z)=f(z),~zin D quad Leftrightarrowquad forall varepsilon>0quad exists N(varepsilon,z)colon, bigl|f_n(z)-f(z)bigr|<varepsilon$ для n>N(varepsilon,z),~zin D .

Заметим, что в отличие от числовой последовательности (см. соответствующее определение) номер зависит не только от varepsilon , но и от .

Это естественно, так как для каждого фиксированного zin D получает определенная числовая последовательность и для нее номер , начиная с которого выполняется соответствующее неравенство, свой при одном и том же выбранном значении varepsilon . Для различных значений z_kin D получаем различные N(varepsilon,z_k) , т.е. последовательность номеров N_k,~k=1,2,ldots .

Равномерная сходимость функциональной последовательности

2. Если последовательность N_k,~k=1,2,ldots ограничена, т.е. существует N=N(varepsilon) , такое, что N_k<N для любого , то говорят, что функциональная последовательность f_n(z) сходится к f(z) на множестве равномерно, что обозначается f_n(z)Rightarrow f(z) . Таким образом,

f_n(z)Rightarrow f(z),~zin Dquad Leftrightarrowquad forall varepsilon>0quad exists N(varepsilon)colon, bigl|f_n(z)-f(z)bigr|<varepsilon для n>N(varepsilon) и forall zin D .

Функциональный ряд в комплексной области

3. Ряд, членами которого являются функции комплексного переменного u_n(z),~ n=1,2,ldots , определенные на некотором множестве комплексной плоскости, называется функциональным рядом в комплексной плоскости и обозначается

$sum_{n=1}^{infty}u_n(z).$

(3.1)

4. Последовательность $bigl{S_n(z)bigr}_{ninmathbb{N}}$ , где $S_n(z)= sum_{k=1}^{n}u_k(z)$ , называется последовательностью частичных сумм ряда (3.1), где S_1(z)= u_1(z),S_2(z)=u_1(z)+u_2(z),ldots — частичные суммы.

5. Ряд (3.1) называется сходящимся ни множестве , если на множестве сходится последовательность его частичных сумм, т.е. существует предел этой последовательности, который называется суммой ряда S(z)colon

$lim_{ntoinfty}S_n(z)=S(z),~ zin D;qquad sum_{n=1}^{infty}u_n(z)=S(z),~ zin D.$

(3.2)

Область сходимости и равномерная сходимость рядов

6. Множество точек zin D , для которых сходится ряд, называется областью сходимости ряда (3.1). Очевидно, для суммы S(z) ряда в области сходимости справедливо неравенство

$bigl|S_n(z)-S(z)bigr|<varepsilonquad text{for}quad n>N(varepsilon,z),~ zin D.$

(3.3)

7. Ряд (3.1) называется равномерно сходящимся на множестве , если на этом множестве равномерно сходится последовательность ${S_n(z)}$ , то есть

$bigl|S_n(z)-S(z)bigr|<varepsilonquad text{for}quad n>N(varepsilon),~ forall zin D.$

(3.4)

Равномерно сходящиеся ряды (и последовательности) непрерывных функций комплексной переменной, как и аналогичные ряды в действительной области, обладают свойствами конечных сумм, в частности сумма такого ряда является функцией, непрерывной на множестве, где ряд сходится равномерно. Кроме того, ряд можно почленно интегрировать. Это означает, что полученный ряд, т.е. ряд, членами которого являются интегралы от членов данного ряда, сходится и его сумма равна интегралу от суммы данного ряда:

$sum_{n=1}^{infty}int u_n(z),dz= int sum_{n=1}^{infty}u_n(z),dz= int S(z),dz,.$

(3.5)

Признак Вейерштрасса и равномерная сходимость

8. Для исследования функционального ряда на равномерную сходимость и нахождения области его равномерной сходимости можно использовать, как и в действительной области, достаточный признак равномерной сходимости.

Теорема 3.1 (признак Вейерштрасса). Если ряд (3.1) на множестве мажорируется сходящимся числовым рядом с положительными членами, то он сходится на равномерно, т.е. из условия

$bigl|u_n(z)bigr|<c_n,~ n>k,~ kgeqslant1,~ zin D;qquad sum_{n=1}^{infty}c_n~ text{shoditsya},~c_n>0$

(3.6)

следует равномерная сходимость ряда (3.1) на множестве .

9. Для равномерно сходящихся рядов аналитических функций справедливы отмеченные выше свойства непрерывности суммы ряда и почленного интегрирования. Кроме того, имеет место свойство, связанное с почленным дифференцированием ряда.

Теорема Вейерштрасса для рядов аналитических функций

Теорема 3.2 (теорема Вейерштрасса для рядов аналитических функций). Если ряд (3.1) аналитических в области функций u_n(z) равномерно сходится внутри , т.е. на любом замкнутом подмножестве overline{B}subset D , то сумма S(z) ряда аналитична в ; ряд можно почленно дифференцировать любое число раз, причем ряд, членами которого являются производные $u_n^{(k)}(z)$ , равномерно сходится на любом overline{B}subset D , и сумма такого ряда равна производной $S^{(k)}(z)$ от суммы исходного ряда, т.е.

$sum_{n=1}^{infty}u_{n}^{(k)}(z)= S_{n}^{(k)}(z),quad kin mathbb{N}.$

(3.7)

Нахождение области сходимости рядов

Так как по определению ряд (3.1) сходится в точке z_0 , если сходится числовой ряд $sum_{n=1}^{infty}u_n(z_0)$ , то для нахождения всех таких точек, т.е. области сходимости ряда, можно использовать известные признаки сходимости числовых рядов (признаки абсолютной сводимости). Так, можно найти пределы:

$lim_{ntoinfty}left|frac{u_{n+1}(z)}{u_n(z)}right|=bigl|f(z)bigr|,qquad lim_{ntoinfty}sqrt[LARGE{n}]{bigl|u_n(z)bigr|}= bigl|f(z)bigr|.$

(3.8)

Согласно признакам Даламбера (в первом случае) и Коши (во втором случае) область абсолютной сходимости ряда образуют те точки , для которых |f(z)|<1 .

Граничные точки, т.е. точки, для которых выполняется равенство |f(z)|<1 , могут быть как точками абсолютной или условной сходимости, так и точками расходимости.

Примеры исследования сходимости рядов с комплексными членами

Пример 3.1. Исследовать сходимость рядов с комплексными членами:

а) $sum_{n=1}^{infty}z^n$ ; б) $frac{z^n}{2^n}$ ; в) $sum_{n=1}^{infty} n!z^n$ ; г) $sum_{n=1}^{infty}frac{z^n}{n!}$ .

Решение

Все ряды, очевидно, сходятся в точке z=0 , так как $lim_{ntoinfty}S_n(0)=0$ . Исследуем их сходимость в других точках. Для первых двух рядов используем признак Коши (найдем $lim_{ntoinfty}sqrt[LARGE{n}]{|u_n(z)|}=|f(z)|$ ), а для других — признак Даламбера (найдем $lim_{ntoinfty} left|frac{u_{n+1}(z)}{u_n(z)}right|= |f(z)|$ ).

а) Имеем $lim_{ntoinfty}sqrt[LARGE{n}]{|z|^n}=|z|$ ; неравенство |z|<1 определяет область сходимости ряда. Границей области является окружность |z|<1 или, в комплексной форме, $z=e^{ivarphi},~ 0leqslantvarphi<2pi$ . Для точек границы получаем числовые ряды вида $sum_{n=1}^{infty}e^{invarphi}$ , или $sum_{n=1}^{infty} cos nvarphi+ i sum_{n=1}^{infty}sin nvarphi$ , очевидно, расходящиеся, так как пределы $lim_{ntoinfty}cos nvarphi$ и $lim_{ntoinfty}sin nvarphi$ не существуют. Область сходимости ряда — круг |z|<1 .

б) $lim_{ntoinfty}sqrt[LARGE{n}]{left|frac{z^n}{2^n}right|}= frac{|z|}{2}<1$ . Неравенство |z|<2 определяет область сходимости ряда. В точках границы, уравнение которой $z=2e^{ivarphi}$ , получаем расходящиеся ряды. Область сходимости ряда — круг |z|<2 .

в) $lim_{ntoinfty}left|frac{(n+1)!z^{n+1}}{n!z^n}right|= |z| lim_{ntoinfty}(n+1)=infty$ для любого zne0 . Ряд сходится только в одной точке z=0 .

г) $lim_{ntoinfty}left|frac{z^{n+1}n!}{(n+1)!z^n}right|= |z|lim_{ntoinfty}frac{1}{n+1}= 0<1$ для любого zne0 . Ряд сходится всюду, во всей комплексной плоскости mathbb{C} .

Пример 3.2. Исследовать сходимость комплексных функциональных рядов:

а) $sum_{n=1}^{infty}frac{1}{z^n}$ ; б) $sum_{n=1}^{infty}frac{2^n}{z^n}$ ; в) $sum_{n=1}^{infty}frac{1}{n!z^n}$ ; г) $sum_{n=1}^{infty}frac{n!}{z^n}$ .

Решение

Пример 3.3. Найти области сходимости рядов: а) $sum_{n=1}^{infty}3^n(z-i)^n$ ; б) $sum_{n=1}^{infty}frac{n}{2^{n^2}(z+i)^n}$ .

Решение

Пример 3.4. Исследовать сходимость комплексного ряда $sum_{n=1}^{infty} left(frac{2^n}{z^n}+ frac{z^n}{3^n}right)$ .

Решение

Общий член данного ряда имеет вид $u_n(z)= frac{2^n}{z^n}+ frac{z^n}{3^n}$ , то есть

$u_1(z)= frac{2}{z}+frac{z}{3}=frac{6+z^2}{3z},quad u_2(z)= frac{4}{z^2}+ frac{z^2}{9}= frac{36+z^4}{9z^2},quad ldots$

Рассмотрим два вспомогательных ряда $sum_{n=1}^{infty}frac{2^n}{z^n}$ и $sum_{n=1}^{infty}frac{z^n}{3^n}$ , найдем их области сходимости. Первый ряд сходится в области |z|>2 , второй — в круге |z|<3 (см. п. «б» примеров 3.1 и 3.2). Пересечение областей сходимости рядов образует кольцо 2<|z|<3 . В любой точке этого кольца сходятся оба ряда, т.е. сходятся соответствующие числовые ряды. По свойствам числовых рядов сходящиеся ряды можно складывать, общий член полученного при сложении ряда равен сумме общих членов рядов — слагаемых. В данном случае, складывая два ряда, сходящиеся при любом , принадлежащем кольцу 2<|z|<3 , получим ряд с общим членом $left(frac{2^n}{z^n}+ frac{z^n}{3^n}right)$ . Следовательно, исходный функциональный ряд сходится в кольце 2<|z|<3 .

Пример 3.5. Найти область сходимости ряда $sum_{n=1}^{infty} left(frac{z-2i}{z+i}right)^n$ .

Решение

Находим предел $lim_{ntoinfty}sqrt[LARGE{n}]{|u_n(z)|}= lim_{ntoinfty}sqrt[LARGE{n}]{left|frac{z-2i}{z+i}right|^n|}= left|frac{z-2i}{z+i}right|$ . Область сходимости определяем из неравенства $left|frac{z-2i}{z+i}right|<1$ , то есть |z-2i|<|z+i| . Границей множества является линия, комплексное уравнение которой |z-2i|= |z+i| . Геометрически — это прямая, проходящая через середину отрезка, соединяющего точки z=2i и z=-i перпендикулярно этому отрезку. Уравнение этой линии $y=frac{1}{2}$ , то есть $operatorname{Im}z= frac{1}{2}$ . Эта линия разделяет плоскость на две части: $operatorname{Im}z>frac{1}{2}$ и $operatorname{Im}z<frac{1}{2}$ . Областью сходимости ряда будет Imz > —, так как, например, для точки z=i , принадлежащей этой области, неравенство |z-2i|< |z+i| выполняется.

Пример 3.6. Доказать, что ряд $sum_{n=1}^{infty}frac{z^n}{3^n}$ сходится равномерно в круге |z|<1 .

Решение

Для точек , удовлетворяющих неравенству |z|<1 , выполняется неравенство $left|frac{z^n}{3^n}right|<frac{1}{3^n}$ , т.е. функциональный ряд в круге |z|<1 мажорируется числовым рядом $sum_{n=1}^{infty}frac{1}{3^n}$ . Так как ряд $sum_{n=1}^{infty}left(frac{1}{3}right)^n$ сходится, то по признаку Вейерштрасса данный функциональный ряд в круге |z|<1 сходится равномерно.

Заметим, что, очевидно, ряд сходится равномерно и в большей области, а именно в любой области overline{B} вида |z|leqslant r,~ 0<r<3 , так как мажорируется в этой области сходящимся числовым рядом: $left|frac{z}{3}right|^n leqslant left(frac{r}{3} right)^n=q^n$ , а при q<1 ряд $sum_{n=1}^{infty}q^n$ сходящийся. Как отмечено выше, в таком случае говорят, что ряд сходится равномерно внутри круга |z|<3 .

Пример 3.7. Найти область равномерной сходимости ряда $sum_{n=1}^{infty} frac{e^{nz}}{n^2}$ .

Решение

Воспользуемся признаком Вейерштрасса. Поскольку числовой ряд $sum_{n=1}^{infty}frac{1}{n^2}$ сходится, то область равномерной сходимости данного ряда будут составлять те , для которых справедливо неравенство $|e^{nz}|<1$ , так как при этом справедливо неравенство $left|frac{e^{nz}}{n^2} right|<frac{1}{n^2}$ . Учитывая равенство $|e^z|=e^{operatorname{Re}z}$ , получаем $|e^{nz}|=e^{nx}$ . Для нахождения области равномерной сходимости нужно рассмотреть неравенство $e^{nx}<1$ , которое, очевидно, выполняется при любых отрицательных значениях . Поэтому областью равномерной сходимости данного ряда является множество operatorname{Re}z<0 — левая полуплоскость, или любое множество вида operatorname{Re}zleqslant a,~ a<0 .

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

(схема 48)

Числовым рядом (или просто рядом) называется бесконечная сумма вида

, (9.1)

где – действительные или комплексные числа, называемые членами
ряда, u_n–
общим
членом ряда.

Если известен общий член ряда как функция его номера n: u_n=f(n), то ряд
считают заданным.

Сумма первых n членов ряда (9.1) называется n-ой частичной суммой ряда S_n, то есть S_n = u₁ + u₂ +…+ u_n.

Рассмотрим последовательность частичных сумм ряда
(9.1):

. (9.2)

Если существует конечный предел последовательности
частичных сумм (9.2), то этот предел называют суммой
ряда, а сам ряд – сходящимся числовым рядом. При этом
записывают:.

Если не существует или , то ряд (9.1) называют расходящимся. Говорят, что такой ряд
суммы не имеет.

Ряд называется остатком
ряда после n-го члена или n-ым остатком ряда.

Сформулируем некоторые свойства числовых рядов.

1. Если ряд (9.1) сходится и его сумма равна S, то ряд

(9.3)

где
c – произвольное
число, также сходится и его сумма равна cS. Если же ряд (9.1) расходится и c ≠ 0, то и ряд (9.3) расходится.

2. Если сходится ряд (9.1) и сходится ряд , при этом S₁ и S₂ – их соответствующие суммы, то сходятся также ряды, причём сумма каждого равна
соответственно S₁± S₂.

Следствие.
Сумма (разность)
сходящегося и расходящегося рядов есть расходящийся ряд

Примечание. Сумма (разность) двух расходящихся рядов
может быть как сходящимся, так и расходящимся рядом.

3. Если к ряду (9.1) прибавить или отбросить конечное
число членов, то полученный ряд и ряд (9.1) сходятся или расходятся
одновременно.

Следствие. Если ряд (9.1) сходится, то
его n-ый остаток r_n
стремится к нулю при n→∞, то есть .

Теорема 9.1
(необходимый признак сходимости числового ряда). Если ряд (9.1)
сходится, то его общий член u_n стремится к нулю при неограниченном возрастании n, то есть .

Следствие (достаточное
условие расходимости ряда). Если или этот предел не
существует, то ряд расходится

Таким образом, из того, что общий член
ряда стремится к нулю при n→∞, еще не следует, что ряд сходится.

Пример 9.1. Исследовать на сходимость ряд .

Решение. Вычислим предел общего члена ряда:

, то есть выполняется достаточное условие расходимости ряда.
Следовательно, заданный ряд расходится

Во многих случаях на вопрос о
сходимости или расходимости числового ряда можно ответить с помощью достаточных
признаков.

Сходимость или расходимость знакоположительного ряда
часто устанавливается путем сравнения его с другим рядом, о котором известно,
сходится он или нет. Подобное сравнение базируется на теоремах 9.2 и 9.3.

Теорема 9.2
(признак сравнения числовых знакоположительных рядов). Пусть даны два знакоположительных ряда

(9.4) и (9.5)

Если для всех n, начиная с некоторого номера N, выполняется неравенство , то из сходимости ряда (9.5) следует сходимость ряда (9.4),
а из расходимости ряда (9.4) следует расходимость ряда (9.5)

В этом случае ряд (9.4) называется минорантным,
а ряд (9.5) – мажорантным рядом.

Пример 9.2. Исследовать на сходимость ряд .

Решение. Общий член заданного ряда. Рассмотрим минорантный ряд с общим членом, который расходится (гармонический ряд (9.6)). Следовательно, заданный по условию ряд
(мажорантный) расходится и подавно

Теорема 9.3.
(признак сравнения в предельной форме)

Пусть даны два знакоположительных ряда (9.4) и (9.5).
Если существует конечный, отличный от нуля, предел , то ряды (9.4) и (9.5) сходятся или расходятся одновременно

Теорема 9.4
(признак Даламбера). Если в ряде (9.1) с положительными членами отношение последующего члена ряда к
предыдущему при n→∞ имеет конечный или бесконечный предел , то при
l<1 ряд сходится и расходится
при l>1

Примечание. Если l=1, то ряд (9.1) может быть как сходящимся, так и
расходящимся

Признак Даламбера целесообразно применять, когда общий
член ряда содержит факториалы и показательные выражения.

Пример 9.3. Исследовать на сходимость ряд .

Решение. Согласно теореме 9.4 вычислим величину . Следовательно, по признаку Даламбера
заданный ряд сходится

Теорема 9.5
(радикальный признак Коши). Если для ряда (9.1) с положительными членами существует
конечный или бесконечный предел , то при при
l<1 ряд сходится и расходится
при l>1

Пример 9.4. Исследовать на сходимость ряд .

Решение. Учитывая теорему 9.5 и второй замечательный предел (3.13), вычисляем:

. Следовательно, по
радикальному признаку Коши заданный ряд сходится

Теорема 9.6
(интегральный признак Коши). Если
члены знакоположительного числового ряда  могут быть
представлены как числовые значения некоторой непрерывной монотонно убывающей на
промежутке [1;∞) функции f(x) так, что u₁= f(1), u₂= f(2), …,
u_n= f(n), …, то если  сходится, то сходится
и ряд (9.1); если расходится, то
расходится также и ряд (9.1)

Пример 9.5. Исследовать на сходимость ряд .

Решение. Для исследования ряда на сходимость применим интегральный признак Коши – рассмотрим несобственный интеграл

Так как несобственный интеграл от общего члена ряда сходится, то и исходный ряд также сходится (согласно теореме 9.6)

Особое значение в теории числовых рядов (в частности,
при их сравнении) имеет обобщенный гармонический ряд

, (9.6)

где
p>0 –
действительное число. Для
исследования ряда (9.6) применим теорему 9.6 (интегральный признак Коши).

Рассмотрим функцию . Она непрерывна и монотонно убывает на промежутке [1;∞), при этом . При p ≠ 1 имеем:

При p = 1
имеем гармонический ряд , который расходится . Итак, ряд (9.6) сходится при p>1, расходится при p≤1.

Примечание. Знакоотрицательный ряд переходит в
знакоположительный путем умножения его
на (–1), что не влияет на сходимость
ряда

Помимо знакоположительных числовых рядов существует
важный класс знакопеременных рядов, в которых члены ряда имеют произвольные
знаки.

Числовой ряд , содержащий бесконечное множество положительных и
бесконечное множество отрицательных членов, называется знакопеременным.

Теорема 9.7
(общий достаточный признак сходимости). Пусть
дан знакопеременный ряд

u₁ + u₂ +…+ u_n (9.7)

Если сходится ряд

(9.8)

составленный
из модулей членов данного ряда, то сходится и сам знакопеременный ряд (9.7)

Знакопеременный ряд называется абсолютно сходящимся,
если ряд, составленный из модулей его членов, сходится.

Знакопеременный ряд называется условно сходящимся, если
сам он сходится, а ряд, составленный из модулей его членов, расходится.

Сформулируем основные свойства абсолютно сходящихся
рядов.

1. Если ряд абсолютно сходится и имеет сумму S, то ряд,
полученный из него перестановкой членов, также сходится и имеет ту же сумму S, что и
исходный ряд.

2. Абсолютно сходящиеся ряды с суммами S₁ и S₂ можно
почленно складывать (вычитать). В результате получается абсолютно сходящийся
ряд, сумма которого равна S₁ + S₂ (S₁ – S₂).

3. Произведение двух абсолютно сходящихся рядов с
суммами S₁ и S₂ есть абсолютно сходящийся ряд, сумма которого равна S₁ ∙ S₂.

Примечание. В случае условно сходящихся рядов подобные свойства,
вообще говоря, места не имеют.

Используя указанные свойства, математические действия и операции производят только над абсолютно сходящимися
рядами. Для установления абсолютной сходимости используют все признаки
сходимости знакоположительных рядов, заменяя всюду общий член ряда его модулем.

Частным случаем знакопеременных рядов являются знакочередующиеся
ряды, члены которых имеют строго
чередующиеся знаки:

, (9.9)

где
u_n>0 для всех .

Для знакочередующихся рядов имеет место следующий
достаточный признак сходимости.

Теорема 9.8
(признак Лейбница). Знакочередующийся
ряд (9.9) сходится, если последовательность абсолютных величин его членов монотонно убывает (u₁ > u₂ > u₃>…> u_n>) и общий член ряда по абсолютной величине стремится к
нулю при n→∞, то есть . При этом сумма S ряда (9.9) удовлетворяет неравенствам 0 < S < u₁

Пример 9.6. Исследовать на сходимость ряд .

Решение. Это знакочередующийся ряд, для которого выполняются
условия теоремы 9.8. Действительно, предел общего члена ряда и члены ряда монотонно
убывают по абсолютной величине:. Следовательно, заданный ряд сходится. Однако, ряд,
составленный из модулей его членов, то есть ряд – расходится, так как
является гармоническим. Значит, заданный по условию знакочередующийся ряд
сходится условно

Ряд, членами которого являются функции от переменной x, называется функциональным:

(9.10)

Придавая x определённое значение x₀, мы
получим числовой ряд , который может быть как сходящимся, так и расходящимся.

Если полученные числовой ряд сходится, то точка x₀ называется точкой сходимости ряда (9.10); если
же ряд расходится – точкой расходимости функционального ряда. Совокупность числовых
значений аргумента x, при которых функциональный ряд сходится, называется
его областью
сходимости.

В области сходимости функционального ряда его сумма
является некоторой функцией от x: S= S(x), которая определяется равенством:

– частичная сумма
ряда.

Частным случаем
функционального ряда является степенной ряд, члены которого представляют
собой степенные функции аргумента x:

(9.11)

Действительные (или комплексные) числа называются коэффициентами
ряда (9.11), – действительная
переменная.

Ряд (9.11) называется разложением по степеням x. На практике часто работают со
степенным рядом, разложенным по степеням (x
– x₀):

(9.12)

где x₀–
некоторое постоянное число.

Рассмотрим вопрос о нахождении области сходимости
степенного ряда.

Теорема 9.9
(Абеля о сходимости степенного ряда). Если
степенной ряд сходится при некотором значении x₀ ≠ 0, то
он абсолютно сходится при всех значениях x, удовлетворяющих неравенству |x|<| x₀|; если ряд
(9.11) расходится при x = x₁, то он
расходится при всех x,
удовлетворяющих неравенству |x|>| x₁|

Из теоремы Абеля следует, что если x₀ ≠ 0 есть точка сходимости степенного ряда, то интервал (–|x₀|;|x₀|) весь
состоит из точек сходимости данного ряда; при всех значениях x вне этого
интервала ряд (9.11) расходится (рис. 9.1). Интервал (–|x₀|;|x₀|)
называют интервалом сходимости степенного ряда. Положив |x₀|=R, интервал сходимости можно записать в виде (–R;R). Число R называют радиусом
сходимости степенного ряда, то есть R > 0 – это
такое число, что при всех x, для которых |x| < R,
ряд (9.11) абсолютно сходится, а при |x| > R
ряд расходится.

Если ряд (9.11) сходится в одной точке x₀ = 0, то полагают, что R=0. Если же он сходится при всех действительных
значениях x, то его радиус сходимости R=∞.

На практике радиус сходимости степенного ряда (9.11)
отыскивают с помощью признака Даламбера. Для этого составляют ряд из модулей
членов ряда:

и применим к нему
признак Даламбера. Допустим, что существует предел

По теореме 9.4 ряд сходится, если, то есть ряд сходится при тех значениях x, для
которых. Ряд, составленный из
модулей членов ряда (9.11), расходится при тех значениях x, для
которых . Таким образом, для ряда (9.11) радиус абсолютной сходимости
вычисляется по формуле:

. (9.13)

С помощью радикального признака Коши (теоремы 9.5) можно
показать, что радиус сходимости также вычисляется по формуле:

. (9.14)

Примечание. Интервал сходимости степенного ряда (9.12) находят из
неравенства |x– x₀| < R; он имеет вид (x₀–R; x₀+R)

Пример 9.7. Найти область сходимости ряда .

Решение. Воспользуемся формулой (9.13) : .

Следовательно,
данный ряд абсолютно сходится в единственной точке х = 0.

Область
сходимости степенного ряда (9.11) уточняют на концах полученного интервала
сходимости, симметричного относительно начала координат. На его левом конце,
при  получают
знакочередующийся числовой ряд, сходимость которого исследуют с помощью
признака Лейбница (теорема 9.8). На правом конце интервала сходимости, при x=R получают
числовой ряд с положительными членами, который исследуют на сходимость с
помощью рассмотренных выше достаточных признаков – теорем
9.2-9.6. Если при  и (или) x=R получают
сходящийся числовой ряд, то
соответствующую точку включают в область сходимости степенного ряда. Если при  и (или) x=R получают
расходящийся числовой ряд, то
соответствующую точку включают в область расходимости степенного ряда.
Уточненный на концах интервал сходимости представляет собой область сходимости
степенного ряда (9.11).

Пример 9.8. Написать первые три члена ряда и найти его область сходимости.

Решение. Беря последовательно n = 1, 2, 3, …, запишем данный ряд в виде:

Для нахождения области сходимости ряда применим
признак Даламбера:

Данный ряд сходится абсолютно при тех значениях x, которые удовлетворяют неравенству

Исследуем сходимость ряда на концах полученного
интервала.

При заданный ряд принимает
вид . Последний ряд является знакочередующимся; абсолютная
величина его общего члена стремится к нулю при n→∞; члены ряда убывают по абсолютной
величине. Следовательно, по признаку
Лейбница этот ряд сходится. Значит, принадлежит области
сходимости данного ряда.