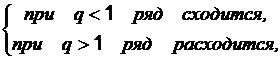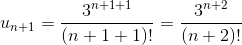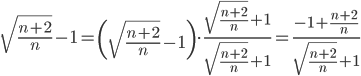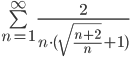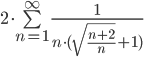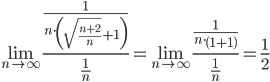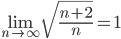Как найти сходящиеся ряды онлайн - Исправление недочетов и поиск решений вместе с Examum.ru

Признаки сходимости ряда

Определение. Числовым рядом называется бесконечная сумма членов последовательности:

.

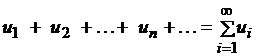
Признаки сходимости знакопостоянного числового ряда можно разделить на необходимый и достаточные.

Необходимый признак сходимости состоит в том, что: .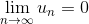

Если этот признак не выполняется, то ряд расходится.

Решение онлайн
Видеоинструкция

Правила ввода данных

В качестве переменной используйте только n.
Все математические операции выражаются через общепринятые символы (+ , - , * , / , ^ ). Например, 4ⁿ, записываем как 4^n.

Примеры

≡ n^2/(n+2)

≡ n+sqrt(n-1)

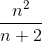
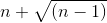
Это поле предназначено для ввода знаменателя дроби.

Правила ввода данных

Все математические операции выражаются через общепринятые символы ( + , - , * , / , ^ ). Например, 4ⁿ, записываем как 4^n.

Примеры

≡ n^2/(n+2)

≡ n+sqrt(n-1)

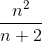
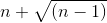
Рассмотрим четыре достаточных признака сходимости числового ряда .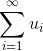

1. Признак Даламбера.

Если 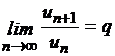, то

при q = 1 получаем неопределенность.

2. Радикальный признак Коши.

Если ,

при q = 1 получаем неопределенность.

3. Интегральный признак Коши.

Если 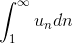существует, то ряд сходится; если интеграл не существует (т. е. равен ±∞) – ряд расходится.

4. Признак сравнения.

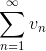
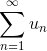
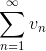
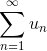
Если сходится и u_n ≤ v_n, то также сходится, если расходится и u_n ≥ v_n, то также расходится.

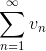
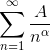
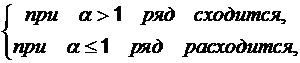
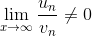
Для признака сравнения в качестве ряда часто используется , который , A — произвольная постоянная величина; причем .

5. Предельный признак сравнения.

Если предел отношений исходного ряда u_n с расходимым рядом v_n равен конечному числу, отличному от нуля, то ряд u_n расходится.

Если предел отношений исходного ряда u_n со сходимым рядом v_n равен конечному числу, отличному от нуля, то ряд v_n сходится.

Схема определения сходимости или расходимости ряда

ДаНетДаНетДаНетДаДаНетДаНетДаНетПреобразование и упрощениеЗамена на замечательные эквивалентностиФункция ограниченаЗамена на VnПризнаки сходимостиПризнаки сходимостиVn сходитсяUn≤VnVn расходитсяРяд Un сходитсяСходимость не определенаUn≥VnРяд Un расходитсяСходимость не определенаРяд сходитсяРяд Un сходитсяРяд расходитсяРяд Un расходитсяСходимость не определена

Пример 1. Исследовать ряд 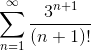на сходимость.

Решение:

Применим признак Даламбера:

;

= = ряд сходится.

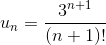
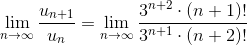
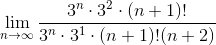
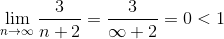
Пример 2. Исследовать ряд 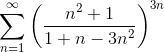на сходимость.

Решение:

Применим радикальный признак Коши:

ряд сходится.

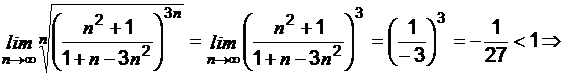
Замечание: 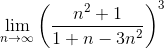вычисляем следующим образом: так как в числителе и знаменателе дроби старшие степени переменной n равны, то выписываем коэффициенты при n² соответственно из числителя и знаменателя.

Пример 3. Исследовать ряд 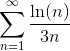на сходимость.

Решение:

Применим интегральный признак Коши:

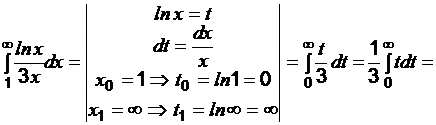
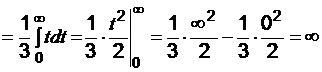
, так как интеграл не существует, то ряд расходится.

Пример 4. Исследовать ряд 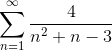на сходимость.

Решение:

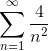
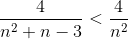
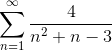
Сравним ряд с , который сходится, так как степень α переменной n: α=2 > 1. При этом , следовательно ряд также сходится.

Пример 5. Исследовать ряд 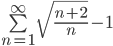на сходимость.

Решениие.

Исходное выражение преобразуем к виду:

Тогда исходный ряд можно представить в виде:

Коэффициент общего члена не влияет на сходимость или расходимость ряда, поэтому выносим его за пределы суммы:

Применим сравнительный признак. Рассмотрим ряд: , .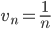

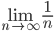
Поскольку u_n≤v_n, то если ряд v_n будет сходиться, то будет сходиться и исходный u_n.

По определению этот ряд расходится, здесь α≤1.

Проведя анализ ряда 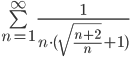можно сделать вывод, что признак сравнения здесь не применим (по условию ряд должен был сходиться, а он расходится). Поэтому продолжаем исследования далее. Используем предельный признак сравнения.

Сравним исследуемый ряд с расходящимся рядом:

здесь

Получено конечное число, отличное от нуля, значит, исследуемый ряд расходится.

Следовательно, ряд 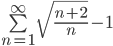расходится.

Источник

Проверить сходимость ряда можно несколькими способами. Во-первых можно просто найти
сумму ряда.
Если в результате мы получим конечное число, то такой
ряд сходится. Например, поскольку

то данный ряд сходится. Если нам не удалось найти сумму ряда, то следует использовать другие методы для проверки сходимости ряда.

Одним из таких методов является
признак Даламбера, который записывается следующим образом:

здесь

и

соответственно

и

члены ряда, а сходимость определяется значением
. Если

— ряд сходится, если

— расходится. При

— данный признак не даёт ответа и нужно проводить дополнительные исследования.

В качестве примера, исследуем сходимость ряда

с помощью признака Даламбера. Сначала запишем выражения для

и
.
Теперь найдем соответствующий
предел:

Поскольку
,
в соответствии с признаком Даламбера, ряд сходится.

Еще одним методом, позволяющим проверить сходимость ряда является
радикальный признак Коши, который записывается следующим образом:

здесь

— n-ый член ряда, а сходимость, как и в случае признака Даламбера, определяется значением
. Если

— ряд сходится, если

— расходится. При

— данный признак не даёт ответа и нужно проводить дополнительные исследования.

В качестве примера, исследуем сходимость ряда

с помощью радикального признака Коши. Сначала запишем выражение для

Теперь найдем соответствующий предел:

Поскольку
,
в соответствии с радикальным признаком Коши, ряд расходится.

Стоит отметить, что наряду с перечисленными, существуют и другие признаки сходимости рядов, такие как интегральный признак Коши, признак Раабе и др.

Наш онлайн калькулятор, построенный на основе системы Wolfram Alpha позволяет протестировать сходимость ряда. При этом, если калькулятор в качестве суммы ряда выдает конкретное число, то ряд сходится. В противном случае, необходимо обращать внимание на пункт «Тест сходимости ряда». Если там присутствует словосочетание «series converges», то ряд сходится. Если присутствует словосочетание «series diverges», то ряд расходится.

Ниже представлен перевод всех возможных значений пункта «Тест сходимости ряда»:

Текст на английском языке	Текст на русском языке
By the harmonic series test, the series diverges.	При сравнении исследуемого ряда с гармоническим рядом , исходный ряд расходится.
The ratio test is inconclusive.	Признак Даламбера не может дать ответа о сходимости ряда.
The root test is inconclusive.	Радикальный признак Коши не может дать ответа о сходимости ряда.
By the comparison test, the series converges.	По признаку сравнения, ряд сходится
By the ratio test, the series converges.	По признаку Даламбера, ряд сходится
By the limit test, the series diverges.	На основнии того, что , или указанный предел не существует, сделан вывод о том, что ряд расходится.

Источник

Сходимость ряда

Примеры суммы рядов

Тест сходимости ряда
```
n/(n^3-n^2-1)
```
Признак Даламбера ответа
```
(-1)^n/n!
```
Признак Коши (радикальный)
```
csc(n)^2/n^3
```
По интегральному признаку ряд сходится
```
(3*n - 1)/(-5)^n
```

Источник

bold{mathrm{Basic}}

bold{alphabetagamma}

bold{mathrm{ABGamma}}

bold{sincos}

bold{gedivrightarrow}

bold{overline{x}spacemathbb{C}forall}

bold{sumspaceintspaceproduct}

bold{begin{pmatrix}square&square\square&squareend{pmatrix}}

bold{H_{2}O}

square^{2}

x^{square}

sqrt{square}

nthroot[msquare]{square}

frac{msquare}{msquare}

log_{msquare}

theta

infty

int

frac{d}{dx}

ge	le	cdot	div	x^{circ}	(square)	\|square\|	(f:circ:g)	f(x)	ln	e^{square}
left(squareright)^{‘}	frac{partial}{partial x}	int_{msquare}^{msquare}	lim	sum	sin	cos	tan	cot	csc	sec

alpha	beta	gamma	delta	zeta	eta	theta	iota	kappa	lambda	mu
nu	xi	pi	rho	sigma	tau	upsilon	phi	chi	psi	omega

A	B	Gamma	Delta	E	Z	H	Theta	K	Lambda	M
N	Xi	Pi	P	Sigma	T	Upsilon	Phi	X	Psi	Omega

sin	cos	tan	cot	sec	csc	sinh	cosh	tanh	coth	sech
arcsin	arccos	arctan	arccot	arcsec	arccsc	arcsinh	arccosh	arctanh	arccoth	arcsech

begin{cases}square\squareend{cases}	begin{cases}square\square\squareend{cases}	=	ne	div	cdot	times	<	>	le	ge
(square)	[square]	▭:longdivision{▭}	times twostack{▭}{▭}	+ twostack{▭}{▭}	— twostack{▭}{▭}	square!	x^{circ}	rightarrow	lfloorsquarerfloor	lceilsquarerceil

overline{square}	vec{square}	in	forall	notin	exist	mathbb{R}	mathbb{C}	mathbb{N}	mathbb{Z}	emptyset
vee	wedge	neg	oplus	cap	cup	square^{c}	subset	subsete	superset	supersete

int	intint	intintint	int_{square}^{square}	int_{square}^{square}int_{square}^{square}	int_{square}^{square}int_{square}^{square}int_{square}^{square}	sum	prod
lim	lim _{xto infty }	lim _{xto 0+}	lim _{xto 0-}	frac{d}{dx}	frac{d^2}{dx^2}	left(squareright)^{‘}	left(squareright)^{»}	frac{partial}{partial x}

(2times2)	(2times3)	(3times3)	(3times2)	(4times2)	(4times3)	(4times4)	(3times4)	(2times4)	(5times5)
(1times2)	(1times3)	(1times4)	(1times5)	(1times6)	(2times1)	(3times1)	(4times1)	(5times1)	(6times1)	(7times1)

mathrm{Радианы}	mathrm{Степени}	square!	(	)	%	mathrm{очистить}
arcsin	sin	sqrt{square}	7	8	9	div
arccos	cos	ln	4	5	6	times
arctan	tan	log	1	2	3	—
pi	e	x^{square}	0	.	bold{=}	+

Подпишитесь, чтобы подтвердить свой ответ

Войдите, чтобы сохранять заметки

Войти

Номер Строки

Примеры

sum_{n=0}^{infty}frac{3}{2^n}
sum_{n=1}^{infty}frac{1}{n(n+1)}
sum_{n=1}^{infty}frac{(-1)^n}{n}
sum_{n=0}^{infty}frac{sin(n)}{n^2}
sum_{n=0}^{infty}frac{x^{n}}{n!}
sum_{n=1}^{infty}nx^{n}
Показать больше

Описание

Поэтапный признак сходимости рядов

series-calculator

Блог-сообщения, имеющие отношение к Symbolab

The Art of Convergence Tests

Infinite series can be very useful for computation and problem solving but it is often one of the most difficult…

Введите Задачу

Сохранить в блокнот!

Войти

Источник

Данный калькулятор предназначен для исследования ряда на сходимость.
Под числовым рядом понимается сумма членов числовой последовательности следующего вида: ∑^∞_n=1a_n=a₁+a₂+a₃+…, где все a — это числа. Если говорить о функциональном ряде, то все члены последовательности являются функциями: ∑^∞_n=1f_n(x)=f₁(x)+f₂(x)+f₃(x)+… Ряд, членами которого являются степенные функции, называется степенным рядом: ∑^∞_n=1a_nxⁿ.
Чтобы найти сходимость числового ряда, функционального ряда или степенного ряда, необходимо знать признаки сходимости рядов. Существует необходимый признак сходимости ряда: если ряд ∑^∞_n=1a_n сходится, то (lim)┬(n→∞)⁡an=0.

Однако данный признак не является гарантией сходимости ряда, поэтому рассматриваются также достаточные признаки сходимости. Признаки сравнения рядов заключаются в следующем. Даны два ряда ∑^∞_n=1a_n и ∑^∞_n=1b_n, при этом 0 < a_n < b_n. В таком случае, если ∑^∞_n=1b_n сходится, то также должен сходиться ряд ∑^∞_n=1a_n. Если ∑^∞_n=1a_n расходится, то ∑^∞_n=1b_n тоже расходится. Предельные признаки сравнения рядов состоят в следующем. Даны два ряда ∑^∞_n=1a_n и ∑^∞_n=1b_n, при этом a_n и b_n – положительны. Тогда, во-первых, если 0 < lim ⁡a_n/b_n < 0, то оба ряда сходятся или расходятся. Во-вторых, если lim a_n/b_n=0, то ∑^∞_n=1a_n сходится, если сходится ∑^∞_n=1b_n. В-третьих, если lim a_n/b_n=∞, то ∑^∞_n=1a_n расходится, если расходится ∑^∞_n=1b_n.
Калькулятор поможет определить сходимость или расходимость ряда онлайн. Расшифровка ответов следующая:

Для получения полного хода решения нажимаем в ответе Step-by-step.

converges — ряд сходится
not converges — ряд расходится.

Пожалуйста напишите с чем связна такая низкая оценка:

Для установки калькулятора на iPhone — просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android — просто добавьте страницу
«На главный экран»

Источник