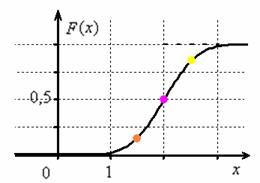
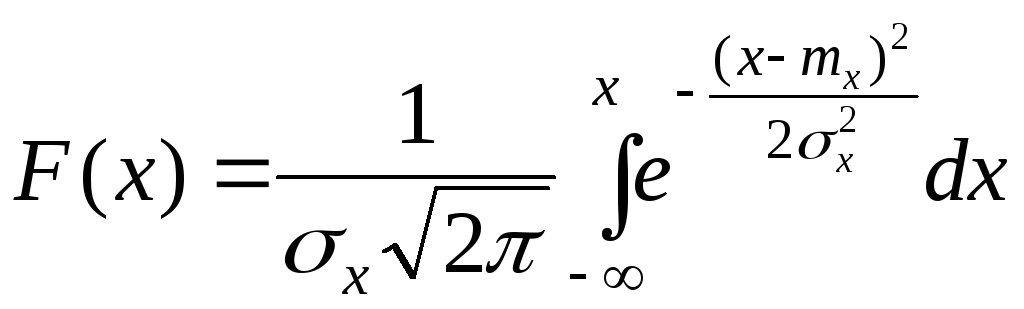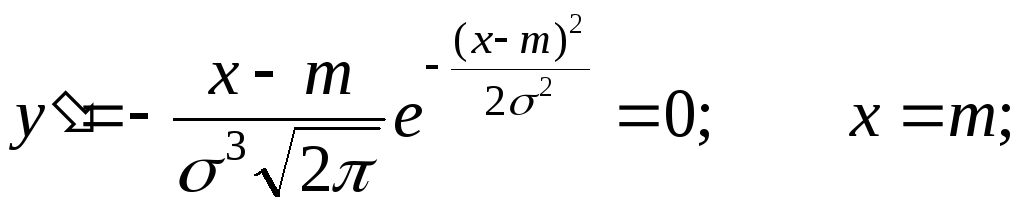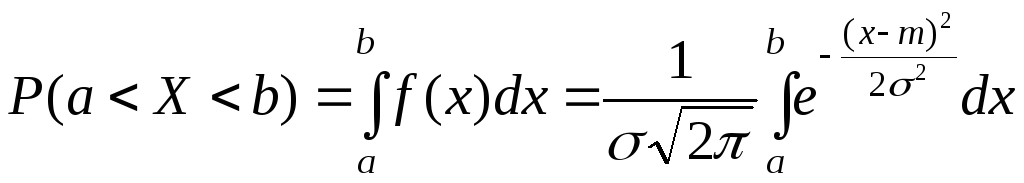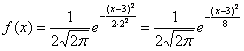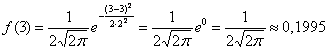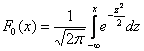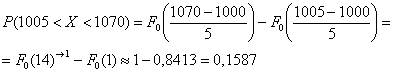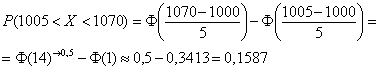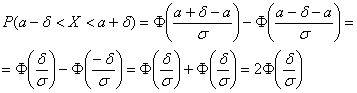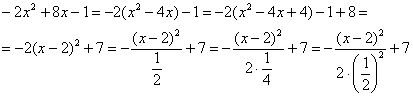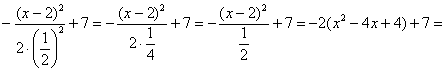Правило трех сигм
Содержание:
- В чем заключается правило трех сигм (3-sigma rule) в статистике
- Нормальное распределение случайной величины
- Примеры решения задач
В чем заключается правило трех сигм (3-sigma rule) в статистике
Определение
Математическое ожидание — это среднее значение случайной величины. Обозначается как (mu).
Определение
Стандартное или среднеквадратичное отклонение — это наиболее частый показатель рассеивания значений величины относительно математического ожидания. Обозначается символом (sigma), который произносится как «сигма».
Определение
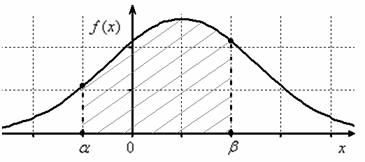
Правило трех сигм заключается в том, что при нормальном распределении практически все значения величины с вероятностью 0,9973 лежат не далее трех сигм в любую сторону от математического ожидания, то есть находятся в диапазоне (left[mu-3sigma;;mu+3sigmaright]).
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
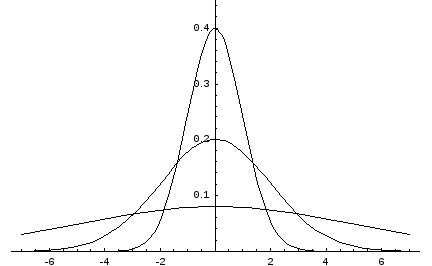
Приблизительно 99,7% всех значений лежат в пределе трех сигм от математического ожидания, около 95% — в пределах двух сигм, а примерно 68% значений лежат в пределах всего одной сигмы.
Те значения, которые выходят за рамки 3 сигм, принято считать грубыми ошибками. Большое количество таких ошибок может свидетельствовать о том, что распределение на самом деле не является нормальным. В этом заключается практическая польза правила 3 сигм.
Нормальное распределение случайной величины
Определение
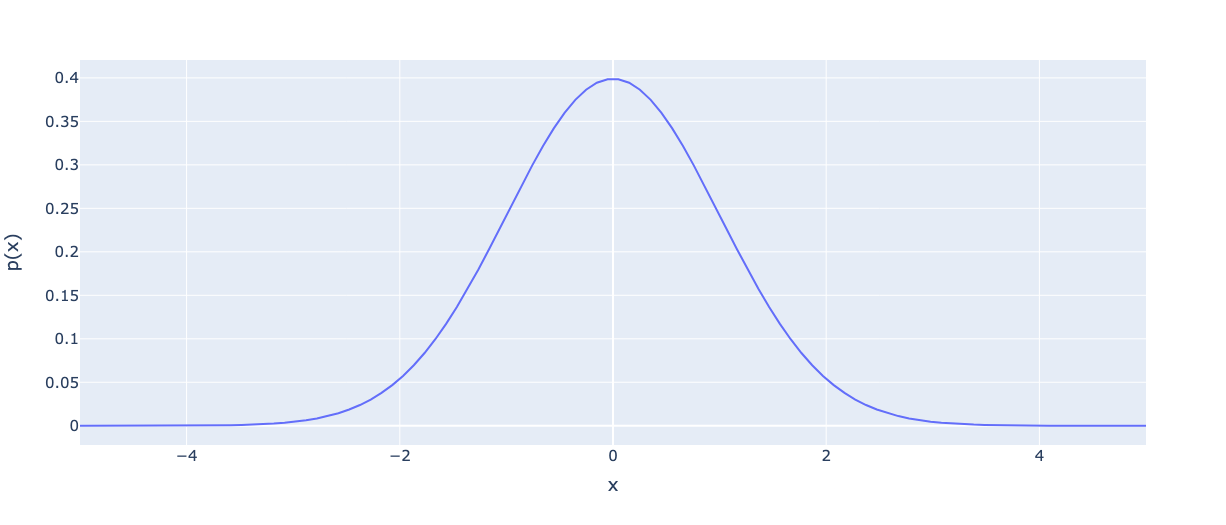
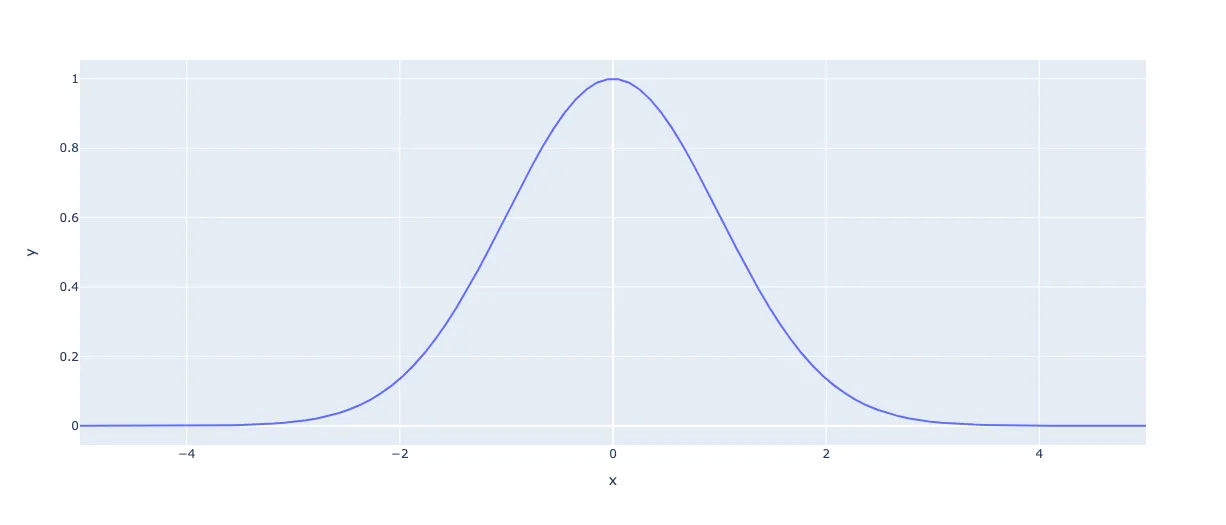
Нормальное распределение (распределение Гаусса) — это такое распределение вероятностей, функция плотности которого совпадает с функцией Гаусса.
(fleft(xright)=frac1{sigmasqrt{2pi}}expleft(-frac{left(x-muright)^2}{2sigma^2}right))
где (mu) — значение математического ожидания, (sigma) – величина среднеквадратического отклонения, (sigma^2) — дисперсия распределения.
Определение
Функция плотности — это функция, которая характеризует сравнительную вероятность реализации определенных значений случайной переменной или переменных.
Иными словами, функция плотности показывает, с какой вероятностью случайное значение будет равно заданному. Чем «выше» значение по оси ординат, тем больше вероятность, что случайное значение будет равно данному по оси абсцисс. Таким образом, на графике нормального распределения наиболее вероятно то значение, которое совпадает с точкой максимума. А те значения, которые находятся в «основании» графика, то есть находятся низко по оси Y, менее вероятны.
Нормальное распределение величины центрировано и нормировано.
График нормального распределения тесно связан с центральной предельной теоремой (ЦПТ). Согласно ЦПТ, сумма достаточно большого количества слабо зависимых случайных величин имеет распределение, близкое к нормальному.
Пример
Нормальное распределение не является абстрактным понятием. Ему соответствуют некоторые характеристики живых организмов в популяции, отклонение от мишени при стрельбе, измерения и их погрешности. Во всех этих случаях наиболее распространена группа близких значений, но есть отклонения как в большую, так и в меньшую сторону.
Примеры решения задач
Рассмотрим несколько простых задач на применение правила 3 сигм.
Задача 1
Имеется выборка жителей богатого дома. Средняя зарплата жильцов составляет 150 000 рублей, среднеквадратичное отклонение равно 20 000 рублей. Определите, жители с какой зарплатой вряд ли могут жить в этом доме: А) 205 000 рублей; Б) 95 000; В) 230 000; Г) 87 000.
Решение
Чтобы решить данную задачу, необходимо определить, каковы верхние и нижние границы возможных зарплат в доме. Для этого воспользуемся правилом 3 сигм.
(s_{нижн.}=mu-3sigma=150;000-3cdot20;000=150;000-60;000=90;000)
(s_{верх.}=mu+3sigma=150;000+3cdot20;000=150;000+60;000=210;000)
Значения А, Б входят в диапазон (left[90;000;;210;000right]). Значения В, Г не входят в него и, следовательно, являются искомыми грубыми ошибками.
Ответ: В, Г.
Задача 2
Завод выпускает партии по 100 цилиндрических деталей. Диаметр каждой детали — случайная величина, распределенная по нормальному закону. Математическое ожидание равно 65 мм, а среднее отклонение составляет 0,9 мм. Для упаковки партии используют коробки шириной 6600 мм. Детали кладут в один ряд. Если детали не поместятся в одну коробку, придется брать еще одну. Найдите вероятность, что понадобится только одна коробка.
Решение
Т. к. диаметр каждой детали распределен нормально, то и их общий диаметр также будет распределен нормально.
Чтобы все детали поместились в одну коробку, необходимо, чтобы отклонение диаметра всех деталей отклонялось от ожидаемого не более чем на 100 мм. Это следует из того, что математическое ожидание общего диаметра всех деталей равно (65cdot100=6500). А ширина коробки составляет 6600 мм.
Для расчета воспользуемся формулами дисперсии и правилом 3 сигм, чтобы вычислить вероятность, что понадобится только одна коробка.
(Pleft|X-M(X)right|<100;Rightarrow2Phileft[frac{100}{100sigma}right]=2Phileft[1,111right]=2cdot0,3665=0,733)
Ответ: 0,733
Нормальным называют распределение вероятностей непрерывной случайной величины
, плотность которого имеет вид:
где
–
математическое ожидание,
–
среднее квадратическое отклонение
.
Вероятность того, что
примет
значение, принадлежащее интервалу
:
где
– функция Лапласа:
Вероятность того, что абсолютная
величина отклонения меньше положительного числа
:
В частности, при
справедливо
равенство:
Асимметрия, эксцесс,
мода и медиана нормального распределения соответственно равны:
, где
Правило трех сигм
Преобразуем формулу:
Положив
. В итоге получим
если
, и, следовательно,
, то
то есть вероятность того, что
отклонение по абсолютной величине будет меньше утроенного среднего квадратического отклонение, равна 0,9973.
Другими словами, вероятность того,
что абсолютная величина отклонения превысит утроенное среднее квадратическое отклонение, очень мала, а именно равна
0,0027. Это означает, что лишь в 0,27% случаев так может произойти. Такие
события исходя из принципа невозможности маловероятных
событий можно считать практически невозможными. В этом и состоит
сущность правила трех сигм: если случайная величина распределена нормально, то
абсолютная величина ее отклонения от математического ожидания не превосходит
утроенного среднего квадратического отклонения.
На практике правило трех сигм
применяют так: если распределение изучаемой случайной величины неизвестно, но
условие, указанное в приведенном правиле, выполняется, то есть основание
предполагать, что изучаемая величина распределена нормально; в противном случае
она не распределена нормально.
Смежные темы решебника:
- Таблица значений функции Лапласа
- Непрерывная случайная величина
- Показательный закон распределения случайной величины
- Равномерный закон распределения случайной величины
Пример 2
Ошибка
высотометра распределена нормально с математическим ожиданием 20 мм и средним
квадратичным отклонением 10 мм.
а) Найти
вероятность того, что отклонение ошибки от среднего ее значения не превзойдет 5
мм по абсолютной величине.
б) Какова
вероятность, что из 4 измерений два попадут в указанный интервал, а 2 – не
превысят 15 мм?
в)
Сформулируйте правило трех сигм для данной случайной величины и изобразите
схематично функции плотности вероятностей и распределения.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
а) Вероятность того, что случайная величина, распределенная по
нормальному закону, отклонится от среднего не более чем на величину
:
В нашем
случае получаем:
б) Найдем
вероятность того, что отклонение ошибки от среднего значения не превзойдет 15
мм:
Пусть событие
– ошибки 2
измерений не превзойдут 5 мм и ошибки 2 измерений не превзойдут 0,8664 мм
– ошибка не
превзошла 5 мм;
– ошибка не
превзошла 15 мм
в)
Для заданной нормальной величины получаем следующее правило трех сигм:
Ошибка высотометра будет лежать в интервале:
Функция плотности вероятностей:
График плотности распределения нормально распределенной случайной величины
Функция распределения:
График функции
распределения нормально распределенной случайной величины
Задача 1
Среднее
количество осадков за июнь 19 см. Среднеквадратическое отклонение количества
осадков 5 см. Предполагая, что количество осадков нормально-распределенная
случайная величина найти вероятность того, что будет не менее 13 см осадков.
Какой уровень превзойдет количество осадков с вероятностью 0,95?
Задача 2
Найти
закон распределения среднего арифметического девяти измерений нормальной
случайной величины с параметрами m=1.0 σ=3.0. Чему равна вероятность того, что
модуль разности между средним арифметическим и математическим ожиданием
превысит 0,5?
Указание:
воспользоваться таблицами нормального распределения (функции Лапласа).
Задача 3
Отклонение
напряжения в сети переменного тока описывается нормальным законом
распределения. Дисперсия составляет 20 В. Какова вероятность при изменении
выйти за пределы требуемых 10% (22 В).
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 4
Автомат
штампует детали. Контролируется длина детали Х, которая распределена нормально
с математическим ожиданием (проектная длинна), равная 50 мм. Фактическая длина
изготовленных деталей не менее 32 и не более 68 мм. Найти вероятность того, что
длина наудачу взятой детали: а) больше 55 мм; б) меньше 40 мм.
Задача 5
Случайная
величина X распределена нормально с математическим ожиданием a=10и средним
квадратическим отклонением σ=5. Найти
интервал, симметричный относительно математического ожидания, в котором с
вероятностью 0,9973 попадает величина Х в результате испытания.
Задача 6
Заданы
математическое ожидание ax=19 и среднее квадратическое отклонение σ=4
нормально распределенной случайной величины X. Найти: 1) вероятность
того, что X примет значение, принадлежащее интервалу (α=15;
β=19); 2) вероятность того, что абсолютная величина отклонения значения
величины от математического ожидания окажется меньше δ=18.
Задача 7
Диаметр
выпускаемой детали – случайная величина, распределенная по нормальному закону с
математическим ожиданием и дисперсией, равными соответственно 10 см и 0,16 см2.
Найти вероятность того, что две взятые наудачу детали имеют отклонение от
математического ожидания по абсолютной величине не более 0,16 см.
Задача 8
Ошибка
прогноза температуры воздуха есть случайная величина с m=0,σ=2℃. Найти вероятность
того, что в течение недели ошибка прогноза трижды превысит по абсолютной
величине 4℃.
Задача 9
Непрерывная
случайная величина X распределена по нормальному
закону: X∈N(a,σ).
а) Написать
плотность распределения вероятностей и функцию распределения.
б) Найти
вероятность того, что в результате испытания случайная величина примет значение
из интервала (α,β).
в) Определить
приближенно минимальное и максимальное значения случайной величины X.
г) Найти
интервал, симметричный относительно математического ожидания a, в котором с
вероятностью 0,98 будут заключены значения X.
a=5; σ=1.3;
α=4; β=6
Задача 10
Производится измерение вала без
систематических ошибок. Случайные ошибки измерения X
подчинены нормальному закону с σx=10. Найти вероятность того, что измерение будет
произведено с ошибкой, превышающей по абсолютной величине 15 мм.
Задача 11
Высота
стебля озимой пшеницы — случайная величина, распределенная по нормальному закону
с параметрами a = 75 см, σ = 1 см. Найти вероятность того, что высота стебля:
а) окажется от 72 до 80 см; б) отклонится от среднего не более чем на 0,5 см.
Задача 12
Деталь,
изготовленная автоматом, считается годной, если отклонение контролируемого
размера от номинала не превышает 10 мм. Точность изготовления деталей
характеризуется средним квадратическим отклонением, при данной технологии
равным 5 мм.
а)
Считая, что отклонение размера детали от номинала есть нормально распределенная
случайная величина, найти долю годных деталей, изготовляемых автоматом.
б) Какой
должна быть точность изготовления, чтобы процент годных деталей повысился до
98?
в)
Написать выражение для функции плотности вероятности и распределения случайной
величины.
Задача 13
Диаметр
детали, изготовленной цехом, является случайной величиной, распределенной по
нормальному закону. Дисперсия ее равна 0,0001 см, а математическое ожидание –
2,5 см. Найдите границы, симметричные относительно математического ожидания, в
которых с вероятностью 0,9973 заключен диаметр наудачу взятой детали. Какова
вероятность того, что в серии из 1000 испытаний размер диаметра двух деталей
выйдет за найденные границы?
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 14
Предприятие
производит детали, размер которых распределен по нормальному закону с
математическим ожиданием 20 см и стандартным отклонением 2 см. Деталь будет
забракована, если ее размер отклонится от среднего (математического ожидания)
более, чем на 2 стандартных отклонения. Наугад выбрали две детали. Какова вероятность
того, что хотя бы одна из них будет забракована?
Задача 15
Диаметры
деталей распределены по нормальному закону. Среднее значение диаметра равно d=14 мм
, среднее квадратическое
отклонение σ=2 мм
. Найти вероятность того,
что диаметр наудачу взятой детали будет больше α=15 мм и не меньше β=19 мм; вероятность того, что диаметр детали
отклонится от стандартной длины не более, чем на Δ=1,5 мм.
Задача 16
В
электропечи установлена термопара, показывающая температуру с некоторой
ошибкой, распределенной по нормальному закону с нулевым математическим
ожиданием и средним квадратическим отклонением σ=10℃. В момент когда термопара
покажет температуру не ниже 600℃, печь автоматически отключается. Найти
вероятность того, что печь отключается при температуре не превышающей 540℃ (то
есть ошибка будет не меньше 30℃).
Задача 17
Длина
детали представляет собой нормальную случайную величину с математическим
ожиданием 40 мм и среднеквадратическим отклонением 3 мм. Найти:
а)
Вероятность того, что длина взятой наугад детали будет больше 34 мм и меньше 43
мм;
б)
Вероятность того, что длина взятой наугад детали отклонится от ее
математического ожидания не более, чем на 1,5 мм.
Задача 18
Случайное
отклонение размера детали от номинала распределены нормально. Математическое
ожидание размера детали равно 200 мм, среднее квадратическое отклонение равно
0,25 мм, стандартами считаются детали, размер которых заключен между 199,5 мм и
200,5 мм. Из-за нарушения технологии точность изготовления деталей уменьшилась
и характеризуется средним квадратическим отклонением 0,4 мм. На сколько
повысился процент бракованных деталей?
Задача 19
Случайная
величина X~N(1,22). Найти P{2
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 20
Заряд пороха для охотничьего ружья
должен составлять 2,3 г. Заряд отвешивается на весах, имеющих ошибку
взвешивания, распределенную по нормальному закону со средним квадратическим
отклонением, равным 0,2 г. Определить вероятность повреждения ружья, если максимально
допустимый вес заряда составляет 2,8 г.
Задача 21
Заряд
охотничьего пороха отвешивается на весах, имеющих среднеквадратическую ошибку
взвешивания 150 мг. Номинальный вес порохового заряда 2,3 г. Определить
вероятность повреждения ружья, если максимально допустимый вес порохового
заряда 2,5 г.
Задача 21
Найти
вероятность попадания снарядов в интервал (α1=10.7; α2=11.2).
Если случайная величина X распределена по
нормальному закону с параметрами m=11;
σ=0.2.
Задача 22
Плотность
вероятности распределения случайной величины имеет вид
Найти
вероятность того, что из 3 независимых случайных величин, распределенных по
данному закону, 3 окажутся на интервале (-∞;5).
Задача 23
Непрерывная
случайная величина имеет нормальное распределение. Её математическое ожидание
равно 12, среднее квадратичное отклонение равно 2. Найти вероятность того, что
в результате испытания случайная величина примет значение в интервале (8,14)
Задача 24
Вероятность
попадания нормально распределенной случайной величины с математическим
ожиданием m=4 в интервал (3;5) равна 0,6. Найти дисперсию данной случайной
величины.
Задача 25
В
нормально распределенной совокупности 17% значений случайной величины X
меньше 13% и 47% значений случайной величины X
больше 19%. Найти параметры этой совокупности.
Задача 26
Студенты
мужского пола образовательного учреждения были обследованы на предмет
физических характеристик и обнаружили, что средний рост составляет 182 см, со
стандартным отклонением 6 см. Предполагая нормальное распределение для роста,
найдите вероятность того, что конкретный студент-мужчина имеет рост более 185
см.
Нормально разбираемся в Нормальном распределении
Уровень сложности
Средний
Время на прочтение
6 мин
Количество просмотров 12K
Всем привет. Это пост про интуитивное понимание Нормального распределения.
Обычный курс теории вероятностей проходит следующим образом. Сначала вам даются понятные и относительно простые концепции. Все легко объясняется «на пальцах»: подбрасывание монеток, красные и белые шары в урнах, кролики в клетках и так далее.
Но в следующей теме вас бросают в яму к этому монстру:
Внезапно больше нет ни монет, ни урн, ни шаров. Вам только говорят запомнить эту функцию плотности вероятности Нормального распределения, что это очень важно и что график похож на колокол. В остальном вы предоставлены сами себе.
Но что это такое? Почему там экспонента? Почему минус? Зачем делить на 2 сигма-квадрат? Откуда взялось число Пи? Куда делись монеты, шары, урны и кролики? Почему мы от интуитивных объяснений перешли к тупому запоминанию?
Каждая формула несет некоторую идею. В этом посте мы будем препарировать нормальное распределение, пока не поймем, что оно в себе несет. В конце мы выведем функцию плотности вероятности, чтобы понять, откуда она берется.
Я покажу, что, несмотря на пугающий вид, Нормальное распределение это не конь в вакууме. Это все еще про броски монеток, урны и другие вещи из реального мира.
Самореклама
Эта статья является переводом моей статьи из Substack Understanding the Normal Distribution for Real. Переходите туда если вам удобнее читать на английском или хочется получать такой контент по почте.
Так же у меня есть телеграм канал @boris_again
Препарируем монстра
Начнем изнутри. Разберемся в идеях, стоящих за этим куском:
Режем монстра на части.
Где это среднее, один из параметров распределения.
Посмотрим на график функции при
:
Мы видим параболу. Она похожа на форму колокола, но перевернутую. Также заметьте, что ось произвольна, а не находится в диапазоне
, так что это пока не распределение.
Обратите внимание, что чем дальше от среднего значения, тем больше значение функции. Во-вторых, квадрат позволяет нам одинаково относиться к отрицательным и положительным значениям. Он делает форму колокола симметричной.
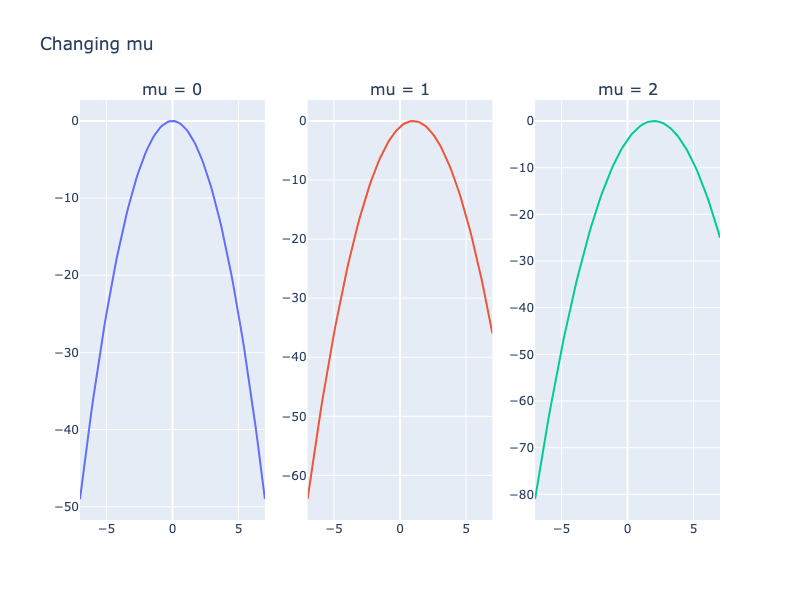
Идея: определяет местоположение вершины колокола, и распределение становится симметричным.
Наконец-то, форма колокола! Но значения y отрицательны. Естественно у нас не может быть отрицательных вероятностей.
Что будет если менять ?
Вывод: Изменение перемещает пик колокола в другое место.
Добавим следующий кусок, деление на сигма квадрат:
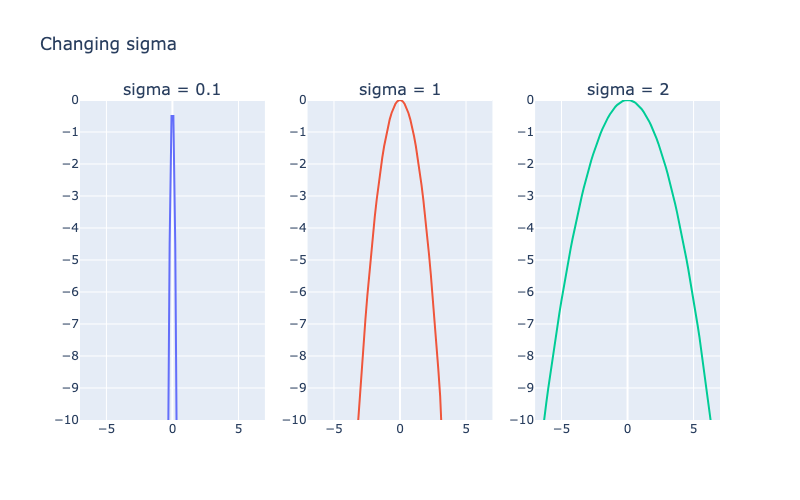
Здесь сигма — это второй параметр распределения: стандартное отклонение. Квадрат сигмы — это дисперсия. Что это дает нашему распределению?
Попробуем поменять ее:
Идея: знаменатель с сигмой задает скорость изменения значения функции по мере удаления от среднего. Меньшие сигмы создают более узкие колоколообразные формы.
Мы можем рассматривать сигму как меру неопределенности. Малые сигмы указывают на то, что среднее значение более вероятно. Большие сигмы распределяют вероятность по более широкому диапазону.
Сигма возводится в квадрат, чтобы показать: неопределенность возрастает квадратично (быстро), а не линейно (медленно). Другими словами, небольшая вариация данных сильно меняет колоколообразную кривую.
Отлично, у нас есть колоколообразная кривая. Но она не похожа на распределение вероятностей. Чтобы это было распределение, выходы должны находиться в пределах и в сумме равняться 1. Вот здесь и появляется экспонента.
Давайте построим на график около нуля:
Обратите внимание: экспонента отображает любой отрицательный вход в значение между 0 и 1. В нашем случае аргумент всегда отрицательный.
Отлично! Теперь все значения находятся между , и у нас получилась нужная нам колоколообразная кривая. Мы закончили.
На самом деле нет. Это прекрасная колоколообразная кривая, но в сумме значения не равны 1. Один только пик почти равен 1.
Как сделать так, чтобы сумма была равна 1? Нормализовать!
Как бы вы нормализовали такую последовательность чисел, как: ? Легко: разделить на сумму.
В нашем случае функция — это не просто последовательность чисел. Она непрерывна. Тем не менее, идея та же. Чтобы получить сумму давайте проинтегрируем:
Теперь, когда у нас есть сумма, давайте разделим функцию на нее:
Наконец, мы собрали все части, чтобы получить нормальное распределение.
Если вм нужны подробности вычисления интеграла, то я рекомендую это видео:
Связь с Биномиальным распределением
Нормальное распределение тесно связано с биномиальным. Давайте отвлечемся и рассмотрим биномиальное распределение поближе. Это поможет нам получить полное представление о нормальном распределении.
Представьте, что у вас есть Substack рассылка, и вы собираетесь запустить рекламную кампанию, нацеленную на 100 человек. Вы знаете свою конверсию в подписку: 10%. Какова вероятность того, что подпишутся ровно 5 человек?
Давайте представим каждого пользователя в виде броска монеты. Он либо регистрируются с вероятностью , либо нет. Это может быть описано распределением Bernoulli(n, p), которое имеет следующую функцию массы вероятности:
Идея: это бросок монеты, есть два возможных исхода, и с вероятностью выпадает орел.
Это распределение позволяет отвечать на вопросы типа «Какова вероятность выпадения орла для этой монеты?» или, более практично, «Какова вероятность того, что пользователь подпишется?».
Мы можем сложить несколько случайных величин Бернулли и получить Биномиальное распределение . Оно говорит нам о вероятности получения
успехов из
независимых испытаний Бернулли с вероятностью
.
Биномиальное распределение объединяет все независимые испытания, чтобы ответить на новые вопросы: «Какова вероятность выпадения 3 орлов из 3 бросков?» или «Сколько пользователей мы можем ожидать при регистрации?»
Вот PMF Биномиального распределения:
Где это Биномиальный коэффициент.
Биномиальный коэффициент используется для того, чтобы учесть множество способов регистрации человек. Например, при наличии четырех посетителей существует шесть способов зарегистрироваться двум из них.
Давайте подставим наши значения, чтобы найти вероятность того, что зарегистрируются ровно пять человек:
Ожидаемое количество подписчиков среди 5 пользователей равно просто умноженное на
, то есть 3.387. Мы также можем получить вероятность регистрации хотя бы 5 подписчиков, просуммировав по
и получим 0.94242.
Теперь давайте посмотрим, что происходит по мере роста числа испытаний.
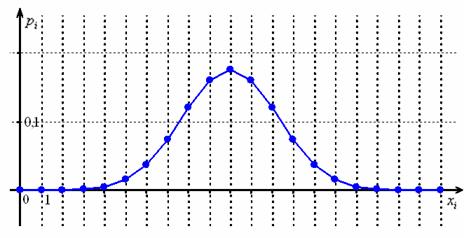
Обратите внимание: с ростом результирующая PMF приближается к знакомой колоколообразной форме Нормального распределения.
Оказывается, что Нормальное распределение является предельным случаем биномиального распределения. Биномиальное распределение отвечает на вопрос: «Насколько вероятно получить k орлов из n бросков монеты?» Нормальное распределение имеет ту же идею, но дает приблизительный результат.
Нас интересует это приближение, потому что вычисление коэффициентов биномиального распределения для больших значений требует огромных вычислительных затрат. Факториалы в формуле являются самой большой проблемой. Например, для биномиальный коэффициент равен 75287520. Это очень дорогое вычисление, особенно если вам нужно суммировать по многим
.
Вместо вычисления биномиальной PMF мы можем аппроксимировать его вычислением PDF нормального распределения. Это гораздо быстрее: нужно только подставить несколько чисел в формулу. Этот подход часто используется в опросах.
Основная идея нормального распределения: число успехов в большом количестве независимых испытаний типа «да или нет» распределено симметрично вокруг среднего значения, а форма распределения описывается функцией Гаусса.
Надеюсь, теперь PMF нормального распределения больше не является просто страшной формулой в вакууме. Она по-прежнему связана с подбрасыванием монет и реальной жизнью, как и Биномиальное распределение
Выводим Нормальное распределение
Почему именно такая функция позволяет нам аппроксимировать Биномиальное распределение? Чтобы ответить на этот вопрос, нам нужно будет вывести PMF нормального распределения. Есть несколько способов сделать это, но мы будем использовать наши знания о том, что нормальное распределение является предельным случаем биномиального распределения. Я опишу только основные шаги, так как детали вывода довольно длинные, но вы можете найти полный вывод в этой статье.
Нормальное распределение является предельным случаем Биномиального, если не очень мало, и выполняется условие:
Если это не так, мы получаем распределение Пуассона, что тоже круто, но выходит за рамки этого поста.
Помните биномиальный PMF? Предположим, у нас есть последовательность испытаний Бернулли, каждое с вероятностью успеха , и мы повторяем этот эксперимент
раз. Пусть
— количество успехов в n испытаниях. Тогда
имеет биномиальное распределение с параметрами
. Функция массы вероятности
определяется как:
Самая тяжелая часть — факториал. Давайте воспользуемся приближением Cтирлинга, чтобы вычислить факториалы быстрее:
Подставив это в Биномиальный коэффициент мы получаем:
Это может выглядеть пугающе, но на самом деле это просто замена и некоторая перестановка терминов.
Подставляя это приближение в PMF Биномиального распределения, мы получаем:
Это функция плотности вероятности нормального распределения при , и квадратом
:
Вывод: гауссиана появляется, когда мы заменяем вычисления факториалов в биномиальном приближении.
Завершение
Мы разобрали нормальное распределение на его компоненты, исследовали связь между биномиальным и нормальным распределением и, наконец, получили нормальную PDF. Надеюсь, теперь для вас это не столько таинственный монстр, сколько прекрасный способ описания явлений реального мира.
Код для графиков вы можете найти в этом коллабе.
Спасибо за внимание! Если вам нравится такой контент, то подписывайтесь на мой телеграм канал @boris_again и substack.
Определение.
Нормальным называется
распределение вероятностей непрерывной
случайной величины, которое описывается
плотностью вероятности
Нормальный
закон распределения также называется
законом
Гаусса.
Нормальный
закон распределения занимает центральное
место в теории вероятностей. Это
обусловлено тем, что этот закон проявляется
во всех случаях, когда случайная величина
является результатом действия большого
числа различных факторов. К нормальному
закону приближаются все остальные
законы распределения.
Можно
легко показать, что параметры
и
,
входящие в плотность распределения
являются соответственно математическим
ожиданием и среднеквадратическим
отклонением случайной величиныХ.
Найдём
функцию распределения F(x).
График
плотности нормального распределения
называется нормальной
кривой или
кривой Гаусса.
Нормальная
кривая обладает следующими свойствами:
1)
Функция определена на всей числовой
оси.
2)
При всех х
функция распределения принимает только
положительные значения.
3)
Ось ОХ является горизонтальной асимптотой
графика плотности вероятности, т.к. при
неограниченном возрастании по абсолютной
величине аргумента х,
значение функции стремится к нулю.
4)
Найдём
экстремум функции.
Т.к.
при y’
> 0 при x
< m
и y’
< 0 при x
> m
, то в точке х
= т функция
имеет максимум, равный
.
5)
Функция является симметричной относительно
прямой х = а,
т.к. разность
(х
– а) входит
в функцию плотности распределения в
квадрате.
6)
Для нахождения точек перегиба графика
найдем вторую производную функции
плотности.
При
x
= m
+
и x
= m
—
вторая производная равна нулю, а при
переходе через эти точки меняет знак,
т.е. в этих точках функция имеет перегиб.
В
этих точках значение функции равно
.
Построим
график функции плотности распределения
(рис. 5).
Рис.
5
Построены
графики при т
=0 и трёх возможных значениях
среднеквадратичного отклонения
= 1,
= 2 и
= 7. Как видно, при увеличении значения
среднего квадратичного отклонения
график становится более пологим, а
максимальное значение уменьшается.
Если
а
> 0, то график сместится в положительном
направлении, если а
< 0 – в отрицательном.
При
а
= 0 и
= 1 кривая называется нормированной.
Уравнение нормированной кривой:
-
Функция Лапласа
Найдём
вероятность попадания случайной
величины, распределенной по нормальному
закону, в заданный интервал.
Обозначим
Тогда
Т.к.
интеграл
не выражается через элементарные
функции, то вводится в рассмотрение
функция

которая
называется функцией
Лапласа или
интегралом
вероятностей.
Значения
этой функции при различных значениях
х
посчитаны и приводятся в специальных
таблицах.
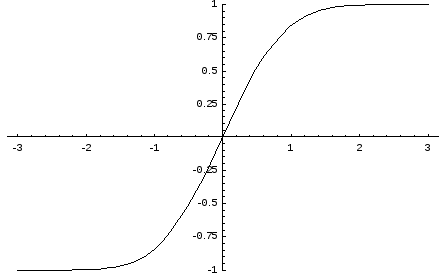
На
рис. 6 показан график функции Лапласа.
Рис.
6
Функция
Лапласа обладает следующими свойствами:
1) Ф(0)
= 0;
2) Ф(-х)
= — Ф(х);
3) Ф()
= 1.
Функцию
Лапласа также называют функцией
ошибок и
обозначают erf
x.
Е
используетсянормированная
функция
Лапласа, которая связана с функцией
Лапласа соотношением:
На
рис. 7 показан график нормированной
функции Лапласа.
Рис.
7
-
Правило
трёх сигм
При рассмотрении
нормального закона распределения
выделяется важный частный случай,
известный как правило
трёх сигм.
Запишем
вероятность того, что отклонение
нормально распределенной случайной
величины от математического ожидания
меньше заданной величины :
Если
принять
= 3,
то получаем с использованием таблиц
значений функции Лапласа:
Т.е.
вероятность того, что случайная величина
отклонится от своего математического
ожидание на величину, большую чем
утроенное среднее квадратичное
отклонение, практически равна нулю.
Это
правило называется правилом
трёх сигм.
Не
практике считается, что если для
какой-либо случайной величины выполняется
правило трёх сигм, то эта случайная
величина имеет нормальное распределение.
Заключение
по лекции:
В лекции мы
рассмотрели законы распределения
непрерывных величин В ходе подготовки
к последующей лекции и практическим
занятиям вы должны самостоятельно при
углубленном изучении рекомендованной
литературы и решения предложенных задач
дополнить свои конспекты лекций.
Приложения
2.5.3. Нормальный закон распределения вероятностей
Без преувеличения его можно назвать философским законом. Наблюдая за различными объектами и процессами окружающего мира, мы часто
сталкиваемся с тем, что чего-то бывает мало, и что бывает норма. Перед вами принципиальный вид функции плотности нормального распределения вероятностей:
Какие можно примести примеры? Их просто тьма. Это, например, рост, вес людей (и не только), их физическая сила, умственные способности и
т.д. Существует «основная масса» (по тому или иному признаку) и существуют отклонения в обе стороны.
Это различные характеристики неодушевленных объектов (те же размеры, вес). Это случайная продолжительность процессов…, снова пришёл
на ум грустный пример, и поэтому скажу время «жизни» лампочек 
быстрые, но большинство двигаются со «стандартными» скоростями.
Более того, даже дискретные распределения бывают близкИ к нормальному, и в конце
урока мы раскроем важную предпосылку «нормальности». А сейчас математика, математика, математика, которая в древности не зря считалась
философией!
Непрерывная случайная величина , распределённая по нормальному закону, имеет функцию
плотности 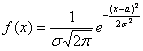
определяется параметрами и
.
Эта функция получила фамилию некоронованного короля математики, К.Ф. Гаусса и в своё время была изображена вместе с его портретом
на купюре в 10 немецких марок. Для функции Гаусса выполнены общие свойства плотности, а
именно (почему?) и
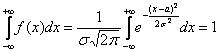
распределённая случайная величина достоверно примет одно из действительных значений. Теоретически – какое
угодно, практически – узнаем позже.
Следующие замечательные факты я тоже приведу без доказательства:
– то есть, математическое ожидание нормально распределённой случайной величины в точности равно «а», а
среднее квадратическое отклонение в точности равно «сигме»: .
Эти значения выводятся с помощью общих формул, и желающие могут найти подробные выкладки в учебной литературе.
Ну а мы переходим к насущным практическим вопросам. Практики будет много, и она будет интересна не только «чайникам», но и более
подготовленным читателям:
Задача 118
Нормально распределённая случайная величина задана параметрами . Записать её функцию плотности и построить график.
Несмотря на кажущуюся простоту задания, в нём существует немало тонкостей.
Первый момент касается обозначений. Они стандартные: матожидание обозначают буквой (реже
или
(«мю»)), а стандартное отклонение – буквой
. Кстати, обратите внимание, что в условии ничего не
сказано о сущности параметров «а» и «сигма», и несведущий человек может только догадываться, что это такое.
Решение начнём шаблонной фразой: функция плотности нормально
распределённой случайной величины имеет вид 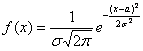
и:
Первая, более лёгкая часть задачи выполнена. Теперь график. Вот на нём-то, на моей памяти, студентов «заворачивали» десятки раз,
причём, многих неоднократно. По той причине, что график функции Гаусса обладает несколькими принципиальными
особенностями, которые нужно обязательно отобразить на чертеже.
Сначала полная картина, затем комментарии:
На первом шаге декартову систему координат. При выполнении чертежа от руки во многих случаях оптимален следующий масштаб:
по оси абсцисс: 2 тетрадные клетки = 1 ед.,
по оси ординат: 2 тетрадные клетки = 0,1 ед., при этом саму ось следует расположить из тех соображений, что в точке функция достигает
максимума, и вертикальная прямая (на чертеже её нет) является линией симметрии
графика.
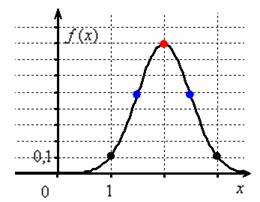
И логично, что в первую очередь удобно найти максимум функции:
Отмечаем вершину графика (красная точка).
Далее вычислим значения функции при , а точнее только одно из них – в силу симметрии графика они
равны:
Отмечаем синим цветом.
Внимание! и
– это точки перегиба нормальной кривой. На интервале
график является
выпуклым вверх, а на крайних интервалах – вогнутым вниз.
Далее отклоняемся от центра влево и право ещё на одно стандартное отклонение и рассчитываем высоту:
Отмечаем точки на чертеже (зелёный цвет) и видим, что этого вполне достаточно.
На завершающем этапе аккуратно чертим график, и особо аккуратно отражаем его выпуклость /
вогнутость! Ну и, наверное, вы давно поняли, что ось абсцисс – это горизонтальная асимптота, и «залезать» за неё
категорически нельзя!
Поговорим о том, как меняется форма нормальной кривой в зависимости от значений и
.
При увеличении или уменьшении «а» (при неизменном «сигма») график сохраняет свою форму и перемещается вправо или
влево соответственно. Так, при (уменьшили «а» на 3) функция принимает вид
и наш график «переезжает»
на 3 единицы влево – ровнехонько в начало координат:
Нормально распределённая величина с нулевым математическим ожиданием получила вполне естественное название – центрированная; её
функция плотности 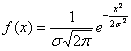
чётная, и график симметричен относительно оси ординат.
В случае изменения «сигмы» (при постоянном «а»), график «остаётся на месте», но меняет форму. При увеличении он становится более
низким и вытянутым, словно осьминог, растягивающий щупальца. И, наоборот, при уменьшении график становится более узким и высоким
– как «удивлённый осьминог». Так, при уменьшении «сигмы» в два раза: предыдущий график сужается и вытягивается вверх в два
раза:
Нормальное распределёние с единичным значением «сигма» называется нормированным, а если оно ещё и центрировано (наш
случай), то такое распределение называют стандартным. Оно имеет ещё более простую функцию плотности, которая уже встречалась в локальной теореме Лапласа: . Стандартное распределение нашло широкое применение, и
очень скоро мы окончательно поймём его предназначение.
И как-то незаслуженно осталась в тени функция распределения вероятностей.
Вспоминаем её определение:
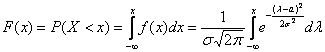
вероятность того, что случайная величина примет значение, МЕНЬШЕЕ, чем переменная
, которая «пробегает» все
действительные значения до «плюс» бесконечности.
Внутри интеграла используют другую букву, чтобы не возникало «накладок» с обозначениями, ибо здесь каждому значению ставится в соответствие
несобственный интеграл 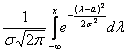
. Почти все значения
не поддаются
абсолютно точному расчету, но с современными вычислительными мощностями с этим нет никаких трудностей (ролик на Ютубе).
Так, например, график функции 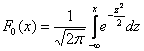
имеет следующий вид:

На чертеже хорошо видно выполнение всех свойств функции распределения, и из
технических нюансов здесь следует обратить внимание на горизонтальные асимптоты и точку перегиба .
Теперь вспомним одну из ключевых задач темы, а именно выясним, как найти – вероятность того, что
нормальная случайная величина примет
значение из интервала . Геометрически эта вероятность равна площади между
нормальной кривой и осью абсцисс на соответствующем участке:
но каждый раз вымучивать приближенное значение 
«лёгкую» формулу:
! Вспоминает также, что:
Тут можно снова задействовать Эксель, но есть пара весомых «но»: во-первых, он не всегда под рукой, а во-вторых, «готовые» значения
, скорее всего,
вызовут вопросы у преподавателя. Почему?
Об этом я неоднократно рассказывал ранее: в своё время (и ещё не очень давно) роскошью был обычный калькулятор, и в учебной
литературе до сих пор сохранился «ручной» способ решения рассматриваемой задачи. Его суть состоит в том, чтобы свести решение к
стандартному распределению:
, где
Зачем это нужно? Дело в том, что значения скрупулезно подсчитаны нашими предками и сведены в
специальную таблицу, которая есть во многих книгах по терверу. Но ещё чаще встречается таблица значений функции Лапласа:
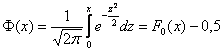
функцией и этой таблицей (см. Приложение Таблицы) мы уже имели дело в интегральной теореме Лапласа.
Итак, вероятность того, что нормальная случайная величина с параметрами
и
примет значение из интервала
, можно вычислить по формуле:
, где
– функция Лапласа.
Таким образом, наша задача становится чуть ли не устной! Порой, здесь хмыкают и говорят, что метод устарел. Может быть…, но
парадокс состоит в том, что «устаревший метод» очень быстро приводит к результату!
И ещё в этом заключена большая мудрость – если вдруг пропадёт электричество или восстанут машины, то у человечества останется
возможность заглянуть в бумажные таблицы и спасти мир =) Классика жанра:
Задача 119
Из пункта ведётся стрельба из орудия вдоль прямой
. Предполагается, что дальность
полёта распределена нормально с математическим ожиданием 1000 м и средним квадратическим отклонением 5 м. Определить (в процентах) сколько
снарядов упадёт с перелётом от 5 до 70м.
Решение: в задаче рассматривается нормально распределённая случайная величина – дальность полёта снаряда, и по
условию .
Так как речь идёт о перелёте за цель, то . Вычислим вероятность
– того, что снаряд упадёт в пределах этой
дистанции.
Если в вашей методичке дана таблица значений функции 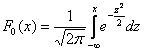
:
Для самопроверки можно «забить» и затем
в Пункт 9
Калькулятора, и кроме того, для стандартного нормального распределения в Экселе существует прямая функция
=НОРМСТРАСП(z).
Но гораздо чаще, и в этом курсе в частности, встречается таблица значений функции Лапласа 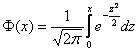
Дробные значения традиционно округляем до 4 знаков после запятой, как это сделано в типовой таблице. И для контроля есть Пункт
5 макета.
Напоминаю, что . Всегда контролируйте, таблица КАКОЙ функции
перед вашими глазами.
Ответ требуется дать в процентах, поэтому рассчитанную вероятность нужно умножить на 100 и снабдить результат
содержательным комментарием:
– с перелётом от 5 до 70 м упадёт примерно 15,87% снарядов
Тренируемся самостоятельно:
Задача 120
Диаметр подшипников, изготовленные на заводе, представляет собой случайную величину, распределенную нормально с математическим
ожиданием 1,5 см и средним квадратическим отклонением 0,04 см. Найти вероятность того, что размер наугад взятого подшипника колеблется от
1,4 до 1,6 см.
В образце решения и далее я буду использовать функцию Лапласа, как самый распространённый вариант. Кстати, обратите внимание, что
согласно формулировке, в этой задаче корректнее будет включить концы интервала в рассмотрение.
И уже в этом примере нам встретился особый случай – когда интервал симметричен относительно математического ожидания. В
такой ситуации его можно записать в виде и, пользуясь нечётностью функции Лапласа
, упростить рабочую
формулу :
Параметр «дельта» называют отклонением от математического ожидания, и двойное неравенство удобно «упаковать» с помощью модуля:
–
вероятность того, что значение случайной величины отклонится от математического ожидания менее чем на
.
Таким, образом задача про подшипники решается гораздо короче:
–
вероятность того, что диаметр наугад взятого подшипника отличается от 1,5 см не более чем на 0,1 см.
Результат этой задачи получился близким к единице, но хотелось бы ещё бОльшей надежности – а именно, узнать границы, в которых
находится диаметр почти всех подшипников. Существует ли какой-нибудь критерий на этот счёт? Существует! На этот вопрос отвечает
так называемое правило «трех сигм».
Его суть состоит в том, что практически достоверным является тот факт, что
нормально распределённая случайная величина примет значение из промежутка
. И в самом деле, вероятность
отклонения от матожидания менее чем на составляет:
или
99,73%
В «пересчёте на подшипники» – это 9973 штуки с диаметром от 1,38 до 1,62 см и всего лишь 27 «некондиционных» экземпляров.
Продолжаем решать суровые советские задачи:
Задача 121
Случайная величина ошибки взвешивания распределена по нормальному закону
с нулевым математическим ожиданием и стандартным отклонением 3 грамма. Найти вероятность того, что очередное взвешивание будет проведено с
ошибкой, не превышающей по модулю 5 грамм.
Решение очень простое. По условию, и сразу заметим, что по правилу «трёх сигм», при
очередном взвешивании (чего-то или кого-то) мы почти 100% получим погрешность менее 9 грамм. Но в задаче фигурирует более узкое
отклонение и по
формуле :
–
вероятность того, что очередное взвешивание будет проведено с ошибкой, не превышающей 5 грамм.
Ответ:
Этот пример принципиально отличается от вроде бы похожей задачи параграфа о равномерном распределении. Там была погрешность округления результатов измерений,
здесь же речь идёт о случайной погрешности самих измерений. Такие погрешности возникают в связи с техническими характеристиками самого
прибора (диапазон допустимых ошибок, как правило, указывают в его паспорте), а также по вине самого экспериментатора – когда мы,
например, «на глазок» снимаем показания со стрелки механических весов.
Помимо прочих, существуют ещё так называемые систематические ошибки измерения. Это уже неслучайные ошибки, которые
возникают по причине некорректной настройки или эксплуатации прибора. Так, например, неотрегулированные напольные весы могут стабильно
«прибавлять» килограмм, а продавец систематически обвешивать покупателей. Или не систематически, ведь можно обсчитать 
случае, случайной такая «ошибка» не будет, и её матожидание отлично от нуля.
…срочно разрабатываю курс по подготовке продавцов =)
Самостоятельно решаем обратную задачу:
Задача 122
Диаметр валика – случайная нормально распределенная случайная величина, среднее квадратическое отклонение ее равно мм. Найти длину интервала,
симметричного относительно математического ожидания, в который с вероятностью попадет длина диаметра валика.
Пункт 5* Калькулятора в помощь. Обратите внимание, что здесь не известно математическое ожидание,
но это нисколько не мешает решить поставленную задачу.
И экзаменационное задание, которое я настоятельно рекомендую для закрепления материала:
Задача 123
Нормально распределенная случайная величина задана своими параметрами
(математическое ожидание) и
(среднее квадратическим отклонение).
Требуется:
а) записать плотность вероятности и схематически изобразить ее график;
б) найти вероятность того, что примет значение из интервала
;
в) найти вероятность того, что отклонится по модулю от
не более чем на
;
г) применяя правило «трех сигм», найти значения случайной величины .
Такие задачи предлагаются повсеместно, и за годы практики мне их довелось решить сотни и сотни штук. Обязательно попрактикуйтесь в
ручном построении чертежа и использовании таблицы 
Задача 124
Плотность распределения вероятностей случайной величины имеет вид
. Найти
, математическое ожидание
, дисперсию
, функцию распределения
, построить графики плотности и
функции распределения, найти .
Решение: прежде всего, обратим внимание, что в условии ничего не сказано о характере случайной величины. Само по
себе присутствие экспоненты ещё ничего не значит: это может оказаться, например, показательное или вообще произвольное непрерывное распределение. И поэтому «нормальность» распределения ещё нужно обосновать:
функция определена при любом действительном значении
, и если её
удастся привести к виду 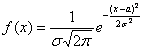
распределена по нормальному закону.
Пробуем привести. Для этого выделяем полный квадрат и
организуем трёхэтажную дробь:
Обязательно выполняем проверку, возвращая показатель в исходный вид:
, что мы и
хотели увидеть.
Таким образом, мы действительно имеем дело с нормальным распределением:
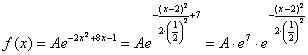
правилу действий со степенями «отщипываем» . И здесь можно сразу записать очевидные числовые
характеристики:
Теперь найдём значение параметра . Поскольку множитель нормального распределения имеет
вид и
, то:
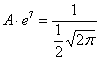
выражаем и
подставляем в нашу функцию:
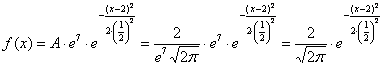
ещё раз пробежим глазами и убедимся, что полученная функция имеет вид 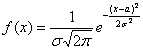
Построим график плотности:
и график функции распределения 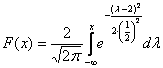
Пару слов на счёт ручного построения последнего графика – на случай отсутствия под рукой Экселя или даже обычного калькулятора. В
точке функция
распределения принимает значение и здесь находится перегиб графика (малиновая точка).
Кроме того, для более или менее приличного чертежа желательно найти ещё хотя бы пару точек. Берём традиционное значение и
стандартизируем его по формуле . Далее по таблице значений функции Лапласа находим:
– жёлтая точка на
чертеже. С симметричной оранжевой точкой никаких проблем: и:
.
После чего аккуратно проводим интегральную кривую, не забывая о перегибе и двух горизонтальных асимптотах.
Да, и ещё нужно вычислить:
–
вероятность того, что случайная величина примет значение из данного отрезка.
Задача была непростой, и посему блеснём академичным стилем, ответ:
А теперь обещанный секрет:
понятие о центральной предельной теореме.
которую также называют теоремой Ляпунова. Её суть состоит в том, что если случайная величина является суммой очень большого числа взаимно
независимых случайных величин , влияние каждой из которых на всю сумму ничтожно мало, то
имеет
распределение, близкое к нормальному.
В окружающем мире условие теоремы Ляпунова выполняется очень часто, и поэтому нормальное распределение встречается буквально на
каждом шагу.
Так, например, молекул воздуха очень и очень много, и каждая из них своим движением оказывает ничтожно малое влияние на всю
совокупность. Поэтому скорость молекул воздуха распределена нормально.
Большая популяция некоторых особей. Каждая из них (или подавляющее большинство) оказывает несущественное влияние на жизнь всей
популяции, следовательно, продолжительность жизни этих особей тоже распределена по нормальному закону.
Теперь вернёмся к знакомой задаче, где проводится независимых
испытаний, в каждом из которых некое событие может появиться с постоянной вероятностью
. Эти испытания можно
считать попарно независимым случайными величинами , и при достаточно большом значении «эн» биномиальное распределение случайной величины
– числа появлений события
в
испытаниях – очень близко к
нормальному распределению.
Уже при и
в многоугольнике биномиального распределения хорошо просматривается нормальная кривая:
И чем больше , тем ближе будет сходство. Причём, вероятность
может быть любой, но
не слишком малой.
Именно этот факт мы и использовали в теоремах Лапласа – когда приближали биномиальные
вероятности соответствующими значениями функций нормального распределения.
Подчёркиваю, что теорема Ляпунова носит статус теоремы, а значит, строго доказана в теории.
И в заключение книги хочется ответить на один философский вопрос: имеет ли в нашей жизни значение случайность? Безусловно! Везение
играет немаловажную, а порой, и огромную роль: встретить хороших друзей, встретить «своего» человека, найти деятельность по душе и т.д. –
всё это нередко происходит благодаря случаю….
Но, с другой стороны, гораздо более важнА системная и упорная деятельность, после которой следуют закономерные результаты.
Желательно, полезные, конечно J
Дополнительную информацию можно найти в соответствующем разделе портала mathprofi.ru (ссылка
на карту раздела). Из учебной литературы рекомендую:
Гмурман В. Е. Теория вероятностей и математическая статистика (уч. пособие);
Гмурман В. Е. Руководство к решению задач по теории вероятности (задачник с примерами решений).
Везения в главном!

| Оглавление |
Полную и свежую версию этой книги в pdf-формате,
а также курсы по другим темам можно найти здесь.
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
С наилучшими пожеланиями, Александр Емелин