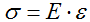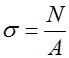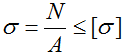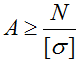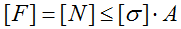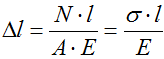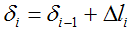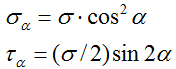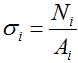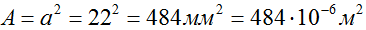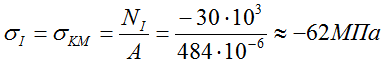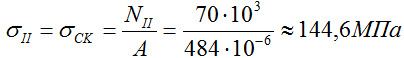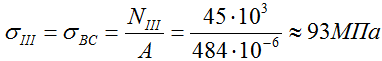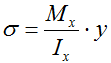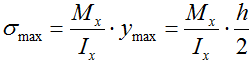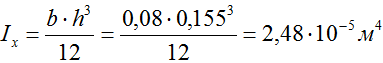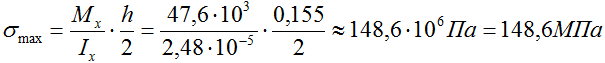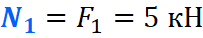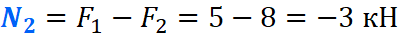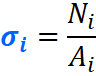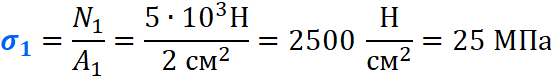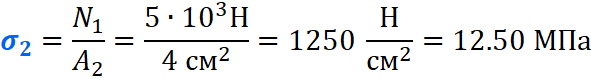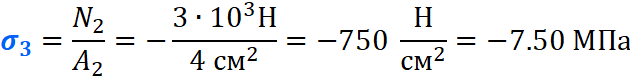Как найти сигму сжатия

1. Основные теоретические сведения и расчетные формулы

1. Определение понятия «растяжение
(сжатие) бруса»

Центральное
(осевое) растяжение и сжатие — это такой
вид деформации бруса, при котором в
поперечных сечениях бруса (стержня)
возникают продольные силы, параллельные
его оси, а все остальные внутренние
усилия равны нулю. Стержень в продольном
направлении удлиняется при растяжении
и укорачивается при сжатии, в поперечном
направлении его размеры уменьшаются
при растяжении и увеличиваются при
сжатии, ось стержня остается прямой.
Внешние силы, приложенные к торцевым
или промежуточным сечениям, должны быть
направлены по оси стержня, либо приводиться
к равнодействующей силе, направленной
вдоль этой оси.

2. Определение
продольных сил. Построение эпюр продольных
сил

Продольная,
или нормальная, сила N,
действующая в поперечном сечении, –
это равнодействующая равномерно
распределенных по сечению внутренних
усилий. Продольная сила N
условно считается положительной при
растяжении и отрицательной при сжатии.

Ее
величина может быть найдена методом
сечений:
продольная
сила N
численно равна алгебраической сумме
проекций на ось бруса всех вне­­­­­­­ш­­­них
сил, приложенных к брусу по одну сторону
от рассматриваемого се­чения.

В
Международной системе единиц (СИ) сила
выражается в ньютонах, в расчетах чаще
применяется величина в тысячу раз
большая – килоньютон (кН), 1кН
=10³
Н.

Примечание:
существуют конструкции, внутренние
усилия в которых невозможно определить
только из уравнений их статического
равновесия. Подобные конструкции
называются статически
неопределимыми.
для их расчета приходится, кроме уравнений
статики, записывать дополнительные
уравнения, учитывающие способность
конструкции деформироваться под
действием внешних нагрузок, изменения
температуры ее элементов и из-за
несоответствия размеров элементов
конструкции ее геометрической схеме.

Продольная сила N
может изменяться по длине стержня.
График, показывающий изменение силы N
при переходе от одного сечения к другому,
называется эпюрой
продольных сил. Каждая
ордината эпюры численно равна продольной
силе, действующей в данном сечении.

Построение
эпюры N
рекомендуется
проводить в следующей последовательности:

—
разбить брус на участки. Участок
– это часть
бруса, расположенная между сечениями,
в которых приложены внешние сосредоточенные
силы, начинается или заканчивается
нагрузка, распределенная по его длине;

—
применяя метод сечений, составить
выражения для определения продольной
силы N
в произвольном
сечении каждого участка и вычислить ее
величину как алгебраическую сумму
проекций всех внешних сил, приложенных
к брусу слева или справа от рассматриваемого
сечения;

—
при наличии в пределах участка нагрузки,
распределенной по его длине, вычислить
величину силы N
на границах участков;

—
параллельно оси бруса провести прямую
линию – ось (базу) эпюры;

—
выбрав масштаб графика, отложить в
граничных сечениях перпендикулярно
оси эпюры вверх положительные значения
продольной силы, вниз – отрицательные.
Если ось бруса вертикальна, вправо
откладываются положительные значения
продольной силы, влево — отрицательные.

—
соединить полученные точки прямыми
линиями и заштриховать эпюру прямыми,
перпендикулярными базе, поставить на
эпюре в кружочке знак плюс для
растягивающего усилия или минус – для
сжимающего. На границах участков
проставить числа, соответствующие
продольным силам, действующим в этих
граничных сечениях.

Примечание:
если на стержень действуют только
сосредоточенные силы, эпюра ограничена
прямыми линиями, параллельными ее оси,
т.е. состоит из прямоугольников и имеет
скачки в сечениях, в которых приложены
внешние сосредоточенные силы. На
участках, находящихся под действием
нагрузки, равномерно распределенной
по длине бруса, эпюра
N
ограничена наклонной прямой.

Пример 1.1. Построить
эпюру продольных сил N
для бруса, показанного на рис.1.1.

Рис. 1.1. Схема бруса

Решение.

Заданный
брус разбиваем на три участка:
АВ, ВС,
CD
(рис.
1.2,а).

Записываем
выражения для определения продольных
сил, действующих в пределах каждого из
участков, мысленно рассекая брус (рис.
1.2,б,в,г)
произвольными сечениями с координатами

(
и

отсчитываются от левого торцевого
сечения,

— от правого, что упрощает вычисления).

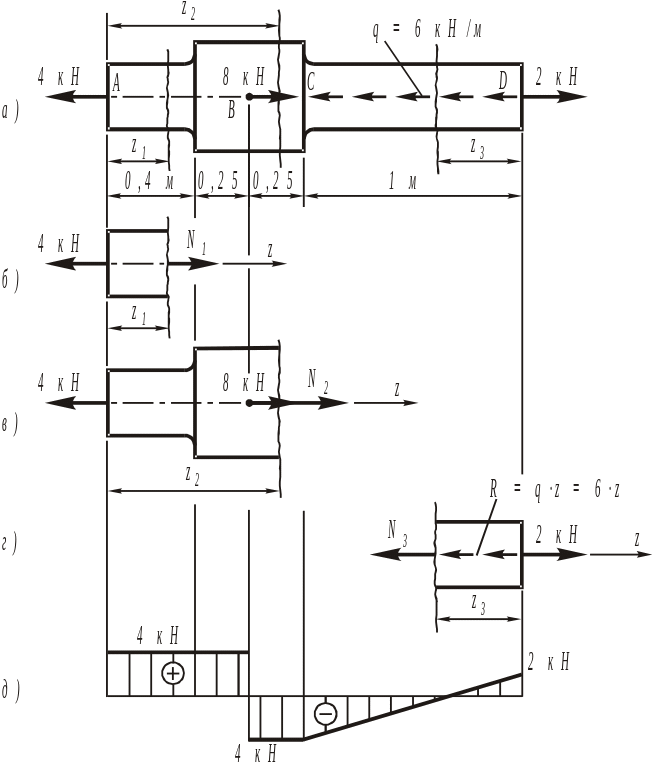
Рис. 1.2. К определению продольных сил в
поперечных сечениях бруса и построению
эпюры продольных сил: а) схема бруса;
(б—г) определение

продольных сил; д) эпюра продольных
сил

Участок
АВ:

Участок
ВС:

Участок
CD:

Из
выражений, приведенных выше, следует,
что на участках
АВ и ВС
эпюра ограничена прямыми, параллельными
оси эпюры N,
а на участке
CD
продольная сила изменяется по линейному
закону, и эпюра N
ограничена наклонной прямой. Вычисляем
значения продольных сил на границах
участков — в сечениях А,
В,
С и
D.

;

.

Для
вычисления продольной силы в сечении
D
подставим в уравнение

значение z
= 0:

.

Если подставить z
= 1 м,
получим значение силы, действующей в
сечении С:

,
что соответствует ранее полученному
результату. Эпюра продольных сил,
построенная по методическим рекомендациям,
приведенным выше, представлена на (рис.
2.2,д).

3. Нормальные
напряжения в поперечном сечении. Эпюра
нормальных напряжений

При
осевом растяжении-сжатии в поперечном
сечении бруса действуют только
нормальные напряжения,
характеризующие интенсивность равномерно
распределенных по сечению внутренних
усилий.

Нормальные
напряжения, обозначаемые греческой
буквой

(сигма), одинаковы во всех точках
поперечного сечения и могут быть
оп­­ределены по формуле

, (1.1)

где
N
— продольная сила в поперечном сечении
(Н);
F
— его пло­щадь (м²).

Растягивающие
напряжения считаются положительными,
сжимающие – отрицательными.

Примечание: в
учебной литературе площадь фигуры
иногда обозначается латинской буквой
А (от английского слова area
— площадь).

Как
видно из формулы (1.1), величина
нормальных напряжений не зависит от
материала бруса.

В
Международной системе единиц (СИ)
нормальное напряжение выражается в
паскалях. В практических расчетах
напряжения чаще всего выражаются в
мегапаскалях
(МПа), 1МПа = 10⁶
Па. В справочной и учебной литературе,
изданной ранее, сила может быть выражена
в кГс,
а напряжение — в
кГссм²
или же в
кГс
мм²
.

Для
наглядного изображения изменения
нормальных напряжений в поперечных
сечениях по длине бруса строится эпюра
нормальных напряжений.

Пример 1.2. Построить
эпюру продольных сил N
и эпюру нормальных напряжений


для бруса, показанного на рис. 1.3,а.

Решение.

Применяя
метод сечений, вычислим, как это было
сделано в примере 1.1, продольные силы,
действующие в поперечных сечениях бруса
участков AB, BC, CD
и DE:

По
найденным значениям продольных сил
строим эпюру N (рис. 1.3,б).

Вычисляем
нормальные напряжения, действующие в
поперечных сечениях бруса участков
AB, BC, CD и DE:

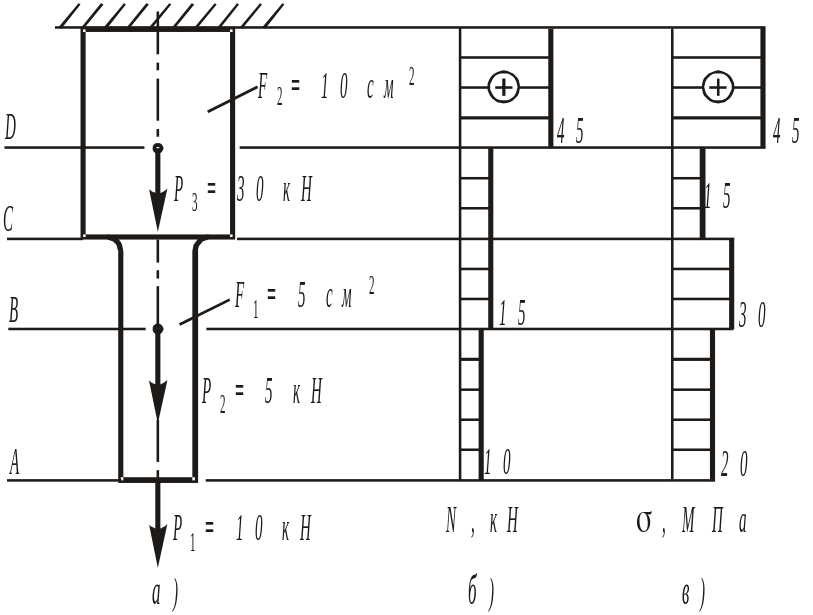
Рис. 1.3. К построению эпюр продольных
сил и нормальных напряжений в поперечных
сечениях бруса а) схема бруса; б)
эпюра продольных сил;

в)
эпюра нормальных напряжений.

Эпюра
нормальных напряжений представлена на
рис. 1.3,в.

На рис.
1.3,б и 1.3,в можно видеть, что эпюра
продольных сил имеет два скачка — в
сечениях B и D, где приложены
внешние силы, а эпюра нормальных
напряжений – три: в сечениях B и D,
где приложены внешние силы, и в месте
изменения площади поперечного сечения
(сечение С).

4. Деформации растянутого (сжатого) бруса

При растяжении
длина бруса увеличивается, а поперечные
размеры умень­шаются, при сжатии
наблюдается обратная картина (рис. 1.4)

а)
б)

Рис.
1.4. Деформации бруса: а)
при растяжении, б)
при сжатии

Поперечные
сечения при растяжении — сжатии остаются
плоскими, смещаясь параллельно своему
начальному положению.

Изменение
первоначальной длины бруса

называется его абсолютным
удлинением
и определяется из выражения:

(1.2)

где
l
— начальная длина бруса; l_к
– длина бруса после его нагружения.

Частное
от деления абсолютного удлинения бруса
на его начальную длину называется
продольной
линейной деформацией
(относительным
удлинением)
бруса

(1.3)

При растяжении l
> 0 и 
> 0, при сжатии эти величины отрицательны.

Абсолютное
поперечное сужение (абсолютная поперечная
деформация)

(1.4)

где
b
— первоначальный
поперечный размер бруса;
b_к
— его величи­на после нагружения.

Относительное поперечное сужение
(относительная поперечная деформация)

. (1.5)

Абсолютная величина
отношения

,
обозначаемая греческой буквой

(мю)
или

(ню),
называется коэффициентом
Пуассона

.
(1.6)

Она является в
пределах упругих деформаций постоянной
величиной для каждого материала и
характеризует его упругие свойства.

Изменение начальных размеров бруса
может произойти не только от действия
приложенных к брусу внешних сил, но и
от действия собственного веса бруса, а
также от изменения температуры материала,
из которого он изготовлен. Большинство
реальных физических тел при нагревании
расширяются, а при охлаждении сжимаются.
Вычислить удлинение бруса при изменении
его температуры можно по формуле

,
(1.7)

где

—
абсолютное удлинение бруса,

—
коэффициент линейного расширения его
материала,

—
температура, на которую нагревается
или охлаждается брус,

—
длина бруса до изменения температуры.

5. Закон Гука. Вычисление продольного
удлинения бруса.

Между
нормальным напряжением, действующим в
поперечном сечении бруса, и его
относительным удлинением существует
прямая пропорциональная зависимость,
называемая законом
Гука:

,
(1.8)

где
E
— коэффициент пропорциональности (модуль
упругости первого рода, или
модуль Юнга).

Модуль
упругости — это физическая величина,
характеризующая жесткость материала
и измеряе­мая в тех же единицах, что
и нормальное напряжение.

Если
N,
E,
F
на участке бруса длиной l
постоянны, его абсолютное удлинение
можно найти по формуле:

. (1.9)

Примечание:
Величина EF,
стоящая в знаменателе, называется
жесткостью
бруса
при осевом растяжении-сжатии.

Если
величины N,
E,
F
(или хотя бы одна из них), не изменяются
в пределах участка, но изменяются по
длине бруса, полное абсолютное удлинение
бруса подсчитывается как алгебраическая
сумма удли­нений участков, в пределах
которых N,
E,
F
постоянны.

.
(1.10)

Пример 1.3. Определить
абсолютное удлинение бруса, показанного
на рис. 1.5 .
Модули
упругости стали и меди: Е_с
=
,
Е_м
=
.

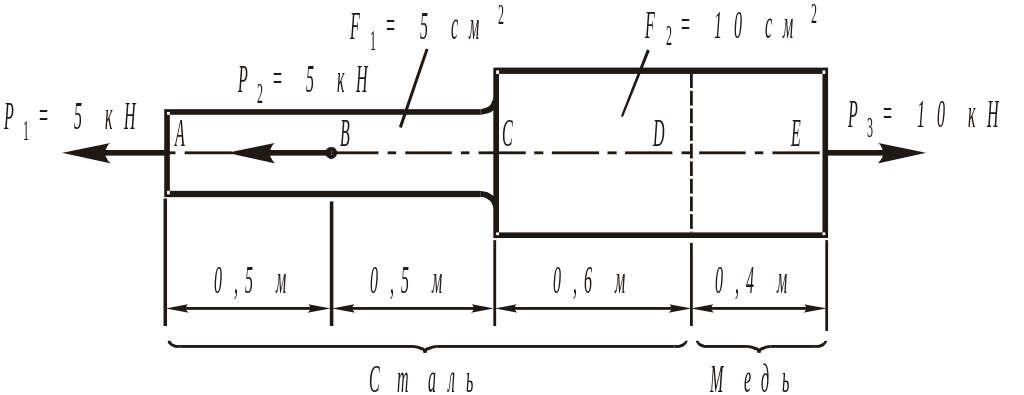
Рис. 1.5. Расчетная
схема бруса

Решение.

Абсолютное удлинение

заданного
бруса следует вычислять по формуле
(1.10)

Методом сечений
определяем продольные силы, действующие
в сечениях AB,
BC,
CD,
DE:

Подставив численные значения, получим

Если же величины N
и F
изменяются по длине бруса по непрерывному
закону, его абсолют­ное удли­не­ние
следует вычислять по формуле

. (1.11)

Пример
1.4. Определить
абсолютное удлинение растянутого бруса,
имеющего коническую форму (рис. 1.6,а).
Р = 20 кН,
d
= 2см,
l
= 1м,  Е =
.

Решение.

Поскольку
площадь поперечного сечения заданного
бруса непрерывно меняется по его длине,
для вычисления абсолютного удлинения
бруса следует воспользоваться формулой
(1.11).

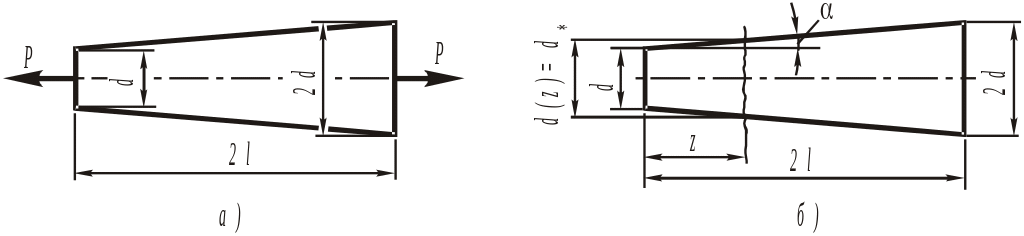
Рис.
1.6. К определению удлинения бруса
переменного сечения:

а)
схема бруса, б)
определение диаметра бруса в его
произвольном

сечении

Очевидно,
что в любом поперечном сечении

,
и под знаком интеграла находится только
одна переменная величина —
.

Из рис. 1.6,б
следует, что

Площадь
поперечного сечения бруса

.

По
формуле 1.11 удлинение бруса

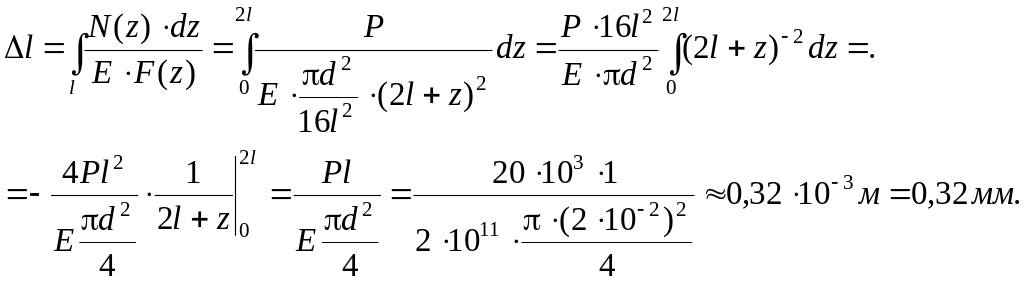
6. Продольные
перемещения поперечных сечений при
растяжении-сжатии

В
ряде задач требуется определить
перемещение
какого-либо поперечного сечения стержня.
Следует иметь ввиду, что перемещение
сечения зависит не от деформации всего
стержня, а лишь от деформации его части,
заключенной между этим сечением и
неподвижной заделкой. Если же нужно
определить изменение расстояния между
двумя поперечными сечениями бруса, то
для этого сле­дует определить
удлинение части бруса, расположенной
между этими сечениями.

Аналогично
эпюрам продольных сил и напряжений
можно построить эпюру
перемещений.

Пример
1.5. Для стального
бруса показанного на рис.1.7а,
построить эпюры продольных сил, нормальных
напряжений и эпюру перемещений поперечных
сечений. Модуль упругости стали принять

Решение.

Очевидно,
что по длине бруса сила не изменяется
и равна 20 кН. Нормальные напряжения
на участках AB и BC соответственно
равны

Эпюры
продольных сил и нормальных напряжений
(рис. 1.7,б,в)
построены так же, как это делалось в
примере 1.2.

Для
построения эпюры перемещений рассмотрим
сечение, находящееся на расстоянии

от
заделки. Его перемещение равно удлинению
части бруса, заключенной между заделкой
и этим сечением и определяется по формуле

в пределах

.

Рис.1.7. К построению эпюр продольных
сил, нормальных напряжений и эпюры
перемещений поперечных сечений бруса:
а) схема бруса; б) эпюра продольных
сил; в) эпюра нормальных напряжений,

г) эпюра перемещений поперечных
сечений бруса

При

,

при

.

В
пределах участка АВ
перемещение изменяется по линейному
закону, следовательно, на этом участке
эпюра имеет вид треугольника. Рассмотрим
далее сечение, находящееся на расстоянии

от места изменения поперечных размеров.
Его перемещение равно сумме удлинений
участков АВ
и z₂,
т.е.

в пределах

.

Таким
образом, при

имеем

.

В
свою очередь при

получим

,

то
есть на участке ВС
эпюра перемещений представляет собой
трапецию, что и показано на рис.1.7,г.

Методы
определения нормальных напряжений и
линейных деформаций используются при
расчетах растянутого или сжатого бруса
на прочность
и жесткость.

7. Расчет бруса на прочность по допускаемым
напряжениям

Рассмотрим
задачи, связанные с расчетом бруса на
прочность по допускаемым напряжениям.
Очевидно, что прочность бруса как
элемента конструкции будет обеспечена,
если величина максимального нормального
напряжения _max,
действующего в его поперечном сечении,
не превышает некоторой величины [],
называемой допускаемым
напряжением.

Условие
прочности материала бруса
при растяжении
— сжатии
записывается в виде двух выражений

,

,
(1.12)

где

,

— соответственно максимальные растягивающие
и сжимающие (по абсолютной величине)
напряжения,

и

— допускаемые напряжения материала при
растяжении и сжатии.

Максимальные
по абсолютной величине напряжения
действуют в сечении или сечениях,
ко­­торые называются опасными.

Центральное растяжение или сжатие возникает в случае, когда на стержень действуют нагрузки, направленные параллельно его оси . При этом в каждом сечении по длине стержня возникает внутреннее усилие, называется оно продольная сила. Продольная сила направлена вдоль оси и удерживает стержень от разрушения.

Величины, которые используются при растяжении — сжатии

$N$ — продольная сила [Н, кН, МН].

$sigma$ — напряжения [Па, кПа, МПа].

$epsilon$ — относительная деформация [безразмерная величина].

$Delta l$ — абсолютная деформация, удлинение [м, мм].

$E$ — модуль упругости [Па, МПа, ГПа].

$nu$ — коэффициент Пуассона [безразмерная величина].

iSopromat.ru

Пример решения задачи на построение эпюры нормальных напряжений σ при растяжении и сжатии стального стержня квадратного сечения.

Задача

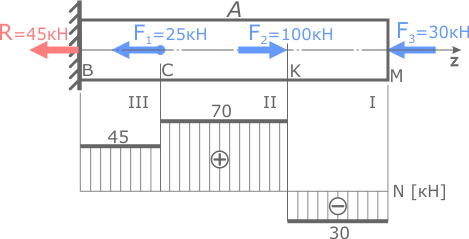
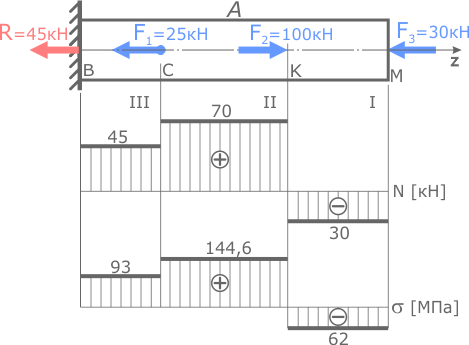
Построить эпюру нормальных напряжений для стержня постоянного сечения, нагруженного продольными силами.

Решение

Предыдущие пункты решения задачи:

т.е. напряжения в рассматриваемом сечении определяются отношением соответствующей величины внутренней силы к площади поперечного сечения стержня.

Площадь поперечного сечения стержня постоянна по всей его длине, и составляет

Очевидно, что в пределах участка стержня, на котором внутренняя сила и площадь постоянны, напряжения так же будут иметь одинаковую величину.

Здесь, при одинаковой площади, внутренние силы различаются на трех силовых участках. Соответственно на этих участках нормальные напряжения тоже будут отличаться.

Знак напряжений зависит от знака соответствующей внутренней продольной силы.
Значения внутренних сил принимаются с построенной ранее эпюры N.

Расчет напряжений

Нормальные напряжения на I силовом участке (KM)

По этим данным строим эпюру нормальных напряжений.

По построенной эпюре видно, что напряжения не превышают заданных допустимых значений, следовательно, рассчитанные размеры стержня обеспечивают его прочность.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

iSopromat.ru

Пример решения задачи на построение эпюры нормальных напряжений σ при изгибе стальной балки прямоугольного сечения.

Задача

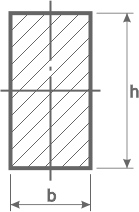
Построить эпюру распределения нормальных напряжений для подобранного ранее прямоугольного сечения двухопорной балки с размерами h=155мм и b=80мм.

Пример решения

Предыдущие пункты решения задачи:

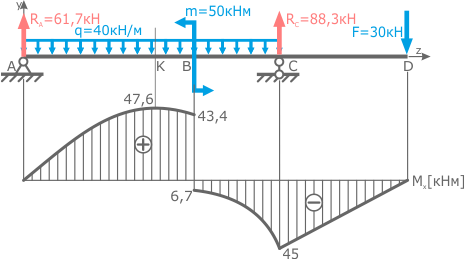
Рассмотрим пример построения эпюры распределения нормальных напряжений в опасном сечении балки.

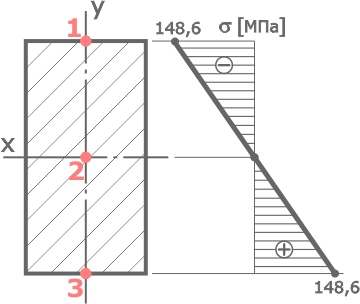
Прямоугольное сечение имеет три характерных точки:

Для построения эпюры достаточно найти значения в любых двух точках, потому что при изгибе нормальная составляющая полных напряжений по высоте сечения меняется линейно.

где I_x – осевой момент инерции сечения,
y – расстояние от оси х проходящей через центр тяжести сечения до точки в которой рассчитывается напряжение.

Очевидно, что на самой оси x (точка №2) где координата y=0 напряжения отсутствуют.

Наибольшие значения нормальных напряжений будут на максимальном удалении от оси x, то есть при y_max=h/2 (в точках 1 и 3).

При изгибе верхний и нижний слой балки испытывают продольную деформацию разных знаков.

Знаки напряжений в точках 1 и 3 определяются по построенной ранее эпюре изгибающих моментов M_x.

В данном случае по ней видно, что в опасном сечении балки эпюра моментов имеет положительное значение (+47,6 кНм), что согласно правила знаков при изгибе говорит о том, что в рассматриваемом месте балки сжимаются верхние слои (нижние соответственно растягиваются).

Поэтому в соответствии с правилом знаков для напряжений, нормальные напряжения в верхней точке 1 будут отрицательны (потому что сжатие), а в точке 3 – положительны (растяжение) или σ _т1=-148,6МПа, σ _т3=148,6МПа.

По полученным данным строим эпюру

Как видно по построенной эпюре, нормальные напряжения не превышают заданных допустимых значений, что говорит о том, что размеры прямоугольного сечения были подобраны верно, и прочность балки обеспечена.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

Построение эпюр при растяжении и сжатии: продольных сил и нормальных напряжений для ступенчатого стержня (бруса)

Автор: Константин Вавилов · Опубликовано 23.11.2017 · Обновлено 14.03.2021

Приветствую, друзья! Сегодня дебютирует наш курс – «сопромат для чайников», Вы находитесь на сайте проекта SoproMats, который связан с сопроматом и не только. На этой страничке будет выложен первый урок из заявленного экспресс курса, который связан с таким простейшим видом деформации как растяжение (сжатие). В частности, будем учиться строить эпюры для бруса (стержня), который загружен растягивающей и сжимающей силой. Как правило, такое домашнее задание, одним из первых, дают всем студентам, которые начинают знакомиться с сопроматом. После изучения материалов данного урока вы научитесь строить следующие эпюры: продольных сил и нормальных напряжений. Не пугайтесь мудреных названий, на самом деле все эти эпюры строятся очень просто. Что же давайте приступим к изучению!

Построение эпюры продольных сил

Так как это курс для чайников, я многие моменты буду упрощать и рассказывать только самое основное, чтобы написанное здесь, было понятно даже самому неподготовленному студенту — заочнику. Если вы хотите более детально изучить рассматриваемые здесь вопросы, то могу предложить Вам другие материалы нашего сайта. Например, что касается данного блока статьи, то у нас есть материалы про продольную силу, где представлено полное досье на данный внутренний силовой фактор: что эта за сила, зачем нужна и т.д. Но если Вам некогда залазить в эти дебри, и хотите по-быстрому освоить продольную силу, то оставайтесь здесь, сейчас покажу как строится первая эпюра!

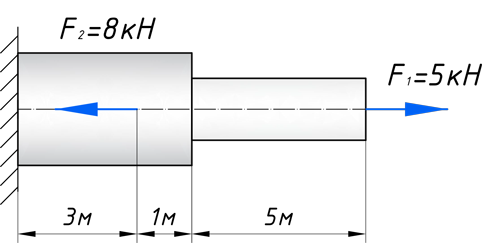
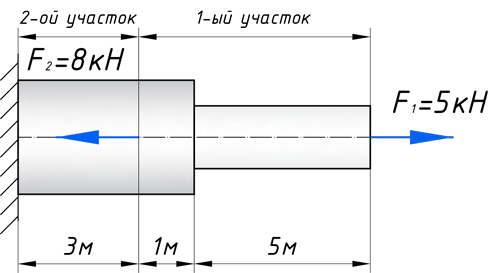
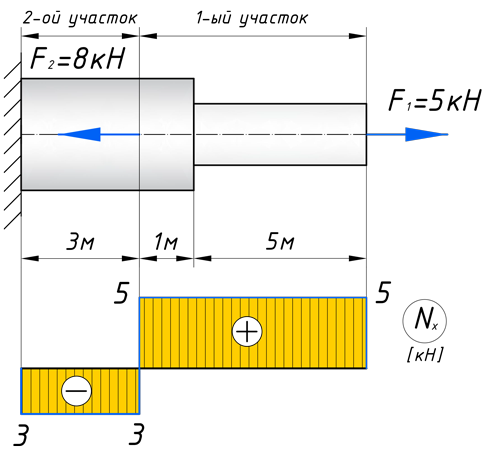
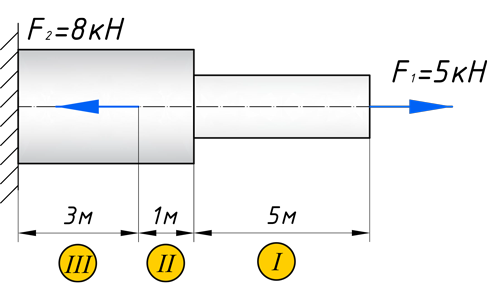
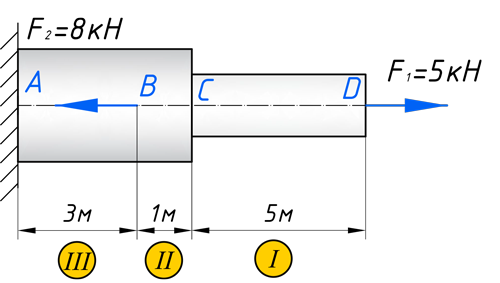
Кстати, вот объект нашего сегодняшнего исследования:

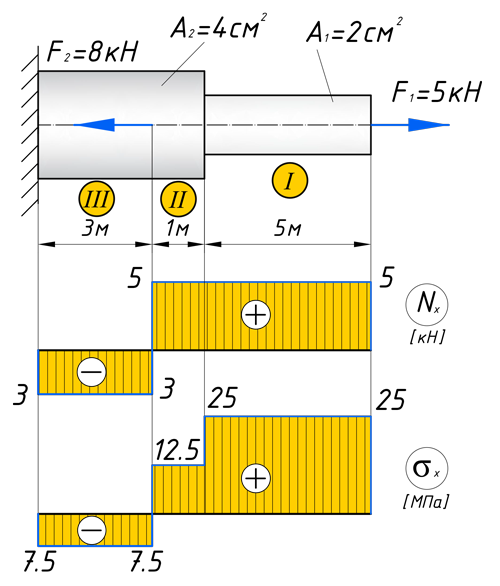
Чтобы построить эпюру продольных сил, нужно разбить наш брус на несколько участков, на которых эта эпюра будет иметь постоянное значение. Конкретно, для продольной эпюры, границами участков служат те точки, где прикладываются силы. То бишь, для нашего примера, нужно рассмотреть всего 2 участка:

Важно! На эпюру продольных сил, никак не влияет форма бруса, в отличие от других эпюр, которые будем дальше рассчитывать и строить.

На первом участке сила F₁ растягивает брус на величину 5кН, поэтому на этом участке, продольная сила будет положительной и равной:

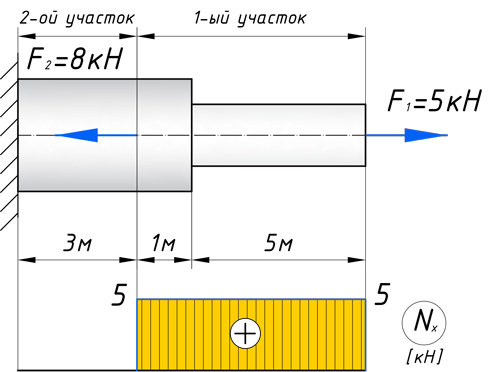
Откладываем это значение на графике. Эпюры в сопромате, принято штриховать перпендикулярно нулевой линии, а также для продольных сил, на эпюрах проставляются знаки:

На втором же участке, сила F₂ сжимает брус, тем самым в уравнение продольных сил, она пойдет с минусом:

Откладываем полученное значение на эпюре:

Вот так, достаточно просто, строится эта эпюра!

Построение эпюры нормальных напряжений

Переходим к эпюре нормальных напряжений. В отличие от продольных сил, нормальные напряжения зависят от формы бурса, а если точнее, то от площади его поперечных сечений и вычисляются они, по следующей формуле:

То бишь, чтобы найти нормальное напряжение в любом сечении бруса, нужно: продольную силу в этом сечении разделить на его площадь.

Для того чтобы построить эпюру нормальных напряжений, нужно рассчитать ее для любого сечения, каждого участка. В отличие, от продольной силы, здесь границами участков также служат места изменения геометрии бруса. Таким образом, для нашего подопытного бруса, нужно наметить три участка и вычислить напряжение, соответственно, 3 раза:

Зададим брусу на первом участке (I) площадь поперечного сечения A₁=2 см 2 , а вторая ступень бруса, допустим, будет иметь площадь A₂=4 см 2 (II, III участки). В вашей домашней задаче, эти величины будут даны по условию. Также в задачах, часто, просят определить эти площади из условия прочности, с учетом допустимого напряжения, обязательно сделаю статью про это.

Вычисляем напряжения на каждом участке:

По полученным значениям строим эпюру нормальных напряжений:

Вот так, достаточно просто можно построить эпюры для бруса, работающего на растяжение (сжатие). В рамках статьи, была рассмотрена достаточно простая расчетная схема, если Вы хотите развить свои навыки по построению эпюр, то приглашаю Вас на страничку про различные эпюры, где можно найти примеры расчета более сложных брусьев с распределенными нагрузками, где о каждой эпюре подготовлена отдельная статья.

Если Вам понравилась статья, расскажите о ней своим друзьям, подписывайтесь на наши социальные сети, где публикуется информация о новых статьях проекта. Также, там можно задать любой интересующий Вас вопрос о сопромате и не только.

Источник

Построение эпюры перемещений

Построение эпюры нормальных напряжений

Переходим к эпюре нормальных напряжений. В отличие от продольных сил, нормальные напряжения зависят от формы бурса, а если точнее, то от площади его поперечных сечений и вычисляются они, по следующей формуле:

То бишь, чтобы найти нормальное напряжение в любом сечении бруса, нужно: продольную силу в этом сечении разделить на его площадь.

Для того, чтобы построить эпюру нормальных напряжений, нужно рассчитать ее для любого сечения, каждого участка. В отличие, от продольной силы, здесь границами участков также служат места изменения геометрии бруса. Таким образом, для нашего подопытного бруса, нужно наметить три участка и вычислить напряжение, соответственно, 3 раза:

Зададим брусу на первом участке (I) площадь поперечного сечения A₁=2 см 2 , а вторая ступень бруса, допустим, будет иметь площадь A₂=4 см 2 (II, III участки). В вашей домашней задаче, эти величины будут даны по условию.

Вычисляем напряжения на каждом участке:

По полученным значениям строим эпюру нормальных напряжений:

Построение эпюры перемещений

Самое время перейти к последней эпюре, которая называется эпюрой осевых перемещений поперечных сечений. Для краткости, ее еще называют просто эпюрой перемещений. Для расчета данного графика, пользуются следующей формулой:

Эта формула, является следствием закона Гука. Также ее можно записать как:

Сейчас покажу как ею пользоваться. Все характерные сечения бруса назовем буквами английского алфавита, чтобы потом в решении, было удобно ссылаться на них:

Традиционно расчет перемещений начинают с жестко защемленного торца. Так как сечение в заделке, не имеет возможности перемещаться, то и в решение записываем, что перемещение этого сечения равно нулю:

Далее, для построения эпюры нужно вычислить перемещения в характерных сечениях, которые находятся на границах участков (B, C и D). Этого будет достаточно, так как в пределах участков, эпюра будет меняться по линейному закону. Исключениями могут быть участки, на которых действует распределенная нагрузка, но это тема отдельной статьи.

Приступаем к расчету перемещения сечения B. По формуле, оно будет равно площади эпюры σ, на третьем участке, деленной на модуль упругости — E. При этом, обязательно, учитываем знак эпюры:

Для других сечений, перемещения будут вычисляться аналогичным образом:

ВАЖНО! Вы, наверное, заметили, что для каждого последующего сечения, в расчетах учитывается перемещение предыдущего. Это обязательно необходимо делать.

По полученным значениям, откладываем эпюру перемещений

Вот так, достаточно просто можно построить эпюры для бруса, работающего на растяжение (сжатие).

Эпюры построения смотри ниже.

Решить задачу(домашняя работа)

Для консольного бруса переменного сечения (рис.3.1) построить эпюры нормальной силы, нормальных напряжений, а также максимальное удлинение.

Принять А=200 мм², А₁=400мм 2 ,l=2м, а=4м,в=3м,с=2м,Е=2 ·10 5 МПа.

Источник

Условие прочности при растяжении (сжатии):,где

 —площадь поперечного сечения; — максимальная продольная сила;

 —максимальное нормальное напряжение;  или — допускаемое напряжение   

Если расчет ведется по методу предельных состояний,то  в расчет вместо допускаемого напряжения вводится расчетное сопротивление материала R.

Три типа задач при расчете на прочность при растяжении (сжатии)

1. Проверочный расчет 

2. Проектный расчет или подбор сечения

3. Определение допускаемой нагрузки 

Рассмотрим схему, согласно которой стержень  растягивается силой Р. Ширина стержня b, длина ℓ. 

Под   действием силы Р стержень удлиняется на величину ∆ℓ (абсолютная деформация), а его поперечное  сечение уменьшается и становится равным b^‘. Тогда найдем величину отношения абсолютной деформации к первоначальной длине бруса:

 Эта безразмерная величина называется относительной продольной деформацией. 

 Это относительная поперечная деформация.

Отношение   называется коэффициентом Пуассона, который для каждого материала имеет свое значение и изменяется в приделах от 0 до 0,5 (0,5 — каучук ,0 — пробка):

медь, μ = 0,31  :  0,34; сталь, μ = 0,25  :  0,33;  чугун, μ = 0,19  :  0,27;                                            бетон, μ = 0,08  :  0,18 

Коэффициент Пуассона характеризует физические свойства материала.

Влияние собственного веса на напряжения и деформации.В длинных вертикальных брусьях существенную  роль играет собственный вес, он вызывает напряжения и деформации, которые нельзя не учитывать. Вес материала G представляет собой нагрузку, равномерно распределенную по объему бруса. Рассмотрим схему, согласно которой стержень подвергается действию собственного веса G (а).

Схема к учету собственного веса: а) общее нагружение; б) для определения напряжений; в) для определения удлинений

Проведем сечение 1 – 1 и рассмотрим равновесие отсеченной части (рис. б). В сечении 1 – 1 будет действовать неизвестное усилие от собственного веса  N_G, Составим уравнение равновесия на ось z:

 , где  — это удельный вес, т.е. вес единицы объема материала в естественном состоянии (вместе с порами).

Определим напряжение от собственного веса:

 Как видно из формулы, напряжения от собственного веса не зависят от площади сечения. Наибольшие напряжения возникают в верхнем ,закрепленном сечении ,где z=l.

 (1)

Теперь разберемся с деформациями. Так как напряжения возрастают пропорционально расстоянию z, то и относительные удлинения бесконечно малых по длине  элементов бруса dz согласно закону Гука пропорциональны величине z:

Абсолютное удлинение элемента dz составляет:

Полное удлинение всего бруса складывается из удлинений отдельных элементов:

 (2)Умножим числитель и знаменатель на А:

 (3), где  -вес всего стержня.

Если сравнить формулу (3) и формулу закона Гука для деформаций:  увидим, что абсолютное удлинение бруса от собственного веса равно половине того удлинения, которое получит тот же брус от силы,  равной его весу и приложенной к свободному концу.

Иными словами, абсолютное удлинение от собственного веса равно удлинению, которое получит брус, если его вес будет сосредоточен в центре тяжести.

Вывод закона Гука при растяжении – сжатии. В ходе многочисленных экспериментов установлена зависимость между нагрузкой, приложенной к стержню, и перемещениями сечений, к которым эта нагрузка приложена:

 (1), где ∆ℓ – абсолютное удлинение стержня, ℓ – длина этого стержня, А – площадь сечения стержня , Е – модуль упругости первого рода (модуль Юнга), характеризует жесткость материала, то есть способность материала сопротивляться действию внешних сил, чем жестче материал, тем меньше он деформируется при данной величине напряжений… Размерность Е —  [МПа]. Для каждого из материалов величина модуля упругости имеет свое значение: сталь, Е = 2^.10⁵ МПа,          медь, Е = 1^.10⁵ МПа,  алюминий, Е = 0,7^.10⁵ МПа. Значение модуля упругости устанавливается экспериментально.

Произведение ЕА – называется жесткостью сечения стержня при растяжении – сжатии.

Учитывая, что F/А = σ, выражение (1) можно записать так: В этой формуле поделим левую и правую части на ℓ , тогда в правой части длины  ℓ  сократятся, а в левой получим:

  получаем величину относительной продольной деформации.

Тогда:  Или, собственно, закон Гука при растяжении-сжатии:

Этот закон был предложен в 1660 г. английским физиком Гуком (закон был опубликован только в 1678 г.).  В 1680 г. этот же закон независимо от Гука открыл французский ученый Мариотт.

Температурные напряжения. При нагреве или охлаждении в элементах конструкций возникают напряжения. Рассмотрим стержень, защемленный с двух сторон и подвергающийся нагреву, т.е. имеем: t₂>t₁.

Схема к расчету нагретого стержня

В случае, если при нагреве или охлаждения стержня, ничего не препятствует изменению его длины, то в нем не возникает никаких напряжений.  Другое дело в статически неопределимых системах. При нагреве бруса, жестко защемленного обоими концами (см. схему), заделки препятствуют его свободному удлинению, и в них возникают реактивные силы Р₁ и Р₂ , вызывающие сжатие бруса.

Составим уравнение статики:            Р₁ – Р₂ = 0      Как видим, задача статически неопределима.

Если мысленно снять правое защемление, то под действием усилия  распора и температуры возникнут перемещения:

, где α – коэффициент линейного расширения материала. Тогда имеем:

Напряжения, вызванные изменением температуры в стержне постоянного сечения, не зависят от его длины, площади поперечного сечения, а зависят от модуля упругости, коэффициента линейного расширения α  и разности температур ∆t.

При нагреве стержня в нем возникают сжимающие напряжения при невозможности свободного удлинения  (а), при охлаждении – растягивающие, поскольку брус будет испытывать растяжение, не имея возможности свободно укорачиваться (б). Вообще при изучении температурных напряжений следует строго разграничивать понятия: растяжение и удлинение, сжатие и укорочение, так как в некоторых задачах стержни могут удлиняться, испытывая при этом сжатие и наоборот.

Растяжение  (сжатие) – это такой   вид нагружения стержня, при котором в его поперечном сечении возникает внутренняя продольная сила Ν, действующая вдоль центральной оси z.

Продольная сила Ν – это равнодействующая всех внутренних нормальных сил в сечении. Для вычисления продольной силы применяется метод сечений.

Продольная сила Ν численно равна алгебраической сумме проекций всех сил, действующих по одну сторону от рассматриваемого сечения,  на продольную ось бруса.

Правило знаков для продольной силы Ν: при растяжении продольная сила положительна, при сжатии – отрицательна.

График изменения продольных сил по длине стержня называется эпюрой. Эпюра N строится методом сечений на характерных участках бруса. Строится эпюра для использования ее при расчете бруса на прочность. Она дает возможность найти наибольшие значения продольных сил и положение сечений, в которых они возникают.

При растяжении (сжатии) возникают только нормальные напряжения. Согласно гипотезе Я. Бернулли (или гипотеза плоских сечений) в поперечных сечениях, удаленных от места приложения нагрузок, нормальные напряжения распределяются по сечению практически равномерно, а сами сечения, перпендикулярные к оси стержня z, остаются плоскими в процессе нагружения.

Нормальные напряжения в сечении при  растяжении (сжатии) вычисляются по формуле

где А – площадь поперечного сечения.

Правило знаков для σ совпадает с правилом знаков для N.

В наклонном сечении, нормаль к которому составляет угол α с осью стержня z,

При растяжении в продольном направлении стержень удлиняется, а его поперечные размеры уменьшаются, при сжатии, напротив, в продольном направлении стержень укорачивается, а его поперечные размеры увеличиваются; Δℓ — абсолютное удлинение или укорочение участка стержня длиной ℓ, Δb – абсолютная поперечная деформация.

Относительное удлинение или укорочение участка стержня длиной ℓ, называемое линейной деформацией, определяется следующим образом

ε=Δℓ/ℓ.

Экспериментально установлено, что в определенной области нагрузок при упругом поведении материала между нормальными напряжениями и линейными деформациями существует линейная зависимость (закон Гука для напряжений)

σ=εЕ,

где Е – модуль продольной упругости или модуль Юнга, это физическая const. Для каждого из материалов величина модуля упругости имеет свое значение:

сталь, Е = 2^.10⁵ МПа,

медь, Е = 1^.10⁵ МПа,

алюминий, Е = 0,7^.10⁵ МПа.

Значение модуля упругости устанавливается экспериментально.

Согласно закону Гука (данную запись называют законом Гука для деформаций)

Δℓ=Νℓ/ЕА

Произведение ЕА – называется жесткостью стержня при растяжении – сжатии.

Перемещение произвольного сечения ступенчатого стержня

w=∑Δℓ_i

Относительная поперечная деформация:

ε′=Δb/b

где b – поперечный размер стержня.

Эксперименты также показывают, что в упругой стадии деформирования между продольной и поперечной деформациями существует взаимосвязь

μ  =│ε′⁄ε│ — const,

где   μ —  коэффициент Пуассона, берется по модулю ,поскольку у продольной и поперечной деформации разные знаки (при растяжении продольные волокна увеличиваются, а поперечные уменьшаются в размере).

Для твердых материалов имеет значения коэффициент Пуассона

0≤μ ≤0,5

Изменение температуры стержня вызывает его удлинение (при нагревании) или укорочение (при охлаждении)

где — a- коэффициент линейного температурного расширения; Δtº=(tº_к-tº_н) — изменение температуры между значениями начальным (tº_н) и конечным (tº_к).

Статически неопределимыми называют системы, имеющие лишние связи – внешние или внутренние.

Для определения внутренних усилий в таких системах недостаточно рассматривать только уравнения равновесия.

В этом случае требуются дополнительные уравнения, число которых равно количеству лишних связей. Дополнительные уравнения составляются на основе анализа картины деформирования системы и использования законов деформирования ее элементов.

Алгоритм решения подобных задач включает следующее:

1)   Статическая часть. Составляются уравнения равновесия с включением неизвестных усилий, действующих по направлению лишних связей.

2)    Геометрическая часть. Составляются уравнения, описывающие взаимосвязь перемещений характерных точек, удлинений и укорочений отдельных стержней между собой.

3)   Физическая связь. Записываются законы деформирования отдельных стержней системы.

Порядок расчета статически неопределимых брусьев

1.  Задаться направлениями возможных опорных реакций и составить уравнение      статики для всей системы в целом.
2. Определить степень статической неопределимости и использовать метод сечений с целью выразить неизвестные усилия через неизвестные опорные реакции. При этом неизвестные продольные силы (N) следует предполагать положительными и поэтому направлять «от сечения».
3. Сформулировать условие совместности деформаций участков бруса.
4. В процессе превращения условия совместности в уравнение совместности деформаций различий в характере деформаций участков не учитывать.

Порядок расчета статически неопределимых шарнирно-стержневых систем

1. Задаться направлениями опорных реакций, но уравнений равновесия для всей системы не составлять, а сразу использовать метод сечений и составить уравнения статики для выделенной части системы.
2. Определить степень статической неопределимости как разницу между количеством всех неизвестных, оказавшихся в уравнениях статики, и числом самих этих уравнений.
3. Рассмотреть (изобразить) любую возможную картину деформаций системы и из ее анализа сформулировать условия совместности деформаций стержней системы (столько, какова степень статической неопределимости).
4. В процессе преобразования условий совместности в уравнения совместности деформаций обязательно учитывать различие в характере деформаций стержней (т.е. вводить удлинение со знаком «плюс», а укорочение со знаком «минус») в соответствии с той картиной деформации, которую мы рассматриваем.