Как найти силовые линии электрического поля

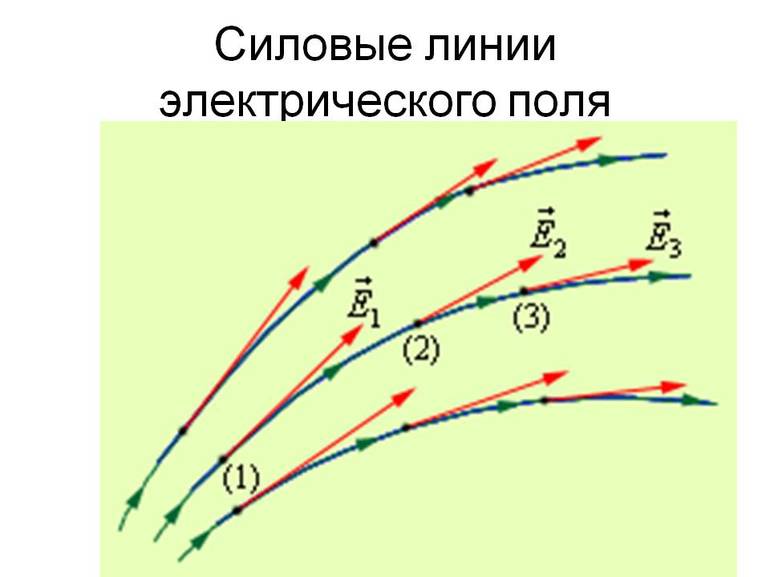
Вектор напряженности электрического поля

По теории близкодействия взаимодействия между заряженными телами, удаленными друг от друга, происходит с помощью электромагнитных полей, создаваемых этими телами в окружающем их пространстве. Если поле было создано неподвижными частицами, то его относят к электростатическому. Когда происходят изменения во времени, получает название стационарного. Электростатическое поле является стационарным. Оно считается частным случаем электромагнитного поля.

Характеристика электрического поля

Силовая характеристика электрического поля – вектор напряженности, который можно найти по формуле:

E → = F → q , где F → — сила, действующая со стороны поля на неподвижный (пробный) заряд q . Его значение должно быть настолько мало, чтобы отсутствовала возможность искажать поле, напряженность которого с его помощью и измеряют. По уравнению видно, что напряженность совпадает по направлению с силой, с которой поле действует на единичный положительный пробный заряд.

У напряженности электростатического поля нет зависимости от времени. Когда она во всех точках поля одинакова, тогда поле называют однородным. В другом случае – неоднородным.

Силовые линии

Чтобы изобразить электростатические поля графически, необходимо задействовать понятие силовых линий.

Силовые линии – это линии, касательные к которым в каждой точке поля совпадают с направлениями векторов напряженности в этих точках.

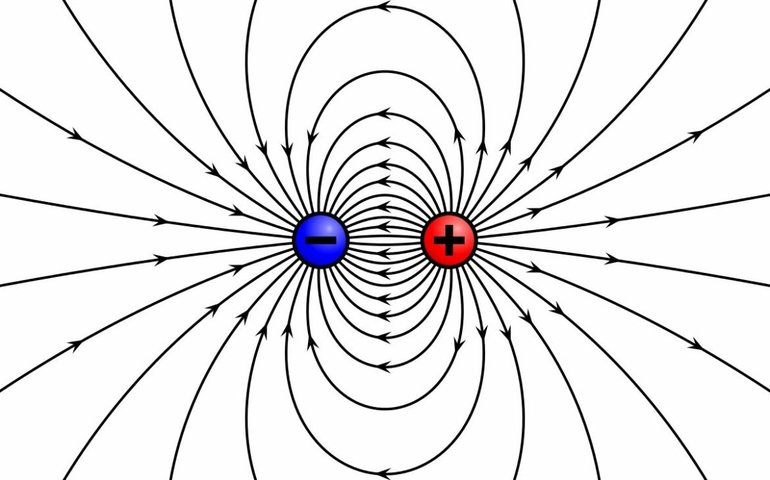
Такие линии в электростатическом поле разомкнутые. Они начинаются на положительных зарядах и заканчивают на отрицательных. Реже уходят в бесконечность или возвращаются из нее. Силовые линии поля не могу пересекаться.

Вектор напряженности электрического поля подчиняется принципу суперпозиции, а именно:

E → = ∑ i = 1 n E → i .

Результирующий вектор напряженности сводится к нахождению векторной суммы напряженностей, составляющих его «отдельные» поля. При распределении непрерывного заряда, поиск суммарной напряженности поля производится по формуле:

Интегрирование E → = ∫ d E → проводится по области распределения зарядов. Если их распределение идет по линии ( τ = d q d l — линейная плотность распределения заряда), то интегрирование E → = ∫ d E → тоже. Когда распределение зарядов идет по поверхности и поверхностная плоскость обозначается как σ = d q d S , тогда интегрируют по поверхности.

Интегрирование по объему выполняется, если имеется объемное распределение заряда:

ρ = d q d V , где ρ — объемная плотность распределения заряда.

Что называется напряженностью электрического поля

Напряженность поля в диэлектрике равняется векторной сумме напряженностей полей, которые создают свободные E 0 → и связанные E p → заряды:

Зачастую бывают случаи, когда диэлектрик изотропный. Тогда запись напряженности поля имеет вид:

E → = E 0 → ε , где ε обозначает относительную диэлектрическую проницаемость среды в рассматриваемой точке поля.

Отсюда следует, что по выражению E → = E 0 → ε имеется однородный изотропный диэлектрик с напряженностью электрического поля в ε меньше, чем в вакууме.

Напряженность электростатического поля системы точечных зарядов равняется:

E → = 1 4 π ε 0 ∑ i = 1 n q i ε r i 3 r i → .

В системе СГС напряженность поля точечного заряда в вакууме:

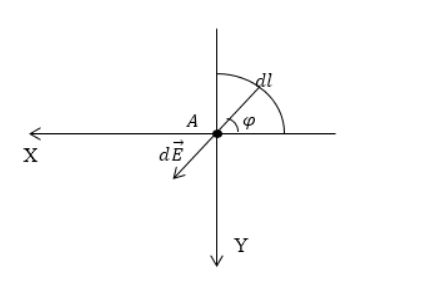
Дан равномерно распределенный заряд по четверти окружности радиуса R с линейной плотностью τ . Необходимо найти напряженность поля в точке А , являющейся центром окружности.

Решение

Произведем выделение на заряженной части окружности элементарного участка d l , который будет создавать элемент поля в точке А . Следует записать выражение для напряженности, то есть для d E → . Тогда формула примет вид:

d E → = d q R 3 R → R .

Проекция вектора d E → на ось О х составит:

d E x = d E cos φ = d q cos φ R 2 .

Произведем выражение d q через линейную плотность заряда τ :

d q = τ d l = τ · 2 πRdR .

Необходимо использовать d q = τ d l = τ · 2 πRdR для преобразования d E x = d E cos φ = d q cos φ R 2 :

d E x = 2 π R τ d R cos φ R 2 = 2 π τ d R cos φ R = τ cos φ d φ R ,

где 2 π d R = d φ .

Далее перейдем к нахождению полной проекции E x при помощи интегрирования d E x = 2 π R τ d R cos φ R 2 = 2 π τ d R cos φ R = τ cos φ d φ R ,

по d φ с изменением угла 0 ≤ φ ≤ 2 π .

E x = ∫ 0 2 π τ cos φ d φ R = τ R ∫ 0 2 π cos φ d φ = τ R sin φ 0 2 π = τ R .

Перейдем к проекции вектора напряженности на О у :

d E y = d E sin φ = τ R sin φ d φ .

Следует проинтегрировать с изменяющимся углом π 2 ≤ φ ≤ 0 :

E y ∫ π 2 0 τ R sin φ d φ = τ R ∫ π 2 0 sin φ d φ = — τ R cos φ π 2 0 = — τ R .

Произведем нахождение модуля вектора напряженности в точке А , применив теорему Пифагора:

E = E x 2 + E y 2 = τ R 2 + — τ R 2 = τ R 2 .

Ответ: E = τ R 2 .

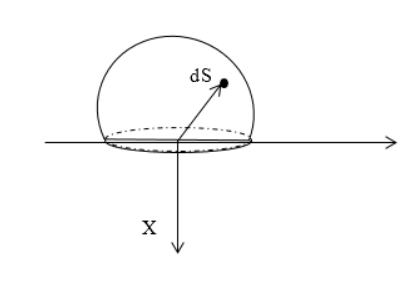
Найти напряженность электростатического поля равномерно заряженной полусферы с радиусом R . Поверхностная плотность заряда равняется σ .

Решение

Следует выделить на поверхности заряженной сферы элементарный заряд d q , располагаемый на элементе площади d S . Запись, используя сферические координаты d S , равняется:

d S = R 2 sin θ d θ d φ ,

при 0 ≤ φ ≤ 2 π , 0 ≤ θ ≤ π 2 .

Элементарная напряженность поля точечного заряда в системе С И :

d E → = d q 4 π ε 0 R 3 R → R .

Необходимо спроецировать вектор напряженности на О х :

d E x = d q cos θ 4 π ε 0 R 2 .

Произведем выражение заряда через поверхностную плотность заряда:

Подставим d q = σ d S в d E x = d q cos θ 4 π ε 0 R 2 , используя d S = R 2 sin θ d θ d φ , проинтегрируем и запишем:

E x = σ R 2 4 π ε 0 R 2 ∫ 0 2 π d φ ∫ 0 π 2 cos θ sin θ d θ = σ 4 π ε 0 2 π · 1 2 = σ 4 ε 0 .

Отсюда следует, что E = E x .

Ответ: напряженность полусферы в центре равняется E = σ 4 ε 0 .

Как найти уравнение силовые линий

Для наглядного представления векторных полей используют картину силовых линий. Силовая линия есть воображаемая математическая кривая в пространстве, направление касательной к которой в каждой точке, через которую она проходит, совпадает с направлением вектора поля в той же точке (рис. 1.17 ).
Рис. 1.17 :
Условие параллельности вектора E → и касательной можно записать в виде равенства нулю векторного произведения E → и элемента дуги d r → силовой линии:

[ d r → , E → ] = 0 .

(9.1)

Векторное уравнение (9.1 ) есть система трёх скалярных уравнений, но только два из них независимы. В декартовой системе его обычно записывают следующих образом: d x E x = d y E y = d z E z .

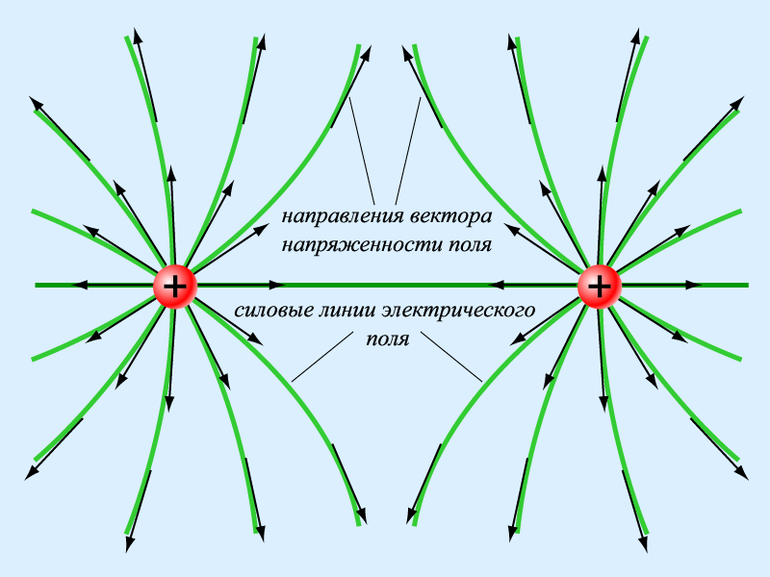
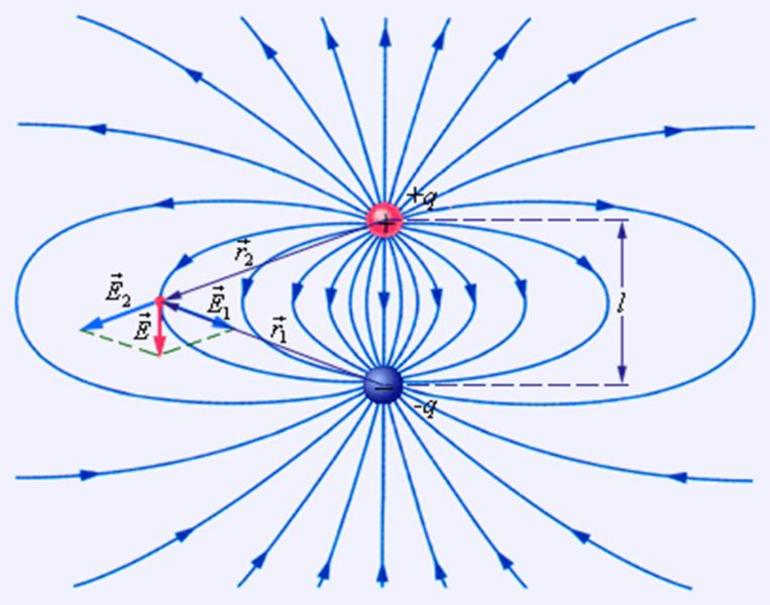
За положительное направление силовой линий принимают направление самого вектора поля E → . При таком соглашении можно сказать, что электрические силовые линии начинаются от положительных зарядов и оканчиваются на отрицательных. На рис. 1.18 изображены силовые линии положительного и отрицательного зарядов.

Эквипотенциалью называют поверхность, на которой постоянна величина электрического потенциала ϕ . В поле точечного заряда, как показано на рис. 1.18 , эквипотенциальными являются сферические поверхности с центров в месте расположения заряда; это видно из уравнения ϕ = q ∕ r = const .

Анализируя геометрию электрических силовых линий и эквипотенциальных поверхностей, можно указать ряд общих свойств геометрии электростатического поля.

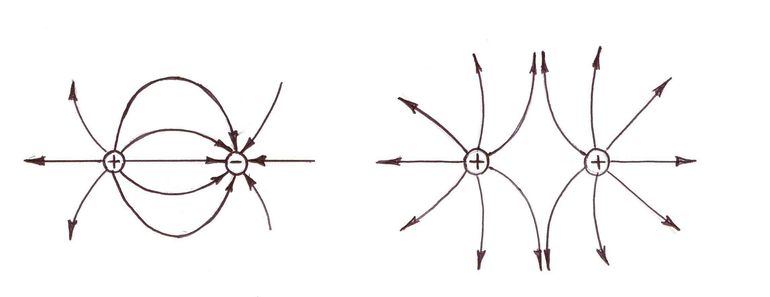
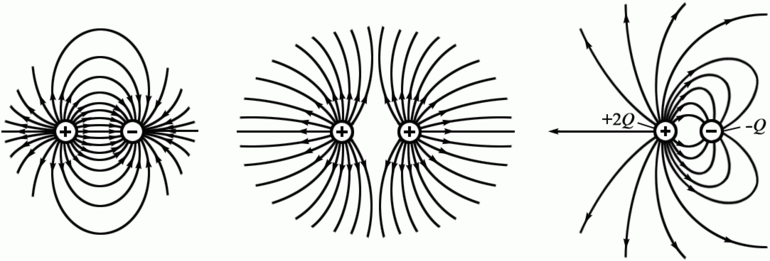
Во-первых, силовые линии начинаются на зарядах. Они либо уходят на бесконечность, либо заканчиваются на других зарядах, как на рис. 1.19 .

Во-вторых, в потенциальном поле силовые линии не могут быть замкнуты. В противном случае можно было бы указать такой замкнутый контур, что работа электрического поля при перемещении заряда по этому контуру не равна нулю.

В-третьих, силовые линии пересекают любую эквипотенциаль по нормали к ней. Действительно, электрическое поле всюду направлено в сторону скорейшего уменьшения потенциала, а на эквипотенциальной поверхности потенциал постоянен по определению (рис. 1.20 ).
Рис. 1.20 :
И наконец, силовые линии нигде не пересекаются за исключением точек, где E → = 0 . Пересечение силовых линий означает, что поле в точке пересечения есть неоднозначная функция координат, а вектор E → не имеет определенного направления. Единственным вектором, который обладает таким свойством, является нулевой вектор. Структура электрического поля вблизи точки нуля будет проанализирована в задачах к ?? .

Метод силовых линий, конечно, применим для графического представления любых векторных полей. Так, в главе ?? мы встретим понятие магнитных силовых линий. Однако геометрия магнитного поля совершенно отлична от геометрии электрического поля.

Рис. 1.21 :
Представление о силовых линиях тесно связано с понятием силовой трубки. Возьмем какой-либо произвольный замкнутый контур L и через каждую точку его проведём электрическую силовую линию (рис. 1.21 ). Эти линии и образуют силовую трубку. Рассмотрим произвольное сечение трубки поверхностью S . Положительную нормаль проведём в ту же сторону, в какую направлены силовые линии. Пусть N — поток вектора E → через сечение S . Нетрудно видеть, что если внутри трубки нет электрических зарядов, то поток N остаётся одним и тем же по всей длине трубки. Для доказательства нужно взять другое поперечное сечение S ′ . По теореме Гаусса, поток электрического поля через замкнутую поверхность, ограниченную боковой поверхностью трубки и сечениями S , S ′ , равен нулю, так как внутри силовой трубки нет электрических зарядов. Поток через боковую поверхность равен нулю, так как вектор E → касается этой поверхности. Следовательно, поток через сечение S ′ численно равен N , но противоположен по знаку. Внешняя нормаль к замкнутой поверхности на этом сечении направлена противоположно n → . Если же направить нормаль в ту же сторону, то потоки через сечения S и S ′ совпадут и повеличине, и по знаку. В частности, если трубка бесконечно тонкая, а сечения S и S ′ нормальны к ней, то

Получается полная аналогия с течением несжимаемой жидкости. В тех местах, где трубка тоньше, поле E → сильнее. В тех местах, где она шире, поле E → сильнее. Следовательно, по густоте силовых линий можно судить о напряженности электрического поля.

До изобретения компьютеров для экспериментального воспроизведения силовых линий брали стеклянный сосуд с плоским дном и наливали в него жидкость, не проводящую электрически ток, например, касторовое масло или глицерин. В жидкости равномерно размешивали истертые в порошок кристаллики гипса, асбеста или какие-либо другие продолговатые частицы. В жидкость погружали металлические электроды. При соединении с источниками электричества, электроды возбуждали электрическое поле. В этом поле частицы электризуются и, притягиваясь друг к другу разноименно наэлектризованными концами, располагаются в виде цепочек вдоль силовых линий. Картина силовых линий искажается течениями жидкости, вызываемыми силами, действующими на неё в неоднородном электрическом поле.

To Be Done Yet
Рис. 1.22 :
Лучшие результаты получаются по методу, применявшемуся Робертом В. Полем (1884–1976). На стеклянную пластинку наклеиваются электроды из станиоля, между которыми создается электрическое напряжение. Затем на пластинку насыпают, слегка постукивая по ней, продолговатые частички, например, кристаллики гипса. Они располагаются по ней вдоль силовых линий. На рис. ?? изображена полученная таким образом картина силовых линий между двумя разноименно заряженными кружками из станиоля.

Записать уравнение силовых линий в произвольных ортогональных координатах.

Записать уравнение силовых линий в сферических координатах.

Как найти уравнение силовые линий

«Физика — 10 класс»

Что является посредником, осуществляющим взаимодействие зарядов?
Как определить, какое из двух полей более сильное? Предложите пути сравнения полей.

Напряжённость электрического поля.

Электрическое поле обнаруживается по силам, действующим на заряд. Можно утверждать, что мы знаем о поле всё, что нам нужно, если будем знать силу, действующую на любой заряд в любой точке поля. Поэтому надо ввести такую характеристику поля, знание которой позволит определить эту силу.

Если поочерёдно помещать в одну и ту же точку поля небольшие заряженные тела и измерять силы, то обнаружится, что сила, действующая на заряд со стороны поля, прямо пропорциональна этому заряду. Действительно, пусть поле создаётся точечным зарядом q₁. Согласно закону Кулона (14.2) на точечный заряд q действует сила, пропорциональная заряду q. Поэтому отношение силы, действующей на помещаемый в данную точку поля заряд, к этому заряду для каждой точки поля не зависит от заряда и может рассматриваться как характеристика поля.

Отношение силы, действующей на помещаемый в данную точку поля точечный заряд, к этому заряду, называется напряжённостью электрического поля.

Подобно силе, напряжённость поля — векторная величина; её обозначают буквой :

Отсюда сила, действующая на заряд q со стороны электрического поля, равна:

=q. (14.8)

Направление вектора совпадает с направлением силы, действующей на положительный заряд, и противоположно направлению силы, действующей на отрицательный заряд.

Единица напряжённости в СИ — Н/Кл.

Силовые линии электрического поля.

Электрическое поле не действует на органы чувств. Его мы не видим. Однако мы можем получить некоторое представление о распределении поля, если нарисуем векторы напряжённости поля в нескольких точках пространства (рис. 14.9, а). Картина будет более наглядной, если нарисовать непрерывные линии.

Линии, касательная в каждой точке которых совпадает с вектором напряжённости электрического поля, называют силовыми линиями или линиями напряжённости поля (рис. 14.9, б).

Направление силовых линий позволяет определить направление вектора напряжённости в различных точках поля, а густота (число линий на единицу площади) силовых линий показывает, где напряжённость поля больше. Так, на рисунках 14.10—14.13 густота силовых линий в точках А больше, чем в точках В. Очевидно, что _А > _B.

Не следует думать, что линии напряжённости существуют в действительности вроде растянутых упругих нитей или шнуров, как предполагал сам Фарадей. Линии напряжённости помогают лишь наглядно представить распределение поля в пространстве. Они не более реальны, чем меридианы и параллели на земном шаре.

Силовые линии можно сделать видимыми. Если продолговатые кристаллики изолятора (например, хинина) хорошо перемешать в вязкой жидкости (например, в касторовом масле) и поместить туда заряженные тела, то вблизи этих тел кристаллики выстроятся в цепочки вдоль линий напряжённости.

На рисунках приведены примеры линий напряжённости: положительно заряженного шарика (см. рис. 14.10), двух разноимённо заряженных шариков (см. рис. 14.11), двух одноимённо заряженных шариков (см. рис. 14.12), двух пластин, заряды которых равны по модулю и противоположны по знаку (см. рис. 14.13). Последний пример особенно важен.

На рисунке 14.13 видно, что в пространстве между пластинами силовые линии в основном параллельны и находятся на равных расстояниях друг от друга: электрическое поле здесь одинаково во всех точках.

Электрическое поле, напряжённость которого одинакова во всех точках, называется однородным.

В ограниченной области пространства электрическое поле можно считать приближённо однородным, если напряжённость поля внутри этой области меняется незначительно.

Силовые линии электрического поля не замкнуты, они начинаются на положительных зарядах и оканчиваются на отрицательных. Силовые линии непрерывны и не пересекаются, так как пересечение означало бы отсутствие определённого направления напряжённости электрического поля в данной точке.

Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский

Электростатика — Физика, учебник для 10 класса — Класс!ная физика

1. Электрический заряд. Закон сохранения
   электрического заряда. Закон Кулона.

Электри́ческий заря́д — это физическая
скалярная величина, определяющая
способность тел быть источником
электромагнитных полей и принимать
участие в электромагнитном взаимодействии.

В замкнутой системе алгебраическая
сумма зарядов всех частиц остается
неизменной.

( … но, не числа заряженных частиц,
т.к. существуют превращения элементарных
частиц).

Замкнутая система

— система частиц, в которую не входят
извне и не выходят наружу заряженные
частицы.

Закон Кулона

— основной закон электростатики.

Сила взаимодействия двух точечных
неподвижных заряженных тел в вакууме
прямо пропорциональна

произведению модулей заряда и обратно
пропорциональна квадрату расстояния
между ними.

Когда тела считаются точечными? — если
расстояние между ними во много раз
больше размеров тел.

Если у двух тел есть электрические
заряды, то они взаимодействуют по закону
Кулона.

1. Напряженность электрического поля.
   Принцип суперпозиции. Расчёт
   электростатического поля системы
   точеных зарядов на основе принципа
   суперпозиции.

Напряжённость электри́ческого по́ля
— векторная физическая величина,
характеризующая электрическое поле в
данной точке и численно равная отношению
силы
действующей на неподвижный[ пробный
заряд, помещенный в данную точку поля,
к величине этого заряда
:

.

При́нцип суперпози́ции — один из самых
общих законов во многих разделах физики.
В самой простой формулировке принцип
суперпозиции гласит:

результат воздействия на частицу
нескольких внешних сил есть векторная
сумма воздействия этих сил.

Наиболее известен принцип суперпозиции
в электростатике, в которой он утверждает,
что напряженность электростатического
поля, создаваемого в данной точке
системой зарядов, есть сумма напряженностей
полей отдельных зарядов.

3.

Электрическое поле
изображают с помощью силовых линий.

Силовые линии указывают
направление силы, действующей на
положительный заряд в данной точке
поля.

Свойства силовых линий электрического поля

• Силовые линии электрического
  поля имеют начало и конец. Они начинаются
  на положительных зарядах и заканчиваются
  на отрицательных.

• Силовые линии электрического
  поля всегда перпендикулярны поверхности
  проводника.

• Распределение
  силовых линий электрического поля
  определяет характер поля. Поле может
  быть радиальным (если
  силовые линии выходят из одной точки
  или сходятся в одной точке), однородным(если
  силовые линии параллельны)
  и неоднородным (если
  силовые линии не параллельны).

Силовые линии электрического поля

стр. 448

9.5. Поток вектора напряженности электрического поля. Теорема Гаусса

Как
и для любого векторного поля важно
рассмотреть свойства потока электрического
поля. Поток электрического поля
определяется традиционно.

Выделим
малую площадку площадью ΔS,
ориентация которой задается единичным
вектором нормали  (рис.
157).

В
пределах малой площадки электрическое
поле можно считать однородным ^[1],
тогда поток вектора напряженности
ΔФ_E определяется
как произведение площади площадки на
нормальную составляющую вектора
напряженности

 .
(1)

где  —
скалярное произведение векторов  и ; E_n —
нормальная к площадке компонента вектора
напряженности.

В
произвольном электростатическом поле
поток вектора напряженности через
произвольную поверхность, определяется
следующим образом (рис. 158):

—
поверхность разбивается на малые
площадки ΔS (которые
можно считать плоскими);

—
определяется вектор напряженности  на
этой площадке (который в пределах
площадки можно считать постоянным);

—
вычисляется сумма потоков через все
площадки, на которые разбита поверхность

 .

Эта
сумма называется потоком
вектора напряженности электриче-ского
поля через заданную поверхность.

Непрерывные линии, касательные к которым в каждой точке, через которую они проходят, совпадают с вектором напряженности, называются силовыми линиями электрического поля или линиями напряженности.
Густота линий больше там, где напряженность поля больше. Силовые линии электрического поля, созданного неподвижными зарядами не замкнуты: они начинаются на положительных зарядах и заканчиваются на отрицательных. Электрическое поле, напряженность которого одинакова во всех точках пространства, называется однородным.Густота линий больше вблизи заряженных тел, где напряженность больше. Силовые линии одного и того же поля не пересекаются.На любой заряд в электрическом поле действует сила. Если заряд под действием этой силы перемещается, то электрическое поле совершает работу. Работа сил по перемещению заряда в электростатическом поле не зависит от траектории движения заряда и определяется только положением начальной и конечной точек.Рассмотрим однородное электрическое поле, образованное плоскими пластинами, заряженными разноименно. Напряженность поля во всех точках одинакова. Пусть точечный заряд q перемещается из точки А в точку B вдоль кривой L. При перемещении заряда на небольшую величину D L работа равна произведению модуля силы на величину перемещения и на косинус угла между ними, или, что то же самое, произведению величины точечного заряда на напряженность поля и на проекцию вектора перемещения на направление вектора напряженности. Если подсчитать полную работу по перемещению заряда из точки А в точку B, то она независимо от формы кривой L, окажется равной работе по перемещению заряда q вдоль силовой линии в точку B1. Работа по перемещению из точки B1в точку B равна нулю, так как вектор силы и вектор перемещения перпендикулярны.

5. Теорема Гаусса для электрического
поля в вакууме

Общая
формулировка: Поток
вектора напряжённости
электрического поля через
любую произвольно выбранную замкнутую
поверхность пропорционален заключённому
внутри этой поверхности электрическому
заряду.

СГС	СИ

где

• —
  поток
  вектора напряжённости электрического
  поля через замкнутую поверхность .

• —
  полный
  заряд, содержащийся в объёме, который
  ограничивает поверхность .

• — электрическая
  постоянная.

Данное
выражение представляет собой теорему
Гаусса в интегральной форме.

• Замечание:
  поток вектора напряжённости через
  поверхность не зависит от распределения
  заряда (расположения зарядов) внутри
  поверхности.

В
дифференциальной форме теорема Гаусса
выражается следующим образом:

СГС	СИ

Здесь —
объёмная плотность заряда (в случае
присутствия среды — суммарная
плотность свободных и связанных зарядов),
а — оператор
набла.

• Теорема
  Гаусса может быть доказана как теорема
  в электростатике исходя из закона
  Кулона (см.
  ниже).
  Формула однако также верна в
  электродинамике, хотя в ней она чаще
  всего не выступает в качестве доказываемой
  теоремы, а выступает в качестве
  постулируемого уравнения (в этом смысле
  и контексте ее логичнее называть законом
  Гаусса^[2].

6. Применение теоремы Гаусса к расчету
электростатического поля равномерно
заряженной длинной нити (цилиндра)

Поле
равномерно заряженного бесконечного
цилиндра (нити).
Бесконечный цилиндр радиуса R (рис. 6)
равномерно заряжен слинейной
плотностью τ
(τ = –dQ/dt заряд, который приходится на
единицу длины). Из соображений симметрии
мы видим, что линии напряженности будут
направлены по радиусам круговых сечений
цилиндра с одинаковой густотой во все
стороны относительно оси цилиндра.
Мысленно построим в качестве замкнутой
поверхности коаксиальный цилиндр
радиуса r и высотой l.
Поток вектора Е сквозь
торцы коаксиального цилиндра равен
нулю (торцы и линии напряженности
параллельны), а сквозь боковую поверхность
равен 2πrlЕ.
Используя теорему Гаусса, при r>R 2πrlЕ
= τl/ε₀,
откуда 

 (5) 

Если
r<R, то замкнутая поверхность внутри
зарядов не содержит, поэтому в этой
области E=0. Значит, напряженность поля
вне равномерно заряженного бесконечного
цилиндра задается выражением (5), внутри
же его поле равно нулю. 

7. Применение теоремы Гаусса к расчету
электростатического поля равномерно
заряженной плоскости

 Поле
равномерно заряженной бесконечной
плоскости.
Бесконечная плоскость (рис. 1) заряжена
с постоянной поверхностной
плотностью +σ
(σ = dQ/dS — заряд, который приходится на
единицу поверхности). Линии напряженности
перпендикулярны данной плоскости и
направлены от нее в каждую из сторон.
Возьмем в качестве замкнутой поверхности
цилиндр, основания которого параллельны
заряженной плоскости, а ось перпендикулярна
ей. Так как образующие цилиндра параллельны
линиям напряженности поля (соsα=0), то
поток вектора напряженности сквозь
боковую поверхность цилиндра равен
нулю, а полный поток сквозь цилиндр
равен сумме потоков сквозь его основания
(площади оснований равны и для основания
Е_n совпадает
с Е), т. е. равен 2ES. Заряд, который заключен
внутри построенной цилиндрической
поверхности, равен σS. Согласно теореме
Гаусса, 2ES=σS/ε₀,
откуда 

 (1) 

Из
формулы (1) следует, что Е не зависит от
длины цилиндра, т. е. напряженность поля
на любых расстояниях равна по модулю,
иными словами, поле равномерно заряженной
плоскости однородно. 

8. Применение теоремы Гаусса к расчету
электростатического поля равномерно
заряженной сферы и объемно заряженного
шара.

Поле
равномерно заряженной сферической
поверхности.
Сферическая поверхность радиуса R с
общим зарядом Q заряжена равномерно
с поверхностной
плотностью +σ.
Т.к. заряд распределен равномернопо
поверхности то поле, которое создавается
им, обладает сферической симметрией.
Значит линии напряженности направлены
радиально (рис. 3). Проведем мысленно
сферу радиуса r, которая имеет общий
центр с заряженной сферой. Если r>R,ro
внутрь поверхности попадает весь заряд
Q, который создает рассматриваемое поле,
и, по теореме Гаусса, 4πr²E
= Q/ε₀ ,
откуда 

 (3) 

При
r>R поле убывает с расстоянием r по
такому же закону, как у точечного заряда.
График зависимости Е от r приведен на
рис. 4. Если r'<R, то замкнутая поверхность
не содержит внутри себя зарядов, значит
внутри равномерно заряженной сферической
поверхности электростатическое поле
отсутствует (E=0). 

 Поле
объемно заряженного шара.
Шар радиуса R с общим зарядом Q заряжен
равномерно с объемной
плотностью ρ
(ρ = dQ/dV – заряд, который приходится на
единицу объема). Учитывая соображения
симметрии, аналогичные п.3, можно доказать,
что для напряженности поля вне шара
получится тот же результат, что и в
случае (3). Внутри же шара напряженность
поля будет иная. Сфера радиуса r'<R
охватывает заряд Q’=(4/3)πr’³ρ
. Поэтому, используя теорему Гаусса,
4πr’²E=Q’/ε₀=(4/3)πr’³ρ/ε₀ .
Т.к. ρ=Q/(4/3πR³))
получаем

 (4) 

Значит,
напряженность поля вне равномерно
заряженного шара описывается формулой
(3), а внутри его изменяется линейно с
расстоянием r’ согласно зависимости
(4). График зависимости Е от r для
рассмотренного случая показан на рис.
5. 

9.
Работа сил электрического поля при
перемещении заряда. Теорема о циркуляции
напряженности электрического поля.

Элементарная
работа, совершаемая силой F при перемещении
точечного электрического заряда  из
одной точки электростатического поля
в другую на отрезке пути  ,
по определению равна

где  —
угол между вектором силы F и направлением
движения .
Если работа совершается внешними силами,
то dA0. Интегрируя последнее выражение,
получим, что работа против сил поля при
перемещении пробного заряда  из
точки “а” в точку “b” будет равна

где  —
кулоновская сила, действующая на пробный
заряд  в
каждой точке поля с напряженностью Е.
Тогда работа

Пусть
заряд  перемещается
в поле заряда q из точки “а”, удалённой
от q на расстоянии  в
точку “b”, удаленную от q на расстоянии  (рис
1.12).

Как
видно из рисунка  тогда
получим

Как
было сказано выше, работа сил
электростатического поля, совершаемая
против внешних сил, равна по величине
и противоположна по знаку работе внешних
сил, следовательно

Теорема
о циркуляции электрического поля.

Напряженность и потенциал –
это две характеристики одного и того
же объекта – электрического поля,
поэтому между ними должна существовать
функциональная связь. Действительно,
работа сил поля по перемещению заряда q из
одной точки пространства в другую может
быть представлена двояким образом:

Откуда
следует, что 

Или

Это
и есть искомая связь между
напряженностью и потенциалом электрического
поля в дифференциальномвиде.

 —
вектор, направленный из точки с меньшим
потенциалом в точку с большим потенциалом
(рис.2.11).

, .

Рис.2.11.
Векторыи gradφ.
.

Из
свойства потенциальности электростатического
поля следует, что работа сил поля по
замкнутому контуру (φ₁=
φ₂)
равна нулю:

,

поэтому
можем написать

Последнее
равенство отражает суть второй основной
теоремы электростатики
– теоремы
о циркуляцииэлектрического поля,
согласно которой циркуляция
поля вдоль произвольного
замкнутого контура равна нулю. Эта
теорема является прямым
следствием потенциальности электростатического
поля.

10. Потенциал электрического поля. Связь
между потенциалом и напряжонностью.

Электростатический
потенциа́л (см.
также кулоновский
потенциал) — скалярная энергетическая характеристикаэлектростатического
поля,
характеризующая потенциальную
энергию поля,
которой обладает единичный заряд,
помещённый в данную точку поля. Единицей
измерения потенциала
является, таким образом, единица
измерения работы,
деленная на единицу измерения заряда (для
любой системы единиц; подробнее о
единицах измерения — см.
ниже).

Электростатический
потенциал —
специальный термин для возможной замены
общего термина электродинамики скалярный
потенциал в
частном случае электростатики (исторически
электростатический потенциал появился
первым, а скалярный потенциал
электродинамики — его обобщение).
Употребление термина электростатический
потенциал определяет
собой наличие именно электростатического
контекста. Если такой контекст уже
очевиден, часто говорят просто
о потенциале без
уточняющих прилагательных.

Электростатический
потенциал равен отношению потенциальной
энергии взаимодействия заряда с
полем к величине этого заряда:

Напряжённость
электростатического поля  и
потенциал  связаны
соотношением^[1]

или
обратно^[2]:

Здесь — оператор
набла,
то есть в правой части равенства стоит
минус градиент потенциала —
вектор с компонентами, равными частным
производным от
потенциала по соответствующим
(прямоугольным) декартовым координатам,
взятый с противоположным знаком.

Воспользовавшись
этим соотношением и теоремой
Гаусса для
напряжённости поля ,
легко увидеть, что электростатический
потенциал удовлетворяетуравнению
Пуассона.
В единицах системы СИ:

где —
электростатический потенциал
(в вольтах), —
объёмная плотность
заряда (в кулонах на
кубический метр), а — диэлектрическая
проницаемостьвакуума
(в фарадах на
метр).

11. Энергия системы неподвижных точечных
электрических зарядов.

 Энергия
системы неподвижных точечных зарядов.
Как мы уже знаем, электростатические
силы взаимодействия консервативны;
значит, система зарядов обладает
потенциальной энергией. Будем искать
потенциальную энергию системы двух
неподвижных точечных зарядов Q₁ и
Q₂,
которые находятся на расстоянии r друг
от друга. Каждый из этих зарядов в поле
другого обладает потенциальной энергией
(используем формулу потенциала уединенного
заряда): 

 

где
φ₁₂ и
φ₂₁ —
соответственно потенциалы, которые
создаются зарядом Q₂ в
точке нахождения заряда Q₁ и
зарядом Q₁ в
точке нахождения заряда Q₂.
Согласно, 

 и  

поэтому
W₁ =
W₂ =
W и 

 

Добавляя
к нашей системе из двух зарядов
последовательно заряды Q₃,
Q₄,
… , можно доказать, что в случае n
неподвижных зарядов энергия взаимодействия
системы точечных зарядов равна 

 (1) 

где
φ_i —
потенциал, который создается в точке,
где находится заряд Q_i,
всеми зарядами, кроме i-го. 

12. Диполь в электрическом поле. Полярные
и неполярные молекулы. Поляризация
диэлектриков. Поляризованность.
Сегнетоэлектрики.

Если поместить диэлектрик во внешнее
электрическое поле, то он поляризуется,
т. е. получит неравный нулю дипольный
момент pV=∑piгдеpi— дипольный момент
одной молекулы. Чтобы произвести
количественное описание поляризации
диэлектрика вводят векторную величину
— поляризованность, которая определяется
как дипольный момент единицы объема
диэлектрика:

(1)

Из опыта известно, что для большого
класса диэлектриков (за исключением
сегнетоэлектриков, см. далее)
поляризованность Р зависит от напряженности
поля Е линейно . Если диэлектрик
изотропный и Е численно не слишком
велико, то

(2)

Сегнетоэлектрики —
диэлектрики, которые обладают в
определенном интервале температур
спонтанной (самопроизвольной)
поляризованностью, т. е. поляризованностью
в условиях отсутствия внешнего
электрического поля. К сегнетоэлектрикам
относятся, например, подробно изученные
И. В. Курчатовым (1903—1960) и П. П. Кобеко
(1897—1954) сегнетова соль NaKC₄H₄O₆•4Н₂O
(от нее и было получено данное название)
и титанат бария ВаТiO₃. 

Поляризация
диэлектриков —
явление, связанное с ограниченным
смещением связанных зарядов в диэлектрике или
поворотом электрических диполей,
обычно под воздействием внешнего электрического
поля,
иногда под действием других внешних
сил или спонтанно.

Поляризацию
диэлектриков характеризует вектор
электрической поляризации.
Физический смысл вектора электрической
поляризации — это дипольный
момент,
отнесенный к единице объема диэлектрика.
Иногда вектор поляризации коротко
называют просто поляризацией.

Электрический
диполь —
идеализированная электронейтральная
система, состоящая из точечных и равных
по абсолютной величине положительного
и отрицательного электрических
зарядов.

Другими
словами, электрический диполь представляет
собой совокупность двух равных по
абсолютной величине разноимённых
точечных зарядов, находящихся на
некотором расстоянии друг от друга

Произведение
вектора  проведённого
от отрицательного заряда к положительному,
на абсолютную величину зарядов  называется
дипольным моментом: 

Во
внешнем электрическом поле  на
электрический диполь действует момент
сил  который
стремится повернуть его так, чтобы
дипольный момент развернулся вдоль
направления поля.

Потенциальная
энергия электрического диполя в
(постоянном) электрическом поле равна  (В
случае неоднородного поля это означает
зависимость не только от момента диполя
— его величины и направления, но и от
места, точки нахождения диполя).

Вдали
от электрического диполя напряжённость
его электрического
поля убывает
с расстоянием  как  то
есть быстрее, чем у точечного
заряда ().

Любая
в целом электронейтральная система,
содержащая электрические заряды, в
некотором приближении (то есть собственно
в дипольном
приближении)
может рассматриваться как электрический
диполь с моментом  где —
заряд -го
элемента, —
его радиус-вектор. При этом дипольное
приближение будет корректным, если
расстояние, на котором изучается
электрическое поле системы, велико по
сравнению с её характерными размерами.

Поля́рные
вещества́ в химии — вещества, молекулы которых
обладают электрическим
дипольным моментом.
Для полярных веществ, в сравнении с
неполярными, характерны высокая диэлектрическая
проницаемость (более
10 в жидкой фазе), повышенные температура
кипения и температура
плавления.

Дипольный
момент обычно возникает вследствие
разной электроотрицательности составляющих
молекулу атомов,
из-за чегосвязи в
молекуле приобретают полярность.
Однако, для приобретения дипольного
момента требуется не только полярность
связей, но и соответственное их расположение
в пространстве.
Молекулы, имеющие форму, подобную
молекулам метаналибо двуокиси
углерода,
являются неполярными.

Полярные растворители наиболее
охотно растворяют полярные
вещества, а также обладают
способностью сольватироватьионы.
Примерами полярного растворителя
являются вода, спирты и
другие вещества.

13. Напряженность электрического поля
в диэлектрики. Электрическое смещение.
Теорема Гаусса для поля в диэлектрики.

Напряженность
электростатического поля, согласно
(88.5), зависит от свойств среды: в однородной
изотропной среде напряженность
поля Е обратно
пропорциональна .
Вектор напряженности Е,
переходя через границу диэлектриков,
претерпевает скачко­образное изменение,
создавая тем самым неудобства при
расчетах электростатических полей.
Поэтому оказалось необходимым помимо
вектора напряженности характеризо­вать
поле еще вектором
электрического смещения, который
для электрически изотроп­ной среды,
по определению, равен

 (89.1)

Используя формулы
(88.6) и (88.2), вектор электрического смещения
можно выразить как

 (89.2)

Единица
электрического смещения — кулон на
метр в квадрате (Кл/м²).

Рассмотрим,
с чем можно связать вектор электрического
смещения. Связанные заряды появляются
в диэлектрике при наличии внешнего
электростатического поля, создаваемого
системой свободных электрических
зарядов, т. е. в диэлектрике на
электростатическое поле свободных
зарядов накладывается дополнительное
поле свя­занных зарядов.Результирующее
поле в
диэлектрике описывается вектором
напряжен­ности Е,
и потому он зависит от свойств диэлектрика.
Вектором D описывается
электростатическое поле, создаваемое свободными
зарядами. Связанные
заряды, воз­никающие в диэлектрике,
могут вызвать, однако, перераспределение
свободных заря­дов, создающих поле.
Поэтому вектор D характеризует
электростатическое поле, создаваемое свободными
зарядами (т.
е. в вакууме), но при таком их распределении
в пространстве, какое имеется при
наличии диэлектрика.

Аналогично,
как и поле Е,
поле D изображается
с помощью линий
электрического смещения, направление
и густота которых определяются точно
так же, как и для линий напряженности
(см. §79).

Линии
вектора Е могут
начинаться и заканчиваться на любых
зарядах — свободных и связанных, в то
время как линии вектора D — только
на свободных зарядах. Через
области поля, где находятся связанные
заряды, линии вектора D проходят
не прерываясь.

Для
произвольной замкнутой поверхности S поток
вектора D сквозь
эту поверх­ность

где D_n —
проекция вектора D на
нормаль n к
площадке dS.

Теорема
Гаусса для электростатического
поля в диэлектрике:

 (89.3)

т. е.
поток вектора смещения электростатического
поля в диэлектрике сквозь произ­вольную
замкнутую поверхность равен алгебраической
сумме заключенных внутри этой
поверхности свободных электрических
зарядов. В
такой форме теорема Гаусса справедлива
для электростатического поля как для
однородной и изотропной, так и для
неоднородной и анизотропной сред.

Для
вакуума D_n = ₀E_n ( =1),
тогда поток вектора напряженности Е сквозь
произ­вольную замкнутую поверхность
(ср. с (81.2)) равен

Так
как источниками поля Е в
среде являются как свободные, так и
связанные заряды, то теорему Гаусса
(81.2) для поля Е в
самом общем виде можно записать как

где —
соответственно алгебраические суммы
свободных и связанных зарядов, охватываемых
замкнутой поверхностью S. Однако
эта формула неприемлема для описания
поля Е в
диэлектрике, так как она выражает
свойства неизвестного поля Е через
связанные заряды, которые, в свою очередь,
определяются им же. Это еще раз доказывает
целесообразность введения вектора
электрического смещения.

.
Напряженность электрического поля в
диэлектрике.

В
соответствии с принципом
суперпозиции электрическое
поле в диэлектрике векторно складывается
из внешнего поля  и
поля поляризационных зарядов  (рис.3.11).

 или
по абсолютной величине

Мы
видим, что величина напряженности
поля  в
диэлектрике меньше, чем вакууме. Другими
словами, любой диэлектрик ослабляет внешнее
электрическое поле.

Рис.3.11.
Электрическое поле в диэлектрике.

Индукция
электрического поля ,
где , ,
то есть .
С другой стороны, ,
откуда находим, что ε₀Е₀ =
ε₀εЕ и,
следовательно, напряженность электрического
поля в изотропном диэлектрике
есть:

Эта
формула раскрывает физический
смысл диэлектрической
проницаемости и показывает, что
напряженность электрического поля в
диэлектрике в  раз меньше,
чем в вакууме. Отсюда следует простое
правило: чтобы
написать формулы электростатики в
диэлектрике, надо в соответствующих
формулах электростатики вакуума рядом
с  приписать .

В
частности, закон
Кулона в
скалярной форме запишется в виде:

14. Электрическая емкость. Конденсаторы
(плоский, сферический, цилиндрический),
их емкости.

Конденсатор
состоит из двух проводников (обкладок),
которые разделены диэлектриком. На
емкость конденсатора не должны влиять
окружающие тела, поэтому проводникам
придают такую форму, чтобы поле, которое
создавается накапливаемыми зарядами,
было сосредоточено в узком зазоре между
обкладками конденсатора. Этому условию
удовлетворяют: 1) две плоские пластины;
2) две концентрические сферы; 3) два
коаксиальных цилиндра. Поэтому в
зависимости от формы обкладок конденсаторы
делятся на плоские,
сферические и цилиндрические. 

Так
как поле сосредоточено внутри конденсатора,
то линии напряженности начинаются на
одной обкладке и кончаются на другой,
поэтому свободные заряды, которые
возникают на разных обкладках, равны
по модулю и противоположны по знаку.
Под емкостьюконденсатора
понимается физическая величина, равная
отношению заряда Q, накопленного в
конденсаторе, к разности потенциалов
(φ₁ —
φ₂)
между его обкладками: 

(1) 

Найдем
емкость плоского конденсатора, который
состоит из двух параллельных металлических
пластин площадью S каждая, расположенных
на расстоянии d друг от друга и имеющих
заряды +Q и –Q. Если считать, что расстояние
между пластинами мало по сравнению с
их линейными размерами, то краевыми
эффектами на пластинах можно пренебречь
и поле между обкладками считать
однородным. Его можно найти используя
формулу потенциала поля двух бесконечных
параллельных разноименно заряженных
плоскостей φ₁-φ₂=σd/ε₀.
Учитывая наличие диэлектрика между
обкладками: 

(2) 

где
ε — диэлектрическая проницаемость.
Тогда из формулы (1), заменяя Q=σS, с учетом
(2) найдем выражение для емкости плоского
конденсатора: 

 (3) 

Для
определения емкости цилиндрического
конденсатора, который состоит из двух
полых коаксиальных цилиндров с радиусами
r₁ и
r₂(r₂ >
r₁),
один вставлен в другой, опять пренебрегая
краевыми эффектами, считаем поле
радиально-симметричным и действующим
только между цилиндрическими обкладками.
Разность потенциалов между обкладками
считаем по формуле для разности
потенциалов поля равномерно заряженного
бесконечного цилиндра с линейной
плотностью τ =Q/l (l—длина
обкладок). При наличии диэлектрика между
обкладками разность потенциалов 

 (4) 

Подставив
(4) в (1), найдем выражение для емкости
цилиндрического конденсатора: 

 (5) 

Чтобы
найти емкость сферического конденсатора,
который состоит из двух концентрических
обкладок, разделенных сферическим слоем
диэлектрика, используем формулу для
разности потенциалов между двумя
точками, лежащими на расстояниях r₁ и
r₂ (r₂ >
r₁)
от центра заряженной сферической
поверхности. При наличии диэлектрика
между обкладками разность
потенциалов 

 (6) 

Подставив
(6) в (1), получим 

 

Электрическая
ёмкость —
характеристика проводника, мера его
способности накапливать электрический
заряд.
В теории электрических цепей ёмкостью
называют взаимную ёмкость между двумя
проводниками; параметр ёмкостного
элемента электрической схемы,
представленного в виде двухполюсника.
Такая ёмкость определяется как отношение
величины электрического заряда к разности
потенциалов между
этими проводниками.

В
системе СИ ёмкость
измеряется в фарадах.
В системе СГС в сантиметрах.

Для
одиночного проводника ёмкость равна
отношению заряда проводника к его
потенциалу в предположении, что все
другие проводники бесконечно удалены
и что потенциал бесконечно удалённой
точки принят равным нулю. В математической
форме данное определение имеет вид

 где — заряд, —
потенциал проводника.

Ёмкость
определяется геометрическими размерами
и формой проводника и электрическими
свойствами окружающей среды (её
диэлектрической проницаемостью) и не
зависит от материала проводника. К
примеру, ёмкость проводящего шара
радиуса Rравна
(в системе СИ):

где ε₀ — электрическая
постоянная, ε — относительная
диэлектрическая проницаемость.

Понятие
ёмкости также относится к системе
проводников, в частности, к системе двух
проводников, разделённых диэлектриком иливакуумом, —
к конденсатору.
В этом случае взаимная
ёмкость этих
проводников (обкладок конденсатора)
будет равна отношению заряда, накопленного
конденсатором, к разности потенциалов
между обкладками. Для плоского конденсатора
ёмкость равна:

где S —
площадь одной обкладки (подразумевается,
что они равны), d —
расстояние между обкладками, ε — относительная
диэлектрическая проницаемость среды
между обкладками, ε₀ =
8.854·10⁻¹² Ф/м — электрическая
постоянная.

Конденса́тор (от лат. condensare —
«уплотнять», «сгущать») — двухполюсник с
определённым значением ёмкости и
малой омической проводимостью;
устройство для накопления заряда и
энергии электрического поля. Конденсатор
является пассивным электронным
компонентом. Обычно состоит из двух
электродов в форме пластин
(называемых обкладками),
разделённых диэлектриком,
толщина которого мала по сравнению с
размерами обкладок.

15. Соединение конденсаторов (параллельное
и последовательное)

Помимо
показанного на рис. 60 и 61, а также на рис.
62, а параллельного соединения конденсаторов,
при котором соединены между собой все
положительные и все отрицательные
обкладки, иногда соединяют конденсаторы
последовательно, т. е. так,   чтобы
отрицательная обкладка

Рис.
62. Соединение конденсаторов: а)
параллельное; б) последовательное
первого
конденсатора была соединена с положительной
обкладкой второго, отрицательная
обкладка второго — с положительной
обкладкой третьего и т. д. (рис. 62, б). В
случае параллельного соединения все
конденсаторы заряжаются до одной и той
же разности потенциалов U, но заряды на
них могут быть различными. Если емкости
их равны С1, С2,…, Сn, то соответствующие
заряды будут

Общий
заряд на всех конденсаторах

и,
следовательно, емкость всей системы
конденсаторов

(35.1)
Итак,
емкость группы параллельно соединенных
конденсаторов равна сумме емкостей
отдельных конденсаторов.

В
случае последовательно соединенных
конденсаторов (рис. 62, б) одинаковы заряды
на всех конденсаторах. Действительно,
если мы поместим, например, заряд +q на
левую обкладку первого конденсатора,
то вследствие индукции на правой его
обкладке возникнет заряд —q, а на левой
обкладке второго конденсатора — заряд
+q. Наличие этого заряда на левой обкладке
второго конденсатора опять-таки
вследствие индукции создает на правой
его обкладке заряд —q, а на левой обкладке
третьего конденсатора — заряд +q и т. д.
Таким образом, заряд каждого из
последовательно соединенных конденсаторов
равен q. Напряжение же на каждом из этих
конденсаторов определяется емкостью
соответствующего конденсатора:
 
где
Сi — емкость одного конденсатора.
Суммарное напряжение между крайними
(свободными) обкладками всей группы
конденсаторов

Следовательно,
емкость всей системы конденсаторов

определяется
выражением
(35.2)
Из
этой формулы видно, что емкость группы
последовательно соединенных конденсаторов
всегда меньше емкости каждого из этих
конденсаторов в отдельности.

16.
Энергия электрического поля и её объёмная
плотность.

Энергия
электрического поля. Энергию
заряженного конденсатора можно выразить
через величины, характеризующие
электрическое поле в зазоре между
обкладками. Сделаем это на примере
плоского конденсатора. Подстановка
выражения для емкости в формулу для
энергии конденсатора дает

Частное U / d равно
напряженности поля в зазоре;
произведение S·d представляет
собой объем V,
занимаемый полем. Следовательно, 

Если
поле однородно (что имеет место в плоском
конденсаторе при расстоянии dмного
меньшем, чем линейные размеры обкладок),
то заключенная в нем энергия распределяется
в пространстве с постоянной плотностью w.
Тогда объемная
плотность энергии электрического
поля равна 

C
учетом соотношения можно
записать 

В
изотропном диэлектрике направления
векторов D и E совпадают
и 
Подставим
выражение ,
получим 

Первое
слагаемое в этом выражении совпадает
с плотностью энергии поля в вакууме.
Второе слагаемое представляет собой
энергию, затрачиваемую на поляризацию
диэлектрика. Покажем это на примере
неполярного диэлектрика. Поляризация
неполярного диэлектрика заключается
в том, что заряды, входящие в состав
молекул, смещаются из своих положений
под действием электрического поляЕ.
В расчете на единицу объема диэлектрика
работа, затрачиваемая на смещение
зарядов q_i на
величину dr_i,
составляет 

Выражение
в скобках есть дипольный момент единицы
объема или поляризованность диэлектрика Р.
Следовательно, .
Вектор P связан
с вектором E соотношением .
Подставив это выражение в формулу для
работы, получим

Проведя
интегрирование, определим работу,
затрачиваемую на поляризацию единицы
объема диэлектрика

.

Зная
плотность энергии поля в каждой точке,
можно найти энергию поля, заключенного
в любом объеме V.
Для этого нужно вычислить интеграл:

17. Постоянный электрический ток, его
характеристики и условия существования.
Закон Ома для однородного участка цепи
(интегральная и дифференциальная формы)

Для существования
постоянного электрического тока
необходимо наличие свободных заряженных
частиц и наличие источника тока. в
котором осуществляется преобразование
какого-либо вида энергии в энергию
электрического поля.

Источник
тока —
устройство, в котором осуществляется
преобразование какого-либо вида энергии
в энергию электрического поля. В источнике
тока на заряженные частицы в замкнутой
цепи действуют сторонние силы. Причины
возникновения сторонних сил в различных
источниках тока различны. Например в
аккумуляторах и гальванических элементах
сторонние силы возникают благодаря
протеканию химических реакций, в
генераторах электростанций они возникают 
при движении проводника в магнитном
поле, в фотоэлементах — при действия
света на электроны в металлах и
полупроводниках.

Электродвижущей
силой источника тока называют
отношение работы сторонних сил к величине
положительного заряда, переносимого
от отрицательного полюса источника
тока к положительному.

Свойства и форма изображения распределения позволяет судить о течении явления, определять его главные характеристики. То есть анализировать поле, находить его неоднородности и величину напряжённости.

Общие сведения

Неким фундаментальным свойством природы является электрический заряд. Один из разделов физики занимается изучением его свойств и взаимодействия, называется он электродинамикой. Наиболее интересно для учёных изучение влияния друг на друга заряженных тел.

Бум исследования электрических явлений пришёлся на XIX век. В это время появилось две теории, одна из которых оказалась ошибочной и была опровергнута экспериментами. Эта догадка называлась правилом дальнодействия. Согласно ей один заряд непосредственно действует на другой. То есть чем больше расстояние между взаимодействующими телами, тем меньше сила действия.

Но на самом деле электрические заряды влияют друг на друга по-другому. Эта теория получила название «Правило близкодействия». Как оказалось, если взять два заряженных тела, например, положительно, то первый заряд на второй не действует. Он просто изменяет вокруг себя пространство, создавая нечто. Эта материя и получила название «Электрическое поле». Именно оно и воздействует на второе тело. Другими словами, на заряд действует материя, создаваемая первой частицей. При этом распространяется она с довольно большой, но конечной, скоростью.

Опыты, проводимые Фарадеем, показали, что если из системы убрать одно из тел, то сила, действующая на вторую частицу, не изменится мгновенно, хотя это и произойдёт довольно скоро. Именно Фарадей и является открывателем электромагнитного поля. В дальнейшем Максвелл смог описать явление теоретически.

Им было установлено, что заряд испытывает влияние поля, даже если поблизости его нет других частиц. Эта сила представляет собой электромагнитную волну.

Электрическое поле можно обнаружить, поместив в неё другой заряд, и исследовать действие наблюдающийся силы. Электромагнитную материю можно описать количественно, поэтому, зная характеристики поля и заряда, можно определить величину силы.

К основным параметрам электростатического поля, то есть материи, созданной неподвижной частицей в пространстве, относят:

• напряжённость;
• потенциал.

Таким образом, если есть система заряженных тел, то в любой её точке будет существовать силовое электрическое поле. Его можно исследовать через силу, действующую на заряд, находящийся в этой материи.

Так как визуально вектор увидеть нельзя, то используют так называемые силовые линии, указывающие, куда направлено воздействие.

Свойство линий

За величину силы электрополя в пространстве окутывающего тело принимают количество заряда обратного квадрату расстояния до него. Принято, что направление распространения действия направлено от положительного потенциала к отрицательному. Обозначают поле буквой E, а напряжённость H. Причём это векторная величина, представляемая в виде стрелки с определённой длиной и направлением.

Так как заряд — это источник, то его окружает множество векторов напряжённости. Чтобы не изображать их бесчисленное число, используют силовые линии. Другое их название — интегральные кривые. По сути, это объединённые векторы, где они сами являются касательными к точкам.

Распространение силовых кривых подчиняется определённым правилам.

К основным из них относят следующие:

• линии имеют начало и конец;
• если силы выходят из одной точки или сходятся в ней, то такое распределение будет радиальным;
• когда кривые не пересекаются, то материя считается однородной, в ином же случае неоднородной (силовые линии не параллельны);
• силы электрического поля всегда перпендикулярны поверхности тела.

Изображение линий подчиняется различными правилами. Так, для частиц с большим зарядом плотность линий должна быть выше, чем с меньшим. Если заряд недалеко от источника, то плотность силовых линий гуще. Для кривых проходящих перпендикулярно первичным силам используют эквипотенциальное изображение. Такой тип образуют замкнутые контуры. В них каждая точка напряжённости будет иметь одинаковое значение потенциала. При пересечении частицей линий говорят о совершении работы.

С помощью линий наглядно показывают направление вектора напряжённости в разных точках материи. Для этого их рисуют так, что касательная к каждой будет параллельна напряжённости. Но из-за того, что прямая указывает направление вектора с точностью до 180°, задают полярность обхода. Поэтому стрелку чертят так, чтобы она была сонаправлена с напряжённостью.

Силы электрического поля не могут пересекаться, а эквипотенциальные кривые образуют замкнутые контуры. В тех же точках, где линии перекрещиваются друг с другом, взаимодействие происходит в перпендикулярной плоскости.

Иными словами, на рисунке получается изображение, напоминающее собой координатную сетку. Причём по точкам пересечения и описывают характер электрополя.

Напряжённость поля

Взаимодействие между заряженными телами описывается количественной характеристикой, определяющей структуру материи. Эта величина называется напряжённостью и определяется из отношения E = F / q, где F — сила, а q — заряд, помещённый в поле. Для однородной изотропной среды выражение можно получить, используя закон Кулона: E = (1 / 4 pE) * (q * r / er ² r), где r — радиус-вектор.

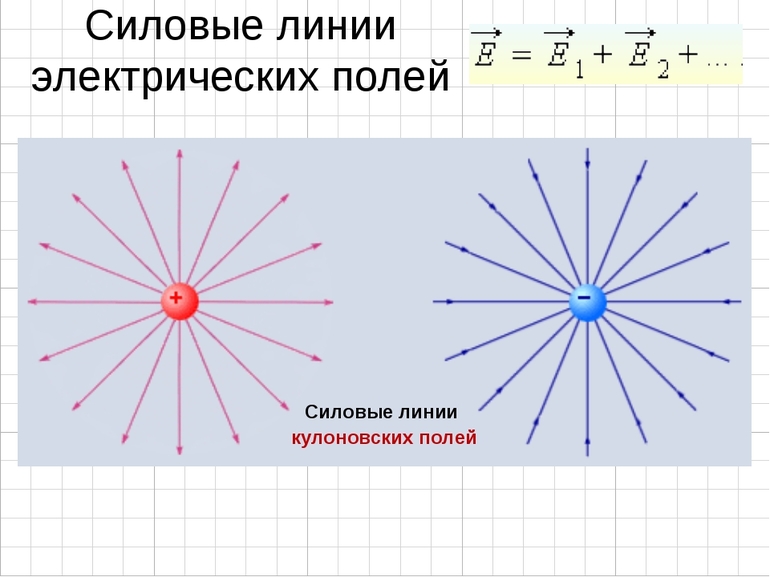
Линии распространения напряжённости поля одинокого заряда во всех точках имеют радиальный вид. Кривые лежат от частицы при q > 0, к телу при q < 0. Для нескольких же носителей вводится понятие — пробный заряд. Он представляет собой результирующую напряжённость, определяемую суммой векторов сил, разделённых на значение введённой характеристики. Такой подход определения называется принципом суперпозиции.

Используя его, можно определить напряжённость как для системы одиночных носителей, так и проводника в целом. В последнем случае происходит непрерывное перераспределение. Именно поэтому заряженное тело можно представить как совокупность элементарных частиц dq.

Изображать непрерывными линиями напряжённости невидимое поле было предложено Майклом Фарадеем. С их помощью стало возможным определить количественное значение действующей силы. Показывают её с помощью изменения плотности, которую выбирают пропорционально векторам напряжённости по модулю. Другими словами, определяют число кривых, пронизывающих единичную площадь перпендикулярно к поверхности.

Поток вектора напряжённости можно вычислить по формуле: F = E * S * cos (a). Для неоднородного поля выражение проекции находят как произведение вектора площади на энергию материи: dF = E * dS. И в первом, и во втором случае поток считается скалярной величиной. Когда же рассматриваемая поверхность криволинейная, то площадь разбивается на простые контуры. В этом случае поток находится как сумма пронизывающих линий через элементарные поверхности. В любом случае поток, являясь алгебраической величиной, зависит от конфигурации поля и направления.

Изображение напряжённости даёт возможность получить полную картину, которая наглядно показывает, чему равна напряжённость в каждой точке поля и как она изменяется. Какой густоты рисовать линии — неважно.

Главное, их нужно изображать в примерном соотношении. Но хоть плотность векторов ничем не ограничивается при изображении, нужно учитывать их направление. Стрелки как раз и указывают, в какую сторону распространяются волны.

Физика распространения

Если рассматривать одинокую частицу, то линии силы будут исходить от неё в радиальном направлении. При взаимодействии же двух и более зарядов на вид распространения влияет напряжённость. Чтобы нарисовать, как будут выглядеть линии, следует сложить векторы напряжённости. Их результирующая и будет характеризовать суммарное поле.

При составлении картинки распространения поля нужно учитывать, что точки соприкосновения на силовой линии определяются вектором напряжённости. Чтобы математически описать силовые кривые, необходимо составить уравнения. Вектора в них будут являться производными первого порядка. По сути, это обыкновенные касательные.

Каждая частица, добавленная в электромагнитное поле, оказывает на него влияние. Соответственно будет изменяться и узор кривых сил. Но в любом случае основой для построения визуализированного рисунка будет вектор напряжённости каждого источника поля. При этом правило, что линии напряжённости начинаются на положительном заряде, а заканчиваются на отрицательном, условное.

Довольно интересным для изучения является процесс возникновения электрического поля между заряженными бесконечными плоскостями. Созданная однородная материя между пластинками будет распространяться в параллельном направлении, то есть линии пересекаться не будут. Если же в зазор между ними внести точечный заряд, то кривые начнут изгибаться по дуге, поле станет неоднородным, а значение напряжённости будет зависеть от плотности.

Распространение поля подчиняется следующим правилам:

• излучается во все направления;
• изменяет свой рисунок при оказании внешнего воздействия;
• уменьшается при удалении от источника;
• может быть как однородным, так и неоднородным.

Электрические силы при внесении заряженной частицы в поле совершают работу. При незначительном воздействии её можно описать так: A = F * l * cos (a) = E * q * L. Таким образом, структура распространения зависит от расстояния между частицами.

Если же изменить направление перемещения заряженного тела на противоположное, то знак поменяет и работа. А это значит, что замкнутая траектория кулоновских сил будет равна нулю.