Как найти силу давления перегрузка на груз

Условие задачи:

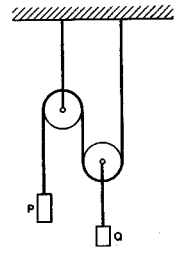
Два одинаковых груза массами 0,1 кг связаны между собой нитью, перекинутой через блок. На один из грузов кладут перегрузок массой 0,05 кг. Определить, с какой силой будет давить перегрузок на груз.

Задача №2.2.5 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

(M=0,1) кг, (m=0,05) кг, (N-?)

Решение задачи:

Сила, с которой давит перегрузок на груз, равна сила реакции (N) по третьему закону Ньютона.

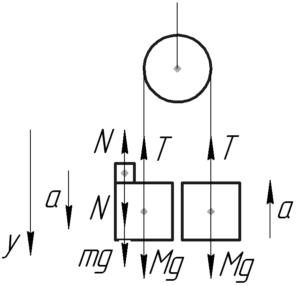
Очевидно, что после установки перегрузка система придет в движение, и один из грузов, на который поставили перегрузок, начнет движение вниз, а второй груз – вверх.

Изобразив на схеме два груза и на одним из них перегрузок, покажем все силы, действующие на тела и запишем для каждого из них второй закон Ньютона в проекции на вертикальную ось.

[left{ begin{gathered}
Mg + N – T = Ma ;;;;(1)hfill \
mg – N = ma ;;;;(2)hfill \
Mg – T = – Ma ;;;;(3)hfill \
end{gathered} right.]

К равенству (1) прибавим равенство (2) и отнимем (3), тогда:

[Mg + N – T + mg – N – Mg + T = 2Ma + ma]

[mg = aleft( {2M + m} right)]

[a = frac{{mg}}{{2M + m}}]

Отлично, теперь из равенства (2) выразим искомое (N).

[N = mg – ma]

Подставим в эту формулу полученное ранее выражение для ускорения:

[N = mg – frac{{{m^2}g}}{{2M + m}}]

Приведем под общий знаменатель:

[N = frac{{mgleft( {2M + m} right) – {m^2}g}}{{2M + m}} = frac{{2Mmg + {m^2}g – {m^2}g}}{{2M + m}}]

[N = frac{{2Mmg}}{{2M + m}}]

Теперь можно считать ответ:

[N = frac{{2 cdot 0,1 cdot 0,05 cdot 10}}{{2 cdot 0,1 + 0,05}} = 0,4; Н = 400; мН]

Ответ: 400 мН.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.2.4 Два грузика массами m1=0,3 кг и m2=0,2 кг соединены нитью, перекинутой через блок
2.2.6 Две гири неравной массы висят на концах нити, перекинутой через невесомый блок
2.2.7 Через невесомый блок перекинута нерастяжимая нить, к одному из концов которой

2020-12-12   

Грузы Р и Q находятся в равновесии с системой блоков (рис.). На груз Q кладут перегрузок массой $m = 0,2 кг$, и система приходит в движение. Определите силу давления перегрузка на груз Q. Масса груза Р $M = 0,3 кг$.

Решение:

Определим силы, действующие на грузы при равновесии: $M vec{g}, M_{1} vec{g}$ — силы тяжести, $vec{T}, vec{T}_{1}$ — силы реакции нитей. Силы показаны на рисунке. Сила $vec{T}_{1}$ и сила $vec{T}_{1}^{ prime }$ равны и противоположно направлены по третьему закону Ньютона: $vec{T}_{1} = — vec{T}_{1}^{ prime }$. При равновесии сумма сил, действующих на каждое тело, равна нулю.

$begin{cases} Mg — T = 0, \ 2T — T_{1} = 0, \ M_{1}g — T_{1} = 0. end{cases}$ (1)

Из системы (1) видно, что масса груза Q $M_{1} = 2M$. Рассмотрим движение грузов после того, как положили перегрузок. Силы в этом случае показаны на рисунке. Уравнения второго закона Ньютона для каждого груза запишем в проекции на направление движения:

$begin{cases} T — Mg = Ma, \ 2MG + f_{д} — 2T = 2M frac{a}{2}, \ mg — N = m frac{a}{2}. end{cases}$ (2)

$vec{f}_{д} = — vec{N}$ по третьему закону Ньютона. Определяем давление перегрузка на груз:

$f_{д} = frac{6Mgm}{6M + m}$.

При составлении уравнений системы (2) учитывается, что реакция нити $T_{1} = 2T$; это было показано при рассмотрении равновесия системы. Второе уравнение системы (1) остается таким же, так как мы пренебрегаем массой блоков. Ускорение груза Q и перегрузка в 2 раза меньше ускорения груза Р, так как при перемещении груза Р на высоту $h$ груз с перегрузкой опустится только на высоту $h/2$ за это же время — этот груз висит на двух «отрезках» нити.

Ответ: $f_{д} = frac{6Mgm}{6M + m}, f_{д} approx 1,8 Н$.

Блоки, нити, грузы и перегрузки

Задача 1.  К телу массой кг подвешено на веревке тело массой кг. Масса веревки кг. Вся система движется ускоренно вверх под действием силы Н, приложенной к верхнему телу (рис.1). Найти натяжение веревки в ее центре и в точках крепления тел и .

Представим всю систему единым телом массой . Будем действовать на эту систему с силой . Тогда по второму закону Ньютона

Откуда найдем ускорение системы:

Теперь вернемся к первому рисунку и запишем уравнения по второму закону Ньютона для верхнего  и нижнего грузов:

Откуда

Очевидно, что посередине веревки сила ее натяжения будет средним арифметическим найденных двух сил:

Ответ: Н, Н, Н.

Задача 2. Маляр массой кг работает в подвесном кресле. Ему понадобилось срочно подняться вверх. Он начинает тянуть веревку с такой силой, что сила давления на кресло уменьшается до Н. Масса кресла кг. Чему равно ускорение маляра? Чему равна нагрузка на блок?

Расставим силы. Отметим все силы, действующие не маляра, и силы, действующие на люльку:

Теперь можно написать уравнения:

Вычитаем уравнения:

Ответ: м/с.

Задача 3.

Через легкий неподвижный блок перекинута невесомая нерастяжимая нить с двумя грузами на концах, массы которых и , . Система приходит в движение, причем нить не проскальзывает относительно блока. Определить ускорение грузов, силу натяжения нити и силу давления на ось блока.

Понятно, что больший груз перетянет и начнет двигаться вниз, а меньший – подниматься. Запишем для них уравнение по второму закону:

Сложим уравнения:

Откуда

Теперь можно найти и силу натяжения нити:

Сила давления на блок равна :

Ответ: , ,
.

Задача 4.

Через блок перекинута нить, на концах которой висят два груза с одинаковыми массами . Одновременно на каждый из грузов кладут по перегрузку: справа  массой , слева (рис. 2). Определить ускорение системы, силу натяжения нити и силу давления перегрузков на основные грузы.

Запишем уравнение по второму закону Ньютона для обоих грузов с учетом массы перегрузков:

Сложение уравнений даст нам

Сила натяжения нити найдется подстановкой найденного ускорения в любое уравнение системы:

Определим силу давления меньшего перегрузка массой на груз :

Для большего перегрузка

Ответ: , , , .

Задача 5.

Через неподвижный блок перекинута нить, к которой подвешены три одинаковых груза массой кг каждый (рис. 3). Найти ускорение системы и силу натяжения нити между грузами 1 и 2. Какой путь пройдут грузы за первые с движения? Трением пренебречь.

Сначала мысленно объединим два груза слева в один и запишем уравнение по второму закону:

Для правого грузика

Складываем уравнения:

Определим силу натяжения нити между грузиками. Обозначим ее . Тогда для самого нижнего грузика слева:

Определяем путь грузиков за 4 с:

Ответ: м/с, Н, м.

Задача 6.

Определить ускорение грузов и силы натяжения всех нитей в системе, изображенной на рисунке. Масса каждого груза , массой блока пренебречь.

Сначала определяем ускорение. Для этого записываем уравнение по второму закону для грузиков справа и слева, пока не вспоминая о том, что их там несколько. Для нас сейчас это  груз массой  справа и слева. Силу натяжения основной нити обозначим :

Складываем уравнения:

Тогда

Рассмотрим теперь грузы, висящие справа. Обозначим натяжение нити между ними . Для нижнего груза справа

Осталось определить и . Для верхнего грузика слева

Откуда

А для нижнего грузика слева

Ответ: , , , , .

Задача 7.

Два груза массами г и г соединены нерастяжимой нитью, перекинутой через невесомый блок (рис.). Грузы прижимаются друг к другу с постоянными силами Н. Коэффициент трения между ними . Найти ускорение, с которым движутся грузы.

Записываем уравнение по второму закону:

Тогда

Ответ: .

Задача 8.

Невесомая нить, перекинутая через неподвижный блок, пропущена через щель (рис.). При движении нити на нее действует постоянная сила трения . На концах нити подвешены грузы, массы которых и . Определить ускорение грузов.

Давайте предположим, что . Тогда левый груз начинает движение вверх, правый – вниз. Записываем для них уравнение  по второму закону с учетом наличия силы трения:

Складывая уравнения, имеем:

Откуда

Но, если бы , тогда

Тогда, чтобы учесть обе возможности, запишем ответ так:

Ответ: .

Задача 9.

Через невесомый блок перекинута легкая нерастяжимая нить, к одному концу которой привязан груз массой г, а по другому
скользит кольцо массой г (рис.). С каким ускорением движется кольцо, если груз  неподвижен?

Сила трения кольца в данном случае и порождает силу натяжения нити, то есть это одна и та же сила. Поэтому для неподвижного груза

А для кольца

Ответ: 6 м/с.

4 комментария

Если я правильно понял, то такой рисунок:

Обозначим груз, который находится на правом конце, как (1), на левом — (2), перегрузок — (3).

По 2 закону Ньютона для (1): T + Mg = Ma.

y| Mg − T = −Ma,

T − Mg = Ma.

По 2 закону Ньютона для (2): T + Mg + F_д = Ma.

y| Mg + F_д − T = Ma.

По 2 закону Ньютона для (3): N + mg = ma.

y| mg − N = ma.

Имеем систему из (1), (2) и (3). Теперь:

По 3 закону Ньютона для (3): F_д = N.

Из (1) выразим натяжение нити: T = Mg + Ma.

Из (3) выразим ускорение: a = mg − F_д/m.

Натяжение нити и ускорение подставим в (2) и в итоге получим: F_д = 2Mmg / (m + 2M).