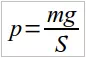{p = dfrac{F}{S}}
Давление — физическая величина, равная отношении силы, приложенной перпендикулярно поверхности на площадь этой поверхности. Единица измерения давления — Паскаль (обозначается Па).
На странице приведены два варианта нахождения давления:
- если известно давление и площадь опоры
- если известна масса тела и площадь опоры
Содержание:
- калькулятор давления твердых тел
- формула давления твердых тел через силу и площадь опоры
- формула давления твердых тел через массу и площадь опоры
- примеры задач
Очевидно, что давление будет тем больше, чем больше сила и чем меньше площадь, на которую эта сила действует. Другими словами, человек, стоящий на одной ноге будет оказывать на землю бОльшее давление, чем когда он стоит на двух ногах (так как сила одна и та же, а площадь в первом случае меньше). Человек на лыжах будет оказывать на землю меньшее давление, чем человек без лыж.
Формула давления твердых тел через силу и площадь опоры
{p = dfrac{F}{S}}
p — давление
F — сила
S — площадь опоры
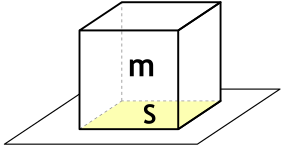
Если учесть, что на тело действует только сила тяжести, то формулу {p=dfrac{F}{S}} можно преобразовать, заменив силу на вес тела ({F=mcdot g}. Тогда мы получим зависимость давления от массы: {p=dfrac{m cdot g}{S}}.
Формула давления твердых тел через массу и площадь опоры
{p = dfrac{m cdot g}{S}}
p — давление
m — масса тела
g — ускорение свободного падения (9,80665 м/с²)
S — площадь опоры
Примеры задач на нахождение давления твердых тел
Задача 1
Гусеничный трактор ДТ-75М массой 6610 кг имеет опорную площадь обеих гусениц 1,4 м². Определите давление этого трактора на почву.
Решение
Так как в условии указана масса трактора, воспользуемся формулой давления через массу и площадь опоры. Подставим в нее значения массы и площади и произведем вычисления. Значение ускорения свободного падения примем равным 9.8 м/с².
p = dfrac{m cdot g}{S} = dfrac{6610 cdot 9.8}{1.4} = dfrac{6610 cdot 9.8}{1.4} = dfrac{64778}{1.4} = dfrac{64778}{1.4} = 46270 Па = 46.27 кПа
Ответ: 46.27 кПа
Получившийся результат просто проверить с помощью калькулятора .
Задача 2
Найдите давление которое оказывает тело массой 20 кг на пол, если площадь опоры 200 см².
Решение
Задача похожа на ту, которую мы решили выше. И процесс ее решения будет аналогичный. Значение g также будем считать равным 9.8 м/с². Площадь опоры дана в квадратных сантиметрах, ее необходимо преобразовать в квадратные метры: 200 см² = 0.02 м².
p = dfrac{m cdot g}{S} = dfrac{20 cdot 9.8}{0.02} = 1000 cdot 9.8 = 9800 Па = 9.8 кПа
Ответ: 9.8 кПа
Проверим ответ на калькуляторе .
Задача 3
Найдите давление которое оказывает тело массой 350 кг, если его длина 15 см а ширина 25 см.
Решение
Еще одна похожая задача, для решения которой мы будем использовать вторую формулу. Как видим, нам прямо не указана площадь опоры, но даны ее размеры. Из них понятно, что точка опоры имеет прямоугольную форму, а найти площадь прямоугольника не составит труда — достаточно умножить длину на ширину:
S = a cdot b = 15 cdot 25 = 375 см^2
Теперь необходимо перевести квадратные сантиметры в квадратные метры, разделив 375 см² на 10000:
375 см^2 = dfrac{375 см^2}{10000} = 0.0375 м^2
Осталось произвести расчет по формуле:
p = dfrac{m cdot g}{S} = dfrac{350 cdot 9.8}{0.0375} = 91 560 Па = 91.56 кПа
Ответ: 91.56 кПа
Проверка .
Давление твердых тел
- Опора
- Сила давления и давление
- Единицы измерения давления
- Задачи
п.1. Опора
По определению, вес тела – это сила, с которой тело действует на подвес или опору (см. §22 данного справочника). В свою очередь, в подвесе или опоре возникают силы реакции, которые по своей природе являются силами упругости и уравновешивают нагрузку.
Практически все тела вокруг нас на что-то «опираются»: опорой для фундамента дома служит грунт, опорой для стен – фундамент, опорой для плит перекрытий – стены, опорой для настила пола – плита перекрытия, опорой для стола – пол, опорой для компьютера – стол, ну, и опорой для пыли – компьютер.
Не обязательно сила, действующая на опору, будет силой тяжести, направленной вертикально вниз. Ветер оказывает на здания и сооружения в основном горизонтальное воздействие. А используемые в различных механизмах распорки могут действовать на опоры за счет сил упругости не только горизонтально, но и под любыми другими углами, если необходимо.
п.2. Сила давления и давление
Силу, действующую перпендикулярно опоре, называют силой давления.
 |
На рисунке девушка опирается на пол и стену в трёх различных точках; поэтому моделируем её действие на опоры с помощью трёх сил давления, каждая из которых направлена перпендикулярно опоре.
Если девушка снимет обувь на каблуках и примет ту же позу, силы давления останутся такими же. Однако, опыт подсказывает, что от каблуков на стенах и на полу могут остаться вмятины и трещины, а от босых ног – вряд ли. |
Давление – физическая величина, равная отношению силы давления к площади опоры, на которую она действует: $$ p=frac FS $$
Давление – скалярная величина, имеющая только числовое значение.
А сила давления – векторная величина, имеющая не только числовое значение, но и направление – перпендикулярно поверхности, на которую она действует.
п.3. Единицы измерения давления
В системе СИ (см. §2 данного справочника) сила измеряется в ньютонах, площадь – в квадратных метрах. А для измерения давления используется «паскаль».
Единицей давления в системе СИ является паскаль ((1 text{Па})) – действие силы давления величиной (1 text{Н}) на поверхность площадью (1 text{м}^2): $$ 1 text{Па}=1 text{Н/м}^2 $$
На практике могут использоваться и другие внесистемные единицы, например:
1 атм – атмосфера;
1 мм рт.ст. – миллиметр ртутного столба;
1 кгс – килограмм-сила и т.д.
п.4. Задачи
Задача 1. Площадь ступни человека 180 см2. Какое давление создает человек массой 70 кг, если он стоит на обеих ногах?
Дано:
(S=180 text{см}^2=0,018 text{м}^2)
(m=70 text{кг})
(gapprox 10 text{м/с}^2)
__________________
(p-?)
Сила давления, с которой человек давит на опору, равна силе тяжести: (F=mg)
Давление равно отношению силы тяжести к удвоенной площади стопы (человек стоит на двух ногах): $$ p=frac{P}{2S}=frac{mg}{2S} $$ Получаем: $$ p=frac{70cdot 10}{2cdot 0,018}approx 19444 (text{Па})approx 19,4 (text{кПа}) $$ Ответ: ≈19,4 кПа
Задача 2. Площадь стопы слона 700 см2. Стоя на четырех ногах, он создает давление 107 кПа. Какова масса слона (в тоннах)?
Дано:
(S=700 text{см}^2=0,07 text{м}^2)
(p=107 text{кПа}=1,07cdot 10^5 text{Па})
(gapprox 10 text{м/с}^2)
__________________
(m-?)
Сила давления, с которой слон давит на опору, равна силе тяжести: (F=mg)
Давление, если слон стоит на четырех ногах: $$ p=frac{F}{4S}=frac{mg}{4S} $$ Откуда масса слона: $$ m=frac{4pS}{g} $$ Получаем: $$ m=frac{4cdot 10,7cdot 10^5cdot 0,07}{10}=2996 (text{кг})approx 3 (text{т}) $$ Ответ: ≈3 т
Задача 3. Масса охотника со снаряжением 120 кг. Рассчитайте для него ширину лыж длиной 1,6 м, если снег не проваливается при давлении до 5 кПа. Учтите, что опора может быть на одну лыжу. Ответ запишите в сантиметрах.
Дано:
(m=120 text{кг})
(gapprox 10 text{м/с}^2)
(a=1,6 text{м})
(p=5 text{кПа}=5cdot 10^3 text{Па})
__________________
(b-?)
Считаем поверхность лыжи прямоугольной. Площадь поверхности одной лыжи (S=ab)
Сила давления равна силе тяжести: (F=mg)
Давление охотника на снег на одной лыже $$ p=frac{F}{S}=frac{mg}{ab} $$ Откуда ширина лыжи $$ b=frac{mg}{ap} $$ Получаем: $$ b=frac{120cdot 10}{1,6cdot 5cdot 10^3}=0,15 (text{м})=15 (text{см}) $$ Ответ: 15 см
Задача 4. Лист стекла, лежащий на полу, оказывает на него давление 200 Па. Какова толщина листа, если плотность стекла 2500 кг/м3? Ответ укажите в миллиметрах.
Дано:
(p=200 text{Па})
(rho=2500 text{кг/м}^3)
(gapprox 10 text{м/с}^2)
__________________
(h-?)
Пусть лист имеет длину (a) и ширину (b). Тогда его площадь (S=ab), объем (V=abh).
Масса листа (m=rho V=rhocdot abh)
Давление листа на пол $$ rho=frac{mg}{S}=frac{rhocdot abhcdot g}{ab}=rho hg $$ Откуда толщина листа $$ h=frac{p}{rho g} $$ Получаем: $$ h=frac{200}{250cdot 10}=8cdot 10^{-3} (text{м})=8 (text{мм}) $$ Ответ: 8 мм
Задача 5*. На столе стоят два куба из одного и того же материала. Длина ребра одного куба в 2 раза больше, чем длина ребра другого. Какой куб оказывает большее давление на стол и во сколько раз?
Пусть ребро меньшего куба равно (a). Тогда у большего куба оно равно (2a).
Площадь грани меньшего куба (S_1=a^2), объем (V_1=a^3).
Масса меньшего куба (m_1=rho V_1=rho a^3).
Давление меньшего куба на опору $$ p_1=frac{m_1g}{S_1}=frac{rho a^3g}{a^2}=rho ag $$ Аналогично, для большего куба begin{gather*} S_2=(2a)^2=4a^2, V_2=(2a)^3=8a^3, m_2=rho V_2=8rho a^3\[7px] p_2=frac{m_2g}{S_2}=frac{8rho a^3g}{4a^2}=2rho ag end{gather*} Получаем: $$ frac{p_2}{p_1}=2 $$ Давление большего куба больше в 2 раза.
Ответ: больший куб; в 2 раза
Задача 6*. Полый медный куб с длиной ребра 10 см оказывает на стол давление 5 кПа. Найдите объем полости, если плотность меди равна 8900 кг/м3. Ответ запишите в кубических сантиметрах.
Дано:
(a=10 text{см}=0,1 text{м})
(gapprox 10 text{м/с}^2)
(p=5 text{кПа}=5cdot 10^3 text{Па})
(rho=8900 text{кг/м}^3)
__________________
(V_0-?)
Объем куба (V=a^3). Этот объем является суммой объема полости и объема вещества: $$ V=V_0+V_m $$ Объем вещества: $$ V_m=frac{m}{rho} $$ Давление куба на опору: $$ p=frac{mg}{S}=frac{mg}{a^2}Rightarrow m=frac{pa^2}{g} $$ Получаем: begin{gather*} V_0=V-V_m=a^3-frac{m}{rho}=a^3-frac{pa^2}{rho g}\[7pt] V_0=a^2left(a-frac{p}{rho g}right) end{gather*} Подставляем: $$ V_0=0,1^2left(0,1-frac{5cdot 10^3}{8900cdot 10}right)approx 4,38cdot 10^{-4} (text{м}^3)=438 (text{см}^3) $$ Ответ: 438 см3
Задача 7*. Говорят, что йоги практикуют своеобразный «отдых» на доске, утыканной гвоздями. Рассчитайте, сколько гвоздей понадобится йогу, чтобы безопасно лечь на доску, если острие каждого гвоздя имеет площадь 0,1 мм2, масса йога 70 кг, а кожа человека способна выдерживать давление до 3 МПа. Ответ округлите с избытком до целых.
Дано:
(s_0=1 text{мм}^2=10^{-6} text{м}^2)
(m=70 text{кг})
(p=3cdot 10^6 text{Па})
(gapprox 10 text{м/с}^2)
__________________
(N-?)
Общая площадь (N) гвоздей (S=N_{S0})
Давление гвоздей на кожу $$ pfrac FS=frac{mg}{N_{S0}} $$ Откуда необходимое количество гвоздей $$ N=frac{mg}{p_{S0}} $$ Получаем: begin{gather*} N=frac{70cdot 10}{3cdot 10^6cdot 10^{-6}}approx 233,3approx 234 end{gather*} Ответ: 234 гвоздя
Давление
Известно, что человеку удобнее ходить по глубокому снегу на лыжах, так как при этом он меньше проваливается под снег. А разрезать предметы удобнее остро отточенным ножом. Причина этого – давление. В первом случае мы стремимся уменьшить давление на снег, а во втором случае, мы стараемся максимально увеличить давление.
Формула давления твердого тела
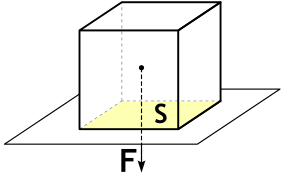
Рассмотрим твердое тело, например, кирпич. Пусть он лежит на горизонтальной поверхности и давит на нее своим весом (рис. 1).
Рис. 1. Твердое тело опирается на поверхность площадью S и давит на нее своим весом mg
На рисунке символом S обозначена нижнее основание тела – это площадь, на которую тело опирается (давит). Сила, с которой тело давит на поверхность – это сила тяжести mg.
Давление, которое твердое тело оказывает на поверхность, можно рассчитать так:
[ large boxed{ P = frac{F_{perp}}{S} }]
Примечание: Эта формула подходит для расчета давления твердых тел. Существует еще одна формула, с помощью которой рассчитывают давление жидкостей.
( P left( text{Па}right) ) – давление;
( F_{perp} left(H right) ) – сила, которая давит (сила давления). Эта сила располагается под прямым углом к поверхности;
( S left( text{м}^{2}right) ) – площадь, на которую давит сила.
Иногда в условии задачи указывают площадь в квадратных сантиметрах, или других единицах, отличающихся от основных единиц, принятых в СИ. Чтобы правильно рассчитать давление, нужно уметь переводить площадь в квадратные метры.
В системе СИ давление измеряется в Паскалях.
[ large 1 text{Па} = frac{1 H}{1 text{м}^{2}} ]
Поэтому, перед решением задач, нужно давление переводить в Паскали, если в условии встретятся другие единицы измерения давления.
В некоторых школьных задачах просят найти не давление, а силу давления. Нужно уметь их различать.
Сила давления, как и любая сила, измеряется в Ньютонах. Именно она давит на поверхность.
А давление — это дробь, в числителе расположена сила, которая давит, а в знаменателе — площадь поверхности, на которую давят. Давление измеряют в Паскалях.
Примечание: Давление – это сила, деленная на площадь. Сила должна располагаться перпендикулярно поверхности (рис. 2а).
Когда сила не перпендикулярна поверхности
Силу раскладываем на проекции, если она направлена к поверхности не под прямым углом (рис. 2б). Выберем часть силы, расположенную перпендикулярно поверхности. Именно эту часть силы и нужно подставлять в формулу для расчета давления.
Рис. 2. Если сила, которая давит на поверхность, направлена не под прямым углом к поверхности, раскладываем силу на проекции и выбираем часть, которая располагается к поверхности перпендикулярно
Оценка статьи:
Загрузка…
Краткое описание документа:
7. Задача на расчет давления твердых тел
Задача: Станок весом 12000 Н имеет площаль опоры 2,5 м2. Определите давление станка на фундамент.
Дано:
P=12000 Н
S=2,5 м2
p — ?
Решение:
p=P/S
F=P
=> p=P/S
p=12000 Н/2,5 м2=4,8 кПа
Ответ. p=4,8 кПа
Задача: Ящик весом 960 Н оказывает на опору давление 5 кПа. Какую площадь опоры имеет ящик?
Дано:
P=960 Н
p=5 кПа
S — ?
СИ
=5*103 Па
Решение:
p=F/S
P=F
=> p=P/S
=> S=P/p
S=960 Н/5*103 Па=0,192 м2
Ответ. S=0,192 м2
Задача: Двухосный прицеп с грузом имеет массу 2,5 т. рассчитайте давление, производимое прицепом на дорогу, если площадь соприкосновения каждого колеса с дорогой равна 125 см2.
Дано:
m=2,5 т
S=125 см2
2 оси;
4 колеса
g=10 Н/кг
p — ?
СИ
=2,5*103кг
=125*10-4м2
Решение:
p=F/S
F=m*g
S=4Sк
=> p=m*g/4Sк
p=2,5*103кг*10Н/кг/4*125*10-4м2=5*105Па
Ответ. p=5*105Па
Мальчик массой 48 кг оказывает давление на опору. Рассчитайте, какое давление он оказывает, если общая площадь его подошв составляет 320 см2.
Проанализировав условие, запишем его в краткой форме, указав массу мальчика и площадь его подошв (Рис. 1). Затем в отдельной колонке запишем в системе СИ те величины, которые в условии приведены во внесистемных единицах. Масса мальчика приведена в системе СИ, а вот площадь, выраженную в квадратных сантиметрах, следует выразить в квадратных метрах:
320 см2 = 320∙(0,01 м)2 = 320∙0,0001 м2 = 0,032 м2.
Рис. 1. Краткое условие задачи №1
Для нахождения давления нам необходимо силу, с которой мальчик действует на опору, разделить на площадь опоры:
Значение силы нам неизвестно, однако в условие задачи входит масса мальчика. Сила, с которой он действует на опору, – это его вес. Предполагая, что мальчик неподвижен, можно считать, что его вес равен силе тяжести, которая равна произведению массы мальчика на ускорение свободного падения
Теперь мы можем объединить обе формулы в одну конечную. Для этого вместо силы F мы подставим в первую формулу произведение mg из второй формулы. Тогда расчетная формула будет иметь вид:
Следующий этап – проверка размерности полученного результата. Размерность массы [m] = кг, размерность ускорения свободного падения [g] = Н/кг, размерность площади [S] = м2. Тогда
Наконец, подставим числовые данные из условия задачи в конечную формулу:
Не забываем записать ответ. В ответе мы можем использовать кратные величины
Ответ: p = 15 кПа.
(Если в ответе вы запишете = 15 000 Па, то тоже будет правильно.)
Полное решение в окончательном виде будет выглядеть так (Рис. 2):
Рис. 2. Полное решение задачи №1
2. Задача №2
Брусок действует на опору с силой 200 Н, при этом он оказывает давление 4 кПа. Какова площадь опоры бруска?
Запишем краткое условие и выразим давление в системе СИ (4 кПа = 4000 Па) (Рис. 3).
Рис. 3. Краткое условие задачи №2
Величина площади поверхности входит в известную нам формулу для расчета давления.
Из этой формулы нам необходимо выразить площадь опоры. Вспомним математические правила. Сила F – делимое, площадь опоры S – делитель, давление p – частное. Чтобы найти неизвестный делитель, необходимо делимое разделить на частное. Мы получим:
Проверим размерность полученного результата. Площадь должна выражаться в квадратных метрах.
Выполняя проверку, мы паскали заменили ньютонами на квадратный метр, а дробную черту – знаком деления. Вспомним, что деление дробей заменяется умножением. При этом дробь, которая является делителем, переворачивается, то есть ее числитель и знаменатель меняются местами. После этого ньютон в числителе (перед дробью) и ньютон в знаменателе дроби сокращаются, и остаются квадратные метры.
Отметим, что проверка размерности является очень важным этапом решения задачи, так как позволяет обнаружить ошибки, случайно допущенные при выполнении математических преобразований.
После проверки размерности результата проведем расчет числового значения площади, подставляя данные из краткого условия:
Не забудем зафиксировать ответ.
Ответ: S = 0,05 м2.
Полностью оформленное решение задачи будет выглядеть так (Рис. 4):
Рис 4. Полное решение задачи №2
Давление твёрдых тел
/Статья для учеников 7 класса/
§ Содержание:
1. Что такое давление?
2. Способы увеличения и уменьшения давления.
3. Давление в живой природе.
4. Давление в технике.
5. Решение задач на расчёт давления.
6. Экспериментальные задания.
7. Просто интересные задачи.
1.Что такое давление?
Представьте, что вы отправились на лыжную прогулку. Лыжи скользят по снегу, оставляя совсем неглубокий след. Что произойдёт, если снять лыжи? Конечно, вы сразу провалитесь в снег. Давайте разберёмся, почему это происходит. Вес, т.е сила, с которой человек давит на снег, осталась такой же. А что изменилось? Только площадь опоры (сравните подошвы ботинок и лыжи). Значит, можно предположить, что результат действия силы зависит не только от самой силы — точки приложения, направления, модуля — но и от площади соприкосновения.
Чтобы проверить это, проведём эксперимент. Возьмите поролоновую губку и кусок мыла. Поставим мыло на губку самой большой стороной. Обратите внимание на деформацию губки. А теперь переверните мыло на ребро. Что изменилось? Теперь мы можем сделать вывод:результат действия силы зависит и от самой силы, и от площади её воздействия. Следовательно, нужна физическая величина, учитывающая оба фактора. Эта величина называется давлением. Отношение силы F к площади поверхности S при условии, что сила действует перпендикулярно поверхности, называется давлением.
p = F/S
Единицы измерения давления вычисляем по формуле: 1 Н/кв.м = 1 Па (паскаль).Единица измерения названа в честь известного учёного Блеза Паскаля. Кроме основных единиц, используют также и приставки:
1 кПа = 1000 Па, 1 МПа = 1 000 000 Па
Подумайте, используют ли приставки «милли», «микро»? Почему?
2. Способы увеличения и уменьшения давления.
Сначала ответим на вопрос: а для чего это нужно? Вы видели, какие следы оставляют тяжёлые машины, трактора на земле? Такие глубокие колеи возникают как раз из- за высокого давления. Значит, в таких случаях его нужно снижать. Так как давление зависит от силы и площади, изменять его можно, меняя эти величины.
Зачем увеличивать давление? Попробуйте тупым ножом порезать хлеб. Чем тупой нож отличается от острого?Конечно,площадью лезвия и создаваемым давлением. Поэтому все режущие и колющие инструменты должны быть очень острыми.
3. Давление в живой природе.
Об этом можно прочитать здесь: [1]
4. Давление в технике
Давление необходимо учитывать и в машиностроении, и в архитектуре, и на транспорте.Выше уже говорилось о машинах,деформирующих почву. Они наносят непоправимый вред экологии. Например, при освоении Крайнего Севера гусеничными тракторами были уничтожены огромные площади ягеля — основного корма оленей, что отрицательно сказалось на их популяции. Чтобы избежать этого, необходимо уменьшить давление, т.е.либо уменьшить силу давления, либо увеличить площадь. Уменьшить силу сложно:для этого нужно уменьшать массу, применяя более лёгкие материалы. Но эти вещества либо непрочные, либо очень дорогие. Поэтому чаще всего используют именно увеличение площади.Сделать это можно разными способами: применение гусениц на тракторах, увеличение диаметра шин, использование парных колёс.Большое значение имеет и то, как накачены шины, ведь от этого тоже зависит площадь соприкосновения.Гусеницы значительно снижают давление (см.таблицу),повышая проходимость механизма, но при этом сильно повреждают верхние слои почвы.Очень важен учёт давления и в архитектуре, строительстве. Фундамент здания используется для снижения давления.С древних времён при строительстве использовали полые колонны. Имея достаточную прочность, они гораздо легче сплошных, а следовательно и создаваемое давление тоже меньше.
Механизм
Давление, в кПа
Гусеничные тракторы(болотные) с уширенными гусеницами
20 -30
Гусеничные тракторы
40 -50
Колёса легкового автомобиля
230 -300
Колёса железнодорожного вагона на рельсы
300 000
5. Решение задач на расчёт давления.
§ 1) На полу находится кирпич размерами: высота -5 см,ширина — 10 см,длина — 20 см. Его масса 2 кг.Какое давление оказывает кирпич на пол, находясь в трёх различных положениях?
§ 2) Какова длина лыж, если стоящий на них человек массой 80 кг оказывает на снег давление 2,5 кПа? Ширина лыжи 8 см.
§ 3) Какое давление на почву оказывает гусеничный трактор , если масса трактора 3,2 т, а площадь одной гусеницы 0,8 кв.м?
6. Экспериментальные задания.
§ 1) Определите давление стакана с чаем на стол. Изменится ли давление, если чай выпить? Во сколько раз?
§ 2) Во сколько раз изменится давление учебника физики на стол, если его поставить на ребро? а если учебник по физике заменить на историю?
7.Просто интересные задачи.
§ 1)Разведчик должен пересечь реку по тонкому льду. Придумайте устройство, уменьшающее риск переправы.
§ 2)Почему рельсы не кладут прямо на землю?
§ 3) Почему острой бритвой нечаянно порезаться легче, чем ножом?
§ 4)На деревянную стенку надавили с силой в 200 Н сначала ладонью, потом с такой же силой шилом. Силы равны по величине, почему же результат различный?
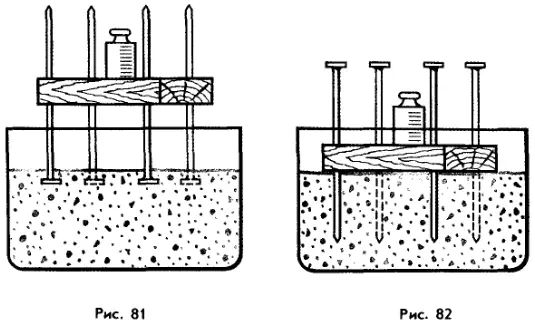
Проделаем опыт. Возьмем небольшую доску, в углы которой вбиты четыре гвоздя, и поместим ее остриями вверх на песок. Сверху на нее положим гирю (рис. 81). Мы увидим, что шляпки гвоздей лишь незначительно вдавятся в песок. Если же мы перевернем доску и снова поставим ее (вместе с гирей) на песок, то теперь гвозди войдут в него значительно глубже (рис. 82). В обоих случаях вес доски был одним и тем же, однако эффект оказался разным. Почему?
Вся разница в рассматриваемых случаях заключалась в том, что площадь поверхности, на которую опирались гвозди, в одном случае была больше, а в другом меньше. Ведь сначала песка касались шляпки гвоздей, а затем их острия.
Мы видим, что результат воздействия зависит не только от силы, с которой тело давит на поверхность, но и от площади этой поверхности. Именно по этой причине человек, способный скользить по рыхлому снегу на лыжах, сразу же проваливается в него, как только их снимет (рис. 83).
Но дело не только в площади. Важную роль играет и величина прикладываемой силы. Если, например, на ту же. доску (см. рис. 81) положить еще одну гирю, то гвозди (при той же площади опоры) погрузятся в песок еще глубже.
Силу, прикладываемую перпендикулярно поверхности, называют силой давления на эту поверхность.
Силу давления не следует путать с давлением. Давление — это физическая величина, равная отношению силы давления, приложенной к данной поверхности, к площади этой поверхности:
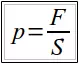
где
р — давление, F — сила давления, S — площадь.
Итак, чтобы определить давление, надо силу давления разделить на площадь поверхности, на которую оказывается давление.
При одной и той же силе давление больше в том случае, когда площадь опоры меньше, и, наоборот, чем больше площадь опоры, тем давление меньше.
В тех случаях, когда силой давления является вес находящегося на поверхности тела (F = P = mg), давление, оказываемое телом, можно найти по формуле
Если давление р и площадь S известны, то можно определить силу давления F; для этого надо давление умножить на площадь:
F = pS (32.2)
Сила давления (как и любая другая сила) измеряется в ньютонах. Давление же измеряется в паскалях. Паскаль (1 Па) — это такое давление, которое производит сила давления в 1 Н, будучи приложенной к поверхности площадью 1 м2:
1 Па = 1 Н/м2.
Используются также другие единицы давления — гектопаскаль (гПа) и килопаскаль (кПа):
1 гПа = 100 Па, 1 кПа = 1000 Па.
1. Приведите примеры, показывающие, что результат действия силы зависит от площади опоры, на которую действует эта сила. 2. Почему человек, идущий на лыжах, не проваливается в снег? 3. Почему острая кнопка легче входит в дерево, чем тупая? 4. Что называют давлением? 5. Какие вы знаете единицы давления? 6. Чем отличается давление от силы давления? 7. Как можно найти силу давления, зная давление и площадь поверхности, к которой приложена сила?