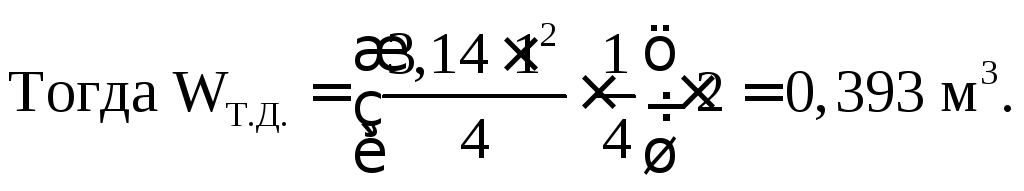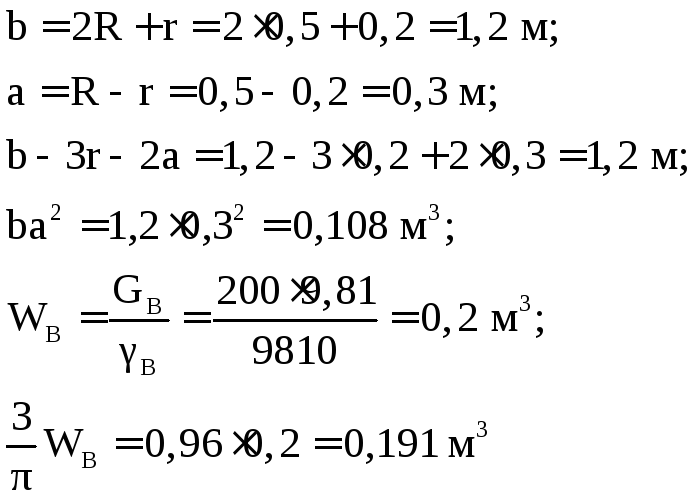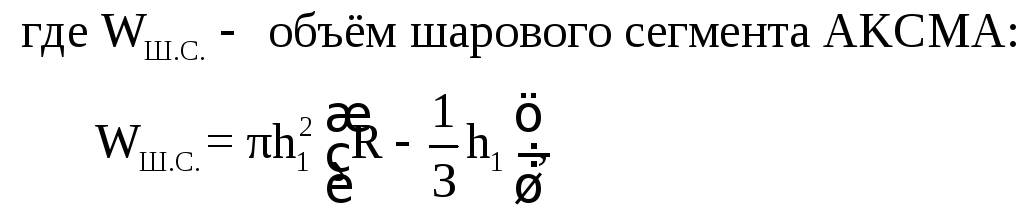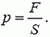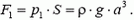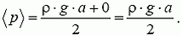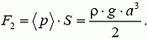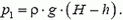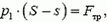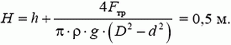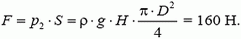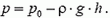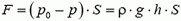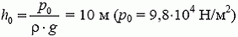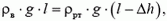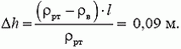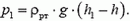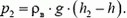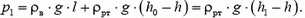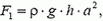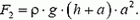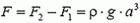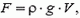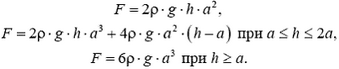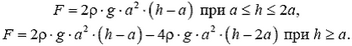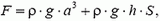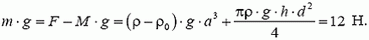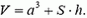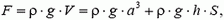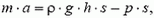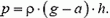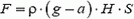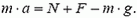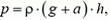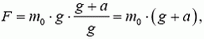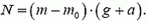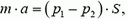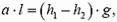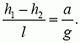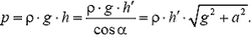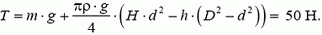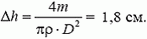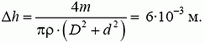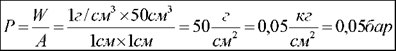Как найти силу давления трубы

1. Гидростатическое давление

Гидростатическое давление — это
внутренняя сжимающая сила, обусловленная
действием внешних сил, приложенная в
данной точке жидкости. Такое давление
по всем направлениям одинаково и зависит
от положения точки в покоящейся жидкости.

Размерность гидростатического давления
в системе МКГСС—кг/см2или т/м2,
в системе СИ — Н/м2.

Основные соотношения единиц измерения
давления:

	кг/см2	Н/м2
Техническая атмосфера	1	98066,5
Миллиметр водяного столба	0,0001	9,80665
Миллиметр ртутного столба	0,00136	133,32

При практических расчетах 1 техническая
атмосфера = 1 кг/см2= 10 м вод. ст. =
735 мм рт. ст. = 98070 Н/м2.

Для несжимаемой жидкости, находящейся
в равновесии под дей­ствием силы
тяжести, полное гидростатическое
давление в точке:

p=p+
h,

где р— давление на свободной
поверхности жидкости;

h— вес (сила тяжести) столба жидкости
высотойhс площадью

поперечного сечения, равной единице;

h— глубина погружения
точки;

— удельный вес жидкости.

Для некоторых жидкостей значения
удельного веса, используемые при решении
задач, приведены в приложении (табл.
П-3).

Величина превышения давления над
атмосферным (p_a)
называется манометрическим, или
избыточным, давлением:

Если давление на свободной поверхности
равно атмосферному, то избыточное
давление р_м=
h.

Недостающая до атмосферного давления
величина называется ва­куумом:

р_вак= р_а– р.

Решение большинства задач данного
раздела связано с использова­нием
основного уравнения гидростатики

где z— координата или
отметка точки.

1. Общие сведения по гидравлическому расчету трубопроводов

При расчете
трубопроводов рассматривается
установившееся, равномерное напорное
движение любой жидкости, отвечающее
турбулентному режиму, в круглоцилиндрических
трубах. В напорных трубопроводах жидкость
находится под избыточным давлением, а
поперечные сечения их полностью
заполнены. Движение жидкости по
трубопроводу происходит в результате
того, что напор в начале его больше, чем
в конце.

Гидравлический
расчет производится с целью определения
диаметра трубопровода d
при известной
длине для обеспечения пропуска
определенного расхода жидкости Q
или установления
при заданном диаметре и длине необходимого
напора и расхода жидкости. Трубопроводы
в зависимости от длины и схемы их
расположения подразделяются на простые
и сложные. К простым трубопроводам
относятся трубопроводы, не имеющие
ответвлений по длине, с постоянным
одинаковым расходом.

Трубопроводы
состоят из труб одинакового диаметра
по всей длине или из участков труб разных
диаметров и длин. Последний случай
относится к последовательному соединению.

Простые трубопроводы
в зависимости от длины с участком местных
сопротивлений разделяют на короткие и
длинные. Короткими
трубопроводами
являются
трубопроводы с достаточно малой длиной,
в которых местные сопротивления
составляют более 10% гидравлических
потерь по длине. Например, к ним относят:
сифонные трубопроводы, всасывающие
трубы лопастных насосов, дюкеры (напорные
водопроводные трубы под насыпью дороги),
трубопроводы внутри зданий и сооружений
и т.п.

Длинными
трубопроводами
называют
трубопроводы сравнительно большой
длины, в которых потери напора по длине
значительно преобладают над местными
потерями. Местные потери составляют
менее 510%
потерь по длине трубопровода, и поэтому
ими можно пренебречь или ввести при
гидравлических расчетах увеличивающий
коэффициент, равный 1,051,1.
Длинные трубопроводы входят в систему
водопроводных сетей, водоводов насосных
станций, водоводов и трубопроводов
промышленных предприятий и
сельскохозяйственного назначения и
т.п.

Сложные трубопроводы
имеют по длине различные ответвления,
т.е. трубопровод состоит из сети труб
определенных диаметров и длин. Сложные
трубопроводы подразделяются на
параллельные, тупиковые (разветвленные),
кольцевые (замкнутые) трубопроводы,
которые входят в водопроводную сеть.

Гидравлический
расчет трубопровода сводится, как
правило, к решению трех основных задач:

• определение
  расхода трубопровода Q,
  если известны
  напор H,
  длина l
  и диаметр d
  трубопровода,
  с учетом наличия определенных местных
  сопротивлений или при их отсутствии;

• определение
  потребного напора H,
  необходимого для обеспечения пропуска
  известного расхода Q
  по трубопроводу
  длиной l
  и диаметром d;

• определение
  диаметра трубопровода d
  в случае
  известных величин напора H,
  расхода Q
  и длины l.

Скорость течения жидкости равна

где q > расчетный расход жидкости, м3/с;

– площадь живого сечения трубы, м2.

Коэффициент сопротивления трения λ определяется в соответствии с регламентами свода правил СП 40-102-2000 «Проектирование и монтаж трубопроводов систем водоснабжения и канализации из полимерных материалов. Общие требования»:

где b – некоторое число подобия режимов течения жидкости; при b > 2 принимается b = 2.

где Re – фактическое число Рейнольдса.

где ν – коэффициент кинематической вязкости жидкости, м²/с. При расчетах холодных водопроводов принимается равным 1,31 · 10-6 м²/с – вязкость воды при температуре +10 °С;

Reкв >- число Рейнольдса, соответствующее началу квадратичной области гидравлических сопротивлений.

где Кэ – гидравлическая шероховатость материала труб, м. Для труб из полимерных материалов принимается Кэ = 0,00002 м, если производитель труб не дает других значений шероховатости.

В тех случаях течения, когда Re ≥ Reкв, расчетное значение параметра b становится равным 2, и формула ( 4 ) существенно упрощается, обращаясь в известную формулу Прандтля:

При Кэ = 0,00002 м квадратичная область сопротивлений наступает при скорости течения воды (ν= 1,31 · 10-6 м²/с), равной 32,75 м/с, что практически недостижимо в коммунальных водопроводах.

Для повседневных расчетов рекомендуются номограммы, а для более точных расчетов – «Таблицы для гидравлических расчетов трубопроводов из полимерных материалов», том 1 «Напорные трубопроводы» (А.Я. Добромыслов, М., изд>во ВНИИМП, 2004 г.).

При расчетах по номограммам результат достигается одним наложением линейки – следует прямой линией соединить точку со значением расчетного диаметра на шкале dр с точкой со значением расчетного расхода на шкале q (л/с), продолжить эту прямую линию до пересечения со шкалами скорости V и удельных потерь напора 1000 i (мм/м). Точки пересечения прямой линии с этими шкалами дают значение V и 1000 i.

Как известно, затраты электроэнергии на перекачку жидкости находятся в прямой пропорциональной зависимости от величины Н (при прочих равных условиях). Подставив выражение ( 3 ) в формулу ( 2 ), нетрудно увидеть, что величина i (а, следовательно и Н) обратнопропорциональна расчетному диаметру dр в пятой степени.

Выше показано, что величина dр зависит от толщины стенки трубы e: чем тоньше стенка, тем выше dр и тем, соответственно, меньше потери напора на трение и затраты электроэнергии.

Если в дальнейшем по каким-либо причинам меняется значение MRS трубы, ее диаметр и толщина стенки (SDR) должны быть пересчитаны.

Следует иметь в виду, что в целом ряде случаев применение труб с MRS 10 взамен труб с MRS 8, тем более труб с MRS 6,3 позволяет на один размер уменьшить диаметр трубопровода. Поэтому в наше время применение полиэтилена РЕ 80 (MRS и PE 100 (MRS 10) взамен полиэтилена РЕ 63 (MRS 6,3) для изготовления труб позволяет не только уменьшить толщину стенки труб, их массу и материалоемкость, но и снизить затраты электроэнергии на перекачку жидкости (при прочих равных условиях).

В последние годы (после 2013) трубы изготовленные из полиэтилена ПЭ80 практически полностью вытеснены из производства трубами изготовленные из полиэтилена марки ПЭ100. Объясняется это тем, что сырье из которого производятся трубы поставляется из-за границы маркой ПЭ100. А еще тем, что полиэтилен 100 марки имеет более прочностные характеристики, благодаря чему, трубы выпускаются с теми же характеристиками, что трубы из ПЭ80, но с более тонкой стенкой, за счет чего увеличивается пропускная способность полиэтиленовых трубопроводов.

Номограмма для определения потерь напора в трубах диаметрами 6 , 100 мм.

Номограмма для определения потерь напора в трубах диаметрами 100 , 1200 мм.

Критерий Рейнольдса

Такую зависимость вывел английский физик и инженер Осборн Рейнольдс (1842 — 1912).

Критерий, который помогает ответить на вопрос, есть ли необходимость учитывать вязкость, является число Рейнольдса Re. Оно равно отношению энергии движения элемента текущей жидкости к работе сил внутреннего трения.

Рассмотрим кубический элемент жидкости с длиной ребра n. Кинетическая энергия элемента равна:

Согласно закону Ньютона, сила трения, действующая на элемент жидкости, определяется так:

Работа этой силы при перемещении элемента жидкости на расстояние n составляет

а отношение кинетической энергии элемента жидкости к работе силы трения равно

Сокращаем и получаем:

Re — называется числом Рейнольдса.

Таким образом, Re — это безразмерная величина, которая характеризует относительную роль сил вязкости.

Например, если размеры тела, с которым соприкасаются жидкость или газ, очень малы, то даже при небольшой вязкости Re будет незначительно и силы трения играют преобладающую роль. Наоборот, если размеры тела и скорость велики, то Re >> 1 и даже большая вязкость почти не будет влиять на характер движения.

Однако не всегда большие числа Рейнольдса означают, что вязкость не играет никакой роли. Так, при достижении очень большого (несколько десятков или сотен тысяч) значения числа Re плавное ламинарное (от латинского lamina — «пластинка») течение превращается в турбулентное (от латинского turbulentus — «бурный», «беспорядочный»), сопровождающееся хаотическими, нестационарными движениями жидкости. Этот эффект можно наблюдать, если постепенно открывать водопроводный кран: тонкая струйка течёт обычно плавно, но с увеличением скорости воды плавность течения нарушается. В струе, вытекающей под большим напором, частицы жидкости перемещаются беспорядочно, колеблясь, всё движение сопровождается сильным перемешиванием.

Появление турбулентности весьма существенно увеличивает лобовое сопротивление. В трубопроводе скорость турбулентного потока меньше скорости ламинарного потока при одинаковых перепадах давления. Но не всегда турбулентность плоха. В силу того что перемешивание при турбулентности очень значительно, теплообмен — охлаждение или нагревание агрегатов — происходит существенно интенсивнее; быстрее идёт распространение химических реакций.

Уравнение Бернулли стационарного движения

Одно из важнейших уравнений гидромеханики было получено в 1738 г. швейцарским учёным Даниилом Бернулли (1700 — 1782). Ему впервые удалось описать движение идеальной жидкости, выраженной в формуле Бернулли.

Идеальная жидкость — жидкость, в которой отсутствуют силы трения между элементами идеальной жидкости, а также между идеальной жидкостью и стенками сосуда.

Уравнение стационарного движения, носящее его имя, имеет вид:

где P — давление жидкости, ρ − её плотность, v — скорость движения, g — ускорение свободного падения, h — высота, на которой находится элемент жидкости.

Смысл уравнения Бернулли в том, что внутри системы заполненной жидкостью (участка трубопровода) общая энергия каждой точками всегда неизменна.

В уравнении Бернулли есть три слагаемых:

• ρ⋅v2/2 — динамическое давление — кинетическая энергия единицы объёма движущей жидкости;
• ρ⋅g⋅h — весовое давление — потенциальная энергия единицы объёма жидкости;
• P — статическое давление, по своему происхождению является работой сил давления и не представляет собой запаса какого-либо специального вида энергии («энергии давления»).

Это уравнение объясняет почему в узких участках трубы растёт скорость потока и падает давление на стенки трубы. Максимальное давление в трубах устанавливается именно в месте, где труба имеет наибольшее сечение. Узкие части трубы в этом отношении безопасны, но в них давление может упасть настолько, что жидкость закипит, что может привести к кавитации и разрушению материала трубы.

Уравнение Навье — Стокса для вязких жидкостей

В более строгой формулировке линейная зависимость вязкого трения от изменения скорости движения жидкости называется уравнением Навье — Стокса. Оно учитывает сжимаемость жидкостей и газов и, в отличие от закона Ньютона, справедливо не только вблизи поверхности твёрдого тела, но и в каждой точке жидкости (у поверхности твёрдого тела в случае несжимаемой жидкости уравнение Навье — Стокса и закон Ньютона совпадают).

Любые газы, для которых выполняется условие сплошной среды, подчиняются и уравнению Навье — Стокса, т.е. являются ньютоновскими жидкостями.

Вязкость жидкости и газа обычно существенна при относительно малых скоростях, потому иногда говорят, что гидродинамика Эйлера — это частный (предельный) случай больших скоростей гидродинамики Навье — Стокса.

При малых скоростях в соответствии с законом вязкого трения Ньютона сила сопротивления тела пропорциональна скорости. При больших скоростях, когда вязкость перестаёт играть существенную роль, сопротивление тела пропорционально квадрату скорости (что впервые обнаружил и обосновал Ньютон).

Последовательность выполнения гидравлического расчета

1.
Выбирается главное циркуляционное
кольцо системы отопления (наиболее
невыгодно расположенное в гидравлическом
отношении). В тупиковых двухтрубных
системах это кольцо, проходящее через
нижний прибор самого удаленного и
нагруженного стояка, в однотрубных –
через наиболее удаленный и нагруженный
стояк.

Например,
в двухтрубной системе отопления с
верхней разводкой главное циркуляционное
кольцо пройдет от теплового пункта
через главный стояк, подающую магистраль,
через самый удаленный стояк, отопительный
прибор нижнего этажа, обратную магистраль
до теплового пункта.

В
системах с попутным движением воды в
качестве главного принимается кольцо,
проходящее через средний наиболее
нагруженный стояк.

2.
Главное циркуляционное кольцо разбивается
на участки (участок характеризуется
постоянным расходом воды и одинаковым
диаметром). На схеме проставляются
номера участков, их длины и тепловые
нагрузки. Тепловая нагрузка магистральных
участков определяется суммированием
тепловых нагрузок, обслуживаемых этими
участками. Для выбора диаметра труб
используются две величины:

а)
заданный расход воды;

б)
ориентировочные удельные потери давления
на трение в расчетном циркуляционном
кольце R_ср.

Для
расчета R_cp
необходимо знать длину главного
циркуляционного кольца и расчетное
циркуляционное давление.

3.
Определяется расчетное циркуляционное
давление по формуле

,
(5.1)

где
—
давление, создаваемое насосом, Па.
Практика проектирования системы
отопления показала, что наиболее
целесообразно принять давление насоса,
равное

,
(5.2)

где

—
сумма длин участков главного циркуляционного
кольца;

—
естественное давление, возникающее при
охлаждении воды в приборах, Па, можно
определить как

,
(5.3)

где
—
расстояние от центра насоса (элеватора)
до центра прибора нижнего этажа, м.

Значение
коэффициента можно
определить из табл.5.1.

Таблица
5.1 — Значение в
зависимости от расчетной температуры
воды в системе отопления

(),C	, кг/(м3К)
85-65	0,6
95-70	0,64
105-70	0,66
115-70	0,68

—
естественное давление, возникающее в
результате охлаждения воды в трубопроводах
.

В
насосных системах с нижней разводкой
величиной
можно пренебречь.

1. Определяются
   удельные потери давления на трение

,
(5.4)

где
к=0,65 определяет долю потерь давления
на трение.

5.
Расход воды на участке определяется по
формуле

(5.5)

где
Q
– тепловая нагрузка на участке, Вт:

(t_г
— t_о)
– разность температур теплоносителя.

6.
По величинам
иподбираются стандартные размеры труб
.

6.
Для выбранных диаметров трубопроводов
и расчетных расходов воды определяется
скорость движения теплоносителя v
и устанавливаются фактические удельные
потери давления на трение R_ф.

При
подборе диаметров на участках с малыми
расходами теплоносителя могут быть
большие расхождения между
и.
Заниженные потерина
этих участках компенсируются завышением
величинна других участках.

7.
Определяются потери давления на трение
на расчетном участке, Па:

.
(5.6)

Результаты
расчета заносят в табл.5.2.

8.
Определяются потери давления в местных
сопротивлениях, используя или формулу:

,
(5.7)

где
— сумма коэффициентов местных сопротивлений
на расчетном участке .

Значение ξ
на каждом участке сводят в табл. 5.3.

Таблица 5.3 —
Коэффициенты местных сопротивлений

№ п/п	Наименования участков и местных сопротивлений	Значения коэффициентов местных сопротивлений	Примечания

9.
Определяют суммарные потери давления
на каждом участке

.
(5.8)

10. Определяют
суммарные потери давления на трение и
в местных сопротивлениях в главном
циркуляционном кольце

.
(5.9)

11. Сравнивают Δр
с Δр_р.
Суммарные потери давления по кольцу
должны быть меньше величины Δр_р
на

.
(5.10)

Запас располагаемого
давления необходим на неучтенные в
расчете гидравлические сопротивления.

Если условия не
выполняются, то необходимо на некоторых
участках кольца изменить диаметры труб.

12. После расчета
главного циркуляционного кольца
производят увязку остальных колец. В
каждом новом кольце рассчитывают только
дополнительные не общие участки,
параллельно соединенные с участками
основного кольца.

Невязка потерь
давлений на параллельно соединенных
участках допускается до 15% при тупиковом
движении воды и до 5% – при попутном.

Таблица
5.2 — Результаты гидравлического расчета
для системы отопления

На схеме трубопровода

По предварительному расчету

По окончательному расчету

Номер участка

Тепловая нагрузка Q, Вт

Расход теплоносителя G, кг/ч

Длина участка l, м

Диаметр d, мм

Скорость v, м/с

Удельные потери давления на трение R, Па/м

Потери давления на трение Δртр, Па

Сумма коэффициентов местных сопротивлений ∑ξ

Потери давления в местных сопротивлениях Z

d, мм

v, м/с

R, Па/м

Δртр, Па

∑ξ

Z, Па

Rl+Z, Па

Занятие 6

Изменение температуры газа по длине газопровода

При стационарном движении газа массовый
расход в газопроводе составляет

. (2.41)

Фактически движение газа в газопроводе
всегда является неизотермическим. В
процессе компримирования газ нагревается.
Даже после его охлаждения на КС температура
поступающего в трубопровод газа
составляет порядка 2040С,
что существенно выше температуры
окружающей среды (T).
Практически температура газа становится
близкой к температуре окружающей среды
лишь у газопроводов малого диаметра
(Dу0.
Кроме того следует учесть, что
транспортируемый по трубопроводу газ
является реальным газом, которому присущ
эффект Джоуля-Томпсона, учитывающий
поглощение тепла при расширении газа.

При изменении температуры по длине
газопровода движение газа описывается
системой уравнений:

удельной энергии ,

неразрывности ,

состояния ,

теплового баланса .

Рассмотрим в первом приближении уравнение
теплового баланса без учета эффекта
Джоуля-Томпсона. Интегрируя уравнение
теплового баланса

,

получим

, (2.42)

где ;

K_СР– средний на участке полный
коэффициент теплопередачи от газа в
окружающую среду;

G– массовый расход газа;

c_P–
средняя изобарная теплоемкость газа.

Величина a_tLназывается безразмерным критерием
Шухова

(2.43)

Таким образом, температура газа в конце
газопровода составит

. (2.44)

На удалении xот начала
газопровода температура газа определяется
по формуле

. (2.45)

Изменение температуры по длине газопровода
имеет экспоненциальный характер (рис.
2.6).

Рассмотрим
влияние изменения температуры газа на
производительность газопровода.

Умножив обе части уравнения удельной
энергии на 2и выразив,
получим

. (2.46)

Выразим плотность газа в левой части
выражения (2.46) из уравнения состояния
,
произведениеwиз уравнения неразрывности,dxиз уравнения теплового
баланса.

С учетом этого уравнение удельной
энергии принимает вид

(2.47)

или

. (2.48)

Обозначив
и интегрируя левую часть уравнения
(2.48) отP_НдоP_К, а правую отT_НдоT_К, получим

. (2.49)

Произведя замену

, (2.50)

имеем

. (2.51)

Произведя интегрирование в указанных
пределах, получим

. (2.52)

С учетом (2.42)

или

, (2.53)

где – поправочный коэффициент, учитывающий
изменение температуры по длине газопровода
(неизотермичность газового потока).

С учетом (2.53) зависимость для определения
массового расхода газа примет вид

. (2.54)

Значение _Нвсегда больше единицы, следовательно,
массовый расход газа при изменении
температуры по длине газопровода
(неизотермическом режиме течения) всегда
меньше, чем при изотермическом режиме
(T=idem). Произведение T_Нназывается среднеинтегральной
температурой газа в газопроводе.

При значениях числа Шухова Шу4
течение газа в трубопроводе можно
считать практически изотермическим
при T=idem. Такой температурный
режим возможен при перекачке газа с
небольшими расходами по газопроводам
малого (менее 500 мм) диаметра на значительное
расстояние.

Влияние изменения температуры газа
проявляется при значениях числа Шухова
Шу

При
перекачке газа наличие дроссельного
эффекта приводит к более глубокому
охлаждению газа, чем только при теплообмене
с грунтом. В этом случае температура
газа может даже опуститься ниже
температурыT(рис.
2.7).

Рис. 2.7. Влияние эффекта Джоуля-Томпсона
на распределение температуры газа по
длине газопровода

1 – без учета Di; 2 – с
учетомDi

Тогда с учетом коэффициента Джоуля-Томпсона
закон изменения температуры по длине
принимает вид

, (2.55)

5 Гидравлические потери

Разность
давлений масла в двух сечениях одного
и того же трубопровода при условии, что
первое расположено выше по течению, а
второе – ниже, определяется уравнением
Бернулли

,

где
h₂
– h₁
– разность высот центров тяжести
сечений от произвольно выбранного
горизонтального уровня;

v₁,
v₂
– cредние скорости масла в сечениях;

g – ускорение силы
тяжести;

–сумма
гидравлических потерь при движении
масла из первого сечения во второе.

Уравнение
Бернулли в полном виде используется
для расчета всасывающих линий насосов;
в остальных случаях первым слагаемым,
как правило, пренебрегают и считают:

Гидравлические
потери обычно разделяют на местные
потери и потери на трение по длине
трубопровода (линейные).

1.5.1
Местные потери
энергии обусловлены местными
гидравлическими сопротивлениями,
вызывающими деформацию потока. Местными
сопротивлениями являются: сужения,
расширения, закругления трубопроводов,
фильтры, аппаратура управления и
регулирования и пр. При протекании
жидкости через местные сопротивления
изменяется её скорость и обычно возникают
крупные вихри.

Потери
давления от местных сопротивлений
определяют по формуле Вейсбаха:

МПа
(или
Па),

где
 (кси) – коэффициент сопротивления или
потерь,

v
– средняя по сечению скорость потока
в трубе за местным сопротивлением, м/с;

,
Н/м3;
g=9,81 м/с2.

Каждое
местное сопротивление характеризуется
своим значением коэффициента
.
При турбулентном течении значенияопределяются, в основном, формой местных
сопротивлений и очень мало изменяются
с изменением размеров сечения, скорости
потока и вязкости жидкости. Поэтому
принимают, что они не зависят от числа
Рейнольдса Re.

Значения
,
например, для тройников с одинаковыми
диаметрами каналов, принимают равными,
если:

потоки
складываются, расходятся; поток
проходящий;

=0,5-0,6

=1,5-2=0,3=1-1,5=0,1=0,05

=0,7

=0,9-1,2=2

при
повороте трубопровода

= 1,5-2 и т.д.

Значения
для конкретных сопротивлений, встречающихся
в гидросистемах оборудования, берут из
справочной литературы.

При
ламинарном режиме (Re

Потери
давления от местных сопротивлений при
ламинарном режиме определяются по
формуле:

МПа,

где

_л
= аи поправочный коэффициент ламинарности

Величины
потерь давления в стандартных
гидравлических устройствах для
номинального расхода жидкости обычно
приводятся в их технических характеристиках.

1.5.2
Потери на
трение по длине
— это потери энергии, которые возникают
в прямых трубах постоянного сечения,
т.е. при равномерном течении жидкости,
и возрастают пропорционально длине
трубы. Эти потери обусловлены внутренним
трением в жидкости, а поэтому имеют
место и в шероховатых, и в гладких трубах.

Потери
давления на трение в трубопроводе
определяется по формуле Дарси:

МПа,

где
– коэффициент трения в трубопроводе;

l
и d
– длина и внутренний диаметр трубопровода,
мм.

Эта
формула применима как при ламинарном,
так и при турбулентном течении; различие
заключается лишь в значениях коэффициента

.

При
ламинарном режиме (Re

При
турбулентном течении коэффициент трения
является не только функцией числа Re, но
зависит и от шероховатости внутренней
поверхности трубы. Для гидравлически
гладкой трубы,
т.е. с такой шероховатостью, которая
практически не влияет на ее сопротивление,
коэффициент трения при турбулентном
режиме можно определить по формуле П.К.
Конакова:

Трубу
считают гидравлически гладкой, если
(d/k)>(Re/20),
где k – эквивалентная шероховатость,
мм. Например, для новых бесшовных стальных
труб k≈0,03
мм, а после нескольких лет эксплуатации
k≈0,2
мм, для новых цельнотянутых труб из
цветных металлов k≈0,005
мм. Такие трубы часто используются в
гидросистемах металлорежущих станков.

Коэффициент
трения при турбулентном режиме можно
определить по формуле Альтшуля,
являющейся универсальной (т.е. применимой
в любых случаях):

2. Расходная характеристика трубопровода модуль расхода

Вспомним
формулу линейных потерь – формулу Дарси
– Вейсбаха:
.

Выразим
в этой формуле скорость V
через расход Q
из соотношения
:

.
(6.1)

Для
трубопровода определенного диаметра
комплекс величин
в выражении (6.1) можно считать величиной
постоянной (1/К2),
кроме коэффициента гидравлического
трения λ. На основании понятия
среднеэкономической скорости V_с.э
покажем, что и указанный коэффициент λ
можно отнести к этому комплексу, т.к. в
этом случае, число Рейнольдса будет
иметь определенное значение:
,
и на графике Никурадзе коэффициент λ в
этом случае будет иметь конкретное
значение.

Обоснуем
правомерность введения понятия
среднеэкономической скорости следующими
рассуждениями.

Гидравлическую
систему, например водопроводную, для
пропуска определенного расхода можно
выполнить из труб разного диаметра. При
этом с увеличением диаметра d,
следовательно, уменьшением скорости V
капитальные затраты будут расти, а
эксплуатационные затраты будут
уменьшаться из-за снижения гидравлических
потерь. Скорость, при которой суммарные
затраты будут иметь минимальное значение,
будем называть среднеэкономической
скоростью V_с.э
= 0,8…1,3 м/с (рис.6.1).

рис.6.1

Тогда
формула линейных потерь (6.1) примет вид

,
(6.2)

где
К – расходная характеристика трубопровода
(модуль расхода), зависит от материала
трубопровода, диаметра и расхода. берется
из таблиц.

Силу гидростатического давления на
криволинейную поверхность определяют
по формуле

где
—
составляющие силы избыточного давления
по соответствующим координатным осям.
В случае цилиндрической криволинейной
поверхности

где

и
— горизонтальная и вертикальная
составляющие силыР.

Горизонтальная составляющая избыточного
давления Р_х равна
си­ле давления на вертикальную проекцию
криволинейной поверхности

где р_м — манометрическое
давление на поверхности жидкости,

h_ц —
глубина погружения центра тяжести
вертикальной проекции криволинейной
поверхности;

—
площадь вертикальной проекции
криволинейной поверхности. Если
манометрическое давление на свободной
поверхности жид­кости равно нулю
(р_o= р_а), то

В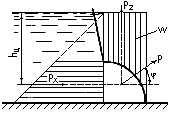ертикальная
составляющая
равна весу жидкости в объеме тела
давления. Тело давления располо­жено
между вертикальными плос­костями,
проходящими через край­ние образующие
цилиндрической по­верхности, самой
цилиндрической поверхностью и свободной
поверх­ностью жидкости или ее
продолже­нием.

Если давление на свободной поверхности
жидкости
,
то тело давления ограничивается сверху
пьезометрической плоскостью, удаленной
от свободной поверхности жидкости на
расстояние

Направление силы Р определяется
тангенсом угла:

Если криволинейная поверхность не
цилиндрическая, то горизон­тальную
составляющую Р_y
определяют аналогично силеР_х.

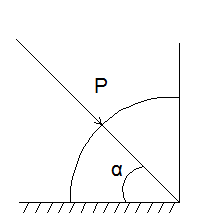
Примеры

2.28. Определить силу давления воды
на деталь, имеющую форму четверти
кругового цилиндра радиуса =0,5 м. Найти
угол,
под котором эта сила направлена к
горизонту. Расчет вести на единицу
ширины конструкции. Высота конструкции
Н=5 м.

Р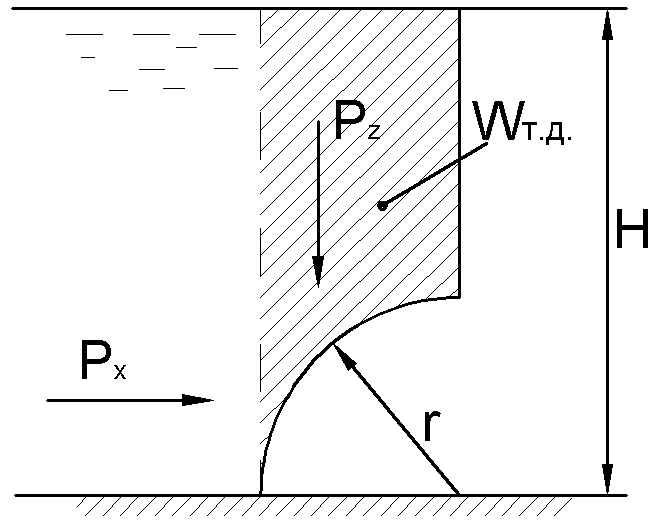ешение:

Найдем горизонтальную составляющую
силы гидростатического давления воды:

Р_x=,

где h_c=H-;
;

=
^Н.

Найдем
вертикальную составляющую:

P_z=.

Для чего
определим объем тела давления:

^Wт.д=м3.

^{Тогда
Pz
=H.}

Результирующая
сила найденных составляющих равна:

^Р
=3,31Н.

Угол между
линией действия этой силы и линией
горизонта равен:

Ответ:P= 3, 31
H;
.

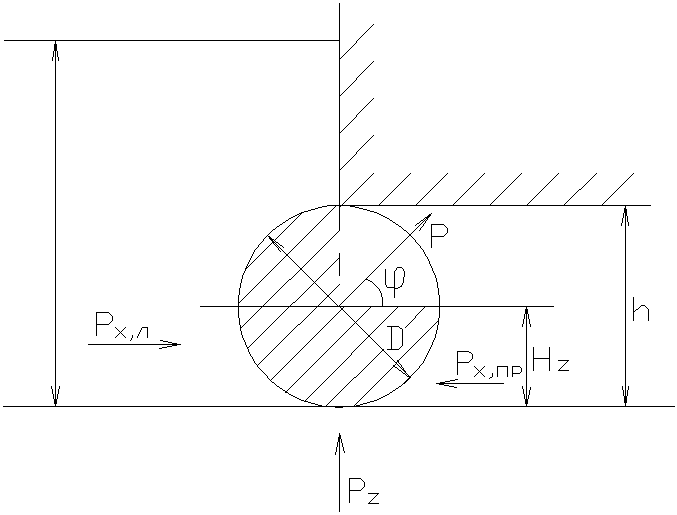
2.29. Определить величину Р и направление
угол α равнодействующей силы давления
на цилиндрический затвор плотины,
перекрывающий прямоугольное отверстиеh=D= 1,0 м и
ширинойb= 5,0 м. Глубина
воды слева -H₁= 3,4 м,
справа -H₂=D/2.

Решение: 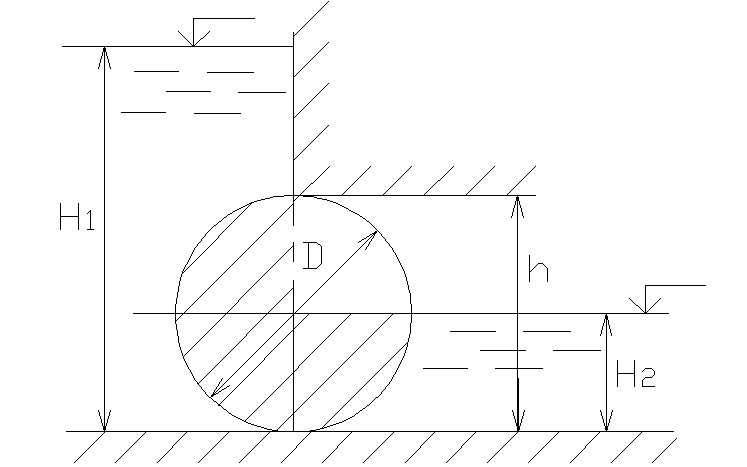Для
нахождения силы гидростатического
давления на цилиндр необходимо
использовать зависимость:

,

^{где
– горизонтальная
составляющая}

полной силы гидростатического
давления воды;

^{– вертикальная
составляющая}полной силы
гидростатического давления воды.

Направление равнодействующей силы
гидростатического давления воды найдем
по формуле:

Горизонтальная составляющая силы
давления воды:

— слева

— справа

Их равнодействующая величина равна
алгебраической сумме:

.

Вертикальная составляющая силы
давления на затвор равна весу воды в
объеме тела давления (на рисунке
заштриховано):

.

Результирующая сила гидростатического
давления на цилиндрический затвор
составит:

.

Направление этой силы, т.е. угол
наклона к горизонту составит:

.

^Ответ:

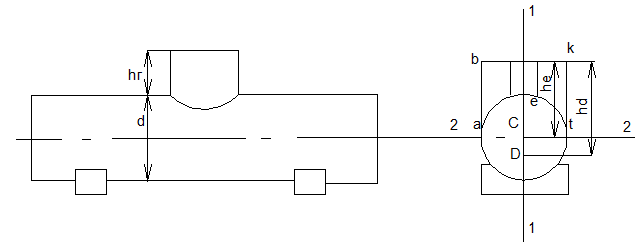
2.30.Определить силу суммарного
давления на торцовую плоскую стенку
цилиндрической цистерны диаметроми точку её приложения. Высота горловины.
Цистерна заполнена бензином до верха
горловины.

Решение. Сила суммарного давления
бензина на торцовую стенку цистерны
равна

где
—
плотность бензина (табл. П-3).

Точка приложения (центр давления) силы
суммарного давления расположена на
глубине (от верхней кромки горловины)

Ответ:

2.31.Определить силу суммарного
давления на секторный затвор и её
направление. Глубина воды перед затвором
Н=4м, длина затвораL=8м,
угол.

Решение.Горизонтальная составляющая
полной силы давления на секторный затвор
равна силе давления на вертикальную
проекцию затвора:

.

Вертикальную составляющую полной силы
давления на секторный затвор определяем
по формуле:

,

где W- объём тела давленияabcдлинойL;

—
площадь фигурыabc;

Найдем элементы
и площадь фигурыabc:

;

;

;

;

;

;

;

.

Равнодействующую сил давлений определяем
по формуле:

.

Направление этой силы определяется
углом
:

;.

Ответ: ;.

2.32.По стальному трубопроводу
диаметромподаётся вода под давлениемОпределить напряжение в стенке трубы,
если ее толщина.

Решение.Суммарная сила давления,
разрывающая трубу в продольном
направлении, равна гидростатическому
давлению, умноженному на площадь
вертикальной проекции криволинейной
стенки:

Разрыв происходит по двум продольным
сечениям стенки трубы. Напряжение,
возникающее в материале стенки, равно

Ответ: МПа

2.33.Определить силы, разрывающие
горизонтальную, наполненную бензином
цистерну длинойпо сечениями,
если диаметр цистерны,
а высота горловины.
Цистерна заполнена бензином плотностью=740кг/до верха горловины.

Решение.Сила, разрывающая цистерну
по сечению,
равна горизонтальной составляющей силы
давления воды на криволинейную стенкуили:

.

Силы, растягивающие цистерну по сечению
2-2, равны силам, действующим на криволинейные
стенки aetиaft. Эти силы также направлены противоположно
друг другу. Сила давления на криволинейную
стенкуaet

,

где W– объём телаabkt;

ω – площадь фигуры abktea;

.

Подставляя цифровые значения, находим:

.

Ответ: ;.

2.34. Для выпуска сточных вод в море
построен трубопровод диаметром,
уложенный по дну на глубине.
Определить силы, действующие на
трубопровод, когда он не заполнен.

Решение. Сила, действующая на
трубопровод сверху, определяется как
вертикальная составляющая суммарных
сил давления на криволинейную поверхность.
Она равна весу воды в объёме тела,
т.е. (надлины трубопровода)

где
—
плотность морской воды (табл. П-3).

Сила
,
действующая на трубопровод снизу, больше
силына величину веса воды в рассматриваемом
участке трубопровода, т.е.;
собственный вес трубыдолжен быть равендля того, чтобы исключить возможность
её всплывания.

Силы, действующие на трубопровод по
горизонтали, равны и направлены
противоположно друг другу .Каждая из
этих сил равна горизонтальной составляющей
сил давления воды на криволинейную
стенку, которая, в свою очередь, равна
силе суммарного давления воды на
вертикальную проекцию трубы, т.е. (на
длины трубопровода)

Ответ:
.

2.35.Определить силу гидростатического
давления воды на
ширины нижней криволинейной части
сооружения, если

Решение.

1) Горизонтальная составляющая силы
давления воды на криво­линейную часть
сооружения равна силе давления на
вертикальную проекцию этой поверхности

2) Вертикальная составляющая

равна весу жидкости в объеме тела
давле­ния. Обозначим площадь фигуры
через.
Тогда:

3) Суммарная сила давления воды на
криволинейную часть сооружения

4) Расстояние от свободной поверхности
воды до линии действия горизонталь­ной
составляющей Р_х.

5)
Вертикальная составляющая
проходит через центр тяжести фигуры.
Расстояниецентра тяжести фигурыот линии
равно стати­ческому моменту этой
фигурыотносительно линии,
деленному на площадь фигуры,
причем расстояние центра тяжести
четверти круга
от линии:

;

Сила
проходит через точку пересеченияc
линий действия горизонтальной и
вертикальной составляющих под угломк горизонту, причем

Заметим, что при круговой цилиндрической
поверхности сила
всегда проходит через центр круга.

Ответ:

2.36.Определить величину и направление
силы гидростатического давления воды
на
ширины вальцового затвора диаметром.

Решение.

1) Горизонтальная составляющая

2) Вертикальная составляющая

3) Суммарная сила давления

4) Составляющая Р_х проходит
на расстоянии у_дот свободной
поверхности:

составляющая
проходит на расстоянииот линии,
равном

5) Равнодействующая Р приложена в
точкеО под угломк горизонту и про­ходит через центр
круга, причем

Ответ: ;.

2.37. Определить силу гидростатического
давления воды на 1м ширины вальцового
затвора диаметромприи.

Решение.1) Горизонтальная составляющая
силы давления воды слева

справа

2) Вертикальная составляющая силы
давления воды, равная весу жидкости в
объеме тела давления (на рисунке
заштриховано):

где
— площадь фигуры,
для определения которой рассмотрим
треуголь­ник:

,

3) Суммарная сила давления

4) Угол наклона силы Рк горизонту
определяется по тангенсу угла
:

Ответ:

2.38. Определить силу давления воды
на
ширины затвора, перекрывающего канал
между двумя смежными камерами, если
глубина воды в левой камерев правой

Решение. 1) Горизонтальная составляющая
силы давления воды на затвор слева

справа

откуда

2) Вертикальная составляющая P_z
равна весу жидкости в объеме тела
давления (на рисунке заштриховано):

где d – длина
основания тела давления;

b= 1м– его
ширина. Для определениярассмотрим треугольникиАВОиАВС:

Угол

3) Суммарная сила давления на затвор

Сила Рпроходит через шарнирОпод угломк горизонту, причем

Ответ:

2.39.Цилиндр радиусоми длинойперекры­вает отверстие в дне резервуара
размерамисм.
Определить: силу давления воды на цилиндр
при.

Решение.1) Горизонтальная составляющая
силы давления воды на ци­линдр равна
нулю, так как и на его основания и на
продольные вертикальные проекции
действуют соответственно равные и
противоположно направленные силы.

2) Вертикальная составляющая равна весу
жидкости в объёме тела давления (на
рисунке заштриховано):

Из рисунка видно, что

.

Тогда площади сегментов s₁
иs₂определяются
по формулам

Ответ:

2.40. На горизонтальной плите установлен
стальной сосуд без дна в форме усеченного
конуса с толщиной стенкимм. Определить при каком уровне воды в
сосудеhон оторвется от
плиты, если известныD=2
м,d=0,5 м, Н=2 м.

Решение: Сосуд может оторваться от
плиты в том случае, если вертикальная
сила гидростатического давления воды
на

наклонные (конические) стенки сосуда
превысит силу веса самого сосуда.
Составим уравнение равновесия этих
сил:

G=_т.д.;

Где G=,

т/м³=8,5Н/м³;

S_бок=—
боковая поверхность конуса;

l-длина образующей:

^l=м,

тогда S_бок=м².

^{Вес сосуда равен
G=8,4Н.}

Тело давления –это заштрихованная
фигура, которая создает вертикальную
отрывающую силу F_z.

Запишем объем тела давления:

^Wт.д.=,
()

где r₁–является
неизвестной величиной. Выразим ее через
глубину воды в сосудеh.

Для этого cоставим
пропорцию для подобных треугольников
АВС и АМN:

АМ=х.

^{Тогда,
откуда х =}.

^{Тогда d1=2r1=D—}.

Теперь выразим радиус r₁:

^r1=.

Подставим значение r₁в уравнение ():

^Wт.д.=,

Раскрываем скобки, приведем подобные
элементы, получим:

=1,04h-0,4h²-0,15h³.

^{Учитывая, что}м³,

Окончательно получаем:

0,15h³-0,4h²+1,04h-0,5=0

Способом подстановок “h”
в это уравнение найдем значение:

h=0,58 м.

^{Проверка: 0,15};

0,6333-0,6350.

Ответ: h=0,58 м.

2.41. Определить силу натяжения троса,
удерживающего криволинейный затвор,
представляющий собой четверть кругового
цилиндра радиусаR=1 м,
перекрывающего канал прямоугольного
сечения ширинойb=3 м.
Глубина наполнения канала водойH=2
м.

Решение:Для определения силы
натяжения троса составим

уравнение моментов всех сил, действующих
на затвор, относительно

точки О:

;

ТR=P_zl_p+P_xl_b.

Для чего найдем составляющие Р_хи Р_z

силы гидростатического давления на
криволинейный

(цилиндрический) затвор:

Р_x==10⁴=
=H.

Точка приложения этой составляющей
находится на расстоянии l_bот оси шарнира 0:

L_b=l_д-(H-R),

L_д=l_c+;

l_b=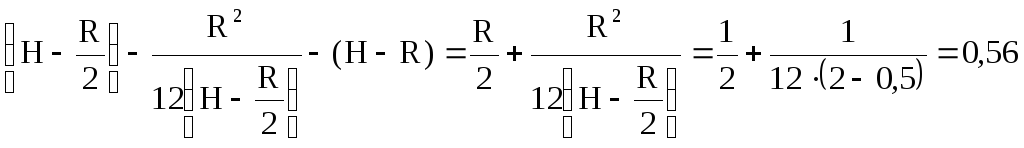м.

Составляющая P_zнаходится через объем тела давленияW_т.д.:

P_z=,

где W_т.д.=.

Тогда P_z=H.

Линия действия этой вертикальной
составляющей проходит через центр
тяжести фигуры 1-0-2-3-4. Расстояние l_р
центра тяжести фигуры 1-0-2-3-4 от линии
0-2 равно статическому моменту этой
фигурыSотносительно
линии 1-0-2, поделенному на площадь фигурыF(причем расстояние центра
тяжести четверти круга 1-0-4 от линии
1-0-2 равно е=0,4244R).

^м.

Тогда Т= H.

^{Ответ: Т=4,52Н.}

2.42. Найти величину и направление
силы гидростатического давления воды
на 1м ширины криволинейного затвора,
если известны

Решение:Результирующая
сила гидростатического давления равна.
Найдём составляющие этой силыи:

Найдём параметры затвора:

Тогда горизонтальная составляющая
равна :

Найдём вертикальную составляющую,
для чего вычислим объём тела давления:,

;;;.

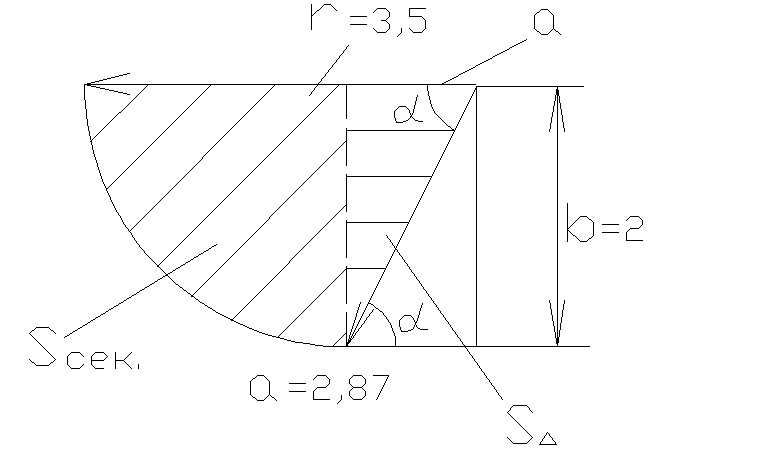
Найдём площадь треугольника:

S_∆.

Площадь сектора составит:

.

Площадь тела давления:

.

Тогда объём тела давления составит:

.

.

Полная сила гидростатического давления
на затвор составит:

,

а направление этой силы определяется
углом φ:

.

Ответ:
,.

2.43. Определить горизонтальнуюи вертикальнуюсоставляющие силы давления воды на
горизонтальный цилиндр диаметромd= 30 см, который вставлен чepeз
отверстие в наклонной стенке (α = 30º)
внутрь резервуара на расстоянииl= 0,8 м. Уровень воды над осью цилиндра Н
= 1,0 м.

Pешение:

Горизонтальная составляющая силы
давления на цилиндр определяется
так:

где—
заглубление центра тяжести

вертикальной проекции криволи-

нейной поверхности , т.е.

,

—
площадь вертикальной проекции цилиндра:

.

Тогда:

Вертикальная составляющая силы давления
воды на цилиндр равна:

гдеW– объём тела давления,
который найдём из геометрии.

Рассмотрим ∆ АВС и ∆ МСD.
Они равны,

так как АС = СМ =
;
ВС =CD=;

Поэтому объёмы будут равны:

Тогда объём тела давления определяется
так:

.

Либо объём тела давления найдём так.

Из ∆ АВС:

из ∆ МСD:

Тогда:

Найдём:

.

Окончательно:

Ответ:

2.44. В прямоугольном окне вертикальной
стенке установлен цилиндрический затвор
(270º) диаметромD= 100 см и
длинойb= 2,0 м. Определить
усилие Р на цапфы и момент М от воздействия
жидкости на затвор. Весом затвора
пренебречь. Напор над осью крепления Н
= 1,0 м.

Решение:

Так как затвор выполнен в виде цилиндра,

то для нахождения усилия на цапфы
используем

расчетные формулы для определения сил

гидростатического давления на
криволинейную поверхность:

где Р_х– горизонтальная составляющая
силы гидростатического давления,
определяется по формуле:

,

где h_C– заглубление центра тяжести вертикальной
проекции криволинейной поверхности
под уровень свободной поверхности (в
данном случае);

−
площадь вертикальной проекции
криволинейной поверхности:

.

Тогда

,

где

− удельный вес воды приt= 20ºС [1, табл. 1 Приложения].

P_Z–
вертикальная составляющая силы
гидростатического давления, которая
равна весу жидкости в объеме тела
давления ( тело давления показано на
расчетной схеме):

Полная сила гидростатического давления,

действующая на цапфы, расположенные
на

горизонтальной оси цилиндра, равна:

.

Направление этой силы определяется
тангенсом угла α:

.

Линия действия (приложения) силы Р
проходит через центр цилиндра (через
цапфы).

Найдем теперь момент от воздействия
жидкости на затвор – М.

Этот момент в общем случае состоит
из
— момента от горизонтальной
составляющей силы
;
—
момента от вертикальной составляющей
силы.

Момент от горизонтальной составляющей,
в свою очередь, состоит из двух моментов:
— от горизонтальной составляющей,
действующей на верхнюю (криволинейную
поверх- ность)

— от горизонтальной
составляющей, действующей на нижнюю
часть цилиндра.

Однако эти две горизонтальные
составляющие можно привести к одной со
своим плечом действия:

где

– момент инерции проекции,

Тогда

.

Таким образом, момент от горизонтальной
составляющей будет:

(вращает против часовой стрелки).

Момент от вертикальной составляющей
будет определяться силой
и плечом.

Сила
будет
равна выталкивающей силе (архимедовой)
численно равной весу жидкости (воды) в
объеме, вытесненной 1/4 объема цилиндра:

.

Составляющая
проходит на расстоянииот линииab(см. расчетную
схему).

Тогда момент от
равен:

(вращает по часовой стрелки).

Суммарный момент от воздействия жидкости
на затвор составит:

(вращает против часовой стрелки).

Ответ:
.

2.45. В шарообразном углублении радиусаналита вода весом.
В воду погружен шарик радиусом.
Каким должен быть вес шарика,
чтобы он плавал в положении, концентричном
углублению?

Решение:

Составим равенство объемов:

,

где
– объем воды в углублении;

– объем погруженной части

шарика в воду;

– суммарный объем воды и погруженной
части шарика.

Тогда
или.

Из рисунка следует, что
или.

Обозначим
.
Тогда уравнение примет вид:

или

,
где.

Тогда
.

Вычислим значения:

подставим в предыдущее уравнение
и запишем его относительно h:

Решение этого квадратного уравнения
будет h= 0,109 м.

Так как
,
то вес шарикаили

.

Ответ:

2.46.
Определить величину и направление
равнодействующей силы давления воды
на цилиндрический затвор плотины,
перекрывающий донное отверстие высотойh=D=1,2 м.
и ширинойb= 6 м. Глубина
воды слева Н₁= 3,8 м, справа Н₂=D/2.

Решение:Равнодействующая сила
давления воды на цилиндрический затвор
определяется так:

,

где P_Xгоризонтальная составляющая силы
давления воды;

P_Z–
вертикальная составляющая силы давления
воды.

Найдем горизонтальную составляющую P_X. Она складывается из силы давления
воды, действующей слеваP_Xли справаP_Xпр:

P_Xл= р_С.лω_{z л}
= γ(Н₁ +)Db.

Аналогично:

P_Xпр= р_с.пр ω_z
пр = γb.

Тогда равнодействующая горизонтальных
сил составит:

P_X
=P_Xл-P_Xпр
= γ(Н₁ +)Db– γb= γb[(H₁ −)D−];

P_X
= 998 ∙ 9,81 ∙ 6 ∙ [(3,8 −)
∙ 1,2 −]
= 215 кН.

Найдем вертикальную составляющую P_Z.
Она равна весу жидкости в объеме тела
давления ( на рисунке заштриховано):

P_Z
= γW= γb=γb(3/16)πD²;

P_Z
= 998 ∙ 9,81 ∙ 6 ∙ (3/16) ∙ 3,14 ∙ 1,2²=
49,8 кН.

Суммарная сила давления:

.

Угол наклона силы Pк
горизонту:

γ=arctg=arctg
=13º5′.

Ответ: P= 220,7 кН ; γ =
13º5′.

2.47. Стальной шарик радиусомR= 7 см закрывает отверстие диаметромD= 10 см в плоской стенке, удерживаясь
силой гидростатического давления.
Определить, при каком напоре водыhшарик оторвется от отверстия.

Решение:

Н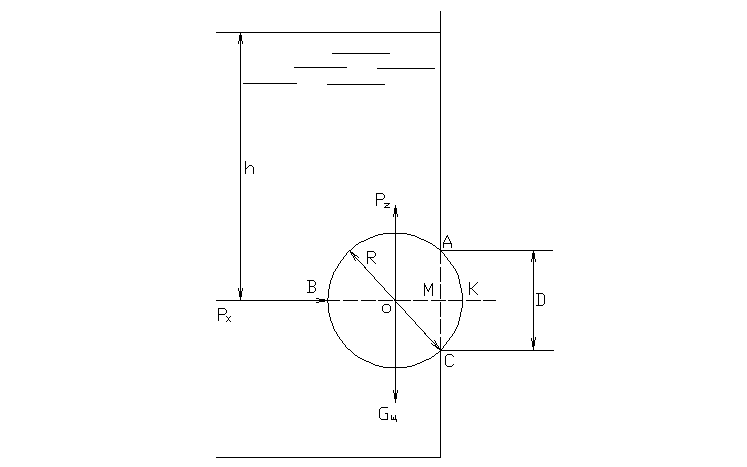айдём
вес шарика:Вертикальная составляющая силы
гидростатического давления воды на
шарик:

Вес шарика в воде будет на величину
меньше,
т.е.

Для сохранения равновесия необходимо
составить уравнение моментов сил
относительно точки C:

,

Тогда

откуда найдём

Ответ:

2.48. Определить величину и направление
действия силы на сегментный затвор
ширинойb3,0м,
радиусомR2,0м,
если известны углы,,.

Решение:

Сила давления жидкости на сегментный
затвор равна:

,

а её направление определяется углом
:

,

где
;

,

где
— объём тела давления, равный величине

Найдём эти величины из геометрии:

;;

;

;

;

=;

;;

;

;

;

,;

;

;

Тогда объём тела давления равняется

.

Найдём составляющие полной силы
гидростатического давления. Горизонтальная,
действующая слева, горизонтальная,
действующая справа

H;

H.

Их сумма равна H.

Вертикальна составляющаяH.

Полная сила гидростатического давления
на затвор составит

H=54,6кН.

tgоткуда.

Ответ:Р=54,6кН;.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

По специальной договоренности с редколлегией и редакцией журнала «Квант»

Давление и силы давления

Жидкость оказывает давление на стенки сосуда, в котором она находится, или на любую другую поверхность, соприкасающуюся с ней. Давление – величина скалярная. Оно измеряется абсолютной величиной нормальной (перпендикулярной поверхности) силы, действующей со стороны жидкости на единицу площади поверхности:

Давление в различных точках поверхности может быть разным. Поэтому площадь S мы должны брать достаточно маленькой.

По закону Паскаля давление жидкости не зависит от ориентации поверхности. Как бы ни была расположена поверхность в данном месте жидкости, давление на нее будет одним и тем же.

Сила давления всегда перпендикулярна поверхности. В обычных условиях она направлена так, как если бы жидкость стремилась расшириться.

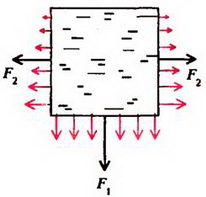
Задача 1. В сосуд, имеющий форму куба с ребром a, налита доверху жидкость плотностью ρ. Определите силы давления жидкости на дно и стенки сосуда.

Давление жидкости на дно сосуда равно весу столба жидкости высотой a с площадью основания, равной единице: 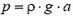, где g – ускореннее свободного падения. (Для простоты здесь и в других задачах, где это специально не оговорено, предполагается, что атмосферное давление отсутствует). Сила давления на дно сосуда (рис. 1, а)

а

б

Рис. 1

Давление на боковую грань куба будет зависеть от расстояния до поверхности жидкости. На глубине h давление 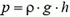. Так как давление изменяется с глубиной по линейному закону (рис. 1. б), для определения силы давления мы должны среднее давление

умножить на площадь боковой грани

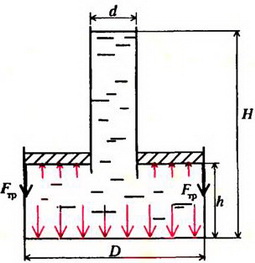
Задача 2. В цилиндрический сосуд диаметром D = 0,7 м вставлен поршень с длинной вертикальной трубкой диаметром d = 0,05 м (рис. 2). Максимальная сила трения между поршнем и стенками сосуда F_тp = 100 Н. Через трубку в сосуд наливают воду. При каком уровне воды в трубке H поршень начнет двигаться? Чему будет равна при этом сила давления воды на дно сосуда? Поршень расположен на высоте h = 0,2 м от дна сосуда. Плотность воды ρ = 10³ кг/м³. Массой поршня с трубкой пренебречь.

Рис. 2

Давление в жидкости на уровне поверхности поршня определяется расстоянием от этого уровня до свободной поверхности жидкости:

Поршень начнет двигаться, когда сила давления на него со стороны жидкости станет равной максимальной силе трения:

где 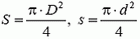 – плошали поперечных сечений сосуда и трубки соответственно. Подставляя сюда выражение для p₁, находим

Давление на дно сосуда .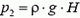

Сила давления

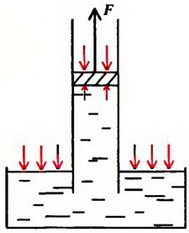
Задача 3. Длинная вертикальная труба с поршнем опущена одним концом в сосуд с водой. Вначале поршень находится у поверхности воды, затем его медленно поднимают. Как зависит сила, прикладываемая к поршню, от высоты h ее поднятия? Площадь поперечного сечения трубы S, атмосферное давление p₀. Изменением уровня воды в сосуде, массой поршня и ею трением о стенки трубы пренебречь.

При поднятии поршня вода под действием атмосферного давления будет вначале заполнять трубу (рис 3, а). Давление в трубе на уровне жидкости в сосуде равно атмосферному давлению p₀. Давление воды на поршень меньше атмосферного на величину веса столба жидкости высотой h и площадью основания, равной единице:

а

б

Рис. 3

Сверху на поршень по-прежнему действует атмосферное давление. Поэтому для удержания поршня на высоте h к нему надо приложить силу, равную

и направленную вверх.

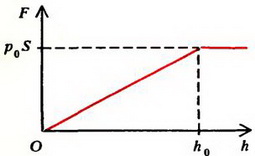
С увеличением h давление воды на поршень будет уменьшаться. На высоте

давление обратится в ноль. При дальнейшем поднятии поршня уровень воды в трубе изменяться не будет, тан как сила атмосферного давления, действующая на столб жидкости в трубе снизу, уравновесится силой тяжести. Для удержания поршня на высоте h > h₀ к нему надо приложить силу .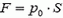

Зависимость прикладываемой к поршню силы F от высоты его поднятия h изображена графически на рисунке 3, б.

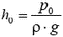
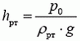
Высота столба воды в трубе , очевидно, может служить для измерения атмосферного давлении p₀. Однако обычно в барометрах используют ртуть, и нормальному атмосферному давлению тогда соответствует значительно меньшая высота столба ртути  = 0,76 м (плотность ртути ρ_рт = 1,36×10⁴ кг/м³).

Примером другого гидростатического устройства, широко используемого в практике, являются сообщающиеся сосуды. Известен закон сообщающихся сосудов: если давление над жидкостью в сосудах одинаково, то уровни жидкости в них равны. Нетрудно доказать этот закон для случая цилиндрических сосудов (рис. 4). Так как жидкость в соединительной трубке находится в равновесии, то давления на нее с обеих сторон должны быть одинаковы. Поэтому равны и уровни жидкости в сосудах.

Рис. 4

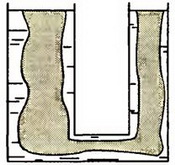
В общем случае для доказательства закона сообщающихся сосудов можно воспользоваться принципом отвердевания, который часто используют в гидростатике. Суть этого принципа заключается в следующем: всегда можно представить себе, что часть жидкости отвердела – равновесие оставшейся части жидкости от этого не нарушится. Так, в цилиндрических сообщающихся сосудах мы можем мысленно выделить часть жидкости, которая заполняла бы сообщающиеся сосуды любой извилистой формы (см. рис. 4), и представить себе, что остальная часть жидкости отвердевает. Тогда равновесие выделенной нами части жидкости не нарушится, и, следовательно, уровни жидкости в извилистых сообщающихся сосудах будут такими же, какими были в цилиндрических сосудах, т.е. одинаковыми.

Закон сообщающихся сосудов справедлив только для однородной жидкости. Если в сосуды налиты жидкости разных плотностей, то уровни в сосудах могут быть разными.

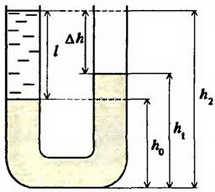
Задача 4. В U – образную трубку налита ртуть. Поверх ртути в одно из колен трубки налили воду (рис. 5, a). Высота столбика воды l = 0,1 м. Определите разность уровней жидкостей в коленах трубки. Нарисуйте график зависимости давления в обоих коленах трубки от высоты. Плотность ртути ρ_рт = 1,36×10⁴ кг/м³, плотность воды ρ_рт = 10³ кг/м³. Атмосферное давление не учитывайте.

а

б

Рис. 5

Давления на ртуть на уровне h_o соприкосновения воды и ртути в обоих коленах должны быть одинаковы (закон сообщающихся сосудов для однородной жидкости). Поэтому

где разность уровней h₂ – h₁ обозначена через Δh. Отсюда

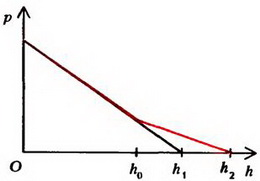
Давление в колене, содержащем только ртуть, меняется с высотой h по закону

Эта формула справедлива и в изогнутой части трубки. (Представите себе, что изогнутое колено сообщается с прямым цилиндрическим сосудом, в котором тоже находится ртуть. Тогда давления на одинаковой высоте в обоих сосудах должны быть равны). В другом колене в области 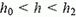, где находится только вода, давление

Ниже уровня h₀ зависимость давления от высоты дается той же формулой, что и в первом колене:

Зависимость давления в коленах трубки от высоты изображена графически на рисунке 5, б. Как видно, выше уровня h₀ давления на одинаковой высоте разные.

---

Выталкивающая сила

На тело, погруженное в жидкость, как известно, действует выталкивающая сила. Эта сила является равнодействующей сил давления жидкости на тело. Найдем, например, выталкивающую силу, действующую на кубик с ребром a целиком погруженный в жидкость плотностью ρ. Сила давления со стороны жидкости на верхнюю грань кубика равна

где h – расстояние от этой грани до поверхности жидкости (для простоты мы считаем, что плоскость верхней грани кубика параллельна поверхности жидкости). На нижнюю грань кубика действует сила

Силы давления на боковые грани кубика уравновешивают друг друга. Равнодействующая сил давлении, т.е. выталкивающая сила, равна

и направлена вертикально вверх. Мы получили закон Архимеда: выталкивающая сила равна силе тяжести, действующей на вытесненную телом жидкость.

В общем случае закон Архимеда можно доказать с помощью принципа отвердевания. Мысленно заменим погруженное тело жидкостью. Очевидно, что эта жидкость будет находиться в равновесии. Следовательно, сила тяжести, действующая на нее, уравновешена силами давления со стороны окружающей жидкости. Если теперь представить себе, что выделенная нами часть отвердела, то равновесие оставшейся части не нарушится, и поэтому не изменятся силы давления на отвердевшую жидкость. Равнодействующая этих сил будет по-прежнему равна силе тяжести.

При доказательстве мы считали, что тело целиком погружено в жидкость. Однако аналогичные рассуждения легко провести и в случае, когда только часть тела находится в жидкости (проделайте это сами). И мы опять получим, что выталкивающая сила равна силе тяжести, действующей на вытесненную телом жидкость:

где ρ – плотность жидкости, V – объем погруженной в жидкость части тела, g –ускорение свободного падения.

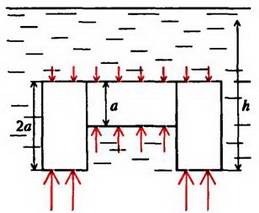
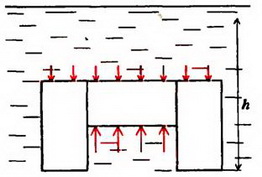
Задача 5. На дне водоема установлена П – образная конструкция из трех одинаковых балок, соединенных между собой (рис. 6). Как зависит сила давления этой конструкции на дно от уровня воды в водоеме? Рассмотрите два случая: 1) вода подтекает под опоры; 2) опоры плотно соприкасаются с дном. Балки имеют квадратное сечение со стороной a, длина балки l = 2a. Плотность материала балок ρ₀. плотность воды ρ.

а

б

в

Рис. 6

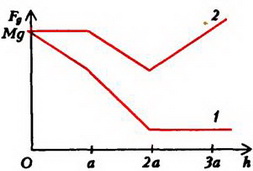
Сила давления F_д на дно определяется разностью силы тяжести конструкции 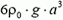 и выталкивающей силы F. В первом случае, когда вода подтекает под опоры (например, если дно водоема покрыто галькой – рисунок 6, а), справедлив закон Архимеда. Зависимость выталкивающей силы от высоты уровня воды h дается формулами:

Соответствующий график для силы F_д изображен на рисунке 6, в – он обозначен цифрой 1.

Во втором случае отсутствует давление воды на опоры снизу (рис.6, б), и пользоваться законом Архимеда уже нельзя. Для определения силы F необходимо найти равнодействующую сил давления:

F = 0 при h ≤ a,

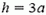
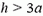
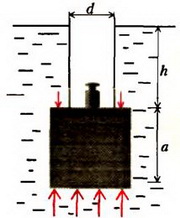
Последнее выражение обращается в нуль при  и при больших h становится отрицательным. Это означает, что при  силы давления не выталкивают конструкцию из воды, а наоборот, прижимают ее ко дну. Зависимость силы давления на дно от высоты уровня воды показана на втором графике рисунка 6, в.

Задача 6. Пробковый кубик с ребром a = 0,1 м погрузили в воду на глубину h = 0,2 м с помощью тонкостенной трубки диаметром d = 0,05 м (рис. 7). Определите, какой груз надо положить в трубку, чтобы кубик от нее оторвался. Плотность пробки ρ₀ = 200 кг/м³, плотность воды ρ = 10³ кг/м³.

Рис. 7

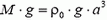
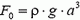
Вес груза равен разности выталкивающей силы F действующей на кубик, и силы тяжести кубика . Если бы кубик был окружен со всех сторон водой, то на него по закону Архимеда действовала бы выталкивающая сила . В нашем случае выталкивающая сила будет большей, так как на часть поверхности верхней грани кубика, «заключенную» в трубку, не действует давление воды:

где 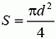 – площадь сечения трубки. Таким образом, сила тяжести грузика

Масса грузика т = 1,2 кг.

Выталкивающую силу, действующую на кубик, можно найти и другим способом. Рассмотрим кубик с трубкой как единое тело, вытесняющее объем воды

Тогда по закону Архимеда на кубик с трубкой действует выталкивающая сила

которая равна выталкивающей силе, действующей на кубик, так как равнодействующая сил давления воды на трубку равна нулю.

Жидкость в движущемся сосуде

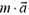
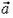
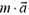
Изучим теперь равновесие жидкости в сосуде, движущемся с ускорением. По второму закону Ньютона в этом случае векторная сумма всех сил, действующих на любой выделенный элемент жидкости, должна равняться , где m – масса выделенной жидкости,  – ускорение сосуда. Но на выделенный элемент жидкости действуют сила тяжести и силы давления со стороны окружающей жидкости. Их равнодействующая и должна быть равна .

Задача 7. Сосуд с жидкостью плотностью ρ падает с ускорением a. Определите давление жидкости на глубине h и силу давления на дно сосуда. Высота уровня воды в сосуде H, площадь дна сосуда s.

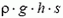
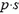
Выделим столбик жидкости высотой h с площадью основания s. На него действуют сила тяжести  и сила давления , направленная вверх. Равнодействующая этик сил создает ускорение столбика:

где 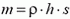 – масса столбика. Для давления p на глубине h отсюда находим

Сила давления на дно сосуда

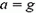
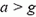
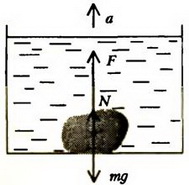
будет тем меньше, чем больше ускорение сосуда a. При  (свободное падение) сила давления жидкости обращается в ноль – наступает состояние невесомости. При  жидкость будет свободно падать с ускорением g, а сосуд – с большим ускорением, и вода вытечет из сосуда.

Задача 8. На дне сосуда с жидкостью лежит тело. Может ли тело всплыть, если сосуд начнет двигаться вверх с ускорением? Определите силу давления тела на дно сосуда, если ускорение сосуда a, плотность жидкости ρ₀, плотность тела ρ, его объем V.

На тело, лежащее на дне сосуда, действуют сила тяжести mg сила реакции дна N и выталкивающая сила F (рис. 8). Если сосуд покоится, то сумма этих сил равняется нулю. При движении сосуда с ускорением a вверх по второму закону Ньютона имеем

Рис. 8

Определим выталкивающую силу F. Аналогично решению предыдущей задачи, легко получить, что при ускоренном движении сосуда, вверх давление на глубине h дается формулой

т.е. давление в 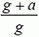 раз больше, чем в неподвижном сосуде. Соответственно будет большей и выталкивающая сила:

где 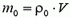 – масса вытесненной телом воды.

Подставляя это выражение в формулу второго закона Ньютона, для силы реакции дна получаем

Легко видеть, что в сосуде, движущемся с ускорением вверх, сила реакции дна всегда больше, чем в неподвижном. Поэтому тело не только не всплывает, а наоборот, сильнее прижимается ко дну.

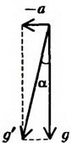
Задача 9. Сосуд с жидкостью движется горизонтально с ускорением a. Определите форму поверхности жидкости в сосуде.

Выделим горизонтальный столбик жидкости длиной l и площадью поперечного сечения S (рис. 9). По второму закону Ньютона

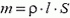
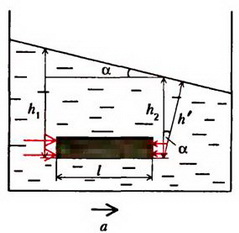
где  – масса столбика, p₁ и p₂ – давления на него слева и справа.

  

Рис. 9

Давление на глубине h определяется по обычной формуле 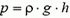 (по вертикали ускорения нет). Подставляя выражения для m и p в уравнение второго закона Ньютона, получаем

или

Но  – это разность высот точек поверхности жидкости. Мы получаем, что поверхность жидкости – плоскость, наклоненная к горизонту под углом α, причем .

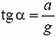
Заметим, что давление жидкости на данной высоте здесь не одно и то же. Линии равного давления параллельны поверхности жидкости. Если ввести расстояние h´ от точки до поверхности жидкости, то давление в этой точке

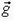
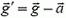
Поэтому можно сказать, что ускоренное движение сосуда эквивалентно замене ускорения свободного падения  на величину . Это утверждение в равной степени относится и к предыдущим двум задачам.

Упражнения

1. Три сосуда, имеющие формы цилиндра, усеченного конуса и перевернутого усеченного конус с одинаковыми площадями оснований и рапными объемами, доверху наполнены водой. Как соотносятся между собой силы давлении воды на дно сосудов?

2. Трубка ртутного барометра подвешена нити. Определите натяжение нити, если высота уровня ртути и трубке Н = 0,76 м, внешний диаметр трубки D = 0,02 м, внутренний d = 0,017 м. нижний конец трубки погружен в ртуть на глубину h = 0,1 м, масса трубки m = 0,3 кг, плотность ртути ρ = 1,36×10⁴ кг/м⁴. Считайте, что торцы трубки плоские.

3. Длинная вертикальная трубка погружена одним концом в сосуд с ртутью. В трубку наливают m = 0,71 кг воды, которая не вытекает из трубки. Определите изменение уровня ртути и сосуде. Диаметр сосуда D = 0,06 м, плотность ртути ρ = 1,36×10⁴ кг/м⁴. Толщиной стоим трубки пренебречь.

4. В сосуде с водой плавает кусок льда. Изменится ли уровень воды в сосуде, если лед растает? Что будет, если в лед вморожен а) кусочек свинца: б) кусочек пробки?

5. В цилиндрические сообщающиеся сосуды диаметрами D = 0,06 м и d = 0,02 м налита вода. Как изменятся уровни воды в сосудах, если в один из сосудов поместить тело массой т = 0,02 кг, которое будет плавать в воде? Плотность воды ρ = 10³ кг/м³.

6. Сосуд с водой скользит без трения по наклонной плоскости с углом наклона α. Определите, как расположится поверхность воды и сосуде.

Ответы

1. Сила давления на дно наибольшая у сосуда, имеющего форму усеченного конуса, наименьшая – у перевернутого конуса.

2.

3.

4. Если лед чистый или в него вморожен кусочек пробки, то уровень воды не изменится. Если же в лед вморожен кусочек свинца, уровень воды понизится.

5.

6. Поверхность параллельна наклонной плоскости.

В данном посте опишу теорию гидравлики простыми словами, чтобы понимать принципы поведения воды в трубе.
Как показала практика, многие работающие с системами автоматического полива люди, имеют ошибочное представление о поведении воды в трубопроводе. Так что опытным монтажникам думаю так же будет полезна данная статья.

Гидравлика изучает поведение жидкости, как в положении покоя, так и при ее движении. Грамотно спроектированная система трубопровода, значительно снижает количество проблем в течение всего жизненного цикла работы системы полива. Поддерживая скорость потока в определенных пределах, вы сможете увеличить значительно срок службы всей системы в целом.
Неверно спроектированная система с неправильными расчетами может привезти к поломке трубопровода, в случаях гидроудара и наводнению на участке.
Грамотный проектировщик учтет же при расчете все факторы, которые будут так или иначе влиять на работу системы, что позволит избежать аварий и существенных поломок в будущем.
Вдобавок неправильное проектное решение по поливу, заставит вас тратить излишнюю воду, а, следовательно, и деньги. Гидравлический анализ системы важен для уменьшения финансовых рисков, увеличения эффективности проекта и для того чтобы избавиться от излишних затрат.
Вода, подчиняясь законам гравитации, стекает в самые низкие точки поверхности и создает на этой поверхности давление. Давление -сила тяжести объема воды на данную площадь.

где Р- давление килограмм на квадратный сантиметр,
F- сила в килограммах,
А- площадь в квадратных сантиметрах
Сила давления в измеряемой точке создается столбом воды находящимся выше этой точки. Для примера на площади равной 1 см2, сила будет просто зависеть от высоты водного столба. Чем больше высота столба воды, больше веса воды действующего на дно, больше сила а, следовательно, и давление. Давление выражается, из выше сказанного, как килограмм на сантиметр квадратный или кг/см2 равный 1 бару.
Пример: На дне сосуда с 1 см2 площадью в основании и высотой водяного столба 50 см- давление будет равно:

Эта связь между давлением и изменением высоты водяного столба известно как напор в метрах. Используя эту закономерность, мы в дальнейшем сможем легко определять статическое (покоя) давление в любом месте трубопровода.

Статическое давление
Статическое давление- характеризует свойства воды когда она в покое т.е она не движется.
Динамическое давление- свойство воды, характеризующее ее при ее движении в заданном направлении по трубопроводу для обеспечения, например полива. Параметры двигающейся воды, с которыми мы будем в дальнейшем иметь дело это расход и давление.
Итак, статическое давление воды мы имеем в закрытой системе (перекрытые клапана) при неподвижном потоке воды. Значения давления в этом случае меняются только с изменением высоты водного уровня. Статическое давление показывает потенциал давления, с которым система сможет работать.
Следует запомнить, что значение статического давления на плоской местности остается постоянным и действующим с одинаковой силой во всех направлениях. Перепады высот оказывают влияние на его значение. Повышение высоты снижает, а снижение высоты повышает уровень статического давления.
Как только мы открываем, клапан или кран, вода начинает двигаться и, в этом случае, мы уже имеем дело с динамическим давлением. В этом случае появляются новые потери давления, а именно потери давления на трение по трубопроводу и местные потери (фитинги, обратные клапана, электромагнитные клапана и т.д.). Шероховатость стенок трубы, турбулентность — вот лишь та малая часть явлений, которые отрицательным образом сказываются на значении давления в трубопроводе при движении воды от магистрали к дождевателям.

Динамическое давление
Динамическое давление или «рабочее давление» отличается от статического тем, что оно зависит от потерь связанных с движением воды, и его необходимо также учитывать, как и изменение статического давления связанного с изменением высоты. Динамическое давление непосредственно связанно с расходом или тем количеством воды, которое проходит по трубе или в месте местного сопротивления.

С увеличением количества воды протекающего по трубопроводу, увеличивается скорость движения потока, увеличивая потери в давлении. Можно найти ряд таблиц с потерями на трение, учитывающих диаметры трубопровода, его материал и скорость потока воды. А также вы всегда сможете найти таблицу местных потерь давления в зависимости от расхода в каталогах производителей поливочного оборудования.

ВАЖНО!!
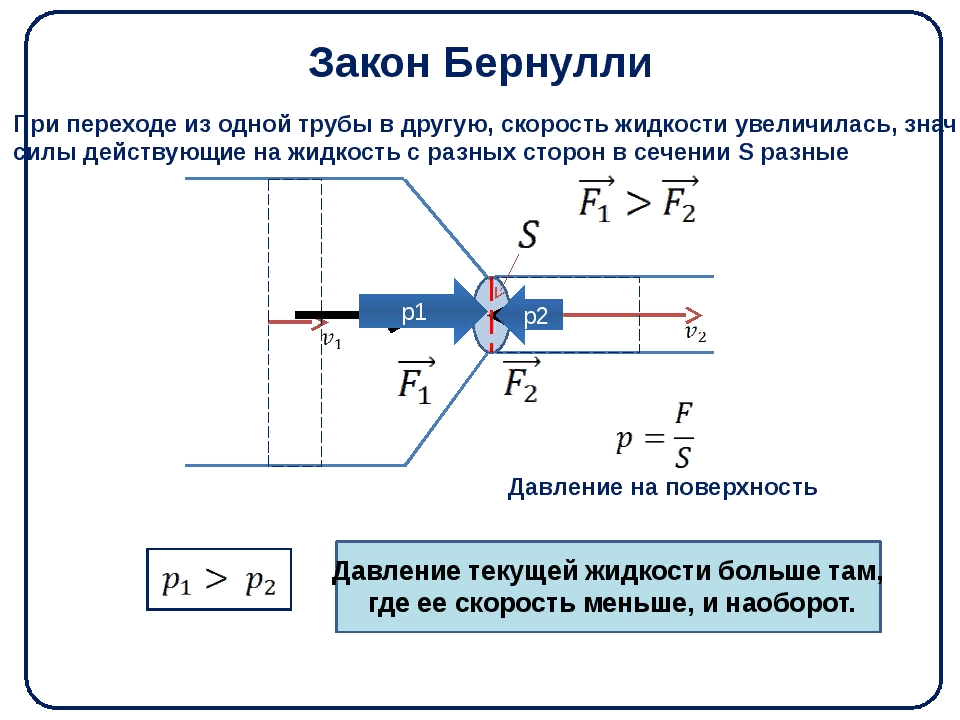
Самое частое заблуждение и стереотип даже у опытных людей, много лет работающих с системами автоматического полива- это святая вера в то, что ПРИ ПОСЛЕДОВАТЕЛЬНОМ ЗАУЖЕНИЕМ ДИАМЕТРА ТРУБОПРОВОДА- СОХРАНЯЕТСЯ ИЛИ УВЕЛИЧИВАЕТСЯ ДАВЛЕНИЕ. Это не ТАК.
Увеличение скорости течения жидкости при переходе из участка трубы с большей площадью поперечного сечения в участок трубы с меньшей площадью поперечного сечения означает, что жидкость движется с ускорением.
Согласно второму закону Ньютона, причиной ускорения является сила. Этой силой в данном случае является разность сил давления, действующих на текущую жидкость в широкой и узкой частях трубы. Следовательно, в широкой части трубы давление жидкости должно быть больше, чем в узкой.
Закон Бернулли

Скорость потока (м3/ч, л/с), значение с которым вода двигается через компоненты трубопровода системы полива, очень важный фактор в анализе гидравлического расчета. Чем быстрее вода движется по трубе, тем выше потери на трение. Слишком большие скорости потока воды могут, также быть причинами других проблем (гидравлические удары, выход из строя запорного оборудования и т.д.).
Опытным путем и с помощью расчетов установлено, что скорость потока равная 1,5 м/с, является оптимальной для движения воды по пластиковым трубам. Дальнейшее увеличение скорости потока, приводит к непропорциональному увеличению значения потерь давления, порой в разы, что может привести к неприятным последствиям, когда на отдаленных зонах вы будете иметь давление, при котором полив осуществляться будет некорректно. А также, при скоростях меньших или равных 1,5 м/с, в системе снижается вероятность появления повреждений, связанных с гидравлическим ударом.

Напомню, что в сервисе по проектированию систем автоматического полива IRRISketch весь гидравлический расчёт делается автоматически, но знать азы всё равно полезно даже опытным работникам.

Ссылка на регистрацию http://bit.ly/irrismax

💪💪💪👍👍👍

@polivmax Всё очень доступно объяснил, спасибо:+1:

@polivmax Очень интересно написано. Но возник вопрос принципиального характера.
В статье утверждается, что резкое повышение скорости потока жидкости (воды) при неправильно проведенном гидравлическом расчете может стать причиной гидравлического удара. Что актуально только в замкнутых системах, типа систем отопления. Именно поэтому в таких системах предусмотрены группы безопасности, которые уберегают замкнутые системы от явлений такого рода. Единственная часть системы полива, в которой возможно возникновение гидавлического удара- это ее напорная часть (магистраль), но напорная часть расчитавыется по максимальному расходу и выполняется трубопроволом одного сечения по всей ее длине. За исключением разве что отводов к гидрантам, но это уже обусловлено экономической целесообразностью.
А вот механизм происхождения гидравлического удара, причиной которого является резкое повышение скорости потока в локальном трубопроводе, в котором и предусмотрено постепенное заужение сечения трубопровода в системе автополива мне не понятен (если разве, что исполнитель не установит всего один дождеватель на линию).
P.S. возможность автоматического проведения гидравлического расчета есть не только в упомянутом серсисе. Такая возможность должна быть как сам-собой разумеющийся факт. В ином случае смысла в таком сервисе нет совсем никакого, разве что, рисовать разметку расположения траншей.

@Eween Всё верно по поводу единого диаметра магистрали. вот только проблема в том, что не многие даже этот диаметр подбирают верно из-за этого уже в магистрали скорость потока превышает 2,5мс. Лично встречал и не раз.
Что же касается сервиса. Опять же для новичков информация не очевидная. Многие в голом автокаде делают и считают гидравлику в ручную. Я сам до того года именно так и делал, хотя знаю кучу специализированных программ. Совсем скоро иррискетч будет считать гидравлику так как не считает ни один подобный сервис.

@Eween

Да опасности возникновения гидравлического удара в системах автополива подвергаются в первую очередь запорные механизмы, эл.магнитные клапаны, клапаны быстрого доступа к воде, и другие завтворы, латеральная часть вне зоны риска, т.к потребители воды не запираются механически. Да и на современных клапанах обеспечена защита от гидроудара благодаря их плавному закрытию. Но никто не отменял кавитации в зонах с резким увеличением скорости потока (на тех самых заужениях с переходом диаметра). Поэтому все-таки не превышать скорость потока очень даже полезно, учитывая то что все собирается зачастую на компрессионых соединениях, которые не так надёжны как паечные. Вообщем, как говорится, соблюдайте скоростной режим:blush:

@filprots Именно так. не однократно видел (даже на видео заснял) как хвалёный ирритековский фитинг от гидроудара срывает на отводе насоса после закрытия гидранта (водяной розетки). так кто в моменте свыше 30атм как я понимаю может создаваться при гидроударе

На мое удивление, до сих пор, БОЛЬШОЕ кол-во профессионалов с пеной у рта пытаются доказать, что заужением диаметра они повышают давление в системе.

@polivmax Теперь мне кажется, что данная статья направлена не ликвидацию безграмотности в среде поливщиков, а на продвижение названанной программы. А про то что, эта программа будет считать так, как ни одна другая, это мне напоминает презентацию K- Pain. Там мы тоже слышали, что они горы свернут))))

@Eween Именно на ЛИКБЕЗ. Упоминание программы, которая, по моему мнению, адекватнее и удобнее аналогов — это то же ликбез. В любом случае это обмен опытом, а право выбора остаётся за каждым.
Так же никто не мешает рекомендовать другие программы, которые считает нужным.

@Eween те в школе в 10 классе нас задолго готовили к появлению Irrisketch?!)) вот это поворот :astonished: )))))))))))))))

• @polivmax процитировал лишь некоторые основы гидродинамики, на примере закона Бернулли. Да, многие программы, тот же ProContractor, RainCAD могут просчитать потери давления в линии на магистрали и узлах, но речь ведь не об этом. Речь о том что неправильный расчет приводит к преждевременному износу узлов системы, сокращая ее фактический срок эксплуатации. Многие специалисты даже не стесняются: выкладывают мп ротатор на котором 5-6 атмосфер, говорят о какой то экономической целесообразности, преимуществах мп перед остальными соплами а по факту что мы имеем — огромный перерасход воды, и дороговизну замены этих сопел, аргумент таких специалистов один — НУ ГАЗОН ЖЕ ЗЕЛЕНЫЙ — значит мы все правильно делаем)

Одно дело когда программа автоматически все делает за тебя, другое дело это понимание процесса. Знание элементарных законов — только возвысит вас в глазах вашего заказчика как специалиста. У меня такие случае были — на объекте установлен был скважинный насос и надо было проверить его хар-ки. Хорошо что у меня всегда с собой расходомер. Произвел замеры и установил рабочую точку в 2,5бар и 33л/мин.. Заказчик меня уверял в том что если из системы убрать гидроаккумулятор то давление возрастет (учитывая даже то, замеры я производил до аккумулятора прямо на выходе из скважины). Да так напористо и уже на повышенных тонах доказывал, что я даже немного стал сомневаться в своей правоте, но не отступил и оказался прав. Получил респект от заказчика и вот уже третий объект сотрудничаем, думаю если бы я тогда слился, заказчик все равно оказался бы не прав — но мнение обо мне у него уже было бы как о сомнительном специалисте.

@polivmax Про чреватость большой скорости потока понятно, но как-то не раскрыта тема меньшей скорости потока и что будет если везде будут как в магистрали, так и в веткахлиниях большие диаметры(типа на всякий пожарный) — скорость потока малая, давление хорошее. Как забабахать всё 40-50 диаметром — точно не ошибёшься!

@Lema а как же гидроудар?

Пользователь @Sergei написал в Основные законы гидравлики:

@Lema а как же гидроудар?

Чем больше диаметр труб, тем ниже скорость потока воды, и, соответственно, гидроудар.
Хотите гидроудар? Повысьте скорость потока в трубах. Хотите повысить скорость потока? Заужайте диаметр.
Ещё гидроудар может быть от резкого скачка давления. От чего в данном случае может быть скачок в трубах большого диаметра как-то не понятно.

@Lema Я не очень понял в чём суть вопроса и вопрос ли это?
Если я правильно понял, то с запасом можно хоть 110 диаметр заложить там, где и 32 подойдёт. Тут главный вопрос в экономической составляющей.

Пользователь @polivmax написал в Основные законы гидравлики:

Я не очень понял в чём суть вопроса и вопрос ли это?

Да, конечно вопрос.
Я про экономическую составляющую понимаю. Конечно труба большего диаметра дороже, но, вопрос в другом, чревато ли ещё чем-то завышение диаметра кроме цены и удобстваскорости монтажа?
Просто может я чего-то не знаю.

@Lema При скорости потока менее 0,2 мс есть вероятность застаивания воды и отложений в трубах

@Lema труба большего диаметра при размотке сильнее бьет по голове)))))

Постановка задачи

Гидравлический расчёт при разработке проекта трубопровода направлен на определение диаметра трубы и падения напора потока носителя. Данный вид расчёта проводится с учетом характеристик конструкционного материала, используемого при изготовлении магистрали, вида и количества элементов, составляющих систему трубопроводов(прямые участки, соединения, переходы, отводы и т. д.), производительности,физических и химических свойств рабочей среды.

Многолетний практический опыт эксплуатации систем трубопроводов показал, что трубы, имеющие круглое сечение, обладают определенными преимуществами перед трубопроводами, имеющими поперечное сечение любой другой геометрической формы:

• минимальное соотношением периметра к площади сечения, т.е. при равной способности, обеспечивать расход носителя, затраты на изолирующие и защитные материалы при изготовлении труб с сечением в виде круга, будут минимальными;
• круглое поперечное сечение наиболее выгодно для перемещения жидкой или газовой среды сточки зрения гидродинамики, достигается минимальное трение носителя о стенки трубы;
• форма сечения в виде круга максимально устойчива к воздействию внешних и внутренних напряжений;
• процесс изготовления труб круглой формы относительно простой и доступный.

Подбор труб по диаметру и материалу проводится на основании заданных конструктивных требований к конкретному технологическому процессу. В настоящее время элементы трубопровода стандартизированы и унифицированы по диаметру. Определяющим параметром при выборе диаметра трубы является допустимое рабочее давление, при котором будет эксплуатироваться данный трубопровод.

Основными параметрами, характеризующими трубопровод являются:

• условный (номинальный) диаметр – D_N;
• давление номинальное – P_N;
• рабочее допустимое (избыточное) давление;
• материал трубопровода, линейное расширение, тепловое линейное расширение;
• физико-химические свойства рабочей среды;
• комплектация трубопроводной системы (отводы, соединения, элементы компенсации расширения и т.д.);
• изоляционные материалы трубопровода.

Условный диаметр (проход) трубопровода (D_N) – это условная  безразмерная величина, характеризующая проходную способность трубы, приблизительно равная ее внутреннему диаметру. Данный параметр учитывается при осуществлении подгонки сопутствующих изделий трубопровода (трубы, отводы, фитинги и др.).

Условный диаметр может иметь значения от 3 до 4000 и обозначается: DN 80.

Условный проход по числовому определению примерно соответствует реальному диаметру определенных отрезков трубопровода. Численно он выбран таким образом, что пропускная способность трубы повышается на 60-100% при переходе от предыдущего условного прохода к последующему.Номинальный диаметр выбирается по значению внутреннего диаметра трубопровода. Это то значение, которое наиболее близко к реальному диаметру непосредственно трубы.

Давление номинальное (PN) – это безразмерная величина, характеризующая максимальное давление рабочего носителя в трубе заданного диаметра, при котором осуществима длительная эксплуатация трубопровода при температуре 20°C.

Значения номинального давления были установлены на основании продолжительной практики и опыта эксплуатации: от 1 до 6300.

Номинальное давление для трубопровода с заданными характеристиками определяется по ближайшему к реально создаваемому в нем давлению. При этом,вся трубопроводная арматура для данной магистрали должна соответствовать тому же давлению. Расчет толщины стенок трубы проводится с учетом значения номинального давления.

Основные положения гидравлического расчета

Рабочий носитель (жидкость, газ, пар), переносимый проектируемым трубопроводом, в силу своих особых физико-химических свойств определяет характер течения среды в данном трубопроводе. Одним из основных показателей характеризующих рабочий носитель, является динамическая вязкость, характеризуемая коэффициентом динамической вязкости – μ.

Инженер-физик Осборн Рейнольдс (Ирландия), занимавшийся изучением течения различных сред, в 1880 году провел серию испытаний,  по результату которых было выведено понятие критерия Рейнолдса (Re) – безразмерной величины, описывающей характер потока жидкости в трубе. Расчет данного критерия проводится по формуле:

Критерий Рейнольдса (Re) дает понятие о соотношении сил инерции к силам вязкого трения в потоке жидкости. Значение критерия характеризует изменение соотношения указанных сил, что, в свою очередь, влияет на характер потока носителя в трубопроводе. Принято выделять следующие режимы потока жидкого носителя в трубе в зависимости от значения данного критерия:

• ламинарный поток (Re<2300), при котором носитель-жидкость движется тонкими слоями, практически не смешивающимися друг с другом;
• переходный режим (2300<Re<4000), который характеризуется нестабильной структурой потока, когда отдельные слои жидкости перемешиваются;
• турбулентный поток (Re>4000) – устойчивый режим, при котором в каждой отдельной точке потока происходит изменение его направления и скорости, что в итоге приводит к выравниванию скорости движения потока по объему трубы.

Критерий Рейнольдса зависит от напора, с которым насос перекачивает жидкость, вязкости носителя при рабочей температуре и геометрических размеров используемой трубы (d, длина). Данный критерий является параметром подобия для течения жидкости,поэтому, используя его, можно осуществлять моделирование реального технологического процесса в уменьшенном масштабе, что удобно при проведении испытаний и экспериментов.

Проводя расчеты и вычисления по уравнениям, часть заданных неизвестных величин можно взять из специальных справочных источников. Профессор, доктор технических наук Ф. А. Шевелев разработал ряд таблиц для проведения точного расчета пропускной способности трубы. Таблицы включают значения параметров, характеризующих как сам трубопровод (размеры, материалы), так и  их взаимосвязь с физико-химическими свойствами носителя. Кроме того, в литературе приводится таблица приближенных значений скоростей движения потока жидкости, пара,газа в трубе различного сечения.

Подбор оптимального диаметра трубопровода

Определение оптимального диаметра трубопровода – это сложная производственная задача, решение которой зависит от совокупности различных взаимосвязанных условий (технико-экономические, характеристики рабочей среды и материала трубопровода, технологические параметры и т.д.). Например, повышение скорости перекачиваемого потока приводит к уменьшению диаметра трубы, обеспечивающей заданный условиями процесса расход носителя, что влечет за собой снижение затрат на материалы, удешевлению монтажа и ремонта магистрали и т.д. С другой стороны, повышение скорости потока  приводит к потере напора, что требует дополнительных энергетических и финансовых затрат на перекачку заданного объема носителя.

Значение оптимального диаметра трубопровода рассчитывается по преобразованному уравнению неразрывности потока с учетом заданного расхода носителя:

 При гидравлическом расчете расход перекачиваемой жидкости чаще всего задан условиями задачи. Значение скорости потока перекачиваемого носителя определяется, исходя из свойств заданной среды и соответствующих справочных данных (см. таблицу).

Преобразованное уравнение неразрывности потока для расчета рабочего диаметра трубы имеет вид:

Расчет падения напора и гидравлического сопротивления

Полные потери напора жидкости включают в себя потери на преодоление потоком всех препятствий: наличие насосов, дюкеров, вентилей, колен, отводов, перепадов уровня при течении потока по трубопроводу, расположенному под углом и т.д. Учитываются потери на местные сопротивления, обусловленные свойствами используемых материалов.

Другим важным фактором, влияющим на потери напора, является трение движущегося потока о стенки трубопровода, которое характеризуется коэффициентом гидравлического сопротивления.

Значение коэффициента гидравлического сопротивления λзависит от режима движения потока и шероховатости материала стенок трубопровода. Под шероховатостью понимают дефекты и неровности внутренней поверхности трубы. Она может быть абсолютной и относительной. Шероховатость различна по форме и неравномерна по площади поверхности трубы. Поэтому в расчетах используется понятие усредненной шероховатости с поправочным коэффициентом (k1). Данная характеристика для конкретного трубопровода зависит от материала, продолжительности его эксплуатации, наличия различных коррозионных дефектов и других причин. Рассмотренные выше величины являются справочными.

Количественная связь между коэффициентом трения, числом Рейнольдса и шероховатостью определяется диаграммой Муди.

Для вычисления коэффициента трения турбулентного движения потока также используется уравнение Коулбрука-Уайта, с использованием которого возможно наглядное построение графических зависимостей, по которым определяется коэффициент трения:

В расчётах используются и другие уравнения приблизительного расчета потерь напора на трение. Одним из наиболее удобных и часто используемых в этом случае считается формула Дарси-Вейсбаха. Потери напора на трение рассматриваются как функция скорости жидкости от сопротивления трубы движению жидкости, выражаемой через значение шероховатости поверхности стенок трубы: 

Потери давления по причине трения для воды рассчитывают по формуле Хазена — Вильямса:

Расчет потерь давления

Рабочее давление в трубопроводе – это на большее избыточное давление, при котором обеспечивается заданный режим технологического процесса. Минимальное и максимальное значения давления, а также физико-химические свойства рабочей среды, являются определяющими параметрами при расчёте расстояния между насосами, перекачивающими носитель, и производственной мощности.

Расчет потерь на падение давления в трубопроводе осуществляют по уравнению:

Примеры задач гидравлического расчета трубопровода с решениями

Задача 1

В аппарат с давлением 2,2 бар по горизонтальному трубопроводу с эффективным диаметром 24 мм из открытого хранилища насосом перекачивается вода. Расстояние до аппарата составляет 32 м. Расход жидкости задан – 80 м³/час. Суммарный напор составляет 20 м. Принятый коэффициент трения равен 0,028.

Рассчитайте потери напора жидкости на местные сопротивления в данном трубопроводе.

Исходные данные:

Расход Q = 80 м³/час = 80·1/3600 = 0,022 м³/с;

эффективный диаметр d = 24 мм;

длина трубы l = 32 м;

коэффициент трения λ = 0,028;

давление в аппарате Р = 2,2 бар = 2,2·10⁵ Па;

общий напор Н = 20 м.

Решение задачи:

Скорость потока движения воды в трубопроводе рассчитывается по видоизмененному уравнению:

w=(4·Q) / (π·d²) = ((4·0,022) / (3,14·[0,024]²)) = 48,66 м/с

Потери напора жидкости в трубопроводе на трение определяются по уравнению:

H_Т = (λ·l) / (d·[w²/(2·g)]) = (0,028·32) / (0,024·[48,66]²) / (2·9,81) = 0,31 м

Общие потери напора носителя рассчитываются по уравнению и составляют:

h_п = H — [(p₂-p₁)/(ρ·g)] — H_г = 20 — [(2,2-1)·10⁵)/(1000·9,81)] — 0 = 7,76 м

Потери напора на местные сопротивления определяется как разность:

7,76 — 0,31=7,45 м

Ответ: потери напора воды на местные сопротивления составляют 7,45 м.

Задача 2

По горизонтальному трубопроводу центробежным насосом транспортируется вода. Поток в трубе движется со скоростью 2,0 м/с. Общий напор составляет 8 м.

Найти минимальную длину прямого трубопровода, в центре которого установлен один вентиль. Забор воды осуществляется из открытого хранилища. Из трубы вода самотеком изливается в другую емкость. Рабочий диаметр трубопровода равен 0,1 м. Относительная шероховатость принимается равной 4·10^-5.

Исходные данные:

Скорость потока жидкости W = 2,0 м/с;

диаметр трубы d = 100 мм;

общий напор Н = 8 м;

относительная шероховатость 4·10^-5.

Решение задачи:

Согласно справочным данным в трубе диаметром 0,1 м коэффициенты местных сопротивлений для вентиля и выхода из трубы составляют соответственно 4,1 и 1.

Значение скоростного напора определяется по соотношению:

w²/(2·g) = 2,0²/(2·9,81) = 0,204 м

Потери напора воды на местные сопротивления составят:

∑ζ_МС·[w²/(2·g)] = (4,1+1)·0,204 = 1,04 м

Суммарные потери напора носителя на сопротивление трению и местные сопротивления рассчитываются по уравнению общего напора для насоса (геометрическая высота Hг по условиям задачи равна 0):

h_п = H — (p₂-p₁)/(ρ·g) — = 8 — ((1-1)·10⁵)/(1000·9,81) — 0 = 8 м

Полученное значение потери напора носителя на трение составят:

8-1,04 = 6,96 м

Рассчитаем значение числа Рейнольдса для заданных условий течения потока (динамическая вязкость воды принимается равной 1·10^-3 Па·с,  плотность воды – 1000 кг/м³):

Re = (w·d·ρ)/μ = (2,0·0,1·1000)/(1·10^-3) = 200000

Согласно рассчитанному значению Re, причем 2320 <Re< 10/e, по справочной таблице рассчитаем коэффициент трения (для режима гладкого течения):

λ = 0,316/Re^0,25 = 0,316/200000^0,25 = 0,015

Преобразуем уравнение и найдем требуемую длину трубопровода из расчетной формулы потерь напора на трение:

l = (H_об·d) / (λ·[w²/(2g)]) = (6,96·0,1) / (0,016·0,204) = 213,235 м

Ответ:требуемая длина трубопровода составит 213,235 м.

Задача 3

В производстве транспортируют воду при рабочей температуре 40°С с производственным расходом Q = 18 м³/час. Длина прямого трубопровода l = 26 м, материал — сталь. Абсолютная шероховатость (ε) принимается для стали по справочным источникам и составляет 50 мкм. Какой будет диаметр стальной трубы, если перепад давления на данном участке не превысит Δp = 0,01 мПа (ΔH = 1,2 м по воде)? Коэффициент трения принимается равным 0,026.

Исходные данные:

Расход Q = 18 м³/час = 0,005 м³/с;

длина трубопровода l=26 м;

для воды ρ = 1000 кг/м³, μ = 653,3·10^-6 Па·с (при Т = 40°С);

шероховатость стальной трубыε = 50 мкм;

коэффициент трения λ = 0,026;

Δp=0,01 МПа;

ΔH=1,2 м.

Решение задачи:

Используя форму уравнения неразрывности W=Q/F и уравнение площади потока F=(π·d²)/4 преобразуем выражение Дарси – Вейсбаха:

∆H = λ·l/d·W²/(2·g) = λ·l/d·Q²/(2·g·F²) = λ·[(l·Q²)/(2·d·g·[(π·d²)/4]²)] = =(8·l·Q²)/(g·π²)·λ/d⁵ = (8·26·0.005²)/(9,81·3,14²)· λ/d⁵ = 5,376·10^-5·λ/d⁵

Выразим диаметр:

d⁵ = (5,376·10^-5·λ)/∆H = (5,376·10^-5·0,026)/1,2 = 1,16·10^-6

d = ⁵√1,16·10^-6 = 0,065 м.

Ответ: оптимальный диаметр трубопровода составляет 0,065 м.

Задача 4

Проектируются два трубопровода для транспортировки невязкой жидкости с предполагаемой производительностью Q₁ = 18 м³/час и Q₂ = 34 м³/час. Трубы для обоих трубопроводов должны быть одного диаметра.

Определите эффективный диаметр труб d, подходящих под условия данной задачи.

Исходные данные:

Q₁ = 18 м³/час;

Q₂ = 34 м³/час.

Решение задачи:

Определим возможный интервал оптимальных диаметров для проектируемых трубопроводов, воспользовавшись преобразованным видом уравнения расхода:

d = √(4·Q)/(π·W)

Значения оптимальной скорости потока найдем из справочных табличных данных. Для невязкой жидкости скорости потока составят 1,5 – 3,0 м/с.

Для первого трубопровода с расходом Q₁ = 18 м³/час возможные диаметры составят:

d_1min = √(4·18)/(3600·3,14·1,5) = 0,065 м

d_1max = √(4·18)/(3600·3,14·3.0) = 0,046 м

Для трубопровода с расходом 18 м³/час подходят трубы с диаметром поперечного сечения от 0,046 до 0,065 м.

Аналогично определим возможные значения оптимального диаметра для второго трубопровода с расходом Q₂ = 34 м³/час:

d_2min = √(4·34)/(3600·3,14·1,5) = 0,090 м

d_2max = √(4·34)/(3600·3,14·3) = 0,063 м

Для трубопровода с расходом 34 м³/час возможные оптимальные диаметром могут быть от 0,063 до 0,090 м.

Пересечение двух диапазонов оптимальных диаметров находится в интервале от 0,063 м до 0,065 м.

Ответ: для двух трубопроводов подходят трубы диаметром 0,063–0,065 м.

Задача 5

В трубопроводе диаметром 0,15 м при температуре Т = 40°C движется поток воды производительностью 100 м³/час. Определите режим течения потока воды в трубе.

Дано:

диаметр трубы d = 0,25 м;

расход Q = 100 м³/час;

μ = 653,3·10^-6 Па·с (по таблице при Т = 40°С);

ρ = 992,2 кг/м³ (по таблице при Т = 40°С).

Решение задачи: 

Режим течения потока носителя определяется по значению числа Рейнольдса (Re). Для расчета Re определим скорость движения потока жидкости в трубе (W), используя уравнение расхода:

W = Q·4/(π·d²) = [100/3600] · [4/(3,14·0,25²)] = 0,57 м/c

Значение числа Рейнольдса определим по формуле:

Re = (ρ·W·d)/μ = (992,2·0,57·0,25) / (653,3·10^-6) = 216422

Критическое значение критерия Re_кр по справочным данным равно 4000. Полученное значение Re больше указанного критического, что говорит о турбулентном характере течения жидкости при заданных условиях.

Ответ: режим потока воды – турбулентный.