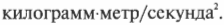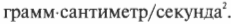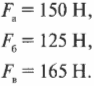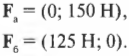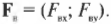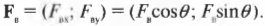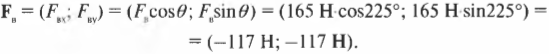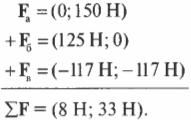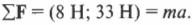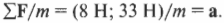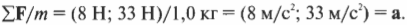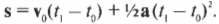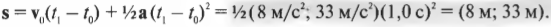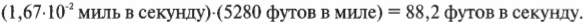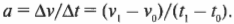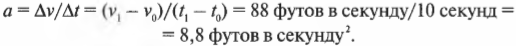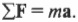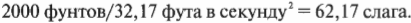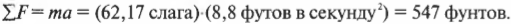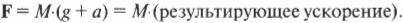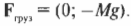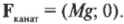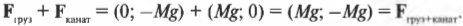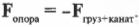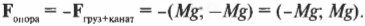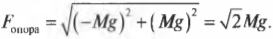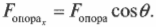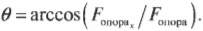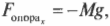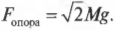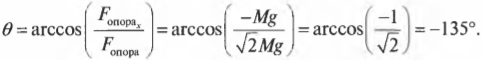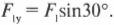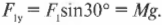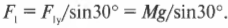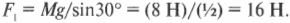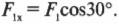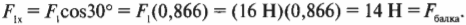Как найти силу если есть перемещение

В этой главе…

• Прилагаем силу
• Открываем три закона Ньютона
• Используем векторы силы для законов Ньютона

В этой главе описываются знаменитые три закона Ньютона. Вероятно, вам уже приходилось встречаться с разными формулировками этих законов, например “всякому действию всегда есть равное ему противодействие”. Эта формулировка не совсем верна, поскольку “всякой силе всегда есть равная ей противоположная сила”. В этой главе будут прояснены различия между этими формулировками. Законы Ньютона в данной главе используются для фокусировки вашего внимания на силах и их влиянии на окружающий нас мир.

Форсируем тему

В окружающем нас мире нельзя избежать встречи с силами: силы используются для открытия двери, нажатия клавиш клавиатуры, управления автомобилем, подъема по ступенькам лестницы к Статуе Свободы, вытаскивания кошелька из кармана, разговора и даже для дыхания. Силы незримо присутствует всюду: во время пешеходной прогулки, катании на коньках, пережевывании хот-дога, открывании бутылки или моргании ресниц вашей ненаглядной спутницы. Сила неразрывно связана с движением объектов, а физика помогает понять, как эта связь работает.

Сила — это на самом деле довольно забавная тема. Как и другие физические темы, она кажется сложной только до настоящего знакомства с ней. Как наши старые “друзья”, перемещение, скорость и ускорение (см. главы 3 и 4), сила является вектором, т.е. имеет величину и направление.

Сэр Исаак Ньютон первым включил силу, массу и ускорение в одно уравнение в XVII веке. (Помните исторический анекдот с падением яблока на его голову, в результате чего он якобы придумал, как математически описать силу тяготения. Подробнее об этом рассказывается в главе 6, где Ньютон также является одним из основных действующих лиц.)

Законы Ньютона и скорость света

Законы Ньютона были пересмотрены Альбертом Эйнштейном в его теории относительности. В ней было показано, что законы Ньютона не выполняются для движения со скоростью, близкой к скорости света. Основная идея теории относительности заключается в том, что скорость света является наибольшей возможной скоростью. Это значит, что любое взаимодействие может происходить только с этой или меньшей скоростью. Следовательно, при приближении к этой скорости нужно учитывать изменяющийся характер взаимодействия; Например, измерение длины ракеты, движущейся со скоростью света, будет отличаться от измерения длины неподвижной ракеты. Как будет показано в главе 21, теория относительности Эйнштейна в значительной степени изменила представленный Ньютоном взгляд на мир и его законы.

Как часто происходит со многими физическими открытиями, Ньютон сначала внимательно наблюдал за поведением объектов, мысленно моделировал его, а затем выразил в математической форме. Зная основные сведения о векторах (которые изложены в главе 4), эта математика не вызовет у вас никаких трудностей.

Ньютон описал свою модель с помощью трех утверждений, которые теперь называются законами Ньютона. Однако нужно помнить, что на самом деле это не окончательные “законы природы”, ведь физики могут создавать лишь модели природы, которые часто впоследствии пересматриваются и уточняются.

Первый закон Ньютона

Барабанную дробь, пожалуйста! Законы Ньютона описывают силы и движение, а его первый закон гласит: “Объект находится в состоянии равновесия или прямолинейном движении с постоянной скоростью, если не подвергается внешнему воздействию”. Нужен перевод? Если вы не прилагаете силу к объекту в покое или “постоянном” движении, то он останется в покое или таком же движении по прямой. Причем вечно!

Например, при игре в хоккей шайба после удара движется к воротам по прямой, скользя по льду почти без трения. В случае удачи соперник не сможет зацепить шайбу своей клюшкой, т.е. не сможет изменить “постоянное” движение шайбы по прямой (и воспрепятствовать голу).

В повседневной жизни объекты не движутся так беспрепятственно, как в случае с шайбой на льду. Большинство окружающих нас объектов испытывает силу трения. Например, при скольжении кофейной чашки по гладкому столу она постепенно замедляет свое скольжение и останавливается (иногда с проливанием кофе не стоит чересчур упражняться, ибо вы рискуете испачкаться или ошпариться горячим кофе). Это совсем не значит, что первый закон Ньютона неверен. Наоборот, именно сила трения принуждает чашку изменить свое движение и остановиться.

Выражение “если не прилагать никакого действия к постоянно движущемуся объекту, он будет двигаться вечно” выглядит так же ужасно, как идея “вечного двигателя”. Однако полностью избавиться от внешнего воздействия сил невозможно, даже если объект находится в межзвездном пространстве. Даже на объекты в самых далеких уголках космоса оказывает воздействие (пусть даже очень слабое) масса других объектов Вселенной. А это значит, что на любое движение всегда оказывается внешнее воздействие, потому вечное постоянное движение в принципе невозможно.

Первый закон Ньютона утверждает лишь то, что единственным способом изменения движения является приложение внешней силы. Иначе говоря, сила является причиной движения. Кроме того, он гласит, что движущийся объект стремится оставаться в движении, что приводит к идее инерции.

Поддерживаем движение: инерция и масса

Инерция — это естественная тенденция объекта оставаться в покое или в движении с постоянной скоростью вдоль прямой линии. Инерция вызвана массой, а масса объекта является мерой инерции. Чтобы привести объект в движение, т.е. изменить его текущее состояние движения, необходимо приложить силу для преодоления инерции.

Представьте себе причал с маленькой шлюпкой и большим танкером с нефтью. Если попробовать толкнуть их ногой, то поведение этих судов будет разным. Шлюпка заскользит по водной глади, а танкер едва “вздрогнет” (да и для этого потребуется невероятно сильный толчок!). Дело в том, что они обладают совершенно разной массой и потому разной инерцией. В ответ на одинаковую силу объект с малой массой (и малой инерцией) ускорится в большей мере, чем объект с малой массой и большей инерцией.

Инерция, т.е. тенденция массы сохранять неизменность текущего состояния движения, иногда может представлять проблему. Например, в рефрижераторе тяжелые туши мороженного мяса подвешены к потолку кузова. Если рефрижератор войдет в крутой поворот на большой скорости, то туши по инерции начнут раскачиваться, как маятники, и их трудно будет остановить. Часто неопытные водители не учитывают инерцию туш мяса, и это приводит к печальным последствиям, например к опрокидыванию машины.

Поскольку масса обладает инерцией, то она сопротивляется изменению движения. Именно поэтому нам приходится прилагать силу для ускорения своего движения. Масса связывает силу и ускорение.

Измеряем массу

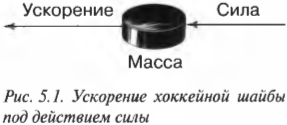
В разных системах измерения физических величин для указания массы (а значит, и инерции) используются разные единицы. В системе СГС используется грамм, а в системе СИ — килограмм, который содержит 1000 грамм.

А какая единица используется в Английской системе мер на основе фута-фунта- дюйма? Наберитесь мужества: в ней используется единица “слаг”, которая эквивалентна 14,5939 килограмма.

Учтите, что масса не равна весу. Масса — это мера инерции, а вес — это сила, которую оказывает сила притяжения Земли, измеренная на ее поверхности. Например, в Английской системе мер на основе фута-фунта-дюйма слаг имеет вес около 32 фунтов.

Леди и джентльмены, встречайте второй закон Ньютона!

Первый закон Ньютона очень и очень серьезен, но не выражается в математической формулировке, которая так необходима физикам. Потому Ньютон предложил свой второй закон: “если результирующая сила ​( sum!F )​ действует на объект массы ​( m )​, то ускорение ​( a )​ объекта можно вычислить по формуле ​( sum!F=ma )​”. В “переводе” это значит: сила равна массе, умноженной на ускорение. Символ ​( sum )​ означает суммирование, а значит, точнее говоря, закон гласит: суммарная, или результирующая, сила равна массе, умноженной на ускорение. (С точки зрения физики процесса, а не формальной математики, ускорение является следствием действия силы, а не наоборот. Потому логичнее было бы сформулировать второй закон Ньютона так: ​( a=sum!F/m )​, т.е. ускорение объекта прямо пропорционально результирующей силе на него и обратно пропорционально массе.)

Согласно первому закону Ньютона, движущееся тело остается в прямолинейном движении с постоянной скоростью, если на него не действует сила. Получается, что на самом деле он является частным случаем второго закона Ньютона, когда ​( sum!F=0 )​. Ведь в таком случае ускорение равняется нулю, о чем говорится в первом законе Ньютона. Взгляните на хоккейную шайбу на рис. 5.1: шайба ускоряется, пока на нее действует сила.

Попробуйте применить уже полученные знания физики в этом примере. Действительно, если даже на долю секунды с помощью клюшки применить силу к шайбе, то она ускорится и, несомненно, попадет в сетку! В данном примере сила применена к клюшке с определенной массой, которая ускорилась и придала это ускорение шайбе.

Чему равно это ускорение? Эта величина зависит не только от единиц измерения массы, но и от единиц измерения силы.

Выбираем единицы измерения силы

Итак, в каких единицах выражается сила? Поскольку ( sum!F=ma ), то, например, в системе СИ сила выражается следующим образом:

Поскольку большинство людей считают эту единицу чересчур сложной, то в системе СИ используется специальная единица — ньютон (угадайте, в честь кого?). Сокращенно “ньютон” записывается как Н. В системе СГС сила выражается следующим образом:

Это тоже довольно неуклюжая единица, и в системе СГС для силы предложено использовать особую единицу — дина, причем 1 ньютон равен 10⁵ динам.

Еще проще выражается единица сила в Английской системе мер на основе фута-фунта-дюйма-секунды — фунт, который выражается следующим образом:

и равен 4,48 ньютонам.

Вычисляем результирующую силу

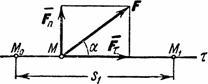
В большинстве учебников вместо полной записи ( sum!F=ma ) используется сокращенная — ( F=ma ), где под ​( F )​ подразумевается результирующая сила. Объект реагирует именно на результирующую силу, которая является суммой всех сил-векторов. Например, на рис. 5.2 показан мяч для игры в гольф и действующие на него силы. Как и в каком направлении будет двигаться мяч?

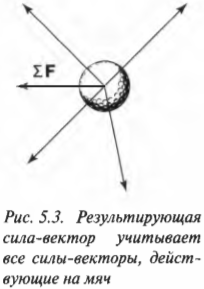
Поскольку во втором законе Ньютона говорится о результирующей силе, то задача упрощается. Все, что нужно сделать, так это сложить все силы-векторы для получения результирующей силы-вектора, как показано на рис. 5.3. Далее, для определения характера движения мяча нужно применить формулу ( sum!F=ma ).

Вычисляем перемещение по известному времени, массе и действующим силам

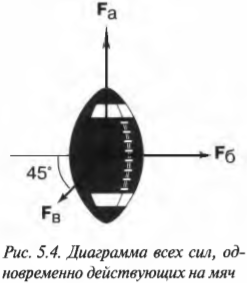
Допустим, что во время игры в мяч вы заинтересовались силами, действующими на мяч. Вот в одной из игровых ситуаций три игрока одновременно пытаются завладеть мячом и действуют на него тремя силами, как показано на рис. 5.4.

Схема на рис. 5.4 в физике называется диаграммой сил, действующих на тело. С ее помощью можно определить компоненты сил и результирующую силу.

Допустим, что с риском для жизни во имя науки вам удалось определить величины сил игроков:

Допустим, что масса мяча точно равна 1,0 кг. Вопрос звучит так: где будет мяч через 1 секунду? Вот те этапы, которые нужно пройти, чтобы вычислить перемещение мяча по известному времени движения и ускорению (которое еще нужно определить по известной массе и действующим силам), т.е. дать окончательный ответ на этот вопрос.

1. Найти результирующую силу ( sum!F) с помощью операции сложения векторов (подробное описание этой операции приводится в главе 4), складывая все силы, действующие на объект.
2. Определить вектор ускорения по формуле ( sum!F=ma ).
3. Вычислить пройденное расстояние за заданное время по формуле ( mathbf{s}=mathbf{v_0}(t_1-t_0)+{}^1!/!_2mathbf{a}(t_1-t_0)^2 ) (см. главу 3, где подробно описывается эта формула).

Пора подставлять числа и доставать калькулятор. Итак, для связи силы, массы и ускорения нужно, прежде всего, определить результирующую силу. Для этого нужно разложить на компоненты все векторы-силы на рис. 5.4, а потом сложить компоненты, чтобы получить компоненты вектора результирующей силы (более подробно операция разбиения вектора на компоненты приводится в главе 4).

Компоненты векторов ​( mathbf{F_а} )​ и ( mathbf{F_б} ) можно определить очень легко, поскольку вектор ( mathbf{F_а} ) ориентирован вдоль положительного направления оси Y, а вектор ( mathbf{F_б} ) — вдоль положительного направления оси X. Это значит, что компоненты этих векторов выражаются следующим образом:

Компоненты вектора ( mathbf{F_в} ) определяются немного сложнее, поскольку нам все придется их вычислить:

Вектор ( mathbf{F_в} ) направлен под углом 45° по отношению к отрицательному направлению оси Х, как показано на рис. 5.4, и под углом ​( theta )​ = 180°+45°=225° к положительному направлению оси X. Тогда компоненты вектора ( mathbf{F_в} ) определяются следующим образом:

После подстановки чисел получим:

Обратите внимание на знак “минус” — оба компонента вектора ( mathbf{F_в} ) отрицательные. Полученный результат всегда можно быстро проверить на непротиворечивость. Вектор ( mathbf{F_в} ) направлен вниз и вправо, т.е. вдоль отрицательных направлений оси X и Y. Это значит, что оба компонента ​( F_{вx} )​ и ( F_{вy} ) должны быть отрицательными. Мне доводилось видеть людей, которые не могли правильно определить знак компонентов вектора, поскольку они не умели выполнять такую простую проверку непротиворечивости.

Всегда сравнивайте знаки компонентов векторов с фактическим направлением вдоль осей. Такая простая и быстрая проверка позволяет избежать многих потенциальных проблем.

Теперь нам известно, что:

И можно приступать к сложению векторов:

Итак, мы вычислили результирующую силу ​( sum!mathbf{F} )​, которая равна (8 Н; 33 Н). Мы тем самым также определили направление движения мяча. На следующем этапе нужно определить ускорение на основании второго закона Ньютона:

Это означает, что:

Поскольку масса мяча равна 1 кг, то, подставляя это значение в предыдущую формулу, получим:

Неплохой прогресс: теперь вы знаете ускорение мяча. Теперь, чтобы узнать расстояние ​( mathbf{s} )​, которое преодолеет мяч за 1 секунду, нужно использовать приведенную ниже формулу (из главы 3):

После подстановки чисел получим:

Ну что ж, совсем неплохо. После 1 секунды движения мяч продвинется на 8 метров вдоль положительного направления оси X и на 33 метра вдоль положительного направления оси Y. Достаньте секундомер, засеките промежуток времени длительностью 1 с и убедитесь, что мяч продвинулся на 8 метров вдоль горизонтальной линии и на 33 метра вдоль вертикальной линии. Вот вам еще один успешный физический эксперимент.

Вычисляем результирующую силу по известному времени и скорости

В предыдущем разделе перемещение объекта было вычислено по известному времени движения с постоянным ускорением. А как поступить, если нужно решить обратную задачу: как определить результирующую силу по известному времени и достигнутой скорости? Допустим, что нужно ускорить автомобиль от 0 до 60 миль в час за 10 секунд. Какую силу нужно приложить для этого? Сначала нужно преобразовать единицы измерения для более удобной работы со значениями скоростей, т.е. мили в час преобразовать в футы в секунды.

Обратите внимание на то, что часы и минуты в итоге сократились, а остались только мили и секунды. Теперь нужно выразить результат в футах в секунду:

Итак, за 10 секунд автомобиль разгонится до скорости около 88 футов в секунду. Если автомобиль весит около 2000 фунтов, то какая сила потребуется для такого ускорения? Сначала найдем величину самого ускорения на основе приведенной ниже формулы (более подробно она описывается в главе 3):

Подставляя числа, получим:

Итак, искомое ускорение равно 8,8 футов в секунду². Согласно второму закону Ньютона:

Нам известно, что вес автомобиля равен 2000 фунтам. Чему равна масса автомобиля в другой системе единиц измерения, а именно в системе на основе фута-фунта-дюйма- секунды или в слагах? В этой системе единиц измерения нужно поделить вес на ускорение свободного падения под действием гравитации, т.е. 32,17 фута в секунду² (эта величина получена после преобразования уже известной нам величины 9,8 метра в секунду²):

Теперь у нас есть все, что нужно для вычисления силы. Какая сила потребуется, чтобы автомобиль весом 62,17 слага двигался с ускорением 8,8 фута в секунду². Нам нужно просто перемножить эти численные значения:

Итак, после округления до 2 значащих цифр получим, что для ускорения автомобиля до скорости 60 миль в час за 10 секунд потребуется сила 550 фунтов.

Учтите, что в данной задаче игнорируются такие особенности, как трение и наклон дороги. Более подробно эти вопросы рассматриваются в главе 6. Даже при движении по плоской поверхности без наклона трение может играть очень большую роль, и для ускорения автомобиля с учетом трения часто требуется приложить силу на 30% больше, чем 550 фунтов.

Торжественный финал: третий закон Ньютона

Этот закон движения особенно популярен среди борцов и инструкторов вождения автомобилей. Он гласит: сила действия одного объекта на другой равна по величине силе противодействия другого объекта, направленной в противоположную сторону.

Наиболее популярной формулировкой этого закона является следующая: “для любого действия всегда найдется равное ему и противоположное действие”. Однако физики предпочитают вместо неконкретного термина “действие” использовать более точный термин “сила”. Дело в том, что под действием часто подразумеваются совершенно разные явления, например характер голосования на избирательном участке или изменение температуры.

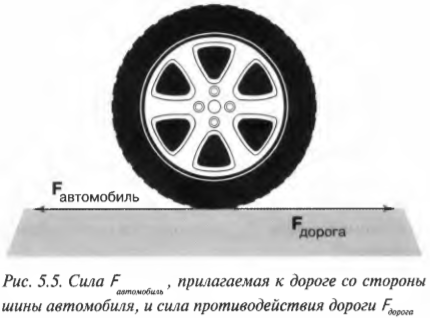
Допустим, что вы едете в автомобиле и для движения шина автомобиля должна прилагать силу к дороге (т.е. отталкиваться от нее), ибо иначе автомобиль не сможет двигаться. В таком случае дорога оказывает такую же силу на шину автомобиля, как показано на рис. 5.5.

Если бы силы действия автомобиля была больше силы противодействия, то шина проскальзывала бы по дороге, как при движении по льду.

У внимательного читателя может возникнуть вопрос: а почему дорога не движется в обратную сторону? На самом деле, верьте или нет, но третий закон Ньютона действует и дорога движется в обратную сторону. Действительно, шина автомобиля прилагает силу к поверхности дороги и приводит в движение Землю. Однако, учитывая, что масса Земли в 6⋅10²¹ раз больше массы автомобиля, это действие практически незаметно.

Учитываем трение

Когда хоккеист бьет клюшкой по шайбе, она ускоряется с места удара и ускоряется сам хоккеист. Если бы шайба имела массу 1000 кг (а не 105-185 г), то хоккеист, несомненно, ощутил бы это ускорение в гораздо большей мере. При таком нереальном соотношении масс хоккеиста и шайбы могло случиться так, что после удара шайба едва сдвинулась бы, а хоккеист заскользил бы в обратном направлении. (Более подробно такая ситуация описывается в части III.)

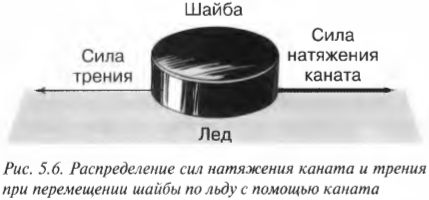
Допустим, что в данном фантасмагорическом примере по окончании игры нужно оттащить такую чудовищно тяжелую шайбу в сторону с помощью каната, как показано на рис. 5.6.

В физических задачах часто используются канаты, а также блоки, причем сила, с которой канат тянут с одного конца, равна силе сопротивления на другом конце каната.

В данном случае 1000-килограммовая шайба будет испытывать силу трения, пусть небольшую, но ощутимую. Итак, результирующая сила равна:

Поскольку сила натяжения каната ​( F_{канат} )​ больше силы трения ( F_{трение} ), то шайба начнет движение, причем ускоренное. Величину ускорения можно определить по известной формуле из второго закона Ньютона:

Одна часть силы натяжения каната ( F_{канат} ) расходуется на ускорение шайбы, а другая — на преодоление силы трения ( F_{трение} ):

Однако сила натяжения каната с одной стороны равна силе натяжения каната с другой, согласно третьему закону Ньютона.

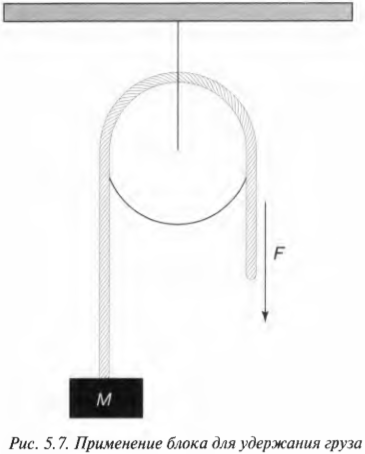
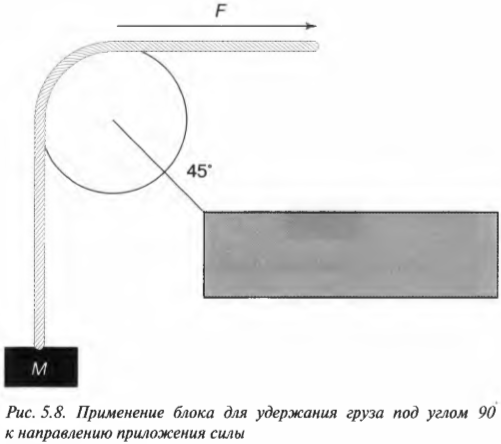
Рассмотрим теперь немного другую ситуацию, показанную на рис. 5.7. Допустим, что канат перекинут через блок и таким образом вам нужно поднять груз массы ​( M )​. Чтобы поднять груз, нужно преодолеть силу тяжести, которая действует на груз весом ​( Mg )​. Здесь ​( g )​ — это ускорение свободного падения под действием гравитации, равное 9,8 см/с² (более подробно сила гравитации описывается в главе 6). На рис. 5.7 показана общая схема приложения силы к канату, необходимая для удержания груза.

Канат и блок используются не только для удержания груза, но и для изменения направления приложения силы. Сила прилагается вниз, а груз под ее действием движется вверх, поскольку канат перекинут через блок, где и происходит изменение направления действия силы. В данном случае, если сила натяжения каната ​( F )​ на свободном конце больше веса груза ​( Mg )​, то груз будет двигаться вверх с ускорением ​( a )​, согласно формуле:

Подсчитаем теперь силу, действующую на потолок, к которому прикреплен блок. Если блок находится в покое, то действующая на него результирующая сила ​( sum!F=0 )​. Это значит, что все силы, которые действуют на блок, в сумме дают 0.

На блок действуют две силы, направленные вниз: сила натяжения каната ​( F )​ на свободном конце и сила со стороны груза с весом ​( Mg )​, движущегося с ускорением ​( a )​. Согласно третьему закону Ньютона, они равны, и сумма двух сил, направленных вниз, равна ​( 2F )​. Поскольку действующая на блок результирующая сила ( sum!F=0 ), то действующая на блок и направленная вверх сила со стороны потолка тоже равна ​( 2F )​.

Ни одна сила не может прилагаться к объекту без возникновения равной по величине и противоположной по направлению силы (даже если какая-то ее часть порождается ускоренным движением объекта). В предыдущем примере канат и блок позволяют изменять направление действия силы. Однако такое изменение направления силы от ​( -F )​ до ​( +F )​ возможно за счет приложение силы ​( 2F )​ к блоку со стороны потолка.

Анализируем углы и величины в третьем законе Ньютона

Чтобы учесть углы приложения силы, нужно вспомнить правила сложения векторов. Взгляните на рис. 5.8, где с помощью каната и блока сила ​( F )​ прилагается для удержания в состоянии покоя груза с массой ​( M )​. Вопрос: с какой величиной и в каком направлении действует сила ​( F_{опора} )​ на опору блока?

Поскольку блок не движется, то действующая на него результирующая сила ​( sum!F=0 )​. Теперь нужно найти все силы, которые действуют на блок. Во-первых, нужно учесть силу тяжести ​( mathbf{F_{груз}}=Mmathbf{g} )​, которая действует на груз. После разложения вектора этой силы на компоненты (подробнее об этом рассказывается в главе 4) получим (Y-компонента силы имеет отрицательный знак, поскольку она направлена вниз, т.е. вдоль отрицательного направления оси Y):

Теперь вычислим силу натяжения каната с другого конца ​( F_{канат} )​. Поскольку груз не движется, то сила натяжения каната на одном конце равна силе натяжения каната на другом конце. После разложения вектора силы натяжения каната на компоненты получим (Х-компонента силы имеет положительный знак, поскольку она направлена вправо, т.е. вдоль положительного направления оси X):

Теперь, чтобы найти результирующую силу, действующую на блок со стороны каната, нужно сложить компоненты сил ( F_{груз} ) и ( F_{канат} ):

Нам известно, что:

где ( F_{опора} ) — это сила, которая действует на опору блока.

Это значит, что:

Следовательно:

Глядя на рис. 5.8, можно легко проверить направление этого вектора. Действительно, блок должен противостоять силе тяжести груза (т.е. возникает сила противодействия, направленная вверх) и натяжению каната (т.е. возникает сила противодействия, направленная вправо).

Попробуем теперь определить величину и направление вектора силы ( F_{опора} ) (подробнее об этом рассказывается в главе 4). Величина этого вектора определяется по теореме Пифагора:

Обратите внимание на то, что здесь (как и в предыдущем примере) величина силы на опору блока больше величины каждой из сил по отдельности. Такова плата за изменение направления силы.

А в каком направлении действует сила ( F_{опора} )? Из рис. 5.8 ясно, что сила ( F_{опора} ) должна быть направлена влево и вверх, а теперь попробуем проверить это предположение с помощью тригонометрии. Если ​( theta )​ — это угол, под которым сила ( F_{опора} ) направлена по отношению к положительному направлению оси X, то Х-компонента силы ( F_{опора} ) имеет вид:

Следовательно:

Нам уже известно, что:

а также:

В итоге получим:

Нетрудно проверить, глядя на рис. 5.8, что найденное значение для направления силы на опору (-135) соответствует нашим предварительным оценкам и ожиданиям.

Если вы не уверены в правильности определения знаков сил, то всегда пробуйте проверить полученные значения с помощью визуального анализа нарисованной схемы распределения сил. Один рисунок порой стоит больше тысячи слов, особенно в физике!

Ищем состояние равновесия

В физике считается, что объект находится в состоянии равновесия, если его ускорение равно нулю, т.е. действующая на него результирующая сила равна 0. При этом объект необязательно должен находиться в покое — он может двигаться даже со скоростью 1000 километров в час, но без ускорения. Конечно, на объект в состоянии равновесия могут действовать самые разные силы, но их векторная сумма должна быть равна нулю.

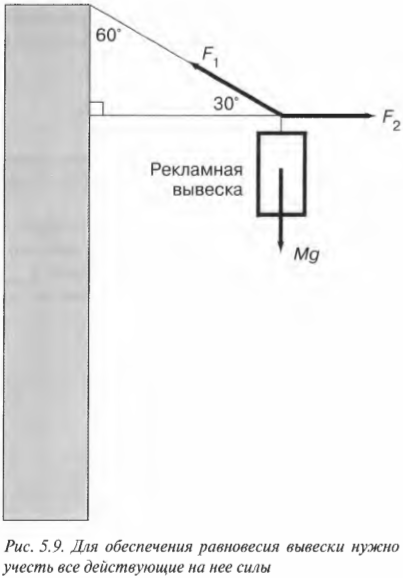
На рис. 5.9 показана схема распределения сил, действующих на рекламную вывеску перед магазином, которую вы собираетесь подвесить на проволоке, выдерживающей силу 15 Н.

Допустим, что вес вывески равен 8 Н. Хватит ли прочности проволоки для ее подвешивания? Иначе говоря, чему равна сила натяжения проволоки ​( F_1 )​ на этой схеме? Вывеска должна быть в состоянии равновесия, значит, результирующая сила на нее ​( sum!F=0 )​. Следовательно, весь вес вывески ​( Mg )​ должен быть уравновешен силой натяжения проволоки ​( F_1 )​.

В данном примере единственная направленная вверх сила — это Y-компонента силы ​( F_1 )​, как показано на рис. 5.9. Сила сопротивления ( F_2 ) горизонтальной балки направлена только по горизонтали, а потому не оказывает никакого влияния на вертикальную компоненту результирующей силы. С помощью навыков тригонометрии (более подробно базовые сведения по тригонометрии приводились в главе 4) можно определить Y-компоненту силы ( F_1 ):

Величина этой компоненты силы равна весу вывески:

Отсюда получаем натяжение проволоки:

Поскольку вес ​( Mg )​ вывески равен 8 Н, то получим

Ну и дела! Похоже, что проволока должна выдерживать силу 16 Н, а мы уже купили проволоку, выдерживающую всего 15 Н. Мораль сей задачи такова: нужно купить проволоку попрочнее!

Допустим, что мы купили более прочную проволоку и теперь интересуемся, достаточно ли прочна горизонтальная балка, чтобы выдержать силу сопротивления ​( F_2 )​, как показано на рис. 5.9. Какую прочность должна иметь балка, чтобы выдержать вес вывески? Иначе говоря, какую силу должна выдержать балка? На рис. 5.9 показаны только две горизонтальные силы: сила сопротивления балки ​( F_2=F_{балка} )​ и Х-компонента силы ​( F_1 )​. Нам уже известно, что ( F_1 ) = 16 Н. Теперь нам осталось только вычислить ( F_2 ). Для начала нужно определить Х-компоненту силы ( F_1 ) Глядя на рис. 5.9 и используя тригонометрию, получим:

Именно эта компонента силы натяжения проволоки равна силе сопротивления балки:

Это значит, что:

Итак, балка должна выдерживать силу около 14 Н.

Для подвешивания вывески весом около 8 Н потребуется проволока, выдерживающая силу около 16 Н, и балка, выдерживающая силу около 14 Н. Посмотрите снова на рис. 5.9: Y-компонента силы натяжения проволоки должна выдерживать вес груза. Такая прочность проволоки и балки нужна для того, чтобы изменить направление силы тяжести груза.

Лекция
2. Работа. Мощность. Теорема об изменении
кинетической энергии точки.

В данной лекции
рассматриваются следующие вопросы:

1. Работа силы.

2. Мощность.

3. Примеры вычисления
   работы.

4. Потенциальная
   энергия

5. Кинетическая
   энергия

6. Теорема об изменении
   кинетической энергии точки.

7. Теорема моментов.

Изучение данных
вопросов необходимо для динамики
движения центра масс механической
системы, динамики вращательного движения
твердого тела, кинетического момента
механической системы, для решения задач
в дисциплинах «Теория машин и механизмов»
и «Детали машин».

Работа силы. Мощность.

Для
характеристики действия, оказываемого
силой на тело при некотором его
перемещении,  вводится
понятие о работе силы.     

Рис.16

При
этом работа характеризует то действие
силы, которым определяется
изменение модуля скорости
движущейся точки.

Введём
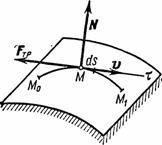
сначала понятие об элементарной работе
силы на бесконечно малом перемещении ds.
Элементарной работой силы  (рис.16)
называется скалярная величина:

,

где  —
проекция силы  на
касательную к траектории, направленную
в сторону перемещения точки, а -бесконечно
малое перемещение точки, направленное
вдоль этой касательной.

Данное
определение соответствует понятию о
работе, как о ха­рактеристике того
действия силы, которое приводит к
изменению модуля скорости точки. В самом
деле, если разложить силу  на
составляющие и ,
то изменять модуль скорости точки будет
только составляющая ,
сообщающая точке касательное ускорение
Составляющая же  или
изменяет направление вектора
скорости v (сообщает
точке нормальное ускорение),
или, при несвободном
дви­жение изменяет давление на связь.
На модуль скорости составляю­щая  влиять
не будет,  т.е.,
как говорят, сила «не
будет про­изводить работу».

Замечая,
что ,
получаем:

.                                            (1)

Таким
образом, элементарная работа силы равна
проекции силы на направление перемещения
точки, умноженной на элементар­ное
перемещение или
элементарная работа силы равна
произведению модуля силы на элементарное
перемещение  и
на косинус угла между направлением силы
и направлением перемещения.

Если
угол острый,
то работа положительна. В
частности, при  элементарная
работа .

Если
угол  тупой,
то работа отрицательна. В
частности, при  элементарная
работа .

Если
угол ,
т.е. если сила направлена перпендикулярно
перемещению, то элементарная работа
силы равна нулю.

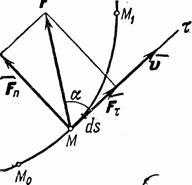
Найдем
аналитическое выражение элементарной
работы. Для этого разложим силу  на
составляющие , ,  по
направлениям координатных осей (рис.17;
сама сила  на
чертеже не показана).

Рис.17

Элементарное
перемещение  слагается
из перемещений , ,  вдоль
координатных осей, где x, y, z —
координаты точки М.
Тогда работу силы  на
перемещении  можно
вычислить как сумму работ её
составляющих , ,  на
перемещениях , , .

Но на
перемещении  совершает
работу только составляющая ,
причем её работа равна .
Работа на перемещениях и  вычисляется
аналогично. Окончательно
находим: .                                                                                                 

Формула дает
аналитическое выражение элементарной
работы силы.

Работа
силы на любом конечном
перемещении М₀М₁ вычисляется
как интегральная сумма соответствующих
элементарных работ и будет равна:

                                                                                                                                              
или

.

Следовательно, работа
силы на любом перемещении М₀М₁ равна
взятому вдоль этого перемещения интегралу
от элементарной работы. Пределы
интеграла соответствуют значениям
пере­менных интегрирования в
точках М₀ и М₁.

                                                                           Рис.18

Если
величина  постоянна
( = const),
то и обозначая перемеще­ние М₀М₁ через  получим: .

Такой
случай может иметь место,  когда
действующая сила  постоянна
по модулю и направлению (F= const),
а точка, к ко­торой приложена сила,
движется прямолинейно (рис.18}. В
этом случае  и
работа силы  .

Единицей
измерения работы в
системе СИ является джоуль (1 дж= 1 hm).

Мощность.

Мощностью называется
величина, определяющая работу, совершаемую
силой в единицу времени. Если работа
совершается равномерно, то мощность

,

где t — время,
в течение которого произведена работа A.
В общем случае

.

Следовательно,
мощность равна произведению касательной
состав­ляющей силы на скорость
движения.

Единицей
измерения мощности в
системе СИ является ватт (1 вт=1 дж/сек). В
технике за единицу мощности часто
принимается 1 лошадиная сила, равная
75 кГм/сек или
736 вт.

Работу,
произведенную машиной, можно измерять
произведением ее мощности на время
работы. Отсюда возникла употребительная
в технике единица измерения работы
киловатт-час (1 квт-ч = 3,6 дж  367100 кГм).

Из
равенства  видно,
что у двигателя, имеющего дан­ную
мощность W, сила
тяги  будет
тем больше, чем меньше ско­рость
движения V. Поэтому,
например, на подъеме или на плохом
участке дороги у автомобиля включают
низшие передачи, позволяю­щие при
полной мощности двигаться с меньшей
скоростью и раз­вивать большую силу
тяги.

Примеры вычисления
работы.

Рассмотренные
ниже при­меры дают результаты, которыми
можно непосредственно пользо­ваться
при решении задач.

1) Работа
силы тяжести. Пусть
точка М, на
которую действует сила тяжести , перемещается
из положения М_­0 (x­₀, у₀, z₀) в
положениеM₁ (х₁,
у₁, z₁). Выберем
оси координат так, чтобы ось Oz была
направлена вертикально вверх (рис.19).

         

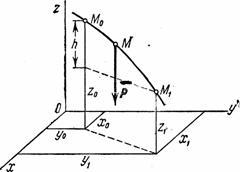
Рис.19                

Тогда Р_x=0, Р_y=0, P_z=
—Р.
Подставляя эти значения и учитывая
перемен­ную интегрирования z:

.                                           

Если
точка M₀ выше М₁, то ,
где h-величина
вер­тикального перемещения
точки;              

Если
же точка M₀ ниже
точки M₁ то .

Окончательно
получаем:  .

Следовательно,
работа силы тяжести равна взятому со
зна­ком плюс или минус произведению
модуля силы на вертикальное перемещение
точки ее приложения. Работа положительна,
если начальная точка выше конечной,
и отрицательна, если начальная точка
ниже конечной. Из полученного результата
следует, что работа силы тяжести не
зависит от вида той траектории, по
которой перемещается точка ее приложения.

Силы, обла­дающие
таким свойством, назы­ваются
потенциальными.

2) Работа
силы упругости. Рассмотрим груз М,
лежащий на горизонтальной плоскости и
прикрепленный к свободному концу
некоторой пружины (рис.20,а). Отметим на
плоскости точкой О поло­жение,
занимаемое концом пружины, когда она
не напряже­на ( — длина
ненапряженной пружины), и примем эту
точку за начало координат. Если теперь
оттянуть груз от равновесного положения О,
удлинив пружину до величины ,
то на груз будет действовать сила
упругости пружины F,
направленная к точке О.

Рис.20

По
закону Гука величина этой силы
пропорциональна удлинению пружины .
Так как в нашем случае ,
то по модулю .

Коэффициент с называется коэффициентом
жесткости пружины.
В технике обычно измеряют
величину с в H/см, полагая
коэф­фициент счисленно
равным силе, которую надо приложить к
пру­жине, чтобы растянуть ее на 1 см.

Найдем
работу, совершаемую силой упругости
при перемещении груза из положения  в
положение . Так
как в данном случае ,  ,
то получим:

.

(Этот
же результат можно получить по графику
зависимости F от х (рис.20, б), вычисляя
площадь  заштрихованной
на чертеже тра­пеции и учитывая знак
работы.) В полученной формуле  представ­ляет
собою начальное удлинение пружины ,
а  конечное
удлинение пружины .
Следовательно,

,

т.е. работа
силы упругости равна половине произведения
коэффи­циента жесткости на разность
квадратов начального и конеч­ного
удлинений (или сжатий) пружины.

Работа
будет положительной, когда ,
т. е. когда конец пружины перемещается
к равновесному положению, и отрица­тельной,
когда ,
т.е. конец пружины удаляется от равновесия
положения. Можно доказать, что формула
ос­тается справедливой и в случае,
когда пе­ремещение точки М не
является прямо­линейным.

Таким
образом, оказывается, что работа
силы F зависит
только от значе­ний  и  и не
зависит от вида траектории точки М.
Следовательно, сила упругости  также
является потенциальной.

Рис.21

3) Работа
силы трения. Рассмотрим
точку, движущуюся по какой-нибудь
шероховатой поверхности (рис. 21) или
кривой. Действующая на точку сила трения
равна по модулю fN,
где f-коэффициент
трения, а -нормальная
реакция поверхности. Направлена сила
трения противоположно перемещению
точки. Следовательно, F_тр=—fN и
по формуле

.

Если
величина силы трения постоянна,
то , где s-длина
дуги кривой М₀М₁ по
которой перемещается точка.  

Таким
образом, работа
силы трения при скольжении всегда
отрицательна. Величина
этой работы зависит от длины
дуги М₀М₁ .Следовательно,
сила трения является силой непотенциальной.

4) Работа
силы, приложенной к телу, вращающемуся
вокруг неподвижной оси.

В этом
случае (рис.22) точка приложения
силы  движется
по окружности радиуса r.
Элементарная работа, по (1), ,
где .

Рис.22

Поэтому .

Но .

Это
нетрудно установить, разложив силу на
три составляющие (рис. 22). (Моменты
сил  и  равны
нулю). Значит,

                                            (2)                        

В
частности, если момент силы относительно
оси ,
работа силы при повороте тела на
угол  равна 

.                                             (3)

Знак работы
определяется знаками момента силы и
угла поворота. Если они одинаковы, работа
положительная.

Из
формулы (3) следует и правило определения
работы пары сил. Если пара с
моментом m расположена
в плоскости перпендикулярной оси
вращения тела, то ее работа при повороте
тела на угол 

.                                                       (4)

Если
же пара сил действует в плоскости не
перпендикулярной оси вращения, то ее
надо заменить двумя парами. Одну
расположить в плоскости перпендикулярной
оси, другую – в плоскости параллельной
оси. Моменты их определяются разложением
вектора момента  по
соответствующим направлениям: . Конечно работу
будет совершать только первая пара с
моментом ,
где  –
угол между вектором  и
осью вращения z,

.                                               (5)  

Потенциальная
энергия

Часть пространства,
в которой на помещенную туда материальную
точку действует сила, зависящая от места
положения точки, называетсясиловым
полем.

Причем,
эта сила определяется  с  помощью
силовой функции u = u(x, y, z). Если
она не зависит от времени, то такое поле
называетсястационарным. Если
во всех точках она одинакова, то поле
– однородное.

Если же проекции
силы на декартовы оси есть частные
производные от силовой функции по
соответствующим координатам

,  ,  ,                                 (6)

то
такое поле называется потенциальным.

Вычислим
работу силы потенциального поля при
перемещении точки из положения М₁ в
положение М_2. (рис.
23).

Рис.23

Элементарная
работа,  

Это есть полный
дифференциал силовой функции.

Работа на конечном
перемещении

                                           (7)

где u₂ и u₁ –
значения силовой функции в точках М₂ и М₁.

Следовательно, работа
силы потенциального поля не зависит от
траектории движения точки, а определяется
лишь значениями силовой функции в
начальном и конечном положениях точки.

Естественно,
если точка вернется в начальное положение,
работа силы  будет
равна нулю. Работа окажется равной  нулю
и при переходе в другую точку М₃,
если там значение силовой функции будет
такое же, как и в начальном положении.

Нетрудно
догадаться, что точки с одинаковыми
значениями силовой функции будут
образовывать целую поверхность. И что
силовое поле – это слоеное пространство,
состоящее из таких поверхностей (рис.
23). Эти поверхности называются поверхностями
уровня или эквипотенциальными
поверхностями. Уравнения
их: u(x, y, z)=C  (C –
постоянная, равная значению u в
точках этой поверхности). А силовую
функцию называют, соответственно, потенциалом поля.

Конечно,
эквипотенциальные поверхности не
пересекаются. Иначе существовали бы
точки поля с неопределенным потенциалом.

Поскольку,
при перемещении точки по эквипотенциальной
поверхности работа силы  равна
нулю, то вектор силы перпендикулярен
поверхности.

Выберем
среди этих поверхностей какую-нибудь
одну и назовем ее нулевой поверхностью
(положим у нее u=u₀).

Работа,
которую совершит силапри
переходе точки из определенного места
М на нулевую поверхность, называют
потенциальной энергией точки в этом
определенном месте М:

.                                                 (8)

Заметим, что
потенциальная энергия в одной и той же
точке поля зависит от выбора нулевой
поверхности.

По (8)
силовая функция .
Поэтому проекции силы на декартовы оси,
по (6), так как ,

 ;   ;                      (9)

и
вектор силы .

Рассмотрим несколько
потенциальных полей.

1) Поле
силы тяжести.

Вблизи
поверхности Земли сила тяжести во всех
точках одинакова ,
равна весу тела. Значит, это силовое
поле однородное. Так как при перемещении
точки в горизонтальной плоскости работа
силы равна нулю, то эквипотенциальными
поверхностями будут горизонтальные
плоскости (рис. 24), а уравнения их: u = z = C.

Рис.24

Если
нулевой поверхностью назначить
плоскость xOy, то
потенциальная энергия точки в
положении М будет
равна работе силы тяжести:

.

2) Поле
упругой силы.

При
деформации упругого тела, например
пружины, появляется сила. То есть около
этого тела возникает силовое поле, силы
которого пропорциональны деформации
тела и направлены в сторону недеформированного
состояния. У пружины – в точку М₀,
где находится конец недеформированной
пружины (рис. 25).

Рис.25

Если
перемещать конец пружины так, чтобы
длина ее не изменялась, то работа упругой
силы  будет
равна нулю. Значит эквипотенциальными
поверхностями являются сферические
поверхности с центром в точке О.

Назначим
нулевой поверхностью сферу, проходящую
через точку М₀,
через конец недеформированной пружины.
Тогда потенциальная энергия пружины в
положении М:  .

При таком выборе
нулевой поверхности потенциальная
энергия всегда будет положительной
(П>0), и в растянутом, и в сжатом состоянии.

Теорема об изменении
кинетической энергии точки.

Рассмотрим
точку с массой т, перемещающуюся
под действием при­ложенных к ней сил
из положения M₀ ,
где она имеет скорость , в
положение М₁ ,
где ее скорость равна .

Для
получения искомой зависимости обратимся
к уравнению выражающему
основной закон динамики. Проектируя
обе части этого равенства на касательную  к
траектории точ­ки М, направленную
в сторону движения, получим:

 

Стоящую слева
величину касательного ускорения можно
пред­ставить в виде

.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

В отличие от повседневной жизни, термин «механическая работа» в физике связан с перемещением тела под воздействием приложенной к нему силы. Примеры работы: малыш тащит на веревочке игрушечный автомобиль, сброшенный с высоты предмет падает на землю, грузчик переносит вещи.

Направление движения не может быть перпендикулярно действию силы. Книга, лежащая на столе, действует на него с силой, направленной перпендикулярно столешнице и равной своему весу. Но стол остается на месте, поэтому работа равна нулю.

Если предмет перемещается в направлении приложенной к нему силы, то совершается положительная работа. Ее величина равна произведению силы и расстояния, на которое переместилось тело.

A = F x D, где:
A — работа;
F — сила, действующая на тело;
D — расстояние, на которое переместилось тело под действием приложенной силы F;

Пример положительной работы: локомотив тянет за собой вагоны.
[A] = 1 Дж = 1 Н x м

Если перемещение противоположно действию силы, то совершается отрицательная работа.
В этом случае A = — F x D.
Например, при запуске летучего змея работа силы тяжести — отрицательная.

Если величина приложенной силы непостоянна или направлена под углом к направлению движения тела, работа рассчитывается по другим, более сложным формулам.

Полная работа определяется как совокупность работы всех сил, действующих на предмет. В зависимости от величины работы и времени на ее выполнение подбирают необходимую мощность машин и механизмов и расход топлива.

Привет! В этом уроке начнём знакомиться с таким видом деформации, как растяжение (сжатие). Обычно, с этой темы и начинают изучать сопротивление материалов — объясняются основные понятия, которые дальше используются на протяжении всего обучения.

Задание, которое будем рассматривать в этой статье, как правило, дается студентам в первую очередь в качестве домашней работы. После изучения материалов этого урока ты научишься строить следующие эпюры: продольных сил, нормальных напряжений, а также осевых перемещений поперечных сечений. Не пугайся мудрёных названий, на самом деле, все эти эпюры строятся очень просто!

Что же давай приступим к изучению!

Построение эпюры продольных сил

В качестве примера возьмём простенькую расчётную схему стержня (также часто ступенчатый стержень, который работает на растяжение или сжатие, называют брусом). Загрузим наш стержень сосредоточенными силами, вот так:

Теперь наша первостепенная задача – построить эпюру продольных сил. И давай сразу будем разбираться в терминологии.

Что такое эпюра?

Эпюра – это график, который принято строить для визуализации распределения какой-либо величины. В нашем случае, продольной силы.

Построив такой график, мы можем увидеть, где определённая величина достигает максимальных или минимальных значений, что может быть полезно при проведении прочностных расчётов и других. Кроме того, эпюры могут служить вспомогательными инструментами для построения других эпюр, о чём мы будем говорить далее.

Что такое продольная сила?

Продольная сила – это внутренняя сила, которая возникает в сечениях стержня, работающего на растяжение или сжатие под действием внешней нагрузки.

Расчёт эпюры продольных сил

Чтобы построить эпюру продольных сил, нужно разбить брус на несколько участков, где эпюра будет иметь постоянное значение. Конкретно, для этого стержня, границами участков служат те точки, где прикладываются сосредоточенные силы.

То есть для нашего примера, нужно рассмотреть всего 2 участка:

Важно! Эпюра продольных сил, никак не зависит от формы бруса, в отличие от других эпюр, которые будем дальше рассчитывать.

Правило знаков для продольных сил

Правило знаков для продольных сил следующее:

• если внешняя сила (F) растягивает брус, то продольная сила (N) в сечениях будет положительная;
• если внешняя сила (F) сжимает брус, то продольная сила (N) в сечениях будет отрицательная.

Расчёт продольных сил на участках

На первом участке сила F₁ растягивает брус на величину 5 кН, поэтому на этом участке, продольная сила будет положительной и равной:

Откладываем это значение на графике — эпюре. Эпюры, принято заштриховывать перпендикулярно к нулевой линии, а также указывать знак продольной силы:

На втором же участке, помимо силы F₁, также действует сила F₂, которая сжимает брус, поэтому в уравнении ее нужно учесть со знаком «минус»:

Откладываем полученное значение на эпюре:

Расчёт реакции в жёсткой заделке

Прежде всего, следует разобраться с тем, что вообще такое реакция. Всё дело в том, что помимо внутренних усилий, возникающих внутри нагруженного элемента конструкции, в том месте, где закреплён этот элемент, также возникают некоторые силы (сила), которые являются реакцией на внешнюю нагрузку и удерживающие эту конструкцию в состоянии статического равновесия.

Например, стул на котором ты сейчас сидишь и давишь на него своим весом, сопротивляется, чтобы удерживать тебя в состоянии равновесия. Если переводить на язык сопромата, твой вес в этом случае это внешняя сила, а сила с которой стул реагирует на твой вес – это реакция опоры, равная по модулю этой силе, но противоположно направленная.

Так и в нашей конструкции, в жёсткой заделке, также возникает реакция! Осталось только научиться — определять эту силу. Так как она должна компенсировать всю нагрузку, которая приложена к стержню, условие равновесия для нашей схемы можно записать так:

То есть, так как система находится в состоянии равновесия, то сумма всех сил, действующих на конструкцию, будет равна нулю.

Из этого условия равновесия и найдём искомую реакцию. Приложим некоторую силу R в месте, где закреплён наш стержень, при этом направить её можно в любую сторону, хоть влево, хоть вправо, главное, чтобы она была направлена горизонтально, так как у нас вся нагрузка, направлена так, то и реакция в заделке будет возникать исключительно — горизонтальная:

Чтобы составить уравнение равновесия, введём продольную ось – x, относительно неё будем составлять это уравнение, при этом силы, которые будут совпадать с положительным направлением оси x, в уравнении будем учитывать с «плюсом», а противоположно направленные с «минусом»:

Находим из этого уравнения реакцию в заделке:

А теперь, давай обсудим, что можем делать с этим теперь. В нашей конкретной задаче реакция может помочь проверить эпюру продольных сил. Если в первом уроке, считали стержень, строго справа налево, то теперь, зная численное значение реакции, можно рассчитать стержень и слева направо. Или как минимум увидеть, что левый участок эпюры, был построен верно.

Да, можно было вполне обойтись, без расчёта этой реакции конкретно в этом случае. Но, чаще всего, решение задач по сопромату начинается как раз с определения реакций, потому что без этого в большинстве случаев, невозможно определить внутренние усилия, а тем самым произвести какие-либо дальнейшие расчёты. Но с этим мы ещё многократно будем сталкиваться в следующих уроках, особенно в задачах на изгиб.

Построение эпюры нормальных напряжений

В отличие от продольных сил, нормальные напряжения уже зависят от формы бруса, а если точнее, то от площади его поперечных сечений.

Формула для определения нормальных напряжений выглядит так:

Таким образом, чтобы найти нормальное напряжение в любом сечении бруса, нужно: продольную силу в этом сечении разделить на площадь сечения.

Нормальные напряжения, как и продольные силы, изменяются по одному закону в пределах участков. Однако, так как форма бруса сказывается на распределении нормальных напряжений, здесь границами участков также служат места изменения геометрии бруса. Таким образом, для нашей расчетной схемы, нужно рассмотреть три участка и вычислить напряжения, соответственно, 3 раза:

Будем считать, что по условию задачи нам известны все параметры бруса, включая площади поперечных сечений: на первом участке площадь поперечного сечения A₁=2 см², а на втором и третьем A₂ = A₃ = 4 см².

Вычисляем напряжения на каждом участке:

По полученным значениям строим эпюру нормальных напряжений:

По полученной эпюре нормальных напряжений, можно определить те поперечные сечения, в которых напряжения будут максимальными (все сечения на участке 1), что полезно при проведении прочностного расчёта.

Построение эпюры осевых перемещений поперечных сечений

Под действием внешней нагрузки поперечные сечения бруса перемещаются вдоль продольной оси. Под нагрузкой брус может как удлиниться, так и укоротиться. И в этом разделе будем учиться определять эти перемещения.

Для начала подготовимся к расчету и расставим точки в характерных сечениях. Чтобы потом к ним привязываться по ходу решения:

Если для первых двух эпюр, расчет начинался справа налево, от свободного конца. То здесь нам нужно начать считать с закрепленного конца, с жесткой заделки и так как сечение A, закреплено жестко, то никакие перемещения этого сечения невозможны, поэтому сразу можем записать:

Эпюра перемещений так же, как и остальные эпюры, меняется по одному закону, в пределах участков. Поэтому, чтобы построить эпюру, достаточно определить эти перемещения в характерных точках.

Перемещение точки B будет складываться из перемещения предыдущего расчетного сечения:

А также удлинения (или укорочения) участка между расчетными сечениями:

В свою очередь, удлинение (или укорочение) любого участка, можно определить по следующей формуле:

Поэтому формулу, для нахождения перемещения сечения B, можно записать и в другом виде:

Подставив все численные значения, найдем искомое перемещение:

Откладываем полученное значение на эпюре:

Также важно отметить, что при вычислении удлинения или укорочения участка (Δl), фактически площадь эпюры продольных сил (ω) делится на жесткость при растяжении или сжатии (EA).

Это свойство нам еще пригодится, когда будем рассматривать более сложную задачу.

Для точек C и D перемещения находятся аналогичным способом, так же как и для точки B, поэтому подробно комментировать не буду, приведу решение.

Точка C

Точка D

Откладываем полученные значения на эпюре:

По полученной эпюре, можно увидеть — в какую сторону и насколько переместится любое поперечное сечение стержня. Наиболее интересной характеристикой здесь является перемещение сечения D, то есть перемещение свободного конца бруса или фактическое удлинение. Как видим, сечение D переместится вправо на величину W_D (т. к. значение W_D — положительное). То есть, под действием всей нагрузки брус удлинится на 0.575 мм.

Учёт распределённой нагрузки

А теперь предлагаю рассмотреть немного измененную задачу. Приложим к нашему брусу дополнительно распределенную нагрузку q с интенсивностью равной 2 кН/м. После чего рассчитаем и построим все те же эпюры: продольных сил, нормальных напряжений и перемещений.

Чтобы учесть распределенную нагрузку, необходимо интенсивность нагрузки (q) умножить на длину участка, на котором действует нагрузка. В чистом виде, только от распределенной нагрузки, эпюра продольных сил будет треугольная.

Расчет продольных сил

На первом участке, сила по-прежнему растягивает стержень, записываем ее в уравнение с «плюсом», а распределенная нагрузка сжимает, соответственно, ее учитываем с «минусом»:

Найдем значения продольной силы на границах первого участка:

Откладываем рассчитанные значения:

На втором участке, распределенная нагрузка будет действовать точно так же, как и сосредоточенная сила:

Рассчитываем продольную силу на третьем участке:

Строим окончательную эпюру продольных сил:

Расчет нормальных напряжений

Нормальные напряжения рассчитываются точно так же, как и для первой задачи, единственное отличие только в том, что на первом участке необходимо рассчитать напряжения два раза — на границах участка:

По полученным значениям строим эпюру нормальных напряжений:

Расчет перемещений

Для точек A, B и С перемещения рассчитываются аналогично, как в первой задаче: 

Строим эпюру перемещений на втором и третьем участке:

Чтобы рассчитать удлинение на первом участке, нужно вычислить площадь эпюры продольных сил на этом участке и разделить на жесткость (EA):

Так как на этом участке, эпюра состоит из двух одинаковых прямоугольных треугольников, но по разные стороны от нулевой линии, с учетом знаков, ожидаемо, получим, что перемещение точки D, будет равно перемещению точки C.

Однако, необходимо учесть еще одну особенность. На участках, где действуют распределенные нагрузки, эпюры перемещений изменяются не по линейному закону, а по квадратичному.

То есть на участке с распределенной нагрузкой, эпюра перемещений всегда будет иметь либо выпуклость, либо вогнутость:

Чтобы понять, как же будет выглядеть эпюра перемещений, на участке с распределённой нагрузкой, нужно проанализировать эпюру продольных сил.

Как видим, начиная от точки C и до пересечения нулевой линии, эпюра продольных сил – отрицательна, а это значит, что эпюра перемещений, на этом отрезке, также должна убывать, как показано зелёной пунктирной линией. Поэтому изображаем эпюру перемещений следующим образом:

Но чтобы окончательно убедиться в верности наших рассуждений, можно также определить экстремум на эпюре перемещений (там, где эпюра достигает своего максимального значения). Или в той точке, где эпюра продольных сил пересекает нулевую линию:

Отмечаем найденное значение на эпюре перемещений: