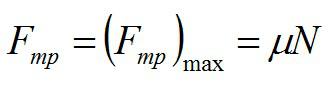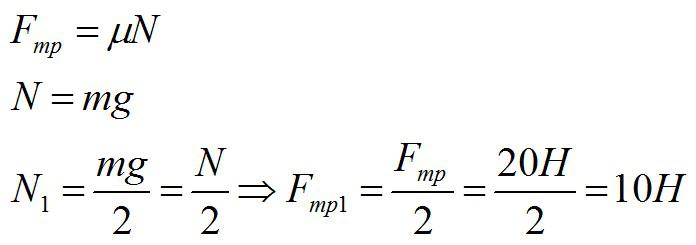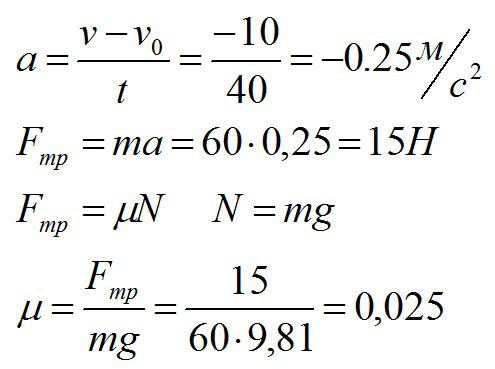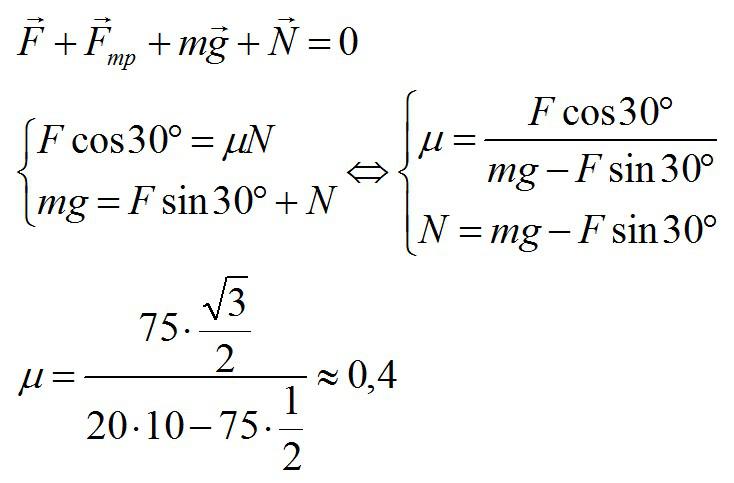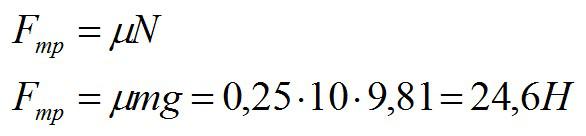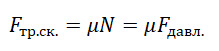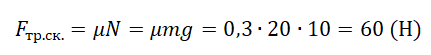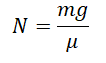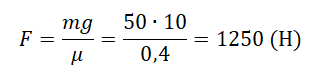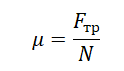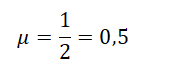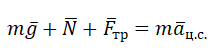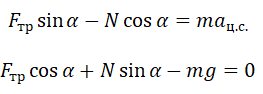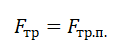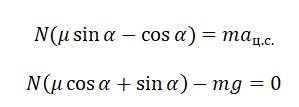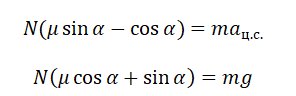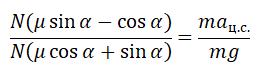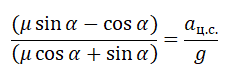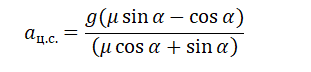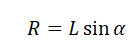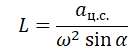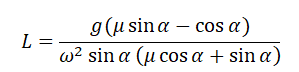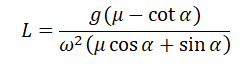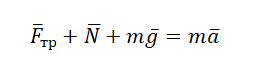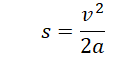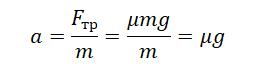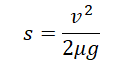Противоположная сила, действующая на тело, называется трением. Разберемся, как найти нормальную силу с коэффициентом трения.
Чтобы узнать, как найти нормальную силу с коэффициентом трения, воспользуемся формулой трения. Трение бывает двух типов: статическое трение и кинетическое трение, и, таким образом, у нас есть статический коэффициент трения и кинетический коэффициент трения. Давайте рассмотрим несколько подходов к тому, как найти нормальную силу с коэффициентом трения.
Мы хорошо знаем нормальную массу; он действует перпендикулярно на объект в направлении вверх. Это нормальная сила, которая удерживает объекты от падения или прохождения через другой объект.
Например, стекло хранится на полке. Мы знаю, что гравитация тянет все предметы вниз. Значит, на стекло тоже будет действовать сила тяжести, и оно должно упасть. Но этого не происходит. Это связано с нормальная сила который действует на стекло в направлении вверх и уравновешивает гравитационное притяжение.
Сила трения является противодействующей силой. Также говорят, что это необходимое зло. Для объекта, который не движется, трение является трением покоя. Точно так же, когда тело находится в движении, возникающее трение является кинетическим.
Когда мы бросаем мяч, он некоторое время катится по земле, постепенно его скорость замедляется, и он останавливается. Это происходит из-за силы трения. Трение — это противодействующая сила, которая действует на объект, ограничивая его движение. Мы можем ходить и писать благодаря трению. Это имеет большое повседневное значение в наших трениях.
Коэффициент трения – это отношение силы трения к нормальной силе. Если трение статическое, то имеем статический коэффициент статического трения, а для кинетическое трение, имеем коэффициент кинетического трения.
Общая формула силы трения f=µN
Вот.
f = сила трения
μ = коэффициент трения
N = нормальная сила.
По этой формуле вычисляем нормальную силу с коэффициентом трения.
N=f/мк
Теперь, если объект удерживается на поверхности и даже после приложения силы он не движется. Тогда трение является трением покоя. В этом случае формула будет такой:
fs= μsN
Н=fs/мкs
Для движущегося объекта сила трения является кинетической; поэтому, чтобы найти нормальную силу, формула принимает вид:
fk= μkN
Н=fk/мкk
Задачи на нахождение нормальной силы с коэффициентом трения
Задача 1) Деревянное бревно массой 2 кг толкают из неподвижного положения, на него действует сила трения 9.8 Н с коэффициентом трения 0.5. Вычислите нормальную силу.
Решение: Для данной задачи дано:
m = 2 кг
μ = 0.5
f = 9.8
Тогда, используя формулу N=f/µ и подставляя значения, получаем:
N=f/мк
N=9.8/0.5
N = 19.6 ньютона
Задача 2) Коробку, лежащую на горизонтальном столе, плавно толкают с силой трения 7.85 Н и коэффициентом трения 0.4. Вычислите нормальную силу.
Решение: Нам дается:
μk = 0.4
fk= 7.85 Н
Тогда нормальная сила будет:
Н=fk/мкk
N = 7.85/0.4
N = 19.625 ньютона
Итак, это все о том, как найти нормальную силу с коэффициентом трения. В случае возникновения дополнительных вопросов прочитайте часто задаваемые вопросы, упомянутые ниже.
Часто задаваемые вопросы (FAQ)
Что такое трение как сила?
Сила трения — это вид силы, которая пытается уменьшить влияние других сил, действующих на тело.
Говоря простым языком, трение противостоит движение, вызванное действующей силой. Например, когда мы пытаемся толкнуть диван, он может не сдвинуться с места, потому что сила трения, действующая на него, будет больше силы, приложенной нами. Другой пример: когда мы нажимаем на тормоз, трение останавливает машину.
Объясните коэффициент трения.
Коэффициент трения дает нам величину силы трения, действующей между поверхностями.
Величина трения также показывает, какая сила требуется, чтобы преодолеть трение и заставить тело двигаться. Меньшее значение коэффициента трения указывает на то, что на объект действует меньшее трение.
Как связаны трение и нормальная сила?
Для тела, удерживаемого на столе или движущегося по горизонтальной поверхности, на него обязательно действуют трение и нормальная сила.
Трение и нормальная сила связаны формулой f∝N. Когда мы убираем знак пропорциональности, мы получаем формулу f=µN, которая связывает силу трения и нормальную силу; с увеличением трения увеличивается нормальная сила, и наоборот.
Что происходит с силой трения при увеличении нормальной силы?
Величина силы трения зависит от нормальной силы.
Для данной ситуации коэффициент трения остается постоянным на всем протяжении. Таким образом, мы узнаем, что трение изменяется с нормальной силой. Поэтому, когда нормальная сила увеличивается, требуется большее трение, чтобы противодействовать движению.
Как найти нормальную силу с коэффициентом трения?
Мы можем найти нормальную силу с коэффициентом трения, используя стандартную формулу трения.
Трение зависит от нормальной силы, действующей на объект. Это дает нам формулу трения f=µN. Из этой формулы мы можем найти нормальную силу, используя коэффициент трения N = f / μ.
Почему трение зависит от нормальной силы, а не от веса тела?
Трение зависит не от веса объекта, а от нормальной силы.
Это так, потому что это нормальная сила, которая давит на тело на поверхности, поэтому, чем больше нормальная сила, тем больше потребуется трения. В то же время вес пытается тянуть тело вниз.
Есть ли у коэффициента трения единица измерения?
Коэффициент трения не удерживает ни одной единицы. Во-первых, это константа, а во-вторых, если мы видим формулу f=мкН , отсюда получаем μ=f/N что является отношением двух сил, и, таким образом, единицы уравновешиваются.
Загрузить PDF
Загрузить PDF
Сила нормальной реакции — сила, действующая на тело со стороны опоры (или сила, противодействующая другим силам в любом данном сценарии). Ее вычисление зависит от конкретных условий и известных величин.
-
1
В случае тела, покоящегося на горизонтальной поверхности, сила нормальной реакции противодействует силе тяжести.
- Представьте себе тело, лежащее на столе. Сила тяжести действует по направлению к земле, но так как тело не разрушает стол и не падает на землю, существует некоторая противодействующая сила. Эта сила и есть сила нормальной реакции.
-
2
Формула для нахождения силы нормальной реакции для тела, покоящегося на горизонтальной поверхности: N = m*g[1]
- В этой формуле N — сила нормальной реакции, m – масса тела, g – ускорение свободного падения.
- В случае тела, находящегося в состоянии покоя на горизонтальной поверхности и на которое не действуют внешние силы, сила нормальной реакции равна весу. Для сохранения тела в состоянии покоя, сила нормальной реакции должна быть равна силе тяжести, действующую на опору. В данном случае сила тяжести, действующая на опору, является весом, то есть произведением массы тела на ускорение свободного падения.
- Пример: найдите силу нормальной реакции, действующую на тело массой 4,2 г.
-
3
Умножьте массу тела на ускорение свободного падения. Вы найдете вес, который в данном случае равен силе нормальной реакции (так как тело в находится в покое на горизонтальной поверхности).
- Обратите внимание, что ускорение свободного падения на поверхности Земли является постоянной величиной: g = 9,8 м/с2.[2]
- Пример: вес = m*g = 4,2*9,8 = 41,16 Н.
- Обратите внимание, что ускорение свободного падения на поверхности Земли является постоянной величиной: g = 9,8 м/с2.[2]
-
4
Запишите ответ.
- Пример: сила нормальной реакции равна 41,16 Н.
Реклама
-
1
Формула для вычисления силы нормальной реакции, действующей на тело, покоящееся на наклонной поверхности: N = m * g * cos(x).[3]
- В этой формуле N — сила нормальной реакции, m – масса тела, g – ускорение свободного падения, х — угол наклона поверхности.
- Пример: найдите силу нормальной реакции, действующую на тело массой 4,2 г, находящегося на наклонной поверхности с углом наклона 45 градусов.
-
2
Найдите косинус угла. Косинус угла равен отношению прилежащей (к этому углу) стороны к гипотенузе. [4]
- Косинус зачастую вычисляется с помощью калькулятора, но вы также можете найти его вручную.
- Пример: соs(45) = 0,71.
-
3
Найдите вес. Вес равен произведению массы тела на ускорение свободного падения.
- Обратите внимание, что ускорение свободного падения на поверхности Земли является постоянной величиной: g = 9,8 м/с2.
- Пример: вес = m*g = 4,2*9,8 = 41,16 Н.
-
4
Перемножьте два найденных значения. Для вычисления силы нормальной реакции умножьте вес на косинус угла наклона.
- Пример: N = m * g * cos(x) = 41,16 * 0,71 = 29,1
-
5
Запишите ответ.
- Обратите внимание, что в случае тела, находящегося на наклонной поверхности, сила нормальной реакции меньше веса.
- Пример: сила нормальной реакции равна 29,1 Н.
Реклама
-
1
Формула для вычисления силы нормальной реакции в случае, когда внешняя сила, действующая на тело, направлена вниз: N = m * g + F * sin(x).
- В этой формуле N — сила нормальной реакции, m – масса тела, g – ускорение свободного падения, х — угол между горизонтальной поверхностью и направлением действия внешней силы.
- Пример: найдите силу нормальной реакции, действующую на тело массой 4,2 г, на которое действует внешняя сила 20,9 Н под углом 30 градусов.
-
2
Найдите вес. Вес равен произведению массы тела на ускорение свободного падения.
- Обратите внимание, что ускорение свободного падения на поверхности Земли является постоянной величиной: g = 9,8 м/с2.
- Пример: вес = m*g = 4,2*9,8 = 41,16 Н.
-
3
Найдите синус угла. Синус угла равен отношению противолежащей (к этому углу) стороны к гипотенузе. [5]
- Пример: sin(30) = 0,5.
-
4
Умножьте синус угла на внешнюю силу.
- Пример: 0,5 * 20,9 = 10,45
-
5
Сложите это значение и вес. Вы найдете силу нормальной реакции.
- Пример: 10,45 + 41,16 = 51,61
-
6
Запишите свой ответ. Обратите внимание, что в случае тела, на которое действует сила, направленная вниз, сила нормальной реакции больше веса.
- Пример: сила нормальной реакции равна 51,61 Н.
Реклама
-
1
Формула для вычисления силы нормальной реакции в случае, когда внешняя сила, действующая на тело, направлена вверх: N = m * g — F * sin(x).
- В этой формуле N — сила нормальной реакции, m – масса тела, g – ускорение свободного падения, х — угол между горизонтальной поверхностью и направлением действия внешней силы.
- Пример: найдите силу нормальной реакции, действующую на тело массой 4,2 г, на которое действует внешняя сила 20,9 Н под углом 50 градусов.
-
2
Найдите вес. Вес равен произведению массы тела на ускорение свободного падения.
- Обратите внимание, что ускорение свободного падения на поверхности Земли является постоянной величиной: g = 9,8 м/с2.
- Пример: вес = m*g = 4,2*9,8 = 41,16 Н.
-
3
Найдите синус угла. Синус угла равен отношению противолежащей (к этому углу) стороны к гипотенузе. [6]
- Пример: sin(50) = 0,77.
-
4
Умножьте синус угла на внешнюю силу.
- Пример: 0,77 * 20,9 = 16,01
-
5
Вычтите это значение из веса. Вы найдете силу нормальной реакции.
- Пример: 41,16 – 16,01 = 25,15
-
6
Запишите свой ответ. Обратите внимание, что в случае тела, на которое действует сила, направленная вверх, сила нормальной реакции меньше веса.
- Пример: сила нормальной реакции равна 25,15 Н.
Реклама
-
1
Формула для вычисления силы трения: F = μ * N.
- В этой формуле F — сила трения, μ — коэффициент трения, N — сила нормальной реакции.
- Коэффициент трения характеризует силу, необходимую для движения одного материала по поверхности другого.
-
2
Перепишите формулу, обособив силу нормальной реакции. Если вам даны сила трения и коэффициент трения, вы можете найти силу нормальной реакции по формуле: N = F / μ.
- Обе части исходной формулы были разделены на μ, в результате чего сила нормальной реакции была обособлена на одной стороне, а сила трения и коэффициент трения — на другой.
- Пример: найдите силу нормальной реакции, когда сила трения равна 40 Н, а коэффициент трения равен 0,4.
-
3
Разделите силу трения на коэффициент трения. Вы найдете силу нормальной реакции.
- Пример: N = F/μ = 40/0,4 = 100
-
4
Запишите ответ. Вы можете проверить ответ, подставив его в исходную формулу для вычисления силы трения.
- Пример: сила нормальной реакции равна 100 Н.
Реклама
Что вам понадобится
- Карандаш
- Бумага
- Калькулятор
Об этой статье
Эту страницу просматривали 59 615 раз.
Была ли эта статья полезной?
Благодаря этой силе автомобили тормозят на светофоре, катер останавливается в воде, колесо буксует в яме. Как вы уже поняли, в этой статье мы будем разбираться, как решать задачи на силу трения.
Сила трения имеет электромагнитную природу. Это значит, что эта сила проявляется в результате взаимодействия частиц, из которых состоит вещество.
Хотите больше полезной и интересной информации по разным темам? Подписывайтесь на наш телеграм-канал.
Что нужно знать о силе трения, чтобы решать задачи
Трение – один из видов взаимодействия тел, которое возникает при их соприкосновении.
Сила трения всегда направлена в сторону, противоположную движению и по касательной к соприкасающимся поверхностям. Между твердыми телами возникает сухое трение, а при движении тел в жидкостях или газах говорят о вязком трении.
Природу этой силы мы уже установили. Помимо этого нужно знать, что бывают разные виды сил трения:
- трение покоя;
- трение скольжения;
- трение качения (при перекатывании тел друг по другу);
- сопротивление среды (для движения в жидкости).
Вот пример на виды силы трения: брусок лежит на столе, и никто его на трогает. В этом случае действуют только сила тяжести и сила нормальной реакции опоры. Если мы начнем толкать брусок, но так сильно, чтобы его сдвинуть, на него будет действовать сила трения покоя, по третьему закону Ньютона равная внешней силе, приложенной к бруску. Сила трения покоя имеет предельное значение. Если внешняя сила будет больше этого значения, брусок начнет скользить по столу. В этом случае говорят о силе трения-скольжения. А вот и простейшая формула для силы трения:
«Мю» — коэффициент трения скольжения. Это безразмерная величина, которая зависит от материалов взаимодействующих тел и от качества их поверхностей. Величина коэффициента трения не превышает единицы.
При решении простых физических задач силу трения скольжения часто принимают равной максимальной силе трения покоя.
Не забывайте также про нашу памятку и подборку полезных формул.
Вопросы по теме «Сила трения»
Вопрос 1. От чего зависит сила трения?
Ответ. Взглянем на формулу выше, и ответ придет сам. Сила трения зависит от свойств соприкасающихся тел, силы нормальной реакции опоры, скорости относительного движения тел.
Вопрос 2. Зависит ли сила трения от площади соприкасающихся поверхностей?
Ответ. Нет, площадь не влияет на силу трения.
Вопрос 3. Какими способами можно уменьшить или увеличить силу трения?
Ответ. Можно уменьшить коэффициент трения, сделав сухое трения вязким. Для увеличения силы трения необходимо увеличить давление на них.
Вопрос 4. Тело покоится на плоскости. Действует ли на него сила трения?
Ответ. Если на тело не действуют внешние силы, то сила трения покоя, по третьему закону Ньютона, равна нулю.
Вопрос 5. Какая из этих сил самая большая по модулю: сила трения покоя, сила трения качения или сила трения скольжения?
Ответ. Сила трения скольжения имеет самое большое значение.
Вопрос 6. Какие есть примеры полезного действия силы трения?
Ответ. Среди полезного использования силы трения можно выделить работу тормозов транспортных средств, добычу огня первобытными людьми.
Задачи на силу трения с решениями
Кстати! Для наших читателей действует скидка 10% на любой вид работы.
Задача №1. Нахождение силы трения
Условие
Брусок массой 5 килограмм скользит по горизонтальной поверхности. Сила трения скольжения равна 20 Н. Найдите силу трения, если масса бруска уменьшится в два раза, а коэффициент трения останется неизменным.
Решение
Применим формулы:
Ответ: 10 Н.
Задача №2. Нахождение коэффициента трения
Условие
Тело скользит по горизонтальной плоскости. Найти коэффициент трения, если сила трения равна 5 Н, а сила давления тела на плоскость – 20 Н.
Решение
Сила давления тела на плоскость равна силе нормальной реакции опоры.
Ответ: 0,25
Задача №3. Нахождение силы трения и коэффициента трения
Условие
Лыжник массой 60 кг, имеющий в конце спуска скорость 10 м/с, останавливается через 40 с после окончания спуска. Определите силу трения и коэффициент трения.
Решение
Сначала найдем ускорение, с которым движется лыжник. Затем по второму закону Ньютона найдем силу, которая действует на него:
Ответ: 15 Н; 0,025.
Задача №4. Нахождение силы трения
Условие
Брусок массой 20 кг равномерно перемещается по горизонтальной поверхности под действием постоянной силы, направленной под углом 30° к поверхности и равной 75 Н. Каков коэффициент трения между бруском и плоскостью?
Решение
Сначала воспользуемся вторым законом Ньютона, учитывая, что ускорение равно нулю. Затем найдем проекции силы на вертикальную и горизонтальную оси:
Ответ: 0,4
Задача №5. Нахождение силы трения покоя
Условие
Ящик массой 10 кг стоит на горизонтальном полу. Коэффициент трения между полом и ящиком равен 0,25. К ящику в горизонтальном направлении прикладывают силу 16 Н. Сдвинется ли он с места. Какова сила трения между ящиком и полом?
Решение
Вычислим максимальную силу трения покоя:
Так как приложенная сила по условию меньше, чем максимальная сила трения покоя, ящик останется стоять на месте. Сила трения между полом и ящиком, по третьему закону Ньютона, равна приложенной силе.
Ответ: 16 Н.
Нужна помощь в решении задач или других заданий? Обращайтесь за ней в профессиональный студенческий сервис.
Трение — вариант взаимодействия двух тел. Оно возникает при движении одного тела по поверхности другого. При этом тела действуют друг на друга с силой, которая называется силой трения. Сила трения имеет электромагнитную природу.
Сила трения — сила, возникающая между телами при их движении или при попытке их сдвинуть. Обозначается как Fтр. Единица измерения — Н (Ньютон).
Трение бывает сухим и жидким. В школьном курсе физике изучается сухое трение.
Виды сухого трения:
- трение скольжения;
- трение качения;
- трение покоя.
Трение скольжения
Трение скольжения — трение, возникающее при скольжении одного тела по поверхности другого. Сила трения скольжения направлена противоположно направлению движения тела: Fтр↑↓v.
Сила трения скольжения определяется формулой:
μ — коэффициент трения, N — сила реакции опоры, Fдавл. — сила нормального давления
Сила реакции опоры и сила нормального давления — равные по модулю, но противоположные по направлению силы. Если тело не перемещается с ускорением относительно оси ОУ, модули силы реакции опоры и силы нормального давления равны модулю силы тяжести, действующей на это тело.
Силу трения скольжения зависит от степени неровности (шероховатости) поверхности. Поэтому ее можно легко менять.
Чтобы увеличить силу трения скольжения, нужно сделать поверхность тела более шероховатой. Так, чтобы зимой автомобили не скользили по голому льду, автомобилисты используют зимние шины. От летних они отличаются глубоким протектором и наличием шипов, создающих дополнительную неровность.
Чтобы уменьшить силу трения скольжения, нужно сделать поверхность более ровной. Ее можно отшлифовать или смазать. Так, чтобы лыжи скользили по снегу лучше, их смазывают специальными мазями или парафинами.
Полезные факты
- Если тело движется по гладкой поверхности, сила трения между ними отсутствует.
- Сила трения скольжения не зависит от площади соприкосновения тел.
- Сила трения качения обычно в несколько раз меньше силы трения скольжения. Поэтому тяжелые грузы перемещают не волоком, а с помощью тележек на колесах.
Пример №1. Конькобежец массой 70 кг скользит по льду. Какова сила трения, действующая на конькобежца, если коэффициент трения скольжения коньков по льду равен 0,002?
Сила реакции опоры по модулю равна силе тяжести, действующей на конькобежца. Отсюда:
Трение покоя
Трение покоя возникает при попытке сдвинуть предмет с места. Трение покоя противоположно направлено приложенной к телу силе (в сторону возможного движения).
Сила трения покоя всегда больше нуля, но всегда меньше силы трения скольжения:
0 < Fтр.пок. < Fтр. ск.
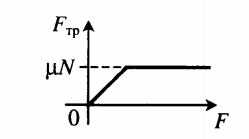
Способы определения вида силы трения, возникающей между телами, и ее модуля:
- Когда к телу прикладывается сила F , модуль которой меньше силы трения скольжения, возникает сила трения покоя. Тело продолжает покоиться. При этом модуль силы трения покоя равен модулю прикладываемой к телу силы. Если F < Fтр. ск., Fтр.пок. = F.
- Когда к телу прикладывается сила, модуль которой равен силе трения скольжения или превышает ее, возникает сила трения скольжения. Тело при этом начинает двигаться. Сила трения определяется формулой силы трения скольжения. Если F ≥ Fтр. ск., Fтр. = Fтр.ск.
Графически это можно изобразить так:
Пример №2. На горизонтальном полу стоит ящик массой 20 кг. Коэффициент трения между полом и ящиком равен 0,3. К ящику в горизонтальном направлении прикладывают силу 36 Н. Какова сила трения между ящиком и полом?
Чтобы определить вид трения, возникающего между ящиком и полом, нужно найти силу трения скольжения и сравнить с ней приложенную к ящику силу.
Сила, приложенная к ящику, меньше силы трения скольжения. Значит, между ящиком и полом возникает сила трения покоя. Модуль силы трения покоя равен модулю приложенной силы:
Fтр.пок. = F = 36 (Н).
Описание движения тел с учетом сил трения
Тело может двигаться по горизонтальной, наклонной или вертикальной плоскости. Оно может покоиться, двигаться равномерно или с ускорением, а сила тяги, под действием которой движется тело, может быть направлена, как в сторону движения тела, так и под углом к плоскости. Поэтому применение законов Ньютона к каждому из случаев имеет свои особенности.
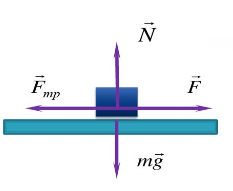
Движение тела по горизонтальной плоскости
Равноускоренное движение по горизонтали, сила тяги параллельная плоскости |
|
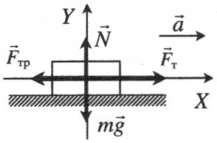 |
Второй закон Ньютона в векторной форме:
mg + N + Fт + Fтр = ma Проекция на ось ОХ: Fт – Fтр = ma Проекция на ось ОУ: N – mg = 0 |
Равнозамедленное движение по горизонтали, сила тяги параллельная плоскости |
|
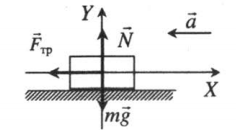 |
Второй закон Ньютона в векторной форме:
mg + N + Fт + Fтр = ma Проекция на ось ОХ: – Fтр = –ma Проекция на ось ОУ: N – mg = 0 |
Ускоренное движение по горизонтали, сила тяги направлена под углом к горизонту (вверх) |
|
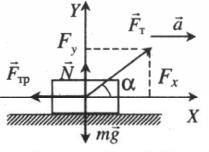 |
Второй закон Ньютона в векторной форме:
mg + N + Fт + Fтр = ma Проекция на ось ОХ: Fтcosα – Fтр = ma Проекция на ось ОУ: Fтsinα + N – mg = 0 |
Ускоренное движение по горизонтали, сила тяги направлена под углом к горизонту (вниз) |
|
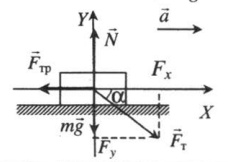 |
Второй закон Ньютона в векторной форме:
mg + N + Fт + Fтр = ma Проекция на ось ОХ: Fтcosα – Fтр = ma Проекция на ось ОУ: N – Fтsinα – mg = 0 |
Внимание! В случаях, когда сила тяги Fт направлена под углом к плоскости движения, сила реакции опоры не равна силе тяжести: N ≠ mg.
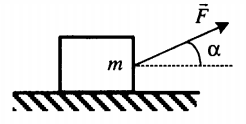
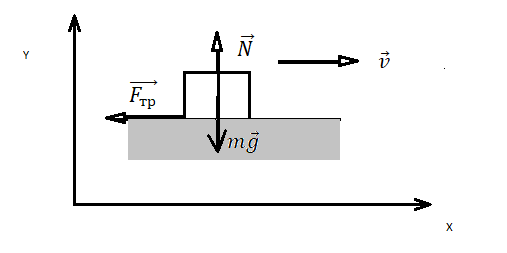
Пример №3. Брусок массой 1 кг движется равноускоренно по горизонтальной поверхности под действием силы 10 Н, как показано на рисунке. Коэффициент трения скольжения равен 0,4, а угол наклона α — 30 градусов. Чему равен модуль силы трения?
Сила трения равна произведению коэффициента трения скольжения на силу реакции опоры:
Fтр = μN
Проекция сил на ось ОУ выглядит так:
N – Fтsinα – mg = 0
Отсюда силы реакции опоры равна:
N = Fтsinα + mg
Подставим ее в формулу для вычисления силы трения и получим:
Fтр = μN = μ (Fтsinα + mg) = 0,4(10∙0,5 + 1∙10) = 6 (Н)
Движение тела по вертикальной плоскости
Тело прижали к вертикальной плоскости и удерживают |
|
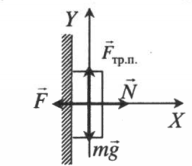 |
Второй закон Ньютона в векторной форме:
mg + N + Fт + Fтр = ma Проекция на ось ОХ: N – F = 0 Проекция на ось ОУ: Fт.п. – mg = 0 |
Тело поднимается под действием силы тяги, направленной под углом к вертикали |
|
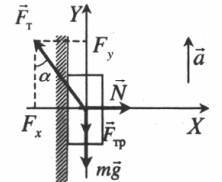 |
Второй закон Ньютона в векторной форме:
mg + N + Fт + Fтр = ma Проекция на ось ОХ: N – Fтsinα = 0 Проекция на ось ОУ: Fтcosα – Fтр – mg = 0 |
Пример №4. Груз массой 50 кг удерживают на вертикальной плоскости, коэффициент трения которой равен 0,4. Определить, какую силу нужно приложить, чтобы груз оставался в состоянии покоя.
Проекция на ось ОХ:
N – F = 0
Отсюда следует, что сила должна быть равна силе реакции опоры.
Проекция на ось ОУ:
Fт.п. – mg = 0
Перепишем, выразив силу трения через силу реакции опоры:
μN – mg = 0
Отсюда выразим силу реакции опоры:
Следовательно:
Движение тела по наклонной плоскости
Движение вниз без трения |
|
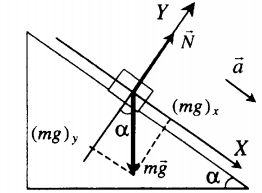 |
Второй закон Ньютона в векторной форме: |
|
mg + N = ma |
|
| Проекция на ось ОХ: | |
|
mg sinα = ma |
|
| Проекция на ось ОУ: | |
|
N – mg cosα = 0 |
|
Тело покоится на наклонной плоскости |
|
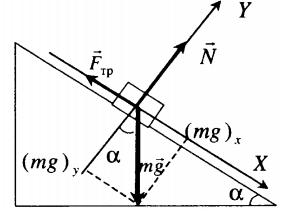 |
Второй закон Ньютона в векторной форме: |
|
mg + N + Fтр = ma |
|
| Проекция на ось ОХ: | |
|
mg sinα – Fтр.п. = 0 |
|
| Проекция на ось ОУ: | |
|
N – mg cosα = 0 |
|
Тело удерживают на наклонной плоскости |
|
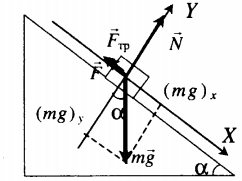 |
Второй закон Ньютона в векторной форме: |
|
mg + N + F + Fтр = ma |
|
| Проекция на ось ОХ: | |
|
F + Fтр. – mg sinα = ma |
|
| Проекция на ось ОУ: | |
|
N – mg cosα = 0 |
|
Равноускоренное движение вверх с учетом силы трения |
|
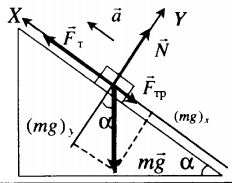 |
Второй закон Ньютона в векторной форме: |
|
mg + N + Fт + Fтр = ma |
|
| Проекция на ось ОХ: | |
|
Fт – mg sinα – Fтр. = ma |
|
| Проекция на ось ОУ: | |
|
N – mg cosα = 0 |
|
Равномерное движение вверх с учетом силы трения |
|
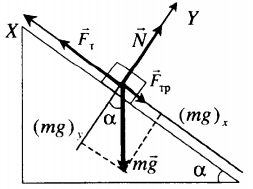 |
Второй закон Ньютона в векторной форме: |
|
mg + N + F + Fтр = ma |
|
| Проекция на ось ОХ: | |
|
Fт – mg sinα – Fтр. = 0 |
|
| Проекция на ось ОУ: | |
|
N – mg cosα = 0 |
Пример №5. Брусок массой 200 г покоится на наклонной плоскости. Коэффициент трения между поверхностью бруска и плоскостью равен 0,6. Определите величину силы трения, если угол наклона плоскости к горизонту равен 30 градусам.
Переведем массу в килограммы: 200 г = 0,2 кг.
Проекция сил, действующих на тело, на ось ОХ:
mg sinα – Fтр.п. = 0
Отсюда сила трения равна:
Fтр.п. = mg sin α
Подставляем известные данные и вычисляем:
Fтр.п. = 0,2∙10∙sin30o = 2∙0,5 = 1 (Н)
Полезная информация
Задание EF18204
При исследовании зависимости силы трения скольжения Fтр от силы нормального давления Fд были получены следующие данные:
|
Fтр, Н |
1,0 |
2,0 |
3,0 |
4,0 |
|
Fд, Н |
2,0 |
4,0 |
6,0 |
8,0 |
Из результатов исследования можно сделать вывод, что коэффициент трения скольжения равен:
а) 0,2
б) 2
в) 0,5
г) 5
Алгоритм решения
1.Записать формулу, связывающую силу трения с силой нормального давления.
2.Выразить из нее коэффициент трения.
3.Взять значения силы трения и силы нормального давления из любого опыта (из любого столбца таблицы).
4.Вычислить коэффициент трения на основании табличных данных.
Решение
Силу трения и силу нормального давления связывает формула:
Fтр = μN
Отсюда коэффициент трения равен:
Сделаем расчет коэффициента трения на основании данных первого опыта (1 столбца):
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17513
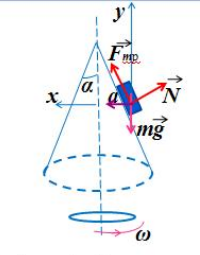
Полый конус с углом при вершине 2α вращается с угловой скоростью ω вокруг вертикальной оси, совпадающей с его осью симметрии. Вершина конуса обращена вверх. На внешней поверхности конуса находится небольшая шайба, коэффициент трения которой о поверхность конуса равен μ. При каком максимальном расстоянии L от вершины шайба будет неподвижна относительно конуса? Сделайте схематический рисунок с указанием сил, действующих на шайбу.
Алгоритм решения
1.Построить чертеж. Указать все силы, действующие на шайбу. Выбрать систему координат.
2.Записать второй закон Ньютона для описания движения шайбы в векторном виде.
3.Записать второй закон Ньютона в виде проекций на оси.
4.Через систему уравнений вывести искомую величину.
Решение
Так как шайба вращается, покоясь на поверхности конуса, на нее действуют четыре силы: сила трения, сила тяжести, сила реакции опоры и центростремительная сила. Изобразим их на чертеже. Выберем систему координат, параллельную оси вращения.
Второй закон Ньютона в векторном виде выглядит следующим образом:
Теперь запишем этот закон в проекциях на оси ОХ и ОУ соответственно:
Так как шайба покоится относительно поверхности конуса, сила трения равна силе трения покоя:
Максимальное значение силы трения равно:
Принимая в учет силу трения покоя, проекции на оси ОХ и ОУ примут следующий вид:
Запишем систему уравнение в следующем виде:
Поделим первое уравнение на второе и получим:
Сделаем сокращения и получим:
Отсюда центростремительное ускорение равно:
Но также известно, что центростремительное ускорение равно произведению квадрата угловой скорости на радиус окружности:
Радиус окружности, по которой вращается шайба вместе с конусом, можно вычислить по формуле:
Отсюда центростремительное ускорение равно:
Выразим искомую величину L:
Подставим в это выражение выведенную для центростремительного ускорения формулу и получим:
Поделим числитель на синус угла α, чтобы упростить выражение, и получим:
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18051
Грузовик массой m, движущийся по прямолинейному горизонтальному участку дороги со скоростью υ, совершает торможение до полной остановки. При торможении колёса грузовика не вращаются. Коэффициент трения между колёсами и дорогой равен μ. Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать.
К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
Алгоритм решения
1.Записать исходные данные.
2.Сделать чертеж. Указать все силы, действующие на грузовик во время торможения. Выбрать систему координат.
3.Записать второй закон Ньютона в векторной форме.
4.Записать второй закон Ньютона в виде проекций на оси ОХ и ОУ.
5.Записать формулу для нахождения силы трения скольжения.
6.Записать формулу для расчета перемещения при движении с постоянным ускорением.
7.Использовать второй закон Ньютона для определения тормозного пути.
Решение
Из условий задачи нам известны следующие величины:
• Начальная скорость грузовика (до начала торможения) v0 = v.
• Коэффициент трения между колесами и дорогой μ.
Выполним чертеж. Выберем такую систему координат, в которой направление движения грузовика во время торможения совпадает с направлением оси ОХ:
Запишем второй закон Ньютона в векторной форме:
Запишем второй закон Ньютона в проекциях на оси:
Fтр = ma
N – mg = 0
Известно, что сила трения скольжения определяется формулой:
Fтр = μN = μmg
Значит, в первую ячейку таблицы мы должны поставить «1».
Перемещение при равнозамедленном движении определяется формулой (учтем, что конечная скорость равна 0, так как грузовик остановился):
Выразим ускорение через проекцию сил на ось ОХ:
Подставим найденное ускорение в формулу тормозного пути и получим:
Следовательно, во вторую ячейку таблицы мы должны поставить «4».
Полный ответ: «14».
Ответ: 14
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 14.6k

{mu = dfrac{F_{тр}}{mg}}
Ускорение свободного падения g
Приводим 2 варианта нахождения коэффициента трения — зная силу трения и массу тела или зная угол наклона. Для обоих вариантов вы найдете удобные калькуляторы и формулы для расчета.
Коэффициент трения представляет собой безразмерную скалярную величину, которая равна отношению силы трения между двумя телами и силы, прижимающей их друг к другу, во время или в начале скольжения.
Коэффициент трения чаще всего обозначают греческой буквой µ («мю»).
Следует помнить, что коэффициент трения (μ) величина безразмерная, то есть не имеет единицы измерения.
Коэффициент трения зависит от качества обработки трущихся поверхностей, скорости движения тел относительно друг друга и материала соприкасающихся поверхностей. В большинстве случаев коэффициент трения находится в пределах от 0,1 до 0,5 (см. таблицу).
Содержание:
- калькулятор коэффициента трения
- формула коэффициента трения через силу трения и массу
- формула коэффициента трения через угол наклона
- таблица коэффициентов трения
- примеры задач
Формула коэффициента трения через силу трения и массу
mu = dfrac{F_{тр}}{mg}
Fтр — сила трения
m — масса тела
g — ускорение свободного падения (в большинстве задач можно принять g=9.81 м/с²)
Формула коэффициента трения через угол наклона
mu = tg(alpha)
α — угол наклона
Таблица коэффициентов трения скольжения для разных пар материалов
| Трущиеся материалы (при сухих поверхностях) | Коэффициенты трения | |
|---|---|---|
| покоя | при движении | |
| Резина по сухому асфальту | 0,95-1,0 | 0,5-0,8 |
| Резина по влажному асфальту | 0,25-0,75 | |
| Алюминий по алюминию | 0,94 | |
| Бронза по бронзе | 0,20 | |
| Бронза по чугуну | 0,21 | |
| Дерево по дереву (в среднем) | 0,65 | 0,33 |
| Дерево по камню | 0,46-0,60 | |
| Дуб по дубу (вдоль волокон) | 0,62 | 0,48 |
| Дуб по дубу (перпендикулярно волокнам) | 0,54 | 0,34 |
| Железо по железу | 0,15 | 0,14 |
| Железо по чугуну | 0,19 | 0,18 |
| Железо по бронзе (слабая смазка) | 0,19 | 0,18 |
| Канат пеньковый по деревянному барабану | 0,40 | |
| Канат пеньковый по железному барабану | 0,25 | |
| Каучук по дереву | 0,80 | 0,55 |
| Каучук по металлу | 0,80 | 0,55 |
| Кирпич по кирпичу (гладко отшлифованные) | 0,5-0,7 | |
| Колесо со стальным бандажем по рельсу | 0,16 | |
| Лед по льду | 0,05-0,1 | 0,028 |
| Метал по аботекстолиту | 0,35-0,50 | |
| Метал по дереву (в среднем) | 0,60 | 0,40 |
| Метал по камню (в среднем) | 0,42-0,50 | |
| Метал по металу (в среднем) | 0,18-0,20 | |
| Медь по чугуну | 0,27 | |
| Олово по свинцу | 2,25 | |
| Полозья деревянные по льду | 0,035 | |
| Полозья обитые железом по льду | 0,02 | |
| Резина (шина) по твердому грунту | 0,40-0,60 | |
| Резина (шина) по чугуну | 0,83 | 0,8 |
| Ремень кожаный по деревянному шкиву | 0,50 | 0,30-0,50 |
| Ремень кожаный по чугунному шкиву | 0,30-0,50 | 0,56 |
| Сталь по железу | 0,19 | |
| Сталь(коньки) по льду | 0,02-0,03 | 0,015 |
| Сталь по райбесту | 0,25-0,45 | |
| Сталь по стали | 0,15-0,25 | 0,09 (ν = 3 м/с)
0,03 (ν = 27 м/с) |
| Сталь по феродо | 0,25-0,45 | |
| Точильный камень (мелкозернистый) по железу | 1 | |
| Точильный камень (мелкозернистый) по стали | 0,94 | |
| Точильный камень (мелкозернистый) по чугуну | 0,72 | |
| Чугун по дубу | 0,65 | 0,30-0,50 |
| Чугун по райбесту | 0,25-0,45 | |
| Чугун по стали | 0,33 | 0,13 (ν = 20 м/с) |
| Чугун по феродо | 0,25-0,45 | |
| Чугун по чугуну | 0,15 |
Примеры задач на нахождение коэффициента трения
Задача 1
Найдите коэффициент трения между полом и ящиком массой 20 кг, который равномерно двигают с силой 50 Н.
Решение
Для решения задачи воспользуемся формулой.
mu = dfrac{F_{тр}}{mg} = dfrac{50}{20 cdot 9.81} = dfrac{50}{196.2} approx 0.25484
Ответ: approx 0.25484
С помощью калькулятора удобно проверить ответ.
Задача 2
Найдите коэффициент трения если угол наклона 30°.
Решение
Для решения этой задачи воспользуемся второй формулой.
mu = tg(alpha) = tg(30°) approx 0.57735
Ответ: approx 0.57735
Проверим полученный ответ с помощью калькулятора .