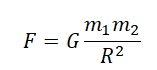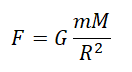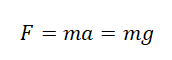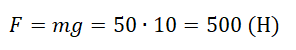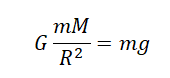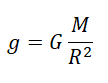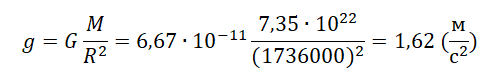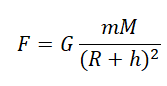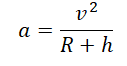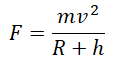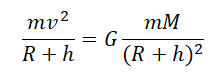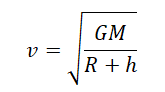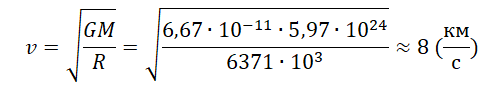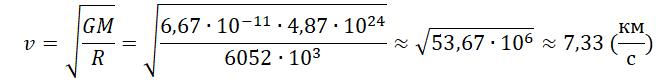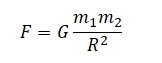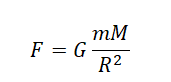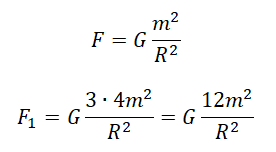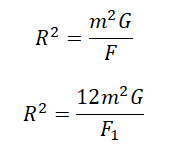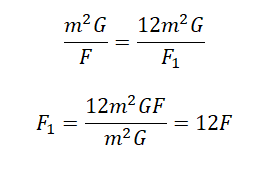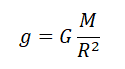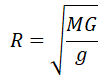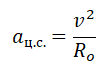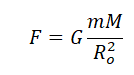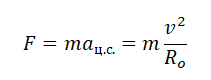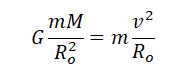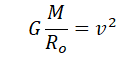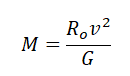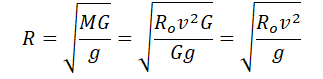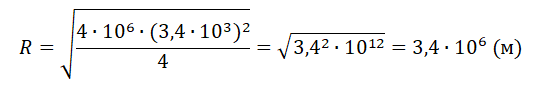Характер и особенности расчета силы притяжения известны еще с древних времен. На основании имеющихся знаний, переданных современному научному сообществу великими исследователями, человек познает не только его окружающий мир, но и Вселенную.
Формула силы притяжения
Со времен Древней Греции философов интересовали явления притяжения тел к земле и свободного падения. К примеру, по утверждениям Аристотеля, из двух камней, брошенных с одинаковой высоты, быстрее достигнет земной поверхности тот, чья масса больше. В IV веке до нашей эры единственными методами научных изысканий служили наблюдения и анализ. К проверке гипотез опытным путем великие мыслители не прибегали. По истечению столетий физик из Италии Галилео Галилей проверил утверждения Аристотеля, используя практические методы исследований.
Итоги проведенных Галилеем опытов были опубликованы в «Беседах и математических доказательствах, касающихся двух новых наук». Ученый использовал псевдоним Сагредо: «пушечное ядро не опередит мушкетной пули при падении с высоты двухсот локтей». Формулировка закона всемирного тяготения была представлена в 1666 году Исааком Ньютоном. В ней фиксировались основные тезисы теоремы Галилея.
Смысл заключался в том, что тела, которые обладают разными массами, падают на землю с одинаковыми ускорениями. Одно тело притягивает другое и, наоборот, с силой, которая прямо пропорциональна их массам и обратно пропорциональна отрезку пути между ними. Согласно определению гравитации от Ньютона, тела, характеризующиеся массой, обладают свойством, благодаря которому притягиваются друг к другу.
Понятие и определение
Силы взаимного притяжения – это силы, которые притягивают любые тела, обладающие массами.
Корректность выводов Ньютона неоднократно подтверждалась путем практических испытаний. Но в начале ХХ века перед учеными-физиками остро стоял вопрос о природе и характере взаимодействия крупных астрономических тел, включая разные виды планетарных систем и галактик в вакууме. Ньютоновского закона уже было недостаточно, чтобы решить эти задачи. Исключить недочеты позволила новая теория, разработанная Альбертом Эйнштейном в начале ХХ столетия. Общая теория относительности объясняет гравитацию не в качестве силы, а представляет ее в виде искривления пространства и времени в четырех измерениях, которое зависит от массы тел, создающих его.
Гравитация представляет собой свойство тел, которые характеризуются массой, притягивать друг друга. Данное физическое явление можно объяснить, как поле, оказывающее дистанционное воздействие на предметы, не связанные между собой никаким другим способом.
Достижение Эйнштейна не противоречит теоретическому объяснению гравитации от Ньютона. Общая теория относительности рассматривает закон всемирного тяготения, как частный случай, применимый для сравнительно небольших расстояний. Данная закономерность в настоящее время также активно используется для поиска решений задач на практике.
Единицы измерения силы притяжения
В разных системах измерений можно встретить несколько отличающиеся обозначения. Единицы измерения силы притяжения следующие:
- система СИ: ([F]=H);
- система СГС: ([F]=дин).
Формула силы притяжения между телами в космосе
Закономерность гравитации, которую обнаружил Ньютон, можно представить в виде математической формулы. Вычисления выглядят следующим образом:
(F=(Gtimes m1times m2times r)/2),
где (m1,m2) — массы объектов, которые притягиваются друг к другу под действием силы (F),
(r) – расстояние, на которое удалены тела,
(G) — т.н. гравитационная постоянная величина, константа, равная 6,67.
Гравитационное взаимодействие объектов будет слабеть, если тела удаляются друг относительно друга. Сила гравитации пропорциональна величине расстояния в квадрате. При этом для нахождения искомой величины расстояние измеряется от центров тяжести тел, а не от поверхностей.
Гравитация в определенных моментах напоминает другие физические явления. Исходя из зависимости интенсивности силы от расстояния в квадрате, гравитацию можно сравнить с электромагнитным взаимодействием сильного и слабого характера.
Формула силы гравитационного притяжения между двумя телами
Квадратичная связь силы, с которой тела притягиваются друг к другу, с расстоянием между ними объясняет тот факт, что люди, находящиеся на поверхности планеты Земля не притягиваются к Солнцу, хотя масса его велика и превышает земную в миллион раз. Земля и центр Солнечной системы удалены примерно на 150 миллионов километров. Дистанция достаточно велика, чтобы ощущаться человеком. Однако эту силу можно зарегистрировать, используя высокоточные приборы. В рамках планеты Земля сила, с которой тела к ней притягиваются, то есть их вес, измеряется следующим образом:
(P=mtimes g),
где (m) – масса тела, на которое воздействует сила притяжение,
(g) – ускорение свободного падения около Земли (если рассматривать систему в условиях любой другой планеты, данная величина будет отличаться).
На разных географических широтах величина ускорения свободного падения может незначительно отличаться. Производя расчеты, данный показатель принимается за 9,81 метров в секунду в квадрате.
В физике понятия массы и веса тел отличаются. Весом называется сила, определяющее притяжение объекта к планете. Масса представляет собой меру инертности вещества. На нее не влияют другие тела, расположенные рядом.
Формула для силы притяжения тел произвольной формы
Расчеты определяются некоторыми условиями. К ним относятся характеристики исследуемых объектов.
Если сила притяжения измеряется между телами, которые обладают произвольной формой, их считают материальными точками:
(dtimes m1=rho1times dV1)
(dtimes m2=rho2times dV2)
где (rho1, rho2) – обозначают плотность веществ материальных точек, характерных для первого и второго объектов,
(dV1 ,dV2) — элементарные объемы выделенных материальных точек.
Исходя из этого, сила притяжения (doverline F), с которой взаимодействуют объекты, равна:
(doverline F=-Gtimes frac{rho _{1}timesrho _{2}times dtimes V_{1}times dtimes V_{2}}{r_{12}^{3}} bar{r_{12}})
Таким образом, сила притяжения первого тела вторым рассчитывается следующим образом:
(bar{F}_{12}=-Gtimesint_{V_{1}}^{rho _{1}times dtimes V_{1}}int_{V_{2}}^{frac{rho _{2}}{r_{12}^{3}}times bar{r}_{12}times dtimes V_{2}})
где интегрирование выполняется по всему объему первого ((V1)) и второго ((V2)) тел. Если тела обладают однородностью, то формула корректируется, таким образом:
(bar{F}_{12}=-Gtimesrho1timesrho2timesint_{V_{1}}^{dtimes V_{1}}int_{V_{2}}^{frac{bar{r}_{12}}{r_{12}^{3}}times dtimes V_{2}})
Формула для силы притяжения твердых тел шарообразной формы
В условиях, когда сила притяжения измеряется между телами, представленных в форме шара или близкой к нему, с плотностью, зависящей лишь от удаленности их центров тяжести, применяется следующая формула:
(bar{F}_{12}=-Gtimes(m1times m2)/R^3times R12)
где (m1,m2) – массы шаров, (R )– радиус – вектор, соединяющий центры шаров.
Пример применения формулы для расчета
Задача. Необходимо рассчитать силу притяжения между двумя идентичными однородными шарами, масса которых составляет по 1 килограмму. При этом их центры тяжести удалены на 1 метр друг от друга.
Решение будет выглядеть следующим образом:
Используя формулу для подсчета силы притяжения между двумя объектами шарообразной формы, получается:
(F_g=6.67times 10^{-11}times frac{1times 1}{1^{2}})
Ответ: (F_g=6.67times 10^{-11})
Выполнить расчет силы притяжения достаточно просто, если правильно выбрать формулу, подходящую под конкретные условия, в которых находятся тела. Если в процессе решения задач по физике или другим дисциплинам возникают проблемы, всегда можно обратиться за помощью к компетентным специалистам портала Феникс.Хелп.
Все тела взаимодействуют друг с другом. Так, две материальные точки, обладающие массой, притягиваются друг к другу с некоторой силой, которую называют гравитационной, или силой всемирного тяготения.
Сила всемирного тяготения — сила, с которой все тела притягиваются друг к другу.
Закон всемирного тяготения
Сила взаимного притяжения двух тел прямо пропорциональна произведению масс этих тел и обратно пропорциональна квадрату расстояния между ними.
F — сила всемирного тяготения, m1 и m2 — массы двух притягивающихся друг к другу тел, R — расстояние между этими телами, G — гравитационная постоянная (G = 6,67∙10–11 Н ∙ м2/кг2).
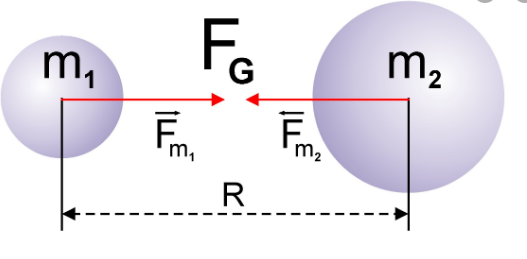
Сила всемирного тяготения направлена по линии, соединяющей центры двух тел.
Гравитационная постоянная численно равна силе притяжения между двумя точечными телами массой 1 кг каждое, если расстояние между ними равно 1 м. Если R = 1 м, m1 = 1 кг и m2 = 1 кг, то F = G.
G = 6,67∙10–11 Н ∙ м2/кг2.
Сила тяжести
Согласно закону всемирного тяготения, все тела притягиваются между собой. Так, Земля притягивает к себе падающий на нее мяч, а мяч притягивает к себе Землю.
Сила тяжести — сила, с которой Земля притягивает к себе тела.
Сила тяжести действует на все тела, находящиеся в поле притяжения Земли. Она всегда направлена к центру нашей планеты.
Расчет силы тяжести на Земле
Силу тяжести можно рассчитать с помощью закона всемирного тяготения. Тогда одна из масс будет равна массе земли. Обозначим ее большой буквой M. Вторая масса будет принадлежать телу, притягивающемуся к Земли. Обозначим его m. В качестве R будет служить радиус Земли. В таком случае сила тяжести будет определяться формулой:
Вывод формулы ускорения свободного падения
Согласно второму закону Ньютона, сила, которая действует на тело, сообщает ему ускорение. Поэтому силу тяжести также можно выразить через это ускорение. Обозначим его g — ускорение свободного падения.
Пример №1. Мальчик массой 50 кг прыгнул под углом 45 градусов к горизонту. Найти силу тяжести, действующую на него во время прыжка.
Сила тяжести зависит только от массы тела и ускорения свободного падения. Направлена она всегда к центру Земли, и от характера движения тела не зависит. Поэтому:
Мы получили две формулы для вычисления силы тяжести: одну — исходя из закона всемирного тяготения, вторую — исходя из второго закона Ньютона. Приравняем правые части формул и получим:
Отсюда:
Формула расчета ускорения свободного падения
Вместо массы и радиуса Земли можно взять массы и радиусы любых планет. Так можно рассчитать ускорение свободного падения для любого космического тела.
Пример №2. Рассчитать ускорение свободного падения на Луне. Считать, что радиус Луны равен 1736 км, а ее масса — 7,35∙1022 кг.
Переведем километры в метры: 1736 км = 1736000 м.
Первая космическая скорость
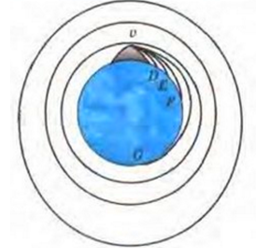
Исаак Ньютон смог доказать, что причиной падения тел на Землю, движения Луны вокруг Земли и движения Земли вокруг Солнца является сила тяготения. Если камень бросить в горизонтальном направлении, его траектория будет отклонена от прямой линии под действием земной силы тяжести. Если же придать этому камню большую скорость, камень приземлится на большем расстоянии. Значит, существует такая скорость, при которой камень не приземлится, а начнет бесконечно вращаться вокруг Земли.
ОпределениеПервая космическая скорость — минимальная (для заданной высоты над поверхностью планеты) горизонтальная скорость, которую необходимо придать объекту, чтобы он совершал движение по круговой орбите вокруг планеты.
Вывод формулы первой космической скорости
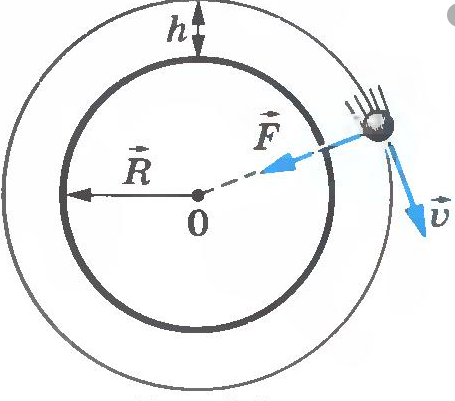
Когда тело массой m вращается на некоторой высоте h, расстояние между ним и центром Земли равно сумме этой высоты и радиуса Земли. Поэтому сила тяготения между этим телом и Землей будет равна:
Движение тела вокруг планеты — частный случай движения тела по окружности с постоянной по модулю скоростью. Мы уже знаем, что такое тело движется с центростремительным ускорением, направленным к центру окружности. В данном случае центростремительное ускорение будет направлено к центру Земли. Это ускорение сообщает телу сила тяготения.
Так как тело движется на некоторой высоте h от поверхности Земли, центростремительное ускорение будет определяться формулой:
Подставив это ускорение в формулу второго закона Ньютона, получим силу, с которой Земля притягивает к себе тело массой m:
Приравняем правые части формул, следующих из закона всемирного тяготения и второго закона Ньютона, и получим:
Отсюда скорость, с которой должно тело массой m бесконечно вращаться вокруг Земли на высоте h, равна:
Скорость бесконечно вращающегося вокруг Земли тела не зависит от его массы. Она зависит только от высоты, на которой оно находится. Чем выше высота, тем меньше скорость его вращения.
Тело, вращающееся вокруг планеты, называется ее спутником. Чтобы любое тело стало спутником Земли, нужно сообщить ему некоторую скорость на поверхности планеты в горизонтальном направлении. Высота h в этом случае равна 0. Тогда эта скорость будет равна:
8 км/с — первая космическая скорость Земли.
Пример №3. Рассчитать первую космическую скорость для Венеры. Считать, что масса Венеры равна 4,87∙1024 кг, а ее радиус равен 6052 км.
Задание EF18521
Сила гравитационного притяжения между двумя шарами, находящимися на расстоянии 2 м друг от друга, равна 9 нН. Какова будет сила притяжения между ними, если расстояние увеличить до 6 м? Ответ выразите в наноньютонах (нН).
Алгоритм решения
- Записать исходные данные.
- Записать закон всемирного тяготения.
- Установить зависимость между силой гравитационного притяжения и расстоянием между телами.
- На основании вывода о зависимости двух величин вычислить гравитационное притяжение между двумя шарами при изменении расстояния между ними.
Решение
Запишем исходные данные:
- Расстояние между двумя шарами в первом случае: R1 = 2 м.
- Расстояние между двумя шарами во втором случае: R2 = 6 м.
- Сила гравитационного притяжения между двумя шарами в первом случае: F1 = 9 нН.
Запишем закон всемирного тяготения:
Из формулы видно, что сила гравитационного притяжения обратно пропорционально квадрату расстояния между телами массами m1 и m2.
R2 больше R1 втрое (6 больше 2 в 3 раза). Следовательно, расстояние между шарами тоже увеличилось втрое. В таком случае сила гравитационного притяжения между ними уменьшится в 32 раз, или в 9 раз. Так как в первом случае эта сила была равна 1 нН, то во втором она составит в 9 раз меньше, или 1 нН.
Ответ: 1
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17569
Две звезды одинаковой массы m притягиваются друг к другу с силами, равными по модулю F. Чему равен модуль сил притяжения между другими двумя звёздами, если расстояние между их центрами такое же, как и в первом случае, а массы звёзд равны 3m и 4m?
а) 7F
б) 9F
в) 12F
г) 16F
Алгоритм решения
1.Записать закон всемирного тяготения.
2.Применить закон всемирного тяготения для первой и второй пары звезд.
3.Из каждого выражения выразить расстояние между звездами.
4.Приравнять правые части уравнений и вычислить силу притяжения между второй парой звезд.
Решение
Закон всемирного тяготения выглядит так:
Примерим этот закон для первой и второй пары звезд:
Выразим квадраты радиусов, так как они в обоих случаях одинаковые:
Приравняем правые части выражений и выразим силу притяжения во втором случае:
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18678
Высота полёта искусственного спутника над Землёй увеличилась с 400 до 500 км. Как изменились в результате этого скорость спутника и его потенциальная энергия?
Для каждой величины определите соответствующий характер изменения:
| 1) | увеличилась |
| 2) | уменьшилась |
| 3) | не изменилась |
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Скорость
спутника |
Потенциальная энергия спутника |
Алгоритм решения
1.Записать закон всемирного тяготения и формулу центростремительного ускорения для движения тела по окружности с постоянной по модулю скоростью.
2.Установить зависимость скорости от высоты спутника над поверхностью Земли.
3.Записать формулу потенциальной энергии и установить, как она зависит от высоты.
Решение
На спутник действует сила притяжения Земли, которая сообщает ему центростремительное ускорение:
F=maц=GmM(R+h)2
Отсюда центростремительное ускорение равно:
aц=GM(R+h)2
Но центростремительное ускорение также равно:
aц=v2(R+h)
Приравняем правые части выражений и получим:
GM(R+h)2=v2(R+h)
v2=MG(R+h)(R+h)2=MG(R+h)
Квадрат скорости спутника обратно пропорционален радиусу вращения. Следовательно, при увеличении высоты увеличивается радиус вращения, а скорость уменьшается.
Потенциальная энергия спутника определяется формулой:
Ep = mgh
Видно, что потенциальная энергия зависит от высоты прямо пропорционально. Следовательно, при увеличении высоты потенциальная энергия спутника тоже увеличивается.
Верная последовательность цифр в ответе: 21.
Ответ: 21
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17578
Искусственный спутник обращается вокруг планеты по круговой орбите радиусом 4000 км со скоростью 3,4 км/с. Ускорение свободного падения на поверхности планеты равно 4 м/с2. Чему равен радиус планеты? Ответ запишите в километрах.
Алгоритм решения
1.Записать исходные данные. Перевести единицы измерения в СИ.
2.Записать формулу ускорения свободного падения и выразить через нее радиус планеты.
3.Записать формулу, раскрывающая взаимосвязь между линейной скоростью и радиусом окружности, по которой движется тело.
4.Записать закон всемирного тяготения применительно к спутнику.
5.Вывести формулу для расчета радиуса планеты.
6.Подставить известные данные и произвести вычисление.
Решение
Запишем исходные данные:
• Линейная скорость спутника: v = 3,4 км/с, или 3,4∙103 м/с.
• Радиус орбиты спутника: Rо = 4000 км, или 4∙106 м.
• Ускорение свободного падения у поверхности планеты: g = 4 м/с2.
Ускорение свободного падения определяется формулой:
Отсюда радиус равен:
Линейная скорость и радиус орбиты связываются формулой:
Используя закон всемирного тяготения, запишем силы, с которой притягивается спутник к планете:
Согласно второму закону Ньютона, сила — это произведение массы на ускорение тела. Следовательно:
Отсюда:
Поделим обе части выражения на массу спутника и радиус его орбиты. Получим:
Из этой формулы выразим массу планеты:
Подставим массу планеты в формулу для нахождения ее радиуса:
Подставляем известные данные и вычисляем:
Этот радиус соответствует 3400 км.
Ответ: 3400
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 18k
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Закон тяготения
Закон всемирного тяготения
Две материальные точки массами (displaystyle m) и (displaystyle M) притягиваются друг к
другу с силой, прямо пропорциональной их массам и обратно пропорциональной квадрату расстояния (displaystyle R) между ними. [F=Gfrac{mM}{R^2}] Гравитационная постоянная — коэффициент пропорциональности
[G=6,67cdot10^{-11} frac{ text{Н}cdot text{м$^2$}}{text{кг$^2$}}]
Сила гравитационного притяжения между двумя шарами равна (F). Во сколько увеличится сила притяжения между шарами, если каждый из них заменить на шар в 4 раза тяжелее, оставив расстояние между шарами неизменным.
По закону всемирного тяготения: [F=Gfrac{M_{1}M_{2}}{R^{2}}] где (M_1) и (M_2) – масса шаров, (R) – радиус между шарами. Так как масса каждого из шаров увеличится в 4, то сила увеличится в 16 раз.
Ответ: 16
Две звезды вращаются вокруг друг друга, сила притяжения между ними равна F. На сколько должно увеличиться расстояние между ними, чтобы сила притяжения осталась неизменной, если масса первой звезды увеличилась в 4 раза?
Сила притяжения между двумя телами равна: [F=Gcdotfrac{M_1M_2}{R^2}] где G – гравитационная постоянная, (M_1), (M_2) – массы тел, R — расстояние между этими телами.
Запишем уравнения до и после того, как изменили массу: [F=
begin{cases}
dfrac{M_1M_2}{R_1^2}\
\
dfrac{4M_1M_2}{R_2^2}
end{cases}
Rightarrow dfrac{M_1M_2}{R_1^2} = dfrac{4M_1M_2}{R_2^2}] [frac{1}{R_1^2}=frac{4}{R_2^2} Rightarrow R_2 =sqrt{R_1^2cdot4} = 2R_1]
Ответ: 2
Сила гравитационного притяжения между двумя шарами равна 200 нН, а расстояние между ними равно 100 м. Какова будет сила притяжения (в нН) между этими шарами, если расстояние между их центрами увеличить в 2 раза
По закону всемирного тяготения: [F=Gfrac{M_{1}M_{2}}{R^{2}}] Составим уравнения для каждого случая, описанного в задаче: [begin{cases}
F_{1}=Gdfrac{M_{1}M_{2}}{R_{1}^2}
\
\
F_{2}=Gdfrac{M_{1}M_{2}}{4R_{1}^2}
end{cases}] Значит сила уменьшится в 4 раза и станет равной 50 нН.
Ответ: 50
Сила гравитационного притяжения между двумя шарами равна (F). Во сколько увеличится сила притяжения между шарами, если один из них заменить на шар в три раза тяжелее, оставив расстояние между шарами неизменным.
По закону всемирного тяготения: [F=Gfrac{M_{1}M_{2}}{R^{2}}] где (M_1) и (M_2) – масса шаров, (R) – радиус между шарами. Так как масса одного из шаров увеличится в три, то и сила увеличится в три раза.
Ответ: 3
Сила гравитационного притяжения между двумя шарами равна (F=100) Н. Какова будет сила притяжения между шарами, если массу каждого из шаров увеличить 2 раза, а расстояние между шарами также увеличить в 2 раза.
По закону всемирного тяготения: [F=Gfrac{M_{1}M_{2}}{R^{2}}] где (M_1) и (M_2) – масса шаров, (R) – радиус между шарами.
Во втором случае сила притяжения равна [F_2=Gfrac{2M_{1}2M_{2}}{4R^{2}}=F=100text{ Н}]
Ответ: 100
Два одинаковых маленьких шарика массой (m) каждый, расстояние между центрами которых равно (r), притягиваются друг к другу с силами, равными по модулю 0,2 пН. Каков модуль сил гравитационного притяжения двух других шариков, если масса каждого из них равна (2m), а расстояние между их центрами равно (2r)? Ответ дайте в пН.
“Демоверсия 2020”
Сила взаимодействия шариков: [F=Gdfrac{mcdot m}{r^2}] Во втором случае: [F=Gdfrac{4m}{4r^2}=Gdfrac{m^2}{r^2}] То есть сила не изменилась
Ответ: 0,2
На Земле на человека действует сила притяжения (F=800) Н. Какая сила будет действовать на этого же человека на Луне, если отношение ускорения свободного падения Луны и Земли равно (dfrac{g_{text{л}}}{g_{text{з}}} = 0,16)? (Ответ дайте в Ньютонах)
Сила приятяжения человека к планете равна: [F = mg] где m – масса человека.
Запишем это уравнение для Земли и Луны соответственно: [F_{text{з}} = mg_{text{з}}] [F_{text{л}} = mg_{text{л}}] Поделив первое уравнение на втрое, получим: [frac{F_{text{з}}}{F_{text{л}}} = frac{g_{text{з}}}{g_{text{л}}} Rightarrow F_{text{л}} = F_{text{з}}cdot frac{g_{text{л}}}{g_{text{з}}}] [F_{text{л}} = 800text{ H}cdot 0,16 = 128text{ H }]
Ответ: 128

УСТАЛ? Просто отдохни
Сила тяжести
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Сила: что это за величина
В повседневной жизни мы часто встречаем, как любое тело деформируется (меняет форму или размер), ускоряется или тормозит, падает. В общем, чего только с разными телами в реальной жизни не происходит. Причиной любого действия или взаимодействия является сила.
Сила — это физическая векторная величина, которую воздействует на данное тело со стороны других тел.
Она измеряется в Ньютонах — это единица измерения названа в честь Исаака Ньютона.
Сила — величина векторная. Это значит, что, помимо модуля, у нее есть направление. От того, куда направлена сила, зависит результат.
Вот стоите вы на лонгборде: можете оттолкнуться вправо, а можете влево — в зависимости от того, в какую сторону оттолкнетесь, результат будет разный. В данном случае результат выражается в направлении движения.
Сила тяготения
В 1682 году Исаак Ньютон открыл Закон Всемирного тяготения. Он звучит так: все тела притягиваются друг к другу, сила всемирного тяготения прямо пропорциональна произведению масс тел и обратно пропорциональна квадрату расстояния между ними.
Формула силы тяготения согласно этому закону выглядит так:
Закон Всемирного тяготения
F = GMm/R2
F — сила тяготения [Н]
M — масса первого тела (часто планеты) [кг]
m — масса второго тела [кг]
R — расстояние между телами [м]
G — гравитационная постоянная
G = 6.67 × 10-11 м3 кг-1 с-2
Когда мы встаем на весы, стрелка отклоняется. Это происходит потому, что масса Земли очень большая, и сила тяготения буквально придавливает нас к поверхности. На более легкой Луне человек весит меньше в шесть раз.
Закон всемирного тяготения используют, чтобы вычислить силы взаимодействия между телами любой формы, если размеры тел значительно меньше расстояния между ними.
Если мы возьмем два шара, то для них можно использовать этот закон вне зависимости от расстояния между ними. За расстояние R между телами в этом случае принимается расстояние между центрами шаров.
Сила тяжести
Сила тяжести — сила, с которой Земля притягивает все тела.
Сила тяжести
F = mg
F — сила тяжести [Н]
m — масса тела [кг]
g — ускорение свободного падения [м/с2]
На планете Земля g = 9,8 м/с2
На первый взгляд сила тяжести очень похожа на вес тела. Действительно, в состоянии покоя на поверхности Земли формулы силы тяжести и веса идентичны. Но разница все-таки есть, давайте разбираться.
Эта формула и правда аналогична силе тяжести. Вес тела в состоянии покоя численно равен массе тела, разница состоит лишь в точке приложения силы.
Сила тяжести — это сила, с которой Земля действует на тело, а вес — сила, с которой тело действует на опору или подвес. Это значит, что у них будут разные точки приложения: у силы тяжести к центру масс тела, а у веса — к опоре.
Также, важно понимать, что сила тяжести зависит исключительно от массы и планеты, на которой тело находится. Вес зависит также от ускорения, с которым движутся тело или опора.
Например, в лифте вес тела зависит от того, куда и с каким ускорением движется тело. А силе тяжести все равно, куда и что движется — она не зависит от внешних факторов.
На второй взгляд сила тяжести очень похожа на силу тяготения. В обоих случаях мы имеем дело с притяжением — значит можем сказать, что это одно и то же. Практически.
Мы можем сказать, что это одно и то же, если речь идет о Земле и каком-то предмете, который к этой планете притягивается. Тогда мы можем даже приравнять эти силы и выразить формулу для ускорения свободного падения.
F = mg
F = GMm/R2
Приравниваем правые части:
mg = GMm/R2
Делим на массу левую и правую части:
g = GM/R2
Это и будет формула ускорения свободного падения. Ускорение свободного падения для каждой планеты уникально, эта формула нужна.
Формула для ускорения свободного падения
g = GM/R2
F — сила тяготения [Н]
M — масса планеты [кг]
R — расстояние между телами [м]
G — гравитационная постоянная
G = 6.67 × 10-11 м3 кг-1 с-2
А теперь задачка
Определить силу тяжести, действующую на тело массой 80 кг.
Решение:
Не смотря на кажущуюся простоту, тут есть над чем подумать.Вроде бы просто нужно взять формулу F = mg, подставить числа и дело в шляпе.
Да, но есть один нюанс: в значении ускорения свободного падения для Земли очень много знаков после запятой. В школе обычно дают то же значения, что мы указывали выше: g = 9,8 м/с2.
В экзаменах ОГЭ и ЕГЭ в справочных данных дают g = 10 м/с2.
Ответ: 800 Н.
Учимся летать
В серии книг Дугласа Адамса «Автостопом по Галактике» говорится, что летать — это просто промахиваться мимо Земли. Если ты промахнулся мимо Земли и достиг первой космической скорости 7,9 км/с, то ты стал искусственным спутником Земли.
Искусственный спутник Земли — космический летательный аппарат, который вращается вокруг Земли по геоцентрической орбите. Чтобы у него так получалось, аппарат должен иметь начальную скорость, равную или большую первой космической скорости.
Кстати, есть еще вторая и третья космические скорости. Вторая космическая скорость — это минимальная скорость, с которой должно двигаться тело, чтобы оно могло без затрат дополнительной работы преодолеть влияние поля тяготения Земли, т. е. удалиться на бесконечно большое расстояние от Земли. А на третьей космической скорости тело вылетит за пределы Солнечной системы.
Подробнее о возможностях полетов и невесомости читайте в нашей статье про вес тела.
Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи!
Сила тяжести, формулы
Основные понятия
Силой тяжести, как физической величиной, является такая сила, которая действует на любое физическое тело, что находится у поверхности Земли или другого небесного тела.
Таким образом, сила тяжести в приповерхностном пространстве состоит из гравитационного притяжения Земли и центробежной силы инерции, которая вызвана вращением планеты вокруг своей оси.
Не нашли что искали?
Просто напиши и мы поможем
Другие силы, к примеру, притяжение Солнца, Юпитера и прочих планет, на поверхности Земли очень малы, и ими пренебрегают. Сила тяжести придаёт всем объектам, в независимости от их размеров и массы, ускорение одной величины, и считается консервативной силой. Её можно рассчитать таким образом:
где (g ⃗ ) – ускорение свободного падения, иными словами, ускорение, придаваемое телу силой притяжения Земли.
На объекты, что перемещаются относительно поверхности Земли, помимо силы тяжести, влияет еще сила Кориолиса. Эта сила имеет место при исследовании перемещения объектов по относительно вращающихся систем отсчета. Учитывая данную силу вместе с физическими силами, что действуют на объект, мы учитываем действие вращения системы отсчёта на перемещение этого объекта.
Различные формулы, касающиеся вычисления силы тяжести
Согласно закону всемирного тяготения, гравитационную силу тяжести, действующую на объект с какой-то массой m на поверхности астрономического сферически симметричного тела с массой M, рассчитывают таким образом:
где (G) – гравитационная постоянная;
(R) – радиус тела.
Данная формула справедлива для тела, у которого масса распределена равномерно по объёму. Причем гравитационная сила тяжести действует на центр тела, то есть центр его тяжести.
Модуль центробежной силы инерции (Q) , что действует на объект, рассчитывается таким образом:
где (a) – отдаленность объекта от оси вращения астрономического тела, в пределах которого рассматривается данная центробежная сила инерции;
(ω) – угловая скорость вращения астрономического тела.
Сложно разобраться самому?
Попробуй обратиться за помощью к преподавателям
Центробежная сила инерции направлена перпендикулярно от оси вращения астрономического тела.
Векторную величину центробежной силы инерции определяют по следующей формуле:
где (vec ) – перпендикулярный к оси вращения вектор, что опущен от неё к указанному объекту, находящемуся у поверхности астрономического тела.
Сила тяжести в данном случае определиться так:
(vec
= vec = vec)
Закон притяжения
Без существования силы тяжести многие явления, кажущаяся для нас привычными, были бы невозможны. Например, дожди, водопады, горные лавины и многие прочие явления. Атмосфера Земли существует исключительно под воздействием силы тяжести. Относительно мелкие астрономические тела не имеют свои атмосферы, так как их силы тяжести недостаточно для их сохранения.
Земная атмосфера играет огромное значение в сохранении всего живого на Земле. Вместе с силой притяжения Земли в приземном пространстве действует сила притяжения Луны. Благодаря её близости на Земле наблюдаются такие явления, как отливы и приливы, а большинство биологических ритмов связаны с вращением Луны. То есть, силу тяжести стоит считать значимой для живой природы.
Если масса одного из тел сильно превышает массу другого, то имеет место гравитационная сила, называемая силой притяжения. Данная сила применима в задачах, которые качаются расчёта силы притяжения на Земле и прочих астрономических телах. Если подставить величину силы притяжения в выражение второго закона Ньютона, то получим:
где (a) – ускорение силы притяжения, которая принуждает объекты притягиваться между собой. Если в задачах задействовано ускорение свободного падения, то данную величину обозначают буквой (g) . Ньютон в своё время математически доказал, при помощи собственного интегрального исчисления, что сила тяжести постоянно сосредоточена в центре тела с большей массой.
Не нашли нужную информацию?
Закажите подходящий материал на нашем сервисе. Разместите задание – система его автоматически разошлет в течение 59 секунд. Выберите подходящего эксперта, и он избавит вас от хлопот с учёбой.
Гарантия низких цен
Все работы выполняются без посредников, поэтому цены вас приятно удивят.
Доработки и консультации включены в стоимость
В рамках задания они бесплатны и выполняются в оговоренные сроки.
Вернем деньги за невыполненное задание
Если эксперт не справился – гарантируем 100% возврат средств.
Тех.поддержка 7 дней в неделю
Наши менеджеры работают в выходные и праздники, чтобы оперативно отвечать на ваши вопросы.
Тысячи проверенных экспертов
Мы отбираем только надёжных исполнителей – профессионалов в своей области. Все они имеют высшее образование с оценками в дипломе «хорошо» и «отлично».
Гарантия возврата денег
Эксперт получил деньги, а работу не выполнил?
Только не у нас!
Деньги хранятся на вашем балансе во время работы над заданием и гарантийного срока
Гарантия возврата денег
В случае, если что-то пойдет не так, мы гарантируем возврат полной уплаченой суммы
Отзывы студентов о нашей работе
«Всё сдал!» — безопасный онлайн-сервис с проверенными экспертами
Используя «Всё сдал!», вы принимаете пользовательское соглашение
и политику обработки персональных данных
Сайт работает по московскому времени:
Принимаем к оплате
Гравитационные силы. Закон всемирного тяготения.
теория по физике 🧲 динамика
Все тела взаимодействуют друг с другом. Так, две материальные точки, обладающие массой, притягиваются друг к другу с некоторой силой, которую называют гравитационной, или силой всемирного тяготения.
Сила всемирного тяготения — сила, с которой все тела притягиваются друг к другу.
Закон всемирного тяготения
Сила взаимного притяжения двух тел прямо пропорциональна произведению масс этих тел и обратно пропорциональна квадрату расстояния между ними.
F — сила всемирного тяготения, m1и m2 — массы двух притягивающихся друг к другу тел, R — расстояние между этими телами, G — гравитационная постоянная (G = 6,67∙10 –11 Н ∙ м 2 /кг 2 ).
Сила всемирного тяготения направлена по линии, соединяющей центры двух тел.
Гравитационная постоянная численно равна силе притяжения между двумя точечными телами массой 1 кг каждое, если расстояние между ними равно 1 м. Если R = 1 м, m1= 1 кг и m2= 1 кг, то F = G.
G = 6,67∙10 –11 Н ∙ м 2 /кг 2 .
Сила тяжести
Согласно закону всемирного тяготения, все тела притягиваются между собой. Так, Земля притягивает к себе падающий на нее мяч, а мяч притягивает к себе Землю.
Сила тяжести — сила, с которой Земля притягивает к себе тела.
Сила тяжести действует на все тела, находящиеся в поле притяжения Земли. Она всегда направлена к центру нашей планеты.
Расчет силы тяжести на Земле
Силу тяжести можно рассчитать с помощью закона всемирного тяготения. Тогда одна из масс будет равна массе земли. Обозначим ее большой буквой M. Вторая масса будет принадлежать телу, притягивающемуся к Земли. Обозначим его m. В качестве R будет служить радиус Земли. В таком случае сила тяжести будет определяться формулой:
Вывод формулы ускорения свободного падения
Согласно второму закону Ньютона, сила, которая действует на тело, сообщает ему ускорение. Поэтому силу тяжести также можно выразить через это ускорение. Обозначим его g — ускорение свободного падения.
Пример №1. Мальчик массой 50 кг прыгнул под углом 45 градусов к горизонту. Найти силу тяжести, действующую на него во время прыжка.
Сила тяжести зависит только от массы тела и ускорения свободного падения. Направлена она всегда к центру Земли, и от характера движения тела не зависит. Поэтому:
Мы получили две формулы для вычисления силы тяжести: одну — исходя из закона всемирного тяготения, вторую — исходя из второго закона Ньютона. Приравняем правые части формул и получим:
Формула расчета ускорения свободного падения
Вместо массы и радиуса Земли можно взять массы и радиусы любых планет. Так можно рассчитать ускорение свободного падения для любого космического тела.
Пример №2. Рассчитать ускорение свободного падения на Луне. Считать, что радиус Луны равен 1736 км, а ее масса — 7,35∙10 22 кг.
Переведем километры в метры: 1736 км = 1736000 м.
Первая космическая скорость
Исаак Ньютон смог доказать, что причиной падения тел на Землю, движения Луны вокруг Земли и движения Земли вокруг Солнца является сила тяготения. Если камень бросить в горизонтальном направлении, его траектория будет отклонена от прямой линии под действием земной силы тяжести. Если же придать этому камню большую скорость, камень приземлится на большем расстоянии. Значит, существует такая скорость, при которой камень не приземлится, а начнет бесконечно вращаться вокруг Земли.
Определение Первая космическая скорость — минимальная (для заданной высоты над поверхностью планеты) горизонтальная скорость, которую необходимо придать объекту, чтобы он совершал движение по круговой орбите вокруг планеты.
Вывод формулы первой космической скорости
Когда тело массой m вращается на некоторой высоте h, расстояние между ним и центром Земли равно сумме этой высоты и радиуса Земли. Поэтому сила тяготения между этим телом и Землей будет равна:
Движение тела вокруг планеты — частный случай движения тела по окружности с постоянной по модулю скоростью. Мы уже знаем, что такое тело движется с центростремительным ускорением, направленным к центру окружности. В данном случае центростремительное ускорение будет направлено к центру Земли. Это ускорение сообщает телу сила тяготения.
Так как тело движется на некоторой высоте h от поверхности Земли, центростремительное ускорение будет определяться формулой:
Подставив это ускорение в формулу второго закона Ньютона, получим силу, с которой Земля притягивает к себе тело массой m:
Приравняем правые части формул, следующих из закона всемирного тяготения и второго закона Ньютона, и получим:
Отсюда скорость, с которой должно тело массой m бесконечно вращаться вокруг Земли на высоте h, равна:
Скорость бесконечно вращающегося вокруг Земли тела не зависит от его массы. Она зависит только от высоты, на которой оно находится. Чем выше высота, тем меньше скорость его вращения.
Тело, вращающееся вокруг планеты, называется ее спутником. Чтобы любое тело стало спутником Земли, нужно сообщить ему некоторую скорость на поверхности планеты в горизонтальном направлении. Высота h в этом случае равна 0. Тогда эта скорость будет равна:
8 км/с — первая космическая скорость Земли.
Пример №3. Рассчитать первую космическую скорость для Венеры. Считать, что масса Венеры равна 4,87∙10 24 кг, а ее радиус равен 6052 км.
Алгоритм решения
- Записать исходные данные.
- Записать закон всемирного тяготения.
- Установить зависимость между силой гравитационного притяжения и расстоянием между телами.
- На основании вывода о зависимости двух величин вычислить гравитационное притяжение между двумя шарами при изменении расстояния между ними.
Решение
Запишем исходные данные:
- Расстояние между двумя шарами в первом случае: R1 = 2 м.
- Расстояние между двумя шарами во втором случае: R2 = 6 м.
- Сила гравитационного притяжения между двумя шарами в первом случае: F1 = 9 нН.
Запишем закон всемирного тяготения:
Из формулы видно, что сила гравитационного притяжения обратно пропорционально квадрату расстояния между телами массами m1 и m2.
R2 больше R1 втрое (6 больше 2 в 3 раза). Следовательно, расстояние между шарами тоже увеличилось втрое. В таком случае сила гравитационного притяжения между ними уменьшится в 3 2 раз, или в 9 раз. Так как в первом случае эта сила была равна 1 нН, то во втором она составит в 9 раз меньше, или 1 нН.
pазбирался: Алиса Никитина | обсудить разбор | оценить
Две звезды одинаковой массы m притягиваются друг к другу с силами, равными по модулю F. Чему равен модуль сил притяжения между другими двумя звёздами, если расстояние между их центрами такое же, как и в первом случае, а массы звёзд равны 3m и 4m?
http://spravochnikvs.com/sila_tyazhesti_formuly
Содержание:
- Определение и формула силы притяжения
- Формула для силы притяжения тел произвольной формы
- Формула для силы притяжения твердых тел шарообразной формы
- Единицы измерения силы притяжения
- Примеры решения задач
Калькулятор расчета силы притяжения
Определение и формула силы притяжения
Определение
Между любыми телами, которые обладают массами, действуют силы, которые притягивают вышеназванные тела друг к другу.
Такие силы называют силами взаимного притяжения.
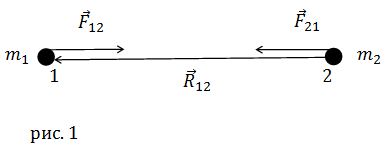
Рассмотрим две материальные точки (рис.1). Они притягиваются с силами прямо пропорциональными произведению масс этих материальных точек и
обратно пропорциональными расстоянию между ними. Так, сила тяготения (
$bar{F}_12$) будет равна:
$$
bar{F}_{12}=-G frac{m_{1} m_{2}}{r^{2}} frac{bar{r}_{12}}{r}(1)
$$
где материальная точка массы m2 действует на материальную точку массы m1 с силой притяжения
$bar{F}_12$; $bar{r}_12$ – радиус – вектор, который проведен из точки 2 в
точку 1, модуль этого вектора равен расстоянию между материальными точками (r); G=6,67•10-11 м3 кг-1
с-2(в системе СИ) – гравитационная постоянная (постоянная тяготения).
В соответствии с третьим законом Ньютона сила, с которой материальная точка 2 притягивается к материальной точке 1 (
$bar{F}_21$) равна:
$$bar{F}_{21}=-bar{F}_{12}=G frac{m_{1} m_{2}}{r^{2}} frac{bar{r}_{12}}{r}=-G frac{m_{1} m_{2}}{r^{2}} frac{bar{r}_{21}}{r}(2)$$
где $bar{r}_12 = — bar{r}_21$
Тяготение между телами осуществляется посредством гравитационного поля (поля тяготения). Силы тяготения являются потенциальными. Это дает возможность ввести такую энергетическую характеристику гравитационного поля как потенциал, который равен отношению потенциальной энергии материальной точки, находящейся исследуемой точке поля к массе данной точки.
Формула для силы притяжения тел произвольной формы
В двух телах произвольной формы и размера выделим элементарные массы, которые можно считать материальными точками, причем:
$$d m_{1}=rho_{1} d V_{1} quad, d m_{2}=rho_{2} d V_{2}$$
где $rho_1, rho_2$ – плотности вещества материальных точек первого и второго тел,
dV1 ,dV2 — элементарные объемы выделенных материальных точек. В таком случае, сила притяжения
($d bar{F}_12$), с которой элемент dm2 действует
на элемент dm1, равна:
$$d bar{F}_{12}=-G frac{rho_{1} rho_{2} d V_{1} d V_{2}}{r_{12}^{3}} bar{r}_{12}(4)$$
Следовательно, сила притяжения первого тела вторым может быть найдена по формуле:
$$bar{F}_{12}=-G int_{V_{1}} rho_{1} d V_{1} quad int_{V_{2}} frac{rho_{2}}{r_{12}^{3}} bar{r}_{12} d V_{2}$$
где интегрирование необходимо произвести по всему объему первого (V1) и второго (V2) тел.
Если тела являются однородными, то выражение можно немного преобразовать и получить:
$$bar{F}_{12}=-G rho_{1} rho_{2} int_{V_{1}} d V_{1} quad int_{V_{2}} frac{bar{r}_{12}}{r_{12}^{3}} d V_{2}$$
Формула для силы притяжения твердых тел шарообразной формы
Если силы притяжения рассматриваются для двух твердых тел шарообразной формы (или близких к шарам), плотность которых зависит только
от расстояний до их центров формула (6) примет вид:
$$bar{F}_{12}=-G frac{m_{1} m_{2}}{R^{3}} bar{R}_{12}(7)$$
где m1,m2 – массы шаров,
$bar{R}_12$ – радиус – вектор, соединяющий центры шаров,
$R=left|bar{R}_{12}right|$
Выражение (7) можно использовать в случае, если одно из тел имеет форму отличную от шарообразной,
но его размеры много меньше, чем размеры второго тела — шара. Так, формулой (7) можно пользоваться для вычислений сил притяжения тел к Земле.
Единицы измерения силы притяжения
Основной единицей измерения силы притяжения (как и любой другой силы) в системе СИ является: [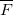
В СГС: [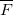
Примеры решения задач
Пример
Задание. Какова сила притяжения двух одинаковых однородных шара масса, которых равна по 1 кг? Расстояние между их центрами равно 1 м.
Решение. Основой для решения задачи служит формула:
$$bar{F}_{g}=-G frac{m_{1} m_{2}}{R^{3}} bar{R}_{12}(1.1)$$
Для вычисления модуля силы притяжения формула (1.1) преобразуется к виду:
$$F_{g}=G frac{m_{1} m_{2}}{R^{2}}$$
Проведем вычисления:
$F_{g}=6,67 cdot 10^{-11} frac{1 cdot 1}{1^{2}}=6,67 cdot 10^{-11}(H)$
Ответ. $F_{g}=6,67 cdot 10^{-11}(H)$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
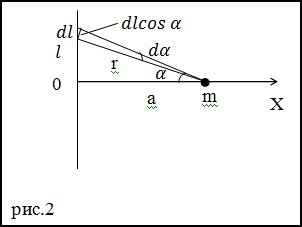
Задание. С какой силой (по модулю) бесконечно длинный и тонкий и прямой стержень притягивает материальную частицу массы m.
Частица расположена на расстоянии a от стержня. Линейная плотность массы вещества стержня равна тау
Решение. Сделаем рисунок
Выделим на стержне элементарный участок массы dm:
$$d m=tau d l(2.1)$$
Силу притяжения между выделенным элементом на стержне и материальной точкой можно найти как:
$$d F=d F_{x}=G frac{d m cdot m}{r^{2}} cos alpha=G frac{tau d l cdot m}{r^{2}} cos alpha$$
Из рис.2 очевидно, что:
$dlcos $alpha=r d alpha$ ( 2.3 )$
Подставим выражение (2.3) в (2.2), имеем:
$$d F=G frac{tau cdot m}{r^{2}} r d alpha=G frac{tau cdot m}{r} d alpha(2.4)$$
Из рис. 2 видно, что:
$$frac{a}{r}=cos alpha rightarrow r=frac{a}{cos alpha}(2.5)$$
Подставим правую часть выражения (2.5) в формулу (2.4), получаем:
$$d F=G frac{tau cdot m}{a} cos alpha d alpha(2.6)$$
Для получения силы, с которой частица притягивается к стержню, проведем интегрирование выражения (2.6). Пределы интегрирования выберем от
0 до пи/2, так как стержень бесконечный умножим выражение на два для того, чтобы интегрирование было выполнено по всему объему стержня.
$$F=2 G frac{tau cdot m}{a} int_{0}^{frac{pi}{2}} cos alpha d alpha=2 G frac{tau cdot m}{a}$$
Ответ. $F=2 G frac{tau cdot m}{a}$
Читать дальше: Формула силы трения.