In the inertial frame of reference (upper part of the picture), the black ball moves in a straight line. However, the observer (red dot) who is standing in the rotating/non-inertial frame of reference (lower part of the picture) sees the object as following a curved path due to the Coriolis and centrifugal forces present in this frame.
In physics, the Coriolis force is an inertial or fictitious force[1] that acts on objects in motion within a frame of reference that rotates with respect to an inertial frame. In a reference frame with clockwise rotation, the force acts to the left of the motion of the object. In one with anticlockwise (or counterclockwise) rotation, the force acts to the right. Deflection of an object due to the Coriolis force is called the Coriolis effect. Though recognized previously by others, the mathematical expression for the Coriolis force appeared in an 1835 paper by French scientist Gaspard-Gustave de Coriolis, in connection with the theory of water wheels.[2] Early in the 20th century, the term Coriolis force began to be used in connection with meteorology.
Newton’s laws of motion describe the motion of an object in an inertial (non-accelerating) frame of reference. When Newton’s laws are transformed to a rotating frame of reference, the Coriolis and centrifugal accelerations appear. When applied to objects with masses, the respective forces are proportional to their masses. The magnitude of the Coriolis force is proportional to the rotation rate, and the magnitude of the centrifugal force is proportional to the square of the rotation rate. The Coriolis force acts in a direction perpendicular to two quantities: the angular velocity of the rotating frame relative to the inertial frame and the velocity of the body relative to the rotating frame, and its magnitude is proportional to the object’s speed in the rotating frame (more precisely, to the component of its velocity that is perpendicular to the axis of rotation). The centrifugal force acts outwards in the radial direction and is proportional to the distance of the body from the axis of the rotating frame. These additional forces are termed inertial forces, fictitious forces, or pseudo forces.[3] By introducing these fictitious forces to a rotating frame of reference, Newton’s laws of motion can be applied to the rotating system as though it were an inertial system; these forces are correction factors that are not required in a non-rotating system.[4]
In popular (non-technical) usage of the term «Coriolis effect», the rotating reference frame implied is almost always the Earth. Because the Earth spins, Earth-bound observers need to account for the Coriolis force to correctly analyze the motion of objects. The Earth completes one rotation for each day/night cycle, so for motions of everyday objects the Coriolis force is imperceptible; its effects become noticeable only for motions occurring over large distances and long periods of time, such as large-scale movement of air in the atmosphere or water in the ocean; or where high precision is important, such as long-range artillery or missile trajectories. Such motions are constrained by the surface of the Earth, so only the horizontal component of the Coriolis force is generally important. This force causes moving objects on the surface of the Earth to be deflected to the right (with respect to the direction of travel) in the Northern Hemisphere and to the left in the Southern Hemisphere. The horizontal deflection effect is greater near the poles, since the effective rotation rate about a local vertical axis is largest there, and decreases to zero at the equator.[5] Rather than flowing directly from areas of high pressure to low pressure, as they would in a non-rotating system, winds and currents tend to flow to the right of this direction north of the equator (anticlockwise) and to the left of this direction south of it (clockwise). This effect is responsible for the rotation and thus formation of cyclones (see Coriolis effects in meteorology).
For an intuitive explanation of the origin of the Coriolis force, consider an object, constrained to follow the Earth’s surface and moving northward in the Northern Hemisphere. Viewed from outer space, the object does not appear to go due north, but has an eastward motion (it rotates around toward the right along with the surface of the Earth). The further north it travels, the smaller the «radius of its parallel (latitude)» (the minimum distance from the surface point to the axis of rotation, which is in a plane orthogonal to the axis), and so the slower the eastward motion of its surface. As the object moves north, to higher latitudes, it has a tendency to maintain the eastward speed it started with (rather than slowing down to match the reduced eastward speed of local objects on the Earth’s surface), so it veers east (i.e. to the right of its initial motion).[6][7]
Though not obvious from this example, which considers northward motion, the horizontal deflection occurs equally for objects moving eastward or westward (or in any other direction).[8] However, the theory that the effect determines the rotation of draining water in a typical size household bathtub, sink or toilet has been repeatedly disproven by modern-day scientists; the force is negligibly small compared to the many other influences on the rotation.[9][10][11]
History[edit]
Image from Cursus seu Mundus Mathematicus (1674) of C.F.M. Dechales, showing how a cannonball should deflect to the right of its target on a rotating Earth, because the rightward motion of the ball is faster than that of the tower.
Image from Cursus seu Mundus Mathematicus (1674) of C.F.M. Dechales, showing how a ball should fall from a tower on a rotating Earth. The ball is released from F. The top of the tower moves faster than its base, so while the ball falls, the base of the tower moves to I, but the ball, which has the eastward speed of the tower’s top, outruns the tower’s base and lands further to the east at L.
Italian scientist Giovanni Battista Riccioli and his assistant Francesco Maria Grimaldi described the effect in connection with artillery in the 1651 Almagestum Novum, writing that rotation of the Earth should cause a cannonball fired to the north to deflect to the east.[12] In 1674, Claude François Milliet Dechales described in his Cursus seu Mundus Mathematicus how the rotation of the Earth should cause a deflection in the trajectories of both falling bodies and projectiles aimed toward one of the planet’s poles. Riccioli, Grimaldi, and Dechales all described the effect as part of an argument against the heliocentric system of Copernicus. In other words, they argued that the Earth’s rotation should create the effect, and so failure to detect the effect was evidence for an immobile Earth.[13] The Coriolis acceleration equation was derived by Euler in 1749,[14][15] and the effect was described in the tidal equations of Pierre-Simon Laplace in 1778.[16]
Gaspard-Gustave Coriolis published a paper in 1835 on the energy yield of machines with rotating parts, such as waterwheels.[17] That paper considered the supplementary forces that are detected in a rotating frame of reference. Coriolis divided these supplementary forces into two categories. The second category contained a force that arises from the cross product of the angular velocity of a coordinate system and the projection of a particle’s velocity into a plane perpendicular to the system’s axis of rotation. Coriolis referred to this force as the «compound centrifugal force» due to its analogies with the centrifugal force already considered in category one.[18][19] The effect was known in the early 20th century as the «acceleration of Coriolis»,[20] and by 1920 as «Coriolis force».[21]
In 1856, William Ferrel proposed the existence of a circulation cell in the mid-latitudes with air being deflected by the Coriolis force to create the prevailing westerly winds.[22]
The understanding of the kinematics of how exactly the rotation of the Earth affects airflow was partial at first.[23] Late in the 19th century, the full extent of the large scale interaction of pressure-gradient force and deflecting force that in the end causes air masses to move along isobars was understood.[24]
Formula[edit]
In Newtonian mechanics, the equation of motion for an object in an inertial reference frame is
where 


Transforming this equation to a reference frame rotating about a fixed axis through the origin with angular velocity 
where
The fictitious forces as they are perceived in the rotating frame act as additional forces that contribute to the apparent acceleration just like the real external forces.[25][26] The fictitious force terms of the equation are, reading from left to right:[27]
Notice the Euler and centrifugal forces depend on the position vector 



As the Coriolis force is proportional to a cross product of two vectors, it is perpendicular to both vectors, in this case the object’s velocity and the frame’s rotation vector. It therefore follows that:
- if the velocity is parallel to the rotation axis, the Coriolis force is zero. For example, on Earth, this situation occurs for a body at the equator moving north or south relative to the Earth’s surface.
- if the velocity is straight inward to the axis, the Coriolis force is in the direction of local rotation. For example, on Earth, this situation occurs for a body at the equator falling downward, as in the Dechales illustration above, where the falling ball travels further to the east than does the tower.
- if the velocity is straight outward from the axis, the Coriolis force is against the direction of local rotation. In the tower example, a ball launched upward would move toward the west.
- if the velocity is in the direction of rotation, the Coriolis force is outward from the axis. For example, on Earth, this situation occurs for a body at the equator moving east relative to Earth’s surface. It would move upward as seen by an observer on the surface. This effect (see Eötvös effect below) was discussed by Galileo Galilei in 1632 and by Riccioli in 1651.[29]
- if the velocity is against the direction of rotation, the Coriolis force is inward to the axis. For example, on Earth, this situation occurs for a body at the equator moving west, which would deflect downward as seen by an observer.
Length scales and the Rossby number[edit]
The time, space, and velocity scales are important in determining the importance of the Coriolis force. Whether rotation is important in a system can be determined by its Rossby number, which is the ratio of the velocity, U, of a system to the product of the Coriolis parameter, 
The Rossby number is the ratio of inertial to Coriolis forces. A small Rossby number indicates a system is strongly affected by Coriolis forces, and a large Rossby number indicates a system in which inertial forces dominate. For example, in tornadoes, the Rossby number is large, in low-pressure systems it is low, and in oceanic systems it is around 1. As a result, in tornadoes the Coriolis force is negligible, and balance is between pressure and centrifugal forces. In low-pressure systems, centrifugal force is negligible and balance is between Coriolis and pressure forces. In the oceans all three forces are comparable.[30]
An atmospheric system moving at U = 10 m/s (22 mph) occupying a spatial distance of L = 1,000 km (621 mi), has a Rossby number of approximately 0.1.
A baseball pitcher may throw the ball at U = 45 m/s (100 mph) for a distance of L = 18.3 m (60 ft). The Rossby number in this case would be 32,000 (at latitude 31°47’46.382″).
Baseball players don’t care about which hemisphere they’re playing in. However, an unguided missile obeys exactly the same physics as a baseball, but can travel far enough and be in the air long enough to experience the effect of Coriolis force. Long-range shells in the Northern Hemisphere landed close to, but to the right of, where they were aimed until this was noted. (Those fired in the Southern Hemisphere landed to the left.) In fact, it was this effect that first got the attention of Coriolis himself.[31][32][33]
Simple cases[edit]
Tossed ball on a rotating carousel[edit]
A carousel is rotating counter-clockwise. Left panel: a ball is tossed by a thrower at 12:00 o’clock and travels in a straight line to the center of the carousel. While it travels, the thrower circles in a counter-clockwise direction. Right panel: The ball’s motion as seen by the thrower, who now remains at 12:00 o’clock, because there is no rotation from their viewpoint.
The figure illustrates a ball tossed from 12:00 o’clock toward the center of a counter-clockwise rotating carousel. On the left, the ball is seen by a stationary observer above the carousel, and the ball travels in a straight line to the center, while the ball-thrower rotates counter-clockwise with the carousel. On the right, the ball is seen by an observer rotating with the carousel, so the ball-thrower appears to stay at 12:00 o’clock. The figure shows how the trajectory of the ball as seen by the rotating observer can be constructed.
On the left, two arrows locate the ball relative to the ball-thrower. One of these arrows is from the thrower to the center of the carousel (providing the ball-thrower’s line of sight), and the other points from the center of the carousel to the ball. (This arrow gets shorter as the ball approaches the center.) A shifted version of the two arrows is shown dotted.
On the right is shown this same dotted pair of arrows, but now the pair are rigidly rotated so the arrow corresponding to the line of sight of the ball-thrower toward the center of the carousel is aligned with 12:00 o’clock. The other arrow of the pair locates the ball relative to the center of the carousel, providing the position of the ball as seen by the rotating observer. By following this procedure for several positions, the trajectory in the rotating frame of reference is established as shown by the curved path in the right-hand panel.
The ball travels in the air, and there is no net force upon it. To the stationary observer, the ball follows a straight-line path, so there is no problem squaring this trajectory with zero net force. However, the rotating observer sees a curved path. Kinematics insists that a force (pushing to the right of the instantaneous direction of travel for a counter-clockwise rotation) must be present to cause this curvature, so the rotating observer is forced to invoke a combination of centrifugal and Coriolis forces to provide the net force required to cause the curved trajectory.
Bounced ball[edit]
Bird’s-eye view of carousel. The carousel rotates clockwise. Two viewpoints are illustrated: that of the camera at the center of rotation rotating with the carousel (left panel) and that of the inertial (stationary) observer (right panel). Both observers agree at any given time just how far the ball is from the center of the carousel, but not on its orientation. Time intervals are 1/10 of time from launch to bounce.
The figure describes a more complex situation where the tossed ball on a turntable bounces off the edge of the carousel and then returns to the tosser, who catches the ball. The effect of Coriolis force on its trajectory is shown again as seen by two observers: an observer (referred to as the «camera») that rotates with the carousel, and an inertial observer. The figure shows a bird’s-eye view based upon the same ball speed on forward and return paths. Within each circle, plotted dots show the same time points. In the left panel, from the camera’s viewpoint at the center of rotation, the tosser (smiley face) and the rail both are at fixed locations, and the ball makes a very considerable arc on its travel toward the rail, and takes a more direct route on the way back. From the ball tosser’s viewpoint, the ball seems to return more quickly than it went (because the tosser is rotating toward the ball on the return flight).
On the carousel, instead of tossing the ball straight at a rail to bounce back, the tosser must throw the ball toward the right of the target and the ball then seems to the camera to bear continuously to the left of its direction of travel to hit the rail (left because the carousel is turning clockwise). The ball appears to bear to the left from direction of travel on both inward and return trajectories. The curved path demands this observer to recognize a leftward net force on the ball. (This force is «fictitious» because it disappears for a stationary observer, as is discussed shortly.) For some angles of launch, a path has portions where the trajectory is approximately radial, and Coriolis force is primarily responsible for the apparent deflection of the ball (centrifugal force is radial from the center of rotation, and causes little deflection on these segments). When a path curves away from radial, however, centrifugal force contributes significantly to deflection.
The ball’s path through the air is straight when viewed by observers standing on the ground (right panel). In the right panel (stationary observer), the ball tosser (smiley face) is at 12 o’clock and the rail the ball bounces from is at position 1. From the inertial viewer’s standpoint, positions 1, 2, and 3 are occupied in sequence. At position 2, the ball strikes the rail, and at position 3, the ball returns to the tosser. Straight-line paths are followed because the ball is in free flight, so this observer requires that no net force is applied.
Applied to the Earth[edit]
The acceleration affecting the motion of air «sliding» over the Earth’s surface is the horizontal component of the Coriolis term
This component is orthogonal to the velocity over the Earth surface and is given by the expression
where
In the northern hemisphere, where the latitude is positive, this acceleration, as viewed from above, is to the right of the direction of motion. Conversely, it is to the left in the southern hemisphere.
Rotating sphere[edit]
Coordinate system at latitude φ with x-axis east, y-axis north, and z-axis upward (i.e. radially outward from center of sphere)
Consider a location with latitude φ on a sphere that is rotating around the north–south axis.[34] A local coordinate system is set up with the x axis horizontally due east, the y axis horizontally due north and the z axis vertically upwards. The rotation vector, velocity of movement and Coriolis acceleration expressed in this local coordinate system (listing components in the order east (e), north (n) and upward (u)) are:
When considering atmospheric or oceanic dynamics, the vertical velocity is small, and the vertical component of the Coriolis acceleration (
where 
By setting vn = 0, it can be seen immediately that (for positive φ and ω) a movement due east results in an acceleration due south. Similarly, setting ve = 0, it is seen that a movement due north results in an acceleration due east.
In general, observed horizontally, looking along the direction of the movement causing the acceleration, the acceleration always is turned 90° to the right (for positive φ) and of the same size regardless of the horizontal orientation.
As a different case, consider equatorial motion setting φ = 0°. In this case, Ω is parallel to the north or n-axis, and:
Accordingly, an eastward motion (that is, in the same direction as the rotation of the sphere) provides an upward acceleration known as the Eötvös effect, and an upward motion produces an acceleration due west.
Meteorology and oceanography[edit]
Due to the Coriolis force, low-pressure systems in the Northern hemisphere, like Typhoon Nanmadol (left), rotate counterclockwise, and in the Southern hemisphere, low-pressure systems like Cyclone Darian (right) rotate clockwise.
Schematic representation of flow around a low-pressure area in the Northern Hemisphere. The Rossby number is low, so the centrifugal force is virtually negligible. The pressure-gradient force is represented by blue arrows, the Coriolis acceleration (always perpendicular to the velocity) by red arrows
Schematic representation of inertial circles of air masses in the absence of other forces, calculated for a wind speed of approximately 50 to 70 m/s (110 to 160 mph).
Cloud formations in a famous image of Earth from Apollo 17, makes similar circulation directly visible
Perhaps the most important impact of the Coriolis effect is in the large-scale dynamics of the oceans and the atmosphere. In meteorology and oceanography, it is convenient to postulate a rotating frame of reference wherein the Earth is stationary. In accommodation of that provisional postulation, the centrifugal and Coriolis forces are introduced. Their relative importance is determined by the applicable Rossby numbers. Tornadoes have high Rossby numbers, so, while tornado-associated centrifugal forces are quite substantial, Coriolis forces associated with tornadoes are for practical purposes negligible.[35]
Because surface ocean currents are driven by the movement of wind over the water’s surface, the Coriolis force also affects the movement of ocean currents and cyclones as well. Many of the ocean’s largest currents circulate around warm, high-pressure areas called gyres. Though the circulation is not as significant as that in the air, the deflection caused by the Coriolis effect is what creates the spiralling pattern in these gyres. The spiralling wind pattern helps the hurricane form. The stronger the force from the Coriolis effect, the faster the wind spins and picks up additional energy, increasing the strength of the hurricane.[36]
Air within high-pressure systems rotates in a direction such that the Coriolis force is directed radially inwards, and nearly balanced by the outwardly radial pressure gradient. As a result, air travels clockwise around high pressure in the Northern Hemisphere and anticlockwise in the Southern Hemisphere. Air around low-pressure rotates in the opposite direction, so that the Coriolis force is directed radially outward and nearly balances an inwardly radial pressure gradient.[37]
Flow around a low-pressure area[edit]
If a low-pressure area forms in the atmosphere, air tends to flow in towards it, but is deflected perpendicular to its velocity by the Coriolis force. A system of equilibrium can then establish itself creating circular movement, or a cyclonic flow. Because the Rossby number is low, the force balance is largely between the pressure-gradient force acting towards the low-pressure area and the Coriolis force acting away from the center of the low pressure.
Instead of flowing down the gradient, large scale motions in the atmosphere and ocean tend to occur perpendicular to the pressure gradient. This is known as geostrophic flow.[38] On a non-rotating planet, fluid would flow along the straightest possible line, quickly eliminating pressure gradients. The geostrophic balance is thus very different from the case of «inertial motions» (see below), which explains why mid-latitude cyclones are larger by an order of magnitude than inertial circle flow would be.
This pattern of deflection, and the direction of movement, is called Buys-Ballot’s law. In the atmosphere, the pattern of flow is called a cyclone. In the Northern Hemisphere the direction of movement around a low-pressure area is anticlockwise. In the Southern Hemisphere, the direction of movement is clockwise because the rotational dynamics is a mirror image there.[39] At high altitudes, outward-spreading air rotates in the opposite direction.[40] Cyclones rarely form along the equator due to the weak Coriolis effect present in this region.[41]
Inertial circles[edit]
An air or water mass moving with speed 

where 



If the rotating system is a parabolic turntable, then 


Other terrestrial effects[edit]
The Coriolis effect strongly affects the large-scale oceanic and atmospheric circulation, leading to the formation of robust features like jet streams and western boundary currents. Such features are in geostrophic balance, meaning that the Coriolis and pressure gradient forces balance each other. Coriolis acceleration is also responsible for the propagation of many types of waves in the ocean and atmosphere, including Rossby waves and Kelvin waves. It is also instrumental in the so-called Ekman dynamics in the ocean, and in the establishment of the large-scale ocean flow pattern called the Sverdrup balance.
Eötvös effect[edit]
The practical impact of the «Coriolis effect» is mostly caused by the horizontal acceleration component produced by horizontal motion.
There are other components of the Coriolis effect. Westward-traveling objects are deflected downwards, while eastward-traveling objects are deflected upwards.[43] This is known as the Eötvös effect. This aspect of the Coriolis effect is greatest near the equator. The force produced by the Eötvös effect is similar to the horizontal component, but the much larger vertical forces due to gravity and pressure suggest that it is unimportant in the hydrostatic equilibrium. However, in the atmosphere, winds are associated with small deviations of pressure from the hydrostatic equilibrium. In the tropical atmosphere, the order of magnitude of the pressure deviations is so small that the contribution of the Eötvös effect to the pressure deviations is considerable.[44]
In addition, objects traveling upwards (i.e. out) or downwards (i.e. in) are deflected to the west or east respectively. This effect is also the greatest near the equator. Since vertical movement is usually of limited extent and duration, the size of the effect is smaller and requires precise instruments to detect. For example, idealized numerical modeling studies suggest that this effect can directly affect tropical large-scale wind field by roughly 10% given long-duration (2 weeks or more) heating or cooling in the atmosphere.[45][46] Moreover, in the case of large changes of momentum, such as a spacecraft being launched into orbit, the effect becomes significant. The fastest and most fuel-efficient path to orbit is a launch from the equator that curves to a directly eastward heading.
Intuitive example[edit]
Imagine a train that travels through a frictionless railway line along the equator. Assume that, when in motion, it moves at the necessary speed to complete a trip around the world in one day (465 m/s). The Coriolis effect can be considered in three cases: when the train travels west, when it is at rest, and when it travels east. In each case, the Coriolis effect can be calculated from the rotating frame of reference on Earth first, and then checked against a fixed inertial frame. The image below illustrates the three cases as viewed by an observer at rest in a (near) inertial frame from a fixed point above the North Pole along the Earth’s axis of rotation; the train is denoted by a few red pixels, fixed at the left side in the leftmost picture, moving in the others 
- The train travels toward the west: In that case, it moves against the direction of rotation. Therefore, on the Earth’s rotating frame the Coriolis term is pointed inwards towards the axis of rotation (down). This additional force downwards should cause the train to be heavier while moving in that direction.If one looks at this train from the fixed non-rotating frame on top of the center of the Earth, at that speed it remains stationary as the Earth spins beneath it. Hence, the only force acting on it is gravity and the reaction from the track. This force is greater (by 0.34%) than the force that the passengers and the train experience when at rest (rotating along with Earth). This difference is what the Coriolis effect accounts for in the rotating frame of reference.
- The train comes to a stop: From the point of view on the Earth’s rotating frame, the velocity of the train is zero, thus the Coriolis force is also zero and the train and its passengers recuperate their usual weight.From the fixed inertial frame of reference above Earth, the train now rotates along with the rest of the Earth. 0.34% of the force of gravity provides the centripetal force needed to achieve the circular motion on that frame of reference. The remaining force, as measured by a scale, makes the train and passengers «lighter» than in the previous case.
- The train travels east. In this case, because it moves in the direction of Earth’s rotating frame, the Coriolis term is directed outward from the axis of rotation (up). This upward force makes the train seem lighter still than when at rest.
Graph of the force experienced by a 10-kilogram (22 lb) object as a function of its speed moving along Earth’s equator (as measured within the rotating frame). (Positive force in the graph is directed upward. Positive speed is directed eastward and negative speed is directed westward).
From the fixed inertial frame of reference above Earth, the train traveling east now rotates at twice the rate as when it was at rest—so the amount of centripetal force needed to cause that circular path increases leaving less force from gravity to act on the track. This is what the Coriolis term accounts for on the previous paragraph.As a final check one can imagine a frame of reference rotating along with the train. Such frame would be rotating at twice the angular velocity as Earth’s rotating frame. The resulting centrifugal force component for that imaginary frame would be greater. Since the train and its passengers are at rest, that would be the only component in that frame explaining again why the train and the passengers are lighter than in the previous two cases.
This also explains why high-speed projectiles that travel west are deflected down, and those that travel east are deflected up. This vertical component of the Coriolis effect is called the Eötvös effect.[48]
The above example can be used to explain why the Eötvös effect starts diminishing when an object is traveling westward as its tangential speed increases above Earth’s rotation (465 m/s). If the westward train in the above example increases speed, part of the force of gravity that pushes against the track accounts for the centripetal force needed to keep it in circular motion on the inertial frame. Once the train doubles its westward speed at 930 m/s (2,100 mph) that centripetal force becomes equal to the force the train experiences when it stops. From the inertial frame, in both cases it rotates at the same speed but in the opposite directions. Thus, the force is the same cancelling completely the Eötvös effect. Any object that moves westward at a speed above 930 m/s (2,100 mph) experiences an upward force instead. In the figure, the Eötvös effect is illustrated for a 10-kilogram (22 lb) object on the train at different speeds. The parabolic shape is because the centripetal force is proportional to the square of the tangential speed. On the inertial frame, the bottom of the parabola is centered at the origin. The offset is because this argument uses the Earth’s rotating frame of reference. The graph shows that the Eötvös effect is not symmetrical, and that the resulting downward force experienced by an object that travels west at high velocity is less than the resulting upward force when it travels east at the same speed.
Draining in bathtubs and toilets[edit]
Contrary to popular misconception, bathtubs, toilets, and other water receptacles do not drain in opposite directions in the Northern and Southern Hemispheres. This is because the magnitude of the Coriolis force is negligible at this scale.[49][50][51][52] Forces determined by the initial conditions of the water (e.g. the geometry of the drain, the geometry of the receptacle, preexisting momentum of the water, etc.) are likely to be orders of magnitude greater than the Coriolis force and hence will determine the direction of water rotation, if any. For example, identical toilets flushed in both hemispheres drain in the same direction, and this direction is determined mostly by the shape of the toilet bowl.
Under real-world conditions, the Coriolis force does not influence the direction of water flow perceptibly. Only if the water is so still that the effective rotation rate of the Earth is faster than that of the water relative to its container, and if externally applied torques (such as might be caused by flow over an uneven bottom surface) are small enough, the Coriolis effect may indeed determine the direction of the vortex. Without such careful preparation, the Coriolis effect will be much smaller than various other influences on drain direction[53] such as any residual rotation of the water[54] and the geometry of the container.[55]
Laboratory testing of draining water under atypical conditions[edit]
In 1962, Ascher Shapiro performed an experiment at MIT to test the Coriolis force on a large basin of water, 2 meters (6 ft 7 in) across, with a small wooden cross above the plug hole to display the direction of rotation, covering it and waiting for at least 24 hours for the water to settle. Under these precise laboratory conditions, he demonstrated the effect and consistent counterclockwise rotation.
He reported that,[56]
Both schools of thought are in some sense correct. For the everyday observations of the kitchen sink and bath-tub variety, the direction of the vortex seems to vary in an unpredictable manner with the date, the time of day, and the particular household of the experimenter. But under well-controlled conditions of experimentation, the observer looking downward at a drain in the northern hemisphere will always see a counter-clockwise vortex, while one in the southern hemisphere will always see a clockwise vortex. In a properly designed experiment, the vortex is produced by Coriolis forces, which are counter-clockwise in the northern hemisphere.
Lloyd Trefethen reported clockwise rotation in the Southern Hemisphere at the University of Sydney in five tests with settling times of 18 h or more.[57]
Ballistic trajectories[edit]
The Coriolis force is important in external ballistics for calculating the trajectories of very long-range artillery shells. The most famous historical example was the Paris gun, used by the Germans during World War I to bombard Paris from a range of about 120 km (75 mi). The Coriolis force minutely changes the trajectory of a bullet, affecting accuracy at extremely long distances. It is adjusted for by accurate long-distance shooters, such as snipers. At the latitude of Sacramento, California, a 1,000 yd (910 m) northward shot would be deflected 2.8 in (71 mm) to the right. There is also a vertical component, explained in the Eötvös effect section above, which causes westward shots to hit low, and eastward shots to hit high.[58][59]
The effects of the Coriolis force on ballistic trajectories should not be confused with the curvature of the paths of missiles, satellites, and similar objects when the paths are plotted on two-dimensional (flat) maps, such as the Mercator projection. The projections of the three-dimensional curved surface of the Earth to a two-dimensional surface (the map) necessarily results in distorted features. The apparent curvature of the path is a consequence of the sphericity of the Earth and would occur even in a non-rotating frame.[60]
Trajectory, ground track, and drift of a typical projectile. The axes are not to scale.
The Coriolis force on a moving projectile depends on velocity components in all three directions, latitude, and azimuth. The directions are typically downrange (the direction that the gun is initially pointing), vertical, and cross-range.[61]: 178
where
Visualization of the Coriolis effect[edit]
Fluid assuming a parabolic shape as it is rotating
Object moving frictionlessly over the surface of a very shallow parabolic dish. The object has been released in such a way that it follows an elliptical trajectory.
Left: The inertial point of view.
Right: The co-rotating point of view.
To demonstrate the Coriolis effect, a parabolic turntable can be used.
On a flat turntable, the inertia of a co-rotating object forces it off the edge. However, if the turntable surface has the correct paraboloid (parabolic bowl) shape (see the figure) and rotates at the corresponding rate, the force components shown in the figure make the component of gravity tangential to the bowl surface exactly equal to the centripetal force necessary to keep the object rotating at its velocity and radius of curvature (assuming no friction). (See banked turn.) This carefully contoured surface allows the Coriolis force to be displayed in isolation.[62][63]
Discs cut from cylinders of dry ice can be used as pucks, moving around almost frictionlessly over the surface of the parabolic turntable, allowing effects of Coriolis on dynamic phenomena to show themselves. To get a view of the motions as seen from the reference frame rotating with the turntable, a video camera is attached to the turntable so as to co-rotate with the turntable, with results as shown in the figure. In the left panel of the figure, which is the viewpoint of a stationary observer, the gravitational force in the inertial frame pulling the object toward the center (bottom ) of the dish is proportional to the distance of the object from the center. A centripetal force of this form causes the elliptical motion. In the right panel, which shows the viewpoint of the rotating frame, the inward gravitational force in the rotating frame (the same force as in the inertial frame) is balanced by the outward centrifugal force (present only in the rotating frame). With these two forces balanced, in the rotating frame the only unbalanced force is Coriolis (also present only in the rotating frame), and the motion is an inertial circle. Analysis and observation of circular motion in the rotating frame is a simplification compared with analysis and observation of elliptical motion in the inertial frame.
Because this reference frame rotates several times a minute rather than only once a day like the Earth, the Coriolis acceleration produced is many times larger and so easier to observe on small time and spatial scales than is the Coriolis acceleration caused by the rotation of the Earth.
In a manner of speaking, the Earth is analogous to such a turntable.[64] The rotation has caused the planet to settle on a spheroid shape, such that the normal force, the gravitational force and the centrifugal force exactly balance each other on a «horizontal» surface. (See equatorial bulge.)
The Coriolis effect caused by the rotation of the Earth can be seen indirectly through the motion of a Foucault pendulum.
Coriolis effects in other areas[edit]
Coriolis flow meter[edit]
A practical application of the Coriolis effect is the mass flow meter, an instrument that measures the mass flow rate and density of a fluid flowing through a tube. The operating principle involves inducing a vibration of the tube through which the fluid passes. The vibration, though not completely circular, provides the rotating reference frame that gives rise to the Coriolis effect. While specific methods vary according to the design of the flow meter, sensors monitor and analyze changes in frequency, phase shift, and amplitude of the vibrating flow tubes. The changes observed represent the mass flow rate and density of the fluid.[65]
Molecular physics[edit]
In polyatomic molecules, the molecule motion can be described by a rigid body rotation and internal vibration of atoms about their equilibrium position. As a result of the vibrations of the atoms, the atoms are in motion relative to the rotating coordinate system of the molecule. Coriolis effects are therefore present, and make the atoms move in a direction perpendicular to the original oscillations. This leads to a mixing in molecular spectra between the rotational and vibrational levels, from which Coriolis coupling constants can be determined.[66]
Gyroscopic precession[edit]
When an external torque is applied to a spinning gyroscope along an axis that is at right angles to the spin axis, the rim velocity that is associated with the spin becomes radially directed in relation to the external torque axis. This causes a torque-induced force to act on the rim in such a way as to tilt the gyroscope at right angles to the direction that the external torque would have tilted it. This tendency has the effect of keeping spinning bodies in their rotational frame.
Insect flight[edit]
Flies (Diptera) and some moths (Lepidoptera) exploit the Coriolis effect in flight with specialized appendages and organs that relay information about the angular velocity of their bodies.
Coriolis forces resulting from linear motion of these appendages are detected within the rotating frame of reference of the insects’ bodies. In the case of flies, their specialized appendages are dumbbell shaped organs located just behind their wings called «halteres».[67]
The fly’s halteres oscillate in a plane at the same beat frequency as the main wings so that any body rotation results in lateral deviation of the halteres from their plane of motion.[68]
In moths, their antennae are known to be responsible for the sensing of Coriolis forces in the similar manner as with the halteres in flies.[69] In both flies and moths, a collection of mechanosensors at the base of the appendage are sensitive to deviations at the beat frequency, correlating to rotation in the pitch and roll planes, and at twice the beat frequency, correlating to rotation in the yaw plane.[70][69]
Lagrangian point stability[edit]
In astronomy, Lagrangian points are five positions in the orbital plane of two large orbiting bodies where a small object affected only by gravity can maintain a stable position relative to the two large bodies. The first three Lagrangian points (L1, L2, L3) lie along the line connecting the two large bodies, while the last two points (L4 and L5) each form an equilateral triangle with the two large bodies. The L4 and L5 points, although they correspond to maxima of the effective potential in the coordinate frame that rotates with the two large bodies, are stable due to the Coriolis effect.[71] The stability can result in orbits around just L4 or L5, known as tadpole orbits, where trojans can be found. It can also result in orbits that encircle L3, L4, and L5, known as horseshoe orbits.
See also[edit]
- Analytical mechanics
- Applied mechanics
- Classical mechanics
- Dynamics (mechanics)
- Earth’s rotation
- Equatorial Rossby wave
- Frenet–Serret formulas
- Gyroscope
- Kinetics (physics)
- Mechanics of planar particle motion
- Reactive centrifugal force
- Secondary flow
- Statics
- Uniform circular motion
- Whirlpool
References[edit]
- ^ Frautschi, Steven C.; Olenick, Richard P.; Apostol, Tom M.; Goodstein, David L. (2007). The Mechanical Universe: Mechanics and Heat, Advanced Edition (illustrated ed.). Cambridge University Press. p. 396. ISBN 978-0-521-71590-4. Extract of page 396
- ^
- ^ Bhatia, V.B. (1997). Classical Mechanics: With introduction to Nonlinear Oscillations and Chaos. Narosa Publishing House. p. 201. ISBN 978-81-7319-105-3.
- ^ Lee, Choonkyu; Min, Hyunsoo (17 April 2018). Essential Classical Mechanics. World Scientific Publishing Company. ISBN 978-981-323-466-6. Retrieved 13 March 2021.
- ^ «Coriolis Effect: Because the Earth turns – Teacher’s guide» (PDF). Project ATMOSPHERE. American Meteorological Society. Archived from the original (PDF) on 14 April 2015. Retrieved 10 April 2015.
- ^ Beckers, Benoit (2013). Solar Energy at Urban Scale. John Wiley & Sons. p. 116. ISBN 978-1-118-61436-5. Extract of page 116
- ^ Toossi, Reza (2009). Energy and the Environment: Resources, Technologies, and Impacts. Verve Publishers. p. 48. ISBN 978-1-4276-1867-2. Extract of page 48
- ^ «MIT: Flow in rotating environments» (PDF). Archived (PDF) from the original on 7 September 2015.
- ^ Shakur, Asif (2014). «Debunking Coriolis Force Myths». The Physics Teacher. 52 (8): 464–465. Bibcode:2014PhTea..52..464S. doi:10.1119/1.4897580.
- ^ «Can somebody finally settle this question: Does water flowing down a drainspin in different directions depending on which hemisphere you’re in? And ifso, why?». Scientific American.
- ^ «Coriolis Force Effect on Drains». Snopes.com.
- ^ Graney, Christopher M. (2011). «Coriolis effect, two centuries before Coriolis». Physics Today. 64 (8): 8. Bibcode:2011PhT….64h…8G. doi:10.1063/PT.3.1195. S2CID 121193379.
- ^ Graney, Christopher (24 November 2016). «The Coriolis Effect Further Described in the Seventeenth Century». Physics Today. 70 (7): 12–13. arXiv:1611.07912. Bibcode:2017PhT….70g..12G. doi:10.1063/PT.3.3610.
- ^ Truesdell, Clifford. Essays in the History of Mechanics. Springer Science & Business Media, 2012., p. 225
- ^ Persson, A. «The Coriolis Effect: Four centuries of conflict between common sense and mathematics, Part I: A history to 1885.» History of Meteorology 2 (2005): 1–24.
- ^ Cartwright, David Edgar (2000). Tides: A Scientific History. Cambridge University Press. p. 74. ISBN 9780521797467.
- ^ G-G Coriolis (1835). «Sur les équations du mouvement relatif des systèmes de corps». Journal de l’École Royale Polytechnique (in French). 15: 142–154.
- ^ Dugas, René and J. R. Maddox (1988). A History of Mechanics. Courier Dover Publications: p. 374. ISBN 0-486-65632-2
- ^ Bartholomew Price (1862). A Treatise on Infinitesimal Calculus : Vol. IV. The dynamics of material systems. Oxford : University Press. pp. 418–420.
- ^ Arthur Gordon Webster (1912). The Dynamics of Particles and of Rigid, Elastic, and Fluid Bodies. B. G. Teubner. p. 320. ISBN 978-1-113-14861-2.
- ^ Edwin b. Wilson (1920). James McKeen Cattell (ed.). «Space, Time, and Gravitation». The Scientific Monthly. 10: 226.
- ^ William Ferrel (November 1856). «An Essay on the Winds and the Currents of the Ocean» (PDF). Nashville Journal of Medicine and Surgery. xi (4): 7–19. Archived from the original (PDF) on 11 October 2013. Retrieved on 1 January 2009.
- ^ Anders O. Persson. «The Coriolis Effect:Four centuries of conflict between common sense and mathematics, Part I: A history to 1885» (PDF). Swedish Meteorological and Hydrological Institute. Archived from the original (PDF) on 11 April 2014. Retrieved 26 February 2006.
- ^ Gerkema, Theo; Gostiaux, Louis (2012). «A brief history of the Coriolis force». Europhysics News. 43 (2): 16. Bibcode:2012ENews..43b..14G. doi:10.1051/epn/2012202.
- ^
Mark P Silverman (2002). A universe of atoms, an atom in the universe (2 ed.). Springer. p. 249. ISBN 978-0-387-95437-0. - ^ Taylor (2005). p. 329.
- ^
Cornelius Lanczos (1986). The Variational Principles of Mechanics (Reprint of Fourth Edition of 1970 ed.). Dover Publications. Chapter 4, §5. ISBN 978-0-486-65067-8. - ^
Morton Tavel (2002). Contemporary Physics and the Limits of Knowledge. Rutgers University Press. p. 93. ISBN 978-0-8135-3077-2.Noninertial forces, like centrifugal and Coriolis forces, can be eliminated by jumping into a reference frame that moves with constant velocity, the frame that Newton called inertial.
- ^ Graney, Christopher M. (2015). Setting Aside All Authority: Giovanni Battista Riccioli and the Science Against Copernicus in the Age of Galileo. Notre Dame, Indiana: University of Notre Dame Press. pp. 115–125. ISBN 9780268029883.
- ^ Lakshmi H. Kantha; Carol Anne Clayson (2000). Numerical Models of Oceans and Oceanic Processes. Academic Press. p. 103. ISBN 978-0-12-434068-8.
- ^ Stephen D. Butz (2002). Science of Earth Systems. Thomson Delmar Learning. p. 305. ISBN 978-0-7668-3391-3.
- ^ James R. Holton (2004). An Introduction to Dynamic Meteorology. Academic Press. p. 18. ISBN 978-0-12-354015-7.
- ^ Carlucci, Donald E.; Jacobson, Sidney S. (2007). Ballistics: Theory and Design of Guns and Ammunition. CRC Press. pp. 224–226. ISBN 978-1-4200-6618-0.
- ^ William Menke; Dallas Abbott (1990). Geophysical Theory. Columbia University Press. pp. 124–126. ISBN 978-0-231-06792-8.
- ^ James R. Holton (2004). An Introduction to Dynamic Meteorology. Burlington, MA: Elsevier Academic Press. p. 64. ISBN 978-0-12-354015-7.
- ^ Brinney, Amanda. «Coriolis Effect – An Overview of the Coriolis Effect». About.com.
- ^ National Geographic Society (17 August 2011). «Coriolis effect». National Geographic Society. Retrieved 17 January 2018.
- ^ Roger Graham Barry; Richard J. Chorley (2003). Atmosphere, Weather and Climate. Routledge. p. 115. ISBN 978-0-415-27171-4.
- ^ Nelson, Stephen (Fall 2014). «Tropical Cyclones (Hurricanes)». Wind Systems: Low Pressure Centers. Tulane University. Retrieved 24 December 2016.
- ^ Cloud Spirals and Outflow in Tropical Storm Katrina from Earth Observatory (NASA)
- ^ Penuel, K. Bradley; Statler, Matt (29 December 2010). Encyclopedia of Disaster Relief. SAGE Publications. p. 326. ISBN 9781452266398.
- ^ John Marshall; R. Alan Plumb (2007). p. 98. Amsterdam: Elsevier Academic Press. ISBN 978-0-12-558691-7.
- ^ Lowrie, William (1997). Fundamentals of Geophysics (illustrated ed.). Cambridge University Press. p. 45. ISBN 978-0-521-46728-5. Extract of page 45
- ^ Ong, H.; Roundy, P.E. (2020). «Nontraditional hypsometric equation». Q. J. R. Meteorol. Soc. 146 (727): 700–706. arXiv:2011.09576. Bibcode:2020QJRMS.146..700O. doi:10.1002/qj.3703. S2CID 214368409.
- ^ Hayashi, M.; Itoh, H. (2012). «The Importance of the Nontraditional Coriolis Terms in Large-Scale Motions in the Tropics Forced by Prescribed Cumulus Heating». J. Atmos. Sci. 69 (9): 2699–2716. Bibcode:2012JAtS…69.2699H. doi:10.1175/JAS-D-11-0334.1.
- ^ Ong, H.; Roundy, P.E. (2019). «Linear effects of nontraditional Coriolis terms on intertropical convergence zone forced large‐scale flow». Q. J. R. Meteorol. Soc. 145 (723): 2445–2453. arXiv:2005.12946. Bibcode:2019QJRMS.145.2445O. doi:10.1002/qj.3572. S2CID 191167018.
- ^ Lowrie, William (2011). A Student’s Guide to Geophysical Equations. Cambridge University Press. p. 141. ISBN 978-1-139-49924-8. Retrieved 25 February 2020.
- ^ «Bad Coriolis». www.ems.psu.edu. Retrieved 21 December 2016.
- ^ «Flush Bosh». www.snopes.com. Retrieved 21 December 2016.
- ^ «Does the rotation of the Earth affect toilets and baseball games?». 20 July 2009. Retrieved 21 December 2016.
- ^ «Can somebody finally settle this question: Does water flowing down a drain spin in different directions depending on which hemisphere you’re in? And if so, why?». www.scientificamerican.com. Retrieved 21 December 2016.
- ^ Larry D. Kirkpatrick; Gregory E. Francis (2006). Physics: A World View. Cengage Learning. pp. 168–9. ISBN 978-0-495-01088-3.
- ^ Y. A. Stepanyants; G. H. Yeoh (2008). «Stationary bathtub vortices and a critical regime of liquid discharge» (PDF). Journal of Fluid Mechanics. 604 (1): 77–98. Bibcode:2008JFM…604…77S. doi:10.1017/S0022112008001080. S2CID 53071268.
- ^ Creative Media Applications (2004). A Student’s Guide to Earth Science: Words and terms. Greenwood Publishing Group. p. 22. ISBN 978-0-313-32902-9.
- ^ Shapiro, Ascher H. (December 1962). «Bath-Tub Vortex». Nature. 196 (4859): 1080–1081. Bibcode:1962Natur.196.1080S. doi:10.1038/1961080b0. S2CID 26568380.
- ^ Trefethen, Lloyd M.; Bilger, R. W.; Fink, P. T.; Luxton, R. E.; Tanner, R. I. (September 1965). «The Bath-Tub Vortex in the Southern Hemisphere». Nature. 207 (5001): 1084–1085. Bibcode:1965Natur.207.1084T. doi:10.1038/2071084a0. S2CID 4249876.
- ^ The claim is made that in the Falklands in WW I, the British failed to correct their sights for the southern hemisphere, and so missed their targets. John Edensor Littlewood (1953). A Mathematician’s Miscellany. Methuen And Company Limited. p. 51. John Robert Taylor (2005). Classical Mechanics. University Science Books. p. 364; Problem 9.28. ISBN 978-1-891389-22-1. For set up of the calculations, see Carlucci & Jacobson (2007), p. 225
- ^ «Do Snipers Compensate for the Earth’s Rotation?». Washington City Paper. 25 June 2010. Retrieved 16 July 2018.
- ^ Klinger, Barry A.; Haine, Thomas W. N. (2019). «Deep Meridional Overturning». Ocean Circulation in Three Dimensions. Thermohaline Overturning. Cambridge University Press. ISBN 978-0521768436. Retrieved 19 August 2019.
- ^ McCoy, Robert L. (1999), Modern Exterior Ballistics, Schiffer Military History, ISBN 0-7643-0720-7
- ^ When a container of fluid is rotating on a turntable, the surface of the fluid naturally assumes the correct parabolic shape. This fact may be exploited to make a parabolic turntable by using a fluid that sets after several hours, such as a synthetic resin. For a video of the Coriolis effect on such a parabolic surface, see Geophysical fluid dynamics lab demonstration Archived 20 November 2005 at the Wayback Machine John Marshall, Massachusetts Institute of Technology.
- ^ For a java applet of the Coriolis effect on such a parabolic surface, see Brian Fiedler Archived 21 March 2006 at the Wayback Machine School of Meteorology at the University of Oklahoma.
- ^ John Marshall; R. Alan Plumb (2007). Atmosphere, Ocean, and Climate Dynamics: An Introductory Text. Academic Press. p. 101. ISBN 978-0-12-558691-7.
- ^ Omega Engineering. «Mass Flowmeters».
- ^ califano, S (1976). Vibrational states. Wiley. pp. 226–227. ISBN 978-0471129967.
- ^ Fraenkel, G.; Pringle, W.S. (21 May 1938). «Halteres of Flies as Gyroscopic Organs of Equilibrium». Nature. 141 (3577): 919–920. Bibcode:1938Natur.141..919F. doi:10.1038/141919a0. S2CID 4100772.
- ^ Dickinson, M. (1999). «Haltere-mediated equilibrium reflexes of the fruit fly, Drosophila melanogaster». Phil. Trans. R. Soc. Lond. 354 (1385): 903–916. doi:10.1098/rstb.1999.0442. PMC 1692594. PMID 10382224.
- ^ a b Sane S., Dieudonné, A., Willis, M., Daniel, T. (February 2007). «Antennal mechanosensors mediate flight control in moths» (PDF). Science. 315 (5813): 863–866. Bibcode:2007Sci…315..863S. CiteSeerX 10.1.1.205.7318. doi:10.1126/science.1133598. PMID 17290001. S2CID 2429129. Archived from the original (PDF) on 22 June 2007. Retrieved 1 December 2017.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ^ Fox, J; Daniel, T (2008). «A neural basis for gyroscopic force measurement in the halteres of Holorusia». Journal of Comparative Physiology. 194 (10): 887–897. doi:10.1007/s00359-008-0361-z. PMID 18751714. S2CID 15260624.
- ^ Spohn, Tilman; Breuer, Doris; Johnson, Torrence (2014). Encyclopedia of the Solar System. Elsevier. p. 60. ISBN 978-0124160347.
Further reading[edit]
Physics and meteorology[edit]
- Riccioli, G. B., 1651: Almagestum Novum, Bologna, pp. 425–427
(Original book [in Latin], scanned images of complete pages.) - Coriolis, G. G., 1832: «Mémoire sur le principe des forces vives dans les mouvements relatifs des machines.» Journal de l’école Polytechnique, Vol 13, pp. 268–302.
(Original article [in French], PDF file, 1.6 MB, scanned images of complete pages.) - Coriolis, G. G., 1835: «Mémoire sur les équations du mouvement relatif des systèmes de corps.» Journal de l’école Polytechnique, Vol 15, pp. 142–154
(Original article [in French] PDF file, 400 KB, scanned images of complete pages.) - Gill, A. E. Atmosphere-Ocean dynamics, Academic Press, 1982.
- Robert Ehrlich (1990). Turning the World Inside Out and 174 Other Simple Physics Demonstrations. Princeton University Press. p. Rolling a ball on a rotating turntable; p. 80 ff. ISBN 978-0-691-02395-3.
- Durran, D. R., 1993: Is the Coriolis force really responsible for the inertial oscillation?, Bull. Amer. Meteor. Soc., 74, pp. 2179–2184; Corrigenda. Bulletin of the American Meteorological Society, 75, p. 261
- Durran, D. R., and S. K. Domonkos, 1996: An apparatus for demonstrating the inertial oscillation, Bulletin of the American Meteorological Society, 77, pp. 557–559.
- Marion, Jerry B. 1970, Classical Dynamics of Particles and Systems, Academic Press.
- Persson, A., 1998 [1] How do we Understand the Coriolis Force? Bulletin of the American Meteorological Society 79, pp. 1373–1385.
- Symon, Keith. 1971, Mechanics, Addison–Wesley
- Akira Kageyama & Mamoru Hyodo: Eulerian derivation of the Coriolis force
- James F. Price: A Coriolis tutorial Woods Hole Oceanographic Institute (2003)
- McDonald, James E. (May 1952). «The Coriolis Effect» (PDF). Scientific American. 186 (5): 72–78. Bibcode:1952SciAm.186e..72M. doi:10.1038/scientificamerican0552-72. Archived from the original (PDF) on 21 March 2016. Retrieved 4 January 2016.
Everything that moves over the surface of the Earth – water, air, animals, machines and projectiles – sidles to the right in the Northern Hemisphere and to the left in the Southern
. Elementary, non-mathematical; but well written.
Historical[edit]
- Grattan-Guinness, I., Ed., 1994: Companion Encyclopedia of the History and Philosophy of the Mathematical Sciences. Vols. I and II. Routledge, 1840 pp.
1997: The Fontana History of the Mathematical Sciences. Fontana, 817 pp. 710 pp. - Khrgian, A., 1970: Meteorology: A Historical Survey. Vol. 1. Keter Press, 387 pp.
- Kuhn, T. S., 1977: Energy conservation as an example of simultaneous discovery. The Essential Tension, Selected Studies in Scientific Tradition and Change, University of Chicago Press, 66–104.
- Kutzbach, G., 1979: The Thermal Theory of Cyclones. A History of Meteorological Thought in the Nineteenth Century. Amer. Meteor. Soc., 254 pp.
External links[edit]
- The definition of the Coriolis effect from the Glossary of Meteorology
- The Coriolis Effect — a conflict between common sense and mathematics PDF-file. 20 pages. A general discussion by Anders Persson of various aspects of the coriolis effect, including Foucault’s Pendulum and Taylor columns.
- The coriolis effect in meteorology PDF-file. 5 pages. A detailed explanation by Mats Rosengren of how the gravitational force and the rotation of the Earth affect the atmospheric motion over the Earth surface. 2 figures
- 10 Coriolis Effect Videos and Games- from the About.com Weather Page
- Coriolis Force – from ScienceWorld
- Coriolis Effect and Drains An article from the NEWTON web site hosted by the Argonne National Laboratory.
- Catalog of Coriolis videos
- Coriolis Effect: A graphical animation, a visual Earth animation with precise explanation
- An introduction to fluid dynamics SPINLab Educational Film explains the Coriolis effect with the aid of lab experiments
- Do bathtubs drain counterclockwise in the Northern Hemisphere? Archived 15 May 2008 at the Wayback Machine by Cecil Adams.
- Bad Coriolis. An article uncovering misinformation about the Coriolis effect. By Alistair B. Fraser, Emeritus Professor of Meteorology at Pennsylvania State University
- The Coriolis Effect: A (Fairly) Simple Explanation, an explanation for the layperson
- Observe an animation of the Coriolis effect over Earth’s surface
- Animation clip showing scenes as viewed from both an inertial frame and a rotating frame of reference, visualizing the Coriolis and centrifugal forces.
- Vincent Mallette The Coriolis Force @ INWIT
- NASA notes
- Interactive Coriolis Fountain lets you control rotation speed, droplet speed and frame of reference to explore the Coriolis effect.
- Rotating Co-ordinating Systems, transformation from inertial systems
-
Мне что-то непонятен первоначальный пример. Автор хочет сказать, что предмет, находящийся в воздухе достаточно долго, может «подождать», пока Земля подставит другой бок?! так было бы лишь в том случае, если бы в момент удара по мячу Земля бы стояла! потом, когда мяч был бы в воздухе, неожиданно закрутилась. Разве нет?
Ответить
-
RedDebil
alnomy
15.08.2006
17:11
Ответить
Скорость точки вылета мяча отличается от скорости в точке его падения, в следствии различного радиуса вращения этих точек и одинаковой угловой скорости.
Ответить
-
Так и есть: в момент удара земля под мячом стоит, а пока мяч летит Земля успевает провернуться.
Ответить
-
-
Слышал о т.н. летающих танках (например M1A1 Abrams модификации «F»), принцип действия которых основан на эффекте Кориолиса. (или его модификациях). Может, кто-нибудь знает, как его применяют?
Ответить
-
Странно, что реально существующую силу называют «фиктивной». В то же время, признается, что именно эта сила закручивает атмосферные вихри и пресловутые воронки в сливах. Эта сила мала по сравнению, например, с центробежной силой, но это не отменяет ее реального действия на объекты, находящиеся на Земле. Кориолисова сила действует везде, где складываются вращательное и поступательное движения. Кстати, если это так, на поверхности Земли все, в том числе и атомы, подвержено действию этой силы. Следовательно, на северном полушарии атомы закручиваются против, а на южном — по часовой стрелке. Это наводит на мысль, что если соединить какие-то точки на противоположных полушариях, можно получить ЭДС! Забавно было бы!
Ответить
-
Не всегда можно сложить вращательное и поступательное движения, а только при условии соприкосновения предметов. Если где-то летит астероид и в это время вращается наша Земля, то никакой связи нет. Также после удара по мячу мяч относительно мирового пространства летит туда куда его пнули, и его не волнует, что в это время провернулась Земля. Во время полета никакой боковой силы на мяч не действует, хотя он смещается относительно земли. Потому и сила — Фиктивная.
Ответить
-
Мяч, до того как его пнули, вращался вместе с Землёй и имел угловую скорость. И атмосфера, по которой летит мяч, тоже вращается вместе с землёй. Скорее в этом случае будет верно высказываение о влиянии разных радиусов земли на полюсе и экваторе, следовательно, разных касательных скоростях на поверхности.
Ответить
-
Речь шла о том, что мяч пнули с полюса, поэтому угловой скорости он не
имел. Если не с полюса, то верно — разные угловые скорости. Просто с
полюса мне кажется проще объяснить людям. На счет атмосферы вы тоже
правы, её никуда не выкинешь, но это уже нюансы. На какой-нибудь планете
без атмосферы(вращающейся естественно) мяч повел бы себя точно так же. И
снаряды бы летели по такому закону, и рельсы бы изнашивались так же.Ответить
-
Здравствуйте!
Подскажите ответ на аналогичный вопрос (поспорили с другом):Если из пушки выстрелить ядром строго(!) вверх. то куда попадет ядро, когда начнет падать обратно? Прямо в пушку, или отклонится от этой точки на некоторое расстояние (из-за того же вращения Земли)?
Естественно, принимаем за условие, что ядро и пушка — идеальны, а также что ветра нет!Заранее спасибо!
Ответить
-
Здравствуйте. Отвечаю — ядро упадет обратно в пушку, смещения не будет. При полете ядра во-первых: широта не меняется, во-вторых линейные скорости пушки и ядра по траектории вращения(векторы скорости по касательной) одинаковы. А вот если бы уронить ядро с какого-нибудь небоскреба, метров 100, то тогда оно упадет не совсем вертикально, а с отклонением, примерно 2,5 см. по ходу вращения Земли(немного вперед). В этом случае широта хоть и не меняется, но линейные скорости разные(чем выше, тем больше).
Ответить
-
Так и с ядром будет та же петрушка. Пока оно вверху, оно сохраняет линейную скорость, а не угловую, поэтому упадет западнее.
Тут есть еще один момент: что автор формулировки понимает под «строго вверх» — в зенит, или по вертикали (отвесу)?Ответить
-
-
-
-
-
-
fatyalink
barjer
25.12.2009
00:20
Ответить
Да не забавно. а реально. на ось и экватор проводок или нагрузку. дело за малым, подцепиться.
во Фарадей у гробу от зависти сам закрутится. а ведь он крутится мысленно!
ну прямо галилей получается. а все таки она вертится!
динамо оно выдумали гео херо магнитное, а ларчик прост как скорлупа от пасхального яйца.Ответить
-
Hmelnikov
barjer
22.02.2012
14:36
Ответить
Вы правы-реально существующую силу называют «фиктивной».
Это потому, что не понимают, о чём разговор.
На самом деле сила Кориолиса возникает при движении тела по радиусу от поверхности вращающегося тела. Для ясности рассмотрим движение единичной массы воды при движении от экватора к Северному ледовитому океану.
Расстояние от оси вращения Земли до единичной массы меняется?
Меняется.
Это приводит к изменению линейной скорости единичной массы при постоянной угловой скорости Земли?
Приводит.
Вот и возникает ускорение Кориолиса.
Естественно, ускорение порождает силу.
В рассматриваемом случае это сила торможения, которая и приводит к подмыванию берегов рек.Ответить
-
iggrs
Hmelnikov
18.05.2014
21:19
Ответить
>>Вот и возникает ускорение Кориолиса. Естественно, ускорение порождает силу.
Противоестественно… естественно — это когда сила порождает ускорение.
Тем не менее, Вы в принципе правы, как раз потому что это сила фиктивная. Система отсчёта связанная с поверхностью Земли — неинерциальна, и законы Ньютона в ней не действуют. Фиктивные силы Кориолиса и центробежную поэтому и вводят, чтобы можно было вести расчеты как в инерциальных. Это в большинстве случаев намного проще. В инерциальной системе, учитывающей вращение Земли, никаких сил Кориолиса нет. Только сила гравитации, сила реакции опоры, сумма которых соответствует центростремительному ускорению от вращения Земли, и та сила, которая вызывает движение исследуемого объекта по поверхности. Всё, никаких фиктивных сил инерции.
Ответить
-
-
-
Вопрос: при пояснениях действия силы Кориолиса в природе приводят в пример движения рек в северном и южном полушариях, и утверждают, что у всех рек, текущих в северном полушарии, правый берег крутой, а в южном — левый. В случае, если река в северном полушарии протекает не с севера на юг, а вдоль меридиана или, наоборот, с юга на север, то у такой реки тоже правый берег круче левого, или все-таки круче тот, который находится западнее от русла реки? спасибо за ответ
Ответить
-
Здравствуйте, хотел задать вопрос: представим ты едешь в поезде и подкидываешь строго вверх предмет ( к примеру мяч ), он упадёт назад в то же место откуда его и кидали или сместиться? учитывая конечно, что поезд едет с постоянной скоростью… и если да, то что в данном случае действует на мяч сила Кориолиса или какая-то другая сила.. ( ситуация интерисует, что ты находишься именно внутри поезда, а не на нём..) заранее спасибо!
Ответить
-
Постоянства скорости мало, надо еще, чтобы во время эксперимента поезд шел по прямой. Тогда в то же место. Если проделывать опыт реально, то лучше не подбрасывать мяч, а отпускать с высоты и смотреть, отвесно он падает, или нет. Для сравнения проделать то же самое, пока поезд стоит на станции.
Ответить
-
ответ понял, но хотел бы ещё кое-что уточнить, почему, взяв теже условия (постоянная скорость, поезд движется по прямой и убрать атмосферное воздействие )мы будем находиться на крыше поезда и опустим мяч, с некоторого расстояния, он сместиться, а находясь внутри поезда он не сместиться… с чем это связано?
Ответить
-
Это связано с тем, что мы не смогли убрать атмосферное воздействие, даже мысленно
Можно предложить два способа решения проблемы: 1) запустить поезд на Луне, где атмосфера отсутствует; 2) построить будку на крыше поезда, закрытую со всех сторон. В обоих случаях мяч упадет отвесно.Как водится, это, конечно же, лишь часть правды. Эксперимент с мячиком довольно груб. На глаз мы можем оценить отвесность падения с точностью несколько сантиметров, что не позволяет обнаружить более тонкие отклонения, вызванные эффектом Кориолиса.
Ответить
-
цитата…..Вопрос первый. Отчего у Вас такая путаница с системами отсчета?
Вопрос второй. Известны ли Вам другие описания эффекта Кориолиса, кроме этой статьи? В них также не акцентируется, что эффект возникает при _движении_ во вращающейся системе отсчета, а на покоящиеся в ней эта фиктивная сила не действует?………Первое.
Это не у меня путаница, это чехарда от придуманной относительности.
Вместо того чтобы прямо заявить, что неподвижная система отсчета какая-либо звезда, нам просто пудрят мозги, короче, чем больше путаница, тем легче скрыть собственное непонимание. Прием известный, а дяденьки Лорентц, Эйнштейн и прочие применяли его гениально.Физический эффект присутствует, но он не может быть объяснен с позиции механики. Никакое физическое движение нельзя разрешить или запретить математической абстракцией – выбором места наблюдения.
Он действительно зависит от вращения земли. Но не напрямую. И фиктивными выдуманными воздействиями объяснен быть не может.
Такое объяснения и будет фикцией.http://elkin52.narod.ru/new/otvet31.htm
Более или менее толково изложена суть явления.
С единственным но, если смотреть на южный полюс отклонения всегда на восток. И это не инерция!!! Хотя и силы инерции тоже фиктивные и классическое их объяснение – фикция, непонимание происходящего. На безрыбье и рак рыба. Посчитали что и так сойдет. Чтоб не забросить формулировку ньютона в мусор. Насчет прямолинейного и равномерного движения.С этим эффектом пытаются связать значительные отклонения от вертикали при определении ускорения свободного падения. Отклонение происходит по ходу вращения земли. Причем для разных материалов разные. Не знаю, учитывается ли это в метрологии (в гравиметрии не учитывается).
Как правило его вообще не учитывают. http://arlenasong.ru/_14/index.php?k=5.htmlhttp://www.inauka.ru/blogs/article91056.html
http://www.kscnet.ru/ivs/publication/tutorials/geophys_studies/chapter2.pdf
сам эффект отклонения обнаружен шахтным методом наблюдений.Кроме того, для намагниченных тел присутствует отклонение в сторону полюсов в зависимости от полушария, мало того имеется и элемент вращения. Это магнитное наклонение и магнитное склонение.
На самом деле все это якобы силами Кариолиса не вызывается.
Кстати, этого отклонения нет вообще на магнитном экваторе, не географическом.Якобы Проявление эффекта с подмывом западных берегов. Множество народа пытается опровергнуть это заблуждение и совершенно правильно. Земля крутится неравномерно, то быстрее то медленнее. Попробуйте походить со стаканом воды в руке, да посмотрите где уровень будет больше. В стороне противоположной направлению движения. И именно за счет подвижности воды,текучести. Показано только для северного полушария, а для южного подходящих примеров нет. Так и суши такой как на севере нет и речек так же текущих.
Напрямую это явление связано с маятником Фуко, плоскость качания которого на экваторе тоже не изменяется. Еще хохма… маятник Фуко запускается ОДИН РАЗ! и колебания не затухают. Есть еще одно! маятник Фуко реагирует на солнечные затмения уж очень непредсказуемо, как магнитная стрелка на полюсе. Работа реального (не математического) маятника Фуко зависит от высоты подвеса.
Чем выше, тем больше скорость. В общем, это второе и главное.Третье.
Некоторые заморочки со вращением (медного диска) и магнитным полем земли обнаружил Фарадей и прекрасно описал в своих трудах. Читаешь и поражаешься, а куда все смотрят?
Тут мужик со светом (сайт я дал) поработал, так еще выясняются и некоторые совпадения с солнечной активностью, с геоактивностью недр.
на луне эффект смещения будет но в ту же сторону направления вращения. но никак не в другую.и все будет сказываться на всех телах, не только движущихся. поскольку земля в пространстве не стоит на месте. а количественная сторона будет зависеть от результирующей скорости, суммы скоростей всех перемещений относительно какого либо выбранного объекта в космосе и желательно неподвижного.
С уважением, АВФОтветить
-
-
-
-
-
цитата……Представьте, что кто-то, находясь на Северном полюсе, бросил мяч кому-то, кто находится на экваторе. Пока мяч летел, Земля немного повернулась вокруг своей оси, и ловящий успел сместиться к востоку. Если бросающий, целясь мячом, не учел этого движения Земли, мяч упал западнее (или левее) ловящего. С точки зрения человека на экваторе получается, что мяч летел левее, чем надо, с самого начала , как только его выпустил из рук бросающий, и до тех пор, пока не приземлился……
А кто это пробовал в натурном экс-е? да это на какую же высоту швырнуть мячик надо, чтоб его ветром сдувать стало.
цитата…Согласно законам механики Ньютона, чтобы движущееся прямолинейно тело отклонилось от изначально заданной траектории, на него должна действовать какая-то внешняя сила. Значит, ловящий на экваторе должен сделать вывод, что брошенный мяч отклонился от прямолинейной траектории под действием некоей силы. Если бы мы смогли посмотреть на летящий мяч из космоса, мы бы увидели, что на самом деле никакая сила на мяч не действовала. Отклонение же траектории было вызвано тем, что Земля успела повернуться под мячом, пока он летел по прямой. Таким образом, действует в подобной ситуации какая-то сила или нет, это целиком зависит от системы отсчета, в которой находится наблюдатель…….
Вопрос к тому же физику: а что это за вращающаяся система отсчета? относительно чего? Звездного неба что-ли? и земля и наблюдатель оба вращаются. и в космосе тоже вращается, и атмосфера тоже вместе с ними.и в космосе тоже вращается. никто на месте не стоит. и даже фиктивной силы нет, иначе бы воздух двигался отдельно от поверхности и хотя бы из-за трения у поверхности все время дул бы в одну сторону обратную вращению планеты ну хоть чуть чуть, но нету этого, не сказывается из-за большой плотности воздуха. Путь кинут в меня каменюкой-эйнштейном! Да, наверху выше 10 километров разреженный воздух меньше притормаживается землей и можно заметить, но причем тут относительность безотносительная.
Действительно с запада на восток самолеты летят дольше чем с востока на запад из меньшего притормаживания. Ветер мешает.Данный эффект никак не обнаруживается в опытах по определению гравитационной постоянной. Нет никакого смещения.
Другое дело происходит с намагниченными телами. И ускоряются и смещаются. И вращаются. Но господа, в каких официальных отчетах хоть упоминается об этом. Да тем кто занимаются этими измерениями и думать об этом запрещено. с магнитами развлекаться.Весь фундамент современной физики порушить ни-ни. Вот альтернативам все можно поскольку за бесплатно.
Вот официоз и приплетает кариолисову чушь. мозги компостирует.
А это уже электродинамика. Объяснить можно, но не средствами классическими, там ветер дует потому, что деревья качаются. От колебательных процессов ребята пляшут и от Максвелла с тем же каменюкой да лоренцом, а зря.
А для правильного понимания этого надо и мозги из нижней части спины приподнять повыше. да и из положения рака на ноги встать.То же касается и воронок в трубах и атмосферных вихрей.
Никакого кариолиса.
Поскольку вращение в одну сторону и с какой стороны не посмотри (точка наблюдения будет двигаться вместе с системой отсчета) а значит вся арифметика полный бред, потому что на экваторе то сидеть совсем необязательно, сядьте просто на противоположный полюс и эффект исчезнет чисто математически. Вправо, влево; никакой разницы.
Вот вам и теория относительности!
Еще вот на луне такого уже показать и в эксперименте не получится! Атмосферы то нету.
Тормозить инерцию нечем.
Правда ньансы есть, если брошенное тело вращается, типа снаряда.
но тут двойное кручение и земля и тело, а ля праща — тоже.правда о таких задачах в механике мало кто понятие имеет.
Некоторые умники еще водовороты в трубах на архитектуру водопроводов сваливают, как будто сами по ним плавали. Еще вариант типа пальцем закручивать.А вращение в северном полушарии влево, а в южном вправо и воды в трубах и всяческих атмосферных вихрей. Только конечно если не насиловать пальцами и змеевиками. И жестко все завязано на электричество, магнетизм и тепловое воздействие.
Есть опыт Фуко с маятником. Но и он не доказывает факта вращения земли путем использования кариолисовых сил. То есть наоборот доказывает отсутствие существование прямой механической силы.
Полный цикл колебаний маятника не зависит от геометрических суток (солнечных суток) и совершается быстрее на четыре минуты. То есть подчиняется длине звездных суток.
Объяснить это официальная физика не в состоянии.
Мало того, имеется странный коэффициент в квадратных скобках.
в произвольной точке с географической широтой j (угол между осью вращения Земли и плоскостью колебаний маятника ) скорость вращения плоскости колебаний идеального маятника Фуко (в градусах в звёздный час) относительно поверхности Земли составляет
15 sin j
Для неидеального маятника Фуко скорость вращения плоскости колебаний зависит и от длины подвеса:15{1-3/8(a/l)**2} sin j
где a амплитуда колебаний груза маятника; l длина нити. Поэтому для демонстраций применяют маятники с максимально возможной длиной подвеса.
Это коэффициент говорит о том что амплитуда движения маятника в течении суток не изменяется!!!! иначе бы о затухании всплыло бы наверняка, ан нет.То есть для показухи маятник не надо все время подталкивать! То есть в деле еще и трос очень длинный занят! Металлический.Часики то без пружинок и гирек.
Мало того на экваторе никакого смещения плоскости колебаний нет! Факт вращения в этом случае недоказуем. Ну, полная с виду фикция.И фокус совсем в другом. А в чем же? Задавайте вопросы….
Ответить
-
Вопрос первый. Отчего у Вас такая путаница с системами отсчета?
Вопрос второй. Известны ли Вам другие описания эффекта Кориолиса, кроме этой статьи? В них также не акцентируется, что эффект возникает при _движении_ во вращающейся системе отсчета, а на покоящиеся в ней тела эта фиктивная сила не действует?Ответить
-
fatyalink
fatyalink
21.12.2009
22:27
Ответить
Sun Dec 20 23:17:47 2009
From: a_b
To: fatyalink
Answer to:
>
цитата……Представьте, что кто-то, находясь на…Вопрос первый. Отчего у Вас такая путаница с системами отсчета?
Вопрос второй. Известны ли Вам другие описания эффекта Кориолиса, кроме этой статьи? В них также не акцентируется, что эффект возникает при _движении_ во вращающейся системе отсчета, а на покоящиеся в ней эта фиктивная сила не действует?Первое.
Это не у меня путаница, это чехарда от придуманной относительности.
Вместо того чтобы прямо заявить, что неподвижная система отсчета какая-либо звезда, нам просто пудрят мозги, короче, чем больше путаница, тем легче скрыть собственное непонимание. Прием известный, а дяденьки Лорентц, Эйнштейн и прочие применяли его гениально.Физический эффект присутствует, но он не может быть объяснен с позиции механики. Никакое физическое движение нельзя разрешить или запретить математической абстракцией – выбором места наблюдения.
Он действительно зависит от вращения земли. Но не напрямую. И фиктивными выдуманными воздействиями объяснен быть не может.
Такое объяснение и будет фикцией.Цитата из «ФИЗИЧЕСКИЙ ЭНЦИКЛОПЕДИЧЕСКИЙ СЛОВАРЬ»
— М.: Советская энциклопедия, 1983 г. стр. 311.«Кориолисова сила — одна из сил инерции; вводится для учета влияния вращения подвижной системы отсчета на относительной движение материальной точки; названная по имени французского ученого Г. Кориолиса.
К.с. равна произведению массы точки на ее Кориолиса ускорение и направлена противоположно этому ускорению. Эффект, учитываемый К.с. состоит в том, что во вращающей системе отсчета материальная точка движущаяся непараллельно оси этого вращения, отклоняется по направлению, перпендикулярному к ее относительной скорости, или оказывает давление на тело, препятствующее этому отклонению. На Земле этот эффект, обусловленный ее суточным вращением, заключается в том, что свободно падающие тела отклоняются от вертикали к востоку, а тела движущиеся вдоль земной поверхности, отклоняются в Северном полушарии — вправо, а в Южном — влево от направления их движения.
Вследствие медленного вращения Земли эти отклонения весьма малы и заметно сказываются или при больших скоростях движения (например., у ракет, самолетов, и у артиллерийских снарядов с большими дальностями полета), или когда движение длится очень долго, например, подмыв соответствующих берегов рек (правые берега рек в Северном полушарии имеют более крутые берега. т.н. закон Бэра), возникновение некоторых воздушных и морских течений и др…»Более или менее толково изложена суть явления.
С несколькими но, если смотреть на южный полюс отклонения всегда на восток.
И что это за разновидность сил инерции?
И это не инерция!!! Хотя и силы инерции тоже фиктивные и классическое их объяснение – фикция, непонимание происходящего. На безрыбье и рак рыба. Посчитали, что и так сойдет. Чтоб не забросить формулировку ньютона в мусор. Начет прямолинейного и равномерного движения. Начисто забывают, что инерция это свойство тела, на которое явно никакие силы не действуют. А значит это внутренняя его энергия. Аккумулированная и расходуемая при сопротивлении среды. Силы есть, но они внутренние а не внешние.
Проявление эффекта только при Непараллельности направления движения оси вращения. О какой непараллельности идет речь? Поверхность земли определяет непараллельность. Но это не факт, что при параллельности этого не будет, поскольку для проверки тоннель рыть надо, что накладно. С другой стороны несоосность не должна влиять на качественную сторону, только на количественную.С этим эффектом пытаются связать значительные отклонения от вертикали при определении ускорения свободного падения методом бросания. Отклонение происходит по ходу вращения земли. Причем для разных материалов разные. Не знаю, учитывается ли это в метрологии (в гравиметрии не учитывается). Растет длина пути.
Как правило его вообще не учитывают. http://arlenasong.ru/_14/index.php?k=5.htmlhttp://www.inauka.ru/blogs/article91056.html
http://www.kscnet.ru/ivs/publication/tutorials/geophys_studies/chapter2.pdf
сам эффект отклонения обнаружен шахтным методом наблюдений.Кроме того, для намагниченных тел присутствует отклонение в сторону полюсов в зависимости от полушария, мало того имеется и элемент вращения. Это магнитное наклонение и магнитное склонение.
На самом деле все это якобы силами Кариолиса не вызывается.
Кстати, этого отклонения нет вообще на магнитном экваторе, не географическом.Якобы Проявление эффекта с подмывом западных берегов. Множество народа пытается опровергнуть это заблуждение и совершенно правильно. Земля крутится неравномерно, то быстрее то медленнее. Попробуйте походить со стаканом воды в руке, да посмотрите где уровень будет больше. В стороне противоположной направлению движения. И именно за счет текучести. Показано только для северного полушария, а для южного подходящих примеров нет. Так и суши такой как на севере нет и речек так же текущих.
Напрямую это явление связано с маятником Фуко, плоскость качания которого на экваторе тоже не изменяется. Еще хохма… маятник Фуко запускается ОДИН РАЗ! и колебания не затухают. Есть еще одно! маятник Фуко реагирует на солнечные затмения уж очень непредсказуемо, как магнитная стрелка на полюсе. Работа реального (не математического) маятника Фуко зависит от высоты подвеса.
Чем выше, тем больше скорость. В общем, это второе и главное.Третье.
Некоторые заморочки со вращением (медного диска) и магнитным полем земли обнаружил Фарадей и прекрасно описал в своих трудах. Читаешь и поражаешься, а куда все смотрят?
Тут мужик со светом (сайт я дал) поработал, так еще выясняются и некоторые совпадения с солнечной активностью.Ответить
-
Ну, вот видите, что это конкретно автор статьи, Дж.Трефил, написал неудачно (рискну предположить, что даже не он сам, а один из его безвестных аспирантов). Экспериментальная проверка эффекта К. проста и когда-то была очень доступна. Не нужно запуливать мячиком с полюса в стратосферу. Надо лишь найти карусель с ровным полом или вращающуюся сцену. Встать на нее, и во время вращения сделать шаг _вдоль радиуса_. Вы почувствуете, как пол делает Вам подсечку в направлении, перпендикулярном шагу. Особенно эффектно делать шаг в направлении _к_ оси вращения — Вы будете заваливаться набок _против_ ветра (это не ветер, конечно, это Вы двигаетесь в неподвижном воздухе).
«Никакое физическое движение нельзя разрешить или запретить математической абстракцией — выбором места наблюдения» Дело не в разрешении/запрещении, дело в ответе на простой вопрос. Представьте, Вы летите в самолете, а в соседнем кресле спит пассажир. Стюардесса спрашивает:»Скажите, он покоится или движется, только ДА или НЕТ?»
Заметьте, что философский ответ «в мире нет покоя, все движется» не прокатит, ибо все мы участвуем в суточном вращении Земли с очень приличной скоростью, но никто не готов на этом основании платить гаишникам штраф или вовсе расставаться с правами на полгода.Ответить
-
-
-
получил вопросы по почте.
Sun Dec 20 23:17:47 2009
From: a_b
To: fatyalink
Answer to:
>
цитата……Представьте, что кто-то, находясь на…Вопрос первый. Отчего у Вас такая путаница с системами отсчета?
Вопрос второй. Известны ли Вам другие описания эффекта Кориолиса, кроме этой статьи? В них также не акцентируется, что эффект возникает при _движении_ во вращающейся системе отсчета, а на покоящиеся в ней эта фиктивная сила не действует?Первое.
Это не у меня путаница, это чехарда от придуманной относительности.
Вместо того чтобы прямо заявить, что неподвижная система отсчета какая-либо звезда, нам просто пудрят мозги, короче, чем больше путаница, тем легче скрыть собственное непонимание. Прием известный, а дяденьки Лорентц, Эйнштейн и прочие применяли его гениально.Физический эффект присутствует, но он не может быть объяснен с позиции механики. Никакое физическое движение нельзя разрешить или запретить математической абстракцией – выбором места наблюдения.
Он действительно зависит от вращения земли. Но не напрямую. И фиктивными выдуманными воздействиями объяснен быть не может.
Такое объяснение и будет фикцией.Цитата из «ФИЗИЧЕСКИЙ ЭНЦИКЛОПЕДИЧЕСКИЙ СЛОВАРЬ»
— М.: Советская энциклопедия, 1983 г. стр. 311.«Кориолисова сила — одна из сил инерции; вводится для учета влияния вращения подвижной системы отсчета на относительной движение материальной точки; названная по имени французского ученого Г. Кориолиса.
К.с. равна произведению массы точки на ее Кориолиса ускорение и направлена противоположно этому ускорению. Эффект, учитываемый К.с. состоит в том, что во вращающей системе отсчета материальная точка движущаяся непараллельно оси этого вращения, отклоняется по направлению, перпендикулярному к ее относительной скорости, или оказывает давление на тело, препятствующее этому отклонению. На Земле этот эффект, обусловленный ее суточным вращением, заключается в том, что свободно падающие тела отклоняются от вертикали к востоку, а тела движущиеся вдоль земной поверхности, отклоняются в Северном полушарии — вправо, а в Южном — влево от направления их движения.
Вследствие медленного вращения Земли эти отклонения весьма малы и заметно сказываются или при больших скоростях движения (например., у ракет, самолетов, и у артиллерийских снарядов с большими дальностями полета), или когда движение длится очень долго, например, подмыв соответствующих берегов рек (правые берега рек в Северном полушарии имеют более крутые берега. т.н. закон Бэра), возникновение некоторых воздушных и морских течений и др…»Более или менее толково изложена сама суть явления.
С несколькими но, если смотреть на южный полюс отклонения всегда на восток.
И что это за разновидность сил инерции? их что немеряно?
И это не инерция!!! Она вообще ни причем. Смещение бы было в другую сторону. Хотя и силы инерции тоже фиктивные и классическое их объяснение – фикция, непонимание происходящего. На безрыбье и рак рыба. Посчитали, что и так сойдет. Чтоб не забросить формулировку ньютона в мусор. Насчет прямолинейного и равномерного движения. Начисто забывают, что инерция это свойство тела, на которое явно никакие силы не действуют. А значит это внутренняя его энергия. Аккумулированная и расходуемая при сопротивлении среды. Силы есть, но они внутренние, а не внешние.
Проявление эффекта только при Непараллельности направления движения оси вращения. О какой непараллельности идет речь? Поверхность земли определяет непараллельность. Но это не факт, что при параллельности этого не будет, поскольку для проверки тоннель рыть надо, что накладно. С другой стороны несоосность не должна влиять на качественную сторону, только на количественную.С этим эффектом пытаются связать значительные отклонения от вертикали при определении ускорения свободного падения методом бросания. Отклонение происходит по ходу вращения земли. Причем для разных материалов разные. Не знаю, учитывается ли это в метрологии (в гравиметрии не учитывается). Растет длина пути.
Как правило его вообще не учитывают. http://arlenasong.ru/_14/index.php?k=5.htmlhttp://www.inauka.ru/blogs/article91056.html
http://www.kscnet.ru/ivs/publication/tutorials/geophys_studies/chapter2.pdf
сам эффект отклонения обнаружен шахтным методом наблюдений.Кроме того, для намагниченных тел присутствует отклонение в сторону полюсов в зависимости от полушария, мало того имеется и элемент вращения. Это магнитное наклонение и магнитное склонение.
На самом деле все это якобы силами Кариолиса не вызывается.
Кстати, этого отклонения нет вообще на магнитном экваторе, не географическом. Нет зависимости от вращения.
При свободном падении сильно заметного движения вдоль поверхности земли нет, а эффект проявляется и не зависит от самого вращения земли, то есть от той самой вращающейся системы отсчета.Якобы Проявление эффекта с подмывом правых берегов в северном полушарии. Множество народа пытается опровергнуть это заблуждение и совершенно правильно. Земля крутится неравномерно, то быстрее то медленнее. скорость вращения на разных широтах разная.Попробуйте походить со стаканом воды в руке, да посмотрите где уровень будет больше. В стороне противоположной направлению движения. И именно за счет подвижности текучести. Показано только для северного полушария, а для южного такого многообразия подходящих примеров нет. Так и суши такой как на севере нет и речек так же текущих.
так что отнесение данного эффекта только на счет Кариолиса
проблематично.http://gatchina3000.ru/brockhaus-and-efron-encyclopedic-dictionary/017/17191.htmНапрямую это явление связано с маятником Фуко, плоскость качания которого на экваторе тоже не изменяется. Еще хохма… маятник Фуко запускается ОДИН РАЗ! и колебания не затухают. Есть еще одно! маятник Фуко реагирует на солнечные затмения уж очень непредсказуемо, как магнитная стрелка на полюсе. Работа реального (не математического) маятника Фуко зависит от высоты подвеса.
Чем выше, тем больше скорость. В общем, это второе и главное.Третье.
Некоторые заморочки со вращением (медного диска) и магнитным полем земли обнаружил Фарадей и прекрасно описал в своих трудах. Читаешь и поражаешься, а куда все смотрят?
Тут мужик со светом (сайт я дал) поработал, так еще выясняются и некоторые совпадения с солнечной активностью.С уважением, АВФ
Ответить
-
согласен, но земля то не плоская карусель и шагнуть так как предлагается не получится…
получается что это смещение не просто от вращения тела, а от вращения тела в магнитном поле да не только собственном собственном земли, а межзвездном … вот откуда ноги у четырехминутной разницы, да еще и вращательном движении магнитного потока. а заморочка с отсутствием смещений на экваторе как раз и есть связь с точно таким же эффектом у постоянных магнитов.Ответить
-
Как раз это не проблема, решается разложением движения на движение вдоль оси вращения и перпендикулярно к ней вдоль радиуса.
Трефиловская статья «Распределенное движение» (http://elementy.ru/trefil/21072) нормальная. Только та составляющая движения дает эффект К., которая изменяет расстояние от оси вращения.
В поведении маятника Фуко на экваторе гораздо меньше загадочного, чем кажется. Все дело в том, что отклонения от начальной плоскости качания в разных полушариях компенсируют друг друга.Ответить
-
Какой к богу радиус. какое разложение.Вы на краю этой Вашей воображаемой карусели находитесь, ногами на ребре ее стоите. За счет инерции вы вообще с места не сдвинетесь вдоль оси вращения, гироскоп знаете ли. Но мы то спокойно ходим. Значит не сказывается. И сносить то к западу должно, опять же из-за инерции да трения. Уменьшение радиуса к полюсам лишь уменьшать должно, окружная скорость меньше. А эффект превышает этот снос. К радиусу поход невозможен, твердь под вами, только если вы рядом с осью, на полюсе… уменьшение радиуса к полюсам лишь уменьшать должно. да в статье этот вопрос (восточное смещение) и не рассматривается. а на экваторе вообще нет отклонений, так что о компенсации и речи быть не может. в противном бы случае маятник бы трясло хотя бы по синусоиде.и не заметить этого невозможно.
нет тут механики! и разницу во времени не объясняет, и направленность.Ответить
-
Нет, не на краю. Да, «карусель»-Земля несколько горбата, но почему это должно смущать? Где у карусели край? Там, где максимальна линейная скорость (окружная в Вашей терминологии). Для Земли это экватор. Что мешает сделать конусовидную карусель? Конечно, угол fi при основании конуса не получится сделать большим, падать начнем от земного притяжения, но довольно очевидно, что для значительного диапазона fi эффект будет сопоставимый с плоской каруселью. А точнее, делая шаг L, получаем эффект, эквивалентный L*cos fi для плоского случая.
О движении вдоль оси вращения. Гироскоп сохраняет _направление_ оси вращения, ну так при движении _вдоль_ оси оно и не пытается измениться. Шар, закрученный вдоль вертикальной оси, упадет с равной высоты _одновременно_ с незакрученным (и одновременно с закрученным вдоль любой другой оси, но это уже отдельная песня).
«Нет отклонений» не бывает. Бывают отклонения меньше погрешности измерений. Давайте прикинем порядок, сравним с погрешностью приборов.
Какова длина подвеса, материал и вес груза маятника?Ответить
-
Есть предложение поехать вместе на экватор, башню либо шахту соорудить и там попробовать.
насчет карусели, подсечка не по физике, а по условному рефлексу. как на эскалаторе для деревенщины.
насчет гироскопа, любое тело находящееся в сцепке с ним, точно также сопротивляется изменению плоскости вращения. об том и речь, что вы то в плоскости этого гироскопа предлагаете двигаться, а на деле получается приблизительно вдоль оси. есть еще одно предложение, покатать шарик по карусели, думается что кроме трения вы особых эффектов не увидите. максимум по спирали пойдет. предсказуемой. хоть она горбатая, хоть плоская.
окружная скорость, линейная скорость разница на глаз как квадратура круга. у вращательного движения физически нет линейной скорости, она только с математической точки зрения линейна, как дифференциал, приближение. так что разница в наименовании вполне обоснована. ну в школе так научили. плохо… всех нас. как и с центростремительным ускорением, которого нет, как и с ускорением при равномерном вращательном движении, которого тоже нет. судьба…
насчет всего остального. надеюсь заметили в определении. материальная точка. нет размеров нет материала. нет среды. абстракция. а физика не имеет дело с абстракциями, потому и физика. математика, аппарат приближения желаемого к той реальности которую имеем. но никак не физика. так что для вращающегося шара, падающего на землю, необходимо с максимальной точностью приводить условия этого падения. это не отдельная песня, это комплексное рассмотрение проблемы.Ответить
-
«поехать вместе на экватор» Так я-то думал, что это уже кто-то проделал, и у Вас есть его результаты, протоколы.
Да, подсечка такая же, условный рефлекс обманут. Только что же, как не изменившаяся физика, тому причиной?
Отчего же нет линейной скорости? Тело, шагнувшее за край карусели именно с этой скоростью, какую имело по величине и направлению в момент отрыва, и продолжит свое движение дальше. Тут никакой абстракции нет.
Насчет Вашего противопоставления физики и математики. Закон Ньютона F=m*a — это, Вы считаете, физика или математика?
Раз Ваши представления расходятся со «школьными», дайте тогда определение скорости и ускорения, а то мы, возможно, употребляя одинаковые термины, подразумеваем под ними _разные_ вещи.Ответить
-
тАк доверяя проверяй.
если не нравится такая постановка. Народ то ездил и проверил. да вот по библиотекам и странам за такой фигней мотаться накладно. есть косвенные упоминания, а «Шерлок Холмс» — следователь-сыщик, кое что и дедуктивным методом додумывал. благо башка на плечах, а не бочка с учебниками. и не физика меняется. меняется восприятие этой физики. тело эту скорость поимеет, когда сорвется и тормоза отпустят. там уже и безбашенность начнется. а до той поры извольте закон своей системы соблюдать!а с законами Ньютона передергивание карт начинается. Вы уже на принцип давите, который еще и до Ньютона известен был за сто лет до того. Кстати, тогда то математики этой еще и не было. все строилось только на принципах пропорциональности. то есть формулировка ньютона звучала так. сила прямо пропорциональна массе и ускорению. что интересно и законы кулона так же выглядели. коэффициенты уже потом появились. подогнанные. классиков в натуре читать надо. серьезно же вас «образовали». багаж большой, вот только до вагона добежать как?Ответить
-
fatyalink
fatyalink
25.12.2009
00:08
Ответить
Есть еще соображения на эту, вроде бы и маловажную, тему. Но это уже для всех, а не в рамках спора с а_в.
я тоже ав, инициалы…
закрутка влево торнадо, циклонов и воронок в ванной у северного полушария, вправо у южного. а почему, собственно? как у Жванецкого. во мужик, хоть и из Одессы, но уважаю! за язык! длинный и не предсказуемый.
заранее предупреждаю, механика ни при делах.
кто что имеет сказать за эту животрепещущую картину маслом при том при всем что я не из Одессы Мамы, и вовсе наоборот. Увважаю, но пить не буду.Ответить
-
«и не физика меняется. меняется восприятие этой физики.»
Есть такие разделы физики. Например, исследующие оптические обманы зрения. Но там можно приложить линейку, и удостовериться, что фигуры имеют одинаковый размер, или что в белых линиях, разделяющих черные квадраты, нет темных точек.
С эскалатором не так. Гипсовая статуэтка, поставленная на стоящий эскалатор удержится, на движущийся — упадет. С рефлексами же у нее, сами понимаете…Ответить
-
все правильно, только можно и свинцовую поставить… не упадет ведь.
Ответить
-
Вот и хорошо, значит мы с Вами надежно исключили рефлексы, как причину различного поведения. И, возвращаясь отсюда к плоской карусели, выводим, что причиной подсечки была все-таки физика. Каковая в данном случае носит наименование эффекта Кориолиса. А трефиловская иллюстрация с Землей — далеко не лучшая. Слишком много посторонних факторов и при этом слабо выраженный эффект из-за малой угловой скорости.
Ответить
-
-
-
-
-
-
Верно. Элементарный закон сохранения импульса плюс инерция. И так бестолково описано в основной статье.
Когда двигаешся на север, приближаешся к оси вращения, и проскальзываешь на миллиметр вправо при каждом следующем шаге, поскольку всегда наступаешь на место, которое движется вправо медленее тебя (ближе к оси вращения).
Если идти на юг, то теперь Земля будет налетать на тебя справа. Поэтому сила Кориолиса отсутствует на экваторе, и заметно возрастает от 30° с. (ю.) ш. и максимальна у полюса. Карусель!!!
Именно поэтому, из-за закона сохранения импульса, в северном полушарии подмывается правый берег, на север или на юг течет вода.Ответить
-
-
-
-
-
Простите за глупый вопрос. Раз уж зашел разговор о смерчах и вращении воды в трубопроводах то как скажется сила Кориолиса на скорость вращения смерча в его верхней части и в его основании?
Ответить
-
Сила Кориолиса действует только на перпендикулярную оси вращения составляющую любого движения (вертикальную на экваторе и на горизонтальную у полюсов!).
Ответить
-
-
Ваше рассуждение применимо и к двум наблюдателям, находящимся вблизи экватора, а там кориолисова сила равна нулю, т.к. она является векторным произведением угловой скорости Земли (направленной вдоль Земной оси вращения) и скорости исследуемой материальной точки (или тела).
Тем, кто изучал курс механики, известно, что сила Кориолиса отлична от нуля лишь в неинерциальных системах отсчёта, а Ваше рассуждение работает и в инерциальных, значит, Ваше рассуждение не имеет ровно никакого отношения к силе Кориолиса.
Ответить
-
Ю.С. Потапов, Л.П. Фоминский, С.Ю. Потапов
http://www.transgasindustry.com/books/Potapov/vvedenie.html
написали книгу «Энергия вращения». В ней, в частности, говорится, что вращение циклонов в Северном полушарии и вращение в Южном не симметричны. Нечто способствует вращению циклонов в Северном и мешает в Южном, поэтому, в Южном полушарии образуется гораздо меньше вихрей.Ответить
-
олег но
mihailvt
19.12.2011
18:59
Ответить
все проблемы в том что дуализм работает только на движение .одно движется относительно второго и наоборот .а вот с вращением всегда можно знать вращается допустим диск или нет причем безотносительно к чему бы то не было. вращение абсолютно .присутствует центр вращения.по опредилению толи ноль толи бесконечность откуда смотреть.дуализьм .а вот то что крутится проявляет свойства.например в далеком невесомом космосе на одной оси вращаются два диска.один относительно второго ,вопрос, вращается один ,оба,или в разные стороны если есть однозначный ответ тогда есть и абсолютная система координат в которой завсегда найдутся невращающаеся волчки с любым положением осей
Ответить
-
олег но
mihailvt
19.12.2011
19:29
Ответить
все проблемы в том что дуализм работает только на движение .одно движется относительно второго и наоборот .а вот с вращением всегда можно знать вращается допустим диск или нет причем безотносительно к чему бы то не было. вращение абсолютно .присутствует центр вращения.по опредилению толи ноль толи бесконечность откуда смотреть.дуализьм .а вот то что крутится проявляет свойства.например в далеком невесомом космосе на одной оси вращаются два диска.один относительно второго ,вопрос вращается один ,оба,или в разные стороны
Ответить
-
-
В статье в начале пишется что сила Кориолиса фиктивная. Однако, какая же она фиктивная если под ее действием вращаются огромные массы воздуха и подмываются берега рек. Скорее это реальная сила просто ее природа еще не изучена.
Ответить
-
(Значит, ловящий на экваторе должен сделать вывод, что брошенный мяч отклонился от прямолинейной траектории под действием некоей силы)
Данный вывод ловца мяча, по определению происходящего действия — неверный. Что, в свою очередь, не даёт право классифицировать этот вывод с точки зрения обоснования данного действия, ловцом. То есть, ни действие инерции является фиктивным, фиктивным является вывод несообразительного ловца и того, кто это обоснование приложил в качестве — научного аргумента.
Я разделяю людей на две ипостаси, т.е. учёного, который, непосредственно наблюдает за действием процесса и делает из наблюдения соответствующие выводы, и людей, которые, выводы делают не на основании личного наблюдения за процессом, а на основании вывода учёного. А если учёный отрок ошибся с выводом, соответственно, второй, будучи не имея желания или способностей делать свои выводы, будет вторить ошибку учёного, отождествляя вывод, в качестве своего личного убеждения. Сказано было «Не сотвори себе кумира»Ответить
-
Работа эфета Кориолиса..
Одно из назначений силы Кориолиса в природе, является формирование водоворотов циклонов и антициклонов. И чтобы в полной мере проявилась сила Кориолиса, должна произойти разбалансировка линейной и угловой скорости, как относительно оси Земли, так и относительно оси Солнца. Сила Кориолиса, также зависит от наклона оси Земли, к плоскости орбиты Земли. И без учета орбитального вращения Земли,и наклона оси Земли, сила Кориолиса, останется в науке, как декорация, бесполезная для научно- практического применения, и задача для развития мышления у школьников. При кажущейся простоте, сила Кориолиса для восприятия крайне трудна. И объективно изучать, и анализировать её, без макета Солнечной системы, невозможно.
«Приливы и отливы-результат прецессии водоворотов».
Форум Кафедры Океанологии Спбгу.»Гипотезы, загадки, идеи, озарения».Воды озер, морей и океанов, северного полушария, вращаются против часовой стрелки, а воды южного полушария, вращаются по часовой стрелке, образуя гигантские водовороты. А все что вращается, в том числе и водовороты, обладают свойством гироскопа(юлы), сохранять вертикальное положение оси в пространстве независимо от вращения Земли.. Если смотреть на Землю со стороны Солнцa, водовороты вращаясь вместе с Землей опрокидываются, два раза в сутки, благодаря чему, водовороты прецессируют, (1-2 градусов) и отражают от себя приливную волну.. Воды Белого моря, вращаются против часовой стрелки, образуя огромный водоворот-гироскоп, прецессируя отражающий приливную волну по всему периметру Белого моря.. Аналогичная схема приливов и отливов, наблюдается во всех озерах, морях и океанах.. Приливную волну реке Амазонка, создает огромный планетарный водоворот диаметром несколько тысяч км, вращающийся между Южной Америкой и Северной Африкой, охватывая и устье реки Амазонка.. Ширина приливной волны, зависит от диаметра водоворота. А высота приливной волны, зависит от скорости опрокидывания водоворота (за 12часов), и скорости вращения водоворота. А скорость вращения водоворота, зависит от силы Кориолиса, от осевой и орбитальной скорости Земли, и от наклона оси Земли. А роль Луны косвенная, создание неравномерной орбитальной скорости Земли.. Воды Средиземного моря, вращаются против часовой стрелки, образуя приливы высотой 10-15 см. Но в заливе Габес, что у побережья Туниса, высота приливов достигает трех метров, а порой и больше. И это считается одной из загадок природы. Но в тоже время, в заливе Габес, вращается водоворот, прецессируя отражающий дополнительную приливную волну. Внутри постоянных океанических и морских водоворотов, вращаются небольшие постоянные и непостоянные вихри и водовороты, создаваемые впадающими в бухты реками, очертанием берегов и местными ветрами. И в зависимости от скорости, и направления вращения небольших прибрежных водоворотов, зависит календарь, амплитуда, и количество приливов и отливов в сутки.. Водоворотную гипотезу приливов, легко проверить, по связи высоты приливной волны, со скоростью вращения водоворотов.. По высоте приливной волны, можно определять местонахождение водоворотов.. Как правило положительные отзывы к гипотезе, пишут мыслители знающие о противоречиях в Лунной теории приливов и отливов, обладающие углубленными знаниями небесной механики, и свойств гироскопа.
Ответить
-
Гравитационное поле имеет не только скалярный потенциал (нормальную составляющую), но и векторный потенциал (вихревую составляющую) rot A ≠ 0, а генератором вихрей является Ñ — градиент плотности. Вертикальный градиент плотности вызывает тангенциальные силы, приводящий различные среды к вращению в горизонтальной плоскости, а горизонтальный градиент плотности вызывает их вертикальные движения (подъём, погружение). Это фундаментальное свойство гравитационного поля.
Во всех пограничных слоях разных сред (оболочек Земли) существует скачёк плотности, который активизирует (генерирует) тангенциальные силы гравитационного поля, а те в свою очередь формируют вихревые потоки. Менее плотные верхние слои плывут по нижним слоям с вращением по часовой стрелке, формируя антициклонический вихрь. Движение этих потоков осложняется рельефом нижнего более плотного слоя. Такие потоки — придонные течения существуют в атмосфере, реках, озёрах, морях и океанах.
За счёт этих же сил верхняя твёрдая оболочка Земли (литосфера) разбита на плиты, а те в свою очередь на более мелкие блоки верхней более твёрдой коры. Все эти плиты и блоки движутся относительно друг друга, вращаясь на более плотном основание и/или перемещаясь в вертикальном направление, при подъёме формируя материки, а при погружении озёра, моря и океаны. Так как эти плиты и блоки плотно упакованы, то никаких горизонтальных перемещений у них быть не может, а иллюзию перемещения создаёт движение в виде погружения одного и подъём другого с обоюдным вращением двух соседних блоков. К тому же материки, моря и океаны являются тонкой плёнкой на поверхности литосферных плит и составляют 1.5-2% от её мощности-толщины.
Поэтому причиной появления (действия) силы Кориолиса является не вращение Земли, а тангенциальная составляющая гравитационного поля, которая всегда существуют, но начинают действовать (работать) при появлении вертикального градиента плотности. Это можно подтвердить с помощью простого примера. В ясную морозную погоду, когда влажность воздуха минимальна, а его плотность максимальная дым поднимаясь из печной трубы буквально вкручивается в воздух, но если на следующий день при повышение температуры, а значит и влажности воздуха, плотности их становятся близкими, то он (дым) стелется по земле успевая только чуть подняться над трубой. Это говорит о том, что причиной такого поведения дыма является разность плотности дыма и воздуха, чем она больше, тем с большей скоростью и выше поднимается дым из трубы.Ответить
-
Интересная идея, ребята. А если кинуть мяч не с полюса на экватор, а наоборот: с экватора на полюс. То обратного эффекта же не будет? При идеальном полёте смещения не должно же быть? И не учли ещё само движение Земли относительно солнца. Я считаю, что при отсутствии воздуха мяч брошенный с полюса на экватор аналогично приземлится там, куда его направили, и не важно, насколько быстро и как вращается Земля. Важно только замедление вращения, но оно ничтожно, чтобы засечь какую-то фиктивную силу.
Ответить
-
Надо менять линию полом… Или пополам, как Демокрит!
Ответить
Написать комментарий
Во время изучения траекторий полета снарядов на дальние расстояния или при исследовании глобальных процессов, происходящих с океанами и атмосферой, необходимо учитывать влияние так называемой силы Кориолиса. В данной статье рассмотрим, что она собой представляет и как вычисляется.
Инерциальные и неинерциальные системы отсчета
Прежде чем приступить к вопросу, что такое кориолисова сила, напомним, что в физике существует два типа систем, относительно которых рассматриваются все законы механического движения.
Инерциальные — это такие системы, в которых законы механики Ньютона выполняются точно. Они либо находятся в состоянии покоя, либо движутся прямолинейно и равномерно.
Неинерциальные — это системы отсчета, которые перемещаются ускоренно. Причем ускорение может быть как линейным, так и угловым или центростремительным. В этих системах законы Ньютона не выполняются, поскольку появляются фиктивные силы, то есть такие, которые не вызваны каким-либо воздействием, а связаны с инерционными свойствами тел. Сила, которую мы рассмотрим в статье, как раз и является фиктивной.
Что такое сила Кориолиса, и когда она возникает?
Под кориолисовой понимают фиктивную силу, которая действует на тело, движущееся в неинерциальной системе отсчета, в частности, во вращающейся. Чаще всего это понятие связывают с нашей планетой. Однако в любой системе, которая вращается вокруг некоторой оси, присутствует эта сила.
Кориолисова сила отличается от центробежной, которая также является фиктивной. Действительно, центробежная сила стремится сдвинуть тело от оси вращения системы. Чтобы тело находилось в состоянии покоя, необходимо наличие противоположной ей силы — центростремительной. Она уже является настоящей. Сила Кориолиса же стремится искривить траекторию перемещения тела, так как в покое не действует.
Названа эта сила в честь французского ученого XIX века Гаспара Кориолиса, который впервые получил формулу для ее вычисления. Кориолисову силу начали учитывать при изучении процессов в мировом океане и атмосфере только с конца XIX-начала XX веков.
Пример с полетом снаряда
Чтобы лучше понять, как себя проявляет сила Кориолиса, приведем следующий простой, но в то же время показательный пример. Предположим, что пушка, которая находится на широте экватора, выполняет выстрел строго по направлению к северному полюсу. Пусть место ее расположения — n меридиан. Если бы наша планета не вращалась с запада на восток, то ядро упало строго бы на n меридиане в Северном полушарии. Однако из-за суточного вращения планеты оказывается, что ядро падает на m меридиане, который находится восточнее, чем n, то есть m>n. Сила, которая привела к изменению траектории полета юг-север ядра, называется кориолисовой.
Объяснить описанный эффект несложно. Дело в том, что экваториальные широты, ввиду шарообразной формы Земли, вращаются с более высокой линейной скоростью, чем широты Северного и Южного полушарий. Когда снаряд, который вылетел с низких широт, оказывается в высоких, то он по инерции движется с более высокой скоростью на восток, чем воздушные массы этих широт. Данный факт приводит к указанному отклонению снаряда от прямой траектории.
Компоненты изучаемой силы
Теперь рассмотрим, из каких компонент состоит кориолисова сила. Предположим, что у нас имеется вращающийся вокруг вертикальной оси горизонтальный диск. На нем лежит тело некоторой массы. Существуют три разные возможности движения тела в данной системе в соответствии с трехмерностью пространства:
- Если тело перемещается вертикально вверх (вниз), то есть параллельно оси вращения, то на него действует только центробежная сила. Иными словами, данное направление движения не вносит вклад в появление силы Кориолиса.
- Если тело перемещается в радиальном направлении, то есть приближается или удаляется от оси, то возникает кориолисова тангенциальная сила. Она направлена по касательной к траектории вращения. Более конкретное направление зависит от направления вращения и движения тела к оси или от нее.
- Если тело движется вдоль окружности, то есть у него появляется дополнительная относительно вращения тангенциальная компонента скорости. В этом случае также возникает кориолисова сила, которая будет стремиться либо приблизить тело к оси, либо удалить его от нее.
Таким образом, существуют две компоненты изучаемой силы: радиальная и касательная.
Формула силы
В данной статье не будем приводить все математические выкладки, чтобы получить формулу силы Кориолиса, а сразу приведем соответствующее выражение:
F = -2*m*[ω*v].
Здесь m — масса тела, ω и v — угловая скорость вращения системы и линейная скорость движения тела во вращающейся системе, соответственно. В квадратных скобках стоит векторное произведение скоростей. Это означает, что направление силы F всегда будет перпендикулярно оси вращения и вектору v. Например, во время перемещения снаряда в атмосфере нашей планеты кориолисова сила всегда направлена перпендикулярно его скорости — вправо от нее.
Записанная формула может быть получена, если рассмотреть закон сохранения момента импульса, а также применить формулу для определения центростремительного ускорения.
Влияние эффекта Кориолиса на земные процессы
Как выше было выяснено на примере полета снаряда в направлении Северного полушария, сила Кориолиса приводит к его смещению в восточном направлении. В ту же сторону будет смещаться тело при движении от экватора к Южному полюсу. Если же движение объекта противоположно указанным направлениям, то и влияние эффекта Кориолиса окажется противоположным.
Рассматриваемая сила оказывает большое влияние на изменение направлений океанических течений и движение воздушных масс. Например, течение Гольфстрим, которое обогревает своими теплыми водами западные берега Европы, в действительности берет начало по другую сторону Атлантического океана, в Мексиканском заливе. Оно пересекает океан с запада на восток, благодаря влиянию кориолисовой силы.
Еще одним известным примером действия рассматриваемой силы являются ветры пассаты. Как известно, они дуют в западном направлении в экваториальных широтах. Происходит это потому, что движущиеся к экватору воздушные массы из полушарий планеты отклоняются в западном направлении, подобно описанному выше полету снаряда.
Эффект Эотвоса (Eötvös effect)
Данный эффект заключается в уменьшении веса тела либо в его увеличении в зависимости от направления движения тела на Земле. Суть эффекта заключается в следующем: когда тело с большой скоростью движется строго на восток, то оно испытывает влияние кориолисовой силы, направленной от земной оси вращения. Поскольку сила гравитационного взаимодействия направлена вертикально вниз, то эффект Кориолиса приведет к уменьшению веса тела. Аналогичные рассуждения позволяют объяснить увеличение веса тела при его движении в западном направлении.
Пример задачи из баллистики
Пушка выстрелила ядро в северном направлении. Оно летело в течение 1 минуты. Его средняя горизонтальная скорость составляла 600 м/с. Необходимо определить расстояние, на которое отклонилось ядро, если выстрел произведен на широте 45o.
Для начала рассчитаем кориолисово ускорение. Сделать это можно по следующей формуле:
a = 2*ω*v*sin(θ).
Появившаяся функция синуса учитывает радиальную скорость приближения ядра к оси вращения Земли. Несложно рассчитать, что для нашей планеты ω = 7,3*10-5 рад/с. Тогда получаем:
a = 2*7,3*10-5*600*sin(45o) = 0,062 м/с2.
Расстояние, на которое сместится ядро, будет равно:
d = 1/2*a*t2 = 1/2*0,062*602 = 111,6 м.
Из этого результата видно, что эффект Кориолиса является существенным при определении траекторий полета снарядов в баллистике.
При вращении диска, более далёкие от центра точки движутся с большей касательной скоростью, чем менее далёкие (группа чёрных стрелок вдоль радиуса). Если мы хотим переместить некоторое тело вдоль радиуса, так, чтобы оно оставалось на радиусе (синяя стрелка из положения «А» в положение «Б»), то нам придётся увеличить скорость тела, то есть, придать ему ускорение. Если наша система отсчёта вращается вместе с диском, то мы ощутим, что тело «не хочет» оставаться на радиусе, а «норовит» уйти влево — это и есть сила Кориолиса.
Движение шарика по поверхности вращающейся тарелки.
Си́ла Кориоли́са (по имени французского учёного Гюстава Гаспара Кориолиса, впервые его описавшего) — одна из сил инерции, существующая в неинерциальной (вращающейся) системе отсчёта из-за вращения и законов инерции, проявляющаяся при движении в направлении под углом к оси вращения. Ускорение Кориолиса было получено Кориолисом в 1833 г., Гауссом в 1803 г. и Эйлером в 1765 г.
Причина появления силы Кориолиса — в кориолисовом (поворотном) ускорении. Для того, чтобы тело двигалось с кориолисовым ускорением, необходимо приложение силы к телу, равной F = ma, где a — кориолисово ускорение. Соответственно, тело действует по третьему закону Ньютона с силой противоположной направленности. FK = − ma. Сила, которая действует со стороны тела, и будет называться силой Кориолиса. Не следует путать Кориолисову силу с другой силой инерции — центробежной силой, которая направлена по радиусу вращающейся окружности.
В инерциальных системах отсчёта действует закон инерции, то есть, каждое тело стремится двигаться по прямой и с постоянной скоростью. Если рассмотреть движение тела, равномерное вдоль некоторого вращающегося радиуса и направленное от центра, то станет ясно, что чтобы оно осуществилось, требуется придавать телу ускорение, так как чем дальше от центра, тем должна быть больше касательная скорость вращения. Это значит, что с точки зрения вращающейся системы отсчёта, некая сила будет пытаться сместить тело с радиуса.
Если вращение происходит по часовой стрелке, то двигающееся от центра вращения тело будет стремиться сойти с радиуса влево. Если вращение происходит против часовой стрелки — то вправо.
Содержание
- 1 Математическое определение
- 1.1 Получение
- 1.2 Физический смысл
- 2 Сила Кориолиса в природе
- 3 См. также
Математическое определение
Сила Кориолиса равна:
где m — точечная масса, 
Кориолисово ускорение — это векторная величина, равная ![vec{a}_k=2 left[ vec omega times vec v right],](https://dic.academic.ru/pictures/wiki/files/55/7b078ba4ad487c59c24ab9381f405b3f.png)
Получение
Пусть тело совершает сложное движение: движется относительно неинерциальной системы отсчёта со скоростью 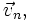
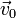
Тогда линейная скорость тела в инерциальной системе координат равна:
где 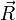
Найдём значение каждого слагаемого в инерциальной системе координат:
![frac{d}{dt} left[ vecomega times vec R right] = left[ vec varepsilon times vec R right] + left[ vecomega times frac{d}{dt} vec R right] = left[ vec varepsilon times vec R right] + left[ vecomega times vec {v}_n right] + left[ vecomega times left[ vecomega times vec R right] right],](https://dic.academic.ru/pictures/wiki/files/101/e5ef1554861e7cb48ef0e7a990349ddd.png)
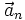
Таким образом, получаем:
![frac{d}{dt}vec v = vec a=vec {a}_0 + vec {a}_n + left[ vec varepsilon times vec R right] + left[ vec omega times left[ vec omega times vec R right] right] + 2left[ vec omega times vec {v}_n right].](https://dic.academic.ru/pictures/wiki/files/99/cee134148f3010b2696e9e0f94b9b9d3.png)
Физический смысл
Пусть тело движется со скоростью 
Тогда данное движение приведёт к изменению расстояния до центра вращения R и, как следствие, абсолютной скорости движения точки неинерциальной системы отсчёта, совпадающей с движущейся точкой.
Как мы знаем, эта скорость движения равна
Данное изменение будет равно:
Проведя дифференцирование по времени, получим ![vec a = left[ vecomega times vec v right]](https://dic.academic.ru/pictures/wiki/files/99/c8317f0075818272e2bc3cd7e7b8b78d.png)
C другой стороны, вектор 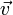
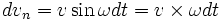
Общее ускорение будет ![vec {a}_k=2 left[ vecomega times vec v right].](https://dic.academic.ru/pictures/wiki/files/50/2852b6463402e829d89a249960f33f2c.png)
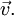
Если тело движется перпендикулярно направлению к центру вращения, то доказательство будет аналогичным. Ускорение из-за поворота вектора скорости останется ![vec a = left[ vecomega times vec v right],](https://dic.academic.ru/pictures/wiki/files/51/3537afd827222e73c0737864244d6b7b.png)
Сила Кориолиса в природе
Самый простой пример использования силы Кориолиса — это эффект ускорения кручения танцоров. Чтобы ускорить свое вращение, человек может начать крутиться с широко разведёнными в стороны руками, а затем — уже в процессе — резко прижать руки к туловищу, что вызовет увеличение круговой скорости (согласно закону сохранения момента импульса). Эффект силы Кориолиса проявится в том, что для такого движения руками придётся прикладывать усилия не только по направлению к телу, но и в направлении по вращению. При этом возникает ощущение, что руки отталкиваются от чего-то, при этом ещё больше ускоряясь.
Сила Кориолиса также проявляется, например, в работе маятника Фуко. Кроме того, поскольку Земля вращается, то сила Кориолиса проявляется и в глобальных масштабах. В северном полушарии сила Кориолиса направлена вправо от движения, поэтому правые берега рек в Северном полушарии более крутые — их подмывает вода под действием этой силы (см. Закон Бэра). В Южном полушарии всё происходит наоборот. Сила Кориолиса ответственна также и за вращение циклонов и антициклонов.
Вопреки расхожему мнению, маловероятно, что сила Кориолиса полностью определяет направление закручивания воды в водопроводе — например, при сливе в раковине. Хотя в разных полушариях она действительно стремится закручивать водяную воронку в разных направлениях, при сливе возникают и побочные потоки, зависящие от формы раковины и конфигурации канализационной системы. По абсолютной величине создаваемые этими потоками силы превосходят силу Кориолиса, поэтому направление вращения воронки как в Северном, так и в Южном полушарии может быть как по часовой стрелке, так и против неё.
См. также
- Центростремительное ускорение
- Кориолисовые расходомеры
Wikimedia Foundation.
2010.
Сила, действующая на объекты, движущиеся в пределах системы отсчета, которая вращается относительно инерциальной системы отсчета. 
В физике сила Кориолиса — это инерционная или фиктивная сила, которые действуют на объекты, которые движутся в системе отсчета вращающегося относительно инерциальной системы отсчета. В системе отсчета, с по часовой стрелке вращение, сила действует влево от движения объекта. В случае вращения против часовой стрелки (или против часовой стрелки) сила действует вправо. Прогиб объекта из-за силы Кориолиса называется эффектом Кориолиса . Хотя это и было признано другими ранее, математическое выражение для силы Кориолиса появилось в 1835 году в статье французского ученого Гаспара-Гюстава де Кориолиса в связи с теорией водяных колес. В начале 20 века номинальная сила Кориолиса Начал учиться в связи с метеорологией.
законы движения Ньютона инерциальной (не движениеускоряющей) системе отсчета ссылка. Когда законы Ньютона преобразуются во вращающуюся систему отсчета, появляются ускорения Кориолиса центробежные. При применении к массивным объектам соответствующие силы пропорциональны их массам. Сила центробежная сила пропорциональна квадрату скорости вращения. Сила поперечной оси вращения и скорости вращения во вращающейся системе координат, и скорости вращения во вращающейся системе координат (точнее, составляющей его скорости, перпикулярной оси вращения). вращения). Центробежная сила действует наружу в радиальном направлении и измеряет расстояния от тела до оси вращающейся рамы. Эти дополнительные силы называются силами инерции, фиктивными силами или псевдосилами. Учет вращения за счет добавления этих фиктивных сил позволяет использовать законы движения Ньютона к вращающейся системе. Это поправочные коэффициенты, которые не требуются в невращающейся системе.
В популярном (нетехническом) применении термина «эффект Кориолиса» подразумевается вращающаяся система почти всегда Земля. Земля вращается, наблюдатели, движущиеся объекты. Земля совершает один оборот для каждого дневного / ночного цикла, поэтому для движущихся обычных объектов, обычно довольно мала по силам с другими силами; его эффекты обычно становятся заметными только для движений, происходящих на больших расстояниях и в течение продолжительных периодов времени, таких как крупномасштабное движение воздуха в атмосфере или воды в океане; или там, где важна высокая точность, например, дальнобойная артиллерия или траектории ракет. Такие движения ограничиваются поверхностью Земли, поэтому обычно важна только горизонтальная составляющая силы Кориолиса. Эта сила заставляет движущиеся объекты на поверхности Земли отклоняться вправо (относительно направления движения) в Северном полушарии и влево в Южном полушарии. Эффект горизонтального отклонения больше около полюсов , поскольку эффективная скорость вращения вокруг вертикальной оси там наибольшая и уменьшается до нуля на экваторе. Вместо того, чтобы течь непосредственно из области высокого давления в области низкого давления, как это было бы в невращающейся системе, ветры и течения имеют тенденцию течь вправо от этого направления к северу от <122 экватора (против часовой стрелки) и к слева от этого направления к югу от него (по часовой стрелке). Этот эффект отвечает за вращение и таким образом, образование циклонов (см. эффекты Кориолиса в метеорологии).
Для интуитивного объяснения происхождения силы Кориолиса рассмотрим объект, который вынужден следовать за поверхностью Земли и движется на север в северном полушарии. Если смотреть из космоса, кажется, что объект движется не на север, а движется на восток (он вращается вправо вместе с поверхностью Земли). Чем дальше на север он движется, тем меньше «диаметр его параллели» (минимальное расстояние от точки поверхности до оси вращения, которая находится в плоскости, ортогональной оси), и поэтому тем медленнее движение его поверхности на восток.. По мере того, как объект движется на север, он имеет тенденцию поддерживать скорость на восток, с которой он начал (вместо того, чтобы замедляться, чтобы соответствовать уменьшенной скорости на восток местных объектов на поверхности Земли), поэтому он поворачивает на восток (т. справа от начального движения).
Хотя это не очевидно из этого примера, в котором движение на север, горизонтальное отклонение происходит одинаково для объектов, движущихся на восток или запад (или в другом направлении). Однако теория том, что этот эффект вращается сливаемой воды в обычной домашней ванне, раковине или унитазе, неоднократно опровергалась современными учеными; сила ничтожно мала по другим другим факторам, влияющим на другие факторы.
Содержание
- 1 История
- 2 Формула
- 3 Шкала длины и число Россби
- 4 Простые случаи
- 4.1 Пушка на поворотном столе
- 4.1.1 Траектория в инерциальной отсчета системе
- 4.1.1.1 Ускорения
- 4.1.1.1.1 Составляющие ускорения
- 4.1.1.1.2 Создание ускорений
- 4.1.1.1 Ускорения
- 4.1.1 Траектория в инерциальной отсчета системе
- 4.2 Подброшенный шар на вращающемся карусель
- 4.3 Отскок мяча
- 4.1 Пушка на поворотном столе
- 5 Применение на Земле
- 5.1 Интуитивное объяснение
- 5.2 Вращающаяся сфера
- 5.3 Метеорология
- 5.3.1 Обтекание области низкого давления
- 5.3. 2 Инерционные круги
- 5.3.3 Другие земные эффекты
- 5.4 Эффект Этвёша
- 5.4.1 Интуитивный пример
- 5.5 Слив в ваннах и туалетах
- 5.6 Баллистические траектории
- 6 Визуализация эффекта Кориолиса
- 7 Эффекты Кориолиса в других областях
- 7.1 Расходомер Кориолиса
- 7.2 Молекулярная физика
- 7.3 Гироскопическая прецессия
- 7.4 Полет насекомых
- 7.5 Стабильность точки Лагранжа
- 8 См. Также
- 9 Нет tes
- 10 Ссылки
- 10.1 Дополнительная литература
- 10.1.1 Физика и метеорология
- 10.1.2 Исторические данные
- 10.1 Дополнительная литература
- 11 Внешние ссылки
История


Итальянский ученый Джованни Баттиста Риччоли и его помощник Франческо Мария Гримальди описали эффект в связи с артиллерией в Almagestum Novum 1651 года, написав это вращение Земли заставить пушечное ядро, выпущенное на север, отклониться на восток. В 1674 году Клод Франсуа Миллиет Дешалес описал в своем Cursus seu Mundus Mathematicus, как вращение Земли должно вызывать отклонение траекторий как падающих тел, так и снарядов, направленных к одному из полюсов планеты. Риччоли, Гримальди и Дешалес описали этот эффект как часть аргумента против гелиоцентрической системы Коперника. Другими словами, они утверждают, что вращение Земли вызывается. Уравнение ускорения Кориолиса было получено Эйлером в 1749 году, и эффект был в уравнениях приливов из Пьера-Симона Лапласа в 1778 году.
Гаспар-Гюставолис опубликовал в 1835 году статью о выходе энергии машин с вращающимися частями таких как водяные. В этой статье рассматривались дополнительные силы, отображаемые во вращающейся системе отсчета. Кориолис разделил эти дополнительные силы на две категории. Вторая категория содержала силу, которая возникает из перекрестного произведения угловой скорости системы системы координат и проекции скорости частиц в плоскость , перпендикулярную оси вращения системы. Кориолис назвал эту силу «сложной центробежной силой» из-за ее аналогии с центробежной силой, уже рассматриваемой в первой категории. Эффект был известен в начале 20 века как «ускорение Кориолиса», а к 1920 году как «сила Кориолиса».
В 1856 году Уильям Феррел использует наличие циркуляционной ячейки в средних широтах, где воздух отклоняется силой Кориолиса, создавая преобладающие западные ветры.
Понимание кинематики того времени, как именно вращается Земля Воздействие на воздушный поток сначала было частичным. В конце 19 века была осознана степень крупномасштабного взаимодействия силы градиента давления и отклоняющей силы, которая в итоге заставляет воздушные массы двигаться по изобарам.
Формула
В механике Ньютона уравнение движения для объекта в инерциальной системе оценки:
- F = ma { displaystyle { boldsymbol {F}} = m { boldsymbol {a}}}
где F { displaystyle { boldsymbol {F}}}


Преобразование этого уравнения в системе отсчета, вращающейся вокруг фиксированной оси через начало координат с угловой скоростью ω { displaystyle { boldsymbol { omega}}}
- F — md ω d t × r ′ — 2 m ω × v ′ — m ω × (ω × r ′) { displaystyle { boldsymbol {F}} — m { frac { operatorname {d} { boldsymbol { omega}}} { operatorname {d} t}} times { boldsymbol {r ‘}} — 2m { boldsymbol { omega}} times { boldsymbol {v ‘}} — m { boldsymbol { omega}} times ({ boldsymbol { omega}} times { boldsymbol {r’}})}
= ma ′ { Displaystyle = m { boldsymbol {a ‘}}}
где
- F { displaystyle { boldsymbol {F}}}
— имеющая сумма физических сил, действующих на объект
- ω { displaystyle { boldsymbol { omega}}}
— это угловая скорость вращающейся системы оценки относительно инерциальной системы отсчета
- v ′ { displaystyle { boldsymbol {v ‘ }}}
— скорость относительно вращающегося re Ference кадр
- г ‘{ displaystyle { boldsymbol {г’}}}
является вектором положения объекта относительно вращающейся системычета
- а ‘{ displaystyle { boldsymbol {a’}}}
— ускорение относительно вращающейся системы отсчета
Фиктивные силы, которые воспринимаются во вращающейся системе координат, как дополнительные силы, способные кажущемуся ускорению, как и реальные внешние силы. Условные обозначения силы в уравнении: слева направо:
Обратите внимание, что эйлеровы и центробежные силы положения от положения положения r ′ { displaystyle { boldsymbol {r ‘}}}



пропорционально сила Кориолиса перекрестному произведению двух векторов, она перпендикулярна к обоим случаям, в данном случае к скорости объекта и вектору вращения кадра. Отсюда следует, что:
- если скорость параллельна оси вращения, сила Кориолиса равна нулю. (Например, на Земле такая ситуация имеет место для тела на экваторе, движущемся на север или юг относительно поверхности Земли.)
- если скорость направлена прямо внутрь оси, сила Кориолиса находится в направлении местное вращение. (Например, на Земле такая ситуация возникает на экваторе, падающем вниз, как на иллюстрации выше, где падающий шар движется дальше на восток, чем башня.)
- если скорость направлена наружу прямо от оси, сила Кориолиса направлена против направления местного вращения. (В примере с башней мяч, запущенный вверх, будет двигаться к западу.)
- , если скорость находится в направлении вращения, сила Кориолиса наружу от оси. Он будет двигаться вверх, как видит наблюдатель на поверхности. Этот эффект (см. Эффект Этвёша ниже) обсуждался Галилео Галилей в работе 1632 и Риччиоли в 1651 году.)
- если скорость направлена против направления вращения, то сила Кориолиса направлена внутрь оси. (На Земле такая ситуация для тела на экваторе, движущееся на запад, которое отклоняется вниз, как это видит наблюдатель.)
Шкалы длины и число Россби
Шкалы времени, пространство и скорость имеют значение для определения важности силы Кориолиса. Важность вращения в системе можно определить по его численности Россби, представляет собой отношение скорости U к системе воспроизведения программы Кориолиса, f = 2 ω sin φ { displaystyle f = 2 omega sin varphi ,}
- R o = U f L. { displaystyle Ro = { frac {U} {fL}}.}
Число Россби — это отношение сил инерции к силам Кориолиса. Маленькое число Россби указывает на то, что на систему оказывает влияние силы Кориолиса, а большое число Россби указывает на систему, в которой преобладают силы инерции. Например, в торнадо число Россби велико, в системе с низким давлением оно низкое, а в океанических системах оно составляет около 1. В результате в торнадо сила Кориолиса незначительна, а баланс находится между давлением и центробежными силами.. В системах с низким давлением центробежная сила незначительна, и баланс находится между силами Кориолиса и давления. В океанах все три силы сопоставимы.
Атмосферная система, движущаяся со скоростью U = 10 м / с (22 мили в час) и занимающее пространственное расстояние L = 1000 км (621 миля), имеет число Россби приблизительно 0,1.
Питчер бейсбола может бросать мяч со скоростью U = 45 м / с (100 миль в час) на расстоянии L = 18,3 м (60 футов). Число Россби в этом случае будет 32000.
Бейсболистам все равно, в каком полушарии они играют. Неуправляемая ракета подчиняется точно такой же физике, что и бейсбольный мяч, но может лететь достаточно долго, чтобы испытать эффект силы Кориолиса. Снаряды дальнего действия в северном полушарии приземлялись, но справа от того места, куда они были нацелены, пока это не было сделано. (Те, кто был запущен в Южном полушарии, приземлились.) Фактически, этот первый эффект привлекательного самого Кориолиса.
Простые случаи
Пушка на поворотном столе




Анимация в верхней части этой статьи является классической иллюстрацией силы Кориолиса. Другая визуализация кориолисовых и центробежных сил — этот анимационный клип.
Учитывая радиус R поворотной платформы в этой анимации, скорость углового вращения ω и скорость пушечного ядра (предполагаемую постоянной) v, правильное угол θ для прицеливания и попадания в цель на краю поворотной платформы.
Инерциальная система отсчета предоставляет один способ решить вопрос: вычислить время до перехвата, которое равно t f = R / v. Затем поворотный стол за это время поворачивается на угол ω t f. Если пушка наведена под углом θ = ω t f = ω R / v, то пушечное ядро достигает периферии в позиции номер 3 одновременно с целью.
Никакое обсуждение силы Кориолиса не может привести к этому решению так просто, поэтому причина для рассмотрения этой проблемы — продемонстрировать формализм Кориолиса в легко визуализируемой ситуации.
Траектория в инерциальной системе отсчета
Траектория в инерциальной системе отсчета (обозначена A) представляет собой прямую радиальную траекторию под углом θ. Положение пушечного ядра в координатах (x, y) в момент времени t составляет:
- r A (t) = v t (cos θ, sin θ). { displaystyle mathbf {r} _ {A} (t) = vt left ( cos theta, sin theta right) .}
В раме поворотного стола (обозначена B) Оси x- y вращаются с угловой скоростью ω, поэтому траектория принимает следующий вид:
- r B (t) = vt (cos (θ — ω t), sin (θ — ω t)), { displaystyle mathbf {r} _ {B} (t) = vt left ( cos ( theta — omega t), sin ( theta — omega t) right) ,}
и три примера этого результата нанесены на рисунок.
Ускорения
Компоненты ускорения
Для определения компонентов ускорения используется общее выражение из статьи фиктивная сила :
- a B = a A — 2 Ω × v B — Ω × (Ω × р В) — d Ω dt × r B { displaystyle mathbf {a} _ {B} = mathbf {a} _ {A} ; — ; 2 { boldsymbol { Omega}} times mathbf {v} _ {B} ; — ; { boldsymbol { Omega}} times left ({ boldsymbol { Omega}} times mathbf { r} _ {B} right) ; — ; { frac {d { boldsymbol { Omega}}} {dt}} times mathbf {r} _ {B}}
, в котором член в -2 Ом × vBпредставляет собой ускорение Кориолиса, а член в -Ом × (Ω× rB) представляет собой центробежное ускорение. Результаты следующие (пусть α = θ — ωt):
- Ω × r B = | i j k 0 0 ω t v cos α t v sin α 0 | = ω t v (- sin α, cos α), Ω × (Ω × r B) = | i j k 0 0 ω — ω t v sin α ω t v cos α 0 | знак равно ω 2 tv (- соз α, — грех α), { displaystyle { begin {align} { boldsymbol { Omega}} times mathbf {r} _ {B} = ; { begin {vmatrix} { boldsymbol {i}} { boldsymbol {j}} { boldsymbol {k}} \ 0 0 omega \ tv cos alpha tv sin alpha 0 end {vmatrix} } ; = omega t , v left (- sin alpha, cos alpha right) , \ { boldsymbol { Omega}} times left ({ boldsymbol { Omega} } times mathbf {r} _ {B} right) = ; { begin {vm atrix} { boldsymbol {i}} { boldsymbol {j}} { boldsymbol {k}} \ 0 0 omega \ — omega tv sin alpha omega tv cos альфа 0 end {vmatrix}} ; = omega ^ {2} t , v left (- cos alpha, — sin alpha right), end {align}}}
Создание ускорений
Создание центробежного ускорения :
- a Cfgl = ω 2 vt (cos α, sin α) = ω 2 r B (t). { displaystyle mathbf {a} _ { text {Cfgl}} = omega ^ {2} vt left ( cos alpha, sin alpha right) = omega ^ {2} mathbf { r} _ {B} (t) .}
Также:
- v B = dr B (t) dt = (v cos α + ω tv sin α, v sin α — ω tv cos α, 0), Ω × v B = | i j k 0 0 ω v cos α + v sin α — ω t v sin α ω t v cos α 0 |, { displaystyle { begin {align} mathbf {v} _ {B} = { frac {d mathbf {r} _ {B} (t)} {dt}} = (v cos alpha + omega tv sin alpha, v sin alpha — omega tv cos alpha, 0) , \ { boldsymbol { Omega}} times mathbf {v} _ {B} = { begin {vmatrix} { boldsymbol {i}} { boldsymbol {j}} { boldsymbol {k}} \ 0 0 omega \ v cos alpha + {} v sin alpha — {} \ quad omega tv sin alpha quad omega tv cos alpha 0 end {vmatrix}} , end {align}}}
с ускорением Кориолиса:
- a Cor = — 2 [- ω v (sin α — ω t cos α), ω v (cos α + ω t sin α)] = 2 ω v (sin α, — cos α) — 2 ω 2 r B (t). { Displaystyle { begin {align} mathbf {a} _ { text {Cor}} = — 2 left [- omega v left ( sin alpha — omega t cos alpha right), omega v left ( cos alpha + omega t sin alpha right) right] \ = 2 omega v left ( sin alpha, — cos alpha справа) -2 omega ^ {2} mathbf {r} _ {B} (t) . end {align}}}
Эти ускорения показаны на диаграммах для конкретного примера.
Видно, что ускорение Кориолиса не только нейтрализует пробежное ускорение, но вместе они обеспечивают чистый «центростремительный», радиально направленный внутрь компонент ускорения (то есть направленный к центру вращения):
- a C ptl = — ω 2 р В (t), { displaystyle mathbf {a _ { mathrm {Cptl}}} = — omega ^ {2} mathbf {r_ {B}} (t) ,}
и дополнительная составляющая ускорения, перпендикулярная rB(t):
- a C ⊥ = 2 ω v (sin α, — cos α). { displaystyle mathbf {a} _ {C perp} = 2 omega v left ( sin alpha, — cos alpha right) .}
«Центростремительный» компонент ускорения напоминает что для кругового движения на радиусе r B, в то время как перпендикулярная зависит от постоянной скорости v и направлена вправо от скорости. Ситуацию можно описать как круговое движение в сочетании с «кажущимся кориолисовым ускорением» 2ωv. Однако это грубая маркировка: точное обозначение истинной центростремительной силы относится к системе отсчета, которая использует направления, нормальные и касательные к траектории, а не координаты, относящиеся к оси вращения.
Эти результаты также могут быть получены непосредственно двумя временными дифференциалами rB(t). Согласование двух подходов показывает, что можно начать с выражения для фиктивного ускорения, приведенного выше, получить траектории, показанные здесь. Однако работа от ускорения к траектории более сложная, чем обратная процедура, используемая здесь, что стало возможным в этом случае, если заранее знать ответ.
В результате этого анализа появляется важный момент: все фиктивные ускорения должны быть включены, чтобы получить правильную траекторию. В частности, ускорения Кориолиса важную роль играет центробежная сила. Из словесных обсужденных проблем, которые сосредоточены на отображении эффекта Кориолиса, легко получить впечатление, что сила Кориолиса — единственный фактор, который используется, но это не так. Поворотный стол, для которого сила Кориолиса является единственным фактором, — это параболический поворотный стол. Несколько более сложная ситуация представляет собой идеализированный пример маршрута полета на больших расстояниях, где центробежной силе траектории и воздушной подъемной силе противодействует гравитационное притяжение.
Подброшенный мяч на вращающемся карусели
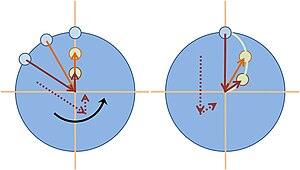
На рисунке показан подброшенный с 12:00 в сторону центра карусели, вращающейся против часовой стрелки. Слева неподвижный наблюдатель видит мяч над каруселью, и мяч движется по прямому к центру, в то время как мяч вращается против часовой стрелки вместе с каруселью. Справа наблюдатель видит мяч, вращающийся вместе с каруселью, поэтому игрок, бросающий мяч, кажется, остается в 12:00. На рисунке показано, как можно построить траекторию шара, видимым вращающимся наблюдателем.
Слева стрелки указывают указание относительно игрока, выполняющего выполняющего бросок. Одна из этих стрелок направлена от центра карусели к мячу, одна из этих стрелок направлена от центра карусели к мячу. (Эта стрелка становится короче по мере приближения шара к центру.) Смещенная версия двух стрелок сначала пунктиром.
Справа та же пара пунктирных стрелок, но теперь они жестко повернуты, так что стрелка, соответствующая линия взгляда метателя мяча по направлению к центру карусели, совмещена с 12: 00 часов. Другая стрелка пары указывает положение мяча относительно центра карусели. Следуя этой процедуре для нескольких положений, устанавливается траектория во вращающейся системе отсчета.
Мяч летит в воздухе, и на нем не действует чистая сила. Для неподвижного наблюдателя мяч движется по прямолинейной траектории, поэтому нет никаких проблем с квадратом этой траектории с нулевой чистой силой. Однако вращающийся наблюдатель видит кривую траекторию. Кинематика настаивает на, что сила (толкающая вправо от мгновенного направления движения для вращения против часовой стрелки) должна присутствовать, чтобы вызвать эту кривизну, поэтому вращающийся наблюдатель вызывает комбинацию центробежных сил и сил Кориолиса, чтобы обеспечить чистую силу, необходимую для создания искотурившейся траектории..
Отскок мяча

На рисунке описана более сложная ситуация, когда подброшенный мяч на поворотной платформе отскакивает от края карусели, а затем возвращается к бросающему мячу, который ловит мяч. Влияние силы кориолиса на его траекторию снова двумя наблюдателями: наблюдаемым «камерой»), который вращается вместе с каруселью. На рисунке показан вид с высоты птичьего полета, основанный на одинаковой скорости мяча на прямом и обратном пути. Внутри каждого круга нанесенные точки показывают одни и те же моменты времени. На левой панели, с точки зрения камеры в центре вращения, тоссер (смайлик) находится в фиксированных местах, и мяч делает очень значительную дугу на своем пути к направляющей и принимает более прямой маршрут на обратном пути. С точки зрения бросающего мяч, кажется, что мяч возвращается быстрее, чем ушел (потому что бросает в сторону мяча при обратном полете).
На карусели, вместо того, чтобы бросать мяч прямо в перила, подбрасывающий должен бросить мяч вправо от мишени, и тогда камеру кажется, что мяч непрерывно движется слева от его направления движения. (влево, потому что карусель вращается по часовой стрелке). Кажется, что мяч движется влево от направления движения как по внутренней, так и по обратной траекториям. Изогнутая траектория требует, чтобы наблюдатель распознал направленную влево чистую силу, действующую на мяч. (Эта сила является «фиктивной», потому что она исчезает для неподвижного наблюдателя, как будет обсуждаться вкратце.) Для некоторых углов запуска траектория имеет участки, где траектория приблизительно радиальна, и сила Кориолиса в первую очередь отвечает за кажущееся отклонение шар (центробежная сила радиальной от центра вращения и небольшое отклонение этих сегментов). Однако, когда траектория отклоняется от радиальной, центробежная сила вносит значительный вклад в отклонение.
Путь мяча в воздухе для наблюдателей, стоящих на земле (правая панель). На правой панели (неподвижный наблюдатель) бросок мяча (смайлик) находится в положении «12 часов», направляющая, от которой отскакивает мяч, находится в положении в 1 (1). С точки зрения инерционного зрителя позиции один (1), два (2), три (3) занимают последовательно. В позиции 2 мяч ударяется о направляющую, а в позицию 3 мяч возвращается в бросок. Прямолинейные траектории следуют, потому что этот мяч находится в свободном полете, поэтому этот наблюдатель требует, чтобы чистая сила не применялась.
Прикладывается к Земле
Сила, влияющая на движение, «скользящего» по поверхности Земли, является горизонтальной составляющей члена Кориолиса
- — 2 Ом × v { displaystyle — 2 , { boldsymbol { Omega times v}}}
Эта составляющая ортогональна скорости над земной поверхностью и задается выражением
- ω v 2 sin ϕ { displaystyle omega , v 2 , sin phi}
где
- ω { displaystyle omega}
— скорость вращения Земли;
- ϕ { displaystyle phi}
— широта, положительная в северном полушарие и отрицательное в южном полушарии
В северном полушарии, где знак положительный, эта сила / ускорение, если смотреть сверху, находится справа от направления движения, в южном полушарии, где знак отрицательный, эта сила / ускорение находится слева от направления движения
Интуитивное объяснение
Когда Земля вращается вокруг своей оси, все, что с ней связано, включая атмосферу re, t urns с ним (незаметно для наших чувств). Объект, который движется без волочения вместе с вращением поверхности или атмосферой, например, объект в баллистическом полете или независимая воздушная масса в атмосфере, движется по прямой над вращающейся Землей. С нашей точки зрения вращения на планете, направление движения объекта в баллистическом полете изменяется по мере его движения, изгибаясь в направлении, противоположном нашему действительному движению.
Если смотреть из неподвижной точки в космосе прямо над северным полюсом, любой объект суши в Северном полушарии поворачивается против часовой стрелки — и, фиксируя взгляд на этом месте, любое другое место в этом полушарии вращается вокруг него так же путь. Отслеживаемая наземная траектория свободно движущегося тела в баллистическом полете, перемещающегося из одной точки в другую, поэтому изгибается в противоположном направлении, по часовой стрелке, что обычно обозначается как «право», где она будет, если направление движения считается «впереди», а «вниз» определяется естественно.
Вращающаяся сфера
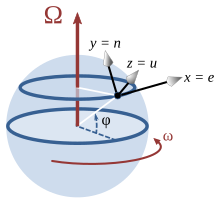
Рассмотрим местоположение с широта φ на сфере, вращающейся вокруг оси север-юг. Устанавливается местная система координат с осью x горизонтально на востоке, осью y горизонтально на севере и осью z вертикально вверх. Вектор вращения, скорость движения и ускорение Кориолиса, выраженные в этой локальной системе координат (перечисляющие компоненты в порядке восток (e), север (n) и вверх (u)):
- Ω = ω (0 cos φ грех φ), { displaystyle { boldsymbol { Omega}} = omega { begin {pmatrix} 0 \ cos varphi \ sin varphi end {pmatrix}} ,}
v = (vevnvu), { displaystyle { boldsymbol {v}} = { begin {pmatrix} v_ {e} \ v_ {n} \ v_ {u} end {pmatrix}} ,}
- a C = — 2 Ω × v = 2 ω (vn sin φ — vu cos φ — ve sin φ ve cos φ). { displaystyle { boldsymbol {a}} _ {C} = — 2 { boldsymbol { Omega times v}} = 2 , omega , { begin {pmatrix} v_ {n} sin varphi -v_ {u} cos varphi \ — v_ {e} sin varphi \ v_ {e} cos varphi end {pmatrix}} .}
При рассмотрении динамики атмосферы или океана вертикальная скорость мала, а вертикальная составляющая ускорения Кориолиса мала по сравнению с ускорением свободного падения. Для таких случаев имеют значение только горизонтальные (восточная и северная) составляющие. Ограничение приведенного выше на горизонтальную плоскость (установка v u = 0):
- v = (vevn), { displaystyle { boldsymbol {v}} = { begin {pmatrix} v_ {e} \ v_ {n} end {pmatrix}} ,}
ac = (vn — ve) f, { displaystyle { boldsymbol {a}} _ {c} = { begin { pmatrix} v_ {n} \ — v_ {e} end {pmatrix}} f ,}
где f = 2 ω sin φ { displaystyle f = 2 omega sin varphi ,}
Если установить v n = 0, сразу видно, что (для положительных φ и ω) движение на восток приводит к ускорению на юге. Аналогичным образом, при установке v e = 0 видно, что движение на север приводит к ускорению на востоке. Как правило, при наблюдении по горизонтали, если смотреть вдоль направления движения, вызывающего ускорение, ускорение всегда поворачивается на 90 ° вправо и одинакового размера независимо от горизонтальной ориентации.
В качестве другого случая рассмотрим установку экваториального движения φ = 0 °. В этом случае Ω параллельно северу или оси n, и:
- Ω = ω (0 1 0), { displaystyle { boldsymbol { Omega}} = omega { begin {pmatrix} 0 \ 1 \ 0 end {pmatrix}} ,}
v = (vevnvu), { displaystyle { boldsymbol {v}} = { begin {pmatrix} v_ {e} \ v_ { n} \ v_ {u} end {pmatrix}} ,}
a C = — 2 Ω × v = 2 ω (- vu 0 ve). { displaystyle { boldsymbol {a}} _ {C} = — 2 { boldsymbol { Omega times v}} = 2 , omega , { begin {pmatrix} -v_ {u} \ 0 \ v_ {e} end {pmatrix}} .}
Соответственно, движение на восток (то есть в том же направлении, что и вращение сферы) обеспечивает восходящее ускорение, известное как эффект Этвёша, а движение вверх ускорение на западе.
Метеорология




Возможно, наиболее важное влияние Кориолиса проявляется в крупномасштабном динамике океанов и атмосферы. В метеорологии и океанографии удобно постулировать вращающуюся систему отсчета, в которой Земля неподвижна. В соответствии с этим предварительным постулатом вводятся центробежные и силы Кориолиса. Их относительная важность поставляется числами Россби. Торнадо имеют высокие числа Россби, поэтому, хотя центробежные силы, связанные с торнадо, весьма существенны, силы Кориолиса, связанные с торнадо, для практических целей пренебрежимо малы.
поверхностные океанические течения вызываются движением. Температура воздуха над водной поверхностью, сила Кориолиса также влияет на движение океанских течений и циклонов. Многие из систем океанских течений циркулируют вокруг теплых областей с высоким давлением, называемых круговоротами. Хотя циркуляция не такая значительная, как в воздухе, отклонение, вызванное эффектом Кориолиса, спиралевидный узор в этих круговоротах. Спиральный ветер сформироваться урагану. Чем сильнее сила эффекта Кориолиса, тем быстрее вращается и набирает дополнительную энергию, увеличивая силу урагана.
Воздух в системе с высоким давлением в таком направлении направляется, что сила Кориолиса направлена радиально внутрь и почти уравновешивается наружу радиальным градиентом давления. В результате воздух движется по часовой стрелке вокруг высокого давления в Северном полушарии и против часовой стрелки в Южном полушарии. Воздух вокруг низкого давления вращается в противоположном направлении, так что сила Кориолиса направлена радиально наружу и почти уравновешивает внутренний радиальный градиент давления.
Обтекание области низкого давления
Если низкое — в атмосфере образует зону давления, воздух стремится втекать к ней, но отклоняется перпендикулярно своей скорости под действием силы Кориолиса. Тогда система равновесия может установить себя, создаваемое круговое движение или циклонический поток. Временное число Росс низкое, баланс сил в основном находится между силой градиента давления, действующей в направлении области низкого давления, и силой Кориолиса, действующей вдали от центра низкого давления.
Вместо того, чтобы течь по градиенту, крупномасштабные движения в атмосфере и океане, как правило, происходит перпендикулярно градиенту давления. Это известно как геострофический поток. На невращающейся планете жидкость будет течь по самой прямой линии, быстро устраняя градиенты давления. Таким образом, геострофический баланс сильно отличается от случая «инерционных движений» (см. Ниже), что объясняет, почему циклоны на средних широтах на порядок больше, чем могли бы быть инерционные круговые потоки.
Эта модель отклонения и направления движения называется законом Байса-Балота. В атмосфере поток называется циклон. В Северном полушарии направление движения вокруг области низкого давления — против часовой стрелки. В Южном полушарии направление движения — по часовой стрелке, потому что динамика вращения там является зеркальным отражением. На больших высотах воздух, распространяющийся наружу, вращается в противоположном направлении. Циклоны редко образуются вдоль экватора из-за слабого эффекта Кориолиса, присутствующего в этой области.
Инерционные круги
Воздушная или водная масса, движущаяся со скоростью v { displaystyle v ,}

- R = vf { displaystyle R = { frac {v} {f}} ,}
где f { displaystyle f}



Если вращающаяся система представляет собой параболический поворотный стол, то f { displaystyle f}


Другие земные эффекты
Эффект Кориолиса сильно влияет на крупномасштабную океаническую и атмосферную циркуляцию, приводя к образованию устойчивых функций, таких как струйные течения и западные пограничные течения. Такие особенности находятся в геострофическом балансе, что означает, что силы Кориолиса и градиента давления уравновешивают друг друга. Ускорение Кориолиса также отвечает за распространение типов волн в океане и атмосфере, включая волны Россби и волны Кельвина. Он также играет важную роль в так называемой динамике Экосистемы в океане и в океане и в в морской среде, называемой балансом Свердрупа.
эффектом Этвёша
воздействие «эффекта Кориолиса» в. в основном вызвано составляющей горизонтального ускорения, создаваемой горизонтальным движением.
Есть и другие компоненты эффекта Кориолиса. Объекты, перемещающиеся на запад, отклоняются вниз, а объекты, перемещающиеся на восток, отклоняются вверх. Это известно как эффект Этвёша. Этот аспект эффекта Кориолиса наиболее силен вблизи экватора. Сила, создаваемая эффектом Этвёша, аналогичная горизонтальной составляющей, но гораздо большие вертикальные силы, обусловленные гравитацией и давлением, предполагают, что она не важна в гидростатическом равновесии. Однако в атмосфере ветры связаны с небольшими отклонениями давления от гидростатического равновесия. В тропической атмосфере порядок величины отклонения давления настолько мал, что вклад эффекта Этвёша в отклонения давления значительный.
Кроме того, движущиеся объекты вверх (т.е. наружу) или вниз (т.е. в) отклоняются на запад или восток соответственно. Этот эффект также наиболее силен вблизи экватора. Вертикальное движение обычно ограничено по протяженности и продолжительности, размер эффекта меньше, и для его обнаружения требуются точные инструменты. Например, идеализированные исследования численного моделирования показывают, что этот эффект может напрямую влиять на крупномасштабное поле ветра примерно на 10% при длительности (2 недели и более) нагревании или тропении в атмосфере. Более того, в случае больших изменений импульса, например, при запуске космического корабля на орбиту, эффект становится значительным. Самый быстрый и наиболее экономичный путь к орбите — это запуск с экватора, который поворачивает в направлении прямо на восток.
Интуитивный пример
Представьте себе поезд, который едет по железной дороге без трения вдоль экватора. Предположим, что в движении он движется с необходимой скоростью, чтобы совершить кругосветное путешествие за один день (465 м / с). Эффект Кориолиса можно рассматривать в трех случаях: когда он движется на запад, когда он находится в состоянии покоя и когда он движется на восток. В каждом случае может быть вычислен сначала из вращающейся системы отсчета на Земле, а сверяться с фиксированной инерциальной системой. На изображении показан три случая с точки зрения наблюдателя в покое в (близкой) инерциальной системе отсчета из фиксированной точки над Северным полюсом вдоль оси вращения Земли ; поезд обозначается красными пикселями, зафиксированными слева на крайнем левом изображении, движущимися с остальными (1 день = ∧ 8 с): { displaystyle (1 { text {day}} ; { overset { land} { =}} ; 8 { text {s}}):}
- 1. Поезд движется на запад: в этом случае он движется против направления. Следовательно, на вращающейся системе координат Земли членолиса направлен внутрь по направлению оси вращения (вниз). Эта сила, направленная вниз, должна сделать более тяжелее при движении в этом направлении поезд.
- Если посмотреть на этот поезд с неподвижной невращающейся рамы наверху центра Земли, то при такой скорости он остается неподвижным, поскольку Земля вращается под ним. Следовательно, единственная сила, действующая на него, — это гравитация и реакция следа. Эта сила больше (на 0,34%), чем сила, которую испытывают пассажиры и поезд в состоянии покоя (вращаясь вместе с Землей). Это различие и объясняется эффектом Кориолиса во вращающейся системе отсчета.
- 2. Поезд останавливается: с точки зрения вращающейся системы, скорость поезда равна нулю Земли, следовательно, сила Кориолиса также равна нулю, и поезд и его пассажиры восстанавливают свой обычный вес.
- Из фиксированной инерциальной системы отсчета над Землей, теперь вращается вместе с остальной Землей. 0,34% силы тяжести обеспечивает центростремительную силу, для достижения кругового движения в этой системе отсчета. Оставшаяся сила, измеренная по шкале, делает поезд и пассажиров «легче», чем в предыдущем случае.
- 3. Поезд идет на восток. В этом случае, поскольку он движется в направлении вращения системы координат Земли, член Кориолиса направлен наружу от оси вращения (вверх). Эта направленная вверх сила заставляет поезд казаться еще легче, чем в состоянии покоя.
-
- Из фиксированной инерциальной системы отсчета над Землей поезд, движущийся на восток, теперь вращается с удвоенной скоростью, чем когда он был в состоянии покоя — таким образом, количество центростремительной силы необходимой для того, чтобы вызвать этот круговой путь. меньше силы тяжести, действующей на путь. Это то, что объясняется термином Кориолиса в предыдущем абзаце.
- В качестве последней проверки можно представить себе систему, обеспечивающую вместе с поездом. Такая рамка будет вращаться с удвоенной угловой скоростью, чем вращающаяся рамка Земли. Результирующая составляющая центробежной силы для этого воображаемого кадра будет больше. Поезд и его пассажиры находятся в состоянии покоя, это был единственный компонент в этом кадре, еще раз объясняющий, почему поезд и его пассажиры легче, чем в предыдущих двух случаях.
Это также объясняет, почему высокоскоростные снаряды, движущиеся на запад, отклоняются вниз, а те, которые идут на восток, отклоняются вверх. Этот вертикальный компонент эффекта Кориолиса называется эффектом Этвёша.
. Приведенный выше пример можно использовать, чтобы объяснить, почему эффект Этвёша начинает уменьшаться, когда объект движется на запад, когда его тангенциальная скорость увеличивается выше Вращение Земли (465 м / с). В приведенном выше примере увеличивает скорость, часть силы тяжести, которая толкает рельсы, составляет центростремительную силу для поддержания его в круговом движении на инерциальной системе отсчета. Как только поезд удваивает свою западную скорость до 930 м / с, эта центростремительная сила становится равной силе, которую поезд испытывает при остановке. С инерциальной системы отсчета обоих случаев он вращается с одинаковой скоростью, но в противоположных направлениях. Таким образом, сила та же самая, полностью отменяющая эффект Этвёша. Любой объект, который движется на запад со скоростью выше 930 м / с, вместо этого испытывает восходящую силу. На рисунке показан эффект Этвеша для 10-килограммового объекта в поезде на разных скоростях. Параболическая форма обусловлена тем, что центростремительная сила пропорциональна квадрату тангенциальной скорости. В инерциальной системе отсчета нижняя часть параболы центрирована в начале координат. Смещение смещения с тем, что этот аргумент использует вращающуюся систему отсчета Земли. График показывает, что эффект Этвеша не является симметричным и что результирующая направленная сила, испытываемая которым движется на запад с высокой скоростью, меньше результирующей восходящей силы, когда он движется на восток с той же скоростью.
Слив в ванне и туалетах
Вопреки распространенному заблуждению, в Северном и Южном полушариях вода из ванн, туалетов и других резервуаров не имеет противоположных направлений. Это потому, что величина силы незначительна в этом масштабе. Силы, определяемые начальными условиями воды (например, геометрия слива, геометрия резервуара, ранее существовавший импульс воды и т. Д. несколько) Вероятно, будут определять направление вращения воды, если таковое имеется. Например, смыв в идентичных унитазах в обоих полушариях происходит в одном направлении, и это направление определяется в схеме унитаза.
В 1962 году профессор Ашер Шапиро провел эксперимент в Массачусетском технологическом институте, чтобы проверить силу Кориолиса на большом бассейне с водой, диаметром 2 метра, с небольшим деревянным крестом над отверстием для пробки, чтобы показать направление вращения, накрыть его и подождать не менее 24 часов, пока вода осядет. В этих точных лабораторных условиях он действует и последовательное вращение против часовой стрелки. Последовательное вращение по часовой стрелке в южном полушарии было подтверждено в 1965 году Ллойдом Трефетеном из Сиднейского университета. См. Статью Шапиро «Вихрь для ванн» в журнале Nature (15 декабря 1962 г., том 196, стр. 1080–1081) и последующую статью доктора Трефетена «Вихрь для ванн в южном полушарии». в том же журнале (4 сентября 1965 г., т. 207, с. 1084-1085).
Шапиро: «Обе точки зрения в некотором смысле верны. Кажется, непредсказуемо изменяется в зависимости от даты, даты и времени. время суток и конкретное жилище экспериментатора. В хорошо контролируемых условиях эксперимент наблюдателя, смотрящий вниз на сток в северном полушарии, всегда будет видеть вихрь против часовой стрелки, а в южном полушарии всегда будет видеть вихрь. вихрь по часовой стрелке.
Трефетен: «Вращение по часовой стрелке наблюдалось во всех пяти последних испытаниях правильно, которые имели время 18 часов или более».
Несмотря на то, что на YouTube есть много видеороликов, показывающих обычную ситуацию, когда эффект не виден, версии тонкого оригинального эксперимента, которые подтверждают эффект, встречаются редко.
Сила Кориолиса все еще влияет на направление потока воды, но только незначительно. Только если вода настолько неподвижна, что эффективная скорость вращения Земли выше, чем скорость вращения воды относительно ее контейнера, и если приложенные извне крутящие моменты (например, которые могут быть вызваны потоком по неровной поверхности дна) достаточно малы, эффект Кориолиса действительно может определять направление вихря. Без такой тщательной подготовки эффект Кориолиса, вероятно, будет намного меньше, чем различные другие воздействия на направление слива, такие как любое остаточное вращение воды и геометрия контейнера. Несмотря на это, идея о том, что в Северном и Южном полушариях отводятся разные воды из туалетов и ванн, была популяризирована в нескольких телевизионных программах и фильмах, в том числе в План побега, Свадебные Крашеры, Симпсоны эпизод «Барт против Австралии », От полюса к полюсу и Секретные материалы эпизод «Die Hand Die Verletzt «. Об этом также говорится в нескольких научных трансляциях и публикациях, в том числе по крайней мере в одном учебнике физики для колледжа.
Образование спирального вихря над пробкой можно объяснить сохранением углового момента : Радиус вращения уменьшается по мере приближения воды к отверстию для пробки, поэтому скорость вращения увеличивается по той же причине, по которой скорость вращения фигуристов увеличивается, когда они втягивают руки. Любое вращение вокруг отверстия для пробки, которое изначально настоящее ускоряется по мере продвижения воды внутрь.
В письме редактору Ричарда Хейка в American Journal of Physics объясняется, как более простые версии экспериментов Шапиро и Трефетена могут быть выполнены на карусели.
Баллистическая траектории
Сила Кориолиса важна в внешней баллистике для расчета траекторий очень дальних артиллерийских снарядов. Самым известным историческим примером является Парижское ружье, которое немцы использовали во время Первой мировой войны для бомбардировки Парижа с расстояния около 120 км (75 миль).. Сила Кориолиса мгновенно изменяет траекторию пули, влияя на точность на очень больших расстояниях. Его настраивают точные стрелки на дальние дистанции, например снайперы. На широте Сакраменто, Калифорния, выстрел на 1000 ярдов (910 м) на север будет отклонен на 2,8 дюйма (71 мм) вправо. Существует также вертикальный компонент, описанный выше в разделе об эффекте Этвёша, который заставляет выстрелы в западном направлении поражать низко, а выстрелы в восточном направлении — высоко.
Влияние силы Кориолиса на баллистические траектории не следует путать с кривизна траекторий ракет, спутников и подобных объектов при нанесении траекторий на двумерные (плоские) карты, такие как проекция Меркатора. Проекции трехмерной изогнутой поверхности Земли на двумерную поверхность (карту) обязательно приводят к искажению деталей. Кажущаяся кривизна траектории является следствием сферичности Земли и будет иметь место даже в невращающейся рамке.
Визуализация эффекта Кориолиса


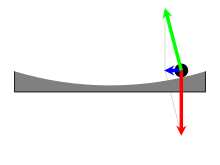
Чтобы продемонстрировать эффект Кориолиса, параболический поворотный стол может быть использован. На плоском поворотном столе инерция объекта, вращающегося в одном направлении, отталкивает его от края. Однако, если поверхность поворотного стола имеет правильную форму параболоида (параболической чаши) (см. Рисунок) и вращается с соответствующей скоростью, компоненты силы, показанные на рисунке, делают компонент силы тяжести касательной к поверхности чаши. точно равняется центростремительной силе, необходимой для поддержания вращения объекта с его скоростью и радиусом кривизны (при условии отсутствия трения). (См. поворот с наклоном.) Эта тщательно очерченная поверхность позволяет изолированно отображать силу Кориолиса.
Диски, вырезанные из цилиндров сухого льда, могут использоваться в качестве шайб, перемещаясь почти без трения по поверхности параболического поворотного стола, позволяя проявиться влиянию Кориолиса на динамические явления. Для того, чтобы получить представление движений, как видно из опорного кадра, вращающийся с поворотным столом, видеокамера прикреплена к поворотной платформе так, чтобы совместно вращаться с поворотным столом, с результатами, как показано на рисунке. На левой панели рисунка, которая является точкой обзора неподвижного наблюдателя, сила тяжести в инерциальной системе отсчета, притягивающая объект к центру (низу) тарелки, пропорциональна расстоянию от объекта до центра. Центростремительная сила такой формы вызывает эллиптическое движение. На правой панели, которая показывает точку обзора вращающейся рамы, внутренняя сила тяжести во вращающейся раме (та же сила, что и в инерционной раме) уравновешивается направленной наружу центробежной силой (присутствует только во вращающейся раме). Когда эти две силы уравновешены, во вращающейся системе координат единственная неуравновешенная сила — это сила Кориолиса (также присутствует только во вращающейся системе координат), а движение представляет собой инерционный круг. Анализ и наблюдение кругового движения во вращающейся системе отсчета является упрощением по сравнению с анализом и наблюдением эллиптического движения в инерциальной системе отсчета.
Поскольку эта система отсчета вращается несколько раз в минуту, а не только один раз в день, как Земля, создаваемое ускорение Кориолиса во много раз больше, и поэтому его легче наблюдать в небольших временных и пространственных масштабах, чем вызванное ускорением Кориолиса. вращением Земли.
В некотором смысле Земля аналогична такому поворотному столу. Вращение заставило планету принять форму сфероида, так что нормальная сила, сила тяжести и центробежная сила точно уравновешивают друг друга на «горизонтальной» поверхности. (См. экваториальная выпуклость.)
Эффект Кориолиса, вызванный вращением Земли, косвенно можно увидеть через движение маятника Фуко.
Эффекты Кориолиса в других областях
расходомер Кориолиса
Практическое применение эффекта Кориолиса — это массовый расходомер, прибор, который измеряет массовый расход и плотность жидкости, протекающей по трубке. Принцип работы заключается в создании вибрации трубки, через которую проходит жидкость. Вибрация, хотя и не полностью круговая, создает вращающуюся систему отсчета, которая вызывает эффект Кориолиса. Хотя конкретные методы различаются в зависимости от конструкции расходомера, датчики отслеживают и анализируют изменения частоты, фазового сдвига и амплитуды колеблющихся расходомерных трубок. Наблюдаемые изменения отражают массовый расход и плотность жидкости.
Молекулярная физика
В многоатомных молекулах движение молекул может быть описано вращением твердого тела и внутренней вибрацией атомов вокруг их положение равновесия. В результате колебаний атомов атомы находятся в движении относительно вращающейся системы координат молекулы. Таким образом, присутствуют эффекты Кориолиса, заставляющие атомы двигаться в направлении, перпендикулярном исходным колебаниям. Это приводит к смешиванию молекулярных спектров между вращательными и колебательными уровнями, по которым могут быть определены константы связи Кориолиса.
Гироскопическая прецессия
При приложении внешнего крутящего момента к вращающемуся гироскопу вдоль оси, которая расположена под прямым углом к оси вращения, скорость обода, связанная со вращением, становится радиально направленной по отношению к оси внешнего крутящего момента. Это заставляет индуцированную крутящим моментом силу воздействовать на обод таким образом, чтобы наклонить гироскоп под прямым углом к направлению, в котором внешний крутящий момент наклонил бы его. Эта тенденция имеет эффект удержания вращающихся тел в их системе вращения.
Стая насекомых
Мухи (Diptera ) и некоторые бабочки (Lepidoptera ) используют эффект Кориолиса в полете с помощью специализированных придатков и органов, передающих информацию об угловой скорости их тел.
Силы Кориолиса, возникающие в результате линейного движения этих придатков, обнаруживаются во вращающейся системе отсчета тел насекомых. В случае мух их специализированные придатки представляют собой органы в форме гантелей, расположенные сразу за их крыльями и называемые «жужжальцами «.
Жужжальцы мухи колеблются в плоскости с той же частотой ударов, что и основные крылья, так что любоевращение тела приводит к боковое отклонение жужжальцев от плоскости их движения.
У мотыльков их антенны, как известно, отвечает за чувствительность кориолисовых силовых так же, как и у жужжальцев у мух. И у мух, и у бабочек. набор механодатчиков в основании отростка чувствителен отклонения в частотах биений, коррелируя с вращением в плоскостях тангажа и крена, и с удвоенной частотой биений, коррелируя с вращением в плоскости рыскание плоскость.
точки стабильности Лагранжа
В астрономии Лагранжа имеют пять положений в плоскости орбиты двух больших орбитальных тел, на которые воздействует только небольшой объект под силой тяжести может быть устойчивой точки. положение относительно два больших тела. Первые три точки Лагранжа (L 1, L 2, L 3) лежат вдоль линии, соединяющей два больших тела, а последние две точки (L 4 и L 5) каждый образуют равносторонний треугольник с двумя большими телами. Точки L 4 и L 5, хотя они соответствуют максимуму эффективно в системе координат, которые вращаются вместе с двумя большими телами, являются стабильными из-за к эффекту Кориолиса. Стабильность может привести к орбитам около L 4 или L 5, известных как орбиты головастиков, где можно найти троянов. Это также может привести к появлению орбитов, окружающих L 3, L 4 и L 5, как известные подковообразные орбиты.
См. Также
Физический портал
- Аналитическая механика
- Прикладная механика
- Классическая механика
- Динамика (физика)
- Вращение Земли
- Экваториальная волна Россби
- формулы Френе-Серре
- Гироскоп
- Кинетика (физика)
- Механика плоского движения частиц
- Реактивная центробежная сила
- Вторичный поток
- Статика
- Равномерное круговое движение
- Whirlpool
Примечания
Ссылки
Дополнительная литература
Физика и метеорология
- Riccioli, GB, 1651: Almagestum Novum, Bologna, pp. 425–427. (Оригинальная книга [на латыни], сканированные изображения полных страниц.)
- Кориолис, Г.Г., 1832: «Память о принципах жизни в духе относительных движений машин». Journal de l’école Polytechnique, Том 13, стр. 268–302.. (Исходная статья [на французском языке], файл PDF, 1,6 МБ, сканированные изображения целых страниц.)
- Кориолис, Г.Г., 1835: «Mémoire sur les équations du движение relatif des systèmes de corps ». Journal de l’école Polytechnique, Vol 15, pp. 142–154. (Исходная статья [на французском языке] PDF-файл, 400 КБ, сканированные изображения целых страниц.)
- Гилл, А.Е. Динамика атмосферы и океана, Academic Press, 1982.
- Роберт Эрлих (1990). Переворачивая мир наизнанку и 174 других простых физических упражнения. Издательство Принстонского университета. п. Катание шара на вращающейся платформе; п. 80 сл.. ISBN 978-0-691-02395-3 .
- Дурран, Д.Р., 1993: Действительно ли сила Кориолиса ответственна за инерционные колебания?, Бык. Амер. Метеор. Soc., 74, стр. 2179–2184; Исправления. Бюллетень Американского метеорологического общества, 75, стр. 261
- Дурран, Д.Р., и С.К. Домонкос, 1996: Устройство для демонстрации инерционных колебаний, бюллетень Американского метеорологического общества, 77, стр. 557–559.
- Мэрион, Джерри Б. 1970, Классическая динамика частиц и систем, Academic Press.
- Перссон, А., 1998 [2] Как мы понимаем силу Кориолиса? Бюллетень Американского метеорологического общества 79, стр. 1373–1385.
- Саймон, Кейт. 1971, Механика, Аддисон-Уэсли
- Акира Кагеяма и Мамору Хёдо: Эйлеров вывод силы Кориолиса
- Джеймс Ф. Прайс: учебник Кориолиса Океанографический институт Вудс-Хоул (2003)
- Макдональд, Джеймс Э. (Май 1952 г.). «Эффект Кориолиса» (PDF). Scientific American. 186 (5): 72–78. DOI : 10.1038 / scientificamerican0552-72. Проверено 4 января 2016 года.
Все, что движется по поверхности Земли — вода, воздух, животные, машины и снаряды — смещается вправо в Северном полушарии и влево в Южном
. Элементарный, нематематический; но хорошо написано.
Исторический
- Граттан-Гиннесс, И., Ред., 1994: Сопутствующая энциклопедия истории и философии математических наук. Тт. I и II. Рутледж, 1840 с.. 1997: История математических наук Фонтана. Фонтана, 817 с. 710 с.
- Хргян А., 1970: Метеорология: исторический обзор. Vol. 1. Кетер Пресс, 387 стр.
- Кун, Т. С., 1977: Сохранение энергии как пример одновременного открытия. Существенное напряжение, Избранные исследования в области научных традиций и изменений, University of Chicago Press, 66–104.
- Куцбах, Г., 1979: Термическая теория циклонов. История метеорологической мысли в девятнадцатом веке. Амер. Метеор. Soc., 254 pp.
Внешние ссылки
- Определение эффекта Кориолиса из Глоссария метеорологии
- Эффект Кориолиса — конфликт между здравым смыслом и математикой PDF-файл. 20 страниц. Общее обсуждение Андерсом Перссоном различных эффектов Кориолиса, включая Маятник Фуко и колонки Тейлора.
- Эффект Кориолиса в метеорологии PDF-файл. 5 страниц. Подробное объяснение Матса Розенгрена того, как гравитационная сила и вращение Земли влияют на движение атмосферы над поверхностью Земли. 2 рисунка
- 10 видеороликов и игр с эффектом Кориолиса — со страницы погоды на сайте About.com
- Сила Кориолиса — из ScienceWorld
- Эффект Кориолиса и дренаж Статья из Веб-сайт NEWTON, обслуживаемый Аргоннской национальной лабораторией.
- Каталог видеороликов Кориолиса
- Эффект Кориолиса: графическая анимация, визуальная анимация Земли с точным объяснением
- Введение в гидродинамику Обучающий фильм SPINLab объясняет эффект Кориолиса с помощью лабораторных экспериментов
- Сливают ли ванны против часовой стрелки в Северном полушарии? Сесила Адамса.
- Плохой Кориолис. Статья, раскрывающая дезинформацию об эффекте Кориолиса. Алистер Б. Фрейзер, заслуженный профессор метеорологии в Государственном университете Пенсильвании
- Эффект Кориолиса: (довольно) простое объяснение, объяснение для непрофессионала
- Посмотрите на анимацию эффекта Кориолиса над Поверхность Земли
- Анимационный ролик, показывающий сцены с точки зрения как инерциальной системы отсчета, так и вращающейся системы координат, визуализирующей кориолисовы и центробежные силы.
- Винсент Маллетт Сила Кориолиса @ INWIT
- Примечания НАСА
- Интерактивный фонтан Кориолиса позволяет управлять скоростью вращения, скоростью капель и системой отсчета для изучения эффекта Кориолиса.
- Вращающиеся системы координат, преобразование из инерциальных систем
















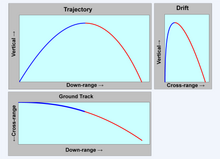






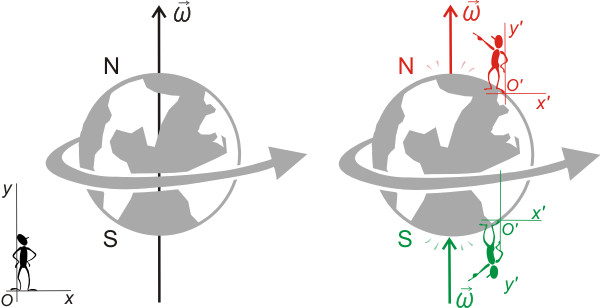


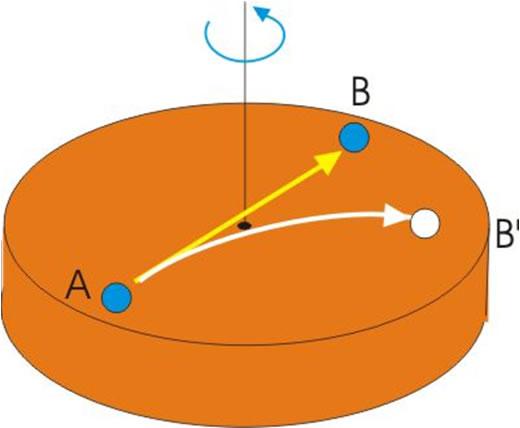

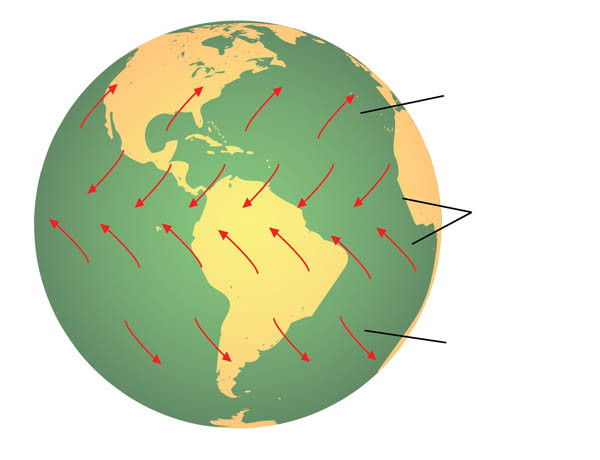
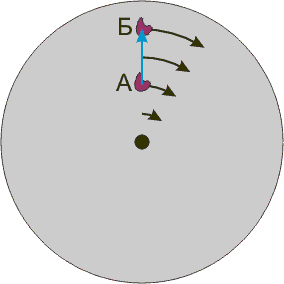

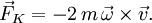
![vec v= vec {v}_0 + left[ vec omega times vec R right] + vec {v}_n,](https://dic.academic.ru/pictures/wiki/files/100/d3ee4158828c2b1125e1761fd6670ab5.png)
![frac{d}{dt}vec v= frac{d}{dt}vec {v}_0 + frac{d}{dt}left[ vec omega times vec R right] +frac{d}{dt} vec {v}_n.](https://dic.academic.ru/pictures/wiki/files/51/3af4b9a812a8b372387d54168f2dba94.png)
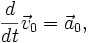
![frac{d}{dt} vec {v}_n = vec {a}_n + left[ vecomega times vec {v}_n right],](https://dic.academic.ru/pictures/wiki/files/53/564bf2b000132c2b979c4abe8bbcd2c5.png)
![vec {v}_e = left[ vec omega times vec R right].](https://dic.academic.ru/pictures/wiki/files/97/aa9de6f46034488f4bbca755d76bc9f5.png)
![d vec {v}_e= left[ vecomega times d vec R right].](https://dic.academic.ru/pictures/wiki/files/48/0baa1c9caf22087ed731e63f30de4be5.png)
 = ma ′ { Displaystyle = m { boldsymbol {a ‘}}}
= ma ′ { Displaystyle = m { boldsymbol {a ‘}}}
 — ускорение относительно вращающейся системы отсчета
— ускорение относительно вращающейся системы отсчета





![{ Displaystyle { begin {выровнено} mathbf {а} _ { текст {Cor}} = - 2 left [- omega v left ( sin alph a - omega t cos alpha right), omega v left ( cos alpha + omega t sin alpha right) right] \ = 2 omega v left ( sin alpha, - cos alpha right) -2 omega ^ {2} mathbf {r} _ {B} (t) . End {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f7bcadd5ccae2f56930c1bf34d7b60818e526a83)



 — скорость вращения Земли;
— скорость вращения Земли; — широта, положительная в северном полушарие и отрицательное в южном полушарии
— широта, положительная в северном полушарие и отрицательное в южном полушарии
