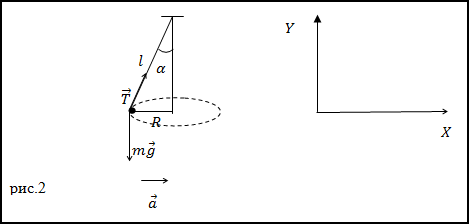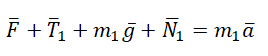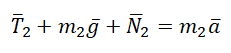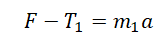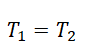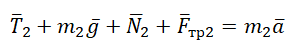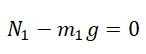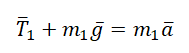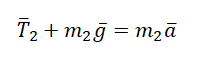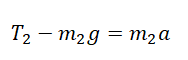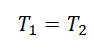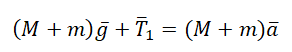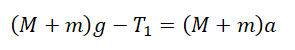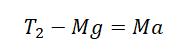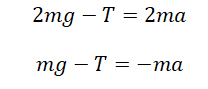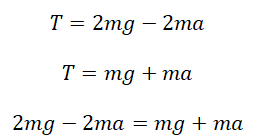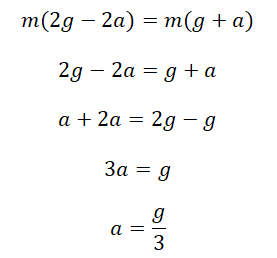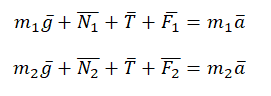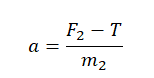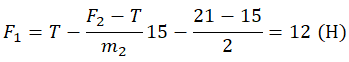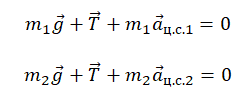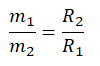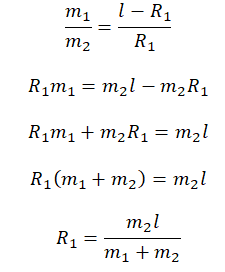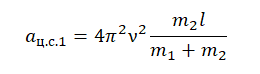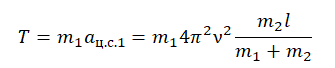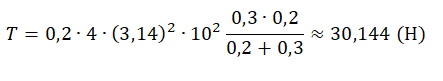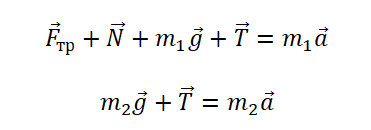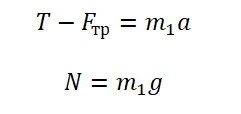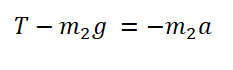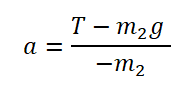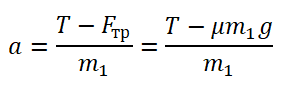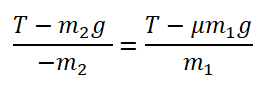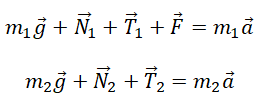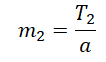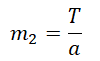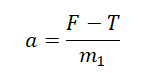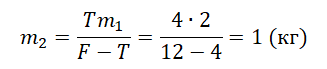Содержание:
- Определение и формула силы натяжения нити
- Единицы измерения силы натяжения нити
- Примеры решения задач
Определение и формула силы натяжения нити
Определение
Силу натяжения определяют как равнодействующую сил $(bar{R})$, приложенных к нити, равную ей по модулю,
но противоположно направленную. Устоявшегося символа (буквы), обозначающего силу натяжения нет. Ее
обозначают и просто $bar{F}$ и
$bar{T}$, и
$bar{N}$ . Математически определение для силы натяжения нити можно записать как:
$$bar{T}=-bar{R}(1)$$
где $bar{R}$ = векторная сумма всех сил, которые действуют на нить. Сила натяжения нити всегда направлена по нити (или подвесу).
Чаще всего в задачах и примерах рассматривают нить, массой которой можно пренебречь. Ее называют невесомой.
Еще одним важной характеристикой нити при расчете силы натяжения является ее растяжимость. Если исследуется невесомая и нерастяжимая
нить, то такая нить считается просто проводящей через себя силу. В том случае, когда необходимо учитывать растяжение нити, применяют
закон Гука, при этом:
$$T=F_{u p r}=k Delta l(2)$$
где k – коэффициент жесткости нити, $Delta l$ – удлинение нити при растяжении.
Единицы измерения силы натяжения нити
Основной единицей измерения силы натяжения нити (как и любой силы) в системе СИ является: [T]=Н
В СГС: [T]=дин
Примеры решения задач
Пример
Задание. Невесомая, нерастяжимая нить выдерживает силу натяжения T=4400Н. С каким максимальным ускорением
можно поднимать груз массой m=400 кг, который подвешивают на эту нить, чтобы она не разорвалась?
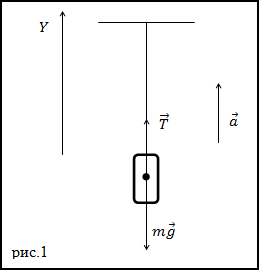
Решение. Изобразим на рис.1 все силы, действующие на груз, и запишем второй закон Ньютона.
Тело будем считать материальной точкой, все силы приложенными к центру масс тела.
$$bar{T}+m bar{g}=m bar{a}(1.1)$$
где $bar{T}$ – сила натяжения нити. Запишем проекцию уравнения (1.1) на ось Y:
$$T-m g=m a(1.2)$$
Из выражения (1.2) получим ускорение:
$$a=frac{T-m g}{m}$$
Все данные в задаче представлены в единицах системы СИ, проведем вычисления:
$$a=frac{4400-400 cdot 9,8}{400}=1,2 mathrm{~m} / mathrm{c}^{2}$$
Ответ. a=1,2м/с2

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Шарик, имеющий массу m=0,1 кг прикрепленный к нити (рис.2) движется по окружности,
расположенной в горизонтальной плоскости. Найдите модуль силы натяжения нити, если длина нити l=5 м, радиус окружности R=3м.
Решение. Запишем второй закон Ньютона для сил, приложенных к шарику, который вращается по окружности с
центростремительным ускорением:
$$bar{T}+m bar{g}=m bar{a}(2.1)$$
Найдем проекции данного уравнения на обозначенные на рис.2 оси X и Y:
$$
begin{array}{c}
X: quad T sin alpha=m a=m omega^{2} R(2.2) \
Y: quad-m g+T cos alpha=0
end{array}
$$
Из уравнения (2.3) получим формулу для модуля силы натяжения нити:
$$T=frac{m g}{cos alpha}(2.4)$$
Из рис.2 видно, что:
$$sin alpha=frac{R}{l} rightarrow cos alpha=sqrt{1-left(frac{R}{l}right)^{2}}$$
Подставим (2.5) вместо $cos alpha$ в выражение (2.4), получим:
$$T=frac{m g}{sqrt{1-left(frac{R}{l}right)^{2}}}=frac{m g l}{sqrt{l^{2}-R^{2}}}$$
Так как все данные в условиях задачи приведены в единицах системы СИ, проведем вычисления:
$$T=frac{0,1 cdot 9,8 cdot 5}{sqrt{5^{2}-3^{2}}}=1,225(H)$$
Ответ. T=1,225 Н
Читать дальше: Формула силы тяги.
Сила натяжения нити — формулировка
Определение
Силой натяжения называют силу, приложенную к концам объекта и создающую внутри него упругую деформацию.
Длина тела, к которому приложена сила, обычно многократно больше, чем его толщина. Примерами таких объектов являются веревка, канат, трос, леска, проволока. Сила натяжения визуально проявляется в следующих примерах:
- создание строительного отвеса;
- установка растяжек для фиксации радиоантенн;
- поведение арматуры внутри напряженного бетона;
- устройство корабельного такелажа.
Как определить силу, формулы
Натяжение проявляется по-разному. Поэтому сила натяжения может рассчитываться определенным образом, в зависимости от окружающих условий.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
С неподвижно закрепленным верхним концом
Простейшим примером проявления силы натяжения является нить с закрепленным на ней грузом. Верхний конец такого подвеса фиксируется неподвижно. В этом случае сила натяжения будет соответствовать силе тяжести, которая действует на тело. Формула для расчета:
(F=F_{тяж}=m*g)
где m – это масса тела, а g представляет собой ускорение свободного падения.
Если нить под углом
В случае, когда груз расположен под определенным углом, характер силы натяжения несколько изменяется. Примером такой системы выступает маятник.
(F_n=m*g*cos(a))
где а равен углу отклонения.
Формула с учетом ускорения и массы
В ситуации, при которой на груз оказывается сила натяжения, приводящая его в движение вверх, следует использовать такую формулу для ее расчета:
(F=F_{тяж}+m*a)
Сила натяжения во вращающейся системе
Описание
Такое явление можно наблюдать, когда система из нити и тела вращается во время раскручивания подвеса вокруг своей оси с закрепленным на одном его конце объектом: центрифуга, маятник, качели. Сила натяжения, возникающая внутри подвеса, характеризуется центробежной силой и в условиях вращения в вертикальной плоскости циклически претерпевает изменения. То есть можно наблюдать зависимость силы от угла отклонения от вертикали:
- приближение к земле приводит к увеличению силы;
- во время удаления от земли сила слабеет.
Формула расчета
Рассчитать силу натяжения в условиях вращающейся системы можно так:
(F=frac{mtimes nu ^{2}}{r})
Обозначение, единица измерения
Существуют определенные стандарты для написания формулы силы натяжения. Как и другие физические силы, натяжение обозначается F. В качестве единицы измерения используют Ньютон (H)
(H=frac{kgtimes m}{c^{2}})
Примеры решения задач
Задание 1
На невесомую нерастяжимую нить действует сила натяжения Т=4400Н. Необходимо определить максимальное ускорение подъема груза, масса которого равна m=400 кг, подвешенного на этой нити. При этом нить должна сохранить целостность.
Решение
Представив все силы, оказывающие действие на тело, необходимо составить формулу второго закона Ньютона. Тело является материальной точкой, а силы приложены к центру его массы.
(bar{T}+mbar{g}=mbar{a})
(bar{T}) является силой натяжения нити.
Проекция уравнения будет иметь следующий вид:
(T – mg = ma)
Данное выражение позволяет рассчитать ускорение:
(a=frac{T-mg}{m})
Так как все величины, изложенные в задании, соответствуют единицам СИ, можно провести корректные вычисления
(a=frac{4400-4*9,8}{400})
Ответ: a = 1.2 (м/с^2)
Задание 2
На иллюстрации изображен шар, который обладает массой m=0.1 кг. Будучи зафиксирован на нити, шарик совершает движение по окружности в горизонтальной плоскости. Длина подвеса составляет l=5 м, а радиус окружности – R=3 м. Требуется вычислить модуль силы натяжения нити.
Решение
Необходимо воспользоваться вторым законом Ньютона и записать его для сил, которые действуют на шар. Центростремительное ускорение при его вращении по окружности будет записано следующим образом:
(bar{T}+mbar{g}=mbar{a})
Проекции данной формулы по осям определяются следующим образом:
X: (T sin α = ma = mω2R)
Y: (-mg + T cos α = 0)
Таким образом, из уравнения Y получаем расчет модуля силы натяжения нити:
(T=frac{mg}{cos alpha })
Анализ рисунка позволяет вывести следующее уравнение:
(sin alpha = frac{R}{l}rightarrow cos alpha = sqrt{1-left(frac{R}{l} right)^{2}})
Если cos α заменить уравнением для расчета модуля силы натяжения нити, то получим следующую формулу:
(T=frac{mg}{sqrt{1-left(frac{R}{l} right)^{2}}}= frac{mgl}{sqrt{l^{2}-R^{2}}})
Значения основных величин, выраженные в СИ, можно подставить в конечную формулу для расчета силы натяжения нити:
(T=frac{0,1*9,8*5}{sqrt{5^{2}-3^{2}}}=1,225left(H right))
Ответ: Т=1,225 H
Понятие силы натяжения
Под силой натяжения понимают силу, приложенную к концам объекта и образующую внутри него упругую деформацию. Длина данного объекта обычно в несколько раз превышает его толщину (нить, веревка, проволока, бечева, трос, шнур и другие похожие объекты).
Увидеть силу натяжения можно в различных областях жизнедеятельности, к примеру, альпинистское снаряжение, вытаскивание ведра из колодца, подвесной мост, ремень безопасности, гитара, буксировка автомобиля, перетягивание каната и в других.
Чему равна сила натяжения нити
Формула
Если в натянутой нити верхний конец крепко закреплен, а нижний находится под действием груза, то определение сила тяжести рассчитывается, как масса груза, умноженная на ускорение свободного падения:
[mathrm{F}=mathrm{F}_{text {тяж }}=mathrm{m} cdot mathrm{g}]
Где m — масса, g — ускорение свободного падения.
Если в натянутой нити верхний конец крепко закреплен, а нижний находится под действием груза, то определение сила тяжести рассчитывается, как масса груза, умноженная на ускорение свободного падения:
Существует и такой случай, когда нить находится под заданным углом, следовательно, формула силы натяжения примет такой вид:
[mathrm{F}_{Pi}=mathrm{m} cdot mathrm{g} cdot cos (alpha)], где α-угол отклонения нити.
Бывает, когда натяжение нити происходит вверх, посредством вертикально закрепленного груза, то в формулу необходимо добавить еще и ускорение, с которым осуществляется это движение:
[mathrm{F}=mathrm{F}_{text {тяж }}+mathrm{m} cdot mathrm{a} ;]
Сила натяжения образуется и во вращающихся системах, к примеру, если процесс раскручивания происходит вокруг оси и на ней закреплен конец нити. Такая сила характерна для качелей, центрифуги, маятника и других подобных устройств. В таком разе напряжение вокруг подвесного груза помогает создавать центробежная сила. Величина центробежной силы прямым образом зависит от массы, радиуса от центра вращения до центра тяжести, а также от скорости движения центра тяжести системы.
[mathrm{Fц} =frac{mathrm{m} cdot mathrm{vartheta}^{2}}{mathrm{r}}]
Вращение может производиться непосредственно в вертикальной площади, а значит, сила натяжения изменяется циклическим образом. При приближении к земле, ее значение увеличивается, а при отдалении от нее, уменьшается. Главным образом, напряжение внутри нити связано с углом отклонения от вертикали (см. пример).
Нет времени решать самому?
Наши эксперты помогут!
Пример задачи на силу натяжения нити
Пример
Маятник длиной 2 метра отклонен от вертикального положения на двадцать градусов и движется со скоростью 2
м/с. Найти силу натяжения нити маятника с массой подвешенного груза 3 кг.
На груз, который подвешен к маятнику, действуют 2 силы:
- сила притяжения;
- центробежная сила.
Поэтому необходимо найти сумму этих сил, чтобы решить данную задачу.
Силу притяжения рассчитаем по формуле: [mathrm{F}_{Pi}=mathrm{m} cdot mathrm{g} cdot cos (alpha)]
Где m — масса, g — ускорение свободного падения, α — угол отклонения. Подставим числовые значения, и получаем:
[Fп=3*9,8*0,95=27,93Н]
Центробежная сила определяется по формуле:
[mathrm{F} ц=frac{mathrm{m} cdot theta^{2}}{mathrm{r}}]
Где ʋ — скорость, r — радиус (длина подвеса).
Подставим числа и получаем:
[mathrm{F} text { Ц }=frac{3 cdot 2^{2}}{2}=6 H]
[Sigma=27,93 mathrm{H}+6 mathrm{H}=33,93 mathrm{H}]
Ответ: сила натяжения нити маятника равна 33,93Н.
Иногда в системе движется не одно, а два связанных между собой тела. Тогда описание движения с применением законов Ньютона включает в себя описания движения каждого из этих тел.
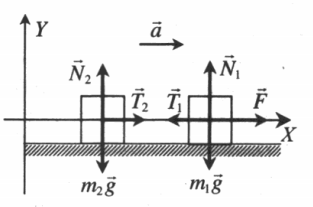
Движение тел по горизонтали без трения
Решение
II закон Ньютона в векторной форме для 1 тела:
II закон Ньютона в векторной форме для 2 тела:
Проекция на ОХ для 1 тела:
Проекция на ОY для 1 тела:
Проекция на ОХ для 2 тела:
Проекция на ОY для 2 тела:
III закон Ньютона:
Движение по горизонтали с учетом сил трения
Решение
II закон Ньютона в векторной форме для 1 тела:
II закон Ньютона в векторной форме для 2 тела:
Проекция на ОХ для 1 тела:
Проекция на ОY для 1 тела:
Проекция на ОХ для 2 тела:
Проекция на ОY для 2 тела:
III закон Ньютона:
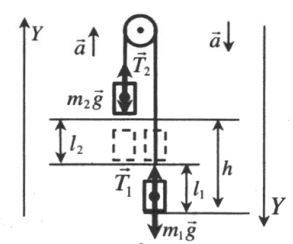
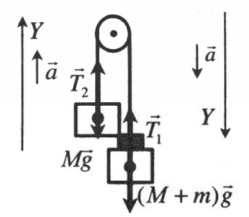
Вертикальное движение тел (m1 > m2)
h — расстояние между телами. l1 и l2 — перемещение тела 1 и тела 2 соответственно. Перемещения обоих тел равны, поэтому: l1 = l2 = l.
Решение
Расстояние между телами определяется формулой: h = l1 + l2 = 2l.
II закон Ньютона в векторной форме для 1 тела:
II закон Ньютона в векторной форме для 2 тела:
Проекция на ОY для 1 тела:
Проекция на ОY для 2 тела:
III закон Ньютона:
На один из грузов положили довесок
Решение
II закон Ньютона для 1 тела:
II закон Ньютона для 2 тела:
Проекция на ось ОУ для 1 тела:
Проекция на ось ОУ для 2 тела:
III закон Ньютона:
Вес довеска определяется по формуле:
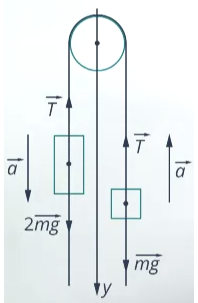
Пример №1. На нити, переброшенной через неподвижный блок, подвешены грузы массами m и 2m. С каким ускорением будут двигаться грузы, если их отпустить? Трением в блоке пренебречь.
Строим чертеж:
Записываем второй закон Ньютона для каждого из тел. Для первого тела он будет иметь вид:
Для второго тела II закон Ньютона примет следующий вид:
Запишем проекции на ось OУ для каждого из тел:
Выразим силы натяжения нити для каждого из тел и приравняем их правые части:
Сделаем несколько преобразований:
Это значит, если отпустить грузы, они будут двигаться с ускорением, втрое меньшим по сравнению с ускорением свободного падения. Приблизительно оно будет равно 3,33 м/с2.
Задание EF17717
а) 6 Н
б) 12 Н
в) 18 Н
г) 21 Н
Алгоритм решения
1.Записать исходные данные.
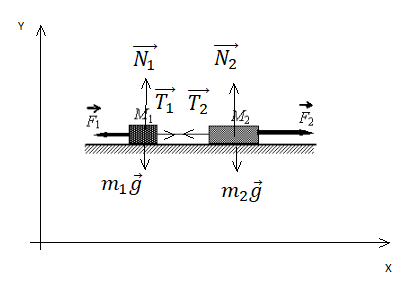
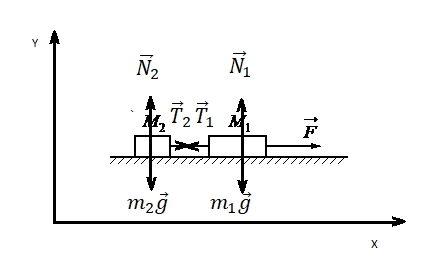
2.Сделать чертеж. Указать все силы, которые действуют на 1 и 2 тело. Выбрать систему координат.
3.Записать для каждого тела второй закон Ньютона в векторной форме.
4.Записать для каждого тела второй закон Ньютона в виде проекций на оси ОХ и ОУ.
5.Выразить формулу для вычисления силы, действующей на первое тело.
6.Подставить известные данные и произвести вычисления.
Решение
Запишем исходные данные:
• Масса тела 1: m1 = 1 кг.
• Масса тела 2: m2 = 1 кг.
• Сила натяжения нити: Т = 15 Н.
• Сила, действующая на второе тело, равна: F2 = 21 Н.
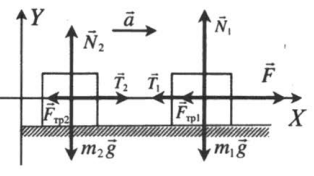
Сделаем чертеж. Систему координат выберем такую, чтобы ось ОУ была параллельная ускорению свободного падения.
Согласно третьему закону Ньютона, два тела действуют друг на друга с равными по модулю, но противоположными по направлению силами. Поэтому модули сил натяжения нити Т1 и T2 равны:
T1 = T2 = T
Учтем это при записи второго закона Ньютона для каждого из тел:
Запишем второй закон Ньютона в проекциях на оси ОХ и ОУ. Сначала для первого тела:
T – F1 = m1a
N1 = m1g
Теперь для второго тела:
F2 – T = m2a
N2 = m2g
Выразим из проекции на ось ОХ для 1 тела модуль первой силы:
F1 = T – m1a
Из проекции на ось ОХ для второго тела выразим ускорение:
Подставим ускорение в формулу для нахождения силы, действующей на первое тело:
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
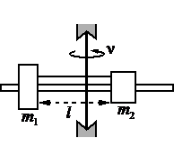
Задание EF18920
Алгоритм решения
1.Записать исходные данные. Перевести их в СИ.
2.Сделать чертеж, обозначив все силы, действующие на систему тел, их направления. Выбрать систему координат.
3.Записать второй закон Ньютона в векторной форме для каждого из тел.
4.Записать второй закон Ньютона для каждого из грузов в виде проекций на ось ОХ.
5.Вывести формулу для радиуса окружности, по которой движется любой из грузов.
6.Вывести формулу для вычисления силы натяжения нити, подставить известные данные и произвести вычисления.
Решение
Запишем исходные данные, сразу переведя их в СИ:
• Масса первого груза m1 = 200 г = 0,2 кг.
• Масса первого груза m2 = 300 г = 0,3 кг.
• Длина нити l = 20 см = 0,2 м.
• Натяжение нити с обеих сторон одинаково, следовательно: T1 = T2 = T.
• Частота вращения штанги ν = 600 об./мин. = 10 об./с.
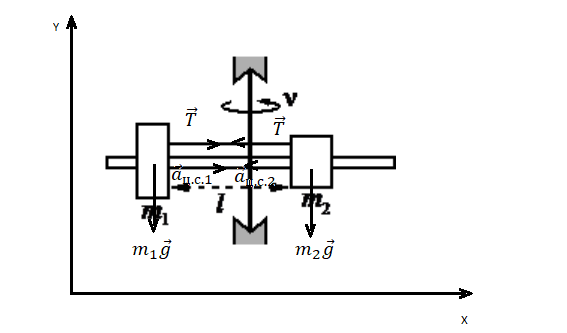
Сделаем чертеж, обозначив все силы. Учтем, что сила натяжения нити равна с обеих сторон. Выберем систему координат, в которой ось ОУ параллельна оси вращения.
Запишем второй закон Ньютона для первого и второго груза соответственно:
Запишем проекции на ось ОХ для каждого из тел:
T = m1aц.с.1
T = m2aц.с.2
Центростремительное ускорение также определяется формулой:
aц.с. = ω2R
Угловая скорость определяется формулой:
ω = 2πν
Следовательно, центростремительное ускорение равно:
aц.с. = 4π2ν2R
Применим эту формулу для обоих грузов:
aц.с.1 = 4π2ν2R1
aц.с.2 = 4π2ν2R2
Сумма радиусов окружностей, по которым вращаются грузы, есть длина нити:
R1 + R2 = l
Выразим радиус окружности, по которой вращается второй груз:
R2 = l – R1
Так как грузы связаны между собой, и ни один из них не перевешивает другой:
m1gR1 = m2gR2
Ускорение свободного падения взаимоуничтожается. Получаем:
Подставим радиус второй окружности и выразим радиус первой окружности:
Следовательно, центростремительное ускорение первого груза равно:
Теперь возьмем проекцию на ось ОХ для первого тела и вставим в формулу найденное центростремительное ускорение для первого тела:
Подставим известные данные и вычислим силу натяжения нити:
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17647
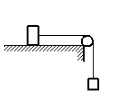
а) 2,25 Н
б) 2,7 Н
в) 3 Н
г) 3,6 Н
Алгоритм решения
• Записать исходные данные.
• Сделать чертеж. Указать все силы, действующие на тела, и их направление. Выбрать систему отсчета.
• Записать второй закон Ньютона для бруска и подвешенного к нити груза в векторной форме.
• Записать второй закон Ньютона для обоих тел в виде проекций на оси.
• Вывести формулу для вычисления искомой величины.
• Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Масса первого тела (движущегося по плоскости) равна: m1 = 0,9 кг.
• Масса второго тела (подвешенного к нити) равна: m2 = 0,3 кг.
• Коэффициент трения первого тела о поверхность плоскости равна: μ = 0,2.
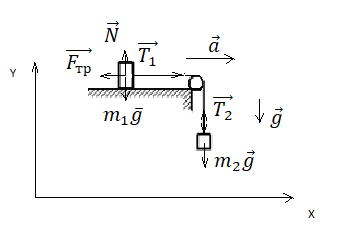
Выполним чертеж и укажем все силы, которые действуют на брусок и груз на нити. Выберем систему координат так, чтобы направление оси ОХ совпадало с направлением движения бруска.
Так как тела связаны, силы натяжения нити на обоих концах равны. Будем обозначать их без индекса. Запишем второй закон Ньютона в векторной форме для первого и второго тела соответственно:
Теперь запишем проекции на ось ОХ и ось ОУ соответственно для бруска:
Запишем проекцию на ось ОУ для груза на нити:
Выразим из этого выражения ускорение и получим:
Из проекции на ось ОХ сил, действующих на брусок, тоже выразим ускорение:
Приравняем правые части уравнений и получим:
Произведем вычисления:
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
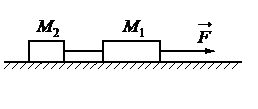
Задание EF22698
Алгоритм решения
1.Записать исходные данные.
2.Выполнить чертеж, указав все силы, действующие на каждый из грузов.
3.Записать второй закон Ньютона для обоих тел.
4.Записать второй закон Ньютона в проекциях на ось ОХ.
5.Применить третий закон Ньютона.
6.Выразить массу второго груза (найти общее решение).
Решение
Запишем исходные данные:
• Масса первого груза равна: m1 = 2 кг.
• Сила натяжения нити равна: T = 4 Н.
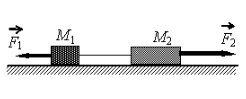
• Модуль силы, которая действует на систему тел: F = 12 Н.
Выполним чертеж:
Запишем второй закон Ньютона для 1 и 2 тела соответственно:
Запишем второй закон Ньютона для 1 и 2 тела в проекции на ось ОХ:
F – T1 = m1a
T2 = m2a
Отсюда масса второго тела равна:
Согласно третьему закону Ньютона, тела действуют друг на друга с равными по модулю, но противоположными по направлению силами. Следовательно, силы натяжения нити равны на обоих концах:
T1 = T2 = T
Поэтому:
T = F – m1a
Из первого выражения выразим ускорение и подставим его во второе:
Подставим в формулу и получим:
Ответ: 1
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 5k
Алексей . Малеев
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Определение 1
Сила натяжения — сила, приложенная к концам объекта и создающая внутри него упругую деформацию. Длина такого объекта, как правило, многократно превышает толщину (веревка, канат, трос, леска, проволока).
Наблюдать силу натяжения можно, на таких примерах, как строительный отвес, растяжки, удерживающие радиоантенны, арматура внутри напряженного бетона, корабельный такелаж и т.п.
В простейшем случае, чтобы определить силу в натянутой под действием веса висящего на ней груза нити с неподвижно закрепленным верхним концом, следует рассчитать силу тяжести как массу груза, умноженную на ускорение свободного падения:
$F = F_{тяж} = m cdot g$
Если подвешенный груз действует на нить не вертикально, а под углом (например, в маятнике), то формула примет вид
$F_п = m cdot g cdot cos(alpha)$
, где $alpha$ — угол отклонения.
Когда нить тянет вертикально подвешенный груз вверх, то в формуле следует учесть еще и ускорение, с которым производится это движение:
$F = F_{тяж} + m cdot a$
Сила натяжения возникает также во вращающейся системе, например, если ее раскручивают вокруг оси, на которой закреплен один из концов нити (например, центрифуга, маятник, качели). В этом случае напряжение внутри подвеса создает еще и центробежная сила. Ее величина зависит от массы, скорости, с которой движется центр тяжести системы, и радиуса от центра вращения до центра тяжести:
$F_ц = frac{m cdot v^2}{r}$
Если вращение производится в вертикальной плоскости, то сила натяжения меняется циклически — нарастает при приближении к земле и ослабевает при удалении от нее, т.е. напряжение внутри нити зависит от угла отклонения от вертикали (см. пример).
Пример 1
Маятник длиной 1 м отклонен от вертикали на двадцать градусов и движется со скоростью 2 м/с. Найти силу натяжения нити маятника при массе подвешенного груза 2 кг.
На груз, подвешенный к маятнику, действуют 2 силы:
- сила притяжения;
- центробежная сила.
Задача сводится к тому, чтобы найти их сумму.
Силу притяжения найдем как
$F_п = m cdot g cdot cos(alpha)$
, где $m$ — масса, $g$ — ускорение свободного падения, $alpha$ — угол отклонения. Подставив числовые значения, получаем:
$F_п = 2 cdot 9,8 cdot 0,95 = 18,64 Н$
Центробежная сила определяется как
$F_ц = frac{m cdot v^²}{r}$
, где $v$ — cкорость, $r$ — радиус (в данном случае длина подвеса). Подставив числовые значения, получаем:
$F_ц = frac{2 cdot 2^²}{1} = 8 Н$
Ответ: сила натяжения нити маятника равна $18,64 + 8 = 26,64 Н$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме