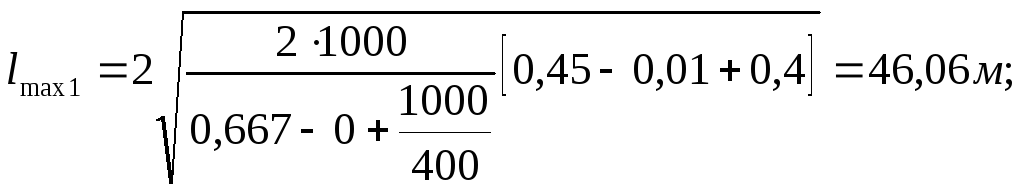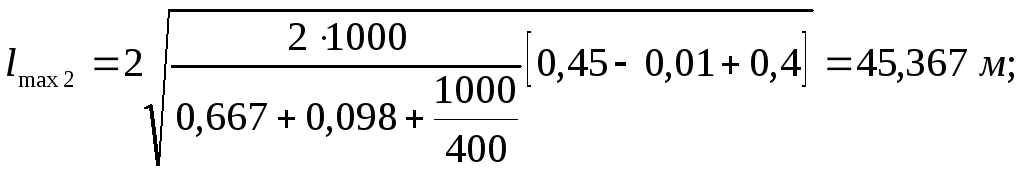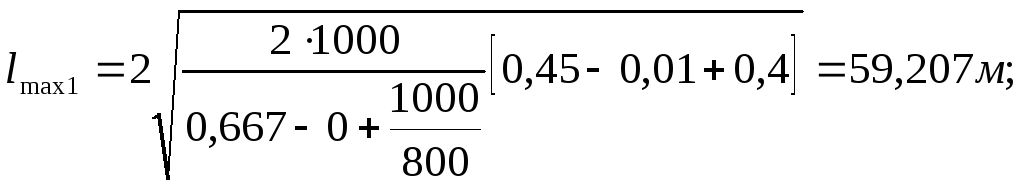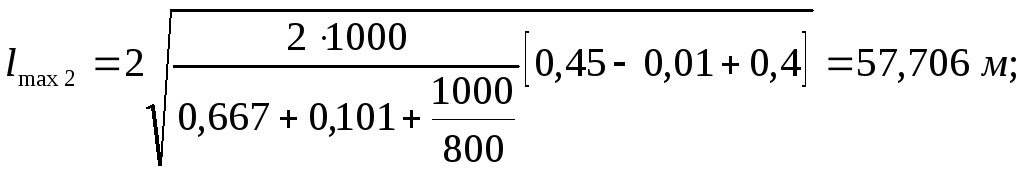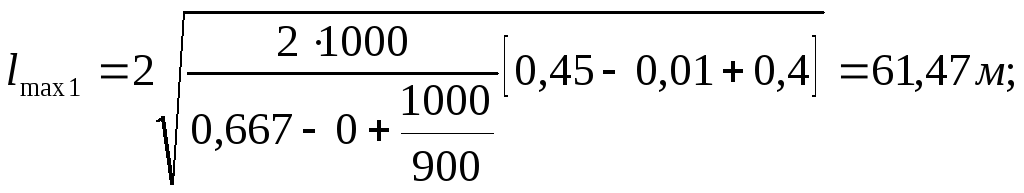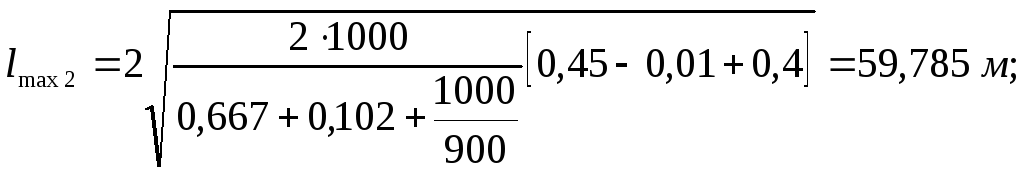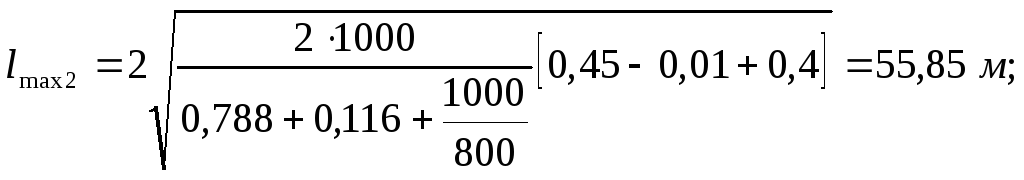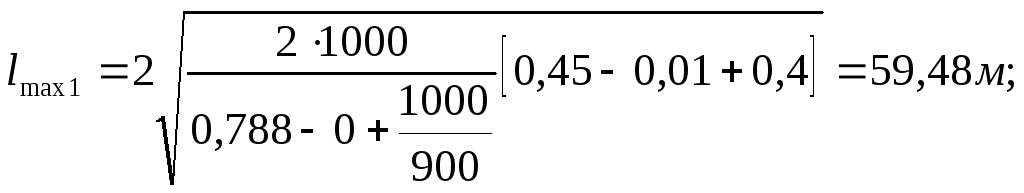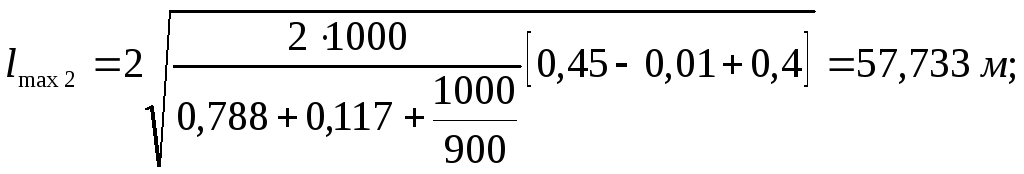Как найти силу натяжения проводов - Исправление недочетов и поиск решений вместе с Examum.ru

Загрузить PDF

В физике, сила натяжения — это сила, действующая на веревку, шнур, кабель или похожий объект или группу объектов. Все, что натянуто, подвешено, поддерживается или качается на веревке, шнуре, кабеле и так далее, является объектом силы натяжения. Подобно всем силам, натяжение может ускорять объекты или становиться причиной их деформации. Умение рассчитывать силу натяжения является важным навыком не только для студентов физического факультета, но и для инженеров, архитекторов; те, кто строит устойчивые дома, должны знать, выдержит ли определенная веревка или кабель силу натяжения от веса объекта так, чтобы они не проседали и не разрушались. Приступайте к чтению статьи, чтобы научиться рассчитывать силу натяжения в некоторых физических системах.

1
Определите силы на каждом из концов нити. Сила натяжения данной нити, веревки является результатом сил, натягивающих веревку с каждого конца. Напоминаем, сила = масса × ускорение. Предполагая, что веревка натянута туго, любое изменение ускорения или массы объекта, подвешенного на веревке, приведет к изменению силы натяжения в самой веревке. Не забывайте о постоянном ускорении силы тяжести — даже если система находится в покое, ее составляющие являются объектами действия силы тяжести. Мы можем предположить, что сила натяжения данной веревки это T = (m × g) + (m × a), где «g» — это ускорение силы тяжести любого из объектов, поддерживаемых веревкой, и «а» — это любое другое ускорение, действующее на объекты.
- Для решения множества физических задач, мы предполагаем идеальную веревку — другими словами, наша веревка тонкая, не обладает массой и не может растягиваться или рваться.
- Для примера, давайте рассмотрим систему, в которой груз подвешен к деревянной балке с помощью одной веревки (смотрите на изображение). Ни сам груз, ни веревка не двигаются — система находится в покое. Вследствие этого, нам известно, чтобы груз находился в равновесии, сила натяжения должна быть равна силе тяжести. Другими словами, Сила натяжения (F_t) = Сила тяжести (F_g) = m × g.
  - Предположим, что груз имеет массу 10 кг, следовательно, сила натяжения равна 10 кг × 9,8 м/с² = 98 Ньютонов.
2
Учитывайте ускорение. Сила тяжести — не единственная сила, что может влиять на силу натяжения веревки — такое же действие производит любая сила, приложенная к объекту на веревке с ускорением. Если, к примеру, подвешенный на веревке или кабеле объект ускоряется под действием силы, то сила ускорения (масса × ускорение) добавляется к силе натяжения, образованной весом этого объекта.
- Предположим, что в нашем примере на веревку подвешен груз 10 кг, и вместо того, чтобы быть прикрепленным к деревянной балке, его тянут вверх с ускорением 1 м/с². В этом случае, нам необходимо учесть ускорение груза, также как и ускорение силы тяжести, следующим образом:
  - F_t = F_g + m × a
  - F_t = 98 + 10 кг × 1 м/с²
  - F_t = 108 Ньютонов.
3
Учитывайте угловое ускорение. Объект на веревке, вращающийся вокруг точки, которая считается центром (как маятник), оказывает натяжение на веревку посредством центробежной силы. Центробежная сила — дополнительная сила натяжения, которую вызывает веревка, «толкая» ее внутрь так, чтобы груз продолжал двигаться по дуге, а не по прямой. Чем быстрее движется объект, тем больше центробежная сила. Центробежная сила (F_c) равна m × v²/r где «m»– это масса, «v» — это скорость, и «r» — радиус окружности, по которой движется груз.
- Так как направление и значение центробежной силы меняются в зависимости от того, как объект движется и меняет свою скорость, то полное натяжение веревки всегда параллельно веревке в центральной точке. Запомните, что сила притяжения постоянно действует на объект и тянет его вниз. Так что, если объект раскачивается вертикально, полное натяжение сильнее всего в нижней точке дуги (для маятника это называется точкой равновесия), когда объект достигает максимальной скорости, и слабее всего в верхней точке дуги, когда объект замедляется.
- Давайте предположим, что в нашем примере объект больше не ускоряется вверх, а раскачивается как маятник. Пусть наша веревка будет длиной 1,5 м, а наш груз движется со скоростью 2 м/с, при прохождении через нижнюю точку размаха. Если нам нужно рассчитать силу натяжения в нижней точке дуги, когда она наибольшая, то сначала надо выяснить равное ли давление силы тяжести испытывает груз в этой точке, как и при состоянии покоя — 98 Ньютонов. Чтобы найти дополнительную центробежную силу, нам необходимо решить следующее:
  - F_c = m × v²/r
  - F_c = 10 × 2²/1.5
  - F_c =10 × 2,67 = 26,7 Ньютонов.
  - Таким образом, полное натяжение будет 98 + 26,7 = 124,7 Ньютона.
4
Учтите, что сила натяжения благодаря силе тяжести меняется по мере прохождения груза по дуге. Как было отмечено выше, направление и величина центробежной силы меняются по мере того, как качается объект. В любом случае, хотя сила тяжести и остается постоянной, результирующая сила натяжения в результате тяжести тоже меняется. Когда качающийся объект находится не в нижней точке дуги (точке равновесия), сила тяжести тянет его вниз, но сила натяжения тянет его вверх под углом. По этой причине сила натяжения должна противодействовать части силы тяжести, а не всей ее полноте.
- Разделение силы гравитации на два вектора сможет помочь вам визуально изобразить это состояние. В любой точке дуги вертикально раскачивающегося объекта, веревка составляет угол «θ» с линией, проходящей через точку равновесия и центр вращения. Как только маятник начинает раскачиваться, сила гравитации (m × g) разбивается на 2 вектора — mgsin(θ), действуя по касательной к дуге в направлении точки равновесия и mgcos(θ), действуя параллельно силе натяжения, но в противоположном направлении. Натяжение может только противостоять mgcos(θ) — силе, направленной против нее — не всей силе тяготения (исключая точку равновесия, где все силы одинаковы).
- Давайте предположим, что, когда маятник отклоняется на угол 15 градусов от вертикали, он движется со скоростью 1,5 м/с. Мы найдем силу натяжения следующими действиями:
  - Отношение силы натяжения к силе тяготения (T_g) = 98cos(15) = 98(0,96) = 94,08 Ньютона
  - Центробежная сила (F_c) = 10 × 1,5²/1,5 = 10 × 1,5 = 15 Ньютонов
  - Полное натяжение = T_g + F_c = 94,08 + 15 = 109,08 Ньютонов.
5
Рассчитайте трение. Любой объект, который тянется веревкой и испытывает силу «торможения» от трения другого объекта (или жидкости), передает это воздействие натяжению в веревке. Сила трения между двумя объектами рассчитывается также, как и в любой другой ситуации — по следующему уравнению: Сила трения (обычно пишется как F_r) = (mu)N, где mu — это коэффициент силы трения между объектами и N — обычная сила взаимодействия между объектами, или та сила, с которой они давят друг на друга. Отметим, что трение покоя — это трение, которое возникает в результате попытки привести объект, находящийся в покое, в движение — отличается от трения движения — трения, возникающего в результате попытки заставить движущийся объект продолжать движение.
- Давайте предположим, что наш груз в 10 кг больше не раскачивается, теперь его буксируют по горизонтальной плоскости с помощью веревки. Предположим, что коэффициент трения движения земли равен 0,5 и наш груз движется с постоянной скоростью, но нам нужно придать ему ускорение 1м/с². Эта проблема представляет два важных изменения — первое, нам больше не нужно рассчитывать силу натяжения по отношению к силе тяжести, так как наша веревка не удерживает груз на весу. Второе, нам придется рассчитать натяжение, обусловленное трением, также как и вызванное ускорением массы груза. Нам нужно решить следующее:
  - Обычная сила (N) = 10 кг & × 9,8 (ускорение силы тяжести) = 98 N
  - Сила трения движения (F_r) = 0,5 × 98 N = 49 Ньютонов
  - Сила ускорения (F_a) = 10 kg × 1 м/с² = 10 Ньютонов
  - Общее натяжение = F_r + F_a = 49 + 10 = 59 Ньютонов.
Реклама

1
Поднимите вертикальные параллельные грузы с помощью блока. Блоки — это простые механизмы, состоящие из подвесного диска, что позволяет менять направление силы натяжения веревки. В простой конфигурации блока, веревка или кабель идет от подвешенного груза вверх к блоку, затем вниз к другому грузу, создавая тем самым два участка веревки или кабеля. В любом случае натяжение в каждом из участков будет одинаковым, даже если оба конца будут натягиваться силами разных величин. Для системы двух масс, подвешенных вертикально в блоке, сила натяжения равна 2g(m₁)(m₂)/(m₂+m₁), где «g» — ускорение силы тяжести, «m₁» — масса первого объекта, «m₂»– масса второго объекта.
- Отметим следующее, физические задачи предполагают, что блоки идеальны — не имеют массы, трения, они не ломаются, не деформируются и не отделяются от веревки, которая их поддерживает.
- Давайте предположим, что у нас есть два вертикально подвешенных на параллельных концах веревки груза. У одного груза масса 10 кг, а у второго — 5 кг. В этом случае, нам необходимо рассчитать следующее:
  - T = 2g(m₁)(m₂)/(m₂+m₁)
  - T = 2(9,8)(10)(5)/(5 + 10)
  - T = 19,6(50)/(15)
  - T = 980/15
  - T = 65,33 Ньютонов.
- Отметим, что, так как один груз тяжелее, все остальные элементы равны, эта система начнет ускоряться, следовательно, груз 10 кг будет двигаться вниз, заставляя второй груз идти вверх.
2
Подвесьте грузы, используя блоки с не параллельными вертикальными нитями. Блоки зачастую используются для того, чтобы направлять силу натяжения в направлении, отличном от направления вниз или вверх. Если, к примеру, груз подвешен вертикально к одному концу веревки, а другой конец держит груз в диагональной плоскости, то непараллельная система блоков принимает форму треугольника с углами в точках с первых грузом, вторым и самим блоком. В этом случае натяжение в веревке зависит как от силы тяжести, так и от составляющей силы натяжения, которая параллельна к диагональной части веревки.
- Давайте предположим, что у нас есть система с грузом в 10 кг (m₁), подвешенным вертикально, соединенный с грузом в 5 кг(m₂), расположенным на наклонной плоскости в 60 градусов (считается, что этот уклон не дает трения). Чтобы найти натяжение в веревке, самым легким путем будет сначала составить уравнения для сил, ускоряющих грузы. Далее действуем так:
  - Подвешенный груз тяжелее, здесь нет трения, так что мы знаем, что он ускоряется вниз. Натяжение в веревке тянет вверх, так что он ускоряется по отношению к равнодействующей силе F = m₁(g) — T, или 10(9,8) — T = 98 — T.
  - Мы знаем, что груз на наклонной плоскости ускоряется вверх. Так как она не имеет трения, мы знаем, что натяжение тянет груз вверх по плоскости, а вниз его тянет только свой собственный вес. Составляющая силы, тянущей вниз по наклонной, вычисляется как mgsin(θ), так что в нашем случае мы можем заключить, что он ускоряется по отношению к равнодействующей силе F = T — m₂(g)sin(60) = T — 5(9,8)(0,87) = T — 42,14.
  - Если мы приравняем эти два уравнения, то получится 98 — T = T — 42,14. Находим Т и получаем 2T = 140,14, или T = 70,07 Ньютонов.
3
Используйте несколько нитей, чтобы подвесить объект. В заключение, давайте представим, что объект подвешен на «Y-образной» системе веревок — две веревки закреплены на потолке и встречаются в центральной точке, из которой идет третья веревка с грузом. Сила натяжения третьей веревки очевидна — простое натяжение в результате действия силы тяжести или m(g). Натяжения на двух остальных веревках различаются и должны составлять в сумме силу, равную силе тяжести вверх в вертикальном положении и равны нулю в обоих горизонтальных направлениях, если предположить, что система находится в состоянии покоя. Натяжение в веревке зависит от массы подвешенных грузов и от угла, на который отклоняется от потолка каждая из веревок.
- Давайте предположим, что в нашей Y-образной системе нижний груз имеет массу 10 кг и подвешен на двух веревках, угол одной из которых составляет с потолком 30 градусов, а угол второй — 60 градусов. Если нам нужно найти натяжение в каждой из веревок, нам понадобится рассчитать горизонтальную и вертикальную составляющие натяжения. Чтобы найти T₁ (натяжение в той веревке, наклон которой 30 градусов) и T₂ (натяжение в той веревке, наклон которой 60 градусов), нужно решить:
  - Согласно законам тригонометрии, отношение между T = m(g) и T₁ и T₂ равно косинусу угла между каждой из веревок и потолком. Для T₁, cos(30) = 0,87, как для T₂, cos(60) = 0,5
  - Умножьте натяжение в нижней веревке (T=mg) на косинус каждого угла, чтобы найти T₁ и T₂.
  - T₁ = 0,87 × m(g) = 0,87 × 10(9,8) = 85,26 Ньютонов.
  - T₂ =0,5 × m(g) = 0,5 × 10(9,8) = 49 Ньютонов.
Реклама

Об этой статье

Эту страницу просматривали 287 682 раза.

Была ли эта статья полезной?

Источник

Romzacultra Участник форумов Сейчас отсутствует	В проекте дано напряжение в проводе в МПа, подскажите как отсюда узнать силу натяжения?

Diego	Вы чем вообще занимаетесь и к чему вам информация подобного толка?
Инженер-проектировщик (Санкт-Петербург, Россия)

Romzacultra

Участник форумов

Сейчас отсутствует

Нужно это для подвеса кабеля сип-3! В проекте даны 2 величины: стрела провеса провода и напряжение в проводе. Как я понимаю мне нужна сила натяжения в Ньютонах, которую я буду видеть при натяжении кабеля на динамометре! как ее вычислить если есть только эти 2 величины? Или может я в чем то ошибаюсь?

Diego	Паскаль равен давлению, вызываемому силой, равной одному ньютону, равномерно распределённой по нормальной к ней поверхности площадью один квадратный метр: 1 Па = 1 Н·м−2.
Инженер-проектировщик (Санкт-Петербург, Россия)

Romzacultra Участник форумов Сейчас отсутствует	При температуре воздуха 15 градусов (что в моем случае) натяжение составляет 14.45 МПа, если это перевести, то получается 14450 кН на кв.метр? но это же невозможно

Diego	Вы в разрядности ошиблись.
Инженер-проектировщик (Санкт-Петербург, Россия)

Diego	А не, перепутал. Все верно. 14.45 мегапаскаль = 14450 килоньютон на кв. метр
Инженер-проектировщик (Санкт-Петербург, Россия)

Romzacultra Участник форумов Сейчас отсутствует	Но такое же невозможно?

Vlad 380 Активный участник форумов Сейчас отсутствует	Но такое же невозможно? Может так возможно? 70 мм2 /1000000 мм2 * 14450 кН·м−2 = 1,0115 кН
Проектировщик электроснабжения (Калининград, Россия)

Romzacultra Участник форумов Сейчас отсутствует	Но такое же невозможно? Может так возможно? 70 мм2 /1000000 мм2 * 14450 кН·м−2 = 1,0115 кН Если не сложно можете объяснить что это за числа? Заранее благодарен!

Vlad 380

Активный участник форумов

Сейчас отсутствует

Как я понимаю мне нужна сила натяжения в Ньютонах, которую я буду видеть при натяжении кабеля на динамометре!

сечение Вашего СИП-3 ( 1 жила 70 мм2 например) переводим в м2 (разделив на 1 млн мм2) и умножаем на кН·м−2:
м2*кН/м2 = кН

Вместо 70 подставьте сечение Вашего проводника

Проектировщик электроснабжения (Калининград, Россия)

Сейчас Вы — Гость на форумах «Проектант». Гости не могут писать сообщения и создавать новые темы.
Преодолейте несложную формальность — зарегистрируйтесь! И у Вас появится много больше возможностей на форумах «Проектант».

Последние сообщения на Электротехническом форуме

Источник

Провода воздушных
линий электропередач рассчитываются
на прочность по допустимому напряжению,
а провода контактной сети – по допустимому
натяжению провода, кН:

(4.1)

где
коэффициент, учитывающий разброс
механических характеристик отдельных
проволок в проводе;

σ_вр
– временное сопротивление разрыву
провода, Па, табл.1.5. [2];

K_j
– коэффициент запаса прочности §1.6 [3];

S
—
расчетная
площадь сечения провода, мм².

Принимаемые в
расчетах наибольшие и номинальные
натяжения проводов приведены в табл.1.8
[2]. Натяжение несущего троса (Т₀)
при беспровесном положении контактного
провода предварительно принимается:

-для медных проводов
—

-для ПБСМ —

Натяжение несущего
троса при ветре набольшей интенсивности
Т_в=0,7Т_дп
при медном и Т_в=0,75Т_дп
при ПБСМ.

Действительные
значения Т₀
и Т_вопределяются
при механическом расчете контактной
подвески.

Главный путь:

Второстепенный
путь:

5.Определение допустимых длин пролетов

Наибольшие длины
пролетов устанавливают в режиме ветра
наибольшей интенсивности. При этом
ветровые отклонения контактного провода
на прямых участках пути не должны
превышать 0,5м, а на кривых – 0,45м. Наибольшее
расстояние между опорами, для обеспечения
надежного токосъема принимается равным
не более 70 м.

Для прямых участков
пути:

(5.1)

для кривых участков
пути:

(5.2)

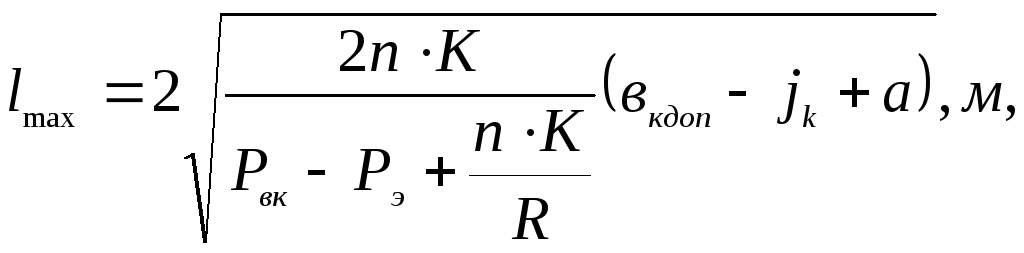
где К
– номинальное
натяжение контактного провода, даН/м;

n
– количество
контактных проводов;

Р_вк
– ветровая нагрузка на контактный
провод, даН/м;

R
– радиус
кривой пути, м;

Р_э
– эквивалентная
нагрузка, передающая с несущего троса
на контактный провод, даН/м;

в_к

доп –
наибольшее допустимое ветровое отклонение
контактного провода, м, (в_кдоп
=0,5 – на прямых; в_кдоп
=0,45 – на кривых);

j_k
– прогиб опоры под действием ветра на
уровне крепления контактного провода,
с.67 [2], ( j_k
=0,01 – 0,015);

Формула для
определения удельной эквивалентной
нагрузки имеет вид:

(5.3)

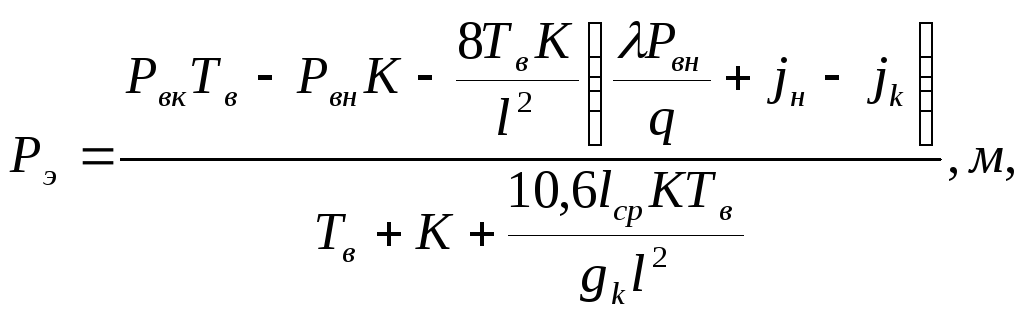
где Р_вн–
ветровая
нагрузка на несущий трос, даН/м;

К – натяжение
контактного провода,( см таблицу 1.2);

Т_в
– натяжение несущего троса в режиме
ветра наибольшей интенсивности, даН;

l
– длина
пролета, м;

λ
– длина гирлянды подвесных изоляторов
и крепительных деталей для несущего
троса, м.
Определяется по [2] с.67, (λ
=0,55 м);

q
– результирующая нагрузка на несущий
трос цепной подвески в режиме ветра
наибольшей интенсивности, даН/м;

g_k
– нагрузка от силы тяжести контактного
провода, (см.пункт 1, раздел 3.1, формула
3.1), даН/м;

j_н
– прогиб опоры под действием ветра на
уровне крепления несущего троса, [2]
с.67, м,
(j_н
=0,015);

l_ср
– средняя длина струн в средней части
пролета, м.
Определяется по формуле:

(5.4)

где h₀
– конструктивная высота цепной подвески,
[2] с.67, м,
(h₀
=1,8 м);

g
– нагрузка
от силы тяжести цепной подвески, (см.пункт
1, раздел 1.1, формула 3.1), даН/м;

T₀
– натяжение несущего троса при
беспровесном состоянии контактного
провода, (см.пункт 2), даН;

а — длина
зигзага, (а=0,3 – на прямых; а=0,4 – на
кривых).

На станции, где
подвески разных путей расположены на
жестких поперечинах, следует брать
меньшую длину пролета. Определение длин
пролета производится по формулам 5.1 и
5.2 при
(простая подвеска), а затем, получив это
значение длины пролета, определяют Р_Э
по формуле 5.3 и снова
с
учетом.
Если длина пролета отличается от
первоначальной не более, чем на 5 м, то
ее принимают за окончательный результат,
если более, то расчеты необходимо
продолжить. Наибольшие длины пролетов
для различных условий трассы, ветровых
районов и контактных подвесок приведены
в табл. 2.7 [2].

Для главного
пути станции:

Для второстепенного
пути станции:

Для главного
пути перегона:

Для главного
пути перегона с кривой R=400
м:

Для главного
пути перегона с кривой R=800
м:

Для главного
пути перегона с кривой R=900
м:

Для главного
пути на насыпи:

Для главного
пути на насыпи с кривой R=800
м:

Для главного
пути на насыпи с кривой R=900
м:

Полученные значения
длин участков сводим в таблицу 5.1

Таблица 5.1 ––
Допустимые длины пролетов

Участок	Длины пролета, м
Р_э= 0	Р_э# 0	Принимаем
Главные пути станции	83,45	78,81	70
Второстепенные пути станции	75,81	74,39	70
Главные пути перегона	72,54	67,64	67
Перегон на кривой R=400	46,06	46,36	35
Перегон на кривой R=800	59,207	57,706	40
Перегон на кривой R=900	61,47	59,785	45
Насыпь прямой участок	66,73	62,206	50
Насыпь на кривой R=800	57,42	55,85	40
Насыпь на кривой R=900	59,48	57,73	45

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

2016-09-08

Участок гибкого провода массой $m$ подвешен так, что его концы закреплены на одинаковой высоте (см. рисунок). Провод находится в однородном горизонтальном магнитном поле с индукцией $B$, и по нему течёт ток $I$. Силы, действующие на провод в точках подвеса, образуют угол $alpha$ с горизонтом. Найдите силу $T$ натяжения провода в его нижней точке. Размеры $L$ и $h$ известны.

Решение:

Обозначим нижнюю точку провода через $A$, верхние точки — через $B$ и $C$ (см. рисунок). Введём в плоскости провода декартову прямоугольную систему координат, направив ось $X$ вправо, ось $Y$ — вверх; обозначим координаты точек $A$ и $C$ как $(x_{A}; y_{A})$ и $(x_{C}; y_{X})$.

Рассмотрим участок провода $AC$. На него действуют направленная вниз сила тяжести $frac{m vec{g}}{2}$, направленная влево сила $vec{T}$ натяжения нити в нижней точке $A$, направленная под углом $alpha$ к горизонту сила натяжения нити $vec{F}$ и сила Ампера $vec{F}_{магн}$, действующая со стороны магнитного поля. Запишем условие равновесия системы в проекциях на оси $X$ и $Y$:

$F_{x}^{магн} + F cos alpha — T = 0, F_{y}^{магн} + F sin alpha — frac{mg}{2} = 0$.

Выражая из второго соотношения неизвестную величину силы $F$ и подставляя её в первое уравнение, находим искомую силу натяжения нити:

$T = F_{x}^{магн} + left ( frac{mg}{2} — F_{y}^{магн} right ) ctg alpha$.

Для получения ответа остаётся найти компоненты силы Ампера $vec{F}^{магн}$. Рассмотрим маленький отрезок провода длиной $Delta l$, составляющий угол $gamma$ с горизонтом и расположенный между точками с координатами $(x; y)$ и $(x + Delta x; y + Delta y)$, где $Delta x = Delta l cdot cos gamma, Delta y = Delta l cdot sin gamma$ (см. рисунок). На этот участок действует сила Ампера $Delta vec{F}^{магн}$, равная по модулю $IB Delta l$ и направленная под углом $gamma$ к

вертикали. Эта сила имеет компоненты

$Delta F_{x}^{магн} = Delta F^{магн} sin gamma = IB Delta l sin gamma = IB Delta y$; $Delta F_{y}^{магн} = — Delta F^{магн} cos gamma = — IB Delta l cos gamma = — IB Delta x$.

Складывая силы Ампера, действующие на все малые отрезки участка $AC$ провода, находим:

$F_{x}^{магн} = IB(y_{C} — y_{A}) = IBh$;

$F_{y}^{магн} = — IB(x_{C} — x_{A}) = — IB frac{L}{2}$.

Подставляя результат в формулу для силы натяжения провода, приходим к ответу:

$T = IBh + frac{mg + IBL}{2} ctg alpha$.

Источник

Сила, которая передается по длине гибкой среды, такой как веревка, кабель, веревка и т. Д., Когда ее тянут или подвешивают силой, действующей на тяжелый объект, называется сила натяжения. В этой статье мы изучим как рассчитать силу натяжения.

Узнайте больше о Что такое частота колебаний

Расчет силы натяжения

Подсчитаем сила натяжения учитывая массу объекта «m» и объекта ускорения «a».

от Второй закон движения Ньютона, мы знаем это

F = m * a

Здесь сила называется сила натяжения так что уравнение становится,

Т = м * а

Случай (i): пусть вес объекта (w) действует вниз, а сила натяжения (T) на веревке, действующая вверх, и ускорение свободного падения равно «g».

Сила натяжения, действующая на объект массой (м)

Тогда сила натяжения будет рассчитана как

Т = Ш

Но мы знаем W = m * g

т.е. T = m * g

Случай (ii): когда объект с определенным ускорение в направлении вниз вес объекта больше, чем натяжение, тогда уравнение принимает следующий вид:

W — T = ma

Но W = m * g,

(м * г) — Т = т * а

Т = м * г — м * а

Или T = m (g — a)

Случай (iii): теперь тело ускоряется в направлении вверх, и вес должен быть меньше напряжения. Тогда уравнение становится,

Т — Ж = м * а

Т — (m * g) = m * a

Т = м * г + м * а

Или T = m (g + a)

Случай (iv): сила натяжения зависит не только от массы объекта и ускорения, но и от угла подвески. Когда объект массой «m» подвешен вертикально под углом θ, силу натяжения можно рассчитать, как показано ниже.

Сила натяжения под определенным углом

Здесь всего одна струна, а разрешающая сила направлена по оси Y.

Т = м * г

Т sin (θ) = m * g

Сходным образом ; когда объект зажат двумя массами горизонтально и составляет угол θ₁ и θ₂тогда сила натяжения будет

T₁ потому что (θ) = Т₂соз (θ)

Узнайте больше о Примеры центробежной силы

Узнайте больше о Трение — консервативная сила

Некоторые решенные примеры

С нижнего конца фонаря свисает предмет массой 24 кг. нерастяжимый кабель. Если верхний конец троса прикреплен к крыше с помощью крючка, то рассчитать силу натяжения, действующую на трос?

Решение:

Дано: масса объекта = 24 кг.

Ускорение свободного падения = 9.8 м / с

Поскольку объект просто подвешен на крыше и нет движения объекта. Следовательно, сила натяжения, действующая на струну, равна весу объекта.

Т = W = мг = 24 × 9.8

= 235.20 Н

Узнайте больше о Примеры простых гармоник

Рассчитайте массу объекта, когда его тянут за веревку, и объект движется вниз с ускорением 8 м / с.². Если сила натяжения, действующая на канат, составляет 286 Н. (Примите ускорение свободного падения как 10 м / с.²).

Решение:

Дано: Сила натяжения, действующая на трос = 286Н

Ускорение объекта, действующего в нисходящем направлении = 8 м / с²

Ускорение свободного падения = 10 м / с²

Мы знаем, что для объекта, ускоряющегося в направлении вниз, сила натяжения определяется выражением

Т = мг — ма

Рассчитать массу объекта; переставляя уравнение, мы получаем

Т = м (г — а)

m = 143 кг

Объект массой 9 кг подвешен на тросе, ускоряющемся вверх. Если сила натяжения, действующая на него, составляет 143 Н, то узнайте ускорение объекта, действующего в восходящем направлении. (Примите ускорение свободного падения как 10 м / с.²).

Решение:

Дано: масса объекта = 9 кг.

Сила натяжения = 143Н

Ускорение свободного падения = 10 м / с²

Мы знаем, что сила натяжения, действующая на объект, когда он ускоряется вверх, равна

Т = мг + ма

143N = (9 кг × 10) + (9 кг × а)

143N = 90 + (9 × а)

143 — 90 = 9a

53 = 9а

a = 5.888 м / с²

К кайту прикреплена тетива, которая образует угол 35 °. За веревку никто не тянет и не тянет. Действующая чистая сила составляет 60 Н. рассчитать натяжение струны.

Решение:

Дано: угол подвеса = 35 °

Чистая сила = м * г = 60 Н

T sin (35) = 60

Т (0.5735) = 60

Т = 104.620 Н

Часто задаваемые вопросы :

Почему работа, проделанная напряжением, всегда нулевая, объяснять?

Ответ: Работа, проделанная чем-либо, дается

Вт = ФС

Где F — сила, а S — смещение

Это означает, что проделанная работа зависит как от силы, так и от смещения. Но напряжение — это сила, в которой не будет смещения.

т.е. S = 0

W = F × 0

W = 0

Следовательно, работа, совершаемая силой натяжения, всегда будет равна нулю.

Сила натяжения — это контактная сила, объясните?

Ответ: Контактная сила — это сила, прилагаемая двумя объектами, находящимися в контакте друг с другом. В силе натяжения сила передается через трос, веревку или жало, когда они туго натягиваются силами, действующими противоположно друг другу. Между передающей средой и объектом существует контакт. Таким образом, сила натяжения — это сила контакта.

Как сила тяжести влияет на силу натяжения?

Ответ: Сила натяжения всегда действует в направлении, противоположном гравитационному притяжению. Если объект висит, он должен быть уравновешен силой натяжения, иначе он должен будет ускоряться в направлении вниз под действием силы тяжести.

Как напряжение зависит от массы?

Ответ: Когда объект подвешивается на веревке, веревке или тросе, возникает только натяжение. Понятно, что когда веревка не тянет за собой какой-либо предмет, натяжение веревки не возникает. Таким образом, напряжение всегда пропорционально массе объекта.

Когда объект определенной массы m тянется с помощью веревки человеком A. Человек B тянет тот же объект в противоположном направлении, то какой будет сила натяжения, действующая на веревку человека A?

Ответ: Из уравнения силы натяжения; сила натяжения, действующая на сторону человека А, равна

T_A = м * а

Сила натяжения со стороны человека B равна

T_B = м * а

Чистая сила будет

F_сеть= Т_A— Т_B

Поскольку сила T_Bдействует в направлении, противоположном T_B

Преобразуя приведенное выше уравнение, мы получаем натяжение веревки A.

T_A= Ф_сеть + T_B

Источник