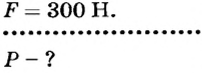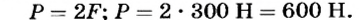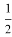Преподаватель который помогает студентам и школьникам в учёбе.
Блоки в физике — виды, формулы и определения с примерами
Содержание:
Блоки:
Всегда ли удобно использовать рычаг
Поднять груз на значительную высоту с помощью рычага очень сложно. Чем высота больше, тем длиннее должен быть рычаг. Такого недостатка нет у блока.
Что такое блок
Блок — это устройство, состоящее из веревки, переброшенной через колесо, которое может вращаться на оси.
Обод колеса, как правило, имеет желоб, в котором прокладывается трос или веревка.
Ось блока может быть неподвижной или перемещаться вместе с колесом. В связи с этим блоки бывают подвижными и неподвижными.
Какой блок называют неподвижным
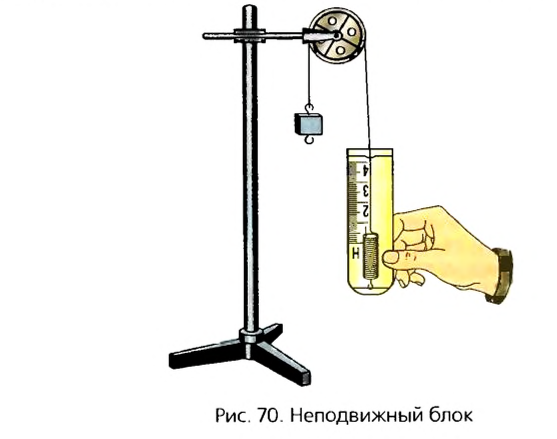
У неподвижного блока ось вращения не изменяет своего положения в пространстве. Она с помощью специальной обоймы закреплена на балке или на другой опоре (рис. 70). Если на конец веревки, переброшенной через блок, подействовать силой, то другой конец начнет двигаться вверх. Если к этому концу прикрепить груз определенной массы, то он будет подниматься вверх. Если на свободный конец веревки действует сила, направленная вниз, то на груз действует сила, направленная вверх. Измерение этих сил показывает, что они равны.
Почему неподвижный блок не дает выигрыша в силе
Неподвижный блок выигрыша в силе не дает, он только изменяет направление действия силы.
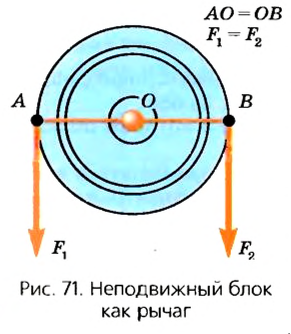
Такую особенность можно легко объяснить, учитывая, что неподвижный блок похож на равноплечий рычаг. Для этого перенесем точки действия сил вверх к точкам А к В, где веревка касается блока (рис. 71). Плечи этих сил OA и ОВ будут одинаковыми, как радиусы окружности. Согласно условию равновесия рычага силы F1 и F2 также должны быть одинаковыми. Опыт подтверждает эти выводы.
- Заказать решение задач по физике
Какой блок называют подвижным
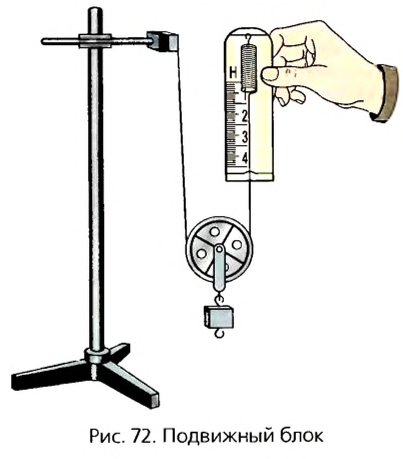
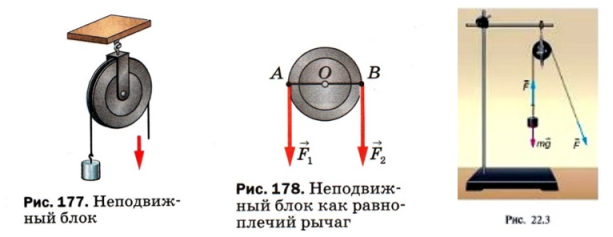
Подвижным называют блок, ось которого перемещается в пространстве. При использовании такого блока обычно один конец веревки или троса закрепляют на опоре, а груз — на обойме, в которой блок закреплен. На рисунке 72 показан опыт с таким блоком. К оси легкого подвижного блока подвешен груз массой 102 г. Итак, на ось блока действует сила 1 Н. Стрелка динамометра, присоединенного к свободному концу веревки, показывает примерно 0,5 Н. Некоторые небольшие различия связаны с тем, что блок сам имеет вес и на него действует сила трения.
Почему подвижный блок дает выигрыш в силе
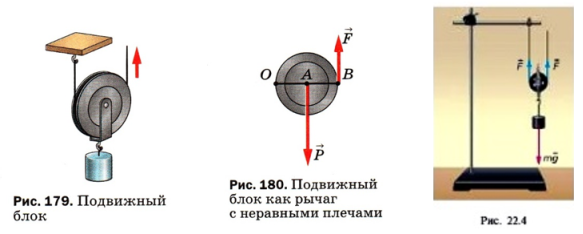
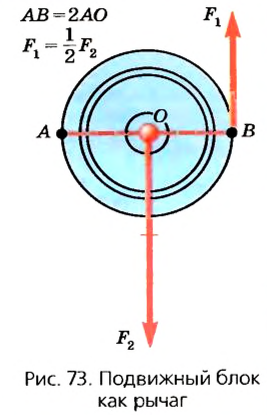
Такую особенность подвижного блока можно объяснить, учитывая свойства рычага (рис. 73). Диск блока можно считать рычагом длиной 2R (где R — радиус колеса). Ось вращения такого рычага проходит через точку А на ободе колеса, а точками приложения сил являются точки О и В. Так как 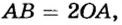
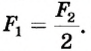
Пример решения задачи
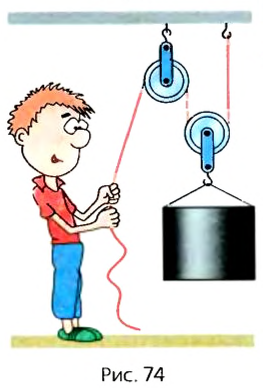
Определить вес груза, который удерживается системой подвижного и неподвижного блоков, если на свободный конец троса действует сила 300 Н (рис. 74).
Дано:
Решение
Неподвижный блок выигрыша в силе не дает. Поэтому вычисления производим с учетом только подвижного блока, который дает выигрыш в силе в два раза. О массе блока в условии задачи не сказано, поэтому весом блока можно пренебречь по сравнению с весом груза. Таким образом,
Ответ. Вес груза равен 600 Н.
- Движение тела под действием нескольких сил
- Наклонная плоскость в физике
- Давление газов и жидкостей
- Движение жидкостей и газов
- Сила давления в физике и единицы давления
- Механическое давление в физике
- Столкновения в физике
- Рычаг в физике
Неподвижный блок
Содержание:
-
Что такое неподвижный блок в физике
- Для чего используется, примеры применения
- Какой выигрыш в силе дает неподвижный блок
- Виды неподвижных блоков и их свойства
- Неподвижные блоки в системах блоков
- Как найти момент силы и работу, формулы
Что такое неподвижный блок в физике
Неподвижный блок — это диск, который вращается вокруг своей оси, и имеет желоб по окружности. Желоб предназначен для скольжения в нем нити (цепи, ремня, каната и т.д.). У неподвижного блока ось закреплена, и при подъеме грузов не поднимается и не опускается.
Неподвижный блок можно представить в виде равноплечего рычага, у которого плечи сил равны радиусу колеса.
В задачах часто используют модель идеального блока.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
В идеальном блоке используется идеальная нерастяжимая и невесомая нить. Проскальзывание нити и силы трения отсутствуют. Сам блок также является невесомым.
Свойства идеального блока:
- Нулевая масса и момент инерции.
- Отсутствие силы трения веревки о блок, блока об ось.
- Отсутствие проскальзывания веревки при вращении блока.
Для чего используется, примеры применения
Неподвижные блоки используют для изменения направления прикладываемой силы.
Неподвижные блоки используются:
- в судоходстве для подъема якорей, стягов, парусов;
- в строительстве для подъема грузов на высоту;
- альпинистами и скалолазами для страховки или поднятия себя;
- для подъема воды в колодце.
Какой выигрыш в силе дает неподвижный блок
Неподвижный блок не дает выигрыша в силе. Для того чтобы поднять груз прикрепленный к одному концу веревки, нужно приложить такую же силу к другому концу веревки.
Неподвижный блок используют не для выигрыша в силе, а для изменения направления прикладываемой силы. Например, тянуть веревку вниз может быть значительно удобнее, чем поднимать наверх.
У неподвижного блока нет выигрыша в силе, но нет и проигрыша в расстоянии. На какое расстояние опустится веревка, к которой применяют силу, на такое же расстояние поднимется груз.
Примечание
КПД реального неподвижного блока всегда будет меньше единицы. Ведь часть работы неподвижного блока тратится на силу трения веревки о желоб.
Виды неподвижных блоков и их свойства
Неподвижные блоки различаются по материалу изготовления, а также по наличию дополнительных элементов.
Материал изготовления диска и тросов влияет на силу трения внутри блока и грузоподъемность блока.
По наличию дополнительных элементов блоки бывают:
- с проушиной;
- с крюком;
- с площадкой крепления и т.д.
Различные дополнительные элементы позволяют крепить разные грузы.
Неподвижные блоки в системах блоков
Для улучшения свойств неподвижные блоки часто используют в системах блоков.
Система из двух неподвижных блоков различного диаметра, насаженных на общую ось, обеспечивает выигрыш в силе или скорости. Ведь плечи сил в такой системе будут неравными.
Полиспаст — система из неподвижных и подвижных блоков.
Полиспаст позволяет получить выигрыш в силе в несколько раз. А также дает возможность менять направление прикладываемой силы.
Как найти момент силы и работу, формулы
Сила, которую нужно приложить для поднятия груза, равна силе, с которой действует на подвес груз.
Согласно правилу моментов:
F1 I1 = F2 I1
Где F1 — сила, с которой действует на точку подвеса груз, F2 — сила, которую прикладывают для того, чтобы груз поднять, I1 — радиус блока.
Формула приобретает вид:
F1 = F2
Условия равновесия неподвижного блока:
F=fmg
Где F — сила, которую нужно приложить, m — масса груза, g — ускорение свободного падения, f — коэффициент сопротивления в блоке.
Для идеального блока коэффициент сопротивления не учитывается.
Неподвижный блок выигрыша в работе не дает. Пути, которые проходят точки приложения сил, одинаковы, равны силы, значит, равны работы.
A1=A2.
Насколько полезной была для вас статья?
Рейтинг: 2.50 (Голосов: 10)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так
Поиск по содержимому
Простые механизмы.
-
Рычаг.
-
Неподвижный блок.
-
Подвижный блок.
-
Наклонная плоскость.
-
Золотое правило механики.
-
КПД механизма.
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: простые механизмы, КПД механизма.
Механизм — это приспособление для преобразования силы (её увеличения или уменьшения).
Простые механизмы — это рычаг и наклонная плоскость.
Рычаг.
Рычаг — это твёрдое тело, которое может вращаться вокруг неподвижной оси. На рис. 1) изображён рычаг с осью вращения . К концам рычага (точкам
и
) приложены силы
и
. Плечи этих сил равны соответственно
и
.
Условие равновесия рычага даётся правилом моментов: , откуда
.
 |
| Рис. 1. Рычаг |
Из этого соотношения следует, что рычаг даёт выигрыш в силе или в расстоянии (смотря по тому, с какой целью он используется) во столько раз, во сколько большее плечо длиннее меньшего.
Например, чтобы усилием 100 Н поднять груз весом 700 Н, нужно взять рычаг с отношением плеч 7 : 1 и положить груз на короткое плечо. Мы выиграем в силе в 7 раз, но во столько же раз проиграем в расстоянии: конец длинного плеча опишет в 7 раз большую дугу, чем конец короткого плеча (то есть груз).
Примерами рычага, дающего выигрыш в силе, являются лопата, ножницы, плоскогубцы. Весло гребца — это рычаг, дающий выигрыш в расстоянии. А обычные рычажные весы являются равноплечим рычагом, не дающим выигрыша ни в расстоянии, ни в силе (в противном случае их можно использовать для обвешивания покупателей).
к оглавлению ▴
Неподвижный блок.
Важной разновидностью рычага является блок — укреплённое в обойме колесо с жёлобом, по которому пропущена верёвка. В большинстве задач верёвка считается невесомой нерастяжимой нитью.
На рис. 2 изображён неподвижный блок, т. е. блок с неподвижной осью вращения (проходящей перпендикулярно плоскости рисунка через точку ).
 |
На правом конце нити в точке закреплён груз весом
. Напомним, что вес тела — это сила, с которой тело давит на опору или растягивает подвес. В данном случае вес
прило жен к точке
, в которой груз крепится к нити.
К левому концу нити в точке приложена сила
.
Плечо силы равно
, где
— радиус блока. Плечо веса
равно
. Значит, неподвижный блок является равноплечим рычагом и потому не даёт выигрыша ни в силе, ни в расстоянии: во-первых, имеем равенство
, а во-вторых, в процессе движении груза и нити перемещение точки
равно перемещению груза.
Зачем же тогда вообще нужен неподвижный блок? Он полезен тем, что позволяет изменить направление усилия. Обычно неподвижный блок используется как часть более сложных механизмов.
к оглавлению ▴
Подвижный блок.
На рис. 3 изображён подвижный блок, ось которого перемещается вместе с грузом. Мы тянем за нить с силой , которая приложена в точке
и направлена вверх. Блок вращается и при этом также движется вверх, поднимая груз, подвешенный на нити
.
 |
В данный момент времени неподвижной точкой является точка , и именно вокруг неё поворачивается блок (он бы «перекатывается» через точку
). Говорят ещё, что через точку
проходит мгновенная ось вращения блока (эта ось направлена перпендикулярно плоскости рисунка).
Вес груза приложен в точке
крепления груза к нити. Плечо силы
равно
.
А вот плечо силы , с которой мы тянем за нить, оказывается в два раза больше: оно равно
. Соответственно, условием равновесия груза является равенство
(что мы и видим на рис. 3: вектор
в два раза короче вектора
).
Следовательно, подвижный блок даёт выигрыш в силе в два раза. При этом, однако, мы в те же два раза проигрываем в расстоянии: чтобы поднять груз на один метр, точку придётся переместить на два метра (то есть вытянуть два метра нити).
У блока на рис. 3 есть один недостаток: тянуть нить вверх (за точку ) — не самая лучшая идея. Согласитесь, что гораздо удобнее тянуть за нить вниз! Вот тут-то нас и выручает неподвижный блок.
 |
На рис. 4 изображён подъёмный механизм, который представляет собой комбинацию подвижного блока с неподвижным. К подвижному блоку подвешен груз, а трос дополнительно перекинут через неподвижный блок, что даёт возможность тянуть за трос вниз для подъёма груза вверх. Внешнее усилие на тросе снова обозначено вектором .
Принципиально данное устройство ничем не отличается от подвижного блока: с его помощью мы также получаем двукратный выигрыш в силе.
к оглавлению ▴
Наклонная плоскость.
Как мы знаем, тяжёлую бочку проще вкатить по наклонным мосткам, чем поднимать вертикально. Мостки, таким образом, являются механизмом, который даёт выигрыш в силе.
В механике подобный механизм называется наклонной плоскостью. Наклонная плоскость — это ровная плоская поверхность, расположенная под некоторым углом к горизонту. В таком случае коротко говорят: «наклонная плоскость с углом
«.
Найдём силу, которую надо приложить к грузу массы , чтобы равномерно поднять его по гладкой наклонной плоскости с углом
. Эта сила
, разумеется, направлена вдоль наклонной плоскости (рис. 5).
 |
Выберем ось так, как показано на рисунке. Поскольку груз движется без ускорения, действующие на него силы уравновешены:
.
Проектируем на ось :
,
откуда
.
Именно такую силу нужно приложить, что двигать груз вверх по наклонной плоскости.
Чтобы равномерно поднимать тот же груз по вертикали, к нему нужно приложить силу, равную . Видно, что
, поскольку
. Наклонная плоскость действительно даёт выигрыш в силе, и тем больший, чем меньше угол
.
Широко применяемыми разновидностями наклонной плоскости являются клин и винт.
к оглавлению ▴
Золотое правило механики.
Простой механизм может дать выигрыш в силе или в расстоянии, но не может дать выигрыша в работе.
Например, рычаг с отношением плеч 2 : 1 даёт выигрыш в силе в два раза. Чтобы на меньшем плече поднять груз весом , нужно к большему плечу приложить силу
. Но для поднятия груза на высоту
большее плечо придётся опустить на
, и совершённая работа будет равна:
т. е. той же величине, что и без использования рычага.
В случае наклонной плоскости мы выигрываем в силе, так как прикладываем к грузу силу , меньшую силы тяжести. Однако, чтобы поднять груз на высоту
над начальным положением, нам нужно пройти путь
вдоль наклонной плоскости. При этом мы совершаем работу
т. е. ту же самую, что и при вертикальном поднятии груза.
Данные факты служат проявлениями так называемого золотого правила механики.
Золотое правило механики. Ни один из простых механизмов не даёт выигрыша в работе. Во сколько раз выигрываем в силе, во столько же раз проигрываем в расстоянии, и наоборот.
Золотое правило механики есть не что иное, как простой вариант закона сохранения энергии.
к оглавлению ▴
КПД механизма.
На практике приходится различать полезную работу A полезн, которую нужно совершить при помощи механизма в идеальных условиях отсутствия каких-либо потерь, и полную работу Aполн,
которая совершается для тех же целей в реальной ситуации.
Полная работа равна сумме:
-полезной работы;
-работы, совершённой против сил трения в различных частях механизма;
-работы, совершённой по перемещению составных элементов механизма.
Так, при подъёме груза рычагом приходится вдобавок совершать работу по преодолению силы трения в оси рычага и по перемещению самого рычага, имеющего некоторый вес.
Полная работа всегда больше полезной. Отношение полезной работы к полной называется коэффициентом полезного действия (КПД) механизма:
=Aполезн/Аполн.
КПД принято выражать в процентах. КПД реальных механизмов всегда меньше 100%.
Вычислим КПД наклонной плоскости с углом при наличии трения. Коэффициент трения между поверхностью наклонной плоскости и грузом равен
.
Пусть груз массы равномерно поднимается вдоль наклонной плоскости под действием силы
из точки
в точку
на высоту
(рис. 6). В направлении, противоположном перемещению, на груз действует сила трения скольжения
.
 |
Ускорения нет, поэтому силы, действующие на груз, уравновешены:
.
Проектируем на ось X:
. (1)
Проектируем на ось Y:
. (2)
Кроме того,
, (3)
Из (2) имеем:
.
Тогда из (3):
.
Подставляя это в (1), получаем:
.
Полная работа равна произведению силы F на путь, пройденный телом вдоль поверхности наклонной плоскости:
Aполн=.
Полезная работа, очевидно, равна:
Аполезн=.
Для искомого КПД получаем:
Если вам нравятся наши материалы — записывайтесь на курсы подготовки к ЕГЭ по физике онлайн
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Простые механизмы.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
07.05.2023
Библиографическое описание:
Шумейко, А. В. Силы, действующие в простом механизме блок / А. В. Шумейко, О. Г. Веташенко. — Текст : непосредственный // Юный ученый. — 2020. — № 2 (32). — С. 38-42. — URL: https://moluch.ru/young/archive/32/1875/ (дата обращения: 29.05.2023).
В учебниках физики для 7 класса при изложении материала о подъёме груза простым механизмом блок авторы учебников рассматривают разное количество сил, действующих на блок или трос. Для выяснения, что за силы и на какие предметы они действуют в простом механизме блок при подъёме груза, и написана эта статья.
Ключевые слова:
неподвижный блок, подвижный блок, сила упругости троса, сила трения.
В учебнике физики для 7 класса автора А. В. Пёрышкина на рис.177 нарисован подъём груза простым механизмом неподвижный блок и на рис.178 силы
F
1
и
F
2
действуют на блок в точках
А
и
В
, а в учебнике О. Ф. Кабардина на рис.22.3 нарисован неподвижный блок, с тросом и сила
F
действует на трос, а сила тяжести
mg
действует на груз.
То же самое происходит и в изложении материала о подвижном блоке: в учебнике А. В. Пёрышкина рис.179, на блок действуют две силы
Р
и
F
рис.180, а в учебнике О. Ф. Кабардина на том же самом подвижном блоке три силы: сила тяжести
mg
на грузе и две силы
F
натяжения троса рис.22.4.
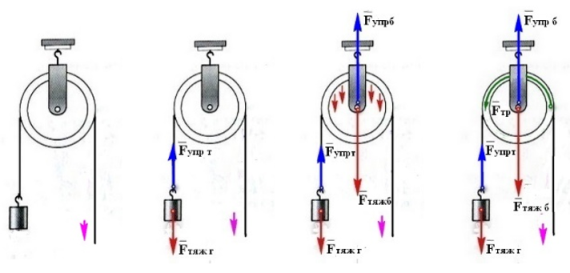
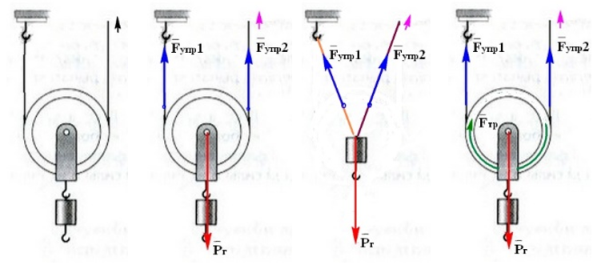
Выяснение сил, действующих в простом механизме блок, начнём с неподвижного блока, изображенного на рис.1. Груз висит на одном из концов троса, далее трос огибает верхнюю полуокружность блока и за второй конец троса происходит подъём груза. На груз действует сила притяжения Земли
F
тяж г
, которая направлена вертикально вниз. Под действием силы тяжести груза в тросу возникает сила упругости
F
упр т
, направленная по тросу и одинаковая по всей длине троса рис.2.
Рис.1. Рис.2. Рис.3. Рис.4.
На рис.3 трос огибает верхнюю полуокружность блока и по всей длине этой полуокружности действуют силы тяжести: груза и троса, а также сила необходимая для подъёма груза. При сложении всех этих параллельных сил равнодействующая сила тяжести
F
тяж б
приложена к центру блока и направлена вертикально вниз, одновременно создавая силу упругости обоймы блока
F
упр б
,
направленную по обойме блока вверх. На рис.4, при подъёме груза, трос движется по верхней полуокружности вращая блок и создавая силу трения скольжения
F
тр
между тросом и блоком.
На рис.5 для определения силы, необходимой для поднятия груза, уберём силу тяжести блока
F
тяж б
и силу упругости блока
F
упр б
, так как они не влияют на величину силы поднятия груза
.
Остались три силы: сила тяжести груза
F
тяж г
, сила упругости троса
F
упр т
и сила трения
F
тр
. Вспомним, что в покое или при равномерном подъёме сила упругости троса равна силе тяжести груза
F
упр т
=
F
тяж г
, а сила трения
F
тр
препятствует подъёму. Поэтому для равномерного подъёма груза необходима сила
F
п,
равная сумме сил упругости троса и силы трения
F
п
=
F
упр т
+
F
тр
. Это равенство справедливо для поднятия груза
полной силой
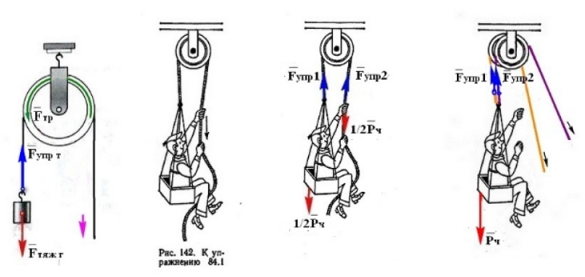
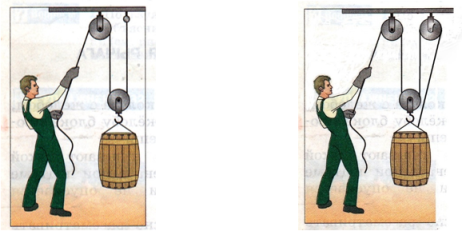
, а на рис.142 в Элементарном учебнике физики под редакцией академика Л. Г. Ландсберга маляры и альпинисты поднимают себя
половинной силой
.
Рис. 5.Рис. 142Рис. 6Рис. 7
На рис.142 человек сидит на сидении, которое прикреплено к тросу, огибающему верхнюю часть неподвижного блока, за второй конец троса человек руками поднимает себя. На рис.6 нарисуем действующие силы подъёма человека. Земля притягивает человека, поэтому на сидение действует половина веса тела человека
Р
ч,
вторая половина веса приходится на руки, которые производят подъём человека. Под действием деления веса человека в тросу возникают силы упругости
F
упр
1
и
F
упр
2
, каждая из которых будет в 2 раза меньше веса человека
F
упр
=
Р
ч.
Наглядно это можно представить как на рис.7, груз поднимают за два независимых троса, и вес груза разделится между тросами, и сила упругости каждого троса будет в два раза меньше веса груза.
F
упр
=
Р
г
.
Подведём итог по силам, действующим на неподвижном блоке:
-
Сила необходимая для подъёма груза на неподвижном блоке равна сумме силы упругости троса и силе трения
F
п
=
F
упр
+
F
тр
.
-
Величина силы упругости троса зависит от способа крепления поднимаемого груза. Если груз закреплён за один из концов троса (за одну ветвь троса) то сила упругости равна весу груза
F
упр
= Р
г
, а если груз закреплён за оба конца троса (за две ветви троса) то сила упругости равна половине веса груза
F
упр
=
Р
г
. Выигрыш в
силе в 2 раза при подъёме груза
половинной силой
с
помощью неподвижного блока даёт трос, а
не неподвижный блок.
-
На рис.178 неподвижный блок нельзя рассматривать как равноплечий рычаг из-за того, что при изменении направления действия силы
F
2
меняется длина рычага
ОВ
на рис.8 (видоизменённом рис.178).
Рис. 178.Рис. 8.
Рассмотрим силы, действующие на подвижный блок рис.9. Груз висит на подвижном блоке, который своей нижней полуокружностью висит на тросу, один конец этого троса закреплён, а подъём подвижного блока с грузом происходит за второй конец троса. На рис.10 обозначим действующие силы на подвижный блок: Земля притягивает груз висящий на подвижном блоке и поэтому в центре подвижного блока действует сила веса груза
Р
г,
а на концах троса силы упругости
F
упр
1
и
F
упр
2
, каждая из которых в 2 раза меньше веса груза из-за того, что вес груза распределился поровну между концами (ветвями) троса, как будто груз висит на двух отдельных тросах рис.11.
Рис. 9.Рис.10.Рис.11.Рис.12.
При подъёме груза блок будет вращаться и создавать силу трения скольжения между подвижным блоком и тросом рис.12, из которого видно, что поднимая груз за один конец троса мы прикладываем силу упругости (которая в 2 раза меньше веса груза) и силу трения
F
п
=
F
упр
2 +
F
тр
. Выигрыш в
силе в 2 раза даёт трос, а
не подвижный блок
и это можно проверить с помощью рис.181 из учебника А. В. Пёрышкина, на котором нарисован неподвижный блок, который не даёт выигрыша в силе и подвижный блок — дающий выигрыш в силе в 2 раза.
Общий выигрыш в
силе этой
комбинации блоков при подъёме груза 2 раза.
Рис.181. Выигрыш в силе 2 разаРис.13 (изменённый рис.181). Выигрыш в силе 3 раза.
Если в этот рисунок добавить еще один неподвижный блок (не дающий выигрыш в силе) и закрепить конец троса за груз рис.13 (изменённый рис.181),
то выигрыш в
силе данной комбинации блоков при подъёме груза будет равен трем, потому что вес груза разделится на три части, так как висит на трёх частях (ветвях) троса.
Отсюда следует, что доказательство в учебнике А. В. Пёрышкина о том, что неподвижный блок не даёт выигрыша в силе, а подвижный блок даёт выигрыш в силе является ошибочным, так как
выигрыш в
силе при подъёме груза на простом механизме блок даёт сила упругости троса (верёвки, цепи), а
модуль выигрыша равен количеству частей (ветвей) троса, на которых висит груз, так как вес груза делится на их количество.
Литература:
- Кабардин О. Ф. Физика. 7 класс: учеб. для общеобразоват. организаций /О. Ф. Кабардин, — 6-е изд. — М.: Просвещение, 2018, — 174 с.: ил. — ISBN 978–5–09–060739–1.
- Ландсберг Г. С.(ред). Элементарный учебник физики, том 1. Механика. Теплота. Молекулярная физика. М. Наука 1985 г.
- Пёрышкин А. В. Физика 7 кл.; учебник / А. В. Пёрышкин, — 9-е изд., пер. — М.: Дрофа, 2019, — 224 с.: ил. ISВN 978–5–358–09796–4.
Основные термины (генерируются автоматически): неподвижный блок, подъем груза, сила, вес груза, трос, конец троса, подвижной блок, подвижный блок, сила трения, сила упругости.
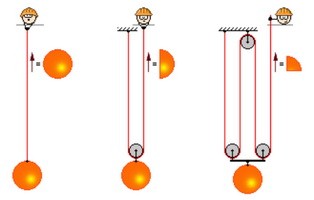
Применение подвижного блока даёт двукратный выигрыш в силе, применение неподвижного — позволяет изменить направление прилагаемой силы. На практике используются комбинации подвижных и неподвижных блоков. При этом каждый подвижный блок позволяет вдвое уменьшить прилагаемое усилие или вдвое увеличить скорость перемещения груза. Неподвижные блоки используют для связи подвижных блоков в единую систему. Такая система подвижных и неподвижных блоков называется полиспаст.
Используется полиспаст в случаях, если необходимо прилагая минимальные усилия поднять или переместить тяжелый груз, обеспечить натяжение и т.п. Простейший полиспаст состоит всего из одного блока и каната, при этом позволяет в два раза снизить тяговое усилие, необходимое для подъема груза.
Рисунок 1. Каждый подвижный блок в полиспасте даёт двукратный выигрыш в силе или скорости
Обычно в грузоподъемных механизмах применяют силовые полиспасты, позволяющие уменьшить натяжение каната, момент от веса груза на барабане и передаточное число механизма (тали, лебедки). Скоростные полиспасты, позволяющие получить выигрыш в скорости перемещения груза при малых скоростях приводного элемента, применяются значительно реже. Они используются в гидравлических или пневматических подъемниках, погрузчиках, механизмах выдвижения телескопических стрел кранов.
Основной характеристикой полиспаста является кратность. Это отношение числа ветвей гибкого органа, на котором подвешен груз, к числу ветвей наматываемых на барабан (для силовых полиспастов), либо отношение скорости ведущего конца гибкого органа к ведомому (для скоростных полиспастов). Условно говоря, кратность это теоретически рассчитанный коэффициент выигрыша в силе или скорости при использовании полиспаста. Изменение кратности полиспаста происходит путем введения или удаления из системы дополнительных блоков, при этом конец каната при четной кратности крепится на неподвижном элементе конструкции, а при нечетной кратности — на крюковой обойме.
Рисунок 2. Крепление каната при чётной и нечётной кратности полиспаста
Выигрыш в силе при применении полиспаста с $n$ подвижных и $n$ неподвижных блоков определяется по формуле: $P=2Fn$, где $Р$ — вес груза, $F$ — сила, прилагаемая на входе полиспаста, $n$ — число подвижных блоков.
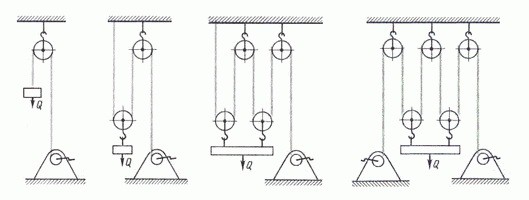
В зависимости от количества ветвей каната, закрепленных на барабане грузоподъемного механизма, можно выделить одинарные (простые) и сдвоенные полиспасты. В одинарных полиспастах, при наматывании или сматывании гибкого элемента вследствие его перемещения вдоль оси барабана, создается нежелательное изменение нагрузки на опоры барабана. Также в случае отсутствия в системе свободных блоков (канат с блока крюковой подвески непосредственно переходит на барабан) происходит перемещение груза не только в вертикальной, но и в горизонтальной плоскости.
Рисунок 3. Одинарные и сдвоенные полиспасты
Для обеспечения строго вертикального подъема груза применяют сдвоенные полиспасты, (состоящие из двух одинарных), в этом случае на барабане закрепляются оба конца каната. Для обеспечения нормального положения крюковой подвески при неравномерной вытяжке гибкого элемента обоих полиспастов применяют балансир или уравнительные блоки.
Рисунок 4. Способы обеспечения вертикальности подъёма груза
Скоростные полиспасты отличаются от силовых тем, что в них рабочая сила, обычно развиваемая гидравлическим или пневматическим цилиндром, прикладывается к подвижной обойме, а груз подвешивается к свободному концу каната или цепи. Выигрыш в скорости при использовании такого полиспаста получается в результате увеличения высоты подъёма груза.
При использовании полиспастов следует учитывать, что используемые в системе элементы не являются абсолютно гибкими телами, а имеют определенную жесткость, поэтому набегающая ветвь не сразу ложится в ручей блока, а сбегающая ветвь не сразу выпрямляется. Это наиболее заметно при использовании стальных канатов.
Вопрос: почему у подъемных строительных кранов крюк, который переносит груз, закреплен не на конце троса, а на обойме подвижного блока?
Ответ: для обеспечения вертикальности подъёма груза.