Мы уже говорили об основах классической механики. Настала пора поговорить о них подробнее и затронуть в обсуждении чуть больше, чем просто основу. В этой статье мы подробно разберем основные законы классической механики. Как вы уже догадались, речь пойдет о законах Ньютона.
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Основные законы классической механики Исаак Ньютон (1642-1727) собрал и опубликовал в 1687 году. Три знаменитых закона были включены в труд, который назывался «Математические начала натуральной философии».
Был долго этот мир глубокой тьмой окутан
Да будет свет, и тут явился Ньютон.
(Эпиграмма 18-го века)
Но сатана недолго ждал реванша —
Пришел Эйнштейн, и стало все как раньше.
(Эпиграмма 20-го века)
Что стало, когда пришел Эйнштейн, читайте в отдельном материале про релятивистскую динамику. А мы пока приведем формулировки и примеры решения задач на каждый закон Ньютона.
Первый закон Ньютона
Первый закон Ньютона гласит:
Существуют такие системы отсчета, называемые инерциальными, в которых тела движутся равномерно и прямолинейно, если на них не действуют никакие силы или действие других сил скомпенсировано.
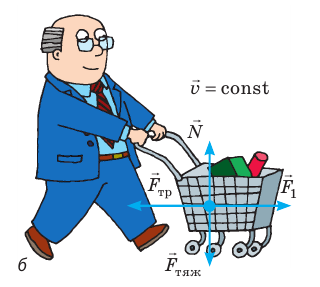
Проще говоря, суть первого закона Ньютона можно сформулировать так: если мы на абсолютно ровной дороге толкнем тележку и представим, что можно пренебречь силами трения колес и сопротивления воздуха, то она будет катиться с одинаковой скоростью бесконечно долго.
Инерция – это способность тела сохранять скорость как по направлению, так и по величине, при отсутствии воздействий на тело. Первый закон Ньютона еще называют законом инерции.
До Ньютона закон инерции был сформулирован в менее четкой форме Галилео Галилеем. Инерцию ученый называл «неистребимо запечатленным движением». Закон инерции Галилея гласит: при отсутствии внешних сил тело либо покоится, либо движется равномерно. Огромная заслуга Ньютона в том, что он сумел объединить принцип относительности Галилея, собственные труды и работы других ученых в своих «Математических началах натуральной философии».
Понятно, что таких систем, где тележку толкнули, а она покатилась без действия внешних сил, на самом деле не бывает. На тела всегда действуют силы, причем скомпенсировать действие этих сил полностью практически невозможно.
Например, все на Земле находится в постоянном поле силы тяжести. Когда мы передвигаемся (не важно, ходим пешком, ездим на машине или велосипеде), нам нужно преодолевать множество сил: силу трения качения и силу трения скольжения, силу тяжести, силу Кориолиса.
Второй закон Ньютона
Помните пример про тележку? В этот момент мы приложили к ней силу! Интуитивно понятно, что тележка покатится и вскоре остановится. Это значит, ее скорость изменится.
В реальном мире скорость тела чаще всего изменяется, а не остается постоянной. Другими словами, тело движется с ускорением. Если скорость нарастает или убывает равномерно, то говорят, что движение равноускоренное.
Если рояль падает с крыши дома вниз, то он движется равноускоренно под действием постоянного ускорения свободного падения g. Причем любой дугой предмет, выброшенный из окна на нашей планете, будет двигаться с тем же ускорением свободного падения.
Второй закон Ньютона устанавливает связь между массой, ускорением и силой, действующей на тело. Приведем формулировку второго закона Ньютона:
Ускорение тела (материальной точки) в инерциальной системе отсчета прямо пропорционально приложенной к нему силе и обратно пропорционально массе.
Если на тело действует сразу несколько сил, то в данную формулу подставляется равнодействующая всех сил, то есть их векторная сумма.
В такой формулировке второй закон Ньютона применим только для движения со скоростью, много меньшей, чем скорость света.
Существует более универсальная формулировка данного закона, так называемый дифференциальный вид.
В любой бесконечно малый промежуток времени dt сила, действующая на тело, равна производной импульса тела по времени.
Третий закон Ньютона
В чем состоит третий закон Ньютона? Этот закон описывает взаимодействие тел.
3 закон Ньютона говорит нам о том, что на любое действие найдется противодействие. Причем, в прямом смысле:
Два тела воздействуют друг на друга с силами, противоположными по направлению, но равными по модулю.
Формула, выражающая третий закон Ньютона:
Другими словами, третий закон Ньютона — это закон действия и противодействия.
Пример задачи на законы Ньютона
Вот типичная задачка на применение законов Ньютона. В ее решении используются первый и второй законы Ньютона.
Десантник раскрыл парашют и опускается вниз с постоянной скоростью. Какова сила сопротивления воздуха? Масса десантника – 100 килограмм.
Решение:
Движение парашютиста – равномерное и прямолинейное, поэтому, по первому закону Ньютона, действие сил на него скомпенсировано.
На десантника действуют сила тяжести и сила сопротивления воздуха. Силы направлены в противоположные стороны.
По второму закону Ньютона, сила тяжести равна ускорению свободного падения, умноженному на массу десантника.
Ответ: Сила сопротивления воздуха равна силе тяжести по модулю и противоположна направлена.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
А вот еще одна физическая задачка на понимание действия третьего закона Ньютона.
Комар ударяется о лобовое стекло автомобиля. Сравните силы, действующие на автомобиль и комара.
Решение:
По третьему закону Ньютона, силы, с которыми тела действуют друг на друга, равны по модулю и противоположны по направлению. Сила, с которой комар действует на автомобиль, равна силе, с которой автомобиль действует на комара.
Другое дело, что действие этих сил на тела сильно отличаются вследствие различия масс и ускорений.
Исаак Ньютон: мифы и факты из жизни
На момент публикации своего основного труда Ньютону было 45 лет. За свою долгую жизнь ученый внес огромный вклад в науку, заложив фундамент современной физики и определив ее развитие на годы вперед.
Он занимался не только механикой, но и оптикой, химией и другими науками, неплохо рисовал и писал стихи. Неудивительно, что личность Ньютона окружена множеством легенд.
Ниже приведены некоторые факты и мифы из жизни И. Ньютона. Сразу уточним, что миф – это не достоверная информация. Однако мы допускаем, что мифы и легенды не появляются сами по себе и что-то из перечисленного вполне может оказаться правдой.
- Факт. Исаак Ньютон был очень скромным и застенчивым человеком. Он увековечил себя благодаря своим открытиям, однако сам никогда не стремился к славе и даже пытался ее избежать.
- Миф. Существует легенда, согласно которой Ньютона осенило, когда на наго в саду упало яблоко. Это было время чумной эпидемии (1665-1667), и ученый был вынужден покинуть Кембридж, где постоянно трудился. Точно неизвестно, действительно ли падение яблока было таким роковым для науки событием, так как первые упоминания об этом появляются только в биографиях ученого уже после его смерти, а данные разных биографов расходятся.
- Факт. Ньютон учился, а потом много работал в Кембридже. По долгу службы ему нужно было несколько часов в неделю вести занятия у студентов. Несмотря на признанные заслуги ученого, занятия Ньютона посещались плохо. Бывало, что на его лекции вообще никто не приходил. Скорее всего, это связано с тем, что ученый был полностью поглощен своими собственными исследованиями.
- Миф. В 1689 году Ньютон был избран членом Кембриджского парламента. Согласно легенде, более чем за год заседания в парламенте вечно поглощенный своими мыслями ученый взял слово для выступления всего один раз. Он попросил закрыть окно, так как был сквозняк.
- Факт. Неизвестно, как бы сложилась судьба ученого и всей современной науки, если бы он послушался матери и начал заниматься хозяйством на семейной ферме. Только благодаря уговорам учителей и своего дяди юный Исаак отправился учиться дальше вместо того, чтобы сажать свеклу, разбрасывать по полям навоз и по вечерам выпивать в местных пабах.
Дорогие друзья, помните — любую задачу можно решить! Если у вас возникли проблемы с решением задачи по физике, посмотрите на основные физические формулы. Возможно, ответ перед глазами, и его нужно просто рассмотреть. Ну а если времени на самостоятельные занятия совершенно нет, специализированный студенческий сервис всегда к вашим услугам!
В самом конце предлагаем посмотреть видеоурок на тему «Законы Ньютона».
Три закона Ньютона
Динамика — раздел механики, изучающий причины движения тел и способы определения их ускорения. В нем движение тел описывается с учетом их взаимодействия.
Большой вклад в развитие динамики внес английский ученый Исаак Ньютон. Он первым смог выделить законы движения, которым подчиняются все макроскопические тела. Эти законы называют законами Ньютона, законами механики, законами динамики или законами движения тел.
Внимание! Законы Ньютона нельзя применять к произвольным телам. Они применимы только к точке, обладающей массой — к материальной точке.
Основное утверждение механики
Для описания движения тела можно взять любую систему отсчета. Обычно для этого используется система отсчета, связанная с Землей. Если какое-то тело меняет свою скорость, рядом с ним всегда можно обнаружить другое тело, которое на него действует. Так, если поднять камень и отпустить, он не останется висеть в воздухе, а упадет вниз. Следовательно, на него что-то подействовало. В данном случае сама Земля притянула камень к себе. Отсюда следует основное утверждение механики:
Основное утверждение механики
Изменение скорости (ускорение) тела всегда вызывается воздействием на него других тел.
Согласно утверждению, если на тело не действуют никакие силы, его ускорение будет нулевым, и оно будет либо покоиться, либо двигаться равномерно и прямолинейно (с постоянной скоростью).
Но в нашем мире мы не всегда это наблюдаем. И этому есть объяснение. Если тело покоится, оно действительно не меняет свою скорость. Так, мяч лежит на траве до тех пор, пока его не пнут. После того, как его пнут, он начинает катиться, но затем останавливается. Пока мяч катится, к нему больше не прикасаются. Казалось бы, согласно основному утверждению механики, мяч должен катиться вечно. Но этого не происходит, потому что на мяч действует сила трения, возникающая между его поверхностью и травой.
Основное утверждение механики можно проиллюстрировать в открытом космосе в месте, где сила притяжения космических тел пренебрежимо мала. Если в космосе придать телу скорость и отпустить, оно будет двигаться с такой скоростью по прямой линии до тех пор, пока на него не подействуют другие силы. Ярким примером служат межгалактические звезды, или звезды-изгои. Гравитационно они не связаны ни с одной из галактик, а потому движутся с постоянной скоростью. Так, звезда HE 0437-5439 удаляется от нашей галактики с постоянной скоростью 723 км/с.
Свободное тело — тело, на которое не действуют другие тела. Свободное тело либо покоится, либо движется прямолинейно и равномерно.
Первый закон Ньютона
Исаак Ньютон, изучая движение тел, заметил, что относительно одних систем отсчета свободные тела сохраняют свою скорость, а относительно других — нет. Он разделил их на две большие группы: инерциальные системы отсчета и неинерциальные. В этом кроется первый закон динамики.
Первый закон Ньютона
Существуют такие системы отсчета, называемые инерциальными, относительно которых тела движутся равномерно и прямолинейно или находятся в состоянии покоя, если на них не действуют другие тела или их действие компенсировано.
Примером инерциальной системы отсчета служит система отсчета, связанная с Землей (геоцентрическая). Другой пример — гелиоцентрическая система отсчета (связанная с Солнцем).
Неинерциальная система отсчета — система отсчета, в которой тела могут менять свою скорость при отсутствии на них действия других тел.
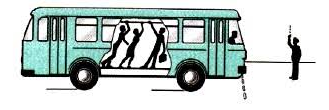
Примером неинерциальной системы отсчета служит автобус. Когда он движется равномерно и прямолинейно, стоящие внутри пассажиры находятся относительно него в состоянии покоя. Но когда автобус останавливается, пассажиры падают вперед, т. е. меняют свою скорость, хотя на них не действуют другие тела.
Второй закон Ньютона
В примере с автобусом видно, что пассажиры стараются сохранить свою скорость относительно Земли — инерциальной системы отсчета. Такое явление называется инерцией.
Инерция — явление, при котором тело сохраняет состояние покоя или равномерного прямолинейного движения.
Инертность — физическое свойство, заключающееся в том, что любое тело оказывает сопротивление изменению его скорости (как по модулю, так и по направлению).
Не все тела одинаково инертны. Вы можете взять мячик и придать ему большое ускорение. Но вы не можете придать такое же ускорение гире, хотя она обладает похожим размером. Но мячик и гиря различаются между собой массой.
Масса — скалярная физическая величина, являющаяся мерой инертности тела. Чем больше масса, тем больше инертность тела.
Масса обозначается буквой m. Единица измерения массы — кг. Прибор для измерения массы — весы.
Чтобы придать одинаковую скорость двум телам с разной инертностью, к телу с большей инертностью придется приложить больше силы. Попробуйте сдвинуть с места стол, а затем — шкаф. Сдвинуть с места стол будет проще.
Если же приложить две одинаковые силы к телам с разной инертностью, будет видно, что тело с меньшей инертностью получает большее ускорение. Если приставить к пружине теннисный шарик, а затем сжать ее и резко отпустить, шарик улетит далеко. Если вместо теннисного шарика взять железный, он лишь откатится на некоторое расстояние.
Описанные выше примеры показывают, что между силой, прикладываемой к телу, и ускорением, которое оно получает в результате прикладывания этой силы, и массой этого тела есть взаимосвязь. Она раскрывается во втором законе Ньютона.
Второй закон Ньютона
Сила, действующая на тело, равна произведению массы этого тела на ускорение, которое сообщает эта сила.
F = ma
где F — сила, которую прикладывают к телу, a — ускорение, которое сообщает эта сила, m — масса тела
Сила — количественная мера действия тел друг на друга, в результате которого тела получают ускорения.
Сила — векторная физическая величина. Обозначается F. Единица измерения — Н (Ньютон). Прибор для измерения силы — динамометр.
Пример №1. Определить, с какой силой действует Земля на яблоко, если, упав с ветки, оно получило ускорение 9,8 м/с2. Масса яблока равна 200 г.
Сначала переведем массу яблока в кг. 200 г = 0,2 кг. Теперь найдем силу, действующую на яблоко со стороны Земли, по второму закону Ньютона:
F = ma = 0,2 ∙ 9,8 = 1,96 (Н)
Равнодействующая сила
Иногда на тело действуют несколько сил. Тогда при описании его движения вводится понятие равнодействующей силы.
Определение
Равнодействующая сила — векторная сумма всех сил, действующих на тело одновременно.
R = F1 + F2 + F3 + …
В этом случае второй закон Ньютона формулируется так:
Второй закон Ньютона через равнодействующие силы
Если на тело действует несколько сил, то их равнодействующая R будет равна произведению массы на ускорение этого тела.
ma = R = F1 + F2 + F3 + …
Правила сложения сил и их проекций
|
Сложение двух сил, направленных вдоль одной прямой в одну сторону |
|
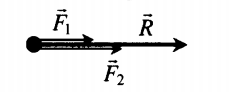 |
Если F1↑↑F2, то:
R = F1 + F2 Равнодействующая сила сонаправлена с обеими силами. |
|
Сложение двух сил, направленных вдоль одной прямой во взаимно противоположных направлениях |
|
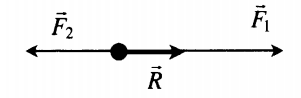 |
Если F1↑↓F2, то:
R = |F1 – F2| Равнодействующая сила направлена в сторону направления большей по модулю силы. |
|
Сложение двух сил, перпендикулярных друг к другу |
|
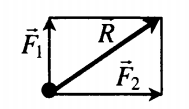 |
Если F1 перпендикулярна F2, то равнодействующая сила вычисляется по теореме Пифагора:
|
|
Сложение двух сил, расположенных под углом α друг к другу |
|
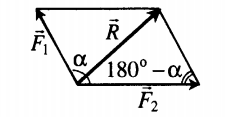 |
Если F1 и F2 расположены под углом α друг к другу, равнодействующая сила вычисляется по теореме косинусов:
|
|
Сложение трех сил |
|
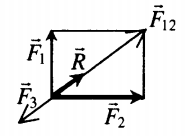 |
Способ сложения определяется правилами сложения векторов. В данном случае:
|
|
Сложение проекций сил |
|
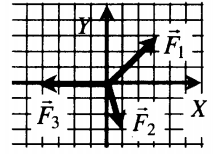 |
Проекция на ось ОХ:
F1x + F2x – F3x = 0 Проекция на ось OY: F1y – F2y = 0 |
Третий закон Ньютона
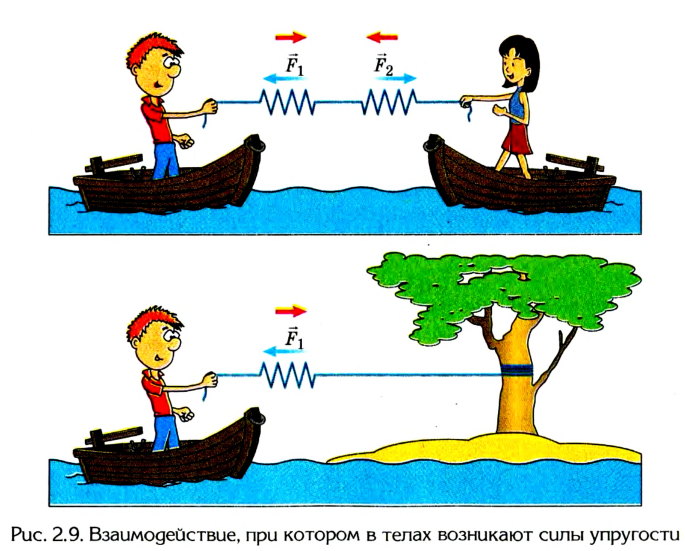
Когда одно тело действует на другое, начинается взаимодействие этих тел. Это значит, если тело А действует на тело В и сообщает ему ускорение, то и тело В действует на тело А, тоже придавая ему ускорение. К примеру, если сжать пружину руками, то руки будут чувствовать сопротивление, оказываемое силой упругости пружины. Если же, находясь в лодке, начать тянуть за веревку вторую лодку, то обе лодки будут двигаться навстречу друг другу. То есть, вы, находясь в своей лодке, тоже будете двигаться навстречу второй лодке.
Иногда на тело действует сразу несколько сил, но тело продолжает покоиться. В этом случае говорят, что силы друг друга компенсируют, то есть их равнодействующая равна нулю.
Две силы независимо от их природы считаются равными по модулю и противоположно направленными, если их одновременное действие на тело не меняет его скорости.
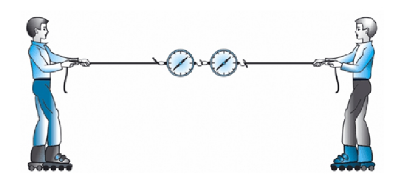
Примером такого явления служит ситуация, когда при перетягивании каната его никто не может перетянуть в свою сторону. Если взять два каната и присоединить между ними два динамометра, а затем начать игру в перетягивание, выяснится, что показания динамометра всегда будут одинаковыми. Это значит, что независимо от масс и придаваемых ускорений два взаимодействующих тела оказывают друг на друга равные по модулю силы. В этом заключается смысл третьего закона Ньютона.
Третий закон Ньютона
Силы, с которыми тела действуют друг на друга, равны по модулям и направлены по одной прямой в противоположные стороны.
FA = –FB
Используя второй закон Ньютона, третий закон механики можно переписать иначе:
m1a1 = –m2a2
Отсюда следует:
Отношение модулей ускорений a1 и a2 взаимодействующих друг с другом тел определяется обратным отношением их масс и совершенно не зависит от характера действующих между ними сил.
Пример №2. Определить ускорение, с которым движется Земля к падающему на нее яблоку. Масса яблока равна 0,2 кг. Ускорение свободного падения принять равной за 10 м/с2. Массу Земли принять равно 6∙1024 кг.
Согласно третьему закону Ньютона модули сил, с которыми взаимодействуют Земли и яблоко, равны. Поэтому:
F1 = F2
Отсюда:
m1a1 = m2a2
Пусть тело 1 будет яблоко, а тело 2 — Земля. Тогда a1 будет равно g. Отсюда ускорение, с которым движется Земля к падающему на нее яблоку, равна:
Задание EF17993
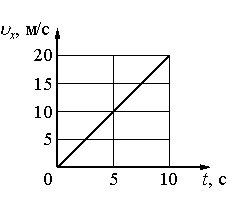
а) 2Н
б) 8 Н
в) 10 Н
г) 20 Н
Алгоритм решения
1.Записать исходные данные.
2.Проанализировать задачу.
3.Записать второй закон Ньютона.
4.Определить ускорение по графику проекции скорости от времени.
5.Подставить найденное ускорение в формулу второго закона Ньютона и произвести вычисления.
Решение
Запишем исходные данные:
Так как графиком скорости является прямая, непараллельная ось времени, тело движется с постоянным ускорением. Если ускорение постоянно, равнодействующая сил тоже будет постоянной в любой момент времени. Поэтому нам достаточно использовать координаты любой, более удобной для их определения точки. К примеру, в точке, соответствующей моменту времени 10 с.
Запишем второй закон Ньютона:
F = ma
Ускорение тела определяется как отношение изменения скорости ко времени, в течение которого эта скорость менялась. Согласно графику, за 10 секунд скорость изменилась на 20 м/с. Следовательно, ускорение равно:
a = 20/10 = 2 (м/с2)
Теперь можем вычислить равнодействующую сил:
F = ma = 5∙2 = 10 (Н)
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18915
Необходимо собрать экспериментальную установку, с помощью которой можно определить коэффициент трения скольжения стали по дереву. Для этого школьник взял стальной брусок с крючком. Какие два предмета из приведённого ниже перечня оборудования необходимо дополнительно использовать для проведения этого эксперимента?
а) деревянная рейка
б) динамометр
в) мензурка
г) пластмассовая рейка
д) линейка
Алгоритм решения
1.Проанализировать задачу. Выяснить, какие предметы необходимы для проведения опыта.
2.Вывести формулу для коэффициента трения.
3.Определить, какую величину нужно измерить, чтобы рассчитать коэффициент трения, и какой прибор для этого нужен.
Решение
Для определения коэффициента трения стали по дереву, нужен не только стальной груз, но и деревянная поверхность. То есть, понадобится деревянная рейка.
Сила трения определяется формулой:
Отсюда коэффициент трения равен:
Ускорение свободного падения известно. Массу можно измерить на весах, но весов в вариантах ответа нет. Силу трения можно измерить динамометром. Следовательно, для опыта нужны только динамометр и деревянная рейка. Рейка из пластика не понадобится, так как цели расчета коэффициента трения стали по пластику нет. Мензурка используется для определения объема жидкости. В данном опыте она тоже не нужна.
Ответ: аб
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17589
Система отсчёта, связанная с Землёй, считается инерциальной. В этом случае систему отсчёта, связанную с самолётом, можно считать инерциальной, если самолёт движется:
а) равномерно и прямолинейно, набирая высоту
б) с постоянным ускорением по горизонтали
в) равномерно, выполняя поворот
г) по взлетной полосе при взлете
Алгоритм решения
- Сформулировать первый закон Ньютона об инерциальных системах отсчета.
- На основании закона сделать вывод, при каких условиях система отсчета, связанная с самолетом, может считаться инерциальной.
- Проанализировать все 4 ситуации, приведенные в вариантах ответа.
- Выбрать тот вариант, который описывает ситуацию, не противоречащую условию, выведенному в шаге 2.
Решение
Первый закон Ньютона формулируется так:
«Существуют такие системы отсчета, называемые инерциальными, относительно которых тела движутся равномерно и прямолинейно или находятся в состоянии покоя, если на них не действуют другие тела или их действие компенсировано».
Чтобы система отсчета, связанная с самолетом, была инерциальной, она должна быть неподвижной или двигаться относительно Земли — инерциальной системы отсчета — равномерно и прямолинейно.
Когда самолет движется равномерно и прямолинейно, набирая высоту, самолет движется с собственным ускорением, которое компенсируется ускорением свободного падения. И это единственный верный ответ, так как:
- Самолет, двигаясь с постоянным ускорением по горизонтали, движется неравномерно, что противоречит условию.
- Самолет, двигаясь равномерно во время поворота, движется непрямолинейно (с центростремительным ускорением).
- Самолет, двигаясь по взлетной полосе при взлете, движется прямолинейно, но неравномерно, так как он разгоняется из состояния покоя.
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22791

Ответ: ( ± ) Н.
Внимание! Записывать ответ следует последовательностью цифр без запятых.
Алгоритм решения
1.Записать исходные данные.
2.Определить цену деления шкалы.
3.Записать значение измерения с учетом погрешности.
Решение
Из условий задачи известно, что погрешность равна цене деления шкалы. Цена деления шкалы определяется отношением разности двух ближайших числовых обозначений на шкале и количеству делений между ними. Возьмем ближайшие значения 1,0 и 1,5. Между ними 5 делений. Следовательно, цена деления шкалы динамометра равна:
Так как погрешность равна цене деления, она также равна 0,1 Н.
Стрелка динамометра показывает 1,1 Н. Следовательно, вес груза равен: 1,1±0,1. Но по условию задачи ответ нужно записать без запятых и прочих знаков. Следовательно, верный ответ: 1101.
Ответ: 1101
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17484
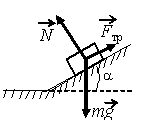
а) N cosα
б) N
в) N sinα
г) mg + Fтр
Алгоритм решения
- Запись второго закона Ньютона в векторном виде.
- Вывод формулы равнодействующей силы трения и силы тяжести.
- Нахождение модуля равнодействующей силы трения и силы тяжести.
Решение
Записываем второй закон Ньютона в векторном виде с учетом того, сто скорость тела не меняется (ускорение равно 0):
N + mg + Fтр = 0
Отсюда равнодействующая силы трения и силы тяжести равна:
mg + Fтр = –N
Следовательно, равнодействующая силы трения и силы тяжести направлена противоположно силе реакции опоры, но равна ей по модулю. Отсюда:
|mg + Fтр| = N
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18548
Алгоритм решения
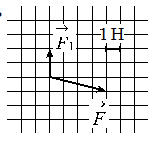
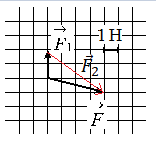
- Изобразить на рисунке второй вектор с учетом правил сложения векторов.
- Записать геометрическую формулу для расчета модуля вектора по его проекциям.
- Выбрать систему координат и построить проекции второй силы на оси ОХ и ОУ.
- По рисунку определить проекции второй силы на оси.
- Используя полученные данные, применить формулу для расчета вектора по его проекциям.
Решение
Построим вектор второй силы. Его начало должно совпадать с концом вектора первой силы, а его конец — с концов равнодействующей этих сил. Этот вывод следует из сложения векторов правилом треугольника.
Модуль вектора равен корню из суммы квадратов его проекций на оси ОХ и ОУ:
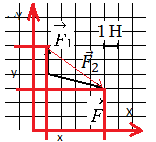
Выберем систему координат и построим проекции второй силы на оси ОХ и ОУ:
Согласно рисунку, проекция второй силы на ось ОХ равна: x = 4 (Н). Ее проекция на ось ОУ равна: y = 3 (Н).
Подставим известные данные в формулу и вычислим модуль вектора второй силы:
Ответ: 5
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 16.5k
Законы Ньютона
Три закона Ньютона лежат в основе классической физики, хотя за прошедшие годы стало понятно, что они — лишь частный случай теории относительности. В нашей статье разбираем формулы и определения законов Ньютона простыми словами
Вплоть до XVII века мировая наука жила в условиях почти религиозной веры в постулаты, заданные великим философом Аристотелем. Покушение на них воспринималось как ересь и безжалостно наказывалось. Доходило даже до инквизиции. В этих условиях деятельность Галилея, Декарта, Ньютона была не только научным, но и человеческим подвигом. Их открытия сегодня могут быть даже переформулированы, не теряя своего смысла и значения.
История открытия законов Ньютона
Про то, как Ньютон открыл закон всемирного тяготения, знают практически все. Это та самая история про яблоко, которое упало ему на голову. На самом деле, яблоко на голову Ньютона не падало, но все это происходило в осеннем яблоневом саду, где яблоки действительно падали.
А вот как были сформулированы три знаменитых закона Ньютона, ставшие фундаментом классической механики, знают далеко не все. Впервые формулировки этих законов появились в книге Ньютона «Математические начала натуральной философии» (1687 год). Название этого труда достаточно известно именно потому, что в них впервые Ньютон дал определения всех трех законов.
Но перед тем, как формулировки этих законов были напечатаны, много чего произошло. Начиная с Древней Греции, многие мыслители пытались облечь в слова фундаментальные законы движения. Потребовалось несколько веков, чтобы сложились предпосылки для этого. Ближе всего к этому подошел Галилей. Но и ему помешали господствующие в научном сообществе иллюзии. Все были безоговорочно уверены, что небесные тела движутся строго по круговым орбитам, потому что это творение Бога, и это творение должно быть совершенно и безупречно. Пошатнуть эти иллюзии удалось Кеплеру. Но и он в своих размышлениях пошел не туда.
Гениальность Ньютона заключается в том, что, изучая труды своих великих предшественников, он смог разглядеть неочевидные вещи, которые даже нам кажутся парадоксальными. Именно Ньютон выдвинул революционную идею, что если на тело не действуют никакие силы, то тело может двигаться прямолинейно и равномерно. В условиях Земли это невозможно, так как действует сила земного тяготения. А вот вне Земли — это обычное дело.
Долгие годы размышлений, черновых набросков, сомнений, которые он выражал в письмах своим коллегам, завершились блестящими формулировками всех трех законов. И эти законы по праву носят имя Ньютона. О каждом из этих законов можно написать отдельную статью — настолько велико и многогранно их значение.
Первый закон Ньютона
Первый закон Ньютона еще называют закон инерции. Фактически он был открыт Галилеем, но именно Исаак Ньютон дал точную его формулировку и включил в число основных законов механики.
Определение
Существуют такие системы отсчёта, называемые инерциальными, относительно которых материальная точка при отсутствии внешних воздействий сохраняет величину и направление своей скорости неограниченно долго. Формулы первый закон Ньютона не имеет.
Второй закон Ньютона
Действие второго закона Ньютона мы можем часто наблюдать в жизни. Возьмём теннисную ракетку и мяч. Если ударить ракеткой по мячу, то мяч приобретёт ускорение равное отношению равнодействующей всех сил к массе.
Определение
В инерциальных системах отсчёта ускорение, приобретаемое материальной точкой, прямо пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки.
Формула
Сила трения
Единицы измерения силы трения, от чего она зависит и какие виды существуют
подробнее
Третий закон Ньютона
Третий закон Ньютона объясняет, как, например, двигаются утки. Они находятся во взаимодействии с водой, отталкивая ее назад лапками, а сами благодаря ответному действию двигаются вперед.
Определение
Материальные точки взаимодействуют друг с другом силами, имеющими одинаковую природу, направленными вдоль прямой, соединяющей эти точки, равными по модулю и противоположными по направлению.
Формула
Популярные вопросы и ответы
Отвечает Андрей Найденов, преподаватель физики и математики в онлайн-школе TutorOnline.
Сколько законов Ньютона изучают в школе?
В школе изучают четыре закона Ньютона. Первые три являются фундаментом классической динамики. С их помощью можно описать любое движение тела, которое движется со скоростью, значительно меньшей скорости света.
Особняком стоит закон всемирного тяготения. Он лежит в основе классической теории гравитации. Этот закон перекликается со вторым законом, касающемся соотношения между ускорением тела, его массой и действующей на него силой. Но все же это разные законы. Так как второй закон Ньютона более универсален, чем закон всемирного тяготения.
Как и где выполняются законы Ньютона в жизни?
Эти законы настолько фундаментальны, что увидеть их можно практически всюду. Пуля из ружья летит туда, куда толкают ее пороховые газы. Ракета летит туда, куда толкают ее продукты горения ракетного топлива. Мяч летит туда, куда пинает его футболист. Это примеры действия первого закона Ньютона.
Второй закон связан с ускорением, которое приобретает тело под действием силы, действующей на это тело. Например, болид «Формулы 1» разгоняется намного быстрее, чем простой серийный легковой автомобиль. На них действуют разные по величине силы тяги их двигателей. Мощность двигателя в спортивной машине на порядок выше, чем у обыкновенной.
Третий закон Ньютона устанавливает закон взаимодействия тел. Сила действия равна силе противодействия. Например, если чашка кофе стоит на столе и не проваливается сквозь него на пол, значит, стол оказывает достаточное противодействие силе тяжести, действующей на чашку. В результате эти две силы уравновешивают друг друга, и чашка стоит на столе без какого-либо движения.
Как Ньютон изменил третий закон Кеплера?
Законы Кеплера — это три соотношения, которые выведены Кеплером на основе астрономических наблюдений. Эти законы описывают идеализированную планету, движущуюся по круговой орбите. Опираясь на третий закон Кеплера, Ньютон сформулировал закон всемирного тяготения. При этом третий закон Кеплера в рамках теории всемирного тяготения Ньютона является решением частной задачи, которая касается двух тел. Другими словами, третий закон Кеплера стал частью более общей теории Ньютона.
Содержание:
Законы ньютона:
Ежедневно мы наблюдаем самые разнообразные механические движения: идут люди и едут машины, летят самолеты и птицы, вращаются колеса велосипедов, автомобилей и карусель в парке.
Почему движется, например, автомобиль? Каждый из вас сразу скажет: потому что работает двигатель автомобиля. Но давайте представим, что колеса автомобиля не соприкасаются с поверхностью Земли (рис. 24), а двигатель работает… Колеса вращаются, а привычное движение автомобиля не происходит. Почему?
Почему для движения автомобиля со скоростью, например, 90
Чтобы ответить на эти вопросы, нужно знать причины, вызывающие механическое движение или изменение состояния движения тел.
Наши жизненные наблюдения, многочисленные опыты показывают, что изменение скорости тела всегда вызывается воздействием на данное тело каких-либо других тел.
Для описания взаимодействий тел друг с другом в физике вводится понятие «сила» (греч. dynamis). Отсюда и название данного раздела — динамика.
Динамика — раздел механики, изучающий различные виды механического движения с учетом взаимодействий между телами.
В динамике решаются две основные задачи:
- устанавливаются законы взаимодействия тел друг с другом;
- определяется влияние этих взаимодействий на механическое движение тел.
Первый закон механики
Некоторое время в физике никто не подвергал сомнению мысль Аристотеля, высказанную им в работе «Механика»: «Движущееся тело останавливается, если сила, толкающая его, прекращает свое действие».
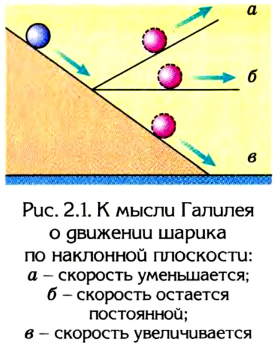
Это ошибочное утверждение, опирающееся на обыденное восприятие явлений природы, впервые опроверг Галилей, сделавший важнейший для науки вывод о вечности, неуничтожаемости движения.
Анализируя движение шарика по наклонной плоскости (рис. 2.1), он писал: «…скорость, которую однажды сообщили телу, будет строго сохранятся, поскольку устранены внешние причины ускорения и замедления, — условие, которое обнаруживается только на горизонтальной плоскости, ибо в случае движения по наклонной плоскости вниз уже существует причина ускорения, в то время как при движении по наклонной плоскости вверх налицо замедление; из этого следует, что движение по горизонтальной плоскости вечно, ибо, если скорость будет постоянной, движение не может быть уменьшено или ослаблено, а тем более уничтожено».
Этот фундаментальный вывод Г. Галилея использовал И. Ньютон в своем знаменитом труде «Математические начала натуральной философии» (1687 г.) при формулировании первого закона динамики (закона инерции):
Всякое тело продолжает удерживаться в своем состоянии покоя или равномерного и прямолинейного движения, поскольку оно не принуждается приложенными силами изменить это состояние.
А. Эйнштейн и Л. Инфельд в работе «Эволюция физики» проще сформулировали этот закон: «Всякое тело сохраняет состояние покоя или равномерного прямолинейного движения, если только оно не вынуждено изменить его под влиянием действующих сил».
Тело большой массы сложнее разогнать до некоторой скоро сти, чем тело малой массы, так как оно более инертно.
Движение шарика по наклонной плоскости рассматривали относительно поверхности Земли, которая считалась неподвижной. Итак, первый закон динамики установлен для систем отсчета, считающихся неподвижными или движущихся относительно последних прямолинейно, равномерно и поступательно. Такие системы называются инерциальными. Инертность тел проявляется в сохранении ими своего состояния покоя или прямолинейного равномерного движения до того времени, пока какая-нибудь внешняя причина не выведет их из этого состояния.
Тело большой массы сложнее разогнать до некоторой скоро сти, чем тело малой массы, так как оно более инертно.
Сущность инертности, которая свойственна всем телам, заключается в том, что для изменения скорости тела необходимо взаимодействие с другим телом. Из двух взаимодействующих тел более инертно то, которое медленнее изменяет свою скорость.
Теоретически инерциальных систем отсчета может быть много, поскольку всегда можно представить тела, которые пребывают в состоянии покоя или движутся равномерно и прямолинейно (без ускорения), и связать с ними соответствующее количество систем координат и устройств для отсчета времени (часов).
Понятие инерциальной системы отсчета является научной абстракцией. В реальной жизни таких систем нет, поскольку в природе не существует абсолютно неподвижных тел (например, тело, которое неподвижно относительно Земли, вращается вместе с ней вокруг земной оси, вокруг Солнца и т. д.).
При решении задач динамики систему отсчета связывают с реальным телом, например Землей или Солнцем.
Поэтому при решении задач динамики систему отсчета связывают с реальным телом. Тогда она может рассматриваться как инерциальная с той или иной степенью приближения.
Так, например, при решении задач в небесной механике и космонавтике с высокой степенью точности инерциальной можно считать гелиоцентрическую систему с началом отсчета на Солнце и осями, направленными на некоторые звезды. Для решения большинства технических задач в качестве инерциальной берут систему отсчета, жестко связанную с Землей.
Первый закон Ньютона
Из личного опыта каждый из нас знает, что скорость тела по величине и направлению может изменяться только под действием других тел. Например, футбольный мяч покоится на ровной поверхности, если по нему не ударить ногой (рис. 25).
Рис. 25
При изучении физики в 7-м классе вы познакомились с утверждением древнегреческого философа Аристотеля, считавшего, что покой — естественное состояние тела, а движение — насильственное состояние, которое необходимо все время поддерживать.
Рассмотрим, какие причины определяют покой и равномерное прямолинейное движение тела.
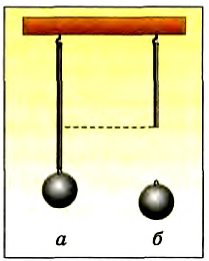
Подвесим шарик на резиновом шнуре (рис. 26, а). Он висит неподвижно, взаимодействуя со шнуром и Землей. Если перерезать шнур, то шарик начнет падать вертикально вниз под действием притяжения Земли, а деформация шнура без воздействия на него шарика станет равной нулю (рис. 26, б).
Рис. 26
Значит, шарик находился в покое потому, что действие резинового шнура компенсировало (уравновешивало) притяжение Земли.
Какие бы тела мы не рассматривали, состояние покоя любого тела сохраняется, если действие на него одних тел компенсируется действием других тел.
Не столь очевидны причины, по которым тело движется с постоянной скоростью, и, возможно, многие из вас будут согласны с мнением Аристотеля о том, что равномерное движение нужно все время поддерживать. Это согласуется с нашим практическим опытом: например, велосипед движется с постоянной скоростью по ровной горизонтальной дороге, если человек крутит педали. Вероятно, поэтому представления Аристотеля господствовали в науке почти 2000 лет.
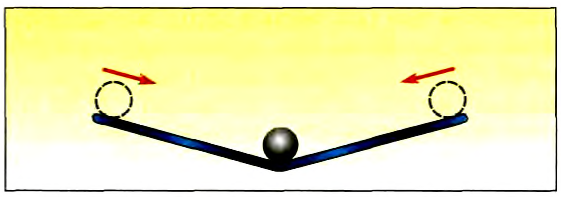
В XVIl в. движение тел начал изучать итальянский ученый Галилео Галилей. В одном из опытов Галилей исследовал движение шара по двум наклонным плоскостям (рис. 27). Он наблюдал, что вниз шар движется ускоренно, а вверх — замедленно, причем в обоих случаях: чем меньше угол наклона плоскости, тем меньше ускорение шара.
Рис. 27
Галилей предположил, что если шар будет двигаться по горизонтальной плоскости, то его ускорение будет равно нулю и, следовательно, движение шара с постоянной скоростью будет продолжаться как угодно долго.
Но на практике шар всегда останавливался (так как двигался замедленно), хотя, чем более гладкой была плоскость, тем дольше продолжалось движение. Галилей установил, что движение шара замедляется из-за сопротивления воздуха и трения о поверхность плоскости.
Таким образом Галилей пришел к выводу:
- тело будет двигаться как угодно долго с постоянной скоростью по идеально гладкой горизонтальной плоскости в безвоздушном пространстве, так как в этом случае воздействия на тело Земли и плоскости компенсируют друг друга, а сопротивление движению отсутствует.
То же самое наблюдалось бы при отсутствии любых взаимодействий тела с другими телами (нет притяжения Земли, нет плоскости, среды и т. п.), хотя этот идеальный вариант трудно представить.
Скорость, с которой при этом движется данное тело, является результатом его предшествующих взаимодействий с другими телами, а ее численное значение и направление зависят от выбранной системы отсчета.
Инерцией (лат. iners — неподвижный, бездеятельный) называется явление сохранения скорости движения тела неизменной (как по модулю, так и по направлению) при отсутствии внешних воздействий на тело.
Поэтому вывод Галилея позднее стали называть законом инерции.
Впоследствии Исаак Ньютон, обобщая результаты работ Галилея и других ученых, а также своих исследований, сформулировал общие законы движения. На первое место среди этих законов он поставил закон инерции, который и стали называть первым законом Ньютона. Простая и близкая к первоначальной формулировка этого закона следующая:
тело движется равномерно и прямолинейно (или покоится), если на него не действуют другие тела (или действие других тел скомпенсировано).
Можно ли проверить выполнение этого закона в земных условиях? Всегда ли он выполняется?
В окружающем нас мире на любое тело действует хотя бы притяжение Земли, т. е. полное отсутствие воздействий невозможно.
Но множество тел вокруг нас покоится потому, что действие на них одних тел скомпенсировано действием других. В некоторых случаях можно наблюдать и равномерное прямолинейное движение тел, т. е. закон инерции выполняется при определенных условиях.
В то же время можно вспомнить и такие случаи, когда и при компенсации воздействий на данное тело других тел этот закон не выполняется.
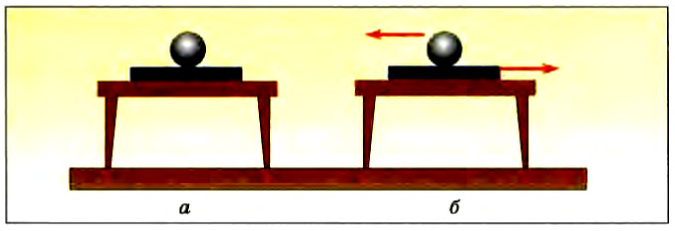
Рассмотрим пример с шаром, который покоится на гладкой неподвижной горизонтальной доске, так как притяжение Земли компенсируется воздействием доски (рис. 28, а). Если потянуть доску в горизонтальном направлении, то можно наблюдать движение шара относительно нее (рис. 28, б). Скорость шара изменяется, хотя воздействия Земли и доски по-прежнему скомпенсированы. В чем дело?
Рис. 28
Дело в том, что любое механическое движение невозможно описать без указания системы отсчета. Шар покоился в неподвижной системе отсчета, связанной с доской, а при воздействии на доску эта система отсчета стала двигаться с ускорением. Множество подобных опытных фактов указывает на то, что первый закон Ньютона выполняется только в определенных системах отсчета.
Поэтому в настоящее время в физике принята следующая формулировка первого закона Ньютона:
- существуют такие системы отсчета (называемые инерциальными), относительно которых поступательно движущееся тело сохраняет свою скорость постоянной (или покоится), если на него не действуют другие тела (или действие других тел скомпенсировано).
Важно понимать, что инерциальная система отсчета — это модель, используемая в физике. Почему это так?
В 7-м классе вы узнали, что точность измерения любой физической величины зависит, прежде всего, от цены деления измерительного прибора. Это относится и к определению значения скорости тела. Кроме того, на практике скорость движения тел практически всегда непостоянна, и различными приборами определяется только ее среднее значение за некоторый промежуток времени.
Например, водитель контролирует скорость движения автомобиля по спидометру с ценой деления, равной 10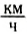
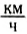
Значит, говоря о постоянном значении скорости тела, нужно понимать, что скорость измерена реальным прибором с определенной точностью.
Инерциальная система отсчета является моделью реальной системы отсчета, движущейся со скоростью, значение которой определяется как постоянное при данной точности измерений.
Таким образом, первый закон Ньютона является постулатом, т. е. утверждением о существовании моделей — инерциальных систем отсчета, и не может быть полностью проверен экспериментально.
Роль первого закона Ньютона в механике в том, что он определяет условия, при которых реальные системы отсчета можно считать инерциальными.
Почему это очень важно? Потому, что практически все физические законы выполняются при определенных условиях. В следующих параграфах вы будете изучать и учиться применять второй и третий законы Ньютона, которые выполняются только в инерциальных системах отсчета.
Главные выводы:
- Инерция — явление сохранения скорости тела постоянной в отсутствии внешних воздействий на него.
- Система отсчета называется инерциальной, если при отсутствии воздействий на данное тело (или их компенсации) скорость тела относительно этой системы отсчета не изменяется.
- Первый закон Ньютона позволяет определить, можно ли считать выбранную систему отсчета инерциальной.
Второй закон механики
Второй закон механики Ньютона устанавливает взаимосвязь между кинематическими и динамическими величинами. Чаще всего он формулируется так: ускорение, которое приобретает тело под действием силы, прямо пропорционально силе, обратно пропорционально массе тела и имеет то же направление, что и сила:
где 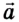
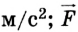
Если по этой формуле определить силу 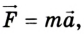
Второй закон механики Ньютона:
И. Ньютон сформулировал второй закон механики несколько иначе, воспользовавшись понятием количества движения (импульса тела).
Импульс или количество движения (от лат. impulsus — удар, толчок) — произведение массы тела на его скорость — одна из мер механического движения: 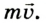
Поскольку ускорение 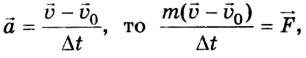
Изменение количества движения тела пропорционально действующей силе и происходит в направлении той прямой, вдоль которой эта сила действует.
По Ньютону второй закон механики звучит так: изменение количества движения тела пропорционально приложенной движущей силе и происходит в направлении той прямой, по которой эта сила действует.
Действие силы не порождает само движение, а лишь изменяет его; сила вызывает изменение скорости (ускорение), а не саму скорость.
Второй закон механики Ньютона обобщил исключительно важный факт: действие силы не порождает само движение, а лишь изменяет его; сила вызывает изменение скорости (ускорение), а не саму скорость.
- Заказать решение задач по физике
Второй закон Ньютона
Как вы уже знаете, изменение скорости тела происходит под действием силы, а быстроту изменения скорости определяет ускорение. Необходимо выяснить, как зависит ускорение тела от действующей на него силы.
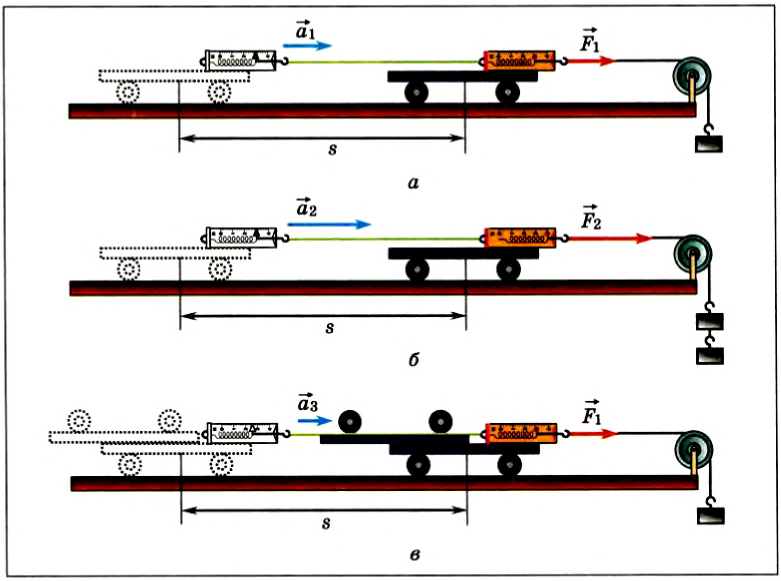
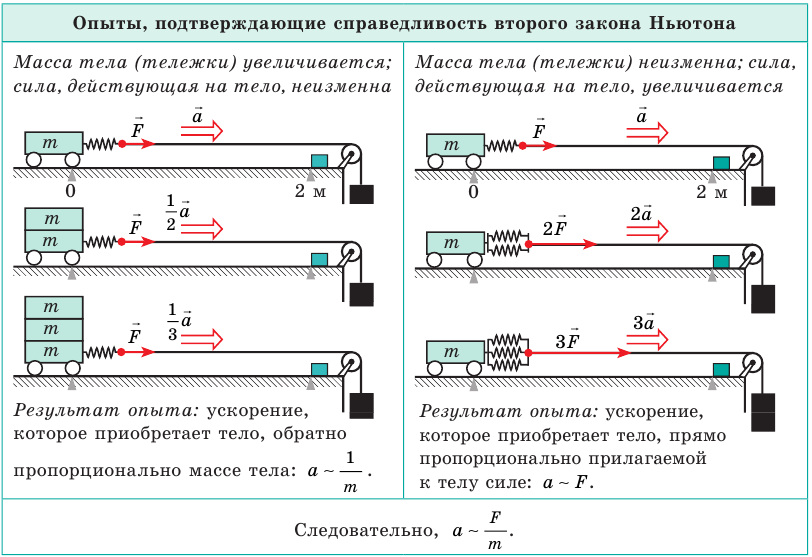
Проведем опыт на неподвижном горизонтальном столе, т. е. в инерциальной системе отсчета. Установим легкую тележку на длинные горизонтальные рельсы, по которым она может двигаться почти без трения. Прикрепим к тележке динамометр, к концу которого присоединим перекинутую через блок нить с грузом (рис. 44, а).
Рис. 44
В вертикальном направлении сила тяжести тележки с динамометром уравновешивается силой реакции рельс. Пренебрегая трением и сопротивлением воздуха, можно считать, что тележка движется вдоль стола с ускорением только под действием горизонтальной силы натяжения нити. Модуль этой силы определяется по показаниям динамометра.
Опыт показывает, что направление вектора ускорения 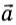
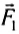
Если увеличить подвешенный к нити груз, то динамометр показывает большее значение действующей на тележку силы 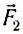
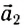
Таким образом, приобретаемое тележкой ускорение по модулю прямо пропорционально действующей, силе и совпадает с ней по направлению.
Изменим условия опыта. Поместим на первую тележку вторую (одинаковой с ней массы) и подберем массу груза так, чтобы показание динамометра вновь стало F1 (рис. 44, в). Масса движущейся тележки с динамометром в первом опыте ml =M + m, а сейчас m3 = 2М + m. При этих условиях тележка с общей массой m3 проходит тот же путь за большее время t3, т. е. ее ускорение m3 меньше . Из расчетов следует, что модуль ускорения 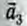
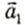
Следовательно, при той же действующей силе модуль ускорения тележки уменьшается во столько же раз, во сколько раз возрастает ее масса.
Многочисленные опыты с различными телами и в других условиях показывают, что, чем больше масса любого тела, тем труднее изменить его скорость на определенную величину, действуя постоянной силой.
Поэтому массу называют основной динамической характеристикой тела — количественной мерой его инертности, т. е. способности тела приобретать ускорение под действием данной силы.
Таким образом, ускорение тела прямо пропорционально действующей силе и обратно пропорционально массе:
Исаак Ньютон, исследуя изменение скорости тела в зависимости от действующей силы, впервые установил подобную закономерность больше 300 лет назад.
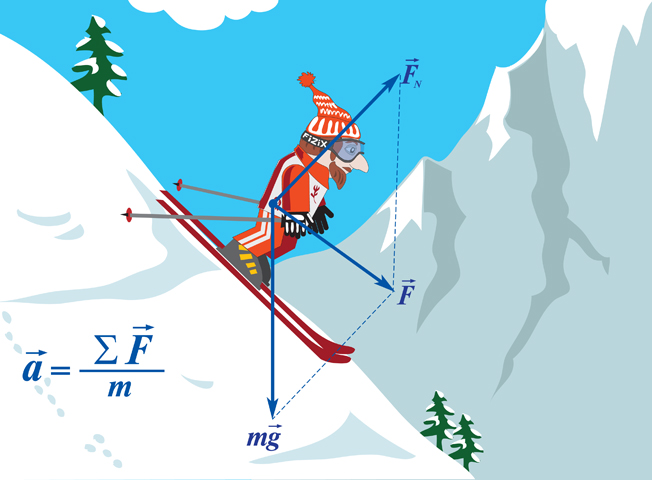
В окружающем мире на тело обычно действует несколько сил, и многочисленные эксперименты в различных условиях (с учетом сил трения и сопротивления; тело на горизонтальной опоре и т. д.) позволили установить, что ускорение тела определяется равнодействующей (результирующей) всех действующих на него сил.
Поэтому принята следующая формулировка второго закона Ньютона:
ускорение, приобретаемое телом, прямо пропорционально равнодействующей всех сил, действующих на тело, и обратно пропорционально его массе:
Для упрощения длинной последовательности n однотипных слагаемых в математике используется специальный знак суммы:
где 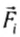
Второй закон Ньютона выполняется только в инерциальных системах отсчета. Следовательно, используя первый закон Ньютона, сначала необходимо выбрать инерциальную систему отсчета, а затем можно в ней применять для расчета ускорения тела второй закон Ньютона.
Часто удобнее использовать второй закон Ньютона в виде
записав в правой части все действующие на тело силы. Поскольку при расчетах целесообразно проводить математические операции со скалярными величинами, то при решении задач записывают второй закон Ньютона для проекций на оси выбранной инерциальной системы отсчета:
- max = Flx+ F2x +F3x+… + Fnx;
- may = Fly+ F2y+F3y+… + Fny.
Второй закон Ньютона позволяет рассчитать ускорение тела в инерциальной системе отсчета при самых разнообразных движениях: при разбеге человека по дорожке (рис. 45) и его катании на карусели, при движении транспорта и выполнении самолетом фигур высшего пилотажа, при вращении деталей станка и старте космического корабля.
Если скорость и координаты тела в начальный момент времени известны, а по второму закону Ньютона определяется его ускорение, можно решить основную задачу механики — определить скорость и координаты тела в любой момент времени.
Главные выводы:
- Модуль ускорения тела прямо пропорционален модулю равнодействующей всех сил и обратно пропорционален массе тела.
- Направление ускорения тела совпадает с направлением равнодействующей всех сил, действующих на него.
- Второй закон Ньютона выполняется только в инерциальных системах отсчета.
Третий закон механики
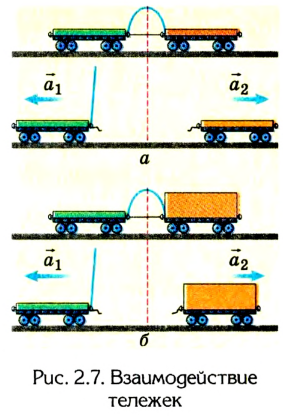
Согласно утверждению Ньютона сила является следствием взаимодействия двух или большего количества тел. Если одно тело действует на другое, то обязательно и второе тело действует на первое, т. е. если есть действие, то есть и противодействие. Понятия действия и противодействия условны, поскольку каждое из них может быть и тем и другим. Возьмем две одинаковые по мае-
се тележки и к одной из них прикрепим плоскую пружину, сжатую прочной нитью. Другую тележку поставим так, чтобы она касалась этой пружины (рис. 2.7, а).
Если нитку, которой сжата пружина, отпустить или поджечь, то пружина распрямится и обе тележки придут в движение. Это означает, что они приобрели ускорение:
Поскольку масса тележек одинакова, то одинаковы их ускорения и расстояния, которые они проходят за определенное время.
Если на одну из тележек положить некоторый груз (увеличить ее массу) и повторить опыт (рис. 2.7, б), то тележка, которая имеет большую массу, пройдет меньшее расстояние.
Таким образом, при взаимодействии двух тел соотношение модулей их ускорений равно обратному соотношению их масс:
Ускорения взаимодействующих тел имеют противоположные направления, поэтому в векторной форме можно записать
Произведение массы тела на его ускорение равно приложенной к телу силе. 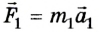
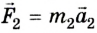
Это равенство и является математическим выражением третьего закона механики. Ньютон его сформулировал так:
- действию всегда есть равное и противоположное противодействие; действия двух тел друг на друга равны между собой и направлены в противоположные стороны.
Существует и такая формулировка: любое действие одного тела на другое имеет характер взаимодействия; силы, с которыми взаимодействуют тела, всегда одинаковы и противоположно направлены.
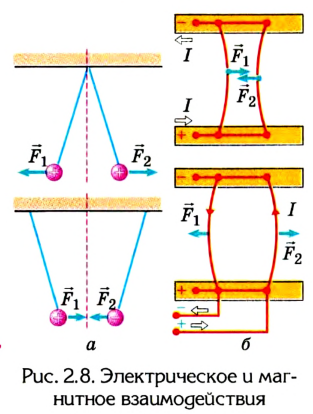
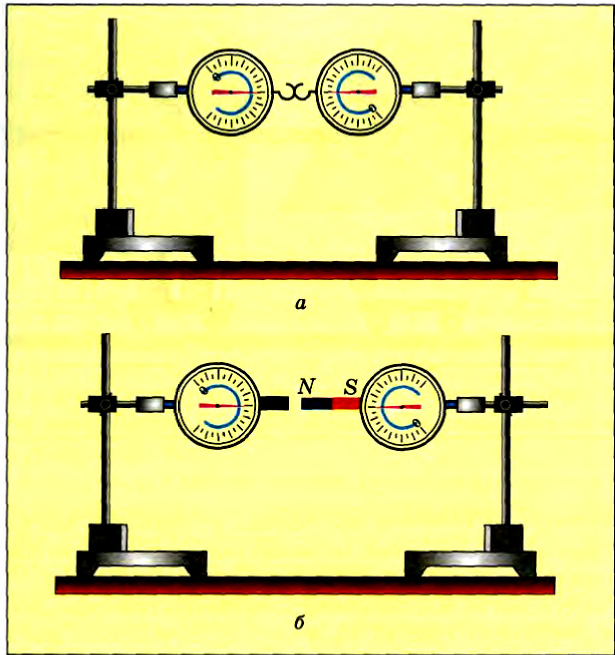
Опыты подтверждают, что силы любой природы во время взаимодействия тел возникают попарно, имеют противоположные направления и одинаковы по модулю. На рисунке 2.8 показаны электрическое (а) и магнитное (б) взаимодействия, а на рисунке 2.9 — взаимодействия в случае возникновения в телах силы упругости (имеют электромагнитную природу).
В третьем законе механики речь идет о силах, приложенных к разным телам. Поэтому, нельзя считать, что сумма сил, приложенных к каждому из взаимодействующих тел, равна нулю. Равнодействующую сил можно находить лишь в том случае, когда силы приложены к одному телу.
Третий закон Ньютона
По второму закону Ньютона можно рассчитать ускорение движущегося тела и при известных начальных условиях найти его скорость и координаты в любой момент времени.
Но на практике недостаточно знать закон движения, например, автомобиля. Важно знать также силу, с которой он действует на опору, чтобы рассчитать, например, конструкцию моста, по которому автомобиль движется. Следовательно, необходимо установить, как соотносятся между собой силы, с которыми действуют друг на друга тела при взаимодействии.
Проведем некоторые опыты и исследуем этот вопрос.
Закрепим в двух штативах динамометры, соединенные крючками (рис. 47, а). Если потянуть в горизонтальном направлении поочередно за один динамометр, за другой или за оба вместе, то в каждом опыте показания приборов равны. Значит, силы, с которыми динамометры действуют друг на друга, равны по модулю и по условиям опыта направлены в противоположные стороны.
Присоединим к одному динамометру кусок железа, а к другому — магнит. При взаимодействии железа и магнита на динамометрах также установятся одинаковые показания (рис. 47, б).
Рис. 47
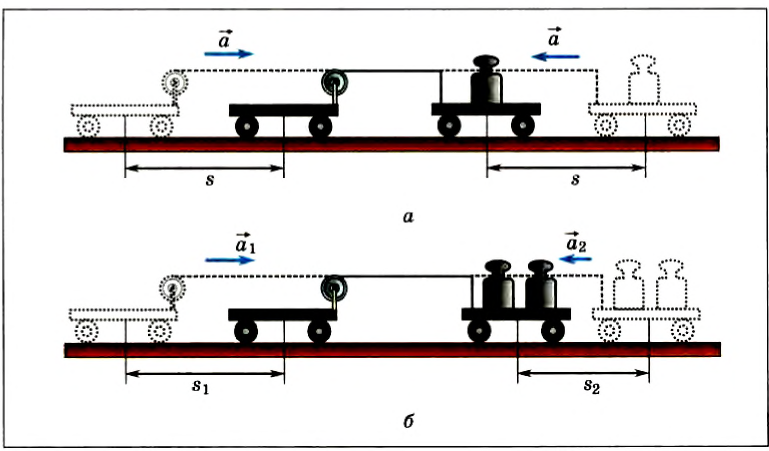
Рассмотрим другой опыт. Пусть на гладких горизонтальных рельсах, закрепленных на неподвижном столе, расположены две тележки одинаковой массы. Закрепим на одной из них моторчик, на ось которого при его работе будет наматываться нить, привязанная к другой тележке. На тележку без моторчика поставим дополнительную гирю, масса которой равна массе моторчика, чтобы общие массы тележек были равны.
При работающем моторчике обе тележки устремляются навстречу друг другу с одинаковыми ускорениями. Их можно рассчитать, измерив пройденный путь и время его прохождения (рис. 48, а).
Если массу одной из тележек изменить, то обратно пропорционально массе изменится ее ускорение (рис. 48, б). А для модулей ускорений двух тележек, если их массы различны, выполняется следующее соотношение:
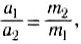
Если учесть, что по второму закону Ньютона m1a1=F1 и m2a2 = F2, а ускорения тележек направлены в противоположные стороны, то можно записать:
Какие бы примеры взаимодействия тел не рассматривались, всегда выполняется установленный Ньютоном третий закон:
силы, с которыми два тела действуют друг на друга, одной природы, равны по модулю, противоположны по направлению и направлены вдоль одной прямой.
Рис. 48
Из третьего закона Ньютона следует, что силы всегда возникают парами и при взаимодействии тел равноправны.
Значит, например, с какой силой каждого человека притягивает наша огромная планета Земля, с такой же силой и человек притягивает Землю.
Третий закон Ньютона выполняется для любых взаимодействий, в том числе и для столкновений тел.
Почему, например, в районах больших аэропортов принимаются специальные меры для удаления из воздушного пространства любых птиц? Столкновение даже небольшой птицы с обшивкой самолета, стеклом иллюминатора или частью двигателя может вызвать их разрушение.
Ускорение и деформация тел при взаимодействии зависят от их массы и от того, с какими другими телами есть еще взаимодействие в данный момент.
Рассмотрим, например, взаимодействие одинаковых бильярдных шаров при различных условиях (рис. 49). Шар, лежащий посередине стола, взаимодействует с опорой и притягивается Землей. Причем силы тяжести и упругости перпендикулярны плоскости стола и равны по модулю. Можно показать, что при центральном ударе по одному шару такого же второго шара бильярдные шары практически обмениваются скоростями (рис. 50).
Если шар лежит у бортика стола, взаимодействуя добавочно и с ним (см. рис. 50), то результат удара совершенно другой. Хотя при этом массы тел не изменились, и скорость движущегося шара перед взаимодействием такая же.
Экспериментально установлено: в каких бы разнообразных взаимодействиях тело не участвовало, третий закон Ньютона выполняется для каждой пары взаимодействующих тел.
Таким образом, третий закон Ньютона утверждает, что силы возникают всегда парами. Любое взаимодействие необходимо характеризовать двумя силами, которые хотя и равны по модулю, но противоположны по направлению и действуют на разные тела.
Главные выводы
- Силы взаимодействия двух тел равны по величине, противоположно направлены и приложены к разным телам.
- Третий закон Ньютона выполняется в инерциальных системах отсчета.
- Результат взаимодействия двух тел зависит от того, в каких еще взаимодействиях каждое из них участвует.
Значение законов Ньютона и принцип относительности в механике
Иногда в разговоре с не очень компетентными людьми можно услышать, что для современного человека важнее последние достижения физической науки, чем законы классической физики, сформулированные Ньютоном больше 300 лет назад.
Такие рассуждения не корректны. Законы Ньютона используются в физике для описания движения различных объектов не только в механике, но и в других разделах физики, в которых изучаются тепловые процессы, электрические и магнитные явления, колебательные системы и т. д.
Законы Ньютона называют основными законами механики, потому что они лежат в основе динамики, в которой устанавливаются количественные зависимости между характером движения тел и действующими на них силами.
Эти законы определяют общие существенные закономерности, свойственные любым механическим движениям. Но механическое движение всегда относительно, а следовательно, для его описания необходимо выбрать систему отсчета.
Первый закон Ньютона позволяет выбрать инерциальную систему отсчета, в которой движение тел однозначно определяется вторым и третьим законами Ньютона.
На основании второго закона Ньютона можно рассчитать ускорение тела при действии на него заданных сил.
Согласно третьему закону Ньютона силы возникают парами при взаимодействии тел, причем модули этих сил равны, независимо от причины, вызвавшей взаимодействие тел.
Законы Ньютона выполняются лишь при определенных условиях. Они хорошо описывают движение макроскопических тел со скоростями, много меньшими скорости света. Поэтому области применения законов Ньютона в окружающем человека мире очень обширны.
Их используют для расчетов результатов самых разнообразных взаимодействий и явлений на Земле и в космосе.
Законы Ньютона применяются при разработках новых двигателей для автомобильного, водного и воздушного транспорта. Без этих законов нельзя рассчитать длину взлетной или посадочной полосы (рис. 51) для различных типов самолетов, параметры (наклон к горизонту и кривизну) скоростных автомобильных дорог.
Рис. 51
Старт космического корабля, его вывод на орбиту вокруг Земли или на определенную траекторию для полета к Луне, другим небесным телам невозможны без предварительных расчетов, в которых используются законы Ньютона.
Кроме этого, законы Ньютона необходимы для расчетов: при строительстве зданий, мостов и других сооружений; при разработке спортивной одежды, обуви, тренажеров; в машиностроении и т. п.
Применив эти законы для описания движения Луны и планет Солнечной системы, Ньютон открыл закон всемирного тяготения, который мы будем изучать в дальнейшем.
Как мы уже обсуждали, чтобы использовать второй и третий законы Ньютона, нужно выбрать с помощью первого закона Ньютона инерциальную систему отсчета. В большинстве задач систему отсчета, связанную с поверхностью Земли, можно считать инерциальной.
Тогда система отсчета, связанная с любым телом, движущимся относительно Земли с постоянной скоростью, также является инерциальной (в пределах той же точности измерений). Таким образом, в любом равномерно движущемся транспорте, на эскалаторе, в лифте и т. п. должны также выполняться второй и третий законы Ньютона.
На этот факт впервые обратил внимание Галилей. Он предположил, что опыты, проведенные в неподвижной системе отсчета, связанной с поверхностью Земли, и «в большой каюте под палубой какого-либо крупного корабля» не должны отличаться друг от друга.
«Если только движение будет равномерным, а не колеблющимся туда и сюда», то капли воды будут падать вертикально вниз, как в неподвижной системе отсчета. Мяч, брошенный вертикально вверх, вернется в точку бросания.
«Ни по одному из этих явлений, ни по чему-либо, что станет происходить с вами самими, вы не сможете удостовериться, движется корабль или стоит неподвижно», — утверждал Галилей.
Таким образом, Галилей выдвинул гипотезу, что относительно всех инерциальных систем отсчета тело получает одинаковое ускорение при одинаковых действиях на него других тел.
Действительно, каждый человек из личного опыта знает, что в вагоне, движущемся с постоянной скоростью по прямолинейной дороге, можно легко вставать, ходить, не теряя равновесия, можно даже играть в теннис (рис. 52).
Рис. 52
В настоящее время положение, высказанное Галилеем, называется принципом относительности Галилея или принципом относительности в механике:
в любых инерциальных системах отсчета все механические явления протекают одинаково при одинаковых начальных условиях.
Почему важны одинаковые начальные условия? Потому, что координата и скорость тела в начальный момент времени относительны, зависят от выбранной системы отсчета. Относительно равномерно движущегося вагона тело будет падать вниз по вертикали так же, как и в случае, когда вагон неподвижен (рис. 53). но относительно наблюдателя, находящегося на Земле, тело, падающее отвесно в вагоне, движется по параболе (см. рис. 53).
Рис. 53
Следовательно, не существует какой-то одной, избранной, инерциальной системы отсчета, все инерциальные системы отсчета равноправны, и при решении задач для упрощения расчетов можно выбирать любую из них.
Например, взвешивание тела и расчет результатов этого действия в любом равномерно движущемся транспорте (или в лифте и т. п.) можно проводить, не учитывая этого движения.
В системах отсчета, движущихся с ускорением (неинерциальных), в сформулированном нами виде законы Ньютона не выполняются. Но эти законы оказались так удобны для расчетов, что в неинерциальных системах отсчета специально вводят особые силы инерции, чтобы учесть ускоренное движение системы отсчета и использовать законы Ньютона.
Главные выводы:
- Законы Ньютона определяют общие существенные закономерности, свойственные любым механическим движениям.
- Принцип относительности Галилея устанавливает равноправие всех инерциальных систем отсчета, так как механические явления и процессы протекают в них одинаково при одинаковых начальных условиях.
- В соответствии с принципом относительности при решении задач можно использовать любую наиболее удобную инерциальную систему отсчета.
Движение по инерции и первый закон НЬЮТОНА
Возможно, во время летних каникул вы наблюдали или сами пережили описанные ниже явления:
- a) велосипедист равномерно движется по прямой дороге;
- b) велосипедист пытается удержать велосипед в состоянии покоя, не касаясь ногами земли;
- c) из-за невнимательности велосипедист не не замечает, как колесо велосипеда сталкивается с камнем, и перелетает через внезапно остановившийся велосипед (а).
Основу динамики составляют три закона Ньютона. Эти законы—результат обобщения моногочисленых наблюдений и экспериментов. Первое обобщение опытов провел Г.Галилей, живший в XVII веке. В результате экспериментов, аналогичных проведенному вами исследованию, он сформулировал принцип инерции:
Если на какое-либо тело действуют другие тела с силами, компенсирующими друг друга, то это тело либо находится в покое, либо движется равномерно и прямолинейно.
Ссылаясь на принцип инерции Галилея, Ньютон сформулировал I закон динамики, называемый также I законом Ньютона:
Существуют такие системы отсчета, относительно которых тела сохраняют свое состояние покоя или равномерного прямолинейного движения при отсутствии всякого внешнего воздействия на них, или если оказываемые на тело действия компенсируют друг друга.
Система отсчета, относительно которой выполняется I закон Ньютона, называется инерциальной системой отсчета (ИСО). С достаточно большой точностью системы тел, находящихся в состоянии покоя или равномерного прямолинейного движения относительно Земли, можно считать инерциальны-ми системами отсчета. Например, систему отсчета, связанную с равномерно и прямолинейно движущимся локомотивом, можно принять за инерциальную систему отсчета.
Отметим, что понятие «инерциальная система отсчета» является научной абстракцией. В реальной жизни такой системы не существует, потому что в природе тел в состоянии абсолютного покоя нет.
Основной закон динамика и второй закон Ньютона
Из исследования было выяснено, что ускорение тела данной массы прямо-пропорционально результирующей силе, действующей на тело:
С другой стороны, тела с разными массами под действием одной и той же результирующей силы получают разные ускорения — ускорения тел обратно-пропорциональны их массам
Ньютон исследовал эту зависимость, и обобщил ее в виде закона. Этот закон, называемый II законом Ньютона, выражается следующим образом:
В инерциальной системе отсчета ускорение, получаемое телом, прямо пропорционально равнодействующей силе и обратно пропорционально массе этого тела:
или
Этот закон можно выразить и так: равнодействующая сил, действующих на тело, равна произведению массы тела на его ускорение:
Из II закона Ньютона определяется единица силы в СИ — ньютон:
1 ньютон — это сила, под действием которой тело массой 1 кг получает ускорение
Сила является причиной изменения скорости движения! Как известно из кинематики, ускорение тела — это быстрота изменения его скорости:
Приняв во внимание это выражение во II законе Ньютона, получим:
Выполнив преобразования, получим:
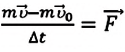
Величина 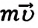
Импульс — векторная физическая величина (иначе называемая количеством механического движения), равная произведению массы тела на его скорость. Обозначается буквой
Единица измерения импульса в СИ:
II закон Ньютона также можно выразить и через импульс:
Изменение импульса (количества движения) тела происходит в направлении равнодействующей силы и пропорционально этой силе:
Произведение силы на время ее действия 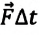
Направление импульса силы, также являющейся векторной величиной, совпадает с направлением вектора силы. Единицей импульса силы в СИ является:
Таким образом, II закон Ньютона обобщил важный факт динамики:
Действие силы приводит к изменению скорости тела, т.е. к возникновению ускорения.
Действие и противодействие и третий закон Ньютона
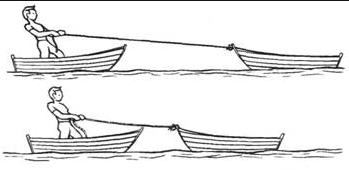
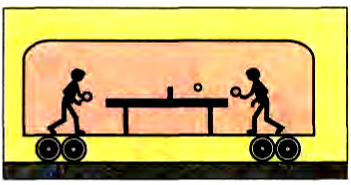
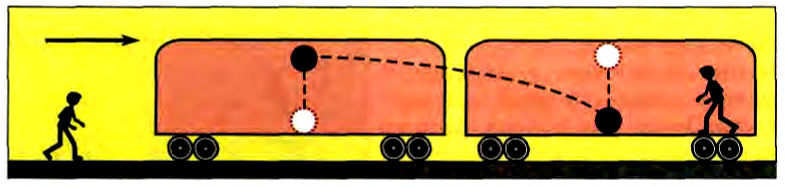
На рисунке изображены две одинаковые лодки, причаливающие к берегу: это достигается с помощью натягивания каната. Так, лодочник в первой лодке тянет за один конец каната, другой конец которого прикреплен к столбику на берегу. Лодочник во второй лодке тянет за конец каната, а за другой конец которого тянет человек на берегу (а). Каждый из них прикладывает к концу каната одинаковую силу. Какая из лодок быстрее причалит к берегу?
Выполнив исследование, вы установили, что при действии динамометров друг на друга силы взаимодействия по модулю равны, а по направлению противоположны (стрелки отклоняются в противоположные направления):
Это равенство выражает III закон Ньютона:
В инерцианальной системе отсчета силы, с которыми два тела действуют друг на друга, равны по модулю и направлены по одной прямой в противоположные стороны.
Этот закон Ньютона показывает, что при взаимодействии тел друг с другом силы всегда возникают попарно. Это означает, что если на произвольное (первое) тело будет действовать с определенной силой другое (второе) тело, то и первое будет действовать на второе тело с той же по модулю силой, только направленной противоположно. Согласно II закону Ньютона, эти силы сообщают телам ускорения в противоположных направлениях:
Где 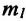
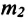
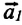
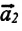
• Силы взаимодействия возникают одновременно и имеют одинаковую природу. Например, силы взаимодействия, возникающие при упругом столкновении тел, оба имеют электромагнитную природу.
Силы, возникающие при взаимодействии тел, прикладываются к разным телам и поэтому не могут уравновешивать друг друга, то есть никогда не компенсируют друг друга. Компенсировать действия друг друга могут только силы, приложенные к одному телу.
Инерциальные системы отсчета
Что является естественным для тела — движение или покой? Древнегреческий философ Аристотель утверждал, что покой, ведь для того, чтобы тело двигалось, нужно действовать на него определенным образом, а если действие прекратится, тело остановится. Кажется, что об этом свидетельствует и наш повседневный опыт. Но действительно ли это так?
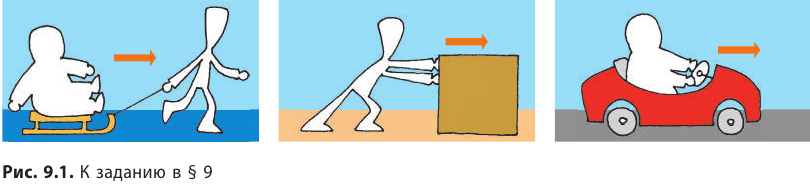
Почему остановятся тела (рис. 9.1), если прекратить их толкать, тянуть и т. п.? Остановятся ли тела, если исчезнет сопротивление их движению?
Надеемся, вы правильно ответили на вопрос и пришли к выводу, к которому в свое время пришел Г. Галилей: «Сообщенная движущемуся телу скорость будет сохраняться, если устранены внешние причины ускорения или замедления движения». Итак, «естественным» для тела является не только состояние покоя, но и прямолинейное равномерное движение.
Закон инерции Галилея: тело движется равномерно прямолинейно или находится в состоянии покоя, если на него не действуют другие тела или действия других тел скомпенсированы.
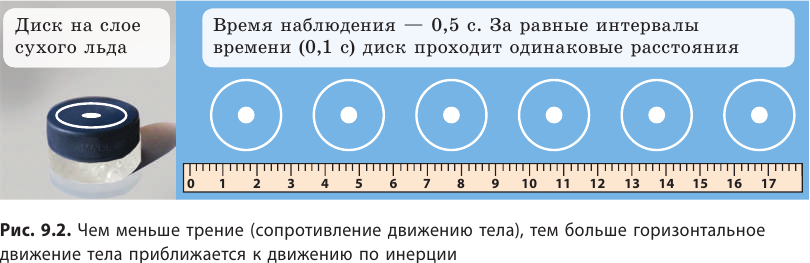
Тело, на которое не действуют другие тела и поля, называют изолированным (свободным), а движение изолированного тела — движением по инерции. В реальности практически невозможно создать условия, когда на тело ничто не действует, поэтому движением по инерции называют равномерное прямолинейное движение при отсутствии или скомпенсированности действия на тело других тел и полей (рис. 9.2).
Справочный материал по первому закону Ньютона
Явление сохранения телом состояния покоя или равномерного прямолинейного движения при условии, что на него не действуют другие тела и поля или их действия скомпенсированы, называют явлением инерции.
Вместе с тем состояние движения и состояние покоя зависят от выбора системы отсчета (СО). А в каждой ли СО наблюдается явление инерции? Из курса физики 9 класса вы хорошо знаете, что не в каждой.
Систему отсчета, относительно которой наблюдается явление инерции, называют инерциальной системой отсчета.
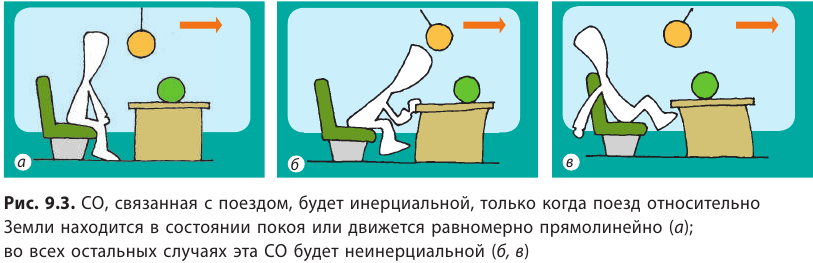
Представьте, что вы сидите в купе поезда, который время от времени увеличивает скорость, тормозит, осуществляет поворот и т. п. Понятно, что СО, связанная с поездом, будет инерциальной только тогда, когда поезд движется равномерно прямолинейно; во всех остальных случаях она будет неинерциальной, ведь относительно нее явление инерции наблюдаться не будет (рис. 9.3).
На каком рисунке (см. рис. 9.3, а–в) показано, что поезд набирает скорость? тормозит? движется равномерно прямолинейно?
Чаще всего в качестве инерциальной выбирают СО, жестко связанную с точкой на поверхности Земли. Но эту систему можно считать инерциальной только условно, поскольку Земля вращается вокруг своей оси. Для более точных измерений используют инерциальную СО, связанную с Солнцем и далекими звездами.
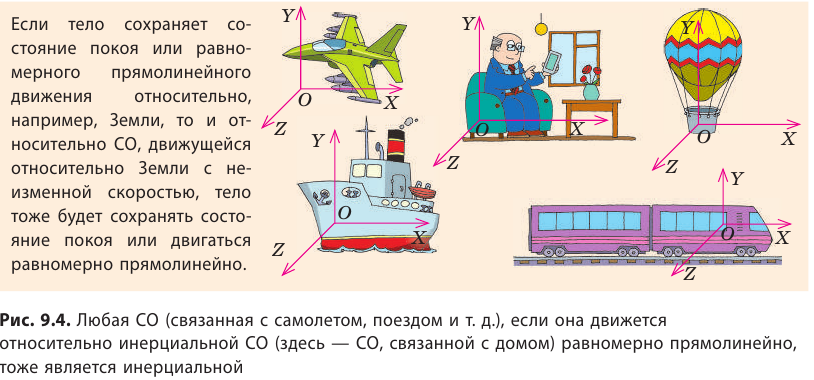
Если мы знаем хотя бы одну инерциальную СО (например, СО, связанную с домом, на рис. 9.4), то можем найти много других (см. рис. 9.4).
Закон инерции Г. Галилея стал первым шагом в установлении основных законов классической механики. Формулируя основные законы движения тел, И. Ньютон назвал этот закон первым законом движения. В современной физике первый закон механики Ньютона формулируют так:
Существуют такие системы отсчета, относительно которых тело сохраняет состояние покоя или равномерного прямолинейного движения, если на него не действуют никакие силы или если эти силы скомпенсированы.
В такой формулировке первый закон Ньютона:
- постулирует существование инерциальных СО (утверждает, что они существуют);
- дает возможность из всех имеющихся СО выделить инерциальные СО;
- содержит закон инерции (условия равномерного прямолинейного движения тела).
Справочный материал по второму закону Ньютона
Поставим на твердую горизонтальную поверхность легкоподвижную тележку и станем тянуть ее с помощью груза. Массу груза для каждого опыта будем подбирать так, чтобы растяжение пружин при движении тележки было одинаковым. Измеряя время t, в течение которого тележка проходит, например, расстояние s = 2 м, будем определять ускорение движения тележки 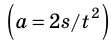
Учитывая, что единицу силы выбирают так, что коэффициент пропорциональности в выражении 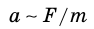
Ускорение, которое приобретает тело в результате действия силы, прямо пропорционально этой силе и обратно пропорционально массе тела:
- Второй закон Ньютона, записанный в виде
, выполняется только в инерциальных системах отсчета.
- Обычно на тело действуют несколько сил. Если тело можно считать материальной точкой, все эти силы можно заменить одной — равнодействующей. Равнодействующая равна геометрической сумме сил, действующих на тело:
(рис. 10.2), поэтому второй закон Ньютона записывают так:
- Направление ускорения движения всегда совпадает с направлением равнодействующей сил, действующих на тело:
.
- Если силы, действующие на тело, скомпенсированы, то есть равнодействующая равна нулю (
), тело не будет изменять скорость своего движения ни по значению, ни по направлению:
= 0 (рис. 10.3), а следовательно, будет двигаться равномерно прямолинейно или находиться в состоянии покоя.
- Тело движется равноускоренно прямолинейно, если равнодействующая сил, приложенных к телу, не изменяется со временем.
Рис. 10.2. Сила 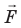
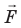
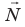
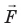
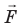
Рис. 10.3. Если равнодействующая сил, приложенных к телу, равна нулю, тело находится в состоянии покоя (а) или движется с постоянной скоростью (б)
Справочный материал по третьему закону Ньютона
«Действию всегда есть равное и противоположное противодействие, иначе: действия двух тел друг на друга между собой равны и направлены в противоположные стороны» — так И. Ньютон сформулировал свою третью и последнюю «аксиому движения».
Силы всегда возникают парами: если тело А действует на тело Б с силой 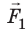
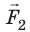
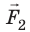
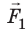
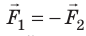
Подчеркнем: «действие» и «противодействие» — это всегда силы одинаковой природы, они всегда направлены вдоль одной прямой (рис. 10.4) — и сформулируем третий закон Ньютона в современном виде:
Тела взаимодействуют с силами, которые имеют одинаковую природу, направлены вдоль одной прямой, равны по модулю и противоположны по направлению:
Рис. 10.4. Силы, возникающие при взаимодействии, имеют одинаковую природу, направлены вдоль одной прямой, равны по модулю и противоположны по направлению
Выводы:
- Сила
— векторная физическая величина, являющаяся мерой взаимодействия тел, в результате которого тела получают ускорения или (и) деформируются. Единица силы в СИ — ньютон (Н). Если на материальную точку одновременно действуют несколько сил, их можно заменить равнодействующей
- Основной закон динамики — второй закон Ньютона: ускорение, которое приобретает тело в результате действия силы, прямо пропорционально этой силе и обратно пропорционально массе тела:
. Этот закон выполняется только в инерциальных СО.
- Третий закон Ньютона — закон взаимодействия: тела взаимодействуют с силами, которые имеют одинаковую природу, направлены вдоль одной прямой, равны по модулю и противоположны по направлению:
. Пара сил, возникающих при взаимодействии двух тел, не уравновешивают друг друга, поскольку приложены к разным телам.
- Гравитационные силы в физике
- Центр тяжести в физике (центр масс)
- Импульс тела в физике
- Замкнутая система в физике
- Кинематика в физике
- Законы сохранения в физике
- Международная система единиц СИ
- Математика — язык физики


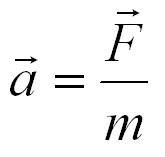
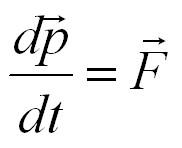
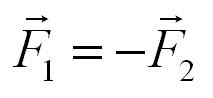

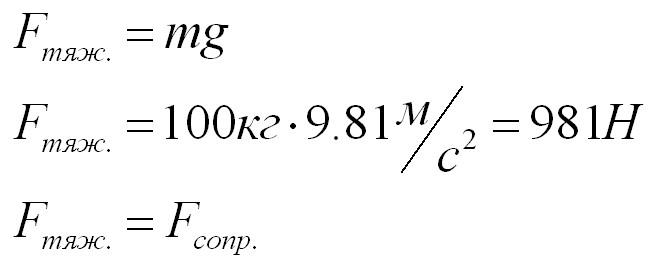
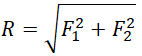
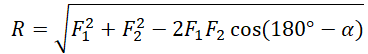
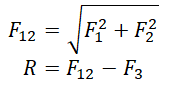
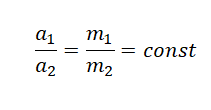
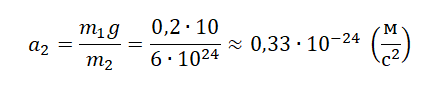
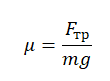
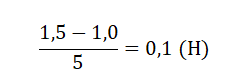
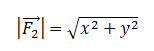
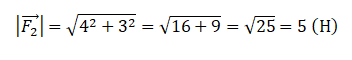






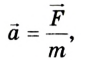
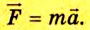
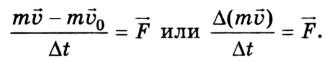
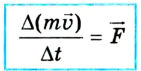
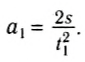
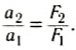
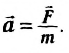
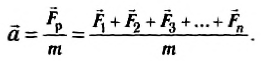
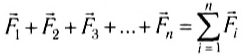
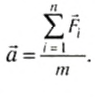
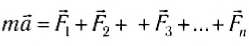
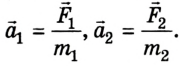
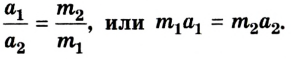
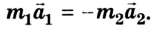
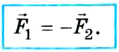
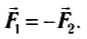


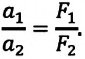
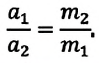


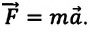
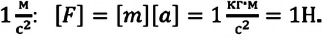
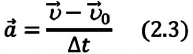
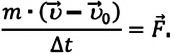
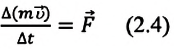
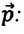
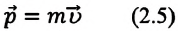
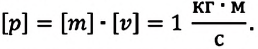
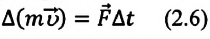
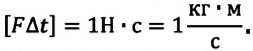

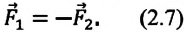
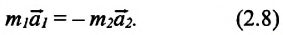
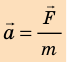
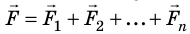 (рис. 10.2), поэтому второй закон Ньютона записывают так:
(рис. 10.2), поэтому второй закон Ньютона записывают так: 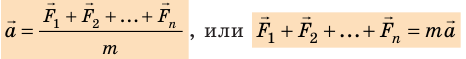
 .
.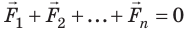 ), тело не будет изменять скорость своего движения ни по значению, ни по направлению:
), тело не будет изменять скорость своего движения ни по значению, ни по направлению: 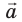 = 0 (рис. 10.3), а следовательно, будет двигаться равномерно прямолинейно или находиться в состоянии покоя.
= 0 (рис. 10.3), а следовательно, будет двигаться равномерно прямолинейно или находиться в состоянии покоя.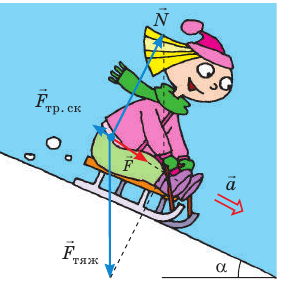
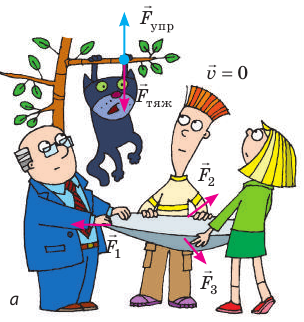
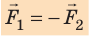

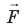 — векторная физическая величина, являющаяся мерой взаимодействия тел, в результате которого тела получают ускорения или (и) деформируются. Единица силы в СИ — ньютон (Н). Если на материальную точку одновременно действуют несколько сил, их можно заменить равнодействующей
— векторная физическая величина, являющаяся мерой взаимодействия тел, в результате которого тела получают ускорения или (и) деформируются. Единица силы в СИ — ньютон (Н). Если на материальную точку одновременно действуют несколько сил, их можно заменить равнодействующей 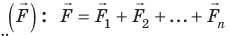
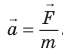 . Этот закон выполняется только в инерциальных СО.
. Этот закон выполняется только в инерциальных СО.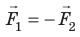 . Пара сил, возникающих при взаимодействии двух тел, не уравновешивают друг друга, поскольку приложены к разным телам.
. Пара сил, возникающих при взаимодействии двух тел, не уравновешивают друг друга, поскольку приложены к разным телам.