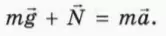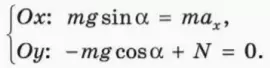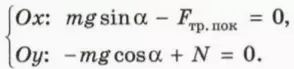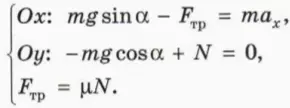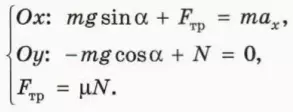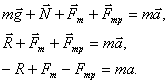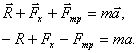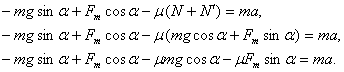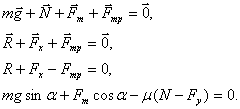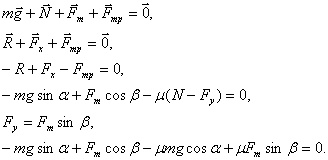Как найти силу реакции наклонной плоскости - Исправление недочетов и поиск решений вместе с Examum.ru

Загрузить PDF

Сила нормальной реакции — сила, действующая на тело со стороны опоры (или сила, противодействующая другим силам в любом данном сценарии). Ее вычисление зависит от конкретных условий и известных величин.

1
В случае тела, покоящегося на горизонтальной поверхности, сила нормальной реакции противодействует силе тяжести.
- Представьте себе тело, лежащее на столе. Сила тяжести действует по направлению к земле, но так как тело не разрушает стол и не падает на землю, существует некоторая противодействующая сила. Эта сила и есть сила нормальной реакции.
2
Формула для нахождения силы нормальной реакции для тела, покоящегося на горизонтальной поверхности: N = m*g^[1]
- В этой формуле N — сила нормальной реакции, m – масса тела, g – ускорение свободного падения.
- В случае тела, находящегося в состоянии покоя на горизонтальной поверхности и на которое не действуют внешние силы, сила нормальной реакции равна весу. Для сохранения тела в состоянии покоя, сила нормальной реакции должна быть равна силе тяжести, действующую на опору. В данном случае сила тяжести, действующая на опору, является весом, то есть произведением массы тела на ускорение свободного падения.
- Пример: найдите силу нормальной реакции, действующую на тело массой 4,2 г.
3
Умножьте массу тела на ускорение свободного падения. Вы найдете вес, который в данном случае равен силе нормальной реакции (так как тело в находится в покое на горизонтальной поверхности).
- Обратите внимание, что ускорение свободного падения на поверхности Земли является постоянной величиной: g = 9,8 м/с2.^[2]
- Пример: вес = m*g = 4,2*9,8 = 41,16 Н.
4
Запишите ответ.
- Пример: сила нормальной реакции равна 41,16 Н.
Реклама

1
Формула для вычисления силы нормальной реакции, действующей на тело, покоящееся на наклонной поверхности: N = m * g * cos(x).^[3]
- В этой формуле N — сила нормальной реакции, m – масса тела, g – ускорение свободного падения, х — угол наклона поверхности.
- Пример: найдите силу нормальной реакции, действующую на тело массой 4,2 г, находящегося на наклонной поверхности с углом наклона 45 градусов.
2
Найдите косинус угла. Косинус угла равен отношению прилежащей (к этому углу) стороны к гипотенузе. ^[4]
- Косинус зачастую вычисляется с помощью калькулятора, но вы также можете найти его вручную.
- Пример: соs(45) = 0,71.
3
Найдите вес. Вес равен произведению массы тела на ускорение свободного падения.
- Обратите внимание, что ускорение свободного падения на поверхности Земли является постоянной величиной: g = 9,8 м/с2.
- Пример: вес = m*g = 4,2*9,8 = 41,16 Н.
4
Перемножьте два найденных значения. Для вычисления силы нормальной реакции умножьте вес на косинус угла наклона.
- Пример: N = m * g * cos(x) = 41,16 * 0,71 = 29,1
5
Запишите ответ.
- Обратите внимание, что в случае тела, находящегося на наклонной поверхности, сила нормальной реакции меньше веса.
- Пример: сила нормальной реакции равна 29,1 Н.
Реклама

1
Формула для вычисления силы нормальной реакции в случае, когда внешняя сила, действующая на тело, направлена вниз: N = m * g + F * sin(x).
- В этой формуле N — сила нормальной реакции, m – масса тела, g – ускорение свободного падения, х — угол между горизонтальной поверхностью и направлением действия внешней силы.
- Пример: найдите силу нормальной реакции, действующую на тело массой 4,2 г, на которое действует внешняя сила 20,9 Н под углом 30 градусов.
2
Найдите вес. Вес равен произведению массы тела на ускорение свободного падения.
- Обратите внимание, что ускорение свободного падения на поверхности Земли является постоянной величиной: g = 9,8 м/с2.
- Пример: вес = m*g = 4,2*9,8 = 41,16 Н.
3
Найдите синус угла. Синус угла равен отношению противолежащей (к этому углу) стороны к гипотенузе. ^[5]
- Пример: sin(30) = 0,5.
4
Умножьте синус угла на внешнюю силу.
- Пример: 0,5 * 20,9 = 10,45
5
Сложите это значение и вес. Вы найдете силу нормальной реакции.
- Пример: 10,45 + 41,16 = 51,61
6
Запишите свой ответ. Обратите внимание, что в случае тела, на которое действует сила, направленная вниз, сила нормальной реакции больше веса.
- Пример: сила нормальной реакции равна 51,61 Н.
Реклама

1
Формула для вычисления силы нормальной реакции в случае, когда внешняя сила, действующая на тело, направлена вверх: N = m * g — F * sin(x).
- В этой формуле N — сила нормальной реакции, m – масса тела, g – ускорение свободного падения, х — угол между горизонтальной поверхностью и направлением действия внешней силы.
- Пример: найдите силу нормальной реакции, действующую на тело массой 4,2 г, на которое действует внешняя сила 20,9 Н под углом 50 градусов.
2
Найдите вес. Вес равен произведению массы тела на ускорение свободного падения.
- Обратите внимание, что ускорение свободного падения на поверхности Земли является постоянной величиной: g = 9,8 м/с2.
- Пример: вес = m*g = 4,2*9,8 = 41,16 Н.
3
Найдите синус угла. Синус угла равен отношению противолежащей (к этому углу) стороны к гипотенузе. ^[6]
- Пример: sin(50) = 0,77.
4
Умножьте синус угла на внешнюю силу.
- Пример: 0,77 * 20,9 = 16,01
5
Вычтите это значение из веса. Вы найдете силу нормальной реакции.
- Пример: 41,16 – 16,01 = 25,15
6
Запишите свой ответ. Обратите внимание, что в случае тела, на которое действует сила, направленная вверх, сила нормальной реакции меньше веса.
- Пример: сила нормальной реакции равна 25,15 Н.
Реклама

1
Формула для вычисления силы трения: F = μ * N.
- В этой формуле F — сила трения, μ — коэффициент трения, N — сила нормальной реакции.
- Коэффициент трения характеризует силу, необходимую для движения одного материала по поверхности другого.
2
Перепишите формулу, обособив силу нормальной реакции. Если вам даны сила трения и коэффициент трения, вы можете найти силу нормальной реакции по формуле: N = F / μ.
- Обе части исходной формулы были разделены на μ, в результате чего сила нормальной реакции была обособлена на одной стороне, а сила трения и коэффициент трения — на другой.
- Пример: найдите силу нормальной реакции, когда сила трения равна 40 Н, а коэффициент трения равен 0,4.
3
Разделите силу трения на коэффициент трения. Вы найдете силу нормальной реакции.
- Пример: N = F/μ = 40/0,4 = 100
4
Запишите ответ. Вы можете проверить ответ, подставив его в исходную формулу для вычисления силы трения.
- Пример: сила нормальной реакции равна 100 Н.
Реклама

Что вам понадобится

Карандаш
Бумага
Калькулятор

Об этой статье

Эту страницу просматривали 59 571 раз.

Была ли эта статья полезной?

Источник

Сила реакции опоры — это сила, с которой опора действует на тело. Она направлена перпендикулярно поверхности, поэтому такую силу называют силой нормальной реакции. Обозначают ее символом N и измеряют в Ньютонах.

Тело находится на выпуклой или вогнутой поверхности

Рассмотрим рисунок 1. Тело находится на опоре и давит на нее своим весом. Опора реагирует на воздействие тела и отвечает ему силой (vec{N}). Эта сила направлена перпендикулярно поверхности, вдоль вектора нормали, поэтому ее называют нормальной силой.

Примечания:

Нормаль – значит, перпендикуляр.
Искривленную, т.е., выпуклую, или вогнутую поверхность, можно считать частью сферы. Центр сферы – точка, она находится внутри сферы, от этой точки к поверхности сферы можно провести радиус.

(vec{N} left( H right) ) – сила, с которой опора действует на тело.

Рис. 1. Тело (шар) опирается на выпуклую – а) и вогнутую – б) поверхность. А поверхность реагирует на вес тела силой нормальной реакции

Когда тело находится на выпуклой поверхности (рис. 1а), реакция направлена вдоль радиуса от центра сферы наружу, за ее пределы.

Если же тело находится на вогнутой части (рис. 1б) поверхности, реакция (vec{N}) направлена по радиусу внутрь сферической поверхности к ее центру.

Тело опирается на поверхность в двух точках

На рисунках 2а и 2б изображено продолговатое тело (к примеру, стержень), опирающееся на поверхности двумя своими точками.

Рис. 2. Однородный стержень опирается на поверхность двумя точками, в каждой из точек сила реакции располагается перпендикулярно поверхности

В точках соприкосновения поверхность отвечает телу силой (vec{N}) своей реакции. Видно, что в каждая сила реакции направлена перпендикулярно поверхности.

Cилы реакции (vec{N_{1}}) и (vec{N_{2}}) имеют различные направления и в общем случае не равны по модулю.

[large vec{N_{1}} ne vec{N_{2}}]

Примечание: Сила — это вектор. Между векторами можно ставить знак равенства, только, когда совпадают характеристики векторов.

Как рассчитать силу нормальной реакции

Пусть тело давит на опору своим весом. В местах соприкосновения тела с опорой наблюдается упругая деформация. При этом опора стремится избавиться от возникшей деформации и вернуться в первоначальное состояние. Силы, с которыми опора упруго сопротивляется воздействию тела, имеют электромагнитную природу. Когда сближаются электронные оболочки атомов тела и опоры, между ними возникает сила отталкивания. Она и является силой реакции опоры на воздействие тела.

Примечание: Сила реакции (vec{N}) распределяется по всей площади соприкосновения тела и опоры. Но для удобства ее обычно считают сосредоточенной силой. Ее изображают на границах соприкасающихся поверхностей исходящей из точки, расположенной под центром масс тела.

Для того, чтобы рассчитать силу реакции, нужно понимать законы Ньютона, уметь составлять силовые уравнения и знать, что такое равнодействующая.

На рисунке 3 изображены тела, находящиеся на горизонтальной – а) и наклонной – б) поверхностях.

Рис. 3. Тело опирается на поверхность горизонтальную – а) и наклонную – б), составляя силовые уравнения для сил, расположенных перпендикулярно соприкасающимся поверхностям, рассчитывают силу реакции опоры

Рассмотрим подробнее рисунок 3а. Тело на горизонтальной поверхности находится в покое. Значит, выполняются условия равновесия тела.

По третьему закону Ньютона, сила, с которой тело действует на опору, равна по модулю весу тела и направлена противоположно весу.

[large boxed{ N = m cdot g }]

(m vec{g} left( H right) ) – сила, с которой тело действует на опору;

(vec{N} left( H right) ) – сила, с которой опора отвечает телу;

Рисунок 3б иллюстрирует тело на наклонной поверхности. Перпендикулярно соприкасающимся поверхностям проведена ось Oy. Проекция силы (m vec{g}) на ось — это (mg_{y}), она будет направлена противоположно реакции опоры (vec{N}) и численно равна ей.

Примечание: Выражение «численно равна» нужно понимать, как «длины векторов равны».

[large boxed{ N = m cdot g cdot cos(alpha) }]

(alpha left(text{рад} right) ) – угол между силой (mg) и осью Oy.

Итоги

Сила, с которой опора сопротивляется воздействию тела, называется силой реакции опоры, она имеет электромагнитную природу.
Ее, как и любую силу, измеряют в Ньютонах, обозначают так: (vec{N}).
Реакция опоры направлена перпендикулярно поверхности, поэтому ее называют силой нормальной реакции.
Сила (vec{N}) распределена по площади соприкосновения, но для удобства ее обычно считают сосредоточенной силой. Ее изображают исходящей из точки, расположенной под центром масс тела на границах между поверхностями тела и опоры.
Чтобы рассчитать силу реакции, нужно знать законы Ньютона, уметь составлять силовые уравнения и понимать, что такое равнодействующая.

Источник

1. Тело на гладкой наклонной плоскости

Напомним: когда говорят о гладкой поверхности, подразумевают, что трением между телом и этой поверхностью можно пренебречь.

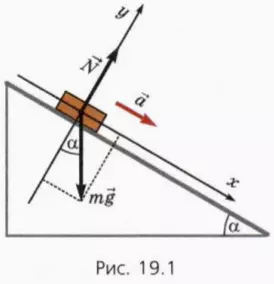
На тело массой m, находящееся на гладкой наклонной плоскости, действуют сила тяжести m и сила нормальной реакции (рис. 19.1).

Удобно ось x направить вдоль наклонной плоскости вниз, а ось y – перпендикулярно наклонной плоскости вверх (рис. 19.1). Угол наклона плоскости обозначим α.

Уравнение второго закона Ньютона в векторной форме имеет вид

? 1. Объясните, почему справедливы следующие уравнения:

? 2. Чему равна проекция ускорения тела на ось x?

? 3. Чему равен модуль силы нормальной реакции?

? 4. При каком угле наклона ускорение тела на гладкой плоскости в 2 раза меньше ускорения свободного падения?

? 5. При каком угле наклона плоскости сила нормальной реакции в 2 раза меньше силы тяжести?

При выполнении следующего задания полезно заметить, что ускорение тела, находящегося на гладкой наклонной плоскости, не зависит от направления начальной скорости тела.

? 6. Шайбу толкнули вверх вдоль гладкой наклонной плоскости с углом наклона α. Начальная скорость шайбы v₀.
а) Какой путь пройдет шайба до остановки?
б) Через какой промежуток времени шайба вернется в начальную точку?
в) С какой скоростью шайба вернется в начальную точку?

? 7. Брусок массой m находится на гладкой наклонной плоскости с углом наклона α.
а) Чему равен модуль силы, удерживающей брусок на наклонной плоскости, если сила направлена вдоль наклонной плоскости? Горизонтально?
б) Чему равна сила нормальной реакции, когда сила направлена горизонтально?

2. Условие покоя тела на наклонной плоскости

Будем теперь учитывать силу трения между телом и наклонной плоскостью.

Если тело покоится на наклонной плоскости, на него действуют сила тяжести m, сила нормальной реакции и сила трения покоя _тр.пок (рис. 19.2).

Сила трения покоя направлена вдоль наклонной плоскости вверх: она препятствует соскальзыванию бруска. Следовательно, проекция этой силы на ось x, направленную вдоль наклонной плоскости вниз, отрицательна:

F_{тр.пок x} = –F_тр.пок

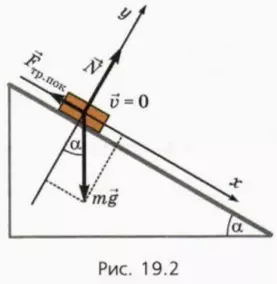
? 8. Объясните, почему справедливы следующие уравнения:

? 9. На наклонной плоскости с углом наклона α покоится брусок массой m. Коэффициент трения между бруском и плоскостью равен μ. Чему равна действующая на брусок сила трения? Есть ли в условии лишние данные?

? 10. Объясните, почему условие покоя тела на наклонной плоскости выражается неравенством

μ ≥ tgα.

Подсказка. Воспользуйтесь тем, что сила трения покоя удовлетворяет неравенству F_тр.пок ≤ μN.

Последнее неравенство можно использовать для измерения коэффициента трения: угол наклона плоскости плавно увеличивают, пока тело не начинает скользить по ней (см. лабораторную работу 4).

? 11.Лежащий на доске брусок начал скользить по доске, когда ее угол наклона к горизонту составил 20º. Чему равен коэффициент трения между бруском и доской?

? 12. Кирпич массой 2,5 кг лежит на доске длиной 2 м. Коэффициент трения между кирпичом и доской равен 0,4.
а) На какую максимальную высоту можно поднять один конец доски, чтобы кирпич не сдвинулся?
б) Чему будет равна при этом действующая на кирпич сила трения?

Сила трения покоя, действующая на тело, находящееся на наклонной плоскости, не обязательно направлена вдоль плоскости вверх. Она может быть направлена и вниз вдоль плоскости!

? 13. Брусок массой m находится на наклонной плоскости с углом наклона α. Коэффициент трения между бруском и плоскостью равен μ, причем и μ < tg α. Какую силу надо приложить к бруску вдоль наклонной плоскости, чтобы сдвинуть его вдоль наклонной плоскости:
а) вниз? б) вверх?

3. Движение тела по наклонной плоскости с учетом трения

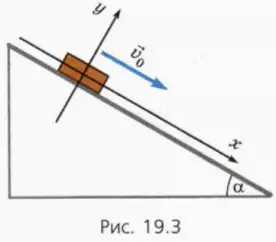
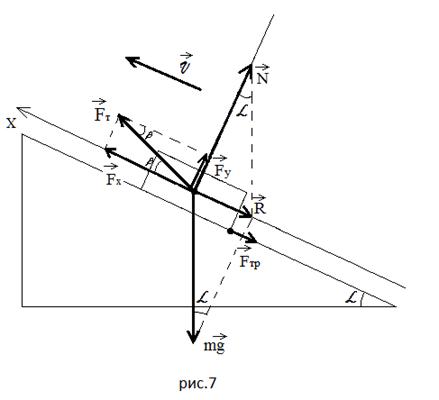
Пусть теперь тело скользит по наклонной плоскости вниз (рис. 19.3). При этом на него действует сила трения скольжения, направленная противоположно скорости тела, то есть вдоль наклонной плоскости вверх.

? 15. Изобразите на чертеже в тетради силы, действующие на тело, и объясните, почему справедливы следующие уравнения:

? 16. Чему равна проекция ускорения тела на ось x?

? 17. Брусок скользит по наклонной плоскости вниз. Коэффициент трения между бруском и плоскостью равен 0,5. Как изменяется со временем скорость бруска, если угол наклона плоскости равен:
а) 20º? б) 30º? в) 45º? г) 60º?

? 18. Брусок начинает скользить по доске, когда ее наклоняют на угол 20º к горизонту. Чему ранен коэффициент трения между бруском и доской? С каким по величине и направлению ускорением будет скользить брусок вниз по доске, наклоненной на угол 30º? 15º?

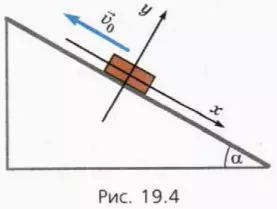
Пусть теперь начальная скорость тела направлена вверх (рис. 19.4).

? 19. Изобразите на чертеже в тетради силы, действующие на тело, и объясните, почему справедливы следующие уравнения:

? 20. Чему равна проекция ускорения тела на ось x?

? 21. Брусок начинает скользить по доске, когда ее наклоняют на угол 20º к горизонту. Брусок толкнули вверх по доске. С каким ускорением он будет двигаться, если доска наклонена на угол: а) 30º? б) 15º? В каком из этих случаев брусок остановится в верхней точке?

? 22.Шайбу толкнули вверх по наклонной плоскости с начальной скоростью v₀. Угол наклона плоскости α, коэффициент трения между шайбой и плоскостью μ. Спустя некоторое время шайба вернулась в начальное положение.
а) Сколько времени двигалась шайба вверх до остановки?
б) Какой путь прошла шайба до остановки?
в) Сколько времени после этого шайба возвращалась в начальное положение?

? 23. После толчка брусок двигался в течение 2 с вверх по наклонной плоскости и затем в течение 3 с вниз до возвращения в начальное положение. Угол наклона плоскости 45º.
а) Во сколько раз модуль ускорения бруска при движении вверх больше, чем при движении вниз?
б) Чему равен коэффициент трения между бруском и плоскостью?

Зацените!! Езда Электро-Велосипеда по воде

Дополнительные вопросы и задания

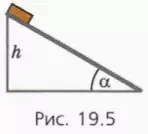
24. Брусок соскальзывает без начальной скорости с гладкой наклонной плоскости высотой h (рис. 19.5). Угол наклона плоскости равен α. Какова скорость бруска в конце спуска? Есть ли здесь лишние данные?

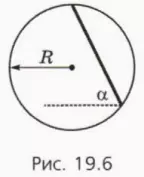
25. (Задача Галилея) В вертикальном диске радиуса R просверлен прямолинейный гладкий желоб (рис. 19.6). Чему равно время соскальзывания бруска вдоль всего желоба из состояния покоя? Угол наклона желоба α, в начальный момент брусок покоится.

26. По гладкой наклонной плоскости с углом наклона α скатывается тележка. На тележке установлен штатив, на котором на нити подвешен груз. Сделайте чертеж, изобразите силы, действующие на груз. Под каким углом к вертикали расположена нить, когда груз покоится относительно тележки?

27. Брусок находится на вершине наклонной плоскости длиной 2 м и высотой 50 см. Коэффициент трения между бруском и плоскостью 0,3.
а) С каким по модулю ускорением будет двигаться брусок, если толкнуть его вниз вдоль плоскости?
б) Какую скорость надо сообщить бруску, чтобы он достиг основания плоскости?

28. Тело массой 2 кг находится на наклонной плоскости. Коэффициент трения между телом и плоскостью 0,4.
а) При каком угле наклона плоскости достигается наибольшее возможное значение силы трения?
б) Чему равно наибольшее значение силы трения?
в) Постройте примерный график зависимости силы трения от угла наклона плоскости.
Подсказка. Если tg α ≤ μ, на тело действует сила трения покоя, а если tg α > μ – сила трения скольжения.

Источник

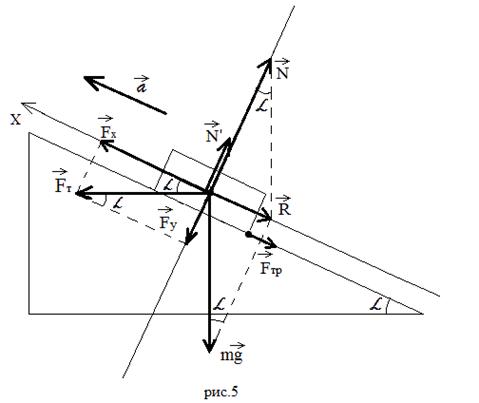
Итак, постараюсь подробно описать ход моих
рассуждений по этому вопросу. На первом уроке
ставлю перед учащимися вопрос: как может тело
двигаться по наклонной плоскости? Вместе
отвечаем: скатываться равномерно, с ускорением;
покоиться на наклонной плоскости; удерживаться
на ней; съезжать под действием силы тяги
равномерно, с ускорением; заезжать под действием
силы тяги равномерно, с ускорением. На рисунках
на двух-трех примерах показываем, какие при этом
на тело действуют силы. Попутно ввожу понятие
скатывающей равнодействующей. Записываем
уравнение движения в векторной форме, затем в нем
заменяем сумму скатывающей
равнодействующей (обозначайте,
как вам нравится). Это делаем по двум причинам:
во-первых, нет необходимости проецировать
векторы сил на ось и решать два уравнения; во-вторых,
правильно будет показано соотношение сил, исходя
из условия задачи.

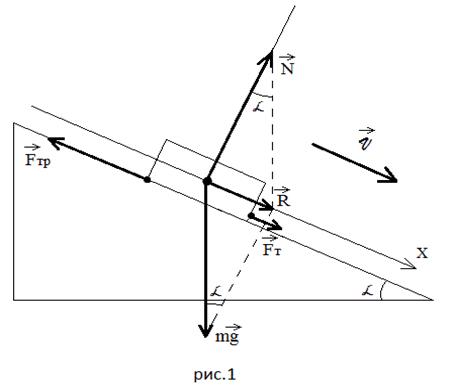
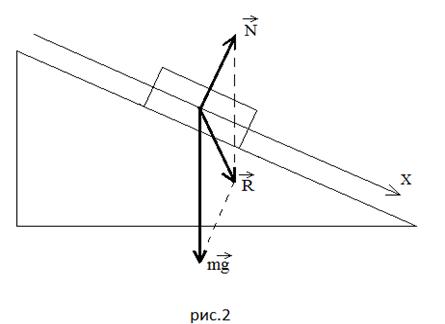
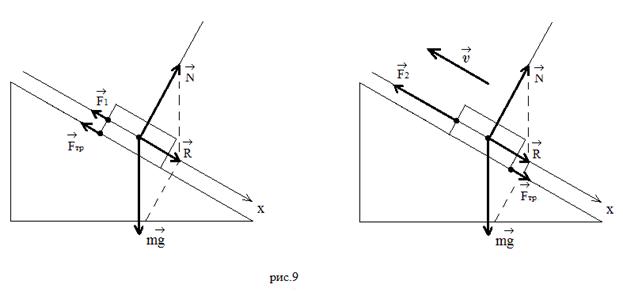
Покажу на конкретных примерах. Пример 1: тело
под действием силы тяги съезжает равномерно
(Рисунок 1).

Ученики первым делом должны усвоить алгоритм
построения рисунка. Изображаем наклонную
плоскость, посередине нее – тело в виде
прямоугольника, через середину тела параллельно
наклонной плоскости проводим ось . Направление оси не
существенно, но в случае равноускоренного
движения лучше показать в сторону вектора , чтобы в
алгебраической форме в уравнении движения в
правой части перед был знак «плюс». Далее строим силы.
Силу тяжести проводим
вертикально вниз произвольной длины (требую
рисунки делать крупными, чтобы всем было все
понятно). Затем из точки приложения силы тяжести
– перпендикуляр к оси , вдоль которого пойдет сила реакции
опоры .
Параллельно этому перпендикуляру из конца
вектора проводим
пунктирную линию до пересечения с осью . Из этой точки –
пунктирную линию, параллельную до пересечения с
перпендикуляром – получаем вектор правильной длины.
Таким образом, мы построили параллелограмм на
векторах и , автоматически
указав правильную величину силы реакции опоры и
построив по всем правилам векторной геометрии
равнодействующую этих сил , которую я называю скатывающей
равнодействующей (диагональ, совпадающая с осью ). В этом месте,
воспользовавшись методом из учебника, на
отдельном рисунке показываю силу реакции опоры
произвольной длины: сначала короче, чем нужно, а
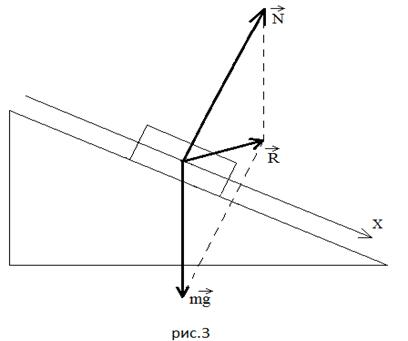
потом длиннее, чем нужно. Показываю
равнодействующую силы тяжести и силы реакции
опоры: в первом случае она направлена вниз под
углом к наклонной плоскости (Рисунок 2), во втором
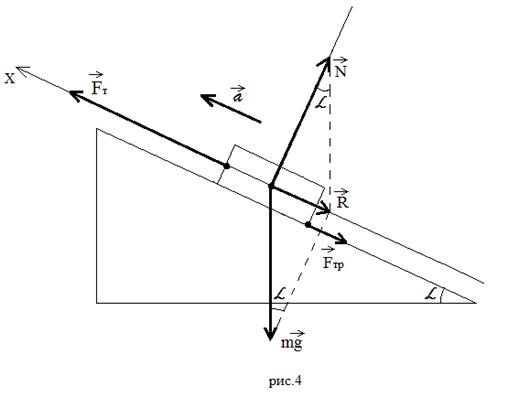
случае – вверх под углом к наклонной плоскости
(Рисунок 3).

Делаем очень важный вывод: соотношение между
силой тяжести и силой реакции опоры должно быть
таким, чтобы тело под их действием (или под
действием скатывающей равнодействующей) в
отсутствие других сил двигалось вниз вдоль
наклонной плоскости. Далее я спрашиваю:
какие еще силы действуют на тело? Ребята
отвечают: сила тяги и сила трения. Я задаю
следующий вопрос: какую силу покажем сначала, а
какую потом? Добиваюсь правильного и
обоснованного ответа: сначала в этом случае надо
показать силу тяги, а затем силу трения, модуль
которой будет равен сумме модулей силы тяги и
скатывающей равнодействующей: , т.к. по условию задачи тело
движется равномерно, следовательно,
равнодействующая всех сил, действующих на тело,
должна равняться нулю согласно первому закону
Ньютона. Для контроля задаю провокационный
вопрос: так сколько сил действует на тело? Ребята
должны ответить – четыре (не пять!): сила тяжести,
сила реакции опоры, сила тяги и сила трения.
Теперь записываем уравнение движения в
векторной форме согласно первому закону Ньютона:

.

Заменяем сумму векторов скатывающей равнодействующей :

.

Получаем уравнение, в котором все векторы
параллельны оси .
Теперь запишем это уравнение через проекции
векторов на ось :

.

Эту запись в дальнейшем можно пропускать.
Заменим в уравнении проекции векторов на их
модули с учетом направлений:

.

Пример 2: тело под действием силы тяги
заезжает на наклонную плоскость с ускорением
(Рисунок 4).

В этом примере ученики должны сказать, что
после построения силы тяжести, силы реакции
опоры и скатывающей равнодействующей следующей
надо показать силу трения, последним – вектор
силы тяги, который должен быть больше суммы
векторов , т.к.
равнодействующая всех сил должна быть
направлена так же, как вектор ускорения согласно второму
закону Ньютона. Уравнение движения тела должны
записать согласно второму закону Ньютона:

Если есть возможность на уроке рассмотреть
другие случаи, то не пренебрегаем этой
возможностью. Если нет, то даю это задание домой.
Кто-то может рассмотреть все оставшиеся случаи,
кто-то некоторые – право выбора учеников. На
следующем уроке проверяем, исправляем ошибки и
переходим к решению конкретных задач,
предварительно выразив из векторных
треугольников и
:

,
.

Равенство (2) желательно проанализировать для
различных углов .
При имеем: , как при движении
горизонтально под действием горизонтальной силы
тяги. С ростом угла его косинус уменьшается,
следовательно, уменьшается и сила реакции опоры
и становится все меньше и меньше силы тяжести.
При угле она
равна нулю, т.е. тело не действует на опору и
опора, соответственно, «не реагирует».

Предвижу вопрос оппонентов: как применить эту
методику для случаев, когда сила тяги
горизонтальна или направлена под углом к
наклонной плоскости? Отвечу на конкретных
примерах.

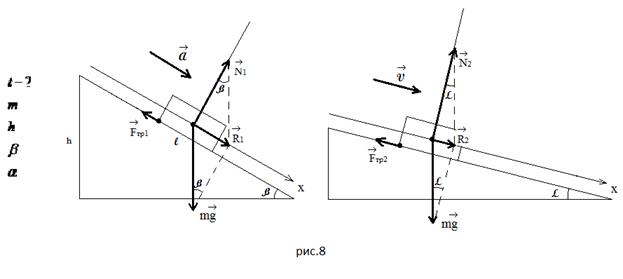
а) Тело с ускорением затаскивают на наклонную
плоскость, прикладывая силу тяги горизонтально
(Рисунок 5).

Горизонтальную силу тяги раскладываем на две
составляющие: вдоль оси – и
перпендикулярную оси – (операция,
обратная построению равнодействующей
перпендикулярных сил). Записываем уравнение
движения:

.

Заменяем скатывающей
равнодействующей, а вместо пишем :

Из векторных треугольников выражаем : и : .

Под действием горизонтальной силы тело не только
поднимается вверх по наклонной плоскости, но еще
и дополнительно прижимается к ней. Поэтому
возникает дополнительная сила давления, равная
модулю вектора и,
согласно третьему закону Ньютона,
дополнительная сила реакции опоры : . Тогда сила трения будет: .

Уравнение движения примет вид:

Вот мы полностью расшифровали уравнение
движения. Теперь осталось выразить из него
искомую величину. Попробуйте решить эту задачу
традиционным способом и вы получите такое же
уравнение, только решение будет громоздче.

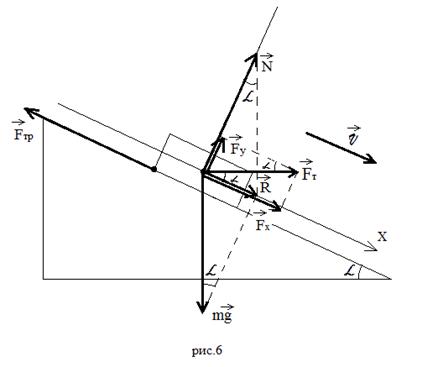
б) Тело стаскивают равномерно с наклонной
плоскости, прикладывая силу тяги горизонтально
(Рисунок 6).

В этом случае сила тяги кроме стаскивания тела
вниз вдоль наклонной плоскости еще и отрывает
его от наклонной плоскости. Итак, окончательное
уравнение имеет вид:

.

в) Тело затаскивают равномерно на наклонную
плоскость, прикладывая силу тяги под углом к наклонной
плоскости (Рисунок 7).

Предлагаю рассмотреть конкретные задачи, дабы
еще убедительнее прорекламировать мой
методический подход к решению таких задач. Но
прежде обращаю внимание на алгоритм решения (я
думаю, все учителя физики на него обращают
внимание учеников, и все мое повествование было
подчинено этому алгоритму):

1) внимательно прочитав задачу, выяснить, как
движется тело;
2) сделать рисунок с правильным, исходя из условия
задачи, изображением сил;
3) записать уравнение движения в векторной форме
согласно первому или второму закону Ньютона;
4) записать это уравнение через проекции векторов
сил на ось x (этот шаг в дальнейшем, когда умение
решать задачи по динамике будет доведено до
автоматизма, можно опустить);
5) выразить проекции векторов через их модули с
учетом направлений и записать уравнение в
алгебраической форме;
6) выразить модули сил по формулам (если есть
необходимость);
7) выразить искомую величину.

Задача 1. За какое время тело массой соскальзывает с наклонной
плоскости высотой и углом наклона , если по наклонной плоскости с
углом наклона оно
движется равномерно?

Каково было бы решать эту задачу привычным
способом!

Задача 2. Что легче: удержать тело на
наклонной плоскости или двигать его по ней
равномерно вверх?

Здесь при объяснении без скатывающей
равнодействующей, на мой взгляд, не обойтись.

Как видно из рисунков, в первом случае сила
трения помогает удерживать тело (направлена в ту
же сторону, что и удерживающая сила), во втором
случае она вместе со скатывающей
равнодействующей направлена против движения. В
первом случае ,
во втором случае .

Источник