Расчет электрических параметров необходим для правильных построений цепей. Поскольку целью использования электричества в электротехнике является задача по выполнению током работы, то встает вопрос о том, как найти силу тока. Данный параметр используют при вычислениях мощности и в расчетах потребления электрической энергии.
Существуют разные способы определения этого важного параметра, которые мы рассмотрим в данной статье.
Формулами
Параметры электрического тока всегда взаимосвязаны. Например, изменение величины нагрузки отображается на показателях других величин. Причем эти изменения подчиняются соответствующим законам, которые выражаются через формулы. Поэтому на практике для нахождения силы тока часто используют соответствующие формулы.
Через заряд и время
Вспомним определение (рис.1): электричество – это величина заряда, движимого силами электрического поля, преодолевающего за единицу времени условную плоскость проводника, называемую поперечным сечением проводника.
Таким образом, если известен электрический заряд, прошедший через проводник за определенное время, то не трудно найти величину этого заряда прошедшего за единицу времени, то есть: I = q/t
Через мощность и напряжение
В паспорте электроприбора обычно указывается его номинальная мощность и параметры электрической сети, для работы с которой он предназначен. Имея в распоряжении эти данные, можно вычислить силу тока по формуле: I = P/U.
Данное выражение вытекает из формулы для расчета мощности: P = IU.
Через напряжение или мощность и сопротивление
Силу электричества на участке цепи определяют по закону Ома. Для этого необходимо знать следующие параметры: сопротивление и напряжение на этом участке. Тогда I = U/R. Если известна мощность нагрузки, то ее можно выразить через квадрат силы тока умноженной на сопротивление участка: P = I2R, откуда
Для полной цепи эту величину вычисляют по закону Ома, но с учетом параметров источника питания.
Через ЭДС, внутреннее сопротивление и нагрузку R
Применяя закон Ома, адаптированный для полной цепи, вы можете вычислить максимальный ток по формуле I = ε / (R+r′), если известны параметры:
- внешнее сопротивление проводников (R);
- ЭДС источника питания (ε);
- внутреннее сопротивление источника, обладающего ЭДС (r′).
Примечание! Реальные источники питания обладают внутренним сопротивлением. Поскольку в электрической цепи
показатель силы тока может уменьшаться в связи с возрастанием сопротивления источника питания или в результате падения ЭДС. Именно из-за роста внутреннего сопротивления садится аккумулятор и ослабевает ЭДС элементов питания.
Закон Джоуля-Ленца
Казалось бы, что расчет силы тока по количеству тепла, выделяющегося в результате нагревания проводника, не имеет практического применения. Однако это не так. Рассмотрим это на примере.
Пусть требуется найти силу тока во время работы электрочайника. Для этого доведите до кипения 1 кг воды и засеките время в секундах. Предположим, начальная температура составляла 10 ºС. Тогда Q = Cm(τ – τ0) = 4200 Дж/кг× 1 кг (100 – 10) = 378 000 Дж.
Из закона Джоуля-Ленца (изображение на рис. 2) вытекает формула:
Измерив сопротивление электроприбора и подставив значения в формулу, получим величину потребляемого тока.
Измерительными приборами
Если под руками имеются измерительные приборы, то с их помощью довольно просто найти силу тока. Необходимо лишь соблюдать правила измерений и не забывать о правилах безопасности.
Амперметром
Пользуясь приборами для измерения ампеража, следует помнить, что они подключаются в цепи последовательно. Внутреннее сопротивление амперметра очень маленькое, поэтому прибор легко выводится из строя, если проводить измерения пределами значений, для которых он рассчитан.
Схема подключения амперметра показана на рисунке 3. Обратите внимание на то, что на участке измеряемой электрической цепи обязательно должна быть нагрузка.
Большинство аналоговых амперметров, например, таких, как на рисунке 4, предназначены для измерений параметров в цепях с постоянными токами.
Обратите внимание распределение шкалы амперметра. Цена первого деления 50 А, а всех последующих – 10 А. Максимальная величина, которую можно измерить данным амперметром не должна превышать 300 А. Для измерений электрической величины в меньших либо в больших пределах следует применять соответствующие приборы, предназначенные для таких диапазонов. В этом смысле универсальность амперметра ограничена.
При измерениях постоянных токов необходимо соблюдать полярность щупов при подключении амперметра. Для подключения прибора требуется разрывать цепь. Это не всегда удобно. Иногда вычисление силы тока по формуле является предпочтительней, особенно если приходится проводить измерения в сложных электротехнических схемах.
Мультиметром
Преимущество мультиметра в том, что этот прибор многофункциональный. Современные мультиметры цифровые. У них есть режимы для измерений в цепях постоянных и переменных токов. В режиме измерения силы тока этот измерительный прибор подключается в цепь аналогично амперметру.
Перед включением мультиметра в цепь, всегда проверяйте режим измерений, а пределы измерения выбирайте заведомо большие предполагаемой силы тока. После первого измерения можно перейти в режим с меньшим диапазоном.
Для работы с переменным напряжением переводите прибор в соответствующий режим. Считывайте значения с дисплея после того, как цифры перестанут мелькать.
Примеры
Покажем на простых примерах, как решать задачи на вычисление силы тока по формуле.
Задача 1.
На участке цепи имеются три параллельно включенных резистора (см. рис. 5). Значения сопротивлений резисторов: R1 = 5 Ом; R2 = 25 Ом; R3 = 50 Ом. Требуется рассчитать силу тока для каждого резистора и на всём участке, если на нем поддерживается постоянное напряжение 100 В.
Решение: При параллельном соединении нагрузочных элементов U = const, то есть, напряжение одинаково на всех резисторах и составляет 100 В. Тогда, по закону Ома I = U/R
- I1 = U/R1 =100/5 = 20 А;
- I2 = U/R2 =100/25 ≈ 4 А;
- I3 = U/R3 =100/50 = 2 А.
Для вычисления искомого параметра на всем участке цепи, нам необходимо знать общее сопротивление этого участка. Учитывая тот факт, что при параллельном соединении нагрузочных элементов в цепи их общее сопротивление равно:
Имеем: 1/R= 1/5 + 1/25 + 1/50 = 13/50; R = 50/13 ≈ 3.85 (Ом)
Тогда: I = U/R = 100 В/3,85 Ом ≈26 А.
Ответ:
- Сила тока на сопротивлениях: I1 =20 А; I2 = 4А; I3 = 2 А.
- Сила тока, поступающего на рассматриваемый участок цепи равна 26 А.
Задача 2.
Мощность электрочайника 2 кВт. Чайник работает от городской сети под напряжением 220 В. Сколько электричества потребляет этот электроприбор?
Решение:
Воспользуемся формулой для нахождения силы тока, включающей напряжение и мощность: I = P/U.
- 2 кВт преобразим в ватты: 2 кВт = 2000 Вт.
- Подставляем данные: I = 2 000 Вт/ 220 В ≈ 9 А
- Ответ: Нагревательный элемент электрочайника рассчитан на 9 А.
Задача 3.
Вычислить силу тока в цепи, если известно, что сопротивление составляет 5 Ом, ЭДС источника питания 6 В, а его внутреннее сопротивление составляет 1 Ом.
Решение.
Применяя закон Ома для полной цепи, запишем: I = ε / (R+r′)
I = 6 В / (5 Ом + 1 Ом) = 1 А.
Ответ: сила тока 1 А.
Задача 4.
Сколько энергии потребляет электроплита за 2 часа работы, если сопротивление нагревательного элемента 40 Ом?
Решение:
За время t электричество выполнит работу A = U*I*t.
Напряжение сети известно – оно составляет 220 В.Силу тока находим по формуле: I = U/R, тогда A = (U2/R)*t или
A = ((220 В)2 / 40 Ом) * 2 ч = 2420 Втч = 2,42 кВтч
Ответ: За 2 часа работы электроплита потребляет 2,42 кВт часов электроэнергии.
Применяя формулы для вычисления параметров электричества, пользуясь фундаментальными законами физики можно находить неизвестные данные для составных элементов цепей и электроприборов с целью оценки их состояния. В каждом отдельном случае необходимо определить известные параметры тока, которые можно использовать в дальнейших вычислениях. Обычно, это напряжение, мощность или сопротивление нагрузки.
Если можно обойтись без измерений амперметром – лучше прибегнуть к вычислениям, даже если при этом потребуется измерить напряжение. Такое измерение можно проводить без разрыва электрической цепи, чего нельзя сделать при помощи амперметра.
Определение
Сила тока — физическая величина, которая позволяет дать количественную характеристику току. Она обозначается буквой I и численно равна заряду, который за единицу времени протекает через поперечное сечение проводника.
Природа происхождения
Определение
Электрический ток — это направленное движение заряженных частиц под воздействием электрического поля.
В качестве частиц выступают:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
- в металлических проводниках — электроны;
- в полупроводниках — дырки или электроны;
- в вакууме — электроны (при определенных условиях);
- в газах — электроны и ионы;
- в растворах и расплавах электролитов — ионы.
Пока по проводнику не течет электрический ток частицы движутся хаотично. И их количество перетекших в одном направлении примерно соответствует и количеству частиц, перетекших в противоположном направлении.
Но ситуация меняется после того, как по проводнику пускают ток. В этом случае количество движущихся в одном направлении частиц значительно возрастает. И чем больше их проходит через поперечное сечение проводника за единицу времени, тем больше и сила тока.
Модель электрической цепи
Лучше понять физический смысл рассматриваемой величины можно на примере механической модели электрической цепи. В качестве ее возьмем водопроводную сеть частного дома.
Для того, чтобы вода начала поступать в водопровод из скважины или колодца необходим насос. Поэтому его можно рассматривать в качестве аналога батареи или иного источника тока. Он создает в системе давление, которое и приводит воду в движение. Соответственно трубы выступают роли проводников, молекулы воды — электронов, а краны — электрических переключателей.
Чем сильнее напор в водопроводной системе, тем большее количество воды, а вернее ее молекул, протекает через поперечное сечение трубы за каждую секунду. Отсюда можно сделать вывод, что чем больше сила тока, тем сильнее и его действие.
Примечание
Воздействие тока силой до 0,5 мА (частота 50 Гц) человек не ощущает. При силе от 2 до 10 мА возникают болезненные сокращения мышц. А удар током силой свыше 100 мА грозит развитием фибрилляции желудочков и остановкой сердечной деятельности.
Единица измерения
Так как сила тока — это количественная величина, то в физике есть и единица ее измерения. Она позволяет проводить сравнительный анализ различных токов и их действий.
В чем измеряется
Формула силы тока записывается так:
(I=frac{triangle q}{triangle t})
где (triangle t) — это единица времени, а (triangle q) — количества электрического заряда, протекшего за указанный промежуток времени через поперечное сечение проводника.
В Интернациональной системе (СИ) заряд измеряется в Кулонах, а время — в секундах. В соответствии с этим единица измерения силы тока — Кулон/секунду. По международному соглашению ее стали называть Ампером.
Примечание
В 1948 году было предложено определять силу тока по взаимодействию двух проводников, расположенных в вакууме на расстоянии одного метра друг от друга и длиной в один метр.
За силу тока в 1 A принимают такой ток, при котором два проводника притягиваются друг к другу (ток течет в одном направлении) или отталкиваются (ток течет в разных направлениях) с силой 0,0000002 H.
На практике очень часто применяются кратные единицы силы тока:
1 кА = 103 А, 1 мкА = 10-6 А, 1 мА = 10-3 А
В честь кого названа единица измерения
Единица измерения силы тока была названа в честь французского ученого Андрэ-Мари Ампер. Его называют «отцом» учения о электромагнетизме. Именно он ввел в науку такие термины как электрический ток, электростатика и электродинамика, гальванометр, напряжение, электродвижущая сила, соленоид. Амперу удалось найти доказательство теоремы «О циркуляции магнитного поля» и описать математически силу взаимодействия между токами.
Как найти силу тока
С проблемой определения силы тока сталкиваются и при решении задач, и в повседневной жизни. Вычислить этот параметр для проводника или электрической цепи можно не только путем проведения измерений, но и при помощи формул.
В проводнике
Основными величинами, характеризующими электрический ток, являются сила, напряжение и сопротивление. Взаимосвязь между ними была установлена экспериментальным путем в 1826 году Георгом Омом. В последствии она была сформулирована в виде закона, который и был назван в честь ученого.
Определение
Закон Ома: сила тока в участке цепи или проводнике обратно пропорциональна сопротивлению и прямо пропорциональна напряжению.
Рассчитать силу тока в проводнике также можно, если разделить мощность на напряжение.
При протекании тока происходит нагревание проводника. И по количеству выделившегося тепла на основании закона Джоуля-Ленца возможно провести вычисление силы тока.
В цепи
Реальный источник тока всегда обладает своим внутренним сопротивлением.
Определение
Закон Ома для полной цепи формулируется так: сила тока в полной цепи прямо пропорциональна электродвижущей силе источника тока и обратно пропорциональна сумме внутреннего и внешнего сопротивления.
Формулы
Закон Ома для участка цепи:
(I=frac UR)
где R — сопротивление проводника, а U — напряжение.
Закон Ома для полной цепи:
(I=fracSigma{R+r})
где ε — электродвижущая сила источника тока, R + r — сумма сопротивлений источника и внешней нагрузки.
Формула, для определения силы тока по мощности и напряжению:
(I=frac PU)
где P — мощность, а U — напряжение.
Определение
Закон Джоуля-Ленца: при протекании по проводнику тока происходит выделение тепла (Q), которое равно произведению квадрата силы тока (I) на время (t), которое он протекал и на сопротивление проводника (R).
Математически формула выглядит так:
(Q=I^2Rt)
Исходя из нее можно вывести еще одну формулу для расчета силы тока:
(I=sqrt{frac Q{Rt}})
Как можно измерить силу тока
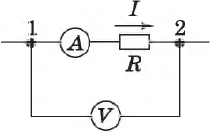
Для измерения силы тока используется прибор, называемый амперметром. На электрических схемах он обозначается буквой А, заключенной в окружность.
В любом проводнике замкнутой цепи, собранной последовательно, протекает электрический ток одинаковой величины. Поэтому для его измерения достаточно просто разомкнуть эту цепь в любом месте и подключить амперметр. Нельзя подключать его к источнику тока при отсутствии устройства потребления.
Ток бывает переменный и постоянный. И для его измерения необходимы разные устройства. На шкале амперметров для постоянного тока имеется одно из следующих обозначений — «-», «DC» или указание на полярность подключения. Амперметры, предназначенные для измерения силы переменного тока обозначаются «(sim)» или «АС».
Амперметр для постоянного тока необходимо включать в цепь с соблюдением полярности, то есть к клемме прибора, имеющей обозначение «+», присоединяют провод, идущий от положительного электрода.
Примечание
Если на источнике тока отсутствует указание полярности, то узнать ее можно по электрической схеме. Короткая линия всегда соответствует «минусу», а длинная — «плюсу».
Амперметр для переменного тока не имеет полярности и подключается без ее учета.
Описание прибора
Амперметр — это один из электроизмерительных приборов. Он обладает очень низким сопротивлением, чтобы не оказывать влияния на величину измеряемой силы тока. Ведь закон Ома гласит, что сила тока прямо пропорциональна напряжению и обратно пропорциональна сопротивлению. Это означает, что чем больше сопротивление проводников, тем меньше сила тока.
Шкала прибора может быть градуирована не только в А, но и в других кратных единицах — мкА, мА, кА.
Амперметры бывают:
- аналоговые (стрелочные);
- цифровые (электронные).
Измерители стрелочного типа не нуждаются в источнике питания, так как потребляют электрический ток непосредственно из измеряемой цепи. Но они показывают величину силы тока с некоторой задержкой, а не мгновенно.
Электронные амперметры практически полностью лишены такого недостатка как инерционность. Современные процессоры, используемые в этих моделях, обеспечивают частоту обновления показателей до 1000 в минуту. Их недостатком является высокая цена и необходимость отдельного источника питания для функционирования.
Примеры нахождения силы тока в задачах
Задача №1
Определите силу тока проводнике, имеющем сопротивление 55 Ом при напряжении в сети 220В.
Решение
(I=frac UR)
Вычисление
(I=frac{220}{50}=4.4;A)
Ответ: сила тока в проводнике 4,4 А.
Задача №2
Сила тока в резисторе при напряжении 100В (U1) составляет 4 А (I1). Если напряжение увеличить на 20В (Δ U), как изменится сила тока (I2), протекающего через этот резистор?
Решение
По условию задачи сопротивление резистора не изменяется. Тогда:
(frac{U1}{I1}=frac{U2}{I2};Rightarrow;I2=frac{I1times U2}{U1})
(U2=U1+triangle U)
(I2=frac{I1timesleft(U1+triangle Uright)}{U1})
Вычисление
(I2=frac{4timesleft(100+20right)}{100}=4.8;A)
Ответ: сила тока станет 4,8 А.
Задача №3
Определите силу тока в цепи с внешним сопротивлением 10 Ом и источником постоянного тока, ЭДС которого составляет 15В, а внутреннее сопротивление – 1 Ом.
Решение
(I=fracvarepsilon{R+r})
Вычисление
(I=frac{15}{10+1}=1.37A)
Ответ: 1,37 А.
Задача №4
При какой силе тока (I) проволока с сопротивлением (R) 20 Ом за 300 секунд (t) выделит 6 кДж теплоты (Q)?
Решение
(I=sqrt{frac Q{Rt}})
Вычисление
(I=sqrt{frac{6000}{20ast300}}=1A)
Ответ: 1 А.
При прохождении электрического тока по цепи мы можем наблюдать различные его действия: тепловое, химическое, магнитное, световое.
Возьмем, к примеру, тепловое действие. Вы можете уверенно сказать, что оно точно может проявляться в разной степени. Это подтверждали наши опыты. Натянутая медная проволока просто нагревалась, а вот вольфрамовая спираль в электрической лампе уж точно нагревалась сильнее. Ведь она накалилась настолько, что начинала излучать свет. Значит, мы могли накалить до похожего состояния и медную проволоку. Что же для этого нужно сделать? Как контролировать силу действия тока? Что эта сила вообще из себя представляет?
На данном уроке вы узнаете ответы на все эти вопросы. Мы рассмотрим, как заряд перемещается по проводнику при прохождении тока. С помощью этих знаний мы подойдем к определению новой силы и ее свойств — силы тока.
Перемещение заряда по проводнику
Как вы уже знаете, электрический ток представляет собой упорядоченное движение заряженных частиц. Мы говорим, что частицы “заряженные” — это означает, что они имеют какой-то определенный заряд $q$.
Соответственно, при движение таких частиц происходит перенос некоторого заряда. Каждый свободный электрон в металле переносит заряд. Каждый ион в растворе кислот, солей или щелочей тоже переносит заряд.
Логично, что чем больше частиц переместится от одного участка цепи к другому, тем больший общий заряд будет ими перенесен.
От чего же зависит интенсивность действий электрического тока? Опытным путем было доказано, что интенсивность (степень действия) электрического тока зависит как раз от величины этого переносимого заряда.
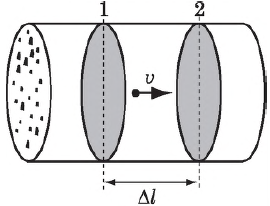
Сила тока
Электрический заряд, проходящий через поперечное сечение проводника в $1 space с$, будет определять такую величину, как сила тока в цепи (рисунок 1).
Сила тока — это физическая величина, равная отношению электрического заряда $q$, прошедшего через поперечное сечение проводника, ко времени его прохождения $t$:
$I = frac{q}{t}$,
где $I$ — сила тока.
Сила взаимодействия проводников с током как основа для определения единицы силы тока
Для того, чтобы определить единицу измерения силы тока, были проведены опыты, которые мы сейчас и рассмотрим. Опыты эти заключались в явлении взаимодействия двух проводников с током.
Возьмем два гибких прямых проводника. Расположим их параллельно друг другу. Подсоединим их к источнику тока (рисунок 2).
После замыкания цепи по ней пойдет электрический ток. Ток будет идти и по нашим подопытным проводникам.
Что мы увидим? Они начнут взаимодействовать друг с другом. А именно, они будут притягиваться друг к другу (рисунок 2, а) или отталкиваться друг от друга (рисунок 2, б). Это будет зависеть от направления тока в них.
Тут же встает вопрос о том, как же измерить эту силу, с которой взаимодействуют проводники? Опыты показали следующее.
Сила взаимодействия между проводниками с током зависит от:
длины проводников;
расстояния между ними;
среды, в которой находятся проводники;
силы тока в проводниках.
Для нас сейчас имеет значение самый последний пункт. Возьмем проводники, для которых все остальные условия будут одинаковы, кроме силы токов. Окажется, что, чем больше сила тока в каждом проводнике, тем с большей силой они взаимодействуют между собой.
Единица измерения силы тока
А теперь представьте себе очень тонкие и очень длинные проводники. Расположены они параллельно друг другу. Расстояние между ними — $1 space м$. Сила тока в них одинакова. И все это в вакууме! Вот здесь и появляется единица измерения силы тока (рисунок 3).
За единицу силы тока принимаю такую силу тока, при которой отрезки параллельных проводников длиной $1 space м$ взаимодействуют с силой $2 cdot 10^{-7} space Н$ ($0.0000002 space Н$).
Имя этой единицы — ампер ($А$). Она названа в честь французского физика Андре Ампера (рисунок 4).

Дольные и кратные единицы силы тока
На практике вы часто можете увидеть следующие единицы: миллиампер ($мА$), микроампер ($мкА$), килоампер ($кА$).
$1 space мА = 0.001 space А = 1 cdot 10^{-3} space А$;
$1 space мкА = 0.000001 space А = 1 cdot 10^{-6} space А$;
$1 space кА = 1000 space А = 1 cdot 10^3 space А$.
Сила тока некоторых электроприборов
Для лучшего понимания, сколько же составляет один ампер на практике, в таблице 1 приведены средние значения силы тока для некоторых электроприборов.
| Устройство | Значение силы тока $I$, А |
| Лампочка карманного фонаря | 0,1 |
| Обычная лампа накаливания | 0,3 — 0,5 |
| Холодильник | 0,8 — 1 |
| Телевизор | 1,2 — 2 |
| Электрический утюг | 3 |
| Пылесос | 4 — 9 |
| Стиральная машина | 6 — 10 |
| Двигатель троллейбуса | 160 — 220 |
| Молния | более 400 000 |
Связь единицы измерения заряда и единицы измерения силы тока
Хоть мы уже и говорили о заряде и единице его измерения (кулон) ранее, в физике принято определять его через ампер.
Выразим из определения силы тока ($I = frac{q}{t}$) сам заряд и получим следующую формулу.
$q = It$.
Если $I = 1 space А$, а $t = 1 space с$, то мы получим единицу электрического заряда — $1 space Кл$.
$1 space кулон = 1 space ампер cdot 1 space с$, или
$1 space Кл = 1 space А cdot 1 space с = 1 space А cdot с$.
За единицу электрического заряда принимают электрический заряд, проходящий сквозь поперечное сечение проводника при силе тока $1 space А$ за время $1 space с$.
Электрический заряд и его зависимость от силы тока и времени
Мы получили формулу, позволяющую по-новому взглянуть на определение электрического заряда: $q = It$.
Делаем вывод:
электрический заряд, проходящий через поперечное сечение проводника зависит от силы тока и времени его прохождения.
Эти знания пригодятся в решении задач. Обратите внимание, что электрический заряд иногда называют количеством электричества.
Например, давайте найдем количество электричества, которое проходит сквозь поперечное сечение спирали лампы за $1 space мин$. Сила тока лампы равна $400 space мА$.
Дано:
$I = 400 space мА$
$t = 1 space мин$
СИ:
$I = 0.4 space А$
$t = 60 space с$
$q — ?$
Показать решение и ответ
Скрыть
Решение:
Используем формулу для электрического заряда, полученную из определения силы тока:
$q = It$.
Рассчитаем этот заряд:
$q = 0.4 space А cdot 60 space с = 24 space Кл$.
Ответ: $q = 24 space Кл$.
Упражнения
Упражнение №1
Выразите в амперах силу тока, равную $2000 space мА$; $100 space мА$; $55 space мА$; $3 space кА$.
Дано:
$I_1 = 2000 space мА$
$I_2 = 100 space мА$
$I_3 = 55 space мА$
$I_4 = 3 space кА$
Показать решение и ответ
Скрыть
Решение:
$I_1 = 2000 space мА = 2000 cdot 10^{-3} space А = 2 space А$.
$I_2 = 100 space мА = 100 cdot 10^{-3} space А = 0.1 space А$.
$I_3 = 55 space мА = 55 cdot 10^{-3} space А = 0.055 space А$.
$I_4 = 3 space кА = 3 cdot 10^3 space А = 3000 space А$.
Ответ: $I_1 = 2 space А$, $I_2 = 0.1 space А$, $I_3 = 0.55 space А$, $I_4 = 3000 space А$.
Упражнение №2
Сила тока в цепи электрической плитки равна $1.4 space А$. Какой электрический заряд проходит через поперечное сечение ее спирали за $10 space мин$?
Дано:
$t = 10 space мин$
$I = 1.4 space А$
СИ:
$t = 600 space с$
$q — ?$
Показать решение и ответ
Скрыть
Решение:
Используем формулу: $q = It$.
$q = 1.4 space А cdot 600 space с = 840 space Кл$.
Ответ: $q = 840 space Кл$.
Упражнение №3
Сила тока в цепи электрической лампы равна $0.3 space А$. Сколько электронов проходит через поперечное сечение спирали за $5 space мин$?
Маленькое напоминание:
заряд одного электрона по модулю равен $|q_e| = 1.6 cdot 10^{-19} space Кл$.
Дано:
$t = 5 space мин$
$I = 0.3 space А$
$|q_e| = 1.6 cdot 10^{-19} space Кл$
СИ:
$t = 300 space с$
$n_e — ?$
Показать решение и ответ
Скрыть
Решение:
Для начала определим суммарный заряд, который проходит через поперечное сечение спирали лампы за указанное время:
$q = It$,
$q = 0.3 space А cdot 300 space с = 90 space Кл$.
А теперь найдем количество электронов, которые в сумме несут этот заряд:
$n_e = frac{q}{|q_e|}$,
$n_e = frac{90 space Кл}{1.6 cdot 10^{-19} space Кл} approx 56 cdot 10^{19}$.
Вот такое огромное количество электронов проходит через поперечное сечение спирали всего за 5 минут.
Ответ: $n_e = 56 cdot 10^{19}$.
Как разными способами найти силу тока
Содержание
- 1 Зачем нужно находить силу тока
- 2 Вычисление тока, если известны мощность и напряжение
- 3 Определение мощности прибора
- 4 Вычисление тока при известных значениях напряжения и сопротивления
- 5 Использование мощности и сопротивления
- 6 Непосредственное измерение силы тока
- 7 Видео по теме
Знание силы тока в электрической цепи является в некоторых случаях необходимым. Ее определяют не только с помощью непосредственного измерения, но и расчетов. В последнем случае нужную информацию можно получить на основе технических характеристик оборудования.
Зависимости между основными электрическими величинами
Зачем нужно находить силу тока
Любое вещество состоит из атомов, которые включают в себя положительно заряженное ядро и вращающиеся вокруг него электроны. При отсутствии электрического поля движение этих частиц является хаотичным. Но как только проводник становится частью электрической цепи, подключённой к источнику питания, электроны начинают двигаться по направлению к положительному полюсу.
Ток проявляется через заряд. Каждый электрон несёт в себе элементарный отрицательный электрический заряд. Сила тока — это количество электронов, проходящих через поперечное сечение проводника за какой-то отрезок времени. Следовательно, можно сделать вывод, что рассматриваемый параметр определяют заряд и время.
Электроток, выраженный через заряд и время
Найти силу тока в проводнике можно только в том случае, когда электрическая цепь подключена к источнику питания. Например, это может быть включение бытового прибора в электросеть с переменным напряжением, равным 220 В. Разным приборам для работы нужна разная мощность. В некоторых случаях даже выключенное оборудование может потреблять небольшое количество электричества, если оставить его вилку в розетке. Поэтому рассчитать силу тока в цепи можно через мощность и напряжение.
Слишком интенсивный электроток способен создавать проблемы. Он может, например, привести к перегреву деталей или к их разрушению. Если большой ток пройдёт через человека, то это нанесет серьёзный вред его здоровью или даже станет опасным для жизни. Для нормального и безопасного функционирования оборудования важно, чтобы электроток соответствовал установленным нормативам. Определение силы тока по мощности и напряжению позволяет проверить, насколько она соответствует требованиям.
Вычисление тока, если известны мощность и напряжение
Есть простой способ, как узнать ток, зная мощность и напряжение. В данном случае рассчитать постоянный ток можно по формуле:
Расчет для переменного тока через мощность усложняется, поскольку его величина и направление постоянно меняются. Это обстоятельство нужно учитывать при расчетах. Если питание однофазное, то используется такая формула:
Чтобы определить силу переменного тока в трехфазной сети, следует воспользоваться формулой:
При рассмотрении переменного тока нужно учитывать не только активную, но и реактивную мощность. Первая связана с активным сопротивлением, а вторая — с реактивным (ёмкостным и индуктивным). Соотношение между различными видами отражается с помощью cos φ.
Косинус угла «фи» обычно указывают в технической документации прибора. Если эту информацию нельзя получить из документации, то в расчетах очень мощных устройств принимают значение 0.8. Для большинства обычных бытовых приборов в вычислениях используют 0.95.
Подставив в формулу, применяемую для определения силы тока на участке цепи, значения напряжения U = 220 В для однофазной цепи и 380 В для трехфазной, а также cos φ = 0.95, получим следующие выражения:
Как видим, сила тока в трехфазной и однофазной сети при одинаковой нагрузке будет разной. В однофазной она втрое больше, чем в трехфазной.
Определение мощности прибора
Перед тем как найти силу электрического тока, нужно определить величину используемой мощности:
- Ее значение должно указываться в технической документации. Однако она не всегда доступна. В частности, документация может быть утеряна.
- На задней панели приборов часто имеется наклейка, на которой приведены важнейшие характеристики устройства. В числе прочих обычно указывают мощность.
Задняя панель прибора с указанием основных данных
- Можно воспользоваться таблицей с указанием средних значений мощности для различных видов устройств.
Мощность разных приборов
При вычислениях необходимо помнить, что пусковая мощность может превышать рабочую. Расчёт силы тока должен учитывать обе этих величины. Когда пусковая мощность вызывает резкое мгновенное увеличение силы тока, оно не должно превышать допустимой величины. Для бытовой техники пусковую мощность указывают редко. Поэтому перед тем как рассчитать силу тока, необходимо обратиться к соответствующим справочникам, чтобы найти определенное значение мощности. Для получения ее точной величины следует провести измерение ваттметром.
Вычисление тока при известных значениях напряжения и сопротивления
Если известно напряжение и сопротивление, то сила тока вычисляется по формуле, вытекающей из закона Ома:
Если известны значения ЭДС, внутреннего сопротивления и нагрузки, то можно найти силу тока, используя закон Ома для полной цепи:
Использование мощности и сопротивления
Как известно, мощность можно находить по формуле.
Применив в данном выражении закон Ома, можно привести его к следующему виду:
Теперь силу тока можно выразить так:
Следовательно, вычислить силу тока можно разными способами.
Непосредственное измерение силы тока
Величину силы тока можно не только рассчитывать, но и измерять, используя такие приборы, как амперметр или мультиметр. Любой из них при измерениях должен стать частью электрической цепи. Поэтому прибор нужно подключать последовательно.
Если нет большой нужды измерять силу тока амперметром, то лучше вычислить этот параметр, используя формулы, даже если для этого придется измерить напряжение. Вольтметром эта процедура осуществляется без разрыва электроцепи, чего нельзя сделать при использовании амперметра.
Также применяется магнитометрический способ. Примером его использования являются токовые клещи. Перед тем как определить силу электротока, их устанавливают так, чтобы они охватывали провод. Поскольку вокруг проводника при протекании тока образуется магнитное поле, которое клещи улавливают, то по его характеристикам прибор определяет силу тока в цепи.
Видео по теме
Закон Ома для участка цепи и полной цепи: формулы и определения
Немецкий физик Георг Симон Ом (1787—1854) открыл основной закон электрической цепи.
Закон Ома для участка цепи:
Определение: Cила тока I на участке электрической цепи прямо пропорциональна напряжению U на концах участка и обратно пропорциональна его сопротивлению R.
- I — сила тока (в системе СИ измеряется — Ампер)
- Сила тока в проводнике прямо пропорциональна напряжению и обратно пропорциональна сопротивлению.
- Формула: I=frac
- U — напряжение (в системе СИ измеряется — Вольт)
- Падение напряжения на участке проводника равно произведению силы тока в проводнике на сопротивление этого участка.
- Формула: U=IR
- R— электрическое сопротивление (в системе СИ измеряется — Ом).
- Электрическое сопротивление R это отношение напряжения на концах проводника к силе тока, текущего по проводнику.
- Формула R=frac
Определение единицы сопротивления — Ом
1 Ом представляет собой электрическое сопротивление участка проводника, по которому при напряжении 1 (Вольт) протекает ток 1 (Ампер).
Закон Ома для полной цепи
Определение: Сила тока в цепи пропорциональна действующей в цепи ЭДС и обратно пропорциональна сумме сопротивлений цепи и внутреннего сопротивления источника
Формула I=frac <varepsilon>
- varepsilon — ЭДС источника напряжения, В;
- I — сила тока в цепи, А;
- R — сопротивление всех внешних элементов цепи, Ом;
- r — внутреннее сопротивление источника напряжения, Ом.
Как запомнить формулы закона Ома
Треугольник Ома поможет запомнить закон. Нужно закрыть искомую величину, и два других символа дадут формулу для её вычисления.
.
- U — электрическое напряжение;
- I — сила тока;
- P — электрическая мощность;
- R — электрическое сопротивление
Смотри также:
Для закрепления своих знаний решай задания и варианты ЕГЭ по физике с ответами и пояснениями.
Источник
Расчет силы тока по мощности, напряжению, сопротивлению
Бесплатный калькулятор расчета силы тока по мощности и напряжению/сопротивлению – рассчитайте силу тока в однофазной или трехфазной сети в ОДИН КЛИК!
Если вы хотите узнать как рассчитать силу тока в цепи по мощности, напряжению или сопротивлению, то предлагаем воспользоваться данным онлайн-калькулятором. Программа выполняет расчет для сетей постоянного и переменного тока (однофазные 220 В, трехфазные 380 В) по закону Ома. Рекомендуем без необходимости не изменять значение коэффициента мощности (cos φ) и оставлять равным 0.95. Знание величины силы тока позволяет подобрать оптимальный материал и диаметр кабеля, установить надежные предохранители и автоматические выключатели, которые способны защитить квартиру от возможных перегрузок. Нажмите на кнопку, чтобы получить результат.
Смежные нормативные документы:
- СП 256.1325800.2016 «Электроустановки жилых и общественных зданий. Правила проектирования и монтажа»
- СП 31-110-2003 «Проектирование и монтаж электроустановок жилых и общественных зданий»
- СП 76.13330.2016 «Электротехнические устройства»
- ГОСТ 31565-2012 «Кабельные изделия. Требования пожарной безопасности»
- ГОСТ 10434-82 «Соединения контактные электрические. Классификация»
- ГОСТ Р 50571.1-93 «Электроустановки зданий»
Формулы расчета силы тока
Электрический ток — это направленное упорядоченное движение заряженных частиц.
Сила тока (I) — это, количество тока, прошедшего за единицу времени сквозь поперечное сечение проводника. Международная единица измерения — Ампер (А / A).
— Сила тока через мощность и напряжение (постоянный ток): I = P / U
— Сила тока через мощность и напряжение (переменный ток однофазный): I = P / (U × cosφ)
— Сила тока через мощность и напряжение (переменный ток трехфазный): I = P / (U × cosφ × √3)
— Сила тока через мощность и сопротивление: I = √(P / R)
— Сила тока через напряжение и сопротивление: I = U / R
Коэффициент мощности cos φ – относительная скалярная величина, которая характеризует насколько эффективно расходуется электрическая энергия. У бытовых приборов данный коэффициент практически всегда находится в диапазоне от 0.90 до 1.00.
Источник
Закон Кулона, конденсатор, сила тока, закон Ома, закон Джоуля – Ленца
Теория к заданию 14 из ЕГЭ по физике
Закон Кулона
Закон Кулона — это один из основных законов электростатики. Он определяет величину и направление силы взаимодействия между двумя неподвижными точечными зарядами.
Под точечным зарядом понимают заряженное тело, размер которого много меньше расстояния его возможного воздействия на другие тела. В таком случае ни форма, ни размеры заряженных тел не влияют практически на взаимодействие между ними.
Закон Кулона экспериментально впервые был доказан приблизительно в 1773 г. Кавендишем, который использовал для этого сферический конденсатор. Он показал, что внутри заряженной сферы электрическое поле отсутствует. Это означало, что сила электростатического взаимодействия меняется обратно пропорционально квадрату расстояния, однако результаты Кавендиша не были опубликованы.
В 1785 г. закон был установлен Ш. О. Кулоном с помощью специальных крутильных весов.
Опыты Кулона позволили установить закон, поразительно напоминающий закон всемирного тяготения.
Сила взаимодействия двух точечных неподвижных заряженных тел в вакууме прямо пропорциональна произведению модулей зарядов и обратно пропорциональна квадрату расстояния между ними.
В аналитическом виде закон Кулона имеет вид:
где $|q_1|$ и $|q_2|$ — модули зарядов; $r$ — расстояние между ними; $k$ — коэффициент пропорциональности, зависящий от выбора системы единиц. Сила взаимодействия направлена по прямой, соединяющей заряды, причем одноименные заряды отталкиваются, а разноименные — притягиваются.
Сила взаимодействия между зарядами зависит также от среды между заряженными телами.
В воздухе сила взаимодействия почти не отличается от таковой в вакууме. Закон Кулона выражает взаимодействие зарядов в вакууме.
Кулон — единица электрического заряда. Кулон (Кл) — единица СИ количества электричества (электрического заряда). Она является производной единицей и определяется через единицу силы тока 1 ампер (А), которая входит в число основных единиц СИ.
За единицу электрического заряда принимают заряд, проходящий через поперечное сечение проводника при силе тока $1$А за $1$с.
Заряд в $1$ Кл очень велик. Сила взаимодействия двух точечных зарядов по $1$ Кл каждый, расположенных на расстоянии $1$ км друг от друга, чуть меньше силы, с которой земной шар притягивает груз массой $1$ т. Сообщить такой заряд небольшому телу невозможно (отталкиваясь друг от друга, заряженные частицы не могут удержаться в теле). А вот в проводнике (который в целом электронейтрален) привести в движение такой заряд просто (ток в $1$ А вполне обычный ток, протекающий по проводам в наших квартирах).
Коэффициент $k$ в законе Кулона при его записи в СИ выражается в $Н · м^2$ / $Кл^2$. Его численное значение, определенное экспериментально по силе взаимодействия двух известных зарядов, находящихся на заданном расстоянии, составляет:
Часто его записывают в виде $k=<1>/<4πε_0>$, где $ε_0=8.85×10^<-12>Кл^2$/$H·м^2$ — электрическая постоянная.
Электрическая емкость конденсатора
Электроемкость
Электроемкостью проводника $С$ называют численную величину заряда, которую нужно сообщить проводнику, чтобы изменить его потенциал на единицу:
Емкость характеризует способность проводника накапливать заряд. Она зависит от формы проводника, его линейных размеров и свойств среды, окружающей проводник.
Единицей емкости в СИ является фарада ($Ф$) — емкость проводника, в котором изменение заряда на $1$ кулон меняет его потенциал на $1$ вольт.
Электрический конденсатор
Электрический конденсатор (от лат. condensare, буквально сгущать, уплотнять) — устройство, предназначенное для получения электрической емкости заданной величины, способное накапливать и отдавать (перераспределять) электрические заряды.
Конденсатор — это система из двух или нескольких равномерно заряженных проводников с равными по величине зарядами, разделенных слоем диэлектрика. Проводники называются обкладками конденсатора. Как правило, расстояние между обкладками, равное толщине диэлектрика, намного меньше размеров самих обкладок, так что поле в конденсаторе практически все сосредоточено между его обкладками. Если обкладки являются плоскими пластинами, поле между ними однородно. Электроемкость плоского конденсатора определяется по формуле:
где $q$ — заряд конденсатора, $U$ — напряжение между его обкладками, $S$ — площадь пластины, $d$ — расстояние между пластинами, $ε_<0>$ — электрическая постоянная, $ε$ — диэлектрическая проницаемость среды.
Под зарядом конденсатора понимают абсолютное значение заряда одной из пластин.
Энергия поля конденсатора
Энергия заряженного конденсатора выражается формулами
которые выводятся с учетом выражений для связи работы и напряжения и для емкости плоского конденсатора.
Энергия электрического поля. Объемная плотность энергии электрического поля (энергия поля в единице объема) напряженностью $Е$ выражается формулой:
где $ε$ — диэлектрическая проницаемость среды, $ε_0$ — электрическая постоянная.
Сила тока
Электрическим током называется упорядоченное (направленное) движение заряженных частиц.
Сила электрического тока — это величина ($I$), характеризующая упорядоченное движение электрических зарядов и численно равная количеству заряда $∆q$, протекающего через определенную поверхность $S$ (поперечное сечение проводника) за единицу времени:
Итак, чтобы найти силу тока $I$, надо электрический заряд $∆q$, прошедший через поперечное сечение проводника за время $∆t$, разделить на это время.
Сила тока зависит от заряда, переносимого каждой частицей, скорости их направленного движения и площади поперечного сечения проводника.
Рассмотрим проводник с площадью поперечного сечения $S$. Заряд каждой частицы $q_0$. В объеме проводника, ограниченном сечениями $1$ и $2$, содержится $nS∆l$ частиц, где $n$ — концентрация частиц. Их общий заряд $q=q_<0>nS∆l$. Если частицы движутся со средней скоростью $υ$, то за время $∆t=<∆l>/<υ>$ все частицы, заключенные в рассматриваемом объеме, пройдут через поперечное сечение $2$. Сила тока, следовательно, равна:
В СИ единица силы тока является основной и носит название ампер (А) в честь французского ученого А. М. Ампера (1755-1836).
Силу тока измеряют амперметром. Принцип устройства амперметра основан на магнитном действии тока.
Оценка скорости упорядоченного движения электронов в проводнике, проведенная по формуле для медного проводника с площадью поперечного сечения $1мм^2$, дает весьма незначительную величину — $∼0.1$ мм/с.
Закон Ома для участка цепи
Сила тока на участке цепи равна отношению напряжения на этом участке к его сопротивлению.
Закон Ома выражает связь между тремя величинами, характеризующими протекание электрического тока в цепи: силой тока $I$, напряжением $U$ и сопротивлением $R$.
Закон этот был установлен в 1827 г. немецким ученым Г. Омом и поэтому носит его имя. В приведенной формулировке он называется также законом Ома для участка цепи. Математически закон Ома записывается в виде следующей формулы:
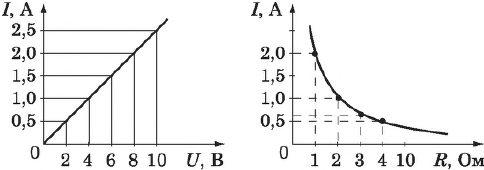
Зависимость силы тока от приложенной разности потенциалов на концах проводника называется вольт-амперной характеристикой (ВАХ) проводника.
Для любого проводника (твердого, жидкого или газообразного) существует своя ВАХ. Наиболее простой вид имеет вольт-амперная характеристика металлических проводников, заданная законом Ома $I=/$, и растворов электролитов. Знание ВАХ играет большую роль при изучении тока.
Закон Ома — это основа всей электротехники. Из закона Ома $I=/$ следует:
- сила тока на участке цепи с постоянным сопротивлением пропорциональна напряжению на концах участка;
- сила тока на участке цепи с неизменным напряжением обратно пропорциональна сопротивлению.
Эти зависимости легко проверить экспериментально. Полученные с использованием схемы, графики зависимости силы тока от напряжения при постоянном сопротивлении и силы тока от сопротивления представлены на рисунке. В первом случае использован источник тока с регулируемым выходным напряжением и постоянное сопротивление $R$, во втором — аккумулятор и переменное сопротивление (магазин сопротивлений).
Электрическое сопротивление
Электрическое сопротивление — это физическая величина, характеризующая противодействие проводника или электрической цепи электрическому току.
Электрическое сопротивление определяется как коэффициент пропорциональности $R$ между напряжением $U$ и силой постоянного тока $I$ в законе Ома для участка цепи.
Единица сопротивления называется омом (Ом) в честь немецкого ученого Г. Ома, который ввел это понятие в физику. Один ом ($1$ Ом) — это сопротивление такого проводника, в котором при напряжении $1$ В сила тока равна $1$ А.
Удельное сопротивление
Сопротивление однородного проводника постоянного сечения зависит от материла проводника, его длины $l$ и поперечного сечения $S$ и может быть определено по формуле:
где $ρ$ — удельное сопротивление вещества, из которого изготовлен проводник.
Удельное сопротивление вещества — это физическая величина, показывающая, каким сопротивлением обладает изготовленный из этого вещества проводник единичной длины и единичной площади поперечного сечения.
Из формулы $R=ρ/$ следует, что
Величина, обратная $ρ$, называется удельной проводимостью $σ$:
Так как в СИ единицей сопротивления является $1$ Ом, единицей площади $1м^2$, а единицей длины $1$ м, то единицей удельного сопротивления в СИ будет $1$ Ом$·м^2$/м, или $1$ Ом$·$м. Единица удельной проводимости в СИ — $Ом^<-1>м^<-1>$.
На практике площадь сечения тонких проводов часто выражают в квадратных миллиметрах (м$м^2$). В этом случае более удобной единицей удельного сопротивления является Ом$·$м$м^2$/м. Так как $1 мм^2 = 0.000001 м^2$, то $1$ Ом$·$м $м^2$/м$ = 10^<-6>$ Ом$·$м. Металлы обладают очень малым удельным сопротивлением — порядка ($1 ·10^<-2>$) Ом$·$м$м^2$/м, диэлектрики — в $10^<15>-10^<20>$ раз большим.
Зависимость сопротивления от температуры
С повышением температуры сопротивление металлов возрастает. Однако существуют сплавы, сопротивление которых почти не меняется при повышении температуры (например, константан, манганин и др.). Сопротивление же электролитов с повышением температуры уменьшается.
Температурным коэффициентом сопротивления проводника называется отношение величины изменения сопротивления проводника при нагревании на $1°$С к величине его сопротивления при $0°$С:
Зависимость удельного сопротивления проводников от температуры выражается формулой:
В общем случае $α$ зависит от температуры, но если интервал температур невелик, то температурный коэффициент можно считать постоянным. Для чистых металлов $α=(<1>/<273>)K^<-1>$. Для растворов электролитов $α
Источник