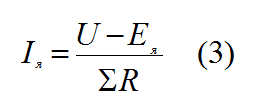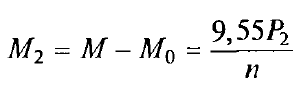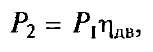Как найти силу тока якоря

Обозначив

и
используя соотношение

(С-7)

можно
найти активный ток якоря как

; (С-8)

В случае расчетов
без использования ЭВМ допускается
использовать приближенное выражение

(С-9)

3.2. Определение результирующей э.Д.С. И м.Д.С.

Для
результирующей э.д.с.

в
соответствии с диаграммой рис. С-1 имеем

(С-11)

При
расчетах без использования ЭВМ допускается
приближенное выражение

(С-11)

Разумеется,
что в выражения (10) или (11) следует
подставить

,
т.е. учитывать опережающий характер
тока якоря.

Для
определения результирующей М.Д.С.

используется «характеристика холостого
хода» синхронной машины (рис.С-2)

Эта
зависимость достаточно точно
апроксимируется выражением

(С-12),

которое следует
использовать для точного определения
Э.Д.С. по М.Д.С. (или наоборот).

3.3 Определение составляющих м.Д.С. Якоря

Из векторной
диаграммы рис. С-1 следует, что

(C-13)

При
невозможности использования ЭВМ
допускается полагать

0

Тогда угол
выбега ротора  в
соответствии с диаграммой может быть
найден как

(с-14)

Приближенное
выражение для :

(С-15)

допускается
при расчетах без использования ЭВМ.

Составляющие
тока якоря ( по осям) определяются как

(С-16)

Необходимо
помнить, что в выражениях (с-13)….(С-17)
составляющая тока якоря

подставляется
отрицательной; углы 
и  также являются
отрицательными.

3.4. Определение тока возбуждения

Из диаграммы
рис. С-1 следует, что

(С-18)

Здесь в
соответствии с (С-16)

является
также отрицательным.

4. Варианты исполнения сд критерия оптимальности

Математическая
модель СД (6) позволяет, таким образом,
при выбранном значении Р_вн
(с учетом разновидности исполнения,
т.е. _н и cos
_н)
определить основные величины, описывающие
рабочий режим (для любой мощности на
валу Р_вт до Р_вм):

• величину тока якоря

  ;

• величину тока возбуждения
  
  ;

• суммарную мощность потерь
  энергии ( с учетом потерь на возбуждение)

(С-19)

Разумеется, что
определение всех этих (и вспомогательных)
величин возможно, если заданы параметры
СД:

• значение сопротивлений

  и
  
  ;

• величина мощности потерь
  

  и
  

  (для і_b=і_b0);

• коэффициент приведения
  м.д.с. якоря к_d;
  к_aq.

Данные о
параметрах десяти вариантов СД, имеющихся
в распоряжении проектанта, приведены
в таблице С-2.

Считается, что
все варианты имеют равную стоимость
(независимо от разновидности, т.е.
значений _н и
cos _н)
и одинаковые характеристики холостого
хода (типа С-17), а также

к_аd=0,9
и к_аq=0,6

Отличие вариантов
состоит прежде всего в величине
предельного допустимого тока возбуждения
i_bmax.
Обращаясь к кривой рис. С-2, можно заметить,
старшие варианты (позволяющие большее
перевозбуждение) обладают меньшей
степенью насыщения стали (поэтому у них
меньше рассеяние полей), но при этом
имеют большие значения сопротивления
якоря.

(С-20)

В качестве
показателей оптимальности варианта СД
следует использовать величину суммарных
потерь энергии

(С-21)

Так как по
условию проекта мощность на валу СД
изменяется случайно и может равновероятно
принимать значения Р_b
:

;

то критерием оптимальности СД
можно считать среднее значение суммарной
мощности потерь энергии

Таким образом,
оптимальным вариантом СД данной
номинальной мощности Р_вн
и разновидности (по значениям _н
и cos _н),
следует считать тот , для которого
выполняются условия:

(С-23)

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Глава   девятая
МАШИНЫ  ПОСТОЯННОГО ТОКА

Соотношение между напряжением, ЭДС и падением напряжения в сопротивлениях цепи якоря определяется на основании второго закона Кирхгофа, согласно которому (см.  рис.  9.22)

Будем считать, что у двигателей последовательного и смешанного возбуждения сопротивление rя включает в себя также и сопротивление последовательной обмотки.

Из (9.18)

Как видно, ток якоря зависит не только от напряжения сети и сопротивлений цепи якоря, но и от ЭДС, индуктируемой в обмотке якоря. При работе двигателя вхолостую М = Мс = 0 и, как было показано ранее, Iя = 0. Из (9.19) следует, что ток Iя может быть равен нулю лишь в том случае, когда Е = U. При увеличении нагрузки двигателя ток Iя возрастает, что можно объяснить только уменьшением ЭДС Е. Поскольку у двигателя параллельного возбуждения при увеличении нагрузки магнитный поток не изменяется, а у двигателей последовательного и смешанного возбуждения он увеличивается, уменьшение ЭДС может происходить лишь вследствие снижения частоты вращения двигателей.

В этой статье описаны основные формулы, величины и их обозначения которые относятся ко всем двигателям постоянного тока.

В результате взаимодействия I_я тока якоря в проводнике L обмотки якоря с внешним магнитным полем возникает электромагнитная сила создающая электромагнитный момент М который приводит якорь во вращение с частотой n.

Противо ЭДС двигателя E_я

При вращении якоря пазовый проводник пресекает линии поля возбуждения с магнитной индукцией B и в соответствии с явлением электромагнитной индукции в проводнике наводится ЭДС E_я направленная навстречу I_я. Поэтому эта ЭДС называется противо ЭДС  и она прямо пропорциональна Ф магнитному потоку и частоте вращения n.

E_я = С_е * Ф * n (1)

C_e — постоянный коэффициент определяемой конструкцией двигателя.

Применив второй закон Кирхгофа получаем уравнение напряжения двигателя.

U = E_я + I_я * ∑R (2)

где ∑R — суммарное сопротивления обмотки якоря включающая сопротивление :

• обмотки якоря
• добавочных полюсов
• обмотки возбуждения (для двигателей с последовательным возбуждением)

Ток якоря I_я

Выразим из формулы 2 ток якоря.

 

Частота вращения якоря

Из формул 1 и 2 выведем формулу для частоты вращения якоря.

Электромагнитная мощность двигателя

P_эм = Е_я I_я (5)

Электромагнитный момент

 где: ω = 2*π*f — угловая скорость вращения якоря, C_м — постоянный коэффициент двигателя (включает в себя конструктивные особенности данного двигателя)

Момент на валу двигателя, т.е. полезный момент, где М₀ момент холостого хода;

Р₂ — полезная мощность двигателя

ПРАКТИЧЕСКАЯ РАБОТА №12

«Расчет параметров двигателей постоянного тока»

ЦЕЛЬ РАБОТЫ: рассчитать ток двигателя в
номинальном режиме, частоту вращения и ток в режиме холостого хода; потери и
КПД двигателя; механические и искусственные характеристики двигателя.   

КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ:

Коллекторные машины обладают
свойством об­ратимости, т. е.
они могут работать как в режиме генератора, так и в режиме двигателя. Поэтому если машину постоянного тока подключить к
источнику энергии постоянного
тока, то в обмотке возбужде­ния
и в обмотке якоря машины появятся токи. Взаи­модействие
тока якоря с полем возбуждения создает на якоре электромагнитный момент М, который
яв­ляется не тормозящим, как это имело место
в гене­раторе, а вращающим.

Под действием электромагнитного момента яко­ря машина начнет вращаться,
т. е. машина будет ра­ботать
в режиме двигателя, потребляя из сети элек­трическую энергию и преобразуя ее в механичес­кую. В процессе работы двигателя его якорь
враща­ется в магнитном поле. В обмотке якоря индуциру­ется ЭДС , направление
которой можно опреде­лить по правилу
«правой руки». По своей природе она не
отличается от ЭДС, наводимой в обмотке якоря
генератора. В двигателе же ЭДС направлена против тока , и поэтому ее называют противоэлектродвижущей силой (противо-ЭДС) якоря.

Для двигателя, работающего с постоянной час­тотой вращения,

                                              
.                                          
     (12.1)

Из (29.1) следует, что
подведенное к двигателю напряжение
уравновешивается противо-ЭДС обмот­ки якоря и падением
напряжения в цепи якоря. На основании (29.1) ток якоря

                                                  
.                                                 
(12.2)

Умножив обе части уравнения (29.1) на ток яко­ря ,
получим уравнение мощности для цепи якоря:

                                             
,                                (12.3)

где  — мощность в цепи
обмотки якоря;   — мощность электрических потерь в цепи якоря.

Для выяснения сущности
выражения  проделаем следую­щее преобразование:

, или
.

Но,

Тогда ,                                
(12.4)

где
 — угловая частота вращения якоря;  — электромаг­нитная
мощность двигателя.

Следовательно, выражение  представляет собой электромаг­нитную мощность двигателя.

Преобразовав выражение (12.3)
с учетом (12.4), получим

                                                            
.

Анализ этого уравнения
показывает, что с увеличением на­грузки на вал двигателя,
т. е. с увеличением электромагнитного момента
М, возрастает мощность в цепи обмотки якоря , т. е.
мощность на входе двигателя. Но так как напряжение, подводимое к двигателю, поддерживается неизменным , то увеличе­ние нагрузки двигателя сопровождается ростом тока в
обмотке якоря  .

В зависимости от способа
возбуждения двигатели постоянного тока, так же как и генераторы, разделяют на
двигатели с возбуждени­ем от постоянных магнитов (магнитоэлектрические) и с
электромаг­нитным возбуждением. Последние в соответствии со схемой включе­ния обмотки возбуждения относительно
обмотки якоря подразделяют на двигатели параллельного (шунтовые),
последовательного (сериесные) и смешанного (компаундные) возбуждения.

В соответствии с формулой ЭДС
 частота вращения двигателя (об/мин)                                                                   .

Подставив
значение  из (12.1), получим (об/мин) ,   (12.5)

Частота вращения двигателя прямо пропорциональна на­пряжению
и обратно пропорциональна магнитному потоку воз­буждения. Физически это объясняется тем, что повышение на­пряжения U или уменьшение потока Ф вызывает увеличение разности ; это,
в свою очередь, ведет к росту тока . Вследствие этого
возросший ток повышает вращающий момент, и
если при этом нагрузочный момент остается неизмен­ным, то частота вращения двигателя увеличивается.

Из (29.5) следует, что регулировать частоту вращения двига­теля
можно изменением либо напряжения U, подводимого к дви­гателю, либо
основного магнитного потока Ф, либо электрическо­го сопротивления
в цепи якоря .

Направление вращения якоря
зависит от направлений магнит­ного потока возбуждения Ф
и тока в обмотке якоря. Поэтому, из­менив направление какой-либо из указанных
величин, можно из­менить направление вращения якоря. Следует иметь в виду, что
переключение общих зажимов схемы у рубильника не дает изме­нения направления вращения якоря, так как при
этом одновремен­но изменяется направление тока и в обмотке якоря, и в
обмотке возбуждения.

Пусковой ток якоря при
полном сопротивлении пускового реостата

                                                    .                                        (12.7)

С появлением тока в цепи
якоря  возникает пусковой мо­мент , под действием которого начинается
вращение якоря. По мере
нарастания частоты вращения увеличивается противо-ЭДС , что ведет к
уменьшению пускового тока и пуско­вого момента.

Схема включения в сеть
двигателя показана на рис.
29.3, а. Характерной особенностью параллельного возбужде­ния
является то, что ток в обмотке возбуждения (ОВ) не за­висит от тока нагрузки (тока якоря). Реостат в цепи
возбуждения  служит
для регулирования тока в обмотке возбуждения и маг­нитного потока
главных полюсов.

Эксплуатационные свойства
двигателя определяются его ра­бочими
характеристиками, под которыми понимают зависимость
частоты вращения n, тока I, полезного момента M₂, вращающего момента M от мощности на валу двигателя Р₂ при  и  (рис.
29.3, 6).

При включении стаби­лизирующей
обмотки согласованно с параллельной обмоткой возбуждения ее МДС
компенсирует размагничивающее
действие реакции якоря так, что поток Ф во всем
диапазоне нагрузок остается практически неизменным.

Изменение частоты вращения
двигателя при переходе от но­минальной
нагрузки к х.х., выраженное в процентах, называют номинальным
изменением частоты вращения:

                                                
,                                   
(29.8)

где  —
частота вращения двигателя в режиме х.х.

Обычно для двигателей
параллельного возбуждения , поэтому характеристику частоты вращения
двигателя па­раллельного возбуждения называют жесткой.

Введение дополнительного
сопротивления в цепь якоря.
Дополнительное сопротивление
(реостат  ) включают в цепь яко­ря аналогично пусковому реостату (ПР).
Однако в отличие от по­следнего оно должно быть рассчитано
на продолжительное проте­кание тока.

При включении сопротивления  в цепь якоря выражение частоты (29.5)
принимает вид

                                         
,                           (29.12)

где  — частота вращения в режиме х.х.;

 —  изменение частоты
вращения, вызван­ное падением напряжения в цепи якоря.

Частоту вращения двигателей
последовательного возбуждения можно
регулировать изменением либо напряжения , либо
маг­нитного потока обмотки
возбуждения. В первом случае в цепь якоря последовательно включают регулировочный реостат  (рис. 29.10, а). С увеличением
сопротивления этого реостата уменьшаются напряжение на входе двигателя и
частота его вра­щения. Этот
метод регулирования применяют главным образом в двигателях небольшой мощности. В случае
значительной мощно­сти двигателя этот способ неэкономичен из-за больших потерь энергии в . Кроме
того, реостат , рассчитываемый на
рабочий ток двигателя,
получается громоздким и дорогостоящим.

Регулировать частоту
вращения двигателя изменением маг­нитного потока можно тремя способами: шунтированием обмотки возбуждения реостатом , секционированием обмотки возбужде­ния и
шунтированием обмотки якоря реостатом . Включение
реостата , шунтирующего обмотку возбуждения, а также уменьшение сопротивления этого
реостата ведет к сниже­нию
тока возбуждения , а следовательно, к росту
частоты вращения. Этот способ
экономичнее предыдущего (см. рис. 29.10, а),
применяется чаще и оценива­ется
коэффициентом регули­рования . Обычно
сопротивление рео­стата  принимается таким, чтобы .

При секционировании об­мотки
возбуждения отключение части витков об­мотки сопровождается ростом частоты вращения. При шунти­ровании обмотки якоря реоста­том увели­чивается ток возбуждения , что вызывает уменьшение  частоты вращения. Этот способ регулирования, хотя и обеспечивает глубокую регулировку, неэкономичен и применяется очень редко.

Потери в машинах постоянного
тока. В машинах
постоянного тока, как и в других электрических машинах, имеют место магнитные, электрические и
механические потери (составляющие группу основных потерь)
и добавочные потери.

Магнитные потери  происходят только в сердечнике якоря, так как только этот элемент
магнитопровода машины постоянного тока подвергается перемагничиванию. Величина магнитных по­терь, состоящих из потерь от гистерезиса и потерь от вихревых токов, зависит от частоты перемагничивания   значений магнитной индукции в
зубцах и спинке якоря, толщины листов электротехнической стали, ее
магнитных свойств и качества изо­ляции этих
листов в пакете якоря.

Электрические потери в
коллекторной машине постоянного тока
обусловлены нагревом обмоток и щеточного контакта. Поте­ри в цепи возбуждения
определяются потерями в обмотке возбуж­дения и в реостате, включенном в цепь
возбуждения:

                                                            
                                        (12.18)

Здесь  — напряжение на зажимах цепи
возбуждения. Потери в
обмотках цепи якоря

                                                    
                                      (12.19)

где сопротивление обмоток в цепи якоря , приведенное к рас­четной рабочей температуре ,
определяется по (13.4) с учетом данных, приведенных в § 13.1 и § 8.4.

Электрические потери также
имеют место и в контакте щеток:

                                                
                                           (12.20)

где
 — переходное падение напряжения, В, на
щетках обеих полярностей, принимаемое в
соответствии с маркой щеток.

Электрические потери в цепи
якоря и в щеточном контакте за­висят от нагрузки машины,
поэтому эти потери называют пере­менными.

Механические потери. В машине
постоянного тока механиче­ские потери
складываются из потерь от трения щеток о коллектор

                                                                                                 (12.21)

трения в подшипниках  и
на вентиляцию

                                               
                                                     (12.22)

где  — коэффициент трения
щеток о коллектор  — поверхность соприкосновения всех щеток
с коллектором, м²;  — удельное давление, Н/м², щетки [для
машин общего назначе­ния =(2÷3)·10⁴ Н/м²];

окружная скорость коллектора
(м/с) диаметром  (м)

                                         .                                                 (12.23)

Механические и магнитные потери при стабильной частоте вращения  можно
считать постоянными.

Сумма магнитных и
механических потерь составляют потери х.х.:

                                    
.                                                    
(12.24)

Если машина работает в качестве двигателя параллельного
возбуждения в режиме х.х., то она потребляет из сети мощность

                 .                   (12.25)

Однако ввиду небольшого
значения тока  электрические по­тери  и весьма малы и обычно не превышают 3% потерь .
Поэтому, не допуская заметной ошибки, можно записать , откуда потери х.х.

                                               
.                                           (12.26)

Таким образом, потери х.х.
(магнитные и механические) могут быть определены экспериментально.

В машинах постоянного тока
имеется ряд трудно учитывае­мых
потерь — добавочных. Эти потери складываются из потерь от вихревых токов
в меди обмоток, потерь в уравнительных соедине­ниях, в стали якоря из-за неравномерного
распределения индукции при
нагрузке, в полюсных наконечниках, обусловленных пульса­цией основного потока из-за наличия зубцов якоря,
и др. Добавоч­ные потери
составляют хотя и небольшую, но не поддающуюся точному учету величину. Поэтому, согласно ГОСТу, в
машинах без компенсационной обмотки значение добавочных
потерь  принимают равным 1% от полезной мощности для генераторов или 1% от подводимой мощности для двигателей. В
машинах с компенсационной
обмоткой значение добавочных потерь прини­мают равным соответственно
0,5%.

Мощность (Вт) на входе
машины постоянного тока (подводимая мощность):

для генератора (механическая
мощность)

                              
                                                 (12.27)

где  — вращающий
момент приводного двигателя, Н∙м;

для двигателя (электрическая
мощность)

                                                                 
.                                                  
(12.28)

Мощность (Вт) на выходе
машины (полезная мощ­ность):

для генератора (электрическая
мощность)

                                                                    
;                                                
(12.29)

для двигателя (механическая
мощность)

                                                        
.                                     (12.30)

Здесь  и  —
момент на валу электрической машины, Н-м;  — частота вращения, об/мин.

Коэффициент полезного
действия. Коэффициент
полезного действия
электрической машины представляет собой отношение мощностей отдаваемой (полезной)  к подводимой (потребляе­мой) ,:

.

Определив суммарную мощность
вышеперечисленных потерь

                                         
,                (12.31)

можно подсчитать КПД машины по одной из следующих
формул:

для генератора

                                     
;                               (12.32)

для двигателя

                                           .                              (12.33)

Обычно КПД машин постоянного
тока составляет 0,75—0,90 для
машин мощностью от 1 до 100 кВт и 0,90—0,97 для машин мощностью свыше 100 кВт. Намного меньше КПД машин
посто­янного тока малой
мощности. Например, для машин мощностью от 5 до 50 Вт  = 0,15÷0,50. Указанные значения
КПД соответст­вуют
номинальной нагрузке машины. Зависимость КПД маши­ны постоянного тока от нагрузки выражается графиком
, форма которого характерна для электрических машин.

Коэффициент полезного
действия электрической машины можно
определять: а) методом непосредственной нагрузки по ре­зультатам
измерений подведенной  и отдаваемой  мощностей; б) косвенным методом по
результатам измерений потерь.

Метод непосредственной
нагрузки применим только для ма­шин малой мощности, для остальных случаев применяется кос­венный метод, как более точный и удобный. Установлено, что при  >
80 % измерять КПД методом непосредственной
нагрузки неце­лесообразно, так как он
дает большую ошибку, чем косвенный метод.

Существует несколько кос­венных способов определения КПД. Наиболее прост способ хо­лостого хода двигателя, когда потребляемая
машиной постоян­ного тока
мощность затрачивает­ся только
на потери х.х. Что же касается
элек­трических потерь, то их определяют расчетным путем
после пред­варительного измерения электрических сопротивлений обмоток и приведения
их к рабочей температуре.

Пример 12.1. Двигатель постоянного тока
параллельного возбуждения
включен в сеть с напряжением 220 В. При номинальной нагрузке и частоте вращения  об/мин
он потребляет ток  = 43 А. Определить КПД
двигателя при номинальной нагрузке, если ток х.х.  = 4 А,
а сопротивления цепей якоря  = 0,25 Ом и возбуждения  = 150 Ом. При каком добавочном сопротивлении ,
включенном последовательно в цепь якоря, частота вращения двигателя будет  = 1000
об/мин (нагрузочный момент )?

Решение. Ток возбуждения  =
220/150 =1,47 А. Ток якоря в ре­жиме х.х. = 4 — 1,47 = 2,53 А. Ток якоря
номинальный  = 43 — 1,47 = 41,53 А. Сумма магнитных и
механических потерь  = 220- 2,53 -2,53²—
0,25 = 555   Вт. Электрические потери в цепи возбуждения по (12.18)

                                                        
 Вт.

Электрические потери в цепи
якоря по (12.19)

                                                     
Вт.

Электрические потери в
щеточном контакте по (12.20)

                                                  
Вт.

Подводимая к двигателю
мощность по (12.28)

                                                       
Вт.

Добавочные потери

                                                  
Вт.

Суммарные потери по (12.31)

                                                   
Вт.

Полезная мощность двигателя

                                             
Вт.

КПД двигателя при номинальной
нагрузке

                                                  
.

Из выражения (29.5) получим

                                                

ЭДС якоря при частоте вращения 1000 об/мин по (12.20)

                                                         
В.

Так как ток якоря прямо
пропорционален моменту , то при  сила тока  после включения  останется
прежней  А. Из выражения тока якоря (12.2) получим

                                           Ом.

Электрические потери в
добавочном сопротивлении

                                        
Вт.

Полезная мощность двигателя при частоте вращения 1000
об/мин

                                         Вт.

Расчет полезной мощности  является приближенным, так как он
не учиты­вает уменьшение
механических потерь двигателя при его переходе на меньшую частоту
вращения.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ:

1.     
Решить
задачу №1. Двигатель постоянного тока параллельного возбуж­дения имеет
следующие данные: номинальная мощность Р_ном, на­пряжение питания U_ном,
номинальная частота вращения n_ном,
сопротивление обмоток в цепи якоря Σr,
сопротивление цепи возбужде­ния r_в, падение
напряжения в щеточном контакте щеток ∆U_щ
= 2 В. Значения перечисленных
параметров приведены в табл. 12.1. Требуется определить потребляемый двигателем
ток в режиме номинальной нагрузки I_ном,
сопротивление пускового реостата R_п.р., при
котором начальный пусковой ток в цепи якоря двигателя был бы равен 2,5 I_аном,
начальный пусковой момент М_п, частоту вращения n₀
и
ток I₀ в режиме
холостого хода, номинальное изменение частоты вращения якоря двигателя при
сбросе нагрузки. Влиянием реакции якоря пренебречь.

Таблица 12.3.

Решение:

—       
определить
потребляемую двигателем мощность при номинальной на­грузке Р_1ном;

—       
определить
ток, потребляемый двигателем при номинальной нагрузке I_ном;

—       
определить
ток в цепи обмотки возбуждения I_в;

—       
определить
ток в обмотке якоря I_аном;

—       
определить
начальный пусковой ток якоря при заданной кратности 2,5 I_п.р.;

—       
определить
требуемое сопротивление цепи якоря при заданной кратности пускового тока 2,5 R_а= R_п.р.+
Σr= U_ном/ I_ап;

—       
определить
сопротивление пускового реостата R_п.р.;

—       
определить
ЭДС якоря в режиме номинальной нагрузки I_аном, используя
уравнение напряжений;

—       
определить
отношение коэффициентов с_M/c_e=[pN/2πɑ]/ [pN/(60ɑ)];

—       
определить
начальный пусковой момент при заданной кратности пуско­вого тока 2,5

—       
М_п= с_MФ I_ап;

—       
определить
момент на валу двигателя при номинальной нагрузке М_2ном;

—       
определить
электромагнитную мощность при номинальной нагрузке Р_эм.ном;

—       
определить
электромагнитный момент при номинальной нагрузке М_ном;

—       
определить
момент холостого хода М₀
=
М_ном — М_2ном;

—       
определить
ток якоря в режиме холостого хода I_аном= М₀/( с_MФ);

—       
определить
ЭДС якоря в режиме холостого хода E_a,
используя уравнение напряжений (принимаем ∆U_щ
= 0);

—       
определить
частоту вращения якоря в режиме холостого хода n₀=
E_a0/( с_еФ);

—       
определить
номинальное изменение частоты вращения двигателя при сбросе нагрузки .

2.      Решить
задачу №2. В табл. 12.1 даны значения параметров двигателя по­стоянного тока
независимого возбуждения: номинальная мощность двигателя Р_ном,
напряжение питания цепи якоря U_ном , напряжение
питания цепи возбуждения U_B, частота
вращения якоря в номиналь­ном режиме n_ном;
сопротивления цепи якоря Σr; и цепи возбужде­ния
r_в,
приведенные к рабочей температуре, падение напряжения в щеточном контакте при
номинальном токе ∆U_щ
= 2 В, номиналь­ное изменение
напряжения при сбросе нагрузки  = 8,0 %, ток якоря в режиме
холостого хода I₀. Требуется
определить все виды потерь и КПД двигателя.

Таблица 12.2.

Решение:

 — определить частоту вращения в режиме холостого
хода n₀;

— определить ЭДС якоря в режиме холостого
хода (падением напряжения в щеточном контакте пренебрегаем ввиду его
незначительной вели­чины в режиме холостого хода) Е_а0;

— определить момент в режиме холостого
хода М₀;

— определить момент на валу двигателя в
режиме номинальной нагрузки М_2ном;

— определить электромагнитный момент
двигателя при номинальной на­грузке М_ном;

— определить электромагнитная мощность
двигателя в режиме номиналь­ной нагрузки Р_эм.ном;

— определить тока якоря в режиме
номинальной нагрузки через ЭДС якоря в режиме холостого хода можно представить
как , с_M/c_e=9,55;

— определить сумму магнитных и
механических потерь двигателя, которая пропор­циональна моменту холостого хода 0,105
М₀n₀;

— определить электрические потери в цепи
обмотки якоря Р_а.э;

— определить электрические потери в
щеточном контакте якоря Р_щ.э;

— определить мощность, подводимая к цепи
якоря, в номинальном режиме Р_1аном;

— определить ток в обмотке возбуждения I_в;

— определить мощность в цепи возбуждения Р_в;

— определить мощность, потребляемую
двигателем в режиме номинальной нагрузки Р_1ном;

—
определить КПД двигателя в номинальном режиме η_ном.

3.      Решить
задачу №3. В табл. 12.3 приведены данные каталога на двигате­ли постоянного
тока независимого возбуждения серии 2П: номи­нальная мощность Р_Ном,
номинальное
напряжение, подводимое к цепи якоря, U_ном, номинальная
частота вращения n_ном, КПД
двига­теля η_ном,
сопротивление цепи якоря, приведенное к рабочей температуре Σr. Требуется определить сопротивление
добавочного ре­зистора г_д, который следует включить в цепь якоря,
чтобы при но­минальной нагрузке двигателя частота вращения якоря составила 0,5п_1ном;
построить естественную и искусственную механические ха­рактеристики двигателя.

Таблица
12.3.

Решение.

— определить ток в цепи якоря в режиме
номинальной нагрузки при п_ном== 750
об/мин I _aном;

— определить ЭДС в режиме номинальной
нагрузки (падением напряжения в щеточном контакте пренебрегаем) Е_ном
;

— определить частоту вращения идеального
холостого хода (пограничная ча­стота вращения) n_оо ; — —
определить номинальный момент на валу двигателя М_2ном;

— по полученным данным построить
естественную механическую характе­ристику (рис. 12.1, график 1);

— определить частоту вращения при включе­нии
резистора п’_ном = 0,5
п_ном;

— по вычисленным данным построить
искусственную механическую характеристику двигателя (рис. 12.1, график 2);

— определить
сопротивление резистора r_Д.

4.     
Оформить отчет по практической работе.

5.     
Ответить на контрольные вопросы.

6.     
Сделать вывод о проделанной работе.

Рисунок 12.1.Механические характеристики
двигателя постоянного тока

КОНТРОЛЬНЫЕ ВОПРОСЫ:

1.    Каким свойством обладают коллекторные машины?

2.    Охарактеризуйте вращающий момент. Где он возникает?

3.    Почему в двигателе постоянного тока ЭДС
называется противоэлектродвижущей силой (противо-ЭДС) якоря?

4.    Что является рабочими характеристиками
двигателя?

5.    Как можно регулировать частоту вращения двигателей
последовательного возбуждения?

6.    От чего зависит направление вращения
якоря?

7.    Виды потерь двигателя постоянного тока и
их характеристики.