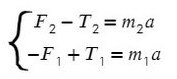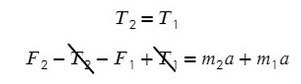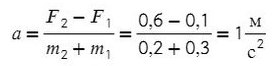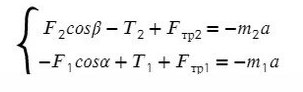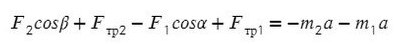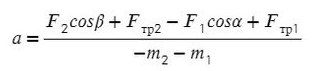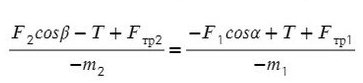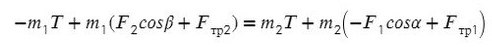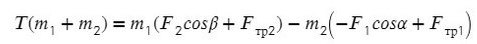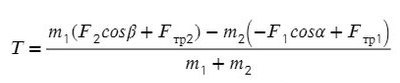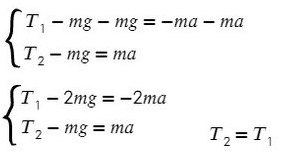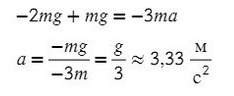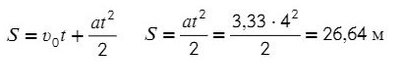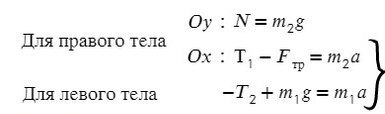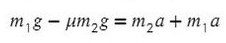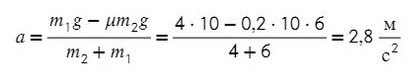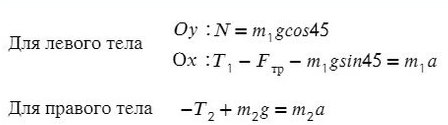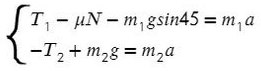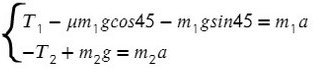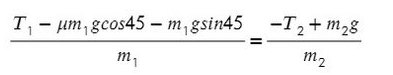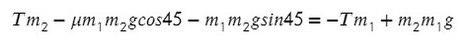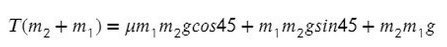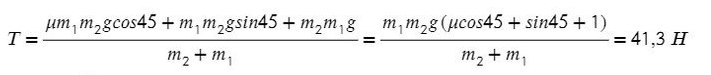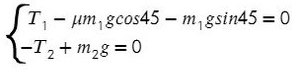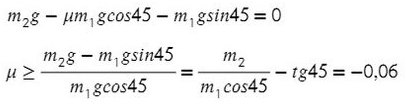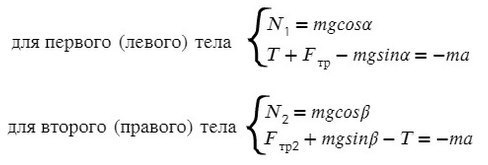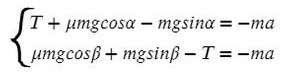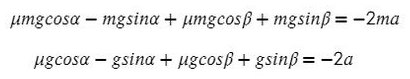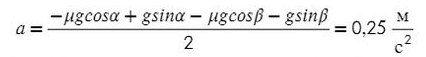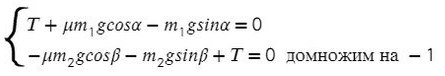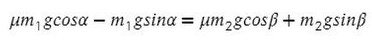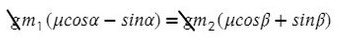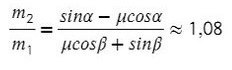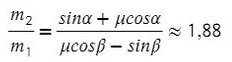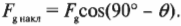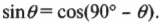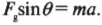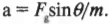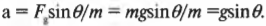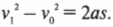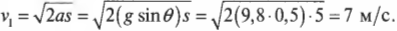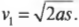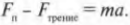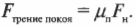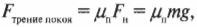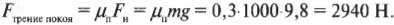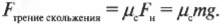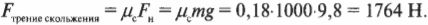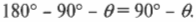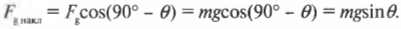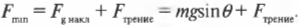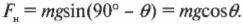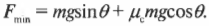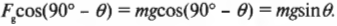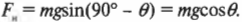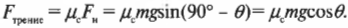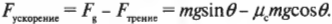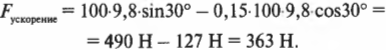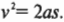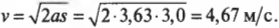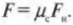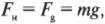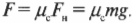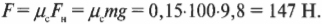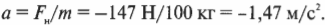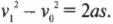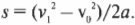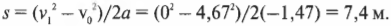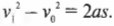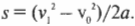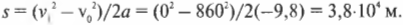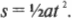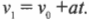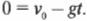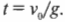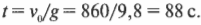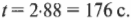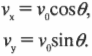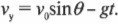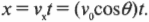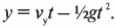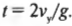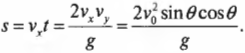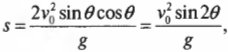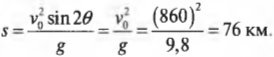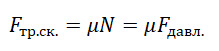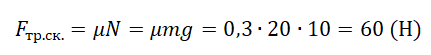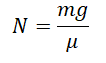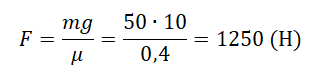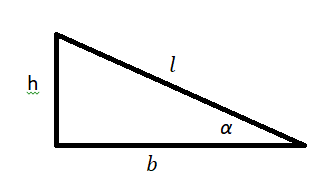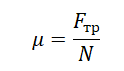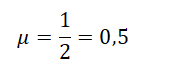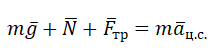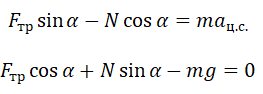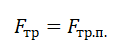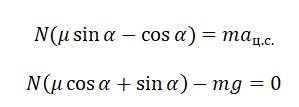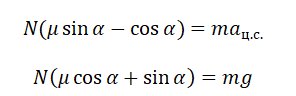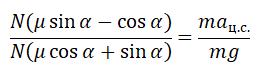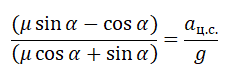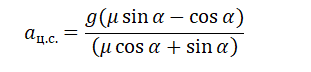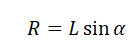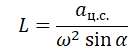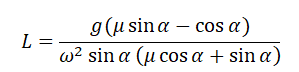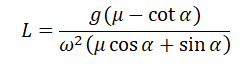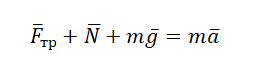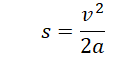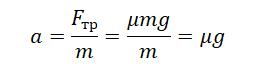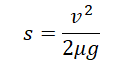Динамика: движения системы связанных тел.
Проецирование сил нескольких объектов.
Действие второго закона Ньютона на тела, которые скреплены нитью
Если ты, дружок, позабыл, как силушку проецировать, советую мыслишки в своей головушке освежить.
А для тех, кто все помнит, поехали!
Задача 1. На гладком столе лежат два связанных невесомой и нерастяжимой ниткой бруска с массой 200 г левого и массой правого 300 г. К первому приложена сила 0,1 Н, к левому — в противоположном направлении сила 0,6 Н. С каким ускорением движутся грузы?
Движение происходит только на оси X.
Т.к. к правому грузу приложена большая сила, движение данной системы будет направлено вправо, поэтому направим ось так же. Ускорение у обоих брусков будет направлено в одну сторону — сторону большей силы.
По II з. Ньютона спроецируем силы обоих тел на Ох:
Сложим верхнее и нижнее уравнение. Во всех задачах, если нет каких-то условий сила натяжения у разных тел одинакова T₁ и Т₂.
Выразим ускорение:
Ответ: 1 м/с²
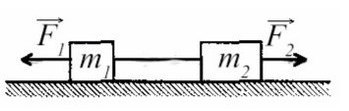
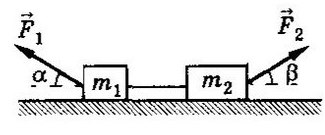
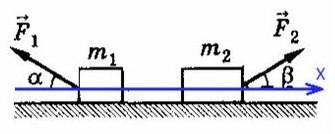
Задача 2. Два бруска, связанные нерастяжимой нитью, находятся на горизонтальной плоскости. К ним приложены силы F₁ и F₂, составляющие с горизонтом углы α и β. Найти ускорение системы и силу натяжения нити. Коэффициенты трения брусков о плоскость одинаковы и равны μ. Силы F₁ и F₂ меньше силы тяжести брусков. Система движется влево.
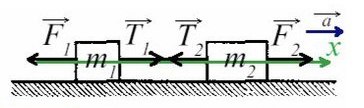
Cистема движется влево, однако ось можно направить в любую сторону (дело лишь в знаках, можете поэксперментировать на досуге). Для разнообразия направим вправо, против движения всей системы, мы же любим минусы! Спроецируем силы на Ох (если с этим сложности — вам сюда ).
По II з. Ньютона спроецируем силы обоих тел на Ох:
Сложим уравнения и выразим ускорение:
Выразим натяжение нити. Для этого приравняем ускорение из обоих уравнений системы:
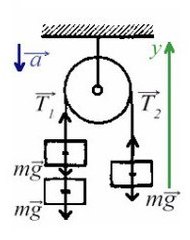
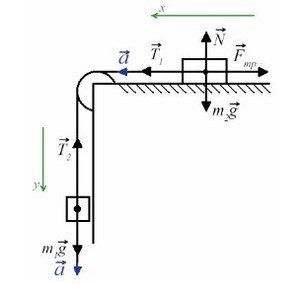
Задача 3. Через неподивжный блок перекинуты нить, к которой подвешены три одинаковых груза (два с одной стороны и один с другой) массой 5 кг каждый. Найти ускорение системы. Какой путь пройдут грузы за первые 4 с движения?
В данной задаче можно представить, что два левых груза скреплены вместе без нити, это избавит нас от проецирования взаимно равных сил.
Вычтем из первого уравнения второе:
Зная ускорение и то, что начальная скорость равна нулю, используем формулу пути для равноускоренного движения:
Ответ: 26,64 м
Задача 4. Два груза массами 4 кг и 6 кг соединены легкой нерастяжимой нитью. Коэффициенты трения между грузом и столом μ = 0,2. Определите ускорение, с которым будут двигаться грузы.
Запишем движение тел на оси, из Oy найдем N для силы трения (Fтр = μN):
(Если сложно понять, какие уравнения понадобятся для решения задачи, лучше запишите все)
Сложим два нижних уравнения для того, чтобы T сократилось:
Выразим ускорение:
Ответ: 2,8 м/с²
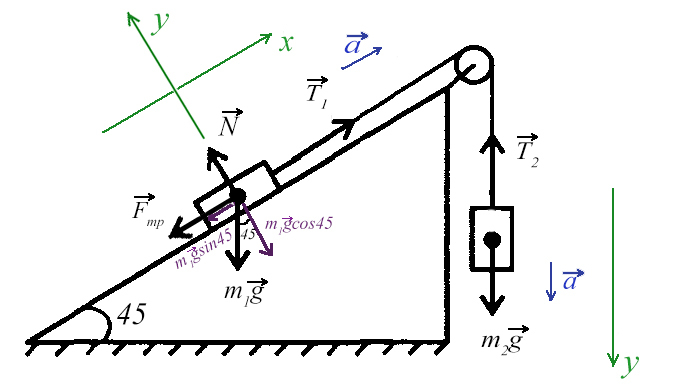
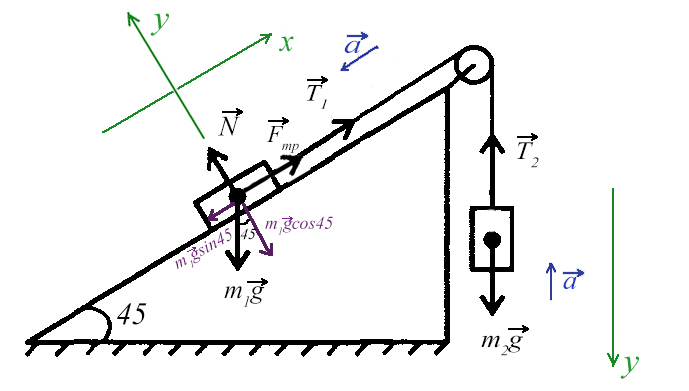
Задача 5. На наклонной поскости с углом наклона 45° лежит брускок массой 6 кг. Груз массой 4 кг присоединен к бруску при помощи нити и перекинут через блок. Определите натяжение нити, если коэффициент трения бруска о плоскость μ = 0,02. При каких значениях μ система будет в равновесии?
Ось направим произвольно и предположим, что правый груз перевешивает левый и поднимает его вверх по наклонной плоскости.
Из уравнения на ось Y выразим N для силы трения на ось Х (Fтр = μN):
Решим систему, взяв уравнение для левого тела по оси Х и для правого тела по оси Y:
Выразим ускорение, чтобы осталась одна неизвестная T, и найдем ее:
Система будет в равновесии. Это означает, что сумма всех сил, действующих на каждое из тел, будет равна нулю:
Получили отрицательный коэффициент трения, значит, движение системы мы выбрали неверно (ускорение, силу трения). Можно это проверить, подставив силу натяжения нити Т в любое уравнение и найдя ускорение. Но ничего страшного, значения остаются теми же по модулю, но противоположными по направлению.
Значит, правильное направление сил должно выглядить так, а коэффициент трения, при котором система будет в равновесии, равен 0,06.
Ответ: 0,06
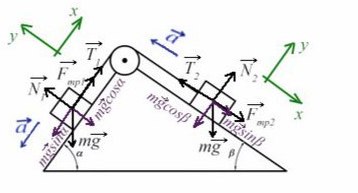
Задача 6. На двух наклонных плоскостях находится по грузу массами 1 кг. Угол между горизонталью и плоскостями равен α = 45° и β = 30°. Коэффициент трения у обеих плоскостей μ = 0,1. Найдите ускорение, с которым движутся грузы, и силу натяжения нити. Каким должно быть отношение масс грузов, чтобы они находились в равновесии.
В данной задаче уже потребуются все уравнения на обе оси для каждого тела:
Найдем N в обоих случаях, подставим их в силу трения и запишем вместе уравнения для оси Х обоих тел:
Сложим уравнения и сократим на массу:
Выразим ускорение:
Подставив в любое уравнение найденное ускорение, найдем Т:
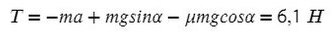
Сложим уравнения
Все, что с одной массой, перенесем в одну часть, все остальное — в другую часть уравнения:
Получили, что отношение масс должно быть таким:
Однако, если мы предположим, что система может двигаться в другом направлении, то есть правый груз будет перевешивать левый, направление ускорения и силы трения изменится. Уравнения останутся такими же, а вот знаки будут другими, и тогда отношение масс получится таким:
Тогда при соотношении масс от 1,08 до 1,88 система будет находиться в покое.
У многих может сложиться впечатление, что соотношение масс должно быть каким-то конкретным значением, а не промежутком. Это правда, если отстутвует сила трения. Чтобы уравновешивать силы тяжести под разными углами, найдется только один варинт, когда система находится в покое.
В данном же случае сила трения дает диапазон, в котором, пока сила трения не будет преодолена, движения не начнется.
Ответ: от 1,08 до 1,88
Задачи для закрепления.
Система связанных тел.
Будь в курсе новых статеек, видео и легкого технического юмора.
В этой главе…
- Постигаем гравитацию
- Изучаем влияние наклона плоскости
- Учитываем силы трения
- Измеряем дальность полета под действием силы тяжести
Сила гравитационного притяжения — вот основная тема этой главы. В главе 5 было показано, что для ее преодоления требуется применять силу. В этой главе будет представлены способы влияния гравитационного притяжения и трения на движение объектов по наклонным плоскостям. Кроме того, будет показано, как гравитация влияет на траекторию полета объекта.
Содержание
- Разбираемся с гравитацией
- Движемся по наклонной плоскости
- Вычисляем углы
- Ищем компоненту вектора силы Fg вдоль наклонной плоскости
- Вычисляем скорость вдоль наклонной плоскости
- Разбираемся с ускорением
- Вычисляем углы
- Преодолеваем трение
- Вычисляем силу трения и нормальную силу
- Разбираемся с коэффициентом трения
- Знакомимся со статическим и кинетическим трением
- Изучаем статическое трение
- Поддерживаем движение вопреки трению скольжения
- Тянем груз в гору и боремся с трением
- Вычисляем компоненту силы тяжести
- Определяем силу трения
- Вычисляем путь скольжения холодильника до полной остановки
- Вычисляем ускорение скольжения
- Вычисляем путь скольжения по полу
- Как гравитация влияет на свободное падение объектов
- Стреляем вверх: максимальная высота
- Время подъема ядра
- Общее время полета
- Стреляем под углом
- Разбиваем движение ядра на компоненты
- Определяем максимальную дальность полета ядра
Разбираемся с гравитацией
На поверхности Земли сила гравитационного притяжения ( mathbf{F_g} ) (или сила тяжести) постоянна и равна ( mmathbf{g} ), где ( m ) — это масса объекта, a ( mathbf{g} ) — ускорение свободного падения под действием силы тяжести, равное 9,8 м/с2.
Ускорение — это вектор, а значит, он имеет величину, направление и точку приложения (подробнее об этом см. главу 4). Уравнение ( mathbf{F_g}=mmathbf{g} ) интересно тем, что ускорение свободного падения объекта ( g ) не зависит от массы объекта.
Поскольку ускорение свободного падения не зависит от массы объекта, то более тяжелый объект падает нисколько не быстрее, чем более легкий объект. Сила тяжести сообщает свободно падающим телам одинаковое направленное вниз ускорение ( mathbf{a} ) (на поверхности Земли равное ( mathbf{g} )), независимо от их массы.
Сказанное выше относится к объектам вблизи поверхности Земли, а в главе 7 рассматриваются другие ситуации вдали от Земли (например, на орбите Луны), где сила тяжести и ускорение свободного падения имеют другие значения. Чем дальше вы находитесь от центра Земли, тем меньше сила тяжести и ускорение свободного падения. В примерах этой главы ускорение свободного падения направлено вниз. Но это не значит, что оно влияет только на движение предметов вертикально вниз. Здесь рассматриваются также примеры движения объектов под углом к вертикали.
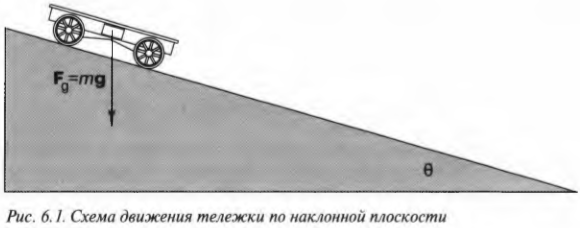
Движемся по наклонной плоскости
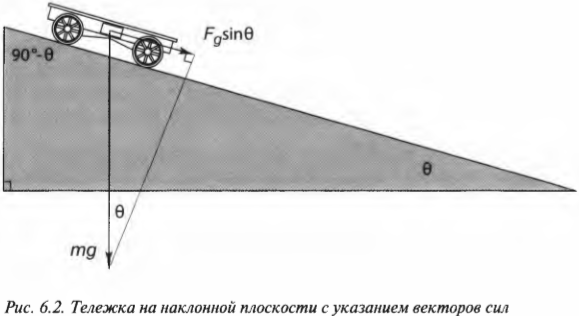
В курсе физики часто упоминаются наклонные плоскости и рассматривается движение объектов по ним. Взгляните на рис. 6.1. На нем показана тележка, которая скатывается по наклонной плоскости. Тележка движется не строго вертикально, а вдоль плоскости, наклоненной под углом ( theta ) к горизонтали.
Допустим, что угол ( theta ) = 30°, а длина наклонной плоскости равна 5 метрам. До какой скорости разгонится тележка в конце наклонной плоскости? Сила тяжести сообщит тележке ускорение, но учтите, что вдоль наклонной плоскости ускорение будет отличаться от ускорения свободного падения. Дело в том, что разгон вдоль наклонной плоскости будет выполнять только компонента силы тяжести вдоль этой наклонной плоскости.
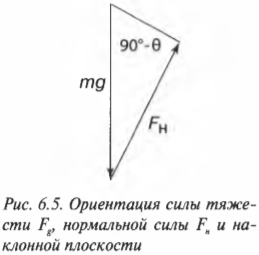
Чему равна компонента силы тяжести, действующей вдоль наклонной плоскости, если на тележку действует направленная вертикально сила тяжести ( mathbf{F_g} )? Взгляните на рис. 6.2, на котором показаны упомянутые выше угол ( theta ) и вектор силы ( mathbf{F_g} ) (подробнее о векторах см. главу 4). Для определения компоненты силы тяжести, действующей вдоль наклонной плоскости, нужно определить угол между вектором силы ( mathbf{F_g} ) и наклонной плоскостью. Для этого потребуются элементарные сведения из геометрии (подробности см. в главе 2), а именно то, что сумма углов треугольника равна 180°. Угол между вектором силы ( mathbf{F_g} ) и основанием наклонной плоскости равен 90°, а угол между наклонной плоскостью и ее основанием равен ( theta ). Поэтому, глядя на рис. 6.2 , можно легко определить угол между вектором силы ( mathbf{F_g} ) и наклонной плоскостью: 180°-90°-( theta ) или 90°-( theta ).
Вычисляем углы
Преподаватели физики используют особый способ вычисления углов между векторами и наклонными плоскостями. Однако читателям книги можно раскрыть этот “секрет” определения угла ( theta ). Для начала обратите внимание на то, что если ( theta ) стремится к 0°, то угол между вектором силы ( mathbf{F_g} ) и наклонной плоскостью стремится к 90°. И наоборот, если ( theta ) стремится к 90°, то угол между вектором силы ( mathbf{F_g} ) и наклонной плоскостью стремится к 0°. На основании этого простого наблюдения можно предположить, что угол между вектором силы ( mathbf{F_g} ) и наклонной плоскостью равняется 90°-( theta ). Как видите, для определения взаимосвязи между углами бывает полезно попробовать поменять значения некоторых углов от 0° до 90°.
Ищем компоненту вектора силы Fg вдоль наклонной плоскости
Итак, зададимся вопросом: чему равна компонента вектора силы ( mathbf{F_g} ) вдоль наклонной плоскости? Теперь мы знаем, что угол между вектором силы ( mathbf{F_g} ) и наклонной плоскостью равняется 90°-( theta ). Значит, компонента вектора силы вдоль наклонной плоскости ( F_{g,накл} ) равна:
Если вы добросовестно учили тригонометрию, то вам наверняка должно быть известно (а если нет, то обратитесь к главе 2), что:
(Часто это знать совсем не обязательно, и может сгодиться предыдущее уравнение.)
Следовательно:
Полученное выражение можно легко проверить следующим образом. Когда ( theta ) стремится к 0°, то значение компоненты силы вдоль наклонной плоскости ( F_{g,накл} ) стремится к 0, поскольку наклонная плоскость стремится к горизонтальному положению. А когда ( theta ) стремится к 90°, то значение компоненты силы вдоль наклонной плоскости ( F_{g,накл} ) стремится к ( F_g ) поскольку наклонная плоскость стремится к вертикальному положению. Итак, если вдоль наклонной плоскости на тележку с массой 800 кг действует сила ( F_gsintheta ), то каким будет ускорение тележки? Это легко определить по известной формуле:
Следовательно:
Задача упрощается, если вспомнить, что ( F_g=mg ) и тогда:
Итак, теперь нам известно, что ускорение тележки вдоль наклонной плоскости равно ( a=gsintheta ). Это соотношение справедливо для любого объекта, ускоряющегося под действием силы тяжести, если не учитывать силы трения.
Вычисляем скорость вдоль наклонной плоскости
Логично было бы поинтересоваться: а какова скорость тележки в конце наклонной плоскости? Для этого нам потребуется следующее уравнение, которое было выведено в главе 3:
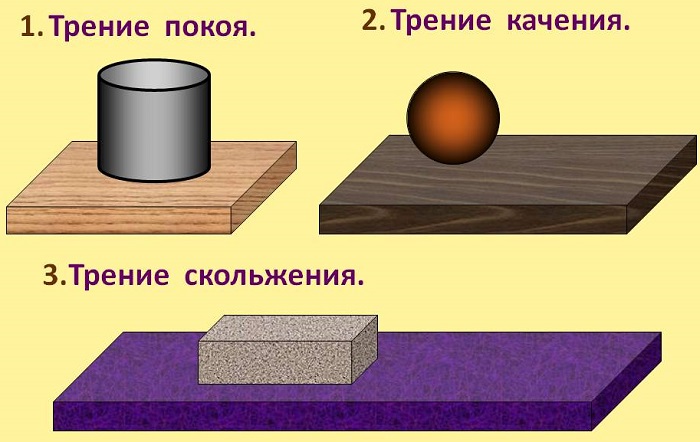
Поскольку начальная скорость ( v_0 ) = 0, а длина наклонной плоскости ( s ) = 5 м, то получим:
Итак, скорость тележки в конце наклонной плоскости ( v_1 ) = 7 метров в секунду. Хотя это не такая уж и большая скорость для автомобиля, но все же не рекомендуется проводить такие эксперименты в домашних условиях. Имейте в виду, что на самом деле скорость будет несколько ниже, поскольку часть энергии расходуется на вращение колес, движение других частей автомобиля, трение и т.д.
Разбираемся с ускорением
Блиц-вопрос: а какую скорость в конце наклонной плоскости приобретет кубик льда при скольжении без трения? Ответ: он будет иметь такую же скорость, что и тележка в предыдущем примере, т.е. 7 м/с. Ускорение любого объекта, движущегося без трения вдоль наклонной плоскости под углом ( theta ), равно ( gsintheta ). Как видите, имеет значение не масса объекта, а компонента ускорения свободного падения вдоль наклонной плоскости. Если нам известно ускорение движения кубика льда и пройденное расстояние ( s ), то получим значение скорости по известной формуле:
Итак, масса не входит в формулу для определения конечной скорости.
Преодолеваем трение
Трудно представить себе повседневную жизнь без трения. Без трения автомобили не могли бы ездить, люди — ходить, а руки — брать любые предметы. Трение создает проблемы, но без него жизнь была бы просто невозможной.
Трение возникает из-за взаимодействия между поверхностными неровностями. Поверхность состоит из множества микроскопических выступов и впадин. При соединении двух поверхностей эти выступы одной поверхности и впадины другой поверхности сцепляются и препятствуют свободному проскальзыванию.
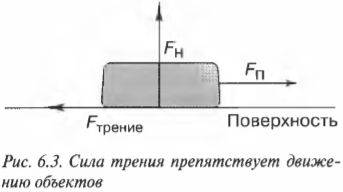
Допустим, что ваши сбережения хранятся в виде огромного золотого слитка, который показан на рис. 6.3, и некий злоумышленник задумал украсть его, но не может нести такой огромный слиток в руках, а может только тащить его волоком. Этот воришка стремится приложить силу к слитку, чтобы ускорить его и сбежать от преследующей его полиции. Однако благодаря силе трения вор не сможет развить большого ускорения.
Определим количественно влияние силы трения на движение объектов. Результирующая сила на слиток и создаваемое ею ускорение определяется как разность приложенной силы ( F_п ) и силы трения ( F_{трение} ) вдоль оси X:
Эта формула выглядит очень просто, но как определить силу трения? Как будет показано ниже, она зависит от нормальной силы.
Вычисляем силу трения и нормальную силу
Сила трения ( F_{трение} ) всегда противодействует приложенной силе, которая вызывает движение. Причем сила трения пропорциональна приложенной силе.
Как показано на рис. 6.3, слиток золота давит на горизонтальную поверхность с силой, равной весу слитка, ( mg ). А поверхность с той же силой действует на слиток. Эту силу называют нормальной силой (или силой нормального давления), ( F_н ).(Нормальной называется компонента силы со стороны поверхности, направленная по нормали к поверхности, т.е. перпендикулярно к поверхности.) Нормальная сила по величине не всегда совпадает с силой тяжести, поскольку нормальная сила всегда перпендикулярна поверхности, по которой движется объект. Иначе говоря, нормальная сила — это сила взаимодействия поверхностей разных объектов, и чем она больше, тем сильнее трение.
В примере на рис. 6.3 слиток скользит вдоль горизонтальной поверхности, поэтому нормальная сила равна весу объекта, т.е. ( F_н=mg ) Итак, у нас есть нормальная сила, которая равна силе давления слитка на горизонтальную поверхность. Для чего она нам нужна? Для определения силы трения.
Разбираемся с коэффициентом трения
Сила трения определяется характеристиками поверхностей соприкасающихся материалов. Как физики теоретически описывают их? Никак. У физиков есть множество общих уравнений, которые предсказывают общее поведение объектов, например ( sum!F=ma ) (см. главу 5). Однако у физиков нет полного теоретического понимания механизмов взаимодействия поверхностей материалов. Поэтому поверхностные характеристики материалов известны, в основном, из опыта.
А из опыта известно, что нормальная сила непосредственно связана с силой трения. Оказывается, что с большой точностью эти две силы пропорциональны друг другу и их можно связать с помощью константы ( mu ) следующим образом:
Согласно этому уравнению, чтобы определить силу трения, нужно умножить нормальную силу на некую постоянную величину, т.е. константу ( mu ). Такая константа называется коэффициентом трения, и именно она характеризует свойства сцепления шероховатостей данных поверхностей.
Величина коэффициента трения находится в диапазоне от 0 до 1. Значение 0 возможно только в идеализированном случае, когда трение отсутствует вообще. А значение 1 соответствует случаю, когда сила трения максимальна и равна нормальной силе. Это значит, что максимальная сила трения для автомобиля не может превышать его веса.
Обратите внимание, что уравнение ( F_{трение}=mu F_н ) не является соотношением между векторами, поскольку эти векторы направлены в разные стороны. Например, на рис. 6.3 они перпендикулярны друг другу. Действительно, нормальная сила ( mathbf{F_н} ) всегда перпендикулярна поверхности, а сила трения ( mathbf{F_{трение}} ) — параллельна. Эти направления определяются их природой: нормальная сила ( mathbf{F_н} ) определяет степень сжатия поверхностей, а сила трения ( mathbf{F_{трение}} ) — степень противодействия скольжению вдоль поверхностей.
Сила трения не зависит от площади соприкосновения двух поверхностей. Это значит, что слиток с той же массой, но вдвое длиннее и вдвое ниже исходного будет испытывать точно такую же силу трения при скольжении по поверхности. При этом увеличивается вдвое площадь соприкосновения, но уменьшается вдвое давление, т.е. величина силы, которая приходится на единицу площади.
Итак, мы получили предварительные сведения и готовы вычислить силу трения? Не так быстро. Оказывается, что коэффициент трения бывает двух типов.
Знакомимся со статическим и кинетическим трением
Два разных коэффициента трения соответствуют двум разным типам трения: статическому трению (или трению покоя) и кинетическому трению (или трению скольжения).
Дело в том, что эти типы трения соответствуют двум разным физическим процессам. Если две поверхности не движутся относительно друг друга, то на микроскопическом уровне они взаимодействуют более интенсивно, и этот случай называется трением покоя. А когда поверхности уже скользят относительно друг друга, то микроскопические неровности не успевают вступить в интенсивное взаимодействие, и этот случай называется трением скольжения. На практике это значит, что для каждого из этих двух типов трения используются свои коэффициенты трения: коэффициент трения покоя ( mu_п ) и коэффициент скольжения ( mu_с ).
Изучаем статическое трение
Трение покоя сильнее трения скольжения, т.е. коэффициент трения покоя ( mu_п ) больше коэффициента трения скольжения ( mu_с ). Это можно упрощенно объяснить следующим образом. В состоянии покоя соприкасающиеся поверхности интенсивно взаимодействуют на микроскопическом уровне, а при скольжении поверхности успевают вступить в интенсивное взаимодействие только на более крупном макроскопическом уровне.
Трение покоя возникает тогда, когда нужно привести в движение покоящийся объект. Именно такую силу трения нужно преодолеть для начала скольжения объекта.
Предположим, что в примере на рис. 6.3 коэффициент трения покоя между слитком и поверхностью равен 0,3, а масса слитка равна 1000 кг (очень приличный слиток). Какую силу должен приложить воришка, чтобы сдвинуть слиток? Из предыдущих разделов нам уже известно, что:
Поскольку поверхность горизонтальна, то нормальная сила направлена противоположно силе тяжести слитка и имеет ту же величину:
где ( m ) — масса слитка, a ( g ) — ускорение свободного падения, вызванное силой притяжения со стороны Земли. Подставляя численные значения, получим:
Итак, воришке потребуется приложить силу 2940 Н, чтобы сдвинуть с места неподвижный слиток. Довольно большая сила! А какая сила потребуется ему, чтобы поддерживать скольжение слитка? Для ответа на этот вопрос нужно рассмотреть трение скольжения.
Поддерживаем движение вопреки трению скольжения
Сила трения скольжения, возникающая из-за скольжения двух соприкасающихся поверхностей, не так велика, как сила трения покоя. Но это совсем не значит, что коэффициент трения скольжения можно легко вычислить теоретически, даже если нам известен коэффициент трения покоя. Оба коэффициента трения приходится определять из опыта.
Именно из опыта известно, что трение покоя больше трения скольжения. Представьте себе, что вы разгружаете неподвижный ящик на наклонной плоскости, но он вдруг начинает скользить вниз. Достаточно заблокировать его движение ногой и с большой вероятностью ящик останется в состоянии покоя, если аккуратно убрать ногу. Именно так, в состоянии покоя, проявляется трение покоя, а в процессе движения ящика — трение скольжения.
Пусть слиток на рис. 6.3 имеет массу 1000 кг, а коэффициент трения скольжения ( mu_c ) равен 0,18. Какую силу должен приложить воришка, чтобы сдвинуть с места неподвижный слиток? Для ответа на этот вопрос нужно воспользоваться следующей формулой:
Подставляя численные значения, получим:
Воришке потребуется приложить силу 1764 Н, чтобы поддерживать скольжение слитка. Не такая уж и маленькая сила, если, конечно, воришке не помогают его верные друзья. Однако это не так уж и легко, и полиция быстро сможет догнать этого воришку. Зная законы физики, полицейские вряд ли захотят прилагать лишние усилия: “Слиток-то мы нашли, а вот домой тащите его сами”.
Тянем груз в гору и боремся с трением
В предыдущих примерах со слитком описывалось трение на горизонтальной поверхности. А как определить силу сопротивления со стороны трения на наклонной плоскости?
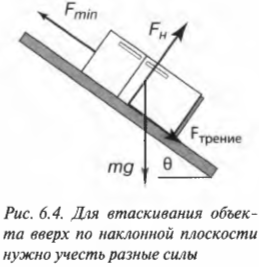
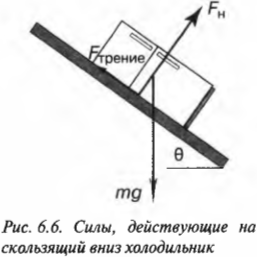
Допустим, что, собираясь на рыбалку, вы решили захватить с собой холодильник массой 100 кг. Единственный способ погрузить его в багажник автомобиля — это втащить холодильник по наклонной плоскости, как показано на рис. 6.4. Пусть наклонная плоскость расположена под углом 30°, коэффициент трения покоя равен 0,2, а коэффициент трения скольжения — 0,15. Хорошая новость заключается в том, что вам помогают два друга, а плохая — в том, что каждый из вас способен приложить силу не более 350 Н.
Ваши друзья растеряны? “Не стоит беспокоиться, немного физики — и все будет в порядке”, — можете ответить им вы, доставая калькулятор. Итак, нам нужно вычислить минимальную силу, которую нужно приложить, чтобы втащить холодильник вверх по наклонной плоскости в багажник автомобиля вопреки силе трения и силе тяжести.
Вычисляем компоненту силы тяжести
Для этого нужно внимательно изучить схему на рис. 6.4. Сила тяжести действует на холодильник и направлена вертикально вниз. Сумма углов треугольника, образованного вектором силы тяжести, наклонной плоскостью и ее основанием, равна 180°. Угол между вектором силы тяжести и основанием наклонной плоскости равен 90°, а угол между наклонной плоскостью и ее основанием — ( theta ). Поэтому угол между наклонной плоскостью и вектором силы тяжести равен:
Компонента силы тяжести, действующая вдоль наклонной плоскости, равна:
Таким образом, минимальная сила, с которой нужно толкать холодильник вверх по наклонной плоскости, равна сумме силы трения, ( F_{трение} ), и этой компоненты ( F_{g,накл} ), т.е.:
Определяем силу трения
Следующий вопрос: чему равна сила трения, ( F_{трение} )? Какой коэффициент трения нужно использовать для ее определения: покоя или скольжения? Поскольку коэффициент трения покоя больше коэффициента трения скольжения, то для оценки минимально необходимой силы имеет смысл учесть коэффициент трения покоя. Ведь после того как холодильник удастся сдвинуть с места, для скольжения придется прикладывать меньшую силу. Итак, с учетом коэффициента трения покоя, получим для силы трения
Для определения этой силы трения нам потребуется вычислить нормальную силу, ( F_н ) (более подробно эта сила описывается выше в этой главе). Она равна компоненте силы тяжести, которая направлена перпендикулярно (т.е. по нормали, откуда и происходит ее название) к наклонной плоскости. Как мы уже выяснили, угол между наклонной плоскостью и вектором силы тяжести равен 90°-( theta )(рис. 6.5).
С помощью тригонометрических соотношений (см. главу 2) получим:
Чтобы проверить справедливость этого выражения, попробуйте устремить угол ( theta ) к нулю, при котором нормальная сила ( F_н ) становится равной ( mg ), что и следовало ожидать. Теперь получаем:
После подстановки численных значений получим:
Итак, три человека должны приложить минимально необходимую силу 660 Н, т.е. по 220 Н каждый, что меньше максимально возможной силы 350 Н. С радостным призывом “Приступим!” вы приступаете к работе, втаскиваете холодильник на самый верх наклонной плоскости. Допустим, что из-за несогласованности действий кто-то из вас перестал прикладывать силу. Как результат, холодильник после непродолжительной остановки неожиданно заскользил вниз, а после достижения основания продолжил движение по полу до полной остановки.
Вычисляем путь скольжения холодильника до полной остановки
Допустим, что наклонная плоскость и пол имеют одинаковые коэффициенты трения скольжения. Каким будет путь скольжения холодильника до полной остановки? Пусть сначала холодильник скользит из состояния покоя до основания наклонной плоскости длиной 3 м, как показано на рис. 6.6. Во время такого скольжения холодильник разгоняется и вполне может столкнуться с автомобилем на расстоянии 7,5 м. О, Боже! Неужели они столкнутся? Нужно немедленно достать калькулятор и приступить к расчетам.
Вычисляем ускорение скольжения
При скольжении вниз действующие на холодильник силы направлены иначе, чем при скольжении вверх. Теперь вы и ваши друзья уже не прилагают свои силы, а холодильник скользит только под действием компоненты силы тяжести, направленной вдоль наклонной плоскости. А ей противодействует лишь сила трения. Чему же равна результирующая сумма этих сил? Из предыдущих разделов уже известно, что компонента силы тяжести вдоль наклонной плоскости равна:
А нормальная сила равна:
Это значит, что сила трения скольжения равна:
Результирующая сила, которая действует на холодильник в направлении движения и определяет его ускорение, равна:
Обратите внимание на то, что сила трения, ( F_{трение} ), имеет отрицательный знак, т.е. она направлена противоположно компоненте силы тяжести вдоль наклонной плоскости, которая приводит в движение холодильник. После подстановки численных значений получим:
Поскольку масса холодильника равна 100 кг, то он скользит с ускорением 363 Н/100 кг = 3,63 м/с2 вдоль наклонной плоскости длиной 3 м. Для вычисления конечной скорости холодильника, ( v ), в конце наклонной плоскости нужно использовать следующую известную нам формулу:
После извлечения квадратного корня и подстановки численных значений получим:
Такой будет скорость холодильника в конце наклонной плоскости.
Вычисляем путь скольжения по полу
Как на основе данных, полученных в предыдущем разделе, определить путь скольжения холодильника по полу? Столкнется ли холодильник с автомобилем?
Итак, нам известно, что холодильник начинает движение по полу со скоростью 4,67 м/с. Вопрос: какое расстояние он пройдет до полной остановки? Теперь в горизонтальном направлении на него действует только сила трения, а компонента силы тяжести по горизонтали равна нулю. Поэтому холодильник постепенно замедляется и рано или поздно остановится. Но уцелеет ли при этом стоящий поодаль автомобиль? Как обычно, сначала вычисляем суммарную силу ( F ), действующую на холодильник в направлении движения и определяющую его ускорение. В данном случае она равна силе трения:
Поскольку холодильник движется вдоль горизонтальной поверхности, то нормальная сила ( F_н ) равна силе тяжести ( F_g ), действующей на холодильник:
т.е. суммарная сила равна:
После подстановки численных значений получим:
Именно такая сила сопротивления действует на холодильник и… терроризирует всю округу! Итак, насколько длинным будет тормозной путь холодильника? Подставим численные значения и получим:
Здесь отрицательный знак обозначает замедление холодильника (см. главу 2).
По формуле:
найдем тормозной путь холодильника:
Поскольку конечная скорость ( v_1 ), равна 0, то эта формула упрощается и принимает вид:
Вот это да! Холодильник проедет расстояние 7,4 м и остановится всего в 10 см от автомобиля, который находится на расстоянии 7,5 м от основания наклонной плоскости. Можно расслабиться и понаблюдать за вашими друзьями, которые охвачены паникой и с ужасом в глазах ожидают столкновения холодильника и автомобиля.
Как гравитация влияет на свободное падение объектов
В главе 7 сила гравитационного притяжения (или сила тяжести) описывается в космическом масштабе, а здесь она рассматривается только вблизи поверхности Земли. В физике часто встречаются задачи с учетом силы тяжести. Этот раздел посвящен тому, как сила тяжести влияет на свободное падение объектов, и его следует рассматривать, как переходный между материалом предыдущей главы и материалом главы 7.
Стреляем вверх: максимальная высота
Зная ускорение свободного падения и начальную скорость объекта, можно легко вычислить дальность его полета. Эти знания могут пригодиться при подготовке праздничных фейерверков!
Предположим невероятное: на день рождения друзья подарили вам пушку, способную разгонять ядро весом 10 кг до начальной скорости 860 м/с. С изумлением рассматривая ее, гости начали спорить: а на какую максимальную высоту эта пушка способна выстрелить? Поскольку вы уже владеете всеми необходимыми знаниями, то можете быстро дать ответ на этот вопрос.
Нам известна начальная скорость ядра, ( v_0 ), и ускорение свободного падения ( g ) под действием силы тяжести. Как определить максимальную высоту подъема ядра? В точке максимального подъема ядра его скорость будет равна нулю, а затем оно начнет обратное движение вниз. Следовательно, для вычисления максимальной высоты подъема ядра, ( s ), можно использовать следующую формулу, в которой конечная скорость ( v_1 ) равна нулю:
Отсюда получим:
Подставляя численные значения для начальной скорости ( v_0 ) = 860 м/с2, ускорения свободного падения под действием силы тяжести ( g ) = —9,8 м/с2 (минус обозначает направление ускорения, противоположное направлению перемещения), получим:
Ого! Ядро улетит на высоту 38 км. Совсем неплохо для пушки, подаренной на день рождения. Интересно, а сколько же времени придется его ждать обратно?
Время подъема ядра
Итак, сколько времени потребуется для того, чтобы ядро поднялось на максимальную высоту? В примере из главы 4, где мяч для игры в гольф падал с вершины обрыва, для вычисления дальности его полета использовалось следующее уравнение:
Однако это уравнение представляет собой всего один из многих возможных вариантов поиска ответа на заданный вопрос.
Нам известно, что в точке максимального подъема скорость ядра равна 0. Поэтому для определения времени полета до максимальной высоты можно использовать следующее уравнение:
Поскольку ( v_1 ) = 0 и ( a ) = ( -g ), то:
Иначе говоря, получим:
После подстановки численных значений получим:
Итак, ядру потребуется 88 с, чтобы достичь максимальной высоты. А каково общее время полета?
Общее время полета
Сколько времени потребуется ядру, чтобы достичь максимальной высоты 38 км и вернуться обратно к пушке, если на подъем ему потребовалось 88 с? Общее время полета вычислить очень просто, поскольку обратный путь вниз симметричен прямому пути вверх. Это значит, что скорость ядра в каждой точке обратного пути вниз равна по величине и имеет противоположное направление по сравнению с прямым путем вверх. Поэтому время падения равно времени подъема и общее время полета равно удвоенному времени подъема:
Итак, общее время полета равно 176 с, или 2 минуты и 56 секунд.
Стреляем под углом
В предыдущих разделах пушка стреляла вертикально вверх. Попробуем теперь поразить цель, стреляя ядром из пушки под углом, как показано на рис. 6.7.
Разбиваем движение ядра на компоненты
Как характеризовать движение ядра при стрельбе под углом? Поскольку любое движение всегда можно разбить на компоненты по осям X и Y, а в данном примере сила притяжения действует только вдоль оси Y, то задача упрощается. Разобьем начальную скорость на компоненты (подробнее об этом рассказывается в главе 4):
Эти компоненты независимы, а сила притяжения действует только в направлении оси Y. Это значит, что компонента ( v_x ) остается постоянной, а меняется только компонента ( v_y ):
Теперь легко определить координаты ядра в любой момент. Например, координата ядра по оси X выражается формулой:
Поскольку сила тяжести влияет на движение ядра по вертикали, то координата ядра по оси Y выражается формулой:
Из предыдущего раздела нам уже известно, что общее время полета ядра по вертикали равно:
Теперь, зная время, можно легко определить дальность полета ядра по оси X:
Итак, для вычисления дальности полета ядра по горизонтали нужно знать начальную скорость ядра, ( v_0 ), и угол, ( theta ), под которым сделан выстрел.
Определяем максимальную дальность полета ядра
При каком угле выстрела ( theta ) ядро улетит на максимальное расстояние по горизонтали? Из тригонометрии известно, что ( 2sinthetacostheta=sin2theta ).
Тогда:
и расстояние ( s ) будет максимальным при максимальном значении ( sin2theta=1 ), т.е. при ( theta ) = 45°.
В таком случае:
Совсем неплохо для пушки, подаренной на день рождения!
Глава 6. Запрягаемся в упряжку: наклонные плоскости и трение
3 (59.07%) 43 votes
Трение — вариант взаимодействия двух тел. Оно возникает при движении одного тела по поверхности другого. При этом тела действуют друг на друга с силой, которая называется силой трения. Сила трения имеет электромагнитную природу.
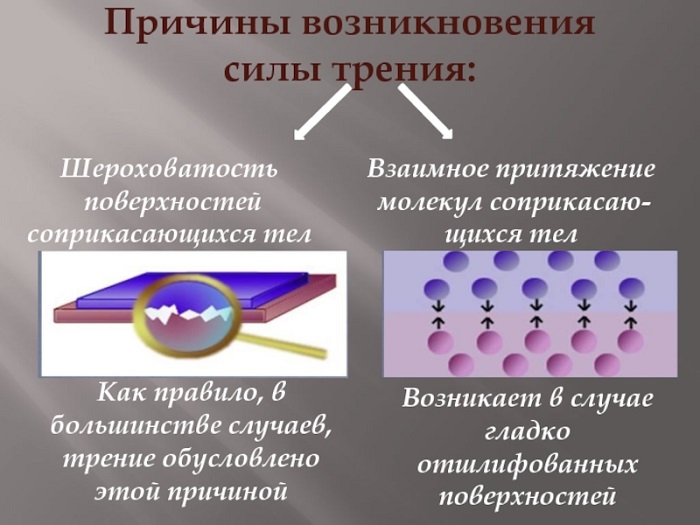
Сила трения — сила, возникающая между телами при их движении или при попытке их сдвинуть. Обозначается как Fтр. Единица измерения — Н (Ньютон).
Трение бывает сухим и жидким. В школьном курсе физике изучается сухое трение.
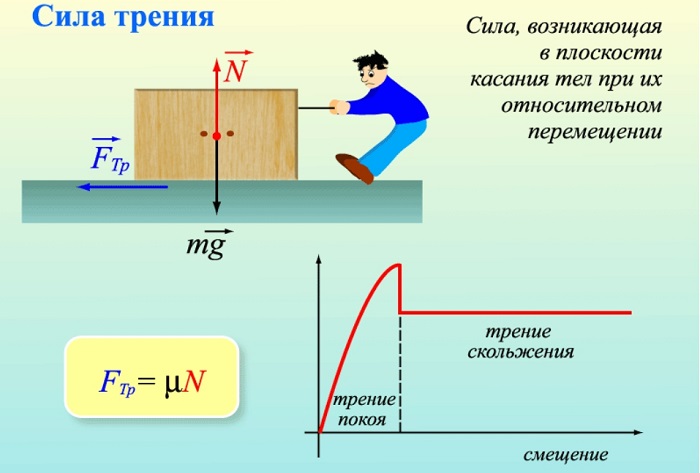
Виды сухого трения:
- трение скольжения;
- трение качения;
- трение покоя.
Трение скольжения
Трение скольжения — трение, возникающее при скольжении одного тела по поверхности другого. Сила трения скольжения направлена противоположно направлению движения тела: Fтр↑↓v.
Сила трения скольжения определяется формулой:
μ — коэффициент трения, N — сила реакции опоры, Fдавл. — сила нормального давления
Сила реакции опоры и сила нормального давления — равные по модулю, но противоположные по направлению силы. Если тело не перемещается с ускорением относительно оси ОУ, модули силы реакции опоры и силы нормального давления равны модулю силы тяжести, действующей на это тело.
Силу трения скольжения зависит от степени неровности (шероховатости) поверхности. Поэтому ее можно легко менять.
Чтобы увеличить силу трения скольжения, нужно сделать поверхность тела более шероховатой. Так, чтобы зимой автомобили не скользили по голому льду, автомобилисты используют зимние шины. От летних они отличаются глубоким протектором и наличием шипов, создающих дополнительную неровность.
Чтобы уменьшить силу трения скольжения, нужно сделать поверхность более ровной. Ее можно отшлифовать или смазать. Так, чтобы лыжи скользили по снегу лучше, их смазывают специальными мазями или парафинами.
Полезные факты
- Если тело движется по гладкой поверхности, сила трения между ними отсутствует.
- Сила трения скольжения не зависит от площади соприкосновения тел.
- Сила трения качения обычно в несколько раз меньше силы трения скольжения. Поэтому тяжелые грузы перемещают не волоком, а с помощью тележек на колесах.
Пример №1. Конькобежец массой 70 кг скользит по льду. Какова сила трения, действующая на конькобежца, если коэффициент трения скольжения коньков по льду равен 0,002?
Сила реакции опоры по модулю равна силе тяжести, действующей на конькобежца. Отсюда:
Трение покоя
Трение покоя возникает при попытке сдвинуть предмет с места. Трение покоя противоположно направлено приложенной к телу силе (в сторону возможного движения).
Сила трения покоя всегда больше нуля, но всегда меньше силы трения скольжения:
0 < Fтр.пок. < Fтр. ск.
Способы определения вида силы трения, возникающей между телами, и ее модуля:
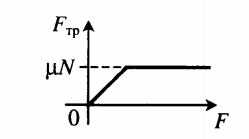
- Когда к телу прикладывается сила F , модуль которой меньше силы трения скольжения, возникает сила трения покоя. Тело продолжает покоиться. При этом модуль силы трения покоя равен модулю прикладываемой к телу силы. Если F < Fтр. ск., Fтр.пок. = F.
- Когда к телу прикладывается сила, модуль которой равен силе трения скольжения или превышает ее, возникает сила трения скольжения. Тело при этом начинает двигаться. Сила трения определяется формулой силы трения скольжения. Если F ≥ Fтр. ск., Fтр. = Fтр.ск.
Графически это можно изобразить так:
Пример №2. На горизонтальном полу стоит ящик массой 20 кг. Коэффициент трения между полом и ящиком равен 0,3. К ящику в горизонтальном направлении прикладывают силу 36 Н. Какова сила трения между ящиком и полом?
Чтобы определить вид трения, возникающего между ящиком и полом, нужно найти силу трения скольжения и сравнить с ней приложенную к ящику силу.
Сила, приложенная к ящику, меньше силы трения скольжения. Значит, между ящиком и полом возникает сила трения покоя. Модуль силы трения покоя равен модулю приложенной силы:
Fтр.пок. = F = 36 (Н).
Описание движения тел с учетом сил трения
Тело может двигаться по горизонтальной, наклонной или вертикальной плоскости. Оно может покоиться, двигаться равномерно или с ускорением, а сила тяги, под действием которой движется тело, может быть направлена, как в сторону движения тела, так и под углом к плоскости. Поэтому применение законов Ньютона к каждому из случаев имеет свои особенности.
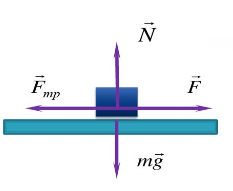
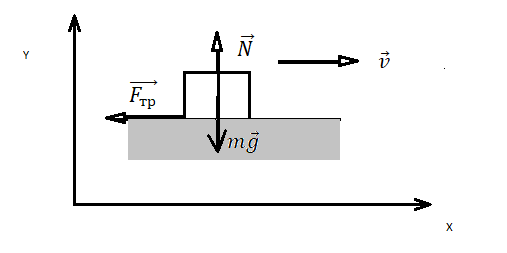
Движение тела по горизонтальной плоскости
Равноускоренное движение по горизонтали, сила тяги параллельная плоскости |
|
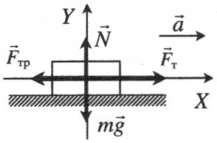 |
Второй закон Ньютона в векторной форме:
mg + N + Fт + Fтр = ma Проекция на ось ОХ: Fт – Fтр = ma Проекция на ось ОУ: N – mg = 0 |
Равнозамедленное движение по горизонтали, сила тяги параллельная плоскости |
|
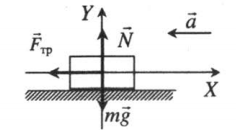 |
Второй закон Ньютона в векторной форме:
mg + N + Fт + Fтр = ma Проекция на ось ОХ: – Fтр = –ma Проекция на ось ОУ: N – mg = 0 |
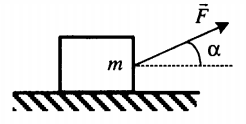
Ускоренное движение по горизонтали, сила тяги направлена под углом к горизонту (вверх) |
|
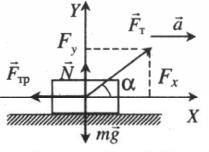 |
Второй закон Ньютона в векторной форме:
mg + N + Fт + Fтр = ma Проекция на ось ОХ: Fтcosα – Fтр = ma Проекция на ось ОУ: Fтsinα + N – mg = 0 |
Ускоренное движение по горизонтали, сила тяги направлена под углом к горизонту (вниз) |
|
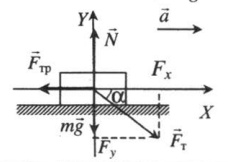 |
Второй закон Ньютона в векторной форме:
mg + N + Fт + Fтр = ma Проекция на ось ОХ: Fтcosα – Fтр = ma Проекция на ось ОУ: N – Fтsinα – mg = 0 |
Внимание! В случаях, когда сила тяги Fт направлена под углом к плоскости движения, сила реакции опоры не равна силе тяжести: N ≠ mg.
Пример №3. Брусок массой 1 кг движется равноускоренно по горизонтальной поверхности под действием силы 10 Н, как показано на рисунке. Коэффициент трения скольжения равен 0,4, а угол наклона α — 30 градусов. Чему равен модуль силы трения?
Сила трения равна произведению коэффициента трения скольжения на силу реакции опоры:
Fтр = μN
Проекция сил на ось ОУ выглядит так:
N – Fтsinα – mg = 0
Отсюда силы реакции опоры равна:
N = Fтsinα + mg
Подставим ее в формулу для вычисления силы трения и получим:
Fтр = μN = μ (Fтsinα + mg) = 0,4(10∙0,5 + 1∙10) = 6 (Н)
Движение тела по вертикальной плоскости
Тело прижали к вертикальной плоскости и удерживают |
|
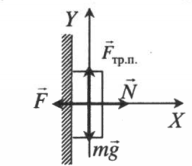 |
Второй закон Ньютона в векторной форме:
mg + N + Fт + Fтр = ma Проекция на ось ОХ: N – F = 0 Проекция на ось ОУ: Fт.п. – mg = 0 |
Тело поднимается под действием силы тяги, направленной под углом к вертикали |
|
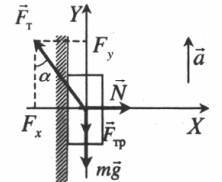 |
Второй закон Ньютона в векторной форме:
mg + N + Fт + Fтр = ma Проекция на ось ОХ: N – Fтsinα = 0 Проекция на ось ОУ: Fтcosα – Fтр – mg = 0 |
Пример №4. Груз массой 50 кг удерживают на вертикальной плоскости, коэффициент трения которой равен 0,4. Определить, какую силу нужно приложить, чтобы груз оставался в состоянии покоя.
Проекция на ось ОХ:
N – F = 0
Отсюда следует, что сила должна быть равна силе реакции опоры.
Проекция на ось ОУ:
Fт.п. – mg = 0
Перепишем, выразив силу трения через силу реакции опоры:
μN – mg = 0
Отсюда выразим силу реакции опоры:
Следовательно:
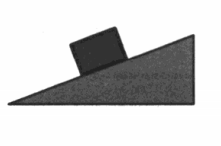
Движение тела по наклонной плоскости
Движение вниз без трения |
|
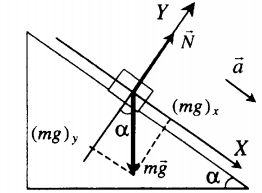 |
Второй закон Ньютона в векторной форме: |
|
mg + N = ma |
|
| Проекция на ось ОХ: | |
|
mg sinα = ma |
|
| Проекция на ось ОУ: | |
|
N – mg cosα = 0 |
|
Тело покоится на наклонной плоскости |
|
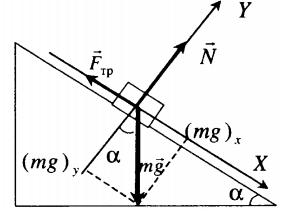 |
Второй закон Ньютона в векторной форме: |
|
mg + N + Fтр = ma |
|
| Проекция на ось ОХ: | |
|
mg sinα – Fтр.п. = 0 |
|
| Проекция на ось ОУ: | |
|
N – mg cosα = 0 |
|
Тело удерживают на наклонной плоскости |
|
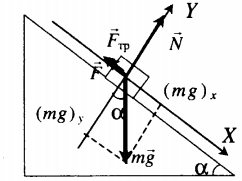 |
Второй закон Ньютона в векторной форме: |
|
mg + N + F + Fтр = ma |
|
| Проекция на ось ОХ: | |
|
F + Fтр. – mg sinα = ma |
|
| Проекция на ось ОУ: | |
|
N – mg cosα = 0 |
|
Равноускоренное движение вверх с учетом силы трения |
|
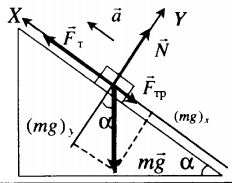 |
Второй закон Ньютона в векторной форме: |
|
mg + N + Fт + Fтр = ma |
|
| Проекция на ось ОХ: | |
|
Fт – mg sinα – Fтр. = ma |
|
| Проекция на ось ОУ: | |
|
N – mg cosα = 0 |
|
Равномерное движение вверх с учетом силы трения |
|
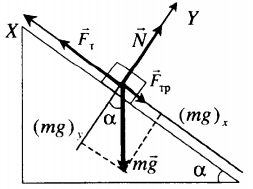 |
Второй закон Ньютона в векторной форме: |
|
mg + N + F + Fтр = ma |
|
| Проекция на ось ОХ: | |
|
Fт – mg sinα – Fтр. = 0 |
|
| Проекция на ось ОУ: | |
|
N – mg cosα = 0 |
Пример №5. Брусок массой 200 г покоится на наклонной плоскости. Коэффициент трения между поверхностью бруска и плоскостью равен 0,6. Определите величину силы трения, если угол наклона плоскости к горизонту равен 30 градусам.
Переведем массу в килограммы: 200 г = 0,2 кг.
Проекция сил, действующих на тело, на ось ОХ:
mg sinα – Fтр.п. = 0
Отсюда сила трения равна:
Fтр.п. = mg sin α
Подставляем известные данные и вычисляем:
Fтр.п. = 0,2∙10∙sin30o = 2∙0,5 = 1 (Н)
Полезная информация
Задание EF18204
При исследовании зависимости силы трения скольжения Fтр от силы нормального давления Fд были получены следующие данные:
|
Fтр, Н |
1,0 |
2,0 |
3,0 |
4,0 |
|
Fд, Н |
2,0 |
4,0 |
6,0 |
8,0 |
Из результатов исследования можно сделать вывод, что коэффициент трения скольжения равен:
а) 0,2
б) 2
в) 0,5
г) 5
Алгоритм решения
1.Записать формулу, связывающую силу трения с силой нормального давления.
2.Выразить из нее коэффициент трения.
3.Взять значения силы трения и силы нормального давления из любого опыта (из любого столбца таблицы).
4.Вычислить коэффициент трения на основании табличных данных.
Решение
Силу трения и силу нормального давления связывает формула:
Fтр = μN
Отсюда коэффициент трения равен:
Сделаем расчет коэффициента трения на основании данных первого опыта (1 столбца):
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17513
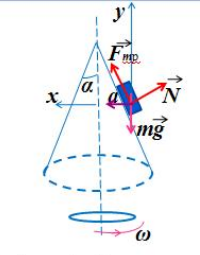
Полый конус с углом при вершине 2α вращается с угловой скоростью ω вокруг вертикальной оси, совпадающей с его осью симметрии. Вершина конуса обращена вверх. На внешней поверхности конуса находится небольшая шайба, коэффициент трения которой о поверхность конуса равен μ. При каком максимальном расстоянии L от вершины шайба будет неподвижна относительно конуса? Сделайте схематический рисунок с указанием сил, действующих на шайбу.
Алгоритм решения
1.Построить чертеж. Указать все силы, действующие на шайбу. Выбрать систему координат.
2.Записать второй закон Ньютона для описания движения шайбы в векторном виде.
3.Записать второй закон Ньютона в виде проекций на оси.
4.Через систему уравнений вывести искомую величину.
Решение
Так как шайба вращается, покоясь на поверхности конуса, на нее действуют четыре силы: сила трения, сила тяжести, сила реакции опоры и центростремительная сила. Изобразим их на чертеже. Выберем систему координат, параллельную оси вращения.
Второй закон Ньютона в векторном виде выглядит следующим образом:
Теперь запишем этот закон в проекциях на оси ОХ и ОУ соответственно:
Так как шайба покоится относительно поверхности конуса, сила трения равна силе трения покоя:
Максимальное значение силы трения равно:
Принимая в учет силу трения покоя, проекции на оси ОХ и ОУ примут следующий вид:
Запишем систему уравнение в следующем виде:
Поделим первое уравнение на второе и получим:
Сделаем сокращения и получим:
Отсюда центростремительное ускорение равно:
Но также известно, что центростремительное ускорение равно произведению квадрата угловой скорости на радиус окружности:
Радиус окружности, по которой вращается шайба вместе с конусом, можно вычислить по формуле:
Отсюда центростремительное ускорение равно:
Выразим искомую величину L:
Подставим в это выражение выведенную для центростремительного ускорения формулу и получим:
Поделим числитель на синус угла α, чтобы упростить выражение, и получим:
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18051
Грузовик массой m, движущийся по прямолинейному горизонтальному участку дороги со скоростью υ, совершает торможение до полной остановки. При торможении колёса грузовика не вращаются. Коэффициент трения между колёсами и дорогой равен μ. Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать.
К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
Алгоритм решения
1.Записать исходные данные.
2.Сделать чертеж. Указать все силы, действующие на грузовик во время торможения. Выбрать систему координат.
3.Записать второй закон Ньютона в векторной форме.
4.Записать второй закон Ньютона в виде проекций на оси ОХ и ОУ.
5.Записать формулу для нахождения силы трения скольжения.
6.Записать формулу для расчета перемещения при движении с постоянным ускорением.
7.Использовать второй закон Ньютона для определения тормозного пути.
Решение
Из условий задачи нам известны следующие величины:
• Начальная скорость грузовика (до начала торможения) v0 = v.
• Коэффициент трения между колесами и дорогой μ.
Выполним чертеж. Выберем такую систему координат, в которой направление движения грузовика во время торможения совпадает с направлением оси ОХ:
Запишем второй закон Ньютона в векторной форме:
Запишем второй закон Ньютона в проекциях на оси:
Fтр = ma
N – mg = 0
Известно, что сила трения скольжения определяется формулой:
Fтр = μN = μmg
Значит, в первую ячейку таблицы мы должны поставить «1».
Перемещение при равнозамедленном движении определяется формулой (учтем, что конечная скорость равна 0, так как грузовик остановился):
Выразим ускорение через проекцию сил на ось ОХ:
Подставим найденное ускорение в формулу тормозного пути и получим:
Следовательно, во вторую ячейку таблицы мы должны поставить «4».
Полный ответ: «14».
Ответ: 14
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 14.5k
Сила трения появляется, когда две поверхности соприкасаются и движутся относительно друг друга. Процесс изучает физика, в частности механика. Она рассматривает основные законы, которым поддаются тела при их движении и взаимодействии, выясняет причины, влияющие на изменение положения предметов.
Определение и природа силы трения
Сила трения Fтр возникает при касании двух тел. Она создает препятствия для их дальнейшего движения.
Это происходит при взаимодействии атомов и молекул, из которых состоят предметы. Поэтому природа ее появления – электромагнитные волны. Она действует в двух направлениях, направлена на оба тела.
При этом ее значение по модулю не изменяется. Если на одно из двух соприкасающихся тел действует сила, то она оказывает влияние и на другое.
На предмет, остающийся без движения, влияет сила трения покоя. Пока ее значение не превысит внешнее вмешательство, пытающееся сместить предмет, он не изменит положение.
Когда же ее величина возрастет до определенного предела, произойдет перемещение в новое место. Тогда появляется сила трения скольжения, ее направление противоположно смещению предмета.
Благодаря действию трения невозможно перемещаться вечно. Движение закончится через определенное время. Если же внешняя сила вновь превысит значение трения покоя, то перемещение возобновится.
Виды силы трения
Основные виды силы трения:
-
Покоя. Она сопротивляется внешним факторам, пытающимся сдвинуть тело. При их отсутствии ее значение приравнивают к нулю.
-
Скольжения. Она находится в прямой зависимости от коэффициента трения и значения силы, с которой поверхность оказывает давление на тело. Ее направление действия всегда перпендикулярно поверхности. Она обычно ниже, чем максимальная сила трения покоя.
-
Качения. Она возникает, когда одно тело катится по поверхности другого. Например, при соприкосновении колеса едущего велосипеда с дорогой или при работе подшипникового механизма. Она оказывает гораздо меньшее действие, чем трение скольжения, если остальные условия считать неизменными. Ее открытие стало незаменимым для техники. Колеса и круглые детали, вращающиеся и меняющие положение, являются основой многих механизмов и работы транспортных средств.
-
Верчения. Она появляется, когда один предмет начинает вращаться по поверхности другого.
Само трение может быть нескольких видов:
-
Сухим. Проявляется при соприкосновении твердых поверхностей. На них не наблюдаются другие материалы и слои. Такое в природе и жизни встречается крайне редко.
-
Вязким. Его еще называют жидкостным. Возникает при взаимодействии твердого тела с жидкостью или газом. Они могут течь мимо неподвижного предмета. Или он перемещается в жидкой или газообразной субстанции. Например, лодку тянут на канате по реке. Тело заставляет перемещаться верхний слой жидкости или газа. Словно тянет его за собой. Он в свою очередь действует на другой слой, расположенный ниже. Чем дальше от тела, тем ниже скорость движения слоев. Это происходит из-за уменьшения влияния твердого предмета. Между слоями возникает сила трения, так как тела движутся относительно друг друга. Она приводит к их торможению, а значит и действует на твердое тело, останавливая его. Температура определяет степень вязкости веществ. Например, она снижается при нагревании масла. Это наглядно видно на работе автомобильного мотора. Когда машина долго находилась на холоде, двигатель нужно сначала разогреть, чтобы увеличить скорость его вращения. У газов обратная зависимость. Вязкость растет с увеличением температуры.
-
Смешанным. Оно наблюдается, когда между телами, соприкасающимися поверхностями, есть слой смазки.
Также трение разделяют на внутреннее и внешнее. Последнее возникает при взаимодействии твердых тел. Значит к нему можно отнести сухое трение.
Внутреннее же характеризуется вязкостью. Именно при взаимодействии жидкостей или газа смещение происходит внутри одного тела, когда слои движутся относительно друг друга.
Как найти силу трения
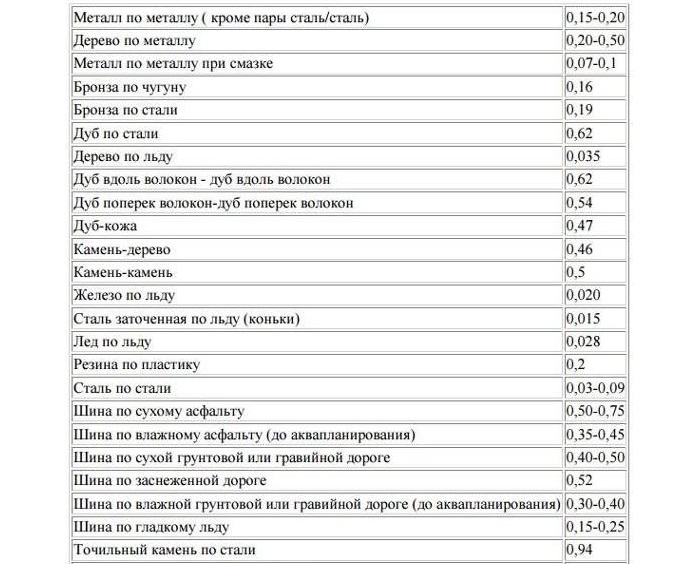
Чтобы найти силу трения, нужно знать коэффициент трения k, зависящий от свойств поверхности. Это постоянная величина, значение которой берется из таблиц.
Также понадобится сила реакции опоры N. Нужная величина определяется произведением двух значений:
Fтр = k * N
Буквой k обозначается коэффициент. Также можно встретить символ µ. Обычно он находится в пределах от 0,1 до 1.
Например, для резины, перемещающейся по сухому асфальту, при движении он колеблется от 0,5 до 0,8. При скольжении металла по дереву – 0,4, железа по чугуну – 0,18.
Сила реакции опоры не отличается от величины силы тяжести, зависящей от веса тела. Поэтому ее значение равно произведению массы тела (m) на ускорение свободного падения (g).
N = m * g
Это постоянная величина, составляющая 9,8 м/с². Это правило действует, когда приходится иметь дело с горизонтальной поверхностью. Сила тяжести и реакция опоры уравновешивают друг друга. Поэтому их считают равными величинами.
Если же происходит движение по наклонной плоскости, ход рассуждений несколько меняется. На предмет по-прежнему действуют силы тяжести и реакция опоры, но не в одном направлении.
При знании угла наклона плоскости к горизонту, формула трансформируется и приобретает следующий вид:
N = k * m *·g *·cosα
Здесь необходимо руководствоваться тем, что косинус это отношение катета, прилежащего к углу, к гипотенузе треугольника. Это один из тех случаев, доказывающих тесную взаимосвязь физики и тригонометрии.
Пример решения задачи
Задача, на применение полученных знаний, связанных с силой трения, поможет закрепить материал.
Условие задачи. На полу стоит коробка весом 7 кг. Коэффициент трения между ней и полом составляет 0,3. К коробке прикладывают силу, равную 14 Н. Сдвинется ли она с места?
Решение.
Коробка находится на горизонтальной плоскости. Она подвержена действию силы тяжести, которую уравнивает реакция опоры. Они направлены перпендикулярно коробке и полу. Значит, для определения силы реакции опоры, нужно умножить массу коробки на ускорение:
N = m * g;
N = 10 кг * 9,8 м/с² = 98 кг * м/с² = 98 Н;
Fтр = k * N;
Fтр = 0,3·* 98Н = 29,4 Н.
Ответ: полученное значение превышает усилия, приложенные к коробке со стороны, так как 29,4 Н > 14 Н. Значит, она останется на первоначальном месте.
Сила трения присутствует в жизни постоянно. Она мешает предметам сдвинуться с места и противится их длительному скольжению и перемещению. Ее значение зависит от поверхностей, с которыми приходится соприкасаться, их свойств и характеристик.
Площадь соприкосновения не учитывается, зато имеет значение положение тела. Например, сила, возникающая при движении автомобиля по ровной поверхности, отличается от величины при перемещении по горной местности, расположенной под углом к горизонту. А если машине приходится двигаться на мокрой дороге, то значение снова меняется.
Движение тела по поверхности другого тела всегда связано с преодолением силы трения. Насколько она замедляет передвижение? В какую сторону направлена? Зависит ли от присутствия между соприкасающимися поверхностями жидкости? Это вопросы, на которые отвечает специальный раздел физики.
Сила трения — что это за показатель?
Соприкосновение двух поверхностей неизменно ведет к появлению силы трения. Ее величина зависит от состояния тел и особенностей их движения:
- между неподвижными телами присутствует трение покоя;
- перекачивающимися — трение качения;
- скользящими — трение скольжения;
- в жидкой среде такой процесс носит название силы сопротивления среды.
Сила, появление которой зависит от соприкосновения двух поверхностей, называется силой трения.
Другими словами, каждое поверхностное движение тем слабее, чем выше трение соприкасающихся сторон. Объясняется это тем, что сила трения всегда направлена против этого движения и распространяется в плоскости, направленной по касательной.
Для понимания данного процесса важно опираться на прямо пропорциональную зависимость силы нормального давления и свойств соприкасающихся поверхностей. Она, в свою очередь, объясняется существованием электромагнитного поля определенной величины.
Естественно, что трение, возникающее внутри механизмов, носит название внутреннего, снаружи — внешнего. Так, если работающий прибор не движется в пространстве, в нем возникают внутренние cилы трения. Если он перемещается относительно других тел, он должен преодолевать внешнюю силу трения.
Действие силы трения можно наблюдать на примере:
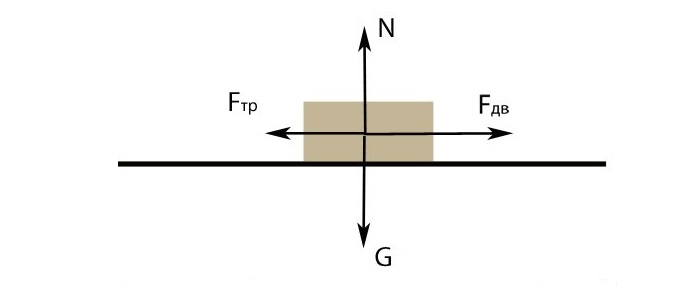
Тело на горизонтальной поверхности, при отсутствии воздействия на него посторонних сил, лежит неподвижно. Начиная применять некую силу движения Fдв происходит попытка сдвинуть его с места.
Сначала это не удается из-за того, что Fтр превышает величину внешней силы. Увеличивая модель последней, добиваются уравновешивания, а затем — превышение силы движения. В данном случае, сила трения — это сила покоя.
Даже максимальное трение не определяется площадью соприкасающихся поверхностей тел, но зависит от силы (N) (нормальное давление) и коэффициента трения покоя (mu0).
(Fтр;пок=mu0N)
Продолжая увеличивать давление, добиваются того, что тело начинает скользить. Теперь при его движении действует сила трения скольжения, на преодоление которой также должно хватать значения внешней силы.
Если рассматриваемый предмет круглой формы, его движение сопровождается силой трения качения. Коэффициент трения при этом гораздо меньше, хотя особенности процесса идентичны.
Тело, находящееся по поверхности под наклоном, испытывает на себе воздействие дополнительной силы — силы опоры.
Понятие и определение, в каких единицах измеряется
Классической формулой для определения Fтр предмета, лежащего на горизонтальной опоре, является:
(F=;kast N)
где (k) — коэффициент трения. Это постоянная величина, которая отражается в специальных технических таблицах и зависит от природы вещества.
(N) — реакция опоры.
Kоэффициент k может встречаться в виде буквы mu.
Помимо него, важно правильно определить реакцию опоры. Она высчитывается по формуле: (N=mast g,) где (m) — известная масса тела, g — показатель свободного падения, равный 9,8м/с2.
Предмет, совершающий движение по наклонной поверхности, испытывает на себе воздействие нескольких сил. Поэтому формула для его Fтр принимает вид:
(Fтр=kast mast gastcosalpha)
В формуле используется гравитационная постоянная g. Ее величина равна 9,8 м/с2.
Для измерения силы трения в СИ существует единица Н (Ньютон). В системе CГС она измеряется в динах (дин).
Выразить смысл единицы Ньютон можно формулой:
(H=кгast м/с2)
Задачи на силу трения, решение типовых примеров
Задания по теме «Сила трения» могут иметь разные направления:
- На определение силы трения.
- На определение коэффициента трения.
- На определение силы трения покоя.
- На определение силы трения скольжения.
- На определение коэффициента трения скольжения.
Пример №1
Масса тела, находящегося на столе, составляет (5 кг. µ=0,2). К телу прилагают внешнюю силу, равную (2,5Н). Какая сила трения при этом возникает (по модулю)?
Решение: по формуле для максимальной силы трения (Fмакс;тр=mu mg=0,2ast5ast10=10Н)
Внешняя сила по условию задачи меньше, максимальной, поэтому тело находится в покое. Fтр уравновешивает внешнюю силу. Следовательно, она равняется (2,5Н.)
Пример №2
Брусок из металла весит 4 кг и лежит на горизонтальной поверхности. Известно, что подвинуть его можно, приложив силу 20 Н, имеющую горизонтальное направление. Если на эту же поверхность положить предмет из пластика с массой 2 кг, необходимая сила значительно изменится. Какой величине она будет равна, если коэффициент трения пластикового предмета в 2 раза меньше металлического.
Решение:
На брусок из металла действует сила согласно формуле (F1=m1ast gast;µ1), на пластиковый — (F2=m2ast gast;µ2=µ1/2m2ast g).
В начале действия (F=Fтр).
Формула, позволяющая решить задачу, имеет следующий вид: (F2=F1/2ast m2/m1=1/2ast20ast2/4=5Н).
Пример №3
Санки весят 5 кг. При скольжении по горизонтальной поверхности на полозья действует сила трения 6 Н. Определить коэффициент трения, если ускорение свободного падения в данной ситуации равно 10 м/с2.
Решение: при скольжении полозьев санок по поверхности сила трения скольжения обуславливается силой реакции опоры, а также коэффициентом µ. Формула имеет следующий вид: (F=;µN). С другой стороны, второй закон Ньютона диктует, что (N=mg). Отсюда вытекает, что (µ=F/mg=6H/5кгast10м/с2=0,12).
Пример №4
Тело имеет массу 5 кг. Оно совершает движение в горизонтальной плоскости. При этом сила трения составляет 10 Н. Определить величину силы трения скольжения при условии, что масса уменьшится на 2 кг, а коэффициент останется без изменений.
Решение: сила трения имеет формулу (F=;µast N). Если тело движется горизонтально по опоре, согласно второму закону Ньютона, его (N) равняется произведению (mast g).
Исходя из этого, (Fтр) будет пропорциональна массе, умноженной на (µ). При неизменном коэффициенте трения уменьшение массы тела в 2 раза приведет к уменьшению силы трения скольжения также в 2 раза. Поэтому:
(10H/2=5H.)
Пример №5
Тело, движущееся по ровной горизонтальной плоскости, давит на нее с силой 20 Н. Сила трения при этом составляет 5 Н. Определить величину коэффициента трения скольжения.
Решение: Поскольку (F=;µast P,µ=;Fтр/P). Подставляя значения, получаем расчет: (5Н/20Н=0,25.)
Ответ: (µ=0,25).
Получить знания или подготовить контрольную работу по теме «Сила трения» можно быстро и грамотно, если обратиться за помощью на Феникс.Хелп.