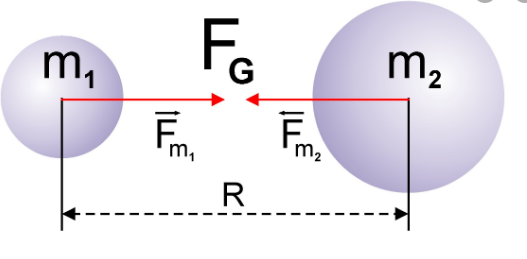
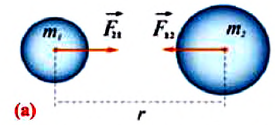
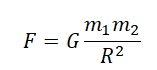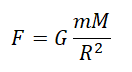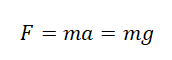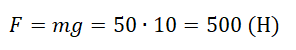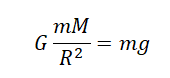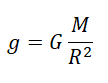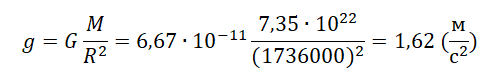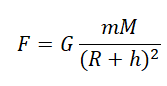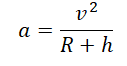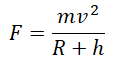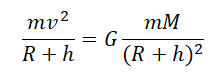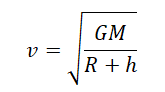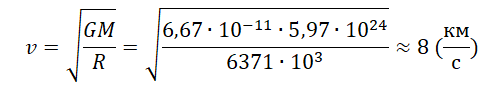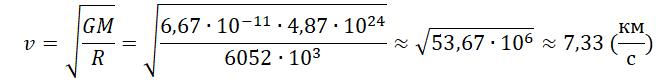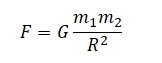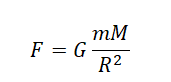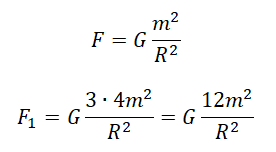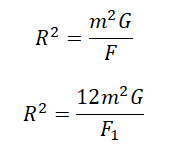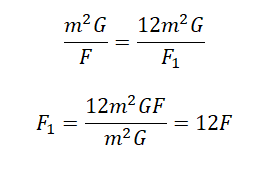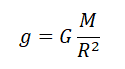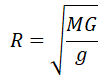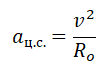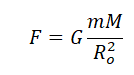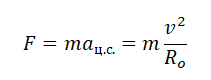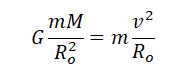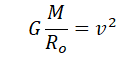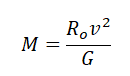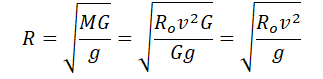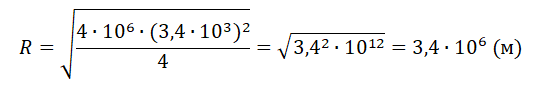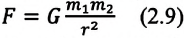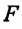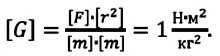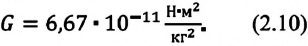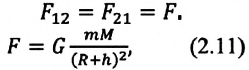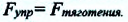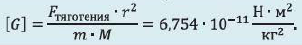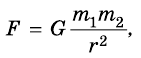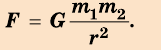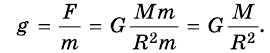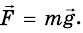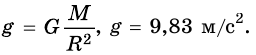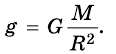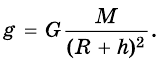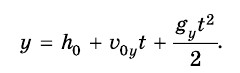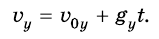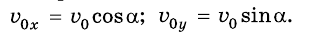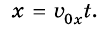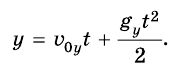Все тела взаимодействуют друг с другом. Так, две материальные точки, обладающие массой, притягиваются друг к другу с некоторой силой, которую называют гравитационной, или силой всемирного тяготения.
Сила всемирного тяготения — сила, с которой все тела притягиваются друг к другу.
Закон всемирного тяготения
Сила взаимного притяжения двух тел прямо пропорциональна произведению масс этих тел и обратно пропорциональна квадрату расстояния между ними.
F — сила всемирного тяготения, m1 и m2 — массы двух притягивающихся друг к другу тел, R — расстояние между этими телами, G — гравитационная постоянная (G = 6,67∙10–11 Н ∙ м2/кг2).
Сила всемирного тяготения направлена по линии, соединяющей центры двух тел.
Гравитационная постоянная численно равна силе притяжения между двумя точечными телами массой 1 кг каждое, если расстояние между ними равно 1 м. Если R = 1 м, m1 = 1 кг и m2 = 1 кг, то F = G.
G = 6,67∙10–11 Н ∙ м2/кг2.
Сила тяжести
Согласно закону всемирного тяготения, все тела притягиваются между собой. Так, Земля притягивает к себе падающий на нее мяч, а мяч притягивает к себе Землю.
Сила тяжести — сила, с которой Земля притягивает к себе тела.
Сила тяжести действует на все тела, находящиеся в поле притяжения Земли. Она всегда направлена к центру нашей планеты.
Расчет силы тяжести на Земле
Силу тяжести можно рассчитать с помощью закона всемирного тяготения. Тогда одна из масс будет равна массе земли. Обозначим ее большой буквой M. Вторая масса будет принадлежать телу, притягивающемуся к Земли. Обозначим его m. В качестве R будет служить радиус Земли. В таком случае сила тяжести будет определяться формулой:
Вывод формулы ускорения свободного падения
Согласно второму закону Ньютона, сила, которая действует на тело, сообщает ему ускорение. Поэтому силу тяжести также можно выразить через это ускорение. Обозначим его g — ускорение свободного падения.
Пример №1. Мальчик массой 50 кг прыгнул под углом 45 градусов к горизонту. Найти силу тяжести, действующую на него во время прыжка.
Сила тяжести зависит только от массы тела и ускорения свободного падения. Направлена она всегда к центру Земли, и от характера движения тела не зависит. Поэтому:
Мы получили две формулы для вычисления силы тяжести: одну — исходя из закона всемирного тяготения, вторую — исходя из второго закона Ньютона. Приравняем правые части формул и получим:
Отсюда:
Формула расчета ускорения свободного падения
Вместо массы и радиуса Земли можно взять массы и радиусы любых планет. Так можно рассчитать ускорение свободного падения для любого космического тела.
Пример №2. Рассчитать ускорение свободного падения на Луне. Считать, что радиус Луны равен 1736 км, а ее масса — 7,35∙1022 кг.
Переведем километры в метры: 1736 км = 1736000 м.
Первая космическая скорость
Исаак Ньютон смог доказать, что причиной падения тел на Землю, движения Луны вокруг Земли и движения Земли вокруг Солнца является сила тяготения. Если камень бросить в горизонтальном направлении, его траектория будет отклонена от прямой линии под действием земной силы тяжести. Если же придать этому камню большую скорость, камень приземлится на большем расстоянии. Значит, существует такая скорость, при которой камень не приземлится, а начнет бесконечно вращаться вокруг Земли.
ОпределениеПервая космическая скорость — минимальная (для заданной высоты над поверхностью планеты) горизонтальная скорость, которую необходимо придать объекту, чтобы он совершал движение по круговой орбите вокруг планеты.
Вывод формулы первой космической скорости
Когда тело массой m вращается на некоторой высоте h, расстояние между ним и центром Земли равно сумме этой высоты и радиуса Земли. Поэтому сила тяготения между этим телом и Землей будет равна:
Движение тела вокруг планеты — частный случай движения тела по окружности с постоянной по модулю скоростью. Мы уже знаем, что такое тело движется с центростремительным ускорением, направленным к центру окружности. В данном случае центростремительное ускорение будет направлено к центру Земли. Это ускорение сообщает телу сила тяготения.
Так как тело движется на некоторой высоте h от поверхности Земли, центростремительное ускорение будет определяться формулой:
Подставив это ускорение в формулу второго закона Ньютона, получим силу, с которой Земля притягивает к себе тело массой m:
Приравняем правые части формул, следующих из закона всемирного тяготения и второго закона Ньютона, и получим:
Отсюда скорость, с которой должно тело массой m бесконечно вращаться вокруг Земли на высоте h, равна:
Скорость бесконечно вращающегося вокруг Земли тела не зависит от его массы. Она зависит только от высоты, на которой оно находится. Чем выше высота, тем меньше скорость его вращения.
Тело, вращающееся вокруг планеты, называется ее спутником. Чтобы любое тело стало спутником Земли, нужно сообщить ему некоторую скорость на поверхности планеты в горизонтальном направлении. Высота h в этом случае равна 0. Тогда эта скорость будет равна:
8 км/с — первая космическая скорость Земли.
Пример №3. Рассчитать первую космическую скорость для Венеры. Считать, что масса Венеры равна 4,87∙1024 кг, а ее радиус равен 6052 км.
Задание EF18521
Сила гравитационного притяжения между двумя шарами, находящимися на расстоянии 2 м друг от друга, равна 9 нН. Какова будет сила притяжения между ними, если расстояние увеличить до 6 м? Ответ выразите в наноньютонах (нН).
Алгоритм решения
- Записать исходные данные.
- Записать закон всемирного тяготения.
- Установить зависимость между силой гравитационного притяжения и расстоянием между телами.
- На основании вывода о зависимости двух величин вычислить гравитационное притяжение между двумя шарами при изменении расстояния между ними.
Решение
Запишем исходные данные:
- Расстояние между двумя шарами в первом случае: R1 = 2 м.
- Расстояние между двумя шарами во втором случае: R2 = 6 м.
- Сила гравитационного притяжения между двумя шарами в первом случае: F1 = 9 нН.
Запишем закон всемирного тяготения:
Из формулы видно, что сила гравитационного притяжения обратно пропорционально квадрату расстояния между телами массами m1 и m2.
R2 больше R1 втрое (6 больше 2 в 3 раза). Следовательно, расстояние между шарами тоже увеличилось втрое. В таком случае сила гравитационного притяжения между ними уменьшится в 32 раз, или в 9 раз. Так как в первом случае эта сила была равна 1 нН, то во втором она составит в 9 раз меньше, или 1 нН.
Ответ: 1
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17569
Две звезды одинаковой массы m притягиваются друг к другу с силами, равными по модулю F. Чему равен модуль сил притяжения между другими двумя звёздами, если расстояние между их центрами такое же, как и в первом случае, а массы звёзд равны 3m и 4m?
а) 7F
б) 9F
в) 12F
г) 16F
Алгоритм решения
1.Записать закон всемирного тяготения.
2.Применить закон всемирного тяготения для первой и второй пары звезд.
3.Из каждого выражения выразить расстояние между звездами.
4.Приравнять правые части уравнений и вычислить силу притяжения между второй парой звезд.
Решение
Закон всемирного тяготения выглядит так:
Примерим этот закон для первой и второй пары звезд:
Выразим квадраты радиусов, так как они в обоих случаях одинаковые:
Приравняем правые части выражений и выразим силу притяжения во втором случае:
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18678
Высота полёта искусственного спутника над Землёй увеличилась с 400 до 500 км. Как изменились в результате этого скорость спутника и его потенциальная энергия?
Для каждой величины определите соответствующий характер изменения:
| 1) | увеличилась |
| 2) | уменьшилась |
| 3) | не изменилась |
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Скорость
спутника |
Потенциальная энергия спутника |
Алгоритм решения
1.Записать закон всемирного тяготения и формулу центростремительного ускорения для движения тела по окружности с постоянной по модулю скоростью.
2.Установить зависимость скорости от высоты спутника над поверхностью Земли.
3.Записать формулу потенциальной энергии и установить, как она зависит от высоты.
Решение
На спутник действует сила притяжения Земли, которая сообщает ему центростремительное ускорение:
F=maц=GmM(R+h)2
Отсюда центростремительное ускорение равно:
aц=GM(R+h)2
Но центростремительное ускорение также равно:
aц=v2(R+h)
Приравняем правые части выражений и получим:
GM(R+h)2=v2(R+h)
v2=MG(R+h)(R+h)2=MG(R+h)
Квадрат скорости спутника обратно пропорционален радиусу вращения. Следовательно, при увеличении высоты увеличивается радиус вращения, а скорость уменьшается.
Потенциальная энергия спутника определяется формулой:
Ep = mgh
Видно, что потенциальная энергия зависит от высоты прямо пропорционально. Следовательно, при увеличении высоты потенциальная энергия спутника тоже увеличивается.
Верная последовательность цифр в ответе: 21.
Ответ: 21
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17578
Искусственный спутник обращается вокруг планеты по круговой орбите радиусом 4000 км со скоростью 3,4 км/с. Ускорение свободного падения на поверхности планеты равно 4 м/с2. Чему равен радиус планеты? Ответ запишите в километрах.
Алгоритм решения
1.Записать исходные данные. Перевести единицы измерения в СИ.
2.Записать формулу ускорения свободного падения и выразить через нее радиус планеты.
3.Записать формулу, раскрывающая взаимосвязь между линейной скоростью и радиусом окружности, по которой движется тело.
4.Записать закон всемирного тяготения применительно к спутнику.
5.Вывести формулу для расчета радиуса планеты.
6.Подставить известные данные и произвести вычисление.
Решение
Запишем исходные данные:
• Линейная скорость спутника: v = 3,4 км/с, или 3,4∙103 м/с.
• Радиус орбиты спутника: Rо = 4000 км, или 4∙106 м.
• Ускорение свободного падения у поверхности планеты: g = 4 м/с2.
Ускорение свободного падения определяется формулой:
Отсюда радиус равен:
Линейная скорость и радиус орбиты связываются формулой:
Используя закон всемирного тяготения, запишем силы, с которой притягивается спутник к планете:
Согласно второму закону Ньютона, сила — это произведение массы на ускорение тела. Следовательно:
Отсюда:
Поделим обе части выражения на массу спутника и радиус его орбиты. Получим:
Из этой формулы выразим массу планеты:
Подставим массу планеты в формулу для нахождения ее радиуса:
Подставляем известные данные и вычисляем:
Этот радиус соответствует 3400 км.
Ответ: 3400
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 18k
Характер и особенности расчета силы притяжения известны еще с древних времен. На основании имеющихся знаний, переданных современному научному сообществу великими исследователями, человек познает не только его окружающий мир, но и Вселенную.
Формула силы притяжения
Со времен Древней Греции философов интересовали явления притяжения тел к земле и свободного падения. К примеру, по утверждениям Аристотеля, из двух камней, брошенных с одинаковой высоты, быстрее достигнет земной поверхности тот, чья масса больше. В IV веке до нашей эры единственными методами научных изысканий служили наблюдения и анализ. К проверке гипотез опытным путем великие мыслители не прибегали. По истечению столетий физик из Италии Галилео Галилей проверил утверждения Аристотеля, используя практические методы исследований.
Итоги проведенных Галилеем опытов были опубликованы в «Беседах и математических доказательствах, касающихся двух новых наук». Ученый использовал псевдоним Сагредо: «пушечное ядро не опередит мушкетной пули при падении с высоты двухсот локтей». Формулировка закона всемирного тяготения была представлена в 1666 году Исааком Ньютоном. В ней фиксировались основные тезисы теоремы Галилея.
Смысл заключался в том, что тела, которые обладают разными массами, падают на землю с одинаковыми ускорениями. Одно тело притягивает другое и, наоборот, с силой, которая прямо пропорциональна их массам и обратно пропорциональна отрезку пути между ними. Согласно определению гравитации от Ньютона, тела, характеризующиеся массой, обладают свойством, благодаря которому притягиваются друг к другу.
Понятие и определение
Силы взаимного притяжения – это силы, которые притягивают любые тела, обладающие массами.
Корректность выводов Ньютона неоднократно подтверждалась путем практических испытаний. Но в начале ХХ века перед учеными-физиками остро стоял вопрос о природе и характере взаимодействия крупных астрономических тел, включая разные виды планетарных систем и галактик в вакууме. Ньютоновского закона уже было недостаточно, чтобы решить эти задачи. Исключить недочеты позволила новая теория, разработанная Альбертом Эйнштейном в начале ХХ столетия. Общая теория относительности объясняет гравитацию не в качестве силы, а представляет ее в виде искривления пространства и времени в четырех измерениях, которое зависит от массы тел, создающих его.
Гравитация представляет собой свойство тел, которые характеризуются массой, притягивать друг друга. Данное физическое явление можно объяснить, как поле, оказывающее дистанционное воздействие на предметы, не связанные между собой никаким другим способом.
Достижение Эйнштейна не противоречит теоретическому объяснению гравитации от Ньютона. Общая теория относительности рассматривает закон всемирного тяготения, как частный случай, применимый для сравнительно небольших расстояний. Данная закономерность в настоящее время также активно используется для поиска решений задач на практике.
Единицы измерения силы притяжения
В разных системах измерений можно встретить несколько отличающиеся обозначения. Единицы измерения силы притяжения следующие:
- система СИ: ([F]=H);
- система СГС: ([F]=дин).
Формула силы притяжения между телами в космосе
Закономерность гравитации, которую обнаружил Ньютон, можно представить в виде математической формулы. Вычисления выглядят следующим образом:
(F=(Gtimes m1times m2times r)/2),
где (m1,m2) — массы объектов, которые притягиваются друг к другу под действием силы (F),
(r) – расстояние, на которое удалены тела,
(G) — т.н. гравитационная постоянная величина, константа, равная 6,67.
Гравитационное взаимодействие объектов будет слабеть, если тела удаляются друг относительно друга. Сила гравитации пропорциональна величине расстояния в квадрате. При этом для нахождения искомой величины расстояние измеряется от центров тяжести тел, а не от поверхностей.
Гравитация в определенных моментах напоминает другие физические явления. Исходя из зависимости интенсивности силы от расстояния в квадрате, гравитацию можно сравнить с электромагнитным взаимодействием сильного и слабого характера.
Формула силы гравитационного притяжения между двумя телами
Квадратичная связь силы, с которой тела притягиваются друг к другу, с расстоянием между ними объясняет тот факт, что люди, находящиеся на поверхности планеты Земля не притягиваются к Солнцу, хотя масса его велика и превышает земную в миллион раз. Земля и центр Солнечной системы удалены примерно на 150 миллионов километров. Дистанция достаточно велика, чтобы ощущаться человеком. Однако эту силу можно зарегистрировать, используя высокоточные приборы. В рамках планеты Земля сила, с которой тела к ней притягиваются, то есть их вес, измеряется следующим образом:
(P=mtimes g),
где (m) – масса тела, на которое воздействует сила притяжение,
(g) – ускорение свободного падения около Земли (если рассматривать систему в условиях любой другой планеты, данная величина будет отличаться).
На разных географических широтах величина ускорения свободного падения может незначительно отличаться. Производя расчеты, данный показатель принимается за 9,81 метров в секунду в квадрате.
В физике понятия массы и веса тел отличаются. Весом называется сила, определяющее притяжение объекта к планете. Масса представляет собой меру инертности вещества. На нее не влияют другие тела, расположенные рядом.
Формула для силы притяжения тел произвольной формы
Расчеты определяются некоторыми условиями. К ним относятся характеристики исследуемых объектов.
Если сила притяжения измеряется между телами, которые обладают произвольной формой, их считают материальными точками:
(dtimes m1=rho1times dV1)
(dtimes m2=rho2times dV2)
где (rho1, rho2) – обозначают плотность веществ материальных точек, характерных для первого и второго объектов,
(dV1 ,dV2) — элементарные объемы выделенных материальных точек.
Исходя из этого, сила притяжения (doverline F), с которой взаимодействуют объекты, равна:
(doverline F=-Gtimes frac{rho _{1}timesrho _{2}times dtimes V_{1}times dtimes V_{2}}{r_{12}^{3}} bar{r_{12}})
Таким образом, сила притяжения первого тела вторым рассчитывается следующим образом:
(bar{F}_{12}=-Gtimesint_{V_{1}}^{rho _{1}times dtimes V_{1}}int_{V_{2}}^{frac{rho _{2}}{r_{12}^{3}}times bar{r}_{12}times dtimes V_{2}})
где интегрирование выполняется по всему объему первого ((V1)) и второго ((V2)) тел. Если тела обладают однородностью, то формула корректируется, таким образом:
(bar{F}_{12}=-Gtimesrho1timesrho2timesint_{V_{1}}^{dtimes V_{1}}int_{V_{2}}^{frac{bar{r}_{12}}{r_{12}^{3}}times dtimes V_{2}})
Формула для силы притяжения твердых тел шарообразной формы
В условиях, когда сила притяжения измеряется между телами, представленных в форме шара или близкой к нему, с плотностью, зависящей лишь от удаленности их центров тяжести, применяется следующая формула:
(bar{F}_{12}=-Gtimes(m1times m2)/R^3times R12)
где (m1,m2) – массы шаров, (R )– радиус – вектор, соединяющий центры шаров.
Пример применения формулы для расчета
Задача. Необходимо рассчитать силу притяжения между двумя идентичными однородными шарами, масса которых составляет по 1 килограмму. При этом их центры тяжести удалены на 1 метр друг от друга.
Решение будет выглядеть следующим образом:
Используя формулу для подсчета силы притяжения между двумя объектами шарообразной формы, получается:
(F_g=6.67times 10^{-11}times frac{1times 1}{1^{2}})
Ответ: (F_g=6.67times 10^{-11})
Выполнить расчет силы притяжения достаточно просто, если правильно выбрать формулу, подходящую под конкретные условия, в которых находятся тела. Если в процессе решения задач по физике или другим дисциплинам возникают проблемы, всегда можно обратиться за помощью к компетентным специалистам портала Феникс.Хелп.
Одна из важнейших в природе сил — сила гравитации, или сила тяготения. Она действует на все тела во Вселенной.
Существует миф о том, что Ньютон открыл закон всемирного тяготения после того, как ему на голову упало яблоко. Так это или нет доподлинно неизвестно, но именно Ньютон изучал движение планет вокруг Солнца и открыл математическую формулу для расчета взаимодействия тел определенной массы. Эту формулу мы называем законом всемирного тяготения.
Сила взаимодействия двух тел прямо пропорциональна массе каждого из этих тел и обратно пропорциональной квадрату расстояния между центрами этих тел:
, где
G=6,67⋅10−11Н⋅м2кг2
— гравитационная постоянная,
R
— расстояние между центрами тел.
Для решения задач закон всемирного тяготения применяют, если
1. тела являются точечными (т.е. размеры тел значительно меньше расстояния между ними);
2. тела представляют собой два однородных шара;
3. тело неопределенной формы находится на поверхности шарообразного и однородного тела большого размера и массы (по сравнению с телом неопределенной формы).
Рис. (1). Случаи применения закона всемирного тяготения
Третий закон Ньютона мы используем для расчёта силы тяжести на поверхности Земли или вблизи неё. Поэтому за расстояние между телами берём радиус Земли: (R=6370) км.
Рис. (2). Взаимодействие Земли и яблока
Сила притяжения яблока к Земле равна силе притяжения Земли к яблоку по модулю: (|vec{F_я}|=|vec{F_З}|).
Силы притяжения между телами равны по модулю, но противоположны по направлению: (vec{F_я}=-vec{F_З}).
Значение ускорения Земли, обусловленное притяжением со стороны яблока настолько мало, что при расчёте задач его не учитывают.
Источники:
Рис. 1. Случаи применения закона всемирного тяготения. © ЯКласс.
Рис. 2. Взаимодействие Земли и яблока. © ЯКласс. Планета. Указание автора не требуется, 2021-08-26, Pixabay License, https://pixabay.com/images/id-11015/. Яблоко. Указание автора не требуется, 2021-08-26, Pixabay License, https://pixabay.com/images/id-1834639/.
Содержание:
Закон всемирного тяготения:
В таблице представлены орбитальные скорости планет и карликовых планет Солнечной системы. Исследуя эту информацию, с легкостью можно определить, что небесные тела этой системы, близко расположенные к Солнцу, имеют более высокую орбитальную скорость.
Орбитальная скорость Луны вокруг Земли, по сравнению со скоростями из повседневной жизни, так же очень большая: -3682,8 км/час. Однако эта скорость во много раз меньше скорости Земли вокруг Солнца.
| Планеты и карликовые планеты | Орбитальная скорость | |
| км/с | км/с | |
| Меркурий | 47,87 | 172 332 |
| Венера | 35,02 | 126 072 |
| Земля | 29,78 | 107 208 |
| Марс | 24,13 | 86 868 |
| Церера | 17,88 | 64 368 |
| Юпитер | 13,07 | 47 052 |
| Сатурн | 9,69 | 34 884 |
| Уран | 6,81 | 24 516 |
| Нептун | 5,43 | 19 548 |
| Плутон | 4,67 | 16 812 |
| Хаумеа | 4,48 | 16 128 |
| Макемаке | 4,41 | 15 876 |
| Эрида | 3,44 | 12 384 |
Вы знаете, что все тела во Вселенной, имеющие массу — звезды, галактики, Солнце и планеты, тела Земной системы, молекулы, атомы и другие, взаимно притягиваются друг к другу с силой, называемой силой тяготения (или гравитационной силой). Исследовав, от каких величин и как зависит эта сила, Исаак Ньютон сформулировал закон всемирного тяготения.
Закон всемирного тяготения
Между любыми двумя материальными точками действует сила взаимного притяжения, прямо пропорциональная произведению их масс и обратно пропорциональная квадрату расстояния между ними:
Где
Гравитационная постоянная
Единица гравитационной постоянной в СИ:
Гравитационная постоянная численно равна силе притяжения друг к другу двух материальных точек массами по 1 кг каждый, если расстояние между ними равно 1 м.
Численное значение гравитационной постоянной опытным путем определил английский ученый Генри Кавендиш (1731—1810) в 1798 году. Это значение одинаково для всех тел во Вселенной вне зависимости от их размеров и масс:
Как видно, численное значение гравитационной постоянной очень мало. Поэтому между телами с относительно малыми массами сила притяжения не чувствуется. Эта сила принимает ощутимые значения при взаимодействии тел с очень большой массой, например, между звездой и планетой, планетой и спутником и т.д.
Формула закона всемирного тяготения
Сила притяжения между двумя произвольными телами, не являющимися материальными точками при данных условиях, также определяется формулой закона всемирного тяготения. В этом случае эти тела рассматриваются как совокупность материальных точек, вычисляются силы притяжения между всеми материальными точками этих тел, результаты вычислений суммируются и определяются сила притяжения между этими телами. Такие вычисление представляет собой сложную математическую операцию. Однако формула Всемирного тяготения легко применяется для тел шарообразной формы. За расстояние между телами при этом принимается расстояние между их центрами (а). Поэтому для вычисления силы притяжения между произвольным телом и Землей можно применить формулу закона всемирного тяготения. В этом случае расстояние между ними берется до центра Земли: 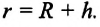
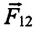
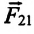
Согласно III закону Ньютона 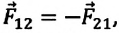
Где 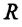
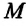
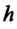
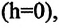
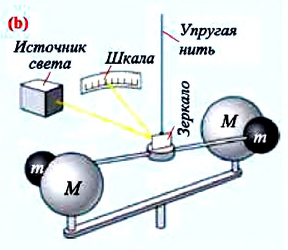
Измерение гравитационной постоянной
С этой целью Г. Кавендиш использовал крутильные весы. Схема весов показана на рисунке: на концах стержня длиной 2 м он установил два свинцовых шарика массой по 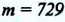
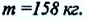
Зная угол поворота, можно определить силу упругости 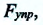
Таким образом, ученый, подставив известные величины в формулу закона всемирного тяготения, получил для гравитационной постоянной значение, очень близкое к его современному значению:
Что такое закон всемирного тяготения
Все тела во Вселенной, как небесные, так и находящиеся на Земле, взаимно притягиваются. Даже если мы не замечаем притягивания между обычными предметами, которые окружают нас в повседневной жизни (например, между книгами, тетрадями, мебелью и т. п.), то это потому, что оно в таких случаях очень слабое.
Взаимодействие, свойственное всем телам во Вселенной и проявляющееся взаимным притягиванием друг к другу, называют гравитационным, а само явление всемирного тяготения — гравитацией (лат. gravitas — «тяжесть»).
Гравитационное взаимодействие осуществляется с помощью особенного вида материи, который называют гравитационным полем. Такое поле существует вокруг любого тела — планеты, камня, человека или листа бумаги. При этом тело, создающее гравитационное поле, действует им на любое другое тело так, что у того появляется ускорение, всегда направленное к источнику поля. Появление такого ускорения и значит, что между телами возникает притяжение.
Гравитационное поле не следует путать с электромагнитными полями, существующими вокруг наэлектризованных тел, проводников с током и магнитов.
Интересной особенностью гравитационного поля, которую не имеют электромагнитные поля, является его всепроникающая способность. Если от электрических и магнитных полей можно защититься с помощью специальных металлических экранов, то от гравитационного поля защититься ничем нельзя: оно проникает сквозь любые материалы.
Выражение для силы притяжения Исаак Ныотон получил еще в 1666 г., когда ему было 24 года. Сначала ученый установил, как зависит от расстояния ускорение свободного падения. Он заметил, что вблизи поверхности Земли, то есть на расстоянии 6400 км от ее центра, это ускорение равно 9,8 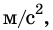
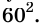
Окончательную формулу силы притяжения можно получить, если учесть, что эта сила должна быть пропорциональна массам тел
где G — гравитационная постоянная.
Так, Ньютон нашел выражение для силы гравитационного взаимодействия Земли с телами, которые притягивались ею. Но интуиция подсказывала ему, что по данной формуле можно рассчитывать и силу притяжения, действующую между любыми другими телами Вселенной, если только их размеры малы по сравнению с расстоянием г между ними. Поэтому он начал рассматривать полученное выражение как закон всемирного тяготения, который выполняется и для небесных тел, и для тел на Земле.
Сила гравитационного притяжения любых двух частиц прямо пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между ними:
Закон всемирного тяготения сформулирован для частиц, размеры которых значительно меньше расстояния г между ними. Однако одна особенность закона дает возможность использовать его и в некоторых иных случаях. Такой особенностью является обратно пропорциональная зависимость силы притяжения именно от квадрата расстояния между частицами, а не от третьей или четвертой степени расстояния. Расчеты показывают, что благодаря этой особенности формулу 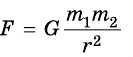
Формула 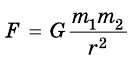
Когда Ньютон открыл закон всемирного тяготения, он не знал ни одного числового значения масс небесных тел, в том числе и Земли. Неизвестно ему было и значение постоянной.
Вместе с тем, гравитационная постоянная G имеет для всех тел Вселенной одно и то же значение и является одной из фундаментальных физических констант. Каким же образом можно определить ее значение? Из закона всемирного тяготения следует, что 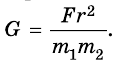
Первые измерения гравитационной постоянной были осуществлены в середине XVIII в. Оценить, правда очень грубо, значение G в то время удалось в результате рассмотрения притягивания маятника к горе, масса которой была определена с помощью геологических методов.
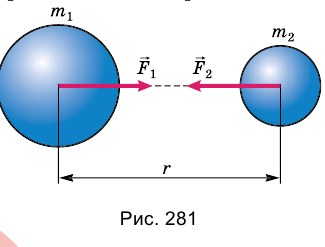
Точные измерения гравитационной постоянной впервые осуществил в 1798 г. Генри Кавендиш — английский физик, член Лондонского королевского общества. С помощью так называемых крутильных весов (рис. 282) ученый по углу закручивания нити А сумел измерить ничтожно малую силу притяжения между маленькими и большими металлическими шарами. Для этого ему пришлось использовать очень чувствительные приборы, потому что даже слабые воздушные потоки могли исказить измерение. Во избежание посторонних влияний, Кавендиш разместил свои приборы в ящике, который оставил в комнате, а сам проводил наблюдение за приборами с помощью телескопа из другого помещения.
Опыты показали, что
Физическое содержание гравитационной постоянной заключается в том, что она определяется силой, с которой притягиваются два тела массами 1 кг каждое, находящиеся на расстоянии 1 м друг от друга.
Если на тело действует только одна сила, направленная вниз (а все другие уравновешены), то оно осуществляет свободное падение. Ускорение свободного падения можно определить, применив второй закон Ньютона:
Отсюда следует, что ускорение свободного падения 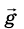
Теперь для силы притяжения можно записать выражение:
По существу говоря, формула 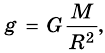
Приведенные значения показывают, что ускорение свободного падения в разных районах земного шара отличается очень мало от значения, вычисленного по формуле
Поэтому при грубых подсчетах пренебрегают неинерциальностые системы отсчета, связанной с поверхностью Земли, и отличием формы Земли от сферической. Ускорение свободного падения считают всюду одинаковым и вычисляют по формуле
В некоторых районах земного шара ускорение свободного падения отличается от приведенного выше значения еще по одной причине. Такие отклонения наблюдаются там, где в недрах Земли залегают породы, плотность которых больше или меньше средней плотности Земли. Там, где есть залежи пород, имеющих большую плотность, значение g больше. Это дает возможность геологам по измерениям значения g находить месторождения полезных ископаемых.
Следовательно, сила притяжения, а значит, и ускорение свободного падения изменяются с отдалением от поверхности Земли. Если тело находится на высоте h над поверхностью Земли, то выражение для модуля ускорения свободного падения g следует записывать следующим образом:
Так, на высоте 300 км ускорение свободного падения уменьшается на 1 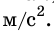
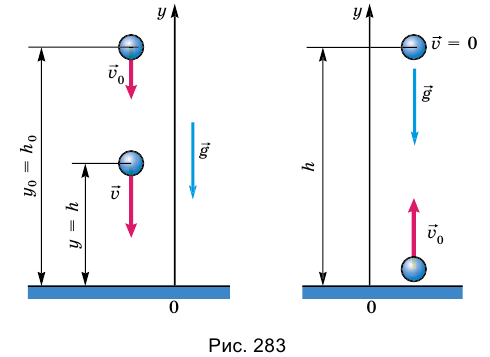
Движение тела под действием силы притяжения: тело движется по вертикали. Если предоставить телу начальную скорость д0, направленную вверх, то это не изменит ни направления, ни значения ускорения тела, потому что толчок вверх не может изменить силу притяжения. В обоих случаях траекторией тела является вертикальная прямая.
Решая задачи на такое движение, за тело отсчета удобно выбирать Землю с началом отсчета на ее поверхности или в любой точке выше или ниже от поверхности, а координатную ось направлять по вертикали вверх или вниз. Высоту тела над определенной поверхностью принято обозначать буквой h (рис. 283).
Тогда координата y тела — это просто его высота h над точкой начала отсчета. Проекция вектора перемещения тела соответствует изменению высоты и равна h — 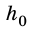
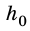
Формулы для вычисления координат (высот) и скоростей ничем не отличаются от формул для прямолинейного равноускоренного движения.
Координата тела (высота):
Скорость тела в любой момент времени:
Скорость тела в любой точке траектории:
Проекция 
- Заказать решение задач по физике
Движение тела под действием силы притяжения: начальная скорость тела направлена под углом к горизонту. Часто приходится рассматривать движения тел, начальная скорость которых не параллельна силе притяжения, а направлена под определенным углом к ней (или к горизонту). Когда, например, спортсмен толкает ядро, бросает диск или копье, он придает этим предметам именно такую скорость. При артиллерийской стрельбе стволы пушек имеют определенный угол поднятия, так что снаряд в стволе также получает начальную скорость, направленную под углом к горизонту.
Будем считать, что силой сопротивления воздуха можно пренебречь. Как в этом случае движется тело?
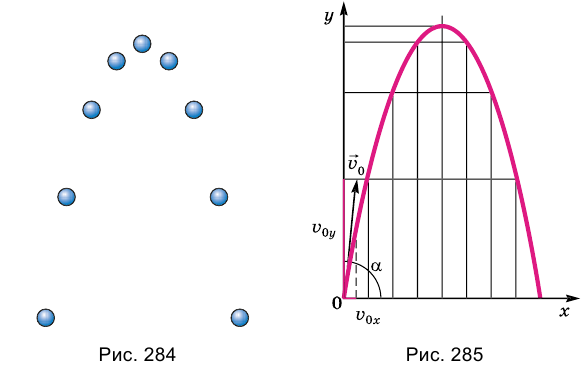
На рисунке 284 показан стробоскопический снимок шарика, брошенного под углом 60° к горизонту. Соединив последовательно положения шарика плавной кривой, получим траекторию движения шарика — параболу.
Если пренебречь влиянием воздуха на движение тела, то на тело, брошенное под углом к горизонту, как и на свободно падающее тело, или на тело, которое получило начальную скорость, направленную вертикально, действует только сила притяжения. Как бы ни двигалось тело, сила притяжения может сообщить ему только ускорение 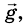
Предположим, что из некоторой точки О брошено тело с начальной скоростью 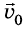
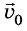
Поскольку на тело действует сила притяжения, то при движении тела будет меняться только проекция 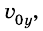
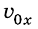
А координата у меняется так же, как при прямолинейном равноускоренном движении:
Чтобы найти траекторию движения тела, надо подставить в уравнение значения времени t, какие последовательно увеличиваются, и вычислить координаты х и у для каждого значения t, если известны значения модуля начальной скорости 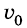
Что будет если тело брошено горизонтально
Тело можно бросить и так, что его начальная скорость 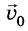
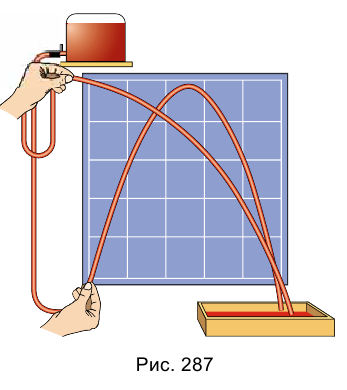
Траекторию движения тел, брошенных горизонтально или под углом к горизонту, можно показать на опыте. Сосуд, заполненный водой, размещают на определенной высоте над столом и соединяют его резиновой трубкой с наконечником, который имеет кран (рис. 287). Выпущенные струи воды непосредственно показывают траектории частиц воды. Таким образом можно наблюдать траекторию для разных значений угла а и скорости
Мы рассмотрели несколько примеров движения тел под действием силы притяжения. Во всех случаях тело движется с ускорением свободного падения, которое не зависит от того, имело ли тело еще и скорость в горизонтальном направлении или нет. Например, пуля, выпущенная стрелком из винтовки в горизонтальном направлении, упадет на землю одновременно с пулей, которую случайно уронил стрелок в момент выстрела. Но вторая пуля упадет у ног стрелка, а пуля, вылетевшая из ствола винтовки, — на определенном расстоянии.
История:
Попытки объяснить наблюдаемую картину мира, и прежде всего строение Солнечной системы, делали многие ученые. Что связывает планеты и Солнце в единую систему? Каким законам подчиняется их движение?
Во II в. н. э. древнегреческий ученый Клавдий Птолемей разработал геоцентрическую систему мира, согласно которой все наблюдаемые перемещения небесных светил объяснялись их движением вокруг неподвижной Земли.
В XVI в. польский астроном Миколай Коперник предложил гелиоцентрическую систему мира: в центре находится Солнце, а вокруг него движутся планеты и их спутники. Что же удерживает планеты, в частности Землю, когда они движутся вокруг Солнца?
Если придерживаться утверждений Аристотеля и связывать силу притяжения тел со скоростью их движения, а не с ускорением, то причиной движения планет является именно направление скорости.
Ньютон связал силу с ускорением. Именно силу притяжения Солнца естественно считать причиной вращения вокруг него Земли и планет.
Но не только планеты притягиваются к Солнцу. Солнце также притягивается планетами. Да и сами планеты взаимодействуют между собой. Одним из первых, кто это понял, был английский ученый Роберт Гук. В 1674 г. он писал: «Все небесные тела имеют притяжение, или силу тяготения к своему центру, вследствие чего они не только притягивают собственные части и препятствуют им разлетаться, как наблюдаем на Земле, но притягивают также все другие небесные тела, находящиеся в сфере их действия. Поэтому не только Солнце и Луна имеют влияние на движение Земли, но и Меркурий, и Венера, и Марс, и Юпитер, и Сатурн также своим притяжением имеют значительное влияние на ее движение. Подобным образом и Земля притяжением влияет на движение каждого из этих тел».
В своем труде «Математические начала натуральной философии» Ньютон сформулировал три фундаментальных закона (известны как законы Ньютона). В соответствии с данными законами, все тела Вселенной, как небесные, так и те, которые находятся на Земле, склонны к взаимному тяготению, причем силы, с которыми притягиваются все эти тела, имеют одинаковую природу и подчиняются одному и тому же закону.
Согласно легенде, мысль о всемирном тяготении озарила Ньютона в тот момент, когда он, отдыхая в своем саду, увидел яблоко, которое падает. Рассказывают даже, что знаменитой яблоне, плод которой сумел так «вовремя» упасть к ногам Ньютона, не дали исчезнуть бесследно и кусочки этого дерева якобы хранятся в Англии и в настоящее время.
Открытие закона всемирного тяготения дало возможность Ньютону создать теорию движения небесных тел, основанную на строгих математических доказательствах. Ничего подобного в науке до того времени не было.
Эта теория, бесспорно, поразила современников Ньютона, но у них возник вопрос: почему все тела притягиваются друг к другу? Ответа на него выдающийся физик не дал. «Причину же свойств силы тяготения я до сих пор не мог вывести из явлений, гипотез же я не выдумываю, — писал он в своих «Математических началах”. — Достаточно того, что притяжение в действительности существует, и действует согласно изложенному закону, и является полностью достаточным для объяснения всех движений небесных тел и моря».
Говоря о море, Ньютон имел в виду явление приливов, обусловленных притягиванием воды Луной и Солнцем. За две тысячи лет до Ньютона над причинами этого явления рассуждал Аристотель, который, однако, объяснить его не смог. Для философа это оказалось трагедией. «Наблюдая длительное время это явление со скалы Негро-понта, он, охваченный отчаянием, бросился в море и нашел там добровольную смерть», — утверждал Г. Галилей.
- Свободное падение тела
- Равнодействующая сила и движение тела под действием нескольких сил
- Сила давления в физике и единицы давления
- Механическое давление в физике
- Деформация в физике
- Плотность вещества в физике
- Сила трения в физике
- Вес тела в физике
Сила тяготения.
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: силы в механике, закон всемирного тяготения, сила тяжести, ускорение свободного падения, вес тела, невесомость, искусственные спутники Земли.
Любые два тела притягиваются друг к другу — по той лишь одной причине, что они имеют массу. Эта сила притяжения называется силой тяготения или гравитационной силой.
Закон всемирного тяготения.
Гравитационное взаимодействие любых двух тел во Вселенной подчиняется достаточно простому закону.
Закон всемирного тяготения. Две материальные точки массами и
притягиваются друг к другу с силой, прямо пропорциональной их массам и обратно пропорциональной квадрату расстояния
между ними:
(1)
Коэффициент пропорциональности называется гравитационной постоянной. Это фундаментальная константа, и её численное значение было определено на основе эксперимента Генри Кавендиша:
Порядок величины гравитационной постоянной объясняет, почему мы не замечаем взаимного притяжения окружающих нас предметов: гравитационные силы оказываются слишком малыми при небольших массах тел. Мы наблюдаем лишь притяжение предметов к Земле, масса которой примерно кг.
Формула (1), будучи справедливой для материальных точек, перестаёт быть верной, если размерами тел пренебречь нельзя. Имеются, однако, два важных для практики исключения.
1. Формула (1) справедлива, если тела являются однородными шарами. Тогда — расстояние между их центрами. Сила притяжения направлена вдоль прямой, соединяющей центры шаров.
2. Формула (1) справедлива, если одно из тел — однородный шар, а другое — материальная точка, находящаяся вне шара. Тогда сстояние от точки до центра шара. Сила притяжения направлена вдоль прямой, соединяющей точку с центром шара.
Второй случай особенно важен, так как позволяет применять формулу (1) для силы притяжения тела (например, искусственного спутника) к планете.
Сила тяжести.
Предположим, что тело находится вблизи некоторой планеты. Сила тяжести — это сила гравитационного притяжения, действующая на тело со стороны планеты. В подавляющем большинстве случаев сила тяжести — это сила притяжения к Земле.
Пусть тело массы лежит на поверхности Земли. На тело действует сила тяжести
, где
— ускорение свободного падения вблизи поверхности Земли. С другой стороны, считая Землю однородным шаром, можно выразить силу тяжести по закону всемирного тяготения:
,
где — масса Земли,
км — радиус Земли. Отсюда получаем формулу для ускорения свободного падения на поверхности Земли:
. (2)
Эта же формула, разумеется, позволяет найти ускорение свободного падения на поверхности любой планеты массы и радиуса
.
Если тело находится на высоте над поверхностью планеты, то для силы тяжести получаем:
.
Здесь — ускорение свободного падения на высоте
:
.
В последнем равенстве мы воспользовались соотношением
которое следует из формулы (2).
Вес тела. Невесомость.
Рассмотрим тело, находящееся в поле силы тяжести. Предположим, что есть опора или подвес, препятствующие свободному падению тела. Вес тела — это сила, с которой тело действует на опору или подвес. Подчеркнём, что вес приложен не к телу, а к опоре (подвесу).
 |
| Рис. 1. Сила тяжести, реакция опоры и вес тела |
На рис. 1 изображено тело на опоре. Со стороны Земли на тело действует сила тяжести (в случае однородного тела простой формы сила тяжести приложена в центре симметрии тела). Со стороны опоры на тело действует сила упругости
(так называемая реакция опоры). На опору со стороны тела действует сила
— вес тела. По третьему закону Ньютона силы
и
равны по модулю
и противоположны по направлению.
Предположим, что тело покоится. Тогда равнодействующая сил, приложенных к телу, равна нулю. Имеем:
С учётом равенства получаем
. Стало быть, если тело покоится, то его вес равен по модулю силе тяжести.
Задача. Тело массы вместе с опорой движется с ускорением
, направленным вертикально вверх. Найти вес тела.
Решение. Направим ось вертикально вверх (рис. 2).
 |
| Рис. 2. Вес тела больше силы тяжести. |
Запишем второй закон Ньютона:
Перейдём к проекциям на ось :
.
Отсюда . Следовательно, вес тела
.
Как видим, вес тела больше силы тяжести. Такое состояние называется перегрузкой.
Задача. Тело массы вместе с опорой движется с ускорением
, направленным вертикально вниз. Найти вес тела.
Решение. Направим ось вертикально вниз (рис. 3).
 |
| Рис. 3. Вес тела меньше силы тяжести. |
Схема решения та же. Начинаем со второго закона Ньютона:
Переходим к проекциям на ось :
.
Отсюда c. Следовательно, вес тела
.
В данном случае вес тела меньше силы тяжести. При (свободное падение тела с опорой) вес тела обращается в нуль. Это — состояние
невесомости, при котором тело вообще не давит на опору.
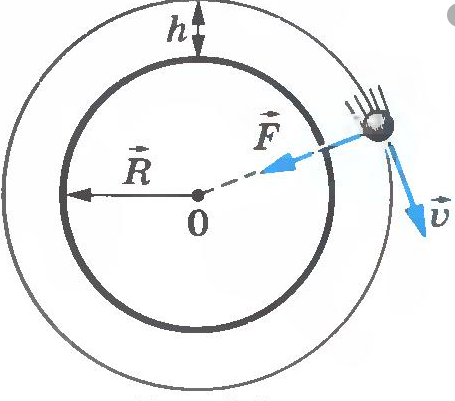
Искусственные спутники.
Для того, чтобы искусственный спутник мог совершать орбитальное движение вокруг планеты, ему нужно сообщить определённую скорость. Найдём скорость кругового движения спутника на высоте над поверхностью планеты. Масса планеты
, её радиус
(рис. 4)
 |
| Рис. 4. Спутник на круговой орбите. |
Спутник будет двигаться под действием единственной силы — силы всемирного тяготения, направленной к центру планеты. Туда же направлено и ускорение спутника — центростремительное ускорение
.
Обозначив через массу спутника, запишем второй закон Ньютона в проекции на ось, направленной к центру планеты:
, или
.
Отсюда получаем выражение для скорости:
.
Первая космическая скорость — это максимальная скорость кругового движения спутника, отвечающая высоте . Для первой космической скорости имеем
,
или, с учётом формулы ( 2),
.
Для Земли приближённо имеем:
км/с.
Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Сила тяготения.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
07.05.2023