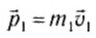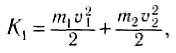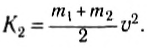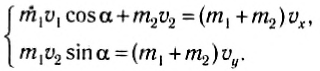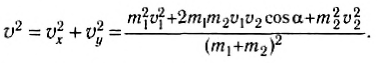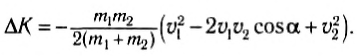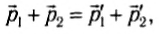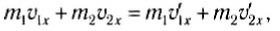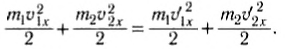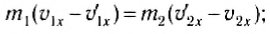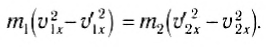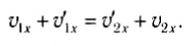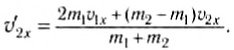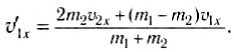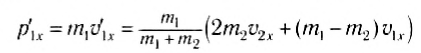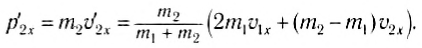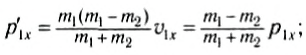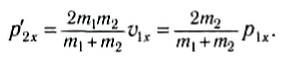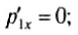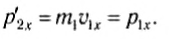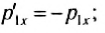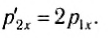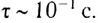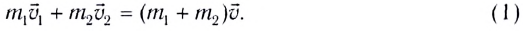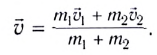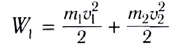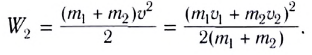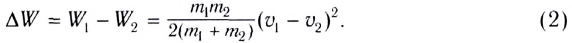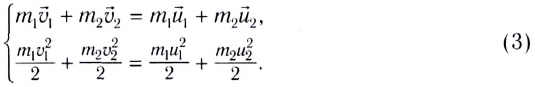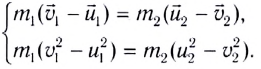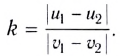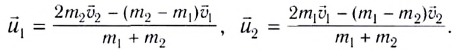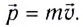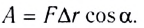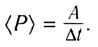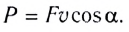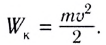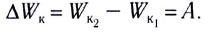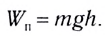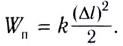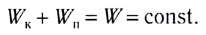Impact force is defined as a situation when some work is done to move an object a specific distance. It can be interpreted as the force produced when two items collide. An object collision occurs when one object collides with another. The impact force has a huge impact on an object in a short period of time. It is denoted by the symbol F. it is unit of measurement is Newtons (N) and the dimensional formula is given by [M1L1T-2]. Its formula equals the product of mass and velocity of a body to the twice time taken. In other words, it is the ratio of kinetic energy possessed by a body to the distance traveled by it.
Impact Force Formula
F = mv/2t
where,
F is the impact force,
m is the mass of the body,
v is the velocity of the body,
t is the time taken.
Derivation
Consider an object of mass m which moves with a velocity v when some work W is done on it. The force applied is F and it moves the object to a distance of d units for t seconds.
We know the work done equals the product of force applied and distance travelled.
W = Fd ⇢ (1)
Also, the work done equals the kinetic energy of the body.
W = K.E. = 1/2 mv2 ⇢ (2)
From (1) and (2) we get,
Fd = 1/2 mv2
F = mv2/2d
Putting d = vt, we get,
F = mv2/2vt
F = mv/2t
This derives the formula for impact force acting on a body.
Sample problems
Problem 1: Calculate the impact force acting on an object of mass 2 kg, velocity 4 m/s for 2 seconds.
Solution:
m = 2
v = 4
t = 2
Using the formula we get,
F = mv/2t
= 2 (4) / 2 (2)
= 8/4
= 2 N
Problem 2: Calculate the impact force acting on an object of mass 3 kg, velocity 8 m/s for 3 seconds.
Solution:
m = 3
v = 8
t = 3
Using the formula we get,
F = mv/2t
= 3 (8) / 2 (3)
= 24/6
= 4 N
Problem 3: Calculate the mass of the body if the impact force acting on an object is 10 N, and velocity is 5 m/s for 4 seconds.
Solution:
F = 10
v = 5
t = 4
Using the formula we get,
F = mv/2t
=> m = 2Ft/v
= 2 (10) (4) / 5
= 16 kg
Problem 4: Calculate the velocity of the body if the impact force acting on an object is 14 N mass is 2 kg for 2 seconds.
Solution:
We have,
F = 14
m = 2
t = 2
Using the formula we get,
F = mv/2t
=> v = 2Ft/m
= 2 (14) (2) / 2
= 28 m/s
Problem 5: Calculate the time taken by the body if the impact force acting on an object is 30 N, mass is 4 kg, and velocity is 15 m/s.
Solution:
F = 30
m = 4
v = 15
Using the formula we get,
F = mv/2t
=> t = mv/2F
= 4 (15) / 2 (30)
= 60/60
= 1 s
Problem 6: Calculate the impact force acting on an object of kinetic energy 20 J if the distance traveled is 2 m.
Solution:
E = 20
d = 2
Using the formula we get,
F = E/d
= 20/2
= 10 N
Problem 7: Calculate the kinetic energy of a body if the impact force acting on an object is 40 N and the distance traveled is 4 m.
Solution:
F = 40
d = 4
Using the formula we get,
F = E/d
=> E = Fd
= 40 (4)
= 160 J
Last Updated :
15 May, 2022
Like Article
Save Article
Расчет силы удара
Сила удара — это сила, которая действует на физическое тело при контакте с другим физическим телом.
Формула расчета силы удара:
F = m * (V1 — V2) / dt, где
F — сила удара в ньютонах;
m — масса тела в килограммах;
V1 — скорость в начале удара в м/с;
V2 — скорость после удара в м/с;
dt — время контакта в секундах.
Быстро выполнить эту математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.
На этой странице представлен самый простой онлайн калькулятор расчета силы удара по простой физической формуле в зависимости от массы тела, скорости и времени контакта. С помощью этого калькулятора вы в один клик сможете определить силу удара.
Как посчитать силу удара?
Формула силы тяжести Fт=m*g, где m-масса тела, g-ускорение свободного падения.
Сколько кг удар у боксера?
Сила удара мужчины колеблется от 200 до 1000 килограммов. 200 килограммов – это довольно хороший удар для боксера, вес которого 60-70 килограммов. Ну а тысяча – это уже предел супертяжеловеса. «Вырубить» оппонента можно ударом в 150 ньютонов (это примерно 15 килограммов).
Какие факторы влияют на силу удара?
Сила — это масса умноженная на ускорение. От сюда следует, что для увеличения силы удара, важна как скорость, с которой Вы выполняете удар, так и мышечная масса руки и всего тела в целом.
Как рассчитать силу удара при столкновении?
Импульс движущегося тела p=mV.
Получаем, что F = mV / t — сила, с которой препятствие тормозит движущееся тело, и (по третьему закону Ньютона) движущееся тело действует на препятствие, т. е. сила удара: F = mV / t, где t — время удара.
Как рассчитать скорость падения тела?
где m — это масса тела (она сокращается и не важна), v — искомая скорость, h — высота падения. Отсюда сразу получаем выражение для скорости v: v = sqrt(2gh), где sqrt — квадратный корень.
Какая сила удара у Кличко?
Как показали датчики, сила удара украинского чемпиона равняется 700 кг (. ), обрушивающихся на голову соперника. Это сравнимо с ударом от взрослого быка! Уже в эту субботу силу удара Владимира на себе сможет ощутить Франческо Пьянета, с которым Кличко сойдется в ринге на SAP-арене в Мангейме, Германия.
Какая сила удара у Брюса Ли?
5. Брюс был слишком сильным для боксерской груши Одним боковым ударом ногой Брюс Ли мог разбить стандартную 150 lb (68 кг) боксерскую грушу, поэтому груши для тренировок ему делали на заказ — в двое тяжелле (300 lb) и с металлическим основанием.
Сколько кг удар у Нганну?
10 мая в Джексонвилле (США) состоялся долгожданный турнир UFC 249. Одно из главных событий — бой между супертяжеловесами Фрэнсисом Нганну и Жаирзиньо Розенстрайком. Оба весят под 120 килограммов (лимит категории) и обладают ударом устрашающей силы. Рефери остановил поединок уже на 20-й секунде.18 мая 2020 г.
Какие мышцы работают при работе с грушей?
Вы проработаете самостоятельно дельтовидные мышцы, бицепсы, все мышцы предплечья, шеи, кисти и пальцы. Если хотите выглядеть мощнее, то груша вам необходима.31 мая 2014 г.
Какие группы мышц работают в боксе?
Это мышцы рук, ног, плечевого пояса, груди, пресса.
Можно ли выжить при лобовом столкновении?
Среди водителей бытует мнение, что при лобовом столкновении выжить практически невозможно. Исходя из законов физики, просчеты верны, но в реальности все по-другому. На самом деле значение имеет не скорость транспортного средства, а его вес, ведь чем тяжелее машина, тем больше шансов, что люди в ней останутся живы.
Какая скорость при лобовом столкновении?
Принято считать, что при лобовом столкновении скорости автомобилей суммируются и результат будет одинаков при столкновении с бетонной стеной на этой же суммарной скорости. … А эквивалентно тому, если бы одно из них въехало в стену на скорости 80 км/час.13 мая 2010 г.
Какая скорость смертельна при дтп?
Исходя из приведенных цифр – при скорости столкновения 80 км/час, вероятность гибели людей в машине в 20 раз больше, чем при аварии на скорости 30 км/час.
Как рассчитать силу удара?
Чтобы рассчитать силу удара, разделить кинетическую энергию на расстояние.
Аналогично, как рассчитать силу удара падающего предмета? Кинетическая энергия непосредственно перед ударом равна его гравитационной потенциальной энергии на высоте, с которой он был брошен: KE = J. Но одно это не позволяет вычислить силу удара! Средняя сила удара = F = Н.
Каковы силы удара? Сила удара сила, возникающая при встрече объектов. Чем быстрее вы едете, тем больше ударная или ударная сила вашего автомобиля. Законы физики определяют, что сила удара увеличивается пропорционально квадрату увеличения скорости.
Похожие страницы:Блог
Какие есть 3 вида налогов?
Как найти среднюю точку между двумя точками?
Как вы делаете кадровые прогнозы?
Как найти начальную скорость, зная только время?
Какие три фактора определяют силу удара?
- скорость.
- Весом воды для заваривания
- расстояние между местом удара и местом остановки.
Во-вторых, каковы 5 уравнений Сувата? Уравнения движения, также известные как уравнения SUVAT, используются, когда ускорение a постоянно. Они известны как уравнения SUVAT, потому что они содержат следующие переменные: s – расстояние, u – начальная скорость, v – скорость в момент времени t, a – ускорение и t – время.
Какие три фактора могут повлиять на силу удара quizlet?
Три фактора, которые изменят силовое воздействие вашего автомобиля при столкновении: скорость, вес и расстояние между ударом и остановкой.
Затем Какие 4 фактора влияют на ваше сцепление в повороте? Вот основные факторы, влияющие на сцепление с дорогой во время движения:
- Материал, из которого изготовлено дорожное покрытие. …
- Состояние дороги. …
- Состояние ваших шин. …
- Вес вашего автомобиля. …
- Баланс вашего автомобиля.
Какие три фактора влияют на ваш автомобиль в повороте? Скорость вашего автомобиля, резкость поворота, крен поворота и загрузка вашего автомобиля. повлияет на контроль, который у вас есть на кривой. Скорость Вы не можете контролировать резкость поворота, но можете регулировать скорость.
Как рассчитывается суват?
Как доказать суват?
Что такое 4-е уравнение движения?
(6) V = и- + 2ас (4) Четвертое уравнение движения: По определению … (7) мгновенной скорости мы можем написать v = “. dt dS = v. dt = (u +at) dt Когда время = (t-1) секунды, пройденное расстояние = S-1 Когда время = t секунд, пройденное расстояние = S, Таким образом, интегрирование уравнения.
Что больше всего влияет на силу удара при столкновении? Сила удара – это сила столкновения объекта с другим объектом. К факторам, влияющим на силу удара, относятся вес объекта, скорость и расстояние, пройденное после первого контакта.
К чему нужно быть готовым при спуске с горы?
Когда вы начинаете возвращаться вниз по склону, используйте свой двигатель и трансмиссию, чтобы замедлить машину вместо тормозов. Переключитесь на более низкую передачу перед тем, как начать движение вниз по склону, так как это поможет замедлить машину без необходимости ехать на тормозах, говорит Служба национальных парков.
Какие три фактора влияют на время удара при столкновении?
- влияние времени столкновения на величину силы, которую испытывает объект, и.
- эффект отскока на изменение скорости и, следовательно, количество силы, которую испытывает объект.
Какие 3 фактора могут вызвать потерю тяги? ПРИЧИНЫ ЗАНОСА И ПОТЕРИ ТЯГИ. Причины заноса (потеря сцепления с дорогой) можно разделить на три группы: (1) состояние дороги, (2) состояние транспортного средства и (3) действия водителя. Лед, снег или иней.
Какие шесть факторов могут повлиять на ваш тормозной путь? Термины в этом наборе (7)
- Скорость. Чем выше ваша скорость, тем длиннее ваш тормозной путь.
- Состояние автомобиля. Транспортному средству с изношенными шинами, амортизаторами или тормозами требуется большее расстояние для остановки.
- Поверхностная проезжая часть. …
- Способность водителя. …
- Антиблокировочная тормозная система (ABS)…
- Холмы. …
- Нагрузки.
Какие условия влияют на тягу?
Зимой потеря сцепления с дорогой может произойти в любое время и в любом месте – при слишком быстром прохождении поворота, при сухие условия быстро сменяются дождем или льдом, при неправильной парковке на обледенелой возвышенности или слишком сильном торможении (что приводит к блокировке колес). Любое из этих действий может иметь разрушительные последствия.
Какие четыре фактора влияют на торможение? Тормозное расстояние
- плохие дорожные и погодные условия, например, мокрые или обледенелые дороги.
- плохое состояние автомобиля, например, изношенные тормоза или изношенные шины.
- большую скорость.
- масса автомобиля – чем больше масса, тем больше тормозной путь.
Что может сделать водитель, чтобы уменьшить силу удара?
2/ выполненная работа= Сила х расстояние. Таким образом, сила удара уменьшается по мере увеличения расстояния. Чем больше время удара, тем меньше сила удара. Функции безопасности автомобиля, такие как зоны деформации, увеличивают время удара и, следовательно, уменьшают силу.
Какие шесть факторов влияют на тормозной путь? Термины в этом наборе (7)
- Скорость. Чем выше ваша скорость, тем длиннее ваш тормозной путь.
- Состояние автомобиля. Транспортному средству с изношенными шинами, амортизаторами или тормозами требуется большее расстояние для остановки.
- Поверхностная проезжая часть. …
- Способность водителя. …
- Антиблокировочная тормозная система (ABS)…
- Холмы. …
- Нагрузки.
Как найти уравнение движения?
Как Суват вычисляет скорость?
Как рассчитать ускорение от суват?
Уравнения «сувата»
- s = ½ (u + v)t.
- с = ут + ½ ат. …
- v 2 = ты 2 + 2ас.
Когда можно использовать суват? Используются уравнения СУВАТ когда ускорение постоянно, а скорость меняется. Если скорость постоянна, вы можете использовать скорость, расстояние и временной треугольник. Их можно использовать для определения начальной и конечной скорости, времени, интервала и ускорения, если известны как минимум три величины.
Как можно рассчитать смещение?
Чтобы рассчитать смещение, просто нарисуйте вектор от начальной точки до конечной позиции и решите длину этой линии. Если ваша начальная и конечная позиции совпадают, например, ваш круговой маршрут 5K, тогда ваше смещение равно 0. В физике смещение представлено Δs.
С какой силой Земля притягивает яблоко, висящее на ветке? Вы скажите, с силой тяжести этого яблока. Но вот Ньютон этого не знал, когда сидел под яблоней. Несчастный первооткрыватель также не знал, с какой силой падающее яблоко приложится к его голове. На самом деле то, что Ньютон открыл свой великий закон притяжения после падения яблока, является лишь мифом, догадкой, легендой. Но не в этом суть. Иногда у нас возникают такие вопросы: «с какой силой боксёр бьёт грушу, человека?», «как её определить?», «от чего она зависит?», «как уцелеть в автомобильной аварии?» и, наконец, «как сильно яблоко ударило Ньютона?».
Яблоко, висящее на дереве, действительно притягивается к земле с силой своей тяжести. Эта сила постоянна во времени, то есть не меняется, и численно равна произведению массы яблока (например, 0,2 килограмма) на ускорение свободного падения (около 10 м/с*с).
То есть получим силу в 2 Ньютона. Именно такую силу нужно приложить, чтобы держать в руке наше яблоко.
Чтобы узнать ускорение свободного падения, можно бросить тело с высокой башни и вычислить из кинематических соображений быстроту, с которой тело набирало скорость, падая. Так и сделал в своё время Галилей. Формулу силы тяжести можно вывести и интуитивно: чем больше масса яблока и чем больше быстрота, с которой яблоко, падая, набирало скорость, тем больше его сила тяжести. Итак, с висящим яблоком разобрались. Теперь рассмотрим, с какой силой яблоко ударяется об голову Ньютона. Для наглядности перейдём к другой ситуации, а потом вернёмся к учёному.
Боксёр решил, что он натренировал свой кулак достаточно, и ударил с определённой силой по бетонной стене. В следующий миг, он усомнился в своих кулаках, испытав жгучую боль. Тогда боксёр надевает свои перчатки и снова бьёт в стену, причём с той же определённой силой. На этот раз боли он почти не почувствовал. Вы скажите, перчатки смягчили энергию удара, а может силу… Так что же именно? Перчатки не могут уменьшить энергию удара (вообще они её уменьшают, но не значительно). Они уменьшают лишь силу удара, а она по 3-ему закону нашего Ньютона как раз равна силе, с которой стена отталкивает назад кулак боксёра. Именно эта сила нам и нужна. А за счёт чего перчатки уменьшили силу удара? За счёт того, что они «размазали» или продлили удар во времени. Перчатки увеличили время контакта кулака со стеной. Без них время контакта было на несколько тысячных долей секунды меньше, чем с ними. Но этих миллисекунд хватает, чтобы время контакта в перчатках было больше времени контакта без них в несколько раз. Пусть в 5 раз. Тогда в 5 раз слабее ударит по стене боксёр и в 5 раз меньше боли при этом испытает. Естественно, я говорю о средней силе контакта, ведь на самом деле силу удара сначала увеличивается, потом уменьшается. Выведем интуитивно формулу для вычисления силы удара. Чем больше скорость, с которой двигался кулак до столкновения, чем больше его масса и чем меньше время контакта его со стеной, тем больше будет среднее значение силы, с которой кулак ударяется о стену. Только что мы с вами вывели 2-ой закон Ньютона в общем виде. Эта формула выглядит так:
в числителе стоит разница между скоростью кулака до удара и после него. В нашем примере кулак потом остановился, значит, скорость V2 будет равна нулю. Из нашей формулы видно, что в бетонную стену бить больнее, чем в деревянную (ведь у деревянной стены время контакта больше, следовательно, знаменатель дроби больше и поэтому сила отдачи меньше), и что не следует бегать босиком по бетонному полу (ведь в этом случае нагрузка на коленный сустав в несколько раз выше, чем в случае, когда бегаешь по деревянному полу в обуви). Предостерегу: будете бегать босиком по бетону или кирпичу – износите свой коленный сустав и начнутся проблемы. Даже в тапках этого делать не следует. Лучше обувь с толстой подошвой. Это я заявляю вам из собственного жизненного опыта.
Возвращаясь к Ньютону и яблоку, оценим силу удара последнего. Падая с высота 3 метра, яблоко будет иметь скорость до удара порядка 8 метров в секунду. Пусть после удара оно отлетит в обратном направлении со скорость 2 метра в секунду (со знаком «–» раз в обратном направлении). И пусть время контакта – 0,004 секунды, то есть 4 миллисекунды. Это время можно измерять с помощью высокоскоростной камеры. Тогда по нашей формуле сила удара яблока составит 500 Ньютон, а это в 250 раз больше, чем сила притяжения яблока к Земле. Выглядит это неправдоподобно. Кажется, такая сила просто раздавит несчастного учёного. Но приняв тот факт, что сила эта действует на его голову лишь доли секунды, сказанное становится более реалистичным. Из всего этого можно сделать вывод: не сидите под яблонями.
Из вышесказанного следует: чем меньше время контакта в ударе, тем больше сила удара. Поэтому в автомобильных авариях везёт больше тем, кто сидит на задних сиденьях или у кого срабатывает подушка безопасности, ведь в этом случае они будут тормозить большее время и сила удара «размажется» во времени.
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Во время удара энергия движущегося объекта преобразуется в работу, и сила играет важную роль. Чтобы создать уравнение для силы любого удара, вы можете задать уравнения для энергии и работы, равные друг другу, и решить для силы. Отсюда относительно легко вычислить силу удара.
TL; DR (слишком длинный; Не читал)
Чтобы рассчитать силу удара, разделите кинетическую энергию на расстояние.
Удар и энергия
Энергия определяется как способность выполнять работу. Во время удара энергия объекта превращается в работу. Энергия движущегося объекта называется кинетической энергией и равна половине массы объекта, умноженной на квадрат его скорости:
KE = frac {1] {2} mv ^ 2
Думая о силе удара падающего объекта, вы можете рассчитать энергию объекта в его точке удара, если вы знаете высоту, с которой он был сброшен. Этот тип энергии известен как гравитационная потенциальная энергия и равен массе объекта, умноженной на высоту, с которой он был сброшен, и ускорение свободного падения:
PE = mgh
Воздействие и работа
Работа происходит, когда сила применяется для перемещения объекта на определенное расстояние. Следовательно, работа равна силе, умноженной на расстояние:
W = Fd
Поскольку сила — это компонент работы, а удар — это преобразование энергии в работу, вы можете использовать уравнения для энергии и работы, чтобы найти силу удара. Расстояние, пройденное при выполнении работы путем удара, называется дистанцией остановки. Это расстояние, пройденное движущимся объектом после удара.
Удар падающего объекта
Предположим, вы хотите узнать силу удара камня массой в один килограмм, который падает с высоты двух метров и погружается на два сантиметра в пластиковую игрушку. Первый шаг — установить уравнения для гравитационной потенциальной энергии и работы, равные друг другу, и решить для силы.
W = PE = Fd = mgh подразумевает F = frac {mgh} {d}
Второй и последний шаг — подставить значения из задачи в уравнение силы. Не забывайте использовать метры, а не сантиметры для всех расстояний. Расстояние остановки в два сантиметра должно быть выражено как две сотых метра. Кроме того, ускорение свободного падения на Земле всегда составляет 9,8 метра в секунду в секунду. Сила удара от камня составит:
F = frac {(1) (9,8) (2)} {0,02} = 980 text {N}
Удар от горизонтально движущегося объекта
Теперь предположим, что вы хотите узнать силу удара 2200-килограммового автомобиля, движущегося со скоростью 20 метров в секунду, который врезается в стену во время проверки безопасности. Расстояние остановки в этом примере — это зона деформации автомобиля или расстояние, на которое автомобиль укорачивается при ударе. Предположим, что автомобиль сдавлен настолько, что он на три четверти метра короче, чем был до удара. Опять же, первый шаг — это составить уравнения для энергии — на этот раз кинетической энергии — и работать, равные друг другу, и решить для силы.
W = KE = Fd = frac {1} {2} mv ^ 2 подразумевает F = frac {1/2 mv ^ 2} {d}
Последний шаг — подставить значения из задачи в уравнение для силы:
F = frac {1/2 (2,200) (20) ^ 2} {0,75} = 586,667 text {N}
Содержание:
Столкновения:
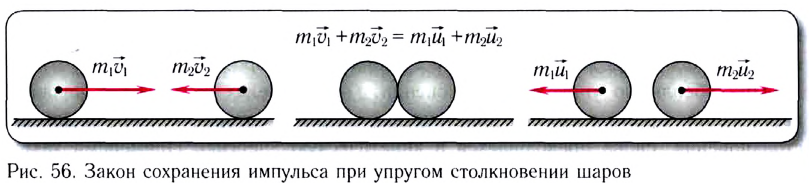
Наиболее общим явлением, наблюдаемым в природе, является взаимодействие материальных тел. Бильярдные шары, сближаясь, в момент соприкосновения взаимодействуют друг с другом. В результате этого меняются скорости шаров, их кинетические энергии. О таком взаимодействии шаров говорят как об их столкновениях.
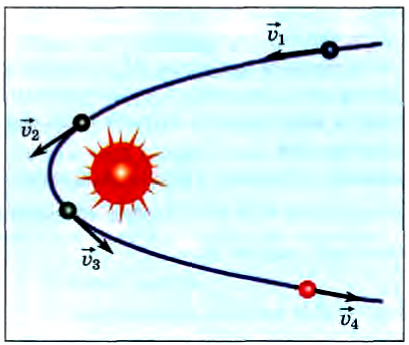
Но понятие «столкновение» относится не только к взаимодействиям, происходящим в результате соприкосновения материальных тел. Комета, прилетевшая из отдаленных областей пространства и прошедшая в окрестности Солнца, меняет свою скорость и удаляется. Этот процесс также является столкновением. хотя непосредственного соприкосновения между кометой и Солнцем не произошло, а осуществлено оно было посредством сил тяготения.
Характерная особенность этого взаимодействия, дающая нам возможность рассматривать его как столкновение, заключается в том, что область пространства, в котором оно произошло, относительно мала. Заметное изменение скорости кометы происходит вблизи Солнца (рис. 129).
Приведенные примеры позволяют нам дать следующее определение столкновения.
Что такое столкновение
Столкновением называется взаимодействие двух и большего числа тел, которое происходит в относительно малой области пространства в течение относительно малого промежутка времени. Вне этого промежутка времени можно говорить о начальных и конечных импульсах тел, когда тела можно считать невзаимодействующими.
Столкновение материальных тел часто называется ударом. Удар определяется как процесс, при котором изменяются импульсы соударяющихся тел без существенного изменения их положений. Это частный случай столкновения, например столкновение шаров, шайб, автомобилей и т. п.
Процессы столкновения являются чрезвычайно сложными. Например, при столкновении двух шаров в момент их соприкосновения начинается деформация шаров. В результате часть кинетической энергии переходит в потенциальную энергию деформации. Затем энергия деформации снова превращается в кинетическую, однако не полностью — часть энергии превращается во внутреннюю. Кроме того, после столкновения шары будут вращаться по иному, чем до столкновения.
Главный интерес при рассмотрении столкновений заключается в знании не самого процесса, а результата. Ситуация до столкновения называется начальным состоянием, а после — конечным. Между величинами, характеризующими начальное и конечное состояния, соблюдаются определенные соотношения. независящие от детального характера взаимодействия. Такими величинами. в частности, являются импульс и энергия системы тел.
В зависимости от характера изменения кинетической энергии тел все столкновения делятся на упругие и неупругие.
Если при столкновении кинетическая энергия тел сохраняется, то столкновение называется упругим, если же не сохраняется — неупругим.
Рассмотрим вначале абсолютно неупругое столкновение (абсолютно неупругий удар). Это частный случай неупругого столкновения, при котором после столкновения тела «слипаются» и движутся вместе.
Пусть в некоторой инерциальной системе отсчета первое тело массой m1 движется до столкновения со скоростью υ1, а второе тело массой m2 — со скоростью υ2. Следовательно, импульсы тел до столкновения равны соответственно:
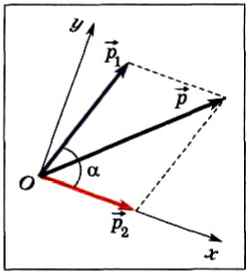
Процесс столкновения обычно наглядно представляют с помощью векторной диаграммы импульсов (рис. 130). Нетрудно убедиться, что кинетическая энергия системы не сохраняется. До столкновения она составляет:
после столкновения —
Изменение кинетической энергии:
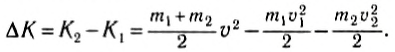
Для расчета выберем оси координат так, как показано на рисунке 130, и спроектируем на них равенство (1). B результате получим:
Рис. 130
Отсюда легко находится квадрат скорости тел после столкновения:
Подставив полученное выражение в (2), получим после несложных преобразований:
Как видно, кинетическая энергия системы уменьшилась. Часть кинетической энергии превратилась в теплоту.
Если тела при столкновении не «слипаются», то скорости тел после столкновения можно найти из закона сохранения импульса:
где штрихом отмечены импульсы тел после столкновения.
При этом кинетическая энергия может как уменьшаться, так и увеличиваться. Последнее происходит, например, при различных взрывах. В этом случае часть внутренней энергии превращается в кинетическую энергию осколков.
Как уже отмечалось, при упругом столкновении выполняется закон сохранения импульса и механической энергии.
Рассмотрим вначале лобовое столкновение, т. е. такое столкновение, при котором импульсы тел до и после столкновения параллельны некоторой прямой. Эту прямую мы примем за ось Ox (рис. 131). Закон сохранения импульса в этом случае примет вид:
а закон сохранения кинетической энергии —
Из этих уравнений найдем скорости тел после удара. Для этого перепишем (3) и (4) следующим образом:
Воспользовавшись тем, что a2 — b2 = (a-b)(a + b), из выражений (5) и (6) легко получить:
Выразив отсюда, например, 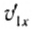
Аналогично:
Проекции импульсов тел после столкновения равны соответственно:
и
Проанализируем полученные выражения для некоторых частных случаев.
Предположим, что тело 2 до столкновения покоилось, т. е. 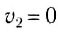
Тогда
При равных массах тел m1 = m2 получим:
Значит, первое тело остановится, а второе придет в движение с таким же импульсом.
Теперь предположим, что масса второго тела намного больше массы первого. Тогда, пренебрегая m1 по сравнению с m2 , получим:
Значит, первое тело отскочит назад с таким же по модулю импульсом, а тело 2 получит импульс, равный удвоенному значению импульса первого тела.
Найдем кинетическую энергию тел после столкновения для случая, когда 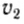
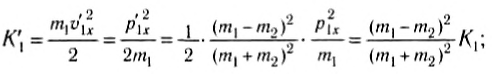
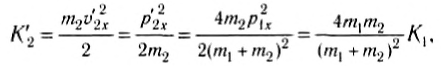
где K1 — кинетическая энергия первого тела до столкновения.
Из полученных выражений следует, что при m1 = m2 первое тело останавливается, а второе приобретает ту же энергию. Если масса второго тела m2 намного больше массы первого m1 то из (10) и (11) следует, что 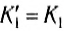
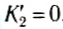
- Заказать решение задач по физике
Главные выводы:
- Столкновением называется взаимодействие двух и большего числа тел, которое происходит в относительно малой области пространства в течение относительно малого промежутка времени.
- Удар определяется как процесс, при котором изменяются импульсы соударяющихся тел без существенного изменения их положений.
- Столкновение тел называется упругим, если кинетическая энергия тел сохраняется. При неупругом столкновении кинетическая энергия тел не сохраняется.
- При столкновениях тел выполняется закон сохранения импульса.
Определение столкновения
Законы сохранения энергии и импульса позволяют провести теоретическое исследование процессов столкновения тел без описания сил, действующих между ними.
Под столкновениями понимают механические процессы взаимодействия между телами, происходящие за очень короткий промежуток времени. При этом силы взаимодействия между сталкивающимися телами настолько велики, что внешними силами, действующими на систему, можно пренебречь.
Вследствие того, что длительность столкновения мала по сравнению со временем наблюдения, различают механические состояния до и после столкновения, причем тела, находящиеся на большом расстоянии друг от друга, считают свободными.
Длительность столкновения бильярдных шаров 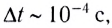
Различают упругие (абсолютно упругие) и неупругие столкновения. В первом случае не происходит выделения теплоты, и механическая энергия сохраняется. Во втором случае выделяется некоторое количество теплоты, поэтому механическая энергия после столкновения уменьшается.
Примером упругих столкновений служат столкновения металлических шаров, а примером неупругих — столкновения пластилиновых шаров, которые при этом слипаются и продолжают движение как одно целое.
Для макроскопических тел в большей степени характерными являются неупругие столкновения, в то время как для физики элементарных частиц, ядер атомов, молекул определяющую роль играет упругое взаимодействие.
Если в процессе столкновения тел на них не действуют внешние силы, то к телам применим закон сохранения импульса, а во многих случаях — и закон сохранения механической энергии. Именно эти законы позволяют, зная скорости тел до столкновения, определить их скорости после столкновения, совершенно не интересуясь тем, что происходило во время него.
При абсолютно неупругом столкновении скорости обоих взаимодействующих тел оказываются одинаковыми. Примером таких тел являются тела из различных пластичных веществ. Такое столкновение можно наблюдать, если подвесить тары из пластилина, развести их в разные стороны и отпустить. После столкновения они оба будут двигаться вместе с одинаковой скоростью.
При абсолютно упругом столкновении в обоих телах не остается никаких деформаций. Кроме того, вся кинетическая энергия, которой тела обладали до столкновения, снова превращается в кинетическую энергию. Примерами таких тел являются шары из стали или слоновой кости.
Рассмотрим простейшее столкновение — центральное, когда скорости тел находятся на линии, соединяющей их центры. Очень часто такое столкновение называют лобовым.
Скорость движения 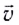
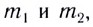
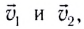
Откуда находим
Определим «потери» механической энергии, найдя кинетическую энергию
тел до столкновения:
и после столкновения:
Тогда часть механической энергии, перешедшая во внутреннюю, определяется выражением:
Следовательно, она зависит от масс сталкивающихся тел и относительной скорости 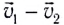
Задача о центральном абсолютно неупругом столкновении впервые была решена Дж. Валлисом в 1669 г.
При абсолютно упругом столкновении двух тел массами 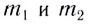
Здесь 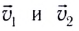
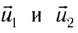
Преобразуем систему уравнений (3), перенеся в правую часть все величины, относящиеся к первому телу, а в левую — ко второму:
Разделив второе уравнение на первое, получим
Перепишем это уравнение в виде 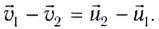
Из него следует, что при центральном абсолютно упругом столкновении тел любой массы их относительная скорость до и после столкновения не изменяется.
Теперь можно дать еще одно определение неупругого столкновения: если относительная скорость тел при центральном столкновении изменяется, то такое столкновение называется неупругим.
Меру неупругости k можно определить как отношение относительных скоростей сталкивающихся тел после и до столкновения:
Она называется коэффициентом восстановления и впервые была измерена Ньютоном в 1687 г. В частности, Ньютон получил значения коэффициента для стали k = 0,55 и стекла k = 0,94, которые приводят и современные справочники.
Абсолютно неупругим является столкновение, при котором скорости тел после столкновения равны 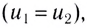
Решая уравнение (4) совместно с первым уравнением системы (3), находим скорости тел после столкновения:
На самом деле при столкновении всегда происходят «потери» механической энергии, т. е. переход части ее в теплоту. Но при малых «потерях» действительный процесс достаточно хорошо описывается абсолютно упругим столкновением.
Задача о центральном абсолютно упругом столкновении впервые была решена X. Гюйгенсом и К. Реном в 1669 г.
Отметим, что осуществить центральное, или лобовое, столкновение на практике очень трудно. Подавляющее число столкновений являются нецентральными.
Основные формулы
Импульс тела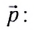
Закон изменения импульса системы тел:
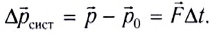
Закон сохранения импульса системы тел:
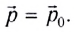
Работа:
Средняя мощность:
Мгновенная мощность:
Кинетическая энергия:
Теорема о кинетической энергии:
Потенциальная энергия:
Потенциальная энергия упруго деформированного тела:
Закон сохранения механической энергии:
- Рычаг в физике
- Блоки в физике
- Движение тела под действием нескольких сил
- Наклонная плоскость в физике
- Свободное падение тела
- Равнодействующая сила и движение тела под действием нескольких сил
- Сила давления в физике и единицы давления
- Механическое давление в физике