Тема: Два заряда (Прочитано 4304 раз)
0 Пользователей и 1 Гость просматривают эту тему.
С какой силой взаимодействуют два заряда 0,66*10-7 и 1,1*10-5 Кл в воде на расстоянии 3,3 см? На каком расстоянии их следует поместить в вакууме, чтобы сила взаимодействия осталась прежней? Сделать рисунок.
Записан
Решение:
Силы взаимодействия неподвижных зарядов прямо пропорциональны произведению модулей зарядов и обратно пропорциональны квадрату расстояния между ними: [ F=kfrac{|{{q}_{1}}|cdot |{{q}_{2}}|}{varepsilon cdot {{r}^{2}}},(1) ]
где k — коэффициент пропорциональности [ k=frac{1}{4pi {{varepsilon }_{0}}}=9cdot {{10}^{9}}frac{Hcdot {{м}^{{2}}}}{{{Кл}^{2}}}. ]
Сила взаимодействия зарядов в воде (εвода=81) равна
[ {{F}_{}}=kfrac{|{{q}_{1}}|cdot |{{q}_{2}}|}{varepsilon cdot r_{1}^{2}}=9cdot {{10}^{9}}frac{0,66cdot {{10}^{-7}}cdot 1,1cdot {{10}^{-5}}}{81cdot {{(3,3cdot {{10}^{-2}})}^{2}}}=0,074H=74 мН. ]
Fвода = Fвакуум.(2)
Из (1) найдем расстояние на которое их нужно поместить в вакууме (εвакуум = 1), чтобы сила взаимодействия осталась прежней (2):
[ begin{align}
& {{r}_{2}}=sqrt{kfrac{|{{q}_{1}}|cdot |{{q}_{2}}|}{varepsilon cdot {{F}_{}}}}, \
& {{r}_{2}}=sqrt{9cdot {{10}^{9}}frac{0,66cdot {{10}^{-7}}cdot 1,1cdot {{10}^{-5}}}{1cdot 0,074}}=0,297 м=29,7см. \
end{align} ]
Ответ: 74 мН, 29,7 см.
« Последнее редактирование: 02 Апреля 2016, 06:42 от alsak »
Записан
1)Найдите силу взаимодействия двух точечных зарядов в воде , если заряды и расстояние между ними равны : 32 нКл , 16 нКл, 40 см.
Заряды и вектор силы изобразите на схематическом рисунке.
2)Найдите потенциал электрического поля точечного заряда 18мкКл на расстоянии 30 см.
3)Найдите заряд который накопит конденсатор электроемкостью 12 мкФ если его зарядить до напряжения 200 в.
На странице вопроса 1)Найдите силу взаимодействия двух точечных зарядов в воде , если заряды и расстояние между ними равны : 32 нКл , 16 нКл, 40 см? из категории Физика вы найдете
ответ для уровня учащихся 10 — 11 классов. Если полученный ответ не
устраивает и нужно расшить круг поиска, используйте удобную поисковую
систему сайта. Можно также ознакомиться с похожими вопросами и ответами
других пользователей в этой же категории или создать новый вопрос. Возможно,
вам будет полезной информация, оставленная пользователями в комментариях, где
можно обсудить тему с помощью обратной связи.
Печатать книгу
| Сайт: | Профильное обучение |
| Курс: | Физика. 10 класс |
| Книга: | § 17. Взаимодействие точечных зарядов. Закон Кулона |
| Напечатано:: | Гость |
| Дата: | Среда, 24 Май 2023, 21:10 |
Оглавление
- Взаимодействие точечных зарядов. Закон Кулона
- Закон Кулона
- Взаимодействие системы точечных зарядов
- Диэлектрическая проницаемость вещества
- Примеры решения задач
- Упражнение 13
Электрически заряженные тела (частицы) взаимодействуют друг с другом. Но как определить силу, которой одно заряженное тело притягивает или отталкивает другое?
Вы уже встречались с физическими моделями при изучении механики (материальная точка) и молекулярной физики (идеальный газ). В электростатике при изучении взаимодействия электрически заряженных тел эффективной оказывается модель «точечный заряд».
Точечный заряд — заряд такого заряженного тела, размеры которого значительно меньше расстояния от этого тела до точки наблюдения и до других тел (т. е. размерами заряженного тела в условиях данной задачи можно пренебречь).
Вспомните, закон всемирного тяготения также сформулирован для точечных тел (материальных точек).
Закон Кулона. Кулон детально исследовал взаимодействие неподвижных точечных зарядов. Он на опыте изучил зависимость сил электрического взаимодействия тел от модулей зарядов этих тел и расстояния между ними.
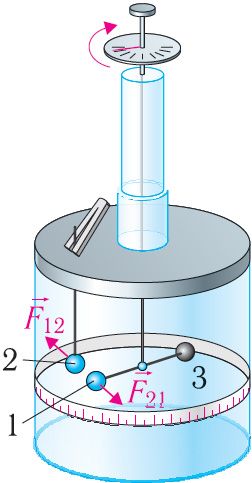
В своих опытах Кулон использовал специальный прибор — крутильные весы (рис. 98). Крутильные весы представляют собой два стеклянных цилиндра, внутри которых на тонкой серебряной нити подвешено лёгкое непроводящее коромысло. На одном конце коромысла закреплён проводящий шар 1, а на другом — бумажный противовес 3. Шар 1 можно заряжать с помощью такого же проводящего шара 2. Он находится на изолирующем стержне, закреплённом на крышке нижнего цилиндра. При соприкосновении шара 1 с заряженным шаром 2 заряд распределяется между ними поровну, и шары отталкиваются.
Используя крутильные весы, Кулон получил зависимость модуля сил взаимодействия двух заряженных шаров от величин зарядов и от расстояния между ними. По углу закручивания нити, отсчитываемому по шкале прибора, можно определить силу взаимодействия заряженных шаров. Кулон установил, что модуль сил взаимодействия двух заряженных шаров обратно пропорционален квадрату расстояния между ними:
.
Для измерения зависимости модуля сил взаимодействия шаров от их зарядов учёный нашёл простой способ. Разряжая шар 2 прикосновением руки, а затем касаясь им уже заряженного шара 1, Кулон смог получить на нём заряды, модуль которых в 2, 4, 8 и т. д. раз меньше первоначального. Он выяснил, что при неизменном расстоянии модуль сил взаимодействия двух неподвижных небольших заряженных тел прямо пропорционален произведению модулей электрических зарядов каждого из них: .
Обобщив экспериментальные данные, Кулон сформулировал закон, получивший его имя.
Закон Кулона: модули сил взаимодействия двух неподвижных точечных заряженных тел в вакууме прямо пропорциональны произведению модулей зарядов этих тел, обратно пропорциональны квадрату расстояния между ними, а сами силы направлены вдоль прямой, соединяющей эти тела:
(17.1)
где k — коэффициент пропорциональности, зависящий от выбора единиц физических величин; |q1| и |q2| — модули точечных зарядов; r — расстояние между ними.
В СИ коэффициент пропорциональности
где — электрическая постоянная.
От теории к практике
Два маленьких положительно заряженных шарика закреплены на расстоянии r друг от друга. Как изменится модуль сил электростатического взаимодействия шариков, если: 1) уменьшить заряд каждого шарика в четыре раза; 2) увеличить расстояние между шариками в четыре раза; 3) увеличить заряд каждого шарика и расстояние между ними в два раза?
Как изменились бы силы электростатического взаимодействия шариков, если бы: 1) шарики были заряжены отрицательно; 2) один из шариков зарядить отрицательно, а другой положительно?
Интересно знать
Экспериментальные факты свидетельствуют о том, что воздействие неподвижного в данной инерциальной системе отсчёта точечного заряда на движущийся точечный заряд может быть описано законом Кулона с приемлемой точностью. Так, описание рассеяния α-частиц на ядрах атомов золота в опытах Резерфорда с помощью модели точечного заряда, на который действует кулоновская сила со стороны неподвижного ядра, согласуется с экспериментальными данными в пределах точности последних.
Два и более движущихся в данной инерциальной системе заряда не могут характеризоваться только кулоновским взаимодействием, так как каждый из них создаёт в окружающем пространстве магнитное поле, которое действует магнитной силой на остальные заряды, движущиеся в нём.
Взаимодействие системы точечных зарядов. Экспериментально установили, что силы взаимодействия двух точечных зарядов не изменяются при появлении третьего точечного заряда или любого числа точечных зарядов. В этом случае силы воздействия ,
, …,
каждого из зарядов q2, q3, …, qn на заряд q1 определяют по закону Кулона. Результирующая сила является векторной суммой сил, которыми каждый из этих зарядов в отдельности воздействует на заряд q1 (принцип суперпозиции).
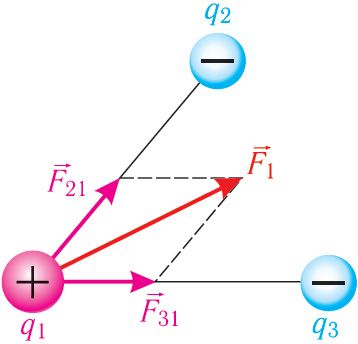
Используя принцип суперпозиции и закон Кулона, можно описать электростатическое взаимодействие любой системы точечных зарядов. На рисунке 100 представлены три взаимодействующих между собой точечных электрических заряда: q1 > 0, q2 < 0, q3 < 0. Результирующей сил, действующих на заряд q1 со стороны зарядов q2 и q3, является сила , которая равна векторной сумме сил
и
:
. Силы
и
воздействия зарядов q2 и q3 на заряд q1 определяют по закону Кулона.
От теории к практике
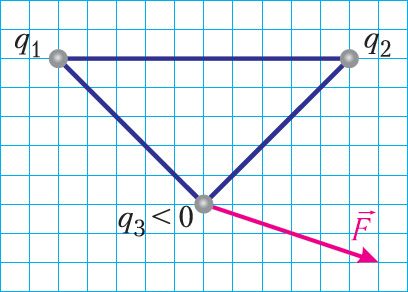
Точечные заряды q1, q2 и q3 закреплены в вершинах треугольника. Направление результирующей электростатической силы, действующей на отрицательный заряд q3 со стороны зарядов q1 и q2, представлено на рисунке 101. Каковы знаки зарядов q1 и q2? Во сколько раз отличаются модули зарядов q1 и q2?
Интересно знать
Понятие электрического заряда в некоторой степени сходно с понятием гравитационной массы. Электрический заряд определяет интенсивность электромагнитных взаимодействий, а масса — гравитационных. Закон Кулона, описывающий электростатическое взаимодействие, формально похож на закон всемирного тяготения Ньютона, определяющий силы гравитационного взаимодействия:
В обоих случаях модуль сил взаимодействия:
– обратно пропорционален квадрату расстояния между материальными точками;
– прямо пропорционален величинам, характеризующим те свойства тел (материальных точек), которые определяют взаимодействия, — массам в одном случае и электрическим зарядам — в другом.
Для измерения сил электрического отталкивания (Ш. Кулон, 1785 г.) и гравитационной постоянной (Г. Кавендиш, 1788 г.) учёные использовали похожие по устройству экспериментальные установки.
Однако между силами гравитационного и электростатического взаимодействий существует и важное различие. Ньютоновские силы тяготения — это всегда силы притяжения. кулоновские же силы взаимодействия зарядов могут быть как силами притяжения (между разноимёнными зарядами), так и силами отталкивания (между одноимёнными зарядами).
От теории к практике
Известно, что масса электрона mе = 9,1· 10–31 кг. Во сколько раз модуль сил электрического отталкивания между двумя электронами больше модуля сил их гравитационного притяжения?
Диэлектрическая проницаемость вещества. Из опытов следует, что взаимодействие электрически заряженных тел в воздухе практически не отличается от их взаимодействия в вакууме. Если заряженные тела находятся в воде, керосине, масле или какой-нибудь другой непроводящей среде, то модуль сил их взаимодействия оказывается меньше, чем в вакууме. Чтобы учесть влияние среды, ввели её специальную характеристику, называемую диэлектрической проницаемостью.
Диэлектрическая проницаемость вещества — физическая величина, показывающая, во сколько раз модуль сил электростатического взаимодействия зарядов в данной однородной среде меньше модуля сил взаимодействия этих же зарядов в вакууме:
(17.2)
где F0 и F — модули сил электростатического взаимодействия зарядов в вакууме и в однородной среде соответственно.
С учётом соотношения (17.2) закон Кулона можно записать следующим образом:
Диэлектрическая проницаемость вакуума равна 1. За 1 принимают и диэлектрическую проницаемость воздуха, поскольку её значение (при нормальном атмосферном давлении) 1,0006. Диэлектрические проницаемости других однородных сред всегда больше единицы. Например, у воды диэлектрическая проницаемость 81, у глицерина — 56, а у керосина — 2.
От теории к практике
Как и во сколько раз отличаются модули сил электростатического взаимодействия двух точечных зарядов, находящихся на одинаковом расстоянии друг от друга в воде, керосине и глицерине?
Интересно знать
Диэлектрическая проницаемость дистиллированной воды при температуре 25 °C равна 78,54, а при температуре 0 °C — 88. Обычно без указания температуры диэлектрическую проницаемость воды полагают равной 81.
1. К какому виду взаимодействий относят взаимодействие неподвижных электрических зарядов (заряженных тел)?
2. Заряды каких заряженных тел можно считать точечными?
3. Опишите эксперименты Кулона по исследованию взаимодействия электрических зарядов.
4. Сформулируйте закон Кулона. Каковы условия применимости закона Кулона?
5. Чему равен в СИ коэффициент k? Выразите наименование коэффициента пропорциональности k в законе Кулона в основных единицах СИ.
6. В чём суть принципа суперпозиции для электрического взаимодействия точечных зарядов?
7. Что называют диэлектрической проницаемостью среды?
Примеры решения задач
Пример 1. Два точечных заряда находятся в керосине на расстоянии r1 = 42 см. Определите, на каком расстоянии должны находиться эти заряды в глицерине, чтобы модуль сил их электростатического взаимодействия остался прежним. Диэлектрические проницаемости керосина ε1 = 2,0, глицерина ε2 = 56,2.
Дано:
r1 = 42 см
Fк1 = Fк2
ε1 = 2,0
ε2 = 56,2
r2 — ?
Решение: Поскольку Fк1 = Fк2, то, воспользовавшись законом Кулона, можно записать: .
Следовательно, .
Ответ: r2 = 7,9 см.
Пример 2. Точечные заряды q1 = 3,4 нКл и q2 = –5,6 нКл находятся в вакууме на расстоянии r = 36 см. Определите модуль и направление результирующей силы, действующей на заряд q3 = 3,2 нКл, помещённый в точку пространства, находящуюся на середине отрезка, соединяющего эти заряды.
Дано:
q1 = 3,4 нКл = 3,4 · 10–9 Кл
q2 = –5,6 нКл = –5,6 · 10–9 Кл
r = 36 см = 0,36 м
q3 = 3,2 нКл = 3,2 · 10–9 Кл
— ?
Решение: Изобразим на рисунке силы и
, действующие на точечный заряд q3 со стороны точечных зарядов q1 и q2 соответственно. Построив векторную сумму сил
и
, определим, что результирующая
этих сил направлена к заряду q2 (рис. 102).
Поскольку силы и
направлены одинаково, то модуль результирующей силы
.
Таким образом,
Ответ: Fp = 8,0 мкН; сила направлена к заряду q2.
Пример 3. Две бусинки, электрические заряды которых q1 = 40 нКл и q2 = 90 нКл, закреплены на непроводящем стержне на расстоянии r = 40 см друг от друга. Определите: а) где надо поместить третью бусинку, имеющую заряд q3, чтобы она оказалась в равновесии; б) каким должен быть заряд q3 третьей бусинки, чтобы результирующая сила электростатического взаимодействия каждой из трёх бусинок с остальными двумя равнялась нулю.
Дано:
q1 = 40 нКл = 4,0·10–8 Кл
q2 = 90 нКл = 9,0·10-8 Кл
r = 40 см = 0,40 м
х — ?
q3 — ?
Решение: а) Третья бусинка, имеющая заряд q3, будет находиться в равновесии, если её поместить в некоторую точку А между зарядами q1 и q2 на прямой, соединяющей эти заряды (рис. 102.1). Пусть заряд q3 < 0. Тогда со стороны зарядов q1 и q2 на заряд q3 будут действовать противоположно направленные кулоновские силы притяжения и
. Согласно второму закону Ньютона, эта бусинка будет покоиться, если модули сил F13 и F23 равны. Тогда, приняв расстояние от заряда q1 до точки А равным х, запишем:
. Так как k и q3 не равны нулю, то это выражение можно сократить:
. Извлечём из обеих частей равенства квадратный корень
. Отсюда:
Такое же значение х мы получим, если примем заряд q3 бусинки положительным (проверьте это самостоятельно).
б) Результирующая сила электростатического взаимодействия каждой из трёх бусинок с остальными двумя равна нулю, если, например, третья бусинка притягивает вторую силой, модуль которой равен модулю силы
, какой её отталкивает первая бусинка (рис. 102.2). При этом заряд третьей бусинки должен быть отрицательным, т. е. q3 < 0. Тогда
. Отсюда
.
Ответ: х = 16 см, расстояние до бусинки с зарядом q3 не зависит от значения и знака её заряда; если заряд бусинки q3 = ‒14 нКл, то результирующая сила электростатического взаимодействия каждой из трёх бусинок с остальными двумя равна нулю.
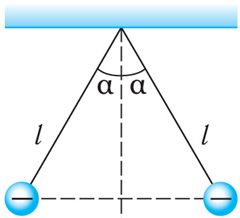
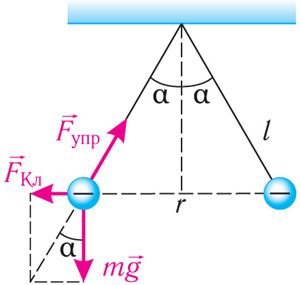
Пример 4. Два одинаковых маленьких проводящих шарика массой m = 20 мг каждый подвешены в воздухе на лёгких нерастяжимых нитях длиной l = 0,20 м, закреплённых в одной точке подвеса. Один из шариков отвели в сторону, сообщили ему заряд q < 0 и отпустили. После столкновения шарики разошлись так, что угол между нитями составил 2α = 60° (рис. 102.3). Определите заряд, который был сообщён первому шарику, а также количество избыточных электронов на каждом из шариков после их столкновения.
Дано:
m = 20 мг = 2,0·10–5 кг
l = 0,20 м
2α = 60°
q – ?
N – ?
Решение: Воспользуемся законом сохранения электрического заряда. При столкновении двух одинаковых проводящих шариков сообщённый одному из них заряд разделился поровну и на каждом шарике оказался избыточный отрицательный заряд . На каждый шарик действуют сила тяжести
сила электростатического взаимодействия
и сила упругости нити
(рис. 102.4). После столкновения шарики разошлись, и установилось равновесие. Векторная сумма сил, действующих на каждый шарик, стала равной нулю:
. Модуль силы электростатического взаимодействия
. Поскольку шарики разошлись симметрично относительно вертикали, проходящей через точку подвеса нитей, то
(рис. 102.4). Следовательно,
. Так как
, то
, откуда
. Примем
.
Количество избыточных электронов на каждом шарике .
Ответ: q = ‒45 нКл, N = 1,4 · 1011.
Упражнение 13
1. Определите модуль сил взаимодействия двух одинаковых неподвижных точечных зарядов q1 = q2 = 9,0 нКл, находящихся на расстоянии r = 0,30 м в вакууме. Во сколько раз уменьшится или увеличится модуль сил взаимодействия этих зарядов при помещении их в керосин, диэлектрическая проницаемость которого ε = 2,0?
2. Определите, во сколько раз следует увеличить расстояние между двумя неподвижными точечными зарядами, чтобы модуль сил взаимодействия остался прежним при увеличении численного значения одного из зарядов в α = 4 раза.
3. Два одинаковых маленьких проводящих шарика, заряды которых отличаются в два раза, находятся на расстоянии r = 50 см. Определите расстояние, на которое необходимо развести шарики после соприкосновения, чтобы модуль сил их взаимодействия остался прежним.
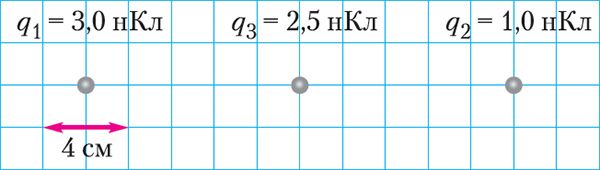
4. Точечные заряды q1 и q2 закреплены в вакууме (рис. 103). Определите модуль и направление результирующей силы, действующей на заряд q3, помещённый в точку, находящуюся на середине отрезка, соединяющего эти заряды.
5. Заряды двух одинаковых маленьких шариков массой m = 40 г каждый одинаковые. Расстояние между шариками существенно превышает их размеры. Определите модуль зарядов шариков, если кулоновская сила их отталкивания уравновешивает силу гравитационного притяжения этих шариков.
6. Небольшой шарик, заряд которого q1 = 20 нКл и масса m = 60 мг, подвешен в воздухе на шёлковой нити. После того как на вертикали, проходящей через центр шарика, на расстоянии r = 15 см ниже его поместили другой маленький шарик, заряженный отрицательно, модуль силы упругости нити увеличился в два раза. Определите заряд второго шарика.
7. Три первоначально закреплённых одинаковых точечных заряда q1 = q2 = q3 = q0 = 1,0 мкКл расположены в вершинах равностороннего треугольника. Определите, какой точечный заряд нужно поместить в центр треугольника, чтобы вся система находилась в равновесии после освобождения первоначально закреплённых зарядов.
ЧАСТЬ I. СТРОЕНИЕ И КАТАЛИЗ
Я верю, что использование методов структурной химии для решения проблем физиологии позволит показать, что роль водородных связей в физиологии больше, чем любых других структур.
Лайнус Полинг, Природа химической связи, 1939
2. ВОДА
Вода — самое распространенное вещество в живой природе; массовая доля воды в большинстве живых организмов составляет 70% и более. Первые живые организмы на Земле, несомненно, появились в водной среде, и ход эволюции определялся свойствами того водного окружения, в котором возникла жизнь.
Данная глава начинается с рассмотрения физических и химических свойств воды, к которым адаптированы все структурные элементы и функции живой клетки. Для структуры и функций биомолекул необычайно важное значение имеют силы притяжения между молекулами воды и ее слабая ионизованность. При рассмотрении вопроса об ионизации мы поговорим о константах равновесия, pH и кривых титрования, а также покажем, как водные растворы слабых кислот и оснований и их соли действуют в качестве буферов, препятствуя изменениям pH в биологических системах. Молекула воды и продукты ее ионизации (Н+ и ОН—) оказывают глубокое влияние на структуру, процесс сборки и свойства всех клеточных компонентов, в том числе белков, нуклеиновых кислот и липидов. Свойства воды как растворителя, включая способность образовывать водородные связи между собственными молекулами и молекулами растворенных веществ, решающим образом влияют на нековалентные взаимодействия, ответственные за силу и специфичность «узнавания» среди биомолекул.
2.1. Слабые взаимодействия в водных средах
Наличие водородных связей приводит к большому внутреннему сцеплению между молекулами воды и делает ее жидкой при комнатной температуре, а также способствует образованию высокоупорядоченной кристаллической структуры льда (твердое состояние). Полярные биомолекулы легко растворяются в воде, поскольку они способны вытеснить воду из связи вода-вода с образованием энергетически более выгодной связи вода-растворенное вещество. Напротив, неполярные вещества мешают взаимодействию вода-вода, но не способны образовывать связь вода-растворенное вещество, другими словами, неполярные вещества плохо растворяются в воде. В водных растворах неполярные вещества часто образуют кластеры.
Водородные связи, ионные, гидрофобные (от греч. боящийся воды) и ван-дер-ваальсовы взаимодействия по отдельности довольно слабые, однако вместе они оказывают весьма значительное влияние на трехмерную структуру белков, нуклеиновых кислот, полисахаридов и мембранных липидов.
Таблица 2-1. Температура плавления, температура кипения и теплота испарения некоторых обычных растворителей
|
Температура плавления (°С) |
Температура кипения (°С) |
Теплота испарения (Дж/г)* |
|
|
Вода |
0 |
100 |
2 260 |
|
Метанол (СН3ОН) |
298 |
65 |
1 100 |
|
Этанол (СН3СН2ОН) |
2117 |
78 |
854 |
|
Пропанол (СН3СН2СН2ОН) |
2127 |
97 |
687 |
|
Бутанол (СН3(СН2)2СН2ОН) |
290 |
117 |
590 |
|
Ацетон (СН3СОСН3) |
295 |
56 |
523 |
|
Гексан (СН3(СН2)4СН3) |
298 |
69 |
423 |
|
Бензол (С6Н6) |
6 |
80 |
394 |
|
Бутан (СН3(СН2)2СН3) |
2135 |
20,5 |
381 |
|
Хлороформ (СНС13) |
263 |
61 |
247 |
*Количество тепловой энергии, необходимое для превращения 1,0 г жидкости при температуре ее кипения и атмосферном давлении в газообразное состояние при тех же значениях температуры и давления. Эта величина является мерой той энергии, которую нужно затратить на преодоление сил притяжения между молекулами в жидкой фазе.
Необычные свойства воды обусловлены наличием водородных связей
По сравнению с большинством других жидкостей вода имеет высокие температуры плавления и кипения и теплоту испарения (табл. 2-1). Эти особенности воды являются результатом сильного притяжения между ее соседними молекулами, вследствие чего жидкая вода характеризуется большим внутренним сцеплением. Причину подобных межмолекулярных взаимодействий можно понять, если рассмотреть электронную структуру молекулы Н2O.
Каждый атом водорода в молекуле воды имеет общую пару электронов с центральным атомом кислорода. Геометрия молекулы определяется формой внешних электронных орбита- лей кислорода, которые имеют структуру, аналогичную связывающим sp3 орбиталям углерода (рис. 1-14). Эти орбитали располагаются в форме неправильного тетраэдра, имеющего по одному атому водорода в каждом из двух углов и неподеленные электронные пары кислорода в двух других углах (рис. 2-1, а). Угол, образуемый связью Н-О-Н, составляет 104,5° — чуть меньше, чем в правильном тетраэдре (109,5°), что связано с взаимным отталкиванием неподеленных электронных пар кислорода.
Рис. 2-1. Строение молекулы воды, а) Биполярная природа молекулы воды показана с помощью шаростержневой модели. Пунктирными линиями обозначены несвязывающие орбитали. Электронные пары, расположенные на внешних электронных орбиталях, образуют вокруг атома кислорода неправильный тетраэдр. Каждый атом водорода несет частичный положительный (δ+), а атом кислорода — частичный отрицательный заряд (2δ—). б) Две молекулы Н2О связаны водородной связью (здесь и далее водородная связь обозначается тремя голубыми черточками), соединяющей атом кислорода верхней молекулы и атом водорода нижней молекулы. Водородные связи длиннее и слабее, чем ковалентные связи О-Н.
Ядро атома кислорода притягивает электроны сильнее, чем ядро водорода (протон), т. е. кислород является более электроотрицательным. В результате положение поделенной нары электронов между кислородом и водородом не равноудаленное — электроны чаще расположены ближе к атому кислорода, чем к атому водорода. Такая асимметрия приводит к образованию в молекуле воды двух электрических диполей — но одному вдоль каждой связи Н-О. В результате на водороде сосредоточивается частичный положительный заряд (δ+), а на кислороде — частичный отрицательный, равный по модулю сумме двух частичных положительных зарядов (2δ-). Этим и объясняется электростатическое притяжение между атомом кислорода одной молекулы воды и атомом водорода другой молекулы (рис. 2-1, б), называемое водородной связью. В данной книге мы будем изображать водородную связь в виде трех голубых параллельных черточек, как на рис. 2-1,6.
Водородные связи сравнительно слабые. Энергия диссоциации (энергия, необходимая для разрыва связи) водородной связи в жидкой воде составляет 23 кДж/моль, тогда как энергия диссоциации ковалентной связи О-Н воды равна 470 кДж/моль, а ковалентной С-С-связи 348 кДж/моль. В образование водородной связи 10% вносят ковалентные взаимодействия (за счет перекрывания электронных орбиталей), а 90% — электростатические взаимодействия. При комнатной температуре тепловая энергия водного раствора (кинетическая энергия движения отдельных атомов и молекул) имеет тот же порядок величины, что и энергия диссоциации водородной связи. Повышение температуры при нагревании воды приводит к ускорению отдельных молекул. В каждый момент времени большинство молекул жидкой воды участвует в образовании водородных связей, однако время жизни каждой водородной связи составляет лишь от 1 до 20 пикосекунд (1 пс = 10-12 с). При разрыве одной водородной связи через 0,1 пс образуется другая — с тем же или с новым партнером. Короткоживущие группы молекул воды, связанные водородными связями, были удачно названы «мерцающими кластерами». Все водородные связи между молекулами определяют сильное внутреннее сцепление жидкой воды. Протяженные сети связанных водородными связями молекул воды включают в себя и молекулы растворенных веществ (белков, нуклеиновых кислот и др.), что позволяет большим молекулам взаимодействовать друг с другом на расстояниях нескольких нанометров без прямого физического контакта.
Поскольку расположение электронных орбиталей вокруг атома кислорода близко к тетраэдрическому (рис. 2-1, а), каждая молекула воды способна образовать водородные связи максимум с четырьмя соседними молекулами воды. Так как в жидком состоянии при атмосферном давлении молекулы воды находятся в непрерывном движении, то считают, что каждая молекула в любой момент времени образует водородные связи в среднем с 3,4 других молекул. Напротив, во льду молекулы зафиксированы в пространстве и оказываются связанными с максимально возможным количеством соседей; при этом образуется регулярная пространственная решетка (рис. 2-2). Для того чтобы разорвать достаточное число водородных связей и нарушить кристаллическую решетку льда, требуется много тепловой энергии, что выражается в сравнительно высокой температуре плавления воды (табл. 2-1). При плавлении льда или испарении воды затрачивается тепловая энергия:
Н2О (твердая) —> Н2О (жидкая)
∆Н = +5,9 кДж/моль
Н2О (жидкая) —> Н2О (газ)
∆Н = +44,0 кДж/моль
Рис. 2-2. Водородные связи между молекулами воды во льду. Каждая молекула воды во льду связана с четырьмя другими молекулами воды (максимально возможное число для воды), так что при этом образуется регулярная кристаллическая решетка. В жидкой воде при комнатной температуре и при атмосферном давлении каждая молекула воды связана водородными связями приблизительно с 3,4 молекул. Кристаллическая решетка льда более рыхлая (лед имеет меньшую плотность, чем вода), и поэтому лед плавает на поверхности воды.
В процессе плавления или испарения энтропия системы повышается, поскольку высокоорганизованная структура молекул (лед) переходит в менее организованное (вода) или в полностью дезорганизованное состояние (пар). При комнатной температуре плавление льда и испарение воды происходят самопроизвольно: стремление молекул воды ассоциировать посредством образования водородных связей оказывается слабее энергетической выгоды от перехода к хаотическому состоянию. Вспомним, что для самопроизвольного протекания процесса изменение свободной энергии (∆G) должно быть отрицательной величиной: ∆G = ∆Н — T∆S, где ∆G представляет собой движущую силу процесса, ∆Н — изменение энтальпии, связанное с образованием и разрывом связей, а ∆S отражает изменение упорядоченности системы. Поскольку в процессах плавления и испарения ∆Н >0, то именно повышение энтропии (∆S) делает значение ∆G отрицательным и способствует данным превращениям.
Вода образует водородные связи с полярными растворенными веществами
Водородные связи существуют не только в воде. Они легко образуются между электроотрицательным атомом (акцептором водорода, в качестве которого обычно выступает кислород или азот) и атомом водорода, ковалентно связанным с другим электроотрицательным атомом (донором водорода) в той же самой или в другой молекуле (рис. 2-3). Атомы водорода, связанные ковалентной связью с углеродом, не участвуют в образовании водородных связей, поскольку электроотрицательность атома углерода лишь немного выше, чем водорода, и, следовательно, связь С-Н практически неполярна. Именно этим различием объясняется сравнительно высокая температура кипения бутилового спирта CH3(CH2)2CH2ОH (117 °С) и низкая — у бутана СН3(СН2)2СН3 (-0,5 °С). В молекуле бутилового спирта есть полярная гидроксильная группа, которая может участвовать в образовании межмолекулярных водородных связей. Незаряженные, но полярные биомолекулы (такие как сахара) легко растворяются в воде благодаря стабилизационному эффекту от образования водородных связей между гидроксильными группами или карбонильным кислородом сахара и полярными молекулами воды. Спирты, альдегиды, кетоны и соединения, содержащие связи N-Н, образуют водородные связи с молекулами воды (рис. 2-4) и обычно хорошо растворяются в воде.
Рис. 2-3. Типы водородных связей, наиболее часто встречающиеся в биологических системах. Акцептором водорода обычно служит атом кислорода или азота; донором водорода является другой электроотрицательный атом.
Рис. 2-4. Некоторые водородные связи, имеющие важное значение для биологических систем.
Водородные связи обладают наибольшей прочностью в тех случаях, когда взаимная ориентация связанных между собой молекул обеспечивает максимальную энергию электростатического взаимодействия. Такая ситуация наблюдается, если атом водорода и два делящих его атома расположены на одной прямой, т. е. если акцептор находится на одной линии с ковалентной связью между атомом донора и атомом водорода (рис. 2-5) и, если положительно заряженный ион водорода находится ровно между частичными отрицательными зарядами на атомах кислорода. Другими словами, водородная связь характеризуется определенной направленностью и вследствие этого способна удерживать обе связанные с се помощью молекулы или группы в определенной ориентации. Ниже мы увидим, что именно это свойство водородных связей способствует стабилизации строго определенных трехмерных структур, характерных для молекул белков и нуклеиновых кислот, имеющих большое число внутримолекулярных водородных связей.
Рис. 2-5. Направленность водородной связи. Максимальное притяжение между частичными электрическими зарядами (рис. 2-1) реализуется в том случае, когда три атома (в данном случае О, Н и O), участвующие в образовании водородной связи, лежат на одной прямой. Если группы, участвующие в образовании водородной связи, строго зафиксированы (например, являются частями одной и той же молекулы белка) и такое идеальное расположение невозможно, то образуется более слабая связь.
Между водой и заряженными веществами существуют электростатические взаимодействия
Вода является полярным растворителем. В ней легко растворяется большинство биомолекул, которые обычно представляют собой заряженные или полярные вещества (табл. 2-2). Легко растворяющиеся в воде вещества называют гидрофильными (от греч. любящий воду). Напротив, неполярные растворители (хлороформ, бензол и др.) плохо растворяют полярные биомолекулы, но хорошо растворяют те вещества, которые обладают гидрофобными свойствами, т. е. неполярные молекулы типа липидов и смол.
Вода растворяет такие соли, как NaCl, гидратируя и стабилизируя ионы Na+ и Сl путем ослабления электростатических взаимодействий между ними, тем самым препятствуя их ассоциации с образованием кристаллической структуры (рис. 2-6). Те же принципы применимы и к растворению заряженных биомолекул, содержащих такие функциональные группы, как ионизованная карбоксильная группа (-СОО-), протонированная аминогруппа (-NH3+), а также эфиры или ангидриды фосфорной кислоты. Вода легко растворяет подобные вещества, при этом водородные связи в молекулах растворенных веществ заменяются водородными связями между растворенным веществом и водой, кроме того, экранируются электростатические взаимодействия между молекулами растворенного вещества.
Воду очень удобно использовать для оценки электростатических взаимодействий между растворенными ионами, поскольку она имеет высокую диэлектрическую проницаемость (этот физический параметр отражает количество диполей в растворителе). Сила ионных взаимодействий в растворе (F) зависит от величины заряда (Q), расстояния между заряженными группами (r) и диэлектрической проницаемости растворителя (ε, безразмерная величина), в котором происходит взаимодействие:
Рис. 2-6. Вода как растворитель. Хорошая растворимость в воде многих кристаллических солей обусловлена гидратацией ионов, образующих эти соли. Кристаллическая решетка NаСl распадается, по мере того как молекулы воды окружают ионы и Сl—. Заряды ионов частично нейтрализуются, и электростатическое притяжение, необходимое для образования решетки, ослабевает.
Диэлектрическая проницаемость воды при 25 °С равна 78,5, а для такого неполярного растворителя, как бензол, ε = 4,6. Таким образом, ионные взаимодействия между растворенными ионами сильнее проявляются в неполярных, чем в полярных средах. Зависимость силы ионных взаимодействий от расстояния (от 1/г2) приводит к тому, что в воде притяжение или отталкивание ионов действует лить на очень коротком расстоянии — в диапазоне от 10 до 40 им в зависимости от концентрации электролита.
Таблица 2-2. Примеры полярных, неполярных и амфифильных биомолекул (в ионной форме при рН 7)
При растворении кристаллических веществ энтропия возрастает
При растворении соли NaCl ионы Na+ и Сl покидают кристаллическую решетку и получают большую свободу передвижения (рис. 2-6). Легкость растворения в воде таких солей, как NaCl, во многом объясняется ростом энтропии в системе (усилением беспорядка). В терминах термодинамики, образованию раствора способствует изменение свободной энергии: ∆G = ∆Н — T∆S, где ∆Н имеет небольшое положительное значение, a T∆S — большое положительное значение, отсюда A∆G <0.
Неполярные газы плохо растворяются в воде
Важные для биологических систем молекулы СO2, O2 и N2 неполярны. В молекулах кислорода и азота электроны поделены поровну между обоими атомами. В молекуле СO2каждая связь С=O полярная, однако два диполя имеют противоположное направление и нейтрализуют друг друга (табл. 2-3). Переход молекул из неупорядоченного состояния в газовой фазе в водный раствор нарушает свободу их перемещения и движение молекул воды, т. е. сопровождается снижением энтропии. Неполярная природа молекул и снижение энтропии при переходе из газовой фазы в жидкость определяют очень плохую растворимость этих соединений (табл. 2-3). У некоторых организмов имеются растворимые в воде белки- нереносчики (например, гемоглобин и миоглобин), облегчающие транспорт кислорода. Диоксид углерода образует в воде угольную кислоту (Н2СO3) и переносится в виде иона бикарбоната (НСO3—) либо в свободном состоянии (бикарбонат очень хорошо растворим в воде: -100 г/л при 25 °С), либо в комплексе с гемоглобином. Такие газы, как NН3, NO и Н2S, также важны для жизнедеятельности некоторых организмов; они полярные и хорошо растворяются в воде и ионизированы в водных растворах.
Таблица 2-3. Растворимость некоторых газов в воде
* Стрелками показаны электрические диполи: направление от области с частичным положительным зарядом (δ+, здесь не показано) к области с частичным отрицательным зарядом (δ—).
** Заметьте, что полярные молекулы растворяются в воде даже при низкой температуре лучше, чем неполярные молекулы при повышенной температуре.
Неполярные вещества при растворении вызывают энергетически невыгодные изменения в структуре воды
При смешивании воды с бензолом или гексаном образуются две фазы. Неполярные соединения (бензол и гексан) гидрофобны, т. е. они не способны вступать в энергетически выгодные взаимодействия с молекулами воды и нарушают водородные связи, существующие между молекулами воды. Все молекулы или ионы в водном растворе нарушают эти связи, однако полярные или заряженные вещества, такие как NаСl, компенсируют нарушение связей вода-вода образованием новых связей вода-растворенное вещество. Суммарное изменение энтальпии (∆Н) при растворении таких молекул обычно невелико. Напротив, гидрофобные вещества никак не компенсируют нарушение структуры водородных связей между молекулами воды, поэтому их растворение сопровождается небольшим увеличением энтальпии; разрыв водородных связей между молекулами воды требует определенной энергии, которую необходимо получить из окружающей среды. Кроме этого, растворение в воде гидрофобных веществ приводит к значительному снижению энтропии. Молекулы воды, находящиеся в непосредственной близости от неполярной молекулы, фиксируются в определенной ориентации и формируют высокоупорядоченную оболочку вокруг каждой молекулы растворенного вещества. Молекулы воды, организованные таким образом, имеют не такую упорядоченную структуру, как клатраты (кристаллы неполярных веществ и воды), но эффект в обоих случаях достигается один и тот же — упорядочение молекул воды снижает энтропию. Число упорядоченных молекул воды, а, следовательно, и величина снижения энтропии, пропорциональны площади поверхности гидрофобного вещества, заключенного в оболочку из молекул воды. Таким образом, изменение свободной энергии, сопровождающее растворение неполярного вещества в воде, не благоприятствует этому процессу: ∆G = ∆H — T∆S, где ∆Н — положительное число, ∆S — отрицательное число, отсюда ∆G >0.
Амфифильные соединения имеют как полярные (заряженные), так и неполярные группы (табл. 2-2). При смешивании амфифильного соединения с водой его полярные гидрофильные области стремятся раствориться, однако неполярные гидрофобные области пытаются избежать контакта с растворителем (рис. 2-7, а). Неполярные группы собираются вместе и образуют кластеры с минимальной поверхностью, а полярные группы располагаются так, чтобы максимально увеличить свой контакт с водой (рис. 2-7, б). В результате в воде образуются устойчивые структуры амфифильных веществ, называемые мицеллами, которые могут состоять из сотен или тысяч молекул. Силы, удерживающие вместе неполярные группы молекул растворенного вещества, называют гидрофобными взаимодействиями. Эта сила не связана с каким-либо внутренним притяжением между неполярными остатками. Скорее, это взаимодействие является результатом стремления системы достичь максимальной термодинамической стабильности путем минимизации числа упорядоченны: молекул воды, которые окружают гидрофобные участки молекул растворенного вещества.
Рис. 2-7. Поведение амфифильных соединений в водном растворе, а) Длинноцепочечные жирные кислоты имеют гидрофобные алкильные цепи, которые окружены слоем упорядоченных молекул воды. б) Образование мицелл приводит к минимизации контакта гидрофобной поверхности жирных кислот с водой, кроме того, в такой структуре минимальное число упорядоченных молекул воды задействовано в образовании оболочки вокруг неполярных молекул. Стабилизация мицеллы происходит за счет выигрыша в энергии в результате высвобождения иммобилизованных молекул воды.
Многие биомолекулы являются амфифильными: белки, пигменты, некоторые витамины, а также стеролы и фосфолипиды в мембранах имеют как полярные, так и неполярные участки. Образованные такими молекулами структуры удерживаются за счет гидрофобных взаимодействий между неполярными группами. Гидрофобные взаимодействия между липидами, а также между липидами и белками являются важнейшим принципом построения биологических мембран. Гидрофобные взаимодействия между неполярными аминокислотами играют роль в стабилизации трехмерной структуры белков.
Образование водородных связей между водой и полярными соединениями также приводит к упорядочиванию молекул воды, однако в случае растворения неполярных веществ энергетический эффект меньше. Часть движущей силы, направленной на связывание полярного субстрата (реагирующего вещества) с комплементарной полярной поверхностью фермента, расходуется на повышение энтропии, поскольку фермент выталкивает упорядоченные молекулы воды с поверхности субстрата, а субстрат выталкивает упорядоченные молекулы воды с поверхности фермента (рис. 2-8).
Рис. 2-8. Высвобождение упорядоченных молекул водь способствует образованию фермент-субстратного ком плекса. Как вокруг молекулы фермента, так и вокруг молекулы субстрата существует слой упорядоченных молекул воды. Связывание фермента с субстратом приводит высвобождению некоторого количества упорядоченны: молекул. Наблюдающееся при этом повышение энтро пии является термодинамическим стимулом образовать фермент-субстратного комплекса (см. с. 282).
Ван-дер-ваальсовы взаимодействия являются слабыми силами межатомного притяжения
При слишком близком контакте двух незаряженных атомов происходит взаимодействие окружающих их электронных облаков. Случайные вариации положения электронов вокруг одного ядра могут создавать электрический диполь, который способен индуцировать противоположный электрический диполь в соседнем атоме. Два диполя слабо притягиваются друг к другу, в результате чего ядра сближаются. Такие слабые силы притяжения называют ван-дер-ваальсовым притяжением (или силами Лондона). По мере сближения двух ядер возникает противоположно направленная сила отталкивания их электронных облаков. В точке, где общее притяжение максимально, говорят, что ядра находятся в ван-дер-ваальсовом контакте. Каждый атом характеризуется ван-дер-ваальсовым радиусом, определяющим, насколько близко этот атом позволяет подойти другому атому (табл. 2-4). В приведенных в данной книге СРК-моделях молекул размеры всех атомов соотносятся, как их ван-дер-ваальсовы радиусы.
Таблица 2-4. Ван-дер-ваальсовы радиусы и ковалентные радиусы (при образовании одинарной связи) некоторых элементов
|
Элемент |
Ван-дер-ваальсовы радиусы (нм) |
Ковалентные радиусы (в одинарной связи) (нм) |
|
H |
0,11 |
0,030 |
|
О |
0,15 |
0,066 |
|
N |
0,15 |
0,070 |
|
С |
0,17 |
0,077 |
|
S |
0,18 |
0,104 |
|
P |
0,19 |
0,110 |
|
I |
0,21 |
0,133 |
Источники: значения ван — дер-ваальсовых радиусов приводятся по Chauvin, R. (1992) Explicit periodic trend of van der Waals radii.J. Phys. Chem. 96,9194-9197. Значенияковалентных радиусов приводятся по Pauling. L. (1960) Nature of the chemical bond, 3rd cd.. Cornell University Press, Ithaca, NY.
Замечание: ван-дер-ваальсовы радиусы описывают пространственные размеры атома. Если два атома связаны ковалентной связью, то атомные радиусы в участке связывания меньше ван-дер-ваальсовых радиусов, поскольку связанные атомы объединены обшей электронной парой. Расстояния между ядрами при ваи-дер-ваальсовых взаимодействиях или при образовании ковалентной связи приблизительно равны соответственно сумме ван-дер-ваальсовых или ковалентных радиусов двух атомов. Таким образом, длина одинарной связи С С примерно равна 0,077 нм + 0,077 нм = 0,154 нм.
Слабые взаимодействия играют чрезвычайно важную роль в структуре и функциях макромолекул
Описанные нами выше нековалентные взаимодействия (водородные связи, а также ионные, гидрофобные и ван-дер-ваальсовы взаимодействия) (табл. 2-5) гораздо слабее ковалентных. Энергия разрыва одинарной С-С связи — 350 кДж/ моль, С-Н связи — 410 кДж/моль, а для ван-дер- ваальсовых сил она составляет всего лишь 4 кДж/ моль. Гидрофобные взаимодействия также гораздо слабее ковалентных связей, однако они значительно усиливаются в растворе полярного растворителя (например, в концентрированном солевом растворе). Сила ионных взаимодействий и водородных связей зависит от полярности растворителя и расположения связанных с водородом атомов, но она всегда слабее силы ковалентных связей. Тепловая энергия молекул в водном растворе при 25 °С обычно имеет тот же порядок величины, что и сила слабых взаимодействий, поэтому вероятность взаимодействия между растворенным веществом и растворителем (водой) практически такая же, как и взаимодействия между молекулами растворенного вещества. В связи с этим как водородные связи, так и ионные, гидрофобные и ван-дер-ваальсовы взаимодействия постоянно возникают и распадаются.
Таблица 2-5. Четыре типа нековалентных («слабых») взаимодействий между биомолекулами в водном растворе
Хотя эти четыре типа взаимодействий по отдельности слабее ковалентной связи, суммарный эффект от действия множества взаимодействий такого рода может быть весьма значительным. Например, в нековалентном связывании фермента с субстратом могут быть задействованы как водородные связи, так и ионные, гидрофобные или ван-дер-ваальсовы взаимодействия. Образование каждой из этих слабых связей вносит свой вклад в общее понижение свободной энергии системы. Можно рассчитать устойчивость нековалентного взаимодействия, например, водородной связи между небольшой молекулой и макромолекулой, исходя из энергии связи. Устойчивость, описываемая константой равновесия связи (см. ниже), экспоненциально зависит от энергии связи. Для диссоциации комплекса двух биомолекул (например, фермента и субстрата), связанных множеством слабых сил, необходимо, чтобы все эти взаимодействия были разрушены одновременно. Поскольку данные взаимодействия постоянно появляются и исчезают, одновременный разрыв всех связей маловероятен. Таким образом, молекулярная структура, удерживаемая с помощью 5-20 слабых взаимодействий, оказывается гораздо более устойчивой, чем могло бы показаться при формальном сложении небольших значений энергии связывания.
В таких макромолекулах, как белки, ДНК и РНК, имеется множество участков для образования водородных связей, гидрофобных, ионных и ван-дер-ваальсовых взаимодействий, так что суммарный эффект от действия этих слабых сил может быть огромным. Наиболее стабильная (т. е. нативная) структура макромолекул обычно характеризуется максимальным числом реализованных слабых взаимодействий. В соответствии с этим принципом происходит укладка полипептидпой или пол и нуклеотидной цепи в присущую ей пространственную форму. Связывание антигенов и специфичных к ним антител также зависит от кумулятивного эффекта множества слабых взаимодействий. Как уже говорилось выше, именно энергия, высвобождающаяся при нековалентном связывании фермента с субстратом, является движущей силой каталитической реакции. Связывание гормона или медиатора с клеточным рецептором — это тоже результат слабых взаимодействий. Из-за больших размеров молекул ферментов и рецепторов (но сравнению с их субстратами или лигандами) на их поверхности есть множество участков для реализации слабых взаимодействий. Комплементарность реагирующих макромолекул на молекулярном уровне означает возможность слабых взаимодействий между полярными, заряженными и гидрофобными группами на их поверхности.
При изучении структуры белков, например, таких, как гемоглобин (рис. 2-9), методом рентгеноструктурного анализа (см. доп. 4-5, с. 196) часто выясняется, что молекулы воды связаны с белком настолько сильно, что ведут себя как часть кристаллической структуры. Аналогичное явление наблюдается и в кристаллах РНК или ДНК. Эти связанные молекулы воды, которые в водном растворе можно обнаружить методом ядерного магнитного резонанса, имеют совсем другие свойства, чем молекулы в толще воды. Например, они не обладают осмотической активностью (см. ниже). Связанные молекулы воды играют важную роль в функционировании многих белков. Так, в одной из основных реакций фотосинтеза под действием света протоны проникают сквозь биологическую мембрану по мере того, как электроны передаются в ряду специальных белков-переносчиков (рис. 19-60). Один из этих белков цитохром f — имеет цепочку из пяти связанных молекул воды (рис. 2-10), которые могут обеспечивать перенос протонов через мембрану в соответствии с механизмом, названным «протонными прыжками» (см. ниже). Еще один подобный световой протонный насос — бактериородопсин — по всей видимости, использует для трансмембранного переноса протонов цепочку связанных молекул воды, ориентированных определенным образом (рис. 19-67).
Рис. 2-9. Связывание воды с молекулой гемоглобина (РDВ ID 1А3N). Кристаллическая структура молекулы гемоглобина a) со связанными молекулами воды (красные шарики) и б) без молекул воды. Молекулы воды настолько сильно связаны с белком, что при рентгеноструктурном анализе ведут себя так, как будто являются частью кристаллической структуры. Две α-субъединицы гемоглобина изображены серым, а две β-субъединицы — синим цветом. Каждая субъединица связана с гемом (структура из красных палочек; в данном ракурсе гем виден только в β-субъединицах). Структура и функции гемоглобина обсуждаются в гл. 5.
Рис. 2-10. Цепочка молекул воды в цитохроме/. Молекулы воды связываются в протонном канале мембранного белка цитохрома/, являющегося частью фотосинтетического аппарата в хлоропластах (рис. 19-64). Пять молекул воды связаны между собой и с функциональными группами белка водородными связями; в этом взаимодействии участвуют атомы основных цепей остатков валина, пролина, аргинина и аланина, а также атомы боковых цепей трех остатков аспарагина и двух остатков глутамина. Молекула белка связана с гемом (рис. 5-1), ион железа в котором облегчает перенос электронов в процессе фотосинтеза. Поток электронов сопряжен с процессом переноса протонов через мембрану, возможно, в соответствии с «прыжковым» механизмом переноса протонов по цепочке связанных молекул воды (рис. 2-13).
Растворенные вещества изменяют свойства воды
Любое растворенное вещество изменяет некоторые физические свойства растворителя (воды), в частности давление пара, температуру кипения, температуру плавления (замерзания) и осмотическое давление. Эти свойства называют коллигативными (взаимосвязанными) свойствами, поскольку в основе изменения всех свойств лежит одна и та же причина: концентрация воды в растворе ниже, чем в чистой воде. Изменение коллигативных свойств не зависит от химической природы растворенного вещества, а зависит только от числа растворенных частиц (молекул, ионов) в единице объема растворителя. Например, диссоциирующий в водном растворе NаСl изменяет осмотическое давление в два раза сильнее, чем такое же количество молей недиссоциирующей в воде глюкозы.
Молекулы воды стремятся переместиться из области с более высокой концентрацией воды в область с более низкой концентрацией — в соответствии со стремлением любой природной системы к разупорядочению. При разделении двух водных растворов с разной концентрацией растворенных веществ с помощью полупроницаемой мембраны (позволяющей проходить молекулам воды, но не пропускающей растворенные вещества) молекулы воды диффундируют из области с большей концентрацией воды в область с меньшей концентрацией, оказывая осмотическое давление (рис. 2-11). Осмотическое давление (П) определяется как сила, которую нужно приложить для оказания сопротивления движению воды (рис. 2-11, в), и рассчитывается по уравнению Вант-Гоффа:
П = icRТ
где R — универсальная газовая постоянная, Т — абсолютная температура. Множитель ic, являющийся произведением молярной концентрации раствора (с) и фактора Вант-Гоффа (i), называется осмолярностью раствора и отражает степень диссоциации растворенного вещества на ионы. В разбавленном растворе NаСl происходит полная диссоциация соли на ионы Nа+ и Сl—, что удваивает число частиц растворенного вещества, т. е. i = 2. Для всех недиссоциирующих веществ i = 1. Осмотическое давление в растворе нескольких (n) веществ представляет собой сумму осмотических давлений, оказываемых каждым растворенным веществом:
П = RТ (i1с1 + i2с2 + … +inсn)
Рис. 2-11. Осмос и определение осмотического давления, а) Исходное состояние. В пробирке содержится водный раствор, а в стакане — чистая вода. Полупроницаемая мембрана пропускает воду, но не пропускает растворенное вещество. Вода течет из стакана в пробирку, стремясь сравнять концентрации воды по обе стороны мембраны. б) Конечное состояние. Вода проникла в раствор вещества, молекулы которого не могут проходить сквозь мембрану, в результате чего произошло разбавление раствора. В состоянии равновесия давление столба раствора, имеющего высоту Л, уравновешивает осмотическое давление, характеризующее стремление воды проникнуть в зону с более низкой концентрацией, в) Осмотическое давление (П) определяется как сила, которую нужно приложить к поршню, чтобы уровень раствора в пробирке снизить до уровня воды в стакане. Эта сила пропорциональна высоте столба жидкости (h) в пробирке в состоянии (б).
Явление осмоса, проявляющееся в движении воды через полупроницаемую мембрану под действием разности осмотических давлений, играет важнейшую роль в жизни большинства клеток. Плазматические мембраны клеток гораздо лучше проницаемы для воды, чем для большинства других небольших молекул, ионов и макромолекул. Проникновение воды в клетку частично происходит за счет обычной диффузии молекул воды сквозь двойной липидный слой, а частично связано с наличием в мембране белковых каналов (так называемых аквапоринов, см. рис. 11-46), обеспечивающих селективный транспорт воды. Растворы с осмолярностью, равной осмолярности цитоплазмы клетки, называют изотоническими по отношению к клетке. Количество воды в клетке, помещенной в изотонический раствор, не уменьшается и не увеличивается (рис. 2-12).
Рис. 2-12. Влияние осмолярности внешней среды на движение воды через плазматическую мембрану. Если клетку, находящуюся в осмотическом равновесии с окружающей средой (т. е. находящуюся в изотоническом растворе) (а), перенести в гипертонический (б) или гипотонический раствор (в), то вода начнет проходить сквозь плазматическую мембрану, стремясь уравновесить осмолярность внутри клетки и в окружающей среде.
В гипертоническомрастворе, осмолярность которого превышает осмолярность цитозоля, клетки сжимаются, поскольку вода из них выходит. Напротив, в гипотоническомрастворе, осмолярность которого ниже осмолярности цитозоля, клетки разбухают, поскольку в них усиленно проникает вода. В естественных условиях концентрация биомолекул и ионов в клетках обычно выше, чем в окружающей среде, так что под действием осмотического давления вода должна была бы проникать в клетки. Если не противостоять этому давлению каким-либо образом, то прибывающая вода будет растягивать плазматическую мембрану и в конечном итоге разорвет клетку (осмотический лизис).
У клеток есть несколько механизмов для предотвращения подобной катастрофы. Плазматическая мембрана клеток бактерий и растений окружена нерастяжимой клеточной стенкой, имеющей достаточную жесткость и прочность, чтобы противостоять осмотическому давлению и не допустить осмотического лизиса. Некоторые пресноводные простейшие, обитающие в условиях гипотонической среды, имеют специальные органеллы — сократительные вакуоли, которые выкачивают из клетки воду. У многоклеточных животных плазма крови и интерстициальная жидкость (межклеточная жидкость тканей) имеют осмолярность, близкую к осмолярности цитозоля. Значительный вклад в осмолярность плазмы крови вносит высокая концентрация альбумина и других белков. Кроме того, для поддержания осмотического равновесия с окружающей средой клетки активно выкачивают в интерстициальную жидкость Na+ и некоторые другие ионы.
Поскольку влияние растворенных веществ на осмолярность зависит от числа растворенных частиц, а не от их массы, макромолекулы (белки, нуклеиновые кислоты, полисахариды) оказывают гораздо меньшее действие, чем составляющие их мономерные молекулы в эквивалентном по массе количестве. Например, один грамм полисахарида, состоящего из 1000 остатков глюкозы, оказывает такое же влияние на осмолярность, как один миллиграмм глюкозы. Энергетические запасы клетки хранятся в виде полисахаридов (крахмала или гликогена), а не глюкозы или других простых сахаров, что позволяет избежать невероятного повышения осмотического давления в запасающей клетке.
В растениях осмотическое давление служит для поддержания механической прочности. Вода поступает в клетки растений благодаря очень высокой концентрации растворенных веществ в клеточной вакуоли (рис. 2-12). Возникающее в результате этого осмотическое давление на клеточную стенку (тургорное давление), возрастая, придает жесткость клеткам, тканям и всему растению в целом. Зелень в приготовленном салате вянет, поскольку потеря воды приводит к снижению тургора. Явление осмоса важно учитывать и в лабораторной практике. Например, митохондрии, хлоропласты и лизосомы ограничены полупроницаемыми мембранами. Выделение органелл из разрушенных клеток должно осуществляться в изотоническом растворе (см. рис. 1-8), что позволит избежать проникновения в органеллы избыточного количества воды, сопровождающегося их набуханием и разрушением. В буферах, используемых для фракционирования клеток, обычно содержится достаточная концентрация сахарозы или других инертных веществ, предохраняющих органеллы от осмотического лизиса.
Пример 2-1. Осмотическое давление в органелле. I
Предположим, что основными растворенными веществами в интактных лизосомах являются КСl (-0,1 М) и NaCl (-0,03 М). Какой должна быть концентрация сахарозы в растворе для экстракции лизосом при комнатной температуре (25 °С), чтобы предотвратить их набухание и лизис?
Решение. Нужно найти концентрацию сахарозы, обеспечивающую такое же осмотическое давление, какое создают КСl и NаСl, присутствующие в лизосомах. Для расчета осмотического давления воспользуемся уравнением Вант-Гоффа:
П = КТ (i1с1 + i2с2 + i3с3 +… + inсn)
где R — универсальная газовая постоянная (8,315 Дж/мольК), Т — абсолютная температура (в кельвинах), с1, с2 и с3 — молярные концентрации растворенных веществ, а i1, i2 и i3 — число частиц, которое образуется в растворе в результате растворения каждого вещества (для КСl и NаСl i = 2).
Рассчитаем осмотическое давление в лизосоме:
Плизосома — RT(iКСl + iNаСlCNаСl) = RT [(2) (0,03 моль/л) + (2) (0,1 моль/л)] = RТ (0,26 моль/л)
Поскольку концентрации растворенных веществ известны лишь с точностью до одного знака после запятой, получаем Плизосома = RT (0,3 моль/л).
Осмотическое давление раствора сахарозы определяется по формуле:
Псахароза = RT (iсахароза Cсахароза)
В данном случае iсахароза = 1, поскольку сахароза в воде не ионизирована. Таким образом,
Псахароза = RT Cсахароза
Приравниваем осмотическое давление содержимого лизосом осмотическому давлению раствора сахарозы:
Псахароза = Плизосома
RT (ссахароза) = RT (0,3 моль/л)
cсахароза — 0,3 моль/л
Таким образом, требуемая концентрация сахарозы (мол. масса 342) составляет (0,3 моль/л)(342 г/моль) = 102,6 г/л. Или, если учитывать только значащие цифры, ссахароза = 0,1 кг/л.
Пример 2-2. Осмотическое давление в органелле. II
Предположим, что для уравновешивания осмотического давления внутри лизосом (см. пример 2-1) мы решили использовать раствор полисахарида, например, гликогена. Считая, что линейный полимер состоит из 100 глюкозных звеньев, рассчитайте количество полимера, необходимое для достижения того же осмотического давления, что и в примере 2-1. Мr полимера, состоящего из остатков глюкозы, ~18 000, и, как и сахароза, он не ионизирован в воде.
Решение. Как мы получили в примере 2-1:
Псахароза = RT (0,3 моль/л)
Аналогичным образом,
Пгликоген RT (iгликогенсгликоген) RT (сгликоген)
Для раствора гликогена с тем же осмотическим давлением, что и в растворе сахарозы, можно записать:
Пгликоген = Псахароза
RT (cгликоген) = RT (0,3 моль/л)
сгликоген = 0,3 моль/л = (0,3 моль/л) (18 000 г/моль) = 5,4 кг/л
Если учитывать только значащие цифры, получаем ответ: сгликоген = 5 кг/л — невероятно высокая концентрация!
Как мы увидим позднее (с. 353), клетки печени и мышц запасают углеводы не в виде низкомолекулярных сахаров, таких как глюкоза или сахароза, но в виде высокомолекулярного полимера гликогена, что позволяет минимизировать влияние на осмолярность цитозоля.
Краткое содержание раздела 2.1. Слабые взаимодействия в водных средах
■ Большое различие электроотрицательности атомов Н и О является причиной сильной полярности молекулы воды, благодаря чему она образует водородные связи с другими молекулами воды, а также с молекулами растворенных веществ. Водородные связи непостоянны, имеют в основном электростатическую природу и по прочности слабее ковалентных связей. Вода — хороший растворитель для полярных (гидрофильных) веществ, с которыми она образует водородные связи, и для заряженных веществ, с которыми она вступает в электростатические взаимодействия.
■ Неполярные (гидрофобные) вещества плохо растворяются в воде и не способны образовывать водородные связи с растворителем. При наличии в водном растворе гидрофобных веществ происходит энергетически невыгодное упорядочение молекул воды на их поверхности. Для минимизации обращенной к воде поверхности неполярные вещества, такие как липиды, образуют агрегаты (мицеллы) таким образом, что гидрофобные остатки молекул обращены внутрь мицелл, а полярные группы реагируют с водой. Силы, заставляющие гидрофобные частицы удерживаться вместе в растворе полярного растворителя, называют гидрофобными взаимодействиями.
■ Многочисленные слабые нековалентные взаимодействия играют важную роль в образовании нативной конформации таких макромолекул, как белки и нуклеиновые кислоты. Наиболее устойчивая конформация биомолекулы характеризуется реализацией максимального числа водородных связей внутри самой молекулы, а также между молекулой и растворителем. При этом гидрофобные остатки образуют кластеры внутри биомолекулы, в результате чего их контакт с водой оказывается минимальным.
■ Физические свойства водных растворов сильно зависят от концентрации растворенных веществ. Если два водных раствора разделены полупроницаемой мембраной (такой как плазматическая мембрана, отделяющая клетку от окружающей среды), вода стремится пройти сквозь мембрану и сравнять осмолярность двух растворов. Давление, оказываемое при этом водой, называют осмотическим давлением.
Опубликовано 3 года назад по предмету
Физика
от 097449
-
Ответ
Ответ дан
ПросветительПишем закон Кулона: F = k· (r₁·r₂) /ε· r² = 9·10⁹ · (10⁻⁹·2 · 10⁻⁹) / 81·0,01 = 2,2 · 10⁻⁸Н
Самые новые вопросы
Математика — 3 года назад
Решите уравнения:
а) 15 4 ∕19 + x + 3 17∕19 = 21 2∕19;
б) 6,7x — 5,21 = 9,54
Информатика — 3 года назад
Помогите решить задачи на паскаль.1)
дан массив случайных чисел (количество элементов
вводите с клавиатуры). найти произведение всех элементов массива.2)
дан массив случайных чисел (количество элементов
вводите с клавиатуры). найти сумму четных элементов массива.3)
дан массив случайных чисел (количество элементов
вводите с клавиатуры). найти максимальный элемент массива.4)
дан массив случайных чисел (количество элементов
вводите с клавиатуры). найти максимальный элемент массива среди элементов,
кратных 3.
География — 3 года назад
Почему япония — лидер по выплавке стали?
Математика — 3 года назад
Чему равно: 1*(умножить)х? 0*х?
Русский язык — 3 года назад
В каком из предложений пропущена одна (только одна!) запятая?1.она снова умолкла, точно некий внутренний голос приказал ей замолчать и посмотрела в зал. 2.и он понял: вот что неожиданно пришло к нему, и теперь останется с ним, и уже никогда его не покинет. 3.и оба мы немножко удовлетворим свое любопытство.4.впрочем, он и сам только еле передвигал ноги, а тело его совсем застыло и было холодное, как камень. 5.по небу потянулись облака, и луна померкла.
Информация
Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикации.