Как найти симметрическую разность двух множеств

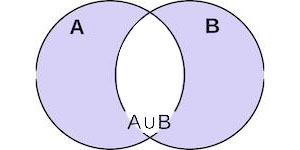
Симметрическая разность множеств

Симметрическую разность можно описать двумя способами:

Например, если А={1,2,3,4}, B={3,4,5,6}, то А Δ В = (А В) ∪ (В А) = {1,2} ∪ {5,6} = {1,2,5,6}

Например, если А={1,2,3,4}, B={3,4,5,6}, то А Δ В = (A ∪ B) (A ∩ B) = {1,2,3,4,5,6} {3,4} = {1,2,5,6}

Онлайн калькулятор позволяет найти симметрическую разность множеств A и B (А Δ B).

Поделиться страницей в социальных сетях:

Симметрическая разность множеств А и В называется множество А Δ В, содержащее в себе только непересекающиеся элементы множества А и B. Пусть A = {1,2,3,4,5}, а B = {3,4,5,6,7,8}. Тогда симметрической разностью этих множеств будет множество вида: A Δ B = {1,2,6,7,8}. Для указания множества, вводите его значения, разделенные запятой.

Разностью
множеств
А и В называют множество, состоящее из
тех и только тех элементов, которые
принадлежат только множеству А и не
принадлежат множеству В. Разность
множеств¹
А и В обозначается АВ. Формально
определение разности множеств А и В
можно записать в виде:

.
1.16

Примеры.

1. Пусть
   имеем А={4,5,8,12,16,21}; B={1,2,5,7,12,17,21,30}.
   Тогда АВ={4,8,16}, а BA={1,2,7,17,30}.

2. A={a,b,c,d};
   B={a,d,e,f,g}.
   В этом
   случае получаем: АВ={b,c}
   и BA={e,f,g}.

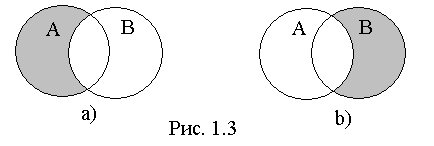
Если как и ранее
множества А и В изобразить в виде точек
кругов А и В соответственно, то разность
множеств будет представляться так, как
это показано на рис. 1.3, где а) соответствует
разности АВ, b)- разности
BA.

1.5.5 Симметрическая разность

Симметрической
разностью
множеств А и В называют множество,
состоящее из объединения множеств
разностей АВ и ВА. Симметрическая
разность множеств А и В обозначается
символом ,
т.е А 
В. Таким образом, по определению

.
1.17

Нетрудно
убедиться, что

.
1.18

Примеры.

1. Имеем:
   А={4,5,8,12,16,21}; B={1,2,5,7,12,17,21,30}.
   Тогда

А

В={1,2,4,7,8,16, 17,30}.

1. A={a,b,c,d};
   B={a,d,e,f,g}.
   В этом
   случае получаем А 
   В={b,c,e,f,g}.

Графически
симметричная разность множеств А и В
может быть представлена как показано
на рис. 1.4. Закрашенные области соответствуют
симметрической разности множеств А и
В.

1.5.6 Универсальное множество

Если
в некотором рассмотрении участвуют
только подмножества некоторого
фиксированного множеств I,
то это самое большое множество называют
универсальным
(или
полным)
множеством.

В различных конкретных случаях роль
универсального множества играют
различные множества. Так, при рассмотрении
студентов института универсальным
(полным) множеством является вся
совокупность студентов. Отдельные
группы (факультеты) можно рассматривать
как подмножества. В некоторых случаях
универсальным множеством может являться
и отдельная группа, в которой имеют
место свои подмножества (отличники;
студенты, проживающие в общежитии;
юноши; девушки и т.п.).

Вполне
очевидно, что для универсального
множества справедливы следующие
соотношения:

и

1.19

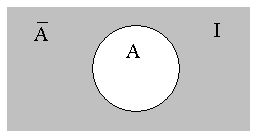
Универсальное
множество удобно изображать графически
в виде множества точек прямоугольника.
Различные области внутри прямоугольника
будут означать различные подмножества
универсального множества. Изображение
множества в виде областей в прямоугольнике,
представляющем универсальное множество,
называют диаграммой Эйлера-Венна.

1.5.7 Дополнение множества

Множество

,
определяемое из соотношения

1.20

называют
дополнением
множества
А (до универсального множества I)

Графически
дополнение множества А может быть
представлено как показано на рис. 1.5.

Формальное
определение дополнения множества А
может быть записано как

1.21

Из
определения дополнения множества
следует, что А и

не имеют общих элементов, т.е.

1.22

Кроме
того,

1.23

Из
симметрии формул 1.22 и 1.23 следует, что
не только

является
дополнением А, но и А является дополнением

.
Но дополнение

есть

.
Таким образом

1.24

Рис.
1.5

С
помощью операции дополнения удобно
представить разность множеств:

=
,
т.е

1.25

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #

Бинарные операции над упорядоченными множествами

В предыдущей статье я писал о бинарных операциях над неупорядоченными множествами. В этой статье мы рассмотрим алгоритмы с меньшей сложностью выполнения, для упорядоченных множеств.

Содержание
I. Пересечение упорядоченных множеств
II. Разность упорядоченных множеств
III. Объединение упорядоченных множеств
IV. Симметрическая разность упорядоченных множеств
Заключение

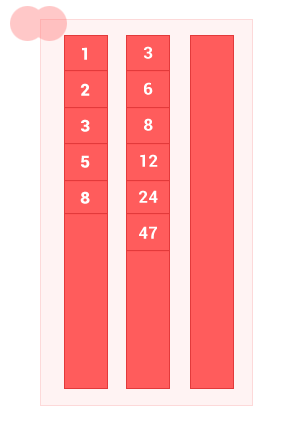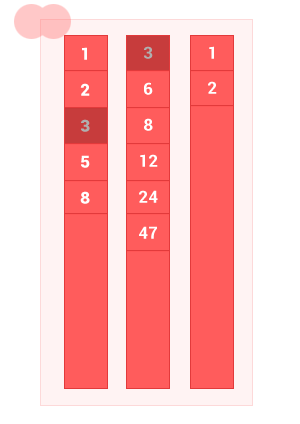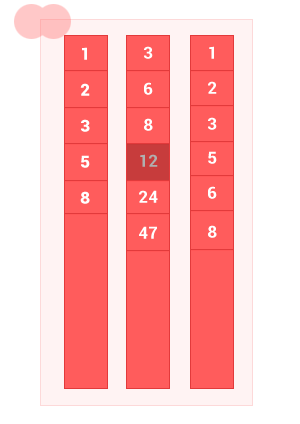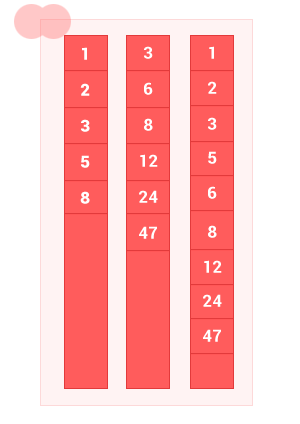
I. Пересечение упорядоченных множеств

Пересечение двух упорядоченных множеств A и B — это множество только с теми элементами A и B, которые одновременно принадлежат обоим множествам, без дублей. Сложность алгоритма O(m+n), где m и n — длины входных множеств A и B соответственно.

Сделал небольшую анимацию, чтобы показать как работает алгоритм.

Пример реализации на javascript:

function intersec_sort_arr(array_1,array_2)
{
	var n = array_1.length, m = array_2.length, i = 0, k = 0, j = 0, array_3 = [];
	while ((i < n) && (j < m)) // пока не дошли до конца массива 
	{
		if (array_1[i] == array_2[j])
		{ 
			array_3[k] = array_1[i]; // запишем элемент в массив array_3
			k++,i++,j++; // и сдвинем позицию во всех 3 массивах
		} else {
			if (array_1[i] < array_2[j]) {
				i++; // сдвинем позицию в первом массиве
			} else {
				j++; // сдвинем позицию во втором массиве
			}
		}
	}
    return array_3;
} 

Обращение к функции:

intersec_sort_arr([1, 2, 3, 5, 8], [3, 6, 8, 12, 24, 47]); // на выходе [3, 8]

II. Разность упорядоченных множеств

Разность двух упорядоченных множеств A и B — это множество с элементами A, не совпадающими с элементами B, без дублей. Сложность алгоритма O(m+n), где m и n — длины входных упорядоченных множеств A и B соответственно.

function diff_sort_arr(array_1,array_2)
{
	var n = array_1.length, m = array_2.length, i = 0, k = 0, j = 0, array_3 = [];
	while ((i < n) && (j < m)) // пока не дошли до конца массива 
	{
		if (array_1[i] == array_2[j])
		{ 
			i++,j++;
		} else {
			if (array_1[i] < array_2[j]) {
				array_3[k] = array_1[i];
				k++;
				i++; // сдвинем позицию в первом массиве
			} else {
				j++; // сдвинем позицию во втором массиве
			}
		}
	}
	while (i < n) {
		array_3[k] = array_1[i];
		k++, i++;
	}
    return array_3;
} 

diff_sort_arr([1, 2, 3, 5, 8], [3, 6, 8, 12, 24, 47]); // на выходе [1, 2, 5]

III. Объединение упорядоченных множеств

Объединение двух упорядоченных множеств A и B — это множество с элементами A и элементы множества B, без дублей. Сложность алгоритма O(m+n), где m и n — длины входных упорядоченных множеств A и B соответственно.

function sum_sort_arr(array_1,array_2)
{
	var n = array_1.length, m = array_2.length, i = 0, k = 0, j = 0, array_3 = [];
	while ((i < n) && (j < m)) // пока не дошли до конца массива 
	{
		if (array_1[i] == array_2[j])
		{ 
			array_3[k] = array_1[i];
			k++,i++,j++;
		} else {
			if (array_1[i] < array_2[j]) {
				array_3[k] = array_1[i];
				k++;
				i++; // сдвинем позицию в первом массиве
			} else {
				array_3[k] = array_2[j];
				k++;
				j++; // сдвинем позицию во втором массиве
			}
		}
	}
	while (i < n) {
		array_3[k] = array_1[i];
		k++, i++;
	}
	while (j < m) {
		array_3[k] = array_2[j];
		k++, j++;
	}
    return array_3;
} 

sum_sort_arr([1, 2, 3, 5, 8], [3, 6, 8, 12, 24, 47]); // на выходе [1, 2, 3, 5, 6, 8, 12, 24, 47]

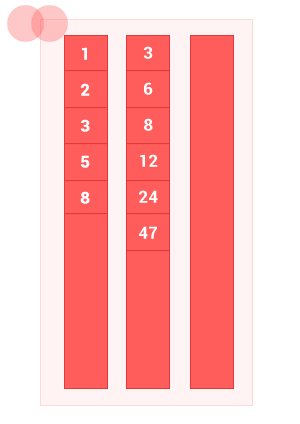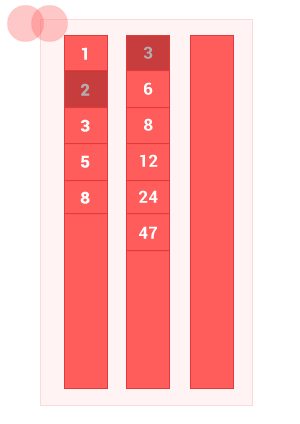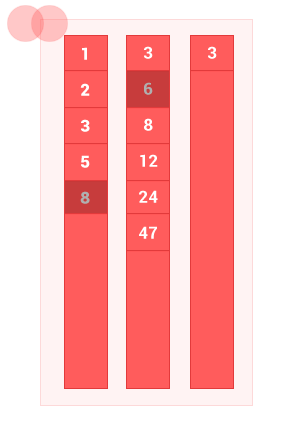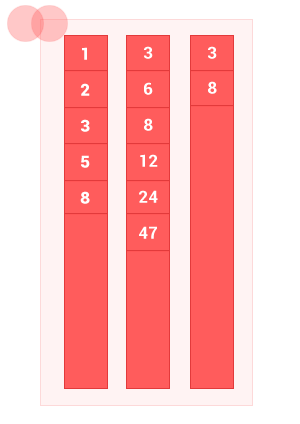
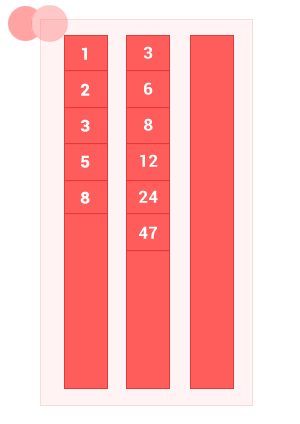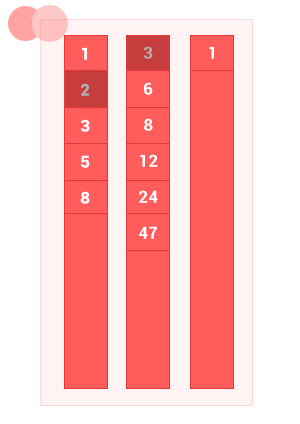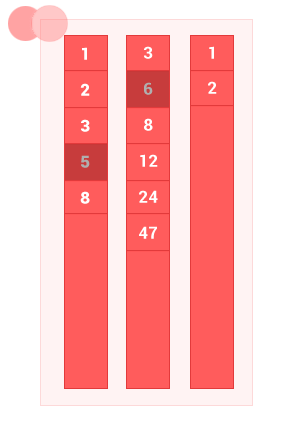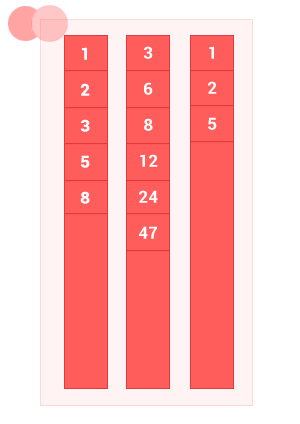
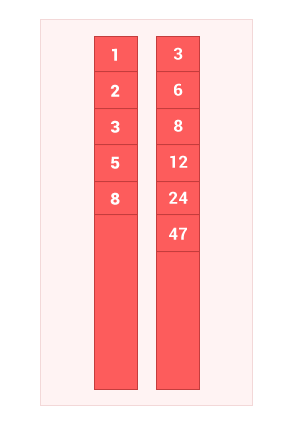
IV. Симметрическая разность упорядоченных множеств

Симметрическая разность двух упорядоченных множеств A и B — это такое множество, куда входят все те элементы первого упорядоченного множества, которые не входят во второе упорядоченное множество, а также те элементы второго упорядоченного множества, которые не входят в первое упорядоченное множество. Сложность алгоритма O(2(m+n)), где m и n — длины входных упорядоченных множеств A и B соответственно.

По сути это вычитание множеств, сначала A из B, затем B из A.

function symmetric_diff_sort_arr(array_1,array_2)
{
    var n = array_1.length, m = array_2.length, i = 0, k = 0, j = 0, array_3 = [];
    while ((i < n) && (j < m)) // пока не дошли до конца массива 
    { 
        if (array_1[i] == array_2[j])
        { 
            i++,j++;
        } else {
            if (array_1[i] < array_2[j]) {
                array_3[k] = array_1[i];
                k++;
                i++; // сдвинем позицию в первом массиве
            } else {
                j++; // сдвинем позицию во втором массиве
            }
        }
    }
    while (i < n) { 
            array_3[k] = array_1[i];
            k++, i++;
    }
	
    n = array_2.length, m = array_1.length, j = 0, i = 0;
    while ((i < n) && (j < m)) // пока не дошли до конца массива 
    { 
        if (array_2[i] == array_1[j])
        { 
            i++,j++;
        } else {
            if (array_2[i] < array_1[j]) {
                array_3[k] = array_2[i];
                k++;
                i++; // сдвинем позицию в первом массиве
            } else {
                j++; // сдвинем позицию во втором массиве
            }
        }
    }
    while (i < n) { 
            array_3[k] = array_2[i];
            k++, i++;
     }
    return array_3;
} 

Способ предложенный 0leGG.

function symmetric_diff_sort_arr(array_1,array_2)
{
    var n = array_1.length, m = array_2.length, i = 0, k = 0, j = 0, array_3 = [];
    while ((i < n) && (j < m)) // пока не дошли до конца массива 
    { 
        if (array_1[i] < array_2[j]) { 
            array_3[k] = array_1[i];
            k++;
            i++; // сдвинем позицию в первом массиве
        } else if (array_1[i] > array_2[j]) {
            array_3[k] = array_2[j];
            k++;
            j++; // сдвинем позицию во втором массиве
        } else {
            i++, j++;
        }
    }
    while (i < n) { 
        array_3[k] = array_1[i];
        k++, i++;
    }
    while (j < m) {
        array_3[k] = array_2[j];
        k++, j++;
    }
    return array_3;
}

symmetric_diff_sort_arr([1, 2, 3, 5, 8], [3, 6, 8, 12, 24, 47]); // на выходе [1, 2, 5, 6, 12, 24, 47]

Заключение

Мне часто приходится работать с отсортированными массивами, поэтому эти алгоритмы очень сильно ускоряют процесс. Пример реализации метода intersec_sort_arr, вы можете посмотреть в моем приложении для vk.com. С помощью данного метода я нахожу общих участников сообществ работая с отсортированными массивами, в миллионы элементов, метод справляется очень быстро. До этого использовал метод описанный в моей предыдущей статье, обработка массивов была очень медленной.

Порой обучение продвигается с трудом. Сложная теория, непонятные задания… Хочется бросить. Не сдавайтесь, все сложности можно преодолеть. Рассказываем, как

Не понятна формулировка, нашли опечатку?

Выделите текст, нажмите ctrl + enter и опишите проблему, затем отправьте нам. В течение нескольких дней мы улучшим формулировку или исправим опечатку

Что-то не получается в уроке?

Загляните в раздел «Обсуждение»:

1. Изучите вопросы, которые задавали по уроку другие студенты — возможно, ответ на ваш уже есть
2. Если вопросы остались, задайте свой. Расскажите, что непонятно или сложно, дайте ссылку на ваше решение. Обратите внимание — команда поддержки не отвечает на вопросы по коду, но поможет разобраться с заданием или выводом тестов
3. Мы отвечаем на сообщения в течение 2-3 дней. К «Обсуждениям» могут подключаться и другие студенты. Возможно, получится решить вопрос быстрее!

Подробнее о том, как задавать вопросы по уроку