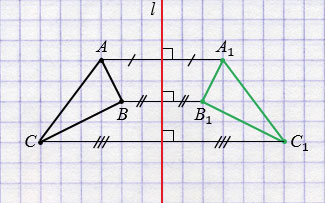Симметрия — соразмерность, соответствие, сходность, порядок в расположении частей. Это слово, как и многие другие математические понятия, произошли от греческих слов.
Смотря на объекты вокруг, мы не раз восклицаем: «Какая симметрия!»

Рис. (1). Симметрия в архитектуре.
Люди с давних времён использовали симметрию в рисунках, орнаментах, предметах быта, в архитектуре, художестве, строительстве.
Но симметрия широко распространена и в природе, где не было вмешательства человеческой руки. Её можно наблюдать в форме листьев и цветов растений, в расположении различных органов животных, в форме кристаллических тел, в порхающей бабочке, загадочной снежинке, морской звезде.
Рис. (2). Симметрия в природе.
Пока рассмотрим две симметрии на плоскости: относительно точки и прямой.
Симметрию относительно точки называют центральной симметрией.
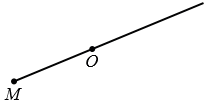
Точки
M
и
M1
симметричны относительно некоторой точки (O), если точка (O) является серединой отрезка
MM1
.
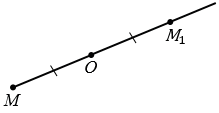
Рис. (3). Центральная симметрия.
Точка (O) называется центром симметрии.
Алгоритм построения центрально-симметричных фигур.
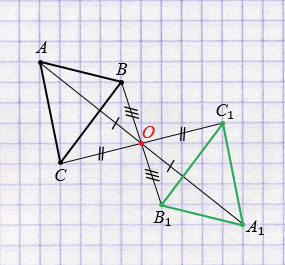
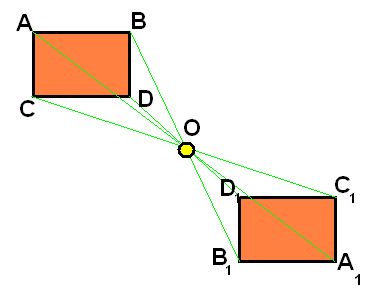
Рис. (4). Треугольники симметричны относительно точки (O).
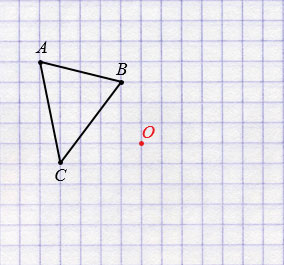
Построим треугольник
A1B1C1
, симметричный треугольнику (ABC) относительно центра (точки) (O).
1. Для этого соединим точки (A), (B), (C) с центром (O) и продолжим эти отрезки.
2. Измерим отрезки (AO), (BO), (CO) и отложим с другой стороны от точки (O) равные им отрезки
AO=OA1;BO=OB1;CO=OC1
;
3. Соединим получившиеся точки отрезками и получим треугольник
A1B1C1
, симметричный данному треугольнику (ABC).
Фигуры, симметричные относительно некоторой точки, равны.
Фигура симметрична относительно центра симметрии, если для каждой точки этой фигуры симметричная ей точка также лежит на этой фигуре. Такая фигура имеет центр симметрии (фигура с центральной симметрией).
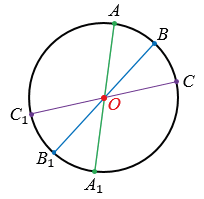
Есть фигуры с центральной симметрией, это, например, окружность и параллелограмм. У окружности центр симметрии — это её центр, у параллелограмма центр симметрии — это точка, в которой пересекаются его диагонали. Есть очень много фигур, у которых нет центра симметрии.
Осевая симметрия
Осевая симметрия — это симметрия относительно проведённой прямой (оси).
Точки
M
и
M1
симметричны относительно некоторой прямой (оси симметрии), если эти точки лежат на прямой, перпендикулярной данной, и на одинаковом расстоянии от оси симметрии.
Рис. (5). Осевая симметрия.
Алгоритм построения фигуры, симметричной относительно некоторой прямой.
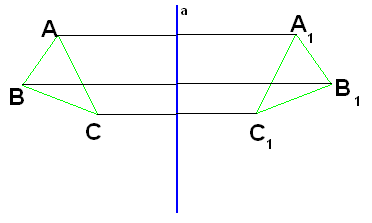
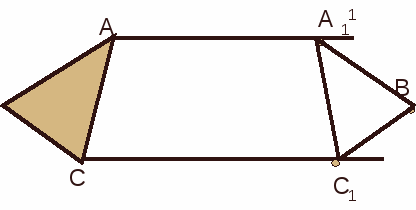
Рис. (6). Треугольники симметричны относительно прямой.
Построим треугольник
A1B1C1
, симметричный треугольнику (ABC) относительно красной прямой.
1. Для этого проведём из вершин треугольника (ABC) прямые, перпендикулярные оси симметрии, и продолжим их дальше на другой стороне оси.
2. Измерим расстояния от вершин треугольника до получившихся точек на прямой и отложим с другой стороны прямой такие же расстояния.
3. Соединим получившиеся точки отрезками и получим треугольник
A1B1C1
, симметричный данному треугольнику (ABC).
Фигуры, симметричные относительно прямой, равны.
Фигура считается симметричной относительно прямой, если для каждой точки рассматриваемой фигуры симметричная для неё точка относительно данной прямой также находится на этой фигуре. Прямая является в этом случае осью симметрии фигуры.
Иногда у фигур несколько осей симметрии:
- для неразвёрнутого угла существует единственная ось симметрии — это биссектриса данного угла.
- Для равнобедренного треугольника есть единственная ось симметрии.
- Для равностороннего треугольника — три оси.
- Для прямоугольника и ромба существуют две оси симметрии.
- Для квадрата — целых четыре.
- Для окружности осей симметрии бесчисленное множество — это каждая прямая, которая проходит через центр этой фигуры.
- Есть фигуры без осей симметрии — это параллелограмм и треугольник, все стороны которого различны.
Источники:
Рис. 1 Симметрия в архитектуре. Указание авторства не требуется, 2021-06-02, Архитектура/Здания, бесплатно для коммерческого использования, https://clck.ru/VFC5B.
Рис. 2. Симметрия в природе. Указание авторства не требуется, 2021-06-02, бесплатно для коммерческого использования, https://clck.ru/VFECn.
Рис. 3. Центральная симметрия, © ЯКласс.
Рис. 4. Треугольники симметричны относительно точки O, © ЯКласс.
Рис. 5. Осевая симметрия, © ЯКласс.
Рис. 6. Треугольники симметричны относительно прямой, © ЯКласс.
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Координаты на плоскости
- Осевая и центральная симметрии
Осевая симметрия
Рассмотрим построение точки, симметричной данной точке А относительно данной прямой 
Пусть дана точка А и прямая 
Точку симметричную точке А относительно прямой 



Пусть прямые 


Получаем точки А и А1, которые симметричны относительно прямой 
Также можно построить фигуры, симметричные относительно прямой.
Построим треугольник А1В1С1, симметричный треугольнику АВС относительно прямой 
Пусть дан треугольник АВС и прямая 
Далее строим точки А1, В1 и С1, симметричные точкам А, В и С относительно прямой 

Обратите внимание, любые две фигуры, симметричные относительно прямой, равны.
Если фигура имеет ось симметрии (прямая 
Центральная симметрия
Точки М и М1 называют симметричными относительно точки О, если точка О является серединой отрезка ММ1 (смотри рисунок ниже).
Рассмотрим построение точки, симметричной данной точке М относительно данной точки О.
Пусть даны точки М и О. Точку, симметричную точке М относительно точки О, можно построит так. Проведем луч МО.
На луче МО отложим отрезок ОN , равный отрезку ОМ.
Точки М и М1, которые симметричны относительно точки О.
Также можно построить фигуры, симметричные относительно точки.
Построим треугольник А1В1С1, симметричный треугольнику АВС относительно точки О.
Пусть дан треугольник АВС и точки О.
Далее строим точки А1, В1 и С1, симметричные точкам А, В и С относительно точки О (алгоритм построения смотри выше), соединив которые получим треугольник А1В1С1, симметричный треугольнику АВС относительно точки О.
Обратите внимание, любые две фигуры, симметричные относительно точки, равны.
Рассмотрим окружность с центром в точке О. Все точки окружности можно разбить на пары точек, симметричных относительно точки О.
В таком случае говорят, что окружность имеет центр симметрии — точку О.
Также центр симметрии имеют такие фигуры, как отрезок, прямоугольник, эллипс.
Советуем посмотреть:
Перпендикулярные прямые
Параллельные прямые
Координатная плоскость
Координаты на плоскости
Правило встречается в следующих упражнениях:
6 класс
Номер 1247,
Мерзляк, Полонский, Якир, Учебник
Номер 1255,
Мерзляк, Полонский, Якир, Учебник
Номер 1256,
Мерзляк, Полонский, Якир, Учебник
Номер 1266,
Мерзляк, Полонский, Якир, Учебник
Номер 1267,
Мерзляк, Полонский, Якир, Учебник
Номер 1268,
Мерзляк, Полонский, Якир, Учебник
Номер 1271,
Мерзляк, Полонский, Якир, Учебник
Номер 1,
Мерзляк, Полонский, Якир, Учебник
Номер 9,
Мерзляк, Полонский, Якир, Учебник
Номер 10,
Мерзляк, Полонский, Якир, Учебник
9.12.2020 г.
Учитель: Семикоз Надежда
Васильевна
Математика, 6 класс
Тема урока: Симметрия
относительно точки.
Урок изучения нового
материала.
Оборудование: учебник Математика 6 класс
С.М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин М., Просвещение,
2017 г., компьютер, проектор, экран, презентация.
Цель урока: Ознакомить учащихся с
понятием симметрии относительно точки. Сформировать навыки строить фигуры на
плоскости, симметричные относительно точки.
Задачи:
формировать понятия о симметричных фигурах
относительно прямой.
Регулятивные цели: учить планировать,
контролировать, оценивать свои действия.
Коммуникативные цели: учить формулировать собственное
мнение и позицию, учить сотрудничать и принимать мнения своих одноклассников.
Личностные цели: учить использовать полученную информацию
для решения образовательных задач.
Метапредметные цели: учить обнаруживать пробелы в
знаниях и уметь их восполнять.
Планируемые
результаты:
Предметные:
Знают понятие симметрии относительно
точки.
Умеютстроить фигуры на плоскости,
симметричные относительно точки.
Метапредметные:
Регулятивные: различают
способ и результат действий.
Познавательные: владеют
общим приёмом решения задач.
Коммуникативные: договариваются о совместной
деятельности, приходят к общему
решению, в том числе в ситуации
столкновения интересов.
Личностные:Имеют способность к
эмоциональному восприятию математических объектов, задач, решений, рассуждений
Методы: словесные, наглядные, практические.
Формы работы: фронтальная, групповая, парная,
индивидуальная.
Дополнительное
методическое и дидактическое обеспечение урока:
«Математика. Методические
рекомендации. 6 класс» М.К. Потапов, А.В. Шевкин. М., Просвещение, 2015 г.
Структура урока:
1. Организационный
момент.
2. Постановка
учебной задачи. Мотивация учебной деятельности учащихся.
3. Актуализация
знаний обучающихся.
4.
Определение темы и целей
урока.
5.
Изучение нового материала.
6. Практическое выполнение
заданий.
7. Физическая минутка.
8. Закрепление изученного.
9. Итоги урока.
10. Постановка домашнего задания
11. Рефлексия
1. Организационный
момент.
Самоопределение к
деятельности.
Цель: проверка готовности обучающихся, их настроя на работу.
-Добрый день, ребята.
-Я пришла к вам на урок с хорошим настроением и хочу передать
вам свой эмоциональный настрой.
Посмотрите друг на друга, улыбнитесь, подарите хорошее
настроение своему однокласснику. И мы начинаем с Вами урок.
2.
Постановка учебной задачи. Мотивация
учебной деятельности учащихся
Цель: мотивация учащихся на
осознание потребности к построению нового способа действий.
В качестве эпиграфа к
уроку я взяла слова древнегреческого философа Платона, ученика Сократа и
учителя Аристотеля – основателя физики. (слайд 2)
3. Актуализация
знаний обучающихся.
Цель: активизировать мыслительную деятельность
обучающихся.
·
Давайте мы попробуем увидеть
прекрасное и научимся его создавать. На слайде представлены изображения. Как Вы
думаете, в чем заключена красота?
·
Какие еще симметричные
фигуры существуют в окружающем мире? Вокруг нас? (слайд 3)
4.
Определение темы и целей
урока.
Цель: с помощью решения ребуса определить тему урока и поставить
цели.
Решить ребус. Поставить цели урока. (слайд 4)
5.
Изучение нового материала.
Цель: Обеспечение восприятия, осмысления и первичного
запоминания учащимися нового материала.
Слово «Симметрия» греческого происхождения.
В переводе на русский язык означает «соразмерность»,
пропорциональность, одинаковость в расположении предметов. (Слайд 5)
Существует
несколько видов симметрии:
·
Симметрия относительно точки
(центральная);
·
Симметрия относительно
прямой (осевая);
·
Зеркальная симметрия.(Слайд
6)
Мы же с Вами на
сегодняшнем уроке познакомимся с симметрией относительно точки.
Открыть тетрадь, записать число и тему.(Слайд
7)
•
Определение. Точки
А и А1 называются симметричными относительно точки О (центр
симметрии), если О – середина отрезка АА1.
•
Точка
О считается симметричной самой себе.(Слайд 
Вывод алгоритма
построения точки, симметричной относительно точки: Через точку и центр
симметрии провести луч и отметить на луче отрезок, равный данному.
6. Практическое выполнение
заданий.
Цель: отработка навыков
построения точек, симметричных относительно прямой, в ходе выполнения
построений.
Пример 1 (Слайд 9). Построить
отрезок А1В1 симметричный отрезку АВ относительно точки
О, не лежащей на отрезке АВ.
Решение.
Требуется построить отрезок А1В1 так,
чтобы он была симметричен отрезку АВ относительно точки О. При этом центр
симметрии О будет серединой каждого из отрезков АА1 и ВВ1.
Проведем из точки А через
центр симметрии О луч АО. На луче АО, с помощью циркуля, отложим отрезок ОА1 так,
чтобы, ОА1 =
ОА.
Проведем из точки В через
центр симметрии О луч ВО. На луче ВО, с помощью циркуля, отложим отрезок ОВ1 так,
чтобы, ОВ1 =
ОВ.
1) (т.к. точки А, А1, О лежат на
одной
прямой и ОА = ОА1).
2) (т.к. точки
В, В1, О лежат на
одной
прямой и ОВ = ОВ1).
3)
Значит .
Пример 2 (слайд 10). Дан
треугольник АВС и точка О вне этого треугольника. Постройте треугольник А1В1С1,
симметричный треугольнику АВС относительно точки О.
Решение.
Требуется построить треугольник
А1В1С1 так, чтобы он была симметричен
треугольнику АВС относительно точки О. При этом центр симметрии О будет
серединой каждого из отрезков АА1, ВВ1и СС1.
Проведем из точки А через
центр симметрии О луч АО. На луче АО, с помощью циркуля, отложим отрезок ОА1 так,
чтобы, ОА1 =
ОА.
Проведем из точки В через
центр симметрии О луч ВО. На луче ВО, с помощью циркуля, отложим отрезок ОВ1 так,
чтобы, ОВ1 =
ОВ.
Проведем из точки С через
центр симметрии О луч СО. На луче СО, с помощью циркуля, отложим отрезок ОС1 так,
чтобы, ОС1 =
ОС.

(т.к. точки А, А1, О лежат на
одной прямой и ОА = ОА1).
2) (т.к. точки В, В1, О лежат на
одной прямой и ОВ = ОВ1).
3)
т.к. точки
С, С1, О лежат на одной прямой и ОС = ОС1.
4)
Значит .
7. Физическая минутка.
Цель: снять
физическое напряжение и усталость.
Встаньте. Расположите руки
так, чтобы они были симметричны относительно грудной клетки. Не симметричны.
Повернулись к соседу, улыбнулись. Сели.
8. Закрепление изученного. Устная работа (Слайды
11-16)
Цель: закрепить
полученные на практики навыки.
Введем определение фигуры,
симметричной относительно точки и определим, какие из предложенных фигур
являются симметричными и чем является их центр симметрии (Слайд 15-16).
Примеры симметричных объектов
(Слайд 17-18)
Цель: увидеть симметрию в объектах
живой природы.

9. Итоги урока.
Цель: подвести итоги уроки,
определить, достигли поставленных в начале урока целей, выявить затруднения,
если такие появились.
1. Что нового вы
узнали на уроке?
2. Что вам
понравилось? Не понравилось?
3. Что показалось
вам трудным в этой теме?
4. Достигли ли мы
своих целей?
10. Постановка домашнего задания.
Цель: закрепление
знаний и навыков построения фигур, симметричных относительно точки. На
листе формата А4 изобразить первую букву своего имени или какой-либо рисунок и
отразить ее симметрично относительно выбранной точки О. (Примеры Выполнения
домашнего задания – слайд 19-24)



11. Рефлексия
Цель: Самооценка
полученного личностного прироста.
Руки вверх – я
полня все. В стороны – есть затруднения. Вниз – ничего не понял.
Дополнение.
Постройте фигуру, симметричную данной, относительно точки О
Постройте фигуру, симметричную данной, относительно точки О
Постройте фигуру, симметричную данной, относительно точки О
Постройте фигуру, симметричную данной, относительно точки О
Центральная и осевая симметрия
«Симметрия» — слово греческого происхождения. Оно означает соразмерность, наличие определенного порядка, закономерности в расположении частей.
Люди с давних времен использовали симметрию в рисунках, орнаментах, предметах быта.
Симметрия широко распространена в природе. Её можно наблюдать в форме листьев и цветов растений, в расположении различных органов животных, в форме кристаллических тел, в порхающей бабочке, загадочной снежинке, мозаике в храме, морской звезде.
Симметрия широко используется на практике, в строительстве и технике. Это строгая симметрия в форме античных зданий, гармоничные древнегреческие вазы, здании Кремля, машинах, самолетах и многом другом. (слайд 4) Примерами использования симметрии являются паркет и бордюр. (смотри гиперссылку об использовании симметрии в бордюрах и паркетах) Рассмотрим несколько примеров, где можно увидеть симметрию в различных предметах, с использованием слайд-шоу (включить значок ).
Определение: Центральная симметрия – это симметрия относительно точки.
Определение: Точки А и В симметричны относительно некоторой точки О, если точка О является серединой отрезка АВ.
Определение: Точка О называется центром симметрии фигуры, а фигура называется центрально-симметричной.
Свойство: Фигуры, симметричные относительно некоторой точки, равны.
Примеры:
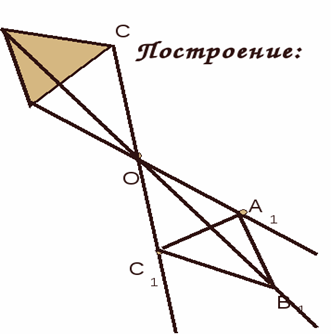
Алгоритм построения центрально-симметричной фигуры
1.Построим треугольник А 1В 1 С 1, симметричный треугольнику АВС, относительно центра (точки) О. Для этого соединим точки А,В,С с центром О и продолжим эти отрезки;
2. Измерим отрезки АО, ВО, СО и отложим с другой стороны от точки О, равные им отрезки (АО=А 1 О 1, ВО=В 1 О 1, СО=С 1 О 1 );
3. Соединим получившиеся точки отрезками А 1 В 1; А 1 С 1; В1 С 1.
Получили ∆А 1 В 1 С 1 симметричный ∆АВС.
Осевая симметрия – это симметрия относительно проведенной оси (прямой).
Определение: Точки А и В симметричны относительно некоторой прямой а, если эти точки лежат на прямой, перпендикулярной данной, и на одинаковом расстоянии.
Определение: Осью симметрии называется прямая при перегибании по которой «половинки» совпадут, а фигуру называют симметричной относительно некоторой оси.
Свойство: Две симметричные фигуры равны.
Примеры:
Алгоритм построения фигуры, симметричной относительно некоторой прямой
Построим треугольник А1В1С1, симметричный треугольнику АВС относительно прямой а.
Для этого:
1. Проведем из вершин треугольника АВС прямые, перпендикулярные прямой а и продолжим их дальше.
2. Измерим расстояния от вершин треугольника до получившихся точек на прямой и отложим с другой стороны прямой такие же расстояния.
3. Соединим получившиеся точки отрезками А1В1, В1С1, В1С1.
Получили ∆ А1В1С1 симметричный ∆АВС.
Представим
себе такую историю…
–
Саша, чем ты занимаешься? – спросил у друга Паша.
–
Я разгадываю ребус, – ответил Саша. – Учитель математики сказал, что, разгадав
его, мы узнаем, о чём будем говорить на следующем уроке. Хочешь разгадаем его
вместе?
–
С удовольствием! – сказал Паша.
–
Смотри, первая картинка в ребусе – лиса, но она перевёрнута, – начал Саша.
–
Это значит, что слово «лиса» надо читать справа налево, то есть «асил», –
рассуждал Паша.
–
А запятые перед и после картинки означают, что первую и последнюю буквы в этом
слове надо убрать, – продолжил Саша. – Тогда у нас останется слог «си».
–
Верно, – сказал Паша. – Затем идёт буква «м», а после нарисован змей.
–
И снова перед и после картинки стоят запятые, – заметил Саша, – а значит, в
слове «змей» мы уберём первую и последнюю буквы и у нас останется слог «ме».
Потом идёт буква «т». А что нарисовано на следующей картинке?
–
Это цирк, – ответил Паша. – Но картинка перевёрнута.
–
Точно, – сказал Саша. – Тогда получается слово «криц».
–
Но не забудь про запятые перед и после этой картинки, – заметил Паша.
–
То есть уберём первую и последнюю буквы и получим слог «ри», – продолжил Саша.
–
И у нас осталась буква «я». Теперь давай посмотрим, что у нас получилось, –
предложил другу Паша.
–
У нас получилось слово «симметрия», – назвал зашифрованное слово Саша.
–
Значит, на следующем уроке математики мы будем говорить о симметрии, – сделал
вывод Паша и предложил, – но давай прежде поговорим о ней с Мудряшом.
–
Ребята, прежде чем мы с вами поговорим, давайте немного разомнёмся и выполним
устные задания, – предложил Мудряш.
–
Теперь сверимся! – сказал Мудряш. –
Посмотрите, что у вас должно было получиться!
–
А сейчас вернёмся к вашему вопросу, – начал Мудряш. – Ребята, в 5 классе
вы уже познакомились с симметричными фигурами.
–
Точно, – вспомнил Саша. – Это фигуры, которые имеют ось симметрии.
–
Верно, – сказал Мудряш. – Также вспомним, что ось симметрии – это
прямая (или воображаемая линия), которая делит геометрическую фигуру на две
зеркально одинаковые фигуры.
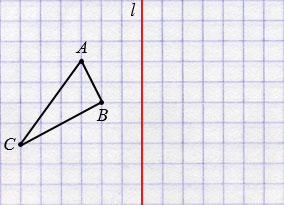
Посмотрите
на следующую фигуру. При перегибании листа бумаги по прямой l
«половинки»
этой фигуры, расположенные по разные стороны от прямой l,
совпадут.
–
То есть прямая l является осью симметрии
для этой фигуры, – сделал вывод Паша.
–
И эта фигура является симметричной относительно прямой l,
– добавил Саша.
–
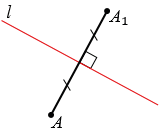
Правильно, – отметил Мудряш. – Теперь посмотрите на следующий рисунок. На нём
изображены прямая l
и треугольник .
Представим, что этот треугольник нарисован чернилами. Тогда перегнув лист бумаги
по прямой l, треугольник оставит
отпечаток, и мы получим треугольник, который назовём .
Теперь
соединим точки и
,
и
,
и
.
Заметим, что отрезки ,
и
перпендикулярны
прямой l. И прямая l
делит каждый из этих отрезков пополам.
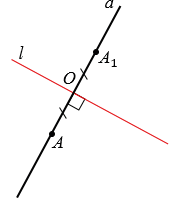
Запомните!
Точки и
называют
симметричными относительно прямой l,
если прямая l перпендикулярна
отрезку и
делит его пополам.
–
Получается, что точки и
,
и
,
и
симметричны
относительно прямой l?
– спросил Саша.
–
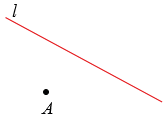
Верно, – ответил Мудряш и продолжил, – пусть нам дана точка и
прямая l. Давайте построим точку,
симметричную точке относительно
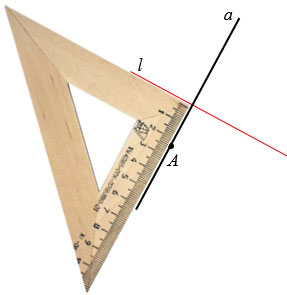
прямой. l Через
точку проведём
прямую ,
перпендикулярную прямой l.
Для этого воспользуемся угольником… Пересечение прямых и
l обозначим точкой О.
Затем отложим на прямой отрезок
,
равный отрезку .
Таким образом, мы построили точку симметричную
точке относительно
прямой l.
–
Построить точку, симметричную данной, совсем не сложно. А вот как построить,
например, треугольник, симметричный треугольнику относительно
прямой l? – спросили у Мудряша
мальчишки.
–
Для этого нам надо в первую очередь построить точки, симметричные точкам ,
и
относительно
прямой l, – начал объяснять
Мудряш. – Построим точку ,
симметричную точке относительно
прямой l, точку ,
симметричную точке относительно
прямой l, и точку ,
симметричную точке также
относительно прямой l.
Соединим эти точки отрезками и получим треугольник .
–
Он и будет симметричным треугольнику ?
– спросил Саша.
–
Да, – ответил Мудряш. – Треугольники и
называют
симметричными относительно прямой l.
–
Мне кажется, что эти треугольники равны, – заметил Паша.
–
Это так, – сказал Мудряш. – Запомните! Любые две фигуры, симметричные
относительно некоторой прямой, равны.
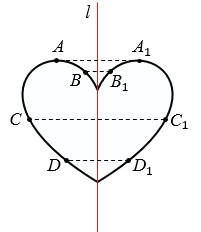
Посмотрите
на фигуру. Прямая l
– ось симметрии этой фигуры. Каждая её точка, не лежащая на оси симметрии, имеет
симметричную себе точку.
Итак,
мы с вами поговорили об осевой симметрии. Теперь
давайте рассмотрим центральную симметрию.
Посмотрите
на следующий рисунок. Здесь точка О
является серединой отрезка .
Тогда можно сказать, что точки и
симметричны
относительно точки О.
Запомните!
Точки и
называют
симметричными относительно точки О,
если точка О является серединой отрезка .
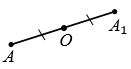
Давайте
построим точку, симметричную точке относительно
точки О. Для этого проведём луч .
Затем отложим на этом луче отрезок ,
равный отрезку .
Тогда точки и
симметричны
относительно точки .
–
А можно ли построить треугольник, симметричный, например, треугольнику относительно
точки О? – спросили у Мудряша Саша и Паша.
–
Конечно, можно, – ответил Мудряш. – Для этого мы построим точку ,
симметричную точке относительно
точки О, точку ,
симметричную точке относительно
точки О, и точку ,
симметричную точке также
относительно точки О.
–
Теперь соединим точки ,
и
отрезками
и получим треугольник ,
– сказал Саша.
–
И этот треугольник является симметричным треугольнику относительно
точки О, – добавил Паша.
–
Молодцы! – похвалил мальчишек Мудряш.
–
Эти треугольники равны, – заметил Паша.
–
Верно, – сказал Мудряш. – Запомните! Любые две фигуры, симметричные
относительно некоторой точки, равны.
Ребята,
а теперь давайте с вами посмотрим на окружность с центром в точке О.
Проведём диаметр .
Диметр состоит из двух радиусов: и
.
Мы знаем, что все радиусы одной окружности равны между собой, а значит, отрезок
равен
отрезку .
Следовательно, точки и
симметричны
относительно точки О.
Таким
образом, все точки окружности можно разбить на пары точек, симметричных
относительно центра этой окружности.
Говорят,
что точка О – центр симметрии окружности.
–
А какие ещё геометрические фигуры имеют центр симметрии? – спросили мальчишки.
–
Например, отрезок имеет
центр симметрии – точку О, которая является его
серединой. Центром симметрии прямоугольника является точка пересечения его диагоналей.
У квадрата центром симметрии также является точка пересечения его диагоналей, –
привёл примеры Мудряш.
С
симметрией вы постоянно встречаетесь в повседневной жизни. Люди используют
симметрию в орнаментах, предметах быта, архитектуре, технике.
Симметрия
также встречается в природе. Например, в форме цветов и листьев растений, в форме
кристаллов и снежинок, в порхающей бабочке и хвосте павлина.
Симметрия
создаёт ощущение соразмерности, порядка, гармонии.
–
Ребята, а сейчас давайте выполним несколько заданий, – предложил Мудряш.
Задание
первое: проверьте с помощью угольника и линейки, симметричны
ли относительно прямой l
точки.
Решение:
проверим,
симметричны точки и
или
нет. Для этого воспользуемся определением. Соединим точки и
и
проверим с помощью угольника, перпендикулярна ли прямая l
отрезку .
Прямая l перпендикулярна отрезку .
Теперь с помощью линейки проверим, делит ли прямая l
отрезок пополам.
Прямая l делит отрезок на
два равных отрезка. Следовательно, точки и
симметричны
относительно прямой l.
Теперь
проверим, симметричны ли точки и
.
Соединим их. С помощью угольника проверим, перпендикулярна ли прямая l
отрезку .
Прямая l перпендикулярна отрезку .
Затем с помощью линейки проверим, делит ли прямая l
отрезок пополам.
Отрезки не равны, а значит, точки и
не
симметричны относительно прямой l.
И
проверим, симметричны ли точки и
.
Соединим их. Приложим угольник к точке пересечения отрезка с
прямой l и увидим, что они не
перпендикулярны. А значит, точки и
не
симметричны относительно прямой l,
хотя прямая делит отрезок пополам.
Второе
задание: проверьте с помощью линейки, симметричны ли относительно
точки О точки и
,
и
.
Решение: чтобы
проверить, симметричны точки и
относительно
точки О, воспользуемся определением.
Соединим точки и
и
с помощью линейки проверим, является ли точка О
серединой отрезка .
Видим, что отрезки и
не
равны, а значит, точки и
не
симметричны относительно точки О.
Теперь
соединим точки и
.
Приложим к отрезку линейку.
Видим, что отрезки и
равны,
следовательно, точки и
симметричны
относительно точки О.
И
ещё одно задание: начертите отрезок и
отметьте точку вне
этого отрезка. Постройте отрезок, симметричный отрезку относительно
точки .
Сравните полученный отрезок и отрезок .
Решение:
начертим
с помощью линейки отрезок ,
равный 5
см. Отметим точку вне
этого отрезка. Чтобы построить отрезок, симметричный данному относительно точки
,
мы в первую очередь построим точки, симметричные точкам А и БЭ относительно
точки .
Проведём
луч и
отложим на нём отрезок ,
равный отрезку .
Затем проведём луч и
отложим на нём отрезок ,
равный отрезку .
Таким образом мы построили точки и
,
симметричные соответственно точкам и
относительно
точки .
Теперь
соединим точки и
и
получим отрезок .
Этот отрезок симметричен отрезку относительно
точки .
Давайте
с помощью линейки измерим полученный отрезок. Видим, что его длина равна пяти
сантиметрам, а значит, отрезок равен
отрезку и
равен 5
см.