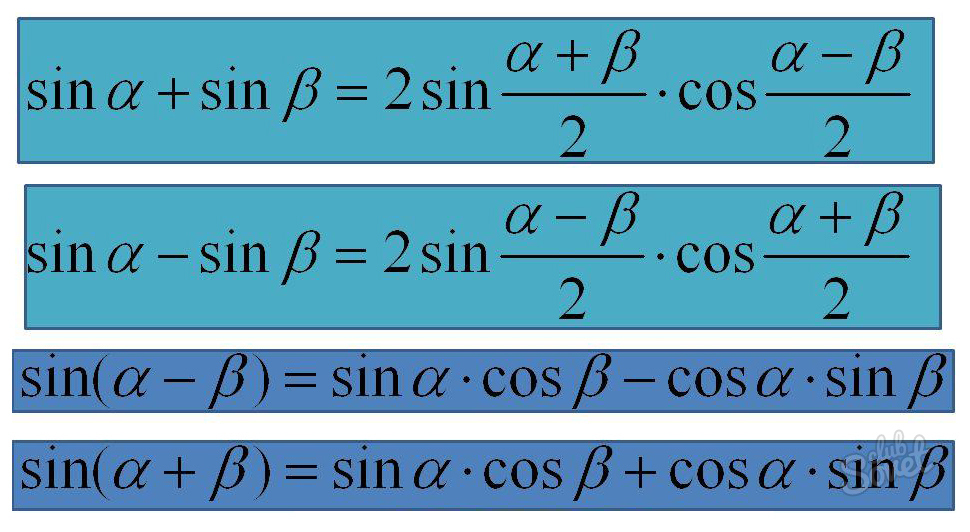Оказывается, найти точное значение синуса восемнадцати градусов, не пользуясь никакими вычислительными приборами или посторонними ресурсами (калькулятором, компьютером, логарифмической линейкой, таблицами Брадиса…) вполне возможно и даже относительно несложно. Впрочем, для кого как. Я рад, что с возрастом разобрался с этим вопросом.
Формулы сложения здесь как бы бессильны. Выручит хитроумное рассуждение.
У нас есть угол θ (тета). Мы знаем: θ = 18°.
Отсюда: 5θ = 5 * 18°; 5θ = 90°.
2θ + 3θ = 90°
2θ = 90° – 3θ
Если углы равны, то и их синусы равны.
sin(2θ) = sin(90° – 3θ)
Справа применим формулу приведения: sin(90° – α) = cosα.
sin(2θ) = cos(3θ)
А теперь слева применим формулу синуса двойного угла, а справа — формулу косинуса тройного угла. Если кто их забыл или не знал, то можно их всегда для себя вывести из формул сложения аргументов триг. функций, если последние Вы таки помните.
[Тем не менее формулы таковы: sin2α = 2sinαcosα; cos3α = 4cos³α – 3cosα.]
2sinθcosθ = 4cos³θ – 3cosθ
Рассуждаем. Может ли в нашем случае cosθ равняться нулю? Очевидно, нет! Решением уравнения cosx = 0 будет: x = п/2 + пn, где n — произвольное целое число. У нас угол отнюдь не прямой. Косинус нулю не равен. Итак, на косинус тета мы имеем право обе части нашего верного равенства разделить.
2sinθcosθ = 4cos³θ – 3cosθ | : cosθ
2sinθ = 4cos²θ – 3
А теперь вспомним ОТТ: cos²θ = 1 – sin²θ. Оно пригодится в правой части.
2sinθ = 4(1 – sin²θ) – 3
2sinθ = 4 – 4sin²θ – 3
2sinθ = –4sin²θ + 1
Теперь соберём всё в левой части.
4sin²θ + 2sinθ – 1 = 0
И сейчас уже, чтобы не таскаться и дальше с этим неудобоваримым синусом тета, мы заменим выражение sinθ на какую-нибудь букву (обозначающую неизвестную искомую величину). Пусть это будет q.
4q² + 2q – 1 = 0
D = b² – 4ac = 2² – 4 * 4 * (–1) = 4 + 16 = 20
q₁ = [–b – √(D)]/(2 * a) = (–2 – √20)/8 = (–1 – √5)/4
q₂ = [–b + √(D)]/(2 * a) = (–2 + √20)/8 = (–1 + √5)/4
Я записал корни в порядке возрастания: сперва меньший, потом больший. Но теперь придётся ещё порассуждать. Один из корней надо исключить. Какой?
Наш угол θ = 18°. К какой четверти (координатному квадранту) он принадлежит? К первому, поскольку 0 < 18° < 90°. А каков знак синуса в 1-м квадранте? В 1-м квадранте синус положителен.
Какое же из наших двух значений q — положительное число?
q₁ = (–1 – √5)/4: знаменатель положителен, а числитель отрицателен, так как там алгебраическая сумма двух отрицательных чисел. Минус делить на плюс даёт минус. Значит, q₁ исключаем — это и есть посторонний корень.
А вот q₂ проверку выдерживает. Знаменатель положителен; в числителе минус единица «тянет» вниз, а второе слагаемое — вверх. Но √5, очевидно, больше, чем √4, а √4 — это два, а 2 > 1. Значит, √5 перетянет, и числитель положителен. Плюс делить на плюс — будет положительное частное.
Итак, окончательно получаем: q = (–1 + √5)/4. Это и будет искомый синус.
Задача решена: sin 18° = (–1 + √5)/4 = (√5 – 1)/4.
Напоследок добавлю, что с практической точки зрения такой ответ будет малополезен. Надо бы ещё найти рациональное приближение. Тут уж можно посоветовать вот что: найти несколько верных знаков числа √5 в столбик, отнять единицу и затем полученную разность разделить на 4. Я решил ограничиться четырьмя значащими цифрами корня; получилось: √5 ≈ 2,236. Отсюда √5 – 1 ≈ 1,236 и далее (√5 – 1)/4 ≈ 1,236 : 4 = 0,309.
Содержание
- — Что такое формула загара?
- — Какова формула Sin Cos Tan?
- — Как найти грех 75 без калькулятора?
- — Как рассчитать касательную?
- — Как найти tan 35 без калькулятора?
- — Как выглядит синусоида?
Что такое формула загара?
1. Чему равен загар? Тангенс x определяется как его синус, деленный на его косинус: тангенс х = грех х / соз х. Котангенс x можно определить как косинус x, деленный на синус x: cot x = cos x / sin x.
Значение функции загара для любого угла θ в терминах sin и cos может быть задано по формуле tan θ = sin θ / cos θ.
Как найти грех 75 без калькулятора?
sin (A + B) = sin A cos B + cos A sin B, мы можем найти синус (45° + 30°) дать синус 75 градусов.
Как рассчитать касательную?
Функция тангенса, наряду с синусом и косинусом, является одной из трех наиболее распространенных тригонометрических функций. В любом прямоугольном треугольнике тангенс угла равен длина противоположной стороны (O), деленная на длину соседней стороны (A). В формуле он записывается просто как «загар».
Как найти tan 35 без калькулятора?
Загар 35 градусов
Загар 35 градусов равен 0,70021, то же самое, что загар 35 градусов в радианах. Чтобы получить 35 градусов в радианах, умножьте 35 ° на / 180 ° = 7/36 . Загар 35 градусов = загар (7/36 ×.
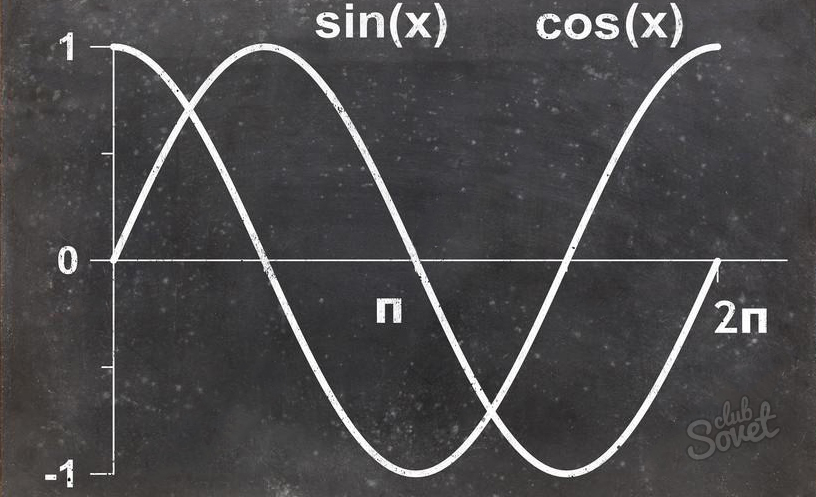
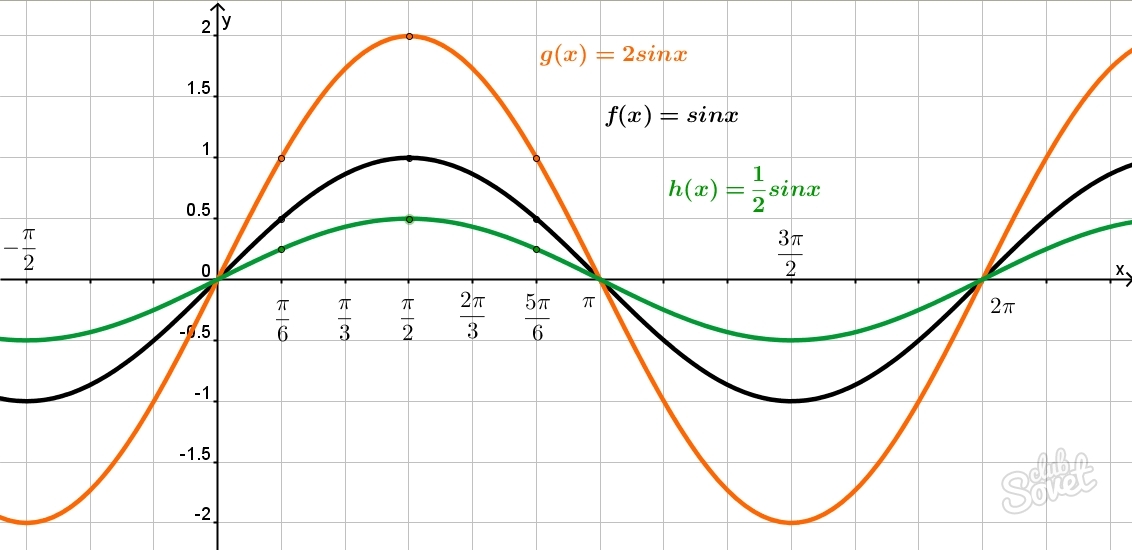
Как выглядит синусоида?
Форма синусоиды то же самое для каждого полного поворота угла поэтому функция называется «периодической». Период функции равен 360 ° или 2π радиан. Вы можете вращать точку сколько угодно раз. Это означает, что вы можете найти синус любого угла, независимо от его размера.
Интересные материалы:
Как использовать быстрый выбор в предложении?
Как использовать Canon EOS 1100D?
Как использовать Cdate в VBA?
Как использовать чаны на PS4?
Как использовать чернильный картридж с защитой HP?
Как использовать чит-движок в Риме 2?
Как использовать Cloudflare DNS?
Как использовать Countif с несколькими условиями?
Как использовать датчик OBD 2?
Как использовать датчик расстояния?
В статье мы расскажем, как находить значения:
(cos300^°), (sin(-540^°)), (cos 510^°), (sin(-135^°))
и других тригонометрических выражений без тригонометрической таблицы.
Как вычисляются синусы и косинусы углов?
Чтобы вычислить косинус и синус некоторого угла нужно:
1. Отложить этот угол на тригонометрическом круге и определить какая точка соответствует этому углу;
2. Найти абсциссу и ординату этой точки. Косинус угла равен — абсциссе, а синус угла — ординате.
Предположим, стоит задача найти косинус и синус угла (30^°). Отложим на круге угол в (30^°) и найдем какая точка соответствует этому углу.
Если построить все точно, то видно, что абсцисса точки равна (0,866)… , что равно числу (frac{sqrt{3}}{2}) , а ордината равна (0,5), то есть (frac{1}{2}).

Получается, (cos 30^° = frac{sqrt{3}}{2}), а (sin30^° =frac{1}{2}).
Аналогично и для любой другой точки на круге: значение абсциссы равно косинусу угла, а ординаты – синусу угла. Поэтому:
В тригонометрии ось абсцисс (ось x) часто называют «ось косинусов», а ординат (ось y) – «ось синусов».
Обычно на осях не отмечают (0,1); (0,2); (0,3) и т.д., а сразу наносят стандартные значения для синуса и косинуса: (±frac{1}{2}=±0,5); (±frac{sqrt{2}}{2} ≈±0,707); (±frac{sqrt{3}}{2} ≈±0,866).
Первый шаг к тому, чтобы находить синусы и косинусы стандартных углов – научится отмечать эти углы на тригонометрическом круге.
Как отметить любой угол на тригонометрическом круге?
Для этого нужно знать несколько фактов:
- Начало отсчета находится в крайней правой точке окружности;
-
Чтоб отложить положительный угол нужно двигаться против часовой стрелки от начала отсчета, чтобы отметить отрицательный – по часовой стрелке;
-
Градусная мера окружности равна (360^°), полуокружности (180^°), а четверти (90^°);
-
Углы в (0^°), (30^°), (45^°) и (60^°) выглядят так:


- Одна точка может соответствовать разным углам;
- Угол может быть больше (360^°). В этом случае он просто сделает полный оборот и пойдет дальше. Фактически, можно (360^°) просто отбросить и откладывать тот угол, который останется – в итоге вы всё равно окажетесь в той же точке.
Пример. Отметьте угол в (90^° ) и (-90^°).
Решение:

Пример. Отметьте угол в (225^° ) и (-135^°).
Решение: (225^°=180^°+45^°)
(-135^°=-90^°-45^°)

Пример. Отметьте угол в (420^° ) и (-390^°).
Решение: (420^°=360^°+60^°)
(-390^°=-360^°-30^°)


Задание 1. Отметьте на окружности точки соответствующие углам: (720^°), (225^°), (300^°), (870^°), (900^°), (-330^°), (-630^°), (-210^°).
Как находить синус и косинус любого угла?
Простой алгоритм:
- Начертите тригонометрический круг и оси косинусов и синусов (не обязательно рисовать прям аккуратно, как на картинке ниже, можно и некрасиво – главное не запутаться какая точка к какому значению относится).
- Отложите на круге угол, синус и косинус которого надо найти, и определите точку на круге, соответствующую этому углу.
- Найдите координаты точки, используя картинку ниже.

Пример. Вычислите (sin300^°) и (cos300^°) .
Решение: (300^°=360^°-60^°)

(cos 300^°=frac{1}{2}), (sin{300^°}=-frac{sqrt{3}}{2}).
Пример . Вычислите (sin(-540^°)) и (cos(-540^°)) .
Решение. (-540^°=-360^°-180^°).

(-540^°) на тригонометрическом круге совпадает с (-1) на оси косинусов. То есть, координаты этой точки: ((-1;0)). Значит, (cos(-540^°)=-1), а (sin(-540^° )=0).
Да, имея перед глазами тригонометрический круг, вычислять синусы и косинусы любых углов легко. Возможно, у вас возник вопрос: «а что делать, если круга нет? Как делать такие вычисления на ЕГЭ?». Ответ очевиден – нарисовать круг самому! Для этого надо понять, как располагаются значения на нем. Подробную методику того, как это делается я рассказывала в этой статье.
Есть и другой способ запомнить тригонометрический круг – внимательно посмотреть на картинку ниже и запомнить максимальное количество элементов. После прикройте страницу и по памяти нарисуйте круг и отметьте всё, что смогли запомнить. Сверьте, что у вас получилось с тем, что было на картинке. Повторяйте эту последовательность действий пока по памяти не получится нарисовать тригонометрический круг со всеми значениями. Это займет 15 минут вашего времени, но сильно поможет в 13 задаче ЕГЭ (и не только в ней).

Примеры вычисления синуса и косинуса из ЕГЭ
В двух следующих примерах я специально рисовала круг от руки, чтобы вы увидели, как выглядят реальные решения.
Пример . Найдите значение выражения (-18sqrt{2}sin(-135^°)).
Решение. (-135^°=-90^°-45^°)

Получается (-18sqrt{2} sin(-135^° )=-18sqrt{2}cdot-frac{sqrt{2}}{2}=frac{18cdotsqrt{2}cdotsqrt{2}}{2}=9cdot 2=18.)
Ответ: (18).
Пример . Найдите значение выражения (54sqrt{3}cos(510^°)).
Решение. (510^°=360^°+150^°=360^°+180^°-30^°.)

(54sqrt{3}cos(510^°)=54sqrt{3}cdot(-frac{sqrt{3}}{2})=-frac{54cdot sqrt{3}cdot sqrt{3}}{2}=-27cdot 3=-81.)
Ответ: (-81).
Смотрите также:
Как найти тангенс и котангенс без тригонометрической таблицы? Из градусов в радианы и наборот
Тригонометрическая таблица с кругом
Почему в тригонометрической таблице такие числа?
Для тех кто хочет закрепить знания:
Задание на вычисление синусов, косинусов, тангенсов и котангенсов
I would suggest a less well-known method that generalises nicely to many other functions and can be quite efficient even when you need to do all the calculations by hand:
The pair $(c,s) = (cos x, sin x)$ (in radians, of course!) can be interpreted as the unique solution to the ordinary differential equation
$$
frac{mathrm{d}}{mathrm{d}x} begin{pmatrix}c\send{pmatrix}
= begin{pmatrix}-s\cend{pmatrix}
$$
with starting condition $c(0) = 1$, $s(0) = 0$. As such, it can be solved approximately by Runge-Kutta solvers. The idea is to start from zero and then approach the target value step by step, effectively using a Taylor expansion around each point. Because the steps are small, Taylor expansion converges much faster here than if you directly put in the target value.
Why this is particularly convenient for manual calculation: you can choose the step-lengths in a way so the numbers will stay reasonably nice in decimal, as long as you make sure the steps are small and add up to the point where you want to go.
I’ll use the Heun scheme, which is the simplest of these iterative solvers that actually gives usable precision. It’s based on a 2nd order Taylor expansion.
So let’s say you want to compute $sin (45^circ) = sin (tfracpi4)$. We know this should come out as $sqrt2/2$, but let’s see. I’ll pick 0.2 as the default step-size. Let’s go:
$x_0=0$, $c_0=1$, $s_0=0$
- $$begin{align}
h_1=&0.2 \ x_1=&0.2
\ tilde c_1 =& c_0 — h_1times s_0 = 1
\ tilde s_1 =& s_0 + h_1times c_0 = 0.2
\ c_1 =& c_0 — frac{h_1}2times (s_0 + tilde s_1) = 1 — 0.1times0.2 = 0.98
\ s_1 =& s_0 + frac{h_1}2times (c_0 + tilde c_1) = 0.2
end{align}$$ - $$begin{align}
h_2=&0.2 \ x_2=&0.4
\ tilde c_2 =& c_1 — h_2times s_1 = 0.98 — 0.2times0.2 = 0.94
\ tilde s_2 =& s_1 + h_2times c_1 = 0.2 + 0.2cdot0.98 = 0.396
\ c_2 =& c_1 — frac{h_2}2times (s_1 + tilde s_2) = 0.98 — 0.1times 0.596 = 0.9204
\ s_2 =& s_1 + frac{h_2}2times (c_1 + tilde c_2) = 0.2 + 0.1times 1.92 = 0.392
end{align}$$ - $$begin{align}
h_3=&0.2 \ x_3=&0.6
\ tilde c_3 =& ldots = 0.9204 — 0.2times 0.392 = 0.842
\ tilde s_3 =& ldots = 0.392 + 0.2times 0.9204 = 0.5768
\ c_3 =& ldots = 0.9204 — 0.1times 0.9688 = 0.82352
\ s_3 =& ldots = 0.392 + 0.1times 1.7624 = 0.56824
end{align}$$ - Ok, if we now did another step of 0.2, we’d end up at 0.8, but $pi/4 approx 0.7854$. So we’ll only do a step of 0.1. Also I’ll start rounding after the fifth decimal here.
$$begin{align}
h_4=&0.1 \ x_4=&0.7
\ tilde c_4 =& ldots = 0.82352 — 0.1times 0.56824 approx 0.76670
\ tilde s_4 =& ldots = 0.56824 + 0.1times 0.82352 approx 0.65059
\ c_4 =& ldots = 0.82352 — 0.05times 1.21883 approx 0.76258
\ s_4 =& ldots = 0.56824 + 0.05times 1.53339 approx 0.64491
end{align}$$ - $$begin{align}
h_5=&0.08 \ x_5=&0.78
\ tilde c_5 =& ldots = 0.76258 — 0.08times 0.64491 approx 0.71099
\ tilde s_5 =& ldots = 0.64491 + 0.08times 0.76258 approx 0.70592
\ c_5 =& ldots = 0.76258 — 0.04times 1.47357 approx 0.70364
\ s_5 =& ldots = 0.64491 + 0.04times 1.35083 approx 0.69894
end{align}$$
Ok, we’re now pretty close to $tfracpi4$, and it’s already good to see how the values for $cos$ and $sin$ become very similar, since theory says $sin(tfracpi4) = cos(tfracpi4) = tfrac{sqrt2}2$. We can further confirm this by quickly squaring: $0.70364^2 approx 0.495$. Reasonably close to $0.5$. Not great, but also I only did five not-that-small steps (since the Heun scheme is 2nd order accurate, making the steps a bit smaller would give really notably better accuracy) and – that’s the main advantage – all of them only involved very simple multiplications, because I could choose the step size so it would be convenient, unlike in a direct Taylor-series evaluation.
That is also the basic idea behind the CORDIC method which was already mentioned in comments. That uses extra properties of sine and cosine to achieve better efficiency, but this is not really needed. Many functions that are defined by an ODE are efficiently evaluated by a Runge-Kutta solver; often the fourth-order version is preferred which gives yet better convergence.
In practice, this method is still only superior to direct Taylor if you need multiple function values. Then it’s very good because a) you make a table of values as you go along b) you compute both sine and cosine, which can then be combined by exploiting the symmetry/periodicity properties.
Как найти синус?
Решение многих как алгебраических, так и геометрических задач невозможно без использования такой тригонометрической функции как синус. Для нахождения величины синуса можно использовать как собственно определение функции, так и соотношения тождеств тригонометрии, формулы приведения, а также теорему синусов. С каждым из данных способов более подробно и познакомит данная статья.
1
Нахождение величины синуса по определению
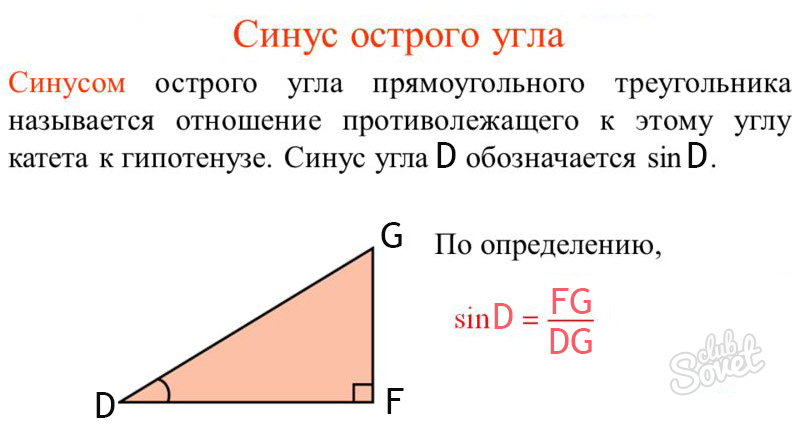
Формулировка термина “синус” определяет данную тригонометрическую величину как соотношение определенных сторон прямоугольного треугольника – отношение катета, лежащего против искомого угла, к гипотенузе.
Рассмотрим ΔDFG, ∠DFG = 90°. Тогда:
- sinD = FG / DG,
- FG — противолежащий катет,
- DG — гипотенуза представленного треугольника.
2
Нахождение величины синуса через формулу теоремы синусов
Данная теорема является универсальной, т.к. позволяет установить соотношение между углами и сторонами не только прямоугольного, то и произвольного треугольника.
Рассмотрим ΔLMN,
- MN = l, NL = m, ML = n.
- ∠M = η, ∠N = μ, ∠L = γ.
Для произвольного треугольника ΔLMN верно соотношение l / sinL = m / sinM = n / sinN – каждая сторона треугольника пропорциональна синусу угла, напротив которого она располагается.
Обозначив радиус описанной около треугольника окружности через R, соотношение теоремы синусов справедливо в следующей форме:
l / sinL = m / sinM = n / sinN = 2R.
Из соотношения следует:
sinL = l / 2R,
sinM = m / 2R,
sinN = n / 2R.
3
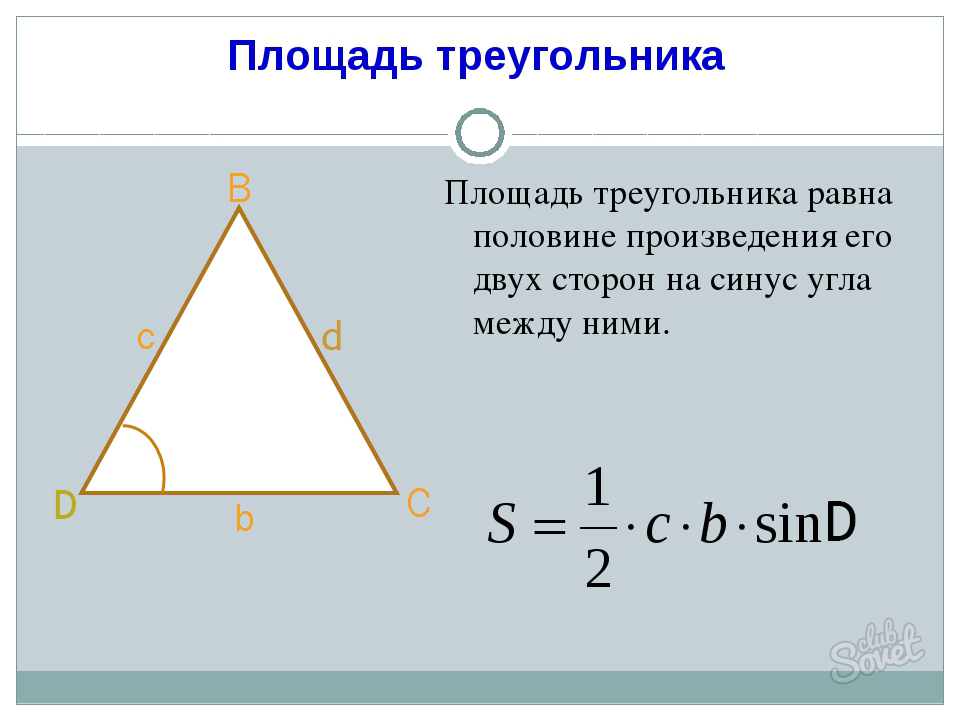
Нахождение величины синуса через площадь треугольника
Перед вами ΔDBC со сторонами
DB = c,
BC = d,
DC = b.
Для нахождения площади треугольника можно воспользоваться соотношением S = bc / 2sinD (или S = cd / 2sinB, или S = bd / 2sinC). Из этого следует, что:
- sinD = bc / 2S,
- sinB = cd / 2S,
- sinC = bd / 2S.
4
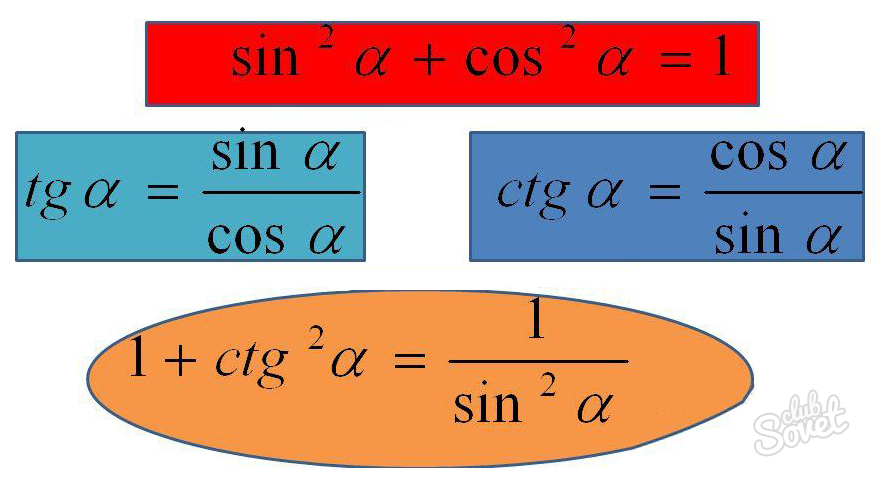
Нахождение величины синуса через тождества тригонометрии
Тождественные выражения справедливы для угла любой градусной меры.
- cos2φ + sin2φ = 1 ⇒ sin2φ = 1 — cos2φ ⇒ ΙsinφΙ = √ 1 — cos2φ ⇒ sinφ = ±√ 1 — cos2φ.
- tgφ = sinφ / cosφ ⇒ sinφ = cosφ * tgφ.
- ctgφ = cosφ / sinφ ⇒ sinφ = cosφ / ctgφ.
- 1/sin2φ = ctg2φ + 1 ⇒ sin2φ = 1 / (ctg2φ + 1) ⇒ ΙsinφΙ = 1 / √ctg2φ + 1 ⇒ sinφ = ± 1 / √ctg2φ + 1.
5
Нахождение величины синуса через формулы преобразования
- sin(η + μ) = sinη * cosμ + cosη * sinμ,
- sin(η – μ) = sinη * cosμ – cosη * sinμ,
- sinη + sinμ = 2sin((η + μ)/2) * cos((η – μ)/2),
- sinη – sinμ = 2cos((η + μ)/2) * sin((η – μ)/2)
- sinη * sinμ = (cos(η – μ) – cos(η + μ))/2,
- sinη = 2tg(η/2) / (1 + tg2(η/2)).
- sin2η =2sinη * cosη,
- sin3η =3sinη – 4sin3η.
6
Нахождение синуса угла – табличные величины
Воспользовавшись таблицей Брадиса, можно определить значение синуса для каждого угла в промежутке от 0° до 360°. Наиболее часто при решении задач школьного курса геометрии используются следующие табличные величины:
- sin0° = 0, sin90° = 1,
- sin30° = 1/2, sin180° = 0,
- sin60° = √3/2, sin270° = -1,
- sin45° = √2/2, sin360° = 0.