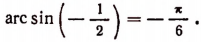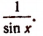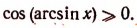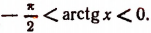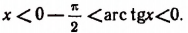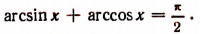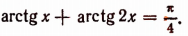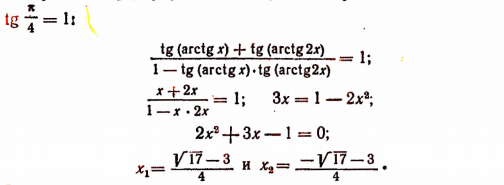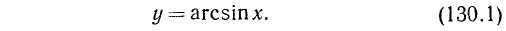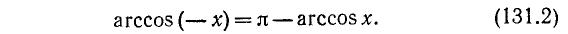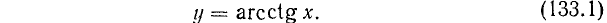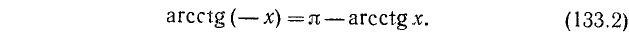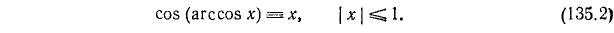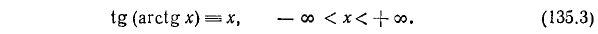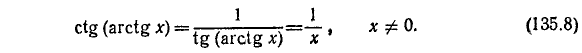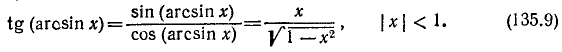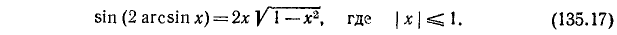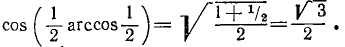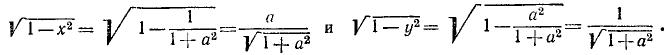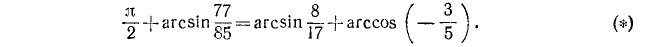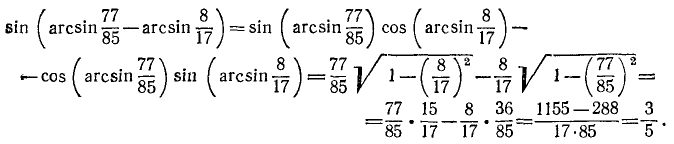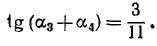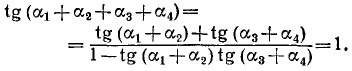Хотя синус арккосинуса ( sin arccos x) несложно найти через тригонометрическую единицу, более простое и наглядное решение можно получить через геометрическую интерпретацию синуса и косинуса, определение арккосинуса и теорему Пифагора.
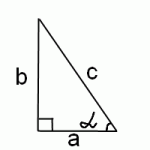
Но в прямоугольном треугольнике косинус равен отношению прилежащего катета к гипотенузе:
Нам нужен синус этого же угла альфа. А он равен отношению противолежащего катета к гипотенузе:
Противолежащий катет находим по теореме Пифагора:
Отсюда
где
Примеры
1) Найти sin (arccos (1/3)).
В этом примере x=1/3, отсюда прилежащий катет a=1, гипотенуза c=3. Находим противолежащий катет b:
Отсюда
2) Найти sin (arccos (3/5)) (или sin (arccos 0,6)).
Арккосинус трех пятых — это число, косинус которого равен 3/5. Косинус — отношение прилежащего катета к гипотенузе. Значит, прилежащий катет а=3, гипотенуза с=5. Отсюда противолежащий катет — 4. Синус — отношение противолежащего катета к гипотенузе. Отсюда
Сферы применения правил обратных тригонометрических функций
Определение
Тригонометрия — раздел математики, объясняющий зависимость между сторонами и углами треугольника, правила используют для расчета углов.
Изучая постулаты тригонометрических функций, ученики и студенты часто задаются вопросом, где эти знания могут пригодиться. Сфер применения достаточно много. Астрономы используют понятия для расчёта положения небесных объектов, тригонометрия помогает выполнять чертежи и создавать архитектурные шедевры, выстраивать модель биологических ритмов. В морской и воздушной навигации, акустике и оптике, в анализе финансового рынка, статистике, медицине, химии, во многих областях используются тригонометрические вычисления. Поэтому так важно научиться применять и выводить формулы самостоятельно.
Обратные функции тригонометрии
Обратными называются функции, которые ещё называют арксинус, арккосинус, арктангенс, арккотангенс.
Название данный вид тригонометрической зависимости, получил от соответствующей прямой функции с приставкой арк — дуга. Взаимосвязь просматривается между длиной дуги единичной окружности и соответствующим определённым отрезком.
Правила обратной функции справедливы в пределах интервалов, например,
формула арксинуса возможна при:
[arcsin (sin mathrm{x})=mathrm{x} text { при }-frac{pi}{2} leq mathrm{x} leq frac{pi}{2}]
[arccos (cos mathrm{x})=mathrm{x} text { при } 0 leq mathrm{x} leq pi]
и так далее.
Формулы с обратными функциями тригонометрии
Уже были рассмотрены обратные тригонометрические функции. Они, как и другие функции имеют между собой связи и зависимости, которые можно выразить в виде формул и использовать для решения задач.
В данной работе мы рассмотрим основные формулы, в которых применяются функции тригонометрии. Разберём их виды, деление на группы, доказательства и способы решения задач с их помощью.
Группировка основных понятий
Сначала проведём группировку формул, для того чтобы сделать более понятной логику объяснений. И объединим все правила и доказательства в одну статью.
Синус от арксинуса для [alpha in(-1 ; 1) sin (arcsin alpha)=alpha, cos (arccos alpha)=alpha]
Тангенса от арктангенса для [alpha in(-infty, infty) operatorname{tg}(operatorname{arctg} alpha)=alpha, operatorname{ctg}(operatorname{arctg} alpha)=alpha].
Указанное в данных выражениях легко выводится из самих определений обратных функций тригонометрии. При необходимости найти arcsin tg, можно использовать приведённые формулы.
Тангенс, арктангенс, котангенс, арккотангенс, синус, арксинус, косинус, арккосинус и формулы
[text{Для }-frac{pi}{2} leq alpha leq frac{pi}{2} arcsin (sin alpha)=alpha],
[text{Для } leq alpha leq pi arccos (cos alpha)=alpha],
[text{Для }-frac{pi}{2}<alpha<frac{pi}{2} operatorname{arctg}(operatorname{tg} alpha)=alpha],
[text{Для } 0<alpha<pi operatorname{arcctg}(operatorname{ctg} alpha)=alpha].
В данном примере собраны тригонометрические выражения, достаточно очевидные, которые можно вывести из определений функций тригонометрии. Необходимо обратить внимание, на то, что высказывания будут верны, если «а» (угол, или числовое значение) будет входить в определённый предел. Если условие не выполняется, расчёт будет не верен и формулу использовать нельзя.
Соотношение между собой обратных тригонометрических функций противоположных чисел
Рассмотрим важное определение:
Обратные функции тригонометрии можно выразить через аркфункции противоположного положительного числа.
[text{Для }alpha in operatorname{open}-1,1] text { arccis }(-alpha)= -operatorname{arc} sin alpha, quad operatorname{arc} cos (-alpha)=pi -a r c cos alpha]
[text { Для } alpha in(-infty, infty) operatorname{arctg}(-alpha)= -operatorname{arctg} alpha, operatorname{arcctg}(-alpha)=pi-operatorname{arcctg} alpha]
Это значит, если расчёты имеют функции отрицательного числа, от них можно избавиться. Для этого необходимо преобразовать их в аркфункции положительных чисел. Такие вычисления проводить проще.
Формулы суммы: arcsin + arccos, arctg +arcctg
Правила суммы выглядят так:
Для [alpha in[-1,1] arcsin alpha+arccos alpha=frac{pi}{2}],
Для [alpha in[-infty, infty] operatorname{arctg} alpha+operatorname{arctg} alpha=frac{pi}{2}].
Отсюда видно, что arcsin определённого числа можно выразить через его arccos , и наоборот. Тоже правило касается и arctg и arcctg, которые выражаются аналогично.
Формулы связи между обратными и прямыми тригонометрическими функциями
Чтобы иметь возможность решить множество задач, требуется знание связей между прямыми тригонометрическими функциями, и их аркфункциями. Рассмотрим, как необходимо поступить, если нужно вычислить тангенс арксинуса. Ниже представлен список основных формул, которые помогут в решении таких задач.
| [-1 leq alpha leq 1], [sin (arcsin alpha)=alpha] |
[-1 leq alpha leq 1], [sin (arccos alpha) =sqrt{1-alpha^{2}}] |
[-infty leq alpha leq+infty], [sin (operatorname{arctg} alpha)=frac{alpha}{sqrt{1+alpha^{2}}}] |
[-infty leq alpha leq+infty], [sin (operatorname{arcctg} alpha)=frac{1}{sqrt{1+a^{2}}}] |
| [-1 leq alpha leq 1], [cos (arcsin alpha)=sqrt{1-alpha^{2}}] |
[-1 leq alpha leq 1], [cos (arccos alpha)=alpha] |
[-infty leq alpha leq+infty], [cos (operatorname{arctg} alpha)=frac{1}{sqrt{1+a^{2}}}] |
[-infty leq alpha leq+infty], [cos (operatorname{arcctg} alpha)=frac{1}{sqrt{1+a^{2}}}] |
| [-1<alpha<1], [operatorname{tg}(arcsin alpha)=frac{alpha}{sqrt{1-alpha^{2}}}] |
[alpha in(-1,0) cup(0,1)], [operatorname{tg}(arccos alpha)=frac{sqrt{1-a^{2}}}{alpha}] |
[-infty leq alpha leq+infty], [operatorname{tg}(operatorname{arctg} alpha)=alpha] |
[alpha neq 0], [operatorname{tg}(operatorname{arcctg} alpha)=frac{1}{alpha}] |
| [alpha in(-1,0) cup(0,1)], [operatorname{ctg}(arcsin alpha)=frac{sqrt{1-alpha^{2}}}{alpha}] |
[-1<alpha<1], [operatorname{ctg}(arccos alpha)=frac{alpha}{sqrt{1-a^{2}}}] |
[alpha neq 0], [operatorname{ctg}(operatorname{arctg} alpha)=frac{1}{alpha}] |
[-infty leq alpha leq+infty], [operatorname{ctg}(operatorname{arcctg} alpha)=alpha] |
Примеры 1 — 2
Нужно найти косинус арктангенса из 5.
Решение. Для этого необходимо воспользоваться формулой следующего вида: [cos (operatorname{arcctg} alpha)=frac{1}{sqrt{1+a^{2}}}]
Подставим необходимое значение: [cos (operatorname{arctg} sqrt{5})=frac{1}{sqrt{1+sqrt{5^{2}}}}=frac{2}{sqrt{6}}]
Определить синус арккосинуса [frac{1}{2}]
Решение. Реализовать решение нам поможет формула: [sin (arccos alpha)=sqrt{1-alpha^{2}}]
Ставим значение и получаем: [sin left(arccos frac{1}{2}right)=sqrt{1-left(frac{1}{2}right)^{2}}=frac{sqrt{3}}{2}]
Заметим, что непосредственное вычисление приведёт к тому же ответу: [sin left(arccos frac{1}{2}right)=sin frac{pi}{3}=frac{sqrt{3}}{2}]
Для правильного вычисления значений прямых и обратных тригонометрических функций, стоит вспомнить начальные материалы.
Доказательство формул синуса от арккосинуса, арккотангенса и арктангенса
Чтобы вывести формулы и разобрать их более наглядно, необходимо применить основные тригонометрические тождества и правила обратных тригонометрических функций, которые были выведены ранее.
Доказательство формул 1
Используя тождества получим:
[sin ^{2} alpha+cos ^{2} alpha=1]
[1+operatorname{ctg}^{2} alpha=frac{1}{sin ^{2} alpha}]
Вспомним тот факт, что tg α *ctg α= 1, следовательно
[sin alpha=sqrt{1-cos ^{2} alpha}, 0 leq alpha leq pi]
[sin alpha=frac{operatorname{tg} alpha}{sqrt{1+operatorname{tg}^{2} alpha}},-frac{pi}{2}<alpha<frac{pi}{2}]
[sin alpha=frac{1}{sqrt{1+c t g^{2} alpha}}, 0<alpha<pi]
Результатом станет вывод синуса через подходящие аркфункции в заданном условии.
В математическое выражение вместо α, ставим arccos α, получаем в итоге формулу синуса арккосинуса.
Во втором случае вместо α подставляем arctg α, соответственно получаем формулу синуса арктангенса.
В третьем варианте проводим аналогичную операцию и подставляем arcctg α для выражения формулы синуса арккотангенса.
Нет времени решать самому?
Наши эксперты помогут!
Доказательство формул для тангенса, обратных функций(arcsin, arccos, arcctg)
В данном разделе рассмотрим доказательство закона тангенса обратных функций тригонометрии.
Доказательство формул 2
- Исходя из: [frac{sin alpha}{sqrt{1-sin alpha^{2}}},-frac{pi}{2}<alpha<frac{pi}{2}]Получим [operatorname{tg}(arcsin alpha)=frac{sin (arcsin alpha)}{sqrt{1-sin ^{2}(arcsin alpha)}}=frac{alpha}{sqrt{1-alpha^{2}}}]При условии [-1<alpha<1]
- Из выражения [operatorname{tg} alpha=frac{sqrt{1-cos ^{2} alpha}}{cos alpha}, alpha inleft[0, frac{pi}{2}right) cupleft(frac{pi}{2}, piright]]
Получаем [operatorname{tg}(arccos alpha)=frac{sqrt{1-cos ^{2}(arccos alpha)}}{cos (arccos alpha)}=frac{sqrt{1-alpha^{2}}}{alpha}] при условии [alpha in(-1,0) cup(0,1)]. - Исходя из [operatorname{tg} alpha=frac{1}{operatorname{ctg} alpha}, alpha inleft(0, frac{pi}{2}right) cupleft(frac{pi}{2}, piright)] получаем [operatorname{tg}(operatorname{arcctg} alpha)=frac{1}{operatorname{ctg}(operatorname{arcctg} alpha)}=frac{1}{alpha}] при условии, что [alpha neq 0].
Далее нам понадобятся понятия котангенсов арксинуса, арккосинуса, арктангенса. Напомним такое тригонометрическое равенство:
[operatorname{ctg} alpha=frac{1}{operatorname{tg} alpha}]
Применяя данное выражение можно вывести необходимые формулы, вставляя выражения тангенса обратных функций тригонометрии. Практически необходимо поменять местами числитель и знаменатель.
Выражение арксинуса с помощью арккосинуса, арктангенса и арккотангенса
Прямые и обратные функции в тригонометрии связаны между собой. Полученные в результате выведения формулы помогут найти связь и между обратными функциями тригонометрии, выразив одни аркфункции через другие. Рассмотрим примеры.
В первом случае меняем арксинус на арккосинус, а арктангенс на арккотангенс, получим следующие формулы арксинуса и арккосинуса:
[begin{aligned}
&arcsin a=left{begin{array}{l}
arccos sqrt{1-a^{2}}, 0 leq a leq 1 \
-arccos sqrt{1-a^{2}},-1 leq a<0
end{array}right. \
&arcsin a=operatorname{arctg} frac{a}{sqrt{1-a^{2}}},-1<a<1 \
&arcsin a=left{begin{array}{l}
operatorname{arcctg} frac{sqrt{1-a^{2}}}{a}, 0<a leq 1 \
operatorname{arcctg} frac{sqrt{1-a^{2}}}{a}-pi,-1 leq a<0
end{array}right.
end{aligned}]
Для арккосинуса также есть свои формулы:
[begin{aligned}
&arccos a=left{begin{array}{l}
arcsin sqrt{1-a^{2}}, 0 leq a leq 1 \
pi-arcsin sqrt{1-a^{2}},-1 leq a<0
end{array}right. \
&arccos a=left{begin{array}{l}
operatorname{arctg} frac{sqrt{1-a^{2}}}{a}, 0<a leq 1 \
pi+operatorname{arctg} frac{sqrt{1-a^{2}}}{a},-1 leq a<0
end{array}right. \
&arccos a=operatorname{arcctg} frac{a}{sqrt{1-a^{2}}},-1<a<1
end{aligned}]
Выражения для арктангенса:
[begin{aligned}
&operatorname{arctg} a=arcsin frac{a}{sqrt{1+a^{2}}},-infty<a<+infty\
&operatorname{arctg} a=left{begin{array}{l}
arccos frac{1}{sqrt{1+a^{2}}}, a geq 0 \
-arccos frac{1}{sqrt{1+a^{2}}}, a<0
end{array}right.\
&operatorname{arctg} a=operatorname{arcctg} frac{1}{a}, a neq 0
end{aligned}]
Последний блок формул покажет преобразование арккотангенса через другие обратные функции тригонометрии:
[begin{aligned}
&operatorname{arcctg} a=left{begin{array}{l}
arcsin frac{1}{sqrt{1+a^{2}}}, a geq 0 \
pi-arcsin frac{1}{sqrt{1+a^{2}}}, a<0
end{array}right.\
&operatorname{arctg} a=arccos frac{a}{sqrt{1+a^{2}}},-infty<a<+infty\
&operatorname{arcctg} a=operatorname{arctg} frac{1}{a}, a neq 0
end{aligned}]
Рассмотренные формулы арксинуса, арккосинуса, арктангенса помогут в решении различных задач. Разберём доказательство с использованием основных определений обратных функций и ранее рассмотренных правил.
Возьмём arcsin [alpha=operatorname{arctg} frac{alpha}{sqrt{1-alpha^{2}}},-1<alpha<1] для выведения доказательства.
Мы имеем выражение [operatorname{arctg} frac{alpha}{sqrt{1-alpha^{2}}}] — число, которое имеет значение от минус половины [pi] до плюс половины [pi]. Используя выражение синуса арктангенса, получаем следующее:
[sin left(operatorname{arctg} frac{alpha}{sqrt{1-alpha^{2}}}right)=frac{frac{alpha}{sqrt{1-alpha^{2}}}}{sqrt{1+left(frac{alpha}{sqrt{1-alpha^{2}}}right)^{2}}}=frac{frac{alpha}{sqrt{1-alpha^{2}}}}{sqrt{1+frac{alpha^{2}}{1-alpha^{2}}}}=frac{frac{alpha}{sqrt{1-alpha^{2}}}}{frac{1}{sqrt{1-alpha^{2}}}}=alpha]
Получается, что [operatorname{arctg} frac{alpha}{sqrt{1-alpha^{2}}}] с условием [-1<alpha<1] — арксинус числа [alpha].
Вывод: [arcsin alpha=operatorname{arctg} frac{alpha}{sqrt{1-alpha^{2}}},-1<alpha<1].
Другие подобные формулы доказываются по аналогичной схеме.
Рассмотрим пример применения полученных истин.
Пример 3
Необходимо вычислить синус арккотангенса — [sqrt{3}]
Решение. Для того чтобы провести решение задачи, необходимо использовать формулу связи арккотангенса и арксинуса: [arcsin alpha=operatorname{arctg} frac{alpha}{sqrt{1-alpha^{2}}}]
Подставим в неё [alpha=-sqrt{3}] и получим [-frac{1}{2}].
Используя непосредственное вычисление ответ был бы такой же: [sin (operatorname{arcctg}(-sqrt{3}))=sin frac{5 pi}{6}=frac{1}{2}]
Можно использовать и следующую формулу:
[sin (operatorname{arcctg} alpha)=frac{1}{sqrt{1+a^{2}}}]
[sin (operatorname{arcctg}(-sqrt{3}))=frac{1}{sqrt{1+(-sqrt{3})^{2}}}=frac{1}{2}]
Другие формулы, в которых используются обратные функции тригонометрии
Разобраны основные функции, которые чаще всего используются для решения задач. Но представлены не все формулы с обратными тригонометрическими функциями, есть некоторые специфичные, употребляемые редко, но они тоже полезны. Учить их нет смысла, лучше вывести при необходимости.
Пример 4
Разберём для примера одну такую формулу. Выглядит она так:
[sin ^{2} frac{alpha}{2}=sqrt{frac{1-cos alpha}{2}}]
Если представленный угол имеет значение больше нуля, но меньше Пи, то получаем:
[sin frac{arccos alpha}{2}=sqrt{frac{1-cos (arccos alpha)}{2}}]
[Leftrightarrow sin frac{arccos alpha}{2}=frac{sqrt{1-alpha}}{2}]
Здесь мы выводим следующую готовую формулировку, арксинус которой выведен через арккосинус:
[frac{arccos alpha}{2}=arcsin sqrt{frac{1-alpha}{2}}]
В тексте рассмотрены лишь некоторые, самые популярные виды связей между прямыми и обратными функциями тригонометрии. Главное не выучить наизусть данные постулаты, а научиться их применять и выводить, исходя из уже известных определений.
Удобно использовать инженерный вид калькулятора, на котором есть, необходимые для вычислений тригонометрические формулы и функции.
Когда задается какое-либо отвлеченное число х и требуется найти sin х, то, как известно, всякий раз для любого определенного значения х мы находим для sin х единственный ответ, а именно некоторое определенное отвлеченное число, заключенное в границах от — 1 до
+ 1 включительно.
Например,
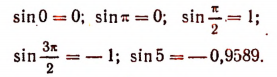
Это замечание относится и к каждой из остальных тригонометрических функций. Поэтому все тригонометрические функции sin х , cos х , tg х являются функциями однозначными.
Если же нам будет задано какое-либо отвлеченное число х в границах от — 1 до +1 включительно и будет предложено отыскать такое отвлеченное число у, синус которого равен числу х , то всякий раз будет получаться не один, а бесконечное множество ответов.
Например, если 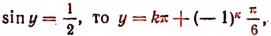
Это замечание относится и к остальным тригонометрическим функциям.
Пусть
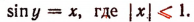
Отсюда следует, что у есть такое отвлеченное число, синус которого равен х. Вместо этого словесного утверждения пишут:
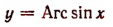
(читают: у равен арксинусу х).
Как уже разъяснялось, выражение Arc sin х для всякого данного значения х, заключенного в границах от — 1 до + 1 включительно, имеет бесконечное множество различных значений.
Приставка Arc неотделима от обозначения sin и вместе с ним образует знак нового математического действия над отвлеченным числом х.
Подобным же образом вводятся математические действия
Arc cos х (арккосинус х)
и
Arc tg х (арктангенс х).
Arc cos х обозначает такие всевозможные отвлеченные числа, что косинус каждого из них равен х;
Arc tg x обозначает такие всевозможные отвлеченные числа, что тангенс каждого из них равен х (здесь х может быть любым числом).
Выражения Arc sin x, Arc cos х, Arc tg x называются обратными тригонометрическими функциями аргумента х.
Как мы уже видели, все обратные тригонометрические функции являются функциями многозначными (с бесконечным множеством значений). В отличие от обратных тригонометрических функций функции sin x, cos x, tg x и т. д. называются прямыми тригонометрическими функциями аргумента х.
Как уже отмечалось, все прямые тригонометрические функции являются функциями однозначными.
Пользоваться обратными тригонометрическими функциями при решении задач не всегда удобно вследствие их многозначности. Поэтому наряду с обратными тригонометрическими функциями Arc sin х, Arc cos x и т. д. вводятся и изучаются еще и другие обратные тригонометрические функции, а именно
arc sin x, arc cos x, arc tg x,
которые определяются так, чтобы каждая из них была функцией однозначной.
Свойства однозначных обратных тригонометрических функций
A. arc sin х
arc sin x есть отвлеченное число в границах от — 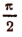
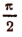
Из этого определения следует, что равенство у = arc sin х равносильно следующим утверждениям:
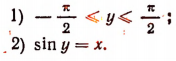
Если 0 <х < 1, то равенство у = arcsin x равносильно следующим утверждениям:
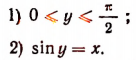
Если —1 <x<0, то равенство у = arc sin x равносильно следующим утверждениям:
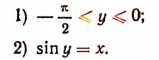
Значение функции arc sin x представляет собой определенное действительное число лишь в том случае, когда
i*i <i.
Из данного определения функции arc sin x следует, что
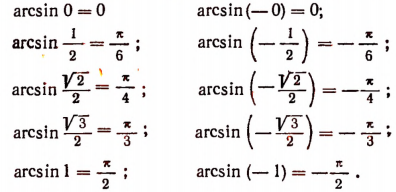
Чтобы найти, например, 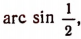
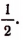
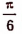
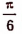
Чтобы найти 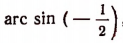
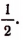
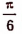
Очевидно, что
Этот результат легко обобщить и получить, что
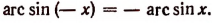
Нетрудно убедиться, что, например,
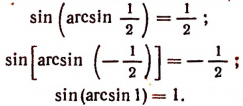
Из определения функции arcsin х следует, что
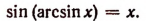
Если над числом х сначала выполняется действие нахождения арксинуса, а затем над полученным результатом действие нахождения синуса, то в результате получится первоначальное число х.
Выражение 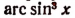
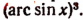
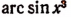
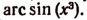
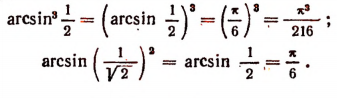
Б. arctg x
arctg х есть отвлеченное число в границах от —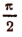
Из этого определения следует, что равенство у = arctg х равносильно следующим утверждениям:
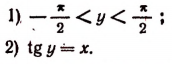
Если то равенство у = arctg х равносильно следующим утверждениям:
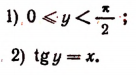
Если х <0, то равенство у = arctg х равносильно следующим утверждениям:
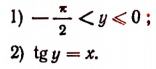
Значение функции arctg х представляет собой определенное действительное число при всяком значении х.
Из данного определения функции arctg х следует, что
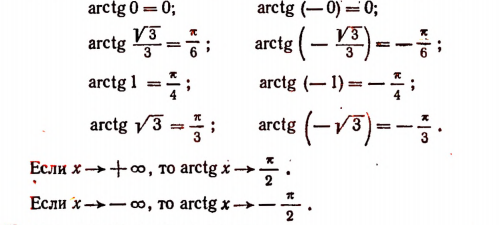
Поэтому иногда условно пишут:
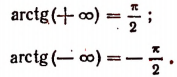
Очевидно, что
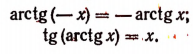
B. arccos x
arccos х есть отвлеченное число в границах от 0 до равное числу радианов, содержащихся в таком угле, косинус которого равен х.
Равенство у = arccos х равносильно следующему:
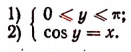
Значение функции arccos х представляет определенное действительное число тогда и только тогда, когда |х| < 1.
Из данного определения функции arccos х следует, что

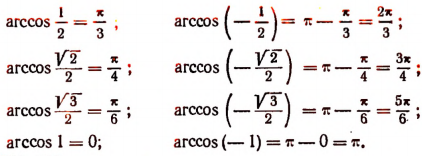
Очевидно, что
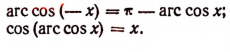
Выражения многозначных обратных тригонометрических функций
Многозначные обратные тригонометрические функции выражаются формулами:
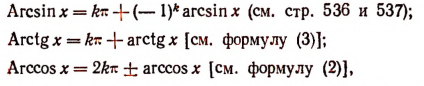
где k — любое целое число (положительное, отрицательное или нуль).
Например,
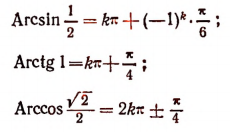
и. т. д.
Функция y = Arcsin х называется функцией, обратной функции у = sinх. Функция же csc х не есть функция, обратная функции sin х, но есть величина, обратная величине sin х, так как csc х =
Из многозначной функции Arcsin х можно выделить сколько угодно однозначных функций. Например, можно выделить однозначную функцию, заключающуюся в границах от 
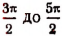
Но во всех теоретических и практических вопросах принято пользоваться преимущественно однозначной функцией арксинуса в границах от— 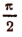
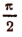
О знаках математических действий
Напишем знаки известных нам математических действий:
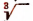
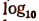
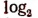
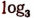
sin — знак синуса;
cos — знак косинуса;
arc sin — знак арксинуса (однозначного);
arc tg — знак арктангенса (однозначного);
Arcsin — знак арксинуса (многозначного);
Arc tg — знак арктангенса (многозначного).
Если под каждым из этих знаков поместить какое-либо число, например число 100, то получим:


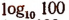
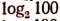

sin 100 — синус числа 100;
cos 100 — косинус числа 100;
arc sin 100 — арксинус (однозначный) числа 100;
arc tg 100 — арктангенс (однозначный) числа 100;
Arc sin 100—арксинус (многозначный) числа 100;
Arc tg 100 — арктангенс (многозначный) числа 100.
Любое из этих математических действий выполняется над отвлеченным числом и в результате опять получается отвлеченное число. Всякое математическое действие выполняется по своему особому правилу.
Пользуясь тем, что эти правила нам известны, мы получим:
Выражаясь образно, можно сказать, что каждый знак математического действия представляет собой как бы простейшую математическую «машину», принимающую к переработке отвлеченные числа. В то время как некоторые из этих «машин» принимают к переработке любые числа, другие принимают не всякие числа.
Например, «машины» 
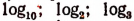
Полученное в результате математических действий число может выражать ту или иную физическую величину в зависимости от той конкретной задачи, которую мы решали с помощью этих математических действий.
Примеры преобразований и вычислений, связанных с однозначными обратными тригонометрическими функциями
1. Упростить выражение sin (arccos х).
Так как 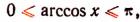

Поэтому, пользуясь формулой 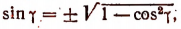
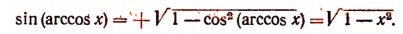
2. Упростить выражение cos (arcsin х).
Так как 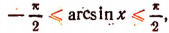
Поэтому, пользуясь формулой 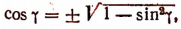
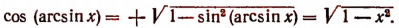
3. Упростить выражение tg (arcctgx).
Пользуясь формулой 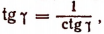
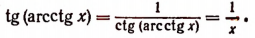
4. Упростить выражение tg (arcsin х).
Пользуясь формулой 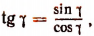
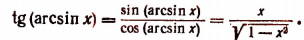
5. Упростить выражение sin (arctg х).
Пусть 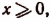
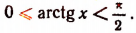
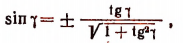
получим, что
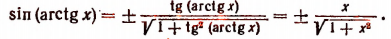
Но из этих двух знаков годным является только знак плюс. Действительно, 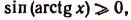
Правая же часть будет положительным числом или нулем, если из двух знаков, стоящих перед ней, выбрать только знак плюс (ведь по условию 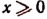
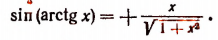
Пусть х < 0, тогда
Пользуясь формулой
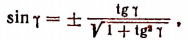
получим, что
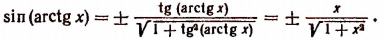
Но из этих двух знаков годным является только знак плюс. Действительно, 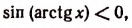
Правая же часть будет отрицательным числом лишь тогда, когда мы из двух знаков, стоящих перед ней, выберем только знак плюс (ведь по условию х < 0). Итак, при х < 0 формула имеет тот же вид, как и при 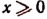
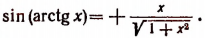
Таким образом, равенство
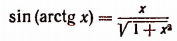
справедливо при всяком значении х.
6. Доказать тождество
Сначала вычислим синус левой части написанного выше равенства:
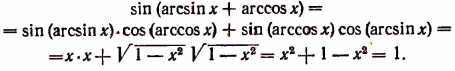
Из одного того факта, что sin (arcsin х + arccos х) = 1, мы еще не можем заключить, что 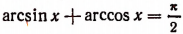
Чтобы удостовериться в том, что сумма arcsin х + arccos х равняется именно 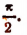
По определению

Складывая, получим:
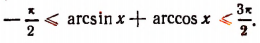
Но среди чисел, больших или равных — 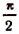
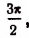
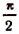
Поэтому
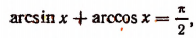
что и требовалось доказать.
Аналогично доказывается и тождество
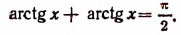
7. Показать справедливость равенства
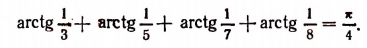
Сначала вычислим тангенс суммы, стоящей в левой части написанного равенства:
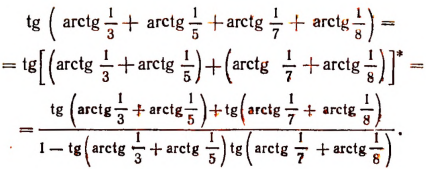
Для сокращения записей вычислим предварительно значения тангенсов, стоящих в числителе последней дроби:
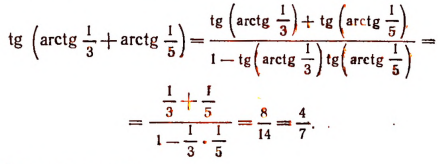
Найдем также, что
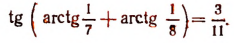
Теперь
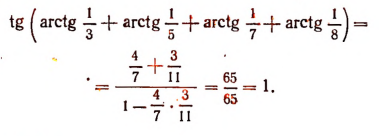
Очевидно, что

Складывая, получим, что
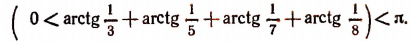
Итак, мы установили два факта:
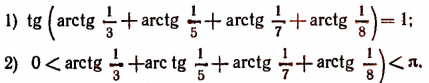
Из этих двух фактов вытекает, что
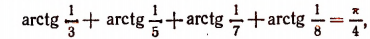
что и требовалось доказать.
8. Решить уравнение arccos х = 2arcsin x.
Если два числа равны, то равны и их косинусы. Поэтому из данного уравнения вытекает уравнение cos (arccos х) = cos(2 arcsin x). Но данное уравнение и вновь полученное, вообще говоря, не равносильны. Всякий корень первого уравнения будет корнем второго, но не всякий корень второго уравнения обязательно должен быть корнем первого, так как из равенства косинусов не обязательно следует равенство чисел, стоящих под знаками косинусов. Поэтому каждый из корней второго уравнения надо испытать подстановкой в первое уравнение и отобрать лишь те, которые удовлетворяют первому уравнению.
Второе уравнение после преобразований примет вид:
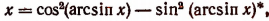
или
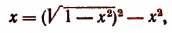
или
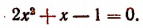
Отсюда
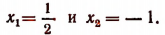
Подставляя в первоначально заданное уравнение вместо неизвестного х число 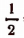
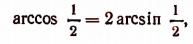
или
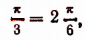
т.е. тождество.
Подставляя число — 1, получим:
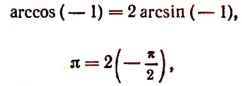
т. е. равенство неверное.
Итак, первоначальное уравнение имеет лишь один корень х =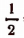
9. Решить уравнение
Преобразуем данное уравнение, взяв тангенсы его левой и правой части:
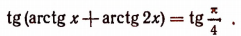
(см. пояснения к примеру 8).’
Применим формулу тангенса суммы и примем во внимание, что
Равенство
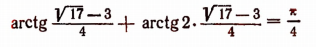
справедливо, так как его левая часть заключена между 0 и 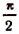
Равенство же
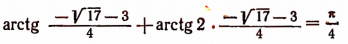
несправедливо, так как его левая часть заключена между — 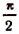
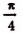
Следовательно, данное уравнение имеет только один корень
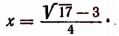
Графики обратных тригонометрических функций
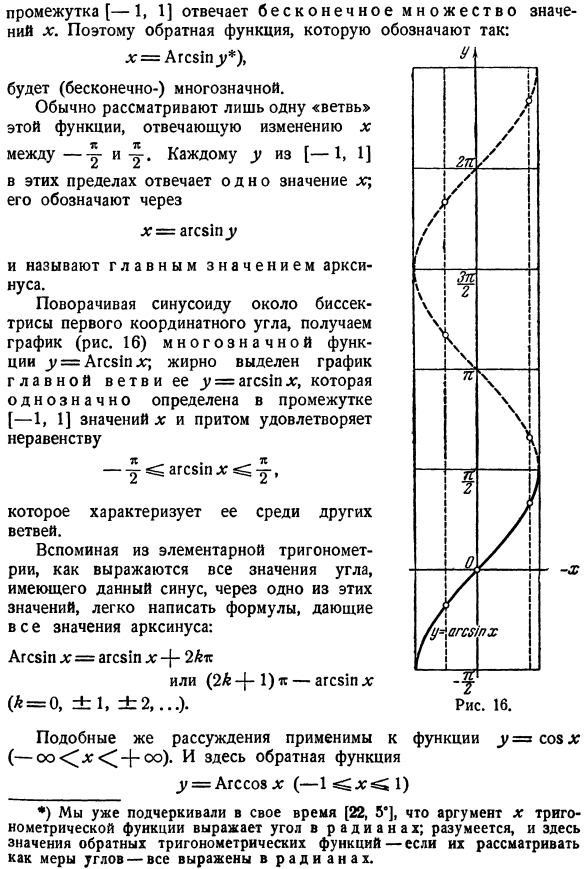
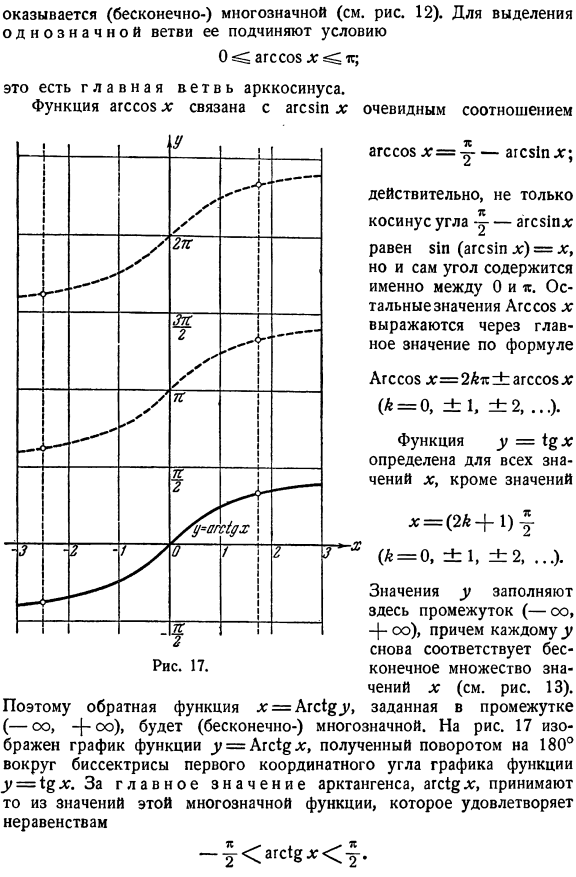
На рисунке 185 изображен график функции у = arcsin х.
На рисунке 186 изображен график функции у = arccos х.
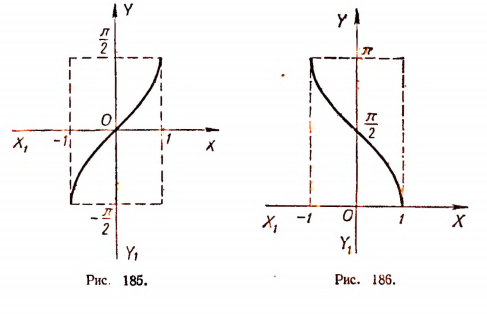
На рисунке 187 изображен график функции у = arctg х.
Дополнение к обратным тригонометрическим функциям
Смотрите также:
Решение задач по математическому анализу
Обратные тригонометрические функции и их графики
Функция y = arcsin x (арксинус).
Рассмотрим функцию y = sin x. Так как область определения этой функции — вся ось Ох (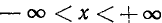
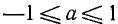
бесконечно много значений аргумента 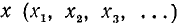
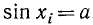
Для того чтобы получить обратную (однозначную) функцию к функции у = sin x, достаточно рассмотреть какой-либо наибольший отрезок оси Ох, на котором функция y = sin x или монотонно возрастает, или монотонно убывает (см. п. 35). Функция у = sin х монотонно возрастает от —1 до +1, например, на отрезке 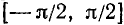
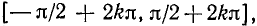
где k = 0, ±1, ±2,… Она монотонно убывает от +1 до —1 на любом отрезке вида
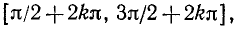
где k = 0, ±1, ±2, …
На всей оси Ох функция y = sin x обратной (однозначной) функции не имеет. На каждом же из отрезков монотонности функция y = sin x имеет обратную функцию. Остается теперь зафиксировать какой-либо из этих отрезков. В качестве отрезка оси Ох, на котором рассматривается функция у = sin x и обратная к ней функция, обычно берут отрезок 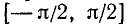
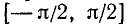
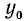
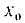
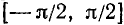
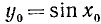
Пример:
Найти а = arcsin (1/2).
Данный пример подробно можно сформулировать так: найти такой аргумент а, лежащий в пределах от 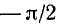
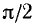
Решение:
Существует бесчисленное множество аргументов, синус которых равен 1/2, например: 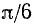
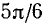
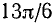
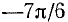
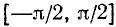
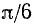
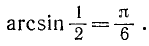
Пример:
Найти 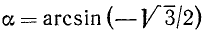
Решение:
Рассуждая так же, как и в примере 1, получим
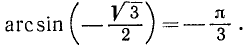
По общему правилу (см. п. 35) график обратной функции симметричен с графиком основной функции относительно биссектрисы I—III координатных углов (рис. 21).
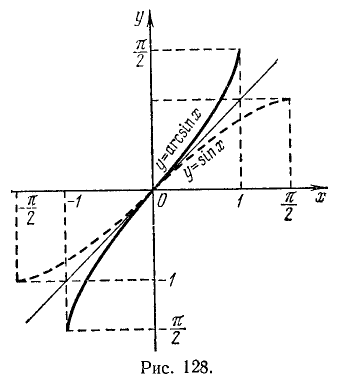
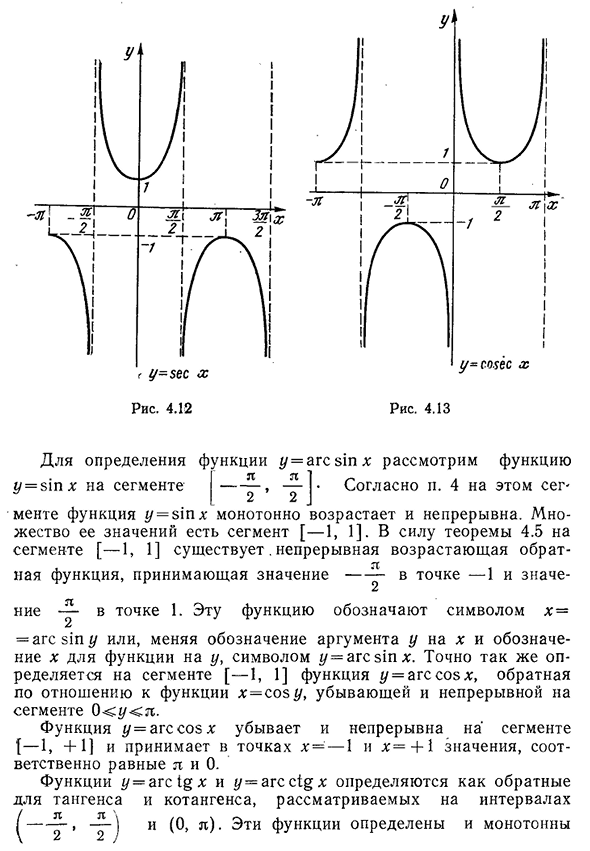
Свойства функции у = arcsin х (рис. 128).
1) Область определения: отрезок [—1, 1].
2) Область изменения: отрезок 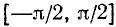
3) Функция у = arcsin х нечетная: arcsin (—x) = — arcsin х.
4) Функция y = arcsin х монотонно возрастающая.
5) График пересекает оси Ох, Оу в начале координат.
6)
Перечисленные свойства вытекают из свойств функции у = sin x на отрезке 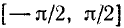
Функция y = arccos x (арккосинус)
Функция у = cos x определена на всей оси Ох (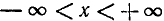
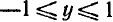
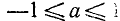
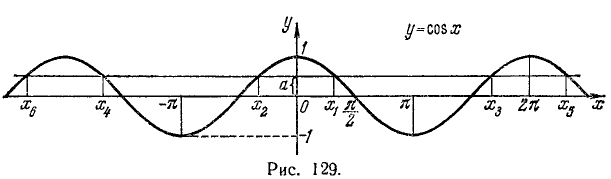
На рис. 129 видно, что существует бесконечно много значений аргумента х (
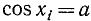
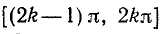
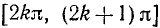
В качестве отрезка оси Ох, на котором рассматривается функция у = cos x и обратная к ней функция, обычно берут отрезок 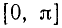
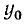
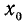
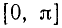
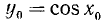
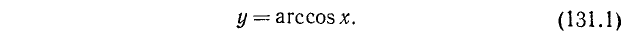
Пример:
Найти 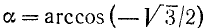
Подробно данный пример можно сформулировать так: найти такой аргумент а, лежащий в пределах от 0 до 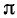
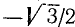
Решение:
Существует бесчисленное множество аргументов, косинус которых равен 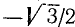
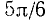
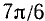
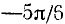
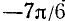
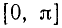
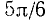
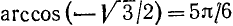
Пример:
Найти 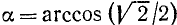
Решение:
Рассуждая так же, как и в предыдущем случае, мы получим 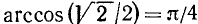
График функции у = arccos х симметричен с графиком функции у = cos x относительно биссектрисы I—III координатных углов (см. рис. 21 в п. 35).
Свойства функции у = arccos х вытекают из соответствующих свойств функции у = cos x на отрезке 
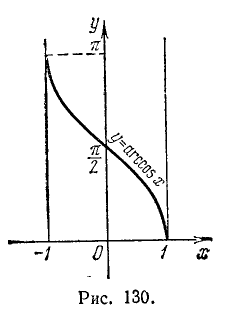
Перечислим эти свойства:
1) Область определения: отрезок [-1, 1].
2) Область изменения: отрезок 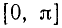
3) Функция у = arccos х ни четная, ни нечетная. Для нее выполняется тождество
4) Функция у = arccos х монотонно убывающая.
5) График пересекает ось Ох в точке (1, 0), а ось Оу в точке 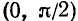
6) 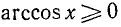
Функция y = arctg x (арктангенс)
Рассмотрим функцию y = tg x. Область определения этой функции — вся ось Ох, за исключением точек вида
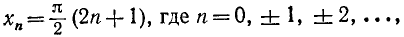
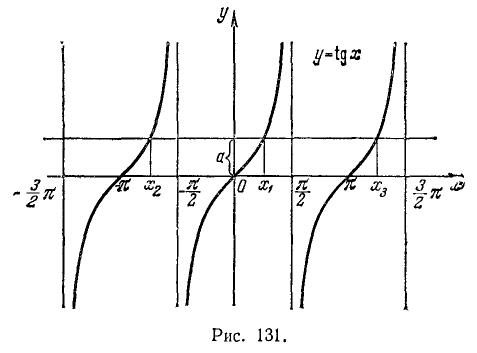
и область изменения значений — вся ось Оу. Об обратной функции (по отношению к функции у = tg x) можно уже говорить для всей оси Оу. Задача нахождения х из уравнения tg х = а и здесь имеет бесчисленное множество решений. На рис. 131 видно, что существует бесконечно много значений аргумента 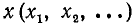
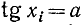
Для того чтобы получить обратную (однозначную) функцию к функции y = tg x, достаточно рассмотреть какой-либо наибольший интервал оси Ох, на котором она монотонно возрастает. Функция у= tg x монотонно возрастает от 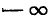
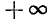
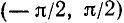
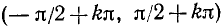
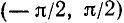
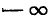
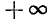
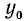
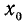
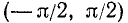
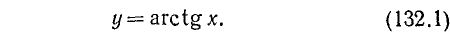
Пример:
Найти 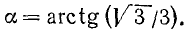
Подробно данный пример можно сформулировать так: найти такой аргумент а, лежащий в пределах от 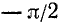
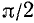
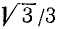
Решение:
Существует бесчисленное множество аргументов, тангенс которых равен 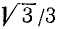
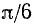
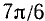
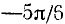
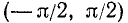
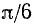
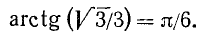
Пример:
Найти 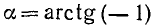
Решение:
Рассуждая так же, как и в предыдущем случае, мы получим 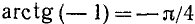
График функции у = arctg х симметричен с графиком функции y = tg x относительно биссектрисы I — III координатных углов (см. рис. 21 в п. 35).
Свойства функции у = arctg x вытекают из соответствующих свойств функции y = tg x на интервале 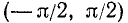
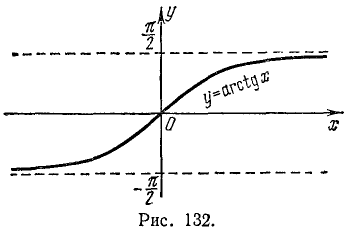
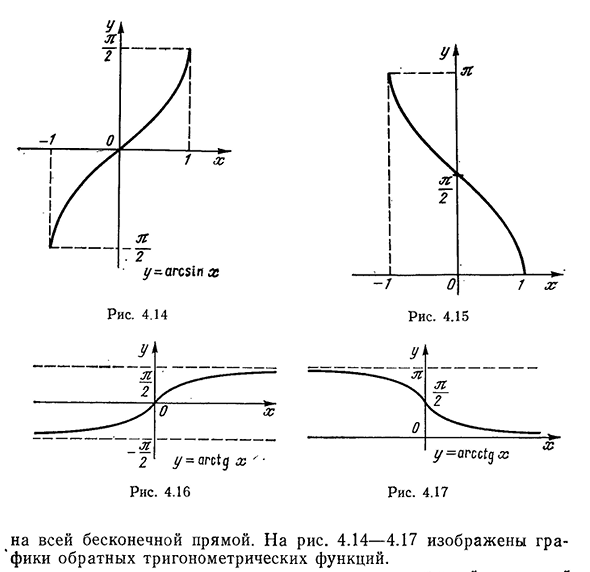
Перечислим эти свойства:
1) Область определения: x — любое действительное число.
2) Область изменения: интервал 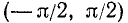
3) Функция y = arctg х нечетная: arctg ( —x) =— arctg x.
4) Функция у = arctg x монотонно возрастающая.
5) График пересекает оси Ох, Оу в начале координат.
6) arctg x < 0 при 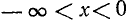
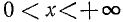
7) Прямые 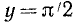

Функция y = arcctg x (арккотангенс)
Функция y = ctg x определена на всей оси Ох, за исключением точек вида 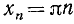
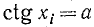
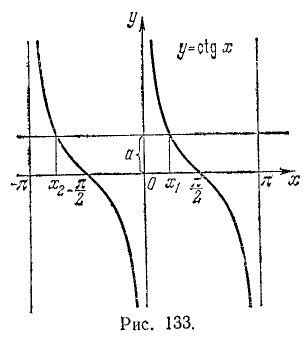
В качестве интервала оси Ох, на котором определяется обратная функция по отношению к функции у = ctg x, берут обычно интервал 
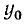
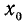
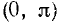
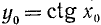
Пример:
Найти 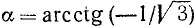
Подробно данный пример можно сформулировать так: найти такой аргумент а, лежащий в пределах от 0 до 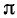
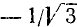
Решение:
Существует бесчисленное множество аргументов, котангенс которых равен 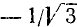
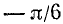
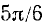
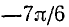
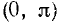
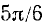
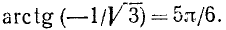
Пример:
Найти а = arcctg 1.
Решение:
Рассуждая так же, как и в предыдущем случае, мы получим 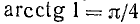
График функции у = arcctg x симметричен с графиком функции у = ctg x относительно углов (см. рис. 21 в п. 35). Свойства функции y = arcctg x вытекают из соответствующих свойств функции y = ctg x на интервале 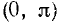
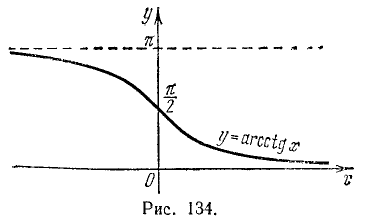
Перечислим эти свойства:
1) Область определения: х — любое действительное число.
2) Область изменения: интервал 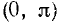
3) Функция у = arcctg х ни четная и ни нечетная. Для нее выполняется тождество
4) Функция у = arcctg x монотонно убывающая.
5) График пересекает ось Оу в точке 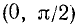
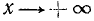
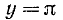
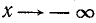
6) arcctg x > 0 при любых х.
Пример:
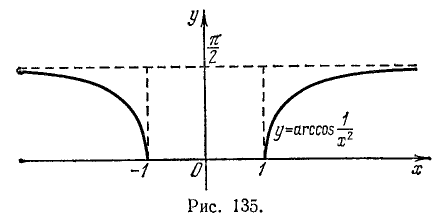
Построим график функции 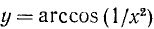
1) Область определения: функция определена для х, удовлетворяющих неравенству
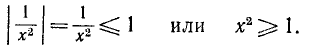
Последнее неравенство удовлетворяется при 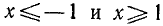
2) Область изменения значений функции: 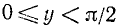
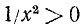
3) Функция четная, так как 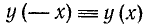
4) Точки пересечения с осями координат:
а) с осью Оу (х = 0) функция не может иметь точек пересечения, так как она определена только при 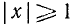
б) с осыо Ох (у = 0) она пересекается в точках (—1, 0) и (1, 0) (нули функции), так как 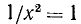
5) Наименьшее и наибольшее значения функции в области определения. В силу четности функции достаточно ее исследовать для 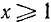
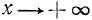
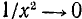
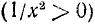
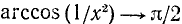
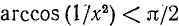
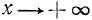
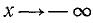
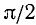
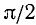
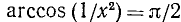
6) Интервалы знакопостоянства: функция всюду в области определения неотрицательна, т. е. 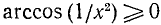
Для построения графика функции найдем некоторые опорные его точки, а затем соединим их плавной линией с учетом свойств функции.
Так как функция 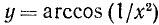

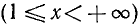
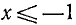
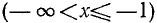
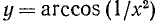
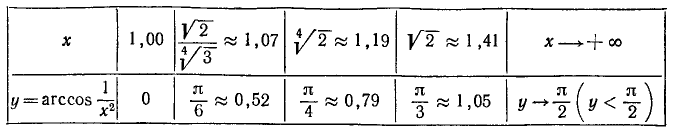
Соединив полученные опорные точки плавной линией и учтя, что прямая 
Продолжив его четным образом на бесконечный полуинтервал 
Операции над обратными тригонометрическими функциями
Тригонометрические операции: Рассмотрим некоторые простейшие тригонометрические операции над обратными тригонометрическими функциями (первая группа формул).
1) y= sin (arcsin х). По определению
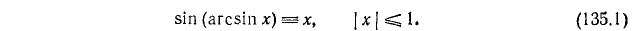
Пример 1. sin (arcsin 0,93) = 0,93.
2) у = cos (arccos х). По определению
Пример:
cos [arccos (— 0,79)] = — 0,79.
Следует подчеркнуть, что тождества (135.1) и (135.2) справедливы только в области определения (существования) арксинуса и арккосинуса, т. е. при 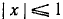
На основании предыдущего заметим также, что функции
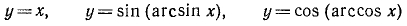
совпадают только в области определения арксинуса и арккосинуса, т. е. на отрезке [—1, 1] оси Ох. Вне этого отрезка последние две функции просто не существуют.
3) y = tg (arctg х). По определению
Пример:
tg (arctg 123) = 123.
4) y = ctg (arcctg x). По определению
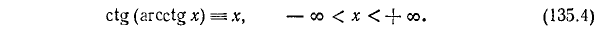
Пример:
ctg [arcctg (— 987)] = — 987.
Функции y = x, y =tg (arctg x), у = ctg (arcctg x) совпадают на всей оси Ox.
5) у = sin (arccos x). Положив arccos x = a, получим cos a = x.
На основании формулы (100.3) будем иметь
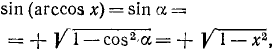
т. е.
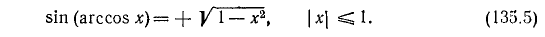
Мы взяли перед корнем знак « + » потому, что а = arccos х удовлетворяет неравенствам 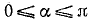
Пример:
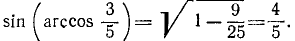
6) у = cos (arcsin x). Положив arcsin x = а, получим sin a = x. На основании формулы (100.1) будем иметь
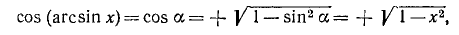
т. e.
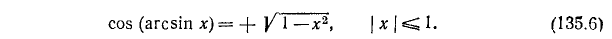
Мы взяли перед корнем знак « + » потому, что угол а = arcsin х удовлетво-ряет неравенствам 
Пример:
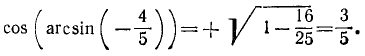
7) На основании тождества tg а = 1 /ctg а имеем
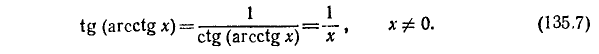
Пример:
tg (arcctg (1/9)) = 9.

Пример:
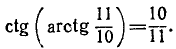
9) На основании формулы 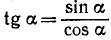
Пример:
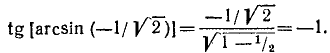
Аналогично предыдущему, можно доказать следующие формулы:

Пример:
Вычислить:
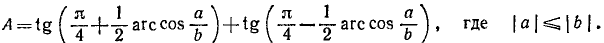
Решение:
На основании формулы (125.5) имеем
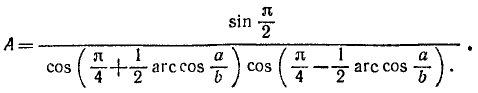
Знаменатель этой дроби преобразуем по формуле (123.2):
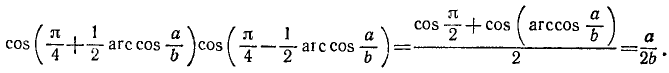
Окончательно найдем: А = 2b/а.
С помощью формул (135.1)—(135.16) получим ряд новых соотношений (вторая группа формул).
10) у = sin (2 arcsin х).
Обозначив arcsin x через а, будем иметь sin 2а = 2 sin а cos а, откуда
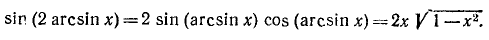
Мы воспользовались формулами (135.1) и (135.6). Итак,
Пример:
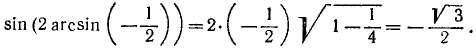
11) у = sin (2 arccos x). Имеем
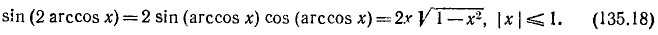
Пример:
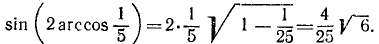
12) у = cos (2 arccos x). Аналогично предыдущему, будем иметь
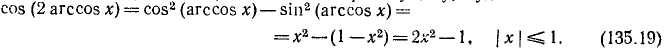
Есть другие возможные случаи, аналогичные случаям 10) —12), можно вывести соответствующие формулы. Например:
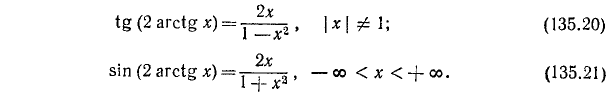
Пример:
Проверить равенство
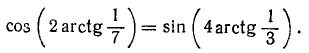
Решение:
Вычислим левую и правую части предполагаемого равенства. Обозначим arctg (1/7) через а, тогда tg a = 1/7. Далее, воспользовавшись формулой (122.2), получим
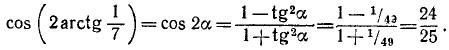
Обозначим arctg (1/3) через 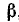
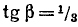
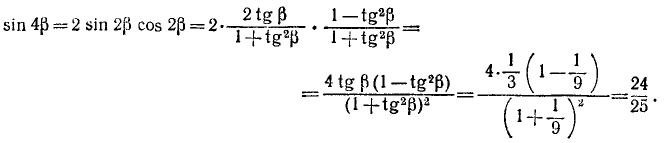
Следовательно, cos (2 arctg (1/7)) = sin (4 arctg (1/3)). Решая пример 13, мы попутно вывели еще две формулы:
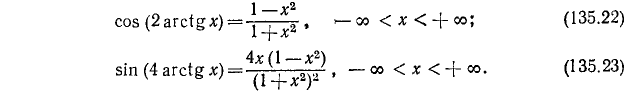
Выведем теперь некоторые формулы для тригонометрических функций от половины обратной тригонометрической функции (третья группа формул).
13) 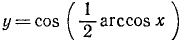
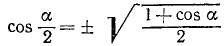
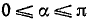
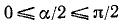
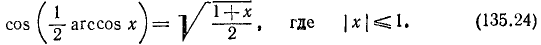
Пример:
14) 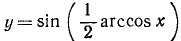
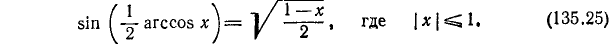
Пример:
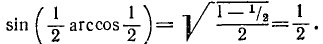
Используя формулы сложения и полученные выше формулы, выведем еще ряд соотношений (четвертая группа формул).
15) А = sin (arcsin + arcsin у). На основании формул (116.1), (135.1) и (135.6) будем иметь
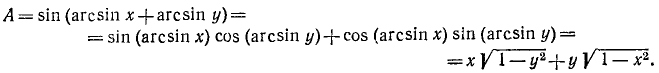
Итак,
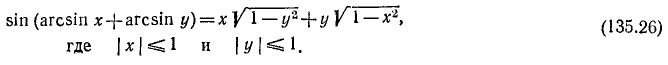
Пример:
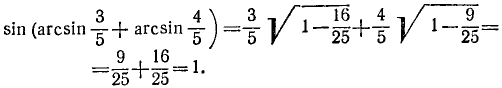
16) А = sin (arccos x + arccos у). На основании формул (116.1), (135.5) и (135.2) будем иметь
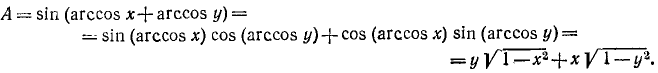
Итак,
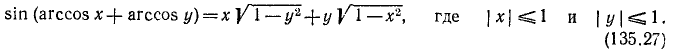
Пример:
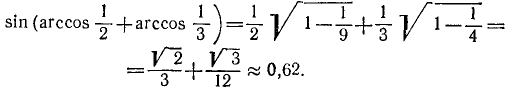
В этой группе формул можно образовать очень много различных соотношений. Запоминать все эти формулы не имеет смысла. В дальнейшем при решении примеров мы в каждом конкретном случае будем выводить ту или иную формулу.
Пример:
Вычислить:
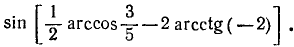
Решение:
В общем виде наш пример можно записать так:
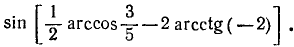
На основании формул (116.2), (135.24), (135.25), (135.21) и (135.22) будем иметь
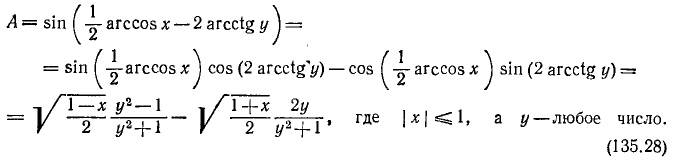
В нашем конкретном случае x = 3/5 и у = —2. Следовательно,
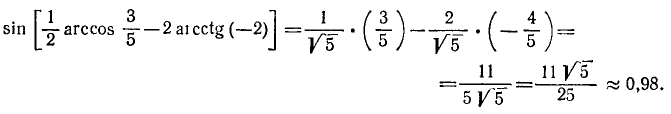
Пример:
Вычислить:
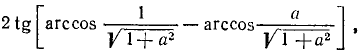
где a > 0.
Решение:
В общем виде наш пример можно записать так:
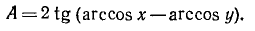
На основании формул (117.3) и (135.12) будем иметь
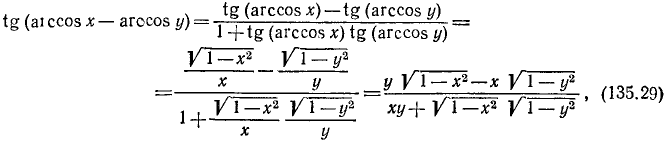
где 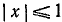
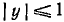
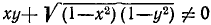
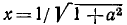
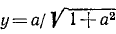
Окончательно получаем:
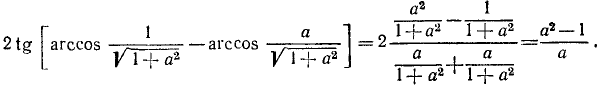
Операции сложения (вычитания)
Выведем теперь некоторые соотношения между обратными тригонометрическими функциями.
Теорема:
Для всех х из отрезка [—1, 1] имеет место тождество
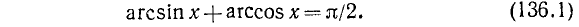
Доказательство:
По определению 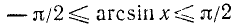
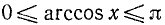
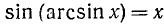
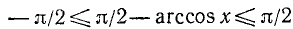
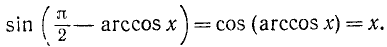
Итак, аргументы arcsin x и 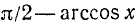
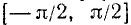
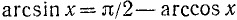
Теорема:
Для всех 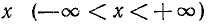
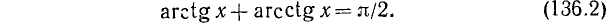
Тождество (136.2) доказывается так же, как и тождество (136.1). Рекомендуем читателю провести это доказательство самостоятельно.
Аналогично предыдущему могут быть получены формулы для arcsin х + arcsin у, arccos x + arccos у, arctg х + arctg у и т. д. Мы не будем их выводить, а приведем ряд примеров, на которых покажем метод решения таких задач.
Пример:
Проверить, имеет ли место равенство
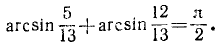
Решение:
Обозначим 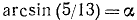
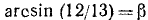
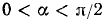
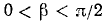
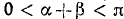
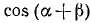
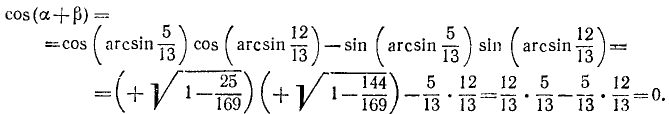
Итак, 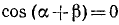
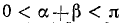
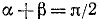
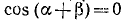
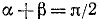
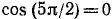
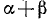
Пример:
Проверить, имеет ли место равенство
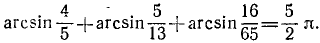
Решение:
Обозначим 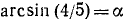
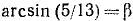
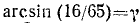
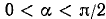
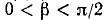
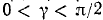
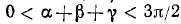
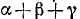
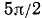
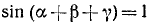
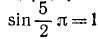
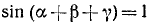
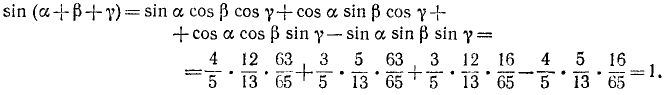
Итак, 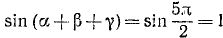
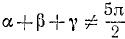
Пример:
Проверить, имеет ли место равенство
Решение:
На основании формулы (131.2)
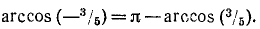
Предполагаемое равенство (*) перейдет в равенство
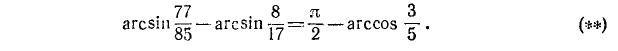
Воспользовавшись формулой (136.1), получим
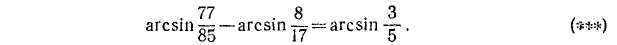
Обозначим 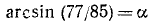
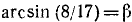
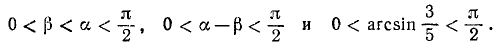
Если мы докажем теперь, что
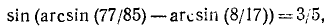
то будет доказано равенство (**), а тем самым и предполагаемое равенство ():
Итак,
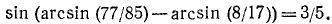
Следовательно, справедливо и равенство (*).
Пример:
Доказать, что
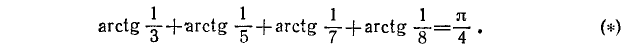
Решение:
Обозначим 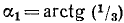
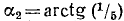
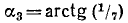
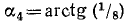
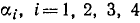
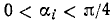
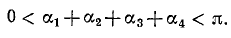
Если нам удастся доказать теперь, что 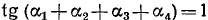
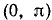
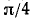
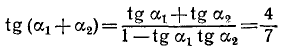
и
Далее,
Следовательно, равенство (*) имеет место.
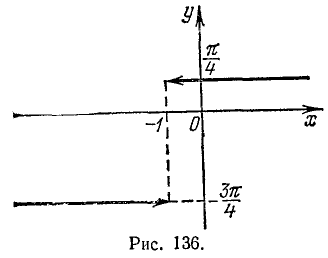
Пример:
Исследовать функцию
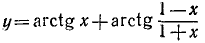
и построить ее график.
Решение:
Функция определена всюду, кроме х =—1. Обозначим 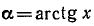
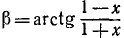
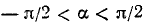
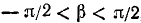
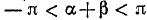
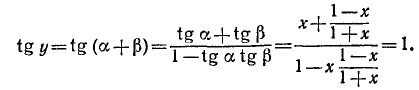
Итак, мы имеем 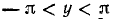
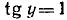
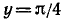
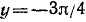
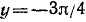
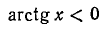
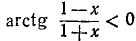
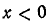
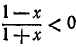
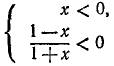
удовлетворяется, если 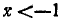

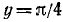
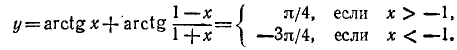
График исследуемой функции изображен на рис. 136.
Обратные тригонометрические операции над тригонометрическими функциями
Функция у = arcsin (sin x)
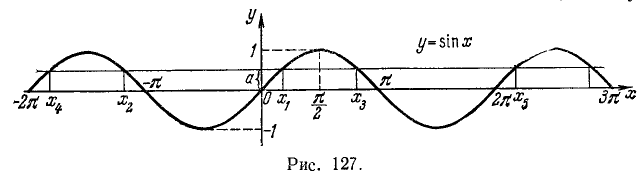
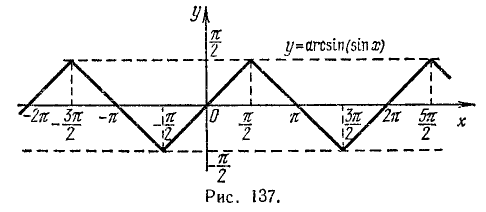
Исследуем функцию y =arcsin (sin х) и построим ее график.
1) Область определения (существования): функция определена для всех x 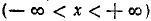
2) Область изменения функции: из определения арксинуса следует, что 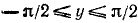
3) Сформулируем словесно правило, определяющее у по заданному х: каждому значению аргумента х 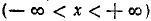
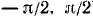
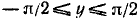
Пример:
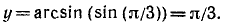
Здесь 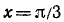
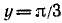
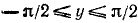
Пример:
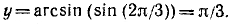
Здесь 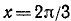
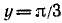
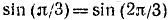
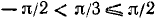
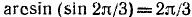
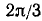
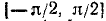
4) Функция нечетна. В самом деле.
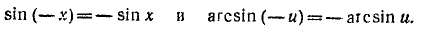
Следовательно,
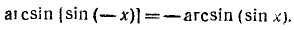
5) Функция периодическая с периодом 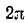
6) График функции y = arcsin (sin х) на отрезке 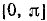
а) При 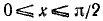
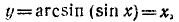
б) При 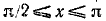
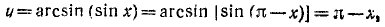
ибо
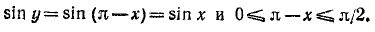
Итак,
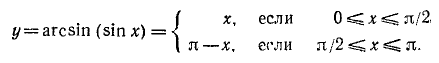
Построив график функции у = arcsin (sin х) на отрезке [
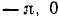
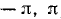
Пример:
Найти а = arcsin (sin 2).
Решение:
Требуется найти угол а, лежащий в пределах от 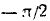
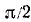
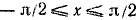
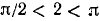
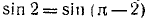

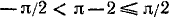
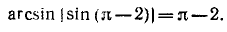
Следовательно, 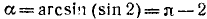
Пример:
Вычислить:
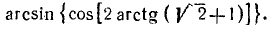
Решение:
Воспользовавшись формулой 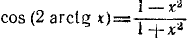
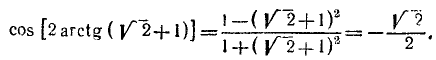
После этого получим
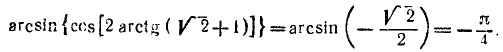
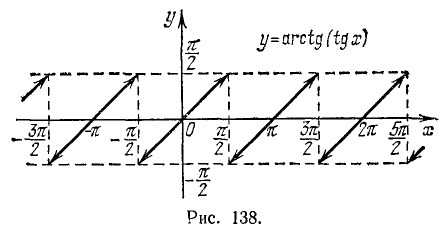
138. Функция y = arctg (tg x). Исследуем функцию y = arctg (tg x) и построим ее график.
1) Область определения (существования): функция определена для всех x, за исключением 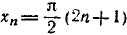
2) Область изменения функции: из определения арктангенса следует, что 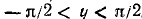
3) Каждому значению х из области определения данной функции ставшей в соответствие значение функции и находящееся в интервале (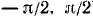
Пример:
y= aictg (tg (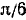
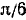
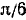
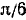
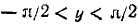
Пример:
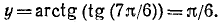
Здесь 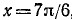
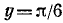
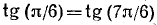
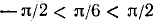
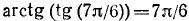
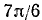
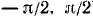
4) Функция нечетна, так как tg (—x) = — tg x и arctg(—u) = — arctg u. Следовательно, arctg (tg (—x)] = — arctg (tg x).
5) Функция периодична с периодом 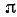
6) График функции y = arctg (tg x) на интервале 
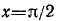
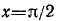
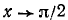
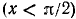
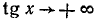
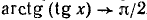
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат