Как найти sinb в треугольнике abc - Исправление недочетов и поиск решений вместе с Examum.ru

Синус, косинус и тангенс острого угла прямоугольного треугольника

Изучение тригонометрии мы начнем с прямоугольного треугольника. Определим, что такое синус и косинус, а также тангенс и котангенс острого угла. Это основы тригонометрии.

Напомним, что прямой угол — это угол, равный 90 градусов. Другими словами, половина развернутого угла.

Острый угол — меньший 90 градусов.

Тупой угол — больший 90 градусов. Применительно к такому углу «тупой» — не оскорбление, а математический термин

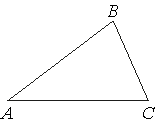
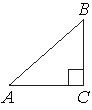
Нарисуем прямоугольный треугольник. Прямой угол обычно обозначается C. Обратим внимание, что сторона, лежащая напротив угла, обозначается той же буквой, только маленькой. Так, сторона, лежащая напротив угла A, обозначается .

Угол A обозначается соответствующей греческой буквой alpha .

Гипотенуза прямоугольного треугольника — это сторона, лежащая напротив прямого угла.

Катеты — стороны, лежащие напротив острых углов.

Катет , лежащий напротив угла alpha , называется противолежащим (по отношению к углу alpha ). Другой катет , который лежит на одной из сторон угла alpha , называется прилежащим.

Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:

sin A $=genfrac{}{}{}{0}{displaystyle a}{displaystyle c}.$

Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе:

cos A $=genfrac{}{}{}{0}{displaystyle b}{displaystyle c}.$

Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:

tg A $=genfrac{}{}{}{0}{displaystyle a}{displaystyle b}.$

Другое (равносильное) определение: тангенсом острого угла называется отношение синуса угла к его косинусу:

tg A $=genfrac{}{}{}{0}{displaystyle sin A}{displaystyle cos A}.$

Котангенс острого угла в прямоугольном треугольнике — отношение прилежащего катета к противолежащему (или, что то же самое, отношение косинуса к синусу):

ctg A $=genfrac{}{}{}{0}{displaystyle cos A}{displaystyle sin A}.$

Обратите внимание на основные формулы для синуса, косинуса, тангенса и котангенса, которые приведены ниже. Они пригодятся нам при решении задач.

sin $displaystyle alpha = frac{a}{c}$	sin ${}^2 alpha +$ cos $displaystyle {}^2 alpha =1$	$alpha + beta = 90 ^{circ}$
cos $displaystyle alpha = frac{b}{c}$	1+tg $displaystyle {}^2 alpha =frac{1}{cos ^2 alpha}$	cos = sin
tg $displaystyle alpha = frac{a}{b}$	1+ctg $displaystyle {}^2 alpha =frac{1}{sin ^2 alpha}$	sin = cos
ctg $displaystyle alpha = frac{b}{a}$		tg = ctg

Давайте докажем некоторые из них.

Сумма углов любого треугольника равна $180^{circ}$ . Значит, сумма двух острых углов прямоугольного треугольника равнa $90^{circ}$ .
С одной стороны, $sin A =genfrac{}{}{}{0}{displaystyle a}{displaystyle c}$ как отношение противолежащего катета к гипотенузе. С другой стороны, $cos B =genfrac{}{}{}{0}{displaystyle a}{displaystyle c}$ , поскольку для угла катет а будет прилежащим. Получаем, что . Иными словами, $cos left( 90^{circ}-A right) = sin A$ .
Возьмем теорему Пифагора: . Поделим обе части на получаем $displaystyle left ( frac{a}{c} right )^2+left ( frac{b}{c} right )^2=left ( frac{c}{c} right )^2 ,$ то есть
Мы получили основное тригонометрическое тождество.
Поделив обе части основного тригонометрического тождества на , получим: $1+tg ^2 A = genfrac{}{}{}{0}{displaystyle 1}{displaystyle cos ^2 A }.$ Это значит, что если нам дан тангенс острого угла , то мы сразу можем найти его косинус. Аналогично, $1+ctg ^2 A =genfrac{}{}{}{0}{1}{sin ^2 A }.$

Хорошо, мы дали определения и записали формулы. А для чего все-таки нужны синус, косинус, тангенс и котангенс?

Мы знаем, что сумма углов любого треугольника равна $180^{circ}$ .

Знаем соотношение между сторонами прямоугольного треугольника. Это теорема Пифагора: .

Получается, что зная два угла в треугольнике, можно найти третий. Зная две стороны в прямоугольном треугольнике, можно найти третью. Значит, для углов — свое соотношение, для сторон — свое. А что делать, если в прямоугольном треугольнике известен один угол (кроме прямого) и одна сторона, а найти надо другие стороны?

С этим и столкнулись люди в прошлом, составляя карты местности и звездного неба. Ведь не всегда можно непосредственно измерить все стороны треугольника.

Синус, косинус и тангенс — их еще называют тригонометрическими функциями угла — дают соотношения между сторонами и углами треугольника. Зная угол, можно найти все его тригонометрические функции по специальным таблицам. А зная синусы, косинусы и тангенсы углов треугольника и одну из его сторон, можно найти остальные.

Мы тоже нарисуем таблицу значений синуса, косинуса, тангенса и котангенса для «хороших» углов от $0^{circ}$ до $90^{circ}$ .

	0	$genfrac{}{}{}{0}{displaystyle pi}{displaystyle 6}$	$genfrac{}{}{}{0}{displaystyle pi}{displaystyle 4}$	$genfrac{}{}{}{0}{displaystyle pi}{displaystyle 3}$	$genfrac{}{}{}{0}{displaystyle pi}{displaystyle 2}$
sin	0	$displaystyle frac{1}{2}$	$displaystyle frac{sqrt{2}}{2}$	$displaystyle frac{sqrt{3}}{2}$
cos		$displaystyle frac{sqrt{3}}{2}$	$displaystyle frac{sqrt{2}}{2}$	$displaystyle frac{1}{2}$	0
tg	0	$genfrac{}{}{}{0}{displaystyle 1}{displaystyle sqrt{3}}$			−
ctg	−			$genfrac{}{}{}{0}{displaystyle 1}{displaystyle sqrt{3}}$	0

Обратите внимание на два прочерка в таблице. При соответствующих значениях углов тангенс и котангенс не существуют.

Докажем теорему:

Если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то синусы этих углов равны, косинусы этих углов равны и тангенсы этих углов равны.

В самом деле, пусть АВС и — два прямоугольных треугольника с прямыми углами С и C_1 и равными острыми углами А и A_1.

Треугольники АВС и подобны по первому признаку подобия треугольников, поэтому $displaystyle frac{AB}{A_1 B_1}=frac{BC}{B_1 C_1}=frac{AC}{A_1 C_1 } .$

Из этих равенств следует, что $displaystyle frac{BC}{AB}=frac{B_1 C_1}{A_1 B_1} ,$ т. е. sin А = sin A_1.

Аналогично, $displaystyle frac{AC}{AB}=frac{A_1C_1}{A_1 B_1},$ т. е. cos А = cos A_1, и $displaystyle frac{BC}{AC}=frac{B_1C_1}{A_1 C_1},$ т. е. tg A = tg A_1.

Это значит, что синус, косинус и тангенс зависят только от величины угла.

Разберем несколько задач по тригонометрии из Банка заданий ФИПИ.

Задача 1. В треугольнике ABC угол C равен $90^{circ}$ , sin A = 0,1. Найдите cos B.

Задача решается за четыре секунды.

Поскольку $A+B = 90^{circ}$ , sin A = cos B = 0,1.

Задача 2. В треугольнике ABC угол равен $90^{circ}$ , AB=5 , $sin A = genfrac{}{}{}{0}{displaystyle 7}{displaystyle 25}$ .

Найдите .

Решение:

$sin A = genfrac{}{}{}{0}{displaystyle a}{displaystyle c} = genfrac{}{}{}{0}{displaystyle BC}{displaystyle AB} = genfrac{}{}{}{0}{displaystyle 7}{displaystyle 25}.$

Отсюда

$BC= genfrac{}{}{}{0}{displaystyle 7}{displaystyle 25} cdot AB = genfrac{}{}{}{0}{displaystyle 7}{displaystyle 5}.$

Найдем AC по теореме Пифагора.

$AC=sqrt{AB^2-BC^2} = genfrac{}{}{}{0}{displaystyle 24}{displaystyle 5} = 4,8.$

Ответ: 4,8.

Задача 3. В треугольнике АВС угол С равен AВ = 13, ВС = 5. Найдите косинус и тангенс острого угла А. Ответ округлите до сотых.

Решение:

Для угла А противолежащий катет – это ВС,

АВ является гипотенузой треугольника, лежит против Значит, sin A $displaystyle = frac{BC}{AB}= frac{5}{13}.$

Катет, прилежащий к angle A – это катет АС, следовательно, cos⁡ А $displaystyle = frac{AC}{AB}=frac{AC}{13}.$

Длину катета АС найдем по теореме Пифагора:

Тогда $AC = sqrt{AB^2-BC^2}=sqrt{(13)^2-5^2}=sqrt{144}=12.$

cos⁡ А $displaystyle = frac{12}{13}=0,923 ... approx 0,92 ;$

tg A $displaystyle = frac{BC}{AC} = frac{5}{12}=0,416...approx 0,42.$

Ответ: 0,92; 0,42.

Заметим, что если катеты прямоугольного треугольника равны 5 и 12, то гипотенуза равна 13. Это одна из так называемых Пифагоровых троек. О них мы расскажем в других статьях сайта.

Задача 4. В треугольнике АВС угол С равен AC = 2, sin A= $displaystyle frac{sqrt{17}}{17} .$

Найдите BC.
Решение:

AC = b = 2, BC = a, AB = c.

Так как sin A $displaystyle = frac{a}{c} = frac{BC}{AB} = frac{sqrt{17}}{17},$ $displaystyle frac{a}{c} = frac{sqrt{17}}{17} ,$ $displaystyle c = frac{17a}{sqrt{17}}=sqrt{17}a.$

По теореме Пифагора получим

$a^2+2^2=(sqrt{17} a)^2;$

$displaystyle a= frac{1}{2}=0,5;$

Ответ: 0,5.

Задача 5. В треугольнике АВС угол С равен AC = 4, tg A = $displaystyle frac{33}{4sqrt{33}} .$ Найдите AB.

Решение:

AC = b = 4, tg A $displaystyle = frac{a}{b}=frac{33}{4sqrt{33}},$

$displaystyle frac{a}{4}=frac{33}{4sqrt{33}},$ $displaystyle a=frac{4 cdot 33}{4 cdot sqrt{33}}=sqrt{33},$

$AB = c = sqrt{a^2+b^2}=sqrt{(sqrt{33})^2+4^2}=sqrt{33+16} =7.$

Ответ: 7.

Задача 6.

В треугольнике АВС угол С равен CH – высота, AB = 13, tg A = $displaystyle frac{1}{5} .$ Найдите AH.

Решение:

AВ = с = 13, tg A = $displaystyle frac{a}{b}=frac{1}{5} ,$ тогда b = 5a.

По теореме Пифагора ABC:

$displaystyle a=sqrt{frac{169}{26}}=frac{13}{sqrt{26}},$ тогда $displaystyle b = 5a=5cdot frac{13}{sqrt{26}}=frac{65}{sqrt{26}}.$

(по двум углам), следовательно $displaystyle frac{AH}{AC}=frac{AC}{AB} ,$ откуда

$displaystyle AH = frac{AC^2}{AB}=frac{b^2}{c}=left ( frac{65}{sqrt{26}}right )^2:13=12,5.$

Ответ: 12,5.

Задача 7. В треугольнике АВС угол С равен

CH – высота, BC = 3, sin A = $displaystyle frac{1}{6} .$

Найдите AH.

Решение:

Так как sin A = $displaystyle frac{a}{c} = frac{BC}{AB} = frac{1}{6},$ тогда $displaystyle frac{3}{c} = frac{1}{6} ,$ c = АВ = 18.

sin A = $displaystyle frac{a}{c}$ = cos⁡ B = $displaystyle frac{1}{6} .$

Рассмотрим BHC:

${cos B= }displaystyle frac{BH}{BC}$ = $displaystyle frac{1}{6} ,$ получим $displaystyle frac{BH}{3}=displaystyle frac{1}{6},$

тогда BH = $displaystyle frac{3}{6}=displaystyle frac{1}{2}$ = 0,5,

AH = AB — BH = 18 — 0,5 = 17,5.

Ответ: 17,5.

Задача 8. В треугольнике АВС угол С равен 90 ${}^circ,$ CH — высота, BC = 3, cos A = $displaystyle frac{sqrt{35}}{6}.$

Найдите АH.

Решение:

Так как для АВС: cos A = $displaystyle frac{AC}{AB}=$ sin В = $displaystyle frac{sqrt{35}}{6},$

а для ВНС: sin В = $displaystyle frac{CH}{BC}$ = $displaystyle frac{sqrt{35}}{6}$ , откуда СН = $displaystyle frac{BC cdot sqrt{35}}{6}=displaystyle frac{3 cdot sqrt{35}}{6}=displaystyle frac{sqrt{35}}{2},$

По теореме Пифагора найдем ВН:

$BH = sqrt{{BC}^2-{CH}^2}=sqrt{3^2-{left(displaystyle frac{sqrt{35}}{2}right)}^2}=$

$=sqrt{9-displaystyle frac{35}{4}}=sqrt{displaystyle frac{1}{4}}=displaystyle frac{1}{2}=0,5.$

Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой. Поэтому для АВС получим:

${CH}^2=AH cdot BH,$ тогда $AH= displaystyle frac{ {CH}^2}{BH}, ; AH= displaystyle frac{ {left(displaystyle frac{sqrt{35}}{2}right)}^2}{0,5}=displaystyle frac{35 cdot 2}{4}=17,5.$

Ответ: 17,5.

Задача 9. В треугольнике АВС угол С равен 90 ${}^circ,$ CH — высота, СН = 24 и BН = 7. Найдите sin A.

Решение:

По определению sin A= $displaystyle frac{a}{c}$ = $displaystyle frac{BC}{AB}$ =

Рассмотрим BHC : ${cos B= }displaystyle frac{BH}{BC}.$

ВС найдем по теореме Пифагора:

ВС= $sqrt{{BH}^2+{CH}^2}=sqrt{7^2+{24}^2}=sqrt{49+576}=sqrt{625}=25,$

тогда ${cos B= }displaystyle frac{BH}{BC}=displaystyle frac{7}{25}=0,28,$ а значит и sin A = = 0,28.

Ответ: 0,28.

Задача 10. В треугольнике АВС угол С равен 90 ${}^circ,$ CH — высота, СН = 8 и BН = 4. Найдите tg A.

Решение:

По определению sin A = $displaystyle frac{a}{c}$ = $displaystyle frac{BC}{AB}$ = cos A = $displaystyle frac{b}{c}$ = $displaystyle frac{AC}{AB}$ =

тогда tg A = $displaystyle frac{sin A}{{cos A }}=displaystyle frac{cosB}{sinB}=ctgB,$ который найдем из BHC:

$ctgB=displaystyle frac{BH}{CH}=displaystyle frac{4}{8}=0,5.$

Ответ: 0,5.

Задача 11. В треугольнике АВС угол С равен 90 ${}^circ,$ CH — высота, BН = 12, tg A = $displaystyle frac{2}{3}.$ Найдите АН.

Решение:

По определению tg A= $displaystyle frac{BC}{AC}=ctgB=displaystyle frac{2}{3}.$

Для BHC: $ctgB=displaystyle frac{BH}{CH}=displaystyle frac{2}{3}$ , значит $displaystyle frac{12}{CH}=displaystyle frac{2}{3},$ СН = $displaystyle frac{12 cdot 3}{2}=18.$

Для АHC: tg A= $displaystyle frac{CH}{AH}=displaystyle frac{2}{3},$ то $displaystyle frac{18}{AH}=displaystyle frac{2}{3},$ AH = $displaystyle frac{18 cdot 3}{2}=27.$

Ответ: 27.

Задача 12. В треугольнике АВС угол С равен 90 ${}^circ,$ CH — высота, BН = 12, sin A = $displaystyle frac{2}{3}.$ Найдите АВ.

Решение:

Так как cos В = $displaystyle frac{BC}{AB}$ = sin A = $displaystyle frac{2}{3}.$

Из СВН имеем cos В = $displaystyle frac{HB}{BC}$ = $displaystyle frac{2}{3},$ тогда ВС = $displaystyle frac{3 cdot HB}{2}=displaystyle frac{3 cdot 12}{2}=18.$

В АВС имеем sinA = $displaystyle frac{BC}{AB}$ = $displaystyle frac{2}{3},$ тогда AВ = $displaystyle frac{3 cdot BC}{2}=displaystyle frac{3 cdot 18}{2}=27.$

Ответ: 27.

Задача 13. В треугольнике АВС угол С равен 90 ${}^circ,$ из вершины прямого угла к гипотенузе проведена высота СН. Найдите cos A, AC и AB, если СН = 12, ВС = 20.

Решение:

Найдем НВ по теореме Пифагора из ВСН:

$HB = sqrt{BC^2-BH^2}=sqrt{20^2-12^2}=sqrt{(20-12)(20+12)}=$

sin В = $displaystyle frac{CH}{BC}$ = $displaystyle frac{12}{20}=displaystyle frac{3}{5}.$

Для АВС: cos A = $displaystyle frac{AC}{AB}=sin B=displaystyle frac{3}{5},$ получили cos A = 0,6.

Найдем АС и АВ несколькими способами.

1-й способ.

Так как cos A = $displaystyle frac{AC}{AB}=displaystyle frac{3}{5},$ то пусть АС = 3х, АВ = 5х,

тогда по теореме Пифагора ${AC}^2+{BC}^2= {AB}^2,$ получим ${(3x)}^2+{(20)}^2= {(5x)}^2$
${25x}^2-{9x}^2= {20}^2 ,$

${16x}^2= {20}^2,$

$x^2= {left(displaystyle frac{20}{4}right)}^2,$
х = 5 ( так как х0). Значит,

2-й способ.

(по двум углам), значит $displaystyle frac{HB}{CB}=frac{HC}{AC}=frac{BC}{AB}$ или $displaystyle frac{16}{20}={12}{AC}={20}{AB} = k,$

k = $displaystyle frac{16}{20}=displaystyle frac{4}{5} ,$ тогда $displaystyle frac{12}{AC}=displaystyle frac{4}{5},$ АС = $displaystyle frac{12 cdot 5}{4}=15$ ; $displaystyle frac{20}{AB}=displaystyle frac{4}{5},$ АВ = $displaystyle frac{20 cdot 5}{4}=25.$

3-й способ.

${CH}^2=AH cdot HB$ (высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой) , тогда ${12}^2=AH cdot 16,$ АН = 144:16 = 9.

АВ = АН + НВ = 9 + 16 = 25.

По теореме Пифагора найдем АС:

$AC = sqrt{{AB}^2-{BC}^2}=sqrt{{25}^2-{20}^2}=sqrt{(25-20)(25+20)}$ =

Ответ: cos A = 0,6; АС = 15, АВ = 25.

Задача 14.

Высота ВН прямоугольного треугольника АВС, проведенная из вершины прямого угла В, равна 24 и отсекает от гипотенузы АС отрезок НС, равный 18.

Найдите АВ и cos А.

Решение:

Из прямоугольного ВНС по теореме Пифагора найдем гипотенузу ВС и cos C:

ВС = $sqrt{{HC}^2+{BH}^2}=sqrt{{18}^2+{24}^2}=sqrt{324+576}$ =

cos C = $displaystyle frac{HC}{BC}=displaystyle frac{18}{30}=displaystyle frac{3}{5}.$

Для АВС: sin А = $displaystyle frac{BC}{AC}$ = cos C = $displaystyle frac{3}{5}.$

Для АНВ: sin А = $displaystyle frac{BH}{AB}$ = $displaystyle frac{3}{5},$ то $displaystyle frac{24}{AB}$ = $displaystyle frac{3}{5},$ АВ = $displaystyle frac{24 cdot 5}{3}=40.$

Из основного тригонометрического тождества найдем

cos A = $sqrt{1-{sin}^2A}=sqrt{1-0,36}=sqrt{0,64}=0,8.$

Ответ: АВ = 40, cos A = 0,8.

Задача 15.

Гипотенуза АС прямоугольного треугольника АСЕ равна 50, sin А = $displaystyle frac{7}{25}.$

Найдите площадь треугольника.

Решение:

В прямоугольном АСЕ sin А = $displaystyle frac{CE}{AC},$

значит $displaystyle frac{7}{25}$ = 14.

Второй катет найдем, используя теорему Пифагора: $AE= sqrt{{AC}^2-{CE}^2};$

$AE = sqrt{{50}^2-{14}^2}=sqrt{(50-14)(50+14)} =sqrt{36cdot 64}=6cdot8=48.$

Площадь прямоугольного треугольника равна S = $displaystyle frac{1}{2}ab,$

поэтому $S_{ACE}= displaystyle frac{1}{2} AEcdot CE=displaystyle frac{48cdot 14}{2}=336.$

Ответ: 336.

Задача 16.

В треугольнике АВС угол С — прямой, катеты АВ = 13 и ВС = 12, СК — высота.

Найдите sin Результат округлите до сотых.

Решение:

A-общий, $angle AKC=angle ACB=90{}^circ$ ),

значит sin $angle ACK=displaystyle frac{AK}{AC}=displaystyle frac{AC}{AB}.$

Найдем АС по теореме Пифагора из САВ:

$AC = sqrt{{AB}^2-{BC}^2}=sqrt{{13}^2-{12}^2}=$

Тогда sin $angle ACK=displaystyle frac{5}{13}=0,384..approx 0,38.$

Ответ: 0,38.

Задача 17. В треугольнике АВС АС = ВС, АВ = 72, cos A = $displaystyle frac{12}{13}.$ Найдите высоту СН.

Решение:

Так как АС = ВС, то АВС — равнобедренный с основанием АВ, тогда

высота СН является медианой, то есть АН = НВ = $displaystyle frac{1}{2}AB=36.$

Поскольку АСН — прямоугольный,

cos A = $displaystyle frac{AH}{AC}=$ $displaystyle frac{12}{13},$ то есть $displaystyle frac{36}{AC}=$ $displaystyle frac{12}{13}$ АС = $displaystyle frac{36 cdot 13}{12}=39.$

По теореме Пифагора ${AH}^2+{CH}^2={AC}^2,$ тогда

$CH = sqrt{{AC}^2-{AH}^2} = sqrt{{39}^2-{36}^2}=$

Ответ: 15.

Задача 18. В треугольнике АВС угол С равен 90 ${}^circ,$ sin A = $displaystyle frac{11}{14},$ AC = 10 Найдите АВ.

Решение:

1-й способ.

Поскольку sin A = $displaystyle frac{BC}{AB}=$ $displaystyle frac{11}{14},$ то можно обозначить

ВС = 11х, АВ = 14х.

По теореме Пифагора $AC^2+{BC}^2={AB}^2;$

${(10sqrt{3})}^2+{(11x)}^2={(14x)}^2;$

${(14x)}^2-{(11x)}^2 = 3 cdot 100;$

(14х- 11х)(14х + 11х) = 3 cdot 100;

x^2=4, учитывая, что длина стороны положительна, х = 2,

следовательно, АВ = 14 cdot 2 = 28.

2-й способ.

Воспользуемся основным тригонометрическим тождеством ${sin}^2A+{cos}^2A=1;$

cos A = $sqrt{1-{sin}^2A}=sqrt{1-{left(displaystyle frac{11}{14}right)}^2}=sqrt{displaystyle frac{196-121}{196}}=sqrt{displaystyle frac{75}{196}}=displaystyle frac{5sqrt{3}}{14}.$

По определению cos A = $displaystyle frac{AC}{AB},$ значит $displaystyle frac{AC}{AB}= displaystyle frac{5sqrt{3}}{14}.$

Так как АС=10 то $displaystyle frac{10sqrt{3}}{AB}= displaystyle frac{5sqrt{3}}{14},$ откуда АВ = $displaystyle frac{10sqrt{3} cdot 14}{5sqrt{3}}$ = 28.

Ответ: 28.

Задача 19. Найдите углы ромба АВСD, если его диагонали АС и ВD равны 4 sqrt{3} и 4.

Решение:

Пусть angle ВАО = alpha .

Диагонали ромба делят его углы пополам, значит, = alpha .

Диагонали ромба взаимно перпендикулярны и точкой пересечения делятся пополам, следовательно, в прямоугольном треугольнике АВО катет АО = $displaystyle frac{1}{2} AC=2sqrt{3},$ а катет ВО = $displaystyle frac{1}{2}BD =2.$

Поэтому tg $alpha =displaystyle frac{BO}{AO}=displaystyle frac{2}{2sqrt{3}}=displaystyle frac{1}{sqrt{3}},$ откуда $alpha =30{}^circ .$

$angle BAD=2alpha =60{}^circ , ; angle ADC=angle ABC=180{}^circ -60{}^circ =120{}^circ .$

Ответ: ${60}^circ,$ ${120}^circ,$ ${60}^circ,$ ${120}^circ .$

Часто в задачах встречаются треугольники с углами $90^{circ},, 30^{circ}$ и $60^{circ}$ или с углами $90^{circ},, 45^{circ}$ и $45^{circ}$ . Основные соотношения для них запоминайте наизусть!

Для треугольника с углами $90^{circ},, 30^{circ}$ и $60^{circ}$ катет, лежащий напротив угла в $30^{circ}$ , равен половине гипотенузы.

Треугольник с углами $90^{circ},, 45^{circ}$ и $45^{circ}$ — равнобедренный. В нем гипотенуза в sqrt{2} раз больше катета.

Задача 20.

В треугольнике АВС угол С равен 90 ${}^circ,$ угол А равен 30 ${}^circ,$ АВ = 2

Найдите высоту CH.

Решение:

Рассмотрим АВС:

По свойству катета, лежащего против угла ${30}^circ,$ имеем ВС = $displaystyle frac{1}{2}$ АВ =

В BHC: $angle BHC=90{}^circ ,; angle B=60{}^circ ,$ то $angle HCB=30{}^circ ,$ следовательно, ВН = $displaystyle frac{1}{2}$ BC = $displaystyle frac{sqrt{3}}{2}.$

По теореме Пифагора найдем НС:

$HC = sqrt{{BC}^2-{BH}^2}=sqrt{{left(sqrt{3}right)}^2-{left(displaystyle frac{sqrt{3}}{2}right)}^2}=sqrt{3-displaystyle frac{3}{4}}=$

$=sqrt{2displaystyle frac{1}{4}}=sqrt{displaystyle frac{9}{4}}=displaystyle frac{3}{2}=1,5.$

Ответ: 1,5.

Задача 21.

В треугольнике АВС угол С равен 90 ${}^circ,$ CH — высота, АВ = 2, $angle A=30{}^circ .$ Найдите АH.

Решение:

Из АВС найдем ВС = $displaystyle frac{1}{2}$ АВ = 1 (по свойству катета, лежащего против угла 30 ${}^circ$ ),

$angle A=30{}^circ ,$ то $angle B=60{}^circ .$

Из ВСН: $angle BHC=90{}^circ , angle B=60{}^circ ,$ то $angle HCB=30{}^circ ,$ следовательно,

ВН = $displaystyle frac{1}{2}$ ВС = $displaystyle frac{1}{2}.$

АН = АВ — НВ = 2 — $displaystyle frac{1}{2}$ = 1,5.

Ответ: 1,5.

Еще раз повторим, что такое синус, косинус и тангенс угла в прямоугольном треугольнике.

Как запомнить эти соотношения? Лучший способ – решать много задач, и на уроках геометрии, и готовясь к ЕГЭ. Тогда все формулы, равенства, соотношения запомнятся сами собой.

Мы рассмотрели задачи на решение прямоугольных треугольников — то есть на нахождение неизвестных сторон или углов. Но это не всё! В вариантах ЕГЭ по математике множество задач, где фигурирует синус, косинус, тангенс или котангенс внешнего угла треугольника. Об этом — в следующей статье.

Если вам понравился разбор данной темы — записывайтесь на курсы подготовки к ЕГЭ по математике онлайн

Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Синус, косинус и тангенс острого угла прямоугольного треугольника» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
08.05.2023

Источник

Синус, косинус, тангенс и котангенс: определения в тригонометрии, примеры, формулы

Тригонометрия — раздел математической науки, в котором изучаются тригонометрические функции и их использование в геометрии. Развитие тригонометрии началось еще во времена античной Греции. Во времена средневековья важный вклад в развитие этой науки внесли ученые Ближнего Востока и Индии.

Данная статья посвящена базовым понятиям и дефинициям тригонометрии. В ней рассмотрены определения основных тригонометрических функций: синуса, косинуса, тангенса и котангенса. Разъяснен и проиллюстрирован их смысл в контексте геометрии.

Синус, косинус, тангенс и котангенс. Определения

Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.

Определения тригонометрических функций

Синус угла ( sin α ) — отношение противолежащего этому углу катета к гипотенузе.

Косинус угла ( cos α ) — отношение прилежащего катета к гипотенузе.

Тангенс угла ( t g α ) — отношение противолежащего катета к прилежащему.

Котангенс угла ( c t g α ) — отношение прилежащего катета к противолежащему.

Данные определения даны для острого угла прямоугольного треугольника!

В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.

Определения синуса, косинуса, тангенса и котангенса позволяют вычислять значения этих функций по известным длинам сторон треугольника.

Область значений синуса и косинуса: от -1 до 1. Иными словами синус и косинус принимают значения от -1 до 1. Область значений тангенса и котангенса — вся числовая прямая, то есть эти функции могут принимать любые значения.

Угол поворота

Определения, данные выше, относятся к острым углам. В тригонометрии вводится понятие угла поворота, величина которого, в отличие от острого угла, не ограничена рамками от 0 до 90 градусов.Угол поворота в градусах или радианах выражается любым действительным числом от — ∞ до + ∞ .

В данном контексте можно дать определение синуса, косинуса, тангенса и котангенса угла произвольной величины. Представим единичную окружность с центром в начале декартовой системы координат.

Начальная точка A с координатами ( 1 , 0 ) поворачивается вокруг центра единичной окружности на некоторый угол α и переходит в точку A 1 . Определение дается через координаты точки A 1 ( x , y ).

Синус (sin) угла поворота

Синус угла поворота α — это ордината точки A 1 ( x , y ). sin α = y

Косинус угла поворота α — это абсцисса точки A 1 ( x , y ). cos α = х

Тангенс угла поворота α — это отношение ординаты точки A 1 ( x , y ) к ее абсциссе. t g α = y x

Котангенс угла поворота α — это отношение абсциссы точки A 1 ( x , y ) к ее ординате. c t g α = x y

Синус и косинус определены для любого угла поворота. Это логично, ведь абсциссу и ординату точки после поворота можно определить при любом угле. Иначе обстоит дело с тангенсом и котангенсом. Тангенс не определен, когда точка после поворота переходит в точку с нулевой абсциссой ( 0 , 1 ) и ( 0 , — 1 ). В таких случаях выражение для тангенса t g α = y x просто не имеет смысла, так как в нем присутствует деление на ноль. Аналогично ситуация с котангенсом. Отличием состоит в том, что котангенс не определен в тех случаях, когда в ноль обращается ордината точки.

Синус и косинус определены для любых углов α .

Тангенс определен для всех углов, кроме α = 90 ° + 180 ° · k , k ∈ Z ( α = π 2 + π · k , k ∈ Z )

Котангенс определен для всех углов, кроме α = 180 ° · k , k ∈ Z ( α = π · k , k ∈ Z )

При решении практических примеров не говорят «синус угла поворота α «. Слова «угол поворота» просто опускают, подразумевая, что из контекста и так понятно, о чем идет речь.

Числа

Как быть с определением синуса, косинуса, тангенса и котангенса числа, а не угла поворота?

Синус, косинус, тангенс, котангенс числа

Синусом, косинусом, тангенсом и котангенсом числа t называется число, которое соответственно равно синусу, косинусу, тангенсу и котангенсу в t радиан.

Например, синус числа 10 π равен синусу угла поворота величиной 10 π рад.

Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Рассмотрим его подробнее.

Любому действительному числу t ставится в соответствие точка на единичной окружности с центром в начале прямоугольной декартовой системы координат. Синус, косинус, тангенс и котангенс определяются через координаты этой точки.

Начальная точка на окружности — точка A c координатами ( 1 , 0 ).

Положительному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t .

Отрицательному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t .

Теперь, когда связь числа и точки на окружности установлена, переходим к определению синуса, косинуса, тангенса и котангенса.

Синус (sin) числа t

Синус числа t — ордината точки единичной окружности, соответствующей числу t. sin t = y

Косинус числа t — абсцисса точки единичной окружности, соответствующей числу t. cos t = x

Тангенс числа t — отношение ординаты к абсциссе точки единичной окружности, соответствующей числу t. t g t = y x = sin t cos t

Последние определения находятся в соответствии и не противоречат определению, данному в начале это пункта. Точка на окружности, соответствующая числу t, совпадает с точкой, в которую переходит начальная точка после поворота на угол t радиан.

Тригонометрические функции углового и числового аргумента

Каждому значению угла α соответствует определенное значение синуса и косинуса этого угла. Также, как всем углам α , отличным от α = 90 ° + 180 ° · k , k ∈ Z ( α = π 2 + π · k , k ∈ Z ) соответствует определенное значение тангенса. Котангенс, как сказано выше, определен для всех α , кроме α = 180 ° · k , k ∈ Z ( α = π · k , k ∈ Z ).

Можно сказать, что sin α , cos α , t g α , c t g α — это функции угла альфа, или функции углового аргумента.

Аналогично можно говорить о синусе, косинусе, тангенсе и котангенсе, как о функциях числового аргумента. Каждому действительному числу t соответствует определенное значение синуса или косинуса числа t. Всем числам, отличным от π 2 + π · k , k ∈ Z соответствует значение тангенса. Котангенс, аналогично, определен для всех чисел, кроме π · k , k ∈ Z.

Основные функции тригонометрии

Синус, косинус, тангенс и котангенс — основные тригонометрические функции.

Из контекста обычно понятно, с каким аргументом тригонометрической функции (угловой аргумент или числовой аргумент) мы имеем дело.

Связь определений sin, cos, tg и ctg из геометрии и тригонометрии

Вернемся к данным в самом начале определениям и углу альфа, лежащему в пределах от 0 до 90 градусов. Тригонометрические определения синуса, косинуса, тангенса и котангенса полностью согласуются с геометрическими определениями, данными с помощью соотношений сторон прямоугольного треугольника. Покажем это.

Возьмем единичную окружность с центром в прямоугольной декартовой системе координат. Повернем начальную точку A ( 1 , 0 ) на угол величиной до 90 градусов и проведем из полученной точки A 1 ( x , y ) перпендикуляр к оси абсцисс. В полученном прямоугольном треугольнике угол A 1 O H равен углу поворота α , длина катета O H равна абсциссе точки A 1 ( x , y ) . Длина катета, противолежащего углу, равна ординате точки A 1 ( x , y ) , а длина гипотенузы равна единице, так как она является радиусом единичной окружности.

В соответствии с определением из геометрии, синус угла α равен отношению противолежащего катета к гипотенузе.

sin α = A 1 H O A 1 = y 1 = y

Значит, определение синуса острого угла в прямоугольном треугольнике через соотношение сторон эквивалентно определению синуса угла поворота α , при альфа лежащем в пределах от 0 до 90 градусов.

Аналогично соответствие определений можно показать для косинуса, тангенса и котангенса.

Синус в треугольнике

Что такое синус в треугольнике? Как найти синус острого угла в прямоугольном треугольнике?

Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.

для угла A треугольника ABC

противолежащий катет — это BC.

Соответственно, синус угла A в треугольнике ABC — это

Для угла B треугольника ABC

противолежащим является катет AC.

Соответственно, синус угла B в треугольнике ABC

равен отношению AC к AB:

Таким образом, синус острого угла в прямоугольном треугольнике — это некоторое число, получаемое в результате деления длины противолежащего катета на длину гипотенузы. Длины отрезков выражаются положительными числами, поэтому синус угла треугольника также является положительным числом.

Поскольку длина катета всегда меньше длины гипотенузы, то синус острого угла прямоугольного треугольника — число, меньшее единицы.

Синус любого острого угла прямоугольного треугольника больше нуля, но меньше единицы:

Синус угла треугольника зависит не от длин сторон треугольника, а от отношения этих длин.

1) В треугольнике ABC катет BC=3 см, а гипотенуза AB=5 см.

2) В треугольнике ABC катет BC=21 дм, гипотенуза AB=35 дм.

Длины сторон треугольника изменилось, но отношения длин остались прежними, поэтому и значение синуса угла A не изменилось.

Что такое синус, косинус, тангенс и котангенс в прямоугольном треугольнике?

Синус, косинус и тангенс острого угла прямоугольного треугольника.

Приветствую Вас дорогие учащиеся.

Сейчас рассмотрим что же такое синус, косинус, тангенс и котангенс в прямоугольном треугольнике?

Это тема не сложная, главное это запомнить правила. И так начнем:

Вспомним, что такое прямоугольный треугольник?

Прямоугольным треугольником, называется треугольник у которого один из углов прямой (составляет 90 градусов). Две стороны которые прилежат к прямому углу, называются катетами, а сторона лежащая напротив прямого угла, называется гипотенузой.

Синус (sin(a)) — это отношение противолежащего катета к гипотенузе;

Косинус (cos(a)) — это отношение прилежащего катета к гипотенузе;

Тангенс (tg(a)) — это отношение противолежащего катета к прилежащему катету;
Другое (равносильное) определение: тангенсом острого угла называется отношение синуса угла к его косинусу;

Котангенс (ctg(a)) — это отношение прилежащего катета к противолежащему.
Другое (равносильное) определение: котангенсом острого угла называется отношение косинуса угла к его синусу;

Пусть дан прямоугольный треугольник ABC с прямым углом C.

Найти sin(a); cos(a); tg(a); ctg(a) Отношение сторон в прямоугольном треугольнике

Аналогично рассуждаем относительно угла B.

Найти sin(b); cos(b); tg(b); ctg(b) Отношение сторон в прямоугольном треугольнике

Пример:

Найти тангенс угла С (tg(C)) треугольника ABC.

Хочешь готовиться к экзаменам бесплатно? Репетитор онлайн бесплатно. Без шуток. ЗДЕСЬ

источники:

Синус в треугольнике

http://tutomath.ru/uroki/sinus-kosinus-tangens.html

Источник

Что такое синус в треугольнике? Как найти синус острого угла в прямоугольном треугольнике?

Определение.

Например,

для угла A треугольника ABC

противолежащий катет — это BC.

Соответственно, синус угла A в треугольнике ABC — это

$[sin angle A = frac{{BC}}{{AB}}]$

Для угла B треугольника ABC

противолежащим является катет AC.

Соответственно, синус угла B в треугольнике ABC

равен отношению AC к AB:

$[sin angle B = frac{{AC}}{{AB}}]$

Вывод:

Синус любого острого угла прямоугольного треугольника больше нуля, но меньше единицы:

Синус угла треугольника зависит не от длин сторон треугольника, а от отношения этих длин.

Например,

1) В треугольнике ABC катет BC=3 см, а гипотенуза AB=5 см.

Тогда

$[sin angle A = frac{{BC}}{{AB}} = frac{3}{5}.]$

2) В треугольнике ABC катет BC=21 дм, гипотенуза AB=35 дм.

Тогда

$[sin angle A = frac{{BC}}{{AB}} = frac{{21}}{{35}} = frac{3}{5}.]$

Угол A в обоих треугольниках одинаков.

Источник

Я так понял, что задача сводится к тому, что нам неизвестен угол треугольника, и нам нужно его найти.

Для того чтобы найти синус угла, а затем и сам угол в произвольном треугольнике, необходимо знать длины двух сторон: стороны, противолежащей искомому углу, и какой-либо другой стороны — и ещё величину угла, противолежащего этой последней стороне.

А затем нужно применить теорему синусов.

Обозначим искомый (неизвестный) угол как A, противолежащую сторону — a, другую известную сторону — b, известный противолежащий этой стороне угол — B.

По теореме синусов: a/sin(A) = b/sin(B).

Отсюда: sin(A) = a * sin(B)/b;

A = arcsin[a * sin(B)/b].

Источник

Вспоминаем, что такое синус, косинус и тангенс в прямоугольном треугольнике.

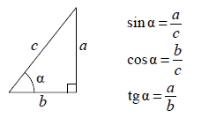
Таким образом, синус и косинус задействуют гипотенузу, а тангенс — только катеты. Синус равен отношению противолежащего катета к гипотенузе; косинус — прилежащего к гипотенузе; тангенс — противолежащего катета к прилежащему.

Если на ОГЭ вы от волнения забудете, как находить косинус, синус и тангенс, загляните в справочные материалы на ваших листах с заданиями, там будут подсказки (в разделе геометрии).

В открытом банке заданий ФИПИ есть следующие задачи на эту тему, которые могут вам попасться на реальном экзамене в этом году.

Задания из банка ФИПИ с sin, cos, tg

Найти катет по известному синусу угла и гипотенузе

В треугольнике ABC угол C равен 90°, sinB=4/15, AB=45. Найдите AC.

Решение:

По определению синуса:
sinB=^AC/_AB
AC=AB*sinB=45*4/15=12

Ответ: 12

D8213E

В треугольнике ABC угол C равен 90°, sinB=7/12, AB=48. Найдите AC.

Решение:

По определению синуса:
sinB=^AC/_AB
AC=AB*sinB=48*7/12=28

Ответ: 28

B972FB

В треугольнике ABC угол C равен 90°, sinB=4/11, AB=55. Найдите AC.

Решение:

По определению синуса:
sinB=^AC/_AB
AC=AB*sinB=55*4/11=20

Ответ: 20

E65720

В треугольнике ABC угол C равен 90°, sinB=5/17, AB=51. Найдите AC.

Решение:

По определению синуса:
sinB=^AC/_AB
AC=AB*sinB=51*5/17=15

Ответ: 15

D893F0

В треугольнике ABC угол C равен 90°, sinB=3/7, AB=21. Найдите AC.

Решение:

По определению синуса:
sinB=^AC/_AB
AC=AB*sinB=21*3/7=9

Ответ: 9

6544F6

В треугольнике ABC угол C равен 90°, sinB=4/9, AB=18. Найдите AC.

Решение:

По определению синуса:
sinB=^AC/_AB
AC=AB*sinB=18*4/9=8

Ответ: 8

F6882F

В треугольнике ABC угол C равен 90°, sinB=5/8, AB=16. Найдите AC.

Решение:

По определению синуса:
sinB=^AC/_AB
AC=AB*sinB=16*5/8=10

Ответ: 10

564758

В треугольнике ABC угол C равен 90°, sinB=3/5, AB=10. Найдите AC.

Решение:

По определению синуса:
sinB=^AC/_AB
AC=AB*sinB=10*3/5=6

Ответ: 6

50A4DC

В треугольнике ABC угол C равен 90°, sinB=5/16, AB=80. Найдите AC.

Решение:

По определению синуса:
sinB=^AC/_AB
AC=AB*sinB=80*5/16=25

Ответ: 25

3D5005

В треугольнике ABC угол C равен 90°, sinB=7/20, AB=40. Найдите AC.

Решение:

По определению синуса:
sinB=^AC/_AB
AC=AB*sinB=40*7/20=14

Ответ: 14

14A018

Найти катет по известному косинусу и гипотенузе

В треугольнике ABC угол C равен 90°, cosB=2/5, AB=10. Найдите BC.

Решение:

По определению косинуса:
cosB=^BC/_AB
BC=АВ*cosB=10*2/5=4

Ответ: 4

1B8713

В треугольнике ABC угол C равен 90°, cosB=5/6, AB=18. Найдите BC.

Решение:

По определению косинуса:
cosB=^BC/_AB
BC=АВ*cosB=18*5/6=15

Ответ: 15

481278

В треугольнике ABC угол C равен 90°, cosB=4/7, AB=21. Найдите BC.

Решение:

По определению косинуса:
cosB=^BC/_AB
BC=АВ*cosB=21*4/7=12

Ответ: 12

D4E48F

В треугольнике ABC угол C равен 90°, cosB=3/8, AB=64. Найдите BC.

Решение:

По определению косинуса:
cosB=^BC/_AB
BC=АВ*cosB=64*3/8=24

Ответ: 24

3F99AC

В треугольнике ABC угол C равен 90°, cosB=7/9, AB=54. Найдите BC.

Решение:

По определению косинуса:
cosB=^BC/_AB
BC=АВ*cosB=54*7/9=42

Ответ: 42

915280

В треугольнике ABC угол C равен 90°, cosB=9/10, AB=60. Найдите BC.

Решение:

По определению косинуса:
cosB=^BC/_AB
BC=АВ*cosB=60*9/10=54

Ответ: 54

56F660

В треугольнике ABC угол C равен 90°, cosB=5/12, AB=60. Найдите BC.

Решение:

По определению косинуса:
cosB=^BC/_AB
BC=АВ*cosB=60*5/12=25

Ответ: 25

CA8E29

В треугольнике ABC угол C равен 90°, cosB=9/14, AB=42. Найдите BC.

Решение:

По определению косинуса:
cosB=^BC/_AB
BC=АВ*cosB=42*9/14=27

Ответ: 27

52D8C1

В треугольнике ABC угол C равен 90°, cosB=11/15, AB=75. Найдите BC.

Решение:

По определению косинуса:
cosB=^BC/_AB
BC=АВ*cosB=75*11/15=55

Ответ: 55

73E3A7

В треугольнике ABC угол C равен 90°, cosB=13/16, AB=96. Найдите BC.

Решение:

По определению косинуса:
cosB=^BC/_AB
BC=АВ*cosB=96*13/16=78

Ответ: 78

D8738D

Найти катет по известному катету и тангенсу

В треугольнике ABC угол C равен 90°, tgB=3/4, BC=12. Найдите AC.

Решение:

По определению тангенса:
tgB=^AC/_BC
AC=BC*tgB=12*3/4=9

Ответ: 9

08FD08

В треугольнике ABC угол C равен 90°, tgB=7/6, BC=18. Найдите AC.

Решение:

По определению тангенса:
tgB=^AC/_BC
AC=BC*tgB=18*7/6=21

Ответ: 21

1BBB13

В треугольнике ABC угол C равен 90°, tgB=9/7, BC=42. Найдите AC.

Решение:

По определению тангенса:
tgB=^AC/_BC
AC=BC*tgB=42*9/7=54

Ответ: 54

14C45C

В треугольнике ABC угол C равен 90°, tgB=8/5, BC=20. Найдите AC.

Решение:

По определению тангенса:
tgB=^AC/_BC
AC=BC*tgB=20*8/5=32

Ответ: 32

1DB806

В треугольнике ABC угол C равен 90°, tgB=11/8, BC=24. Найдите AC.

Решение:

По определению тангенса:
tgB=^AC/_BC
AC=BC*tgB=24*11/8=33

Ответ: 33

EF04D8

В треугольнике ABC угол C равен 90°, tgB=5/9, BC=27. Найдите AC.

Решение:

По определению тангенса:
tgB=^AC/_BC
AC=BC*tgB=27*5/9=15

Ответ: 15

A915AF

В треугольнике ABC угол C равен 90°, tgB=7/12, BC=48. Найдите AC.

Решение:

По определению тангенса:
tgB=^AC/_BC
AC=BC*tgB=48*7/12=28

Ответ: 28

48CB65

В треугольнике ABC угол C равен 90°, tgB=4/7, BC=35. Найдите AC.

Решение:

По определению тангенса:
tgB=^AC/_BC
AC=BC*tgB=35*4/7=20

Ответ: 20

1EB6B0

В треугольнике ABC угол C равен 90°, tgB=7/4, BC=36. Найдите AC.

Решение:

По определению тангенса:
tgB=^AC/_BC
AC=BC*tgB=36*7/4=63

Ответ: 63

93C176

В треугольнике ABC угол C равен 90°, tgB=3/5, BC=30. Найдите AC.

Решение:

По определению тангенса:
tgB=^AC/_BC
AC=BC*tgB=30*3/5=18

Ответ: 18

757BB5

Найти синус по косинусу и наоборот

В решении заданий такого типа используйте основное тригонометрическое тождество

sin²α + cos²α=1

Выражаем то, что нужно найти, и подставляем известные значения.

Синус острого угла А треугольника АВС равен $frac{sqrt{21}}5$. Найдите cosA.

Решение:

Воспользуемся основной тригонометрической формулой:
sin²A+cos²A=1
cos²A = 1 — sin²A =1 — (^√21/₅)²= 1 — ²¹/₂₅= 1 — 0,84 = 0,16
cosA = 0,4

Ответ: 0,4

99B7F9

Синус острого угла А треугольника АВС равен $frac{3sqrt{11}}{10}$. Найдите cosA.

Решение:

Воспользуемся основной тригонометрической формулой:
sin²A+cos²A=1
cos²A = 1 — sin²A =1 — (^3√11/₁₀)²= 1 — ⁹⁹/₁₀₀= 0,01
cosA = 0,1

Ответ: 0,1

E52F99

Синус острого угла А треугольника АВС равен $frac{sqrt{91}}{10}$. Найдите cosA.

Решение:

Воспользуемся основной тригонометрической формулой:
sin²A+cos²A=1
cos²A = 1 — sin²A =1 — (^√91/₁₀)²= 1 — ⁹¹/₁₀₀= 0,09
cosA = 0,3

Ответ: 0,3

5F0BC9

Синус острого угла A треугольника ABC равен $frac{2sqrt6}5$. Найдите cosA.

Решение:

Воспользуемся основной тригонометрической формулой:
sin²A+cos²A=1
cos²A = 1 — sin²A =1 — (^2√6/₅)²= 1 — ²⁴/₂₅= 1-0,96 = 0,04
cosA = 0,2

Ответ: 0,2

DF0885

Синус острого угла A треугольника ABC равен $frac{3sqrt7}8$ . Найдите cosA.

Решение:

Воспользуемся основной тригонометрической формулой:
sin²A+cos²A=1
cos²A = 1 — sin²A =1 — (^3√7/₈)²= 1 — ⁶³/₆₄= 1-0,984375 = 0,015625
cosA = 0,125

Ответ: 0,125

Обратите внимание, что корень придется извлекать самостоятельно, поскольку числа 125 (трехзначного) в таблице квадратов на экзамене не будет.

D56817

Синус острого угла A треугольника ABC равен 4/5 . Найдите cosA.

Решение:

Воспользуемся основной тригонометрической формулой:
sin²A+cos²A=1
cos²A = 1 — sin²A =1 — (⁴/₅)²= 1 — ¹⁶/₂₅= 1-0,64 = 0,36
cosA = 0,6

Ответ: 0,6

F548B1

Синус острого угла A треугольника ABC равен $frac{sqrt7}4$ . Найдите cosA.

Решение:

Воспользуемся основной тригонометрической формулой:
sin²A+cos²A=1
cos²A = 1 — sin²A =1 — (^√7/₄)²= 1 — ⁷/₁₆= 1-0,4375 = 0,5625
cosA = 0,75

Ответ: 0,75

F6FBB5

Синус острого угла A треугольника ABC равен 3/5 . Найдите cosA.

Решение:

Воспользуемся основной тригонометрической формулой:
sin²A+cos²A=1
cos²A = 1 — sin²A =1 — (³/₅)²= 1 — ⁹/₂₅= 1-0,36 = 0,64
cosA = 0,8

Ответ: 0,8

4257EE

Синус острого угла A треугольника ABC равен $frac{sqrt{19}}{10}$ . Найдите cosA.

Решение:

Воспользуемся основной тригонометрической формулой:
sin²A+cos²A=1
cos²A = 1 — sin²A =1 — (^√19/₁₀)²= 1 — ¹⁹/₁₀₀= 1-0,19 = 0,81
cosA = 0,9

Ответ: 0,9

DC7D62

Синус острого угла A треугольника ABC равен $frac{sqrt{15}}4$ . Найдите cosA.

Решение:

Воспользуемся основной тригонометрической формулой:
sin²A+cos²A=1
cos²A = 1 — sin²A =1 — (^√15/₄)²= 1 — ¹⁵/₁₆= 1-0,9375 = 0,0625
cosA = 0,25

Ответ: 0,25

11D7EC

Косинус острого угла A треугольника ABC равен $frac{sqrt{21}}5$ . Найдите sinA.

Решение:

Воспользуемся основной тригонометрической формулой:
sin²A+cos²A=1
sin²A = 1 — cos²A =1 — (^√21/₅)²= 1 — ²¹/₂₅= 1-0,84 = 0,16
sinA = 0,4

Ответ: 0,4

4BD96F

Косинус острого угла A треугольника ABC равен $frac{3sqrt{11}}{10}$ . Найдите sinA.

Решение:

Воспользуемся основной тригонометрической формулой:
sin²A+cos²A=1
sin²A = 1 — cos²A =1 — (^3√11/₁₀)²= 1 — ⁹⁹/100= 1-0,99 = 0,01
sinA = 0,1

Ответ: 0,1

EE565F

Косинус острого угла A треугольника ABC равен $frac{sqrt{91}}{10}$ . Найдите sinA.

Решение:

Воспользуемся основной тригонометрической формулой:
sin²A+cos²A=1
sin²A = 1 — cos²A =1 — (^√91/₁₀)²= 1 — ⁹¹/₁₀₀= 1-0,91 = 0,09
sinA = 0,3

Ответ: 0,3

EE4155

Косинус острого угла A треугольника ABC равен $frac{2sqrt6}5$. Найдите sinA.

Решение:

Воспользуемся основной тригонометрической формулой:
sin²A+cos²A=1
sin²A = 1 — cos²A =1 — (^2√6/₅)²= 1 — ²⁴/₂₅= 1-0,96 = 0,04
sinA = 0,2

Ответ: 0,2

2657CA

Косинус острого угла A треугольника ABC равен $frac{3sqrt7}8$. Найдите sinA.

Решение:

Воспользуемся основной тригонометрической формулой:
sin²A+cos²A=1
sin²A = 1 — cos²A =1 — (^3√7/₈)²= 1 — ⁶³/₆₄= 1-0,984375 = 0,015625
sinA = 0,125

Ответ: 0,125

Обратите внимание, что корень придется извлекать самостоятельно, поскольку числа 125 (трехзначного) в таблице квадратов на экзамене не будет.

857A3B

Косинус острого угла A треугольника ABC равен 4/5. Найдите sinA.

Решение:

Воспользуемся основной тригонометрической формулой:
sin²A+cos²A=1
sin²A = 1 — cos²A =1 — (⁴/₅)²= 1 — ¹⁶/₂₅= 1-0,64 = 0,36
sinA = 0,6

Ответ: 0,6

588CA0

Косинус острого угла A треугольника ABC равен $frac{sqrt7}4$. Найдите sinA.

Решение:

Воспользуемся основной тригонометрической формулой:
sin²A+cos²A=1
sin²A = 1 — cos²A =1 — (^√7/₄)²= 1 — ⁷/₁₆= 1-0,4375 = 0,5625
sinA = 0,75

Ответ: 0,75

5AC6CD

Косинус острого угла A треугольника ABC равен 3/5. Найдите sinA.

Решение:

Воспользуемся основной тригонометрической формулой:
sin²A+cos²A=1
sin²A = 1 — cos²A =1 — (³/₅)²= 1 — ⁹/₂₅= 1-0,36 = 0,64
sinA = 0,8

Ответ: 0,8

3B3235

Косинус острого угла A треугольника ABC равен $frac{sqrt{19}}{10}$. Найдите sinA.

Решение:

Воспользуемся основной тригонометрической формулой:
sin²A+cos²A=1
sin²A = 1 — cos²A =1 — (^√19/₁₀)²= 1 — ¹⁹/₁₀₀= 1-0,19 = 0,81
sinA = 0,9

Ответ: 0,9

4D93A9

Косинус острого угла A треугольника ABC равен $frac{sqrt{15}}4$. Найдите sinA.

Решение:

Воспользуемся основной тригонометрической формулой:
sin²A+cos²A=1
sin²A = 1 — cos²A =1 — (^√15/₄)²= 1 — ¹⁵/₁₆= 1-0,9375 = 0,0625
sinA = 0,25

Ответ: 0,25

A426BF

Найти площадь треугольника по двум сторонам и углу между ними

Вспоминаем формулу нахождения площади треугольника по двум сторонам и углу между ними:

S=¹/₂аb•sinγ, где а и b — стороны треугольника, γ — угол между ними.

Подставляем известные величины и считаем.

Формула так же есть в справочных материалах ОГЭ, на экзамене можете ими воспользоваться.

В треугольнике ABC известно, что AB=6, BC=10, sin∠ABC=1/3. Найдите площадь треугольника ABC.

Решение:

S=¹/₂аb•sinγ=6*10*1/3=20
Ответ: 20

D8DE10

В треугольнике ABC известно, что AB=6, BC=12, sin∠ABC=1/4. Найдите площадь треугольника ABC.

Решение:

S=¹/₂аb•sinγ=6*12*1/4=18
Ответ: 18

510B5D

В треугольнике ABC известно, что AB=20, BC=7, sin∠ABC=2/5. Найдите площадь треугольника ABC.

Решение:

S=¹/₂аb•sinγ=20*7*2/5=56
Ответ: 56

21430B

В треугольнике ABC известно, что AB=15, BC=8, sin∠ABC=5/6. Найдите площадь треугольника ABC.

Решение:

S=¹/₂аb•sinγ=15*8*5/6=100
Ответ: 100

770975

В треугольнике ABC известно, что AB=14, BC=5, sin∠ABC=6/7. Найдите площадь треугольника ABC.

Решение:

S=¹/₂аb•sinγ=14*5*6/7=60
Ответ: 60

845EFC

В треугольнике ABC известно, что AB=12, BC=20, sin∠ABC=5/8. Найдите площадь треугольника ABC.

Решение:

S=¹/₂аb•sinγ=12*20*5/8=150
Ответ: 150

34F484

В треугольнике ABC известно, что AB=12, BC=15, sin∠ABC=4/9. Найдите площадь треугольника ABC.

Решение:

S=¹/₂аb•sinγ=12*15*4/9=80
Ответ: 80

86F9F5

В треугольнике ABC известно, что AB=16, BC=25, sin∠ABC=3/10. Найдите площадь треугольника ABC.

Решение:

S=¹/₂аb•sinγ=16*25*3/10=120
Ответ: 120

6B1EDE

В треугольнике ABC известно, что AB=9, BC=16, sin∠ABC=7/12. Найдите площадь треугольника ABC.

Решение:

S=¹/₂аb•sinγ=9*16*7/12=84
Ответ: 84

521C5A

В треугольнике ABC известно, что AB=12, BC=10, sin∠ABC=8/15. Найдите площадь треугольника ABC.

Решение:

S=¹/₂аb•sinγ=12*10*8/15=64
Ответ: 64

3A3D0B

Найти косинус угла, если известны 3 стороны треугольника

Вспомним теорему косинусов.

Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.

а²= b²+ с²— 2bс • cosα

Нужно выразить косинус и подставить известные величины.

Эта формула так же будет у вас под рукой на экзамене в справочных материалах ОГЭ.

В треугольнике АВС известно, что AB=8, BC=10, AC=12. Найдите cos∠ABC.

Решение:

а²= b²+ с²— 2bс • cosα
2bс • cosα = b²+ с²— а²
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
cosα = (8² +10² — 12²) : 2*8*10 = 20/160 = 0,125

Ответ: 0,125

40840C

В треугольнике ABC известно, что AB=5, BC=7, AC=9. Найдите cos∠ABC.

Решение:

а²= b²+ с²— 2bс • cosα
2bс • cosα = b²+ с²— а²
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{5^2+7^2-9^2}{2ast 5ast 7}$ = -7/70 = -0,1
Ответ: -0,1

112015

В треугольнике ABC известно, что AB=3, BC=8, AC=7. Найдите cos∠ABC.

Решение:

а²= b²+ с²— 2bс • cosα
2bс • cosα = b²+ с²— а²
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{3^2+8^2-7^2}{2ast 3ast 8}$= 24/48 = 0,5
Ответ: 0,5

6E8D8A

В треугольнике ABC известно, что AB=5, BC=10, AC=11. Найдите cos∠ABC.

Решение:

а²= b²+ с²— 2bс • cosα
2bс • cosα = b²+ с²— а²
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{5^2+10^2-11^2}{2ast 5ast 10}$= 4/100 = 0,04
Ответ: 0,04

844A89

В треугольнике ABC известно, что AB=6, BC=7, AC=8. Найдите cos∠ABC.

Решение:

а²= b²+ с²— 2bс • cosα
2bс • cosα = b²+ с²— а²
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{6^2+7^2-8^2}{2ast 6ast 7}$= 21/84 = 0,25
Ответ: 0,25

79B29A

В треугольнике ABC известно, что AB=5, BC=6, AC=4. Найдите cos∠ABC.

Решение:

а²= b²+ с²— 2bс • cosα
2bс • cosα = b²+ с²— а²
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{5^2+6^2-4^2}{2ast 5ast 6}$= 45/60 = 0,75
Ответ: 0,75

6557F1

В треугольнике ABC известно, что AB=6, BC=8, AC=4. Найдите cos∠ABC.

Решение:

а²= b²+ с²— 2bс • cosα
2bс • cosα = b²+ с²— а²
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{6^2+8^2-4^2}{2ast 6ast 8}$= 84/96
Ответ: 0,875

B5CF05

В треугольнике ABC известно, что AB=7, BC=8, AC=13. Найдите cos∠ABC.

Решение:

а²= b²+ с²— 2bс • cosα
2bс • cosα = b²+ с²— а²
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{7^2+8^2-13^2}{2ast 7ast 8}$= -56/112 = -0,5
Ответ: -0,5

91941D

В треугольнике ABC известно, что AB=8, BC=10, AC=14. Найдите cos∠ABC.

Решение:

а²= b²+ с²— 2bс • cosα
2bс • cosα = b²+ с²— а²
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{8^2+10^2-14^2}{2ast 8ast 10}$= -32/160 = -0,2
Ответ: -0,2

755B8F

В треугольнике ABC известно, что AB=2, BC=3, AC=4. Найдите cos∠ABC.

Решение:

а²= b²+ с²— 2bс • cosα
2bс • cosα = b²+ с²— а²
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{2^2+3^2-4^2}{2ast 2ast 3}$= -3/12 = -0,25
Ответ: -0,25

05C64C

Найти синус по двум сторонам

Синус острого угла в прямоугольном треугольнике равен отношению противолежащего катета к гипотенузе. И тот, и другой, известны. Подставляем и считаем.

В треугольнике ABC угол C равен 90°, AC=6, AB=10. Найдите sinB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 6/10 = 0,6
Ответ: 0,6

A67245

В треугольнике ABC угол C равен 90°, AC=4, AB=5. Найдите sinB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 4/5 = 0,8
Ответ: 0,8

46D9DF

В треугольнике ABC угол C равен 90°, AC=7, AB=25. Найдите sinB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 7/25 = 0,28
Ответ: 0,28

6DA700

В треугольнике ABC угол C равен 90°, AC=24, AB=25. Найдите sinB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 24/25 = 0,96
Ответ: 0,96

C7A2A0

В треугольнике ABC угол C равен 90°, AC=6, AB=20. Найдите sinB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 6/20 = 0,3
Ответ: 0,3

ED2D47

В треугольнике ABC угол C равен 90°, AC=11, AB=20. Найдите sinB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 11/20 = 0,55
Ответ: 0,55

F1D3F8

В треугольнике ABC угол C равен 90°, AC=8, AB=40. Найдите sinB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 8/40 = 0,2
Ответ: 0,2

CDC6C7

В треугольнике ABC угол C равен 90°, AC=16, AB=40. Найдите sinB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 16/40 = 0,4
Ответ: 0,4

20BC46

В треугольнике ABC угол C равен 90°, AC=9, AB=25. Найдите sinB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 9/25 = 0,36
Ответ: 0,36

E2F916

В треугольнике ABC угол C равен 90°, AC=13, AB=20. Найдите sinB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 13/20 = 0,65
Ответ: 0,65

2C2621

Найти косинус по двум сторонам треугольника

Косинус острого угла в прямоугольном треугольнике равен отношению прилежащего катета к гипотенузе. Подставляем известные значения и считаем.

В треугольнике ABC угол C равен 90°, BC=8, AB=10. Найдите cosB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 8/10 = 0,8
Ответ: 0,8

36727A

В треугольнике ABC угол C равен 90°, BC=3, AB=5. Найдите cosB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 3/5 = 0,6
Ответ: 0,6

E4988D

В треугольнике ABC угол C равен 90°, BC=14, AB=50. Найдите cosB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 14/50 = 0,28
Ответ: 0,28

B9AA7C

В треугольнике ABC угол C равен 90°, BC=72, AB=75. Найдите cosB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 72/75 = 0,96
Ответ: 0,96

6E5515

В треугольнике ABC угол C равен 90°, BC=14, AB=20. Найдите cosB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 14/20 = 0,7
Ответ: 0,7

E812C8

В треугольнике ABC угол C равен 90°, BC=9, AB=20. Найдите cosB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 9/20 = 0,45
Ответ: 0,45

C759C5

В треугольнике ABC угол C равен 90°, BC=30, AB=40. Найдите cosB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 30/40 = 0,75
Ответ: 0,75

8854A8

В треугольнике ABC угол C равен 90°, BC=26, AB=40. Найдите cosB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 26/40 = 0,65
Ответ: 0,65

C5CD1E

В треугольнике ABC угол C равен 90°, BC=16, AB=25. Найдите cosB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 16/25 = 0,64
Ответ: 0,64

C3A5F2

В треугольнике ABC угол C равен 90°, BC=7, AB=20. Найдите cosB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 7/20 = 0,35
Ответ: 0,35

D58395

Найти тангенс угла по двум катетам

Тангенс острого угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему. Подставляем значения катетов и считаем.

В треугольнике ABC угол C равен 90°, BC=5, AC=2. Найдите tgB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 2/5 = 0,4
Ответ: 0,4

98C7DF

В треугольнике ABC угол C равен 90°, BC=5, AC=3. Найдите tgB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 3/5 = 0,6
Ответ: 0,6

22FD03

В треугольнике ABC угол C равен 90°, BC=10, AC=7. Найдите tgB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 7/10 = 0,7
Ответ: 0,7

C18053

В треугольнике ABC угол C равен 90°, BC=10, AC=8. Найдите tgB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 8/10 = 0,8
Ответ: 0,8

33DA26

В треугольнике ABC угол C равен 90°, BC=15, AC=3. Найдите tgB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 3/15 = 0,2
Ответ: 0,2

DD620C

В треугольнике ABC угол C равен 90°, BC=9, AC=27. Найдите tgB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 27/9 = 3
Ответ: 3

342F0C

В треугольнике ABC угол C равен 90°, BC=5, AC=20. Найдите tgB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 20/5 = 4
Ответ: 4

B800B8

В треугольнике ABC угол C равен 90°, BC=3, AC=18. Найдите tgB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 18/3 = 6
Ответ: 6

FF498A

В треугольнике ABC угол C равен 90°, BC=4, AC=28. Найдите tgB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 28/4 = 7
Ответ: 7

C9E181

В треугольнике ABC угол C равен 90°, BC=7, AC=35. Найдите tgB.

Решение:

∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 35/7 = 5
Ответ: 5

0663D4

Источник