Как найти синус 135 градусов формула

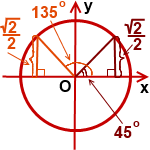
Синус 135 градусов

Синус 135 градусов найдем по формуле приведения для синуса тупого угла от 90 до 180 градусов.

Синус угла альфа на единичной окружности — это ордината точки, полученной из точки (1;0) при повороте на угол альфа вокруг точки O.

Для синуса тупого угла (от 90º до 180º) имеет место следующая формула приведения:

то воспользовавшись этой формулой приведения и значением синуса 45º, получаем:

Как найти синус и косинус углов в градусах без тригонометрической таблицы?

В статье мы расскажем, как находить значения:

и других тригонометрических выражений без тригонометрической таблицы .

Как вычисляются синусы и косинусы углов?

Чтобы вычислить косинус и синус некоторого угла нужно:
1. Отложить этот угол на тригонометрическом круге и определить какая точка соответствует этому углу;
2. Найти абсциссу и ординату этой точки. Косинус угла равен — абсциссе, а синус угла — ординате.

Предположим, стоит задача найти косинус и синус угла (30^°). Отложим на круге угол в (30^°) и найдем какая точка соответствует этому углу.

Если построить все точно, то видно, что абсцисса точки равна (0,866)… , что равно числу (frac<sqrt<3>><2>) , а ордината равна (0,5), то есть (frac<1><2>).

Аналогично и для любой другой точки на круге: значение абсциссы равно косинусу угла, а ординаты – синусу угла. Поэтому:

В тригонометрии ось абсцисс (ось x) часто называют «ось косинусов», а ординат (ось y) – «ось синусов».

Обычно на осях не отмечают (0,1); (0,2); (0,3) и т.д., а сразу наносят стандартные значения для синуса и косинуса: (±frac<1><2>=±0,5); (±frac<sqrt<2>> <2>≈±0,707); (±frac<sqrt<3>> <2>≈±0,866).

Первый шаг к тому, чтобы находить синусы и косинусы стандартных углов – научится отмечать эти углы на тригонометрическом круге.

Как отметить любой угол на тригонометрическом круге?

Чтоб отложить положительный угол нужно двигаться против часовой стрелки от начала отсчета, чтобы отметить отрицательный – по часовой стрелке;

Градусная мера окружности равна (360^°), полуокружности (180^°), а четверти (90^°);

Углы в (0^°), (30^°), (45^°) и (60^°) выглядят так:

• Одна точка может соответствовать разным углам;
• Угол может быть больше (360^°). В этом случае он просто сделает полный оборот и пойдет дальше. Фактически, можно (360^°) просто отбросить и откладывать тот угол, который останется – в итоге вы всё равно окажетесь в той же точке.

Задание 1 . Отметьте на окружности точки соответствующие углам: (720^°), (225^°), (300^°), (870^°), (900^°), (-330^°), (-630^°), (-210^°).

Как находить синус и косинус любого угла?

1. Начертите тригонометрический круг и оси косинусов и синусов (не обязательно рисовать прям аккуратно, как на картинке ниже, можно и некрасиво – главное не запутаться какая точка к какому значению относится).
2. Отложите на круге угол, синус и косинус которого надо найти, и определите точку на круге, соответствующую этому углу.
3. Найдите координаты точки, используя картинку ниже.

(-540^°) на тригонометрическом круге совпадает с (-1) на оси косинусов. То есть, координаты этой точки: ((-1;0)). Значит, (cos⁡(-540^°)=-1), а (sin⁡(-540^° )=0).

Да, имея перед глазами тригонометрический круг, вычислять синусы и косинусы любых углов легко. Возможно, у вас возник вопрос: «а что делать, если круга нет? Как делать такие вычисления на ЕГЭ?». Ответ очевиден – нарисовать круг самому! Для этого надо понять, как располагаются значения на нем. Подробную методику того, как это делается я рассказывала в этой статье .

Есть и другой способ запомнить тригонометрический круг – внимательно посмотреть на картинку ниже и запомнить максимальное количество элементов. После прикройте страницу и по памяти нарисуйте круг и отметьте всё, что смогли запомнить. Сверьте, что у вас получилось с тем, что было на картинке. Повторяйте эту последовательность действий пока по памяти не получится нарисовать тригонометрический круг со всеми значениями. Это займет 15 минут вашего времени, но сильно поможет в 13 задаче ЕГЭ (и не только в ней).

Примеры вычисления синуса и косинуса из ЕГЭ

В двух следующих примерах я специально рисовала круг от руки, чтобы вы увидели, как выглядят реальные решения.

Пример . Найдите значение выражения (54sqrt<3>cos⁡(510^°)).
Решение. (510^°=360^°+150^°=360^°+180^°-30^°.)

Тригонометрические функции на единичной окружности. Тангенс и котангенс

Тригонометрический круг

Углы в радианах

Для математических вычислений тригонометрических функций используются углы не в градусах, а в радианах. Что такое радиан? Угол в радианах равен отношению длины дуги окружности к радиусу. Полный круг в 360° соответствует длине окружности 2 π r. Следовательно 360° в радианах равно 2 π , а 180° равно π радиан.

Как преобразовывать градусы в радианы? Нужно значение в градусах разделить на 180° и умножить на π .

Например, для угла 90° будет 90°180°· π = 12π

Чтобы закрепить свои знания и проверить себя, воспользуйтесь онлайн-тренажером для запоминания значений тригонометрических функций.

Видео

Что такое синус, косинус, тангенс, котангенс в прямоугольном треугольнике

Прямоугольный вид треугольника — это тот, у которого один из углов равен 90°. Он образован катетами и гипотенузой со всеми значениями тригонометрии. Катеты две стороны треугольника, которые прилегают к углу 90°, а третья гипотенуза, она всегда длиннее катетов.

Синусом называется отношение одного из катетов к гипотенузе, косинусом отношение другого катета к ней, а тангенсом отношение двух катетов. Отношение символизирует деление. Также тангенсом является деление острого угла на синус с косинусом. Котангенсом является противоположное тангенсу отношение.

Формулы последних двух отношений выглядят следующим образом: tg(a) = sin(a) / cos(a) и ctg(a) = cos(a) / sin(a).

Тангенс угла

Синус и косинус являются основными, или, как говорят математики, прямыми тригонометрическими ф-циями. Однако есть ещё две производных тригонометрических ф-ций – тангенс и котангенс. Напомним, что тангенс угла в прямоугольном треугол-ке – это отношение противолежащего катета к прилежащему. Однако в тригонометрии куда удобнее пользоваться другим его определением. Тангенс – это отношение синуса угла к его косинусу:

Для получения тангенса на единичной окружности необходимо продолжить прямую, образующую угол α, до её пересечения с прямой х = 1. Точка их пересечения будет иметь координаты (1; tgα):

Заметим, что если α относится ко второй четверти, то тангенс получится отрицательным. Действительно, с одной стороны, соответствующая прямая пересечет линию х = 1 в точке, лежащей ниже оси Ох:

С другой стороны, мы знаем, что во второй четверти синус положителен, а косинус – отрицателен. Тогда их отношение, то есть тангенс, должно быть отрицательным:

Очевидно, что тангенс должен быть периодической ф-цией. Однако его период вдвое меньше 2π и составляет π. Действительно, углы, отличающиеся на π, будут иметь одинаковое значение тангенса, что видно из построения:

Это значит, что справедлива формула:

С другой стороны, это означает, что тангенсы углов из III четверти положительны, ведь они равны тангенсам углов из I четверти. Аналогично можно утверждать, что тангенсы углов из IV четверти отрицательны:

Также тангенс является нечетной ф-цией. Чтобы убедиться в этом, найдем с помощью единичной окружности tgα и tg (– α):

Из построения видно, что tg (– α) = tgα, поэтому тангенс попадает под определение нечетной ф-ции.

Доказать этот факт можно и иначе. Вспомним, что синус – это нечетная ф-ция, а косинус – четная. Тогда, используя определение тангенса, можно записать:

Для вычисления тангенса проще всего использовать его определение. Мы знаем синусы и косинусы стандартных углов, а потому, деля их друг на друга, сможем найти и тангенсы стандартных углов:

Ещё раз отметим, что важнее всего запомнить значения синусов и косинусов стандартных углов. Зная их, школьник всегда сможет самостоятельно вычислить тангенс.

Можно ли вычислить тангенс для угла π/2, то есть для 90°? Сделать это не получится, ведь cosπ/2 равен нулю. Если подставить cosπ/2 в формулу для вычисления тангенса, то получится деление на ноль! Так как тангенс – периодическая ф-ция, то его нельзя вычислить и в тех точках, которые отличаются от π/2 на целое число π.

В частности, тангенс не определен при х = – π/2.

Определение знака синуса, косинуса, тангенса и котангенса

Вообще, этот вопрос заслуживает особого внимания, но здесь все просто: у угла ( displaystyle 30) градусов и синус и косинус положительны (смотри рисунок), тогда берем знак «плюс».

( displaystyle cos 30<>^circ =frac<sqrt<3>><2>)Теперь попробуй на основе вышеизложенного найти синус и косинус углов: ( displaystyle 60<>^circ ) и ( displaystyle 45<>^circ )

Можно схитрить: в частности для угла в ( displaystyle 60<>^circ ) градусов. Так как если один угол прямоугольного треугольника равен ( displaystyle 60<>^circ ) градусам, то второй – ( displaystyle 30<>^circ ) градусам. Теперь вступают в силу знакомые тебе формулы:( displaystyle sin 30<>^circ =cos 60<>^circ )( displaystyle sin 60<>^circ =cos 30<>^circ )Тогда так как ( displaystyle sin 30<>^circ =0,5), то и ( displaystyle cos 60<>^circ =0,5). Так как ( displaystyle cos 30<>^circ =frac<sqrt<3>><2>), то и ( displaystyle sin 60<>^circ =frac<sqrt<3>><2>).

C ( displaystyle 45) градусами все еще проще: так если один из углов прямоугольного треугольника равен ( displaystyle 45) градусам, то и другой тоже равен ( displaystyle 45) градусам, а значит такой треугольник равнобедренный.

Значит, его катеты равны. А значит равны его синус и косинус.

Тогда:( displaystyle si<^<2>>45<>^circ +co<^<2>>45<>^circ =2si<^<2>>45<>^circ =1)( displaystyle si<^<2>>45<>^circ =co<^<2>>45<>^circ =1/2)Откуда: ( displaystyle sin 45<>^circ =cos 45<>^circ =sqrt<1/2>=frac<sqrt<2>><2>)

Теперь найди сам по новому определению (через икс и игрек!) синус и косинус углов в ( displaystyle 0) градусов и ( displaystyle 90) градусов. Здесь уже никакие треугольники нарисовать не получится! Уж слишком они будут плоские!

У тебя должно было получиться:

( displaystyle sin 0<>^circ =0), ( displaystyle cos 0<>^circ =1), ( displaystyle sin 90<>^circ =1), ( displaystyle cos 90<>^circ =0).Тангенс и котангенс ты можешь отыскать самостоятельно по формулам:

( displaystyle textg alpha =frac<sin alpha ><cos alpha >), ( displaystyle ctg alpha =frac)Обрати внимание, что на ноль делить нельзя!!

Теперь все полученные числа можно свести в таблицу:

Здесь приведены значения синуса, косинуса, тангенса и котангенса углов I четверти.

Для удобства углы приведены как в градусах, так и в радианах (но ты-то теперь знаешь связь между ними!). Обрати внимание на 2 прочерка в таблице: а именно у котангенса нуля и тангенса ( displaystyle 90) градусов. Это неспроста!

( displaystyle ctg 0=frac<cos 0><sin 0>=frac<1><0>=. )Поэтому мы с тобой будем считать, что тангенс ( displaystyle 90) градусов и котангенс нуля просто-напросто не определены!

Теперь давай обобщим понятие синус и косинус на совсем произвольный угол. Я рассмотрю здесь два случая:

• Угол лежит в пределах от ( displaystyle 0) до ( displaystyle 360) градусов;
• Угол больше ( displaystyle 360) градусов.

Честно говоря, я скривил немного душой, говоря про «совсем все» углы. Они бывают также и отрицательными! Но этот случай мы с тобой рассмотрим чуть позже. Вначале остановимся на первом случае.

Если угол лежит в 1 четверти – то тут все понятно, мы этот случай уже рассмотрели и даже таблицы нарисовали.

Теперь же пусть наш угол больше ( displaystyle 90) градусов и не больше чем ( displaystyle 360).

Это значит, что он расположен либо во 2, либо в 3 или же в 4 четверти.

Как мы поступаем? Да точно так же!

Давай рассмотрим вместо вот такого случая…

…вот такой:

То есть рассмотрим угол ( displaystyle alpha ), лежащий во второй четверти. Что мы можем сказать про него?

У точки ( displaystyle <_<1>>), которая является точкой пересечения луча и окружности по-прежнему имеет 2 координаты (ничего сверхъестественного, правда?). Это координаты ( displaystyle <_<1>>) и ( displaystyle <_<1>>).

Причем первая координата отрицательная, а вторая – положительная! Это значит, что у углов второй четверти косинус отрицателен, а синус – положителен!

Удивительно, правда? До этого мы еще ни разу не сталкивались с отрицательным косинусом.

Да и в принципе этого не могло быть, когда мы рассматривали тригонометрические функции как отношения сторон треугольника.

Кстати, подумай, у каких углов косинус равен ( displaystyle -1)? А у каких ( displaystyle -1) равен синус?

Аналогично можно рассмотреть углы во всех остальных четвертях. Я лишь напомню, что угол отсчитывается против часовой стрелки! (так, как это показано на последнем рисунке!).

Конечно, можно и отсчитывать в другую сторону, но вот подход к таким углам будет уже несколько другой.

Исходя из приведенных выше рассуждений, можно расставить знаки у синуса, косинуса, тангенса (как синус деленный на косинус) и котангенса (как косинус деленный на синус) для всех четырех четвертей.

Но еще раз повторюсь, нет смысла запоминать этот рисунок. Все, что тебе нужно знать:

Синус – это игрек. Косинус – это икс. Тангенс – это синус деленный на косинус. Котангенс – это косинус деленный на синус.

Тригонометрические функции углового и числового аргумента

Каждому значению угла α соответствует определенное значение синуса и косинуса этого угла. Также, как всем углам α , отличным от α = 90 ° + 180 ° · k , k ∈ Z ( α = π 2 + π · k , k ∈ Z ) соответствует определенное значение тангенса. Котангенс, как сказано выше, определен для всех α , кроме α = 180 ° · k , k ∈ Z ( α = π · k , k ∈ Z ).

Можно сказать, что sin α , cos α , t g α , c t g α — это функции угла альфа, или функции углового аргумента.

Аналогично можно говорить о синусе, косинусе, тангенсе и котангенсе, как о функциях числового аргумента. Каждому действительному числу t соответствует определенное значение синуса или косинуса числа t. Всем числам, отличным от π 2 + π · k , k ∈ Z соответствует значение тангенса. Котангенс, аналогично, определен для всех чисел, кроме π · k , k ∈ Z.

Основные функции тригонометрии

Синус, косинус, тангенс и котангенс — основные тригонометрические функции.

Из контекста обычно понятно, с каким аргументом тригонометрической функции (угловой аргумент или числовой аргумент) мы имеем дело.

Два случая, когда тригонометрическая окружность может пригодиться для решения уравнений

• В ответе у нас не получается «красивый» угол, но тем не менее надо производить отбор корней
• В ответе получается уж слишком много серий корней

Никаких специфических знаний тебе не требуется, кроме знания темы: «Тригонометрические уравнения»

Тему «тригонометрические уравнения» я старался писать, не прибегая к окружности. Многие бы меня за такой подход не похвалили.

Но мне милее формулы, уж что тут поделать. Однако в некоторых случаях формул оказывается мало. Например здесь:

Решите уравнение: ( displaystyle 8co<^<4>>x-10co<^<2>>x+3=0)

Решение:

Ну что же. Решить само уравнение несложно.

Замена ( displaystyle t=co<^<2>>x).

( displaystyle cosx=frac<sqrt<3>><2>) или ( displaystyle cosx=-frac<sqrt<3>><2>)

Отсюда наше исходное уравнение равносильно аж четырем простейшим уравнениям!

Неужели нам нужно будет записывать 4 серии корней?!

источники:

http://cos-cos.ru/ege/zadacha209/357/

http://naiti-ludei.ru/posts/trigonometricheskie-funkcii-na-edinichnoy-okruzhnosti-tangens-i-kotangens/

Один из способов вычисления синуса 135 градусов без технических средств на подобие калькулятора — это использование тригонометрических формул.
К примеру, аргумент 135 градусов можно разложить как сумму 90 и 45 градусов или разность 180 и 45 градусов. Эти значения являются табличными, поэтому можно использовать формулу синуса суммы или разности, а затем вычислить синус 135 градусов при помощи таблицы значений тригонометрических функций, применяя простые арифметические действия.
Начнем с разложения синуса 135 градусов на разность двух аргументов:

   

Используем формулу синуса от разности двух аргументов:

   

Полученные тригонометрические функции можно узнать из таблицы значений синусов и косинусов от 180 и 45 градусов. Подставив эти значения, получим:

   

Можно вычислить приближенное значение получившейся дроби:

   

Также некоторые таблицы значений тригонометрических функций содержат и значения от таких углов, как 135, 225, 315 и т.д. градусов. Поэтому можно использовать сразу их.
Есть еще один способ, который не требует применения формул. Заключается он в использовании таблиц Брадиса.
По таблицам Брадиса для синуса значение синуса 135 градусов равно 0,7071, что соответствует полученному приближенному значению, которое вычислили аналитическим путем.

Вася Иванов

Мореплаватель — имя существительное, употребляется в мужском роде. К нему может быть несколько синонимов.
1. Моряк. Старый моряк смотрел вдаль, думая о предстоящем опасном путешествии;
2. Аргонавт. На аргонавте были старые потертые штаны, а его рубашка пропиталась запахом моря и соли;
3. Мореход. Опытный мореход знал, что на этом месте погибло уже много кораблей, ведь под водой скрывались острые скалы;
4. Морской волк. Старый морской волк был рад, ведь ему предстояло отчалить в долгое плавание.