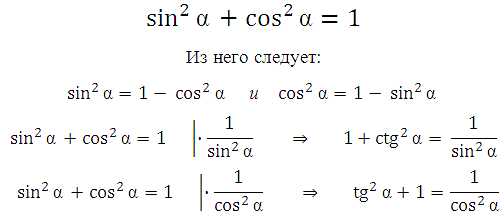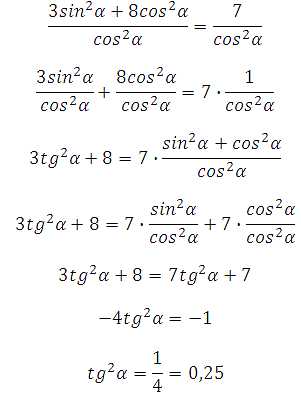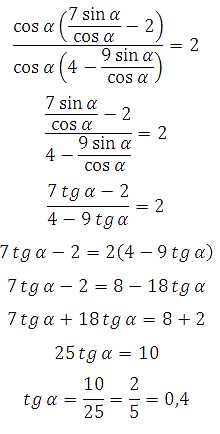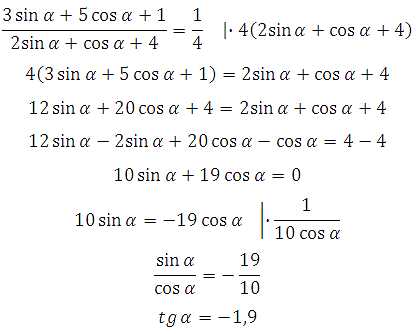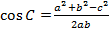Теорема синусов
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Доказательство теоремы синусов
Теорема синусов звучит так: стороны треугольника пропорциональны синусам противолежащих углов.
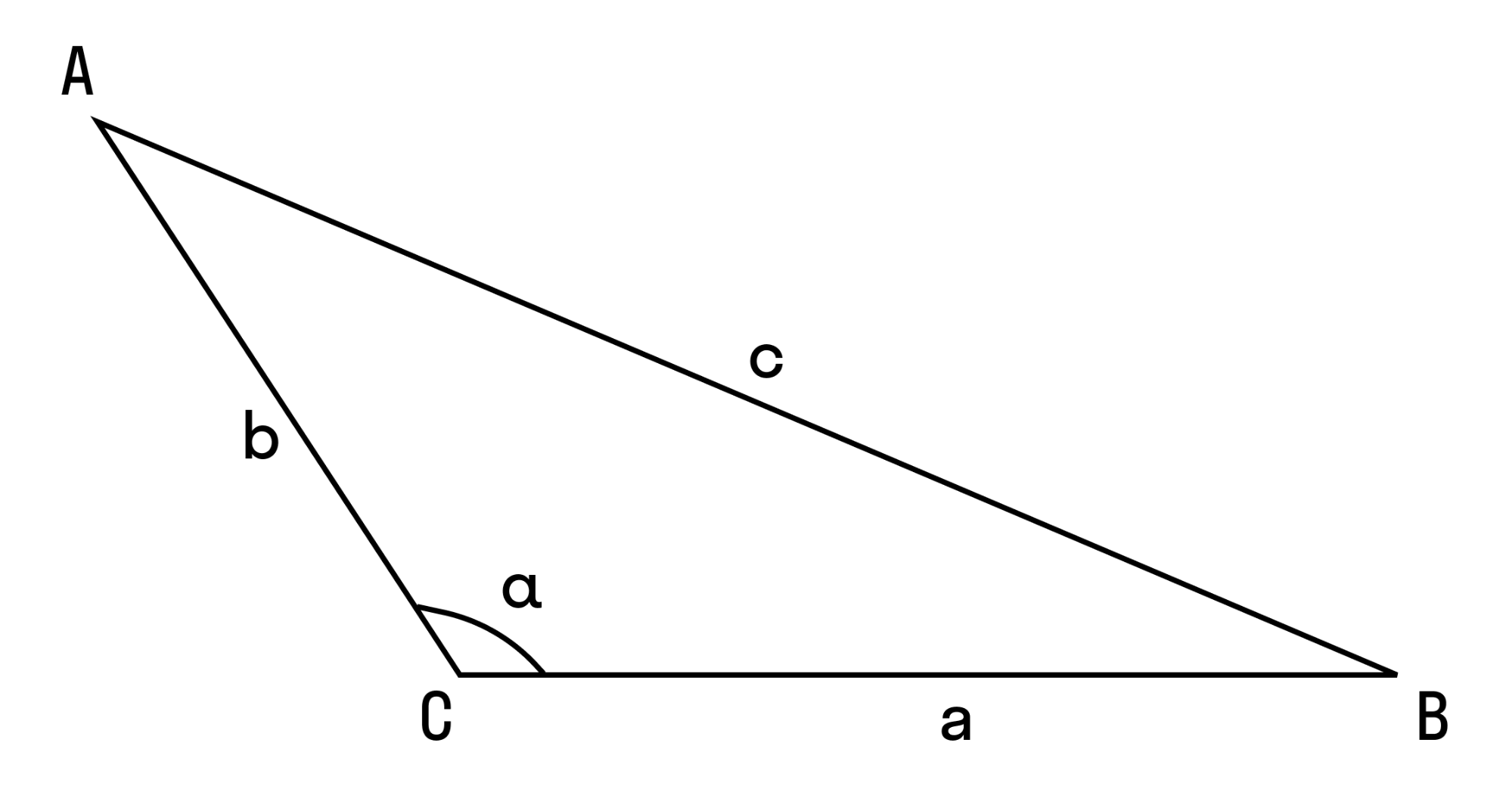
Нарисуем стандартный треугольник и запишем теорему формулой:
Формула теоремы синусов:
Докажем теорему с помощью формулы площади треугольника через синус его угла.
Из этой формулы мы получаем два соотношения:
На b сокращаем, синусы переносим в знаменатели:
bc sinα = ca sinβ
Из этих двух соотношений получаем:
Теорема синусов для треугольника доказана.
Эта теорема пригодится, чтобы найти:
- Стороны треугольника, если даны два угла и одна сторона.
- Углы треугольника, если даны две стороны и один прилежащий угол.
Доказательство следствия из теоремы синусов
У теоремы синусов есть важное следствие. Нарисуем треугольник, опишем вокруг него окружность и рассмотрим следствие через радиус.
где R — радиус описанной около треугольника окружности.
Так образовались три формулы радиуса описанной окружности:
Основной смысл следствия из теоремы синусов заключен в этой формуле:
Радиус описанной окружности не зависит от углов α, β, γ. Удвоенный радиус описанной окружности равен отношению стороны треугольника к синусу противолежащего угла.
Для доказательства следствия теоремы синусов рассмотрим три случая.
1. Угол ∠А = α — острый в треугольнике АВС.
Проведем диаметр BA1. В этом случае точка А и точка А1 лежат в одной полуплоскости от прямой ВС.
Используем теорему о вписанном угле и видим, что ∠А = ∠А1 = α. Треугольник BA1C — прямоугольный, в нём ∠ BCA1 = 90°, так как он опирается на диаметр BA1.
Чтобы найти катет a в треугольнике BA1C, нужно умножить гипотенузу BA1 на синус противолежащего угла.
BA1 = 2R, где R — радиус окружности
Следовательно: R = α/2 sinα
Для острого треугольника с описанной окружностью теорема доказана.
2. Угол ∠А = α — тупой в треугольнике АВС.
Проведем диаметр окружности BA1. Точки А и A1 по разные стороны от прямой ВС. Четырёхугольник ACA1B вписан в окружность, и его основное свойство в том, что сумма противолежащих углов равна 180°.
Следовательно, ∠А1 = 180° — α.
Вспомним свойство вписанного в окружность четырёхугольника:
Также известно, что sin(180° — α) = sinα.
В треугольнике BCA1 угол при вершине С равен 90°, потому что он опирается на диаметр. Следовательно, катет а мы находим таким образом:
α = 2R sin (180° — α) = 2R sinα
Следовательно: R = α/2 sinα
Для тупого треугольника с описанной окружностью теорема доказана.
Часто используемые тупые углы:
- sin120° = sin(180° — 60°) = sin60° = 3/√2;
- sin150° = sin(180° — 30°) = sin30° = 1/2;
- sin135° = sin(180° — 45°) = sin45° = 2/√2.
3. Угол ∠А = 90°.
В прямоугольнике АВС угол А прямой, а противоположная сторона BC = α = 2R, где R — это радиус описанной окружности.
Для прямоугольного треугольника с описанной окружностью теорема доказана.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.
Теорема о вписанном в окружность угле
Из теоремы синусов и ее следствия можно сделать любопытный вывод: если известна одна сторона треугольника и синус противолежащего угла — можно найти и радиус описанной окружности. Но треугольник не задаётся только этими величинами. Это значит, что если треугольник еще не задан, найти радиус описанной окружности возможно.
Раскроем эту тему на примере теоремы о вписанном в окружность угле и следствиях из нее.
Теорема о вписанном угле: вписанный в окружность угол измеряется половиной дуги, на которую он опирается.
∠А = α опирается на дугу ВС. Дуга ВС содержит столько же градусов, сколько ее центральный угол ∠BOC.
Формула теоремы о вписанном угле:
Следствие 1 из теоремы о вписанном в окружность угле
Вписанные углы, опирающиеся на одну дугу, равны.
∠А = ∠BAC опирается на дугу ВС. Поэтому ∠A = 1/2(∠COB).
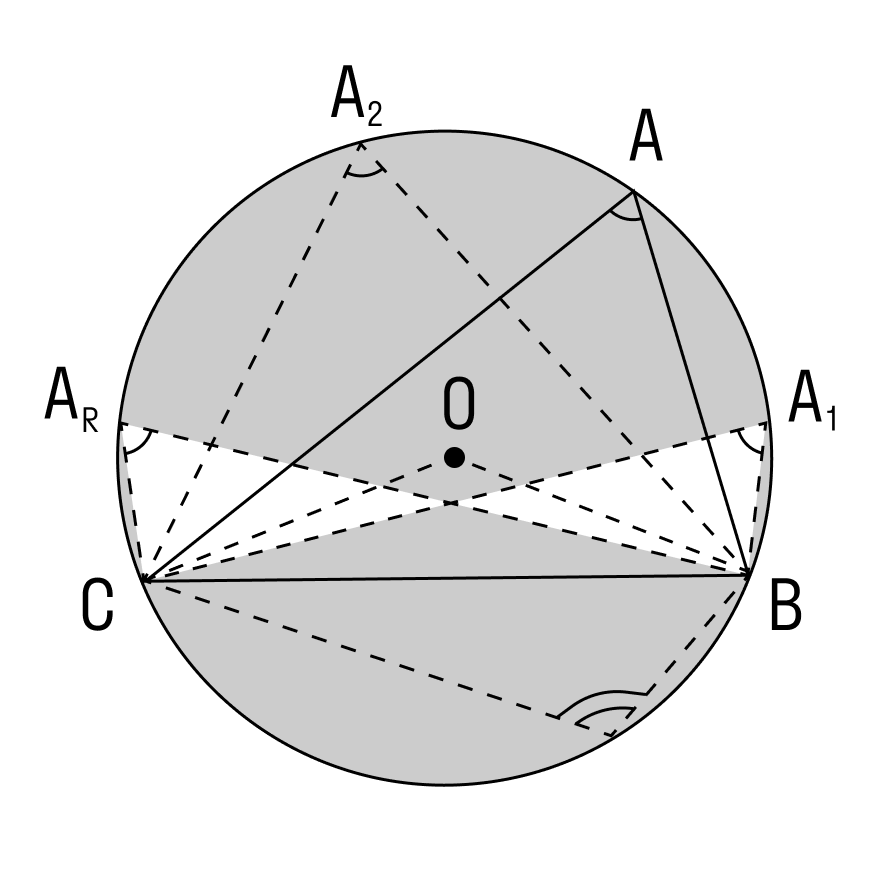
Если мы возьмём точки A1, А2. Аn и проведём от них лучи, которые опираются на одну и ту же дугу, то получим:
На рисунке изображено множество треугольников, у которых есть общая сторона СВ и одинаковый противолежащий угол. Треугольники являются подобными, и их объединяет одинаковый радиус описанной окружности.
Следствие 2 из теоремы о вписанном в окружность угле
Вписанные углы, которые опираются на диаметр, равны 90°, то есть прямые.
ВС — диаметр описанной окружности, следовательно ∠COB = 180°.
Следствие 3 из теоремы о вписанном в окружность угле
Сумма противоположных углов вписанного в окружность четырёхугольника равна 180°. Это значит, что:
Угол ∠А = α опирается на дугу DCB. Поэтому DCB = 2α по теореме о вписанном угле.
Угол ∠С = γ опирается на дугу DAB. Поэтому DAB = 2γ.
Но так как 2α и 2γ — это вся окружность, то 2α + 2γ = 360°.
Следовательно: α + γ = 180°.
Поэтому: ∠A + ∠C = 180°.
Следствие 4 из теоремы о вписанном в окружность угле
Синусы противоположных углов вписанного четырехугольника равны. То есть:
sinγ = sin(180° — α)
Так как sin(180° — α) = sinα, то sinγ = sin(180° — α) = sinα
Примеры решения задач
Теорема синусов и следствия из неё активно используются при решении задач. Рассмотрим несколько примеров, чтобы закрепить материал.
Пример 1. В треугольнике ABC ∠A = 45°,∠C = 15°, BC = 4√6. Найти AC.
-
Согласно теореме о сумме углов треугольника:
∠B = 180° — 45° — 15° = 120°
Пример 2. Гипотенуза и один из катетов прямоугольного треугольника равны 10 и 8 см. Найти угол, который расположен напротив данного катета.
В этой статье мы узнали, что в прямоугольном треугольнике напротив гипотенузы располагается угол, равный 90°. Примем неизвестный угол за x. Тогда соотношение сторон выглядит так:
Значит x = sin (4/5) ≈ 53,1°.
Ответ: угол составляет примерно 53,1°.
Запоминаем
Обычная теорема: стороны треугольника пропорциональны синусам противолежащих углов.
>
Расширенная теорема: в произвольном треугольнике справедливо следующее соотношение:
Теорема синусов. Доказательство
Теорема 1 (теорема синусов). Стороны треугольника пропорциональны синусам противолежащих углов:
Доказательство. Пусть задан треугольник ABC. Проведем высоту hb из вершины B на сторону b (Рис.1).
Из определения синуса (см. страницу Синус и косинус. Онлайн калькулятор) следует, что синус угла α равен hb если предполагать, что c=1. Но поскольку c может иметь любое значение, то имеем
Аналогично можем записать:
Далее, для высоты hc, опущенной из вершины C на сторону c, имеем:
Из (1) и (2) получим:
Теорема 2 (расширенная теорема синусов). Для произвольного треугольника справедливо следующее равенство:
где a, b, c стороны треугольника, а α, β, γ противолежащие им углы, соответственно, R− радиус описанной около треугольника окружности.
Доказательство. Пусть задан треугольник ABC и описанная окружность с радиусом R, проходящей через вершины треугольника.
В теореме 1 мы доказали справедливость равенства (a). Для доказательства (b) достаточно показать, что
Проведем через вершину C диаметр CD описанной окружности и соединим точки D и B.
1. Пусть точки D и A лежат по одну сторону от BC (Рис.2). Полученный треугольник BCD являестся прямоугольным треугольником с прямым углом B, поскольку его одна сторона совпадает с диаметром окружности. А для этого прямоугольного треугольника справедливо равенство:
Но поскольку обе эти углы опираются на дугу BC. Отсюда следует справедливость равенства (3).
2. Пусть точки D и A лежат в разные стороны от BC (Рис.3).
Поскольку BCD прямоугольный треугольник, то справедливо следующее равенство:
Покажем, что . Действительно. Так как вписанный угол измеряется половиной дуги, на которой он упирается, то имеем:
Тогда из (5) и (6) получим:
Учитывая (7), уравнение (4) можно записать так:
Но . Тогда из (8) получим равенство (3).
Примеры и решения
Задание 1. В треугольнике ABC a=8, c=10, угол α=30°. Найти сторону b (Рис.4).
Решение. Из теоремы синусов, имеем:
Поскольку сумма всех углов треугольника равна 180°, то β=180°−30°−36.68°=113.32°.
Далее, из теоремы синусов:
Задание 2. В треугольнике ABC c=16, α=30°, β=45°. Найти стороны a, b (Рис.5).
Четырехугольники. Основные теоремы, формулы и свойства. Виртуальный справочник репетитра по математике
З десь ученики и репетиторы по математике и могут найти основные свойства и формулы площадей четырехугольников, изучаемых в школе по основной программе. Регулярно пользуюсь этими теоретическими сведениями на тематических и обзорных занятиях по геометрии (планиметрии), а также при подготовке к ЕГЭ по математкие. Все математические понятия и факты иллюстрированы с цветовыми выделениями главных особенностей изучаемого.
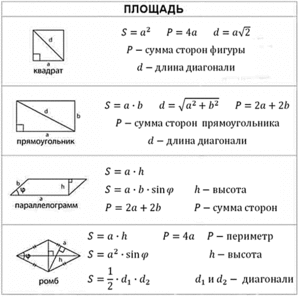
1) Площади четырехугольников
Площадь параллелограмма
произведение основания на высоту
пороизведение сторон на синус угла между ними
полупроизведение диагоналей на синус угла между ними
Площадь трапеции
произведение полусуммы оснований на высоту
произведение средней линии на высоту
полупроизведение диагоналей на синус угла между ними
Площадь произвольного четырехугольника
Площадь произвольного четырехугольника равна полупроизведению его диагоналей на синус угла между ними
2) Свойства параллелограмма
В параллелограмме:
противолежащие стороны и углы равны
диагонали пересекаются и в точке пересечения делятся пополам
3) сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон, то есть
3) Cредняя линия в трапеции
Теорема о средней линии: Средняя линия трапеции параллельна основаниям и равна их полусумме.
То есть и
4) Средняя линия в равнобедренной трапеции
Средняя линия в равнобедренной трапеции равна отрезку нижнего основания, соединяющему вершину основания с снованием проведенной к ней высоты.
То есть
5) Теорема с сдвиге диагонали в трапеции
Теорема: Если в трапеции через вершину В, как показано на рисунке слева , провести отрезок параллельный одной из диагоналей, то окажутся верными следующие факты:
трапеция — равнобедренная равнобедренный
6) Четыре замечательные точки в трапеции
Теорема: В любой трапеции точка пересечения диагоналей, точка пеерсечения продолжений боковых сторон и середины оснований лежат на одной прямой.
То есть точки M, N, K и P лежат на одной прямой
Комментарий репетитора по математкие: Знаний этих свойств по четырехугольникам вполне достаточно для решения задачи С4 на ЕГЭ, то есть ничего сверх этих фактов по четырехугольникам абитуриент знать не обязан. Однако сильным ученикам для решения сложных задач части С или олимпиадных геометрических задач, а также для качественной подготовки к экзамену по математике в МГУ необходимо расширить список. Я бы не советовал репетиторам ограничиваться только задачами на применение этих свойств, так как составителями ЕГЭ по математике закладывается проверка сразу нескольких навыков работы с теорией. В течении всего времени подготовки к ЕГЭ репетитору по математкие необходимо отбирать тренировочные задачи на одновременное использование этих свойств с другими планиметрическими фактами внутри одной задачи, ибо на экзамене может встретиться многоходовая комбинация.
Колпаков Александр Николаевич. Репетитор по математике.
Александр, конечно, есть множество карманных справочников, НО! Было бы здорово сделать для репетиторов по математике скачиваемые материалы в каком-нибудь удобном формате, а также для проработки отдельно задачи к таким шпаргалкам опять же от простого к сложному.
Я выкладывал на каких-то страницах с карточками-памятками готовые теоретические материалы — файлы в формате word, по крайней мере для планиметрии точно. Просмотрите соответствующие разделы сайта. На них ведут ссылки с главной страницы. Задумываю выделить репетиторам по математике для скачивания материалов отдельный раздел сайта. Все упирается в мою занятость реальными учениками. Иначе бы уже давно реализовал все замыслы.
В этой хорошей подборке, на мой взгляд, не достает сведений по углам, например, два внутренних угла параллелограмма, связанных одной стороной в сумме дают 180 градусов.
Принципиально ли в формуле площади через диагонали брать именно меньший угол между ними? Или можно любой?
Александр, если не затруднит, очень хотелось бы получить файлик world на почту или тыкнуть ссылкой на нее. За ранее очень благодарен за титанический труд.
http://matworld.ru/geometry/teorema-sinusov.php
http://ankolpakov.ru/2010/10/11/chetyrexugolniki-osnovnye-teoremy-formuly-i-svojstva-virtualnyj-spravochnik-repetitra-po-matematike/
Содержание материала
- Синус, косинус, тангенс и котангенс. Определения
- Видео
- Теорема косинусов
- Формула Герона
- Решение треугольников
- Пример (решение треугольника по двум сторонам и углу между ними).
- Пример (решение треугольника по стороне и двум прилежащим к ней углам).
- Пример (решение треугольника по трем сторонам).
- Пример
- Пример
- Примеры решения задач с использованием теоремы синусов и теоремы косинусов
- Пример
- Пример
- Пример
- Теорема Стюарта
- Пример
Синус, косинус, тангенс и котангенс. Определения
Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.
Синус угла (sin α) — отношение противолежащего этому углу катета к гипотенузе.
Косинус угла (cosα) — отношение прилежащего катета к гипотенузе.
Тангенс угла (tg α) — отношение противолежащего катета к прилежащему.
Котангенс угла (ctg α) — отношение прилежащего катета к противолежащему.
Данные определения даны для острого угла прямоугольного треугольника!
Приведем иллюстрацию.
В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.
Определения синуса, косинуса, тангенса и котангенса позволяют вычислять значения этих функций по известным длинам сторон треугольника.
Область значений синуса и косинуса: от -1 до 1. Иными словами синус и косинус принимают значения от -1 до 1. Область значений тангенса и котангенса — вся числовая прямая, то есть эти функции могут принимать любые значения.
Видео
Теорема косинусов
Теорема косинусов позволяет выразить длину любой стороны треугольника через длины двух других его сторон и косинус угла между ними (например, длину стороны 

Теорема косинусов. Квадрат любой стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними, т. е.
Доказательство:
Докажем теорему для случая, когда в треугольнике АВС угол А и угол С острые (рис. 166). Проведем высоту ВН к стороне АС. Из 



По основному тригонометрическому тождеству 
Справедливость теоремы для случаев, когда 







• зная две стороны и угол между ними, найти третью сторону треугольника;
• зная две стороны и угол, противолежащий одной из этих сторон, найти третью сторону (рис. 167) (в этом случае возможны два решения).
Рассмотрим следствия из теоремы косинусов, которые дают возможность решить еще целый ряд задач.
Следствие:
Теорема косинусов позволяет, зная три стороны треугольника, найти его углы (косинусы углов). Из равенства 
Для углов 
Пример:
В треугольнике АВС стороны АВ = 8, ВС = 5, АС = 7. Найдем ZB (рис. 168).
По теореме косинусов
Используя записанную выше формулу, можно сразу получить:
Следствие:
С помощью теоремы косинусов можно по трем сторонам определить вид треугольника: остроугольный, прямоугольный или тупоугольный.
Так, из формулы 

- если
то
и угол
острый;
- если
то
и угол
тупой;
- если
то
и угол
прямой.
При определении вида треугольника достаточно найти знак косинуса угла, лежащего против большей стороны, поскольку только больший угол треугольника может быть прямым или тупым.
Пример:
Выясним, каким является треугольник со сторонами a = 2, 6 = 3 и с = 4. Для этого найдем знак косинуса угла у, лежащего против большей стороны с. Так как 


Сформулируем правило определения вида треугольника (относительно углов). Треугольник является:
- остроугольным, если квадрат его большей стороны меньше суммы квадратов двух других его сторон:
- тупоугольным, если квадрат его большей стороны больше суммы квадратов двух других его сторон:
- прямоугольным, если квадрат его большей стороны равен сумме квадратов двух других его сторон:
Следствие:
Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон:
Доказательство:
Пусть в параллелограмме ABCD 






Сложив почленно равенство (1) и равенство (2), получим 
Данная формула дает возможность:
- • зная две соседние стороны и одну из диагоналей параллелограмма, найти другую диагональ;
- • зная две диагонали и одну из сторон параллелограмма, найти соседнюю с ней сторону.
Следствие:
Медиану 
Доказательство:
Рассмотрим 
Проведем отрезки BD и DC. Так как у четырехугольника ABDC диагонали AD и ВС точкой пересечения делятся пополам, то он — параллелограмм. По свойству диагоналей параллелограмма 

Аналогично:
Формула медианы позволяет:
- зная три стороны треугольника, найти любую из его медиан;
- зная две стороны и медиану, проведенную к третьей стороне, найти третью сторону;
- зная три медианы, найти любую из сторон треугольника.
Пример:
а) Дан треугольник АВС, а = 5, 5 = 3, 
Решение:
а) По теореме косинусов







Пример:
Две стороны треугольника равны 6 и 10, его площадь — 
Решение:
Пусть в 







Ответ: 14.
Пример:
Найти площадь треугольника, две стороны которого равны 6 и 8, а медиана, проведенная к третьей стороне, равна 5.
Решение:
Обозначим стороны треугольника 




Формула Герона
Мы знаем, как найти площадь треугольника по основанию и высоте, проведенной к этому основанию: 

Теорема (формула Герона).
Площадь треугольника со сторонами 


Доказательство:






Тогда
Так как

Решение треугольников
Решением треугольника называется нахождение его неизвестных сторон и углов (иногда других элементов) по данным, определяющим треугольник.
Такая задача часто встречается на практике, например в геодезии, астрономии, строительстве, навигации.
Рассмотрим алгоритмы решения трех задач.
Пример (решение треугольника по двум сторонам и углу между ними)
Дано: 
Найти : 
Решение:
Рис. 184 1) По теореме косинусов
2) По следствию из теоремы косинусов
3) Угол 
4) Угол 



Пример (решение треугольника по стороне и двум прилежащим к ней углам)
Дано: 
Найти:
Решение:
1) Угол
2) По теореме синусов 


3) Сторону с можно найти с помощью теоремы косинусов или теоремы синусов: 



Пример (решение треугольника по трем сторонам)
Дано: 
Найти: 
Решение:
1) По следствию из теоремы косинусов
2) Зная 

3) Аналогично находим угол
4) Угол
5) Радиус R описанной окружности треугольника можно найти по формуле 

Замечание*. Вторым способом нахождения R будет нахождение косинуса любого угла при помощи теоремы косинусов 


Пример
Найти площадь S и радиус R описанной окружности треугольника со сторонами 9, 12 и 15.
Решение:
Способ 1. Воспользуемся формулой Герона. Обозначим а = 9, b = 12, с = 15. Получим:









Пример
Найти площадь трапеции с основаниями, равными 5 и 14, и боковыми сторонами, равными 10 и 17.
Решение:
Пусть в трапеции ABCD основания AD = 14 и ВС = 5, боковые стороны АВ = 10 и 



Ответ: 76.
Примеры решения задач с использованием теоремы синусов и теоремы косинусов
Пример:
Внутри угла А, равного 60°, взята точка М, которая находится на расстоянии 1 от одной стороны угла и на расстоянии 2 от другой стороны. Найти расстояние от точки М до вершины угла А (рис. 189, а).
Решение:
Пусть 







Ответ: 
Пример
В прямоугольном треугольнике АВС известно: 
Решение:
Построим 







Пример
Дан прямоугольный треугольник АВС с катетами ВС = а и АС = 
Решение:
Способ 1. Так как 


Пусть СО = х. По теореме косинусов из 
из 
По свойству вписанного четырехугольника 




Способ 2. Используем теорему Птолемея, которая гласит: «Произведение диагоналей вписанного четырехугольника равно сумме произведений его противоположных сторон». Для нашей задачи получаем (см. рис. 191):
Способ 3. Достроим 


Пример
Точка О — центр окружности, вписанной в треугольник АВС, 
Решение:
Пусть 

Отсюда 
С другой стороны, 





Теорема Стюарта
Следующая теорема позволяет найти длину отрезка, соединяющего вершину треугольника с точкой на противоположной стороне.
Теорема Стюарта. «Если а, b и с — стороны треугольника и отрезок d делит сторону с на отрезки, равные х и у (рис. 194), то справедлива формула
Доказательство:
По теореме косинусов из 



Умножим обе части равенства (1) на у, равенства (2) — на 
Сложим почленно полученные равенства: 


Следствие:
Биссектрису треугольника можно найти по формуле (рис. 195)
Доказательство:
По свойству биссектрисы треугольника 



Пример
Доказать, что если в треугольнике две биссектрисы равны, то треугольник — равнобедренный (теорема Штейнера—Лемуса).
Доказательство:
Пусть дан треугольник АВС, 






По формуле биссектрисы треугольника
Из условия 




Теги
Теорема синусов
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Доказательство теоремы синусов
Теорема синусов звучит так: стороны треугольника пропорциональны синусам противолежащих углов.
Нарисуем стандартный треугольник и запишем теорему формулой:
Формула теоремы синусов:
Докажем теорему с помощью формулы площади треугольника через синус его угла.
Из этой формулы мы получаем два соотношения:
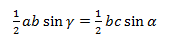
На b сокращаем, синусы переносим в знаменатели:
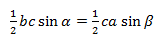
bc sinα = ca sinβ
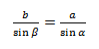
Из этих двух соотношений получаем:
Теорема синусов для треугольника доказана.
Эта теорема пригодится, чтобы найти:
- Стороны треугольника, если даны два угла и одна сторона.
- Углы треугольника, если даны две стороны и один прилежащий угол.
Доказательство следствия из теоремы синусов
У теоремы синусов есть важное следствие. Нарисуем треугольник, опишем вокруг него окружность и рассмотрим следствие через радиус.
где R — радиус описанной около треугольника окружности.
Так образовались три формулы радиуса описанной окружности:
Основной смысл следствия из теоремы синусов заключен в этой формуле:
Радиус описанной окружности не зависит от углов α, β, γ. Удвоенный радиус описанной окружности равен отношению стороны треугольника к синусу противолежащего угла.
Для доказательства следствия теоремы синусов рассмотрим три случая.
1. Угол ∠А = α — острый в треугольнике АВС.
Проведем диаметр BA1. В этом случае точка А и точка А1 лежат в одной полуплоскости от прямой ВС.
Используем теорему о вписанном угле и видим, что ∠А = ∠А1 = α. Треугольник BA1C — прямоугольный, в нём ∠ BCA1 = 90°, так как он опирается на диаметр BA1.
Чтобы найти катет a в треугольнике BA1C, нужно умножить гипотенузу BA1 на синус противолежащего угла.
BA1 = 2R, где R — радиус окружности
Следовательно: R = α/2 sinα
Для острого треугольника с описанной окружностью теорема доказана.
2. Угол ∠А = α — тупой в треугольнике АВС.
Проведем диаметр окружности BA1. Точки А и A1 по разные стороны от прямой ВС. Четырёхугольник ACA1B вписан в окружность, и его основное свойство в том, что сумма противолежащих углов равна 180°.
Следовательно, ∠А1 = 180° — α.
Вспомним свойство вписанного в окружность четырёхугольника:
Также известно, что sin(180° — α) = sinα.
В треугольнике BCA1 угол при вершине С равен 90°, потому что он опирается на диаметр. Следовательно, катет а мы находим таким образом:
α = 2R sin (180° — α) = 2R sinα
Следовательно: R = α/2 sinα
Для тупого треугольника с описанной окружностью теорема доказана.
Часто используемые тупые углы:
- sin120° = sin(180° — 60°) = sin60° = 3/√2;
- sin150° = sin(180° — 30°) = sin30° = 1/2;
- sin135° = sin(180° — 45°) = sin45° = 2/√2.
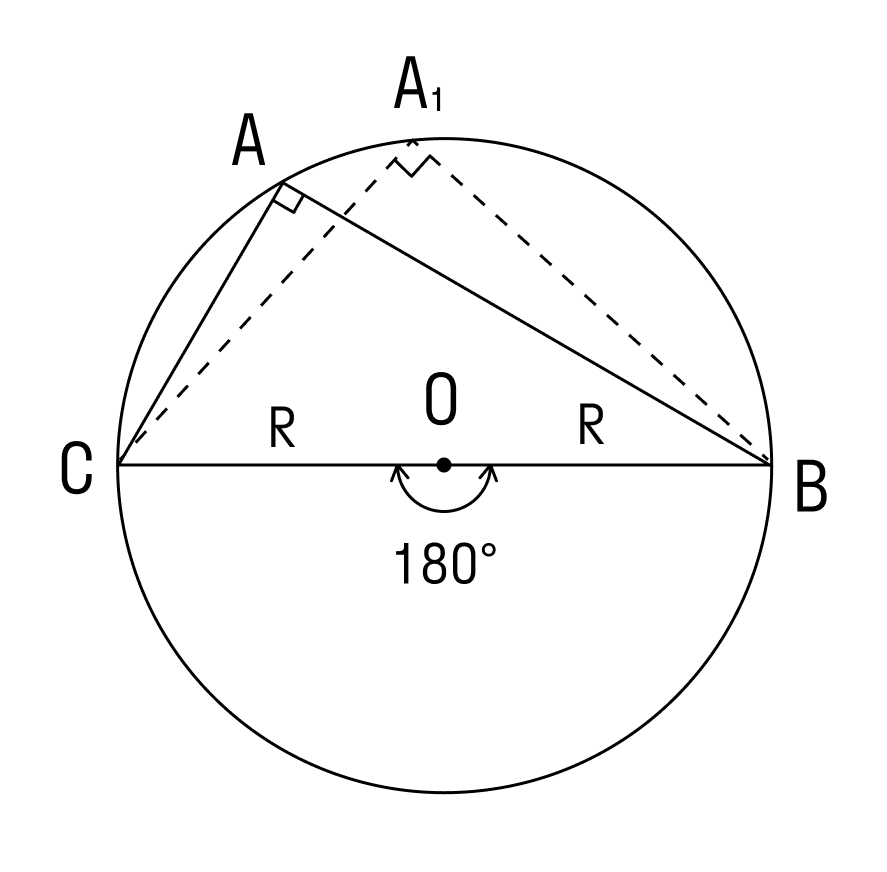
3. Угол ∠А = 90°.
В прямоугольнике АВС угол А прямой, а противоположная сторона BC = α = 2R, где R — это радиус описанной окружности.
Для прямоугольного треугольника с описанной окружностью теорема доказана.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.
Теорема о вписанном в окружность угле
Из теоремы синусов и ее следствия можно сделать любопытный вывод: если известна одна сторона треугольника и синус противолежащего угла — можно найти и радиус описанной окружности. Но треугольник не задаётся только этими величинами. Это значит, что если треугольник еще не задан, найти радиус описанной окружности возможно.
Раскроем эту тему на примере теоремы о вписанном в окружность угле и следствиях из нее.
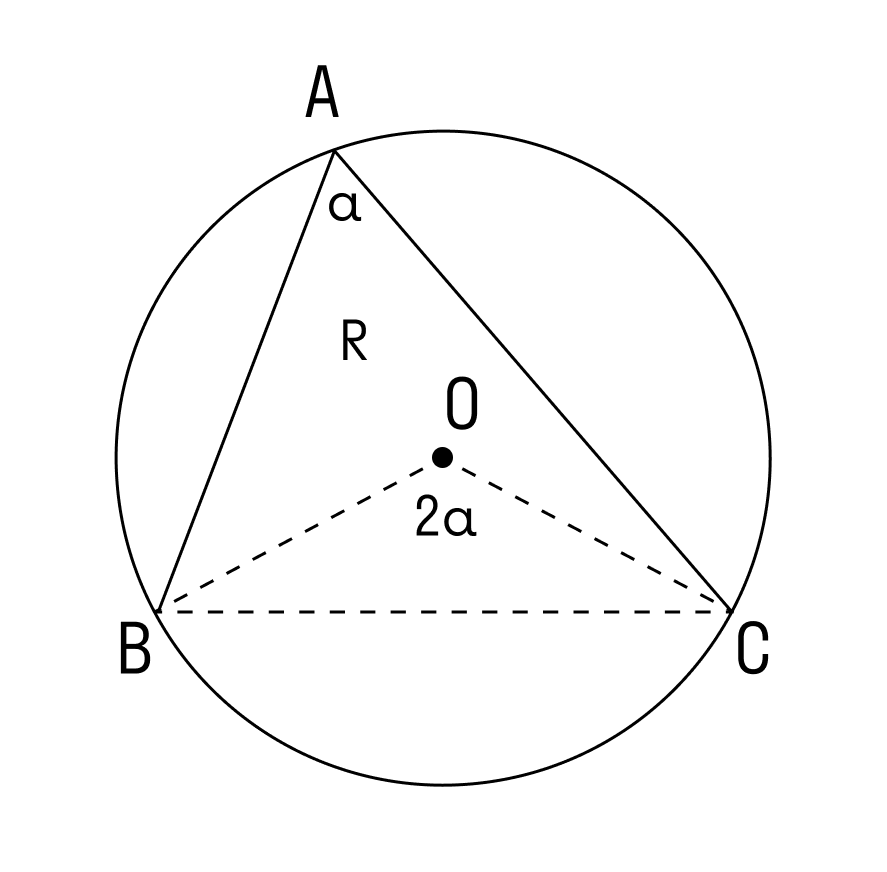
Теорема о вписанном угле: вписанный в окружность угол измеряется половиной дуги, на которую он опирается.
∠А = α опирается на дугу ВС. Дуга ВС содержит столько же градусов, сколько ее центральный угол ∠BOC.
Формула теоремы о вписанном угле:
Следствие 1 из теоремы о вписанном в окружность угле
Вписанные углы, опирающиеся на одну дугу, равны.
∠А = ∠BAC опирается на дугу ВС. Поэтому ∠A = 1/2(∠COB).
Если мы возьмём точки A1, А2. Аn и проведём от них лучи, которые опираются на одну и ту же дугу, то получим:
На рисунке изображено множество треугольников, у которых есть общая сторона СВ и одинаковый противолежащий угол. Треугольники являются подобными, и их объединяет одинаковый радиус описанной окружности.
Следствие 2 из теоремы о вписанном в окружность угле
Вписанные углы, которые опираются на диаметр, равны 90°, то есть прямые.
ВС — диаметр описанной окружности, следовательно ∠COB = 180°.
Следствие 3 из теоремы о вписанном в окружность угле
Сумма противоположных углов вписанного в окружность четырёхугольника равна 180°. Это значит, что:
Угол ∠А = α опирается на дугу DCB. Поэтому DCB = 2α по теореме о вписанном угле.
Угол ∠С = γ опирается на дугу DAB. Поэтому DAB = 2γ.
Но так как 2α и 2γ — это вся окружность, то 2α + 2γ = 360°.
Следовательно: α + γ = 180°.
Поэтому: ∠A + ∠C = 180°.
Следствие 4 из теоремы о вписанном в окружность угле
Синусы противоположных углов вписанного четырехугольника равны. То есть:
sinγ = sin(180° — α)
Так как sin(180° — α) = sinα, то sinγ = sin(180° — α) = sinα
Примеры решения задач
Теорема синусов и следствия из неё активно используются при решении задач. Рассмотрим несколько примеров, чтобы закрепить материал.
Пример 1. В треугольнике ABC ∠A = 45°,∠C = 15°, BC = 4√6. Найти AC.
- Согласно теореме о сумме углов треугольника:
∠B = 180° — 45° — 15° = 120°
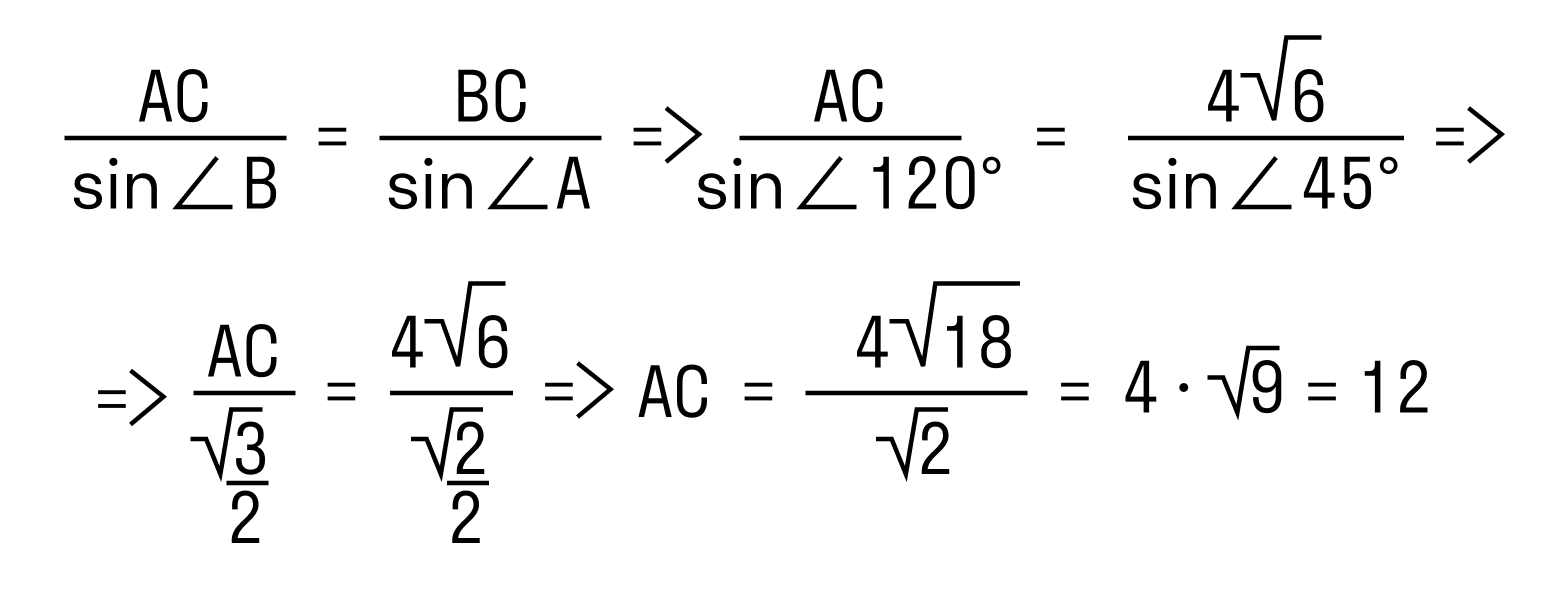
Пример 2. Гипотенуза и один из катетов прямоугольного треугольника равны 10 и 8 см. Найти угол, который расположен напротив данного катета.
В этой статье мы узнали, что в прямоугольном треугольнике напротив гипотенузы располагается угол, равный 90°. Примем неизвестный угол за x. Тогда соотношение сторон выглядит так:
Значит x = sin (4/5) ≈ 53,1°.
Ответ: угол составляет примерно 53,1°.
Запоминаем
Обычная теорема: стороны треугольника пропорциональны синусам противолежащих углов.
>
Расширенная теорема: в произвольном треугольнике справедливо следующее соотношение:
Формулы вычисления площади произвольного четырёхугольника
В школьных математических заданиях часто требуется определить площадь четырёхугольника. Все довольно просто, если задан частный случай фигуры — квадрат, ромб, прямоугольник, трапеция, параллелограмм, ромбоид. В случае же произвольного четырёхугольника все несколько сложнее, но также вполне доступно для среднего школьника. Ниже мы изучим различные методы расчётов площади произвольных четырёхугольников, запишем формулы и рассмотрим различные вспомогательные примеры.
Определения и соглашения
В приведённой ниже таблице будут указаны определения и договорённости, которые будут использоваться в дальнейшем во время наших рассуждений.
Четырёхугольник — это фигура из четырёх точек (вершин), из которых любые три не лежат на одной прямой, и четырёх отрезков (сторон) последовательно их соединяющих.
- Диагональ — отрезок, соединяющий вершины многоугольника не лежащие на одной стороне (её обозначение – латинская буква d).
- Площадь фигуры — это численное значение территории, заключённой внутри многоугольника (её обозначение – латинская буква S).
- Синус угла — это число равное отношению противоположного катета к гипотенузе в прямоугольном треугольнике. (её обозначение – запись sin).
- Косинус угла — это число равное отношению прилежащего катета к гипотенузе в прямоугольном треугольнике. В дальнейшем в статье для его обозначения будем использовать латинскую запись cos.
- Описанная окружность — это окружность, которой принадлежат все вершины многоугольника ( её радиуса обозается буквой R).
- Вписанная окружность — это окружность, которая касается всех сторон многоугольника. В дальнейшем в статье для обозначения её радиуса будем использовать латинскую букву r.
- Угол между сторонами a и b будем обозначать следующей записью (a,b).
Нахождение площади четырёхугольника различными способами и методами
Узнаем как найти площадь четырёхугольника когда даны его диагонали и образуемый при их пересечении острый угол. Тогда площадь четырёхугольника будет вычисляться по формуле: S = 1/2*d1*d2*sin(d1,d2).
Рассмотрим пример. Пусть d1 = 15 сантиметров, d2 = 12 сантиметров, и угол между ними 30 градусов. Определим S. S = 1/2*15*12*sin30 = 1/2*15*12*1/2 = 45 сантиметров квадратных.
Теперь пусть даны стороны и противолежащие углы четырёхугольника.
Пусть a, b, c, d известные стороны многоугольника; p — его полупериметр. Корень квадратный выражения условимся обозначать как rad (от латинского radical). Формула площади четырёхугольника будет находиться по формуле: S = rad(( p − a ) ( p − b ) ( p − c ) ( p − d ) − a b c d ⋅ c o s^2( (a,b) + (c,d))/2), где p = 1/2*(a + b + c + d).
На первый взгляд, формула кажется очень сложной и вычурной. Однако ничего сложного здесь нет, что мы и докажем, рассмотрев пример. Пусть данные нашего условия следующие: a = 18 миллиметров, b = 23 миллиметра, c = 22 миллиметра, d = 17 миллиметров. Противолежащие углы будут равны (a,b) = 0,5 градуса и (c,d) = 1,5 градуса. Для начала находим полупериметр: p = 1/2*(18 + 23 + 22 + 17) = 1/2*80 = 40 миллиметров.
Теперь найдём квадрат косинуса полусуммы противолежащих углов: c o s^2( (a,b) + (c,d))/2) = c o s^2(0,5 + 1,5)/2 = c o s1*c o s1 = (1/2)*(1/2) = 0,9996.
Подставим полученные данные в нашу формулу, получим: S = rad((40 — 18)*(40 — 23)*(40 — 22)*(40 — 17) — 18*23*22*17*0,97) = rad(22*17*18*23 — 18*23*22*17*1/4) = rad((22*17*18*23*(1 — 0,9996)) = rad(154836*0,0004) = rad62 = 7,875 миллиметра квадратного.
Разберёмся как находить площадь с помощью вписанной и описанной окружностей. При решении задач данной темы имеет смысл сопровождать свои действия вспомогательным рисунком, хотя это требование и не является обязательным.
Если есть вписанная окружность и нужно найти площадь четырёхугольника формула имеет вид:
Снова возьмём на рассмотрение пример: a = 16 метров, b = 30 метров, c = 28 метров, d = 14 метров, r = 6 метров. Подставим аши значения в формулу, получим:
S = ((16 +30 + 28 + 14)/2)*6 = 44*6 = 264 метров квадратных.
Теперь займёмся вариантом когда окружность описана вокруг четырёхугольника. Здесь мы сможем воспользоваться следующей формулой:
S = rad((p − a )*( p − b )*( p − c )*( p − d ), где p равно половине длины периметра. Пускай в нашем случае стороны имеют следующие значения a = 26 дециметров, b = 35 дециметров, c = 39 дециметров, d = 30 дециметров.
Первым делом определим полупериметр, p = (26 + 35 + 39 + 30)/2 = 65 дециметров. Подставим найденное значение в нашу формулу. Получим:
S = rad((65 — 26)*(65 — 35)*(65 — 39)*(65 — 30)) = rad(39*30*26*35) = 1032 (округлённо) дециметров квадратных.
Заключение
Внимательно изучив все вышеизложенное, можно сделать вывод — определение площади произвольного четырёхугольника с разными сторонами сложнее, чем у них же специальных видов — квадрата, прямоугольника, ромба, трапеции, параллелограмма. Однако внимательно изучив все приведённые методы, можно с лёгкостью решать задачи необходимые для школьников. Сведём все наши формулы в одну таблицу:
- S = 1/2*d1*d2*sin(d1,d2);
- S = rad(( p − a )*( p − b )*( p − c )*( p − d ) − a*b*c*d*c o s^2( (a,b) + (c,d))/2), где p = 1/2*(a + b + c + d);
- S = ((a + b+ c + d)/2)*r
S = rad((p − a )*( p − b )*( p − c )*( p − d ), где p равно половине периметра.
Таким образом, реально сложной является только формула номер 2, но и она вполне доступна, при условии хорошего понимания данных в статье определений и соглашений.
Видео
Разобраться в этой теме вам поможет видео.
Четырехугольники
теория по математике 📈 планиметрия
Четырехугольник – это геометрическая фигура, состоящая из четырех точек, никакие три из которых не лежат на одной прямой, и отрезков, последовательно соединяющих эти точки.
Выпуклый четырехугольник
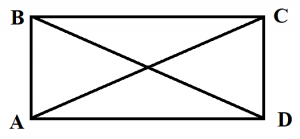
Четырехугольник называется выпуклым, если он находится в одной полуплоскости (то есть все его стороны расположены только с одной стороны прямой, прямая НЕ разбивает фигуру) относительно прямой, содержащей любую его сторону. На рисунке показан выпуклый четырехугольник АВСD.

Диагональ четырехугольника – отрезок, соединяющий любые две не соседние вершины. На рисунке 2 диагоналями являются отрезки АС и BD.
Виды и свойства выпуклых четырехугольников
Сумма углов выпуклого четырехугольника равна 360 градусов.
Прямоугольник
Прямоугольник – это четырехугольник, у которого все углы прямые.

- Противоположные стороны прямоугольника равны (АВ=CD, ВС=АD).
- Диагонали прямоугольника равны (АС=ВD).
- Диагонали пересекаются и точкой пересечения делятся пополам.
- Периметр прямоугольника – это сумма длин всех сторон: Р=(а + b) × 2, где а и b соседние (смежные) стороны прямоугольника
- Площадь прямоугольника – это произведение длин соседних (смежных) сторон, формула для нахождения площади прямоугольника:
S=ab, где a и b соседние стороны прямоугольника.
Квадрат
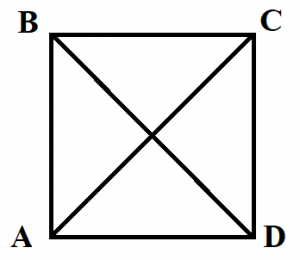
Квадрат – это прямоугольник, у которого все стороны равны.
- Диагонали квадрата равны (BD=AC).
- Диагонали квадрата пересекаются под углом 90 градусов.
- Диагонали квадрата точкой пересечения делятся пополам (BO=OD, AO=OC).
- Периметр квадрата – это сумма длин всех сторон. Так как все стороны квадрата равны, то его можно найти по формуле Р=4×а, где а — длина стороны квадрата.
- Площадь квадрата – это произведение длин соседних сторон, формула для нахождения площади прямоугольника S=a 2 , где a — длина стороны квадрата.
Параллелограмм
Параллелограмм – это четырехугольник, у которого противоположные стороны попарно параллельны.
Ромб – это параллелограмм, у которого все стороны равны.
Трапеция
Трапеция – это четырехугольник, у которого только две противоположные стороны параллельны. Параллельные стороны называются основаниями трапеции, а две другие стороны – боковыми сторонами трапеции.
Виды трапеций
Трапеция называется прямоугольной, если у нее боковая сторона перпендикулярна основаниям. Прямоугольная трапеция имеет два прямых угла.
углы А и С равны по 90 градусов
Средняя линия трапеции
Сделаем чертеж параллелограмма и покажем на нем биссектрисы углов, которые пересекаются в точке N.
Угол ANB равен углу NАD как накрест лежащие при параллельных прямых ВС и АD и секущей AN. А по условию углы BАN и NАD равны (AN биссектриса). Следовательно, углы BАN и BNА равны. Значит, треугольник ABN является равнобедренным, у него АВ= BN.
Аналогично, через равенство углов CND, ADN и CDN доказывается, что треугольник CND является равнобедренным, у него CN=DC.
По условию задачи мы имеем параллелограмм, а по свойству параллелограмма – противолежащие стороны равны, т.е. АВ=СD, значит, АВ=BN=NC=CD. Таким образом, мы доказали, что BN=NC, т.е. N – середина ВС.
Ответ: см. решение
pазбирался: Даниил Романович | обсудить разбор | оценить
Найдите боковую сторону АВ трапеции ABCD, если углы АВС и BCD равны соответственно 30 0 и 135 0 , а СD =17
Сделаем чертеж, выполнив на нём дополнительные построения – высоты АМ и СН, которые равны как расстояния между параллельными сторонами трапеции.
Рассмотрим треугольник CНD, где CD=17, угол Н=90 0 , следовательно, треугольник прямоугольный. Найдем величину угла DCН, 135 0 – 90 0 =45 0 (так как провели высоту CН). Отсюда следует, что угол D=45 0 , так как треугольник прямоугольный. Значит, треугольник является равнобедренным (углы D и DCН равны по 45 градусов).
Найдем катеты CН и DН по теореме Пифагора, как катет равнобедренного треугольника по формуле с=а √ 2 , где с=17. Следовательно, CН = 17 √ 2 . . = 17 √ 2 2 . . .
Рассмотрим прямоугольный треугольник АВМ, где угол В равен 30 градусов, а катет АМ= CН= 17 √ 2 2 . . . Зная, что катет, лежащий напротив угла в 30 градусов, равен половине гипотенузы, найдем АВ (она будет в два раза больше катета). АВ=2 × 17 √ 2 2 . . =17 √ 2
Ответ: см. решение
pазбирался: Даниил Романович | обсудить разбор | оценить
Основания трапеции равны 7 и 11, а высота равна 7. Найти площадь этой трапеции.
Для нахождения площади трапеции в справочном материале есть формула
S = a + b 2 . . h , для которой у нас известны и основания, и высота. Подставим в неё эти значения и вычислим: S = 7 + 11 2 . . ∙ 7 = 18 2 . . ∙ 7 = 9 ∙ 7 = 63
pазбирался: Даниил Романович | обсудить разбор | оценить
Радиус вписанной в квадрат окружности равен 22 √ 2 . Найти диагональ этого квадрата.
Для начала надо сделать построения на чертеже, чтобы увидеть, как располагаются известные и неизвестные элементы и чем они еще могут являться на чертеже.
Обозначим диагональ АВ, точкой О – центр окружности, С – один из углов квадрата. Покажем расстояние от центра окружности до стороны квадрата – радиус r. Если радиус равен 22 √ 2 , то сторона квадрата будет в два раза больше, т.е. 44 √ 2 .
Рассмотрим прямоугольный треугольник АВС, который является равнобедренным (так как по условию дан квадрат) и боковые стороны равны по 44 √ 2 . Нам надо найти диагональ, т.е. гипотенузу данного треугольника. Вспомним, что для нахождения гипотенузы равнобедренного треугольника есть формула с=а √ 2 , где с – гипотенуза, а – катет. Подставим в неё наши данные:
с=44 √ 2 × √ 2 =44 √ 4 =44 × 2=88
pазбирался: Даниил Романович | обсудить разбор | оценить
Площадь четырехугольника можно вычислить по формуле S= d 1 d 2 s i n a 2 . . , где d 1 и d 2 длины диагоналей четырехугольника, а – угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали d 1 , если d 2 =16, sin a= 2 5 . . , a S=12,8
Для выполнения данного задания надо подставить все известные данные в формулу:
12,8= d 1 × 16 × 2 5 . . 2 . .
В правой части можно сократить 16 и 2 на 2: 12,8= d 1 × 8 × 2 5 . . 1 . .
Теперь умножим 8 на дробь 2 5 . . , получим 3,2: 12,8= d 1 × 3 , 2
Найдем неизвестный множитель, разделив 12,8 на 3,2: d 1 =12,8:3,2=4
pазбирался: Даниил Романович | обсудить разбор | оценить
На плане изображен дачный участок по адресу: п. Сосновка, ул. Зеленая, д. 19 (сторона каждой клетки на плане равна 2 м). Участок имеет прямоугольную форму. Выезд и въезд осуществляются через единственные ворота.
При входе на участок слева от ворот находится гараж. Справа от ворот находится сарай площадью 24 кв.м, а чуть подальше – жилой дом. Напротив жилого дома расположены яблоневые посадки. Также на участке есть баня, к которой ведет дорожка, выложенная плиткой, и огород с теплицей внутри (огород отмечен на плане цифрой 6). Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1м х 1м. Между гаражом и сараем находится площадка, вымощенная такой же плиткой. К участку подведено электричество. Имеется магистральное газоснабжение.
Задание №1
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк ответов перенесите последовательность четырех цифр без пробелов, запятых и других символов.
| Объекты | яблони | теплица | сарай | жилой дом |
| Цифры |
Решение
Для решения 1 задачи работаем с текстом и планом одновременно:
при входе на участок слева от ворот находится гараж (слева от входа находится объект под номером 2), итак, гараж — 2. Справа от ворот находится сарай площадью 24 кв.м (справа объект под номером 1), сарай – номер 1. А чуть подальше – жилой дом, следовательно, жилой дом – объект под номером 7. Напротив жилого дома расположены яблоневые посадки, на плане они обозначены цифрой 3. Также на участке есть баня, к которой ведет дорожка, выложенная плиткой, на плане видим, что к объекту под номером 4 ведет дорожка, значит баня – 4. Огород с теплицей внутри (огород отмечен на плане цифрой 6), в огороде расположена теплица – объект 5.
Итак, получили следующее:
1 – сарай; 2 – гараж; 3 – яблоневые посадки; 4 – баня; 5 – теплица; 6 – огород; 7 – жилой дом.
Заполняем нашу таблицу:
| Объекты | яблони | теплица | сарай | жилой дом |
| Цифры | 3 | 5 | 1 | 7 |
Записываем ответ: 3517
Задание №2
Плитки для садовых дорожек продаются в упаковках по 6 штук. Сколько упаковок плиток понадобилось, чтобы выложить все дорожки и площадку между сараем и гаражом?
Решение
Для начала надо определить, как обозначены дорожки, которые надо выложить плиткой, на плане. На плане они показаны серым цветом (мы их обведём голубым цветом).
Теперь ищем в условии задачи, что сказано про плитки и дорожки: «Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1м х 1м».
Сосчитаем, сколько клеточек (плиток) на плане, получаем 65. Зная по условию задачи 1, что плитки продаются в упаковках по 6 штук, разделим 65 на 6. Заметим, что 65 на 6 не делится, получается приблизительно 10,8…Учитывая, что упаковки не делятся, округляем до большего целого числа, нам понадобится 11 упаковок.
Задание №3
Найдите расстояние от жилого дома до теплицы (расстояние между двумя ближайшими точками по прямой) в метрах.
Решение
Из задания 1 знаем, что жилой дом обозначен на плане цифрой 7, а теплица цифрой 5. Следовательно, на плане находим эти объекты и расстояние между двумя ближайшими точками по прямой (обозначим это голубым цветом). Видим, что это расстояние – 2 клетки. На плане показано, что длина стороны одной клетки равна 2 метра, значит, расстояние между двумя этими объектами равно 4 метра.
Задание №4
Найдите площадь, которую занимает гараж. Ответ дайте в квадратных метрах.
Решение
Найдем на плане гараж, это объект под номером 2. Гараж имеет прямоугольную форму, следовательно, нам надо найти площадь прямоугольника. Для этого надо найти длину и ширину. На плане показано, что длина стороны 1 клетки равна 2 метра, значит, длина гаража равна 8 м (4 клетки), а ширина — 6 м (3 клетки).
Зная ширину и длину, находим площадь гаража: 6х8=48 кв.м
Задание №5
Хозяин участка решил покрасить весь забор вокруг участка (только с внешней стороны) в зелёный цвет. Площадь забора равна 232 кв.м., а купить краску можно в одном из двух ближайших магазинов. Цена и характеристика краски и стоимость доставки заказа даны в таблице.
| Номер магазина | Расход краски | Масса краски в одной банке | Стоимость одной банки краски | Стоимость доставки заказа |
| 1 | 0,25 кг/кв.м | 6 кг | 3000 руб. | 500 руб. |
| 2 | 0,4 кг/кв.м | 5 кг | 1900 руб. | 800 руб. |
Во сколько рублей обойдется наиболее дешёвый вариант покупки с доставкой?
Решение
Определим, сколько килограммов краски понадобится для покраски забора площадью 232 кв.м:
1 магазин: 232х0,25=58 кг
2 магазин: 232х0,4=92,8 кг
Вычислим количество банок краски, которое надо купить, зная массу краски в 1 банке:
1 магазин: 58:6=9,7…; так как банки продаются целиком, то надо 10 банок (округляем до наибольшего целого числа)
2 магазин: 92,8:5=18,56; значит надо 19 банок.
Вычислим стоимость краски в каждом магазине плюс доставка:
1 магазин: 10х3000+500=30500 руб.
2 магазин: 19х1900+800=36900 руб.
Из решения задачи видно, что в 1 магазине купить краску выгоднее. Следовательно, наиболее дешёвый вариант покупки с доставкой будет стоить 30500 рублей.
Ответ: см. решение
pазбирался: Даниил Романович | обсудить разбор | оценить
источники:
http://liveposts.ru/articles/education-articles/matematika/formuly-vychisleniya-ploshhadi-proizvolnogo-chetyryohugolnika
http://spadilo.ru/chetyrexugolniki/
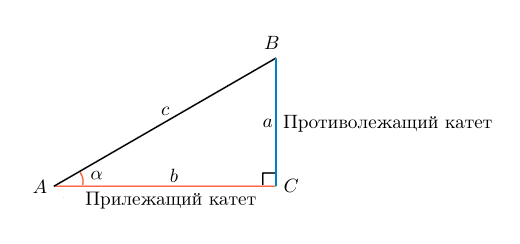
Синусом угла в прямоугольном треугольнике называют отношение противолежащего катета к гипотенузе.
Катетами являются стороны, которые образуют прямой угол в треугольнике, соответственно, гипотенузой является третья (самая длинная) сторона.
Для простоты запоминания можно дать такое определение: синус угла — это отношение дальнего от рассматриваемого угла катета к гипотенузе.
В случае с рисунком, описанным выше: sinα=acsinalpha=frac{a}{c}
В треугольнике, один из углов которого равен 90 градусам, известен катет при угле αalpha и равен он 3 см3text{ см}. Также дано произведение длин катетов и равно 12 см212text{ см}^2. Найдите синус угла αalpha.
Решение
Сначала нужно найти длину неизвестного нам катета. Для этого воспользуемся данным нам произведением. Обозначим неизвестный катет за xx. Тогда, по условию задачи:
3⋅x=123cdot x=12
x=123=4x=frac{12}{3}=4
a=x=4a=x=4
По теореме Пифагора найдем гипотенузу:
a2+b2=c2a^2+b^2=c^2
42+32=c24^2+3^2=c^2
25=c225=c^2
c=5c=5
sinα=ac=45=0.8sinalpha=frac{a}{c}=frac{4}{5}=0.8
Ответ
0.80.8
Вычислите синус 45 градусов.
Решение
Для этого воспользуемся тригонометрической таблицей углов. Находим, что:
sin45∘=π4=0.785sin 45^circ=frac{pi}{4}=0.785
Ответ
0.7850.785
Если в задаче известен косинус угла и нужно найти его синус, то наличие известных длин катетов и гипотенузы не обязательны. Достаточно просто воспользоваться основным тригонометрическим тождеством, которое имеет следующий вид:
sin2α+cos2α=1sin^2alpha+cos^2alpha=1
αalpha — любой угол.
Квадрат косинуса угла в треугольнике равен 0.8. Найдите синус данного угла.
Решение
Воспользуемся основным тригонометрическим тождеством:
sin2α+cos2α=1sin^2alpha+cos^2alpha=1
sin2α+0.8=1sin^2alpha+0.8=1
sin2α=0.2sin^2alpha=0.2
sinα=0.2sinalpha=sqrt{0.2}
sinα≈0.447sinalphaapprox0.447
Ответ
0.4470.447
Испытываете проблемы с вычислением синуса? Оформите задачу по математике на заказ у наших экспертов!
Тест по теме «Вычисление синуса»
Как найти угол альфа формула – Синус угла — sin(A) | Формулы и расчеты онлайн
В данной статье мы с вами разберём некоторые задачи связанные с выражениями. Задания данной группы довольно разнообразны. Если вы запомнили свойства степеней, корней и логарифмов, знаете основные формулы тригонометрии, и постоянно практикуетесь, то большинство задач для вас никакого труда не представят.
Относительную сложность могут вызывать следующие:
— преобразования буквенных иррациональных выражений
— вычисление значений тригонометрических выражений
— преобразования тригонометрических выражений
Если перечислить все группы задач, то они довольно разнообразны.
Они включают в себя: ПОКАЗАТЬ/СКРЫТЬ
Здесь мы с вами разберём задачи на вычисление значений тригонометрических выражений. Конечно, все их в одной статье разобрать невозможно. Но мы обязательно разберём и другие примеры, не пропустите!
Итак, что обязательно вы должны знать и всегда помнить? Это знаки тригонометрических функций в четвертях. ЭТО ВАЖНО.
Как осознать эту информацию и понять следствием чего она является – об этом будет отдельная статья (если вы это знаете, то прекрасно). Пока предлагаю пока просто запомнить:
Основное тригонометрическое тождество:
Формулы тангенса и котангенса:
Выполняются элементарные алгебраические преобразования:
1. Числитель и знаменатель дроби можем умножать и делить на одно и тоже число.
2. Левую и правую часть уравнения можем умножать и делить на одно и тоже число.
В представленных ниже заданиях используется основное тригонометрическое тождество и формула тангенса.
Найдите тангенс альфа, если
В этом и подобных примерах необходимо знать основное тригонометрическое тождество (его вообще нужно помнить всегда), а также формулу тангенса:
Косинус угла нам известен. Из формулы основного тригонометрического тождества мы можем найти значение синуса. Затем подставить их в формулу тангенса.
Теперь ВАЖНЫЙ момент: необходимо определить знак синуса для интервала (3Пи/2;2Пи). Это интервал от 270 до 360 градусов (четвёртая четверть). Как переводить радианы в градусы можно посмотреть здесь. Значение синуса в этой четверти отрицательное, поэтому:
Найдите tg α, если
В этом и подобных примерах необходимо знать основное тригонометрическое тождество (его вообще нужно помнить всегда), а также формулу тангенса:
Cинус угла нам известен. Из формулы основного тригонометрического тождества мы можем найти значение косинуса. Затем подставить их в формулу тангенса.
Определяем знак косинуса для интервала (Пи/2;Пи). Это интервал от 90 до 180 градусов (вторая четверть). Значение косинуса в этой четверти отрицательное (смотрите эскиз). Поэтому
Найдите 5·cos α, если синус альфа
Необходимо найти косинус угла. Из формулы основного тригонометрического тождества следует, что cos 2 x = 1– sin 2 x и
Определим знак косинуса. Угол принадлежит интервалу (3Пи/2;2Пи).
Это интервал от 270 до 360 градусов (четвёртая четверть). Значение косинуса в этой четверти положительное, поэтому:
Таким образом, 5·cos α = 5∙0,7 = 3,5
Найдите 0,1·sin α, если
Необходимо найти синус угла. Из формулы основного тригонометрического тождества следует, что sin 2 x = 1– cos 2 x и
Определим знак синуса. Угол принадлежит интервалу (0; Пи/2).
Это интервал от 0 до 90 градусов (первая четверть). Значение синуса в этой четверти положительное, поэтому:
Таким образом 0,1·sin α = 0,1∙0,3 = 0,03
Общая рекомендация для следующих данных примеров! Если требуется найти тангенс аргумента (квадрат тангенса), то осуществляем деление на косинус (квадрат косинуса). Если требуется найти котангенс аргумента (квадрат котангенса), то осуществляем деление на синус (квадрат синуса). Примеры:
65217. Найдите tg 2 α, если 3sin 2 α + 8 cos 2 α = 7
Требуется найти квадрат тангенса. Разделим обе части уравнения на cos 2 α, получим:
Далее по формуле основного тригонометрического тождества можно найти квадрат синуса и используя формулу тангенса вычислить уже его квадрат:
Преобразуем данное выражение так, чтобы в числителе и знаменателе был тангенс. Разделим числитель и знаменатель на cos α, получим:
Здесь дано значение тангенса. Необходимо сделать так, чтобы в выражении у нас был тангенс. Вынесем cosα за скобки в числителе и знаменателе (или разделим числитель и знаменатель на cosα), получим:
Подставим значение тангенса данное в условии, получим:
*Косинус у нас сократился.
65363. Найдите tg α, если
В левой части в числителе и знаменателе вынесем cosα за скобки, получим:
65423. Найдите tg α, если
Умножим обе части уравнения на 4 (2sinα+cosα+1)
26775. Найдите tg α, если
26776. Найдите tg α, если
26777. Найдите 3cos α, если
26778. Найдите 5sin α, если
26787. Найдите tg 2 α, если
26790. Найдите tg α, если
26791. Найдите tg α, если
Подведём итог, для решения подобных примеров вы:
1. Должны знать на зубок основные формулы тригонометрии.
2. Не забывать определять знак (+ или -) для тригонометрических функций в четвертях. Потерянный знак на экзамене – это ошибка и потерянный бал, будьте внимательны.
Надеюсь, что материал был для вас полезен.
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
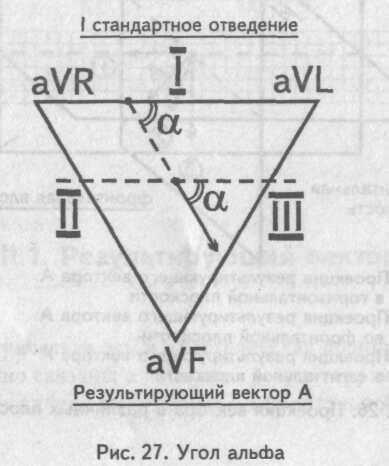
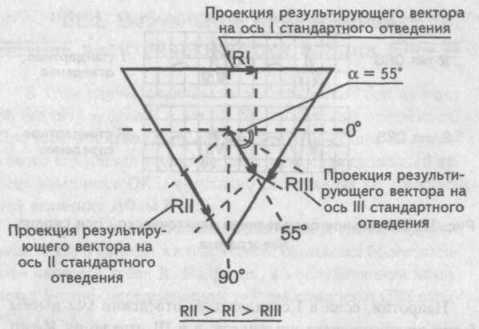
Определение ЭОС
Мысленно поместим результирующий вектор возбуждения желудочков внутрь треугольника Эйнтховена. Угол, образованный направлением результирующего вектора и осью I стандартного отведения, и есть искомый угол альфа.
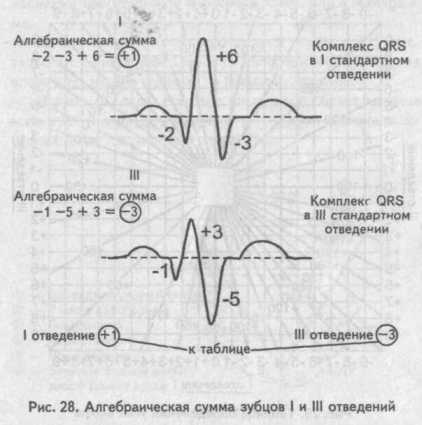
Величину угла альфа находят по специальным таблицам или схемам, предварительно определив на электрокардиограмме алгебраическую сумму зубцов желудочкового комплекса (Q + R + S) в I и III стандартных отведениях. Найти алгебраическую сумму зубцов желудочкового комплекса достаточно просто: измеряют в миллиметрах величину каждого зубца одного желудочкового комплекса QRS, учитывая при этом, что зубцы Q и S имеют знак минус (—), поскольку находятся ниже изоэлектрической линии, а зубец К — знак плюс (+). Если какой-либо зубец на электрокардиограмме отсутствует, то его значение приравнивается к нулю (0).
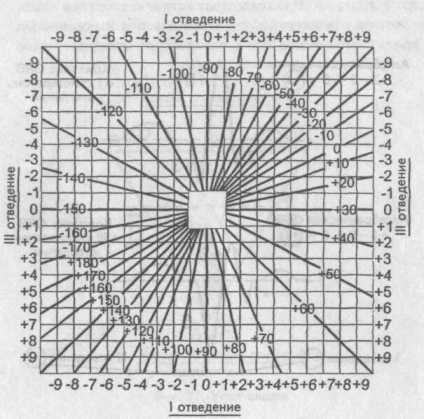
Далее, сопоставляя найденную алгебраическую сумму зубцов для I и III стандартных отведений, по таблице определяют значение угла альфа. В нашем случае он равен минус 70°. Таблица определения положения электрической оси сердца (по Дьеду)
Таблица определения угла альфа
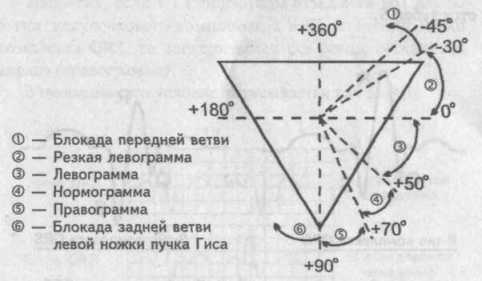
Если угол альфа находится в пределах 50—70°, говорят о нормальном положении электрической оси сердца (электрическая ось сердца не отклонена), или нормограмме. При отклонении электрической оси сердца вправо угол альфа будет определяться в пределах 70—90°. В обиходе такое положение электрической оси сердца называют правограммой.
Если угол альфа будет больше 90° (например, 97°), считают, что на данной ЭКГ имеет место блокада задней ветви левой ножки пучка Гиса. Определяя угол альфа в пределах 50—0° говорят об отклонении электрической оси сердца влево, или о левограмме. Изменение угла альфа в пределах 0 — минус 30° свидетельствует о резком отклонении электрической оси сердца влево или, иными словами, о резкой левограмме. И наконец, если значение у г л а альфа будет меньше минус 30° (например, минус 45°) — говорят о блокаде передней ветви левой ножки пучка Гиса.
Пределы отклонения электрической оси сердца
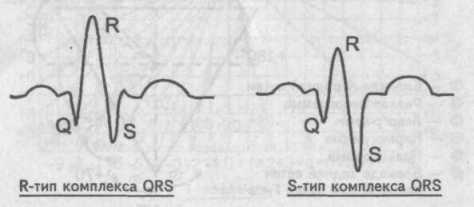
Определение отклонения электрической оси сердца по углу альфа с использованием таблиц и схем производят в основном врачи кабинетов функциональной диагностики, где соответствующие таблицы и схемы всегда под рукой. Однако определить отклонение электрической оси сердца можно и без необходимых таблиц. В этом случае отклонение электрической оси находят по анализу зубцов R и S в I и III стандартных отведениях. При этом понятие алгебраической суммы зубцов желудочкового комплекса комплекса QRS, заменяют визуально понятием «определяющий зубец» сопоставляя по абсолютной величине зубцы R и S . Говорят о «желудочковом комплексе R-типа», подразумевая, что в данном желудочковом комплексе более высоким является зубец К. Напротив, в «желудочковом комплексе S-типа» определяющим зубцом комплекса QRS является зубец S.
Сопоставление зубцов К и 3 комплекса QRS
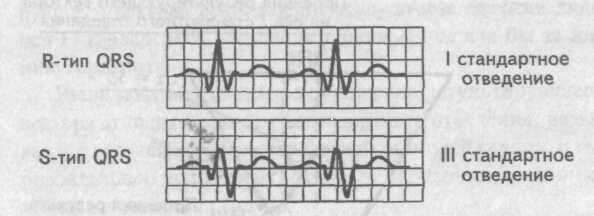
Если на электрокардиограмме в I стандартном отведении желудочковый комплекс представлен R-типом, а комплекс QRS в III стандартном отведении имеет форму S-типа, то в данном случае электрическая ось сердца отклонена влево (левограмма).
Схематично это условие записывается как RI-SIII.
Визуальное определение электрической оси сердца
. Левограмма Напротив, если в I стандартном отведении мы имеем S-тип желудочкового комплекса, а в III отведении R-тип комплекса QRS, то электрическая ось сердца отклонена вправо (правограмма). Упрощенно это условие записывается как SI-RIII.
Визуальное определение электрической оси сердца
. Правограмма Результирующий вектор возбуждения желудочков расположен в норме во фронтальной плоскости так, что его направление совпадает с направлением оси II стандартного отведения.
Нормальное положение электрической оси сердца
(нормограмма) На рисунке видно, что амплитуда зубца R во II стандартном отведении наибольшая. В свою очередь зубец К в I стандартном отведении превосходит зубец RIII. При таком условии соотношения зубцов R в различных стандартных отведениях мы имеем нормальное положение электрической оси сердца (электрическая ось сердца не отклонена). Краткая запись этого условия — RII>RI>RIII.
III.3. Угол альфа
III.3. Угол α
Мысленно поместим результирующий вектор возбуждения желудочков внутрь треугольника Эйнтховена. Угол, образованный направлением результирующего вектора и осью I стандартного отведения, и есть искомый угол α.
Величину угла α находят по специальным таблицам или схемам, предварительно определив на электрокардиограмме алгебраическую сумму зубцов желудочкового комплекса (Q+R+S) в T и III стандартных отведениях.
Найти алгебраическую сумму зубцов желудочкового комплекса достаточно просто: измеряют в миллиметрах величину каждого зубца одного желудочкового комплекса QRS, учитывая при этом, что зубцы Q и S имеют знак минус (-), поскольку находятся ниже изоэлектрической линии, а зубец R – знак плюс (+). Если какой-либо зубец на электрокардиограмме отсутствует, то его значение приравнивается к нулю (0).
Далее, сопоставляя найденную алгебраическую сумму зубцов для I и III стандартных отведений, по таблице определяют значение угла α. В нашем случае он равен мину с 70°.
Если угол α находится в пределах 50-70°, говорят о нормальном положении электрической оси сердца (электрическая ось сердца не отклонена), или нормограмме.
При отклонении электрической ось сердца вправо угол α будет определяться в пределах 70-90°. В обиходе такое положение электрической оси сердца называют правограммой.
Если угол α будет больше 90° (например, 97°), считают, что на данной ЭКГ имеет место блокада задней ветви левой ножки пучка Гиса.
Определяя угол α в пределах 50-0°, говорят об отклонении электрической оси сердца влево, или о левограмме.
Изменение угла α в пределах 0 – минус 30° свидетельствует о резком отклонении электрической оси сердца влево или, иными словами, о резкой левограмме.
И, наконец, если значение угла α будет меньше минус 30° (например, минус 45°) – говорят о блокаде передней ветви левой ножки пучка Гиса.
Определение отклонения электрической оси сердца по углу α с использованием таблиц и схем производят в основном врачи кабинетов функциональной диагностики, где соответствующие таблицы и схемы всегда под рукой.
Однако определить отклонение электрической оси сердца можно и без необходимых таблиц.
Как найти угол в окружности? ? Зная координаты двух точек.
Добрый день! Как найти угол альфа. Если у меня есть воображаемая окружность. Ее центр точка А. и Есть точка В. Мне нужно найти угол. По какой формуле искать. Также точка В может находиться ниже оси OZ, по формуле должен получать градус от 180 до 360.
Как, по какой? Угол равен 180 градусов + Arctg( (Yb — Ya) / (Xb — Xa) ). Если Xa = Xb, то вместо арктангенса прибавляешь 90 градусов.
Ох, насвистел. . .Тебе же нужно в промежутке от 180 до 360.
Тогда еще к этой формуле добавить, а если Arctg() < 0, то складывать его с 360 градусов, а не со 180.
на кой тут окружность и оси координат? Они никакого отношения к задаче вообще не имеют. Да вы еще для пущей путаницы назвали горизонталь OZ, будто это третья ось координат: )
у вас есть точки A и B и горизонталь. опустите из точки B перпендикуляр на линию OZ, получите точку С с координатами Bx, Ау. перед вами треугольник, ваш искомый угол — арксинус |AC| / |AB|
координаты точки А (Х1;У1) точки Б (Х2;У2)
из точку Б опускаешь перпендикуляр на ось ОЗ в точку С — получаем БС. получаешь прямоугольный треугольник.
длина БС = У2-У1. длина АС = Х2-Х1
получаешь длину гипотенузы АБ. получаешь площадь треугольника.
площадь треугольника также вычисляется
С = АБ*АБ + АС*АС — 2*АБ*АС*косинус (угла между сторонам АБ и АС)
отсюда вычисляешь косинус, а из него сам угол.
П. С. правда не понимаю зачем дана окружность. А если нужен угол больше 180, то к найденному прибавь просто 180.
Теорема косинусов и синусов
Для начала вспомним теорему Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Формула Теоремы Пифагора:
a 2 > + b 2 > = c 2 >, где a, b — катеты, с — гипотенуза.
Теорема косинусов звучит так: квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними.
Формула теоремы косинусов:
a 2 = b 2 + c 2 — 2bc cos α
В доказательстве теоремы косинусов используем формулу длины отрезка в координатах. Рассмотрим данную формулу:
В доказательстве теоремы косинусов BC — это сторона треугольника АВС, которая обозначена буквой а. Введем удобную систему координат и найдем координаты нужных нам точек. У точки В координаты (с; 0).
Координаты точки С — (b cos α; b sin α) при α ∈ (0° ; 180°).
cos 2 α + sin 2 α = 1 — основное тригонометрическое тождество.
BC 2 = a 2 = (b cos α — c) 2 + b 2 sin 2 α = b 2 cos 2 α + b 2 sin 2 α — 2bc cos α + c 2 = b 2 (cos 2 α + sin 2 α) — 2bc cos α + c 2
Что и требовалось доказать.
Совет: чтобы быстрее разобраться в сложной теме, запишитесь на онлайн-курсы по математике для детей и подростков.
С помощью теоремы косинусов можно найти косинус угла треугольника:
- Когда b 2 + c 2 — a 2 > 0, угол α будет острым.
- Когда b 2 + c 2 — a 2 = 0, угол α будет прямым.
- Когда b 2 + c 2 — a 2 < 0, угол α будет тупым.
Сформулируем еще одно доказательство теоремы косинусов.
Пусть нам дан треугольник ABC, в котором из вершины C на сторону AB опустили высоту CD. Это значит:
- AD = b × cos α,
- DB = c – b × cos α.
Запишем теорему Пифагора для двух прямоугольных треугольников ADC и BDC:
- h 2 = b 2 — (b × cos α) 2
- h 2 = a 2 — (c – b × cos α) 2
Приравниваем правые части уравнений:
- b 2 — (b × cos α) 2 = a 2 — (c — b × cos α) 2
- a 2 = b 2 + c 2 — 2bc × cos α
Если один из углов при основании тупой (высота упирается в продолжение основания), полностью аналогичен рассмотренному выше.
Определим стороны b и c:
- b 2 = a 2 + c 2 — 2ac × cos β;
- c 2 = a 2 + b 2 — 2ab × cos γ.
Формулировка теоремы для каждой из сторон треугольника
Теорема косинусов справедлива для всех сторон треугольника, то есть:
a 2 = b 2 + c 2 — 2bc cos α
b 2 = c 2 + a 2 — 2ca cos β
c 2 = a 2 + b 2 — 2ab cos γ
Теорема косинусов может быть использована для любого вида треугольника.
Косинусы углов треугольника
Теорема косинусов позволяет найти как косинус, так и угол треугольника. Найдём косинусы углов:
Определение угла с помощью косинуса
А теперь обратим внимание на углы.
Как мы уже знаем, косинус угла из промежутка (0°; 180°) определяет угол (в отличие от его синуса).
Пусть нам дана единичная полуокружность. Если нам задан cos α, то нам задана точка на верхней полуокружности и задан угол α. Следовательно, cos α однозначно определяет точку М(cos α; sin α), и однозначно определяется угол ∠AOM.
Рассмотрение пределов изменения cos α и sin α
Рассмотрим пределы изменения синуса и косинуса α. Вспомним, что если α — угол треугольника, то он лежит в пределах от 0° до 180°.
Предел изменения косинуса: -1 < cos α < 1.
Предел изменения синуса: 0 < sin α ≤ 1.
- Если cos α > 0, то α ∈ (0°;90°)
- Если cos α < 0, то α ∈ (90°;180°)
- Если cos α = 0, то α = 90°
Примеры решения задач
При помощи теоремы косинусов можно решать задачки по геометрии. Рассмотрим интересные случаи.
Пример 1. Дан треугольник АВС. Найти длину СМ.
∠C = 90°, АВ = 9, ВС = 3, AM/MB = 1/2, где М — точка на гипотенузе АВ.
- Так как АМ + МВ = 9, а AM/MB = 1/2, то АМ = 3, МВ = 6.
Из треугольника АВС найдем cos B:
Пример 2. Дан треугольник АВС, в котором a2 + b2 < c2. Доказать, что ∠C — тупой угол.
- Для доказательства нужно вспомнить теорему косинусов для угла ∠C:
- Так как a 2 + b 2 < c 2 , то cos C < 0, следовательно, ∠C — тупой.
Что и требовалось доказать.
Эта задача нам показала, что с помощью теоремы косинусов можно определить тупой угол или острый.















 то
то  и угол
и угол  острый;
острый; то
то  и угол
и угол  тупой;
тупой; то
то  и угол
и угол  прямой.
прямой.








































































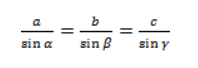
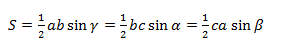
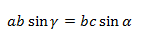
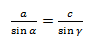
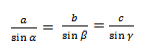

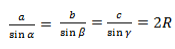

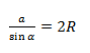


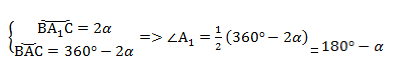

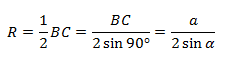
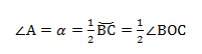
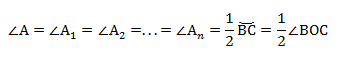
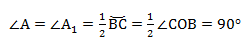

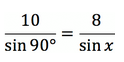
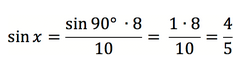

 Четырёхугольник — это фигура из четырёх точек (вершин), из которых любые три не лежат на одной прямой, и четырёх отрезков (сторон) последовательно их соединяющих.
Четырёхугольник — это фигура из четырёх точек (вершин), из которых любые три не лежат на одной прямой, и четырёх отрезков (сторон) последовательно их соединяющих.