Синус двойного угла, формула
Данная формула позволяет найти синус двойного угла зная синус и косинус этого угла по отдельности:
[
sin(2α) = 2sin(α)cos(α)
]
Вычислить, найти синус двойного угла, по формуле (1)
| α° (градусов) | α´ (минут) | α˝ (секунд) |
Вычислить
нажмите кнопку для расчета
Синус двойного угла |
стр. 215 |
|---|
Сегодня будет максимально информативный блок на запоминание формул!
Представляю тебе формулы, которые чаще всего помогают выполнить числовые преобразования.
Синус двойного угла:
sin2α = 2sinα⋅cosα
Косинус двойного угла:
cos2α = cos2α − sin2α = 2cos2α − 1 = 1 − 2sin2α
Тангенс двойного угла:
tg2α = 2tgα/(1 − tg2α)
Аналогично для тройного угла!
👉🏻 Распознать, что требуются именно эти, а не какие-нибудь другие формулы очень просто: если ты видишь выражения сильно похожие на косинус, синус, тангенс двойных углов, то смело можно свернуть выражение в одну из этих формул в первую очередь ✨
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter. Мы обязательно поправим!
Основные понятия. Тригонометрия довольно древняя наука, и ее первые упоминания связаны с необходимостью в практичной жизни, в земледелии, астрономии и строительстве. Впервые именно астрономы вывели такие понятия как отношение сторон треугольника. А официальные названия функций стали появляться позже, например, синус, который получил свое название первым, получил свое название от греческих математиков уже в третьем веке до н.э.. а косинус является относительно молодым, и был выведен как дополнение к синусу. История тригонометрии обширна и интересна, из древней науки о треугольниках она перешла в известную нам науку о тригонометрических функциях. Для того чтобы разобраться в формулах двойного угла, необходимо вспомнить основные понятия тригонометрии. Начнём:
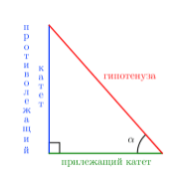
Тригонометрические функции:
- Синус угла — отношение катета напротив угла к гипотенузе:
- Косинус — деление прилежащей стороны треугольника на гипотенузу;
- Тангенс — отношение синуса к косинусу или катета напротив угла к прилежащему;
- Котангенс — деление косинуса на синус, или стороны прилежащей к углу на противолежащую.
Определение
Тригонометрическая окружность — это окружность нанесённая на систему координат, имеющая радиус равный единице и центр в начале координат.
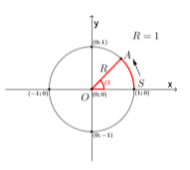
При помощи такой окружность можно наглядно разобраться в тригонометрических формулах и значениях. Например, найти числовые значения функций тригонометрии на системе координат, такие как:
[ sin 60^{circ}=frac{sqrt{3}}{2} ]; [ sin 30^{circ}=frac{1}{2} ]
Данные примеры будут использоваться далее по тексту. Мы можем посмотреть их значение на окружности на рисунке ниже.
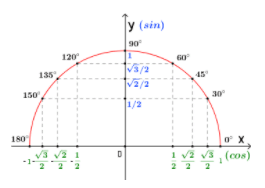
Основное тождество в тригонометрии, звучит так:
- Синус в квадрате угла плюс косинус в квадрате угла равны единице;
- Произведение тангенса и котангенса угла равно единице;
- Тангенс угла равен, делению, синуса этого угла на косинус, а котангенс наоборот косинуса на синус.
Данные тождества также будут применены для выведения формул двойного, тройного и т.д. углов.
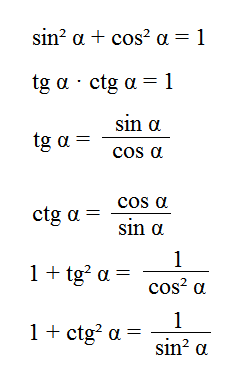
Формулы двойного угла в тригонометрии
Формулы двойного угла тригонометрических функций, необходимы для того чтобы выразить их, при этом угол должен иметь значение 2а, а также используя ТФ этого угла. Для отражения её на графике используют координаты с окружностью.
Список формул двойного угла
Прежде чем преступить к образованию формул двойного угла тригонометрии, давайте вспомним, что в тригонометрии углы принято писать в виде na, в такой записи п — обозначение натурального числа, а а — угол альфа. Обычно такая запись в тригонометрии используется без скобок, значит sin an, это тоже самое что sin (an). А также если рассмотреть запись sinn a, то она тоже имеет аналогичную запись вида (sin а)n . такое правило записи касается всех тригонометрических функций со степенями.
Рассмотрим какие же формулы двойного угла существуют на примерах.
Синус двойного угла формула:
sin 2 α = 2 * sin α * cos α;
Формула косинуса двойного угла:
cos 2 α = cos2α — sin2α, cos 2α = 1 − 2 * sin2α , cos 2α = 2 * cos2α−1;
Тангенс двойного угла формула:
[ operatorname{tg} 2 alpha=frac{2^{*} operatorname{tg} alpha}{1-operatorname{tg}^{2} alpha} ]
Котангенса:
[ operatorname{ctg} 2 alpha=frac{operatorname{ct}^{2} a-1}{2^{*} operatorname{ct} a} ]
Стоит не забывать, что выше приведённые формулы sin и cos, можно применять для любого значения угла. А вот если рассмотреть, формулы для тангенса, то при любых альфа где, tg 2a , имеет смысл, то есть при [a neq frac{pi}{4}+frac{pi}{2} cdot z], где z любое целое число. Что же касается формулы двойного угла котангенса, то при любом a, где ctg 2α определён на α ≠ 2 * z .
Как мы видим косинус с таким видом угла, наделён тремя вариантами записи формул, все они равноправны, а это значит, что результат их применения будет абсолютно одинаковым.
Доказательство формул двойного угла
Для того чтобы, формулы двойного угла были доказаны, вернёмся к истокам, формулам сложения. Сначала рассмотрим формулу синуса суммы, которая выглядит следующим образом:
[ operatorname{Sin}(a+b)=operatorname{Sin} a * cos b+cos a * sin b ]
Косинуса суммы:
[ operatorname{Cos}(a+b)=cos a * cos b-sin a * sin b ]
Если считать что a = b, тогда выходит:
[ operatorname{Sin}(a+a)=sin a * cos a+cos a * sin a=2 * cos a * sin a ]
И также для косинуса:
[ cos (a+a)=cos a * cos a-sin a * sin a=cos ^{2} alpha-sin ^{2} alpha ]
Таким способом мы доказали формулы синуса и косинуса двойного угла.
Формулы которые остались: cos 2α = 1 − 2 * sin2α , cos 2α = 2 * cos2α−1, выразили в таком виде благодаря приведению вместо единицы тождества суммы квадратов, cos2α +sin2α = 1. Поэтому вышло следующее:
Формулы приведения двойного угла: 1 − 2 * sin2α = cos2α +sin2α — 2 * sin2α = cos2α — sin2α.
И так же с третьих примеров формулы двойного угла.
2 * cos2α−1 = 2 * cos2α -( cos2α +sin2α ) = cos2α — sin2α.
Для того, чтобы выполнить доказательство формул для тангенса и котангенса двойного угла тоже применяется равенство следующего вида:
[ operatorname{tg} 2 alpha=frac{sin 2 alpha}{cos 2 alpha} text { и } operatorname{ctg} 2 alpha=frac{cos 2 alpha}{sin 2 alpha} . ]
Сделав замену на данные равенства получим следующие выражения:
[ operatorname{tg} 2 alpha=frac{sin 2 alpha}{cos 2 alpha}=frac{2 cdot sin alpha cdot cos alpha}{cos ^{2} alpha-sin ^{2} alpha} text { и } operatorname{ctg} 2 alpha=frac{cos 2 alpha}{sin 2 alpha}=frac{cos ^{2} alpha-sin ^{2} alpha}{2 cdot sin alpha cdot cos alpha} ]
Представленные выше выражения мы разделим на cos2α, при котором cos2α ≠ 0, а альфа имеет любое значение, когда тангенс угла альфа определён. Со вторым представленным выражением мы также произведём деление, только на sin2α, и он так же не равен нулю, и альфа имеет любое значение, при котором котангенс имеет смысл.
Получим следующие формулы:
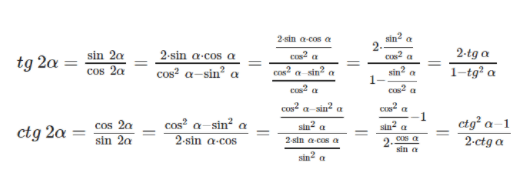
Нет времени решать самому?
Наши эксперты помогут!
Как использовать формулы двойного угла
Рассмотрим, как применяются формулы двойного угла в решении на примерах. Такие примеры помогут закрепить и понять материалы рассмотренный ранее.
Чтобы проверить справедлива ли формула двойного угла для при значении угла альфа в тридцать градусов, необходимо применить функции тригонометрии для этих углов. Если α = 30°, тогда 2α = 60°.
Проверим: sin60° = 2 * sin30° * cos30°cos60° = cos230° — sin230°.
Следующим шагом, подставим эти значения в :
[ operatorname{tg} 60^{circ}=frac{2 cdot operatorname{tg} 30^{circ}}{1-operatorname{tg}^{2} 30^{circ}} text { и } operatorname{ctg} 60^{circ}=frac{operatorname{ctg}^{2} 30^{circ}-1}{2 cdot operatorname{ctg} 30^{circ}} ]
Так как мы знаем, что синус тридцати градусов равен одной второй, косинус этого угла, равен корню из трёх, который поделен на два, тангенс заданного угла это корень из трёх на три, котангенс корень из трёх.
Получается, что синус двойного угла, то есть шестидесяти градусов, равен корню из трёх, который поделен на два; косинус — одной второй; тангенс корню из трёх; а котангенс корню из трёх делённому на три.
Получаем следующие выражения:
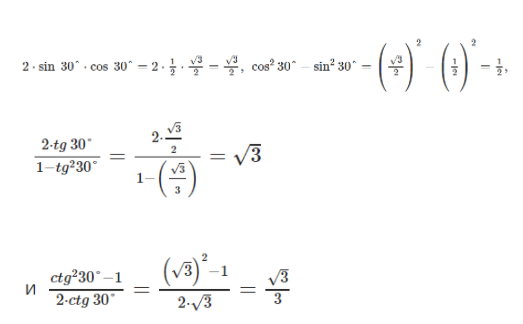
Сделав все операции по вычислению, можно прийти к выводу, что справедливость для угла альфа тридцати градусов, подтверждена.
Теперь мы понимаем, что применение формул тригонометрии двойного угла, это видоизменение тригонометрических выражений. Стоит также рассмотреть пример применения формул двойного угла, в случае, когда угол не равен 2a. К примеру возьмём значение [frac{5 pi}{6}]. Имея такое значение, для решения задания, его необходимо преобразовать, поэтому получаем следующее:
[a=frac{5 pi}{6}: 2=frac{5 pi}{12}], применив данное выражение формула двойного угла для косинуса получит следующий вид:
[ cos frac{5 pi}{6}=cos ^{2} frac{5 pi}{12}-sin ^{2} frac{5 pi}{12} ]
Пример:
Необходимо, через тригонометрические функции представить [sin frac{2 a}{3} text { при } frac{a}{6}].
Решение:
Так как в условии уже [frac{2 a}{3}=4 * frac{a}{6}], то применив дважды выше обозначенную формулу удвоенного угла, что выражая [sin frac{2 a}{3}], через функции угла [frac{a}{6}], с применением формулы двойного угла, выходит , [sin frac{2 a}{3}=2 * sin frac{a}{3} * cos frac{a}{3}], затем к [sin frac{a}{3} text { и } cos frac{a}{3}]в данном примере подставим снова данную формулу удвоенного угла и получим следующее выражение:
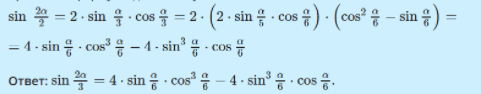
Формулы тройного угла и более углов
Так как зачастую в тригонометрии возникает необходимость вычисления не только двойного угла, но и больше, например тройного, четверного и тд. Стоит рассмотреть примеры их вычисления. Выведение их формул аналогично с выведением формул двойного угла, но для этого будем применять формулы сложения (суммы) двойного угла.
Пример:
sin 3α = sin ( 2 α + α ) = sin 2α * cos α + cos 2 α * sin α = 2 * sin α ⋅ cos α * cos α + ( cos2α — sin2α ) * sin α =
=3 * sin α * cos2α — sin3α
Заменим cos2α, на выражение 1 — sin2α, и теперь получившаяся ранее формула тройного угла sin 3α =3 * sin α * cos2α — sin3α, примет следующий вид: sin 3α = 3 * sin α * cos2α — sin3α = 3 *sin α — 4* sin3α
Аналогично поступим и с формулами cos тройного угла:
cos 3α = cos ( 2 α + α ) = cos 2α * cos α − sin 2α *sin α = ( cos2α — sin2α ) * cos α − 2* sin α * cos α * sin α =
= cos3α − 3* sin2α * cos α
Заменяем sin2α на выражение разности единицы и косинуса, 1 — cos2α, выходит следующая формула : cos 3α =
= -3 * cos α + 4* cos3α
Так как теперь у нас есть формулы тройного угла синуса и косинуса, мы можем вывести формулы тройного угла для тангенса и котангенса, подставив полученные выражения в первичные формулы:

И так далее…
К примеру, чтобы привести формулу угла четыре альфа, для удобства лучше 4а представить, как 2 * 2а, и в результате мы получим, что для выведения формулы для 4а, нужно использовать две формулы двойного угла.
А для выведения формулы угла пятой степени, 5а, необходимо выполнить 5а как сумму тройного и двойного угла, то есть 2а+3а.
В результате мы получим выражение из суммы двух формул двойного и тройного угла. Стоит отметить, что такое же правило будет действовать если необходимо вывести формулу половинного угла.
Область применения
Для того чтобы найти значение тригонометрических функций, берётся окружность на оси координат, у которой радиус равен единице, а диаметры у неё находятся в перпендикулярном положении.
Для такого вычисления нам понадобится отложить от точки, которая принадлежит окружности различные дуги, любой длины. Соответственно если мы отложим их против часовой стрелки они примут положительное значение, а если по часовой, то отрицательное.
Допустим конец дуги имеет некую длину s, в таком случае проекция радиуса в любом выбранном значении диаметра станет значением косинуса данной дуги. Выбранная длина s, или радианная мера угла, будет считаться числом аргумента. А если этот самый аргумент, это тригонометрическая функция угла, то мы знаем, что значение может быть и в градусах.
Мы знаем, что острый угол имеет значения больше нуля, но меньше п2. В таком случае тригонометрическая функция рассматривается как катет делённый на гипотенузу. Такие названия сторон связаны с прямоугольным треугольником, в котором величина угла равна 90 градусов.
Чтобы решить задачи с функциями тригонометрии, используют теорему Пифагора. Такая теорема основана на свойствах того самого прямоугольного треугольника, в котором квадрат гипотенузы равен сумму квадратов катетов.
Так как дуга делит окружность на несколько частей, то мы можем увидеть, что углы лежащие в первой четверти больше нуля. А во второй синус меньше, а косинус больше нуля, а в третьей все функции будут меньше нуля, то есть отрицательными, четвёртая имеет значения противоположные второй. Не стоит забывать, что для построения окружности вам понадобится циркуль.
Как мы видим формулы двойного угла, не так трудно вывести, для этого необходимо знать основные тригонометрические тождества и разобраться в единичной окружности на оси координат. Также необходимо отметить, что формулы двойного угла, как и другие формулы тригонометрии используются в разных сферах жизни:
- В астрономии, учёные с помощью формул вычисляют положение небесных тел, а также расстояние до них;
- Для различного вида навигации, к примеру, морской и воздушной;
- В медицине и биологии, при построении биоритма живых организмов, а также тригонометрия служит основой работы некоторой медицинской техники;
- Архитекторам она важна при создании планов строений;
- но и это не всё, тригонометрия важна и для экономики, в производстве и создании электроники, в различных аналитических вычислениях, акустических построениях и многом другом.
Автор: Виктория Андрианова, менеджер кафедры математики АПО.
Одна из моих учениц обучается в классе «Математическая вертикаль». Рассказала недавно, что начали изучать тригонометрию. Начало 9 класса и сразу тригонометрия. Так еще и на уроке геометрии. Сначала не поняла, начала разбираться в программе. И… мне захотелось этим поделиться.
Как показал опрос подписчиков нашей группы «Олимпиады по математике», большинству тригонометрические функции либо выводили через окружность единичного радиуса, либо вообще не выводили.
Я хочу показать достаточно простой и красивый способ их вывода через геометрию.
Классическое доказательство
Не берусь судить за все школы, но мне в 9 классе, как и большинству, все показывали через окружность с радиусом 1. Давайте сначала разберем это доказательство.
Косинус разности и косинус суммы
Чтобы вывести формулу косинуса суммы, отметим углы a и b так, как показано на рисунке ниже.
Из определений синуса и косинуса узнаем координаты точек А и В. Тогда вектор ОА равен (cos a, sin a), а ОВ равен (cos b, sin b). Также известно, что длины этих векторов равны 1. Давайте запишем скалярное произведение этих вектором двумя различными способами. Напомню необходимые формулы.
Тогда |OA|*|OB|*cos(a-b) = cos a * cos b + sin a * sin b. Но |ОА| = 1 и |ОВ| = 1.
Следовательно, cos(a-b) = cos a * cos b + sin a * sin b.
Формула для косинуса суммы доказывается аналогичным образом.
cos(a+b) = cos a * cos b — sin a * sin b.
Синус разности и синус суммы
Формулы синусов доказываются, когда мы уже вывели формулы для косинусов. Нужно только воспользоваться формулой приведения.
Формула синуса суммы доказывается подобным образом.
Доказательство через геометрию
Для начала давайте разберемся, что если у прямоугольного треугольника гипотенуза равна 1, то его катеты будут равны косинусу и синусу соответствующего угла.
Отсюда легко вывести основное тригонометрическое тождество. Достаточно записать теорему Пифагора для данного треугольника.
Косинус суммы
Когда мы разобрались со сторонами прямоугольного треугольника с единичной гипотенузой, выведем формулу косинуса суммы. Будем пользоваться следующей картинкой
Рассмотрим прямоугольный треугольник АНВ. В нем гипотенуза равна 1. Тогда длина отрезка АН является искомым cos (a+b). АН найдем путем вычитания из длины отрезка AD отрезок HD.
АС = cos (a) из треугольника АВС. Теперь мы можем найти АD из прямоугольного треугольника ACD. АD катет, прилежащий к углу b. Поэтому AD = AC * cos (b) = cos (a) * cos (b).
Заметим далее, что HD = BE (т.к. HDEB прямоугольник). ВС = sin (a) (из треугольника АВС). Тогда ВЕ = ВС * sin (b) = sin (a) * sin (b). НD = sin (a) * sin (b).
Отсюда искомый АН = cos (a+b) = cos (a) * cos (b) — sin (a) * sin (b).
Чтобы вывести формулу для косинуса разности, достаточно вместо угла b подставить угол -b.
cos (a-b) = cos (a) * cos (b) — sin (a) * sin (-b) = cos (a) * cos (b) +sin (a) * sin (b).
Синус суммы
Теперь выведем формулу синуса суммы при помощи той же картинки.
Синусом угла a+b будет отрезок ВН. Найдем его как сумму ЕС и CD.
ЕС = ВС * cos b. ВС = sin a. Тогда ЕС = sin (a) * cos (b).
CD = AC * sin b. AC = cos a. Отсюда CD = sin (b) * cos (a).
Наконец выразим ВН. ВН = sin (a+b) = sin (a) * cos (b) + sin (b) * cos (a).
Ну, а чтобы вывести синус разности, опять подставим в уже имеющуюся формулу угол -b.
sin (a-b) = sin (a) * cos (-b) + sin (-b) * cos (a) = sin (a) * cos (b) -sin (b) * cos (a).
Синус и косинус двойного угла
Конечно, зная формулы косинуса и синуса суммы, можно выразить формулы и для двойных углов. Но я предлагаю вам воспользоваться следующими картинками и вывести их самостоятельно.
Хочу заметить, что треугольники АВС в обоих случаях равны.











