Василий Котеночкин
[24.9K]
более года назад
Для начала было бы неплохо уточнить: единица в каких единицах измеряется? В радианах или в градусах? Впрочем, ни синус одного градуса, ни синус одного радиана аналитически не вычисляются. И находить эти значения можно только на компьютере, калькуляторе или в таблицах Брадиса. Учащимся школ иногда запрещают пользоваться калькуляторами, но таблицы Брадиса не запрещены.
Синус одного радиана равен 0,8414709848.
Синус одного градуса — 0,0174524064
автор вопроса выбрал этот ответ лучшим
комментировать
в избранное
ссылка
отблагодарить
Единичная окружность помогает понять, чему равны sin 1, sin 2, sin 3, sin 4, sin 5, sin 6.
Итак, речь идет об углах в радианах. 1 радиан — это угол, длина дуги которого равна радиусу окружности. Соответственно, определяем приблизительное местонахождение на единичной окружности углов в 2, 3, 4, 5 и 6 радиан, отмечая каждую следующую точку через дугу, длина которой равна радиусу. Впрочем, если вспомнить, что п приближенно равно 3,14, задача существенно упростится.
Рисунок позволяет наглядно определять приблизительные значения sin 1, sin 2, sin 3, sin 4, sin 5, sin 6, а также сравнивать их.
Поскольку синус — это ордината соответствующей точки на единичной окружности (как это легко запомнить — здес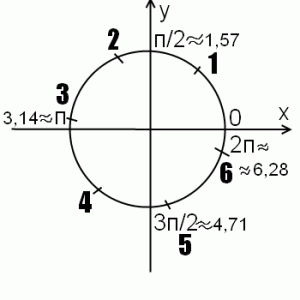
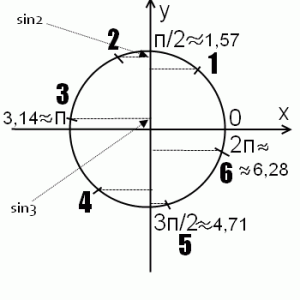
Соответственно внизу синус отрицателен: sin 4<0, sin 5<0, sin 6<o. Поэтому легко сравнить sin2 и sin4, например: sin2>sin4, ведь любое положительное число больше любого отрицательного.
Если требуется сравнить значения синуса одного знака, например, sin2 и sin3, то исходя из геометрических соображений, sin2>sin3.
Если нужно уточнить, чему равен 1 радиан, 2, 3, 4, 5 и 6 радиан в градусах, то приближенные значения таковы:
Приближенно чему равен синус 1, синус 2 и синус 3, можно узнать по таблицам Брадиса:
Используя геометрические соображения, можно найти и приблизительные значения углов, больших 6 радиан.
Узнать ещё
Знание — сила. Познавательная информация
sin x =1
Эта ассоциация помогает легко запомнить значения x, в которых синус равен 1, и быстро решить уравнение sin x =1.
Частные случаи синуса, как и частные случаи косинуса, удобнее всего искать на единичной окружности.
Итак, косинус — колобок. Оба начинаются с ко-, и буква o в имени cos x такая же круглая, как колобок.
Как движется колобок? Влево-вправо, с его круглой фигурой вверх-вниз особо не попрыгаешь. На координатной плоскости влево-вправо движется x. Значит, косинус — это x, а синус — это y.
Поэтому, чтобы определить, где sin x =1, нам надо найти, где на единичной окружности y=1. Двигаемся вверх по оси y и попадаем в точку п/2.
Это только одна из точек, в которых синус равен единице.
Через полный оборот окружности мы снова попадем в эту точку, через два, три и т.д. оборотов — тоже.
Если пойдем по часовой стрелке, то есть -2п, -2п·2, -2п·3 и т.д., то тоже попадем в эту точку.
Чтобы учесть все точки, в которых sin x =1, прибавляем к п/2 2пn, где n — целое число (n принадлежит Z). То есть n=0,±1,±2,±3,…
Таблица СИНУСОВ для углов от 0° до 360° градусов
СИНУС (SIN α) — это одна из прямых тригонометрических функций для углов, в прямоугольном треугольнике синус острого угла равен отношению противолежащего катета к его единственной гипотенузе.
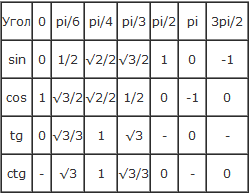
| α (радианы) | 0 | π/6 | π/4 | π/3 | π/2 | π | √3π/2 | 2π |
|---|---|---|---|---|---|---|---|---|
| α (градусы) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| SIN α (СИНУС) | 0 | 1/2 | √ 2/2 | √3 /2 | 1 | 0 | -1 | 0 |
Малая таблица значений тригонометрических функций (в радианах и градусах)
| Угол в градусах | Sin (Синус) |
|---|---|
| 0° | 0 |
| 1° | 0.0175 |
| 2° | 0.0349 |
| 3° | 0.0523 |
| 4° | 0.0698 |
| 5° | 0.0872 |
| 6° | 0.1045 |
| 7° | 0.1219 |
| 8° | 0.1392 |
| 9° | 0.1564 |
| 10° | 0.1736 |
| 11° | 0.1908 |
| 12° | 0.2079 |
| 13° | 0.225 |
| 14° | 0.2419 |
| 15° | 0.2588 |
| 16° | 0.2756 |
| 17° | 0.2924 |
| 18° | 0.309 |
| 19° | 0.3256 |
| 20° | 0.342 |
| 21° | 0.3584 |
| 22° | 0.3746 |
| 23° | 0.3907 |
| 24° | 0.4067 |
| 25° | 0.4226 |
| 26° | 0.4384 |
| 27° | 0.454 |
| 28° | 0.4695 |
| 29° | 0.4848 |
| 30° | 0.5 |
| 31° | 0.515 |
| 32° | 0.5299 |
| 33° | 0.5446 |
| 34° | 0.5592 |
| 35° | 0.5736 |
| 36° | 0.5878 |
| 37° | 0.6018 |
| 38° | 0.6157 |
| 39° | 0.6293 |
| 40° | 0.6428 |
| 41° | 0.6561 |
| 42° | 0.6691 |
| 43° | 0.682 |
| 44° | 0.6947 |
| 45° | 0.7071 |
| 46° | 0.7193 |
| 47° | 0.7314 |
| 48° | 0.7431 |
| 49° | 0.7547 |
| 50° | 0.766 |
| 51° | 0.7771 |
| 52° | 0.788 |
| 53° | 0.7986 |
| 54° | 0.809 |
| 55° | 0.8192 |
| 56° | 0.829 |
| 57° | 0.8387 |
| 58° | 0.848 |
| 59° | 0.8572 |
| 60° | 0.866 |
| 61° | 0.8746 |
| 62° | 0.8829 |
| 63° | 0.891 |
| 64° | 0.8988 |
| 65° | 0.9063 |
| 66° | 0.9135 |
| 67° | 0.9205 |
| 68° | 0.9272 |
| 69° | 0.9336 |
| 70° | 0.9397 |
| 71° | 0.9455 |
| 72° | 0.9511 |
| 73° | 0.9563 |
| 74° | 0.9613 |
| 75° | 0.9659 |
| 76° | 0.9703 |
| 77° | 0.9744 |
| 78° | 0.9781 |
| 79° | 0.9816 |
| 80° | 0.9848 |
| 81° | 0.9877 |
| 82° | 0.9903 |
| 83° | 0.9925 |
| 84° | 0.9945 |
| 85° | 0.9962 |
| 86° | 0.9976 |
| 87° | 0.9986 |
| 88° | 0.9994 |
| 89° | 0.9998 |
| 90° | 1 |
Полная таблица синусов для углов от 0° до 360° с шагом всего в 1°
| Угол в градусах | Sin (Синус) |
|---|---|
| 91° | 0.9998 |
| 92° | 0.9994 |
| 93° | 0.9986 |
| 94° | 0.9976 |
| 95° | 0.9962 |
| 96° | 0.9945 |
| 97° | 0.9925 |
| 98° | 0.9903 |
| 99° | 0.9877 |
| 100° | 0.9848 |
| 101° | 0.9816 |
| 102° | 0.9781 |
| 103° | 0.9744 |
| 104° | 0.9703 |
| 105° | 0.9659 |
| 106° | 0.9613 |
| 107° | 0.9563 |
| 108° | 0.9511 |
| 109° | 0.9455 |
| 110° | 0.9397 |
| 111° | 0.9336 |
| 112° | 0.9272 |
| 113° | 0.9205 |
| 114° | 0.9135 |
| 115° | 0.9063 |
| 116° | 0.8988 |
| 117° | 0.891 |
| 118° | 0.8829 |
| 119° | 0.8746 |
| 120° | 0.866 |
| 121° | 0.8572 |
| 122° | 0.848 |
| 123° | 0.8387 |
| 124° | 0.829 |
| 125° | 0.8192 |
| 126° | 0.809 |
| 127° | 0.7986 |
| 128° | 0.788 |
| 129° | 0.7771 |
| 130° | 0.766 |
| 131° | 0.7547 |
| 132° | 0.7431 |
| 133° | 0.7314 |
| 134° | 0.7193 |
| 135° | 0.7071 |
| 136° | 0.6947 |
| 137° | 0.682 |
| 138° | 0.6691 |
| 139° | 0.6561 |
| 140° | 0.6428 |
| 141° | 0.6293 |
| 142° | 0.6157 |
| 143° | 0.6018 |
| 144° | 0.5878 |
| 145° | 0.5736 |
| 146° | 0.5592 |
| 147° | 0.5446 |
| 148° | 0.5299 |
| 149° | 0.515 |
| 150° | 0.5 |
| 151° | 0.4848 |
| 152° | 0.4695 |
| 153° | 0.454 |
| 154° | 0.4384 |
| 155° | 0.4226 |
| 156° | 0.4067 |
| 157° | 0.3907 |
| 158° | 0.3746 |
| 159° | 0.3584 |
| 160° | 0.342 |
| 161° | 0.3256 |
| 162° | 0.309 |
| 163° | 0.2924 |
| 164° | 0.2756 |
| 165° | 0.2588 |
| 166° | 0.2419 |
| 167° | 0.225 |
| 168° | 0.2079 |
| 169° | 0.1908 |
| 170° | 0.1736 |
| 171° | 0.1564 |
| 172° | 0.1392 |
| 173° | 0.1219 |
| 174° | 0.1045 |
| 175° | 0.0872 |
| 176° | 0.0698 |
| 177° | 0.0523 |
| 178° | 0.0349 |
| 179° | 0.0175 |
| 180° | 0 |
Полная таблица синусов для углов от 91° до 180°
| Угол | Sin (Синус) |
|---|---|
| 181° | -0.0175 |
| 182° | -0.0349 |
| 183° | -0.0523 |
| 184° | -0.0698 |
| 185° | -0.0872 |
| 186° | -0.1045 |
| 187° | -0.1219 |
| 188° | -0.1392 |
| 189° | -0.1564 |
| 190° | -0.1736 |
| 191° | -0.1908 |
| 192° | -0.2079 |
| 193° | -0.225 |
| 194° | -0.2419 |
| 195° | -0.2588 |
| 196° | -0.2756 |
| 197° | -0.2924 |
| 198° | -0.309 |
| 199° | -0.3256 |
| 200° | -0.342 |
| 201° | -0.3584 |
| 202° | -0.3746 |
| 203° | -0.3907 |
| 204° | -0.4067 |
| 205° | -0.4226 |
| 206° | -0.4384 |
| 207° | -0.454 |
| 208° | -0.4695 |
| 209° | -0.4848 |
| 210° | -0.5 |
| 211° | -0.515 |
| 212° | -0.5299 |
| 213° | -0.5446 |
| 214° | -0.5592 |
| 215° | -0.5736 |
| 216° | -0.5878 |
| 217° | -0.6018 |
| 218° | -0.6157 |
| 219° | -0.6293 |
| 220° | -0.6428 |
| 221° | -0.6561 |
| 222° | -0.6691 |
| 223° | -0.682 |
| 224° | -0.6947 |
| 225° | -0.7071 |
| 226° | -0.7193 |
| 227° | -0.7314 |
| 228° | -0.7431 |
| 229° | -0.7547 |
| 230° | -0.766 |
| 231° | -0.7771 |
| 232° | -0.788 |
| 233° | -0.7986 |
| 234° | -0.809 |
| 235° | -0.8192 |
| 236° | -0.829 |
| 237° | -0.8387 |
| 238° | -0.848 |
| 239° | -0.8572 |
| 240° | -0.866 |
| 241° | -0.8746 |
| 242° | -0.8829 |
| 243° | -0.891 |
| 244° | -0.8988 |
| 245° | -0.9063 |
| 246° | -0.9135 |
| 247° | -0.9205 |
| 248° | -0.9272 |
| 249° | -0.9336 |
| 250° | -0.9397 |
| 251° | -0.9455 |
| 252° | -0.9511 |
| 253° | -0.9563 |
| 254° | -0.9613 |
| 255° | -0.9659 |
| 256° | -0.9703 |
| 257° | -0.9744 |
| 258° | -0.9781 |
| 259° | -0.9816 |
| 260° | -0.9848 |
| 261° | -0.9877 |
| 262° | -0.9903 |
| 263° | -0.9925 |
| 264° | -0.9945 |
| 265° | -0.9962 |
| 266° | -0.9976 |
| 267° | -0.9986 |
| 268° | -0.9994 |
| 269° | -0.9998 |
| 270° | -1 |
Таблица синусов для углов 181° — 270°
| Угол | Sin (Синус) |
|---|---|
| 271° | -0.9998 |
| 272° | -0.9994 |
| 273° | -0.9986 |
| 274° | -0.9976 |
| 275° | -0.9962 |
| 276° | -0.9945 |
| 277° | -0.9925 |
| 278° | -0.9903 |
| 279° | -0.9877 |
| 280° | -0.9848 |
| 281° | -0.9816 |
| 282° | -0.9781 |
| 283° | -0.9744 |
| 284° | -0.9703 |
| 285° | -0.9659 |
| 286° | -0.9613 |
| 287° | -0.9563 |
| 288° | -0.9511 |
| 289° | -0.9455 |
| 290° | -0.9397 |
| 291° | -0.9336 |
| 292° | -0.9272 |
| 293° | -0.9205 |
| 294° | -0.9135 |
| 295° | -0.9063 |
| 296° | -0.8988 |
| 297° | -0.891 |
| 298° | -0.8829 |
| 299° | -0.8746 |
| 300° | -0.866 |
| 301° | -0.8572 |
| 302° | -0.848 |
| 303° | -0.8387 |
| 304° | -0.829 |
| 305° | -0.8192 |
| 306° | -0.809 |
| 307° | -0.7986 |
| 308° | -0.788 |
| 309° | -0.7771 |
| 310° | -0.766 |
| 311° | -0.7547 |
| 312° | -0.7431 |
| 313° | -0.7314 |
| 314° | -0.7193 |
| 315° | -0.7071 |
| 316° | -0.6947 |
| 317° | -0.682 |
| 318° | -0.6691 |
| 319° | -0.6561 |
| 320° | -0.6428 |
| 321° | -0.6293 |
| 322° | -0.6157 |
| 323° | -0.6018 |
| 324° | -0.5878 |
| 325° | -0.5736 |
| 326° | -0.5592 |
| 327° | -0.5446 |
| 328° | -0.5299 |
| 329° | -0.515 |
| 330° | -0.5 |
| 331° | -0.4848 |
| 332° | -0.4695 |
| 333° | -0.454 |
| 334° | -0.4384 |
| 335° | -0.4226 |
| 336° | -0.4067 |
| 337° | -0.3907 |
| 338° | -0.3746 |
| 339° | -0.3584 |
| 340° | -0.342 |
| 341° | -0.3256 |
| 342° | -0.309 |
| 343° | -0.2924 |
| 344° | -0.2756 |
| 345° | -0.2588 |
| 346° | -0.2419 |
| 347° | -0.225 |
| 348° | -0.2079 |
| 349° | -0.1908 |
| 350° | -0.1736 |
| 351° | -0.1564 |
| 352° | -0.1392 |
| 353° | -0.1219 |
| 354° | -0.1045 |
| 355° | -0.0872 |
| 356° | -0.0698 |
| 357° | -0.0523 |
| 358° | -0.0349 |
| 359° | -0.0175 |
| 360° | 0 |
Таблица синусов для углов от 271° до 360°
Таблица синусов особенно нужна, когда у вас под рукой нет супер навороченного инженерного калькулятора с маленькой спасительной кнопкой с надписью «sin». В таком случае, чтобы узнать, чему же равняется синус определенного заданного угла, просто найдите информацию о интересующем градусе.
Как распечатать таблицу? Левой кнопкой на компьютерной мишке выделите полностью всё таблицу, на выделенном фоне нажмите уже правую кнопку мишки и в появившемся меню перейдете в пункт «Печать».
Как пользоваться таблицей? Всё гораздо проще, чем Вы думаете, ищем в левой вертикальной колонке, соответствующий градус, и напротив него и будет указано нужное значение синуса для данного нужного нам угла.
Чему равен синус 45? …
— А вот собственно и сам ответ на поставленную задачку.sin 45 = 0.7071
Тригонометрический круг: вся тригонометрия на одном рисунке
Тригонометрический круг — это самый простой способ начать осваивать тригонометрию. Он легко запоминается, и на нём есть всё необходимое.
Тригонометрический круг заменяет десяток таблиц.
Вот что мы видим на этом рисунке:
А теперь подробно о тригонометрическом круге:
Нарисована единичная окружность — то есть окружность с радиусом, равным единице, и с центром в начале системы координат. Той самой системы координат с осями и , в которой мы привыкли рисовать графики функций.
Мы отсчитываем углы от положительного направления оси против часовой стрелки.
Полный круг — градусов.
Точка с координатами соответствует углу ноль градусов. Точка с координатами отвечает углу в , точка с координатами — углу в . Каждому углу от нуля до градусов соответствует точка на единичной окружности.
Косинусом угла называется абсцисса (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .
Синусом угла называется ордината (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .
Всё это легко увидеть на нашем рисунке.
Итак, косинус и синус — координаты точки на единичной окружности, соответствующей данному углу. Косинус — абсцисса , синус — ордината . Поскольку окружность единичная, для любого угла и синус, и косинус находятся в пределах от до :
Простым следствием теоремы Пифагора является основное тригонометрическое тождество:
Для того, чтобы узнать знаки синуса и косинуса какого-либо угла, не нужно рисовать отдельных таблиц. Всё уже нарисовано! Находим на нашей окружности точку, соответствующую данному углу , смотрим, положительны или отрицательны ее координаты по (это косинус угла ) и по (это синус угла ).
Принято использовать две единицы измерения углов: градусы и радианы. Перевести градусы в радианы просто: градусов, то есть полный круг, соответствует радиан. На нашем рисунке подписаны и градусы, и радианы.
Если отсчитывать угол от нуля против часовой стрелки — он положительный. Если отсчитывать по часовой стрелке — угол будет отрицательным. Например, угол — это угол величиной в , который отложили от положительного направления оси по часовой стрелке.
Легко заметить, что
Углы могут быть и больше градусов. Например, угол — это два полных оборота по часовой стрелке и еще . Поскольку, сделав несколько полных оборотов по окружности, мы возвращаемся в ту же точку с теми же координатами по и по , значения синуса и косинуса повторяются через . То есть:
где — целое число. То же самое можно записать в радианах:
Можно на том же рисунке изобразить ещё и оси тангенсов и котангенсов, но проще посчитать их значения. По определению,
http://kvn201.com.ua/table-of-sines.htm
http://ege-study.ru/ru/ege/materialy/matematika/trigonometricheskij-krug/
Синус онлайн калькулятор
Введите число от 0 до 360.
(обязательное поле)
Введите число от 0 до 59.
(не обязательное поле, по умолчанию — 0)
Введите число от 0 до 59.
(не обязательное поле, по умолчанию — 0)
Математика, Геометрия 9 класс.
Cинус 1 градусов.
Cинус 1 градусов таблица.
Синус 1 градусов 0 минут равен = 0.0175
Синус 1 градусов 1 минут равен = 0.0177
Синус 1 градусов 2 минут равен = 0.018
Синус 1 градусов 3 минут равен = 0.0183
Синус 1 градусов 4 минут равен = 0.0186
Синус 1 градусов 5 минут равен = 0.0189
Синус 1 градусов 6 минут равен = 0.0192
Синус 1 градусов 7 минут равен = 0.0195
Синус 1 градусов 8 минут равен = 0.0198
Синус 1 градусов 9 минут равен = 0.0201
Синус 1 градусов 10 минут равен = 0.0204
Синус 1 градусов 11 минут равен = 0.0207
Синус 1 градусов 12 минут равен = 0.0209
Синус 1 градусов 13 минут равен = 0.0212
Синус 1 градусов 14 минут равен = 0.0215
Синус 1 градусов 15 минут равен = 0.0218
Математика, Геометрия 9 класс.
Синус 1 таблица.
Синус 1 градусов 16 минут равен = 0.0221
Синус 1 градусов 17 минут равен = 0.0224
Синус 1 градусов 18 минут равен = 0.0227
Синус 1 градусов 19 минут равен = 0.023
Синус 1 градусов 20 минут равен = 0.0233
Синус 1 градусов 21 минут равен = 0.0236
Синус 1 градусов 22 минут равен = 0.0239
Синус 1 градусов 23 минут равен = 0.0241
Синус 1 градусов 24 минут равен = 0.0244
Синус 1 градусов 25 минут равен = 0.0247
Синус 1 градусов 26 минут равен = 0.025
Синус 1 градусов 27 минут равен = 0.0253
Синус 1 градусов 28 минут равен = 0.0256
Синус 1 градусов 29 минут равен = 0.0259
Синус 1 градусов 30 минут равен = 0.0262
Математика, Геометрия 9 класс.
Синус 1 равен:
Таблица значений синусов 1 градусов.
Синус 1 градусов 31 минут равен = 0.0265
Синус 1 градусов 32 минут равен = 0.0268
Синус 1 градусов 33 минут равен = 0.027
Синус 1 градусов 34 минут равен = 0.0273
Синус 1 градусов 35 минут равен = 0.0276
Синус 1 градусов 36 минут равен = 0.0279
Синус 1 градусов 37 минут равен = 0.0282
Синус 1 градусов 38 минут равен = 0.0285
Синус 1 градусов 39 минут равен = 0.0288
Синус 1 градусов 40 минут равен = 0.0291
Синус 1 градусов 41 минут равен = 0.0294
Синус 1 градусов 42 минут равен = 0.0297
Синус 1 градусов 43 минут равен = 0.03
Синус 1 градусов 44 минут равен = 0.0302
Синус 1 градусов 45 минут равен = 0.0305
Математика, Геометрия 9 класс.
Найти синус 1 градусов:
SIN 1 градусов равен:
Синус 1 градусов 46 минут равен = 0.0308
Синус 1 градусов 47 минут равен = 0.0311
Синус 1 градусов 48 минут равен = 0.0314
Синус 1 градусов 49 минут равен = 0.0317
Синус 1 градусов 50 минут равен = 0.032
Синус 1 градусов 51 минут равен = 0.0323
Синус 1 градусов 52 минут равен = 0.0326
Синус 1 градусов 53 минут равен = 0.0329
Синус 1 градусов 54 минут равен = 0.0332
Синус 1 градусов 55 минут равен = 0.0334
Синус 1 градусов 56 минут равен = 0.0337
Синус 1 градусов 57 минут равен = 0.034
Синус 1 градусов 58 минут равен = 0.0343
Синус 1 градусов 59 минут равен = 0.0346
Синус 1 градусов 60 минут равен = 0.0349
Недавние расчеты
Синус 1 градусов 59 минут и 53 секунд равен = 0.03486558039821
(0.034872648082209 радиан)
Синус 1 градусов 21 минут и 29 секунд равен = 0.023700321542621
(0.023702540869445 радиан)
Синус 1 градусов 17 минут и 47 секунд равен = 0.022624323971467
(0.022626254497382 радиан)
Синус 1 градусов 15 минут и 0 секунд равен = 0.021814885034561
(0.021816615649929 радиан)
Синус 1 градусов 24 минут и 5 секунд равен = 0.024456411593436
(0.024458850211976 радиан)
Синус 1 градусов 56 минут и 37 секунд равен = 0.03391590771776
(0.033922413267234 радиан)
Синус 1 градусов 5 минут и 25 секунд равен = 0.01902778860659
(0.019028936983549 радиан)
Синус 1 градусов 57 минут и 2 секунд равен = 0.034037041159098
(0.034043616687512 радиан)
Синус 1 градусов 6 минут и 31 секунд равен = 0.019347706726416
(0.019348914013082 радиан)
Синус 1 градусов 10 минут и 26 секунд равен = 0.020486792812163
(0.020488226163689 радиан)
В данной таблице представлены значения синусов от 0° до 360°. Таблица синусов нужна, когда у вас под рукой нет калькулятора. Чтобы узнать, чему равен синус угла, просто найдите нужный градус в таблице. Для начала короткая версия таблицы.
https://uchim.org/matematika/tablica-sinusov — uchim.org
Таблица синусов для 0°-180°
|
|
|
|
Таблица синусов для 181°-360°
|
|
|
|
Существуют также следующие таблицы тригонометрических функций: таблица косинусов, таблица тангенсов и таблица котангенсов.
Как легко запомнить таблицу синусов (видео)
Таблицу важно всегда помнить на алгебре, чтобы найти синус.
Всё для учебы » Математика в школе » Таблица синусов углов (градусы, значения)