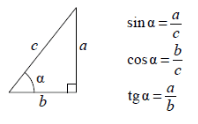6. Геометрия на плоскости (планиметрия). Часть II
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Вычисление синуса, косинуса и тангенса угла треугольника
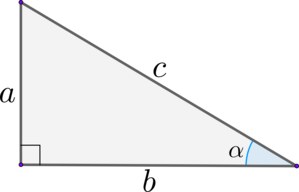
В прямоугольном треугольнике:
(blacktriangleright) Синус острого угла равен отношению противолежащего катета к гипотенузе: [{large{sin alpha =
dfrac{a}{c}}}]
(blacktriangleright) Косинус острого угла равен отношению прилежащего катета к гипотенузе: [{large{cos alpha =
dfrac{b}{c}}}]
(blacktriangleright) Тангенс острого угла равен отношению противолежащего катета к прилежащему: [{large{mathrm{tg}, alpha
= dfrac{a}{b}}}]
(blacktriangleright) Котангенс острого угла равен отношению прилежащего катета к противолежащему: [{large{mathrm{ctg},
alpha =dfrac{b}{a}}}]
Важные формулы:
[{large{begin{array}{|lcl|} hline sin^2 alpha+cos^2 alpha
=1&qquad& mathrm{tg}, alpha cdot mathrm{ctg}, alpha
=1\ &&\
mathrm{tg}, alpha=dfrac{sin alpha}{cos
alpha}&&mathrm{ctg}, alpha
=dfrac{cos alpha}{sin alpha}\&&\
hline
end{array}}}]
[begin{array}{|c|c|c|c|c|c|}
hline & phantom{000}, 0^circ phantom{000}& phantom{000},
30^circ phantom{000} &
phantom{000}, 45^circ phantom{000} & phantom{000}, 60^circ phantom{000}
& phantom{000}, 90^circ phantom{000}\[1ex]
hline sin & 0 ½&frac{sqrt2}2&frac{sqrt3}2 & 1\[1ex]
hline cos & 1 & frac{sqrt3}2&frac{sqrt2}2½ & 0\[1ex]
hline mathrm{tg} & 0 & frac{sqrt3}3&1&sqrt3 & text{не сущ.}\[1ex]
hline mathrm{ctg}& text{не сущ.} &sqrt3&1&frac{sqrt3}3 & 0\[1ex]
hline
end{array}]
Задание
1
#612
Уровень задания: Легче ЕГЭ
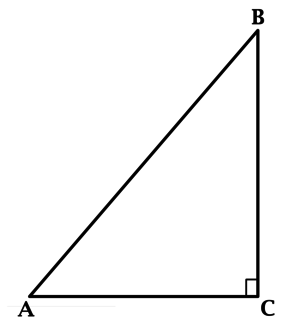
В треугольнике (ABC): (angle C = 90^{circ}), (sin {angle BAC} = dfrac{2}{3}). Найдите (AC), если (AB = 6sqrt{5}).
Синус острого угла в прямоугольном треугольнике равен отношению противолежащего этому углу катета к гипотенузе, тогда [dfrac{BC}{AB} = dfrac{2}{3}qquadRightarrowqquad BC = dfrac{2}{3}AB = 4sqrt{5}.]
По теореме Пифагора (AC^2 = AB^2 — BC^2 = 36cdot 5 — 16cdot 5 = 20cdot 5 = 10^2), тогда (AC = 10).
Ответ: 10
Задание
2
#2098
Уровень задания: Равен ЕГЭ
Дан прямоугольный треугольник (ABC), причем (angle C=90^circ). Известно, что (cos angle B=dfrac13), (AB=9). Найдите (BC).
По определению косинуса [cosangle B=dfrac{BC}{AB}=dfrac13 quad
Leftrightarrow quad BC=dfrac13cdot AB=dfrac13cdot 9=3]
Ответ: 3
Задание
3
#2099
Уровень задания: Равен ЕГЭ
Дан треугольник (ABC), причем (angle C=90^circ). Найдите длину его гипотенузы, если (AC=8, cos angle A=dfrac45).
По определению косинуса [cos angle A=dfrac{AC}{AB}=dfrac45
quad Leftrightarrow quad AB=ACcdot dfrac54=10]
Ответ: 10
Задание
4
#3320
Уровень задания: Равен ЕГЭ
Большее основание равнобедренной трапеции равно (34). Боковая сторона равна (14). Синус острого угла равен (dfrac{2sqrt{10}}7). Найдите меньшее основание.

Проведем (BHperp AD). Из (triangle ABH): [dfrac{2sqrt{10}}7=sinangle A=dfrac{BH}{AB}quadRightarrowquad
BH=4sqrt{10}] Тогда по теореме Пифагора [AH=sqrt{14^2-(4sqrt{10})^2}=6] Так как (AH=0,5(AD-BC)), то (BC=AD-2AH=34-12=22).
Ответ: 22
Задание
5
#3305
Уровень задания: Равен ЕГЭ
В треугольнике (ABC) угол (C=90^circ), (CH) – высота, (AB=13), (mathrm{tg},angle A=0,2). Найдите (AH).
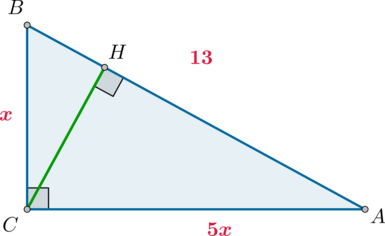
Так как по определению из (triangle ABC): [dfrac{BC}{AC}=mathrm{tg},angle A=dfrac 15] то можно принять (BC=x), (AC=5x). Следовательно, по теореме Пифагора [BC^2+AC^2=AB^2quadRightarrowquad x^2+(5x)^2=13^2quadRightarrowquad
x^2=dfrac{13}2] Из (triangle AHC): [cos angle A=dfrac{AH}{AC}] Из (triangle ABC): [cos angle A=dfrac{AC}{AB}] Следовательно: [dfrac{AH}{AC}=dfrac{AC}{AB}quadRightarrowquad
AH=dfrac{AC^2}{AB}=dfrac{(5x)^2}{13}=dfrac{25}2=12,5]
Ответ: 12,5
Задание
6
#3306
Уровень задания: Равен ЕГЭ
В треугольнике (ABC) угол (C=90^circ), (CH) – высота, (AB=26), (mathrm{tg},angle B=5). Найдите (AH).
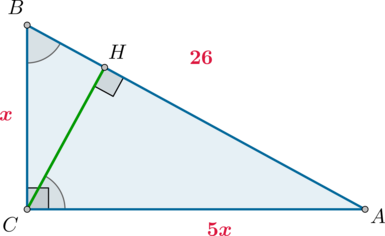
По определению из (triangle ABC): [dfrac{AC}{BC}=mathrm{tg},angle B=dfrac 51] Следовательно, можно принять (AC=5x), (BC=x). Тогда по теореме Пифагора (x^2+(5x)^2=26^2), откуда (x=sqrt{26}).
Тогда [sinangle B=dfrac{AC}{AB}=dfrac5{sqrt{26}}] По свойству прямоугольного треугольника (angle B=angle HCA). Следовательно, из (triangle HCA): [dfrac5{sqrt{26}}=sin angle HCA=dfrac{AH}{AC}quadRightarrowquad
AH=25]
Ответ: 25
Задание
7
#3307
Уровень задания: Равен ЕГЭ
В треугольнике (ABC) угол (C=90^circ), (AB=17), (mathrm{tg},angle A=0,25). Найдите высоту (CH).
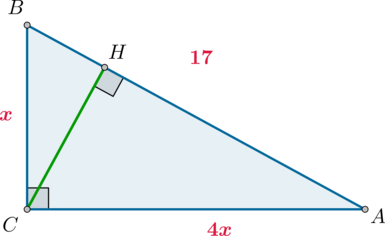
По определению из (triangle ABC): [dfrac{BC}{AC}=mathrm{tg},angle A=dfrac 14] Следовательно, можно принять (AC=4x), (BC=x). Тогда по теореме Пифагора (x^2+(4x)^2=17^2), откуда (x=sqrt{17}).
Так как площадь прямоугольного треугольника (ABC), с одной стороны, равна (0,5CHcdot AB), а с другой стороны, равна (0,5BCcdot AC), то [CHcdot AB=BCcdot ACquadRightarrowquad CH=dfrac{4x^2}{AB}=4]
Ответ: 4
Уметь оперативно и правильно решать задачи ЕГЭ на вычисление элементов многоугольника необходимо всем выпускникам вне зависимости от того, базовый или профильный уровень экзамена они сдают. Причем этой теме традиционно посвящается несколько заданий. Поэтому, если учащийся рассчитывает получить достойные баллы по итогам прохождения ЕГЭ, то ему обязательно стоит уделить внимание задачам, в которых требуется найти синус, косинус и тангенс угла треугольника.
Вместе с образовательным порталом «Школково» вы сможете восполнить пробелы в знаниях и отточить необходимый навык. Весь теоретический и практический материал составлен и изложен таким образом, чтобы все выпускники могли без особых затруднений справляться с задачами ЕГЭ, в которых требуется вычислить тангенс, синус или косинус угла треугольника.
Основные моменты
Первое, что нужно сделать при решении подобных задач в ЕГЭ, — вспомнить, что такое тангенс, косинус и синус угла треугольника. Далее рекомендуется следовать такому алгоритму:
- Выделяем треугольник, в который входит сторона или угол, который требуется найти.
- Определяем известные элементы и выявляем тригонометрическую функцию, которая их связывает.
- Записываем получившееся соотношение и применяем подходящую формулу.
Научившись правильно выполнять упражнения на вычисление элементов многоугольника, а также, например, по теме «Окружность, описанная около многоугольника», которые представлены в данном разделе образовательного портала «Школково», вы сможете закрепить материал и без труда справляться с подобными заданиями на аттестационном экзамене.

Как готовиться к сочинению за 2 дня до ЕГЭ? Четко и без воды
Как готовиться к сочинению за 2 дня до ЕГЭ? Четко и без воды
План урока:
Основное тригонометрическое тождество
Тригонометрические функции суммы и разности
Формулы двойного угла
Формулы понижения степени
Формулы приведения
Сумма тригонометрических функций
Произведение тригонометрических функций
Основное тригонометрическое тождество
Несложно догадаться, что синус и косинус угла – это величины, связанные друг с другом. Отложим на единичной окружности произвольный угол α и опустим из точки А перпендикуляр на ось Ох, в некоторую точку В:
Изучим треугольник АОВ. Он прямоугольный, а потому для него можно записать теорему Пифагора:
АВ2 + ОВ2 = ОА2
Мы рассматриваем единичную окружность, а потому ОА = 1, ОВ = соsα, AB = sinα. Подставив эти величины в равенство, получим тождество:
sin2α + соs2α = 1
Его называют основным тригонометрическим тождеством, ведь именно оно связывает значение двух прямых тригонометрических ф-ций – синуса и косинуса.
Задание. В прямоугольном треугольнике есть угол α. Известно, что sin α = 0,8. Чему равен соsα?
Решение. Подставим в основное тригон-кое тождество значение sinα = 0,8 и получим уравнение:
sin2α + соs2α = 1
0,82 + соs2α = 1
0,64 + соs2α = 1
соs2α = 1 – 0,64
соs2α = 0,36
соsα = – 0,6 или соsα = 0,6
Нашли два возможных значения косинуса. Но по условию α – это острый угол, ведь в прямоугольном треугольнике угол не может быть больше 90°. То есть угол α относится к первой четверти, а потому его косинус положителен. Значит, соsα = 0,6.
Ответ: 0,6.
Рассмотренный пример показал, что одному заданному значению синуса соответствует сразу два противоположных друг другу значения косинуса. Верно и обратное. Действительно, отложим по оси Ох некоторую величину соsα и проведем вертикальную линию, чтобы найти соответствующие ему значения синуса. Она пересечет единичную окружность в двух точках с противоположными ординатами:
По этой причине при решении задач на использование основного тригон-кого тождества обычно указывают, к какой четверти относится угол α.
Задание. Вычислите sinα, если соsα = 0,28 и α принадлежит IV четверти.
Решение.
sin2α + соs2α = 1
0,282 + sin2α = 1
0,0784 + sin2α = 1
sin2α = 1 – 0,0784
sin2α = 0,9216
sin α = –0,96 или sin α = 0,96
Так как α принадлежит IV четверти, то sinα должен быть отрицательным, поэтому sinα = – 0,96.Напомним, что в IV четверти значение косинуса положительно, ведь соответствующая ей дуга единичной окружности располагается правее оси Оу, то есть абсциссы точек, принадлежащих ей, положительны.
Ответ: – 0,96.
Задание. Найдите tgα, если sinα = 5/13 и π/2 < α < π.
Решение. Здесь задача уже в два действия! Сначала определим соsα:
sin2α + соs2α = 1
соs2α = 1 – sin2α = 1 – (5/13)2 = 169/169 – 25/169 = 144/169
соsα = – 12/13 или соsα = 12/13
Условие π/2 < α < π указывает на то, что угол относится ко II четверти, в которой косинус отрицателен, поэтому соsα = – 12/13.
Далее находим тангенс, просто деля синус на косинус:
tgα = sinα:соsα = (5/13):(12/13) = (5/13)•(13/12) = 5/12
Ответ: 5/12
Рассмотренный пример показал нам, что, зная синус, можно рассчитать не только косинус, но и тангенс. А возможно ли совершить обратное действие, найти по тангенсу синус или косинус? Да, но для этого нужно получить новую тригонометрическую формулу.
Запишем тождество
sin2α + соs2α = 1
Далее поделим его на величину соs2α:
Крайнее левое слагаемое – это величина tg2α, а следующая дробь равна единице, так как у неё совпадают числитель и знаменатель:
В итоге нам удалось получить ф-лу, которая связывает значение тангенса и косинуса угла. Есть такая формула и для котангенса. Для ее получения необходимо поделить основное тригон-кое тождество на sin2α:
Задание. Известно, что tgα = 0,75. Найдите соsα и sinα, если угол α принадлежит III четверти.
Решение.
Просто подставляем в ф-лу известное значение тангенса и решаем получившееся уравнение. Для простоты вычислении заменим десятичную дробь 0,75 на обычную 3/4:
Так как угол относится к III четверти, где косинус отрицателен, то
соsα = – 0,8
Синус угла найдем, используя основное тригон-кое тождество:
sin2α + соs2α = 1
sin2α = 1 – соs2α = 1 – (– 0,8)2 = 1 – 0,64 = 0,36
sinα = – 0,6 или sinα = 0,6
С учетом того, что в III четверти синус становится отрицательным, следует выбрать вариант sinα = – 0,6
Ответ: sinα = – 0,6; соsα = – 0,8.
Иногда ф-лы используют не для вычисления значений тригон-ких выражений, а для упрощения выражений. Из тождества sin2α + соs2α = 1 несложно получить из выражения
sin2α = 1 – соs2α
и
соs2α = 1 – sin2α
которые помогают в работе с длинными ф-лами.
Задание. Упростите выражение
4sin2α + 9соs2α – 6
таким образом, чтобы в нем не содержалось синуса.
Решение. Произведем замену sin2α = 1 – соs2α:
4sin2α+ 9соs2α – 6 = 4(1 – соs2α)+ 9соs2α – 6 =
= 4 – 4 соs2α + 9соs2α – 6 = 5соs2α – 2
Видим, что получилось значительно более простое выражение.
Ответ: 5соs2α – 2.
Задание. Избавьтесь от синуса в выражении
sin4α – соs4α
Решение. Воспользуемся ф-лой разности квадратов:
sin4α – соs4α = (sin2α – соs2α)(sin2α + соs2α) = (sin2α – соs2α)•1 =
= 1 – соs2α– соs2α = 1 – 2 соs2α
Ответ:1 – 2 соs2α.
Задание. Упростите дробь
Решение.
Ответ: ctg6α.
Тригонометрические функции суммы и разности
Легко проводить вычисления, когда все тригонометрические действия выполняются над одним углом α. Однако иногда в задачах добавляется ещё один угол, который обычно обозначают как β. Существуют ф-лы, с помощью которых можно вычислять тригон-кие ф-ции от суммы и разности углов α и β.
Вывод этих ф-л достаточно сложен, поэтому сначала мы просто без доказательства приведем две из них, позволяющие вычислять синус суммы и косинус суммы:
Достаточно запомнить их, а далее следующие формулы можно выводить из них. Так, если вместо β подставить угол (–β), то получим формулы для разности. При этом мы используем тот факт, что синус – нечетная ф-ция, то естьsin (– β) = – sinβ, а косинус – четная ф-ция, то есть соs (– β) = соsβ:
Теперь поступим также с ф-лой для косинуса разности:
Итак, нам удалось получить ф-лы для нахождения синуса и косинуса суммы и разности углов.
С помощью этих формул возможно вычислить значение тригон-ких ф-ций для некоторых нестандартных углов. (Стандартными считаются углы в 0°, 30°, 45°, 60° и 90°, ведь для них значение тригон-ких ф-ций можно узнать из таблички.)
Задание. Вычислите соs 150°.
Решение. В табличке стандартных углов есть углы, равные 90° и 60°. Их сумма как раз равна 150°. Поэтому запишем:
Задание. Вычислите синус, косинус и тангенс для угла 15°.
Решение. Угол в 15° можно представить как разность 45° – 30°. Тогда синус будет вычисляться так:
Далее вычислим косинус:
Можно выполнить проверку. Полученные значения должны удовлетворять основному тригон-кому тождеству. И действительно:
Проверка пройдена: сумма квадратов синуса и косинуса оказалась равной единице. Теперь посчитаем tg 15°, используя определение тангенса:
Задание. Вычислите значение тригонометрического выражения
sinπ/7 соsπ/42 + sinπ/42 соsπ/7
Решение: Значение тригон-ких ф-ций для углов π/7 и π/42 мы не знаем, однако это не помешает вычислениям. Можно заметить, что исходное выражение представляет собой синус суммы π/7 и π/42:
sinπ/7 соsπ/42 + sinπ/42 соsπ/7 = sin (π/7 + π/42) = sinπ/6 = 1/2
Ответ: 1/2.
Задание. Упростите выражение
Решение.
Вынесем за скобки множитель 2:
Теперь произведем замену:
C учетом этого можно переписать выражение и использовать ф-лу суммы косинусов:
Ответ: 2соs (π/6 + α).
Формулы двойного угла
Что будет, если формулу синуса суммы подставить не два различных угла α и β, а два одинаковых угла α и α? Получится ф-ла для синуса двойного угла:
Аналогично можно составить ф-лу и для косинуса двойного угла:
Итак, справедливы следующие ф-лы:
Задание. Вычислите sin 120° и соs 120°.
Решение.
Задание. Упростите выражение
соs2t– соs 2t
Решение.
соs2t – соs 2t = соs2t – (соs2 t – sin2t) = соs2t – соs2 t + sin2t = sin2t
Ответ: sin2t.
Задание. Докажите, что функция
является периодической и имеет период, равный π.
Решение. Используем ф-лу квадрата суммы:
Таким образом, исходную ф-цию можно переписать в виде
у = 1 + sin 2x
По определению, ф-ция является периодической с периодом Т, если выполняется условие у(х + Т) = у(х). Поэтому подставим в нашу ф-цию величину х + π:
Получили, что у(х + π) = y(x), то есть ф-ция имеет период, равный π.
Задание. Выведите формулы синуса и косинуса тройного угла.
Решение. Для их получения следует использовать ф-лу синуса суммы углов, в которую подставляют вместо β величину 2α:
Аналогично можно получить и ф-лу для косинуса тройного угла:
Формулы понижения степени
Если нам необходимо узнать косинус угла, который вдвое больше табличного, мы используем ф-лу:
соs 2α = соs2α – sin2α
А что делать, если нам надо вычислить косинус угла, который вдвое меньше известного? Попробуем преобразовать ф-лу косинуса двойного угла:
В результате нам удалось получить тождество, позволяющее по косинусу удвоенного угла найти косинус самого угла! Однако значительно чаще в тригонометрии это равенство записывают в обратном порядке:
и называют ф-лой понижения степени. Действительно, в левой части стоит косинус в квадрате, а справа – косинус без квадрата, но вычисляется он от угла 2α, а не α.
Попробуем получить аналогичную ф-лу и для синуса. Для этого используем основное тригон-кое тождество:
С помощью этих ф-л можно вычислять тригон-кие ф-ции для некоторых малых углов. Так, ранее мы с использованием ф-лу разности синусов определили, что
При этом мы представляли угол 15° как разность 45° – 30°. Но как посчитать соs 7,5°? Этот угол невозможно представить как разницу или сумму известных нам табличных углов (0°, 30°; 45°; 60° и 90°). Однако поможет ф-ла понижения степени. Действительно, ведь 2•7,5° = 15°. Тогда можно записать:
Мы нашли соs2 7,5°. Чтобы узнать соs 7,5°, необходимо извлечь квадратный корень:
Так как угол 7,5° принадлежит I четверти, то его косинус должен быть положительным, поэтому можно записать:
Видно, что получается довольно громоздкое выражение. Используя ф-лу понижения степени, можно найти косинус и угла, который ещё вдвое меньше, то есть равен 3,75°, но в результате получится ещё более громоздкое выражение.
Задание. Вычислите sinπ/8.
Решение. Угол π/4 является табличным (его градусная мера составляет 45°). Поэтому можно записать:
Эти примеры показывают, что тригон-кие ф-ции многих нестандартных углов можно выразить, используя квадратные корни. Возникает вопрос – а любую ли тригонометрическую ф-цию можно выразить таким способом? Оказывается, что нет. Например, sin 10° невозможно найти ни в одной, даже самой подробной тригонометрической таблице. Мы не будем это доказывать, но эту величину невозможно представить в виде выражения, используя арифметические операции и корни. Однако существуют приближенные методы, позволяющие с любой наперед заданной точностью вычислять значение тригонометрических ф-ций.
Формулы приведения
Возможно, вы уже заметили, что синусы и косинусы принимают одинаковые значения в углах, чья сумма равна 90°. Например, sin30° = соs60° = 1/2, и при этом 30° + 60° = 90°. Также мы знаем, что sin 45° = соs 45° (45° + 45° = 90°) и sin60° = соs30° (60° + 30°). В чем причина такой закономерности и справедлива ли она для нестандартных углов?
Используя ф-лу синуса разности, мы можем записать, что
Полученная ф-ла sin (90° – α) = соsα называется формулой приведения. При ее выводе мы использовали тот факт, что sin 90° = 1, а соs 90° = 0, поэтому формула получилась очень простой. Однако синусы и косинусы других углов, кратных 90° (или кратных π/2, если измерять углы в радианах), также равны 0, 1 или – 1, поэтому для них тоже можно получить подобные простые ф-лы, например:
Похожих ф-л можно написать несколько десятков! Все их запоминать не надо, так как существует особое мнемоническое правило, позволяющее записать необходимую ф-лу.
Пусть есть некоторое тригон-кое выражение вида
f(k ± α)
где f – тригонометрическая ф-ция (sin; соs; tg; ctg)
k– угол, кратный π/2 (π/2, π, 3π/2, 2π)
Мы хотим заменить ее другой ф-цией, только от угла α. На первом шаге мы смотрим на слагаемое k. Если оно кратно π (– π, π, 2π), то ф-ция f остается неизменной. Если же слагаемое k – это число π/2 или 3π/2, то ф-цию f надо поменять на так называемую кофункцию (синус меняем на косинус, тангенс на котангенс и наоборот).
Далее надо определить знак, стоящий перед новой ф-цией. Для этого мы предполагаем, что α – это острый угол, то есть он принадлежит I четверти. Далее с учетом этого предположения смотрим, в какую четверть попадает угол k ± α, и какое значение принимает там исходная тригонометрическая ф-ция. Если она отрицательна, то перед новой тригонометрической ф-цией надо поставить минус. В противном случае ничего ставить не надо.
Лучше всего изучить это алгоритм на примерах.
Задание. Упростите выражение соs (π/2 + α).
Решение. Первый шаг – смотрим на слагаемое под знаком косинуса. Это число π/2. Оно НЕ кратно π, а потому мы должны поменять косинус на синус:
sinα
Второй шаг – надо определить, надо ли ставить минус перед синусом. Если α – это острый угол, то угол (π/2 + α) попадет во II четверть:
Во второй четверти косинус отрицателен, а потому перед синусом следует поставить минус:
соs (π/2 + α) = – sinα
Ответ: – sinα.
Важное примечание. В этом примере для составления формулы приведения мы «предположили», что угол α является острым. В результате нам удалось получить формулу соs (π/2 + α) = – sinα. Однако отметим, что полученная нами формула выполняется для абсолютно любых значений угла α, а не только для 0° < α < 90°. Предположение об остроте угла – это лишь часть мнемонического правила для составления формул приведения, позволяющая быстро определить, надо ли в ней перед тригонометрической функцией ставить знак минус или не надо.
Это мнемоническое правило работает абсолютно точно, однако надо понимать, что всё-таки для строгого вывода формул приведения следует использовать формулу косинуса суммы
соs (π/2 + α) = cosπ/2 cos α – sin π/2 sin α = 0•cos α – 1•sin α = – sin α
Получили тот же результат, что и с помощью формулы приведения. При этом нам не потребовалось предположение об остроте угла α, то есть формула верна для любых α. Но практика показывает, что люди просто не могут запомнить формулу косинусов суммы. Поэтому для «упрощения жизни» школьникам рассказывают об относительно простом мнемоническом правиле.
Задание. Составьте ф-лу приведения для выражения tg (α – π).
Решение. Сначала смотрим на слагаемое под знаком тангенса. Это число (– π), кратное π. Поэтому сама ф-ция не меняется на кофункцию:
tgα
Примем, что угол α принадлежит I четверти, тогда угол α – π будет ему противоположен и окажется в III четверти:
Тангенс в III четверти положителен. Значит, минуса перед тангенсом ставить не надо:
tg (α– π) = tgα
Задание. Вычислите sin 7π/6.
Решение. Представим угол 7π/6 как сумму: 7π/6 = π + π/6. Получается, нам надо вычислить величину sin (π + π/6). Составим ф-лу приведения для выражения π + α Так как в скобках стоит слагаемое π, то ф-ция sin остается, а не меняется на косинус:
sinα
Угол (π + α) относится к III четверти, где синус отрицателен. Следовательно, надо добавить знак минус:
sin (π + α) = – sinα
Остается подставить вместо α величину π/6:
sin (π + π/6) = – sinπ/6 = – 1/2
Ответ: – 1/2.
Задание. Чему равен ctg7π/4?
Решение. Угол 7π/4 можно представить как 3π/2 + π/4. Найдем ф-лу приведения для ctg (3π/2 + α). Из-за слагаемого 3π/2, не кратного π, ф-ция должна измениться с котангенса на тангенс:
ctg (3π/2 + α) = tgα
Угол 3π/2 + α попадает в IV четверть, где котангенс отрицателен. Поэтому необходимо добавить знак минуса перед ф-цией:
ctg (3π/2 + α) = –tgα
Ф-ла приведения получена. Осталось подставить в неё значение α = π/4:
ctg (7π/4) = ctg (3π/2 + π/4) = – tgπ/4 = – 1
Ответ: – 1.
Откуда же возникло название «формула приведения»? Дело в том, что с их помощью вычисление тригонометрических ф-ций от углов из диапазона 0 ≤ π ≤ 2π можно привести к вычислению ф-ций от углов из I четверти, то есть из диапазона 0 ≤ α ≤ π/2. Это означает, что нет смысла заучивать большие таблицы, в которых указаны синусы и косинусы углов, больших 90°. Достаточно знать ф-ции от стандартных углов: 0, π/6; π/4, π/3 и π/2.
Если всё же использование ф-л приведения вызывает сложности, то вместо них всегда можно использовать обычные ф-лы косинуса и синуса суммы, которые дадут такой же результат.
В прошлом уроке, строя графики косинуса, мы заметили, что он представляет собой синусоиду, смещенную на π/2 единиц:
Теперь становится ясна причина этого смещения. Дело в ф-ле приведения
соsx = sin (x + π/2)
Она показывает, что точки графика косинуса могут быть получены параллельным переносом точек синусоиды на π/2 единиц влево.
Сумма тригонометрических функций
Мы видим, что тригон-ких формул довольно много. Надо ли все их учить? Этого делать не надо. Достаточно иметь под рукой справочник при решении задач, связанных с преобразованием тригонометрических выражений, в котором все эти ф-лы можно посмотреть. В крайнем случае можно всегда самостоятельно вывести все ф-лы, используя только основное тригон-кое тождество и ф-лы синуса и косинуса суммы. Они, кстати, выдаются в качестве раздаточного материала учащимся при сдаче ЕГЭ. Ещё важно помнить определение тангенса, которое в раздаточном материале не записано.
Пусть есть два произвольных угла s и t. Найдем синусы их разности и суммы:
Сложим эти два уравнения:
Теперь произведем замену. Будем считать, что
x = s + t
у = s – t
Это значит, чтох + у = 2s, или
s = (x + y)/2
С другой стороны
х – у = s + t– (s– t) = 2t
то есть
t = (x – у)/2
Подставляем всё это в ф-лу (1):
Получили формулу, с помощью которой можно найти сумму любых двух синусов! Теперь попытаемся составить аналогичную ф-лу и для их разности синусов. При этом мы учтем нечетность синуса (это значит, что sin (– у) = – sinу):
Задание. Упростите выражения
Решение.
Теперь попробуем составить ф-лы для сложения и вычитания косинусов. Для этого запишем ф-лы для произвольных величин s и t:
Сложив уравнения, мы получим тождество
Далее произведем замены, которые выполняли и ранее:
x = s + t
у = s – t
s = (x + y)/2
t = (x – у)/2
Подставляя всё это в (3), получим:
Получили ф-лу, с помощью которой можно складывать косинусы. Чтобы их можно было вычитать, вычтем из (1) уравнение (2):
Снова произведем замены переменных s и t:
Получили ф-лу и для разности косинусов.
Задание. Упростить тригонометрические выражения
Решение.
в) Здесь мы сталкиваемся с более сложным случаем, так как из косинуса надо вычесть синус. У нас нет готовой ф-лы для такого действия. Однако вспомним, что с помощью формул приведения легко заменить синус на косинус:
sinx = соs (π/2 – х)
Тогда исходное выражение уже можно будет преобразовать:
Произведение тригонометрических функций
В предыдущем разделе, когда мы выводили ф-лы для вычисления суммы синусов и косинусов, мы сначала получали уравнения:
Далее мы производили замену переменных sи t. Однако давайте вместо этого просто поделим первые два уравнения на двойку, а третье – на (– 2):
В случае с последней формулой мы воспользовались правилом, по которому знак минус перед дробью можно убрать, если в числителе поменять местами вычитаемое и уменьшаемое.
Получили ф-лы, которые позволяют заменять произведение тригонометрических ф-ций их суммой.
Задание. Преобразуйте произведение в сумму:
Решение.
На этом наше знакомство с основными тригонометрическими формулами заканчивается. Ещё раз напомним, что в рамках школьного курса заучивать все ф-лы не нужно, можно при необходимости пользоваться смотреть в справочник. Тригон-кие преобразования помогут в будущем при решении сложных тригон-ких уравнений.
В самом конце приведем перечень всех формул, выведенными в этом уроке:

Если конкретно, то дело обстоит так. Косинус (cos) угла — это отношение прилежащего катета к гипотенузе. Cинус (sin) — это отношение противолежащего катета к гипотенузе. Тангенс угла tg(α) — есть отношение противолежащего катета a к прилежащему катету. И еще один лайфхак. Если вы вдруг прям забудете такие простые вещи, мало ли, тоже бывает, то как находить косинус, синус и тангенс, загляните в справочные материалы на ваших листах с заданиями, там будут подсказки (в разделе геометрии).
В открытом банке заданий ФИПИ есть следующие задачи на эту тему, которые могут вам попасться на реальном экзамене в этом году.
Задания из банка ФИПИ с sin, cos, tg
Найти катет по известному синусу угла и гипотенузе
В треугольнике ABC угол C равен 90°, sinB=4/15, AB=45. Найдите AC.
Решение:
По определению синуса:
sinB=AC/AB
AC=AB*sinB=45*4/15=12Ответ: 12
D8213E
В треугольнике ABC угол C равен 90°, sinB=7/12, AB=48. Найдите AC.
Решение:
По определению синуса:
sinB=AC/AB
AC=AB*sinB=48*7/12=28Ответ: 28
B972FB
В треугольнике ABC угол C равен 90°, sinB=4/11, AB=55. Найдите AC.
Решение:
По определению синуса:
sinB=AC/AB
AC=AB*sinB=55*4/11=20Ответ: 20
E65720
В треугольнике ABC угол C равен 90°, sinB=5/17, AB=51. Найдите AC.
Решение:
По определению синуса:
sinB=AC/AB
AC=AB*sinB=51*5/17=15Ответ: 15
D893F0
В треугольнике ABC угол C равен 90°, sinB=3/7, AB=21. Найдите AC.
Решение:
По определению синуса:
sinB=AC/AB
AC=AB*sinB=21*3/7=9Ответ: 9
6544F6
В треугольнике ABC угол C равен 90°, sinB=4/9, AB=18. Найдите AC.
Решение:
По определению синуса:
sinB=AC/AB
AC=AB*sinB=18*4/9=8Ответ: 8
F6882F
В треугольнике ABC угол C равен 90°, sinB=5/8, AB=16. Найдите AC.
Решение:
По определению синуса:
sinB=AC/AB
AC=AB*sinB=16*5/8=10Ответ: 10
564758
В треугольнике ABC угол C равен 90°, sinB=3/5, AB=10. Найдите AC.
Решение:
По определению синуса:
sinB=AC/AB
AC=AB*sinB=10*3/5=6Ответ: 6
50A4DC
В треугольнике ABC угол C равен 90°, sinB=5/16, AB=80. Найдите AC.
Решение:
По определению синуса:
sinB=AC/AB
AC=AB*sinB=80*5/16=25Ответ: 25
3D5005
В треугольнике ABC угол C равен 90°, sinB=7/20, AB=40. Найдите AC.
Решение:
По определению синуса:
sinB=AC/AB
AC=AB*sinB=40*7/20=14Ответ: 14
14A018
Найти катет по известному косинусу и гипотенузе
В треугольнике ABC угол C равен 90°, cosB=2/5, AB=10. Найдите BC.
Решение:
По определению косинуса:
cosB=BC/AB
BC=АВ*cosB=10*2/5=4Ответ: 4
1B8713
В треугольнике ABC угол C равен 90°, cosB=5/6, AB=18. Найдите BC.
Решение:
По определению косинуса:
cosB=BC/AB
BC=АВ*cosB=18*5/6=15Ответ: 15
481278
В треугольнике ABC угол C равен 90°, cosB=4/7, AB=21. Найдите BC.
Решение:
По определению косинуса:
cosB=BC/AB
BC=АВ*cosB=21*4/7=12Ответ: 12
D4E48F
В треугольнике ABC угол C равен 90°, cosB=3/8, AB=64. Найдите BC.
Решение:
По определению косинуса:
cosB=BC/AB
BC=АВ*cosB=64*3/8=24Ответ: 24
3F99AC
В треугольнике ABC угол C равен 90°, cosB=7/9, AB=54. Найдите BC.
Решение:
По определению косинуса:
cosB=BC/AB
BC=АВ*cosB=54*7/9=42Ответ: 42
915280
В треугольнике ABC угол C равен 90°, cosB=9/10, AB=60. Найдите BC.
Решение:
По определению косинуса:
cosB=BC/AB
BC=АВ*cosB=60*9/10=54Ответ: 54
56F660
В треугольнике ABC угол C равен 90°, cosB=5/12, AB=60. Найдите BC.
Решение:
По определению косинуса:
cosB=BC/AB
BC=АВ*cosB=60*5/12=25Ответ: 25
CA8E29
В треугольнике ABC угол C равен 90°, cosB=9/14, AB=42. Найдите BC.
Решение:
По определению косинуса:
cosB=BC/AB
BC=АВ*cosB=42*9/14=27Ответ: 27
52D8C1
В треугольнике ABC угол C равен 90°, cosB=11/15, AB=75. Найдите BC.
Решение:
По определению косинуса:
cosB=BC/AB
BC=АВ*cosB=75*11/15=55Ответ: 55
73E3A7
В треугольнике ABC угол C равен 90°, cosB=13/16, AB=96. Найдите BC.
Решение:
По определению косинуса:
cosB=BC/AB
BC=АВ*cosB=96*13/16=78Ответ: 78
D8738D
Найти катет по известному катету и тангенсу
В треугольнике ABC угол C равен 90°, tgB=3/4, BC=12. Найдите AC.
Решение:
По определению тангенса:
tgB=AC/BC
AC=BC*tgB=12*3/4=9Ответ: 9
08FD08
В треугольнике ABC угол C равен 90°, tgB=7/6, BC=18. Найдите AC.
Решение:
По определению тангенса:
tgB=AC/BC
AC=BC*tgB=18*7/6=21Ответ: 21
1BBB13
В треугольнике ABC угол C равен 90°, tgB=9/7, BC=42. Найдите AC.
Решение:
По определению тангенса:
tgB=AC/BC
AC=BC*tgB=42*9/7=54Ответ: 54
14C45C
В треугольнике ABC угол C равен 90°, tgB=8/5, BC=20. Найдите AC.
Решение:
По определению тангенса:
tgB=AC/BC
AC=BC*tgB=20*8/5=32Ответ: 32
1DB806
В треугольнике ABC угол C равен 90°, tgB=11/8, BC=24. Найдите AC.
Решение:
По определению тангенса:
tgB=AC/BC
AC=BC*tgB=24*11/8=33Ответ: 33
EF04D8
В треугольнике ABC угол C равен 90°, tgB=5/9, BC=27. Найдите AC.
Решение:
По определению тангенса:
tgB=AC/BC
AC=BC*tgB=27*5/9=15Ответ: 15
A915AF
В треугольнике ABC угол C равен 90°, tgB=7/12, BC=48. Найдите AC.
Решение:
По определению тангенса:
tgB=AC/BC
AC=BC*tgB=48*7/12=28Ответ: 28
48CB65
В треугольнике ABC угол C равен 90°, tgB=4/7, BC=35. Найдите AC.
Решение:
По определению тангенса:
tgB=AC/BC
AC=BC*tgB=35*4/7=20Ответ: 20
1EB6B0
В треугольнике ABC угол C равен 90°, tgB=7/4, BC=36. Найдите AC.
Решение:
По определению тангенса:
tgB=AC/BC
AC=BC*tgB=36*7/4=63Ответ: 63
93C176
В треугольнике ABC угол C равен 90°, tgB=3/5, BC=30. Найдите AC.
Решение:
По определению тангенса:
tgB=AC/BC
AC=BC*tgB=30*3/5=18Ответ: 18
757BB5
Найти синус по косинусу и наоборот
В решении заданий такого типа используйте основное тригонометрическое тождество
sin2α + cos2α=1
Выражаем то, что нужно найти, и подставляем известные значения.
Синус острого угла А треугольника АВС равен $frac{sqrt{21}}5$. Найдите cosA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
cos2A = 1 — sin2A =1 — (√21/5)2 = 1 — 21/25 = 1 — 0,84 = 0,16
cosA = 0,4Ответ: 0,4
99B7F9
Синус острого угла А треугольника АВС равен $frac{3sqrt{11}}{10}$. Найдите cosA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
cos2A = 1 — sin2A =1 — (3√11/10)2 = 1 — 99/100 = 0,01
cosA = 0,1Ответ: 0,1
E52F99
Синус острого угла А треугольника АВС равен $frac{sqrt{91}}{10}$. Найдите cosA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
cos2A = 1 — sin2A =1 — (√91/10)2 = 1 — 91/100 = 0,09
cosA = 0,3Ответ: 0,3
5F0BC9
Синус острого угла A треугольника ABC равен $frac{2sqrt6}5$. Найдите cosA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
cos2A = 1 — sin2A =1 — (2√6/5)2 = 1 — 24/25 = 1-0,96 = 0,04
cosA = 0,2Ответ: 0,2
DF0885
Синус острого угла A треугольника ABC равен $frac{3sqrt7}8$ . Найдите cosA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
cos2A = 1 — sin2A =1 — (3√7/8)2 = 1 — 63/64 = 1-0,984375 = 0,015625
cosA = 0,125Ответ: 0,125
Обратите внимание, что корень придется извлекать самостоятельно, поскольку числа 125 (трехзначного) в таблице квадратов на экзамене не будет.
D56817
Синус острого угла A треугольника ABC равен 4/5 . Найдите cosA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
cos2A = 1 — sin2A =1 — (4/5)2 = 1 — 16/25 = 1-0,64 = 0,36
cosA = 0,6Ответ: 0,6
F548B1
Синус острого угла A треугольника ABC равен $frac{sqrt7}4$ . Найдите cosA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
cos2A = 1 — sin2A =1 — (√7/4)2 = 1 — 7/16 = 1-0,4375 = 0,5625
cosA = 0,75Ответ: 0,75
F6FBB5
Синус острого угла A треугольника ABC равен 3/5 . Найдите cosA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
cos2A = 1 — sin2A =1 — (3/5)2 = 1 — 9/25 = 1-0,36 = 0,64
cosA = 0,8Ответ: 0,8
4257EE
Синус острого угла A треугольника ABC равен $frac{sqrt{19}}{10}$ . Найдите cosA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
cos2A = 1 — sin2A =1 — (√19/10)2 = 1 — 19/100 = 1-0,19 = 0,81
cosA = 0,9Ответ: 0,9
DC7D62
Синус острого угла A треугольника ABC равен $frac{sqrt{15}}4$ . Найдите cosA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
cos2A = 1 — sin2A =1 — (√15/4)2 = 1 — 15/16 = 1-0,9375 = 0,0625
cosA = 0,25Ответ: 0,25
11D7EC
Косинус острого угла A треугольника ABC равен $frac{sqrt{21}}5$ . Найдите sinA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
sin2A = 1 — cos2A =1 — (√21/5)2 = 1 — 21/25 = 1-0,84 = 0,16
sinA = 0,4Ответ: 0,4
4BD96F
Косинус острого угла A треугольника ABC равен $frac{3sqrt{11}}{10}$ . Найдите sinA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
sin2A = 1 — cos2A =1 — (3√11/10)2 = 1 — 99/100 = 1-0,99 = 0,01
sinA = 0,1Ответ: 0,1
EE565F
Косинус острого угла A треугольника ABC равен $frac{sqrt{91}}{10}$ . Найдите sinA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
sin2A = 1 — cos2A =1 — (√91/10)2 = 1 — 91/100 = 1-0,91 = 0,09
sinA = 0,3Ответ: 0,3
EE4155
Косинус острого угла A треугольника ABC равен $frac{2sqrt6}5$. Найдите sinA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
sin2A = 1 — cos2A =1 — (2√6/5)2 = 1 — 24/25 = 1-0,96 = 0,04
sinA = 0,2Ответ: 0,2
2657CA
Косинус острого угла A треугольника ABC равен $frac{3sqrt7}8$. Найдите sinA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
sin2A = 1 — cos2A =1 — (3√7/8)2 = 1 — 63/64 = 1-0,984375 = 0,015625
sinA = 0,125Ответ: 0,125
Обратите внимание, что корень придется извлекать самостоятельно, поскольку числа 125 (трехзначного) в таблице квадратов на экзамене не будет.
857A3B
Косинус острого угла A треугольника ABC равен 4/5. Найдите sinA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
sin2A = 1 — cos2A =1 — (4/5)2 = 1 — 16/25 = 1-0,64 = 0,36
sinA = 0,6Ответ: 0,6
588CA0
Косинус острого угла A треугольника ABC равен $frac{sqrt7}4$. Найдите sinA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
sin2A = 1 — cos2A =1 — (√7/4)2 = 1 — 7/16 = 1-0,4375 = 0,5625
sinA = 0,75Ответ: 0,75
5AC6CD
Косинус острого угла A треугольника ABC равен 3/5. Найдите sinA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
sin2A = 1 — cos2A =1 — (3/5)2 = 1 — 9/25 = 1-0,36 = 0,64
sinA = 0,8Ответ: 0,8
3B3235
Косинус острого угла A треугольника ABC равен $frac{sqrt{19}}{10}$. Найдите sinA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
sin2A = 1 — cos2A =1 — (√19/10)2 = 1 — 19/100 = 1-0,19 = 0,81
sinA = 0,9Ответ: 0,9
4D93A9
Косинус острого угла A треугольника ABC равен $frac{sqrt{15}}4$. Найдите sinA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
sin2A = 1 — cos2A =1 — (√15/4)2 = 1 — 15/16 = 1-0,9375 = 0,0625
sinA = 0,25Ответ: 0,25
A426BF
Найти площадь треугольника по двум сторонам и углу между ними
Вспоминаем формулу нахождения площади треугольника по двум сторонам и углу между ними:
S=1/2аb•sinγ, где а и b — стороны треугольника, γ — угол между ними.
Подставляем известные величины и считаем.
Формула так же есть в справочных материалах ОГЭ, на экзамене можете ими воспользоваться.
В треугольнике ABC известно, что AB=6, BC=10, sin∠ABC=1/3. Найдите площадь треугольника ABC.
Решение:
S=1/2аb•sinγ=6*10*1/3=20
Ответ: 20
D8DE10
В треугольнике ABC известно, что AB=6, BC=12, sin∠ABC=1/4. Найдите площадь треугольника ABC.
Решение:
S=1/2аb•sinγ=6*12*1/4=18
Ответ: 18
510B5D
В треугольнике ABC известно, что AB=20, BC=7, sin∠ABC=2/5. Найдите площадь треугольника ABC.
Решение:
S=1/2аb•sinγ=20*7*2/5=56
Ответ: 56
21430B
В треугольнике ABC известно, что AB=15, BC=8, sin∠ABC=5/6. Найдите площадь треугольника ABC.
Решение:
S=1/2аb•sinγ=15*8*5/6=100
Ответ: 100
770975
В треугольнике ABC известно, что AB=14, BC=5, sin∠ABC=6/7. Найдите площадь треугольника ABC.
Решение:
S=1/2аb•sinγ=14*5*6/7=60
Ответ: 60
845EFC
В треугольнике ABC известно, что AB=12, BC=20, sin∠ABC=5/8. Найдите площадь треугольника ABC.
Решение:
S=1/2аb•sinγ=12*20*5/8=150
Ответ: 150
34F484
В треугольнике ABC известно, что AB=12, BC=15, sin∠ABC=4/9. Найдите площадь треугольника ABC.
Решение:
S=1/2аb•sinγ=12*15*4/9=80
Ответ: 80
86F9F5
В треугольнике ABC известно, что AB=16, BC=25, sin∠ABC=3/10. Найдите площадь треугольника ABC.
Решение:
S=1/2аb•sinγ=16*25*3/10=120
Ответ: 120
6B1EDE
В треугольнике ABC известно, что AB=9, BC=16, sin∠ABC=7/12. Найдите площадь треугольника ABC.
Решение:
S=1/2аb•sinγ=9*16*7/12=84
Ответ: 84
521C5A
В треугольнике ABC известно, что AB=12, BC=10, sin∠ABC=8/15. Найдите площадь треугольника ABC.
Решение:
S=1/2аb•sinγ=12*10*8/15=64
Ответ: 64
3A3D0B
Найти косинус угла, если известны 3 стороны треугольника

Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
а2 = b2 + с2 — 2bс • cosα
Нужно выразить косинус и подставить известные величины.
Эта формула так же будет у вас под рукой на экзамене в справочных материалах ОГЭ.
В треугольнике АВС известно, что AB=8, BC=10, AC=12. Найдите cos∠ABC.
Решение:
а2 = b2 + с2 — 2bс • cosα
2bс • cosα = b2 + с2 — а2
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
cosα = (82 +102 + 122) : 2*8*10 = 164/160 = 1,025Ответ: 1,025
40840C
В треугольнике ABC известно, что AB=5, BC=7, AC=9. Найдите cos∠ABC.
Решение:
а2 = b2 + с2 — 2bс • cosα
2bс • cosα = b2 + с2 — а2
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{b^2+с^2-а^2}{2ast bast с}$=
Ответ:
112015
В треугольнике ABC известно, что AB=3, BC=8, AC=7. Найдите cos∠ABC.
Решение:
а2 = b2 + с2 — 2bс • cosα
2bс • cosα = b2 + с2 — а2
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{b^2+с^2-а^2}{2ast bast с}$=
Ответ:
6E8D8A
В треугольнике ABC известно, что AB=5, BC=10, AC=11. Найдите cos∠ABC.
Решение:
а2 = b2 + с2 — 2bс • cosα
2bс • cosα = b2 + с2 — а2
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{b^2+с^2-а^2}{2ast bast с}$=
Ответ:
844A89
В треугольнике ABC известно, что AB=6, BC=7, AC=8. Найдите cos∠ABC.
Решение:
а2 = b2 + с2 — 2bс • cosα
2bс • cosα = b2 + с2 — а2
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{b^2+с^2-а^2}{2ast bast с}$=
Ответ:
79B29A
В треугольнике ABC известно, что AB=5, BC=6, AC=4. Найдите cos∠ABC.
Решение:
а2 = b2 + с2 — 2bс • cosα
2bс • cosα = b2 + с2 — а2
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{b^2+с^2-а^2}{2ast bast с}$=
Ответ:
6557F1
В треугольнике ABC известно, что AB=6, BC=8, AC=4. Найдите cos∠ABC.
Решение:
а2 = b2 + с2 — 2bс • cosα
2bс • cosα = b2 + с2 — а2
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{b^2+с^2-а^2}{2ast bast с}$=
Ответ:
B5CF05
В треугольнике ABC известно, что AB=7, BC=8, AC=13. Найдите cos∠ABC.
Решение:
а2 = b2 + с2 — 2bс • cosα
2bс • cosα = b2 + с2 — а2
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{b^2+с^2-а^2}{2ast bast с}$=
Ответ:
91941D
В треугольнике ABC известно, что AB=8, BC=10, AC=14. Найдите cos∠ABC.
Решение:
а2 = b2 + с2 — 2bс • cosα
2bс • cosα = b2 + с2 — а2
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{b^2+с^2-а^2}{2ast bast с}$=
Ответ:
755B8F
В треугольнике ABC известно, что AB=2, BC=3, AC=4. Найдите cos∠ABC.
Решение:
а2 = b2 + с2 — 2bс • cosα
2bс • cosα = b2 + с2 — а2
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{b^2+с^2-а^2}{2ast bast с}$=
Ответ:
05C64C
Найти синус по двум сторонам
Синус острого угла в прямоугольном треугольнике равен отношению противолежащего катета к гипотенузе. И тот, и другой, известны. Подставляем и считаем.
В треугольнике ABC угол C равен 90°, AC=6, AB=10. Найдите sinB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 6/10 = 0,6
Ответ: 0,6
A67245
В треугольнике ABC угол C равен 90°, AC=4, AB=5. Найдите sinB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 4/5 = 0,8
Ответ: 0,8
46D9DF
В треугольнике ABC угол C равен 90°, AC=7, AB=25. Найдите sinB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 7/25 = 0,28
Ответ: 0,28
6DA700
В треугольнике ABC угол C равен 90°, AC=24, AB=25. Найдите sinB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 24/25 = 0,96
Ответ: 0,96
C7A2A0
В треугольнике ABC угол C равен 90°, AC=6, AB=20. Найдите sinB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 6/20 = 0,3
Ответ: 0,3
ED2D47
В треугольнике ABC угол C равен 90°, AC=11, AB=20. Найдите sinB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 11/20 = 0,55
Ответ: 0,55
F1D3F8
В треугольнике ABC угол C равен 90°, AC=8, AB=40. Найдите sinB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 8/40 = 0,2
Ответ: 0,2
CDC6C7
В треугольнике ABC угол C равен 90°, AC=16, AB=40. Найдите sinB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 16/40 = 0,4
Ответ: 0,4
20BC46
В треугольнике ABC угол C равен 90°, AC=9, AB=25. Найдите sinB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 9/25 = 0,36
Ответ: 0,36
E2F916
В треугольнике ABC угол C равен 90°, AC=13, AB=20. Найдите sinB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 13/20 = 0,65
Ответ: 0,65
2C2621
Найти косинус по двум сторонам треугольника
Косинус острого угла в прямоугольном треугольнике равен отношению прилежащего катета к гипотенузе. Подставляем известные значения и считаем.
В треугольнике ABC угол C равен 90°, BC=8, AB=10. Найдите cosB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 8/10 = 0,8
Ответ: 0,8
36727A
В треугольнике ABC угол C равен 90°, BC=3, AB=5. Найдите cosB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 3/5 = 0,6
Ответ: 0,6
E4988D
В треугольнике ABC угол C равен 90°, BC=14, AB=50. Найдите cosB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 14/50 = 0,28
Ответ: 0,28
B9AA7C
В треугольнике ABC угол C равен 90°, BC=72, AB=75. Найдите cosB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 72/75 = 0,96
Ответ: 0,96
6E5515
В треугольнике ABC угол C равен 90°, BC=14, AB=20. Найдите cosB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 14/20 = 0,7
Ответ: 0,7
E812C8
В треугольнике ABC угол C равен 90°, BC=9, AB=20. Найдите cosB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 9/20 = 0,45
Ответ: 0,45
C759C5
В треугольнике ABC угол C равен 90°, BC=30, AB=40. Найдите cosB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 30/40 = 0,75
Ответ: 0,75
8854A8
В треугольнике ABC угол C равен 90°, BC=26, AB=40. Найдите cosB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 26/40 = 0,65
Ответ: 0,65
C5CD1E
В треугольнике ABC угол C равен 90°, BC=16, AB=25. Найдите cosB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 16/25 = 0,64
Ответ: 0,64
C3A5F2
В треугольнике ABC угол C равен 90°, BC=7, AB=20. Найдите cosB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 7/20 = 0,35
Ответ: 0,35
D58395
Найти тангенс угла по двум катетам
Тангенс острого угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему. Подставляем значения катетов и считаем.
В треугольнике ABC угол C равен 90°, BC=5, AC=2. Найдите tgB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 2/5 = 0,4
Ответ: 0,4
98C7DF
В треугольнике ABC угол C равен 90°, BC=5, AC=3. Найдите tgB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 3/5 = 0,6
Ответ: 0,6
22FD03
В треугольнике ABC угол C равен 90°, BC=10, AC=7. Найдите tgB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 7/10 = 0,7
Ответ: 0,7
C18053
В треугольнике ABC угол C равен 90°, BC=10, AC=8. Найдите tgB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 8/10 = 0,8
Ответ: 0,8
33DA26
В треугольнике ABC угол C равен 90°, BC=15, AC=3. Найдите tgB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 3/15 = 0,2
Ответ: 0,2
DD620C
В треугольнике ABC угол C равен 90°, BC=9, AC=27. Найдите tgB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 27/9 = 3
Ответ: 3
342F0C
В треугольнике ABC угол C равен 90°, BC=5, AC=20. Найдите tgB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 20/5 = 4
Ответ: 4
B800B8
В треугольнике ABC угол C равен 90°, BC=3, AC=18. Найдите tgB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 18/3 = 6
Ответ: 6
FF498A
В треугольнике ABC угол C равен 90°, BC=4, AC=28. Найдите tgB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 28/4 = 7
Ответ: 7
C9E181
В треугольнике ABC угол C равен 90°, BC=7, AC=35. Найдите tgB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 35/7 = 5
Ответ: 5
0663D4
Задачи ОГЭ с развернутым ответом
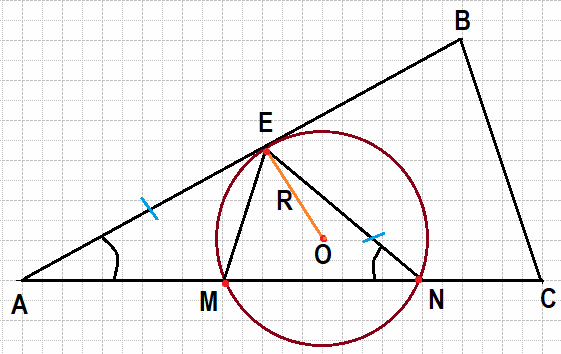
Точки M и N лежат на стороне AC треугольника ABC на расстояниях соответственно 4 и 15 от вершины A. Найдите радиус окружности, проходящей через точки M и N и касающейся луча AB, если cos∠BAC=$frac{sqrt{15}}4$.
Решение:
Найдем AE, по теореме (свойствам) о касательной и секущей. Подробно мы рассказали об этом в другой статье.
Если из одной точки (А) к окружности проведена секущая (АN) и касательная (АE), то произведение всей секущей (АN) на ее внешнюю часть (АM) равно квадрату отрезка касательной (АE).
АE2 = АN·АM
АE2 = 4*15
АE = $sqrt{4ast15}$= $sqrt{60}$Теперь по теореме косинусов найдем EM
EM2 = AE2+AM2 — 2AE*AM*cos∠BAC
EM2 = $sqrt{60}$2 +42 — 2*$sqrt{60}$*4*$frac{sqrt{15}}4$= 60+16-2*$sqrt{60}$*$sqrt{15}$=76-2*30=16
EM = $sqrt{16}$ =4из той же теоремы найдем
EN2 = AE2+AN2 — 2AE*AN*cos∠BAC
EN2 = $sqrt{60}$2 +152 — 2*$sqrt{60}$*15*$frac{sqrt{15}}4$=60+225-($sqrt{900}$*15)/2=285-225=60
EN = $sqrt{60}$Из получившегося значения EN можно сделать вывод, что △AEN равнобедренный, где AE = EN = $sqrt{60}$.
Делаем вывод о том, что △AME подобен треугольнику △AEN по общему углу и по тому, что они равнобедренные.
Теперь из основного тригонометрического тождества найдем ∠BAC или он же ∠ENA, через sin угла.
$sinangle ENA^2+cosangle ENA^2;=1\sinangle ENA^2+left(frac{sqrt{15}}4right)^2;=1\sinangle ENA^2=1-left(frac{sqrt{15}}4right)^2\sinangle ENA^2;=;1;-;frac{15}{16}\sinangle ENA^2;=;frac1{16}\sinangle ENA;=frac14\\\\$
При этом из формулы радиуса описанной окружности получаем.
$R=frac{EM}{2astsinangle;E;N;A};;=frac4{2ast{displaystylefrac14}}=8\\\\$
Ответ: 8
F41EBF
Точки M и N лежат на стороне AC треугольника ABC на расстояниях соответственно 12 и 21 от вершины A. Найдите радиус окружности, проходящей через точки M и N и касающейся луча AB, если cos∠BAC=$frac{sqrt7}4$.
Решение:
Найдем AE, по теореме (свойствам) о касательной и секущей. Подробно мы рассказали об этом в другой статье.
Если из одной точки (А) к окружности проведена секущая (АN) и касательная (АE), то произведение всей секущей (АN) на ее внешнюю часть (АM) равно квадрату отрезка касательной (АE).
АE2 = АN·АM
АE2 = 12*21
АE = $sqrt{12ast21}$= $sqrt{252}$Теперь по теореме косинусов найдем EM
EM2 = AE2+AM2 — 2AE*AM*cos∠BAC
EM2 = $sqrt{252}$2 +122 — 2*$sqrt{252}$*12*$frac{sqrt7}4$= 252+144-2*$sqrt{252}$*12*$frac{sqrt7}4$=396-252=$sqrt{144}$
EM = $sqrt{144}$ =12из той же теоремы найдем
EN2 = AE2+AN2 — 2AE*AN*cos∠BAC
EN2 = $sqrt{252}$2 +212 — 2*$sqrt{252}$*21*$frac{sqrt7}4$=252+441-441=252
EN = $sqrt{252}$Из получившегося значения EN можно сделать вывод, что △AEN равнобедренный, где AE = EN = $sqrt{252}$.
Делаем вывод о том, что △AME подобен треугольнику △AEN по общему углу и по тому, что они равнобедренные.
Теперь из основного тригонометрического тождества найдем ∠BAC или он же ∠ENA, через sin угла.
$sinangle ENA^2+cosangle ENA^2;=1\sinangle ENA^2+left(frac{sqrt7}4right)^2;=1\sinangle ENA^2=1-left(frac{sqrt7}4right)^2\sinangle ENA^2;=;1;-;frac7{16}\sinangle ENA^2;=;frac9{16}\sinangle ENA^;=frac34\\\\$
При этом из формулы радиуса описанной окружности получаем.
$R=frac{EM}{2sinangle ENA}=frac{12}{2{displaystylefrac34}}=frac{48}6=8$
Ответ: 8
23C5ED
Точки M и N лежат на стороне AC треугольника ABC на расстояниях соответственно 8 и 30 от вершины A. Найдите радиус окружности, проходящей через точки M и N и касающейся луча AB, если cos∠BAC=$frac{sqrt{15}}4$.
Решение:
Найдем AE, по теореме (свойствам) о касательной и секущей. Подробно мы рассказали об этом в другой статье.
Если из одной точки (А) к окружности проведена секущая (АN) и касательная (АE), то произведение всей секущей (АN) на ее внешнюю часть (АM) равно квадрату отрезка касательной (АE).
АE2 = АN·АM
АE2 = 8*30
АE = $sqrt{8ast30}$= $sqrt{240}$Теперь по теореме косинусов найдем EM
EM2 = AE2+AM2 — 2AE*AM*cos∠BAC
EM2 = $sqrt{240}$2 +82 — 2*$sqrt{240}$*8*$frac{sqrt{15}}4$=240+64-240=64
EM = 8из той же теоремы найдем
EN2 = AE2+AN2 — 2AE*AN*cos∠BAC
EN2 = $sqrt{240}$2 +302 — 2*$sqrt{240}$*30*$frac{sqrt{15}}4$=240+900-900=240
EN = $sqrt{240}$Из получившегося значения EN можно сделать вывод, что △AEN равнобедренный, где AE = EN = $sqrt{240}$.
Делаем вывод о том, что △AME подобен треугольнику △AEN по общему углу и по тому, что они равнобедренные.
Теперь из основного тригонометрического тождества найдем ∠BAC или он же ∠ENA, через sin угла.
$sinangle ENA^2+cosangle ENA^2;=1\sinangle ENA^2+left(frac{sqrt{15}}4right)^2;=1\sinangle ENA^2=1-left(frac{sqrt{15}}4right)^2\sinangle ENA^2;=;1;-;frac{15}{16}\sinangle ENA^2;=;frac1{16}\sinangle ENA;=frac14\\\\$
При этом из формулы радиуса описанной окружности получаем.
$R=frac{EM}{2sinangle ENA}=frac8{2{displaystylefrac14}}=frac{32}2=16$
Ответ: 16
1D3A90
Точки M и N лежат на стороне AC треугольника ABC на расстояниях соответственно 18 и 22 от вершины A. Найдите радиус окружности, проходящей через точки M и N и касающейся луча AB, если cos∠BAC=$frac{sqrt{11}}6$.
Решение:
Найдем AE, по теореме (свойствам) о касательной и секущей. Подробно мы рассказали об этом в другой статье.
Если из одной точки (А) к окружности проведена секущая (АN) и касательная (АE), то произведение всей секущей (АN) на ее внешнюю часть (АM) равно квадрату отрезка касательной (АE).
АE2 = АN·АM
АE2 = 18*22
АE = $sqrt{18ast22}$= $sqrt{396}$Теперь по теореме косинусов найдем EM
EM2 = AE2+AM2 — 2AE*AM*cos∠BAC
EM2 = $sqrt{396}$2 +182 — 2*$sqrt{396}$*18*$frac{sqrt{11}}6$=396+324-396=324
EM = 18из той же теоремы найдем
EN2 = AE2+AN2 — 2AE*AN*cos∠BAC
EN2 = $sqrt{396}$2 +222 — 2*$sqrt{396}$*22*$frac{sqrt{11}}6$=396+484-484=396
EN = $sqrt{396}$Из получившегося значения EN можно сделать вывод, что △AEN равнобедренный, где AE = EN = $sqrt{396}$.
Делаем вывод о том, что △AME подобен треугольнику △AEN по общему углу и по тому, что они равнобедренные.
Теперь из основного тригонометрического тождества найдем ∠BAC или он же ∠ENA, через sin угла.
$sinangle ENA^2+cosangle ENA^2;=1\sinangle ENA^2+left(frac{sqrt{11}}6right)^2;=1\sinangle ENA^2=1-left(frac{sqrt{11}}6right)^2\sinangle ENA^2;=;1;-;frac{11}{36}\sinangle ENA^2;=;frac{25}{36}\sinangle ENA;=frac56\\\\$
При этом из формулы радиуса описанной окружности получаем.
$R=frac{EM}{2sinangle ENA}=frac18{2{displaystylefrac56}}=frac{21.6}2=10.8$
Ответ: 10.8
35C690
Точки M и N лежат на стороне AC треугольника ABC на расстояниях соответственно 18 и 40 от вершины A. Найдите радиус окружности, проходящей через точки M и N и касающейся луча AB, если cos∠BAC=$frac{sqrt5}3$.
Решение:
Найдем AE, по теореме (свойствам) о касательной и секущей. Подробно мы рассказали об этом в другой статье.
Если из одной точки (А) к окружности проведена секущая (АN) и касательная (АE), то произведение всей секущей (АN) на ее внешнюю часть (АM) равно квадрату отрезка касательной (АE).
АE2 = АN·АM
АE2 = 18*40
АE = $sqrt{18ast40}$= $sqrt{720}$Теперь по теореме косинусов найдем EM
EM2 = AE2+AM2 — 2AE*AM*cos∠BAC
EM2 = $sqrt{720}$2 +182 — 2*$sqrt{720}$*18*$frac{sqrt{5}}3$=720+324-720=324
EM = 18из той же теоремы найдем
EN2 = AE2+AN2 — 2AE*AN*cos∠BAC
EN2 = $sqrt{720}$2 +402 — 2*$sqrt{720}$*40*$frac{sqrt{5}}3$=720+1600-1600=720
EN = $sqrt{720}$Из получившегося значения EN можно сделать вывод, что △AEN равнобедренный, где AE = EN = $sqrt{720}$.
Делаем вывод о том, что △AME подобен треугольнику △AEN по общему углу и по тому, что они равнобедренные.
Теперь из основного тригонометрического тождества найдем ∠BAC или он же ∠ENA, через sin угла.
$sinangle ENA^2+cosangle ENA^2;=1\sinangle ENA^2+left(frac{sqrt5}3right)^2;=1\sinangle ENA^2=1-left(frac{sqrt5}3right)^2\sinangle ENA^2;=;1;-;frac59\sinangle ENA^2;=;frac49\sinangle ENA;=frac23\\\\$
При этом из формулы радиуса описанной окружности получаем.
$R=frac{EM}{2sinangle ENA}=frac18{2{displaystylefrac23}}=frac{54}4=13.5$
Ответ: 13.5
CCD611
Точки M и N лежат на стороне AC треугольника ABC на расстояниях соответственно 9 и 35 от вершины A. Найдите радиус окружности, проходящей через точки M и N и касающейся луча AB, если cos∠BAC=$frac{sqrt{35}}6$.
Решение:
Найдем AE, по теореме (свойствам) о касательной и секущей. Подробно мы рассказали об этом в другой статье.
Если из одной точки (А) к окружности проведена секущая (АN) и касательная (АE), то произведение всей секущей (АN) на ее внешнюю часть (АM) равно квадрату отрезка касательной (АE).
АE2 = АN·АM
АE2 = 9*35
АE = $sqrt{9ast35}$= $sqrt{315}$Теперь по теореме косинусов найдем EM
EM2 = AE2+AM2 — 2AE*AM*cos∠BAC
EM2 = $sqrt{315}$2 +92 — 2*$sqrt{315}$*9*$frac{sqrt{35}}6$=315+81-315=81
EM = 9из той же теоремы найдем
EN2 = AE2+AN2 — 2AE*AN*cos∠BAC
EN2 = $sqrt{315}$2 +352 — 2*$sqrt{315}$*35*$frac{sqrt{35}}6$=315+1225-1225=315
EN = $sqrt{315}$Из получившегося значения EN можно сделать вывод, что △AEN равнобедренный, где AE = EN = $sqrt{315}$.
Делаем вывод о том, что △AME подобен треугольнику △AEN по общему углу и по тому, что они равнобедренные.
Теперь из основного тригонометрического тождества найдем ∠BAC или он же ∠ENA, через sin угла.
$sinangle ENA^2+cosangle ENA^2;=1\sinangle ENA^2+left(frac{sqrt{35}}6right)^2;=1\sinangle ENA^2=1-left(frac{sqrt{35}}6right)^2\sinangle ENA^2;=;1;-;frac{35}{36}\sinangle ENA^2;=;frac1{36}\sinangle ENA;=frac16\\\\$
При этом из формулы радиуса описанной окружности получаем.
$R=frac{EM}{2sinangle ENA}=frac9{2{displaystylefrac16}}=frac{54}2=27$
Ответ: 27
65B0A0
Точки M и N лежат на стороне AC треугольника ABC на расстояниях соответственно 12 и 45 от вершины A. Найдите радиус окружности, проходящей через точки M и N и касающейся луча AB, если cos∠BAC=$frac{sqrt{15}}4$.
Решение:
Найдем AE, по теореме (свойствам) о касательной и секущей. Подробно мы рассказали об этом в другой статье.
Если из одной точки (А) к окружности проведена секущая (АN) и касательная (АE), то произведение всей секущей (АN) на ее внешнюю часть (АM) равно квадрату отрезка касательной (АE).
АE2 = АN·АM
АE2 = 12*45
АE = $sqrt{12ast45}$= $sqrt{540}$Теперь по теореме косинусов найдем EM
EM2 = AE2+AM2 — 2AE*AM*cos∠BAC
EM2 = $sqrt{540}$2 +122 — 2*$sqrt{540}$*12*$frac{sqrt{15}}4$=540+144-540=144
EM = 12из той же теоремы найдем
EN2 = AE2+AN2 — 2AE*AN*cos∠BAC
EN2 = $sqrt{540}$2 +452 — 2*$sqrt{540}$*45*$frac{sqrt{15}}4$=540+2025-2025=540
EN = $sqrt{540}$Из получившегося значения EN можно сделать вывод, что △AEN равнобедренный, где AE = EN = $sqrt{540}$.
Делаем вывод о том, что △AME подобен треугольнику △AEN по общему углу и по тому, что они равнобедренные.
Теперь из основного тригонометрического тождества найдем ∠BAC или он же ∠ENA, через sin угла.
$sinangle ENA^2+cosangle ENA^2;=1\sinangle ENA^2+left(frac{sqrt{15}}4right)^2;=1\sinangle ENA^2=1-left(frac{sqrt{15}}4right)^2\sinangle ENA^2;=;1;-;frac{15}{16}\sinangle ENA^2;=;frac1{16}\sinangle ENA;=frac14\\\\$
При этом из формулы радиуса описанной окружности получаем.
$R=frac{EM}{2sinangle ENA}=frac{12}{2{displaystylefrac14}}=frac{48}2=24$
Ответ: 24
36C43D
Точки M и N лежат на стороне AC треугольника ABC на расстояниях соответственно 9 и 32 от вершины A. Найдите радиус окружности, проходящей через точки M и N и касающейся луча AB, если cos∠BAC=$frac{2sqrt2}3$.
Решение:
Найдем AE, по теореме (свойствам) о касательной и секущей. Подробно мы рассказали об этом в другой статье.
Если из одной точки (А) к окружности проведена секущая (АN) и касательная (АE), то произведение всей секущей (АN) на ее внешнюю часть (АM) равно квадрату отрезка касательной (АE).
АE2 = АN·АM
АE2 = 9*32
АE = $sqrt{9ast32}$= $sqrt{288}$Теперь по теореме косинусов найдем EM
EM2 = AE2+AM2 — 2AE*AM*cos∠BAC
EM2 = $sqrt{288}$2 +92 — 2*$sqrt{288}$*9*$frac{2sqrt2}3$=288+81-288=81
EM = 9из той же теоремы найдем
EN2 = AE2+AN2 — 2AE*AN*cos∠BAC
EN2 = $sqrt{288}$2 +322 — 2*$sqrt{288}$*32*$frac{2sqrt2}3$=288+1024-1024=288
EN = $sqrt{288}$Из получившегося значения EN можно сделать вывод, что △AEN равнобедренный, где AE = EN = $sqrt{288}$.
Делаем вывод о том, что △AME подобен треугольнику △AEN по общему углу и по тому, что они равнобедренные.
Теперь из основного тригонометрического тождества найдем ∠BAC или он же ∠ENA, через sin угла.
$sinangle ENA^2+cosangle ENA^2;=1\sinangle ENA^2+left(frac{2sqrt2}3right)^2;=1\sinangle ENA^2=1-left(frac{2sqrt2}3right)^2\sinangle ENA^2;=;1;-;frac89\sinangle ENA^2;=;frac13\sinangle ENA;=frac13\\\\$
При этом из формулы радиуса описанной окружности получаем.
$R=frac{EM}{2sinangle ENA}=frac9{2{displaystylefrac13}}=frac{27}2=13,5$
Ответ: 13,5
A077B6
Точки M и N лежат на стороне AC треугольника ABC на расстояниях соответственно 24 и 42 от вершины A. Найдите радиус окружности, проходящей через точки M и N и касающейся луча AB, если cos∠BAC=$frac{sqrt7}4$.
Решение:
Найдем AE, по теореме (свойствам) о касательной и секущей. Подробно мы рассказали об этом в другой статье.
Если из одной точки (А) к окружности проведена секущая (АN) и касательная (АE), то произведение всей секущей (АN) на ее внешнюю часть (АM) равно квадрату отрезка касательной (АE).
АE2 = АN·АM
АE2 = 24*42
АE = $sqrt{24ast42}$= $sqrt{1008}$Теперь по теореме косинусов найдем EM
EM2 = AE2+AM2 — 2AE*AM*cos∠BAC
EM2 = $sqrt{1008}$2 +242 — 2*$sqrt{1008}$*24*$frac{sqrt7}4$=1008+576-1008=576
EM = 24из той же теоремы найдем
EN2 = AE2+AN2 — 2AE*AN*cos∠BAC
EN2 = $sqrt{1008}$2 +422 — 2*$sqrt{1008}$*42*$frac{sqrt7}4$=1008+1764-1764=1008
EN = $sqrt{1008}$Из получившегося значения EN можно сделать вывод, что △AEN равнобедренный, где AE = EN = $sqrt{1008}$.
Делаем вывод о том, что △AME подобен треугольнику △AEN по общему углу и по тому, что они равнобедренные.
Теперь из основного тригонометрического тождества найдем ∠BAC или он же ∠ENA, через sin угла.
$sinangle ENA^2+cosangle ENA^2;=1\sinangle ENA^2+left(frac{sqrt7}4right)^2;=1\sinangle ENA^2=1-left(frac{sqrt7}4right)^2\sinangle ENA^2;=;1;-;frac7{16}\sinangle ENA^2;=;frac9{16}\sinangle ENA;=frac34\\\\$
При этом из формулы радиуса описанной окружности получаем.
$R=frac{EM}{2sinangle ENA}=frac{24}{2{displaystylefrac34}}=frac{96}3=32$
Ответ: 32
973563
Точки M и N лежат на стороне AC треугольника ABC на расстояниях соответственно 36 и 44 от вершины A. Найдите радиус окружности, проходящей через точки M и N и касающейся луча AB, если cos∠BAC=$frac{sqrt{11}}6$.
Решение:
Найдем AE, по теореме (свойствам) о касательной и секущей. Подробно мы рассказали об этом в другой статье.
Если из одной точки (А) к окружности проведена секущая (АN) и касательная (АE), то произведение всей секущей (АN) на ее внешнюю часть (АM) равно квадрату отрезка касательной (АE).
АE2 = АN·АM
АE2 = 36*44
АE = $sqrt{36ast44}$= $sqrt{1584}$Теперь по теореме косинусов найдем EM
EM2 = AE2+AM2 — 2AE*AM*cos∠BAC
EM2 = $sqrt{1584}$2 +362 — 2*$sqrt{1584}$*36*$frac{sqrt11}6$=1584+1296-1584=1296
EM = 36из той же теоремы найдем
EN2 = AE2+AN2 — 2AE*AN*cos∠BAC
EN2 = $sqrt{1584}$2 +442 — 2*$sqrt{1584}$*44*$frac{sqrt11}6$=1584+1936-1936=1584
EN = $sqrt{1584}$Из получившегося значения EN можно сделать вывод, что △AEN равнобедренный, где AE = EN = $sqrt{1584}$.
Делаем вывод о том, что △AME подобен треугольнику △AEN по общему углу и по тому, что они равнобедренные.
Теперь из основного тригонометрического тождества найдем ∠BAC или он же ∠ENA, через sin угла.
$sinangle ENA^2+cosangle ENA^2;=1\sinangle ENA^2+left(frac{sqrt{11}}6right)^2;=1\sinangle ENA^2=1-left(frac{sqrt{11}}6right)^2\sinangle ENA^2;=;1;-;frac{11}{36}\sinangle ENA^2;=;frac{25}{36}\sinangle ENA;=frac56\\\\$
При этом из формулы радиуса описанной окружности получаем.
$R=frac{EM}{2sinangle ENA}=frac{36}{2{displaystylefrac56}}=frac{216}{10}=21.6$
Ответ: 21.6
A142B2
Точки M и N лежат на стороне AC треугольника ABC на расстояниях соответственно 16 и 39 от вершины A. Найдите радиус окружности, проходящей через точки M и N и касающейся луча AB, если cos∠BAC=$frac{sqrt{39}}8$.
Решение:
Найдем AE, по теореме (свойствам) о касательной и секущей. Подробно мы рассказали об этом в другой статье.
Если из одной точки (А) к окружности проведена секущая (АN) и касательная (АE), то произведение всей секущей (АN) на ее внешнюю часть (АM) равно квадрату отрезка касательной (АE).
АE2 = АN·АM
АE2 = 16*39
АE = $sqrt{16ast39}$= $sqrt{624}$Теперь по теореме косинусов найдем EM
EM2 = AE2+AM2 — 2AE*AM*cos∠BAC
EM2 = $sqrt{624}$2 +162 — 2*$sqrt{624}$*16*$frac{sqrt{39}}8$=624+256-624=256
EM = 16из той же теоремы найдем
EN2 = AE2+AN2 — 2AE*AN*cos∠BAC
EN2 = $sqrt{624}$2 +392 — 2*$sqrt{624}$*39*$frac{sqrt{39}}8$=624+1521-1521=624
EN = $sqrt{624}$Из получившегося значения EN можно сделать вывод, что △AEN равнобедренный, где AE = EN = $sqrt{624}$.
Делаем вывод о том, что △AME подобен треугольнику △AEN по общему углу и по тому, что они равнобедренные.
Теперь из основного тригонометрического тождества найдем ∠BAC или он же ∠ENA, через sin угла.
$sinangle ENA^2+cosangle ENA^2;=1\sinangle ENA^2+left(frac{sqrt{39}}8right)^2;=1\sinangle ENA^2=1-left(frac{sqrt{39}}8right)^2\sinangle ENA^2;=;1;-;frac{39}{64}\sinangle ENA^2;=;frac{25}{64}\sinangle ENA;=frac58\\\\$
При этом из формулы радиуса описанной окружности получаем.
$R=frac{EM}{2sinangle ENA}=frac{39}{2{displaystylefrac58}}=frac{312}{10}=31.2$
Ответ: 31.2
553368
Точки M и N лежат на стороне AC треугольника ABC на расстояниях соответственно 9 и 11 от вершины A. Найдите радиус окружности, проходящей через точки M и N и касающейся луча AB, если cos∠BAC=$frac{sqrt{11}}6$.
Решение:
Найдем AE, по теореме (свойствам) о касательной и секущей. Подробно мы рассказали об этом в другой статье.
Если из одной точки (А) к окружности проведена секущая (АN) и касательная (АE), то произведение всей секущей (АN) на ее внешнюю часть (АM) равно квадрату отрезка касательной (АE).
АE2 = АN·АM
АE2 = 9*11
АE = $sqrt{9ast11}$= 3$sqrt{11}$Теперь по теореме косинусов найдем EM
EM2 = AE2+AM2 — 2AE*AM*cos∠BAC
EM2 = 32$sqrt{11}$2 +92 — 2*3$sqrt{11}$*9*$frac{sqrt{11}}6$=9*11+81-11*9=81
EM = 9из той же теоремы найдем
EN2 = AE2+AN2 — 2AE*AN*cos∠BAC
EN2 = 32$sqrt{11}$2 +112 — 2*3$sqrt{11}$*11*$frac{sqrt{11}}6$=32$sqrt{11}$2 +121-121 = 32$sqrt{11}$2
EN = 3$sqrt{11}$Из получившегося значения EN можно сделать вывод, что △AEN равнобедренный, где AE = EN = 3$sqrt{11}$.
Делаем вывод о том, что △AME подобен треугольнику △AEN по общему углу и по тому, что они равнобедренные.
Теперь из основного тригонометрического тождества найдем ∠BAC или он же ∠ENA, через sin угла.
$sinangle B;A;C^2+cosangle B;A;C^2=1\sinangle B;A;C^2=1-cosangle B;A;C^2\sinangle B;A;C^2=1-frac{sqrt{11}}6^2\sinangle B;A;C^2;=;1-frac{11}{36}\sinangle B;A;C^2;=frac{25}{36}\sinangle B;A;C;=;frac56\\\\$
При этом из формулы радиуса описанной окружности получаем.
$R=frac{EM}{2astsinangle;B;A;C};;=frac9{2ast{displaystylefrac56}}=5.4\\\\$
Ответ: 5.4
B83171
Каталог заданий.
1. Синус, косинус, тангенс, котангенс
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Тип 29 № 1020
На клетчатой бумаге с размером клетки
изображён угол. Найдите
Решение
·
Помощь
2
Тип 29 № 1024
На клетчатой бумаге с размером клетки
изображён угол. Найдите
Аналоги к заданию № 1024: 1025 Все
Решение
·
Помощь
3
Тип 29 № 1025
На клетчатой бумаге с размером клетки
изображён угол. Найдите
Аналоги к заданию № 1024: 1025 Все
Решение
·
Помощь
4
Тип 29 № 1026
Выведите значения синуса, косинуса, тангенса и котангенса угла 30°.
Решение
·
Помощь
5
Тип 29 № 1027
Выведите значения синуса, косинуса, тангенса и котангенса угла 45°.
Решение
·
Помощь
Пройти тестирование по этим заданиям
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2023
Вспоминаем, что такое синус, косинус и тангенс в прямоугольном треугольнике.
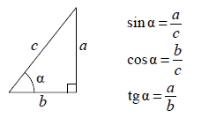
Если на ОГЭ вы от волнения забудете, как находить косинус, синус и тангенс, загляните в справочные материалы на ваших листах с заданиями, там будут подсказки (в разделе геометрии).
В открытом банке заданий ФИПИ есть следующие задачи на эту тему, которые могут вам попасться на реальном экзамене в этом году.
Задания из банка ФИПИ с sin, cos, tg
Найти катет по известному синусу угла и гипотенузе
В треугольнике ABC угол C равен 90°, sinB=4/15, AB=45. Найдите AC.
Решение:
По определению синуса:
sinB=AC/AB
AC=AB*sinB=45*4/15=12Ответ: 12
D8213E
В треугольнике ABC угол C равен 90°, sinB=7/12, AB=48. Найдите AC.
Решение:
По определению синуса:
sinB=AC/AB
AC=AB*sinB=48*7/12=28Ответ: 28
B972FB
В треугольнике ABC угол C равен 90°, sinB=4/11, AB=55. Найдите AC.
Решение:
По определению синуса:
sinB=AC/AB
AC=AB*sinB=55*4/11=20Ответ: 20
E65720
В треугольнике ABC угол C равен 90°, sinB=5/17, AB=51. Найдите AC.
Решение:
По определению синуса:
sinB=AC/AB
AC=AB*sinB=51*5/17=15Ответ: 15
D893F0
В треугольнике ABC угол C равен 90°, sinB=3/7, AB=21. Найдите AC.
Решение:
По определению синуса:
sinB=AC/AB
AC=AB*sinB=21*3/7=9Ответ: 9
6544F6
В треугольнике ABC угол C равен 90°, sinB=4/9, AB=18. Найдите AC.
Решение:
По определению синуса:
sinB=AC/AB
AC=AB*sinB=18*4/9=8Ответ: 8
F6882F
В треугольнике ABC угол C равен 90°, sinB=5/8, AB=16. Найдите AC.
Решение:
По определению синуса:
sinB=AC/AB
AC=AB*sinB=16*5/8=10Ответ: 10
564758
В треугольнике ABC угол C равен 90°, sinB=3/5, AB=10. Найдите AC.
Решение:
По определению синуса:
sinB=AC/AB
AC=AB*sinB=10*3/5=6Ответ: 6
50A4DC
В треугольнике ABC угол C равен 90°, sinB=5/16, AB=80. Найдите AC.
Решение:
По определению синуса:
sinB=AC/AB
AC=AB*sinB=80*5/16=25Ответ: 25
3D5005
В треугольнике ABC угол C равен 90°, sinB=7/20, AB=40. Найдите AC.
Решение:
По определению синуса:
sinB=AC/AB
AC=AB*sinB=40*7/20=14Ответ: 14
14A018
Найти катет по известному косинусу и гипотенузе
В треугольнике ABC угол C равен 90°, cosB=2/5, AB=10. Найдите BC.
Решение:
По определению косинуса:
cosB=BC/AB
BC=АВ*cosB=10*2/5=4Ответ: 4
1B8713
В треугольнике ABC угол C равен 90°, cosB=5/6, AB=18. Найдите BC.
Решение:
По определению косинуса:
cosB=BC/AB
BC=АВ*cosB=18*5/6=15Ответ: 15
481278
В треугольнике ABC угол C равен 90°, cosB=4/7, AB=21. Найдите BC.
Решение:
По определению косинуса:
cosB=BC/AB
BC=АВ*cosB=21*4/7=12Ответ: 12
D4E48F
В треугольнике ABC угол C равен 90°, cosB=3/8, AB=64. Найдите BC.
Решение:
По определению косинуса:
cosB=BC/AB
BC=АВ*cosB=64*3/8=24Ответ: 24
3F99AC
В треугольнике ABC угол C равен 90°, cosB=7/9, AB=54. Найдите BC.
Решение:
По определению косинуса:
cosB=BC/AB
BC=АВ*cosB=54*7/9=42Ответ: 42
915280
В треугольнике ABC угол C равен 90°, cosB=9/10, AB=60. Найдите BC.
Решение:
По определению косинуса:
cosB=BC/AB
BC=АВ*cosB=60*9/10=54Ответ: 54
56F660
В треугольнике ABC угол C равен 90°, cosB=5/12, AB=60. Найдите BC.
Решение:
По определению косинуса:
cosB=BC/AB
BC=АВ*cosB=60*5/12=25Ответ: 25
CA8E29
В треугольнике ABC угол C равен 90°, cosB=9/14, AB=42. Найдите BC.
Решение:
По определению косинуса:
cosB=BC/AB
BC=АВ*cosB=42*9/14=27Ответ: 27
52D8C1
В треугольнике ABC угол C равен 90°, cosB=11/15, AB=75. Найдите BC.
Решение:
По определению косинуса:
cosB=BC/AB
BC=АВ*cosB=75*11/15=55Ответ: 55
73E3A7
В треугольнике ABC угол C равен 90°, cosB=13/16, AB=96. Найдите BC.
Решение:
По определению косинуса:
cosB=BC/AB
BC=АВ*cosB=96*13/16=78Ответ: 78
D8738D
Найти катет по известному катету и тангенсу
В треугольнике ABC угол C равен 90°, tgB=3/4, BC=12. Найдите AC.
Решение:
По определению тангенса:
tgB=AC/BC
AC=BC*tgB=12*3/4=9Ответ: 9
08FD08
В треугольнике ABC угол C равен 90°, tgB=7/6, BC=18. Найдите AC.
Решение:
По определению тангенса:
tgB=AC/BC
AC=BC*tgB=18*7/6=21Ответ: 21
1BBB13
В треугольнике ABC угол C равен 90°, tgB=9/7, BC=42. Найдите AC.
Решение:
По определению тангенса:
tgB=AC/BC
AC=BC*tgB=42*9/7=54Ответ: 54
14C45C
В треугольнике ABC угол C равен 90°, tgB=8/5, BC=20. Найдите AC.
Решение:
По определению тангенса:
tgB=AC/BC
AC=BC*tgB=20*8/5=32Ответ: 32
1DB806
В треугольнике ABC угол C равен 90°, tgB=11/8, BC=24. Найдите AC.
Решение:
По определению тангенса:
tgB=AC/BC
AC=BC*tgB=24*11/8=33Ответ: 33
EF04D8
В треугольнике ABC угол C равен 90°, tgB=5/9, BC=27. Найдите AC.
Решение:
По определению тангенса:
tgB=AC/BC
AC=BC*tgB=27*5/9=15Ответ: 15
A915AF
В треугольнике ABC угол C равен 90°, tgB=7/12, BC=48. Найдите AC.
Решение:
По определению тангенса:
tgB=AC/BC
AC=BC*tgB=48*7/12=28Ответ: 28
48CB65
В треугольнике ABC угол C равен 90°, tgB=4/7, BC=35. Найдите AC.
Решение:
По определению тангенса:
tgB=AC/BC
AC=BC*tgB=35*4/7=20Ответ: 20
1EB6B0
В треугольнике ABC угол C равен 90°, tgB=7/4, BC=36. Найдите AC.
Решение:
По определению тангенса:
tgB=AC/BC
AC=BC*tgB=36*7/4=63Ответ: 63
93C176
В треугольнике ABC угол C равен 90°, tgB=3/5, BC=30. Найдите AC.
Решение:
По определению тангенса:
tgB=AC/BC
AC=BC*tgB=30*3/5=18Ответ: 18
757BB5
Найти синус по косинусу и наоборот
В решении заданий такого типа используйте основное тригонометрическое тождество
sin2α + cos2α=1
Выражаем то, что нужно найти, и подставляем известные значения.
Синус острого угла А треугольника АВС равен $frac{sqrt{21}}5$. Найдите cosA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
cos2A = 1 — sin2A =1 — (√21/5)2 = 1 — 21/25 = 1 — 0,84 = 0,16
cosA = 0,4Ответ: 0,4
99B7F9
Синус острого угла А треугольника АВС равен $frac{3sqrt{11}}{10}$. Найдите cosA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
cos2A = 1 — sin2A =1 — (3√11/10)2 = 1 — 99/100 = 0,01
cosA = 0,1Ответ: 0,1
E52F99
Синус острого угла А треугольника АВС равен $frac{sqrt{91}}{10}$. Найдите cosA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
cos2A = 1 — sin2A =1 — (√91/10)2 = 1 — 91/100 = 0,09
cosA = 0,3Ответ: 0,3
5F0BC9
Синус острого угла A треугольника ABC равен $frac{2sqrt6}5$. Найдите cosA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
cos2A = 1 — sin2A =1 — (2√6/5)2 = 1 — 24/25 = 1-0,96 = 0,04
cosA = 0,2Ответ: 0,2
DF0885
Синус острого угла A треугольника ABC равен $frac{3sqrt7}8$ . Найдите cosA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
cos2A = 1 — sin2A =1 — (3√7/8)2 = 1 — 63/64 = 1-0,984375 = 0,015625
cosA = 0,125Ответ: 0,125
Обратите внимание, что корень придется извлекать самостоятельно, поскольку числа 125 (трехзначного) в таблице квадратов на экзамене не будет.
D56817
Синус острого угла A треугольника ABC равен 4/5 . Найдите cosA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
cos2A = 1 — sin2A =1 — (4/5)2 = 1 — 16/25 = 1-0,64 = 0,36
cosA = 0,6Ответ: 0,6
F548B1
Синус острого угла A треугольника ABC равен $frac{sqrt7}4$ . Найдите cosA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
cos2A = 1 — sin2A =1 — (√7/4)2 = 1 — 7/16 = 1-0,4375 = 0,5625
cosA = 0,75Ответ: 0,75
F6FBB5
Синус острого угла A треугольника ABC равен 3/5 . Найдите cosA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
cos2A = 1 — sin2A =1 — (3/5)2 = 1 — 9/25 = 1-0,36 = 0,64
cosA = 0,8Ответ: 0,8
4257EE
Синус острого угла A треугольника ABC равен $frac{sqrt{19}}{10}$ . Найдите cosA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
cos2A = 1 — sin2A =1 — (√19/10)2 = 1 — 19/100 = 1-0,19 = 0,81
cosA = 0,9Ответ: 0,9
DC7D62
Синус острого угла A треугольника ABC равен $frac{sqrt{15}}4$ . Найдите cosA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
cos2A = 1 — sin2A =1 — (√15/4)2 = 1 — 15/16 = 1-0,9375 = 0,0625
cosA = 0,25Ответ: 0,25
11D7EC
Косинус острого угла A треугольника ABC равен $frac{sqrt{21}}5$ . Найдите sinA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
sin2A = 1 — cos2A =1 — (√21/5)2 = 1 — 21/25 = 1-0,84 = 0,16
sinA = 0,4Ответ: 0,4
4BD96F
Косинус острого угла A треугольника ABC равен $frac{3sqrt{11}}{10}$ . Найдите sinA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
sin2A = 1 — cos2A =1 — (3√11/10)2 = 1 — 99/100 = 1-0,99 = 0,01
sinA = 0,1Ответ: 0,1
EE565F
Косинус острого угла A треугольника ABC равен $frac{sqrt{91}}{10}$ . Найдите sinA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
sin2A = 1 — cos2A =1 — (√91/10)2 = 1 — 91/100 = 1-0,91 = 0,09
sinA = 0,3Ответ: 0,3
EE4155
Косинус острого угла A треугольника ABC равен $frac{2sqrt6}5$. Найдите sinA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
sin2A = 1 — cos2A =1 — (2√6/5)2 = 1 — 24/25 = 1-0,96 = 0,04
sinA = 0,2Ответ: 0,2
2657CA
Косинус острого угла A треугольника ABC равен $frac{3sqrt7}8$. Найдите sinA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
sin2A = 1 — cos2A =1 — (3√7/8)2 = 1 — 63/64 = 1-0,984375 = 0,015625
sinA = 0,125Ответ: 0,125
Обратите внимание, что корень придется извлекать самостоятельно, поскольку числа 125 (трехзначного) в таблице квадратов на экзамене не будет.
857A3B
Косинус острого угла A треугольника ABC равен 4/5. Найдите sinA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
sin2A = 1 — cos2A =1 — (4/5)2 = 1 — 16/25 = 1-0,64 = 0,36
sinA = 0,6Ответ: 0,6
588CA0
Косинус острого угла A треугольника ABC равен $frac{sqrt7}4$. Найдите sinA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
sin2A = 1 — cos2A =1 — (√7/4)2 = 1 — 7/16 = 1-0,4375 = 0,5625
sinA = 0,75Ответ: 0,75
5AC6CD
Косинус острого угла A треугольника ABC равен 3/5. Найдите sinA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
sin2A = 1 — cos2A =1 — (3/5)2 = 1 — 9/25 = 1-0,36 = 0,64
sinA = 0,8Ответ: 0,8
3B3235
Косинус острого угла A треугольника ABC равен $frac{sqrt{19}}{10}$. Найдите sinA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
sin2A = 1 — cos2A =1 — (√19/10)2 = 1 — 19/100 = 1-0,19 = 0,81
sinA = 0,9Ответ: 0,9
4D93A9
Косинус острого угла A треугольника ABC равен $frac{sqrt{15}}4$. Найдите sinA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
sin2A = 1 — cos2A =1 — (√15/4)2 = 1 — 15/16 = 1-0,9375 = 0,0625
sinA = 0,25Ответ: 0,25
A426BF
Найти площадь треугольника по двум сторонам и углу между ними
Вспоминаем формулу нахождения площади треугольника по двум сторонам и углу между ними:
S=1/2аb•sinγ, где а и b — стороны треугольника, γ — угол между ними.
Подставляем известные величины и считаем.
Формула так же есть в справочных материалах ОГЭ, на экзамене можете ими воспользоваться.
В треугольнике ABC известно, что AB=6, BC=10, sin∠ABC=1/3. Найдите площадь треугольника ABC.
Решение:
S=1/2аb•sinγ=6*10*1/3=20
Ответ: 20
D8DE10
В треугольнике ABC известно, что AB=6, BC=12, sin∠ABC=1/4. Найдите площадь треугольника ABC.
Решение:
S=1/2аb•sinγ=6*12*1/4=18
Ответ: 18
510B5D
В треугольнике ABC известно, что AB=20, BC=7, sin∠ABC=2/5. Найдите площадь треугольника ABC.
Решение:
S=1/2аb•sinγ=20*7*2/5=56
Ответ: 56
21430B
В треугольнике ABC известно, что AB=15, BC=8, sin∠ABC=5/6. Найдите площадь треугольника ABC.
Решение:
S=1/2аb•sinγ=15*8*5/6=100
Ответ: 100
770975
В треугольнике ABC известно, что AB=14, BC=5, sin∠ABC=6/7. Найдите площадь треугольника ABC.
Решение:
S=1/2аb•sinγ=14*5*6/7=60
Ответ: 60
845EFC
В треугольнике ABC известно, что AB=12, BC=20, sin∠ABC=5/8. Найдите площадь треугольника ABC.
Решение:
S=1/2аb•sinγ=12*20*5/8=150
Ответ: 150
34F484
В треугольнике ABC известно, что AB=12, BC=15, sin∠ABC=4/9. Найдите площадь треугольника ABC.
Решение:
S=1/2аb•sinγ=12*15*4/9=80
Ответ: 80
86F9F5
В треугольнике ABC известно, что AB=16, BC=25, sin∠ABC=3/10. Найдите площадь треугольника ABC.
Решение:
S=1/2аb•sinγ=16*25*3/10=120
Ответ: 120
6B1EDE
В треугольнике ABC известно, что AB=9, BC=16, sin∠ABC=7/12. Найдите площадь треугольника ABC.
Решение:
S=1/2аb•sinγ=9*16*7/12=84
Ответ: 84
521C5A
В треугольнике ABC известно, что AB=12, BC=10, sin∠ABC=8/15. Найдите площадь треугольника ABC.
Решение:
S=1/2аb•sinγ=12*10*8/15=64
Ответ: 64
3A3D0B
Найти косинус угла, если известны 3 стороны треугольника

Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
а2 = b2 + с2 — 2bс • cosα
Нужно выразить косинус и подставить известные величины.
Эта формула так же будет у вас под рукой на экзамене в справочных материалах ОГЭ.
В треугольнике АВС известно, что AB=8, BC=10, AC=12. Найдите cos∠ABC.
Решение:
а2 = b2 + с2 — 2bс • cosα
2bс • cosα = b2 + с2 — а2
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
cosα = (82 +102 — 122) : 2*8*10 = 20/160 = 0,125Ответ: 0,125
40840C
В треугольнике ABC известно, что AB=5, BC=7, AC=9. Найдите cos∠ABC.
Решение:
а2 = b2 + с2 — 2bс • cosα
2bс • cosα = b2 + с2 — а2
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{5^2+7^2-9^2}{2ast 5ast 7}$ = -7/70 = -0,1
Ответ: -0,1
112015
В треугольнике ABC известно, что AB=3, BC=8, AC=7. Найдите cos∠ABC.
Решение:
а2 = b2 + с2 — 2bс • cosα
2bс • cosα = b2 + с2 — а2
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{3^2+8^2-7^2}{2ast 3ast 8}$= 24/48 = 0,5
Ответ: 0,5
6E8D8A
В треугольнике ABC известно, что AB=5, BC=10, AC=11. Найдите cos∠ABC.
Решение:
а2 = b2 + с2 — 2bс • cosα
2bс • cosα = b2 + с2 — а2
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{5^2+10^2-11^2}{2ast 5ast 10}$= 4/100 = 0,04
Ответ: 0,04
844A89
В треугольнике ABC известно, что AB=6, BC=7, AC=8. Найдите cos∠ABC.
Решение:
а2 = b2 + с2 — 2bс • cosα
2bс • cosα = b2 + с2 — а2
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{6^2+7^2-8^2}{2ast 6ast 7}$= 21/84 = 0,25
Ответ: 0,25
79B29A
В треугольнике ABC известно, что AB=5, BC=6, AC=4. Найдите cos∠ABC.
Решение:
а2 = b2 + с2 — 2bс • cosα
2bс • cosα = b2 + с2 — а2
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{5^2+6^2-4^2}{2ast 5ast 6}$= 45/60 = 0,75
Ответ: 0,75
6557F1
В треугольнике ABC известно, что AB=6, BC=8, AC=4. Найдите cos∠ABC.
Решение:
а2 = b2 + с2 — 2bс • cosα
2bс • cosα = b2 + с2 — а2
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{6^2+8^2-4^2}{2ast 6ast 8}$= 84/96
Ответ: 0,875
B5CF05
В треугольнике ABC известно, что AB=7, BC=8, AC=13. Найдите cos∠ABC.
Решение:
а2 = b2 + с2 — 2bс • cosα
2bс • cosα = b2 + с2 — а2
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{7^2+8^2-13^2}{2ast 7ast 8}$= -56/112 = -0,5
Ответ: -0,5
91941D
В треугольнике ABC известно, что AB=8, BC=10, AC=14. Найдите cos∠ABC.
Решение:
а2 = b2 + с2 — 2bс • cosα
2bс • cosα = b2 + с2 — а2
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{8^2+10^2-14^2}{2ast 8ast 10}$= -32/160 = -0,2
Ответ: -0,2
755B8F
В треугольнике ABC известно, что AB=2, BC=3, AC=4. Найдите cos∠ABC.
Решение:
а2 = b2 + с2 — 2bс • cosα
2bс • cosα = b2 + с2 — а2
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{2^2+3^2-4^2}{2ast 2ast 3}$= -3/12 = -0,25
Ответ: -0,25
05C64C
Найти синус по двум сторонам
Синус острого угла в прямоугольном треугольнике равен отношению противолежащего катета к гипотенузе. И тот, и другой, известны. Подставляем и считаем.
В треугольнике ABC угол C равен 90°, AC=6, AB=10. Найдите sinB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 6/10 = 0,6
Ответ: 0,6
A67245
В треугольнике ABC угол C равен 90°, AC=4, AB=5. Найдите sinB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 4/5 = 0,8
Ответ: 0,8
46D9DF
В треугольнике ABC угол C равен 90°, AC=7, AB=25. Найдите sinB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 7/25 = 0,28
Ответ: 0,28
6DA700
В треугольнике ABC угол C равен 90°, AC=24, AB=25. Найдите sinB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 24/25 = 0,96
Ответ: 0,96
C7A2A0
В треугольнике ABC угол C равен 90°, AC=6, AB=20. Найдите sinB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 6/20 = 0,3
Ответ: 0,3
ED2D47
В треугольнике ABC угол C равен 90°, AC=11, AB=20. Найдите sinB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 11/20 = 0,55
Ответ: 0,55
F1D3F8
В треугольнике ABC угол C равен 90°, AC=8, AB=40. Найдите sinB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 8/40 = 0,2
Ответ: 0,2
CDC6C7
В треугольнике ABC угол C равен 90°, AC=16, AB=40. Найдите sinB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 16/40 = 0,4
Ответ: 0,4
20BC46
В треугольнике ABC угол C равен 90°, AC=9, AB=25. Найдите sinB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 9/25 = 0,36
Ответ: 0,36
E2F916
В треугольнике ABC угол C равен 90°, AC=13, AB=20. Найдите sinB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 13/20 = 0,65
Ответ: 0,65
2C2621
Найти косинус по двум сторонам треугольника
Косинус острого угла в прямоугольном треугольнике равен отношению прилежащего катета к гипотенузе. Подставляем известные значения и считаем.
В треугольнике ABC угол C равен 90°, BC=8, AB=10. Найдите cosB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 8/10 = 0,8
Ответ: 0,8
36727A
В треугольнике ABC угол C равен 90°, BC=3, AB=5. Найдите cosB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 3/5 = 0,6
Ответ: 0,6
E4988D
В треугольнике ABC угол C равен 90°, BC=14, AB=50. Найдите cosB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 14/50 = 0,28
Ответ: 0,28
B9AA7C
В треугольнике ABC угол C равен 90°, BC=72, AB=75. Найдите cosB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 72/75 = 0,96
Ответ: 0,96
6E5515
В треугольнике ABC угол C равен 90°, BC=14, AB=20. Найдите cosB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 14/20 = 0,7
Ответ: 0,7
E812C8
В треугольнике ABC угол C равен 90°, BC=9, AB=20. Найдите cosB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 9/20 = 0,45
Ответ: 0,45
C759C5
В треугольнике ABC угол C равен 90°, BC=30, AB=40. Найдите cosB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 30/40 = 0,75
Ответ: 0,75
8854A8
В треугольнике ABC угол C равен 90°, BC=26, AB=40. Найдите cosB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 26/40 = 0,65
Ответ: 0,65
C5CD1E
В треугольнике ABC угол C равен 90°, BC=16, AB=25. Найдите cosB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 16/25 = 0,64
Ответ: 0,64
C3A5F2
В треугольнике ABC угол C равен 90°, BC=7, AB=20. Найдите cosB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 7/20 = 0,35
Ответ: 0,35
D58395
Найти тангенс угла по двум катетам
Тангенс острого угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему. Подставляем значения катетов и считаем.
В треугольнике ABC угол C равен 90°, BC=5, AC=2. Найдите tgB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 2/5 = 0,4
Ответ: 0,4
98C7DF
В треугольнике ABC угол C равен 90°, BC=5, AC=3. Найдите tgB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 3/5 = 0,6
Ответ: 0,6
22FD03
В треугольнике ABC угол C равен 90°, BC=10, AC=7. Найдите tgB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 7/10 = 0,7
Ответ: 0,7
C18053
В треугольнике ABC угол C равен 90°, BC=10, AC=8. Найдите tgB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 8/10 = 0,8
Ответ: 0,8
33DA26
В треугольнике ABC угол C равен 90°, BC=15, AC=3. Найдите tgB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 3/15 = 0,2
Ответ: 0,2
DD620C
В треугольнике ABC угол C равен 90°, BC=9, AC=27. Найдите tgB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 27/9 = 3
Ответ: 3
342F0C
В треугольнике ABC угол C равен 90°, BC=5, AC=20. Найдите tgB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 20/5 = 4
Ответ: 4
B800B8
В треугольнике ABC угол C равен 90°, BC=3, AC=18. Найдите tgB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 18/3 = 6
Ответ: 6
FF498A
В треугольнике ABC угол C равен 90°, BC=4, AC=28. Найдите tgB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 28/4 = 7
Ответ: 7
C9E181
В треугольнике ABC угол C равен 90°, BC=7, AC=35. Найдите tgB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 35/7 = 5
Ответ: 5
0663D4